How Big Is an Error in the Analytical Calculation of Annular Fin Efficiency?
Abstract
1. Introduction
- (a)
- All temperatures and heat flow operate at steady-state levels.
- (b)
- The contact thermal resistance between the fin and the base surface is negligible.
- (c)
- There are no heat sources in the fin itself.
- (d)
- Radiation heat transfer from the fin is neglected.
- (e)
- The fin thickness is so small compared to its height that temperature gradients normal to the surface may be neglected.
- (f)
- The thermal conductivity of the fin and tube material is temperature-independent and uniform.
- (g)
- The temperature of the surrounding fluid is spatially uniform.
- (h)
- The heat-transfer coefficient is the same over all fin surfaces.
- (i)
- The temperature of the fin base surface is uniform and equal to the temperature of the tube base surface.
2. Materials and Methods
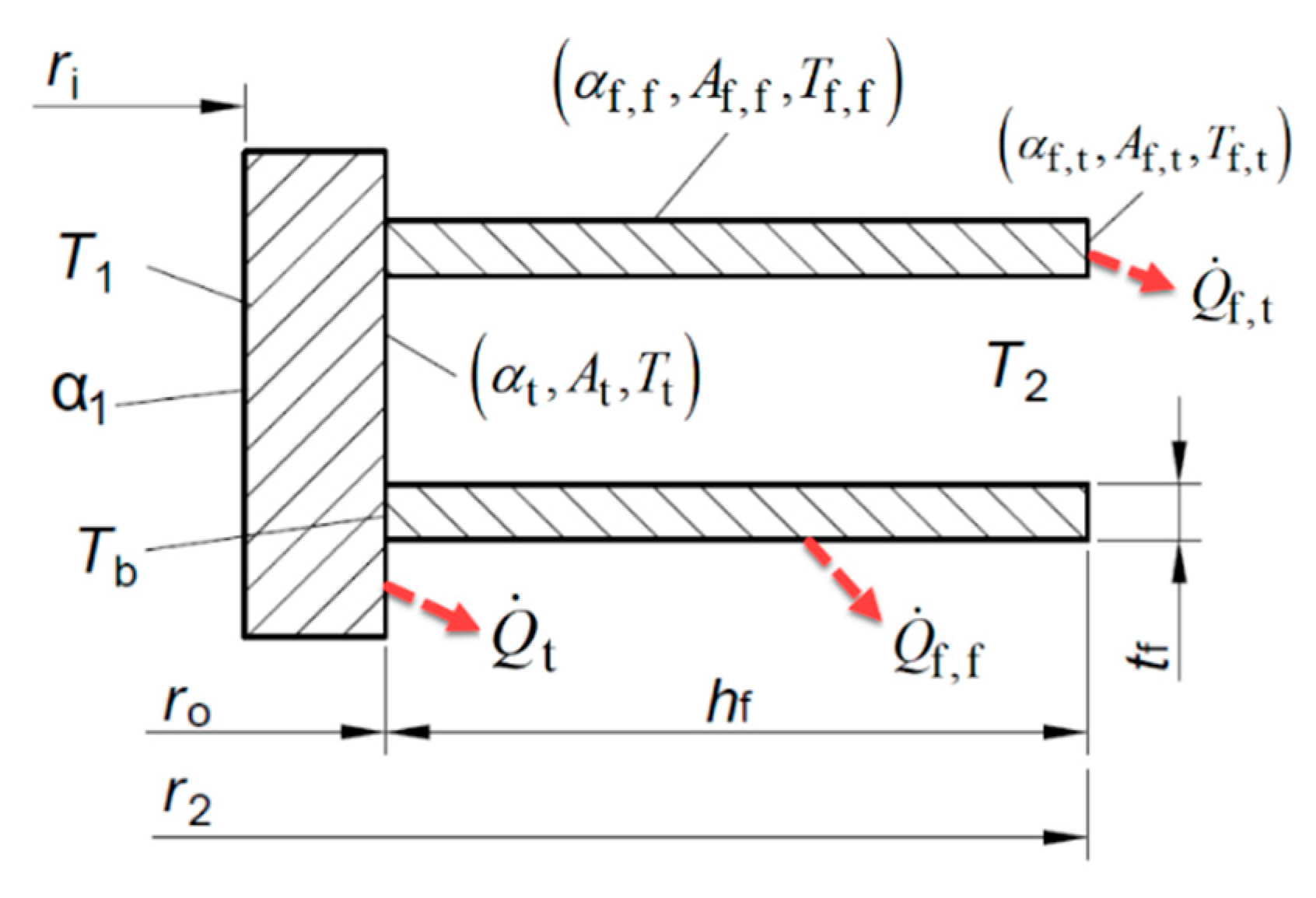
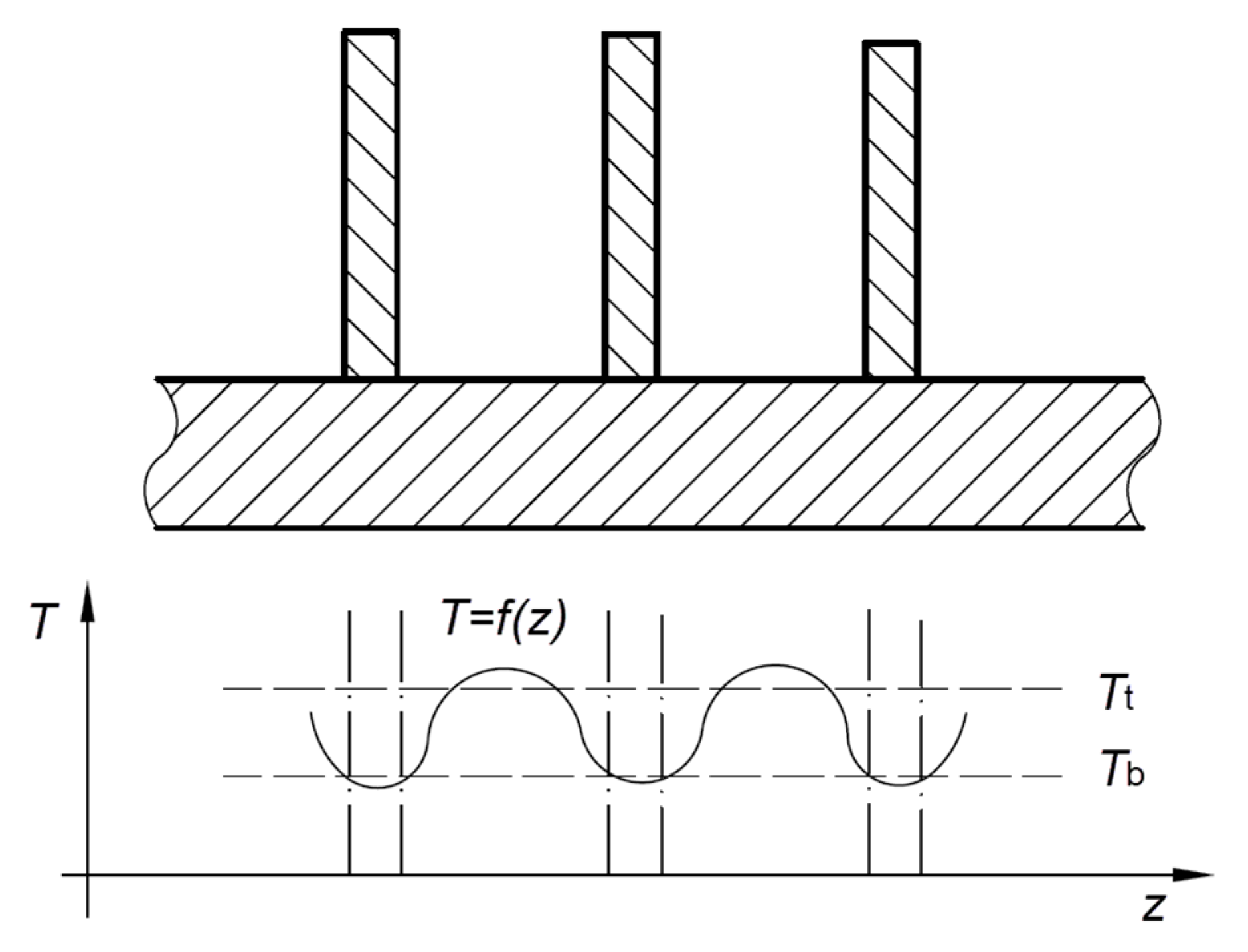
2.1. Physical Basis of Heat Exchange on Finned Surfaces
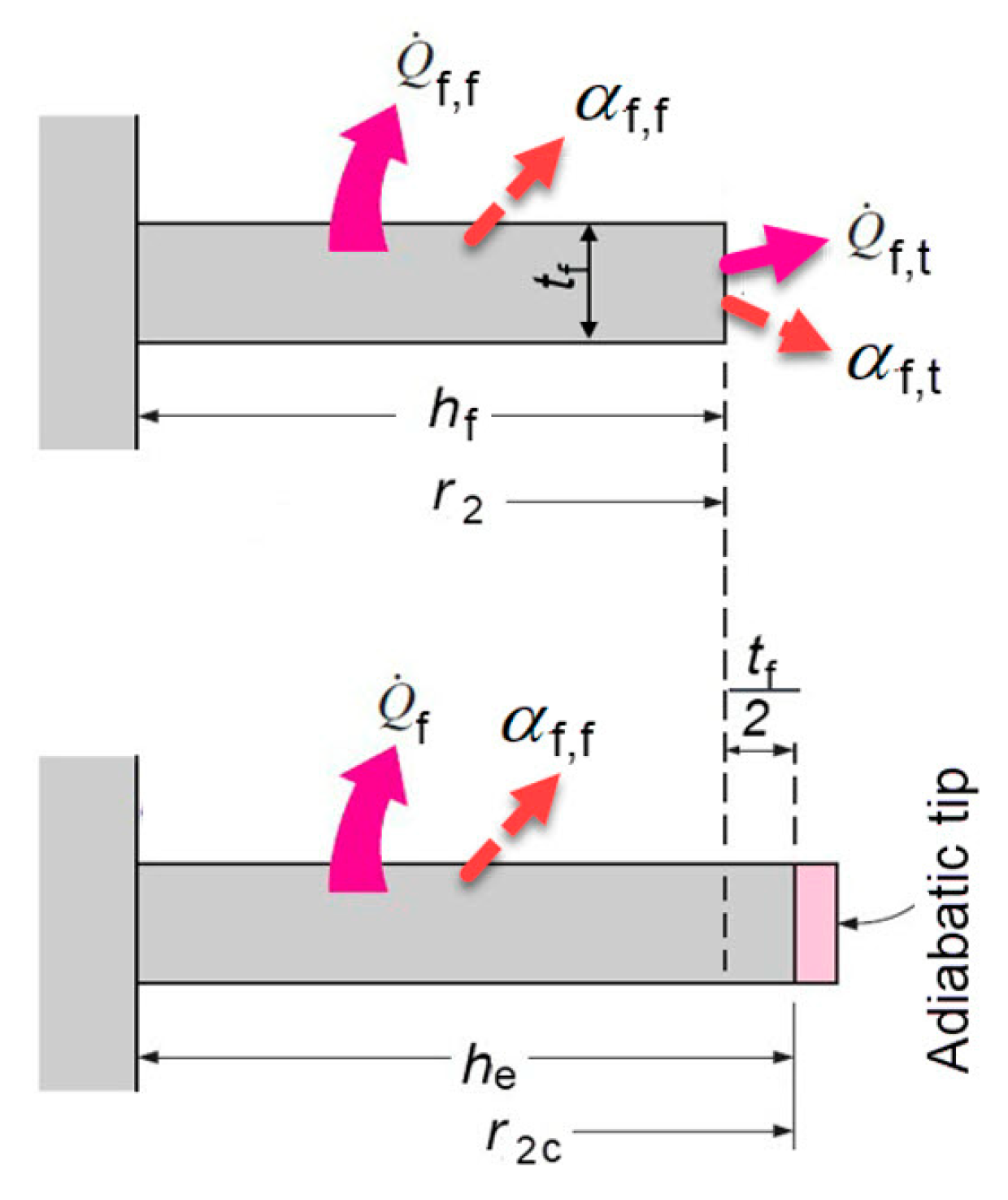
2.2. Analytical Solution of Fin Efficiency
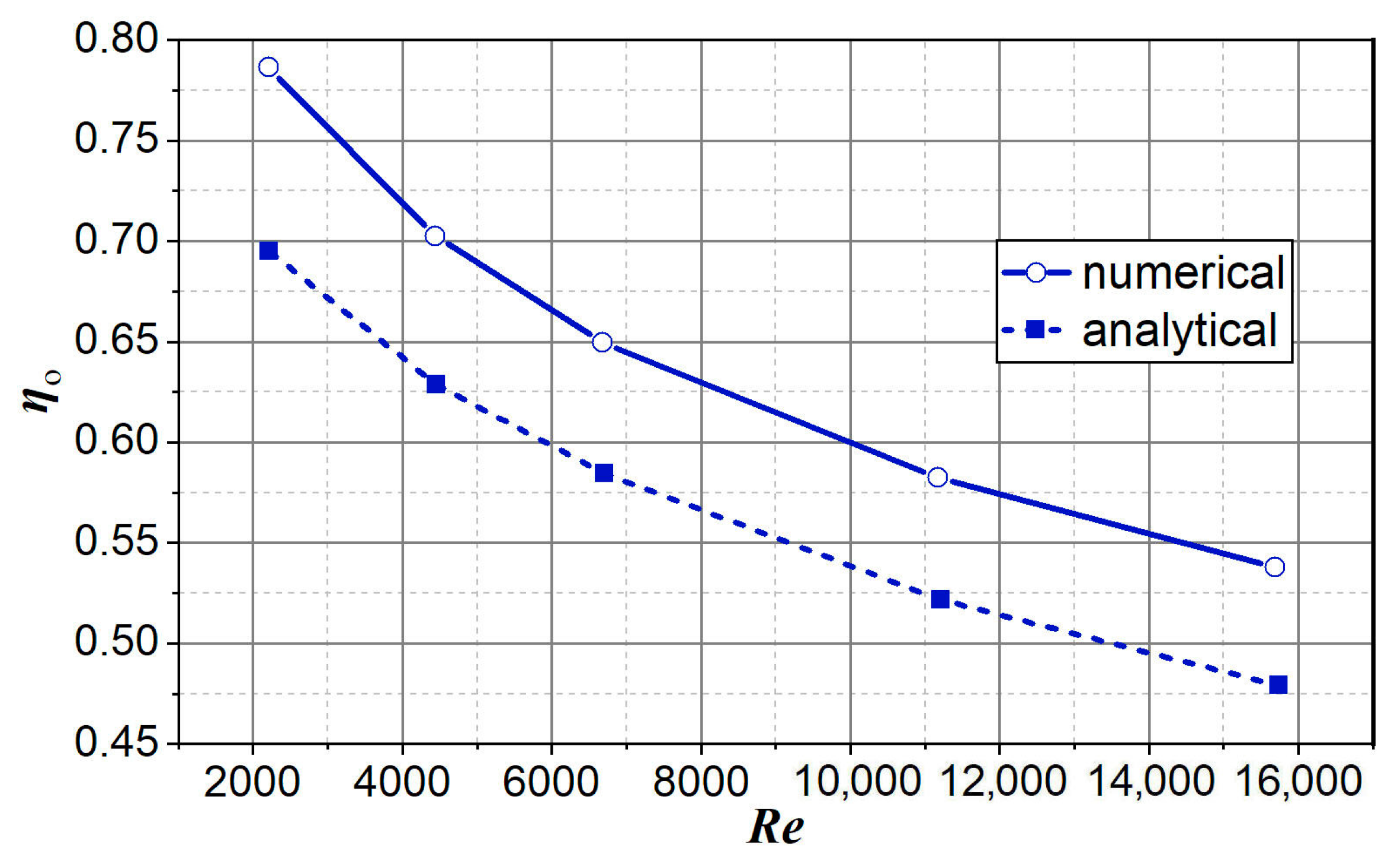
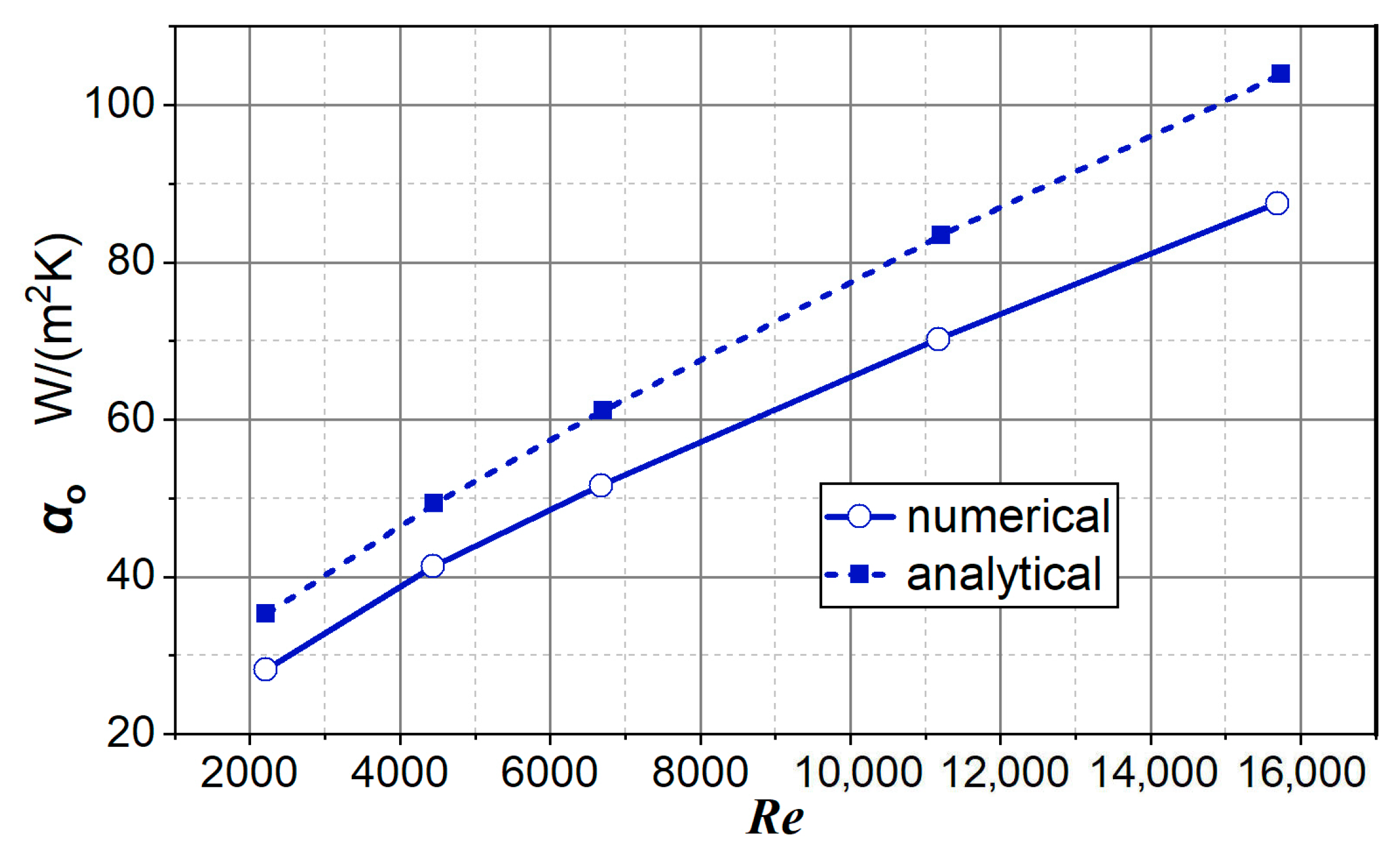
3. Results
3.1. Numerical Analysis
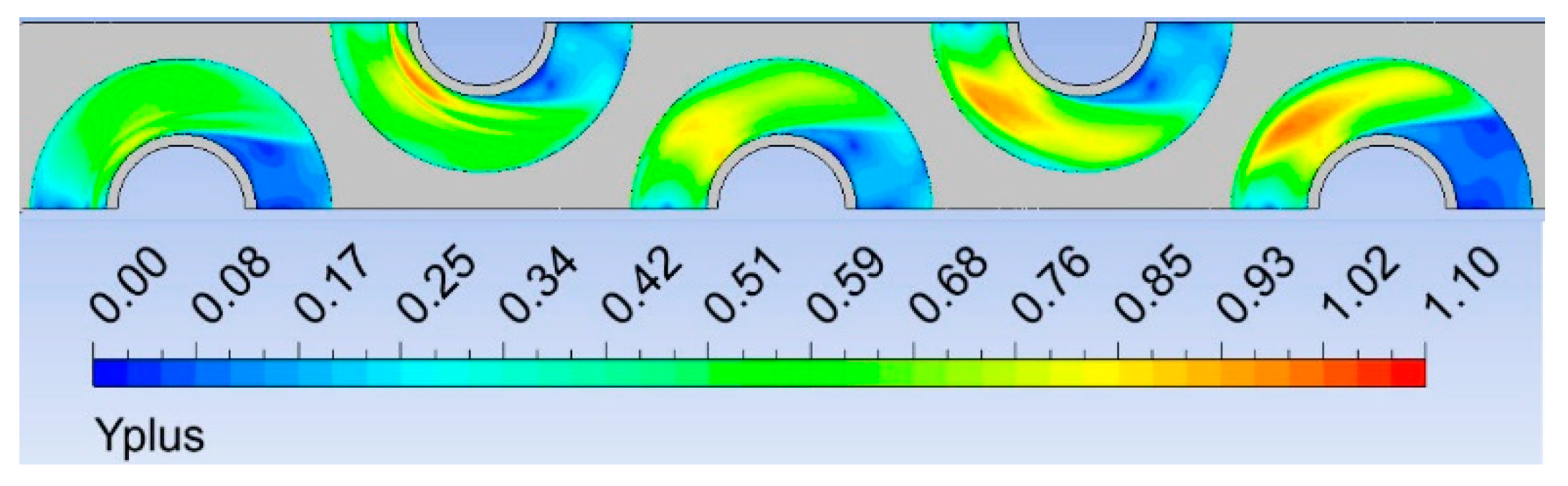
3.1.1. Mathematical Model
3.1.2. Numerical Simulation Results
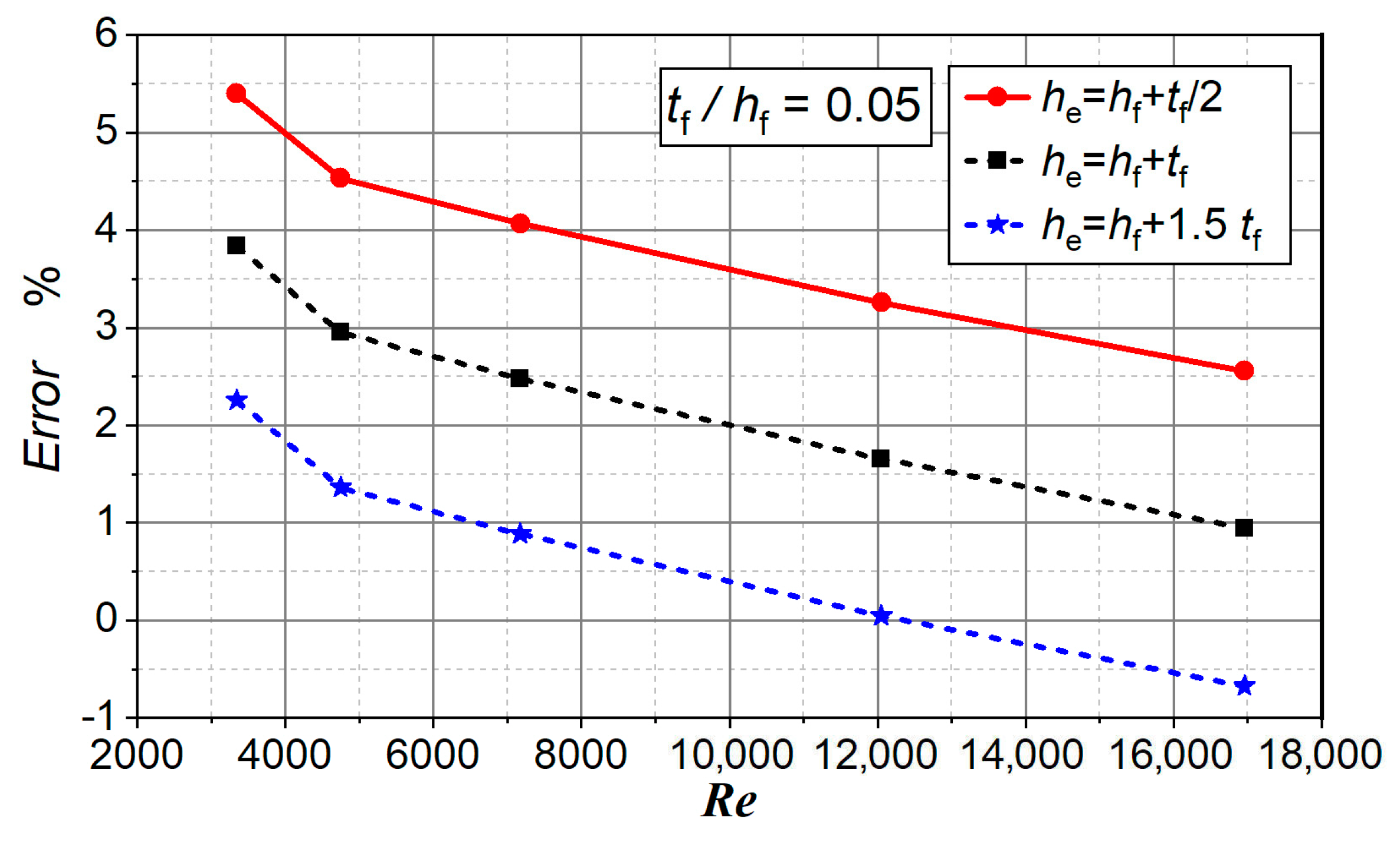
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | surface area on the air side | [m²] |
| E | empirical correction factor to the theoretical fin efficiency for fins | [mm] |
| h | fin high | [mm] |
| m | fin effectiveness parameter | [-] |
| L | tube length | [m] |
| Nt | total number of tubes | [-] |
| heat transfer rate | [W] | |
| r | radius | [mm] |
| t | thickness | [mm] |
| ΔTln | the logarithmic mean temperature difference | [K] |
| T | the average temperature | [K] |
| U | the overall heat transfer coefficient | [W/(m2·K)] |
| λ | the thermal conductivity | [W/(m·K)] |
| α | average convective heat transfer coefficient | [W/(m2·K)] |
| η | efficiency | [-] |
| I0, K0 | modified Bessel functions of the first and second kinds and zero order | [-] |
| I1, K1 | modified Bessel functions of the first and second kinds and first order | [-] |
| Subscripts | ||
| b | fin base | |
| e | effective/equivalent | |
| i | tube inside | |
| in | air inlet | |
| f | fin | |
| f,f | fin face | |
| f,t | fin tip | |
| f,n | fin, numerically | |
| max | maximal (for ideal fin) | |
| o | tube outside/overall | |
| out | air outlet | |
| t | tube/finless tube surface area | |
| th | theoretical | |
| tot | total | |
| 0 | actual | |
| 1 | fluid properties inside tube | |
| 2 | outside fin radius/bulk fluid properties outside tube and fins | |
| 2c | outside corrected fin radius |
References
- Harper, D.R.; Brown, W.B. Mathematical equations for heat conduction in the fins of air cooled engines. NACA R 1922, 158, 32. [Google Scholar]
- Murray, W.M. Heat transfer through an annular disk or fin of uniform thickness. Trans. ASME J. Appl. Mech. 1938, 60, A78–A81. [Google Scholar]
- Gardner, K.A. Efficiency of extended surface. Trans. ASME 1945, 67, 621. [Google Scholar]
- Darvishi, M.T.; Khani, F.; Aziz, A. Numerical investigation for a hyperbolic annular fin with temperature dependent thermal conductivity. Propuls. Power Res. 2016, 5, 55–62. [Google Scholar] [CrossRef]
- Ghai, M.L. Heat transfer in straight fins. In Proceedings of the General Discussion on Heat Transfer, London, UK, 11–13 September 1951. [Google Scholar]
- Zaidan, M.H.; Alkumait, A.A.R.; Ibrahim, T.K. Assessment of heat transfer and fluid flow characteristics within finned flat tube. Case Stud. Therm. Eng. 2018, 12, 557–562. [Google Scholar] [CrossRef]
- Nemati, H.; Moghimi, M. Numerical study of flow over annular-finned tube heat exchangers by different turbulent models. CFD Lett. 2014, 6, 101–112. [Google Scholar]
- Look, D.C., Jr.; Krishnan, A. One-dimensional fin-tip boundary condition correction II. Heat Transf. Eng. 2001, 22, 35–40. [Google Scholar] [CrossRef]
- Nemati, H.; Samivand, S. Performance optimization of annular elliptical fin based on thermo-geometric parameters. Alexandria Eng. J. 2015, 54, 1037–1042. [Google Scholar] [CrossRef][Green Version]
- Chen, H.L.; Wang, C.C. Analytical analysis and experimental verification of trapezoidal fin for assessment of heat sink performance and material saving. Appl. Therm. Eng. 2016, 98, 203–212. [Google Scholar] [CrossRef]
- Lane, H.J.; Heggs, P.J. Extended surface heat transfer-the dovetail fin. Appl. Therm. Eng. 2005, 25, 2555–2565. [Google Scholar] [CrossRef]
- Cléirigh, C.T.Ó.; Smith, W.J. Can CFD accurately predict the heat-transfer and pressure-drop performance of finned-tube bundles? Appl. Therm. Eng. 2014, 73, 679–688. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Kraus, A.D.; Aziz, A.; Welty, J. Extended Surface Heat Transfer; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Sparrow, E.M.; Hennecke, D.K. Temperature depression at the base of a fin. Trans. ASME 1970, 92, 204–206. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Lee, L. Effects of fin base temperature depression in a multifin array. J. Heat Transf. 1975, 97, 463–465. [Google Scholar] [CrossRef]
- Hashizume, K.; Morikawa, R.; Koyama, T.; Matsue, T. Fin efficiency of serrated fins. Heat Transf. Eng. 2002, 23, 7–14. [Google Scholar] [CrossRef]
- Taler, D. Numerical Modelling and Experimental Testing of Heat Exchangers; Springer: Berlin, Germany, 2019; Volume 161. [Google Scholar]
- Könözsy, L. Volume I: Theoretical background and development of an anisotropic hybrid k-omega shear-stress transport/stochastic turbulence model. In A New Hypothesis on the Anisotropic Reynolds Stress Tensor for Turbulent Flows; Springer: Berlin, Germany, 2019; Volume 120. [Google Scholar]
- Bošnjaković, M.; Čikić, A.; Muhič, S.; Stojkov, M. Development of a new type of finned heat exchanger. Tehnical Gazette 2017, 24, 1785–1796. [Google Scholar] [CrossRef]
- Huang, L.J.; Shah, R.K. Assessment of calculation methods for efficiency of straight fins of rectangular profile. Int. J. Heat Fluid Flow 1992, 13, 282–293. [Google Scholar] [CrossRef]
- Suryanarayana, N.W. Two-dimensional effects on heat transfer rates from an array of straight fins. J. Heat Transf. 1977, 99, 129–132. [Google Scholar] [CrossRef]




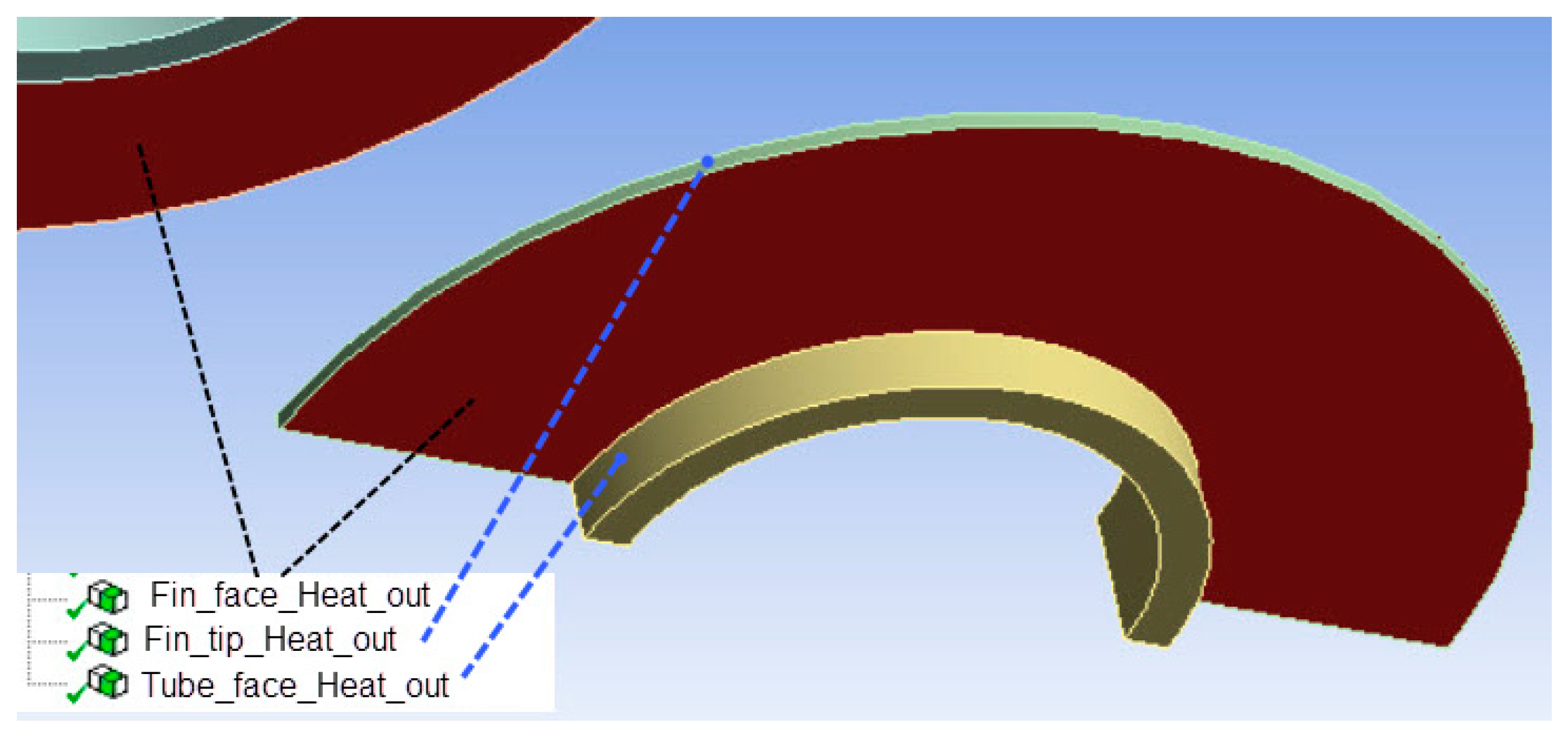
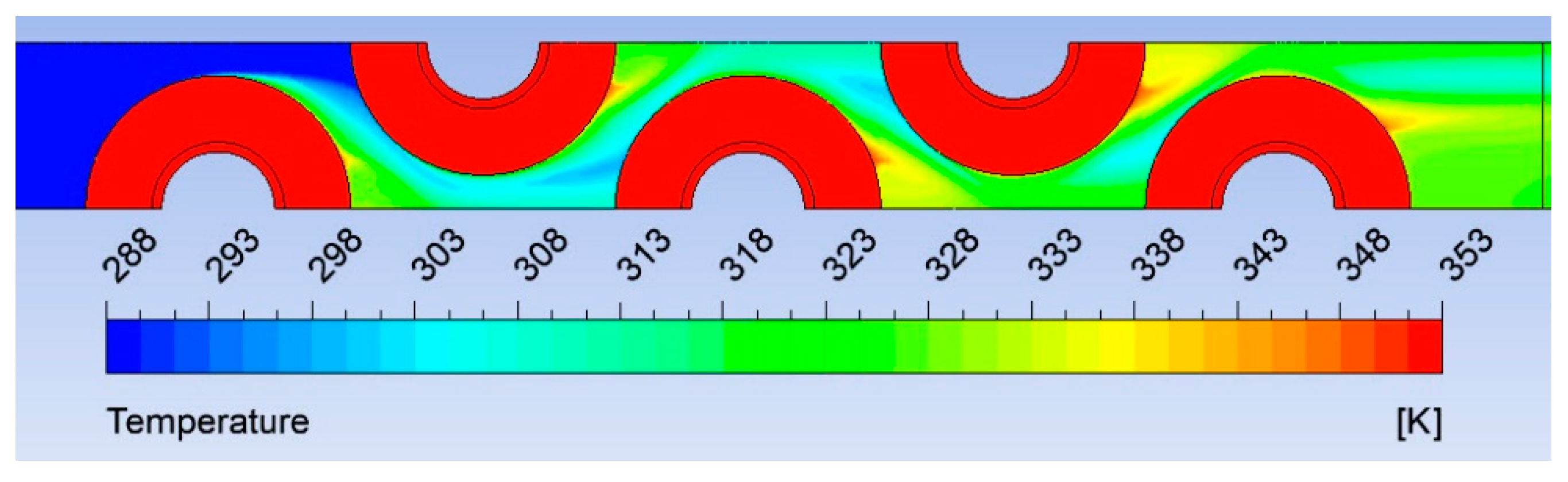
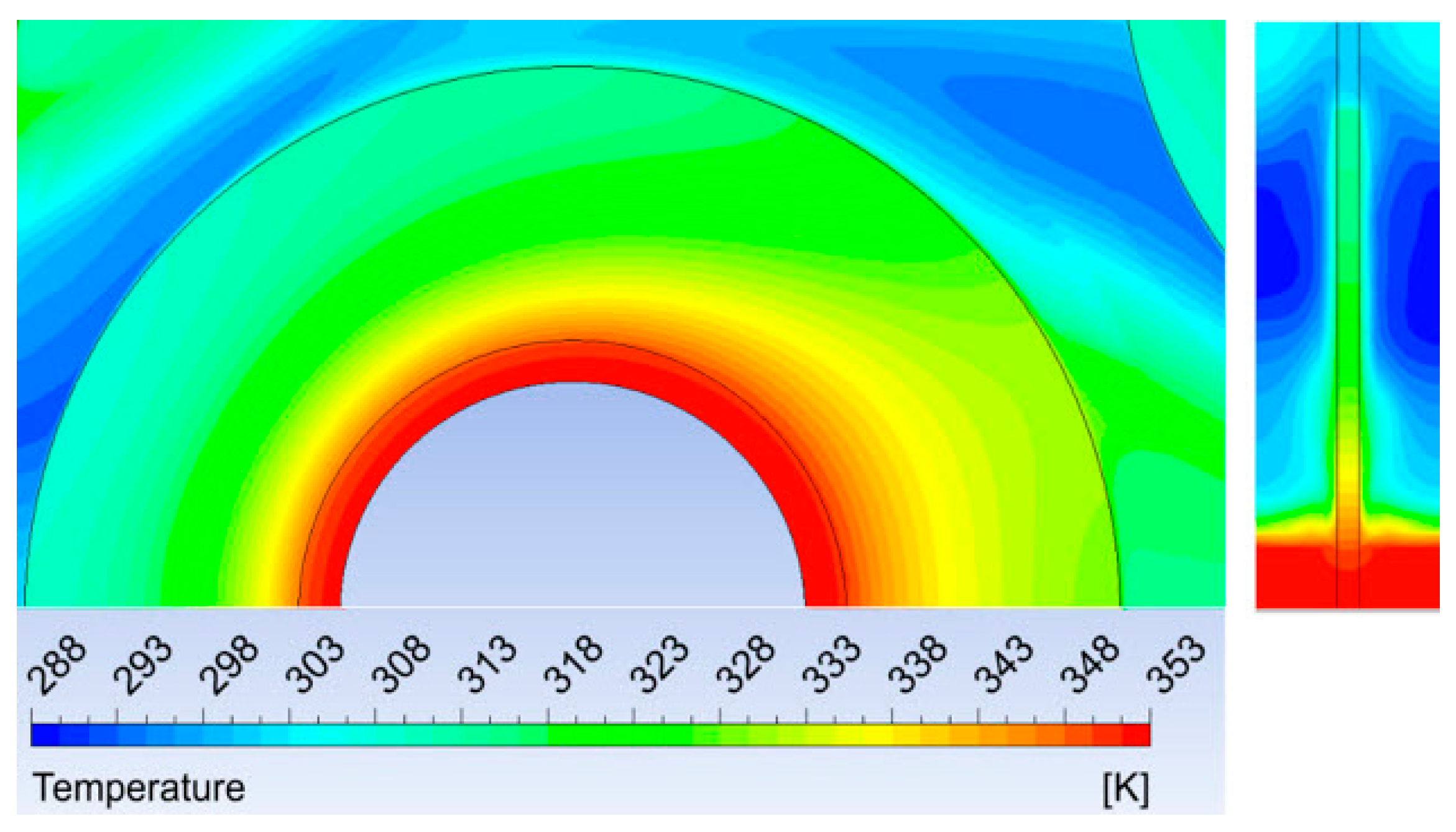
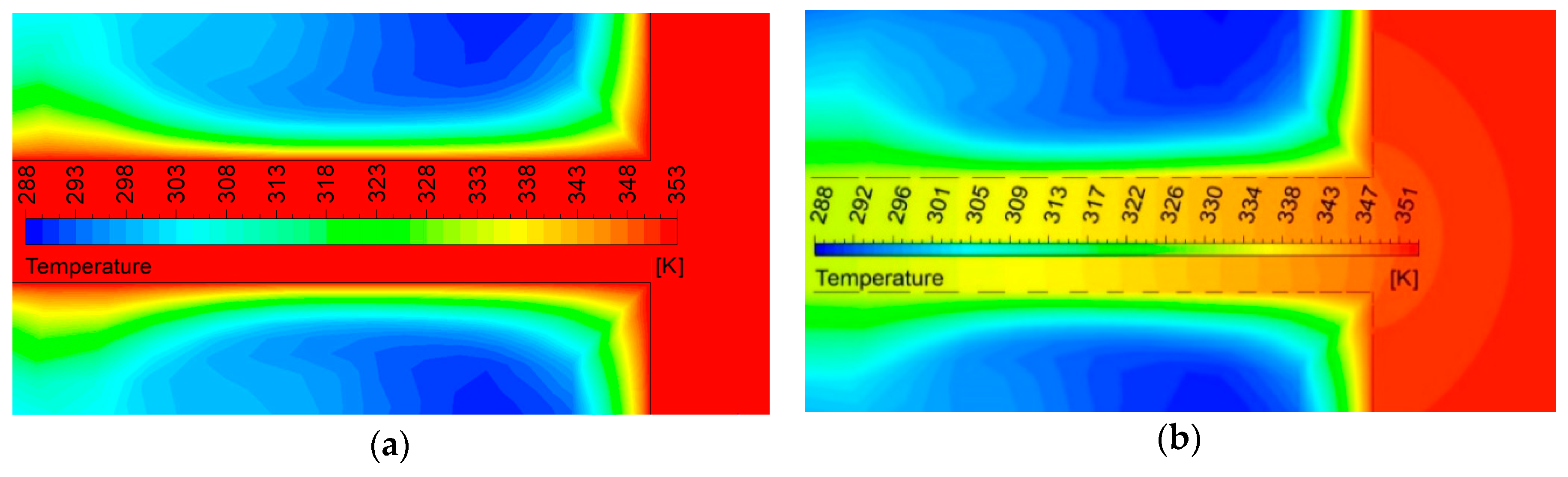
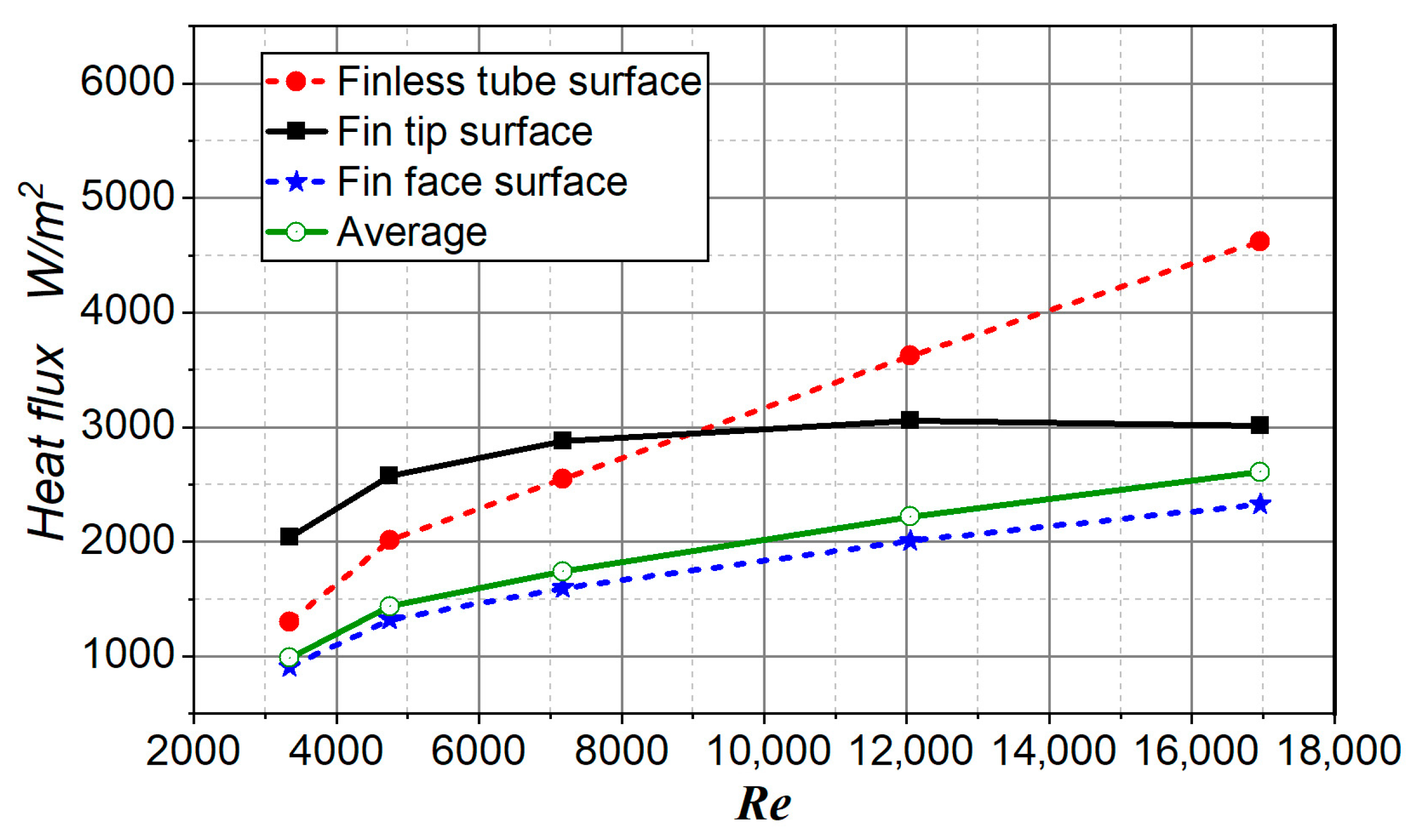
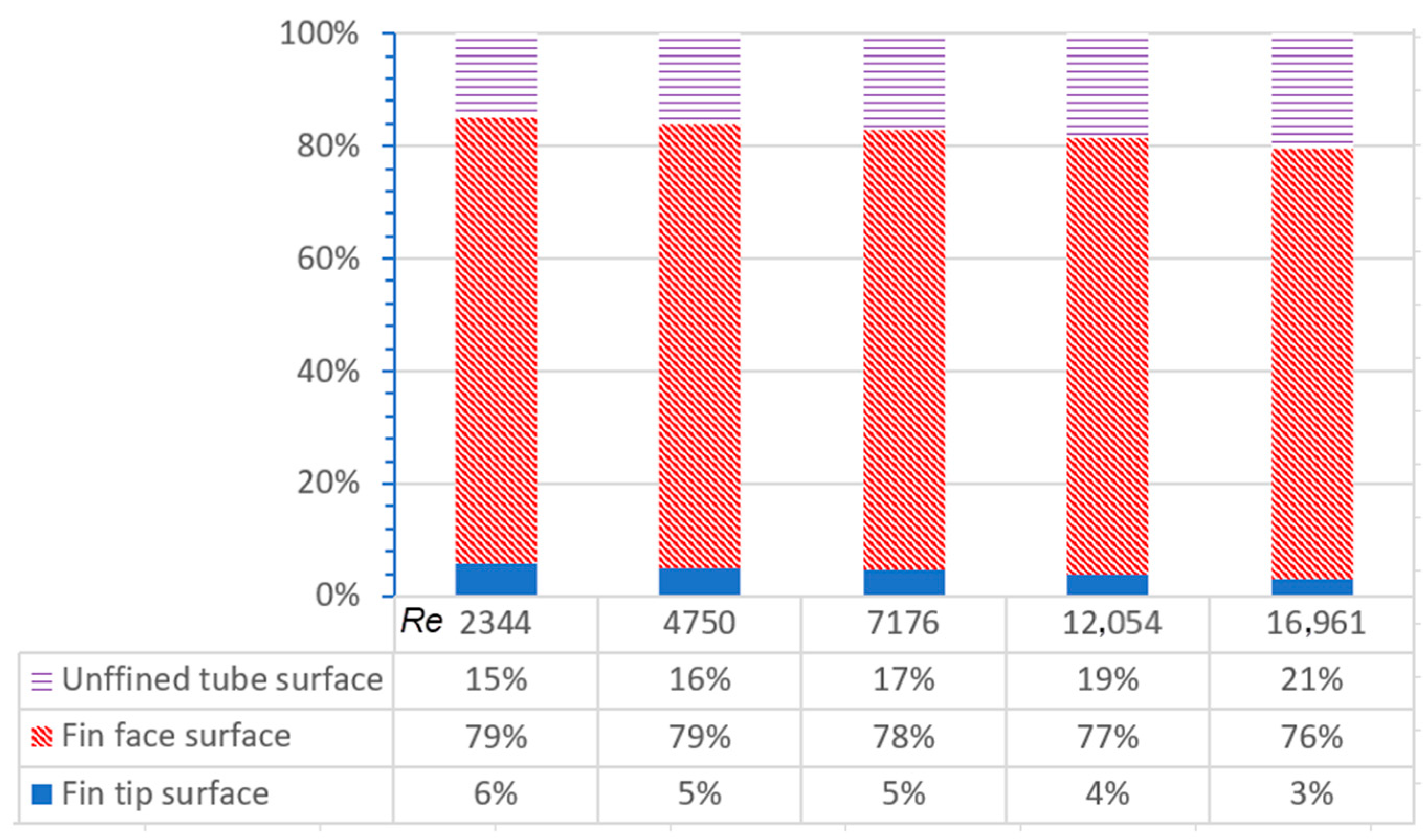
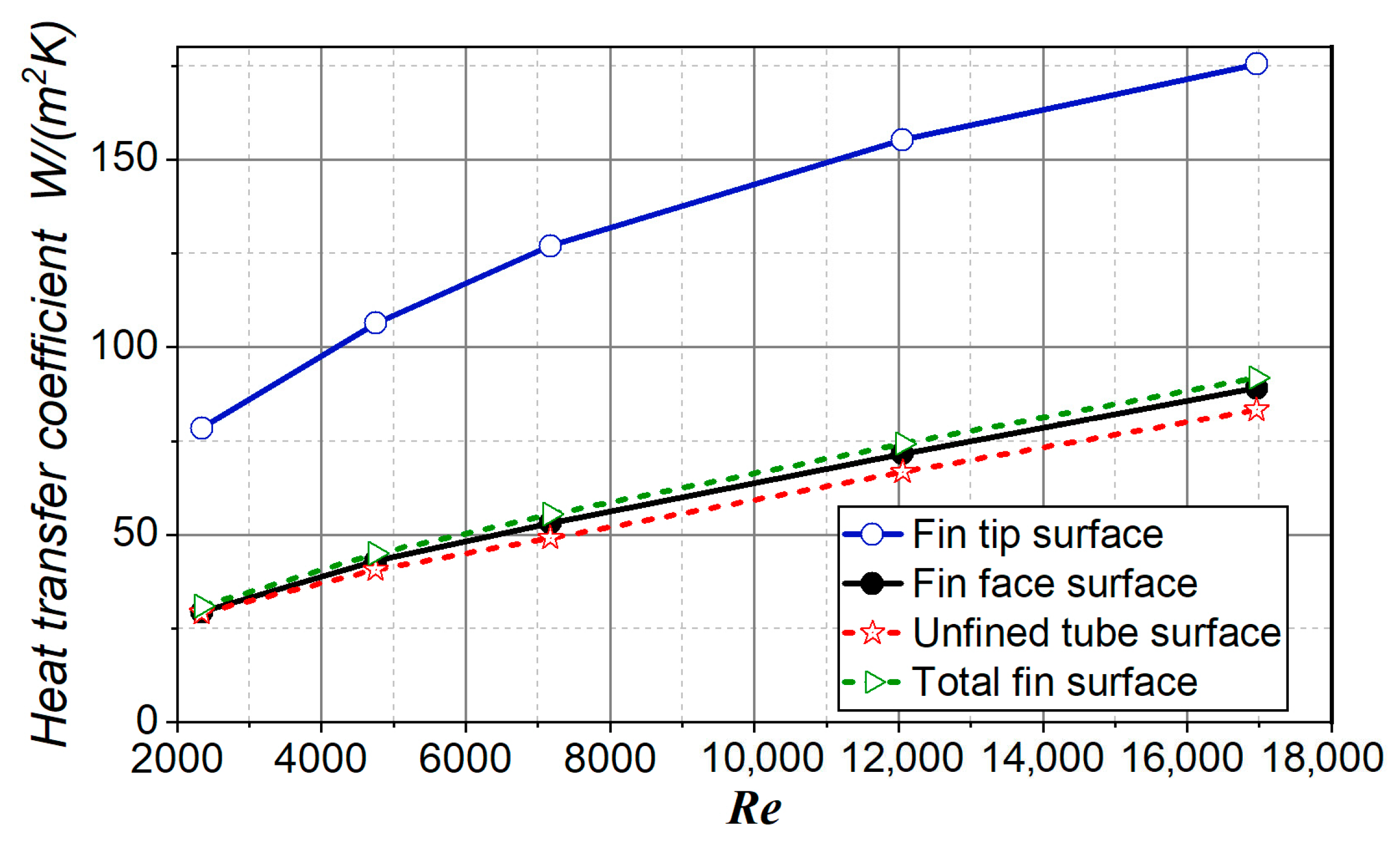
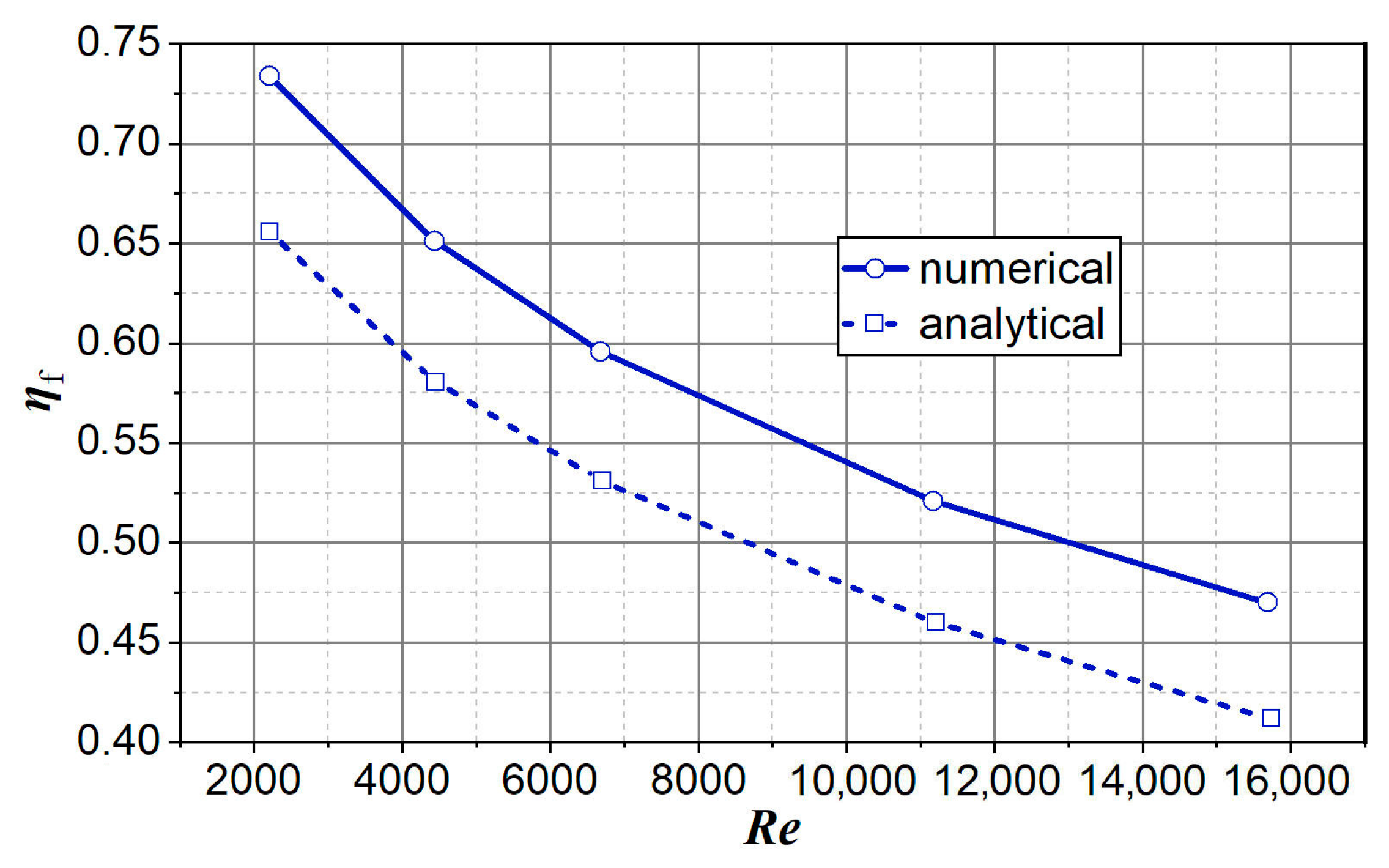
| Surface | Area (mm2) | Share (%) |
|---|---|---|
| Unfinned tube surface | 628.32 | 11.4 |
| Fin face surface | 4712.39 | 85.7 |
| Fin tip surface | 157.08 | 2.9 |
| Total surface area | 5497.78 | 100.0 |
| Tube Outside Diameter | do | mm | 20 |
|---|---|---|---|
| Tube inside diameter | di | mm | 17 |
| Tube rows configuration | - | - | staggered |
| Transverse tube pitch | st | mm | 50 |
| Longitudinal tube pitch | sl | mm | 40 |
| Fin height | hf | mm | 10 |
| Fin thickness | tf | mm | 0.5 |
| Fin pitch | sf | mm | 4.5 |
| Number of tube rows | Nl | - | 5 |
| Inlet Air Temperature | K | 288 |
|---|---|---|
| Air velocity at the inlet of the heat exchanger | m/s | 1, 2, 3, 5, 7 |
| Inlet air turbulence intensity | % | 5 |
| Internal tube wall temperature | K | 353 |
| Outlet air pressure | Pa | 101,325 |
| Wall condition | Hydraulically smooth wall |
| Air Velocity (m/s) | Fin Face Surface Temperature (K) | Fin Tip Surface Temperature (K) | Total Fin Surface Temperature (K) | Outer Unfinned Tube Surface Temp. (K) |
|---|---|---|---|---|
| 1 | 338.8 | 333.8 | 338.6 | 352.4 |
| 2 | 333.4 | 326.8 | 333.2 | 352.1 |
| 3 | 330.0 | 322.7 | 329.8 | 351.9 |
| 5 | 325.3 | 316.9 | 325.0 | 351.5 |
| 7 | 321.9 | 313.0 | 321.6 | 351.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bošnjaković, M.; Muhič, S.; Čikić, A.; Živić, M. How Big Is an Error in the Analytical Calculation of Annular Fin Efficiency? Energies 2019, 12, 1787. https://doi.org/10.3390/en12091787
Bošnjaković M, Muhič S, Čikić A, Živić M. How Big Is an Error in the Analytical Calculation of Annular Fin Efficiency? Energies. 2019; 12(9):1787. https://doi.org/10.3390/en12091787
Chicago/Turabian StyleBošnjaković, Mladen, Simon Muhič, Ante Čikić, and Marija Živić. 2019. "How Big Is an Error in the Analytical Calculation of Annular Fin Efficiency?" Energies 12, no. 9: 1787. https://doi.org/10.3390/en12091787
APA StyleBošnjaković, M., Muhič, S., Čikić, A., & Živić, M. (2019). How Big Is an Error in the Analytical Calculation of Annular Fin Efficiency? Energies, 12(9), 1787. https://doi.org/10.3390/en12091787






