Investigation of Effective Thermal Conductivity for Ordered and Randomly Packed Bed with Thermal Resistance Network Method
Abstract
:1. Introduction
2. Physical Model and Material Thermal Conductivity
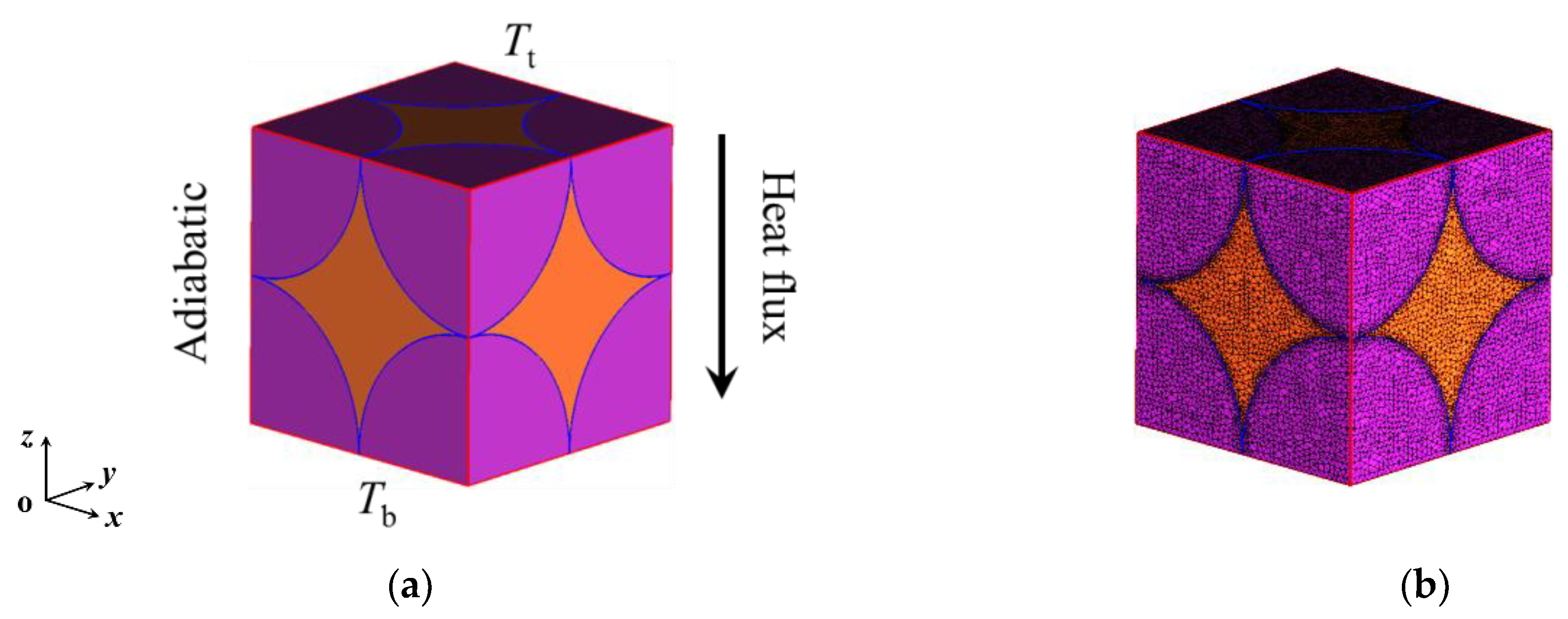
2.1. Physical Model
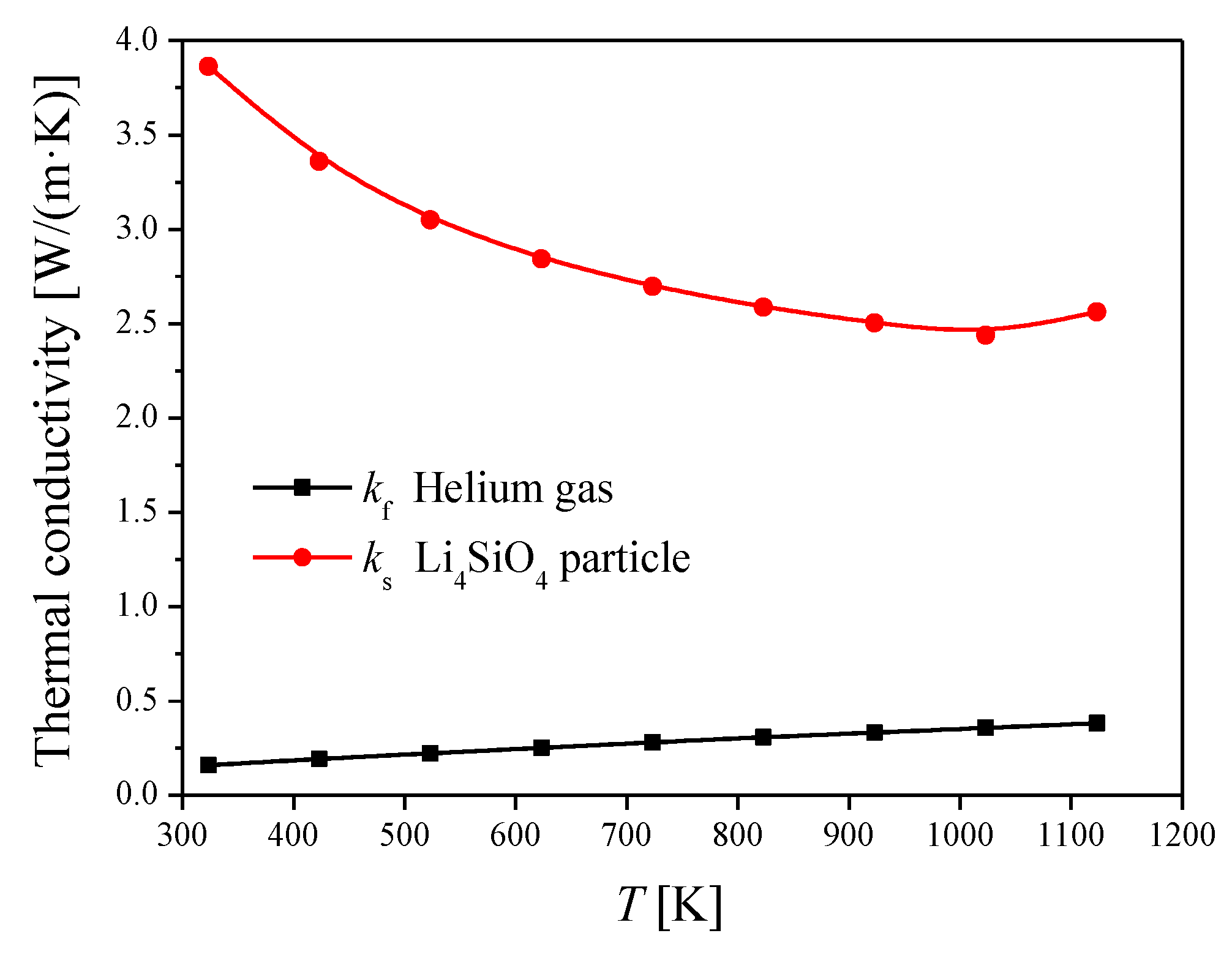
2.2. Material Thermal Conductivity
3. Thermal Resistance Network and Computational Fluid Dynamics (CFD) Methods
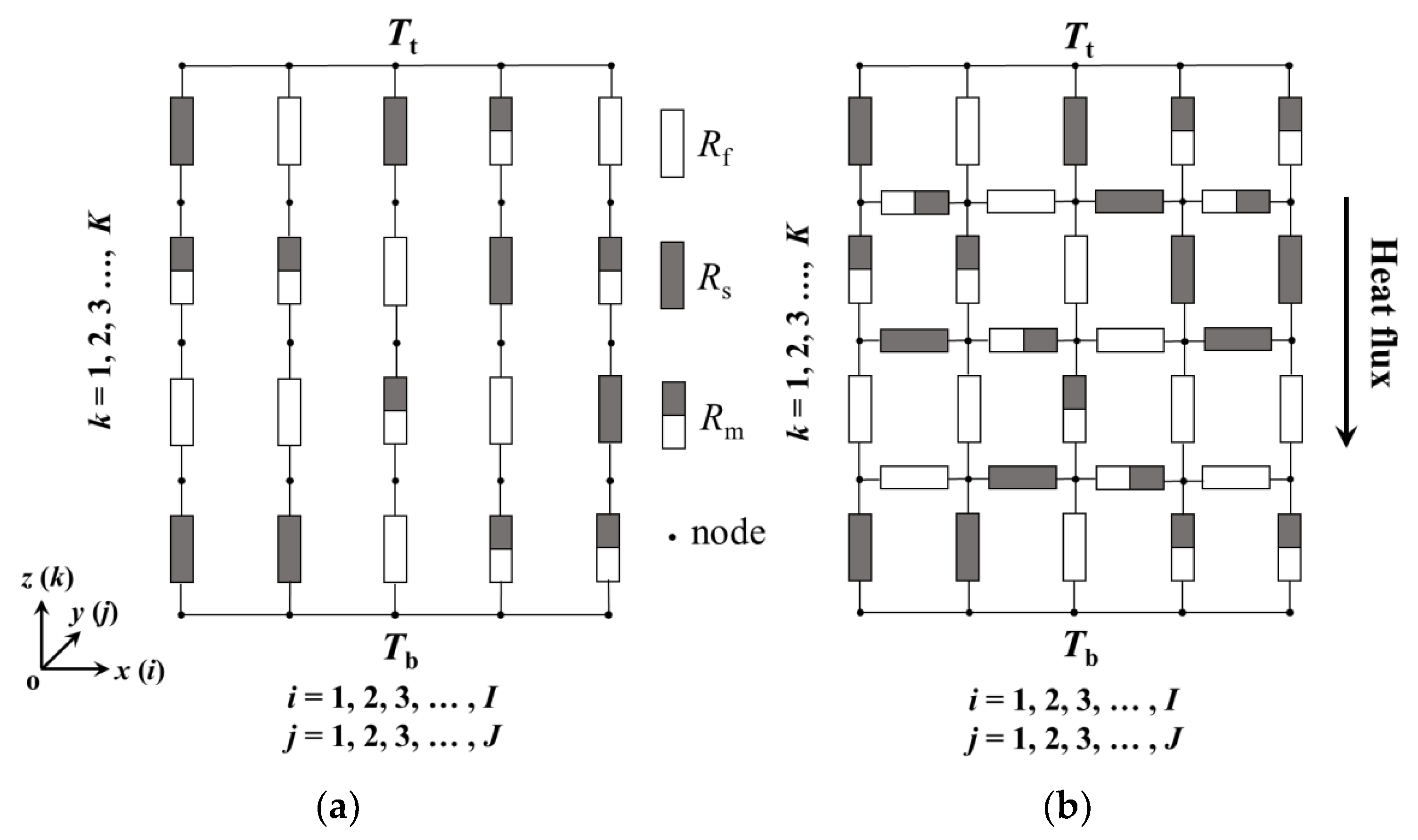
3.1. Thermal Resistance Networks Based on Ohm’s Law and Kirchhoff’s Law
3.2. CFD Simulations
4. Results and Discussion
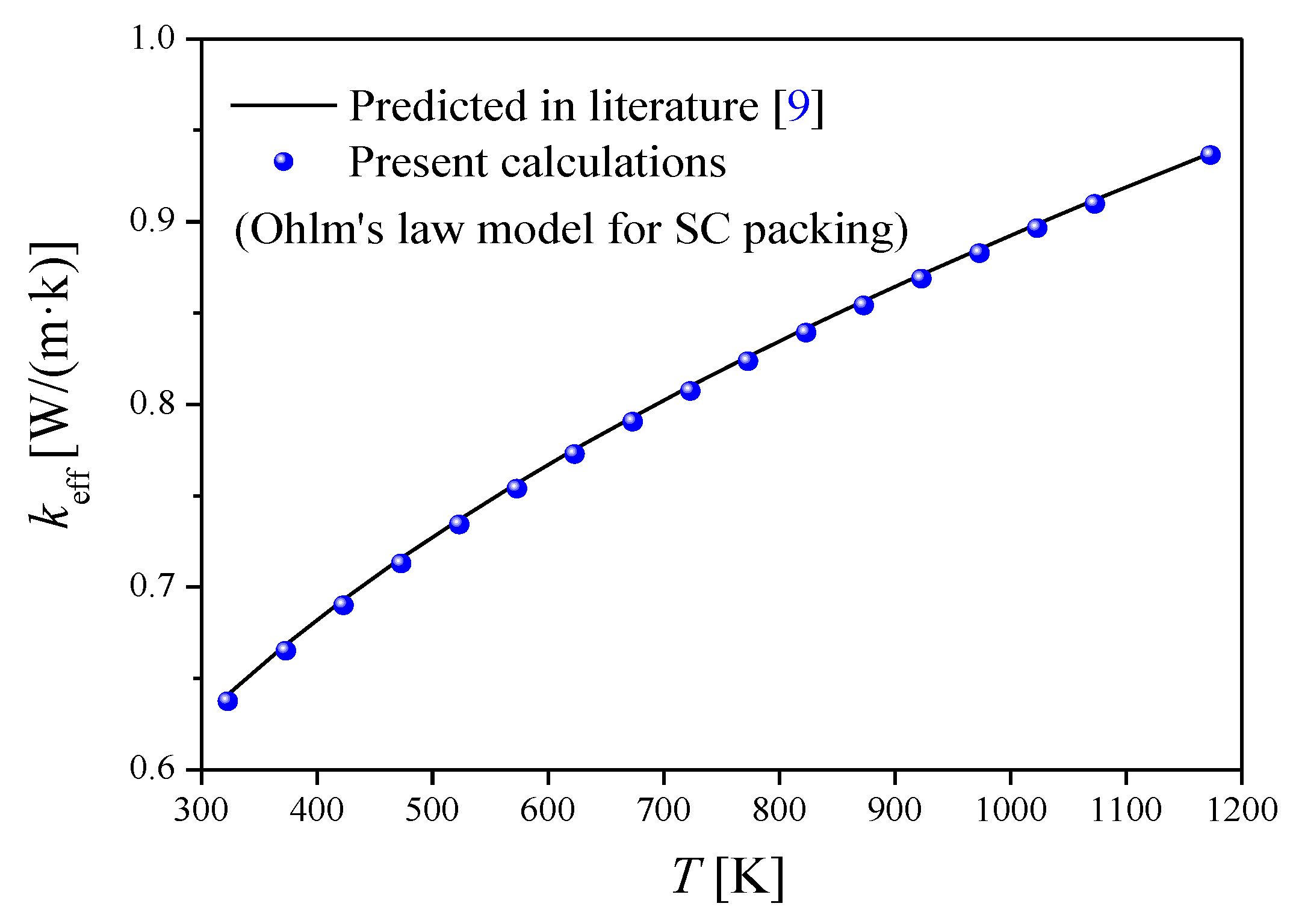
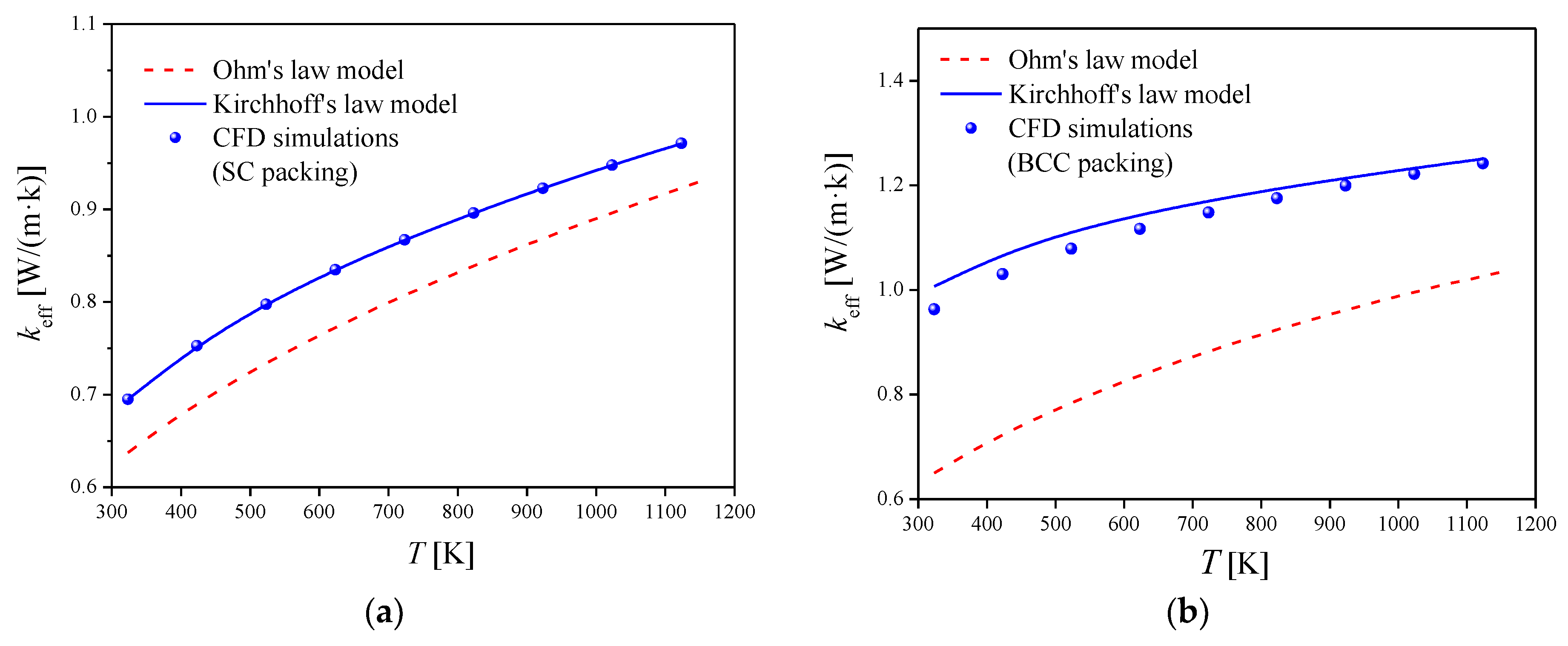
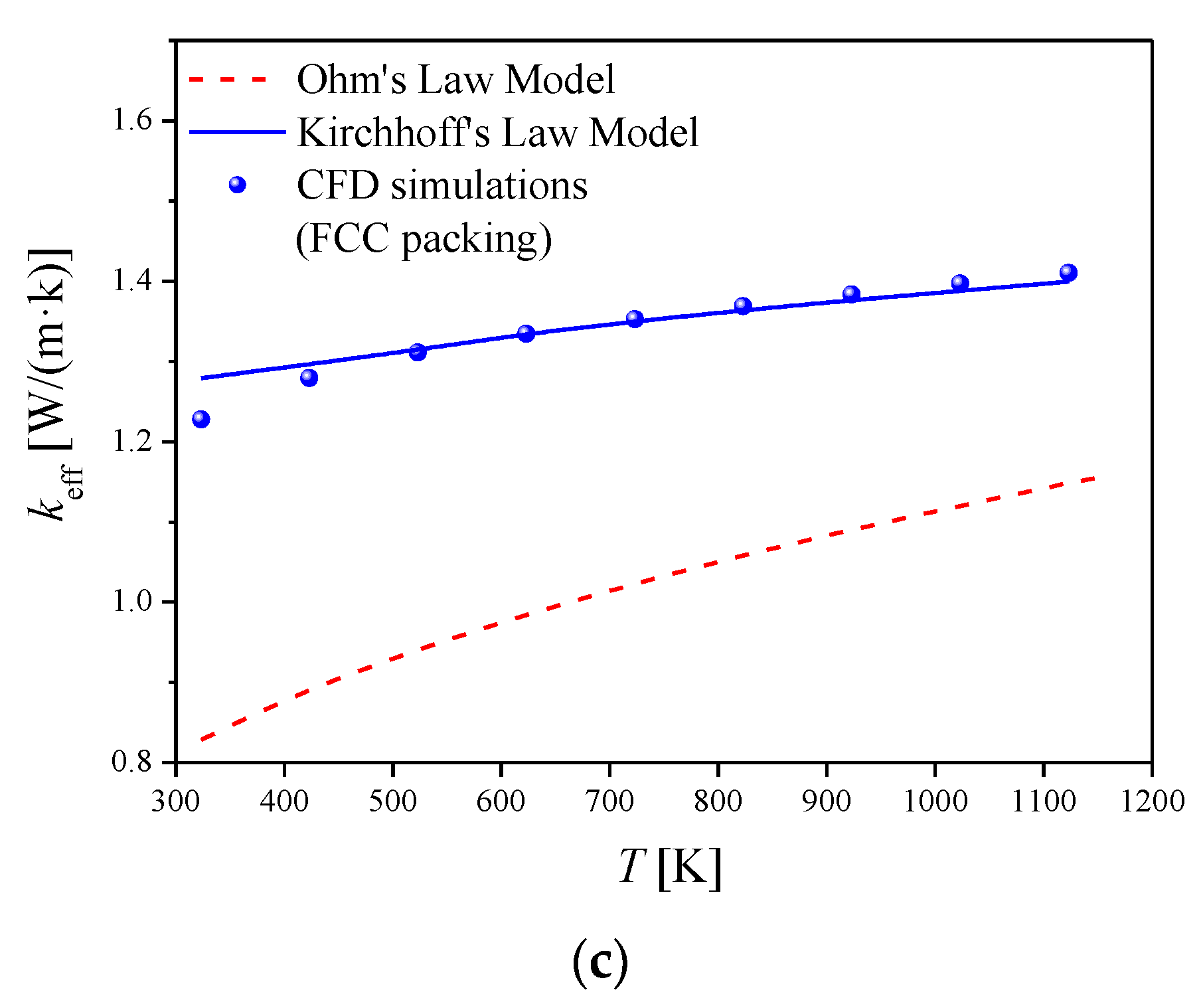
4.1. Effective Thermal Conductivity of Ordered Packings
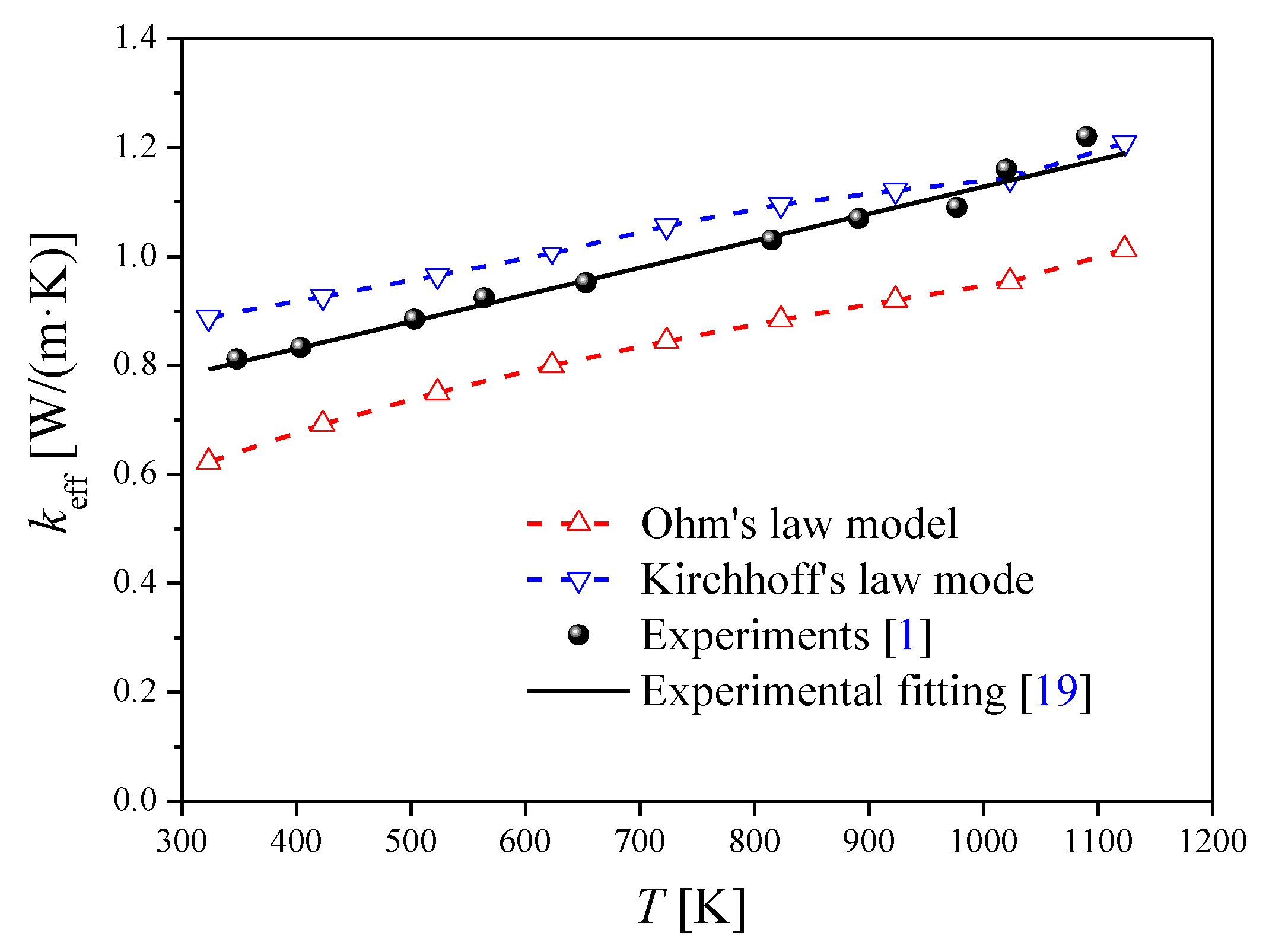
4.2. Effective Thermal Conductivity of Random Packings
4.3. Effect of Packing Factor
5. Conclusions
- (1)
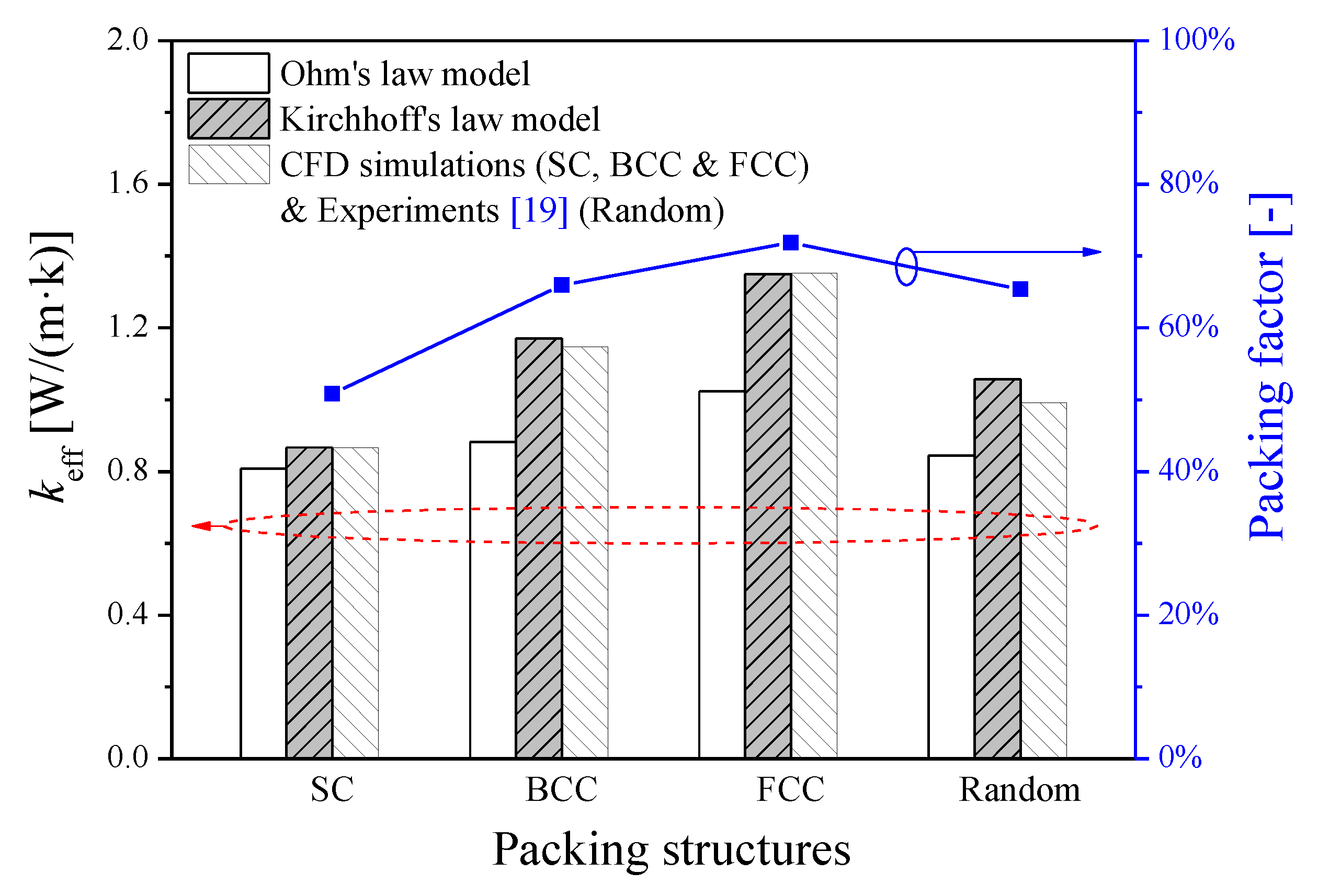
- For ordered packings, the effective thermal conductivities calculated with thermal resistance network of Kirchhoff’s law model fit well with CFD simulation results. While the results calculated with the Ohm’s law model are significantly underestimated. Therefore, when establishing a thermal resistance network, the thermal resistances should be connected along the main heat transfer direction and other heat transfer directions as well in the packing unit.
- (2)
- For random packings, it is proved that, the thermal resistance network method based on the Kirchhoff’s law mode and selected random packing units proposed in the present study would be reliable and accurate for the prediction of effective thermal conductivities in a Li4SiO4-packed bed, while the results calculated with the Ohm’s law model are also significantly underestimated for random packings.
- (3)
- The effect of packing factor is remarkable. As packing factor increases, the effective thermal conductivity (keff) of a packed bed increases, and the deviation of keff between the Ohm’s law model and Kirchhoff’s law model also increases. Furthermore, compared with random packing at a similar packing factor, the effective thermal conductivity of a packed bed might be further improved with an ordered packing method due to its higher coordinate number inside.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | area (m2) |
| dp | particle diameter (m) |
| i | index in x direction |
| I | maximum index in x direction |
| j | index in y direction |
| J | maximum index in y direction |
| k | index in z direction; thermal conductivity (W/(m·K)) |
| K | maximum index in z direction |
| R | thermal resistance (K/W) |
| T | temperature (K) |
| x | location at x coordinate (m) |
| y | location at y coordinate (m) |
| z | location at z coordinate (m) |
| Greek letters | |
| δ | thickness (m) |
| ε | porosity of pebble |
| heat flux (W/m2) | |
| Subscripts | |
| b | bottom surface |
| eff | effective value |
| element | thermal resistance element |
| f | fluid phase |
| m | mean value |
| s | solid phase |
| t | top surface |
| total | total value |
| unit | packing unit |
| x | component in x direction |
| y | component in y direction |
| z | component in z direction |
| Abbreviations | |
| BCC | body center cubic |
| CFD | computational fluid dynamics |
| DEM | discrete element method |
| FCC | face center cubic |
| FEM | finite element method |
| FVM | finite volume method |
| SC | simple cubic |
References
- Donne, M.D.; Goraieb, A.; Piazza, G.; Sordon, G. Measurements of the effective thermal conductivity of a Li4SiO4 pebble bed. Fusion Eng. Des. 2000, 49–50, 513–519. [Google Scholar] [CrossRef]
- Mandal, D.; Sathiyamoorthy, D.; Vinjamur, M. Experimental measurement of effective thermal conductivity of packed lithium-titanate pebble bed. Fusion Eng. Des. 2012, 87, 67–76. [Google Scholar] [CrossRef]
- Hatano, T.; Enoeda, M.; Suzuki, S.; Kosaku, Y.; Akiba, M.; Hatano, T. Effective thermal conductivity of a Li2TiO3 pebble bed for a DEMO blanket. Fusion Sci. Technol. 2003, 44, 94–98. [Google Scholar] [CrossRef]
- Earnshaw, J.W.; Londry, F.A.; Gierszewski, P.J. The effective thermal conductivity of a bed of 1.2-mm-diam lithium zirconate spheres in helium. Fusion Technol. 1998, 33, 31–37. [Google Scholar] [CrossRef]
- Panchal, M.; Chaudhuri, P.; Lew, J.T.V.; Ying, A. Numerical modelling for the effective thermal conductivity of lithium meta titanate pebble bed with different packing structures. Fusion Eng. Des. 2016, 112, 303–310. [Google Scholar] [CrossRef]
- Wang, X.L.; Zheng, J.; Chen, H.L. A prediction model for the effective thermal conductivity of mono-sized pebble beds. Fusion Eng. Des. 2016, 103, 136–151. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Y.H.; Huang, K.; Liu, S.L. Effective thermal property estimation of unitary pebble beds based on a CFD-DEM coupled method for a fusion blanket. Plasma Sci. Technol. 2015, 17, 1083–1087. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Y.H.; Huang, K.; Liu, S.L. Investigation of effective thermal conductivity for packed beds by one-way coupled CFD-DEM method for CFETR-WCCB. Fusion Eng. Des. 2016, 106, 1–8. [Google Scholar] [CrossRef]
- Zhao, Z.; Feng, K.M.; Feng, Y.J. Theoretical calculation and analysis modeling for the effective thermal conductivity of Li4SiO4 pebble bed. Fusion Eng. Des. 2010, 85, 1975–1980. [Google Scholar] [CrossRef]
- Mandal, D.; Gupta, S. Effective thermal conductivity of unary particulate bed. Can. J. Chem. Eng. 2016, 94, 1918–1923. [Google Scholar] [CrossRef]
- Antwerpen, W.V.; Rousseau, P.G.; Toit, C.G.D. Multi-sphere unit cell model to calculate the effective thermal conductivity in packed pebble beds of mono-sized spheres. Nucl. Eng. Des. 2012, 247, 183–201. [Google Scholar] [CrossRef]
- Zhou, F.; Cheng, G.X. Lattice Boltzmann model for predicting effective thermal conductivity of composite with randomly distributed particles: Considering effect of interactions between particles and matrix. Comput. Mater. Sci. 2014, 92, 157–165. [Google Scholar] [CrossRef]
- Cheng, G.J.; Yu, A.B. Particle scale evaluation of the effective thermal conductivity from the structure of a packed bed: Radiation heat transfer. Ind. Eng. Chem. Res. 2013, 52, 12202–12211. [Google Scholar] [CrossRef]
- Antwerpen, W.V.; Toit, C.G.D.; Rousseau, P.G. A review of correlations to model the packing structure and effective thermal conductivity in packed beds of mono-sized spherical particles. Nucl. Eng. Des. 2010, 240, 1803–1818. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Wang, S.C.; Xu, C.Y.; Liu, W.; Liu, Z.C. Numerical study on heat transfer performance in packed bed. Energies 2019, 12, 414. [Google Scholar] [CrossRef]
- Feng, Y.; Li, G.; Meng, Y.F.; Guo, B.Y. A novel approach to investigating transport of lost circulation materials in rough fracture. Energies 2018, 11, 2572. [Google Scholar] [CrossRef]
- Abou-Sena, A.; Ying, A.; Abdou, M. Effective thermal conductivity of lithium ceramic packed beds for fusion blankets: A review. Fusion Sci. Technol. 2005, 47, 1094–1100. [Google Scholar] [CrossRef]
- Reimann, J.; Piazza, G.; Xu, Z.; Goraieb, A.; Harschet, H. Measurements of the Thermal Conductivity of Compressed Beryllium Pebble Beds. Available online: https://www.researchgate.net/profile/Aniceto_Goraieb/publication/239277707_Measurements_of_the_Thermal_Conductivity_of_Compressed_Beryllium_Pebble_Beds_EFDA_reference_TW2-TTBB-007a_D4/links/543bc2e90cf24a6ddb979b85.pdf (accessed on 6 January 2017).
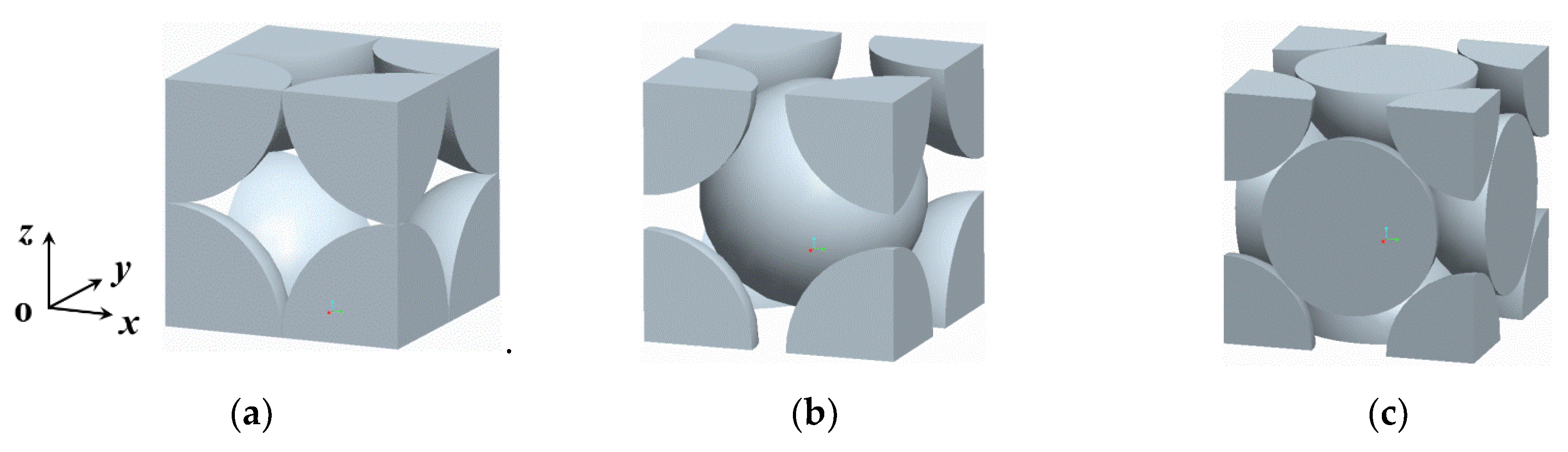
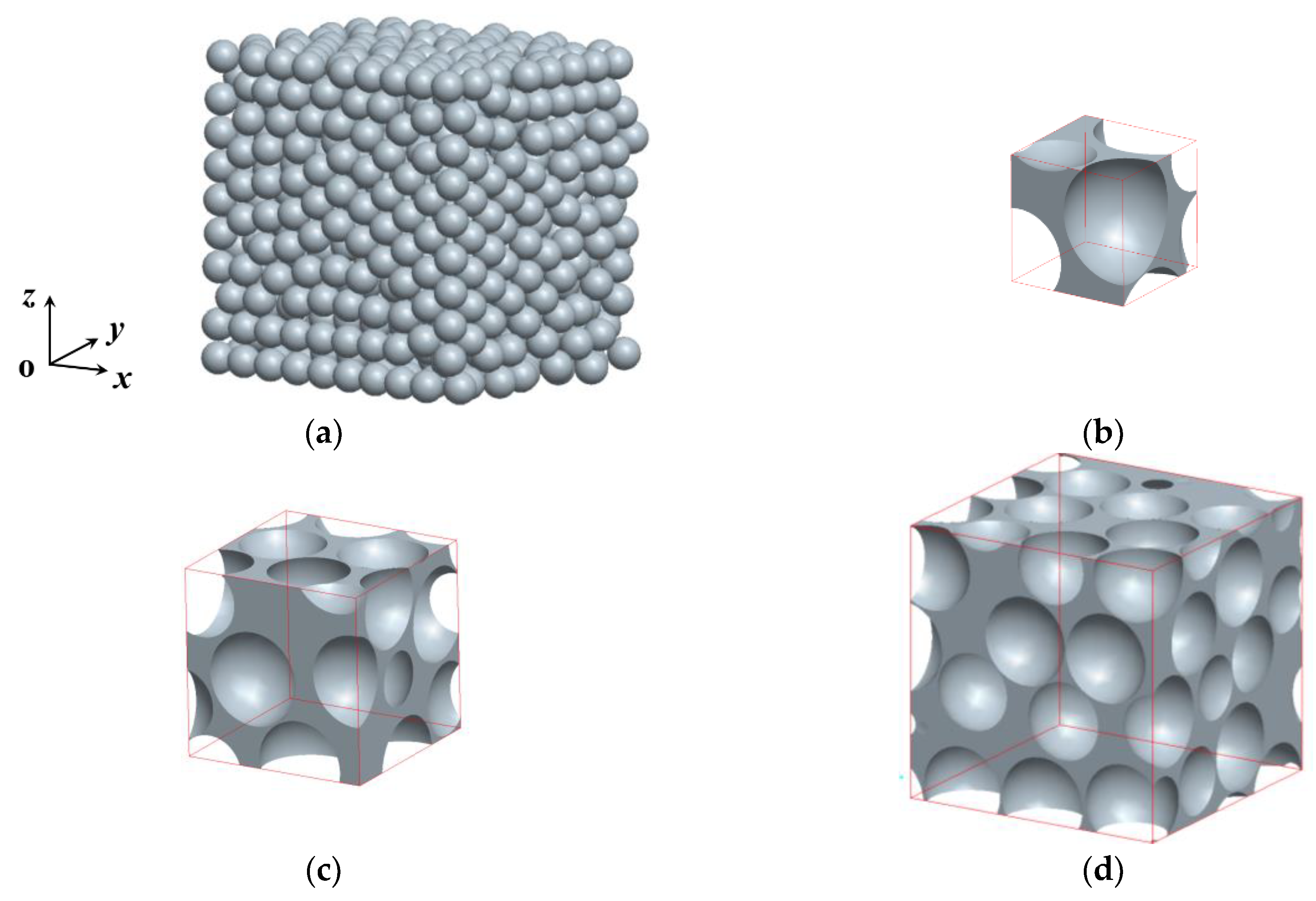
| Packing | dp (mm) | Unit Size | Packing Factor (%) |
|---|---|---|---|
| SC | 0.5 | 1dp × 1dp × 1dp | 50.8 |
| BCC | 0.5 | 1.155dp × 1.155dp × 1.155dp | 66.0 |
| FCC | 0.5 | 1.414dp × 1.414dp × 1.414dp | 71.9 |
| Packing Unit | x (mm) | y (mm) | z (mm) | dp (mm) | Packing Factor (%) | Unit Size |
|---|---|---|---|---|---|---|
| Unit-1 | 1.0–1.5 | 1.0–1.5 | 1.0–1.5 | 0.5 | 62.67 | 1dp × 1dp × 1dp |
| Unit-2 | 1.5–2.0 | 1.5–2.0 | 2.0–2.5 | 0.5 | 65.32 | |
| Unit-3 | 2.0–2.5 | 3.0–3.5 | 3.5–4.0 | 0.5 | 68.73 | |
| Unit-4 | 2.5–3.0 | 2.0–2.5 | 2.5–3.0 | 0.5 | 63.11 | |
| Unit-5 | 3.0–3.5 | 3.5–4.0 | 1.5–2.0 | 0.5 | 65.82 | |
| Unit-6 | 1.0–2.0 | 1.5–2.5 | 3.0–4.0 | 0.5 | 63.99 | 2dp × 2dp × 2dp |
| Unit-7 | 1.5–2.5 | 2.0–3.0 | 2.5–3.5 | 0.5 | 68.88 | |
| Unit-8 | 2.0–3.0 | 3.0–4.0 | 1.0–2.0 | 0.5 | 65.56 | |
| Unit-9 | 1.5–3.0 | 1.5–3.0 | 1.5–3.0 | 0.5 | 64.17 | 3dp × 3dp × 3dp |
| Unit-10 | 2.0–3.5 | 1.0–2.5 | 2.5–4.0 | 0.5 | 65.05 |
| Packing Unit | Packing Factor (%) | keff (W/(m·K)) | Deviation (keff) (%) | Unit Size |
|---|---|---|---|---|
| Unit-1 | 62.67 | 1.085 | 8.42 | 1dp × 1dp × 1dp |
| Unit-2 | 65.32 | 1.139 | 13.77 | |
| Unit-3 | 68.73 | 1.055 | 5.39 | |
| Unit-4 | 63.11 | 0.964 | −3.72 | |
| Unit-5 | 65.82 | 0.981 | −2.02 | |
| Unit-6 | 63.99 | 0.897 | −10.39 | 2dp × 2dp × 2dp |
| Unit-7 | 68.88 | 0.873 | −12.77 | |
| Unit-8 | 65.56 | 1.142 | 14.04 | |
| Unit-9 | 64.17 | 1.026 | 2.54 | 3dp × 3dp × 3dp |
| Unit-10 | 65.05 | 0.848 | −15.26 | |
| Average value | 65.33 | 1.001 | 8.83 | / |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Hu, Y.; Wang, Q. Investigation of Effective Thermal Conductivity for Ordered and Randomly Packed Bed with Thermal Resistance Network Method. Energies 2019, 12, 1666. https://doi.org/10.3390/en12091666
Yang J, Hu Y, Wang Q. Investigation of Effective Thermal Conductivity for Ordered and Randomly Packed Bed with Thermal Resistance Network Method. Energies. 2019; 12(9):1666. https://doi.org/10.3390/en12091666
Chicago/Turabian StyleYang, Jian, Yingxue Hu, and Qiuwang Wang. 2019. "Investigation of Effective Thermal Conductivity for Ordered and Randomly Packed Bed with Thermal Resistance Network Method" Energies 12, no. 9: 1666. https://doi.org/10.3390/en12091666
APA StyleYang, J., Hu, Y., & Wang, Q. (2019). Investigation of Effective Thermal Conductivity for Ordered and Randomly Packed Bed with Thermal Resistance Network Method. Energies, 12(9), 1666. https://doi.org/10.3390/en12091666






