Day-Ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques
Abstract
1. Introduction
2. PV Module Description and Database
2.1. PV Module Description
- -
- PV technology: Silicon mono crystalline
- -
- Rated power: 285 Wp
- -
- Azimuth: 6°30’ (assuming 0° as South direction and counting clockwise)
- -
- Solar panel tilt angle (β): 30°
2.2. Performance Indexes
2.3. Database Clustering
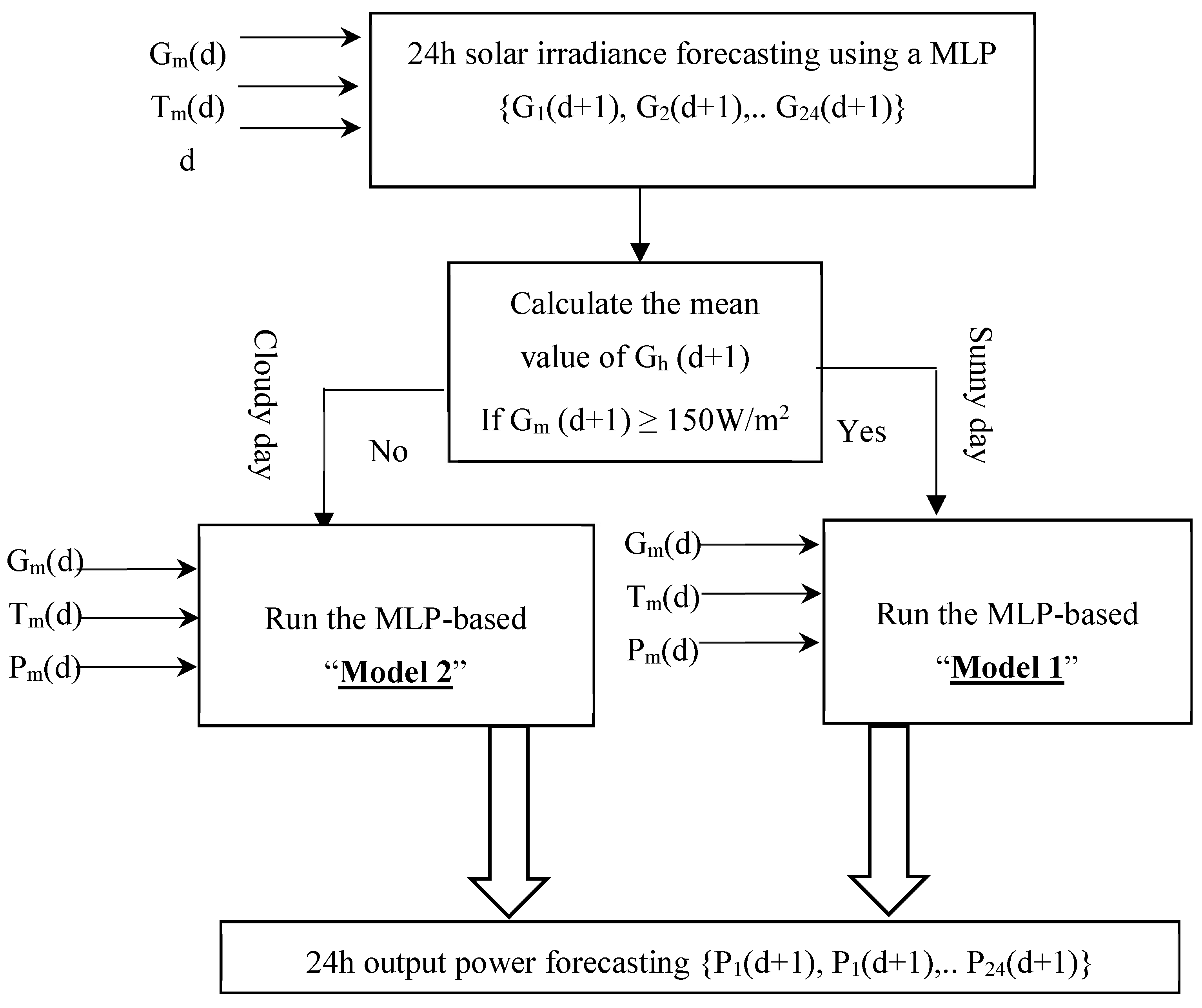
- Sunny days: these are characterized by a mean value of the solar irradiance during 24 h greater than 150 W/m² (i.e., );
- Cloudy days: these are characterized by a mean value of solar irradiance in the range [5–150 W/m²] (i.e., ).
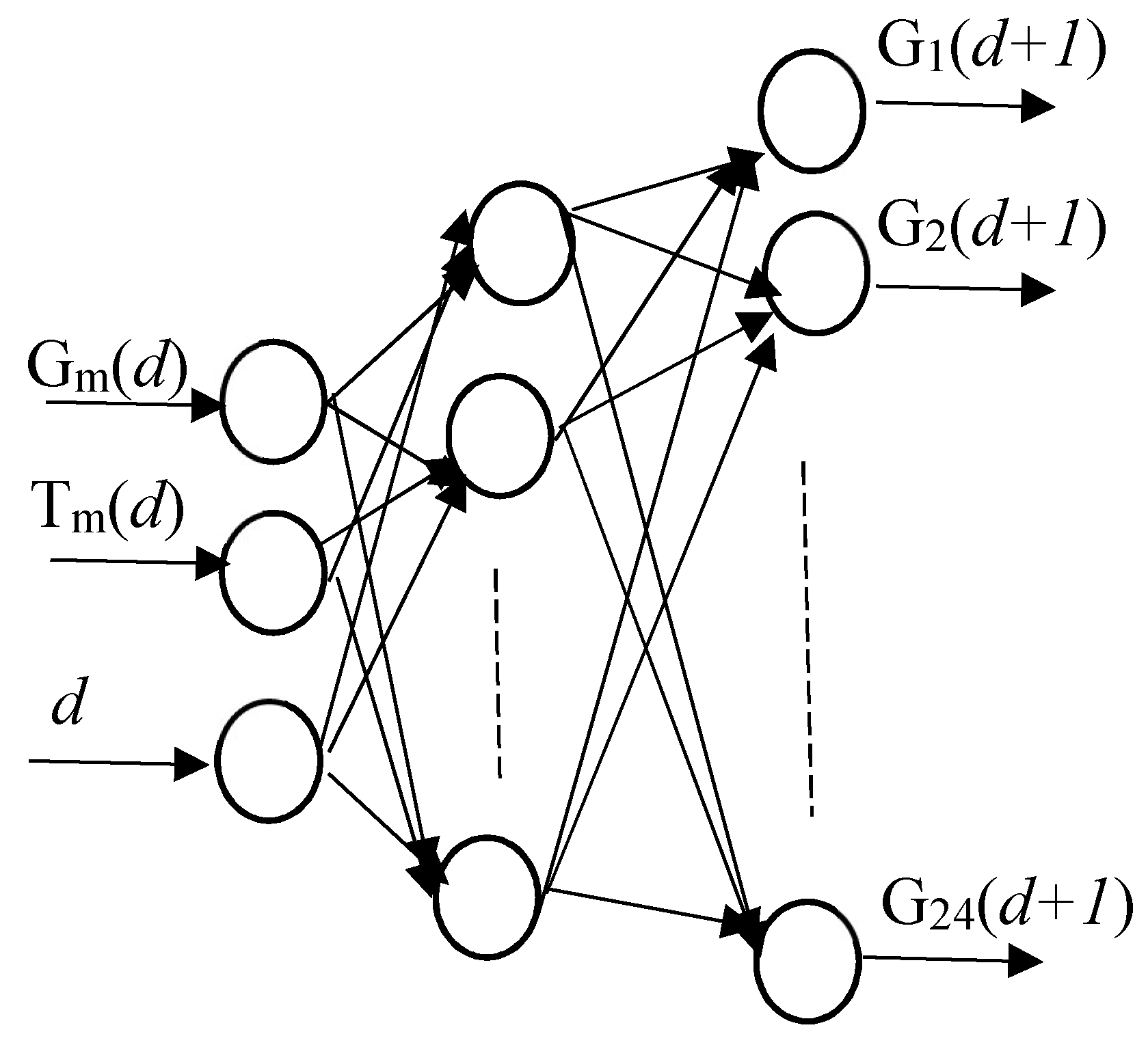
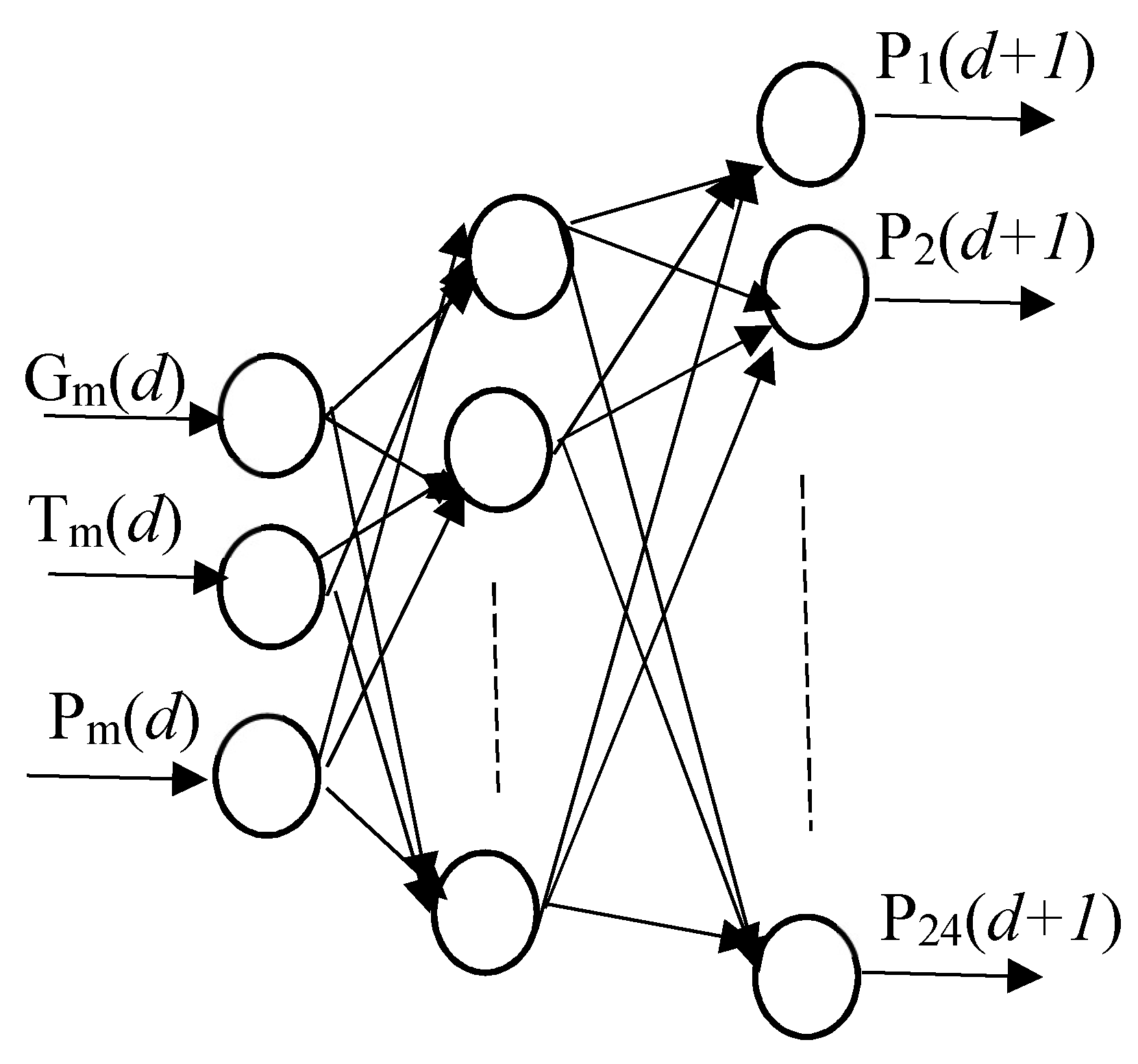
3. Methodology
- Ap1: All the available data are used to train the network (268 days)
- Ap2: The simulations are performed using the dataset comprising all the available data but, in order to train the network, the same number of days available in the sunny and cloudy dataset is used (randomly picked)
- Ap3: The simulations are performed using the “Sunny” and “Cloudy” dataset alternatively.
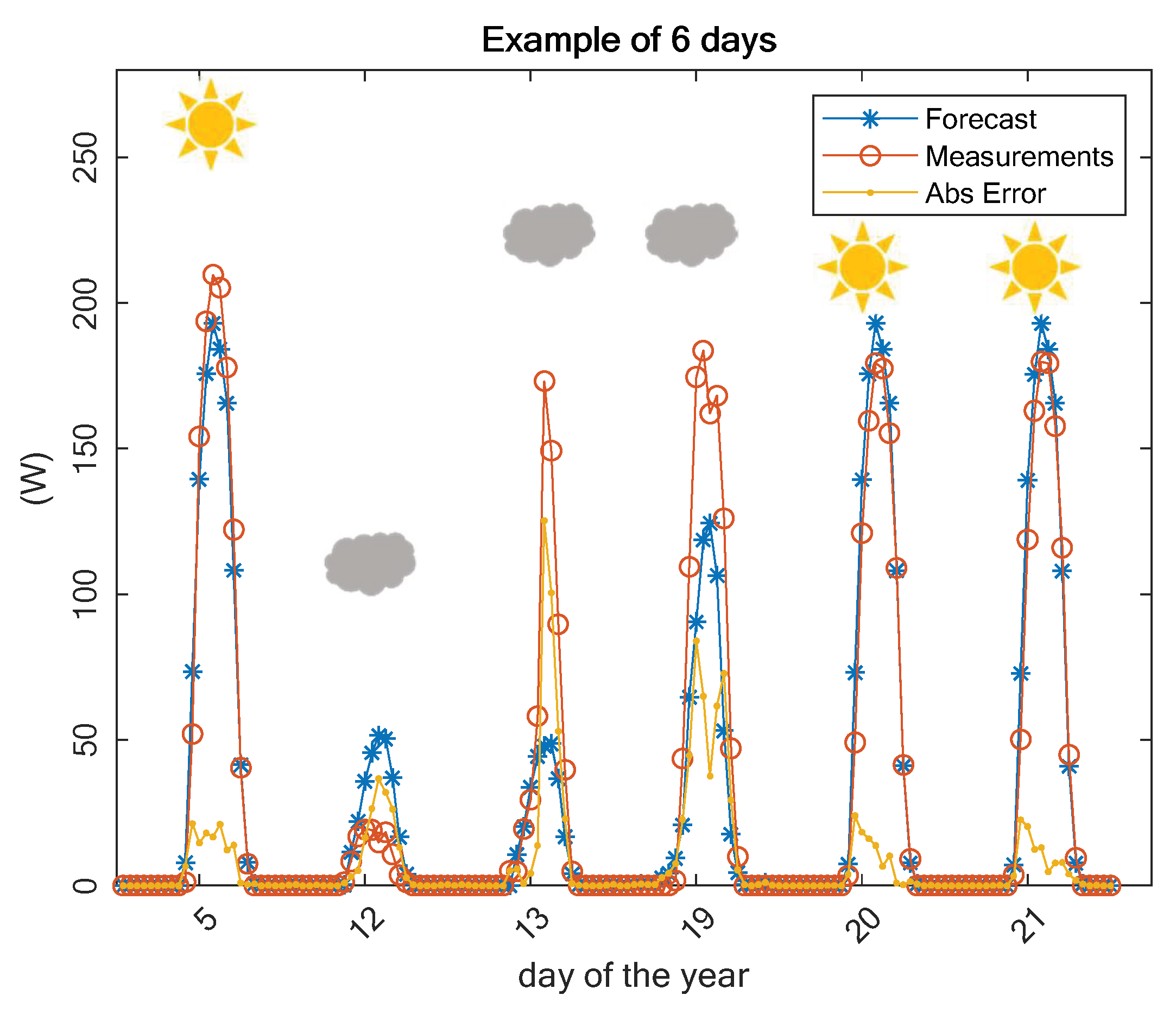
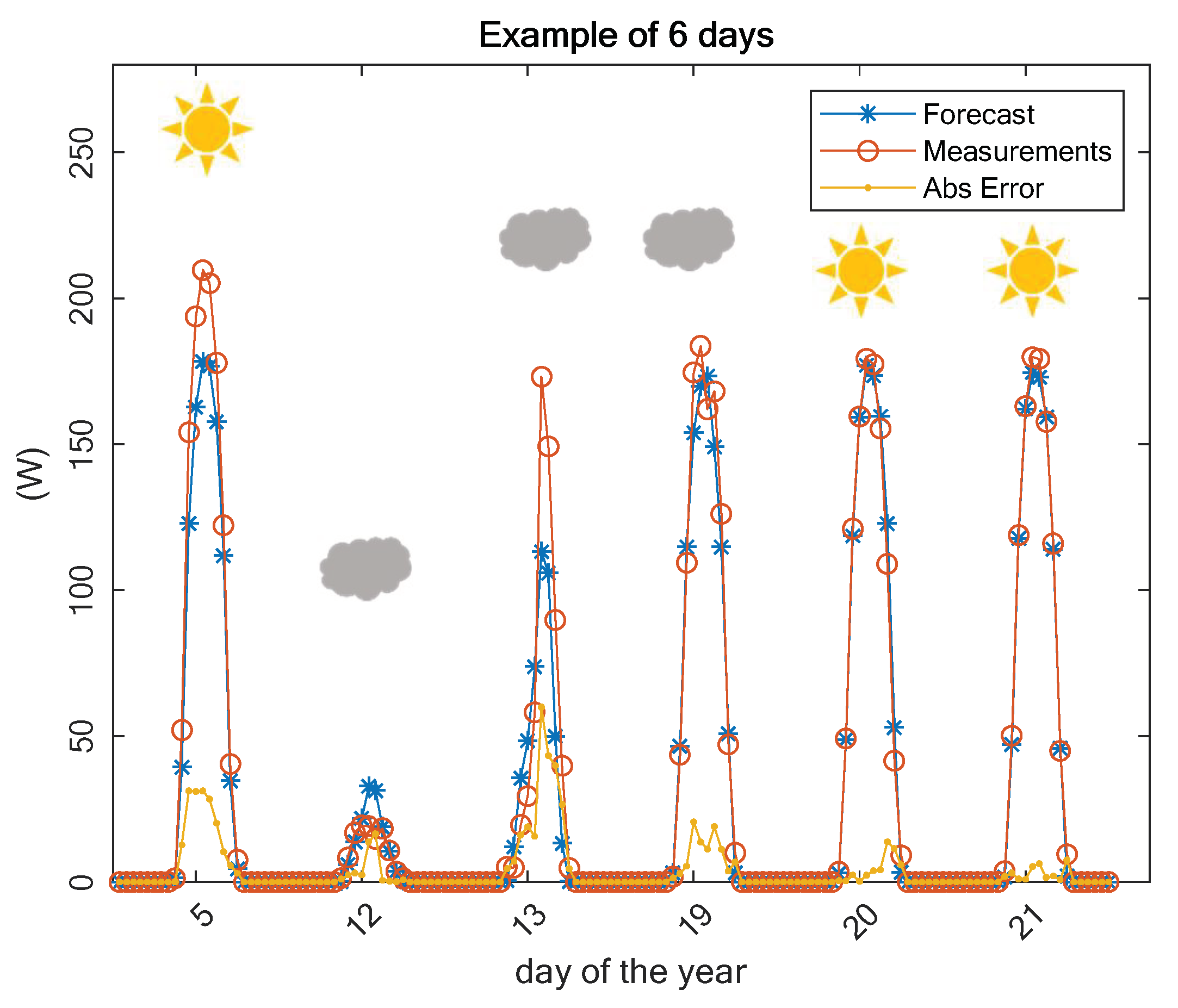
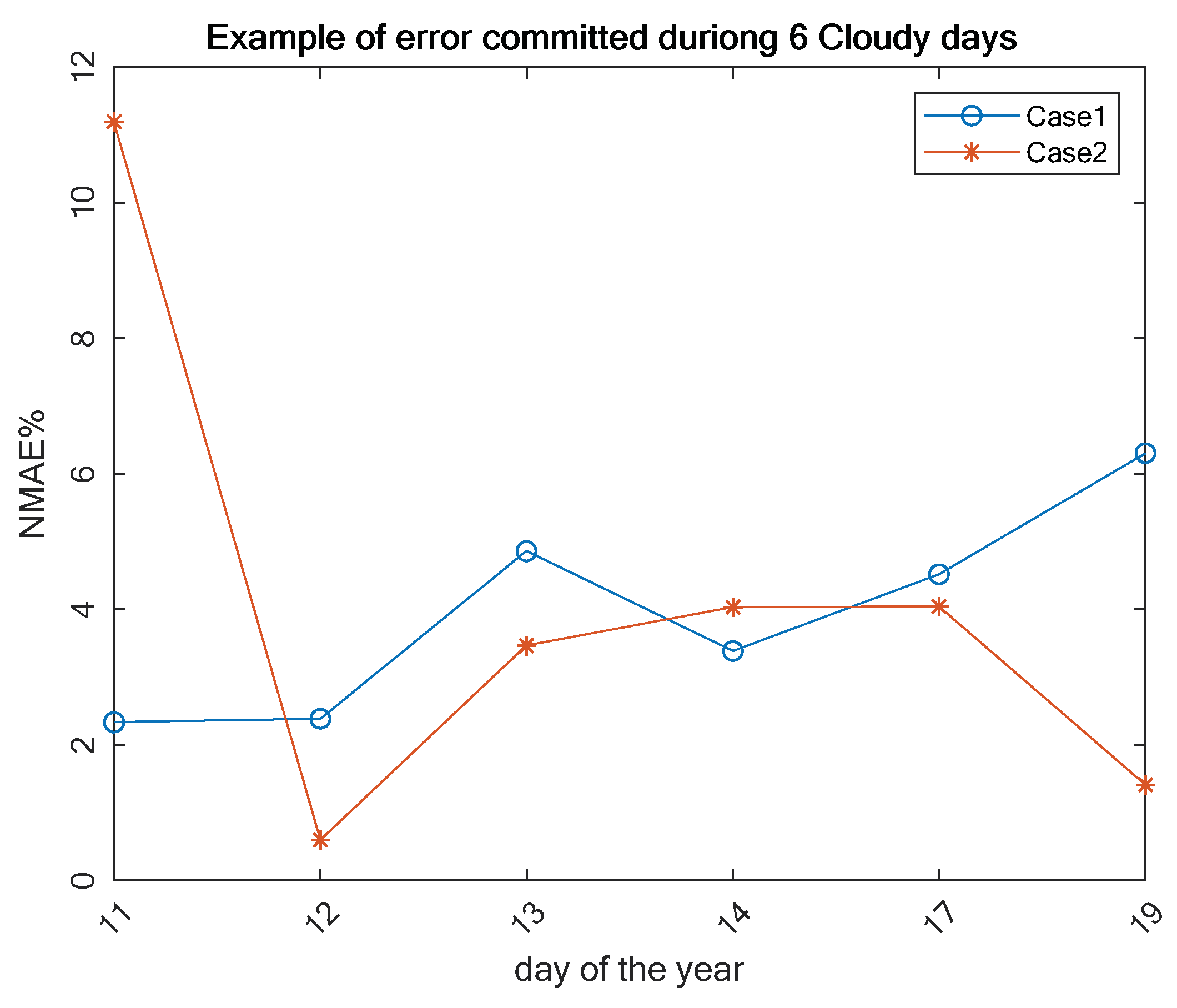
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Executive Summary of the World Energy Investment, 2018. International Energy Agency, 2018. Available online: https://webstore.iea.org/world-energy-investment-2018 (accessed on 22 March 2019).
- Global Warming of 1.5. 2018. Special Report IPCC, 2018. Available online: https://www.ipcc.ch/sr15/ (accessed on 22 March 2019).
- Zhan, D.; Kwan, M.P.; Zhang, W.; Yu, X.; Meng, B.; Liu, Q. The driving factors of air quality index in China. J. Clean. Prod. 2018, 197, 1342–1351. [Google Scholar] [CrossRef]
- Ul’Yanin, Y.A.; Kharitonov, V.V.; Yurshina, D.Y. Forecasting the Dynamics of the Depletion of Conventional Energy Resources. Stud. Russ. Econ. Dev. 2018, 29, 153–160. [Google Scholar] [CrossRef]
- Massi Pavan, A.; Lughi, V.; Rosato, P.; Spertino, F.; Vergura, S. Diminishing cost of electricity from wind power and photovoltaics. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017. [Google Scholar]
- Global landscape of Renewable Energy Finance. IRENA, 2018. Available online: https://www.irena.org/publications/2018/Jan/Global-Landscape-of-Renewable-Energy-Finance (accessed on 22 March 2019).
- D’Alessandro, V.; Di Napoli, F.; Guerriero, P.; Daliento, S. An automated high-granularity tool for a fast evaluation of the yield of PV plants accounting for shading effects. Renew. Energy 2015, 83, 294–304. [Google Scholar] [CrossRef]
- Massi Pavan, A.; Lughi, V. Grid parity in the Italian commercial and industrial electricity market. In Proceedings of the 2013 IEEE 4th International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013. [Google Scholar]
- Massi Pavan, A.; Lughi, V. Photovoltaics in Italy: Toward grid parity in the residential electricity market. In Proceedings of the 2012 24th International Conference on Microelectronics (ICM), Algiers, Algeria, 16–20 December 2012. [Google Scholar]
- Daliento, S.; Aissa, C.; Guerriero, P.; Massi Pavan, A.; Mellit, A.; Moeini, R.; Tricoli, P. Monitoring, diagnosis, and power forecasting for photovoltaic fields: A review. Int. J. Photoenergy 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Massi Pavan, A.; Sulligoi, G.; Lughi, V.; Pauli, F.; Miceli, R.; Di Dio, V.; Viola, F. Leading the way toward fuel parity in photovoltaics: The utility-scale market in Sicily, Italy. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016. [Google Scholar]
- Dolara, A.; Leva, S.; Mussetta, M.; Ogliari, E. PV hourly day-ahead power forecasting in a micro grid context. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016. [Google Scholar]
- Bird, L.; Cochran, J.; Wang, X. Wind and Solar Energy Curtailment: Experience and Practices in the United States; Technical Report NREL/TP-6A20-60983; National Renewable Energy Laboratory: Golden, CO, USA, March 2014. [Google Scholar]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Malvoni, M.; Congedo, P.M. Photovoltaic power forecasting using statistical methods: Impact of weather data. IET Sci. Meas. Technol. 2014, 8, 90–97. [Google Scholar] [CrossRef]
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Connecting the Sun-Solar Photovoltaics on the Road To Large Scale Grid Integration. EPIA, 2012. Available online: http://pvtrin.eu/assets/media/PDF/Publications/other_publications/263.pdf (accessed on 22 March 2019).
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-De-Pison, F.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Mills, A.; Wiser, R. Implications of Wide-Area Geographic Diversity for Short-Term Variability of Solar Power; Technical Report LBNL-3884E; Lawrence Berkeley National Laboratory: Washington, DC, USA, September 2010. [Google Scholar]
- Mills, A.; Botterud, A.; Wu, J.; Zhou, Z.; Hodge, B.M.; Heaney, M. Integrating Solar PV in Utility System Operation; Report ANL/DIS-13/18; Argonne National Laboratory: Lemont, IL, USA, October 2013. [Google Scholar]
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting, 1st ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Mellit, A.; Massi Pavan, A. A 24-h forecast of solar irradiance using artificial neural network: Application for performance prediction of a grid-connected {PV} plant at Trieste, Italy. Sol. Energy 2010, 84, 807–821. [Google Scholar] [CrossRef]
- Mellit, A.; Shaari, S. Recurrent neural network-based forecasting of the daily electricity generation of a photovoltaic power system. Ecolog. Veh. Renew. Energy 2009, 2–7. [Google Scholar]
- Mellit, A.; Saǧlam, S.; Kalogirou, S.A. Artificial neural network-based model for estimating the produced power ofaphotovoltaic module. Renew. Energy 2013, 60, 71–78. [Google Scholar] [CrossRef]
- Mellit, A.; Massi Pavan, A.; Benghanem, M. Least squares support vector machine for short-term prediction of meteorological time series. Theor. Appl. Climatol. 2013, 111, 297–307. [Google Scholar] [CrossRef]
- Reikard, G. Predicting solar radiation at high resolutions: A comparison of time series forecasts. Sol. Energy 2009, 83, 342–349. [Google Scholar] [CrossRef]
- Mellit, A.; Massi Pavan, A.; Lughi, V. Short-term forecasting of power production in a large-scale photovoltaic plant. Sol. Energy 2014, 105, 401–413. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting power output of photovoltaic systems based on weather classification and support vector machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- Yang, C.; Thatte, A.A.; Xie, L. Multitime-scale data-driven spatio-temporal forecast of photovoltaic generation. IEEE Trans. Sustain. Energy 2015, 6, 104–112. [Google Scholar] [CrossRef]
- Yang, H.-T.; Chao-Ming, H.; Huang, Y.-C.; Yi-Shiang, P. A Weather-Based Hybrid Method for one-day Ahead Hourly Forecasting of PV Power Output. IEEE Trans. Sustain. Energy 2014, 5, 917–926. [Google Scholar]
- Chen, C.; Duan, S.; Cai, T.; Liu, B. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Yona, A.; Senjyu, T.; Funabashi, T.; Kim, C.H. Determination method of insolation prediction with fuzzy and applying neural network for long-term ahead PV power output correction. IEEE Trans. Sustain. Energy 2013, 4, 527–533. [Google Scholar] [CrossRef]
- Hoff, T.E.; Perez, R.; Kleissl, J.; Renne, D.; Stein, J. Reporting of irradiance modeling relative prediction errors. Prog. Photovoltaics Res. Appl. 2016, 9, 261–270. [Google Scholar] [CrossRef]
- Pelland, S.; Galanis, G.; Kallos, G. Solar and photovoltaic forecasting through post-processing of the Global Environmental Multiscale numerical weather prediction model. Prog. Photovoltaics Res. Appl. 2011, 9, 261–270. [Google Scholar] [CrossRef]
- Monteiro, C.; Fernandez-Jimenez, L.A.; Ramirez-Rosado, I.J.; Muñoz-Jimenez, A.; Lara-Santillan, P.M. Short-term forecasting models for photovoltaic plants: Analytical versus soft-computing techniques. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Deventer, W.V.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Monteiro, C.; Santos, T.; Fernandez-Jimenez, L.A.; Ramirez-Rosado, I.J.; Terreros-Olarte, M.S. Short-term power forecasting model for photovoltaic plants based on historical similarity. Energies 2013, 6, 2624–2643. [Google Scholar] [CrossRef]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium 2010, Arlington, TX, USA, 26–28 September 2010; pp. 1–8. [Google Scholar]
- Leva, S.; Dolara, A.; Grimaccia, F.; Mussetta, M.; Ogliari, E. Analysis and validation of 24 hours ahead neural network forecasting of photovoltaic output power. Math. Comput. Simul. 2017, 131, 88–100. [Google Scholar] [CrossRef]
- Mandal, P.; Madhira, S.T.S.; Ul haque, A.; Meng, J.; Pineda, R.L. Forecasting power output of solar photovoltaic system using wavelet transform and artificial intelligence techniques. Procedia Comput. Sci. 2012, 12, 332–337. [Google Scholar] [CrossRef]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using AutoEncoder and LSTM Neural Networks. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016. [Google Scholar]
- Omar, M.; Dolara, A.; Magistrati, G.; Mussetta, M.; Ogliari, E.; Viola, F. Day-ahead forecasting for photovoltaic power using artificial neural networks ensembles. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016; pp. 1152–1157. [Google Scholar]
- Fernandez-Jimenez, L.A.; Muñoz-Jimenez, A.; Falces, A.; Mendoza-Villena, M.; Garcia-Garrido, E.; Lara-Santillan, P.M.; Zorzano-Alba, E.; Zorzano-Santamaria, P.J. Short-term power forecasting system for photovoltaic plants. Renew. Energy 2012, 44, 311–317. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. A physical hybrid artificial neural network for short term forecasting of PV plant power output. Energies 2015, 8, 1138–1153. [Google Scholar] [CrossRef]
- Bouzerdoum, M.; Mellit, A.; Massi Pavan, A. A hybrid model (SARIMA-SVM) for short-term power forecasting of a small-scale grid-connected photovoltaic plant. Sol. Energy 2013, 98, 226–235. [Google Scholar] [CrossRef]
- Chicco, G.; Cocina, V.; Di Leo, P.; Spertino, F.; Massi Pavan, A. Error assessment of solar irradiance forecasts and AC power from energy conversion model in grid-Connected photovoltaic systems. Energies 2016, 9, 8. [Google Scholar] [CrossRef]
- Lee, D.; Kim, K. Recurrent Neural Network-Based Hourly Prediction of Photovoltaic Power Output Using Meteorological Information. Energies 2019, 12, 215. [Google Scholar] [CrossRef]
- SolarTech LAB. 2013. Available online: http://www.solartech.polimi.it/ (accessed on 20 April 2019).
- Ulbricht, R.; Fischer, U.; Lehner, W.; Donker, H. First Steps Towards a Systematical Optimized Strategy for Solar Energy Supply Forecasting. ECML/PKDD 2013, 1st Int. Work. Data Anal. Renew. Energy Integr. 2013, 2327, 14–25. [Google Scholar]
- Coimbra, R.; Carlos, F.M.; Kleissl, J.; Marquez, R. Overview of Solar-Forecasting Methods and a Metric for Accurary Evaluation. In Solar Energy Forecasting and Resource Assessment; Academic Press: Cambridge, MA, USA, 2013; pp. 171–193. Available online: https://www.sciencedirect.com/science/article/pii/B9780123971777000085?via%3Dihub (accessed on 20 April 2019).
- Leva, S.; Mussetta, M.; Ogliari, E. PV module fault diagnosis based on micro-converters and day-ahead forecast. IEEE Trans. Ind. Electron. 2018, 66, 3928–3937. [Google Scholar] [CrossRef]
- Mellit, A.; Kalogirou, S.A. Artificial intelligence techniques for photovoltaic applications: A review. Prog. Energy Combust. Sci. 2008, 34, 574–632. [Google Scholar] [CrossRef]
- Bird, R.E.; Riordan, C. Simple Solar Spectral Model for Direct and Diffuse Irradiance on Horizontal and Tilted Planes at the Earth’s Surface for Cloudless Atmospheres. 1986. Available online: https://journals.ametsoc.org/doi/pdf/10.1175/1520-0450%281986%29025%3C0087%3ASSSMFD%3E2.0.CO%3B2 (accessed on 20 April 2019).
- Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. ANN sizing procedure for the day-ahead output power forecast of a PV plant. Appl. Sci. 2017, 7, 622. [Google Scholar] [CrossRef]
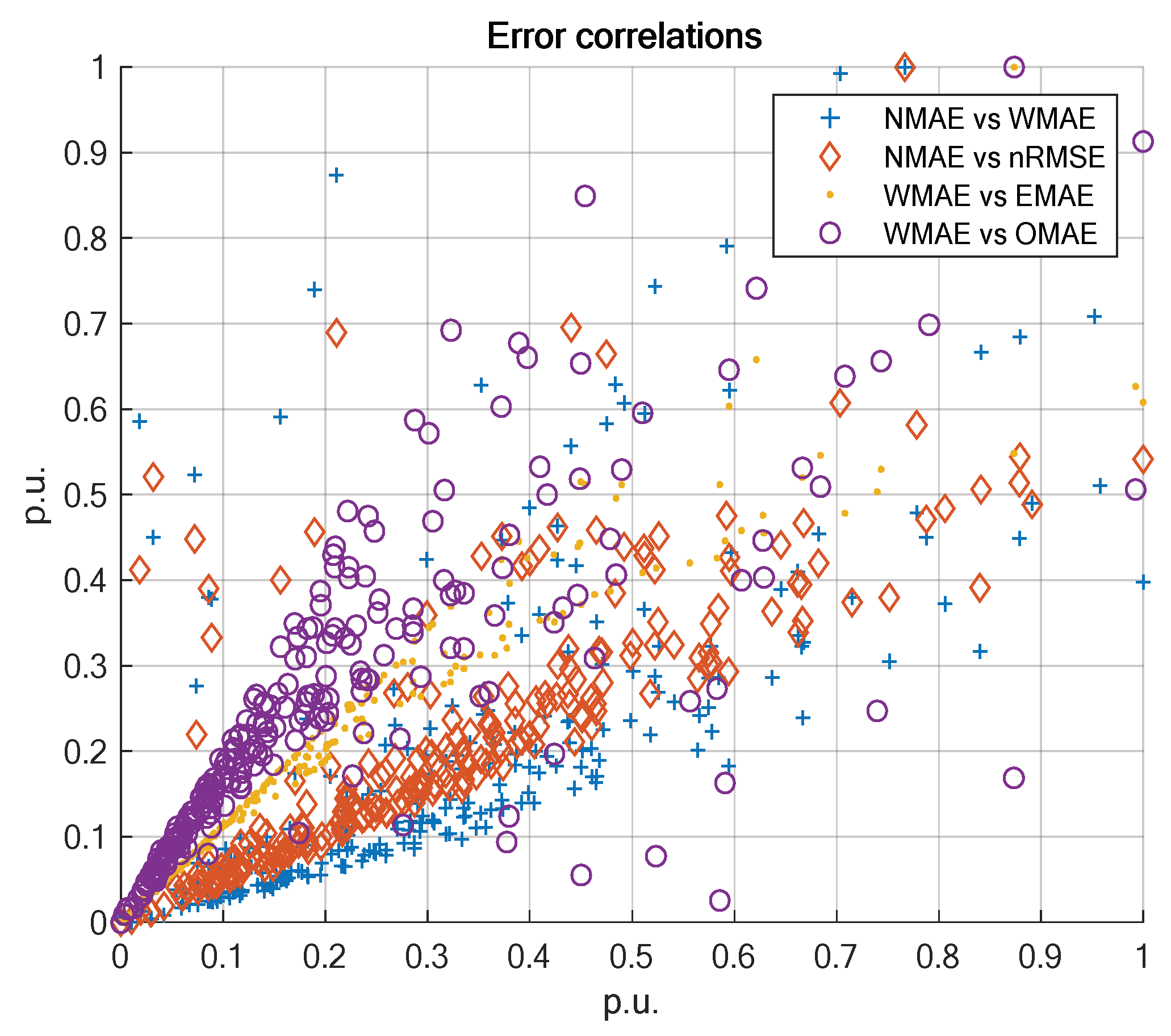


| NMAE | EMAE | WMAE | nRMSE | OMAE | |
|---|---|---|---|---|---|
| NMAE | 1 | 0.59 | 0.37 | 0.40 | 0.90 |
| EMAE | 1 | 0.80 | 0.78 | 0.71 | |
| WMAE | 1 | 0.98 | 0.48 | ||
| nRMSE | 1 | 0.51 | |||
| OMAE | 1 |
| Imposed Threshold on GPOA,f,d | 150 (W/m2) |
|---|---|
| # of days | 268 |
| # of sunny days | 154 |
| # of cloudy days | 114 |
| Sunny | Day 5 | Day 15 | Day 16 | Day 18 | Day 20 | Day 21 |
|---|---|---|---|---|---|---|
| Case 1 | 10.83 | 12.89 | 10.45 | 7.17 | 9.51 | 9.61 |
| Case 2 | 14.95 | 21.43 | 30.39 | 1.96 | 2.22 | 3.29 |
| Cloudy | Day 11 | Day 12 | Day 13 | Day 14 | Day 17 | Day 19 |
|---|---|---|---|---|---|---|
| Case 1 | 156.21 | 143.15 | 57.86 | 26.51 | 42.63 | 42.01 |
| Case 2 | 750.01 | 35.87 | 41.26 | 31.6 | 38.14 | 9.38 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nespoli, A.; Ogliari, E.; Leva, S.; Massi Pavan, A.; Mellit, A.; Lughi, V.; Dolara, A. Day-Ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques. Energies 2019, 12, 1621. https://doi.org/10.3390/en12091621
Nespoli A, Ogliari E, Leva S, Massi Pavan A, Mellit A, Lughi V, Dolara A. Day-Ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques. Energies. 2019; 12(9):1621. https://doi.org/10.3390/en12091621
Chicago/Turabian StyleNespoli, Alfredo, Emanuele Ogliari, Sonia Leva, Alessandro Massi Pavan, Adel Mellit, Vanni Lughi, and Alberto Dolara. 2019. "Day-Ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques" Energies 12, no. 9: 1621. https://doi.org/10.3390/en12091621
APA StyleNespoli, A., Ogliari, E., Leva, S., Massi Pavan, A., Mellit, A., Lughi, V., & Dolara, A. (2019). Day-Ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques. Energies, 12(9), 1621. https://doi.org/10.3390/en12091621








