1. Introduction
The growing concern around rising energy costs, the dependence on fossil fuels, and the environmental impact of energy supply makes it necessary to find economical and environment-friendly energy alternatives. The largest share in newly-installed power capacities around the world is covered by wind and solar plants. Besides those two renewables, geothermal energy also represents large untapped renewable potential and low environmental impact, especially regarding greenhouse gases emissions. Despite many other advantages, like a reliable, constant baseload electricity or direct heat usage and a small land area footprint, geothermal energy is nowadays still a small contributor to the primary energy consumption. Its worldwide installed capacity is estimated at 12.9 GW [
1] and share in total electricity generation of less than 1%. The main reasons are related to the risks and uncertainties of sustained fluid provision from the reservoirs and large upfront costs associated with exploration, well drilling and stimulation [
2]. Furthermore, the traditional hydrothermal systems, based on mature and well-known technology, enable the exploitation of mainly high-enthalpy reservoirs, whereas a huge geothermal potential is present in low permeable, low porosity and low to medium enthalpy bedrock. In order to enhance reservoir productivity in low permeable rocks, Enhanced Geothermal Systems (EGS) technology has been developed. The EGS technique consists of creating a fracture system in the targeted geological formation through which geothermal fluid can circulate. Hydraulic and chemical stimulations are used to create these fractures. The thermal energy stored in the hot rock mass gets extracted by circulating the fluid through the reservoir. The circulation of the fluid is obtained with different extraction technologies, among which the most prominent are so-called injector-producer doublets or borehole heat exchangers.
Aside from exploiting the geothermal heat from low permeable bedrock, additional energy can be recovered from thousands of mature or abandoned oil wells. Mature oil fields have been used for production for a long time, but their production has reached its peak and has started to decline. The typical production pattern of most oil producing wells displays an increase of water with time, from 0% initially to a point, typically above 95%, when it is not economic to produce the remaining oil. Mature oil fields account for more than 70% of world’s oil and gas production, and regarding European oil fields, it is expected that wells are nowadays producing much more water than oil, with average water to a fluid ratio of 90% and with temperature up to 90 °C and sometimes higher. This remaining heat is currently usually wasted, as it is simply re-injected into the reservoir for pressure maintenance or sweep purpose. There are several studies concentrating on energy recovery from mature or abandoned oil fields. In Reference [
3] a preliminary assessment of the potential for geothermal exploitation of the co-produced water from wells in the Villafortuna-Trecate oil field in Italy was made by comparing three different implementation scenarios for the possible use of the co-produced hot water: direct use district heating (DH), electric power generation through Organic Rankine Cycle (ORC) plant, and co-generation of heat and power. In Reference [
4] energy from abandoned oil and gas reservoirs is used by oxidizing the residual oil with the injected air. In Reference [
5] a simulation for the determination of geothermal power production from abandoned oil wells by injecting and retrieving a secondary fluid is performed. Technical feasibility study of acquiring geothermal energy from existing abandoned oil and gas wells is conducted in Reference [
6]. Computational results indicate that the geothermal energy produced from abandoned wells depends largely on the flow rate of the fluid and the geothermal gradient. Moreover, the results also indicate that the distance of the two proposed wells should not be less than 40 m to avoid their interrelationships. A Poland case study on the usage of abandoned oil and gas wells for recovering geothermal heat is given in Reference [
7]. Some important aspects of power generation using the co-produced hot oil and liquid, with temperatures around 120 °C, from Huabei oil field were studied in Reference [
8]. Study on the geothermal power generation using abandoned oil wells is done in Reference [
9] with isobutane as working fluid. Also, some interesting insights are given regarding how to increase obtained heat. The results in Reference [
10] show that it is necessary to consider the oil and gas saturation while estimating geothermal reserve in oil and gas reservoirs. In Reference [
11] the Croatian case of the binary power plant installed in Velika Ciglena is described and in Reference [
12] the economic feasibility of this power plant is presented. Moreover, the thermodynamic cycle optimization of Velika Ciglena power plant is conducted in Reference [
13]. The explorations in Croatia for the national oil company showed a very high temperature of geothermal water in the oil negative well (about 170 °C). Nowadays, the power plant at Velika Ciglena is the largest ORC geothermal power plant in Europe, with design conditions that allow for a 15 MWe installed capacity. The power plant is ORC using the isopentane as a working fluid and an air-cooling system that was chosen for the condensing process. Currently, the plant is producing electricity but there is still enough potential capacity for a DH, for which studies are currently being carried out. Furthermore, in Reference [
14] a global review of 18 significant EGS sites and technologies that have been applied in the EU, Japan, South Korea, Australia, and the USA was given. The results from this study show that the site characteristics are a key factor of successful EGS development. It was concluded that for sites suitable for EGS, the local geological conditions (stress field, temperature field, rock composition, the range of existing permeability, reservoir properties, etc.) mostly determining the amount of recovered geothermal heat by means of EGS techniques.
Many previous studies have focused either on economic assessment [
15,
16] or environmental assessment based on the life cycle environmental impact of geothermal power generation as studied in References [
17,
18]. A review in Reference [
19] presents an analysis of existing software packages for estimating and simulating costs, conventionally used in studying EGS facilities. The focus of the review is the top European software EURONAUT and the US GEOPHIRES package. EURONAUT is implemented based on the studies conducted at the EGS plant in Soultz-sous-Forêts. The root of the program is economic estimation via discontinuous cash flows, and all other calculations are developed as separate modules that can be joined together via various interfaces [
19]. GEOPHIRES, however, is a software tool that combines reservoir, wellbore, and power plant models with capital and operating costs, correlations, and financial levelized cost model to assess the technical and economic performance of EGS. This software differs from the Geothermal Energy Technology Evaluation Model (GETEM) [
20] and Hot Dry Rock economic model (HDRec) [
21], which are two examples of technological/economic models initially used to simulate the operation of EGS plant. The distinction is mainly due to the fact that the currently available packages do not permit the simulation of not only electricity production but also direct-use-heat production and a combined heat and power (CHP) production, which was implemented in GEOPHIRES software.
The rate of geothermal development and implementation has been conditioned not only by mentioned geological conditions, drilling, and stimulation technologies, but also by legal frameworks, and regulative and social constraints. An overview of legislative and socio-economic issues of geothermal energy is available in References [
22,
23]. More on public and political acceptance issues could be found in Reference [
24]. Establishing functional legal frameworks remains a challenge for countries seeking to develop their first geothermal projects to this day.
EGS technology enables exploitation of geothermal energy at a wide range of temperature and on a large geographic scale. However, EGS technology is not yet mature enough to be commercially competitive with other renewable resources. Almost all the EGS pilot plants, currently operating, need to be jointly funded by governments in order to operate or/and develop. Finally, the risks, uncertainties, and costs related to EGS projects mean that it is essential to conduct exhaustive studies involving modelling and simulation of EGS geothermal reservoirs and above-ground power plant facility at any location where it is desired to develop this kind of technology. This requires a holistic approach which should consider different scenarios and various influencing factors, from choosing the right extraction technology to the analysis of the energy prices and market signals. Given the fact that a taken decision will trigger financial consequences over a long period of time, the software for estimating and simulating the costs is an essential tool in order to successfully choose and face an EGS project. This paper presents the concept of such multi-scale Decision-Making Support Tool for Optimal Usage of Geothermal Energy (DMS-TOUGE) and multiple-criteria decision-making (MCDM) matrix that will be fully developed as part of the Horizon 2020 project: Multidisciplinary and multi-context demonstration of EGS exploration and Exploitation Techniques and potentials (MEET, GA No 792037).
The main objective of this work is to present the MCDM matrix and selected weighted criteria used to evaluate and compare different EGS sites and technologies and to demonstrate this MCDM matrix as a means of conducting a rapid preliminary evaluation of the technical and economic feasibility of an EGS project with related environmental and social impact. The MCDM matrix is used in this work for assessment of four different geothermal sites, and by using real data for each of the selected sites the comparison between sites was enabled.
The contribution of this work in relation to other selection matrices is that it provides expanded and detailed criteria related to environmental and social impact giving the necessary emphasis on so far neglected important aspects for successful completion of geothermal projects. Moreover, the novelty of this work is that by combining technical, economic, environmental, and social aspects of geothermal projects, the MCDM presented in this work gives a comprehensive assessment of EGS projects. Namely, since the EGS related projects are high-insensitive investments, for a DM interested in sustainably operate an EGS-plant close to densely populated areas, it is imperative to include many different aspects in techno-economic analysis and decision-making process. It is, however, challenging to predict all possible scenarios and influencing factors. Therefore, the process of developing a DMS-TOUGE and related MCDM matrix is a multiple-stage process. At this stage of the development and modelling process, the tool is intended for an evaluation of an EGS project at early development stage, meaning that a great number of the variables should be approximatively forecasted and estimated. Using optimization, the adequate evaluation of the production for chosen site and technology can be displayed. With progress in time, the tool will be useful for upgrade or extension of an already existing chosen geothermal site. In that case, the DM can provide more detailed information about EGS power plant operating cycle since the plant has already been generating electricity or heat for direct usage.
The rest of paper is organised as follows. Methodology, background, and main components of DMS-TOUGE are explained in
Section 2. In the same chapter one of the main component of DMS-TOUGE, the MCDM is presented in more detail.
Section 3 describes in detail the MCDM matrix and its criterions used in this paper for the evaluation of different EGS sites.
Section 4 describes the case study examples, presents the scenario results, and gives the sensitivity analysis based on these results. The obtained results are discussed.
Section 5 concludes the paper and gives the main directions for future development and research.
3. Multiple-Criteria Decision-Making Analysis
As a subprocess in the DMS-TOUGE, an MCDM analysis will be used and performed using the weighted decision matrix (WDM). For evaluating different EGS options, a set of criterions is defined and presented in this subsection. For evaluation of the relative importance of each criterion in decision making, the weight is associated with each of the listed criterions. Performance,
, of option
on criterion
is arbitrarily defined with a numerical value from 1 to 5, whose higher value means better performance,
. Finally, total performance,
, of
ith EGS option on all criteria,
, is assessed by summing all performance values,
, multiplied by its weight as defined in Equation (1).
where
is the total performance of
ith EGS option,
, where
is a total number of EGS options. The
is weight i.e., relative importance in the decision making of criterion
,
, where
is a total number of criteria. The
is the performance of option
on criterion
. To use WDM successfully while assessing EGS options for a specific geothermal site, a set of well-defined criteria is needed. The criteria on which EGS option will be evaluated is listed below in
Section 3.1,
Section 3.2,
Section 3.3,
Section 3.4,
Section 3.5,
Section 3.6,
Section 3.7,
Section 3.8,
Section 3.9,
Section 3.10,
Section 3.11 and
Section 3.12. It should be noted that, although the Equation (1) shows a simple summation, the actual calculation of total performance for a selected site was performed as an average mean of
performances of each criterion. Also, in this work every criterion
is assumed to have equal relative importance in the decision making. Thereby, all criteria are evaluated assuming all
to be equal and valued with 1. It is worth mentioning that the actual range for
has not been yet precisely defined, as it is a sensitive part of the MCDM matrix. Therefore, such a range must be chosen that will adequately and meaningfully reflect the relative importance of certain criteria in relation to others. In the future work and through a process of validation and verification of the MCDM matrix and DMS-TOUGE, the discrete sequential values for
will be chosen.
3.1. First Criterion: Installed Power,
When considering energy investment, installed power (capacity) is the first and most important parameter [
31]. It later determines both costs (CAPEX, OPEX-O&M) and revenues (power output). According to Reference [
30], performance
of option
i on 1st criterion should be determined by
ratio in p.u. (ratio of installed power,
, of ORC technology in
ith option to the reference installed power,
, e.g., according to Reference [
31] for ORC technology reference installed power ranges from 1 MW to 5 MW depending on site features) (
Table 1).
3.2. Second Criterion: Fluid Heat Flow,
Expected heat flow,
(W), for the two main extraction technologies, a traditional doublet with fluid extraction and reinjection, and wellbore heat exchanger, a closed loop system, is defined with Equation (2):
where
is the fluid flow rate (m
3/s),
is fluid density (kg/m
3),
is specific heat capacity of fluid at constant pressure (J/kg·K).
is the fluid temperature at the wellhead (°C),
is the fluid temperature at the exit of the steam turbine (°C).
Heat flow as a criterion was first proposed in Reference [
31] and is used here with modifications in means of corresponding ranges for temperature. The idea is to emphasize the importance of flow rate and temperature of the produced fluid, and the impact of selected technology on flow rate and temperature. Reference [
31] proposes criterion, here referred to as the
, whose value is based on the ratio between the fluid flow rate,
, and flowing temperature at the wellhead,
. According to [
31] best suited ranges for valuing performance
in heat flow criterion are defined by flow rates between 0 m
3/h and 100 m
3/h and when temperatures are between 80 °C and 160 °C, since those ranges correspond to operative conditions for an ORC plant. For this criterion, the temperature range is modified for the values between 60 °C and 160 °C, since one of the focus of the ongoing H2020 MEET project is to make those temperatures also exploitable (
Table 2).
3.3. Third Criterion: Theoretical Maximum Efficiency,
In this paper, the ORC based power plants are proposed for exclusively electricity generation. It is mainly due to the low-to-medium temperature range of the produced geothermal fluid. The thermal efficiency evaluated at the heat exchanger of the conversion plant in such fields is usually less than 10%, and for the binary power plants, according to Reference [
32] could be calculated with Equation (3).
where the
represents the temperature of the produced fluid at the wellhead in (°C) and
is expressed in (%).
However, in case of power plants different from ORC, meaning other types of conversion plants, the thermal exchanged cycle between the two fluids, one circulating in the primary cycle (geofluid) and other circulating in the secondary circle (working fluid), can be assessed using the Carnot’s ideal efficiency. In those cases, the expected theoretical maximum efficiency of conversion,
expressed in (%), is evaluated using the Equation (4) as according to Reference [
33].
and it depends on the geological site features (the
part, where
in (K) is the outlet temperature from the borehole at the wellhead), technology and environment features (the
part, where
in (K) is the inlet temperature at the wellhead). The performance is valued as shown in
Table 3. Depending on the end-user option the Equations (3) or (4) are used for assessment of the selected site.
3.4. Fourth Criterion: Geothermal Gradient,
When setting the starting point of the geothermal plant feasibility analysis the geological factors should be considered. The efficiency of the heat transfer through the wellbore is highly dependent on the reservoir’s initial temperature, which is a function of the well depth. Also, high thermal conductivity is required, so that the heat stored in the rocks could be transferred to the wellbore fluid. According to Reference [
34], these two influencing factors could be collectively combined and represented with geothermal gradient,
(°C/100 m). The paper also suggested a range of geothermal gradient based on measured gradients for several analyzed oil fields across the world, which was taken for evaluating the performance
in the geothermal gradient criterion (
Table 4).
3.5. Fifth Criterion: The Fluid Temperature at Wellhead,
According to Reference [
31] the outlet temperature of the fluid from the wellhead is one of the main features of the geological site. It later determines installed power, technology, efficiency, revenues, and costs. Namely, this criterion has been defined to emphasize the relevance of this temperature, since it has a great impact on the conversion cycle in the power plant. The higher the fluid temperature at the wellhead, the higher the amount of the heat that can potentially be transferred to the secondary working fluid (depending of course on the heat exchanger technology). Performance
of option on 5th criterion increases linearly depending on fluid temperature,
(
Table 5). Here, the focus is on the utilization of temperatures from 60 °C to 160 °C (although upper bound for analyzed geo sites in the scope of this research is expected to be 90 °C) for cases of smart ORC units. This approach is adapted and modified from the work [
31].
3.6. Sixth Criterion: Global Efficiency,
Aside from the geological setting and wellbore conditions, the supply of heat or/and electricity is directly related to the performance of the plant energy conversion. Therefore, a global efficiency criterion should be established to evaluate the multi-stage heat (energy) loss within the energy conversion cycle and the impact of the ambient temperature on stored heat (
Table 6). According to Reference [
33] the total heat loss is addressed by means of coefficients of the different stages of the conversion cycle resulting in an overall evaluation for plant conversion. Equations (5)–(7) defines those coefficients, where Equation (5) represents the heat loss due to Non-Condensable Gases (NCG), where
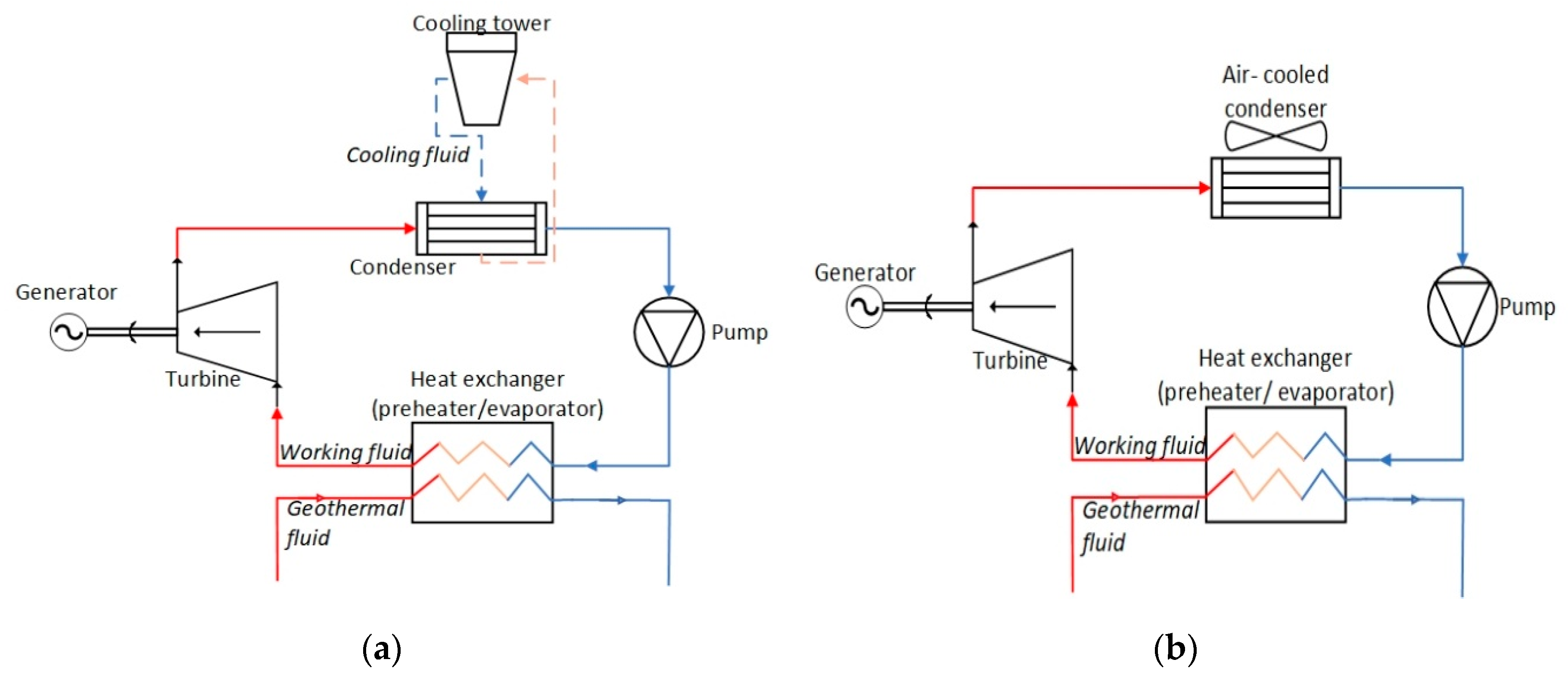
[%] is the estimates of NCG weight, because the presence of NCG can negatively impact the operation of the plant turbine. The Equation (6) represents the parasitic load heat loss, including well pumps, cooling tower, condenser, where
is total parasitic load and
gross thermal power. Moreover, Equation (7) defines the parasitic loss during the working fluid transport where the
is the pipe length in km.
Overall plant efficiency is then calculated according to the Equations (8)–(10), where Equation (8) represents evaluation of the electricity generation, Equation (9) is used to evaluate combined heat-electricity production (CHP), where the second heat exchanger is required to exploit the remaining thermal energy of geothermal water into another district heating fluid, and Equation (10) represents the evaluation of direct usage of heat only in DH systems. Moreover, to measure the operational performance of the turbine and the generator efficiency,
and
, respectively, were included.
where
in the equation related to the CHP represents the efficiency of conversion in ORC for electricity production and
is the efficiency of conversion of the remaining heat from the geothermal fluid for direct heat usage.
3.7. Seventh Criterion: Corrosion and Scaling Hazard,
The corrosive or scaling tendency of the geothermal site is evaluated with the Langelier Saturation Index (LSI) (
Table 7). The LSI later determines O&M costs. The less the LSI, the better the performance of the option will be (see Reference [
31]).
3.8. Eighth Criterion: Distance from Power/Heating Grid,
Construction of power lines and substations for plant connection to the grid imposes significant costs and should be addressed accordingly. Therefore, the distance between the geothermal plant production site and the nearest power and/or district heating system connection point must be addressed. Depending on that distance,
(km), the investment costs and also sLCOE vary. Apart from the distance, considering that the grid connection costs are site-specific, there are many other factors that have an impact on the investment costs. Due to the complexity if all the factors were included, the main influencing factor, namely the distance, was taken for the evaluation of the performance
. The range is shown in
Table 8, finishing with the most favored onsite use, i.e., a very small distance between the plant facility and the connection point.
3.9. Ninth Criterion: Load Factor,
Generally, combined heat and electricity production increases the net efficiency of the power plant, which in turn improves power plant economics. This is even more important in the case of geothermal plants, where thermodynamic efficiencies are typically much lower compared to conventional power plants, due to the lower working fluid temperatures. Considering direct-use systems, heat is only supplied to the process, like greenhouse or district heating, when it is needed. As a result, according to Reference [
34], the load factor,
, can vary from 15% to 75% depending on the application. Reference [
34] examined the costs of the delivered heat as a function of a load factor for U.S. climates. Knowing that industrial applications can have a load factor of 0.30 to 0.75, the space heating only application 0.15 to 0.30, aquaculture 0.50 to 0.80 and greenhouses 0.18 to 0.24, the results showed that the high load factor correlates with lower cost of delivered heat and consequently affects the project’s economic feasibility and sLCOE. As for electricity production, the load factor is typically 0.8 and higher. For combined heat and electricity production, the load factor is higher than in the case of only heat production. Based on forenamed results, the range for performance
of alternative is determined and showed in the
Table 9.
3.10. Tenth Criterion: sLCOE,
The average cost of the project over the lifetime will be addressed by the sLCOE (system LCOE, depending on the end-user option) in (€C/MWh) which also accounts for the costs of integration. This sLCOE will be calculated from all the available external data provided from DM and/or internal data from the internal database of the DMS-TOUGE, and according to Equation (13). Performance
of option
i on sLCOE criterion is determined by
ratio in p.u. (ratio of sLCOE of ORC technology in
ith option to the average market price,
, in different forecasts and for different horizons) shown in
Table 10.
3.11. Eleventh Criterion: Social Impact,
According to Reference [
22], the social acceptability is conditioned by the deviation from the regular condition in the area and utility of the affected parties from the project. As geothermal technologies are site-specific (the geology is different all over Europe and knowledge of the local geological setting is essential) and capital-intensive, the needs regarding exploration, resource development, construction, and O&M are covered by the local workforce. According to Reference [
35], the costs of social acceptance could be presented as the external costs of a geothermal project. Depending on the site, type, and size of the project the amount of those external costs range, on the average, 0.5–2% and 1.5–4% of the total construction costs, i.e., approximately 17,000–220,000 € and 265,000–7,040,000 €, for direct use and multi-purpose projects, respectively. Moreover, employment potential could be divided into direct, indirect, and induced employment effect and quantified in terms of full-time jobs/MW (FT) and person × years of construction and manufacturing employment (
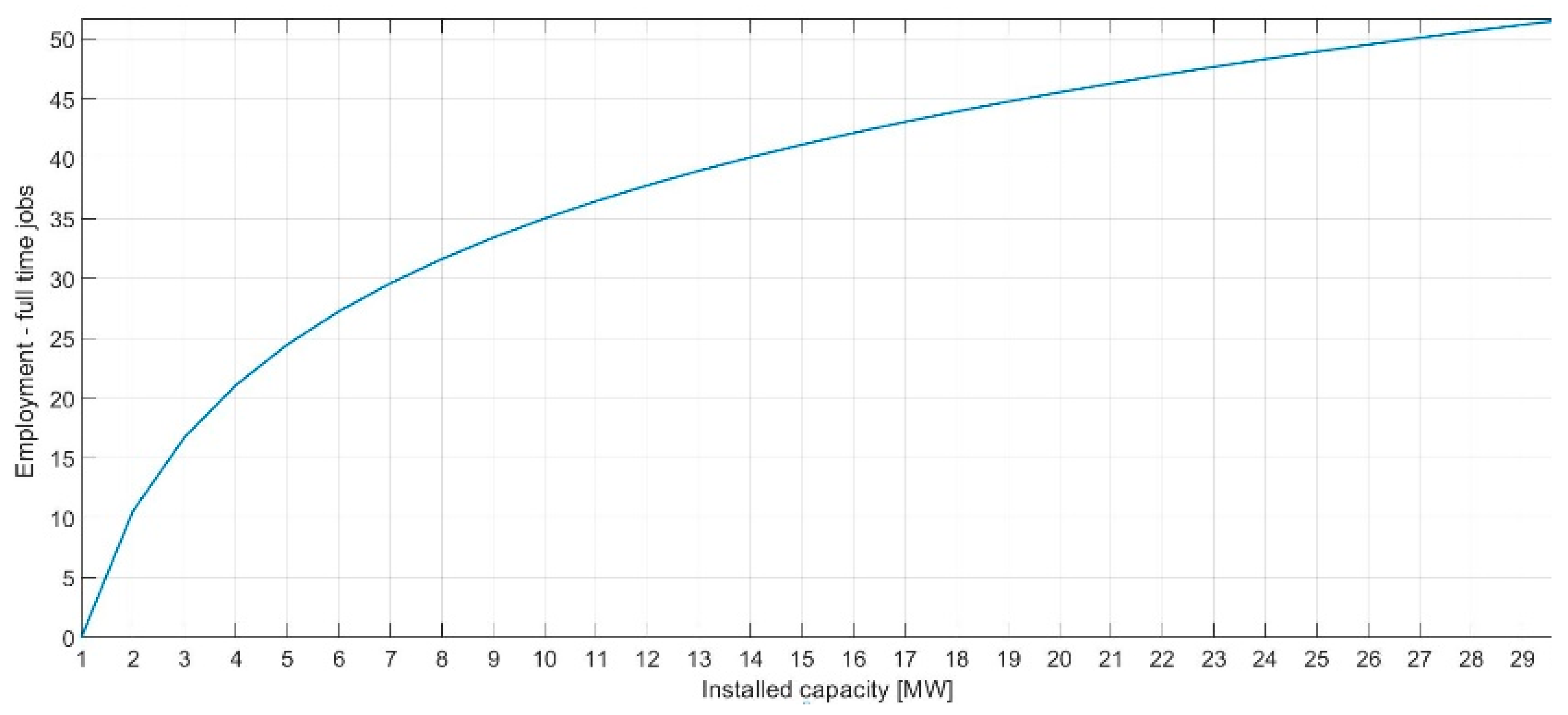
Table 11). Total direct, indirect, and induced employment ratio is a ratio of the installed capacity,
, (MW) and full-time jobs calculated from the Equation (11) (shown in
Figure 6). Equation (12) represents construction and manufacturing employment (C&M), where those jobs are expressed as full-time positions over one year (person × year) as a function of installed capacity,
, (MW). However, those C&M jobs are spread over several years taking into account the development time frame for the new projects. The social impact criterion will be obtained by the average of performances of the following sub-criterions:
social acceptance costs of direct use or electricity production sub-criterion,
social acceptance costs of combined heat-electricity production sub-criterion,
FT employment sub-criterion,
C&M employment sub-criterion. Each sub-criterion will be evaluated with a weight in a range from 1 to 5.
Figure 5 shows the full-time jobs function as a defined in Equation (11).
3.12. Twelfth Criterion: Environmental Impact,
According to Reference [
24], the environmental impact should account for the impact on sustainability, landscape, subsidence, and potentially induced micro-seismicity, and account for the level of noise, atmospheric emissions, potential water contamination, and production of radioactive scaling. The fluid extraction could cause subsidence because of reservoir pressure decline and uplift during borehole drilling activities. This is measured in mm/year of soil decay. Moreover, the pore pressure reduction in production and increase in reinjection operations have been associated with increased induced seismicity, often microseisms of low energy (<2–3 M Richter scale) [
31]. According to Reference [
36] the ranges for this sub-criterion were assigned. The impact on the landscape is measured as land use intensity (LUI) for installed power in m
2/kW, and the range was estimated according to Reference [
37]. The noise impact during routine operation is mainly caused by cooling towers and electrical transformers, and according to Reference [
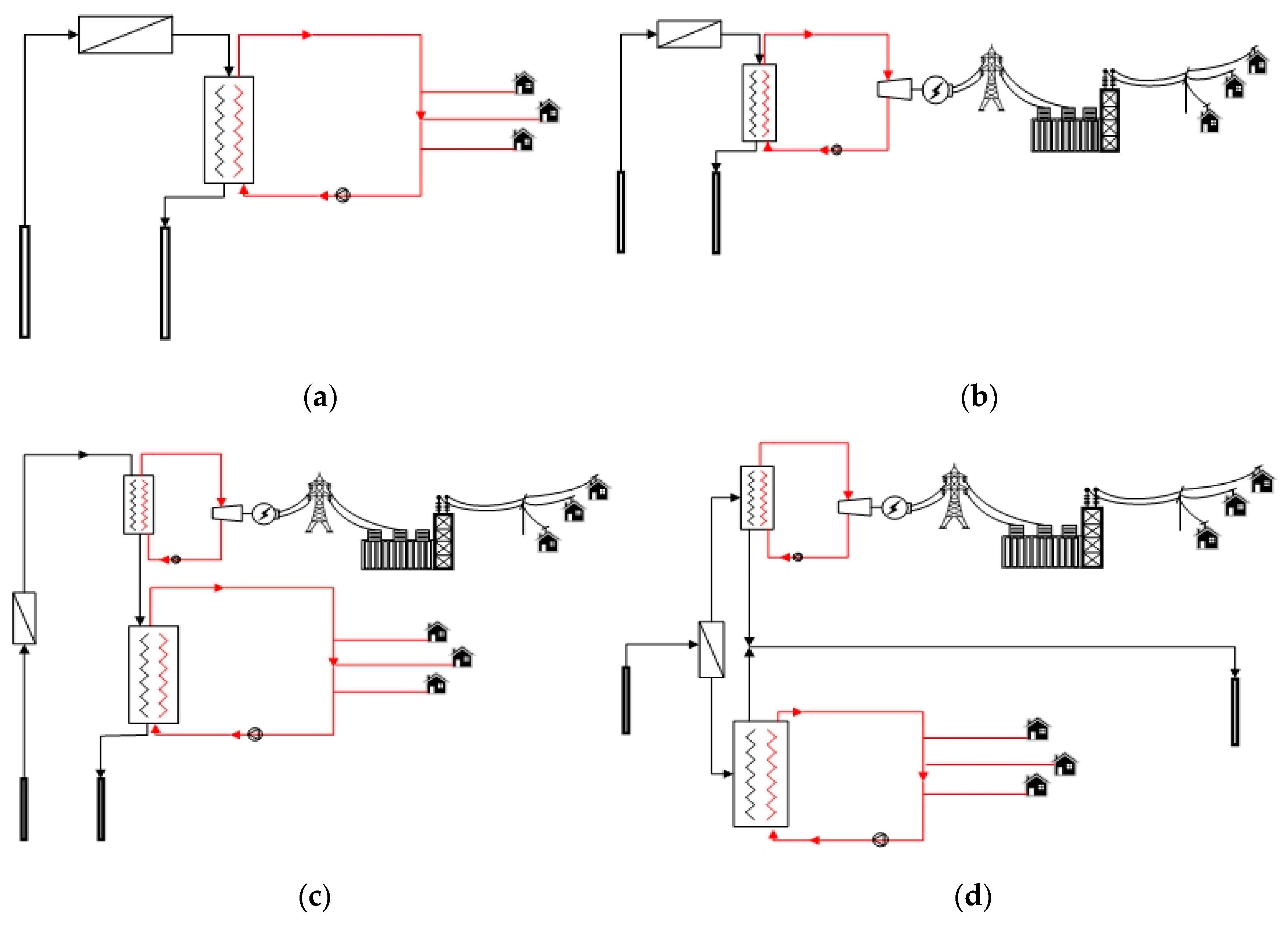
38], typical acceptable levels are 71–83 dB at 900 m distance from the facility. When considering atmospheric emissions, closed cycles, such as binary plants, have no gaseous emissions or they are close to zero and so do not contribute to air pollution. Considering objects of interest in this research (
Figure 3), the impact on surface waters can be excluded. Groundwater contamination may occur if the casings in reinjection wells should fail, allowing fluid to leak. According to WHO, the range of total dissolved solids (TDS) and pH values was determined for the quantification of this sub-criterion. Radioactivity is mainly caused by interaction between the geothermal fluid and certain formations containing radioactive elements. As emphasized in Reference [
39], the content of radionuclides in acidic magmatic rocks is generally higher compared to sedimentary rocks. Furthermore, uranium (U) and thorium (Th) are the most common radioactive elements found in granites. As defined in Reference [
39], different types of rocks can contain different radioelements. Therefore, this sub-criterion is defined with the ranges of the forenamed most common radioactive elements but also taking into account the type of the rock – granitic rocks, shales, basaltic rocks, sandstones, and carbonates - in ascending order of the weights. The environmental impact criterion will be obtained by the average of performances of the following sub-criterions shown in
Table 12:
subsidence sub-criterion,
potential seismicity sub-criterion,
land use sub-criterion,
noise sub-criterion,
potential water contamination sub-criterion, and
radioactivity sub-criterion. Each sub-criterion will be evaluated with a weight in a range from 1 to 5.
5. Conclusions
This paper presents the concept of multi-scale Decision-Making Support Tool for Optimal Usage of Geothermal Energy (DMS-TOUGE) and one of its main features, the multiple-criteria decision-making. These features are used for economic and environmental assessment of enhanced geothermal systems projects. The paper contributes with expanded and detailed criteria related to environmental and social impact giving the necessary emphasis on so far neglected important aspects for successful completion of geothermal projects. Moreover, by combining technical, economic, environmental, and social aspects of geothermal projects, the multiple-criteria decision-making presented in this work gives a comprehensive assessment of enhanced geothermal systems projects. The multiple-criteria decision-making (MCDM) matrix is tested on the case of four operating demonstration geothermal sites where it is used for assessment and comparative analysis. In the application of MCDM matrix, the choice of the weight to assign to the different criterions affects the evaluation of the project. In this work, it is considered that each criterion has equal relative importance in decision making, therefore the weights, , associated with each criterion, are considered identical and are valued with unitary weight. It is, however, important to highlight that the weights assigned to each criterion can vary depending on the DM’s standpoint. Therefore, the results of the final evaluation of the project will vary if a greater weight is assigned to specific criterions according to DM’s assessment. Further steps in tool development are the incorporation of many other relevant decision-making input parameters, not included in the analysis made in this study, testing its capabilities and subsequent verification and validation of the tool. Its proper function is of key importance for work packages and several deliverables of H2020 project such as generation of several layers for mapping (of the main promising European sites where EGS can or should be implemented in a near future) in different resolutions: EU wide layer, layer considering different geologic features, and pilot site layer. The multi-scale Decision-Making Support Tool for Optimal Usage of Geothermal Energy (DMS-TOUGE) will be fully developed as part of the Horizon 2020 project: Multidisciplinary and multi-context demonstration of EGS exploration and Exploitation Techniques and potentials (MEET, GA No 792037). The developed tool will be useful for the decision makers involved in enhanced geothermal system projects associated with applications to nearly unexploited reservoir types (Variscan orogenic belt). This will provide valuable information to decision makers and investors for assessment of enhanced geothermal systems projects considering site-specific environmental, techno-economic and geological features.