Slurry Flow and Erosion Prediction in a Centrifugal Pump after Long-Term Operation
Abstract
1. Introduction
2. Mathematical Model
2.1. Mathematical Model for Liquid Phase
2.2. Mathematical Model for Particles
3. Numerical Methods
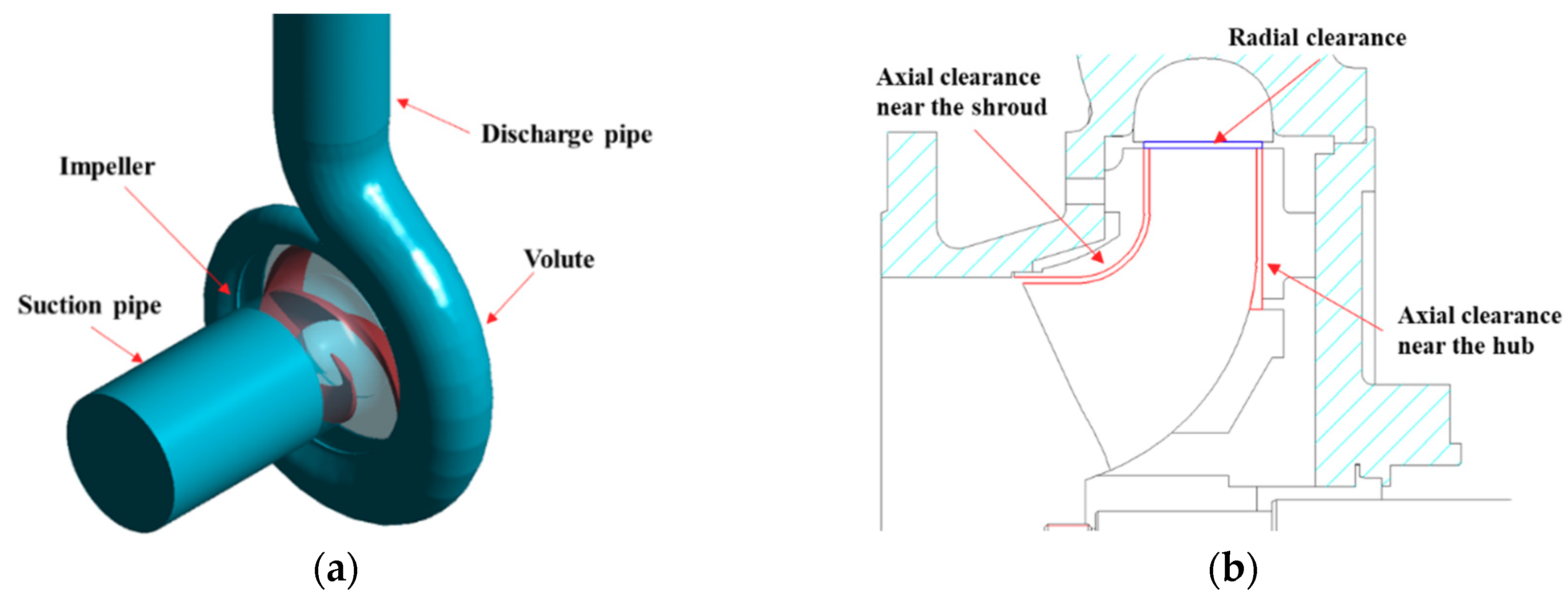
3.1. Pump Model
3.2. Mesh Generation
3.3. Numerical Scheme and Boundary Conditions
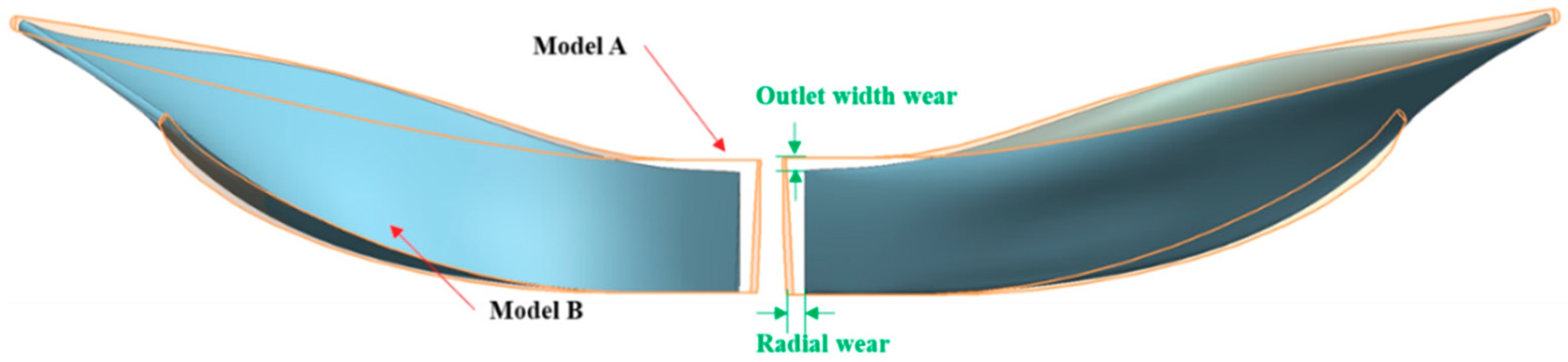
3.4. Numerical Models with Eroded Blades
4. Results and Discussions
4.1. Pump Performances
4.1.1. Pump Performances under Pure Water Conditions
4.1.2. Pump Performance under Two-Phase Conditions
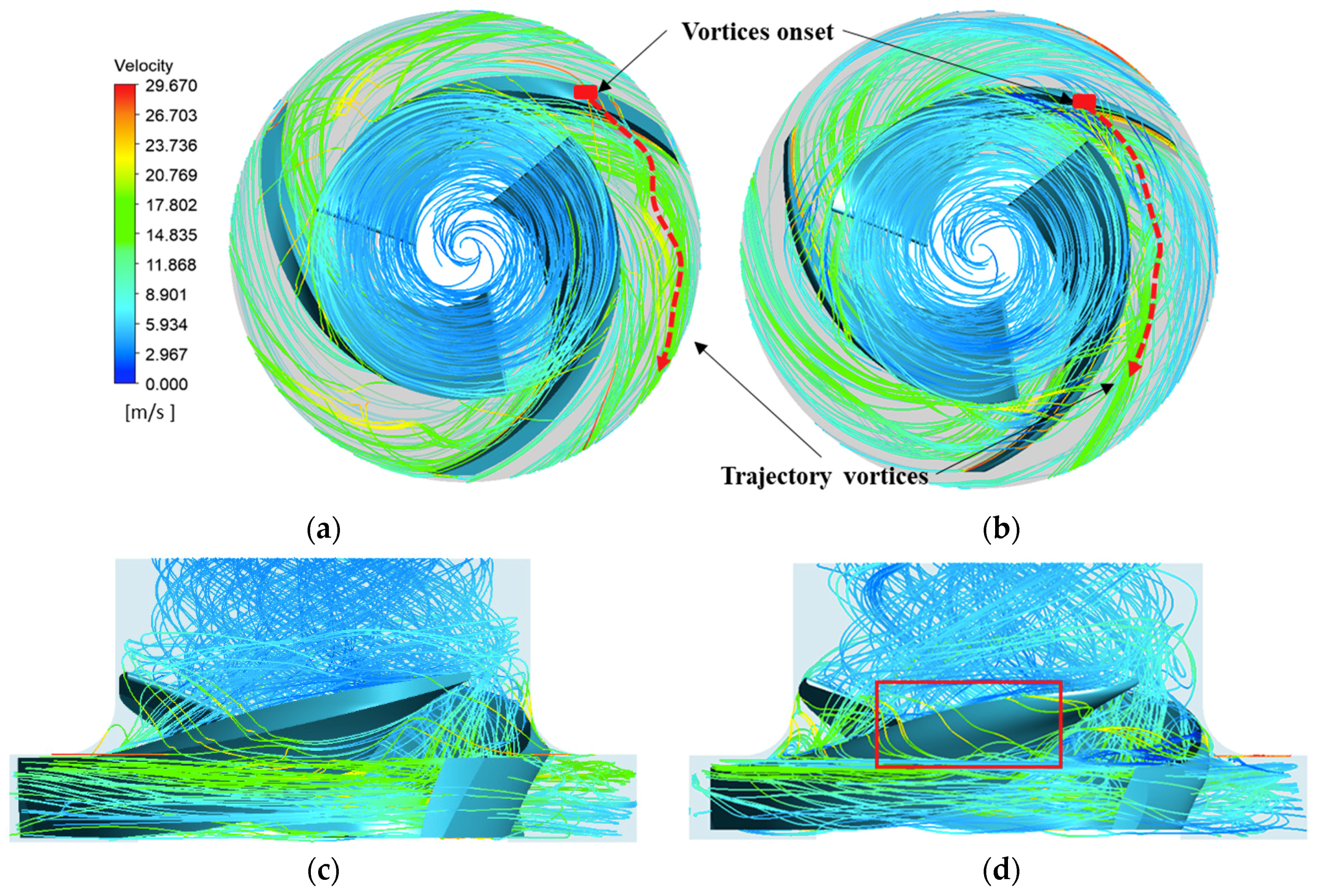
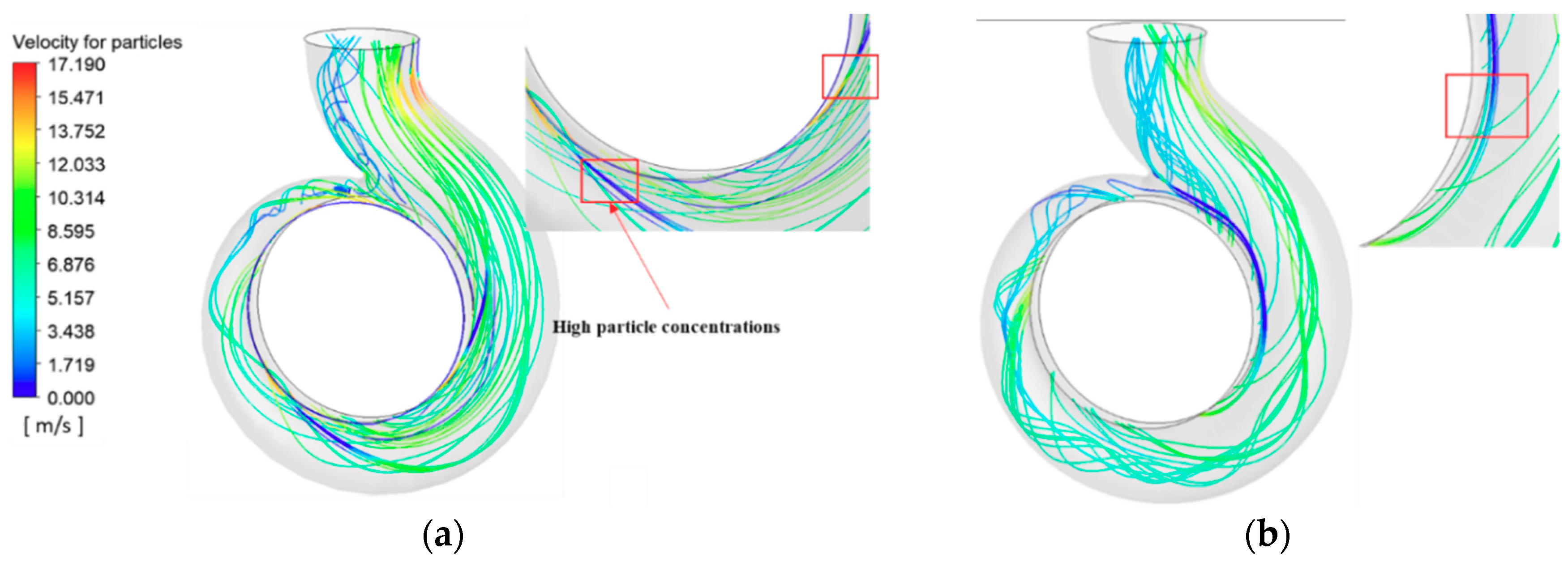
4.2. Particle Trajectories
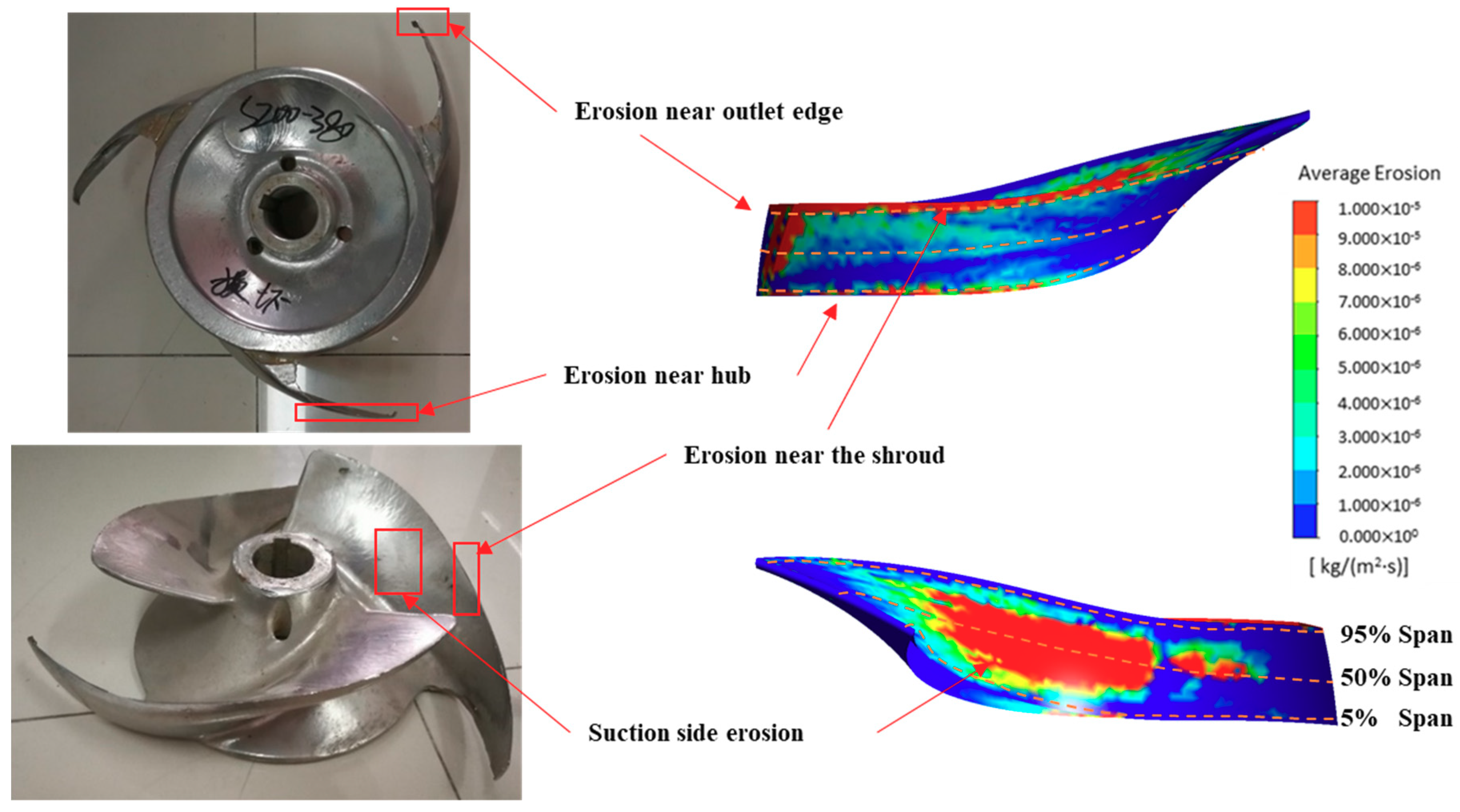
4.3. Erosion Patterns for the Pump
4.3.1. Verification of Numerical Methods
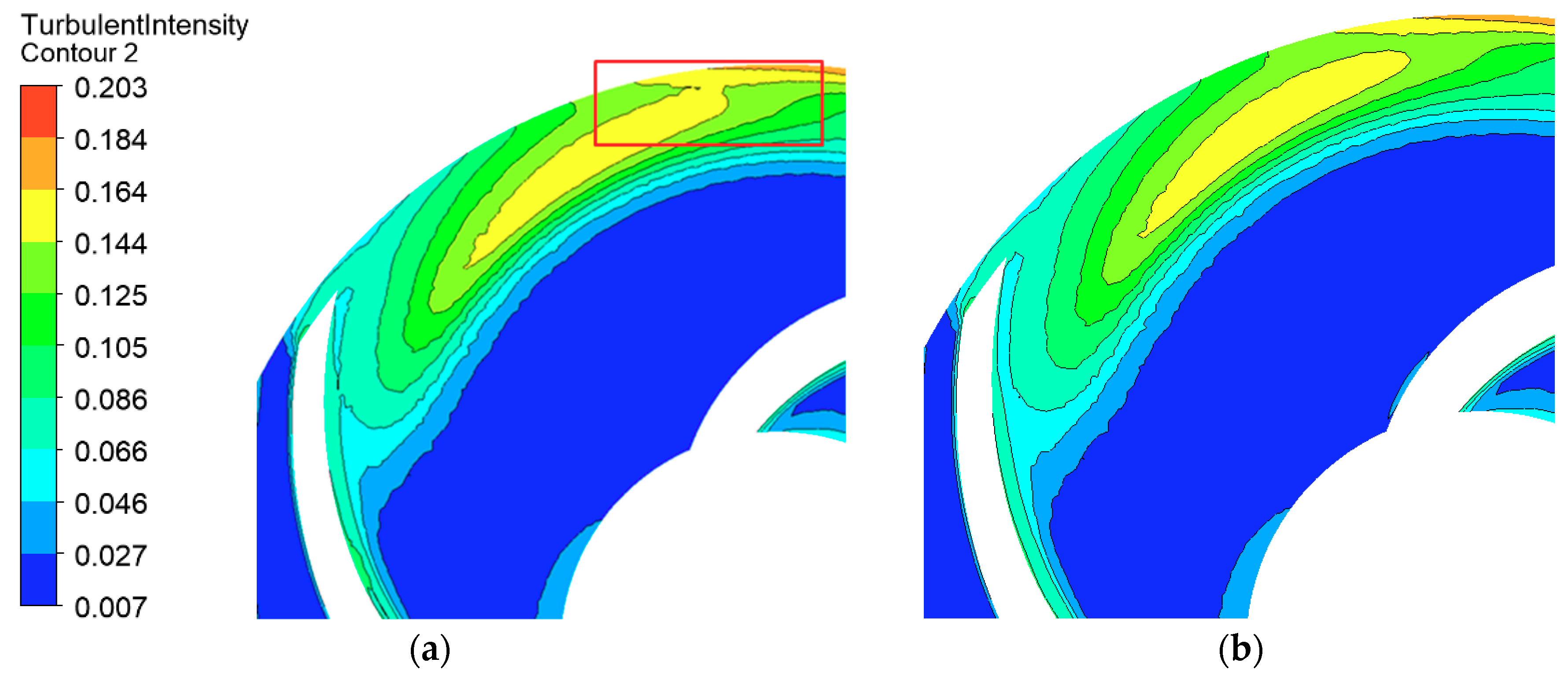
4.3.2. Evolution of Erosion Patterns for the Impeller
4.3.3. Evolution of Erosion Patterns for the Volute
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, X.; Luo, Y.; Wang, Z. A review on fatigue damage mechanism in hydro turbines. Renew. Sustain. Energy Rev. 2016, 54, 1–14. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, Y.; Wang, Z.; Xiao, Y.; Liu, R. Effect of Axial Clearance on the Efficiency of a Shrouded Centrifugal Pump. J. Fluids Eng. 2015, 137, 071101. [Google Scholar]
- Cao, L.; Xiao, Y.; Wang, Z.; Luo, Y.; Zhao, X. Pressure fluctuation characteristics in the sidewall gaps of a centrifugal dredging pump. Eng. Comput. 2017, 34, 1054–1069. [Google Scholar] [CrossRef]
- Ge, J.G.; Li, C.M.; Bao, S.B.; Zhao, W.Y. Vibration analysis of large centrifugal pump rotors. Langenbecks Arch. Surg. 2013, 395, 963–967. [Google Scholar]
- Brennen, C.E. Hydrodynamics of Pumps; Concepts Nrec & Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Hao, Y.; Tan, L. Symmetrical and unsymmetrical tip clearances on cavitation performance and radial force of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 127, 368–376. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, L. Tip clearance on pressure fluctuation intensity and vortex characteristic of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 129, 606–615. [Google Scholar] [CrossRef]
- Pei, J.; Yuan, S.; Benra, F.K.; Dohmen, H.J. Numerical Prediction of Unsteady Pressure Field Within the Whole Flow Passage of a Radial Single-Blade Pump. J. Fluids Eng. 2012, 134, 101103. [Google Scholar] [CrossRef]
- Daily, J.W.; Nece, R.E. Chamber Dimension Effects on Induced Flow and Frictional Resistance of Enclosed Rotating Disks. J. Basic Eng. 1960, 82, 217. [Google Scholar] [CrossRef]
- Zhao, X.; Xiao, Y.; Wang, Z.; Luo, Y.; Cao, L. Unsteady Flow and Pressure Pulsation Characteristics Analysis of Rotating Stall in Centrifugal Pumps under off Design Conditions. J. Fluids Eng. 2017, 140, 021105. [Google Scholar] [CrossRef]
- Araoye, A.A.; Badr, H.M.; Ahmed, W.H.; Habib, M.A.; Alsarkhi, A. Erosion of a multistage orifice due to liquid-solid flow. Wear 2017, 390–391, 270–282. [Google Scholar] [CrossRef]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Grant, G.; Tabakoff, W. Erosion Prediction in Turbomachinery Resulting from Environmental Solid Particles. J. Aircr. 1975, 12, 471–478. [Google Scholar] [CrossRef]
- Oka, Y.I.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact: Part 1: Effects of impact parameters on a predictive equation. Wear 2005, 259, 102–109. [Google Scholar] [CrossRef]
- Chen, X.; Mclaury, B.S.; Shirazi, S.A. Effects of Applying a Stochastic Rebound Model in Erosion Prediction of Elbow and Plugged Tee. In Proceedings of the ASME 2002 Joint U.S.-European Fluids Engineering Division Conference, Mentreal, QC, Canada, 14–18 July 2002; pp. 247–254. [Google Scholar]
- Forder, A.; Thew, M.; Harrison, D. A numerical investigation of solid particle erosion experienced within oilfield control valves. Wear 1998, 216, 184–193. [Google Scholar] [CrossRef]
- Messa, G.V.; Malavasi, S. The effect of sub-models and parameterizations in the simulation of abrasive jet impingement tests. Wear 2017, 370–371, 59–72. [Google Scholar] [CrossRef]
- Zhang, J.; McLaury, B.S.; Shirazi, S.A. Modeling sand fines erosion in elbows mounted in series. Wear 2018, 402–403, 196–206. [Google Scholar] [CrossRef]
- Badr, H.M.; Habib, M.A.; Ben-Mansour, R.; Said, S.A.M.; Al-Anizi, S.S. Erosion in the tube entrance region of an air-cooled heat exchanger. Int. J. Impact Eng. 2006, 32, 1440–1463. [Google Scholar] [CrossRef]
- Nemitallah, M.A.; Ben-Mansour, R.; Habib, M.A.; Ahmed, W.H.; Toor, I.H.; Gasem, Z.M.; Badr, H.M. Solid Particle Erosion Downstream of an Orifice. J. Fluids Eng. 2014, 137, 021302. [Google Scholar] [CrossRef]
- Badr, H.M.; Habib, M.A.; Ben-Mansour, R.; Said, S.A.M. Numerical investigation of erosion threshold velocity in a pipe with sudden contraction. Comput. Fluids 2005, 34, 721–742. [Google Scholar] [CrossRef]
- Habib, M.A.; Ben-Mansour, R.; Badr, H.M.; Kabir, M.E. Erosion and penetration rates of a pipe protruded in a sudden contraction. Comput. Fluids 2008, 37, 146–160. [Google Scholar] [CrossRef]
- Blau, P.J. A multi-stage wear model for grid-to-rod fretting of nuclear fuel rods. Wear 2014, 313, 89–96. [Google Scholar] [CrossRef]
- Blau, P.J. How common is the steady-state? The implications of wear transitions for materials selection and design. Wear 2015, 332–333, 1120–1128. [Google Scholar] [CrossRef]
- Nguyen, V.B.; Nguyen, Q.B.; Liu, Z.G.; Wan, S.; Lim, C.Y.H.; Zhang, Y.W. A combined numerical–experimental study on the effect of surface evolution on the water–sand multiphase flow characteristics and the material erosion behavior. Wear 2014, 319, 96–109. [Google Scholar] [CrossRef]
- Chitrakar, S.; Neopane, H.P.; Dahlhaug, O.G. Study of the simultaneous effects of secondary flow and sediment erosion in Francis turbines. Renew. Energy 2016, 97, 881–891. [Google Scholar] [CrossRef]
- Yuan Zhong, K.M. Measurement of erosion due to particle impingement and numerical prediction of wear in pump casing. Wear 1996, 199, 36–44. [Google Scholar] [CrossRef]
- Noon, A.A.; Kim, M.-H. Erosion wear on centrifugal pump casing due to slurry flow. Wear 2016, 364–365, 103–111. [Google Scholar] [CrossRef]
- Aslam Noon, A.; Kim, M.-H. Erosion wear on Francis turbine components due to sediment flow. Wear 2017, 378–379, 126–135. [Google Scholar] [CrossRef]
- Guangjie, P.; Zhengwei, W.; Yexiang, X.; Yongyao, L. Abrasion predictions for Francis turbines based on liquid–solid two-phase fluid simulations. Eng. Fail. Anal. 2013, 33, 327–335. [Google Scholar] [CrossRef]
- Chongji, Z.; Yexiang, X.; Wei, Z.; Yangyang, Y.; Lei, C.; Zhengwei, W. Pelton turbine Needle erosion prediction based on 3D three- phase flow simulation. Iop Conf. Ser. Earth Environ. Sci. 2014, 22, 052019. [Google Scholar] [CrossRef]
- Messa, G.V.; Mandelli, S.; Malavasi, S. Hydro-abrasive erosion in Pelton turbine injectors: A numerical study. Renew. Energy 2019, 130, 474–488. [Google Scholar] [CrossRef]
- Khanal, K.; Neopane, H.P.; Rai, S.; Thapa, M.; Bhatt, S.; Shrestha, R. A methodology for designing Francis runner blade to find minimum sediment erosion using CFD. Renew. Energy 2016, 87, 307–316. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978; pp. 263–264. [Google Scholar]
- Gosman, A.; Ioannides, E. Aspects of computer simulation of liquid-fuelled combustors. J. Energy 1983, 7, 482–490. [Google Scholar] [CrossRef]
- Gulich, J.F. Effect of reynolds number and surface roughness on the efficiency of centrifugal pumps. J. Fluid Eng. 2003, 125, 670–679. [Google Scholar] [CrossRef]
- Yexiang, X.; Zhengwei, W.; Zongguo, Y.; Mingan, L.; Ming, X.; Dingyou, L. Numerical analysis of unsteady flow under high-head operating conditions in Francis turbine. Eng. Comput. 2010, 27, 365–386. [Google Scholar] [CrossRef]
- Tan, M.; Guo, B.; Liu, H.; Wu, X.; Wang, K. Investigation of radial force and hydraulic performance in a centrifugal pump with different guide vane outlet angle. J. Vibroeng. 2015, 17, 3247–3260. [Google Scholar]
- ANSYS-CFX. ANSYS CFX-Solver Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Shi, B.; Wei, J.; Zhang, Y. A novel experimental facility for measuring internal flow of Solid-liquid two-phase flow in a centrifugal pump by PIV. Int. J. Multiph. Flow 2017, 89, 266–276. [Google Scholar] [CrossRef]
- Rodriguez, C.G.; Egusquiza, E.; Santos, I.F. Frequencies in the Vibration Induced by the Rotor Stator Interaction in a Centrifugal Pump Turbine. J. Fluids Eng. 2007, 129, 1428. [Google Scholar] [CrossRef]








| Parameters | Descriptions |
|---|---|
| Slurry | Pulp and water (5% volume fraction) |
| Slurry density | 75 kg/m3 |
| Particles to fluids density ratio | 0.075 |
| Mean diameter of particles | 0.5 mm |
| Pump material | Stainless steel |
| Model | Description | Radius/mm | Outlet Width/mm | Blade Thickness/mm |
|---|---|---|---|---|
| A | Model with unworn blades | 190 | 50 | 13 |
| B | Model with slightly worn blades | 188 | 42 | 10 |
| Model | Method | Efficiency/% | Head/m | Power/kW |
|---|---|---|---|---|
| Model A | With particle | 73.74 | 21.88 | 55.30 |
| Pure water | 73.56 | 21.59 | 54.98 | |
| Model B | With particle | 57.45 | 11.38 | 36.92 |
| Pure water | 54.01 | 10.89 | 37.77 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Guo, B.; Ahn, S.-H.; Luo, Y.; Wang, Z.; Shi, G.; Li, Y. Slurry Flow and Erosion Prediction in a Centrifugal Pump after Long-Term Operation. Energies 2019, 12, 1523. https://doi.org/10.3390/en12081523
Xiao Y, Guo B, Ahn S-H, Luo Y, Wang Z, Shi G, Li Y. Slurry Flow and Erosion Prediction in a Centrifugal Pump after Long-Term Operation. Energies. 2019; 12(8):1523. https://doi.org/10.3390/en12081523
Chicago/Turabian StyleXiao, Yexiang, Bao Guo, Soo-Hwang Ahn, Yongyao Luo, Zhengwei Wang, Guangtai Shi, and Yanhao Li. 2019. "Slurry Flow and Erosion Prediction in a Centrifugal Pump after Long-Term Operation" Energies 12, no. 8: 1523. https://doi.org/10.3390/en12081523
APA StyleXiao, Y., Guo, B., Ahn, S.-H., Luo, Y., Wang, Z., Shi, G., & Li, Y. (2019). Slurry Flow and Erosion Prediction in a Centrifugal Pump after Long-Term Operation. Energies, 12(8), 1523. https://doi.org/10.3390/en12081523








