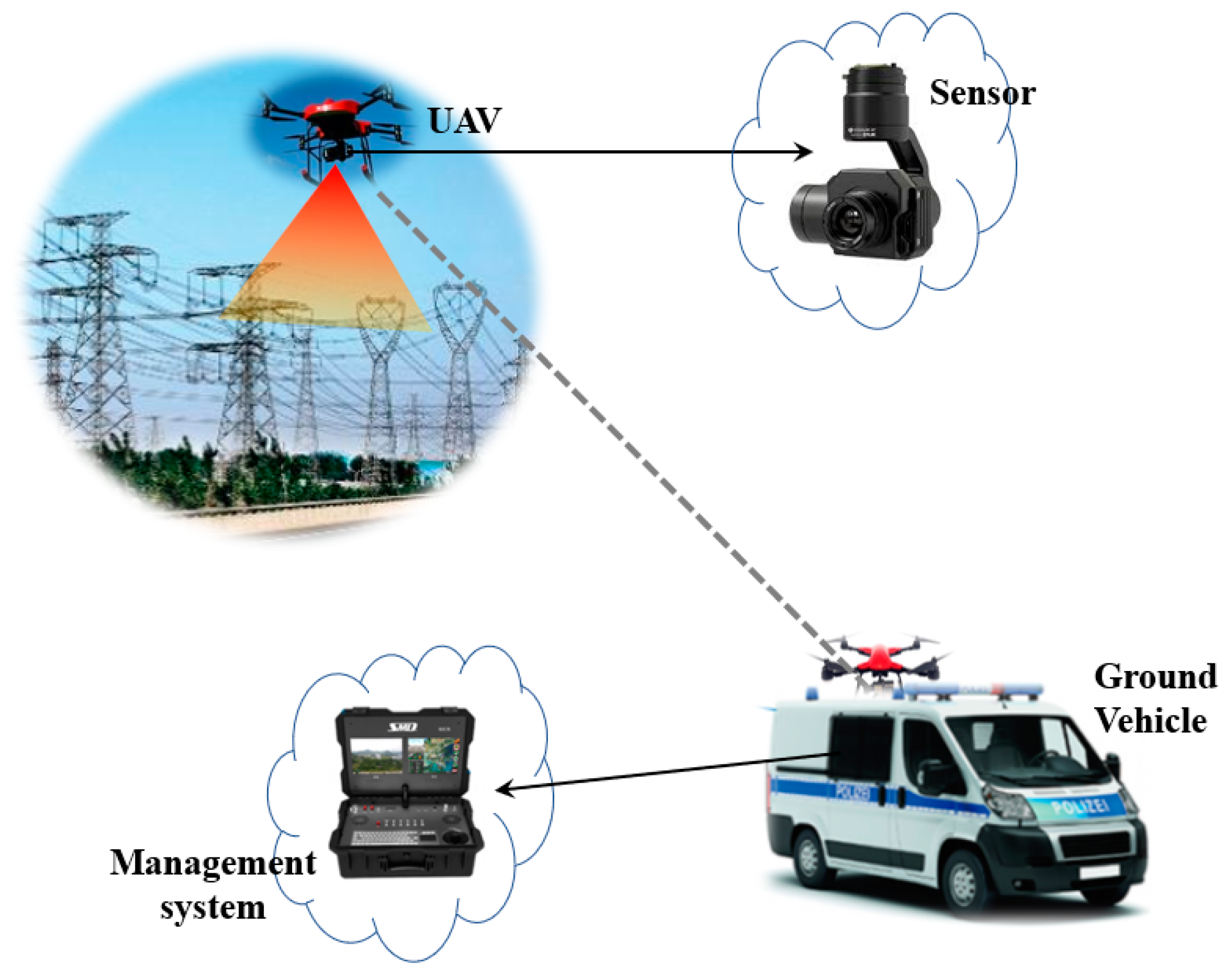
3.1. Problem Description
In the two-layer point-arc routing problem (2L-PA-RP), the vehicle travels on the road network while the drone flies along the transmission line. Ground vehicle can only stop at the predefined parking nodes. The endurance capacity of the drone is limited and known. The problem aims to optimize both drone routes along the powerlines and vehicle routes on the road network, involving the selection of parking locations to minimize the completion time for the whole powerline inspection task.
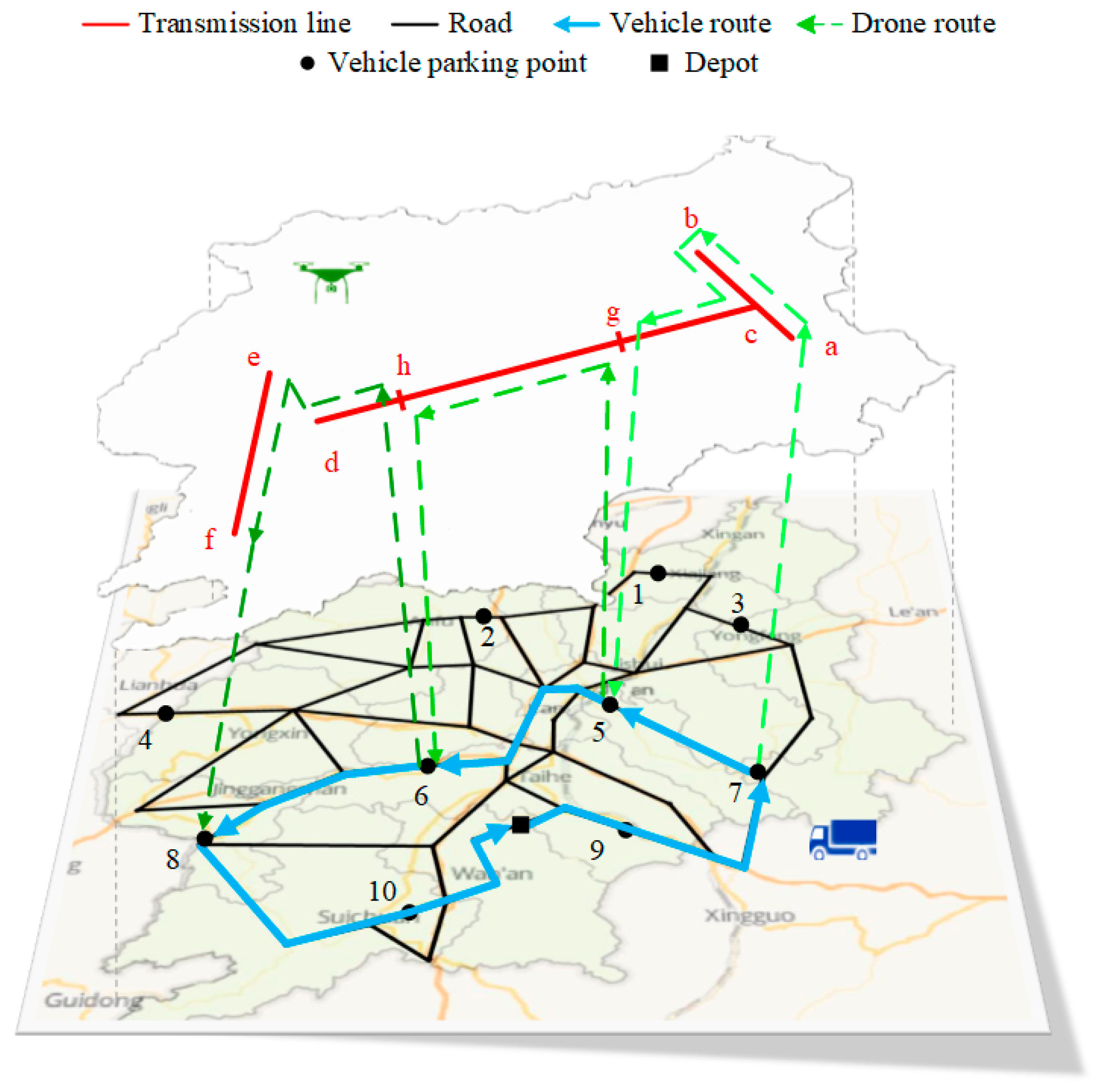
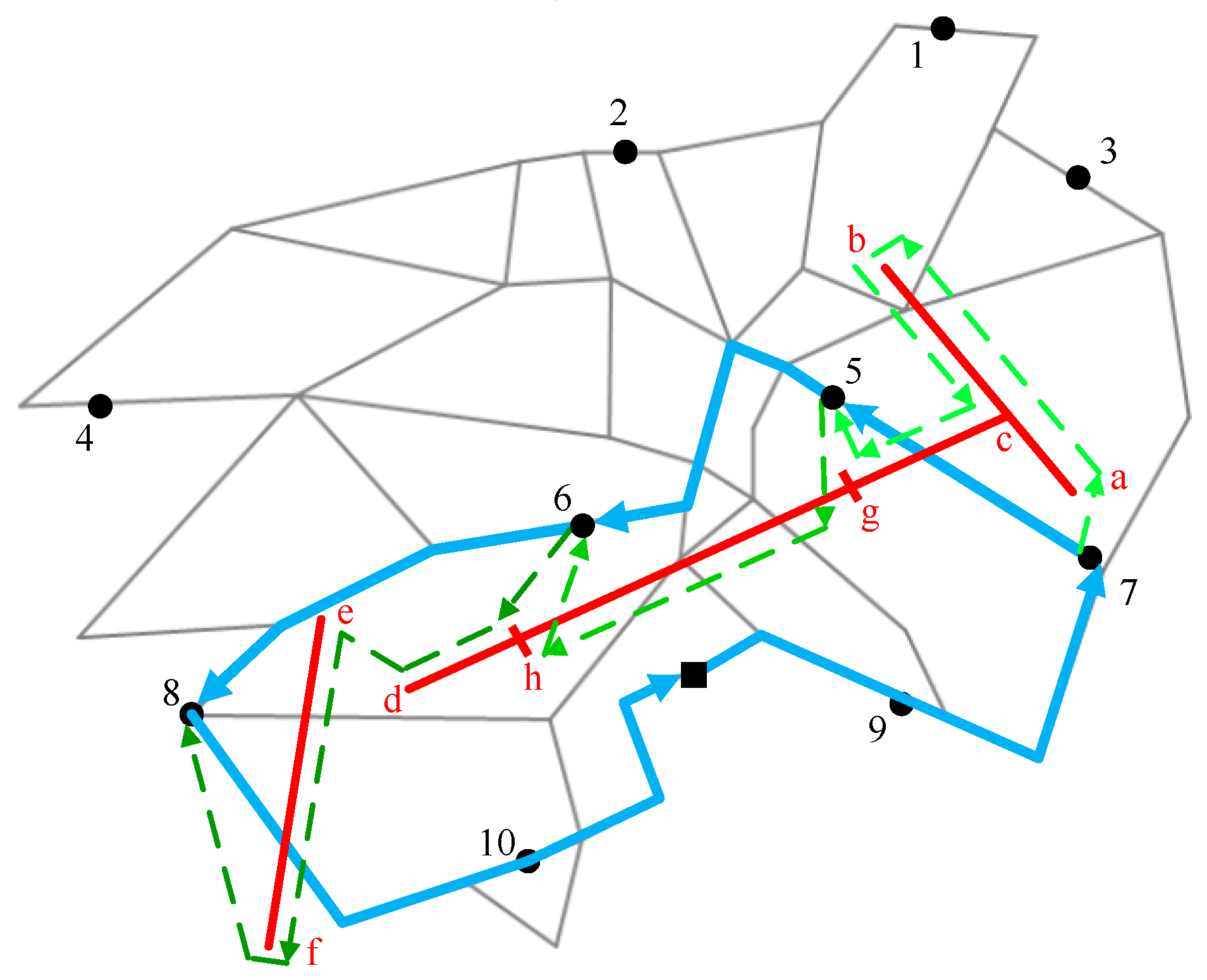
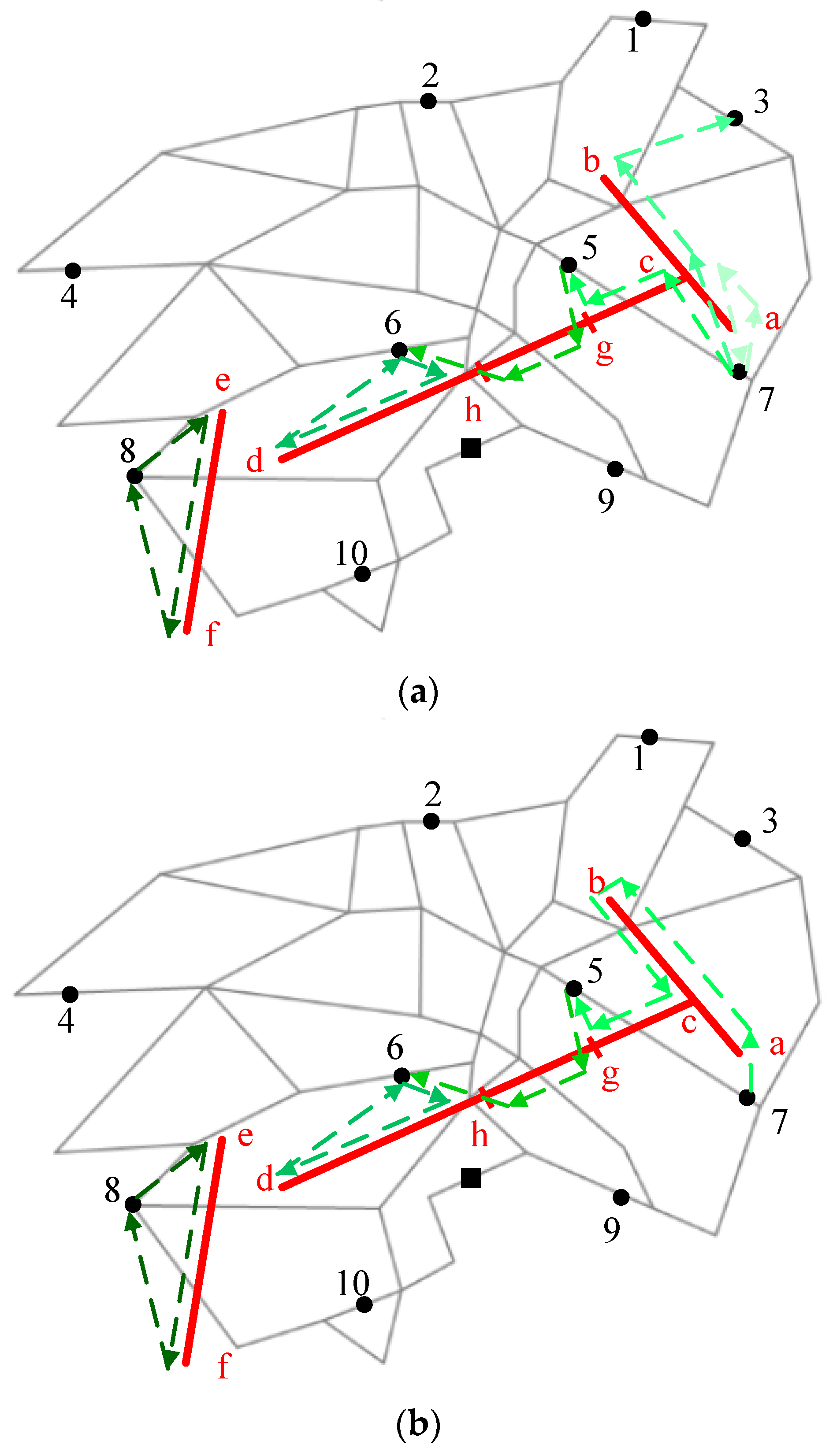
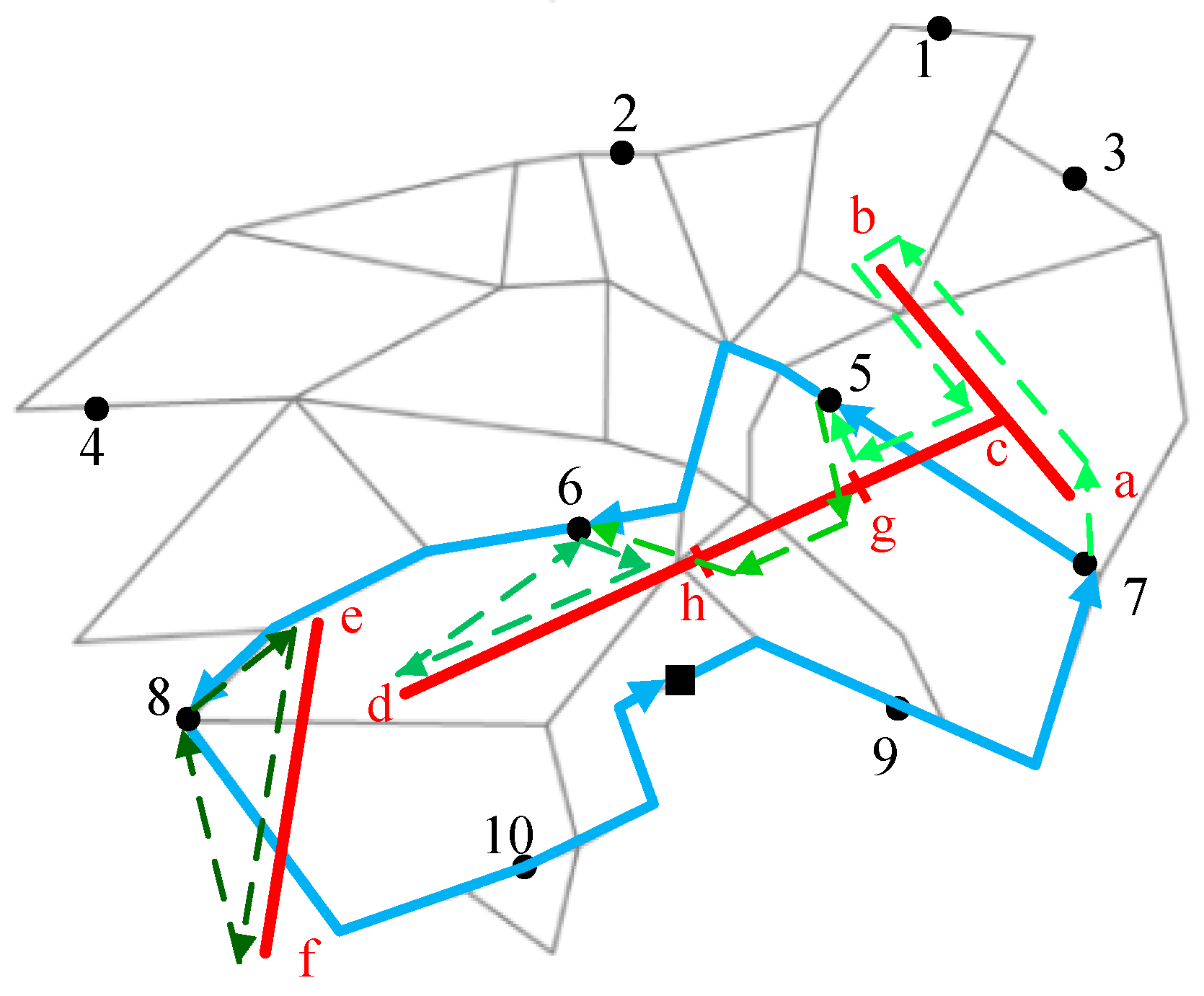
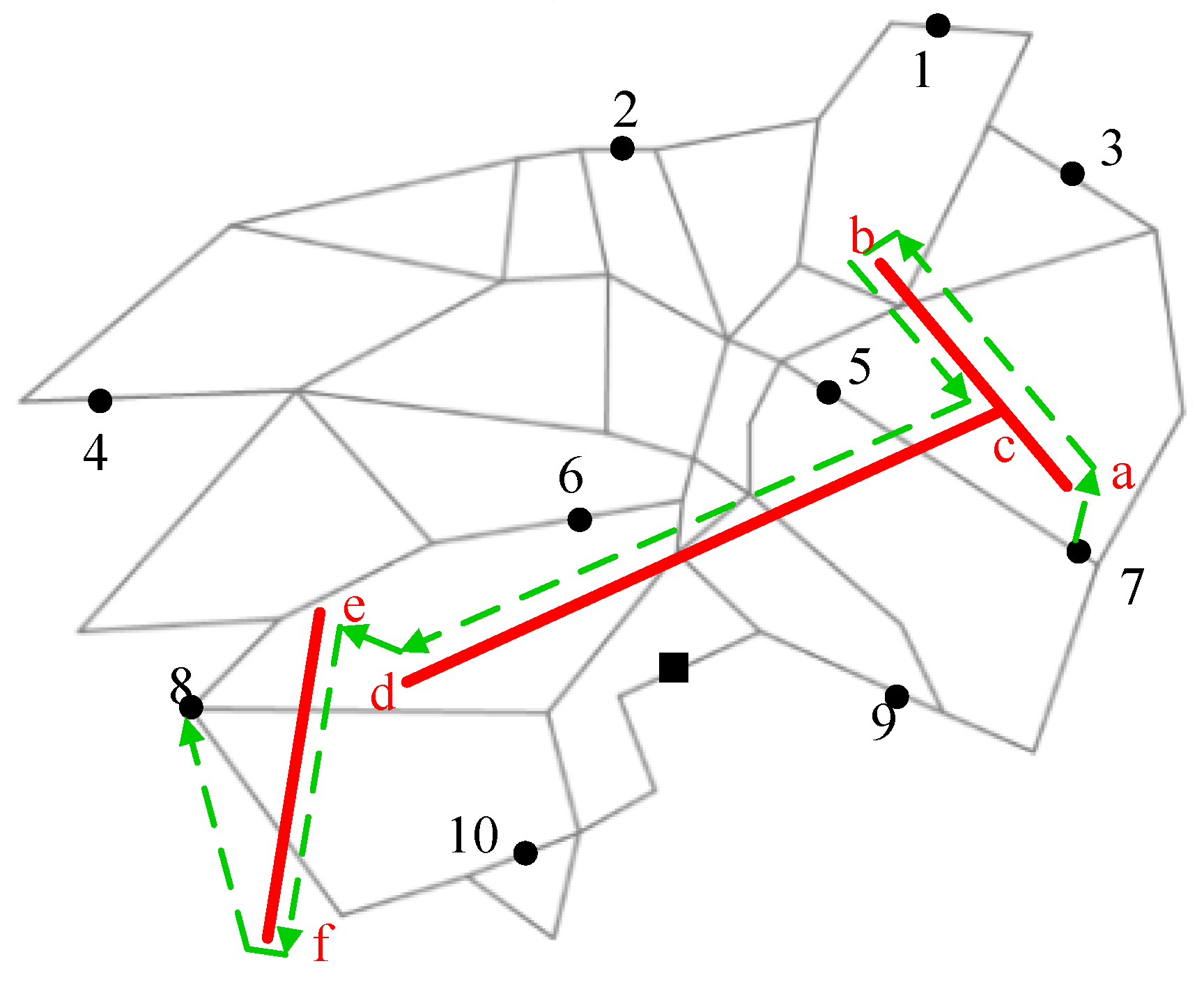
Figure 3 shows the aerial view of the example 2L-PARP in
Figure 2, which contains four powerline arcs (<a,c>, <b,c>, <c,d>, and <e,f>) and 10 potential parking nodes. Arc <e,f> is not connected with other arcs, and this situation appears when different segments represent different-voltage powerlines. The route traveled by the ground vehicle is the lower layer, represented as blue solid lines, whereas the drone routes, depicted as green dashed lines, belong to the upper layer.
More formally, the 2L-PA-RP can be described as follows. Two undirected graphs are defined: GG = (VG, EG) for the road network and GD = (VD, ED) for the powerline network. VG is the set of all parking nodes and VD is the set of all the vertices in the powerline network. EG is the set of edges on the road network while ED contains the edges that can be traveled by the drone.
Specifically, the ground vehicle can travel with the speed of vg only on the edges in EG, which are all located in the lower layer. Each edge eg EG can be represented by < i, j > (i, j VG), and its distance can be calculated as dij1, which is not the Euler distance but the actual travelling distance for the ground vehicle on the road network.
As for the upper layer, let
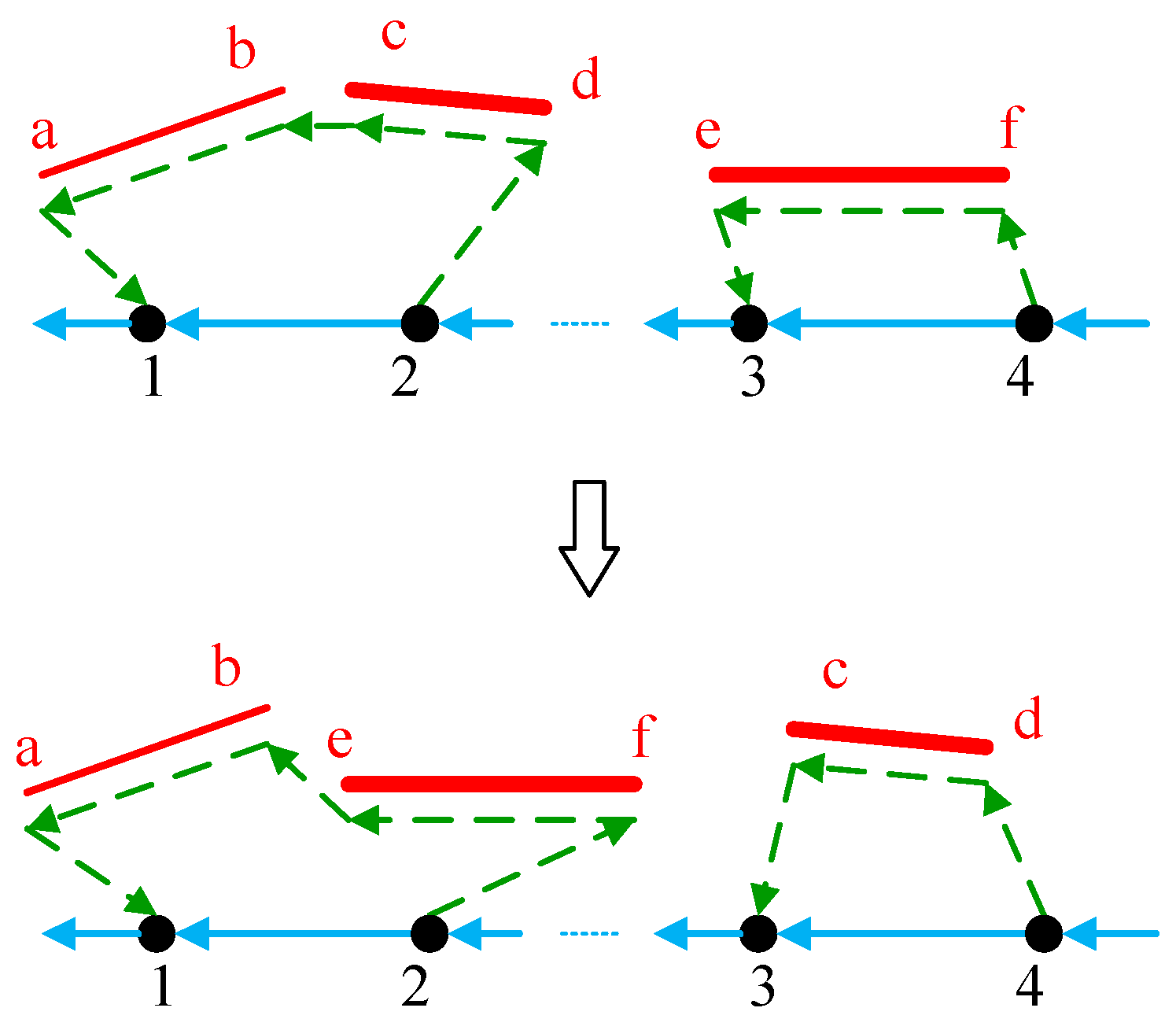
ER ED be the set of edges required to be inspected, which is {<a, c>, <b, c>, <c, d>, <e, f>} in
Figure 3. Represented by <
i,
j > (
i,
j VD), the linear distance of any required edge
er ER can be calculated as
dij2, and the edge is said to be served if and only if the drone traverses the arc for one time. Since the drone can fly into or out of the powerline at any node, each edge
er ER can be served in one flight or several flights. For instance, Edges <a,c> and <b,c> are only included in one drone route while Edge <c,d> is divided into three segments: <c, g> inspected in the first flight, <g,h> inspected in the second flight and <h,d> inspected in the third flight. In one drone route, there are two flight modes, regular flight and inspection flight. The drone can fly quickly from the vehicle to the node on the transmission line (e.g., 7→a) or from one powerline node to another (e.g., b→c), and inspect the powerline with airborne sensors at a slow speed (e.g., a→b). We denote the inspection speed as
vd1 and the regular flight speed as
vd2 (
vd1 ≤
vd2). Besides, the airborne sensors would not work and stay in standby state when the drone is in regular flight. Thus, the power consumption rate of the drone per unit time during inspection, denoted as
p1, is assumed to be higher than that during regular flight,
p2 (
p1 >
p2). The more detailed calculation for the energy consumption process of the drone is presented in
Section 3.2. In addition, since in this problem we utilize the ground vehicle that equips automated systems for launching, recycling and exchanging battery for the drone, it would take only a few seconds for launching, recycling and preparing for the next flight. Thus, compared to the endurance time, over 20 min, the launching and recycling time of the drone can be neglected.
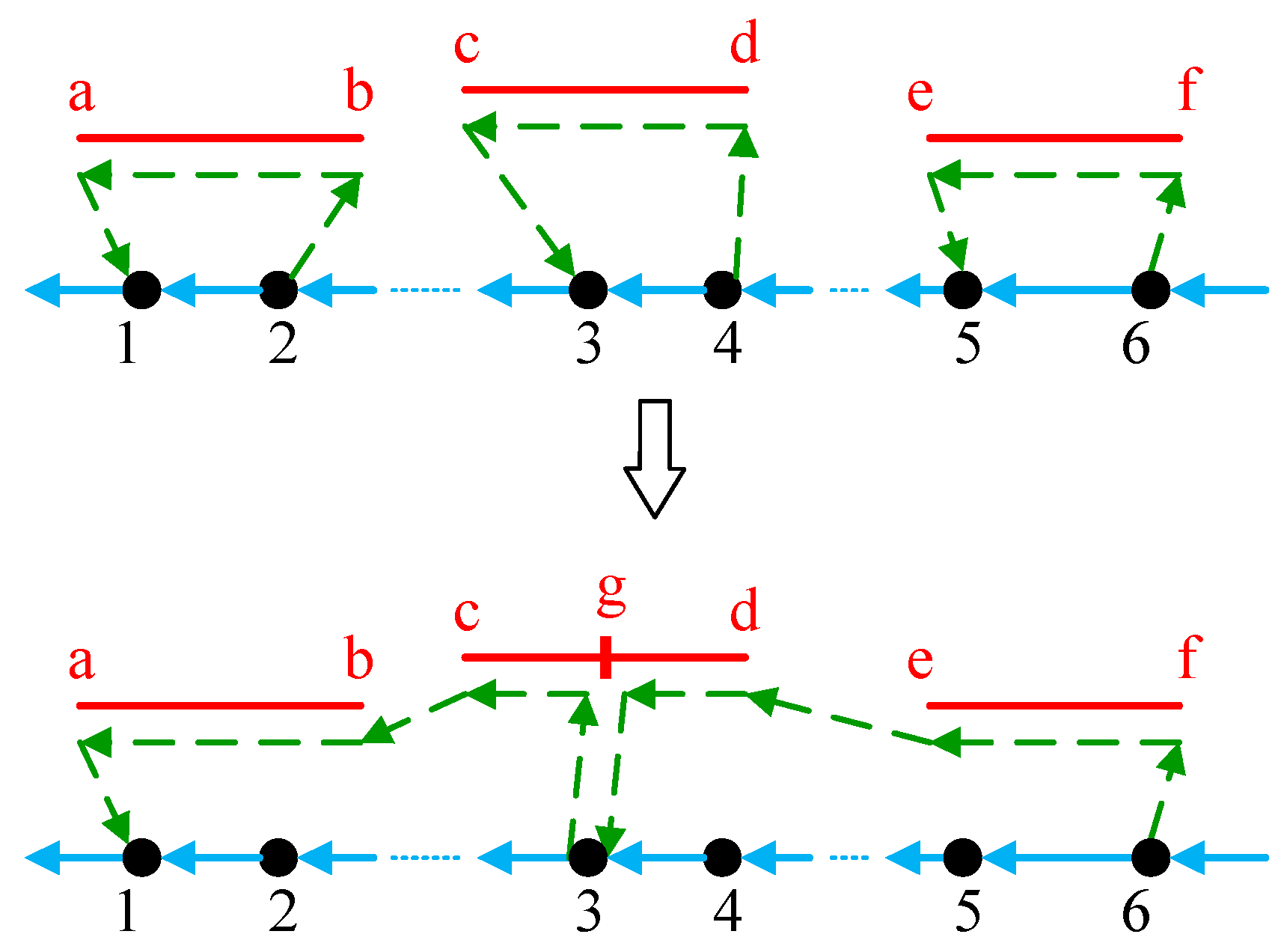
To represent the powerline segments, we introduce a variable
λijm into the edge <
i,
j > (
i,
j VD), representing node
m on the edge, among which
For instance, node g can be described as
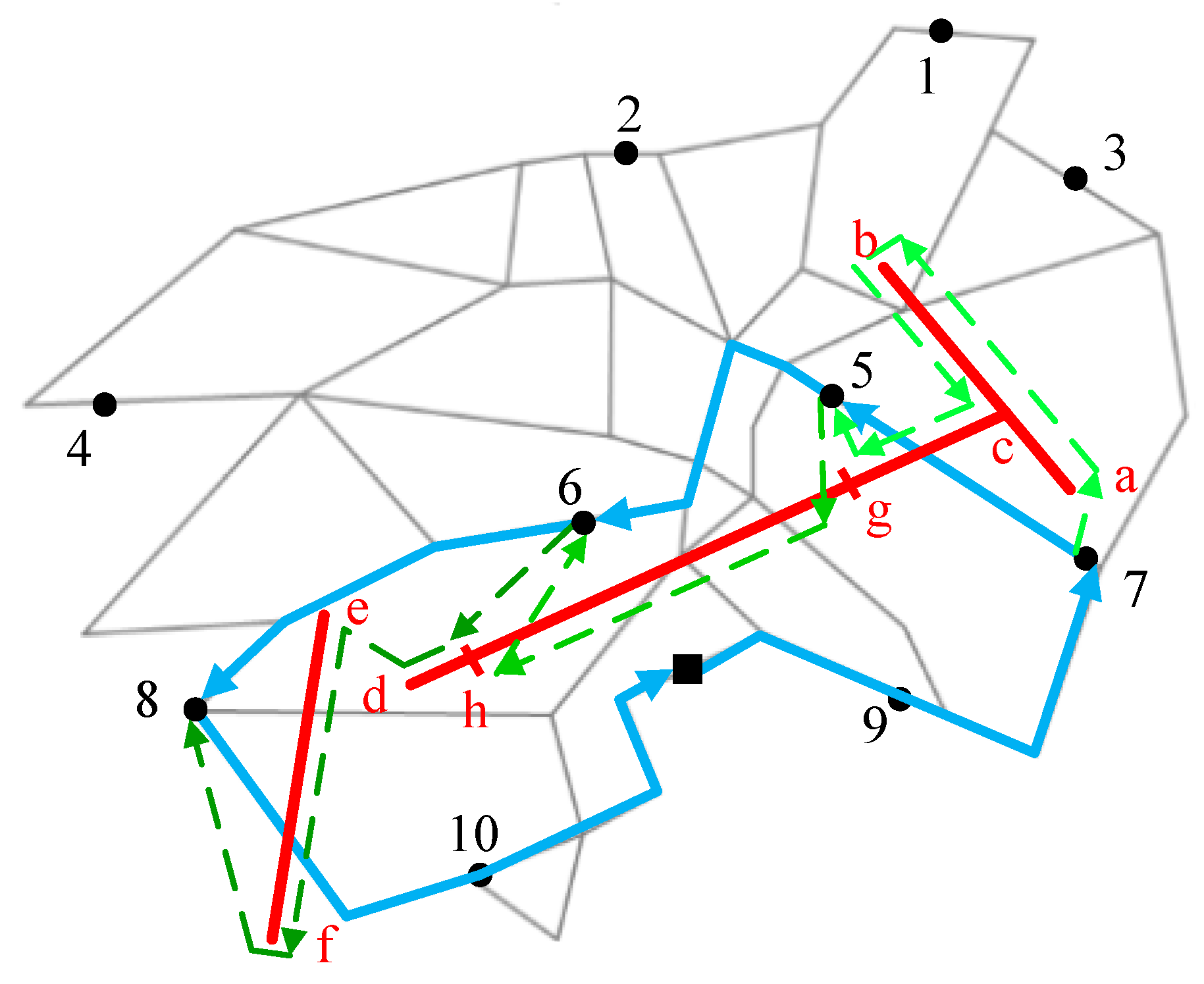
. Thus, each drone flight route can be encoded as an order list
s, in which the first number is the departure road node, the last number is the returning road node, and the middle numbers represent the inspection powerline segments, such as
s1: {7, a, c, b, c, g, 5},
s2:{5, g, h, 6} and
s3:{6, h, e, f, 8} in
Figure 3.
Since the ground vehicle must arrive at the end node before the drone, the drone would spend more time on flight sk than the vehicle on the corresponding road route. Let t1(sk) denote the time that the drone finishes the drone flight sk, which also means the completing time for the sub-solution of sk. In some situations, flight sk is not connected with flight sk+1, and the ground vehicle has to recycle the drone at the end node of sk and carry the drone to the start node of sk+1 to launch it. Let t2(sk, sk+1) denote the time that the vehicle travel from the end node of sub-solution sk to the start node of sub-solution sk+1.
A feasible solution for 2L-PA-RP should satisfy the following constraints:
All the edges of the powerline network must be inspected by the drone, and each edge is visited only once.
The ground vehicle should start at the deport and return to the deport at end.
The ground vehicle has to arrive at the parking node before the drone to recycle it in time.
The drone must return to the truck before its battery is power off.
The route of the ground vehicle must be successive.
Each route of the drone must be successive.
The total time of a feasible solution for completing the inspection task can be calculated as follows.
where
S is the set of all drone’s routes. The objective of 2L-PA-RP is to find the feasible solution that minimizes the time for completing the inspection of the powerline network.
3.2. Energy Consumption Model of the Drone
When the drone flies from the ground vehicle to the transmission line, or from one transmission line to another, the airborne sensors would stay in the standby state, which can save more energy than that during the inspection. In one drone flight, the inspection time is denoted as
t1, and the regular flight time is
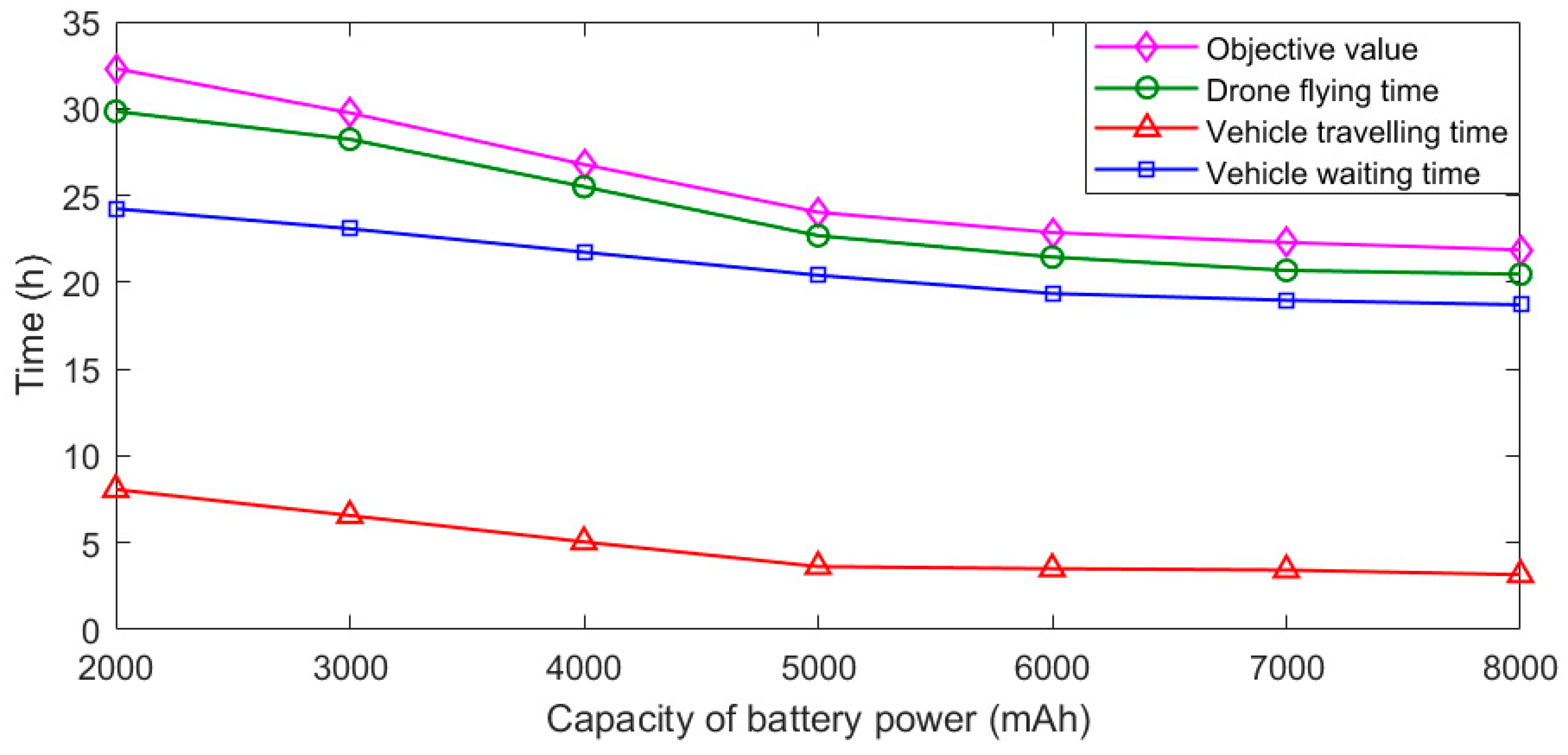
t2. With the maximum capacity of the drone battery,
D, the energy consumption in one drone route must satisfy the constraint:
Since the weight of payload would not be change during the task, we assume that the total weight of the drone with its airborne sensors is
G. The flying speed for powerline inspection is denoted as
vd1 and the flying speed under regular state is denoted as
vd2. According to D’Andrea [
35], the powers power consumption rate of the drone per unit time under different states can be calculated as follows.
where
is the conversion efficiency of the motor,
is the lift ratio,
e is the energy loss of the drone battery, and
ps is the energy consuming rate of the airborne sensors.
Suppose that the drone flies at a constant speed when inspecting the powerline, and let
, which can be calculated with the brand and type of the drone. Similarly, the drone keeps constant speed at the regular flight state. Then, the constraint in Equation (3) can be expressed with inspection distance,
d1, and regular flight distance,
d2, which is