Designing a New Data Intelligence Model for Global Solar Radiation Prediction: Application of Multivariate Modeling Scheme
Abstract
:1. Introduction
2. Methods and Materials
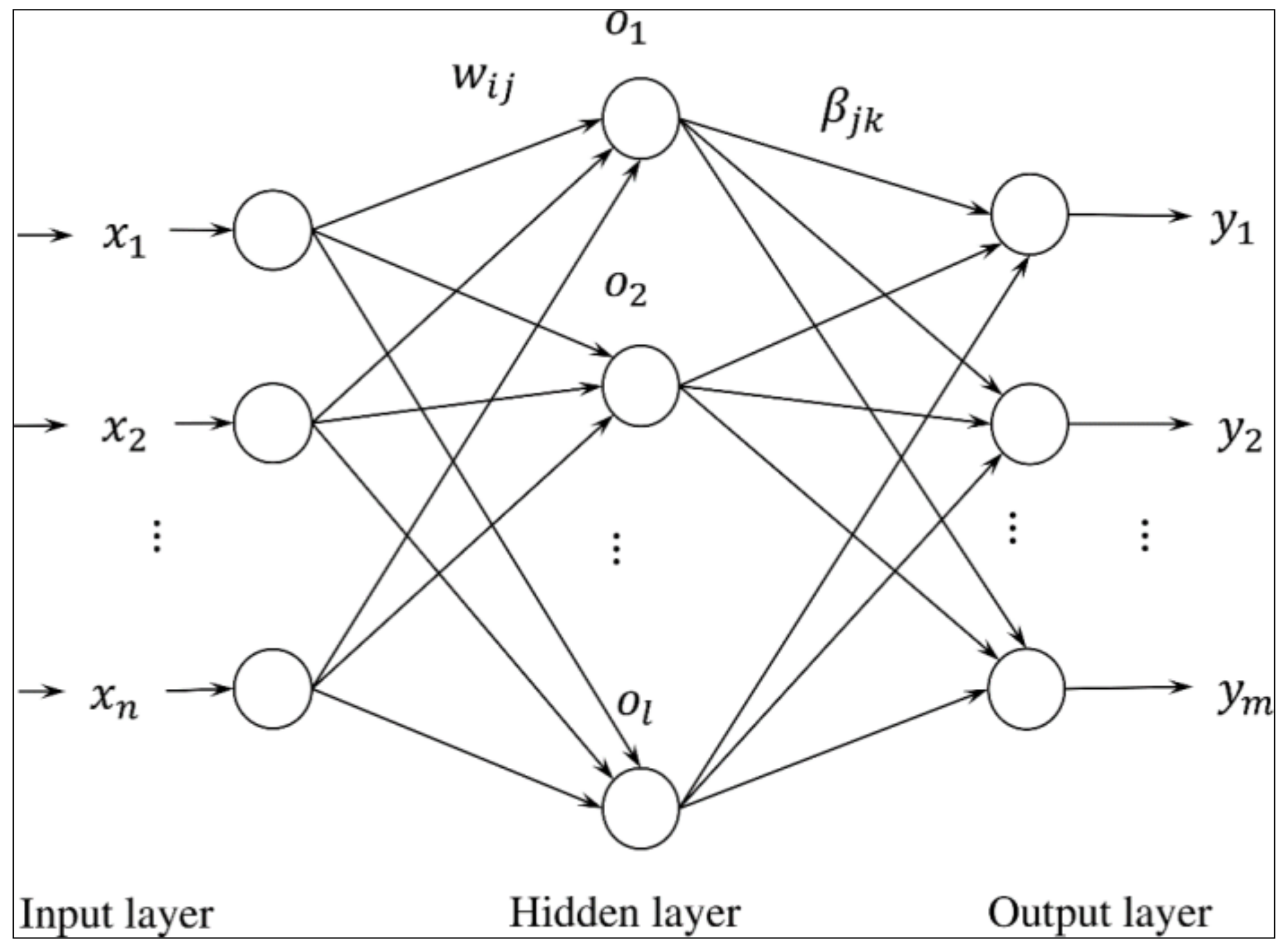
2.1. Self-Adaptive Evolutionary Extreme Learning Machine
2.2. Extreme Learning Machine (ELM)
2.3. Differential Evolution (DE)
- 1.
- Initialization of problem: Number Np parameter vectors are generated randomly through the following equation:
- 2.
- Mutation: There are various mutation strategies [45] that can be applied to produce mutant vector for each individual parameter vector . While there are many mutation strategies, four are utilized here:
- 3.
- Crossover: The crossover procedure is performed on the mutated vectors to increase mutant vectors’ diversity. At generation G, for each mutant vector , a trial vector of is generated using the crossover as follows:
- 4.
- Selection: This is the final step in the DE algorithm that is used to find the individual vectors with minimum error, according to a defined fitness function.
2.4. SaE-ELM Model
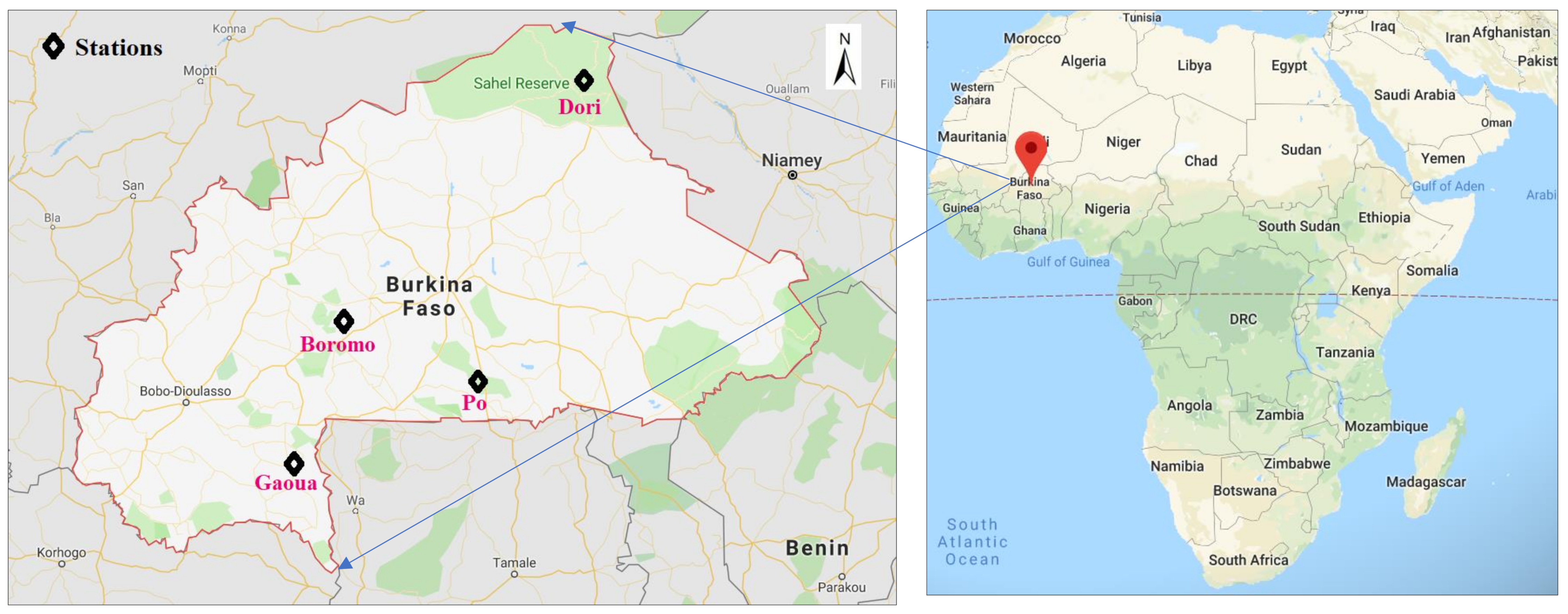
2.5. Case Study and Data Description
3. Application Results and Analysis
3.1. Overall Models Evaluation
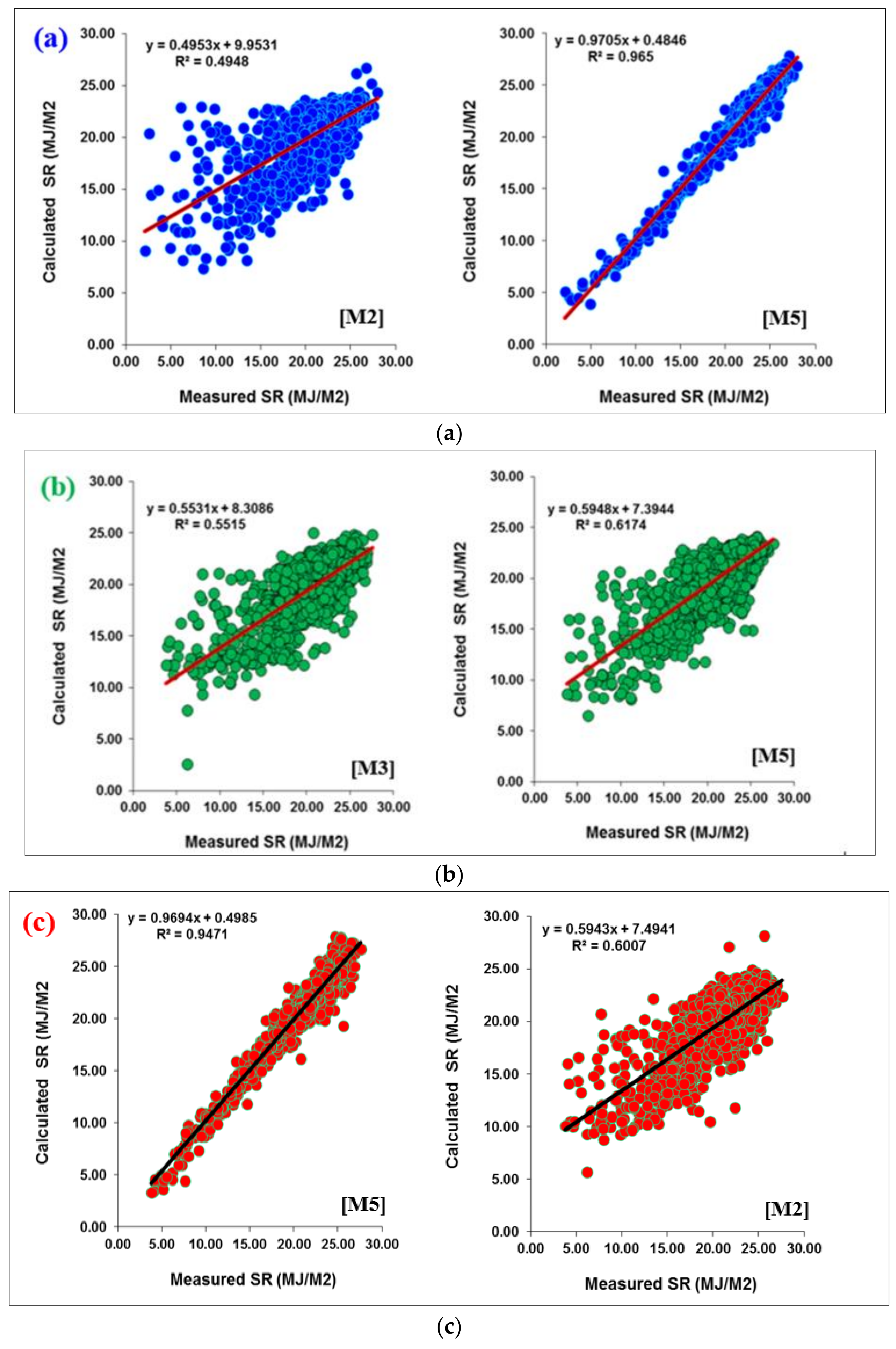
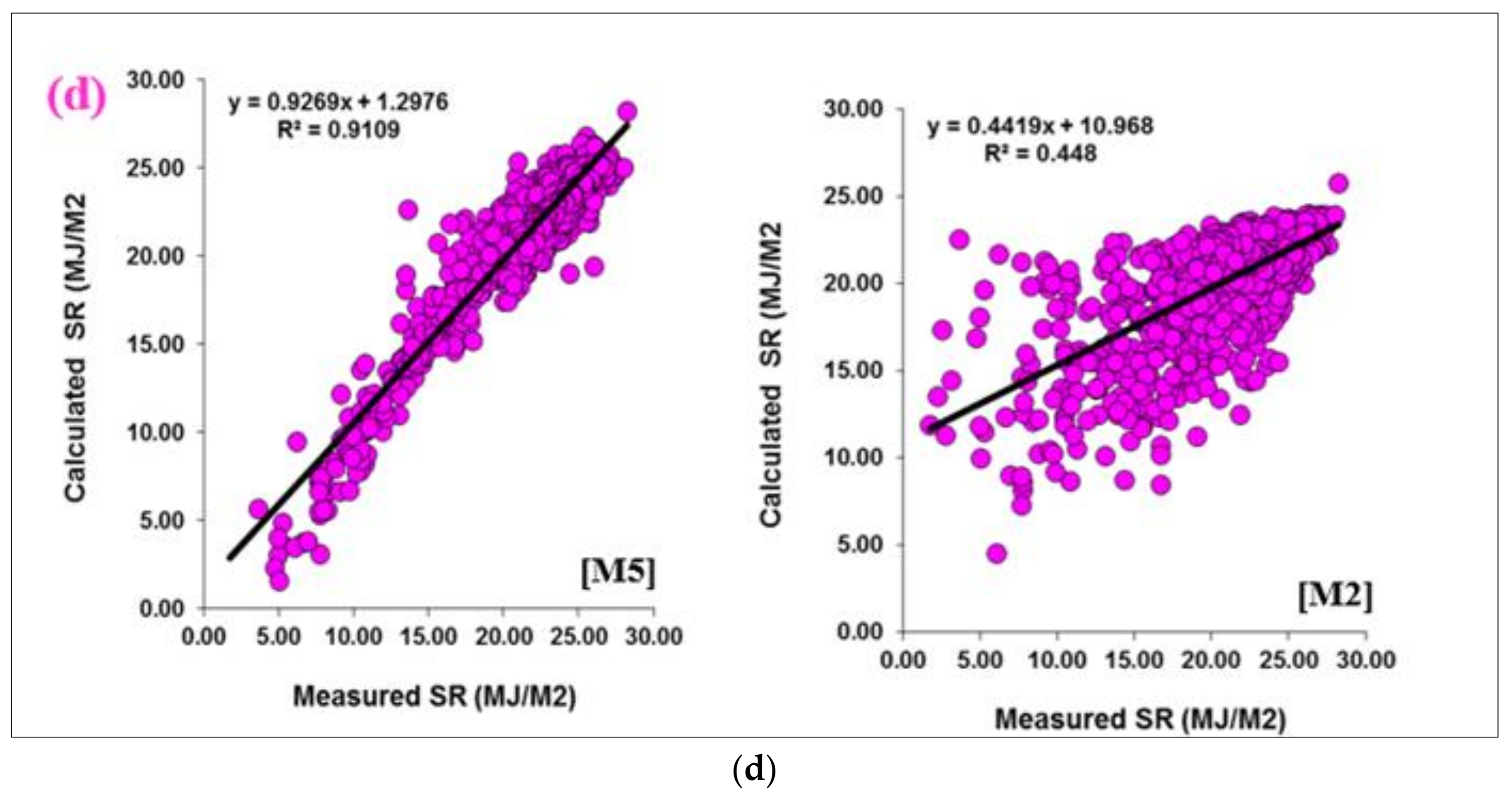
3.2. Model Comparison and Prediction Accuracy
3.3. Usefulness and Assessment of the Developed Models
- (i)
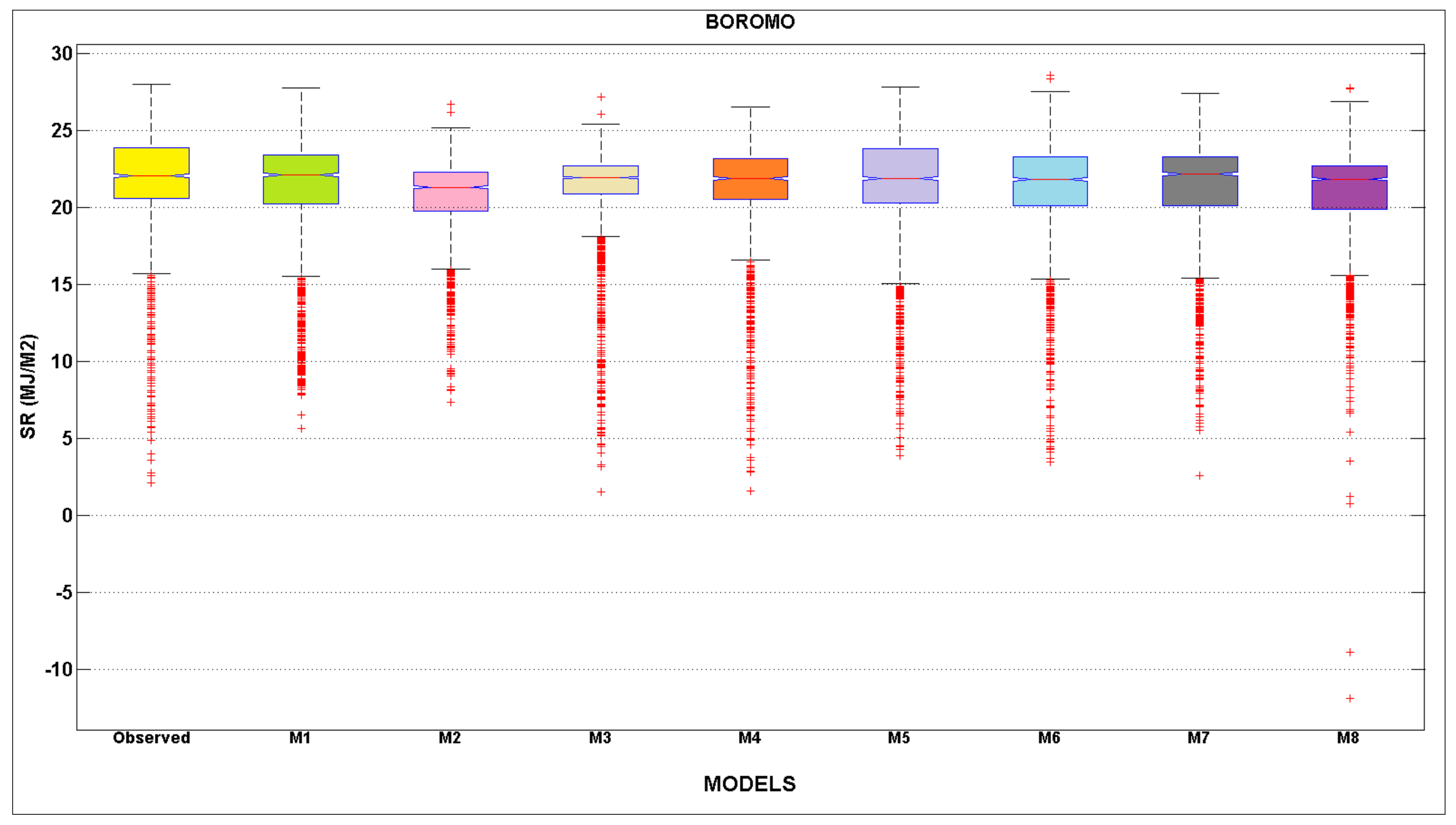
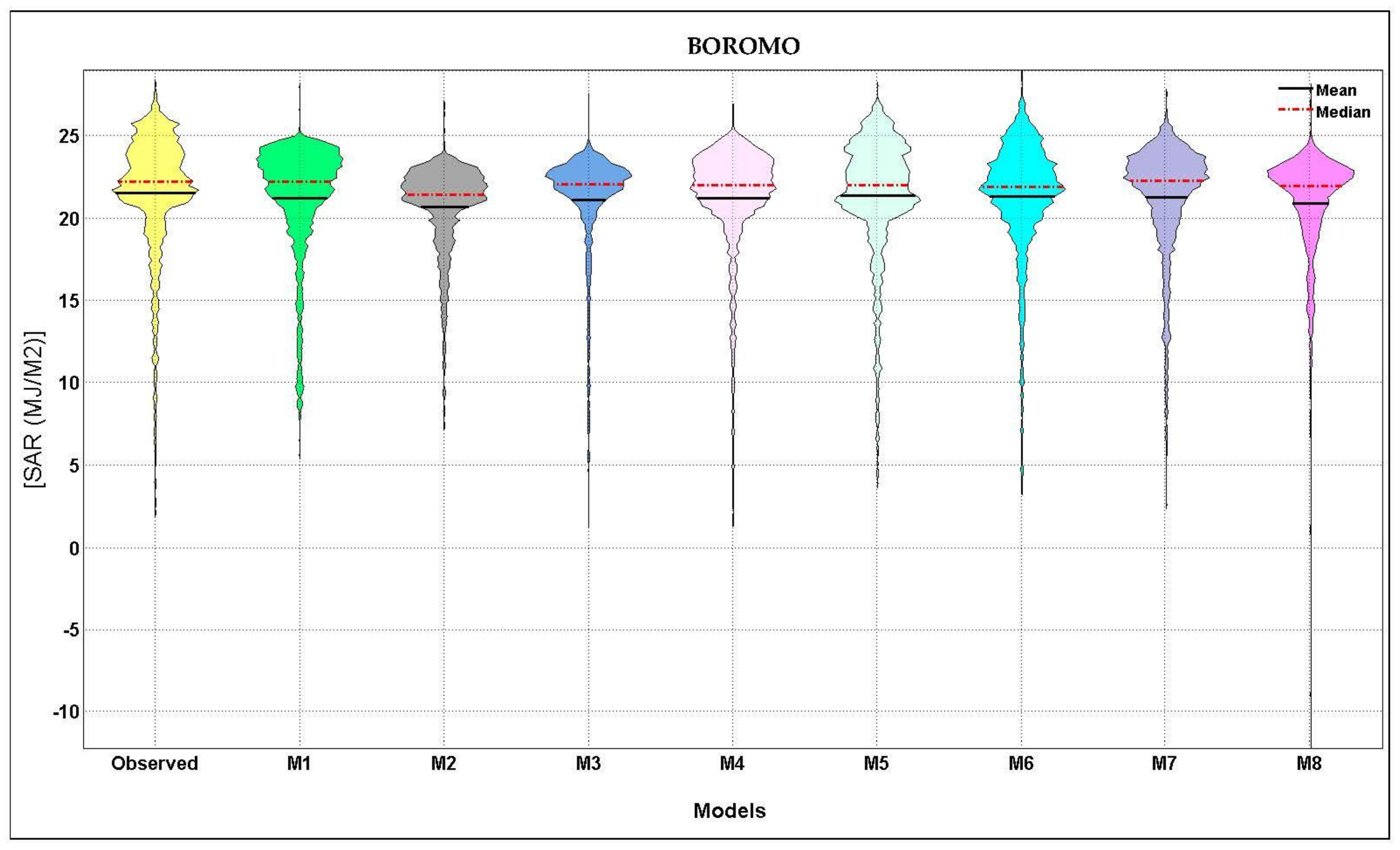
- The statistical indices calculated for the eight models (M1 to M8) show that the accuracy achieved using the M5 model is much higher than that achieved using the all other models with higher R, NSE and VAF values and lower MAE, RMSE and SI values. Specifically, the R, NSE, and VAF computed for M5 model are 0.982, 0.963 and 96.49, respectively. The RMSE, MAE, and SI computed for M5 model are 0.723, 0.544 and 0.034, respectively
- (ii)
- The M5 model has the best prediction accuracy, the M1 model is the second most accurate regarding the R, VAF and MAE indices, and is followed by the M4 and M6 models. However, comparing M1, M4 and M6 models with each other only reveals small and negligible differences in corresponding statistical indices.
3.4. The Modeling Uncertainty Analysis
3.5. Modeling Validation Against the Literature
4. Conclusions
- The integration of the evolutionary algorithm with the self-tuning extreme learning machine model provided a reliable and robust intelligence model for global solar radiation in the Burkina Faso region, West Africa.
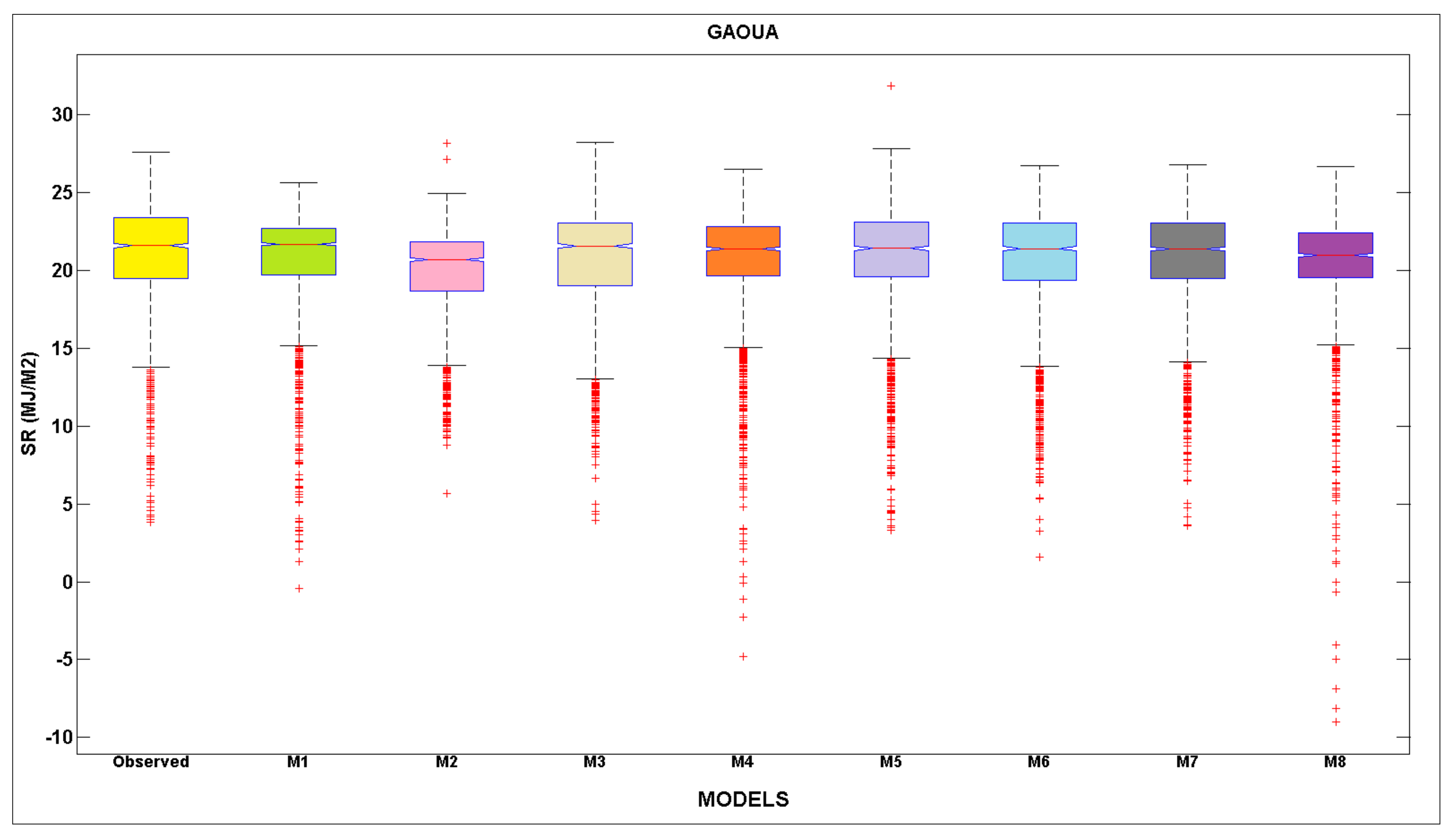
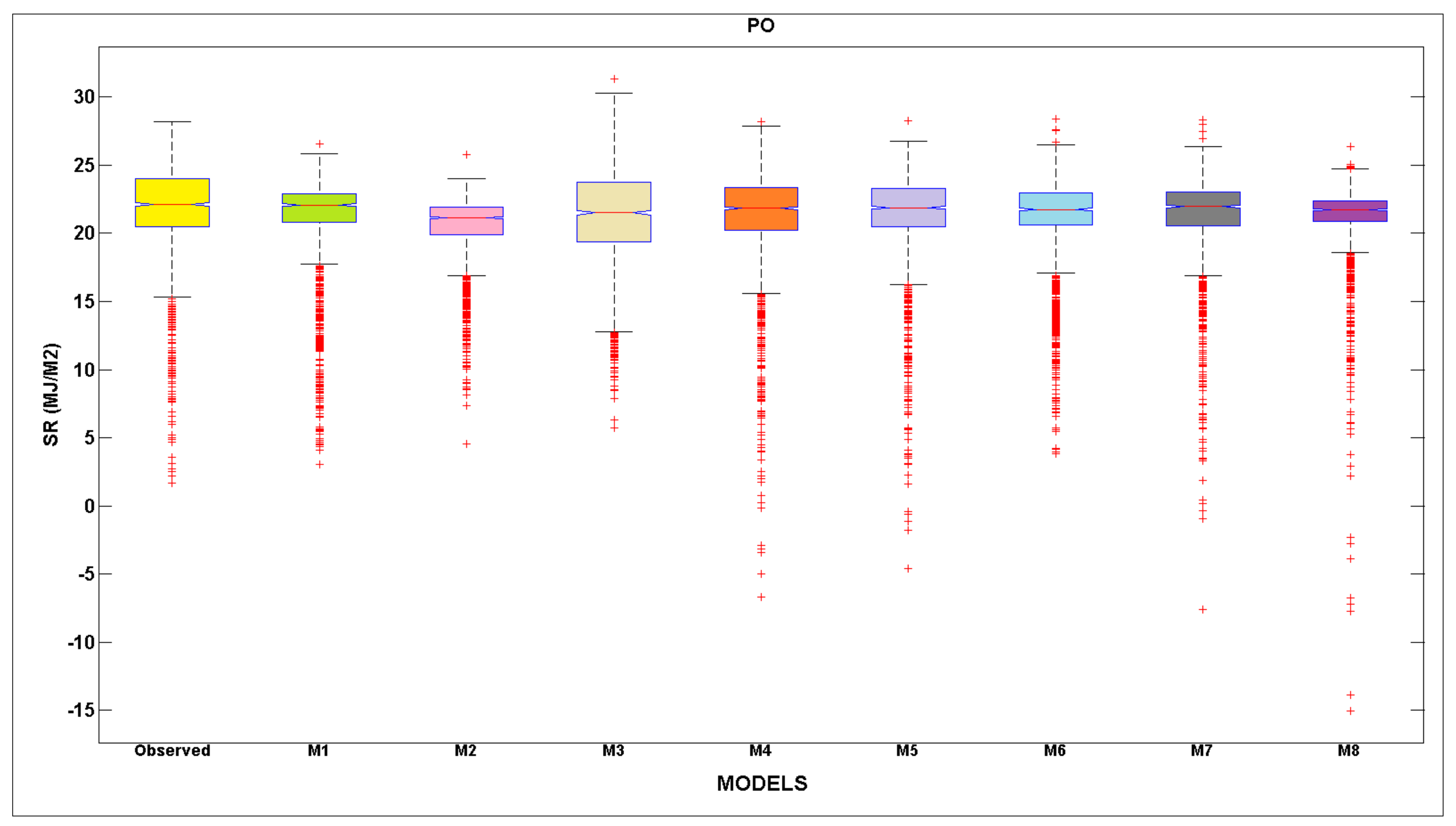
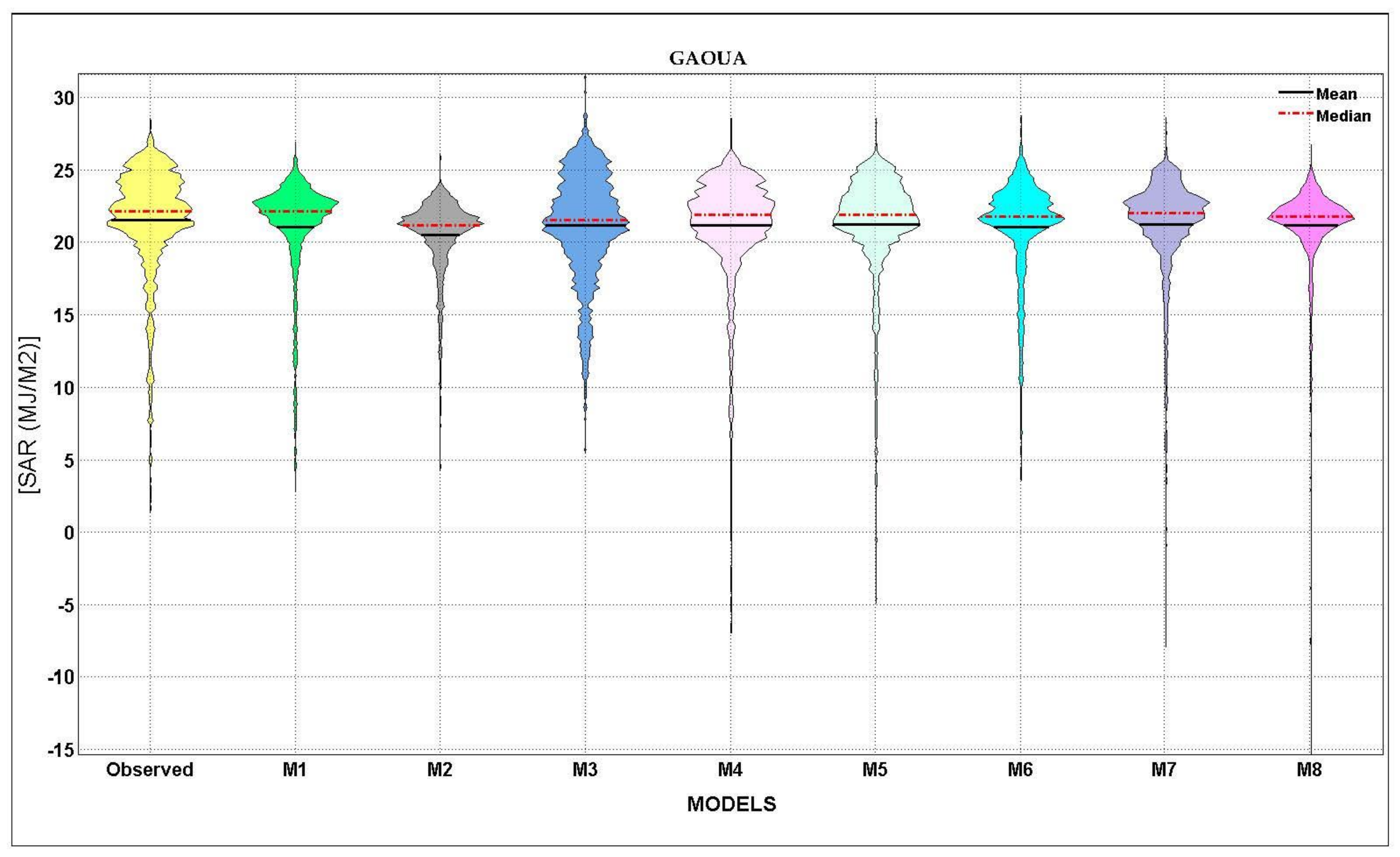
- The modeling results revealed that the best modeling accuracy was obtained for three stations (i.e., Bormo, Gaoua, and Po) using the fifth input combination by incorporating (WS, Tmax, Tmin, Hmin, VPD and Eo) climate variables.
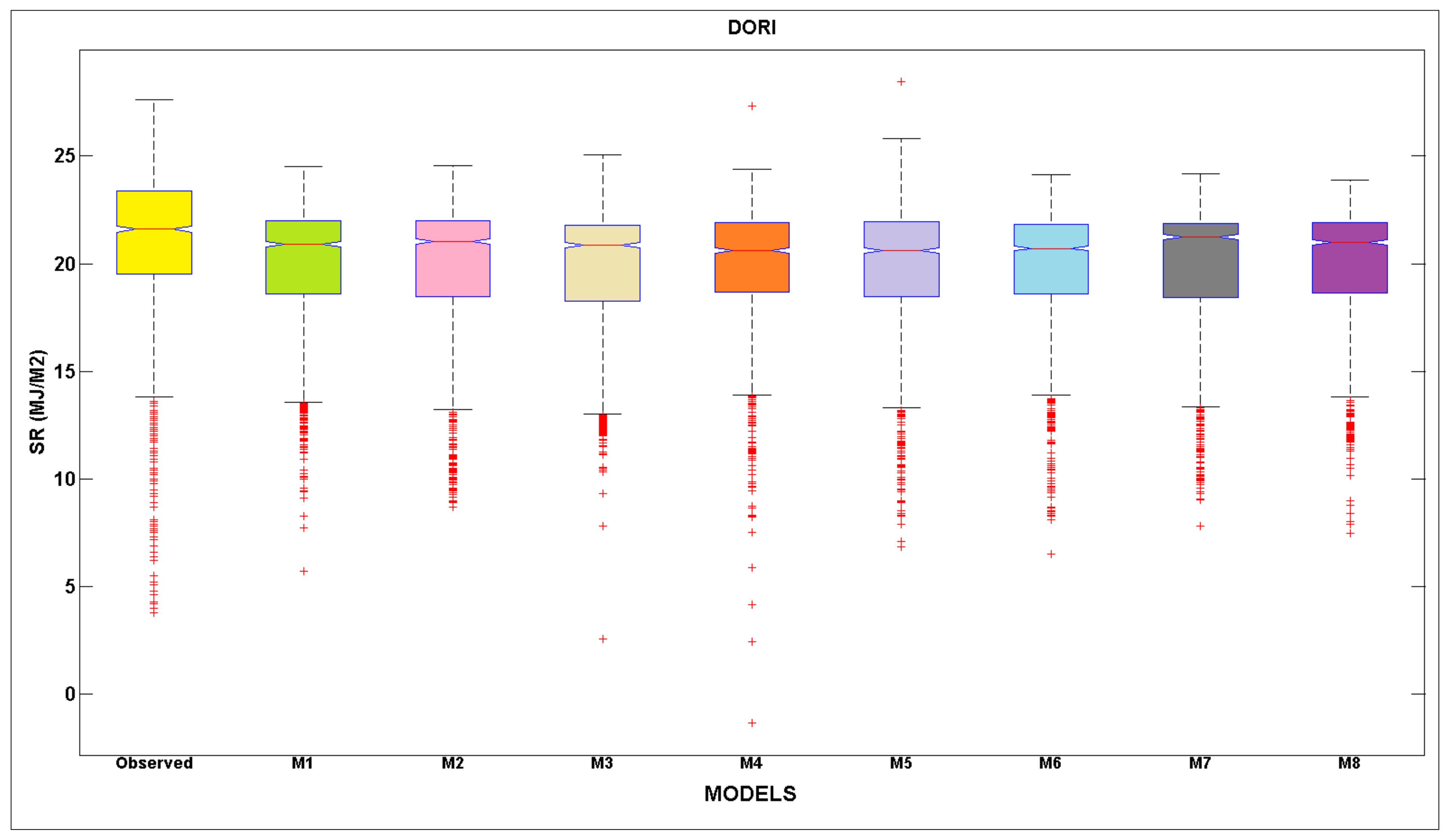
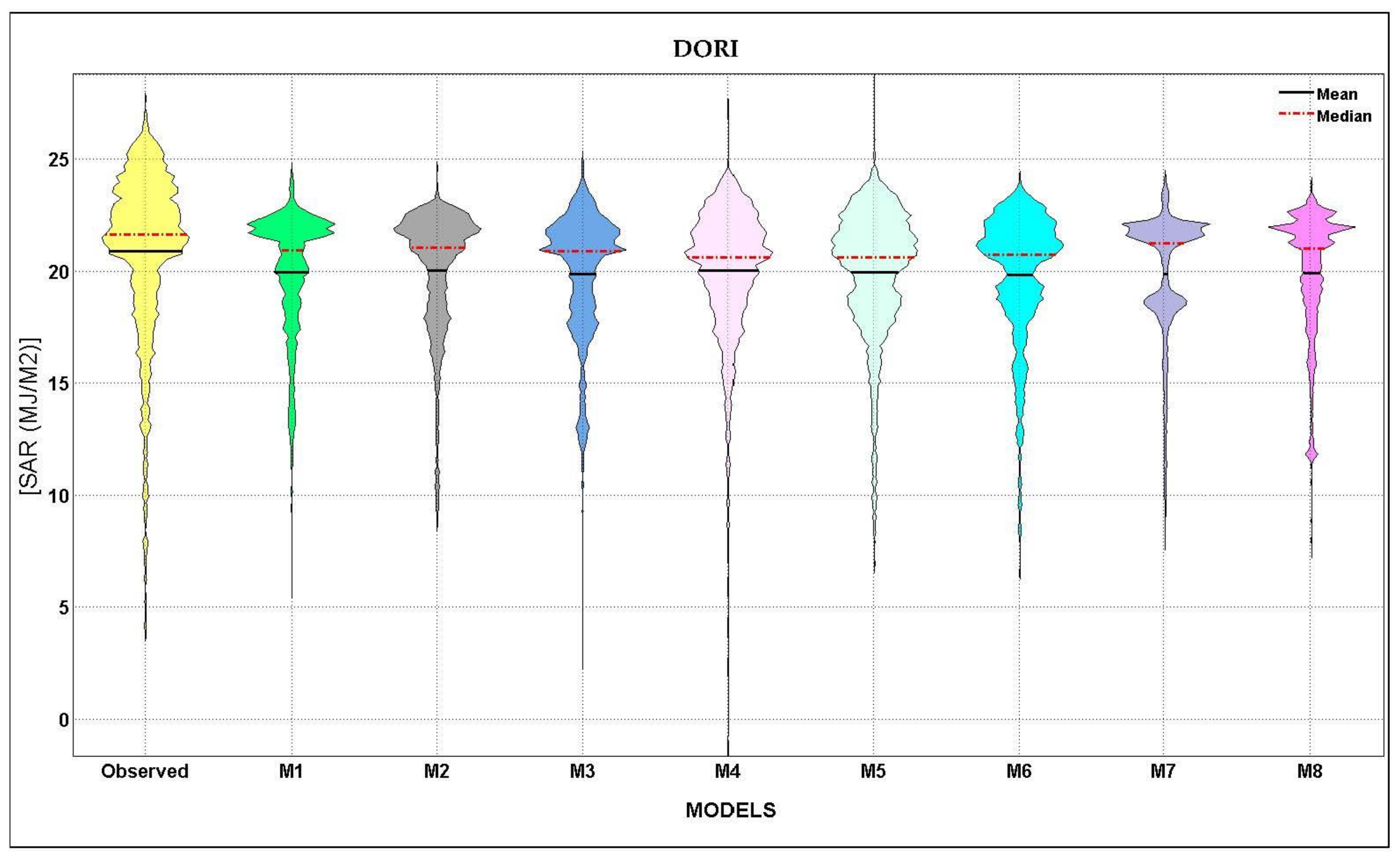
- On the other hand, the Dori station was able to demonstrate best result accuracy using WS, Tmax, Hmax, Hmin, VPD, and Eo as input variables (M6). This was mostly owing to the influence of the climate of the neighbouring area.
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
References
- Qazi, A.; Fayaz, H.; Wadi, A.; Raj, R.G.; Rahim, N.A.; Khan, W.A. The artificial neural network for solar radiation prediction and designing solar systems: A systematic literature review. J. Clean. Prod. 2015, 104, 1–12. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Global solar radiation prediction by ANN integrated with European Centre for medium range weather forecast fields in solar rich cities of queensland Australia. J. Clean. Prod. 2019, 216, 288–310. [Google Scholar] [CrossRef]
- Martin, C.L.; Goswami, D.Y. Solar Energy Pocket Reference; Routledge: Abingdon, UK, 2019; ISBN 1317705343. [Google Scholar]
- Saadi, N.; Miketa, A.; Howells, M. African Clean Energy Corridor: Regional integration to promote renewable energy fueled growth. Energy Res. Soc. Sci. 2015, 5, 130–132. [Google Scholar] [CrossRef]
- Bou-Rabee, M.; Sulaiman, S.A.; Saleh, M.S.; Marafi, S. Using artificial neural networks to estimate solar radiation in Kuwait. Renew. Sustain. Energy Rev. 2017, 72, 434–438. [Google Scholar] [CrossRef]
- Samuel Chukwujindu, N. A comprehensive review of empirical models for estimating global solar radiation in Africa. Renew. Sustain. Energy Rev. 2017, 78, 955–995. [Google Scholar] [CrossRef]
- Şen, Z. Fuzzy algorithm for estimation of solar irradiation from sunshine duration. Sol. Energy 1998, 63, 39–49. [Google Scholar]
- Hou, M.; Zhang, T.; Weng, F.; Ali, M.; Al-Ansari, N.; Yaseen, Z. Global Solar Radiation Prediction Using Hybrid Online Sequential Extreme Learning Machine Model. Energies 2018, 11, 3415. [Google Scholar]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Zhu, R.; Guo, W.; Gong, X. Short-Term Photovoltaic Power Output Prediction Based on k-Fold Cross-Validation and an Ensemble Model. Energies 2019, 12, 1220. [Google Scholar] [CrossRef]
- Han, S.; Qiao, Y.; Yan, J.; Liu, Y.; Li, L.; Wang, Z. Mid-to-long term wind and photovoltaic power generation prediction based on copula function and long short term memory network. Appl. Energy 2019, 239, 181–191. [Google Scholar] [CrossRef]
- De Freitas Viscondi, G.; Alves-Souza, S.N. A Systematic Literature Review on big data for solar photovoltaic electricity generation forecasting. Sustain. Energy Technol. Assess. 2019, 31, 54–63. [Google Scholar] [CrossRef]
- Zou, L.; Wang, L.; Li, J.; Lu, Y.; Gong, W.; Ying, N. Global surface solar radiation and photovoltaic power from Coupled Model Intercomparison Project Phase 5 climate models. J. Clean. Prod. 2019. [Google Scholar] [CrossRef]
- Azoumah, Y.; Ramdé, E.W.; Tapsoba, G.; Thiam, S. Siting guidelines for concentrating solar power plants in the Sahel: Case study of Burkina Faso. Sol. Energy 2010, 84, 1545–1553. [Google Scholar] [CrossRef]
- David, M.; Lauret, P. Solar Radiation Probabilistic Forecasting. In Wind Field and Solar Radiation Characterization and Forecasting A Numerical Approach for Complex Terrain; Springer: Berlin/Heidelberg, Germany, 2018; pp. 201–227. [Google Scholar]
- Fabbri, K.; Canuti, G.; Ugolini, A. A methodology to evaluate outdoor microclimate of the archaeological site and vegetation role: A case study of the Roman Villa in Russi (Italy). Sustain. Cities Soc. 2017, 35, 107–133. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Deng, S.; Xu, W.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S.S. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Izgi, E.; Öztopal, A.; Yerli, B.; Kaymak, M.K.; Şahin, A.D. Short-mid-term solar power prediction by using artificial neural networks. Sol. Energy 2012, 86, 725–733. [Google Scholar] [CrossRef]
- Gutierrez-Corea, F.V.; Manso-Callejo, M.A.; Moreno-Regidor, M.P.; Manrique-Sancho, M.T. Forecasting short-term solar irradiance based on artificial neural networks and data from neighboring meteorological stations. Sol. Energy 2016, 134, 119–131. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Petković, D. Adaptive neuro-fuzzy approach for solar radiation prediction in Nigeria. Renew. Sustain. Energy Rev. 2015, 51, 1784–1791. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Zhu, Z.; Gong, W.; Niu, Z.; Liu, H.; Liu, Z. Prediction of solar radiation in China using different adaptive neuro-fuzzy methods and M5 model tree. Int. J. Climatol. 2017, 37, 1141–1155. [Google Scholar] [CrossRef]
- Jović, S.; Aničić, O.; Marsenić, M.; Nedić, B. Solar radiation analyzing by neuro-fuzzy approach. Energy Build. 2016, 129, 261–263. [Google Scholar] [CrossRef]
- Landeras, G.; López, J.J.; Kisi, O.; Shiri, J. Comparison of Gene Expression Programming with neuro-fuzzy and neural network computing techniques in estimating daily incoming solar radiation in the Basque Country (Northern Spain). Energy Convers. Manag. 2012, 62, 1–3. [Google Scholar] [CrossRef]
- Shavandi, H.; Saeedi Ramyani, S. A linear genetic programming approach for the prediction of solar global radiation. Neural Comput. Appl. 2013, 23, 1197–1204. [Google Scholar] [CrossRef]
- Sharifi, S.S.; Rezaverdinejad, V.; Nourani, V. Estimation of daily global solar radiation using wavelet regression, ANN, GEP and empirical models: A comparative study of selected temperature-based approaches. J. Atmos. Solar-Terrestrial Phys. 2016, 149, 131–145. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Twaha, S.; Al-Turki, Y.A. Investigating the performance of support vector machine and artificial neural networks in predicting solar radiation on a tilted surface: Saudi Arabia case study. Energy Convers. Manag. 2015, 105, 442–452. [Google Scholar] [CrossRef]
- Meenal, R.; Selvakumar, A.I. Assessment of SVM, empirical and ANN based solar radiation prediction models with most influencing input parameters. Renew. Energy 2018, 121, 324–343. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Mohammadi, K.; Petković, D.; Sudheer, C. A support vector machine-firefly algorithm-based model for global solar radiation prediction. Sol. Energy 2015, 115, 632–644. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Tong, C.W.; Arif, M.; Petković, D.; Sudheer, C. A new hybrid support vector machine-wavelet transform approach for estimation of horizontal global solar radiation. Energy Convers. Manag. 2015, 92, 162–171. [Google Scholar] [CrossRef]
- Deo, R.C.; Wen, X.; Qi, F. A wavelet-coupled support vector machine model for forecasting global incident solar radiation using limited meteorological dataset. Appl. Energy 2016, 168, 568–593. [Google Scholar] [CrossRef]
- Wang, J.; Xie, Y.; Zhu, C.; Xu, X. Solar radiation prediction based on phase space reconstruction of wavelet neural network. Procedia Eng. 2011, 15, 4603–4607. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Mohanty, S.; Patra, P.K.; Sahoo, S.S. Prediction and application of solar radiation with soft computing over traditional and conventional approach—A comprehensive review. Renew. Sustain. Energy Rev. 2016, 56, 778–796. [Google Scholar] [CrossRef]
- Aybar-Ruiz, A.; Jiménez-Fernández, S.; Cornejo-Bueno, L.; Casanova-Mateo, C.; Sanz-Justo, J.; Salvador-González, P.; Salcedo-Sanz, S. A novel Grouping Genetic Algorithm-Extreme Learning Machine approach for global solar radiation prediction from numerical weather models inputs. Sol. Energy 2016, 132, 129–142. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, J. A novel hybrid model based on artificial neural networks for solar radiation prediction. Renew. Energy 2016, 89, 268–284. [Google Scholar] [CrossRef]
- Zhang, N.; Behera, P.K. Solar Radiation Prediction based on Recurrent Neural Networks trained by Levenberg-Marquardt Backpropagation Learning Algorithm. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 Janauary 2012. [Google Scholar]
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Self-adaptive differential evolutionary extreme learning machines for long-term solar radiation prediction with remotely-sensed MODIS satellite and Reanalysis atmospheric products in solar-rich cities. Remote Sens. Environ. 2018, 212, 176–198. [Google Scholar] [CrossRef]
- Rabehi, A.; Guermoui, M.; Lalmi, D. Hybrid models for global solar radiation prediction: A case study. Int. J. Ambient Energy 2018, 0, 1–10. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Casanova-Mateo, C.; Pastor-Sánchez, A.; Sánchez-Girón, M. Daily global solar radiation prediction based on a hybrid Coral Reefs Optimization—Extreme Learning Machine approach. Sol. Energy 2014, 105, 91–98. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Wang, M.; Wei, Z.; Sun, G. Estimation and validation of daily global solar radiation by day of the year-based models for different climates in China. Renew. Energy 2019, 135, 984–1003. [Google Scholar] [CrossRef]
- Shamshirband, S.; Mohammadi, K.; Tong, C.W.; Petković, D.; Porcu, E.; Mostafaeipour, A.; Ch, S.; Sedaghat, A. Application of extreme learning machine for estimation of wind speed distribution. Clim. Dyn. 2016, 46, 1893–1907. [Google Scholar] [CrossRef]
- Glezakos, T.J.; Tsiligiridis, T. a.; Iliadis, L.S.; Yialouris, C.P.; Maris, F.P.; Ferentinos, K.P. Feature extraction for time-series data: An artificial neural network evolutionary training model for the management of mountainous watersheds. Neurocomputing 2009, 73, 49–59. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Deo, R.C.; Cornejo-Bueno, L.; Camacho-Gómez, C.; Ghimire, S. An efficient neuro-evolutionary hybrid modelling mechanism for the estimation of daily global solar radiation in the Sunshine State of Australia. Appl. Energy 2018, 209, 79–94. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Sattar, A.M.A.; Bonakdari, H.; Zaji, A.H. Prediction of scour depth around bridge piers using self-adaptive extreme learning machine. J. Hydroinformatics 2017, 19, 207–224. [Google Scholar] [CrossRef]
- Dash, R.; Dash, P.K.; Bisoi, R. A self adaptive differential harmony search based optimized extreme learning machine for financial time series prediction. Swarm Evol. Comput. 2014, 19, 25–42. [Google Scholar] [CrossRef]
- Price, K.V. Differential Evolution. In Intelligent Systems Reference Library; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, L. Convex incremental extreme learning machine. Neurocomputing 2007, 70, 3056–3062. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man. Cybern. B Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Deo, R.C.; Ebtehaj, I.; Bonakdari, H. Hybrid Data Intelligent Models and Applications for Water Level Prediction. In Handbook of Research on Predictive Modeling and Optimization Methods in Science and Engineering; IGI Global: Hershey, PA, USA, 2018. [Google Scholar]
- Al Sudani, Z.A.; Salih, S.Q.; Yaseen, Z.M. Development of Multivariate Adaptive Regression Spline Integrated with Differential Evolution Model for Streamflow Simulation. J. Hydrol. 2019, 573, 1–12. [Google Scholar] [CrossRef]
- REN21. Renewables 2017: Global Status Report; REN21: Paris, France, 2017; Volume 72, ISBN 978-3-9818107-0-7. [Google Scholar]
- Tao, H.; Diop, L.; Bodian, A.; Djaman, K.; Ndiaye, P.M.; Yaseen, Z.M. Reference evapotranspiration prediction using hybridized fuzzy model with firefly algorithm: Regional case study in Burkina Faso. Agric. Water Manag. 2018, 208, 140–151. [Google Scholar] [CrossRef]
- Legates, D.R.; Mccabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Keshtegar, B.; Mert, C.; Kisi, O. Comparison of four heuristic regression techniques in solar radiation modeling: Kriging method vs RSM, MARS and M5 model tree. Renew. Sustain. Energy Rev. 2018, 81, 330–341. [Google Scholar] [CrossRef]
- Kisi, O.; Heddam, S.; Yaseen, Z.M. The implementation of univariable scheme-based air temperature for solar radiation prediction: New development of dynamic evolving neural-fuzzy inference system model. Appl. Energy 2019, 241, 184–195. [Google Scholar] [CrossRef]
- Prasad, R.; Ali, M.; Kwan, P.; Khan, H. Designing a multi-stage multivariate empirical mode decomposition coupled with ant colony optimization and random forest model to forecast monthly solar radiation. Appl. Energy 2019, 236, 778–792. [Google Scholar] [CrossRef]

| Predictive Models | Input Variables | Output Variable |
|---|---|---|
| M1 | WS, Tmax, Tmin, Hmax, Hmin, VPD, Eo | SR |
| M2 | WS, Tmax, Tmin, Hmax, Hmin, VPD | SR |
| M3 | WS, Tmax, Tmin, Hmax, Hmin, Eo | SR |
| M4 | WS, Tmax, Tmin, Hmax, VPD, Eo | SR |
| M5 | WS, Tmax, Tmin, Hmin, VPD, Eo | SR |
| M6 | WS, Tmax, Hmax, Hmin, VPD, Eo | SR |
| M7 | WS, Tmin, Hmax, Hmin, VPD, Eo | SR |
| M8 | Tmax, Tmin, Hmax, Hmin, VPD, Eo | SR |
| Modeling Phases | Input Combinations | R | VAF | RMSE MJ/m2 | SI | MAE MJ/m2 | Nash |
|---|---|---|---|---|---|---|---|
| Training Phase | M1 | 0.930265 | 86.52017 | 1.392039 | 0.06799 | 1.036243 | 0.846698 |
| M2 | 0.634822 | 40.27061 | 2.939233 | 0.143559 | 2.078975 | −0.54626 | |
| M3 | 0.897076 | 80.43472 | 1.679704 | 0.082041 | 1.266132 | 0.763912 | |
| M4 | 0.922551 | 85.07675 | 1.463148 | 0.071464 | 1.103346 | 0.829432 | |
| M5 * | 0.970676 | 94.22108 | 0.907215 | 0.044310 | 0.643799 | 0.938422 | |
| M6 | 0.924674 | 85.49192 | 1.43643 | 0.070159 | 1.069989 | 0.833261 | |
| M7 | 0.900707 | 81.12358 | 1.640405 | 0.080121 | 1.280761 | 0.769113 | |
| M8 | 0.838359 | 70.27836 | 2.074775 | 0.101337 | 1.555200 | 0.579304 | |
| Testing Phase | M1 | 0.946649 | 89.5884 | 1.267718 | 0.059127 | 0.934415 | 0.871137 |
| M2 | 0.703431 | 49.4815 | 2.821365 | 0.131589 | 2.092861 | −0.01726 | |
| M3 | 0.921115 | 84.75038 | 1.545464 | 0.072081 | 1.174501 | 0.792653 | |
| M4 | 0.944293 | 89.10558 | 1.293015 | 0.060307 | 0.963948 | 0.862591 | |
| M5 * | 0.982320 | 96.49205 | 0.722620 | 0.033703 | 0.54431 | 0.962551 | |
| M6 | 0.944095 | 89.12162 | 1.262830 | 0.058899 | 0.949363 | 0.872311 | |
| M7 | 0.914085 | 83.55511 | 1.557891 | 0.072661 | 1.224900 | 0.797607 | |
| M8 | 0.855340 | 73.13868 | 2.056710 | 0.095926 | 1.570392 | 0.596186 |
| Modeling Phases | Input Combinations | R | VAF | RMSE MJ/m2 | SI | MAE MJ/m2 | Nash |
|---|---|---|---|---|---|---|---|
| Training Phase | M1 | 0.905258 | 81.94663 | 1.718238 | 0.085839 | 1.309303 | 0.781138 |
| M2 | 0.612427 | 37.43797 | 3.226028 | 0.161164 | 2.269299 | −0.78704 | |
| M3 | 0.914630 | 83.58584 | 1.638149 | 0.081838 | 1.213962 | 0.791079 | |
| M4 | 0.935026 | 87.36677 | 1.440186 | 0.071948 | 1.106294 | 0.846292 | |
| M5 * | 0.963994 | 92.92267 | 1.074897 | 0.053699 | 0.773968 | 0.922311 | |
| M6 | 0.932506 | 86.76796 | 1.476230 | 0.073749 | 1.082333 | 0.830764 | |
| M7 | 0.939267 | 88.22222 | 1.384733 | 0.069178 | 0.969060 | 0.866117 | |
| M8 | 0.864687 | 74.70987 | 2.040847 | 0.101955 | 1.546622 | 0.638999 | |
| Testing Phase | M1 | 0.924516 | 85.47253 | 1.468869 | 0.070376 | 1.138047 | 0.824449 |
| M2 | 0.775059 | 60.06482 | 2.585672 | 0.123883 | 2.003274 | 0.288351 | |
| M3 | 0.904765 | 81.46193 | 1.650564 | 0.079081 | 1.197077 | 0.798471 | |
| M4 | 0.936090 | 87.27325 | 1.382154 | 0.066221 | 1.031606 | 0.866592 | |
| M5 * | 0.973168 | 94.65295 | 0.887638 | 0.042528 | 0.656585 | 0.944803 | |
| M6 | 0.912247 | 82.31902 | 1.628865 | 0.078041 | 1.180101 | 0.819329 | |
| M7 | 0.914179 | 83.56705 | 1.540293 | 0.073798 | 1.130941 | 0.805704 | |
| M8 | 0.887533 | 78.47722 | 1.818706 | 0.087137 | 1.383960 | 0.744736 |
| Modeling Phases | Input Combinations | R | VAF | RMSE MJ/m2 | SI | MAE MJ/m2 | Nash |
|---|---|---|---|---|---|---|---|
| Training Phase | M1 | 0.596761 | 35.57581 | 3.270526 | 0.163387 | 2.313368 | −0.89387 |
| M2 | 0.594052 | 35.25946 | 3.274283 | 0.163575 | 2.303824 | −0.91372 | |
| M3 | 0.597315 | 35.52598 | 3.277209 | 0.163721 | 2.280505 | −1.01668 | |
| M4 | 0.603950 | 36.45145 | 3.243024 | 0.162013 | 2.308895 | −0.80852 | |
| M5 * | 0.623858 | 38.83679 | 3.188808 | 0.159305 | 2.226632 | −0.70002 | |
| M6 | 0.606662 | 36.7405 | 3.250603 | 0.162392 | 2.251397 | −0.82816 | |
| M7 | 0.588002 | 34.45429 | 3.305049 | 0.165112 | 2.302701 | −1.08256 | |
| M8 | 0.587828 | 34.50788 | 3.298918 | 0.164805 | 2.328470 | −0.99684 | |
| Testing Phase | M1 | 0.755305 | 57.02155 | 2.658639 | 0.127379 | 2.071896 | 0.190999 |
| M2 | 0.757493 | 57.37163 | 2.628870 | 0.125953 | 2.039391 | 0.217939 | |
| M3 | 0.742638 | 55.15065 | 2.734910 | 0.131034 | 2.136888 | 0.169523 | |
| M4 | 0.750326 | 56.29248 | 2.650699 | 0.126999 | 2.018881 | 0.189014 | |
| M5 | 0.770053 | 59.29803 | 2.598160 | 0.124482 | 1.980505 | 0.285795 | |
| M6 * | 0.785724 | 61.65339 | 2.576907 | 0.123463 | 1.999371 | 0.290784 | |
| M7 | 0.758246 | 57.48502 | 2.679643 | 0.128386 | 2.076499 | 0.213567 | |
| M8 | 0.766539 | 58.72635 | 2.622059 | 0.125627 | 2.037424 | 0.236006 |
| Modeling Phases | Input Combinations | R | VAF | RMSE MJ/m2 | SI | MAE MJ/m2 | Nash |
|---|---|---|---|---|---|---|---|
| Training Phase | M1 | 0.901994 | 81.35282 | 1.662271 | 0.081599 | 1.25279 | 0.763189 |
| M2 | 0.550130 | 30.21495 | 3.225583 | 0.158340 | 2.246477 | −1.41327 | |
| M3 | 0.880806 | 77.46188 | 1.819173 | 0.089301 | 1.381514 | 0.683050 | |
| M4 | 0.926815 | 85.84214 | 1.446000 | 0.070982 | 1.103700 | 0.824113 | |
| M5 * | 0.929376 | 86.37367 | 1.413969 | 0.069410 | 1.054562 | 0.840394 | |
| M6 | 0.879309 | 77.31098 | 1.831663 | 0.089914 | 1.295713 | 0.708702 | |
| M7 | 0.908728 | 82.57633 | 1.598182 | 0.078453 | 1.200935 | 0.789833 | |
| M8 | 0.840671 | 70.60883 | 2.075782 | 0.101898 | 1.533630 | 0.606051 | |
| Testing Phase | M1 | 0.919797 | 84.51837 | 1.572986 | 0.073233 | 1.191058 | 0.815071 |
| M2 | 0.669339 | 44.79318 | 3.019014 | 0.140555 | 2.338998 | −0.22922 | |
| M3 | 0.892859 | 79.16279 | 1.783374 | 0.083028 | 1.366748 | 0.769954 | |
| M4 | 0.945065 | 88.99555 | 1.319447 | 0.061429 | 0.963419 | 0.882414 | |
| M5 * | 0.954428 | 91.06514 | 1.175110 | 0.054709 | 0.868936 | 0.900454 | |
| M6 | 0.897851 | 80.61294 | 1.750178 | 0.081482 | 1.284407 | 0.743682 | |
| M7 | 0.916311 | 83.96002 | 1.559401 | 0.072600 | 1.219533 | 0.805511 | |
| M8 | 0.861113 | 74.02332 | 1.986263 | 0.092473 | 1.507260 | 0.609738 |
| Meteorological Station | Input Combinations | Mean Prediction Error | Standard Deviation of Prediction Error | Width of Uncertainty Band | 95% Prediction Error Interval |
|---|---|---|---|---|---|
| Bormo | Model 1 | 1.280 | 1.537 | ±0.300 | (0.980, 1.581) |
| Model 2 | 2.049 | 1.893 | ±0.370 | (1.679, 2.419) | |
| Model 3 | 1.488 | 1.947 | ±0.381 | (1.107, 1.868) | |
| Model 4 | 1.563 | 1.600 | ±0.313 | (1.251, 1.876) | |
| Model 5 | 0.634 | 1.015 | ±0.198 | (0.436, 0.833) | |
| Model 6 | 1.184 | 1.358 | ±0.265 | (0.918, 1.449) | |
| Model 7 | 1.445 | 1.865 | ±0.365 | (1.080, 1.809) | |
| Model 8 | 1.666 | 2.062 | ±0.403 | (1.263, 2.069) | |
| Po | Model 1 | 1.377 | 2.036 | ±0.398 | (0.979, 1.775) |
| Model 2 | 2.587 | 2.210 | ±0.432 | (2.155, 3.019) | |
| Model 3 | 0.474 | 1.798 | ±0.351 | (0.123, 0.826) | |
| Model 4 | 0.894 | 1.579 | ±0.309 | (0.585, 1.202) | |
| Model 5 | 1.160 | 1.633 | ±0.319 | (0.841, 1.480) | |
| Model 6 | 1.526 | 1.851 | ±0.362 | (1.164, 1.888) | |
| Model 7 | 1.278 | 2.017 | ±0.394 | (0.883, 1.672) | |
| Model 8 | 1.582 | 2.023 | ±0.395 | (1.187, 1.977) | |
| Gaoua | Model 1 | 0.896 | 1.812 | ±0.354 | (0.541, 1.250) |
| Model 2 | 1.594 | 2.218 | ±0.433 | (1.161, 2.028) | |
| Model 3 | 0.456 | 1.470 | ±0.287 | (0.169, 0.743) | |
| Model 4 | 0.090 | 1.474 | ±0.288 | (−0.198, 0.378) | |
| Model 5 | 0.235 | 1.161 | ±0.227 | (0.008, 0.462) | |
| Model 6 | 0.307 | 1.068 | ±0.209 | (0.098, 0.516) | |
| Model 7 | 0.026 | 1.432 | ±0.280 | (−0.253, 0.306) | |
| Model 8 | 0.868 | 1.772 | ±0.346 | (0.521, 1.214) | |
| Dori | Model 1 | 1.764 | 2.239 | ±0.438 | (1.326, 2.201) |
| Model 2 | 1.735 | 2.307 | ±0.451 | (1.284, 2.186) | |
| Model 3 | 1.638 | 2.200 | ±0.430 | (1.208, 2.068) | |
| Model 4 | 2.243 | 2.858 | ±0.559 | (1.684, 2.801) | |
| Model 5 | 2.095 | 2.752 | ±0.538 | (1.557, 2.633) | |
| Model 6 | 1.626 | 1.996 | ±0.390 | (1.236, 2.016) | |
| Model 7 | 1.500 | 2.106 | ±0.412 | (1.088, 1.911) | |
| Model 8 | 1.546 | 2.079 | ±0.406 | (1.140, 1.952) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, H.; Ebtehaj, I.; Bonakdari, H.; Heddam, S.; Voyant, C.; Al-Ansari, N.; Deo, R.; Yaseen, Z.M. Designing a New Data Intelligence Model for Global Solar Radiation Prediction: Application of Multivariate Modeling Scheme. Energies 2019, 12, 1365. https://doi.org/10.3390/en12071365
Tao H, Ebtehaj I, Bonakdari H, Heddam S, Voyant C, Al-Ansari N, Deo R, Yaseen ZM. Designing a New Data Intelligence Model for Global Solar Radiation Prediction: Application of Multivariate Modeling Scheme. Energies. 2019; 12(7):1365. https://doi.org/10.3390/en12071365
Chicago/Turabian StyleTao, Hai, Isa Ebtehaj, Hossein Bonakdari, Salim Heddam, Cyril Voyant, Nadhir Al-Ansari, Ravinesh Deo, and Zaher Mundher Yaseen. 2019. "Designing a New Data Intelligence Model for Global Solar Radiation Prediction: Application of Multivariate Modeling Scheme" Energies 12, no. 7: 1365. https://doi.org/10.3390/en12071365
APA StyleTao, H., Ebtehaj, I., Bonakdari, H., Heddam, S., Voyant, C., Al-Ansari, N., Deo, R., & Yaseen, Z. M. (2019). Designing a New Data Intelligence Model for Global Solar Radiation Prediction: Application of Multivariate Modeling Scheme. Energies, 12(7), 1365. https://doi.org/10.3390/en12071365











