Battery Characterization and Dimensioning Approaches for Micro-Grid Systems †
Abstract
:1. Introduction
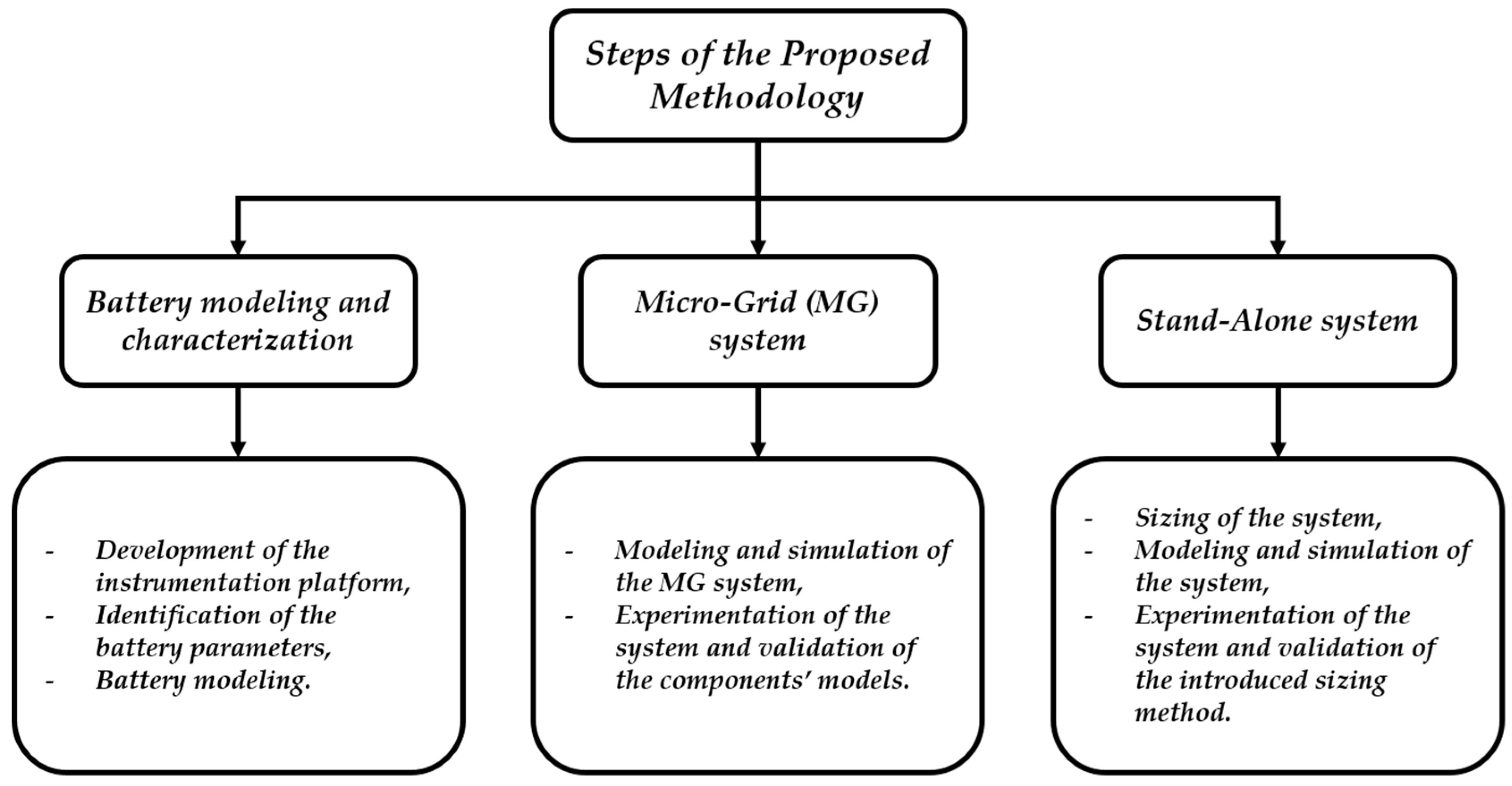
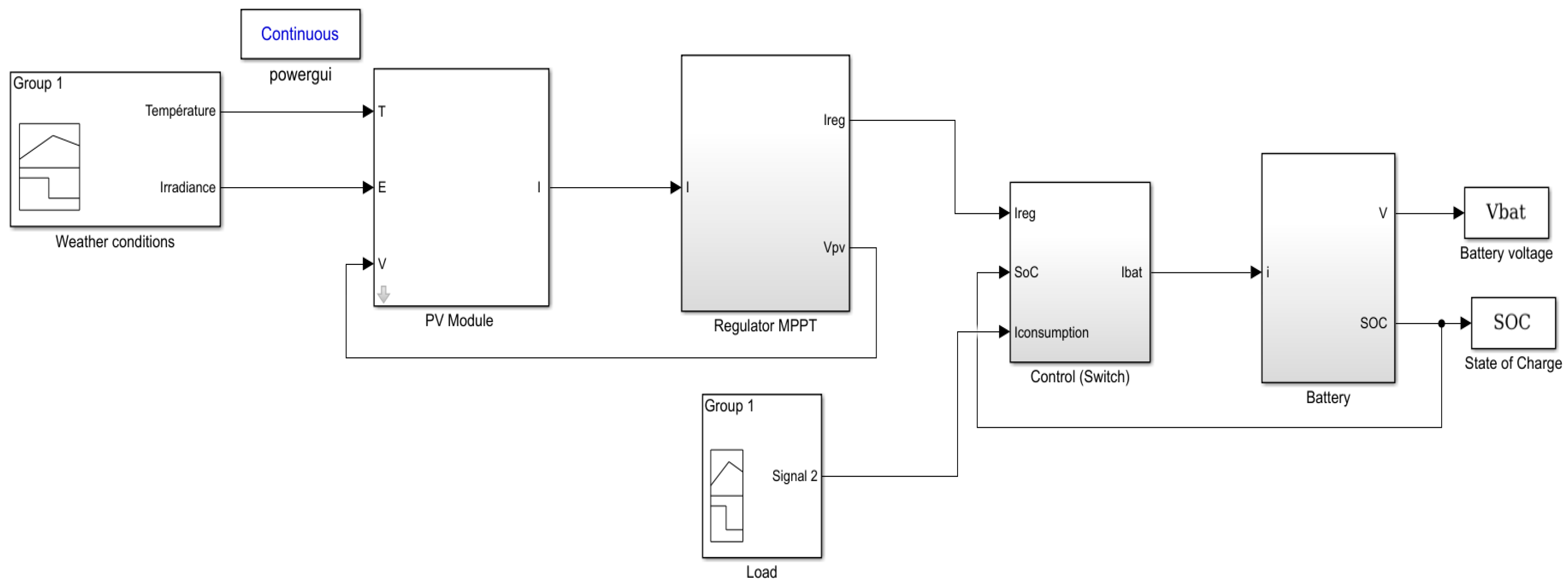
2. Proposed Methodology
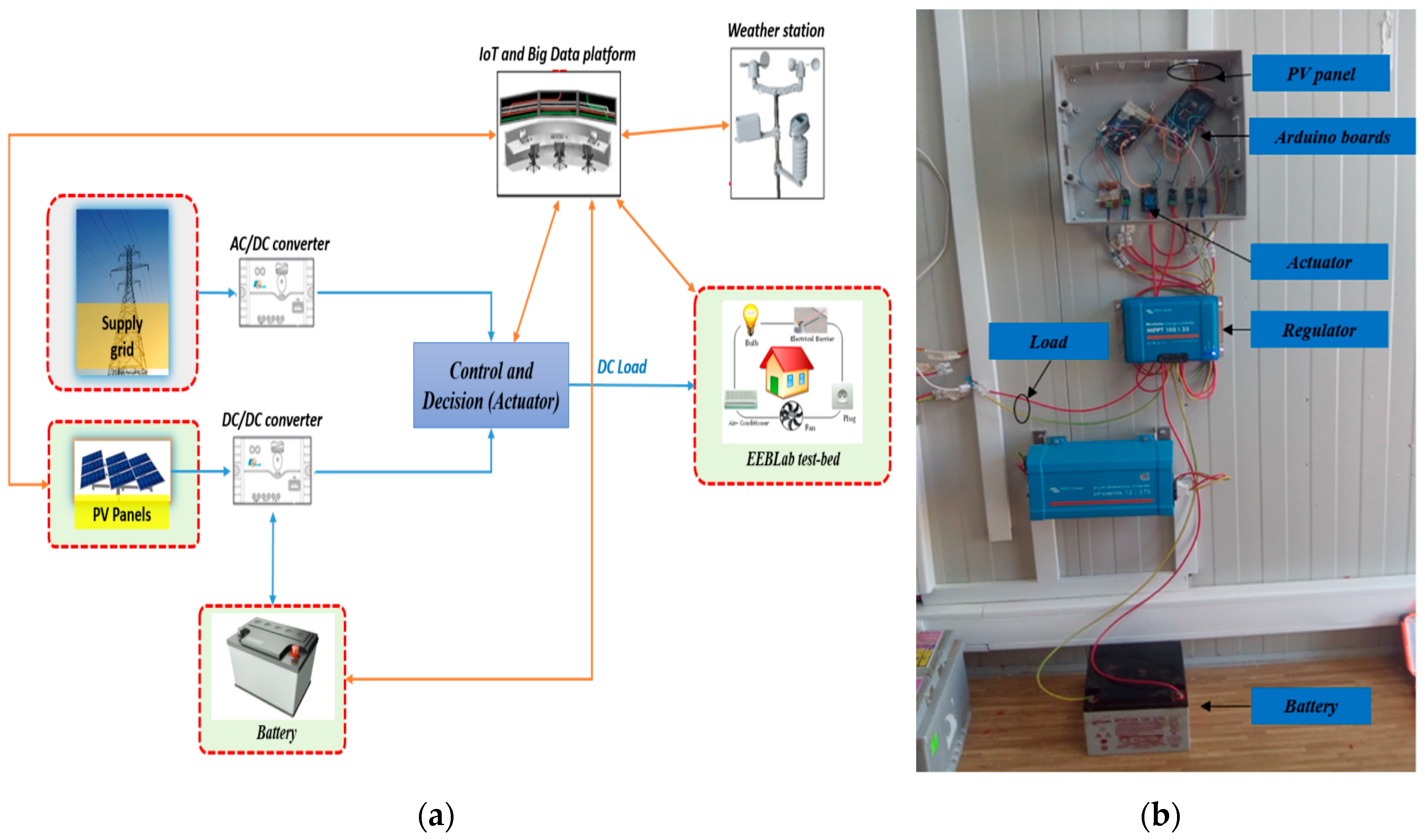
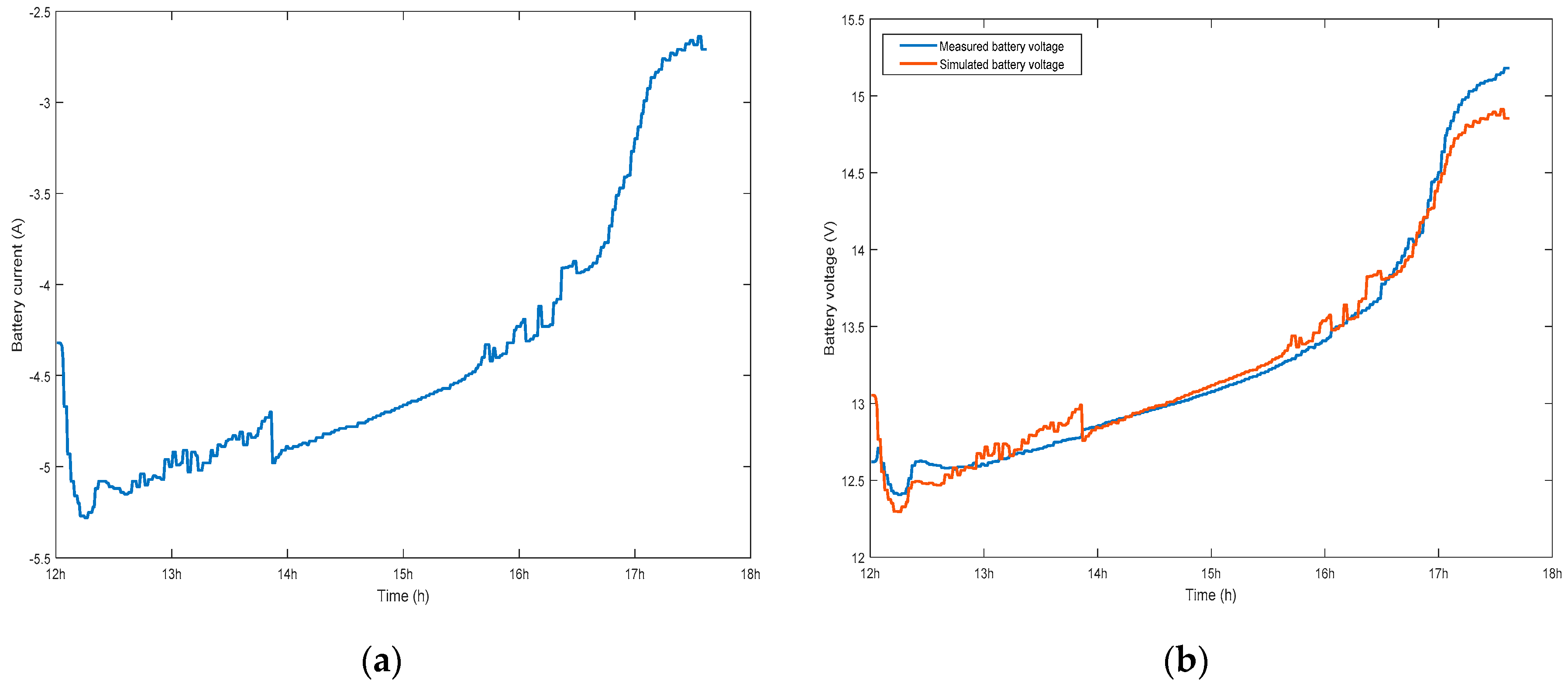
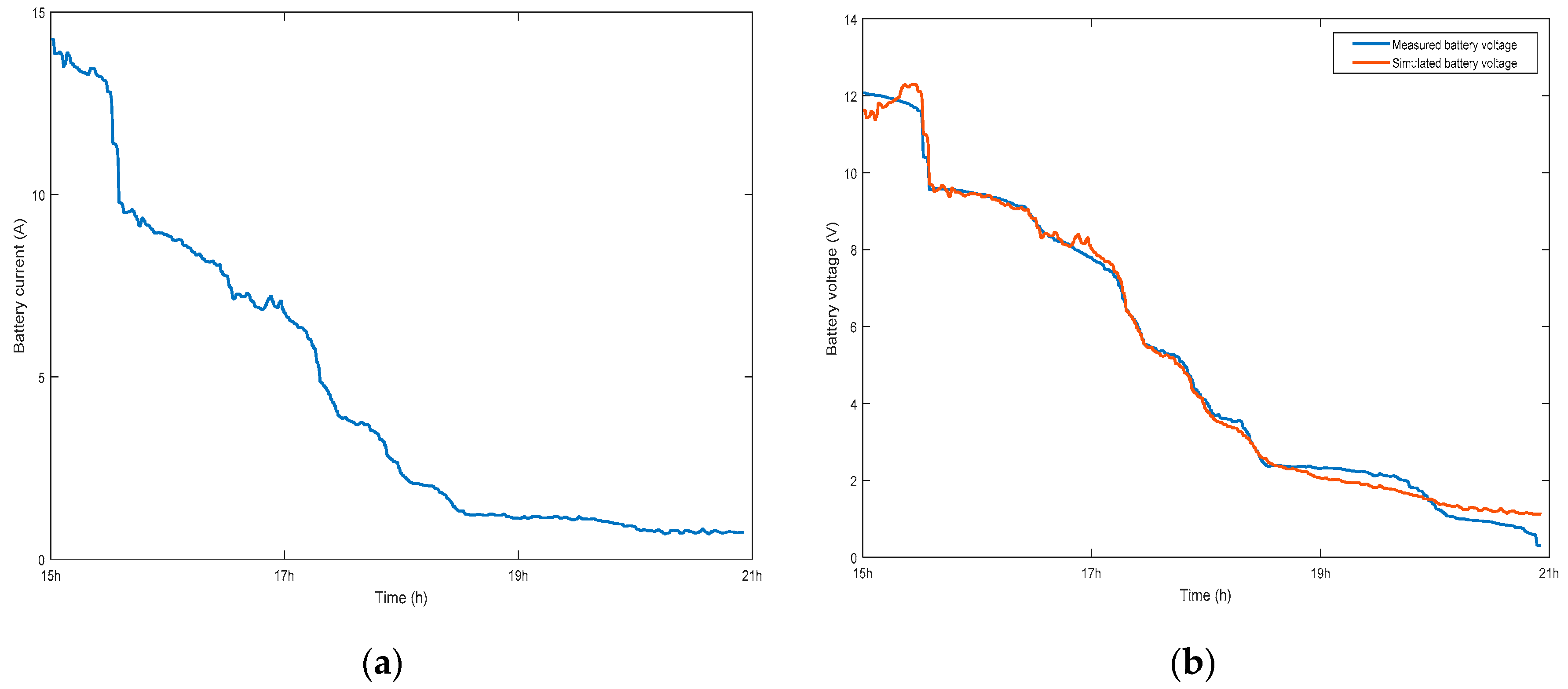
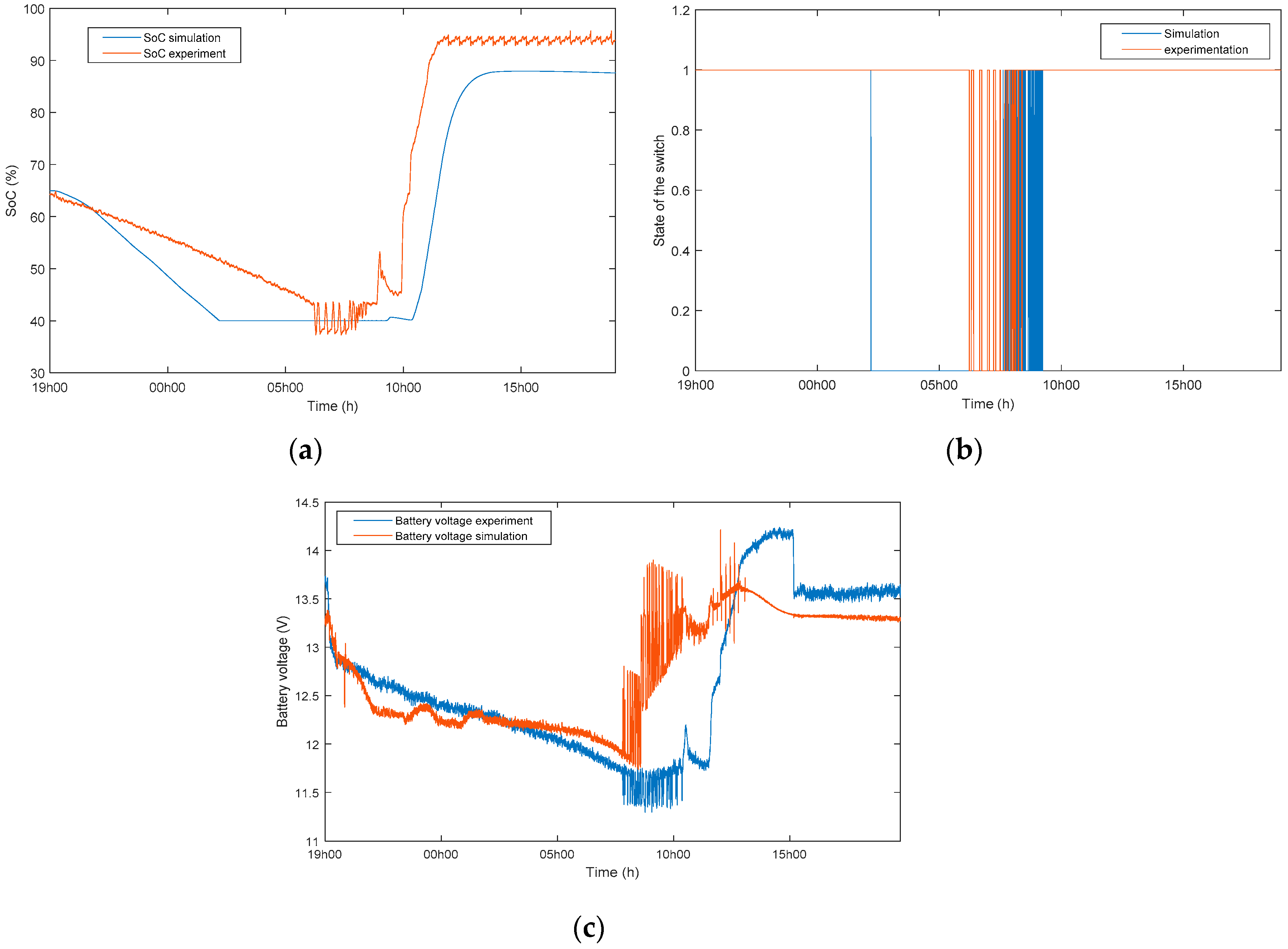
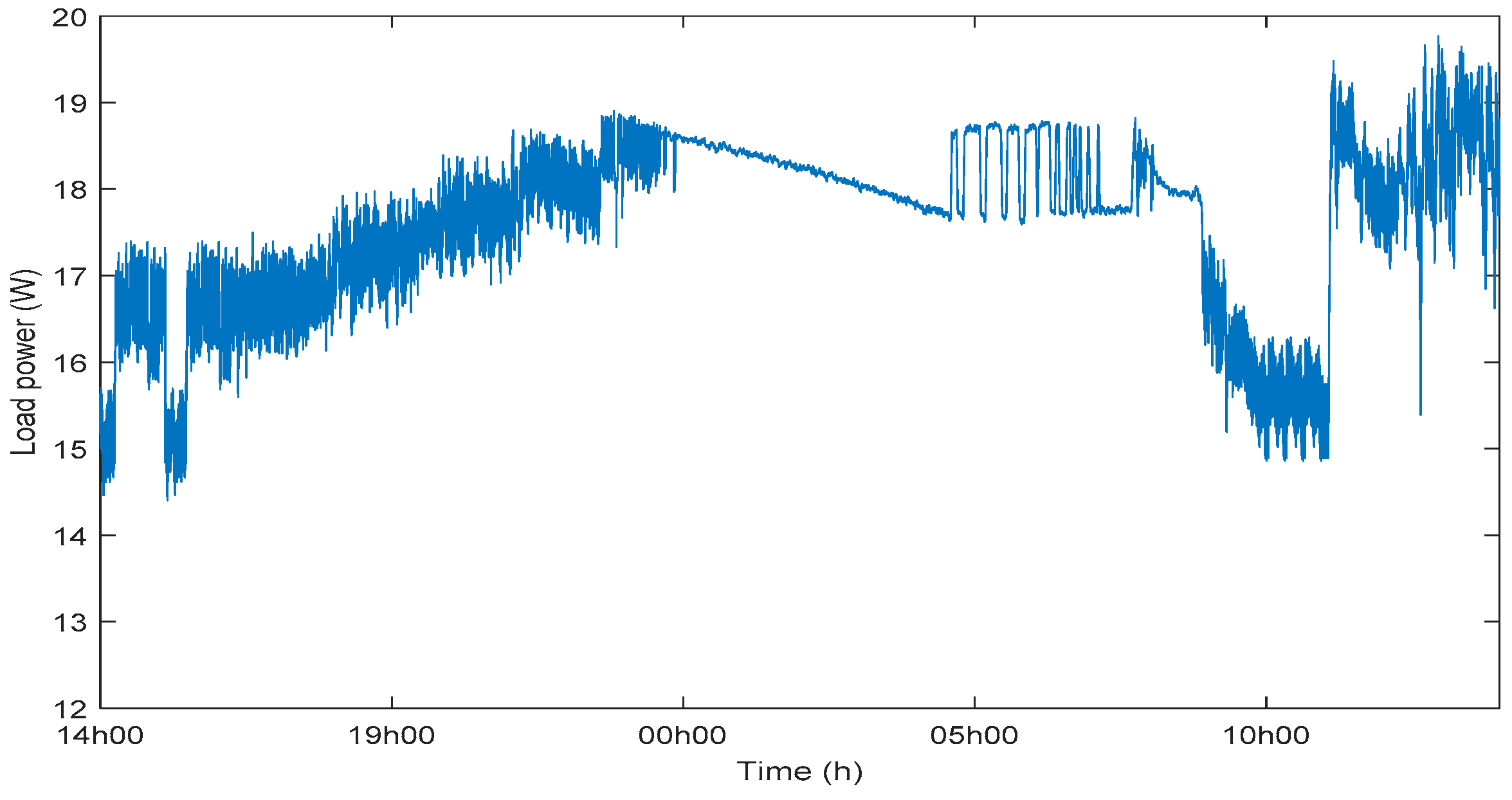
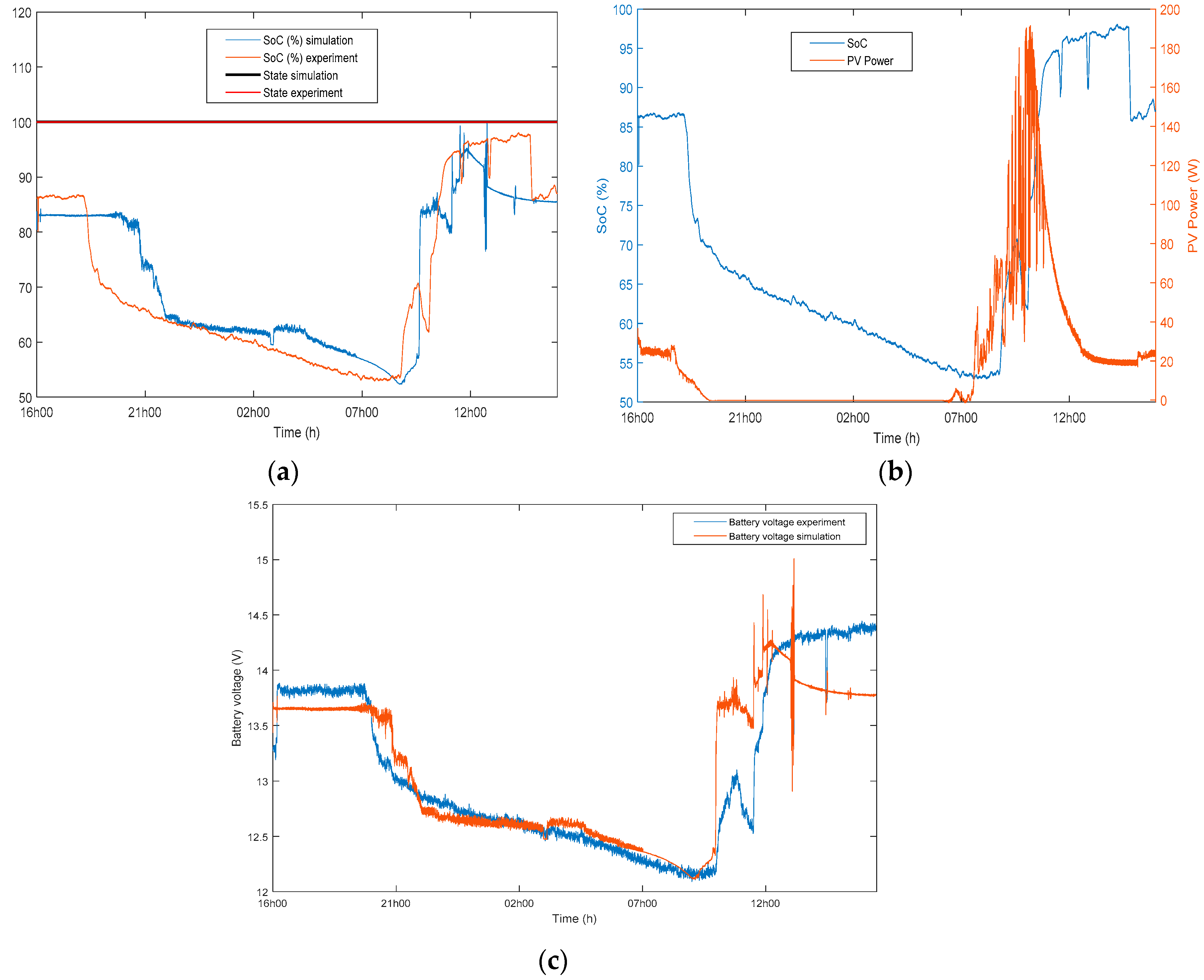
3. Simulation and Experimental Results of the MG System
4. Sizing of the Stand-Alone System
5. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Othieno, H.; Awange, J. Energy Resources in Africa, Distribution, Opportunities and Challenges; Springer: New York, NY, USA, 2016. [Google Scholar]
- Bajracharya, Q. Dynamic Modeling, Monitoring and Control of Energy Storage System. Master’s Thesis, Karlstad University, Karlstad, Sweden, 2013. [Google Scholar]
- Denherder, T. Design and Simulation of Photovoltaic Super System Using Simulink. Ph.D. Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2006. [Google Scholar]
- Berouine, A.; Lachhab, F.; Nait Malek, Y.; Bakhouya, M.; Ouladsine, R. A Smart Metering Platform using Big Data and IoT Technologies. In Proceedings of the CloudTech, Rabat, Morocco, 24–26 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Djafour, A.; Aida, M.S.; Azoui, B. Photovoltaic assisted fuel cell power systems. Energy Procedia 2014, 50, 306–313. [Google Scholar] [CrossRef]
- Boulmrharj, S.; Rabeh, R.; Felix, V.; Ouladsine, R.; Bakhouya, M.; Zine-dine, K.; Khaidar, M.; Siniti, M.; Abid, R. Modeling and dimensioning of grid-connected photovoltaic systems. In Proceedings of the IRSEC’17, Tangier, Morocco, 4–7 December 2017. [Google Scholar] [CrossRef]
- Anoune, K.; Bouya, M.; Astito, A.; Ben Abdellah, A. Sizing methods and optimization techniques for PV-wind based hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2018, 93, 652–673. [Google Scholar] [CrossRef]
- Seaman, A.; Dao, T.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef]
- Sun, K.; Shu, Q. Overview of the types of battery models. In Proceedings of the Chinese Control Conference, Yantai, China, 22–24 July 2011; pp. 3644–3648. [Google Scholar]
- Zhang, C.; Allafi, W.; Dinh, Q.; Ascencio, P.; Marco, J. Online Estimation of Battery Equivalent Circuit Model Parameters and State of Charge using Decoupled Least Squares Technique. Energy 2017. [Google Scholar] [CrossRef]
- Ramadan, H.S.; Becherif, M.; Claude, F. Extended kalman filter for accurate state of charge estimation of lithium-based batteries: A comparative analysis. Int. J. Hydrog. Energy 2017, 29033–29046. [Google Scholar] [CrossRef]
- Xia, B.; Lao, Z.; Zhang, R.; Tian, Y.; Chen, G.; Sun, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M.; et al. Online Parameter Identification and State of Charge Estimation of Lithium-Ion Batteries Based on Forgetting Factor Recursive Least Squares and Nonlinear Kalman Filter. Energies 2018, 11, 3. [Google Scholar] [CrossRef]
- Mauracher, P.; Karden, E. Dynamic Modelling of Lead-acid Batteries using impedance spectroscopy for Parameter Identification. Power Sources 1997, 67, 69–84. [Google Scholar] [CrossRef]
- Shepherd, C.M. Design of Primary and Secondary Ceils: II. An Equation Describing Battery Discharge. J. Electochem. Soc. 1965, 112, 657–664. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.-A. Experimental Validation of a Battery Dynamic Model for EV Applications. World Electr. Veh. J. 2009, 3, 289–298. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.-A.; Dekkiche, A. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the VPPC, Arlington, TX, USA, 9–12 September 2007; pp. 284–289. [Google Scholar] [CrossRef]
- Barillas, J.K.; Li, J.; Günther, C.; Danzer, M.A. A comparative study and validation of state estimation algorithms for Li-ion batteries in battery management systems. Appl. Energy 2015, 155, 455–462. [Google Scholar] [CrossRef]
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
- Windarko, N.A.; Choi, J.; Chung, G. SOC estimation of LiPB batteries using Extended Kalman Filter based on high accuracy electrical mode. In Proceedings of the ICPE, Jeju, Korea, 30 May–3 June 2011. [Google Scholar]
- Vasebi, A.; Partovibakhsh, M.; Taghi Bathaee, S.M. A novel combined battery model for state-of-charge estimation in lead-acid batteries based on extended Kalman filter for hybrid electric vehicle applications. Power Sources 2007, 174, 30–40. [Google Scholar] [CrossRef]
- Vasebi, A.; Partovibakhsh, M.; Taghi Bathaee, S.M. Predicting state of charge of lead-acid batteries for hybrid electric vehicles by extended kalman filter. Energy Convers. Manag. 2008, 49, 75–82. [Google Scholar] [CrossRef]
- Ting, T.O.; Man, K.L.; Lei, C.; Lu, C. State-of-charge for battery management system via Kalman filter. Eng. Lett. 2014, 22, 75–82. [Google Scholar]
- Singh, B.; Singh, B.N.; Chandra, A.; Al-Haddad, K.; Pandey, A.; Kothari, D.P. A Review of Single-Phase Improved Power Quality AC–DC Converters. IEEE Trans. Ind. Electron. 2003, 50. [Google Scholar] [CrossRef]
- Lidula, N.W.A.; Rajapakse, A.D. Microgrids research: A review of experimental microgrids and test systems. Renew. Sustain. Energy Rev. 2011, 15, 186–202. [Google Scholar] [CrossRef]
- Nayar, C.; Tang, M.; Suponthana, W. Wind/PV/Diesel Micro Grid System implemented in Remote Islands in the Republic of Maldives. In Proceedings of the ICSET, Singapore, 24–27 November 2008; pp. 1076–1080. [Google Scholar] [CrossRef]
- Bakhouya, M.; NaitMalek, Y.; Elmouatamid, A.; Lachhab, F.; Berouine, A.; Boulmrharj, S.; Ouladsine, R.; Felix, V.; Zine-dine, K.; Khaidar, M.; et al. Towards a Data-Driven Platform using IoT and Big Data Technologies for Energy Efficient Buildings. In Proceedings of the CloudTech, Rabat, Morocco, 24–26 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Nait Malek, Y.; Kharbouch, A.; El Khoukhi, H.; Bakhouya, M.; Deflorio, V.; Elouadghiri, D.; Latre, S.; Blondia, C. On the use of IoT and Big Data Technologies for Real-time Monitoring and Data Processing. Procedia Comput. Sci. 2017, 113, 429–434. [Google Scholar] [CrossRef]
- Zeng, Z.; Tian, J.; Li, D.; Tian, Y. An Online State of Charge Estimation Algorithm for Lithium-Ion Batteries Using an Improved Adaptive Cubature Kalman Filter. Energies 2018, 11, 59. [Google Scholar] [CrossRef]
- Boulmrharj, S.; NaitMalek, Y.; El Mouatamid, A.; Ouladsine, R.; Bakhouya, M.; Ouldmoussa, M.; Zine-dine, K.; Khaidar, M.; Abid, R. Towards a Battery Characterization Methodology for Performance Evaluation of Micro-Grid Systems. In Proceedings of the SEST, Sevilla, Spain, 10–12 September 2018. [Google Scholar] [CrossRef]
- Stroe, D.-I.; Swierczynski, M.; Stroe, A.-I.; Knudsen Kær, S. Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries. Batteries 2016, 2, 37. [Google Scholar] [CrossRef]
- GuidEnR PHOTOVOLTAIQUE. Available online: http://www.photovoltaique.guidenr.fr/cours-photovoltaique-autonome-1/application-formule-calcul-puissance-crete-photovoltaique.php (accessed on 20 April 2016).
- Elmouatamid, A.; Nait Malek, Y.; Ouladsine, R.; Bakhouya, M.; Elkamoun, N.; Zine-Dine, K.; Khaidar, M.; Abid, R. Towards a Demand/Response Control Approach for Micro-grid Systems. In Proceedings of the ‘CoDIT’2018, Thessaloniki, Greece, 10–13 April 2018. [Google Scholar] [CrossRef]


| Parameters | E0 (V) | R (Ω) | K (Ω or V/Ah) | A (V) | B (Ah−1) |
|---|---|---|---|---|---|
| Values | 13.32 | 0.54306 | 0.0531 | 1.557 × 10−5 | 1.7233 |
| Parameters | E0 (V) | R (Ω) | K (Ω or V/Ah) | A (V) | B (Ah−1) |
|---|---|---|---|---|---|
| Values | 13.64 | 0.514 | 0.0465 | 6.94 × 10−5 | 1.31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boulmrharj, S.; NaitMalek, Y.; Elmouatamid, A.; Bakhouya, M.; Ouladsine, R.; Zine-Dine, K.; Khaidar, M.; Siniti, M. Battery Characterization and Dimensioning Approaches for Micro-Grid Systems. Energies 2019, 12, 1305. https://doi.org/10.3390/en12071305
Boulmrharj S, NaitMalek Y, Elmouatamid A, Bakhouya M, Ouladsine R, Zine-Dine K, Khaidar M, Siniti M. Battery Characterization and Dimensioning Approaches for Micro-Grid Systems. Energies. 2019; 12(7):1305. https://doi.org/10.3390/en12071305
Chicago/Turabian StyleBoulmrharj, Sofia, Youssef NaitMalek, Abdellatif Elmouatamid, Mohamed Bakhouya, Radouane Ouladsine, Khalid Zine-Dine, Mohammed Khaidar, and Mostapha Siniti. 2019. "Battery Characterization and Dimensioning Approaches for Micro-Grid Systems" Energies 12, no. 7: 1305. https://doi.org/10.3390/en12071305
APA StyleBoulmrharj, S., NaitMalek, Y., Elmouatamid, A., Bakhouya, M., Ouladsine, R., Zine-Dine, K., Khaidar, M., & Siniti, M. (2019). Battery Characterization and Dimensioning Approaches for Micro-Grid Systems. Energies, 12(7), 1305. https://doi.org/10.3390/en12071305





