Abstract
Side channel pumps are important machines for handling toxic, explosive or other dangerous liquids in various engineering processes. However, the operational reliability of these pumps is directly affected by the intensity of the pressure and velocity fluctuations, thus the flow fluctuations existing within the pump cannot be neglected because of their direct influence on the noise, vibration and harshness performance. Therefore, describing precisely the zones of highly unsteady and turbulent flow fields is a key research topic. Moreover, the size of the wrapping angle strongly affects the levels of pressure and velocity fluctuations, thus numerical calculations of the pressure and velocity fluctuation intensities in side channel pump models with different wrapping angles were conducted in this work. The results indicated that the pressure fluctuation coefficient increased gradually from the inflow to the outflow. At the interrupter, the flow experienced the most irregular flow patterns in the pump. The flow at the inflow region in both the impeller and side channel passage rendered weak pressure fluctuation intensities. All three pump cases operated with 24 blades but after one complete circulatory cycle, cases 1, 2 and 3 revealed 21, 20 and 19 regular pressure fluctuations respectively in the impeller flow passage. On the other hand, the side channel flow passage rather produced 24 regular pressure fluctuations. Furthermore, the main frequency harmonic excitations for all studied monitoring points in the impeller and side channel flow passages of the three pump cases occurred at 600 Hz (24 × fn), 1200 Hz (48 × fn), and 1800 Hz (72 × fn). For this reason, exchanged flow times between the impeller and side channel is mainly responsible for the pressure fluctuation which subsequently affects the noise and vibration generation in the side channel pump. Hence, the results could be used as a reference for Noise-Vibration-Harshness (NVH) study in turbomachinery especially modifying the side channel pump in order to improve the operational reliabilities for many engineering processes.
1. Introduction
A side channel pump is a kind of small sized regenerative pump with low flow rate but high head. Most side channel pumps can handle toxic, explosive or other dangerous liquids, guaranteeing a high level of safety in various chemical engineering processes. The flow inside the side channel pump is very complex because the fluid travels from the inlet to the outlet through a helical path [1]. Therefore, the operation of this pump experiences vortex and turbulent flows as a result of unsteady pressure and velocity fluctuations. These turbulent effects cause various irregular flow patterns which eventually does not only affect the reliability of the operational system, but also reduces the hydraulic performance of the machine [2,3].
To predict the pressure and velocity fluctuations, the three-dimensional (3D) flows based on the unsteady Reynolds-averaged Navier-Stokes, RANS equations have been studied on other common pumps with the help of computational fluid dynamics, CFD. Cavazzini et al. [4] analyzed the unsteady flows in a radial flow pump caused by the rotor-stator interaction. Rodriguez et al. [5] focused on centrifugal pump turbine for which they studied the frequencies of the unsteady flows which are responsible for the vibrations and noise generated. The time-frequency history of the turbulent patterns of the flow in centrifugal pumps was revealed by Pavesi et al. [6]. The authors of [7,8] simulated unsteady pressure oscillations in different hydraulic machines. Yin et al. [9] also predicted the fluctuating pressure fields in a pump turbine by considering the effects of water compressibility. Pei et al. [10,11] successfully utilized statistical methods to analyze the CFD results to characterize the unsteady pressure zones in a radial single-blade centrifugal pump.
Interestingly, the above researchers concentrated much attention on high-specific speed pumps. Meanwhile, a side channel pump operates at low specific speed (ns) with a magnitude range of 5 to 20 [12]. Due to its unique flow characteristics, it has attracted a lot of research attention after Siemen and Hinsch [13] first designed it. The momentum exchange theory used by Engels [14], Iverson [15] and Grabow [16] has been considered to be more efficient in predicting the flow behavior inside the side channel pump. Badami [17] analyzed the flow pattern in a regenerative pump using the theoretical and experimental methods. The effects of blade angle on the hydraulic performance characteristics of a regenerative pump were also studied by Choi et al. [18]. Maity et al. [19] investigated the inner flow behavior of a regenerative pump using CFD for performance prediction. Zhang et al. [20] reported that axial and radial clearances of a side channel pump greatly affect the magnitude of flow losses as well as the pump efficiency. Fleder and Bӧhle [21] conducted numerical and experimental studies on different geometrical conditions such as blade length, blade width and side channel height to analyze the internal flow characteristics and its influence on the hydraulic performance of a side channel pump. Recently, Zhang et al. [22,23] put forward that the greater blade suction angle, the higher the head performance. Even though, the blade suction angle had a minimal effect on the efficiency, the blades profiled with suction angle 30° produced optimal performance compared to 10° and 20°. Again, Zhang et al. [23] in 2018 studied the transient flow characterization of side channel pump under different time steps.
However, the above studies on side channel pumps concentrated on hydraulic performance rather than unsteady flow fluctuations. Meanwhile, the unsteady flow fluctuations directly affect the operational reliability of the pump which subsequently affects the safety of engineering processes. Therefore, it is absolutely necessary to investigate the pressure and velocity fluctuation intensity in details to help evaluate the 3D unsteady flow fields in side channel pumps. On the other hand, the interrupter is a fundamental part of the side channel pump because it prevents reverse flows from the outflow to the inflow and also has an influence on the pumping region. The interrupter is bounded by an angle called the wrapping angle, φ. However, very few studies have been conducted on the geometry of the interrupter. Pei et al. [24] predicted the hydraulic performance of a side channel pump model using three different wrapping angles. The pump model with the smallest wrapping angle predicted the highest performance at all operating conditions. This present study uses the same side channel pump models employed in the study of Pei et al. [24]. Here, the effects of the size of the wrapping angle on the flow fluctuations are studied by solving the 3D unsteady flow equations using the Shear Stress Transport (SST) k-ω turbulence model. The numerical results are further analyzed using statistical methods to delineate the unsteady flow fields within side channel pump models with different wrapping angles. The results of this study can serve as a point of reference during optimization of geometrical and operational parameters of a side channel pump for engineering processes.
2. Pump Geometry
The pump models in this study are generated using 3D modeling software UG 11. Three different side channel pump models with different wrapping angles are generated. The pump models with wrapping angle, φ 15°, 30° and 45° are labeled as case 1, case 2 and case 3 respectively. The selected wrapping angles are multiples of 15° which equals the blade pitch. The specific speed (ns = nQ0.5/H0.75) of the pump models is 8.6. The models composed of 24 isosceles-triangular shaped impeller blades designed with suction angle 30° and circular side channel as shown in Figure 1. The rotating speed of the shaft is designed to operate at 1500 r/min and the radial and axial gaps are set to 0.2 mm. Table 1 summarizes the main geometrical parameters of the pump models.
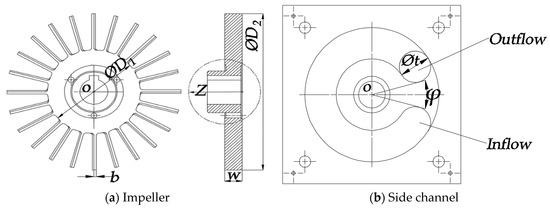
Figure 1.
3D model of a side channel pump.

Table 1.
Main geometrical parameters.
3. Numerical Calculations (CFD) Setup
3.1. Governing Equations
In order to delineate the flow fluctuation intensity caused by the flow exchange between the impeller and side channel, numerical calculations are carried out. For incompressible fluid, the continuity equation and Reynolds averaged Navier-Stokes equations are given as:
Here, is the Reynolds stress tensor which is given as:
is the Kronecker delta, i, j = 1, 2, 3
Menter’s [25,26], SST k-ω turbulence model is utilized to solve the continuity, and momentum fluid equations because of its enhanced prediction of adverse pressure gradient flows. Primarily, the SST model cannot predict flows in rotating frames of reference because its values do not change when arbitrary rotations are applied to its arguments (rotationally invariant) hence the k-ω equations are employed. Wilcox [27,28,29] developed the present equations from the stress transform eddy-viscosity models. One for turbulent kinetic energy, k and the other for turbulent frequency, ω. The k-ω equations are used to calculate flows around the inner boundary layers. The equations switch to k-ε equations which are extremely sensitive to the free-shear layers. Therefore, k-ε equations are modified into k-ω equations with a blending functions F1 and F2.
k-ω equations:
Transformed k-ε model:
The blending functions F1 and F2 are:
The turbulent viscosity, µt is calculated using:
The k-ω equation for the inner boundary layer prediction is applied using the following coefficients: σk1 = 1.176, σω1 = 2.0, β1 = 0.075, α1 = 5/9, β′ = 0.09 [30]. Meanwhile, the k-ε equation for the free-stream flows is solved using the following coefficients: σk2 = 1.0, σω2 =1/0.856, β2 = 0.828 [30].
3.2. Mesh Independence Analysis
The ICEM CFD meshing tool is used to build three dimensional multi-block structured computational grids of the inlet, impeller, side channel and the outlet for all the three pump cases. The mesh independence and grid convergence analyses have been conducted by Pei et al. [24]. Pump case 2 is selected for the analysis of the effect of the mesh number on the head performance at the best efficiency point, QBEP. Figure 2 shows the mesh independence analysis carried out on pump case. The head is calculated using Equation (11). The mesh C which consist 4.5 million is selected for further numerical calculations after following the procedures outlined by Celik et al. [31]. For consistency with the mesh independence analysis, cases 1 and 3 are then gridded with the same blocking method with an approximated grid number of pump cases 1 and 3.
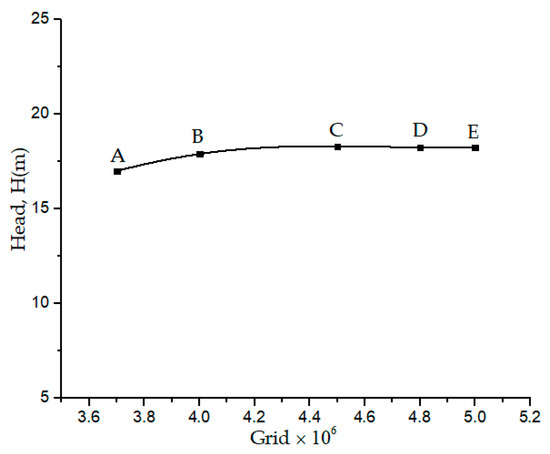
Figure 2.
Mesh independence analysis.
Figure 3 shows the overview of the mesh generated. The impeller, side channel and inlet are meshed with 0.1 million, 3.4 million and 1.0 million, respectively. The grids for the impeller and side channel interface are refined with large numbers for high precision.
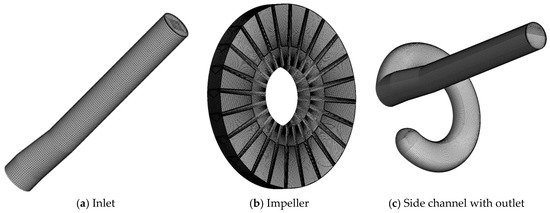
Figure 3.
Structured computational flow domain grids.
3.3. Boundary Conditions Settings
The three-dimensional unsteady RANS equations are solved with the aid of CFX commercial software at different operating conditions. The inlet boundary layer is specified with a total pressure of 1000 Pa and the flow is directed normal to the inlet condition. The outlet boundary layer is set to opening with the corresponding axial cylindrical components at the various operating conditions. The reference pressure value is set to 1 atm. The walls of the impeller blades and side channel are assigned to no slip condition for the flow passage. The temperature of the water used was at 25 °C. In order to predict the highly turbulent flow patterns within the side channel pump, SST k-ω is adopted for the numerical calculations with a 5% turbulent intensity [18,19]. The interface between the impeller and the side channel is set as frozen rotor. The above setting conditions are set for the steady state calculations for 1000 iterations. The solutions from the steady state simulations could not describe precisely thus adopted as an initiation for the unsteady calculations. With the transient calculations, the interface between the impeller and side channel is changed to transient rotor-stator state. The relative position between the moving impeller flow domain and the stationary side channel domain is updated within every time-step of 1.111 × 10−4 s corresponding to one degree. The chosen time step is small enough to acquire the necessary time resolution. A maximum of 10 iterations are carried out at each time step and the convergence criterion at maximum residual is limited to 1.0 × 10−6. Time discretization is carried out with the second order backward Euler scheme. The impeller is set to rotate for six complete revolutions representing a total time of 2.4 × 10−1 s to predict and evaluate the unsteady flow fields at various monitoring points at different operating conditions.
3.4. Monitoring Points
The pressure flow parameter is monitored in the impeller and side channel at different locations as indicated in Figure 4. “D” stands for diameter line in both impeller and side channel while P1, P2 and P3 represent the outer radius, central radius and inner radius of the blade respectively. Furthermore, S1, S2 and S3 represent the side channel flow-in from the impeller, side channel central radius and side channel flow-out to the impeller passage, respectively. A distance of 0.008 m is set between P1–P2, P2–P3, S1–S2 and S2–S3. The angle between D4–D8 is 90° with 15° between each two successive impeller blades. The angle between adjacent diameter lines D1-D5 was 90°. All the static pressure data in the impeller passage are recorded at z = 0.0025 m which is close to the impeller side channel interface whiles in the side channel passage, z is set at −0.007 m.
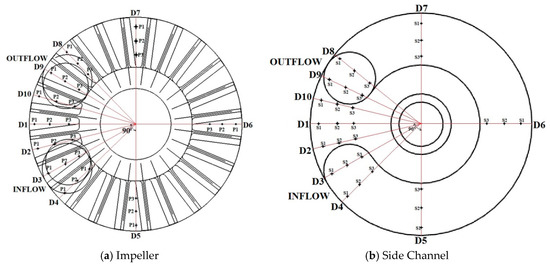
Figure 4.
Monitoring points for three pump cases.
4. Results and Discussion
4.1. Hydraulic Performance Characteristics
To delineate the unsteady flow fields in the pump, verification of the CFD or numerical results with respect to the experimental data is required. Pump case 2 is manufactured for the experimental test measurements to give global view of all the pump cases. For the purpose of numerical calculations, the lengths of inlet and outlet pipes are extended to about four times the pipe diameter. This is done to achieve a fairly stable flow and accurate results. Figure 5 shows a 2D sketch of the experimental test rig used. The experimental test rig is a closed loop system equipped with calibrated device for input power, flow rate, inlet pressure and discharge pressure measurements. The inlet and discharge pressures are obtained by pressure sensors of measuring range 0 to 10 bar with uncertainty of 0.15%. The volumetric flow rate of each operating condition is measured with electromagnetic flow meter (0.9–30 m3h−1) and its maximum measuring error is ±0.5%. The shaft power of the tested pump is driven by variable-speed electric AC motor and controlled by a frequency drive of 0 to 50 Hz. The readings (20 sample data) are taken at constant speed for each valve opening at different flow rates.
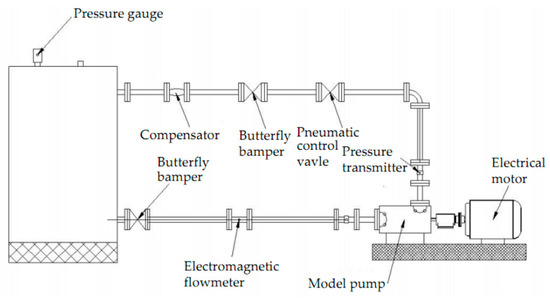
Figure 5.
2D sketch of the experimental test rig.
The hydraulic performance measurements are taken twice and the average values are used. This is done to ensure the reliability of results. The comparison of the hydraulic performance between the CFD and experimental results of the side channel pump model which operated at n = 1500 r/min is shown in Figure 6. The head coefficient, ψ and efficiency, η are subsequently computed using the following relations:
where H is the head, Q is the volumetric flow rate, and M is the torque of the shaft.
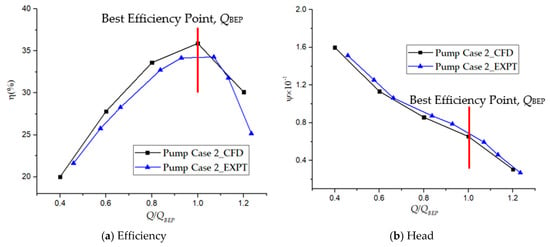
Figure 6.
Performance curves comparison of the test pump.
The CFD heads and efficiencies at all operating conditions are obtained by averaging the values during the last two impeller revolutions. As illustrated in Figure 6a, the efficiency and flow rate ratio Q/QBEP are potted on the y and x axes, respectively. The efficiency curve increases gradually and decreases after the best efficiency, QBEP. The QBEP marks the maximum efficiency and highlighted in red. The value of the QBEP is 10 m3h−1. The CFD efficiency is higher than the experimental measurements at all operating conditions. This is because mechanical losses were not taken into consideration during the numerical calculations. The QBEP of the CFD efficiency curve is 35.9% whereas that of the experimental efficiency is 34.2%. The largest deviation on the efficiency curves occurs at the QBEP and is about 4.90%. Figure 6b shows that higher head values are concurrent with lower flows. The rise in pressure is due to the high circulatory velocity the fluid attains at low flows [32]. Largely, the experimental heads are higher than the CFD heads. The best agreement between the curves occurred at part-load conditions from 0.4 QBEP to 0.8 QBEP. At the QBEP, the deviation between the experimental and CFD head coefficients is 5.27%. This shows that there is a good agreement between the CFD and experimental results thus the CFD results can be used for further analyses. However, the hydraulic performance comparison of the three pump cases has been conducted in details by Pei et al. [24].
4.2. Pressure Fluctuation Intensity
4.2.1. Definition of Pressure Fluctuation Intensity
The pressure fluctuation coefficient is calculated on every grid in the flow domains using the statistical approach. This approach will aid in characterizing the zones in the side channel pump which are of highly unsteady and undesirable flows [33,34]. The instantaneous pressure, p on each grid node is decomposed into two pressure variables defined in Equations (14) and (15). The periodic pressure variable, which is produced as result of the periodical difference in the blade passing frequency (BPF), and the time-averaged variable, .
Time-Averaged Pressure Variable:
Periodic Pressure Variable,
The pressure is then normalized with respect to the density of the fluid and circumferential velocity at the impeller outlet using Equation (16) to predict a non-dimensional pressure fluctuation intensity coefficient, of all grid nodes in one complete oscillation of the blade:
where N is the number of samples during one period, t0 represents the initial time for the transient calculations and is the time-step for the transient calculation, j is the number of time-steps. It is worth noticing that, and defined in Equation (21) are independent of instantaneous rotating time and position.
4.2.2. Impeller Passage
The axial planes generated inside the side channel pump are depicted clearly in Figure 7. Plane 1 is set close to the impeller-side channel interface on the XY axis where z = 0. Plane 2 is set in the side channel also in the XY axis but at z = −0.0021 m. The angular position of the flow is described with reference to the relative position, ϕ = 0.
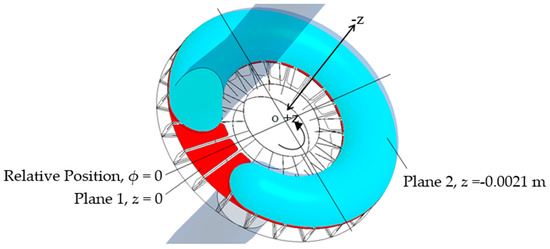
Figure 7.
Axial planes view.
Figure 8 compares the pressure fluctuation intensity in the impeller passage for the three pump cases on the plane 1. It can be seen that, the pressure fluctuation intensity along the suction side is higher than the pressure side around the same region of the three pump cases. On the suction side, the central radius (P2) of the impeller blade is characterized with high pressure fluctuation values compared to inner (P3) and outer radius (P1).
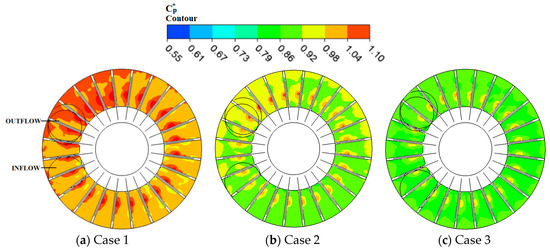
Figure 8.
Pressure fluctuation intensity of impeller passage for three pump cases on plane 1.
Pump cases 1, 2 and 3 at central radius (P2) on the suction side marked values of 1.04~1.10, 0.92~1.10 and 0.79~1.04, respectively. This is largely caused by the fact that there is no energy exchange occurring at the central radius of the impeller blade. The high pressure fluctuation at the central radius increases gradually from inflow to outflow whereas the pressure fluctuation intensity on the outer radius is larger than the inner radius in all cases. Since the flow is incompressible, the strong pressure fluctuation intensity values observed at angular position 292.5° to 322.5° in all three cases are produced by the high energies attained by the fluid as each blade approaches the outflow region. Due to the absence of side channel at the interrupter there was no flow exchange as a result the pressure fluctuation intensity drops. The drop in pressure fluctuation is minimal in case 1 compared to case 2 whiles case 3 experiences the maximal drop. According to this figure, pump case 1 reaches the highest pressure fluctuation intensity ( = 1.04~1.10) within the whole impeller passage at all regions especially around the outflow. The pressure fluctuation intensity within case 2 is moderate ( = 0.86~1.10) while case 3 measures the lowest pressure fluctuation intensity ( = 0.73~1.04) from the inflow to outflow regions. This is because pressure fluctuation intensity decreases with increasing wrapping angle thus the energy exchange between the impeller and side channel passages becomes intense with small wrapping angles.
4.2.3. Side Channel Passage
Largely, the side channel passage of all three pump cases marks higher pressure fluctuation intensity on plane 2 than the impeller passage in Figure 9. The inflow regions of the three cases presented very low pressure fluctuation intensity because of the small centrifugal force imparted unto the incoming flow by the impeller. Around the middle section of the side channel of angular position (172.5°–217.5°) where the flow is assumed to achieve its full flow features, high pressure fluctuation intensities are recognized at the side channel flow-out (S3) for all cases. Figure 10 gives a reason to why high pressure fluctuation, values are observed at S3 because the sudden change geometry of the side channel results in vortex flows developed around angular position (172.5°–217.5°). High of about 1.10 is recorded around the outflow region for case 1 compared to the two pump cases. This is an indication that, the outflow region of case 1 is characterized with weak velocity developing into strong vortices at the outflow compared to cases 2 and 3 as shown in Figure 9. On the other hand, case 2 comparatively reaches higher intensity of pressure fluctuation than case 3 at the outflow region. Generally, higher pressure fluctuation intensities are associated with the vortices generated along the same positions in Figure 8. Subsequently, smaller wrapping angle yields higher pressure fluctuation intensity within the whole pump flow passage.
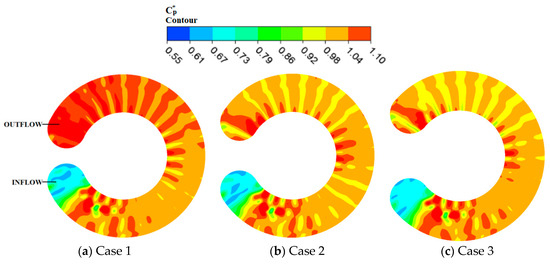
Figure 9.
Pressure fluctuation intensity of side channel passage for three pump cases on plane 2.
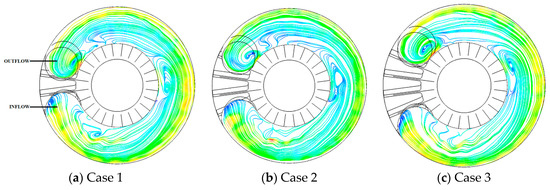
Figure 10.
Velocity streamline plots.
4.3. Time Domain History of Pressure Fluctuation Intensity at Monitoring Points
For the time-dependent history, the non-dimensional pressure coefficient is Cp is defined in Equation (17). This relation is to determine the periodic pressure with respect to time and the impeller rotation angle:
4.3.1. Inflow Region
Figure 11 compares the time domain of static pressure fluctuation intensities, Cp of the inner radius (D3P3) and outer radius (D3P1) inside the impeller passage for all three cases at the inflow region. The pressure coefficient, Cp is plotted on the y and the timestep of the impeller rotation is plotted on the x-axis. The timestep is measured in degree. According to Figure 11, negative Cp value refers to a pressure that is lower than the reference point, which is selected at the inflow. The diameter line, D3 is located 30° from the relative position, ϕ. The pressure amplitudes of all pump cases depict a gentle rise from the inflow to outflow except in the interrupter region where significant amount of pressure energy is lost because there is no exchange of flow. All three pump cases operate with a 24 blade impeller but in case 1 during the flow exchange between the impeller and side channel at both D3P1 and D3P3, 21 regular fluctuations of the pressure appeared in a complete circulatory cycle of the impeller. During the complete circulatory cycle, one blade stays in the interrupter and the other two at the inflow and outflow regions respectively. Case 2 reveals 20 regular pressure fluctuations with two blades in the interrupter while one blade is at inflow region and another in the outflow region in complete circulatory cycle. Pump case 3 on the other hand shows 19 regular pressure fluctuations because it has the largest wrapping angle. Three blades stay in the interrupter in a complete circulatory cycle while the other two are close to the inflow and outflow regions. So, the number of circulations can easily be found as a function of the number of impeller blades.
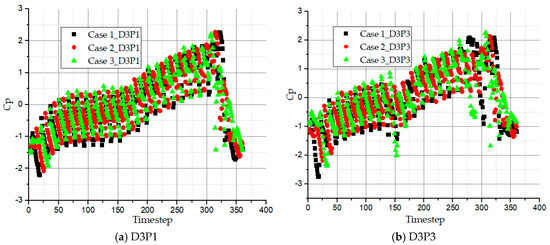
Figure 11.
Time domain history of pressure fluctuation coefficient in impeller passage at inflow region for all pump cases.
It is revealed that the static pressure fluctuation intensity at D3P1 and D3P3 monitoring points are very low for all three pump cases especially in case 3 where Cp = −1.43 and −1.18 at D3P1 and D3P3 respectively. Even though, D3P1 at the inflow region is expected to attain higher static pressure, D3P3 for all three pump cases record higher pressure fluctuation intensity than D3P1. This is due to the fact that at the inflow region, the incident fluid from the inlet pipe begins to experience the centrifugal force imparted by the blades in the impeller flow passage and also the high-pressurized fluid in the blade passage interfered with the low-pressurized flow from the inlet pipe. This phenomenon makes the inflow region highly susceptible to vortex and generation of unwanted noise for all pump cases. The flow exchange between the impeller and side channel is mainly responsible for the pressure fluctuations generated in side channel pumps. The fluctuation times are dependent on the exchange times thus the smaller the wrappings angle the higher fluctuation frequency.
The time domain histories of pressure fluctuations at monitoring points D3S1 and D3S3 respectively in the side channel of the three pump cases are illustrated in Figure 12. Generally, the low regular coefficient of pressure fluctuation intensities at the side channel flow-in and flow-out at the inflow region almost coincide in all pump cases. Pump case 3 marks the weakest pressure fluctuation intensity coefficients at D3S1and D3S3 while case 1 marks the highest. Moderate coefficient pressure fluctuation intensities are registered by pump case 2. In one complete circulatory cycle, the flow at D3S1 and D3S3 in all three pump cases fluctuate 24 times which equal the blade number. This confirms that, the pressure fluctuation times in the side channel depend on its interaction with the rotating impeller and also the side channel coverts the fluid kinetic energy to pressure energy.
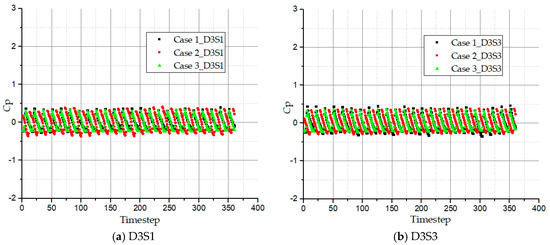
Figure 12.
Time domain history of pressure fluctuation coefficient in side channel passage at inflow region for all pump cases.
4.3.2. 180° Offset Region
The pressure fluctuation coefficient histories of inner radius, D6P1 and outer radius, D6P3 at 180° from the relative position, ϕ are as illustrated in Figure 13. At this angular position, the fluid is expected to develop its full flow characteristics and have sufficient fluid power after undergoing about twelve impeller turns, yet the inner radius D6P3 records greater coefficient of pressure fluctuation than D6P1. This happens because portions of the flow exit from the inner radius due to the sudden change in geometry at this angular position. For cases 1 and 2, the flow leaves the impeller with similar pressure coefficient at the D6P1 at the end of the circulatory cycle which are higher than case 3. This still indicates that the smaller the wrapping angle the stronger the flow exchange in the impeller becomes, therefore the pressure fluctuation intensity increases.
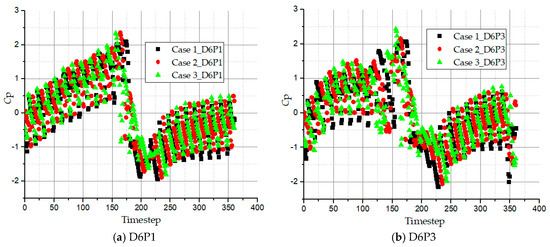
Figure 13.
Time domain history of pressure fluctuation in impeller passage at 180° offset region for all pump cases.
Comparing monitoring points D6S1 and D6S3 in Figure 14 for all pump cases, it is realized that a minimal pressure difference is recorded between side channel flow-in, D6S1 and flow-out, D6S3. It can be established that the side channel hardly add energy to the flow but mainly aids in the transportation of the fluid from inflow to outflow. The pressure fluctuation intensities of these monitoring points show 24 regular pressure fluctuations in a complete circulatory cycle.
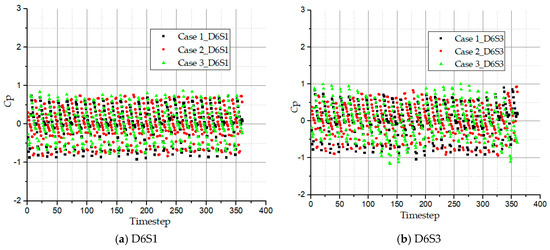
Figure 14.
Time domain history of pressure fluctuation in side channel at 180º offset region for all pump cases.
Overall, case 3 marks the weakest pressure fluctuation coefficient while cases 1 and 2 attain similar magnitudes at both D6S1 and D6S3 points. Again, monitoring points D6S1 and D6S3 show larger coefficient range of the pressure fluctuation values compared to D3S1 and D3S3. Thus, pressure fluctuation intensity in the side channel is mainly influenced by the interaction of the rotating impeller and side channel.
4.3.3. Outflow Region
The outflow region is characterized with high static pressure at D9P1 (blade outer radius) and D9P3 (blade inner radius) because the flow has undergone about 22 impeller turns from the relative position, ϕ to develop a very strong pressure. In Figure 15, the pressure fluctuation coefficient of D9P1 and D9P3 present regular amplitudes except for the interrupter, inflow and outflow regions. As mentioned earlier, the pressure fluctuations of the monitoring points are affected by the flow exchange times which subsequently depend on the size of the wrapping angle. Case 1 reaches the highest pressure at D9P1 and D9P3 than the other two cases at the end of the complete circulatory cycle. Case 1 has the shortest interrupter length therefore the flow is exchanged many times than the other two pump cases.
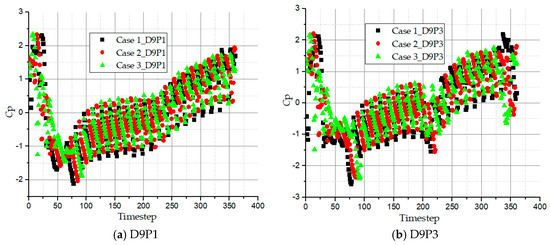
Figure 15.
Time domain history of pressure fluctuation coefficient in impeller passage at outflow region for all pump cases.
Figure 16 depicts the pressure fluctuation coefficients of monitoring points D9S1 and D9S3 in the side channel passage. The pressure fluctuations at these points also reveal 24 regular amplitudes in one complete oscillation which represents the blade number. Similarly, the side channel also records high pressures at the side channel in-flow, D9S1 and out-flow, D9S3. The reason is that, the flow leaves the blade outer radius (D6P1) with very high pressure energy compared to the other monitoring points. The pressure coefficient of the pressure of case 1 at both D9S1 and D9S3 are slightly higher than case 2 while that of case 2 is also higher than case 3. This shows that decreasing the wrapping angle produces high pressure fluctuation intensities.
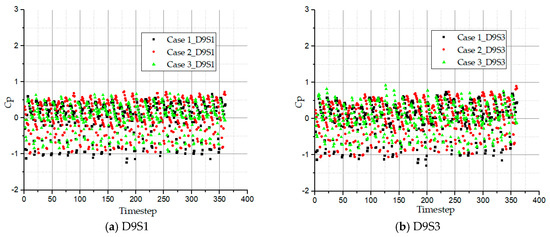
Figure 16.
Time domain history of pressure fluctuation coefficient in side channel passage at outflow region for all pump cases.
4.3.4. Interrupter Region
Figure 17 shows that, the flow depicts a gradual increase of the pressure fluctuation coefficient from the inflow to the outflow until it reaches the interrupter. The time for the abrupt change in the pressure fluctuation coefficient of the two monitoring points for all pump cases is equal to the rotation time for the interrupter. The unsteady pressure fluctuation intensity at the interrupter is due to the absence of the side channel thus the interrupter greatly affects the pressure fluctuation intensity inside the side channel pump. It can be seen that there is no significant difference in pressure fluctuation coefficient between D1P1 and D1P3. There is a sharp decrease in static pressure for case 1 while case 2 displays a moderate decrease. Case 3 with wrapping angle 45° shows a much regular decrease in the pressure amplitudes at the interrupter region. Therefore, smaller wrapping angle causes sharper drop in pressure whereas larger wrapping angle produces fairly even drop.
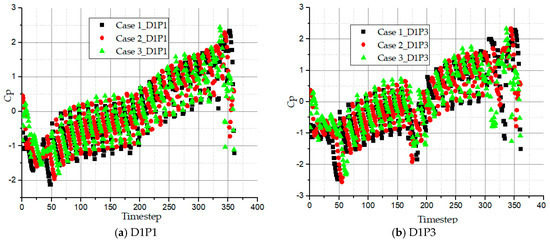
Figure 17.
Time domain history of pressure fluctuation coefficient in impeller passage at interrupter region for all pump cases.
4.4. Frequency Domain History at Monitoring Points
4.4.1. Impeller Passage
Figure 18 presents the history of the frequency domain spectra acquired by using the Fast Fourier Transformation (FFT) analysis of the monitoring points in the impeller passage. The pressure coefficient amplitudes show a decreasing trend with increasing frequency at all monitoring points in the impeller passage. The main pressure fluctuation amplitudes of the frequency domain history in each monitoring point are nearly the same and occurred at the low-frequency region. The pressure intensity amplitudes are mainly subjected to the shaft frequency, fn and the blade passing frequency (BPF). The shaft frequency occurred at 25 Hz while the blade passing frequencies occurred at multiples of the shaft frequency:
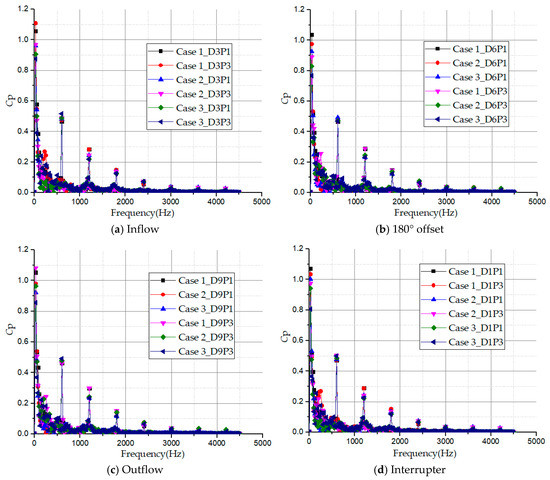
Figure 18.
Frequency domain history of pressure fluctuation in impeller passage for three pump cases.
The frequencies excited by pressure fluctuation occur at 600 Hz (24 × fn), 1200 Hz (48 × fn), 1800 Hz (72 × fn), and continued in the same manner. Here, fn is 25 Hz, the shaft rotating frequency. It is important to note that the excitation of these harmonics is mainly associated with the flow exchange between the impeller and side channel. Likewise, the flow exchange times greatly depends on the size of the wrapping angle and blade numbers. Meanwhile, case 1 marks the highest pressure coefficient amplitude on the blade passing frequency harmonic at all monitoring points in the impeller flow passage. It is therefore obvious that the pressure coefficient amplitudes decreases as the wrapping angle increases from 15° to 45°.
Figure 19 shows much detailed information about the frequency domain (< 600 Hz) at the inflow region in the impeller passage. It can been observed that at shaft frequency, fn at inflow region of case 1 records the highest pressure fluctuation, Cp = 1.06 and 1.11 at D3P1 and D3P3, respectively. Meanwhile, case 3 reaches the lowest Cp at fn and 1st excitation frequency of 600 Hz. In between the shaft and first excitation frequencies are associated noise accompanying flow. These emanating sub-frequencies are from undesirable flow patterns which are mainly caused by the high-pressurized fluid in the impeller passage from outflow to inflow which subsequently tends to mix with the low-pressurized fluid from the suction pipe.
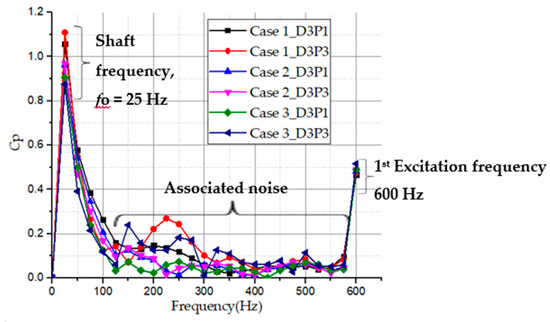
Figure 19.
Detailed frequency domain history of pressure fluctuation in impeller passage for all pump cases below 600 Hz.
4.4.2. Side Channel Passage
The frequency domain history of the monitoring points in the side channel passage is shown in Figure 20. By comparing the frequency coefficient amplitudes in the impeller passage with the side channel passage, the frequencies also excite by pressure fluctuation occurred at 600 Hz (24 × fn), 1200 Hz (48 × fn), 1800 Hz (72 × fn), and continued in the same manner. The pressure fluctuation harmonics of the side channel passage appear at multiples of the shaft frequency and the multiples are related to the blade numbers. Just like the impeller passage, the pressure coefficient amplitudes reduce as the frequency increases. The excited harmonics generated in the side channel also confirm that the pressure fluctuation in the side channel pump is mainly affected by the exchange flow. Predominantly, the pressure coefficient amplitudes at frequencies between 0–200 Hz register relatively low magnitude for all monitoring points especially at the inflow region in Figure 20a. The reason is that the flow receives minimal centrifugal force at the inflow region.
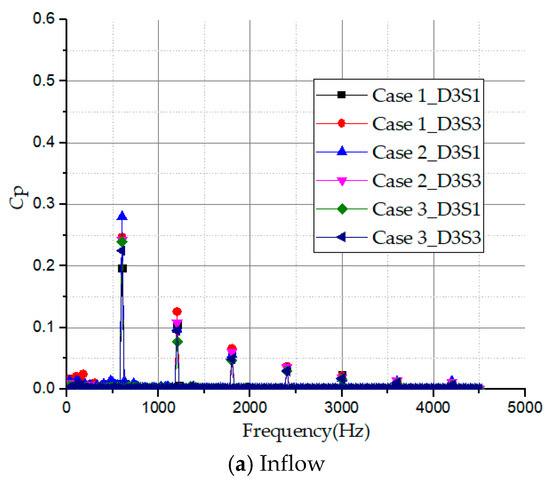
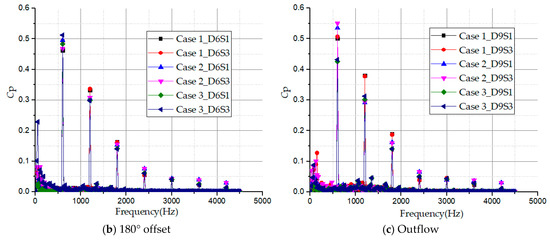
Figure 20.
Frequency domain history of pressure fluctuation coefficient in side channel passage for three pump cases.
4.4.3. Impeller and Side Channel Passages
Figure 21 shows frequency domains of pressure fluctuation in the distinctive monitoring points of the impeller (D3P1) and side channel (D9S3). The main frequencies excited by pressure fluctuation of the impeller and the side channel are the same, namely 600 Hz (24 × fn), 1200 Hz (48 × fn), 1800 Hz (72 × fn) and so on. It still predicts that the flow exchange between the impeller and the side channel is the main reason causing pressure fluctuations both in the impeller and side channel passages. The pressure coefficient amplitude of the selected monitoring point declines gradually with the increasing excited frequency.
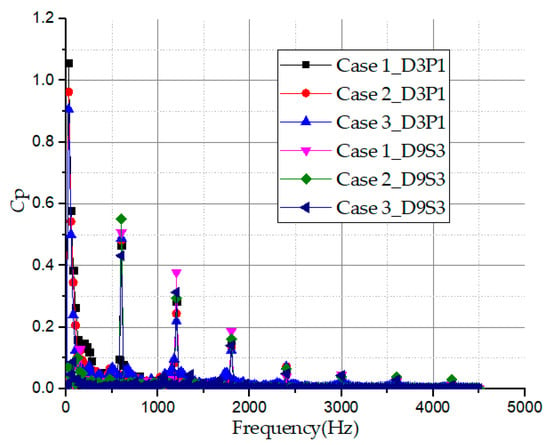
Figure 21.
Frequency domain history of pressure fluctuation of the impeller and side channel passages for three pump cases.
4.5. Relative Velocity Fluctuation Intensity
4.5.1. Definition of Relative Velocity Fluctuation Intensity
The fluctuating velocity intensity is solved with the same method as applied in the case of the pressure fluctuating intensity. On each grid node, the instantaneous relative velocity also comprises two variables which are the time-averaged relative, and the periodic relative, . The relations of these variables are expressed in Equations (19) and (20).
Time-Averaged Relative Velocity Variable:
Periodic Relative Velocity Variable:
The relative velocity is also normalized with respect to the circumferential velocity at the impeller outlet by applying the relation in Equation (21) to determine a non-dimensional relative velocity fluctuation intensity coefficient, of all grid nodes in one complete circulatory cycle:
4.5.2. Impeller Passage
The relative velocity fluctuation intensity is generated on plane 1 (z = 0). As shown in Figure 22, the relative velocity fluctuation intensity on the suction side is greater than the pressure side. In the impeller passage, there is no flow exchange at the central radius which results in large vortex for that reason; the central radius depict the highest relative velocity fluctuation intensity whereas the inner radius mark higher relative velocity fluctuation than the outer radius. As the wrapping angle decreases, the velocity fluctuation intensity on plane 1 of the impeller increases. This is because the velocity fluctuation intensity is affected by the exchange flow between impeller and side channel. The exchange flow times are very dependent on the size of the wrapping angle. The relative velocity intensity of case 3 is the highest. Thus, the vortex magnitude in case 3 is the most intense because of the large wrapping angle compared to the others. Case 2 shows slight increase of relative velocity intensity over case 1 thereby good performance are demonstrated in case 2 and 1 against the vortices developed in the impeller flow passage than case 3. As a result, the smaller the wrapping angle the lower the relative velocity fluctuation.
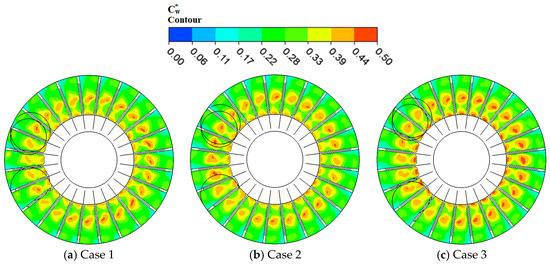
Figure 22.
Velocity fluctuation intensity in impeller passage.
4.5.3. Side Channel Passage
Figure 23 is a representation of the relative velocity fluctuation intensity in the side channel for the pump cases. The relative velocity fluctuation intensity in the impeller passage is higher than the side channel passage. For all the pump cases, at an offset region of about 90° renders a very strong relative velocity fluctuation around the central radius of the side channel which is consistent with the pressure fluctuation intensity in the side channel. This is because the flow around that region acquires minimal centrifugal influence thereby undesirable flows are generated. Furthermore, the side channel flow-out at angular position, 180° and outflow region reveal high relative velocity fluctuation intensity for case 2 while case 3 is low. However, case 1 renders moderate values at these regions. This can be attributed to the irregular flow patterns evolved around these regions.
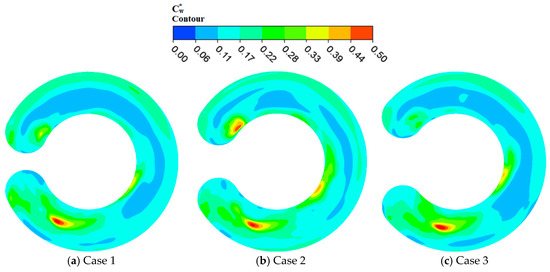
Figure 23.
Velocity fluctuation intensity in side channel passage.
4.6. Turbulent Kinetic Energy Intensity (TKE)
Figure 24 presents the turbulent kinetic energy (TKE) intensity on plane 1 very close to the interface of the impeller and side channel (z = 0) for cases 1, 2 and 3.
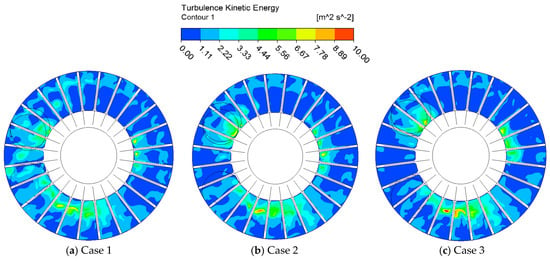
Figure 24.
Turbulent kinetic energy intensity in impeller passage.
TKE is the most important physical quantity in the turbulence model and depends on the turbulence fluctuations, in the turbulent flows within the pump [35]. TKE is defined in Equation (22) as:
The highest TKE within the pump are identified on the impeller inner radius around 82.5°–90°, 172.5°–217.5° offset and outflow regions for all pump cases. The high turbulent kinetic energy corresponds to the increasing kinetic energy which consequently generates high turbulence fluctuations at the impeller inner radius. Thus, the energy dissipation of the fluid is increased which increases the hydraulic loss at the impeller inner radius compared to other regions [27]. Moreover, fairly higher turbulent kinetic energy is recognized at the interrupter region of case 1 compared to case 2 and 3. Averagely, case 1 records the highest turbulent kinetic energy, which suggests that smaller wrapping angle yields higher turbulent kinetic energy.
5. Conclusions
Unsteady flow fields mainly pressure and velocity fluctuations have been studied in details numerically by considering three different wrapping angles 15°, 30° and 45° of side channel pump models. The flow fluctuations monitored at some specific locations in the three pump cases demonstrate interesting results.
The time domain history of the pressure fluctuation coefficients shows a gradual regular increase from the inflow to the outflow regions with the exception of the interrupter. All three pump cases operated with a 24 blade impeller yet cases 1, 2 and 3 revealed 21, 20 and 19 regular pressure fluctuations, respectively, in one complete cycle at all monitoring points in the impeller flow passage. The side channel flow passage rather produced 24 regular pressure fluctuations at all monitoring points in a complete cycle for all three cases. Frequencies excited by pressure fluctuations in both impeller and side channel passages occurred at 600 Hz (24 × fn), 1200 Hz (48 × fn), 1800 Hz (72 × fn), and continued in the same manner. From the time and frequency data, it can be confirmed that the pressure fluctuation intensity is mainly associated with the flow exchange times between the moving impeller and static side channel. The flow exchange is also related to the size of the wrapping angle and the blade number.
The interrupter of the pump experiences the highest pressure fluctuation coefficient due to the absence of the side channel pump causing significant loss of pressure energy. As the wrapping angle reduced the pressure fluctuation intensity became higher because of the effect of the interrupter length. Thus, case 1 predicted the highest and most irregular static pressure fluctuation intensity among case 2 and 3 at the interrupter. The high pressure fluctuation coefficients at the interrupter for the three pump cases are likely to be responsible for the undesirable noise and vibration generation.
Comparing the pressure fluctuation coefficients of the flow that leaves the impeller into the side channel and the flow that re-enters the impeller, it can be concluded that the side channel hardly adds any energy to the flow, but offered a minimal resistance. Therefore, the side channel aids in transportation of the fluid from inflow to outflow. On the whole, case 3 achieved the weakest pressure fluctuation coefficient while cases 1 and 2 attained similar magnitudes, higher than case 3, in the side channel.
In the impeller flow passage, there was little flow exchange at the central radius which resulted in a large vortex; thus, the central radius depicted the highest relative velocity fluctuation intensity in the impeller passage for all pump cases, especially in case 1. The inner radius marked higher relative velocity fluctuation than the outer radius for all pump cases. This makes the central radius and inner radius of the blade key regions to be considered for further studied in order to enhance the vibration and noise performance in side channel pumps. Eventually, case 3 showed the highest relative velocity intensity compared to cases 1 and 2.
Author Contributions
Conceptualization, F.Z. and D.A.; Methodology, D.A. and K.C.; Formal Analysis, B.H.; Resources, S.Y.; Writing—Original Draft Preparation, D.A.; Writing—Review and Editing, K.C. and S.N.A.; Supervision, F.Z. and D.A.
Funding
This research was funded by National Natural Science Foundation of China: 51809121 and 51879121, Natural Science Foundation of Jiangsu Province: BK20170548, Supported by Open Foundation of Zhejiang Provincial Top Key Academic Discipline of Mechanical Engineering (Grant No: ZSTUME02A02) and Senior Talent Research Start-up Foundation of Jiangsu University (Grant No. 17JDG040).
Acknowledgments
The authors express their sincere gratitude to Martin Bӧhle of the SAM in Technical University of Kaiserslautern, Germany for his great support with the experimental test in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| g | Acceleration due to gravity |
| Ω | Angular speed |
| Γ | Auxillary variables in turbulence model |
| s | Axial and radial clearance width |
| Z | Blade number |
| θ | Blade suction angle |
| F1 | Blending or auxillary functions in turbulence model |
| U2 | Circumferential velocity of impeller outlet |
| Cp | Coefficient of pressure fluctuation intensity |
| Cw | Coefficient of velocity fluctuation intensity |
| x, y, z | Coordinates in stationary frame |
| ρ | Density |
| D | Diameter of impeller |
| Δ | Difference |
| ϵ | Dissipation of kinetic energy of turbulence |
| μ | Dynamic viscosity |
| η | Efficiency |
| Q | Flow rate |
| h | Height of the side height |
| ψ | Head coefficient |
| H | Head |
| h | Height of the side height |
| y+ | Non-dimensional wall distance |
| P | Pressure |
| k | Kinetic energy of turbulence |
| δij | Kronecker’s delta |
| n | Rotational speed |
| Reynolds-stress tensor | |
| w | Relative velocity |
| ω | Specific dissipation of turbulence kinetic energy |
| N | Sample number |
| fo | shaft frequency |
| ns | specific speed |
| t | Time |
| M | Torque |
| β*, γ | Turbulence –model coefficients |
| μT | Turbulent viscosity |
| σk, σω | Turbulence-model coefficients |
| ui | Velocity components (u, v, w) in Cartesian directions: x, y, z |
| φ | Wrapping angle |
Subscripts
| 0 | Origin |
| xi | Cartesian coordinates: x, y, z |
| i, j | Components in different directions |
Abbreviations
| BPF | Blade passing frequency |
| 3-D | Three dimensional |
| CFD | Computational fluid dynamics |
| SST | Shear stress transport |
| RANS | Reynolds-averaged Navier-Stokes |
| BEP | Best efficiency point |
| Ave | Average |
References
- Appiah, D.; Zhang, F.; Yuan, S.; Osman, M.K. Effects of the geometrical conditions on the performance of a side channel pump: A review. Int. J. Energy Res. 2017, 42, 416–428. [Google Scholar] [CrossRef]
- Fathi, A.R.; Jalilvand, R.; Shirani, E. Quantitative Evaluation of Influential Coefficients of Regenerative Pumps. In Exergy for a Better Environment and Improved Sustainability 1; Springer: Berlin/Heidelberg, Germany, 2018; pp. 631–643. [Google Scholar]
- Münsterjohann, S.; Becker, S. Wall Pressure and Blade Surface Pressure in a Side Channel Blower. Int. J. Rotating Mach. 2018, 2018, 2308759. [Google Scholar] [CrossRef]
- Cavazzini, G.; Pavesi, G.; Ardizzon, G.; Dupont, P.; Coudert, S.; Caignaert, G.; Bois, G. Analysis of the rotor-stator interaction in a radial flow pump. La Houille Blanche 2009, 5, 141–151. [Google Scholar] [CrossRef]
- Rodriguez, C.; Egusquiza, E.; Santos, I. Frequencies in the vibration induced by the rotor stator interaction in a centrifugal pump turbine. J. Fluids Eng. 2007, 129, 1428–1435. [Google Scholar] [CrossRef]
- Pavesi, G.; Cavazzini, G.; Ardizzon, G. Time–frequency characterization of the unsteady phenomena in a centrifugal pump. Int. J. Heat Fluid Flow 2008, 29, 1527–1540. [Google Scholar] [CrossRef]
- Qian, Z.; Zheng, B.; Huai, W.; Lee, Y. Analysis of pressure oscillations in a Francis hydraulic turbine with misaligned guide vanes. Proc. Inst. Mech. Eng. Part A J. Power Energy 2010, 224, 139–152. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Dou, H.-S.; Zhang, L. Simulations of unsteady cavitating turbulent flow in a Francis turbine using the RANS method and the improved mixture model of two-phase flows. Eng. Comput. 2011, 27, 235–250. [Google Scholar] [CrossRef]
- Yin, J.; Wang, D.; Wang, L.; Wu, Y.; Wei, X. Effects of water compressibility on the pressure fluctuation prediction in pump turbine. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 2030. [Google Scholar] [CrossRef]
- Pei, J.; Yuan, S.; Benra, F.-K.; Dohmen, H.J. Numerical prediction of unsteady pressure field within the whole flow passage of a radial single-blade pump. J. Fluids Eng. 2012, 134, 101103. [Google Scholar] [CrossRef]
- Pei, J.; Wang, W.-J.; Yuan, S.-Q. Statistical analysis of pressure fluctuations during unsteady flow for low-specific-speed centrifugal pumps. J. Cent. South Univ. 2014, 21, 1017–1024. [Google Scholar] [CrossRef]
- Gülich, J.F. Centrifugal Pumps; Springer: Berlin/Heidelberg, Germany, 2008; Volume 2. [Google Scholar]
- Siemen, O.; Hinsch, J. A Circulation Pump Which Acts Partially with Sealing Circling Auxiliary Liquid. Germany Patent No. 413435(3), 1920. [Google Scholar]
- Engels, H. Investigations of Ring Pumps; Tech Hoch Hannover: Hannover, Germany, 1940. [Google Scholar]
- Iversen, H. Performance of the periphery pump. Trans. ASME 1955, 77, 19–22. [Google Scholar]
- Grabow, G. Influence of the number of vanes and vane angle on the suction behaviour of regenerative pumps. In Proceedings of the 5th Conference on Fluid Machinery, Budapest, Hungary, 15–20 September 1975; pp. 351–364. [Google Scholar]
- Badami, M. Theoretical and Experimental Analysis of Traditional and New Periphery Pumps. Available online: https://doi.org/10.4271/971074 (accessed on 6 March 2019).
- Choi, W.C.; Yoo, I.S.; Park, M.R.; Chung, M.K. Experimental study on the effect of blade angle on regenerative pump performance. Proc. Inst. Mech. Eng. Part A J. Power Energy 2013, 227, 585–592. [Google Scholar] [CrossRef]
- Maity, A.; Chandrashekharan, V.; Afzal, M. Experimental and numerical investigation of regenerative centrifugal pump using CFD for performance enhancement. Int. J. Curr. Eng. Technol. 2015, 5, 2898–2903. [Google Scholar]
- Zhang, F.; Martin, B.; Pei, J.; Yuan, S.; Annika, F. Numerical simulation and verification on flow characteristics of impeller axial and radial gaps in side channel pump. Trans. Chin. Soc. Agric. Eng. 2015, 31, 78–83. [Google Scholar]
- Fleder, A.; Böhle, M. A systematical study of the influence of blade length, blade width, and side channel height on the performance of a side channel pump. J. Fluids Eng. 2015, 137, 121102. [Google Scholar] [CrossRef]
- Zhang, F.; Fleder, A.; Böhle, M.; Yuan, S. Effect of suction side blade profile on the performance of a side channel pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 586–597. [Google Scholar] [CrossRef]
- Zhang, F.; Appiah, D.; Zhang, J.; Yuan, S.; Osman, M.K.; Chen, K. Transient flow characterization in energy conversion of a side channel pump under different blade suction angles. Energy 2018, 161, 635–648. [Google Scholar] [CrossRef]
- Pei, J.; Zhang, F.; Appiah, D.; Hu, B.; Yuan, S.; Chen, K.; Asomani, S. Performance Prediction Based on Effects of Wrapping Angle of a Side Channel Pump. Energies 2019, 12, 139. [Google Scholar] [CrossRef]
- Menter, F. Zonal two equation kw turbulence models for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; p. 2906. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Wilcox, D.C. Comparison of two-equation turbulence models for boundary layers with pressure gradient. AIAA J. 1993, 31, 1414–1421. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling; DCW Industries: La Cañada Flintridge, CA, USA, 1993. [Google Scholar]
- Wilcox, D.C. Formulation of the kw turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS Academic Research, Release 15.0, Help System, ANSYS CFX-Solver Theory Guide; 15317; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130, 078001. [Google Scholar]
- Raheel, M.; Engeda, A. Current status, design and performance trends for the regenerative flow compressors and pumps. In Proceedings of the ASME 2002 International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 17–22 November 2002; pp. 99–110. [Google Scholar]
- Benra, F.; Feng, J.; Dohmen, H. Numerical study on pressure fluctuations in a complete stage of a centrifugal pump. In Proceedings of the Eleventh International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 26 February–2 March 2006. Paper No. ISROMAC11-2006-012. [Google Scholar]
- Feng, J.; Benra, F.-K.; Dohmen, H.J. Numerical investigation on pressure fluctuations for different configurations of vaned diffuser pumps. Int. J. Rotating Mach. 2007, 2007, 34752. [Google Scholar] [CrossRef]
- Chen, S.; Pan, Z.; Wu, Y.; Zhang, D. Simulation and experiment of the effect of clearance of impeller wear-rings on the performance of centrifugal pump. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 2017. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).