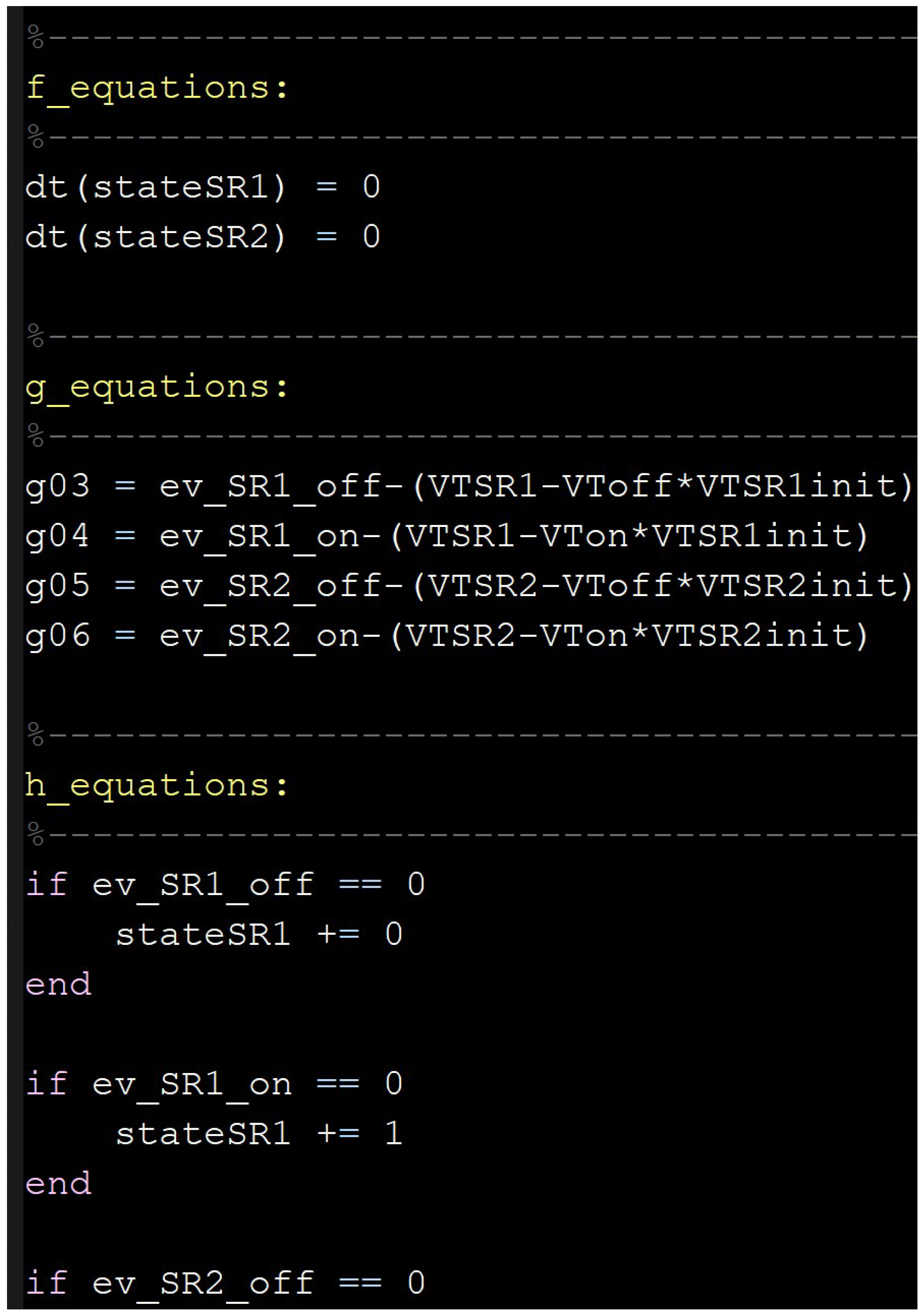
2.1. Switching Overvoltages
Shunt reactors are mostly used in electric transmission systems: their primary function is certainly to regulate the system’s voltage, balancing the reactive power generated by overhead lines in no-load conditions or by cables installed in high and very high voltage systems. Often, the reactors are switched on and off several times a day due to changes in loads and transits on the electrical system. The study of the switching of shunt compensators and of the relative transient has been already discussed in [
4,
5,
6].
When a reactor is de-energized, the chopping of the current and subsequent possible reignitions can results in significant transient overvoltages. The following two types of overvoltages can be generated: overvoltages originated by the premature forcing of current to zero, called chopping overvoltages, with frequencies up to 5 kHz, and overvoltages originated by the possible re-ignition of the circuit breaker after high voltage stress through the poles, called re-ignition overvoltages, with frequencies up to several hundred kHz. The chopping overvoltages are very severe for small reactors (in literature known as small inductive current interruption): in this work, large shunt reactors will be considered and therefore this type of overvoltages is not assumed as relevant to the purposes of the performed analysis. On the other hand, the possible re-ignition with successive overvoltage transients (rather steep) could be critical, and it can damage the insulation or the nearby equipment. The installed overvoltage arresters provide to limit the overvoltages to earth at acceptable levels, but nevertheless they cannot limit the slope of the voltage fluctuations associated to the restarts. A possible solution to this problem can be checking the separation of contacts, with the aim of eliminating the re-ignitions occurrence [
7,
8,
9]. Specific control devices are currently used within circuit breakers in order to control the switching operation of the reactor. Therefore, this type of overvoltages does not represent a critical problem for the application of a de-energizing operation on a shunt reactor.
When a reactor is energized, the switching operation could originate inrush currents with considerable asymmetry and high time constants: however, since the inrush currents are related to the saturation of the magnetic core and since the air-gap used in shunt reactors is such as not to introduce significant saturation effects [
7], this issue is not relevant for the application of an energizing operation of a shunt reactor. The control on closing and the control on opening are usually used together within the breakers of shunt reactors as complementary controls.
2.2. Theoretical Analysis of the Switching Strategy
The power transfer equation of a simple two-bus system is given by:
where P is the active power transfer, V
1 and V
2 are respectively the sending and the receiving end voltage magnitudes, δ is the power angle between V
1 and V
2, and B
12 is a parameter obtained from the equivalent two-port circuit constants and it takes into consideration reactances and capacitances of the link. Equation (1) is valid under the hypothesis that the line resistance is neglected. When a mixed line with shunt reactors is inserted between the two nodes, the opening or the closing of the reactors implies a step change in the value of the parameter B
12, but it results also in a sudden variation of the voltages V
1 and V
2. It is consequent that shunt reactors can have a relevant impact on the transient response of the system [
2,
10]: if properly controlled, they can then contribute to the improvement of the stability of the system when subjected to critical contingencies. The impact of the control action depends obviously on the value of Y
R, which represents the admittance of the shunt reactor: this value increases as the MVAR reactor rating increases. Therefore, the impact of the switching operation becomes more effective with the size of the shunt reactors.
The application of a switching strategy on shunt devices such as capacitors and reactors as improvement of the stability is a known technique in literature, but basically it is conceived as switching-on operation performed on capacitor banks [
11,
12,
13,
14]. However, the switching-on operation of a capacitor is equivalent to the switching-off of a reactor, and vice versa: switching large shunt reactors is expected to have a similar positive impact on the stability of the power system.
The use of a switching procedure as an action supporting system stability can also be imagined as an extension of the simple and only switching-off operation of the device: a more elaborated strategy could involve a series of a couple of switching-off and switching-on operations, applied to the reactors participating to the control action until the system reaches successfully the steady-state after the disturbance. Considering a mechanical analogy, the application of such a strategy could be seen as the insertion of weights on an oscillating mass. Ideally, the connection of these weights should occur in specific instants of the oscillations: these instants correspond to the times when the oscillating system passes through the final equilibrium point. These same considerations can be applied to the case of shunt reactors: the identification of definite instants to trigger the switching operations is a fundamental key in the application of the proposed strategy as help to the system in maintaining the stability. These instants can be identified with the implementation of a simple detection logic on minimum/maximum voltage relays with two thresholds: when the input signal drops below a minimum value defined by the first threshold, the relay activates the disconnection of the reactor; when the input signal raises above a maximum value defined by the second threshold, the relay activates the connection of the reactor. The thresholds are set appropriately in order to achieve the concept of connecting weights at equilibrium point crosses of the oscillating system, as described before in the mechanical analogy. With this approach, the switching strategy considers both the forward and the backward swings of the system, since both can lead to angular separation and therefore to system instability [
11]. The voltage of the reactor node is conveniently used as input signal to the minimum/maximum relay for the implementation of the proposed switching strategy.
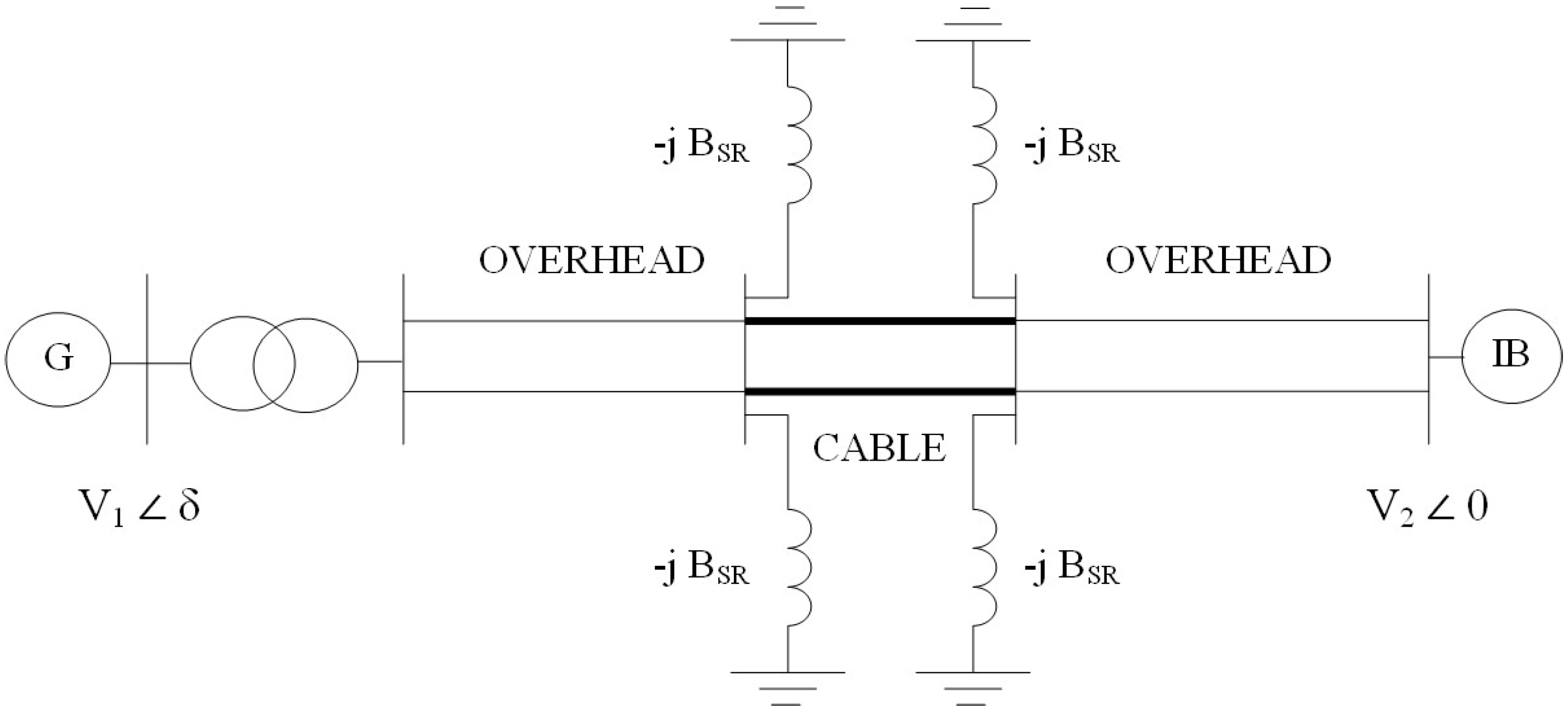
2.3. Single-Machine Infinite-Bus Test System
The switching strategy described in
Section 2.2 is applied to the simple test system shown in
Figure 1: one synchronous machine with step-up transformer is connected to the infinite bus through HV mixed overhead-cable transmission line in double-circuit. The reactive power required by the cables line is compensated by four shunt reactors, installed at the ends of the cable section. The synchronous machine is simulated for the time-domain analysis with a detailed subtransient model. The synchronous machine is equipped with a field-controlled alternator-rectifier excitation system, denominated as AC1A type [
15]. All system data are reported in
Appendix A.
The disturbance applied to the system is the opening of one circuit in the second overhead line (OHL) section: this corresponds to an increase in the value of the overall reactance between the generator and the infinite bus. The line is disconnected at tdist = 1.2 s. Three of the four reactors of the mixed line are involved in the switching operations: the three reactors participating to the control action (about 600 MVAR) are disconnected near the occurrence of the line outage, at tsw = 1.4 s. According to the principles of the switching strategy illustrated in the previous section, the reactors are disconnected and re-connected at precise instants during the oscillations of the system, considering both the forward and the backward swings of the synchronous machine.
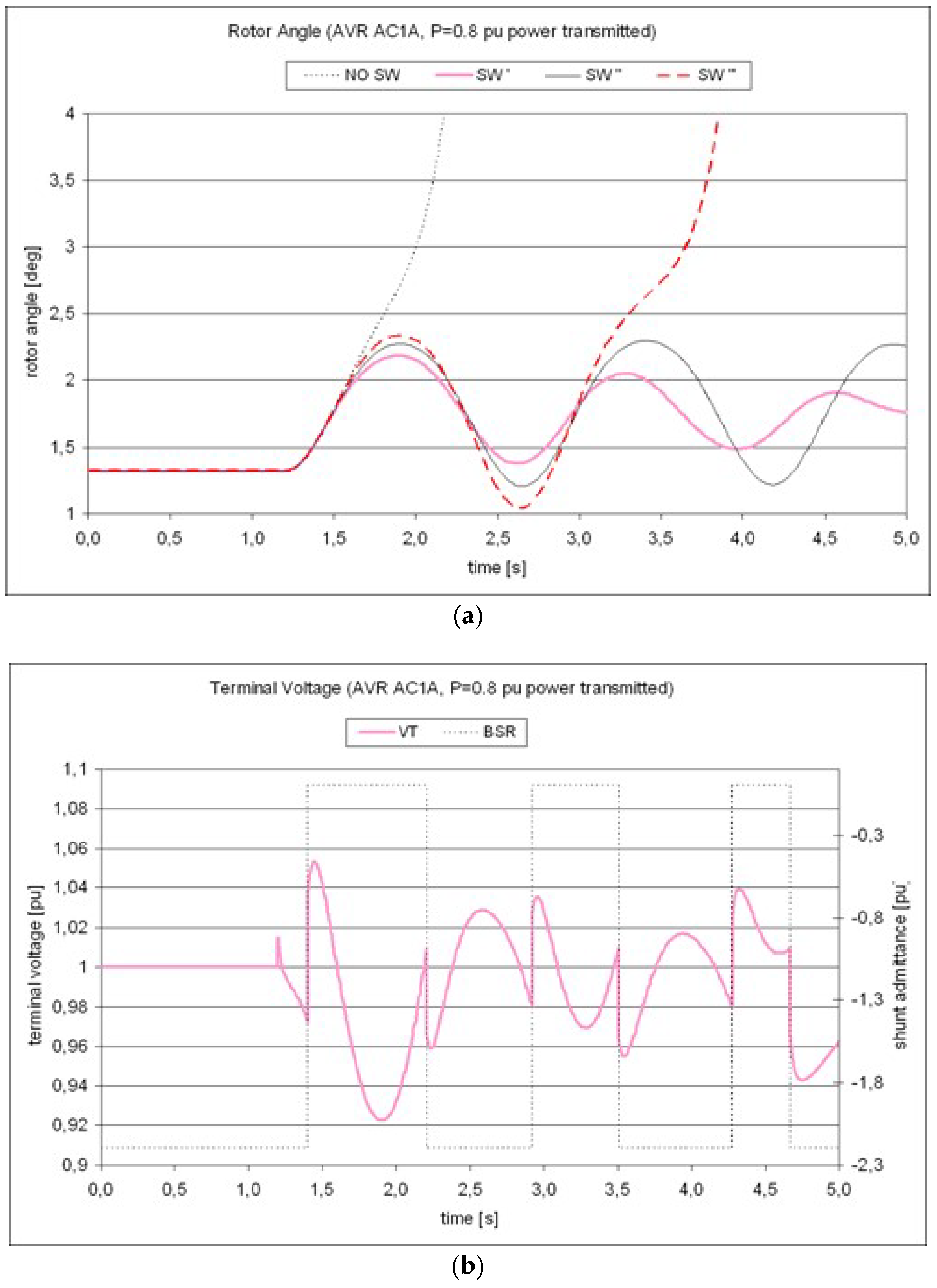
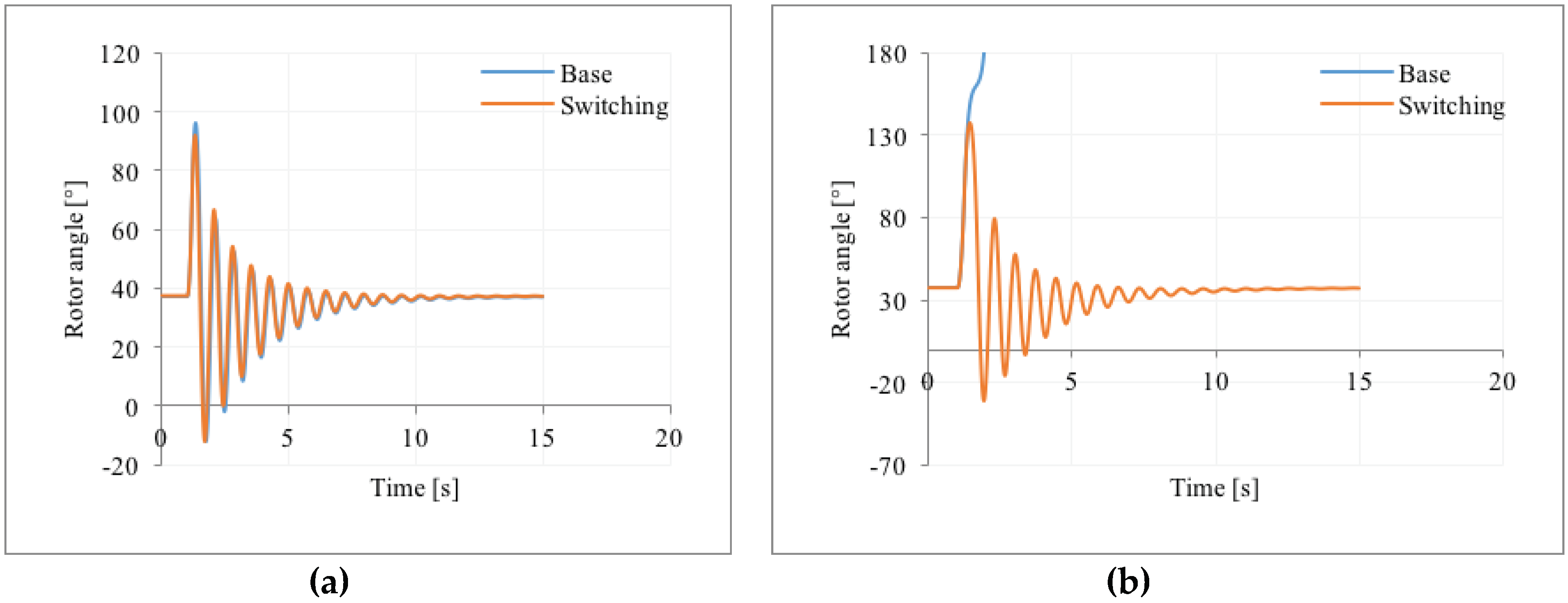
The results of the dynamic analysis are shown in
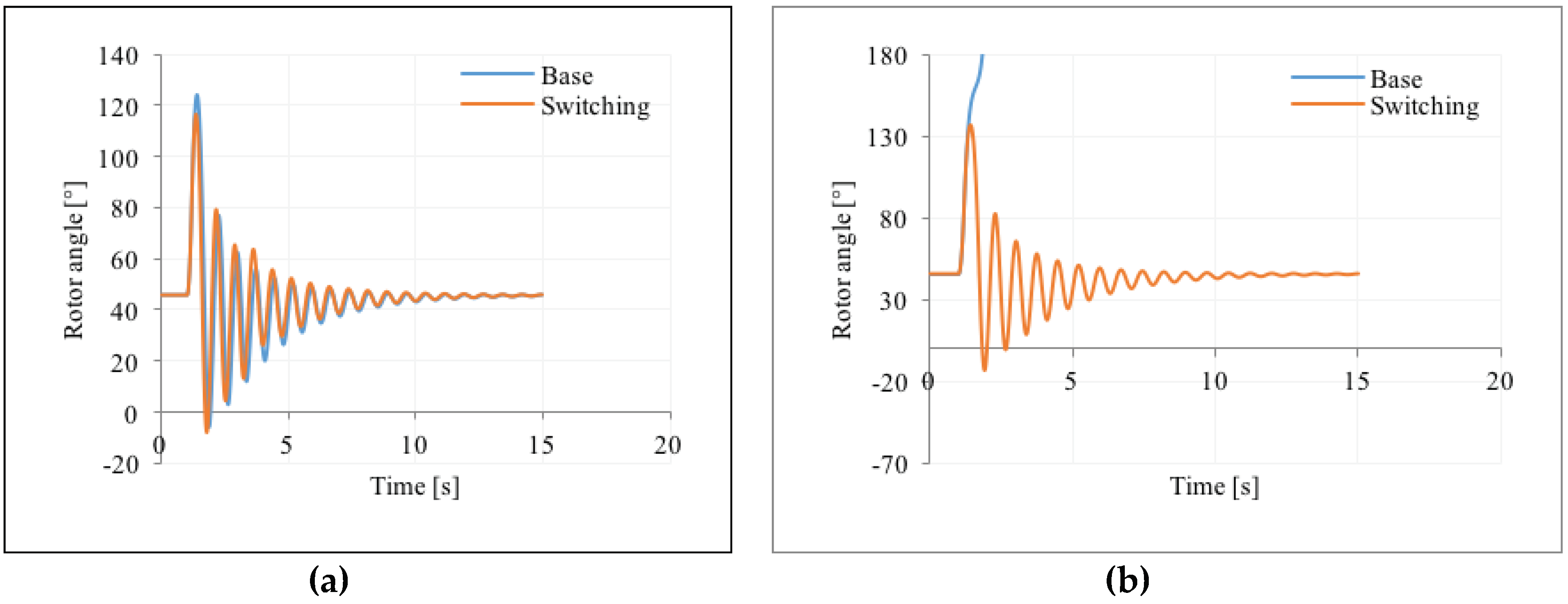
Figure 2. The simulation includes four different scenarios: the base case of no reactor switching and three different switching control cases of the reactors. As shown in
Figure 2a, in the base case of no reactor switching, the system cannot withstand the line tripping: the disturbance brings the system to an unstable condition, and in particular to the so called first-swing instability. In the first switching case (SW′), all three reactors are switched off at t
sw = 1.4 s: two are switched off and on according to the thresholds 0.98 pu and 1.01 pu, while the last reactor is re-connected only if the voltage of the machine terminal exceeds the value of 1.1 pu. In this case, the system is able to maintain the synchronism and the oscillations are well damped. The application of the reactors switching is then crucial in supporting the system to keep stability. For the SW’ case, the voltage of the machine terminal and the shunt admittance of the reactors are shown in
Figure 2b. The second switching case (SW″) is similar to the first, with the difference of the third shunt reactor disconnected later (t
sw = 1.6 s), after the back swing of the generator: as can be seen from
Figure 2a, the system is still stable, but the oscillations of the system after the disturbance are less damped. In the third switching case (SW″), two reactors are switched off too late (t
sw = 1.6 s) after the back swing of the generator: in this case, despite the trigger of disconnections and re-connections applied on the reactors, the system is not stable and it experiences angular separation.
The analysis and the results obtained for the simple test system demonstrate the fundamental role of the identification of specific switching instants for the success of the switching control actions: disconnecting and reconnecting shunt reactors prove to represent a remarkable help for the system in maintaining the stability, and the timing of the switching operations are decisive for the effectiveness of the applied control action.
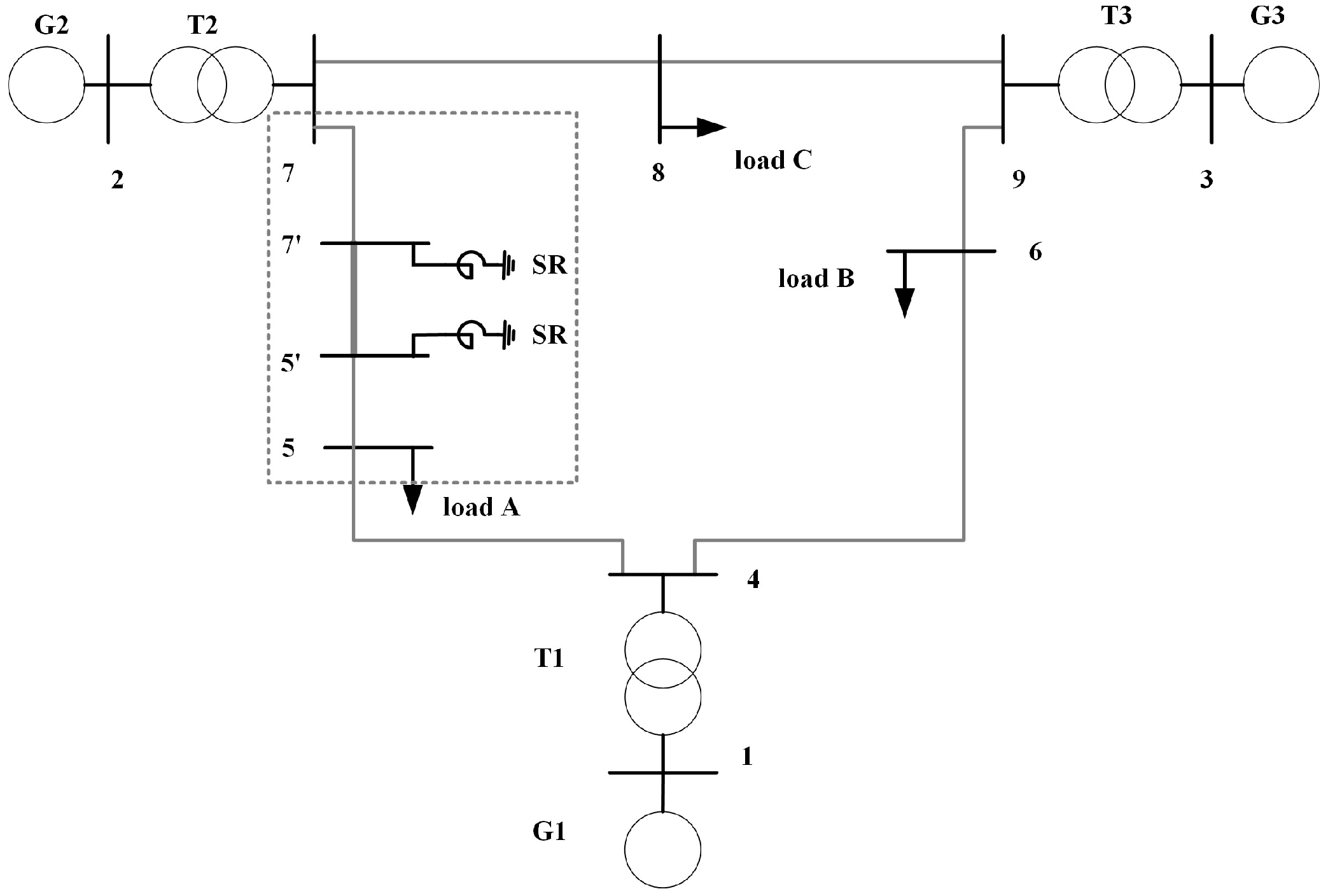
2.4. IEEE 3-Machine 9-Bus Standard Test System
The switching strategy illustrated in
Section 2.2 is also tested using the Western System Coordinating Council (WSCC) IEEE 3-machine 9-bus [
16]: this is a well-known standard test system, normally used in power flow and transient stability studies. The test system is appropriately modified to introduce a mixed overhead-cable line with shunt reactors for the purposes of this work (
Figure 3): the line connecting the bus 5 and the bus 7 is divided in half and a cable line is inserted between the two overhead sections. The cable line has the same parameters of the cable used in the simple system of
Section 2.3. For the considered voltage level of 230 kV, the cable requires a reactive power of about 190 MVAR: two shunt reactors of 100 MVAR each are then installed at the cable ends for the compensation of the reactive power.
Two different system configurations are considered. In the first configuration, the voltage regulator designated as DC1A (also known as IEEE type 1) is included in the system model for generators G2 and G3. In the second configuration, the voltage regulator designated as AC1A is included in the system model for generators G2 and G3. The parameters of the synchronous machine models are derived from [
16] and [
17]. The DC1A type represents DC exciters controlled on-site with DC voltage regulators and it is known that it has been replaced by AC and ST (STatic) excitation system [
15]: however, since several works in literature investigate the 3-machine 9-bus WSCC test system including this type of regulator in the dynamic simulations [
18,
19], the model of this excitation system is considered in this work for sake of comparison.
For the more complex 9-bus 3-machine test system, the proposed control strategy on shunt reactors can be applied with the following settings: the threshold values assigned to voltage relays are set in order to let only one reactor participate to the switching operations, while the operation of the second reactor is activated only if needed, as additional support to the action of the first reactor. The proposed strategy could be also further developed and elaborated, considering different set of thresholds, remote input signal for the minimum/maximum voltage relays, even integrated in the frame of a more coordinated environment of a hierarchical control architecture of the power system.
The results of the application of described switching strategy to the 9-bus WSCC 3-machine test system are reported in the following subsections, respectively for the configuration with DC1A excitation system and for the configuration with the AC1A excitation system. In both cases, the disturbance applied to the system is a three-phase fault on bus 7, applied at tfault = 0.1 s and removed after 23 ms at tclear = 0.33 s.
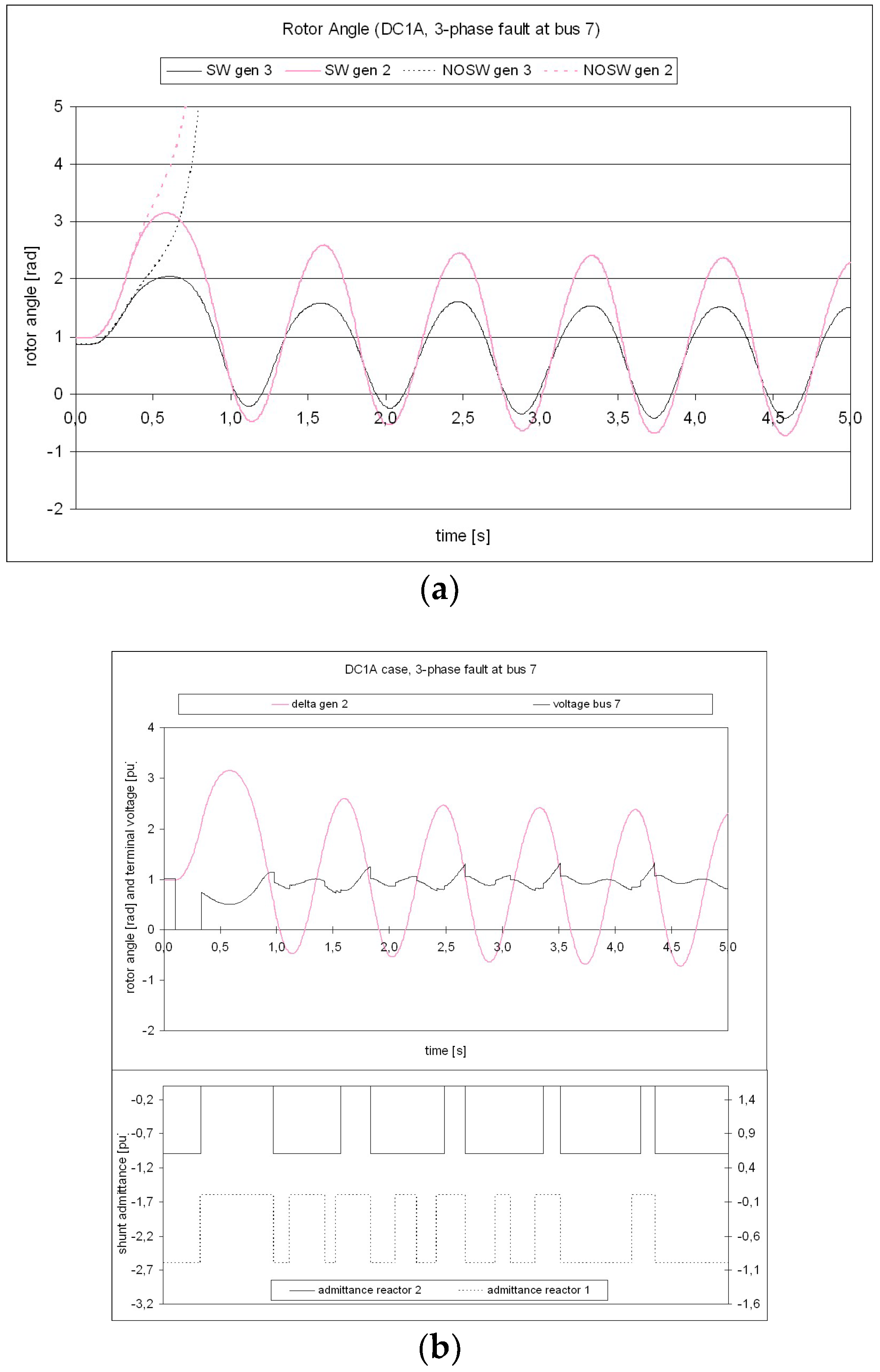
2.4.1. DC1A Type Voltage Regulator
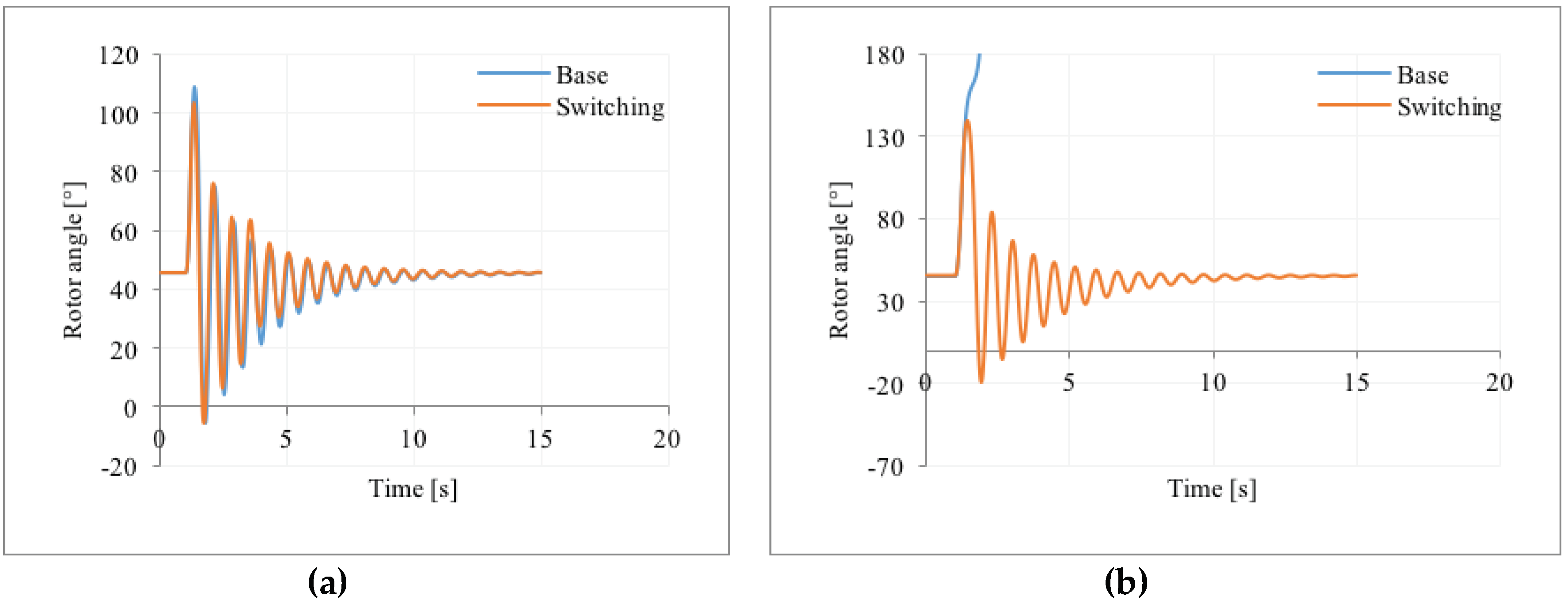
In the case of synchronous machines equipped with DC1A voltage regulators, the results of the dynamic simulations are reported in
Figure 4. When no reactor switching is operated, the power system cannot withstand the fault occurrence and it undergoes first-swing instability (
Figure 4a). When instead the reactors of the mixed line are switched according to the switching strategy described in
Section 2.2, the system is able to maintain stability and the angular separation is avoided. As additional result,
Figure 4b shows the admittances of the two shunt reactors: as it can be seen, one reactor operates eight switching cycles, while the other reactor operates five switching cycles. At the end of the transient due to the disturbance, both reactors return to be connected and the system reaches the final steady-state condition.
In the simulated test system, the voltage relay controlling the first reactor is set with the values of 0.9 pu and 1.01 pu, respectively for the minimum and for the maximum threshold. The voltage relay controlling the second reactor is set instead with the values of 0.8 pu and 1.1 pu, respectively, for the minimum and for the maximum threshold: with these settings, the switching operation of the second reactor is properly activated only as support to the action of the first reactor.
In the case of the analyzed configuration of the IEEE 3-machine 9-bus test system, the application of a switching strategy on the shunt reactors proves to contribute positively and decisively to the stability of the system subjected to a critical contingency.
2.4.2. AC1A Type Voltage Regulator
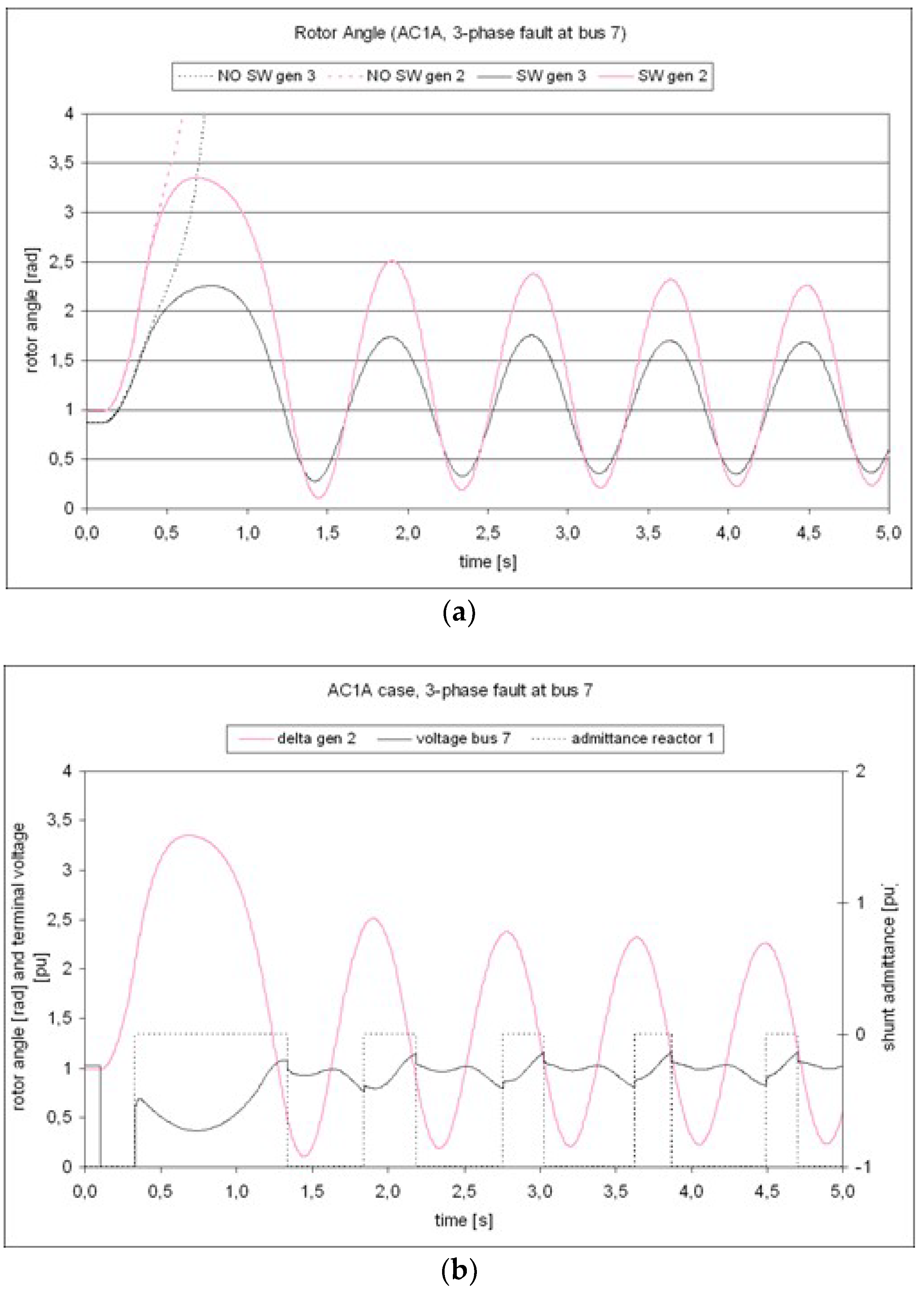
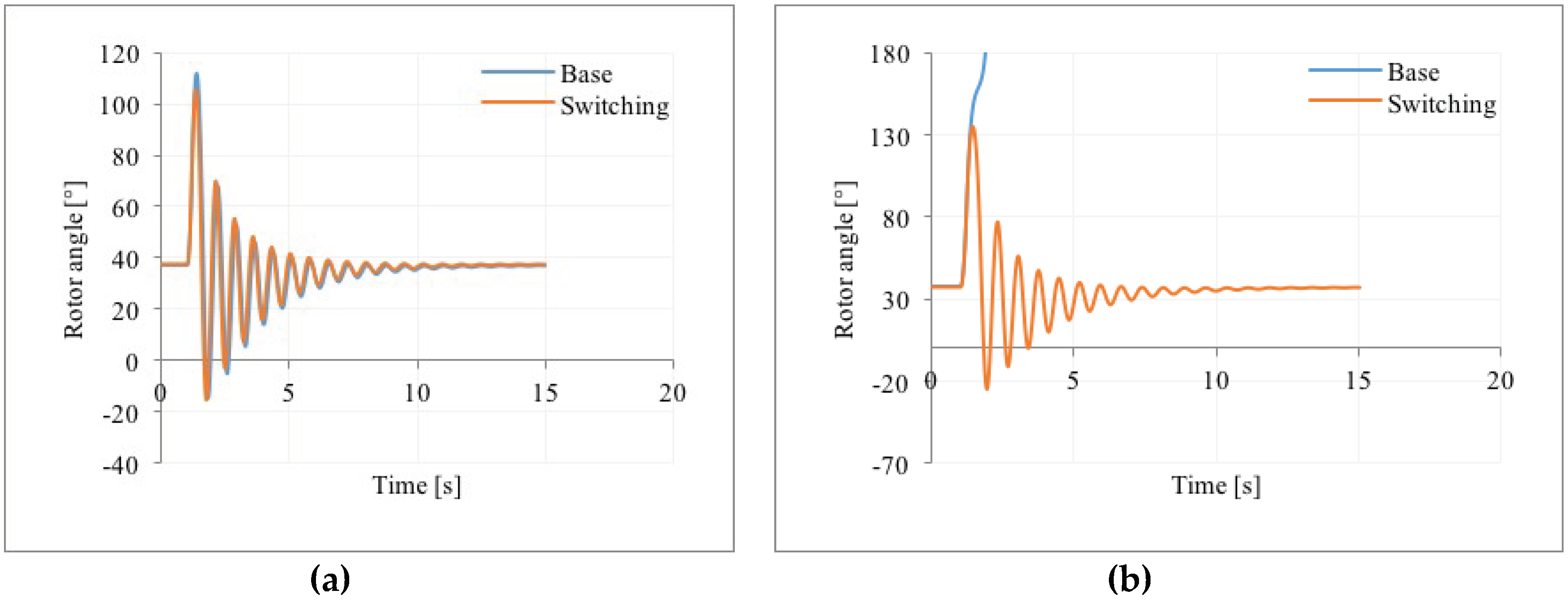
In the case of synchronous machines equipped with AC1A voltage regulators, the results of the dynamic simulations are reported in
Figure 5. Also, in this case, when no reactor switching is operated, the power system is not able to maintain the stability: the generators lose the synchronism and enter in the out-of-step condition, with the consequent tripping of the corresponding protections and the separation of the system (
Figure 5a). When instead the switching strategy is operated on the shunt reactors of the mixed line, the system reacts successfully to the disturbance and it is able to avoid the instability. In this case, the first reactor operates five switching cycles, while the second one is disconnected at the beginning of the control action and afterward kept disconnected for the rest of the transient (
Figure 5b).
In the simulated system, the voltage relays controlling the two reactors have the same thresholds as the previous configuration, except the maximum threshold of the second reactor, which is set in this configuration to 1.2 pu.
Also in the case of this configuration of the IEEE 3-machine 9-bus test system, the control action on the shunt reactors shows to be an effective improvement of the system stability, containing the oscillations after the occurrence of the disturbance and representing an immediate action that could avoid the instability of the system.