A Novel Vector Control Strategy for a Six-Phase Induction Motor with Low Torque Ripples and Harmonic Currents
Abstract
:1. Introduction
2. 6PIM Modelling
2.1. 6PIM Model in Subspace
2.2. 6PIM Model in Subspace
3. Conventional DTC of 6PIM
4. Harmonic Currents Reduction by Duty Cycle Control Strategy
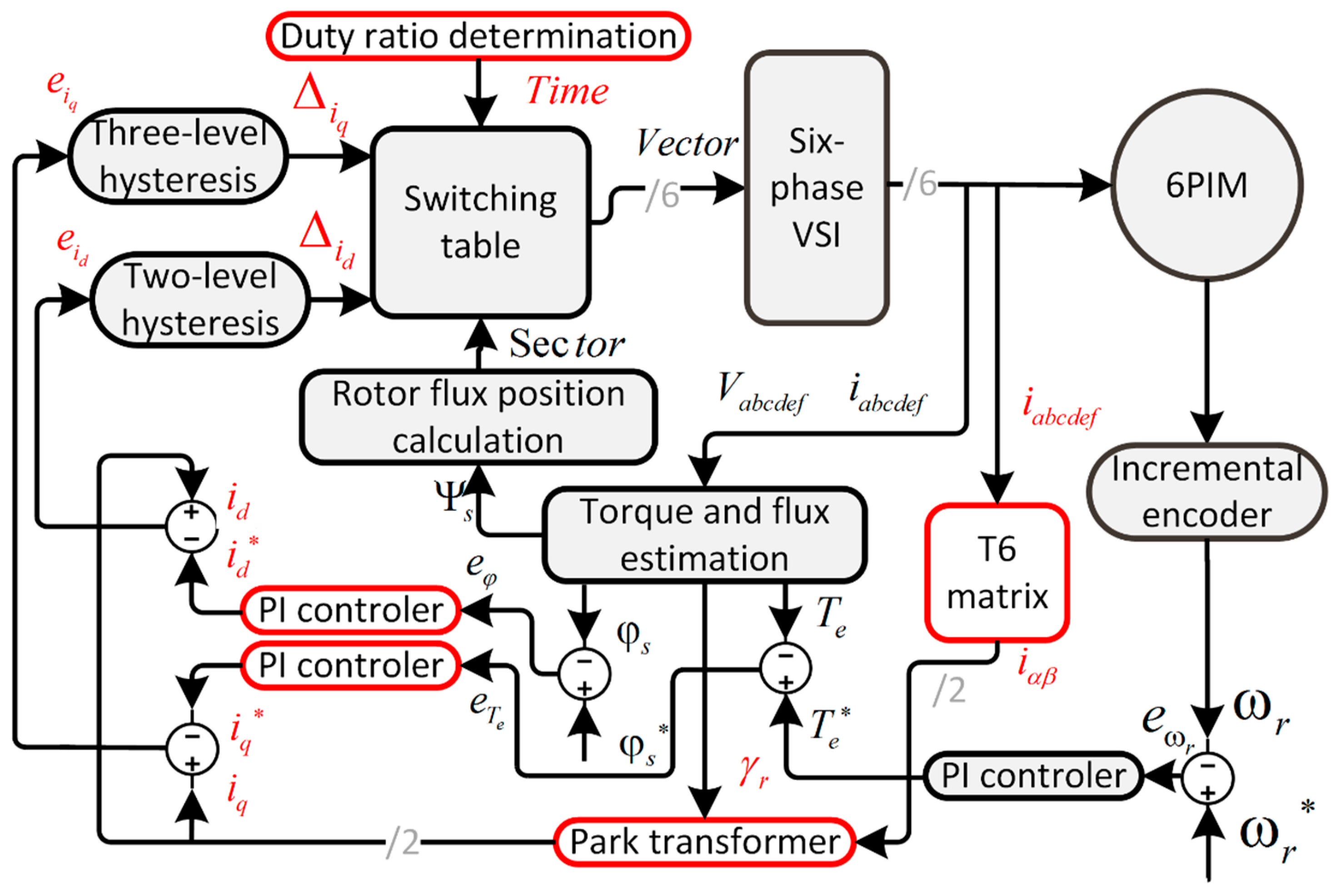
5. Proposed Control Algorithm for the 6PIM Drive
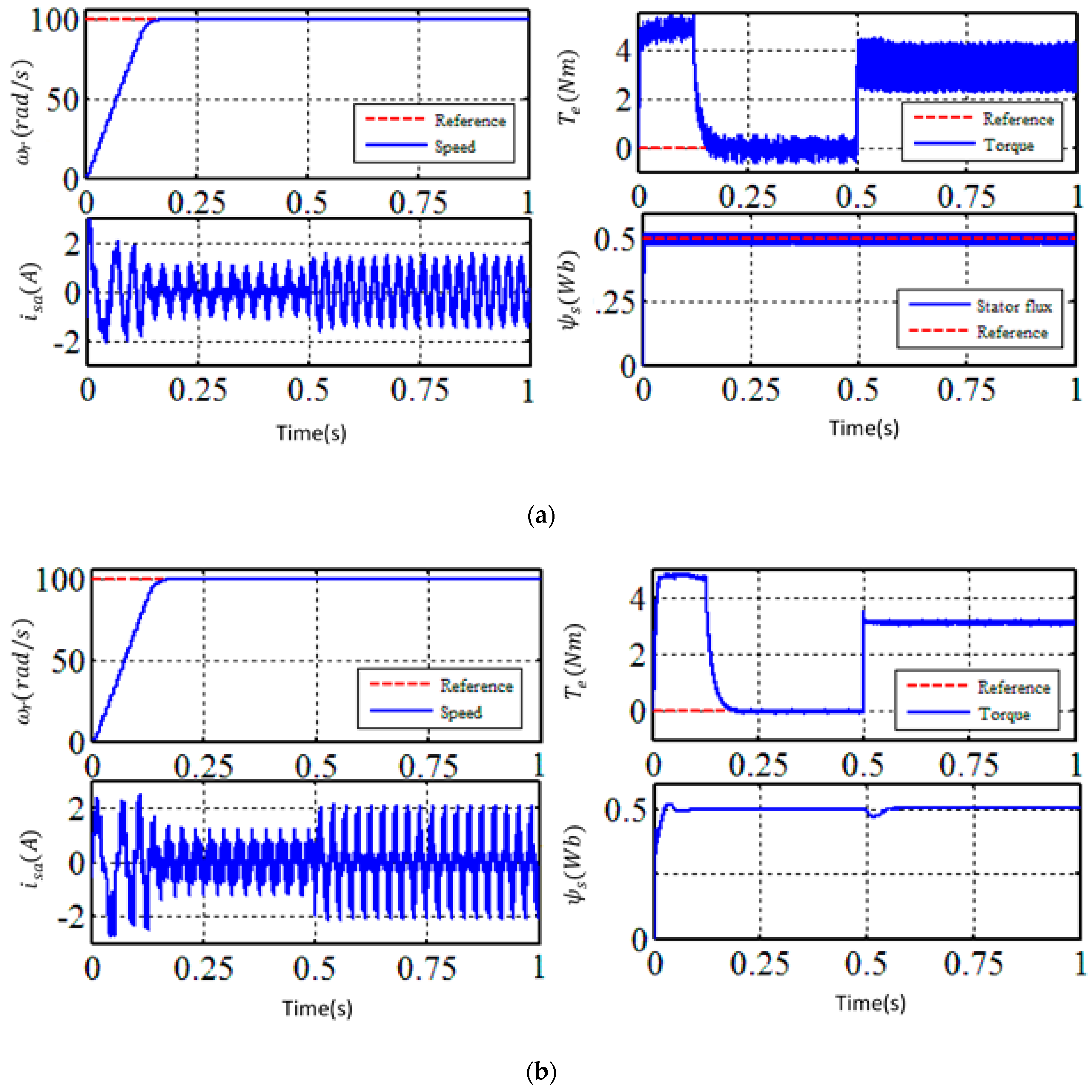
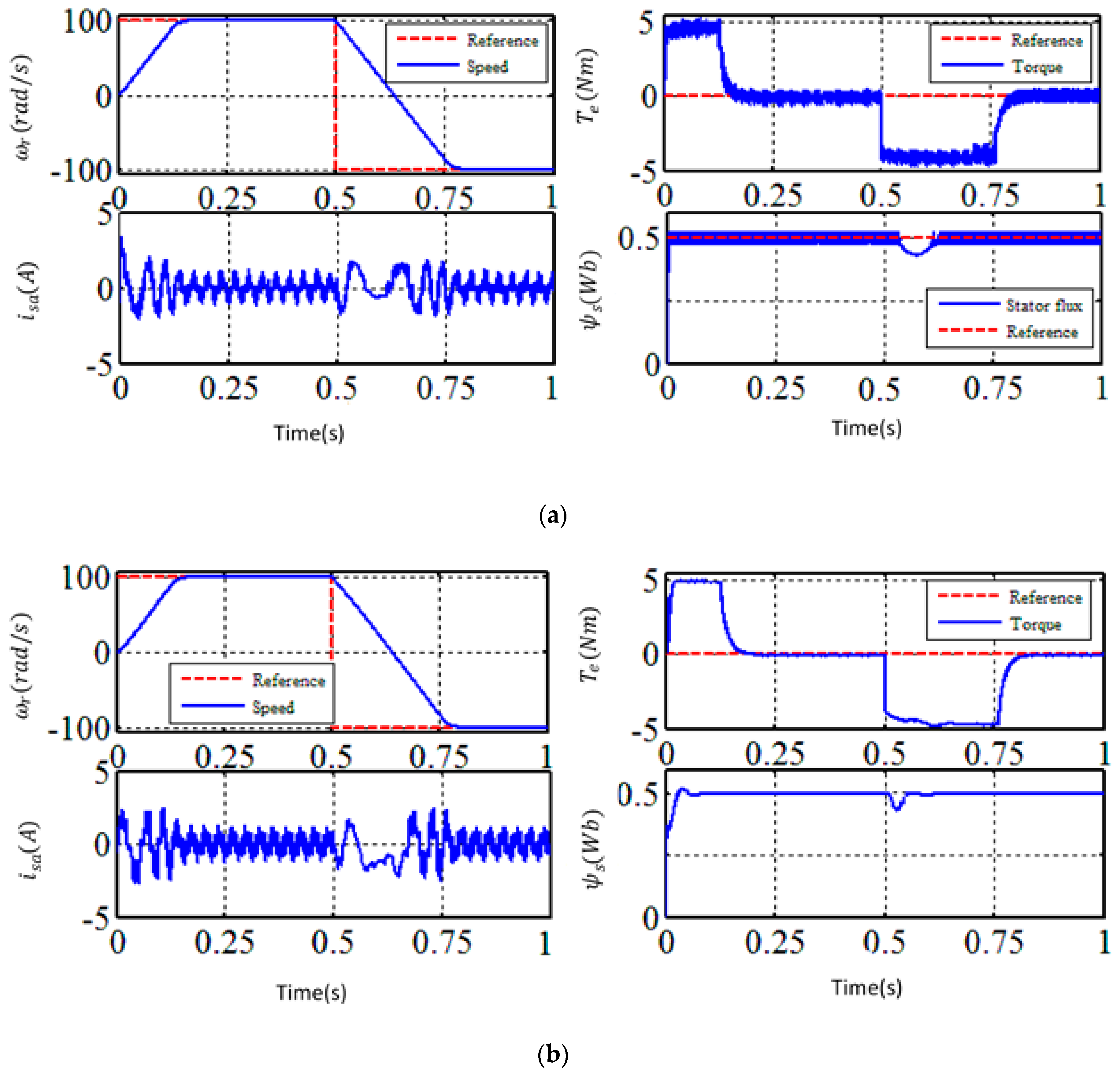
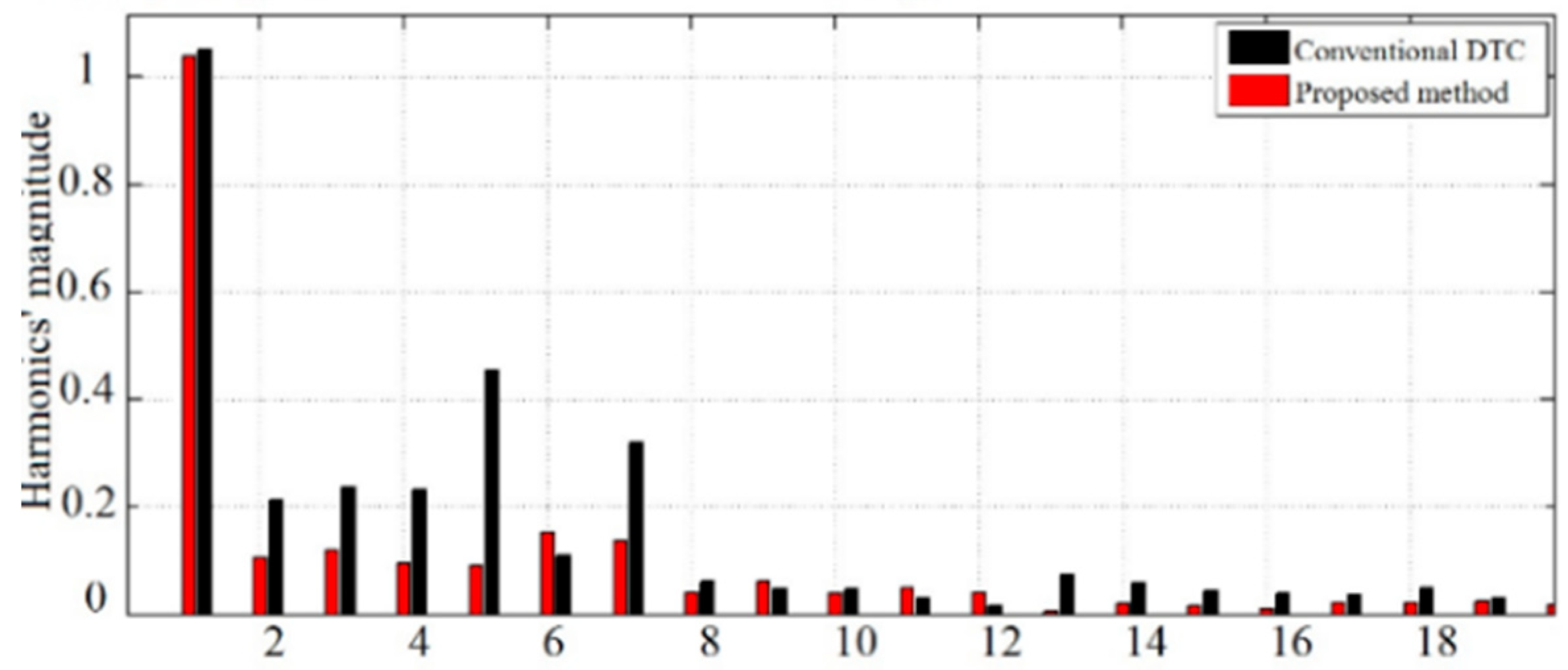
6. Simulation Results
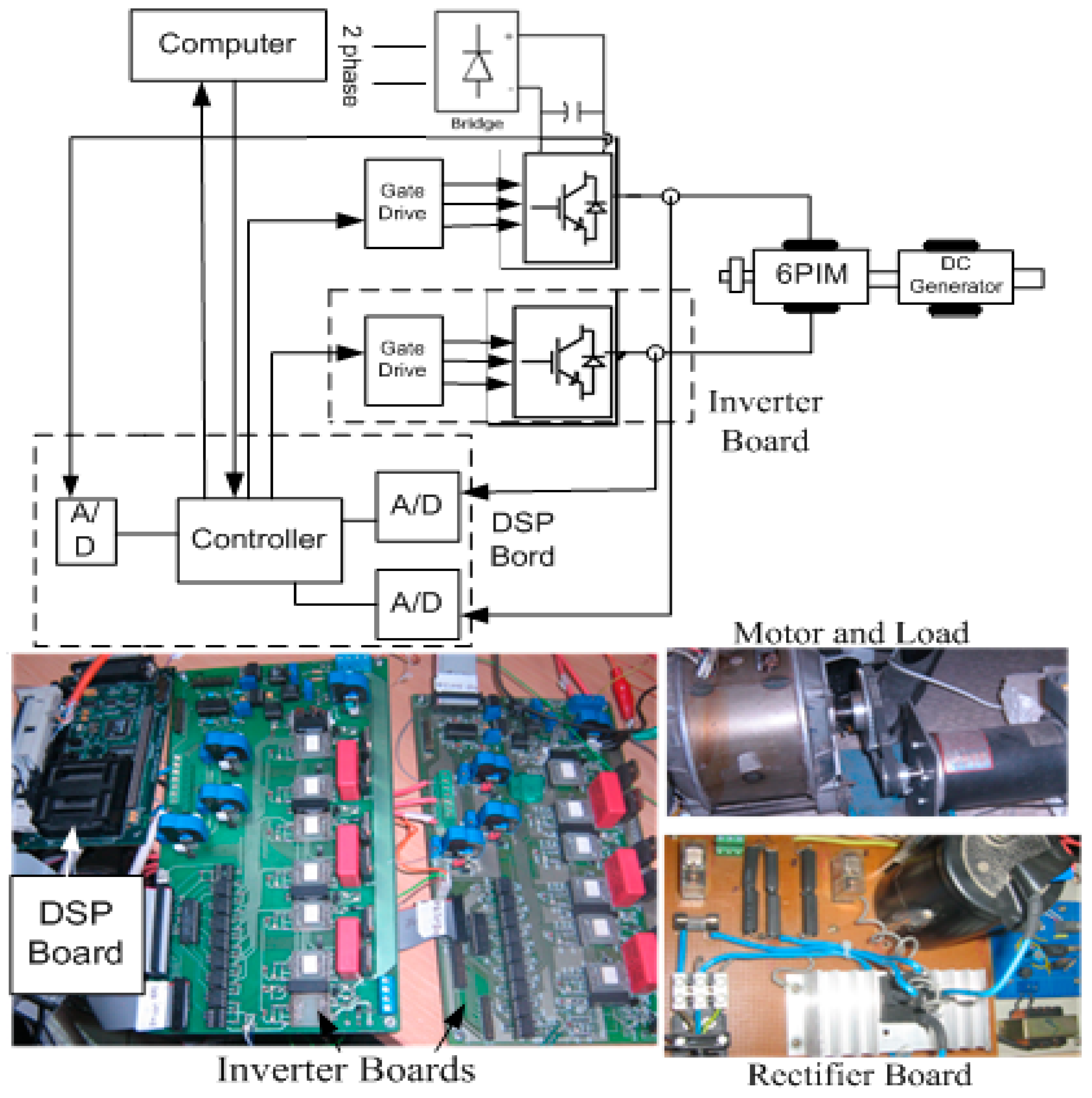
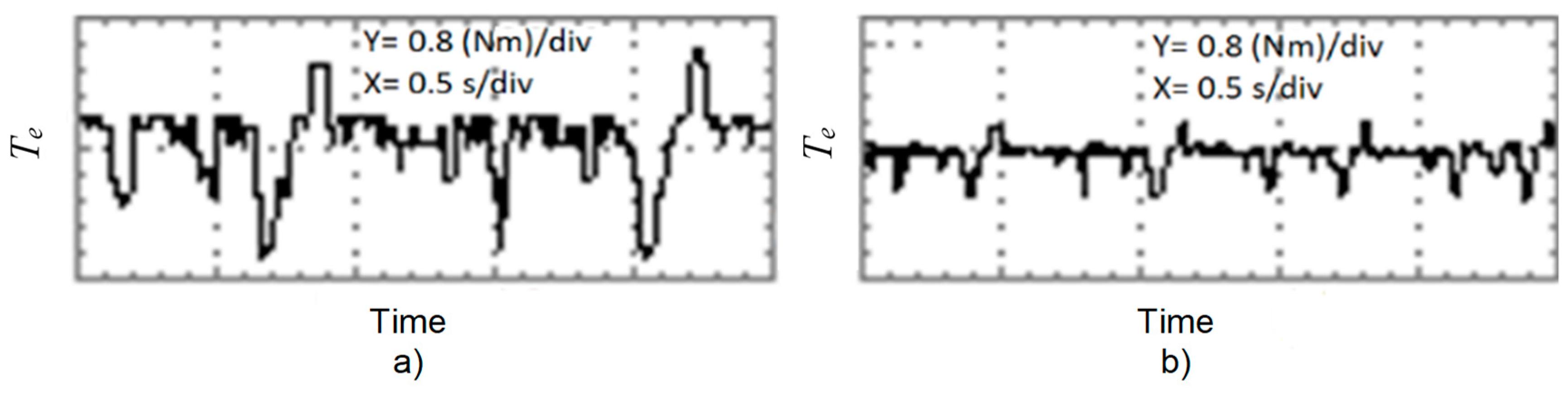
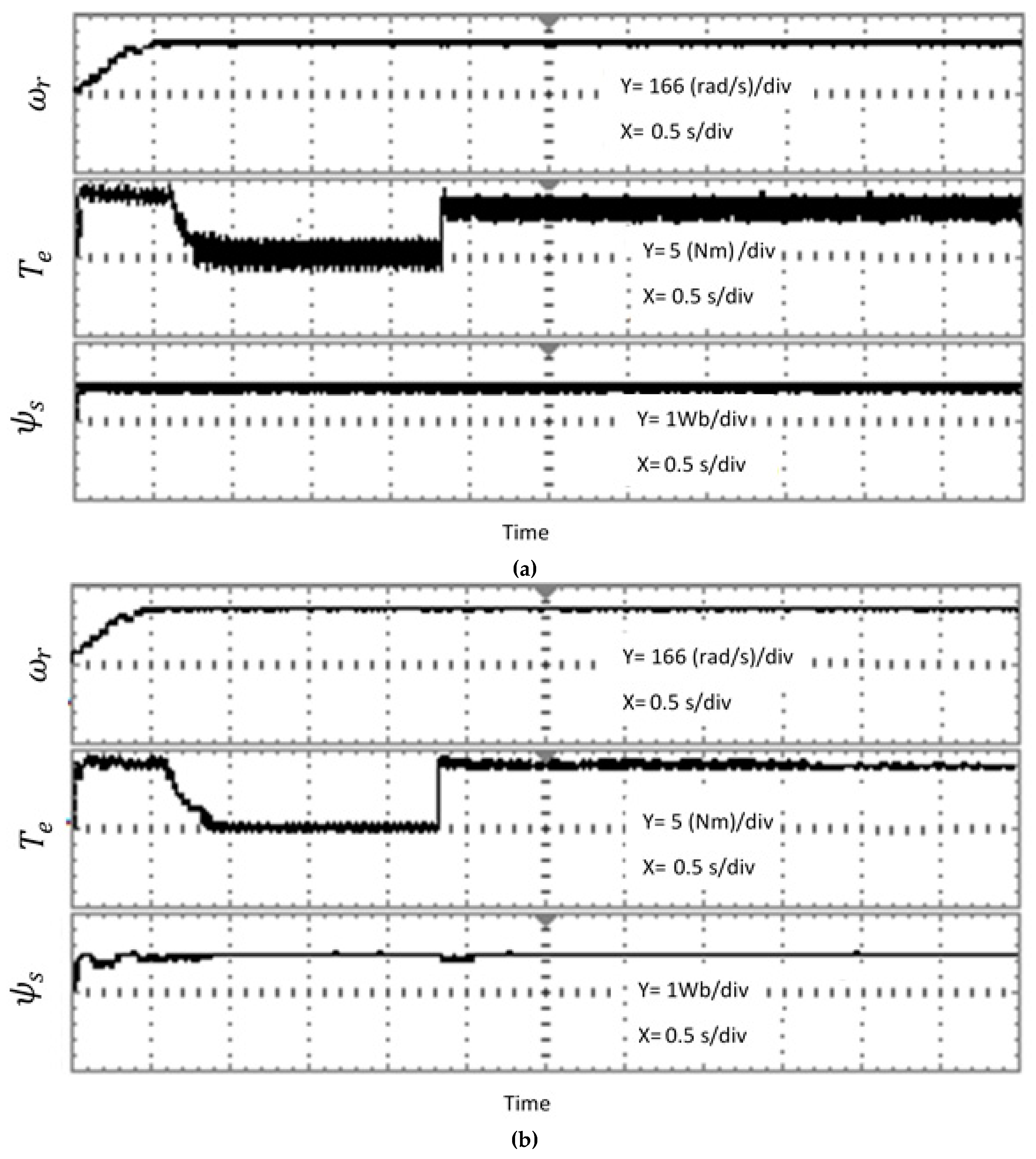
7. Experimental Setup
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Levi, E. Multiphase electric machines for variable-speed applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Holakooie, M.H.; Ojaghi, M.; Taheri, A. Direct Torque Control of Six-Phase Induction Motor with a Novel MRAS-Based Stator Resistance Estimator. IEEE Trans. Ind. Electron. 2018, 65, 7685–7696. [Google Scholar] [CrossRef]
- Che, H.S.; Duran, M.J.; Levi, E.; Jones, M.; Hew, W.P.; Rahim, N.A. Postfault operation of an asymmetrical six-phase induction machine with single and two isolated neutral points. IEEE Trans. Power Electron. 2014, 29, 5406–5416. [Google Scholar] [CrossRef]
- Jahns, T.M. Improved reliability in solid-state drives for large asynchronous ac machines by means of multiple independent phase-drive units. IEEE Trans. Ind. Appl. 1980, IA-16, 321–331. [Google Scholar] [CrossRef]
- Fnaiech, M.A.; Betin, F.; Capolino, G.A.; Fnaiech, F. Fuzzy logic and sliding-mode controls applied to six-phase induction machine with open phases. IEEE Trans. Ind. Electron. 2010, 57, 354–364. [Google Scholar] [CrossRef]
- Parsa, L.; Toliyat, H.A.; Goodarzi, A. Five-phase interior permanent-magnet motors with low torque pulsation. IEEE Trans. Ind. Appl. 2007, 43, 40–46. [Google Scholar] [CrossRef]
- Marouani, K.; Baghli, L.; Hadiouche, D.; Kheloui, A.; Rezzoug, A. A new PWM strategy based on a 24-sector vector space decomposition for a six-phase VSI-Fed dual stator induction motor. IEEE Trans. Ind. Electron. 2008, 55, 1910–1920. [Google Scholar] [CrossRef]
- Pandit, J.K.; Aware, M.V.; Nemade, R.V.; Levi, E. Direct Torque Control Scheme for a Six-Phase Induction Motor with Reduced Torque Ripple. IEEE Trans. Power Electron. 2017, 32, 7118–7129. [Google Scholar] [CrossRef]
- Zheng, L.; Fletcher, J.E.; Williams, B.W.; He, X. A novel direct torque control scheme for a sensorless five-phase induction motor drive. IEEE Trans. Ind. Electron. 2011, 58, 503–513. [Google Scholar] [CrossRef]
- Lokriti, A.; Salhi, I.; Doubabi, S. IM Direct Torque Control with no flux distortion and no static torque error. ISA Trans. 2015, 59, 256–267. [Google Scholar] [CrossRef]
- Ambrozic, A.; Buja, G.S.; Menis, R. Band-Constrained Technique for Direct Torque Control of Induction Motor. IEEE Trans. Ind. Electron. 2004, 51, 776–784. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, Z.Q. Enhancement of steady-state performance in direct-torque-controlled dual three-phase permanent-magnet synchronous machine drives with modified switching table. IEEE Trans. Ind. Electron. 2015, 62, 3338–3350. [Google Scholar] [CrossRef]
- Taheri, A.; Rahmati, A.; Kaboli, S. Comparison of efficiency for different switching tables in six-phase induction motor DTC drive. J. Power Electron. 2012, 12, 128–135. [Google Scholar] [CrossRef]
- Singh, B.; Jain, S.; Dwivedi, S. Torque ripple reduction technique with improved flux response for a direct torque control induction motor drive. IET Power Electron. 2013, 6, 326–342. [Google Scholar] [CrossRef]
- Lai, Y.S.; Chen, J.H. A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction. IEEE Trans. Energy Convers. 2001, 16, 220–227. [Google Scholar]
- Shyu, K.K.; Lin, J.K.; Pham, V.T.; Yang, M.J.; Wang, T.W. Global minimum torque ripple design for direct torque control of induction motor drives. IEEE Trans. Ind. Electron. 2010, 57, 3148–3156. [Google Scholar] [CrossRef]
- Abad, G.; Rodriguez, M.A.; Poza, J. Two-Level VSC Based Predictive Direct Torque Control of the Doubly Fed Induction Machine with Reduced Torque and Flux Ripples at Low Constant Switching Frequency. IEEE Trans. Power Electron. 2008, 23, 1050–1061. [Google Scholar] [CrossRef]
- Wang, T.; Fang, F.; Wu, X.; Jiang, X. Novel filter for stator harmonic currents reduction in six-step converter fed multiphase induction motor drives. IEEE Trans. Power Electron. 2013, 28, 498–506. [Google Scholar] [CrossRef]
- Autsou, S.; Saroka, V.; Karpovich, D.; Rassolkin, A.; Gevorkov, L.; Vaimann, T.; Kallaste, A.; Belahcen, A. Comparative study of field-oriented control model in application for induction and synchronous reluctance motors for life-cycle analysis. In Proceedings of the 2018 25th International Workshop on Electric Drives: Optimization in Control of Electric Drives (IWED), Moscow, Russia, 31 January–2 February 2018. [Google Scholar]
- Nelson, R.H.; Krause, P.C. Induction machine analysis for arbitrary displacement between multiple winding sets. IEEE Trans. Power Appar. Syst. 1974, PAS-93, 841–848. [Google Scholar] [CrossRef]
- Zhao, Y.; Lipo, T.A. Space Vector PWM Control of Dual Three-phase Induction Machine Using Vector Space Decomposition. IEEE Trans. Ind. Appl. 1995, 31, 1100–1109. [Google Scholar] [CrossRef]
- Binder, A.; Muetze, A. Scaling effects of inverter-induced bearing currents in AC machines. IEEE Trans. Ind. Appl. 2008, 44, 769–776. [Google Scholar] [CrossRef]
- Holakooie, M.H.; Taheri, A.; Sharifian, M.B.B. MRAS based speed estimator for sensorless vector control of a linear induction motor with improved adaptation mechanisms. J. Power Electron. 2015, 15, 1274–1285. [Google Scholar] [CrossRef]
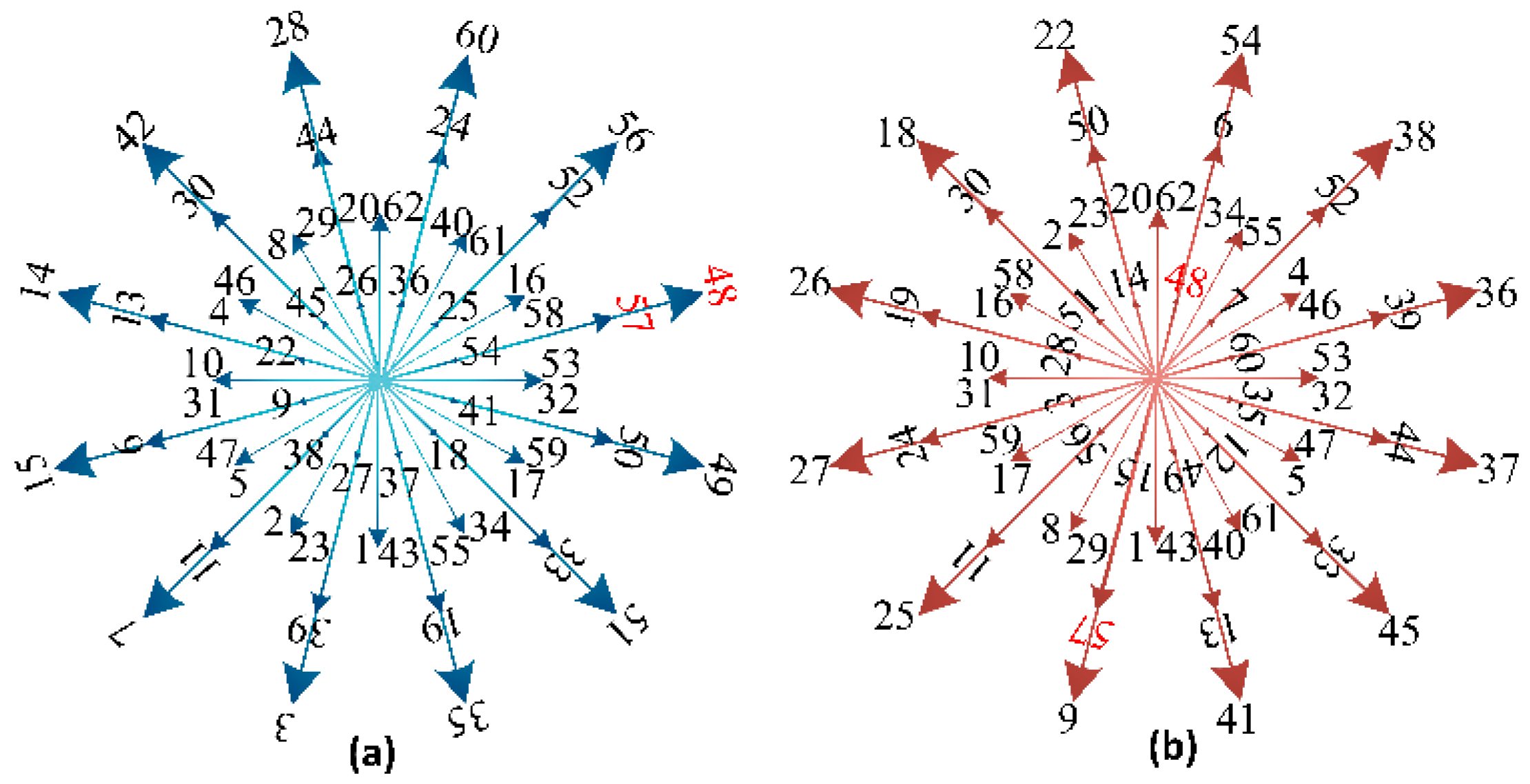


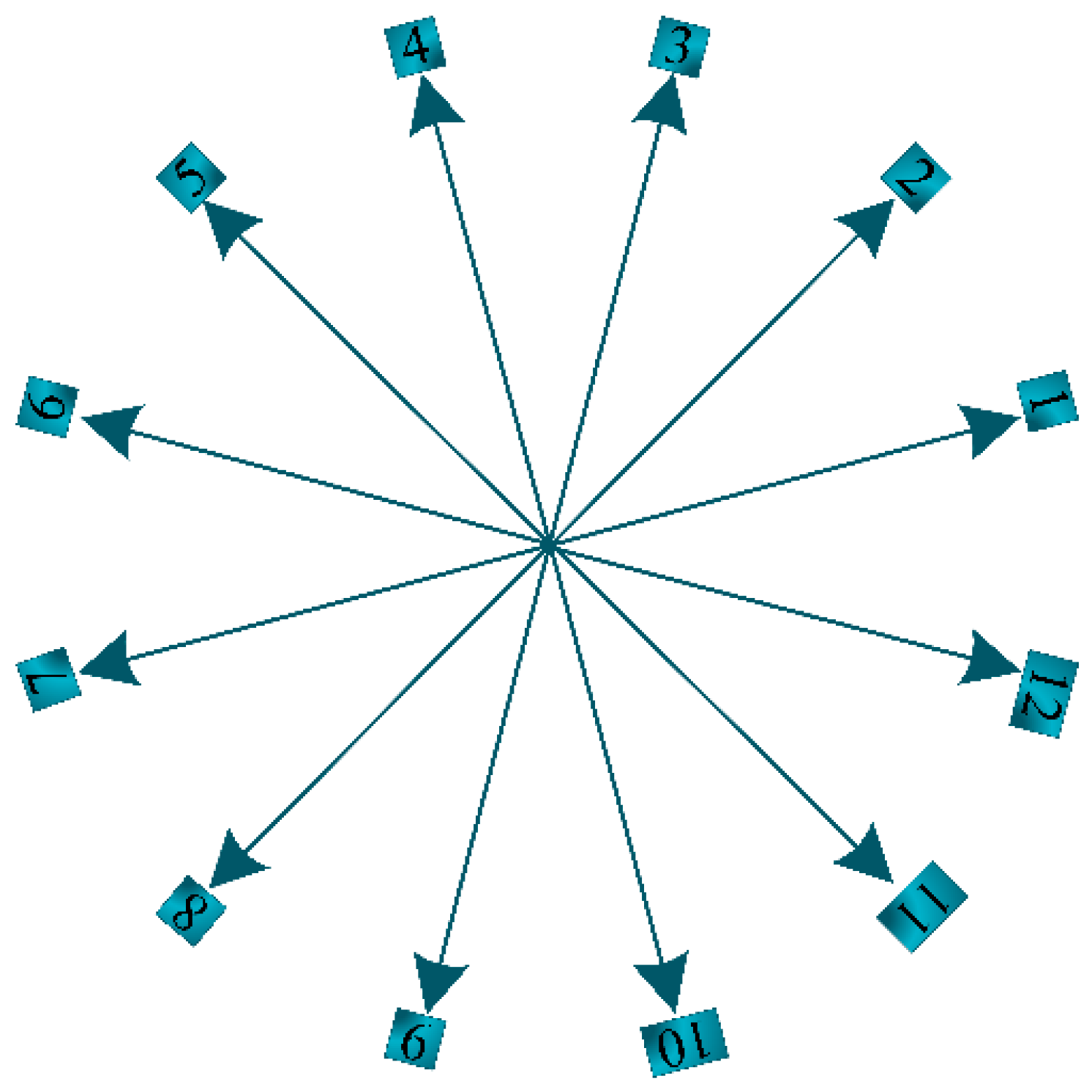

| 0, 21, 42, 63 | 48 | 56 | 60 | 28 | 12 | 14 | 15 | 7 | 3 | 35 | 57 | 49 |
| Parameter, Unit | Value | Parameter, Unit | Value |
|---|---|---|---|
| Rated power, W | 700 | , mH | 588 |
| Rated voltage, V | 200 | , mH | 603.3 |
| Rated current, A | 2 | , mH | 604.4 |
| Rated speed, rpm | 1400 | , | 15.0 |
| Frequency, Hz | 50 | , | 7.91 |
| Method | No-Load | Rated Load | 50% Load |
|---|---|---|---|
| Conventional DTC | %45 | %49 | %47 |
| Duty cycle control | %41 | %37 | %39 |
| Proposed method | %9 | %12 | %10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heidari, H.; Rassõlkin, A.; Vaimann, T.; Kallaste, A.; Taheri, A.; Holakooie, M.H.; Belahcen, A. A Novel Vector Control Strategy for a Six-Phase Induction Motor with Low Torque Ripples and Harmonic Currents. Energies 2019, 12, 1102. https://doi.org/10.3390/en12061102
Heidari H, Rassõlkin A, Vaimann T, Kallaste A, Taheri A, Holakooie MH, Belahcen A. A Novel Vector Control Strategy for a Six-Phase Induction Motor with Low Torque Ripples and Harmonic Currents. Energies. 2019; 12(6):1102. https://doi.org/10.3390/en12061102
Chicago/Turabian StyleHeidari, Hamidreza, Anton Rassõlkin, Toomas Vaimann, Ants Kallaste, Asghar Taheri, Mohammad Hosein Holakooie, and Anouar Belahcen. 2019. "A Novel Vector Control Strategy for a Six-Phase Induction Motor with Low Torque Ripples and Harmonic Currents" Energies 12, no. 6: 1102. https://doi.org/10.3390/en12061102
APA StyleHeidari, H., Rassõlkin, A., Vaimann, T., Kallaste, A., Taheri, A., Holakooie, M. H., & Belahcen, A. (2019). A Novel Vector Control Strategy for a Six-Phase Induction Motor with Low Torque Ripples and Harmonic Currents. Energies, 12(6), 1102. https://doi.org/10.3390/en12061102










