Study and Stability Analysis of Leading Phase Operation of a Large Synchronous Generator
Abstract
:1. Introduction
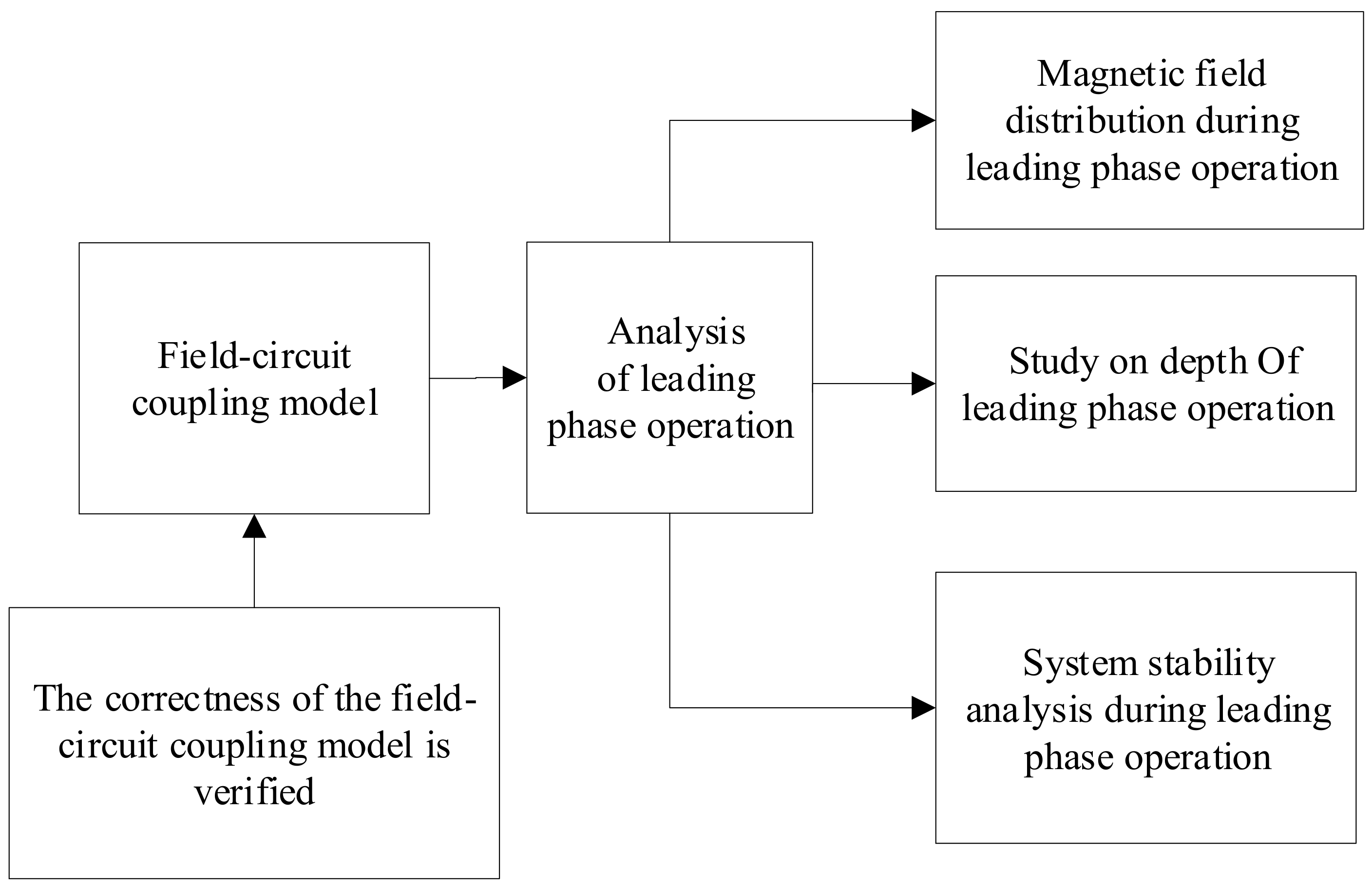
2. Block Diagram of Proposed Research
3. Simulation Analysis of Generator Leading Phase Operation System
- 1)
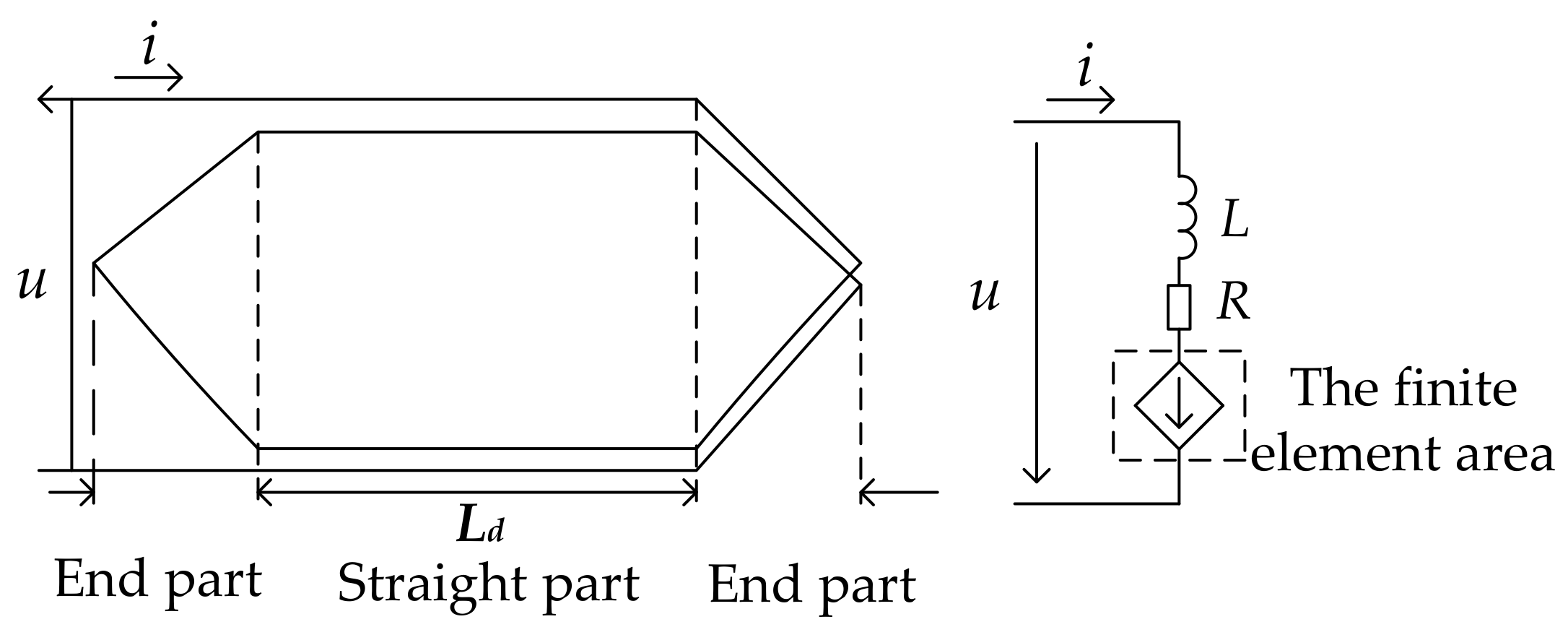
- The magnetic field in the motor has a two-dimensional (2D) distribution, and the stator end effect is described by the constant end leakage reactance;
- 2)
- The material is isotropic, ignoring the hysteresis effect of the ferromagnetic material;
- 3)
- The magnetic field is periodically distributed along the circumferential direction.
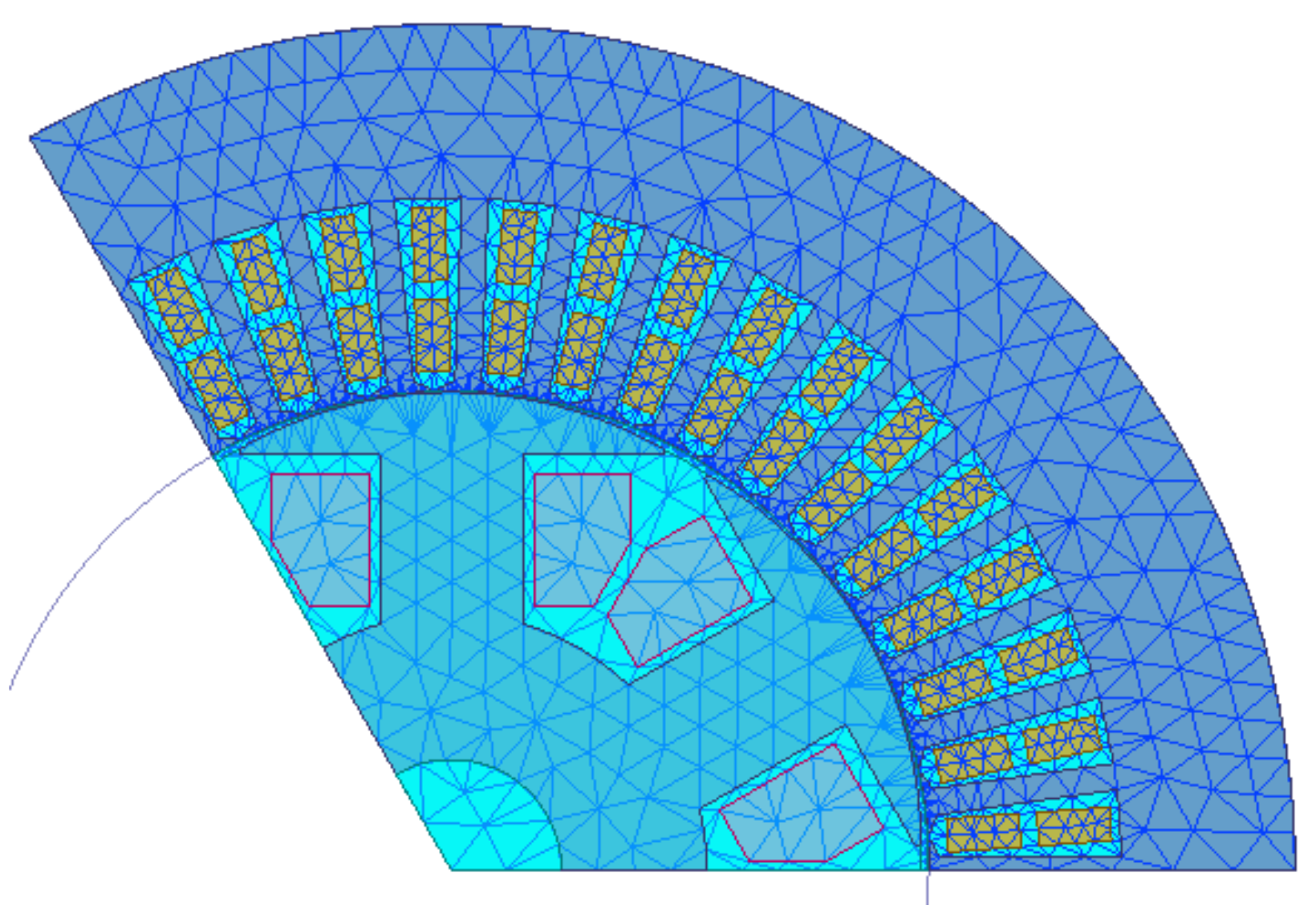
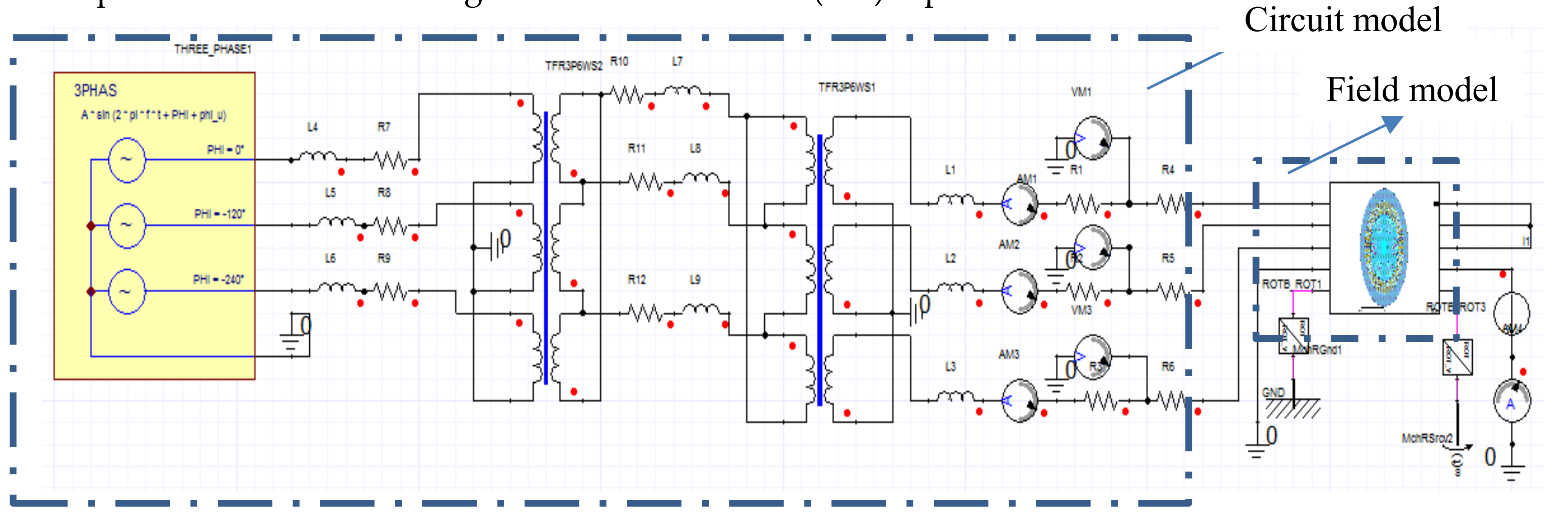
3.1. Modeling
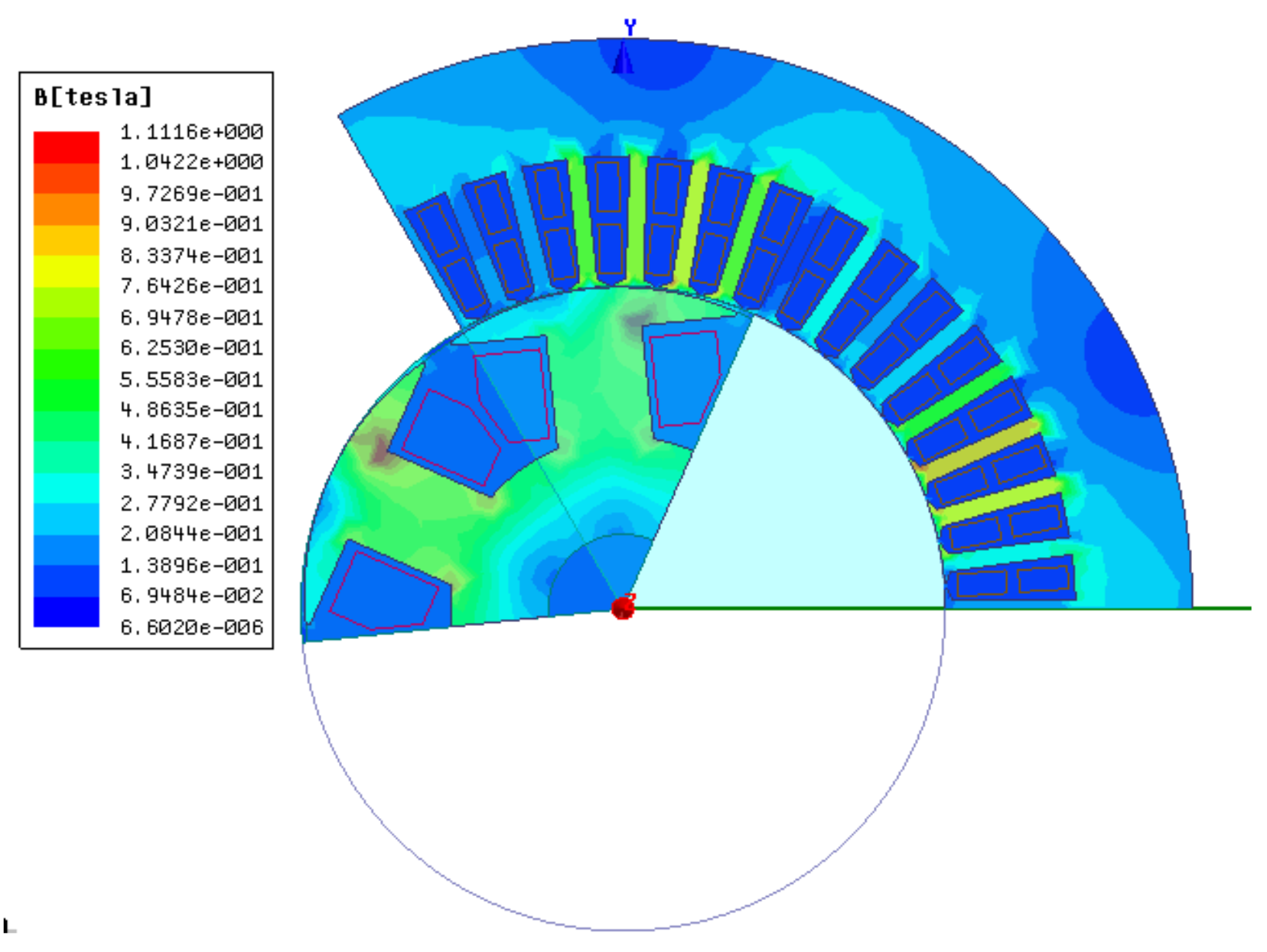
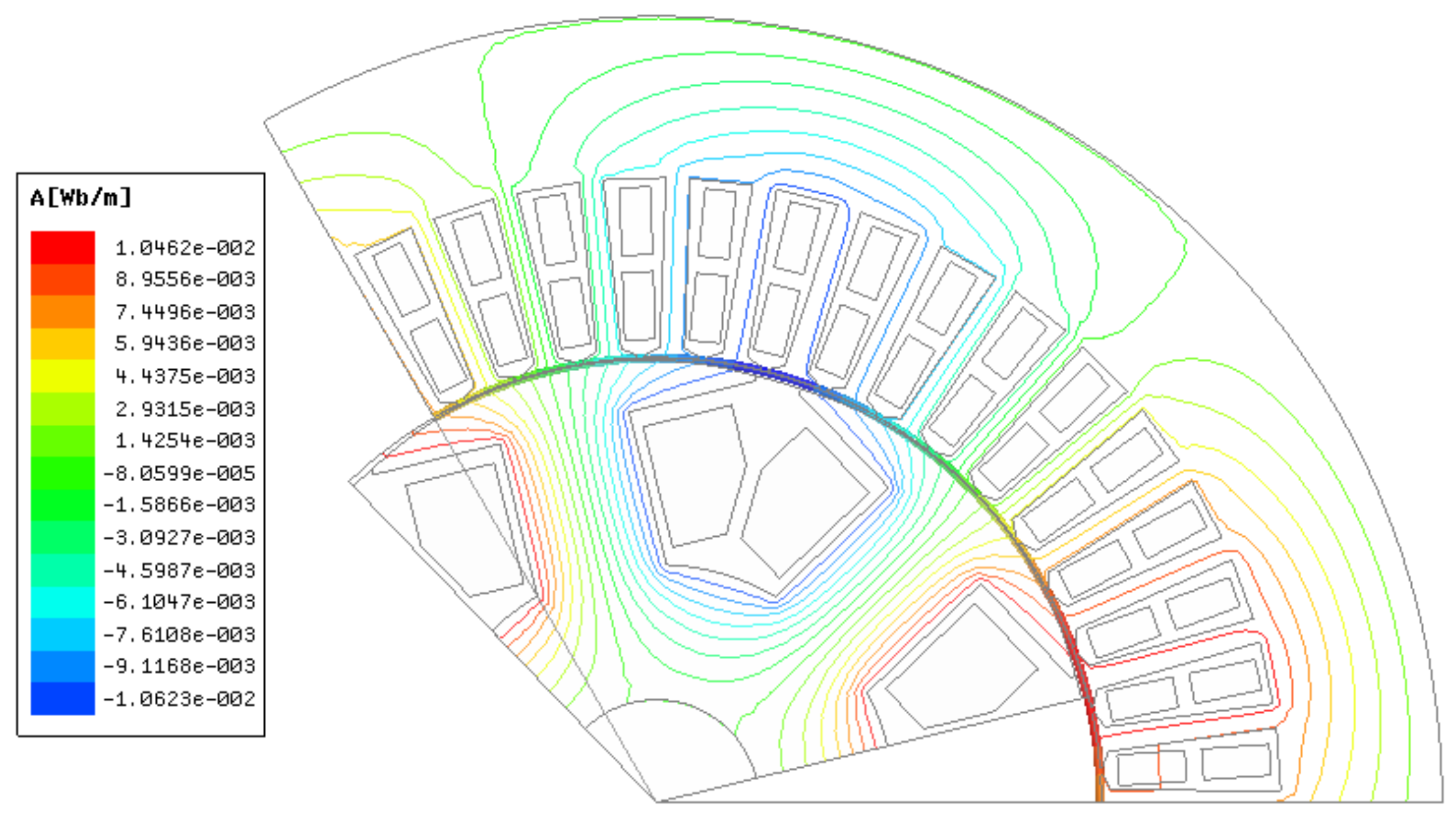
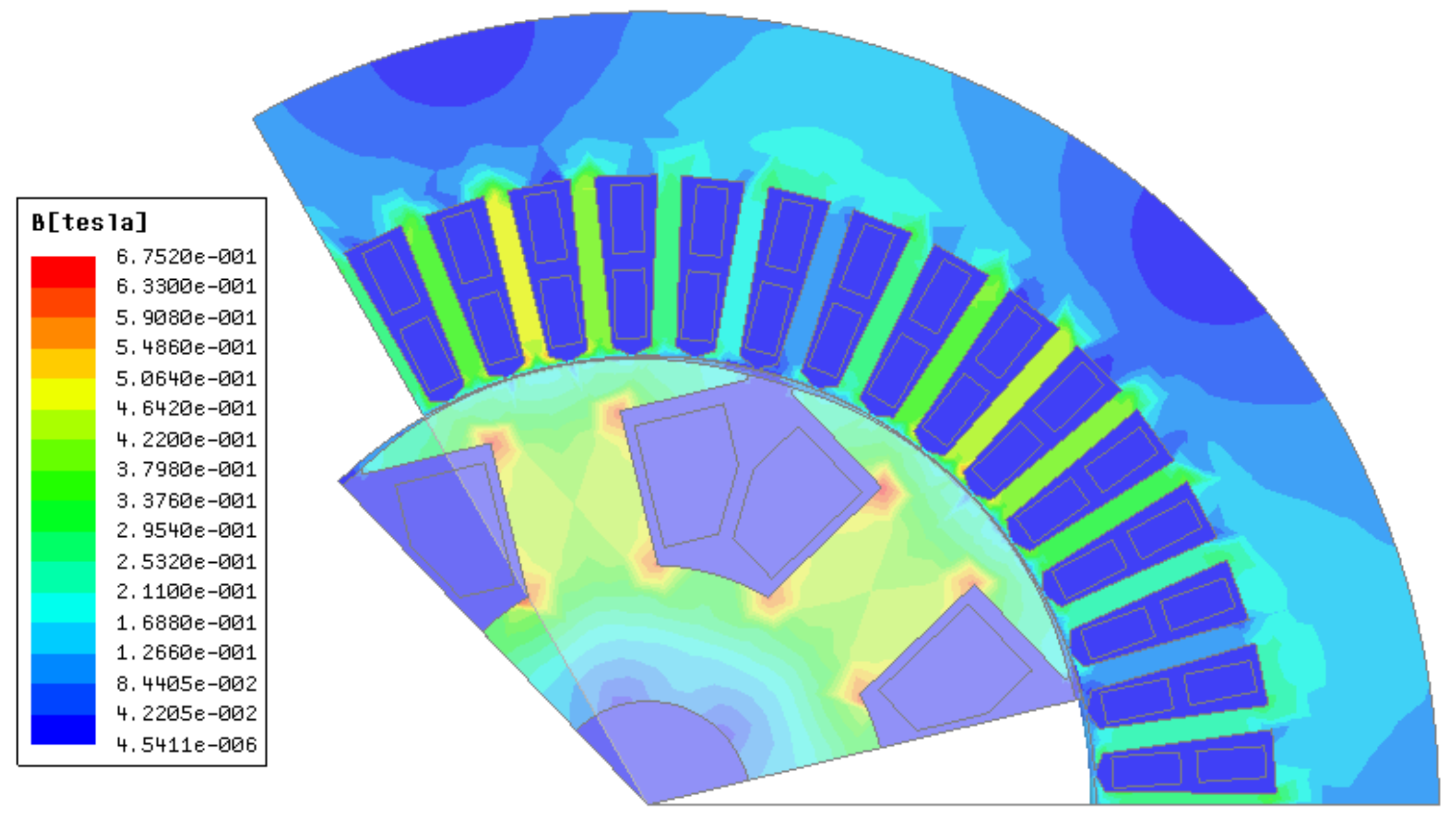
3.2. Modeling Validation
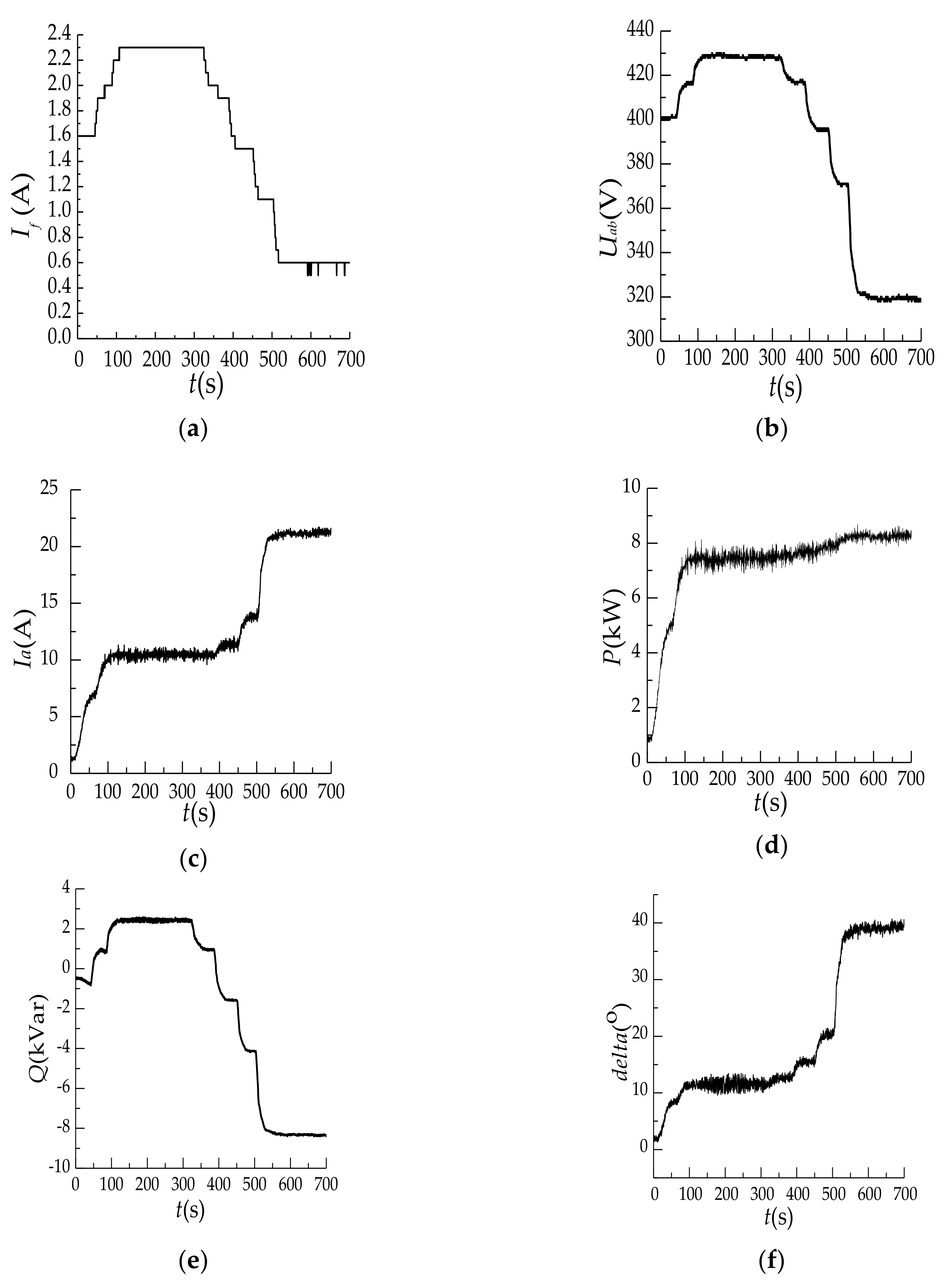
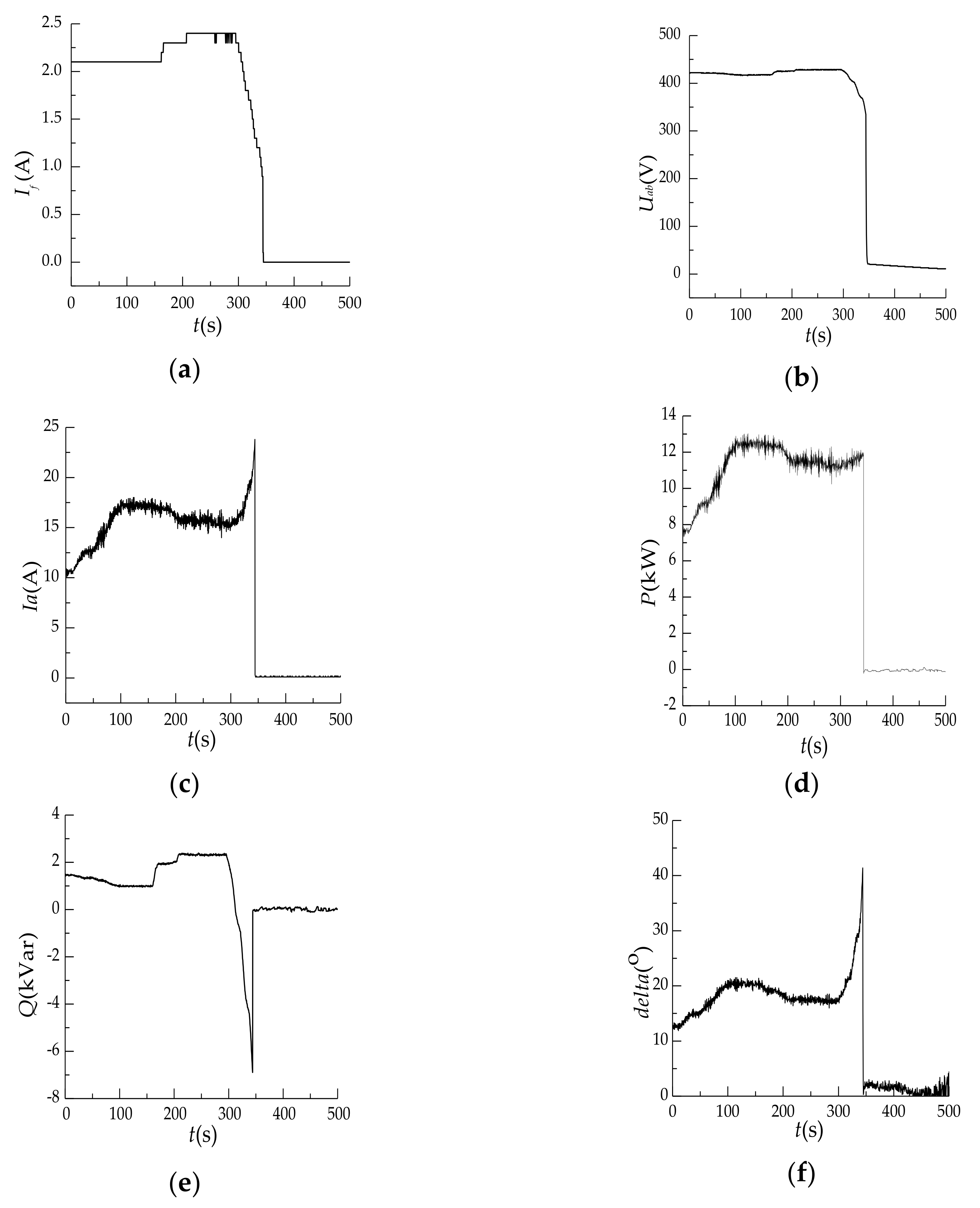
4. Leading Phase Test Analysis
5. Leading Phase Depth and Stability Analysis
6. Conclusions
- 1)
- The field-circuit coupling method was used to establish a field model of the synchronous generator and the field-circuit coupling model of the leading phase operation system of the synchronous generator. The electromagnetic performance of the generator under no-load and rated-load operating conditions was analyzed to verify the accuracy of the model.
- 2)
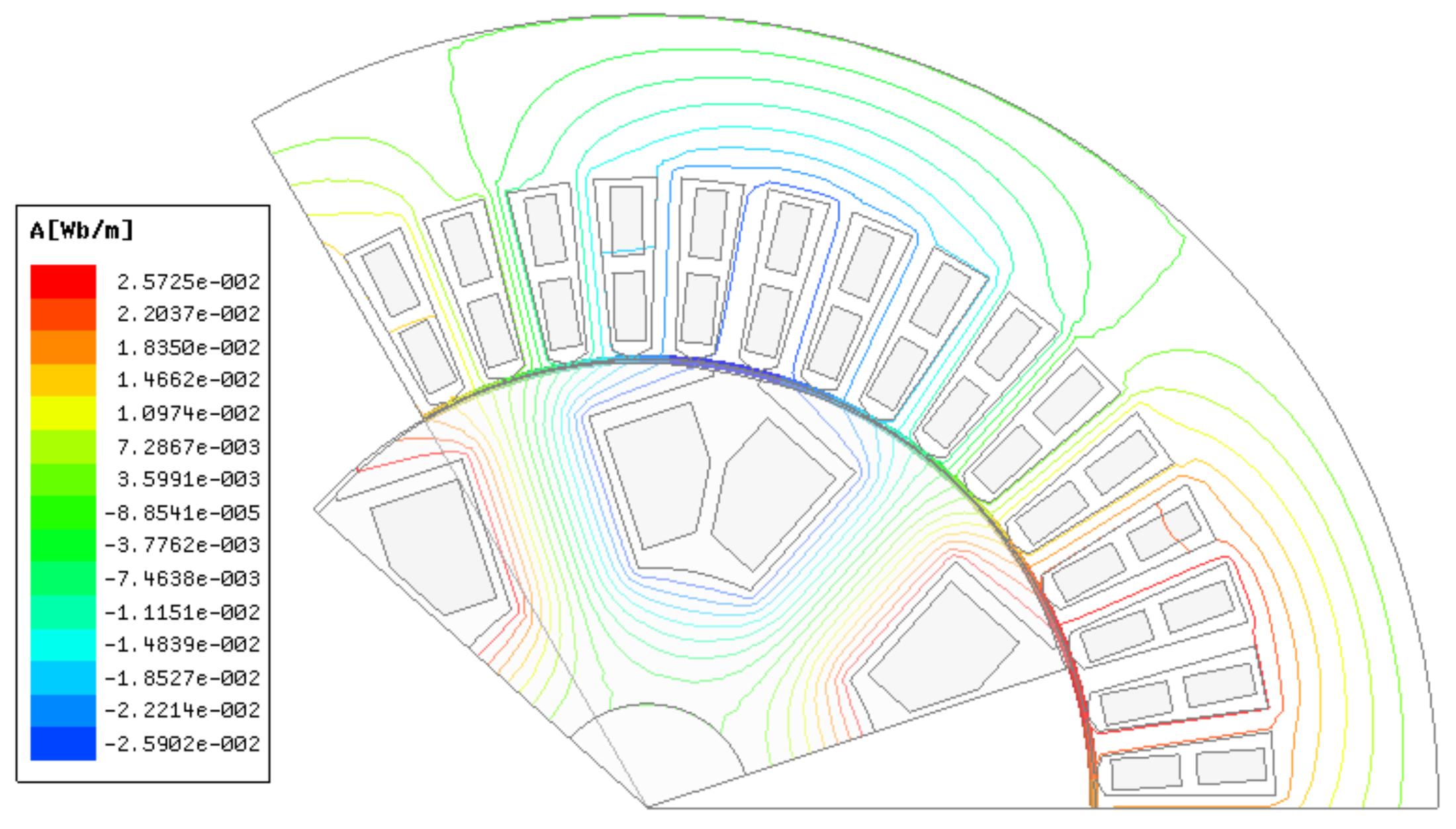
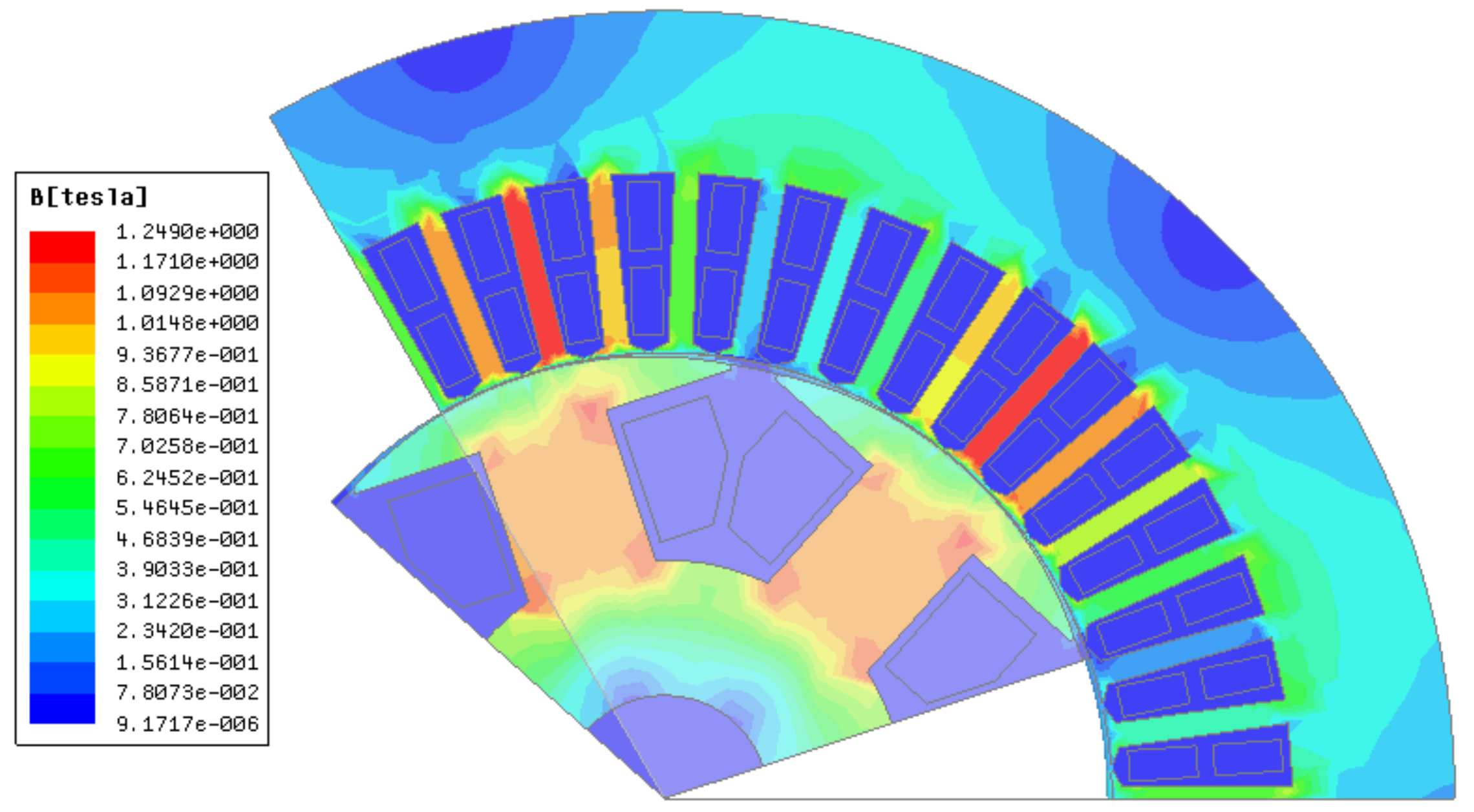
- By analyzing the distribution of magnetic field lines and flux density inside the generator when the large motor is in phase operation under different working conditions, it is concluded that the air-gap flux density increases when the generator is in phase operation with a large load. In particular, close to the end of stator winding, the magnetic field lines are dense, and the greater the power factor is, the more obvious the flux density increases.
- 3)
- Through simulation and experimental analysis, it can be concluded that the field-path coupling method is effective in analyzing the phase feed operation of large motor and provides reference for the phase feed operation of large motor.
Author Contributions
Funding
Conflicts of Interest
References
- Xue, M.; Zheng, H.P.; Yang, W.W. Impact of leading phase operation of 600 MW generator on system voltage. Electr. Eng. 2013, 12, 81–93. [Google Scholar]
- Xia, H.X.; Yao, Y.Y.; Xiong, S.M.; Ni, P.H.; Ni, G.Z.; Liang, X.B.; Xian, Z.-L.; Fan, C.-X. Magnetic-thermal coupling analysis of end region of 1000 MW turbine-generator. Proc. CSEE 2008, 28, 118–122. [Google Scholar] [CrossRef]
- Vicatos, M.S.; Tegopoulos, J.A. Steady state analysis of a doubly-fed induction generator under synchronous operation. IEEE Trans. Energy Convers. 1989, 4, 495–501. [Google Scholar] [CrossRef]
- Wang, X.; Freitas, W. Influence of voltage positive feedback anti-islanding scheme on inverter-based distributed generator stability. IEEE Trans. Power Deliver. 2009, 24, 972–973. [Google Scholar] [CrossRef]
- Wang, C.L.; Wang, C.H. Synchronous generator progress research summary. Electr. Power Autom. Equip. 2012, 32, 131–135. [Google Scholar]
- Li, J.Q.; Li, H.M. Determination of standard temperature of stator iron-core in turbo generator for condition monitoring. Proc. CSEE 2004, 24, 156–160. [Google Scholar] [CrossRef]
- Li, W.; Chai, F.; Zhao, F. Study on eddy current loss and heat-transfer character of stator windings in synchronous generator. In Proceedings of the 2008 International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 479–484. [Google Scholar]
- Choi, S.S.; Jia, X.M. Under excitation limiter and its role in preventing excessive synchronous generator stator end-core heating. IEEE Trans. Power Syst. 2000, 15, 95–101. [Google Scholar] [CrossRef]
- Hammons, T.J. Effect of load and damper modelling on evaluation of negative sequence capability of large generators. IEEE Trans. Energy Convers. 1987, EC-2, 629–637. [Google Scholar] [CrossRef]
- Wang, C.L.; Wang, C.H. Design of the dynamic simulation test for leading phase of large synchronous generator. Electr. Meas. Instrum. 2016, 53, 118–124. [Google Scholar]
- Wang, C.; Wang, H.; Xu, G. System voltage regulation of power grid based on synchronous generator’s leading phase operation. In Proceedings of the CICED 2010, Nanjing, China, 13–16 September 2010; pp. 1–4. [Google Scholar]
- Zhang, C.; Chu, X.; Zhang, B.; Ma, L.; Li, X.; Wang, X.; Wang, L.; Wu, C. A coordinated DC power support strategy for multi-infeed HVDC systems. Energies 2018, 11, 1637. [Google Scholar] [CrossRef]
- Fan, Z.N.; Zhou, Z.T.; Li, J.F.; Wen, K.; Wang, J.; Sun, Z.; Wang, T.; Yao, B. Study on leading-phase operation capability of a 770 MW jumbo hydro-generator based on stability analysis and end-region heat analysis. J. Electr. Eng. Technol. 2018, 13, 1317–1325. [Google Scholar]
- Zeng, C.; Huang, S.; Yang, Y.M. Analysis of electromagnetic forces on involute part of end winding in a 1550 MW nuclear generator. In Proceedings of the 2017 IEEE 2nd IEEE Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 1–4. [Google Scholar]
- Wang, L.; Li, Y.; Li, J. Diagnosis of inter-turn short circuit of synchronous generator rotor winding based on volterra kernel identification. Energies 2018, 11, 2524. [Google Scholar] [CrossRef]
- Xie, Q.; Zhang, Y.; Yu, Y.; Si, G.; Yang, N.; Luo, L. A novel method to magnetic flux linkage optimization of direct-driven surface-mounted permanent magnet synchronous generator based on nonlinear dynamic analysis. Energies 2016, 9, 557. [Google Scholar] [CrossRef]
- Li, Z.Q.; He, F.J.; Chao, H.; FU, Y.L. Numerical analysis of steady state stability limit of salientsynchronous generator in leading power factor operation test. Electr. Mach. Control 2011, 15, 89–95. [Google Scholar] [CrossRef]
- Shi, J.Y.; Shi, Y.S.; Zhao, X.M.; Qu, S.L.; Guo, Y.H.; Zhang, L. The new method of determining the capability of leading phase of generator and realizing the on-line monitoring. Proc. CSEE 2006, 26, 139–143. [Google Scholar] [CrossRef]
- Cui, Y.; Tao, Q.; Chen, D.; Sheng, H.; Fan, Y. Calculation and analysis of leading phase operation of generator based on PSASP. In Proceedings of the 2016 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 9974–9978. [Google Scholar]
- Li, K.; Wang, Y.; Gu, W.; Zhao, B. Modeling of generator leading phase ability based on ant colony optimization and support vector machine. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration, Beijing, China, 26–28 November 2017; pp. 1–5. [Google Scholar]
- Smith, I.R.; Snider, L.A. Prediction of transient performance of isolated saturated synchronous generator. Proc. Inst. Elect. Eng. 1972, 119, 1309–1318. [Google Scholar] [CrossRef]
- Wang, C.; Wang, H.; Xiang, C.; Xu, G. Generator leading phase ability model based on RBF neural network. Trans. China Electron. Soc. 2012, 27, 124–129. [Google Scholar] [CrossRef]
- Wang, C.; Wang, H.; Xu, G. Modeling of generator leading phase ability based on back propagation neural network. Power Syst. Technol. 2011, 35, 136–140. [Google Scholar] [CrossRef]
- Cui, Y.B.; Ling, Z.X.; Sheng, H.X.; Tao, Q.; Fan, Y.P. Simulation research on generator leading phase operation based on measured parameter model. Electr. Eng. 2017, 42, 4–13. [Google Scholar]
- Liu, G.; Song, W.; Song, X. Research on coordination of low excitation limit, loss of excitation protection and out-of-step protection. Power Syst. Prot. Control 2014, 42, 107–112. [Google Scholar]
- Yan, W.; Chen, J.; Shen, Q. Discussion on large non-salient pole generator phase-advancement operation. Autom. Elect. Power Syst. 2007, 31, 94–97. [Google Scholar]
- IEEE Guide for Synchronous Generator Modeling Practices in Stability Analyses; IEEE Standard 1110-1991; IEEE: New York, NY, USA, 1991.
- Tang, R.; Xu, G.; Tian, L.; Zhao, D.; Xu, Y. Calculation of end region magnetic field and circulation losses for turbo-generators using a coupled field and circuit equations method. IEEE Trans. Magn. 1990, 26, 497–500. [Google Scholar] [CrossRef]
- Chen, S.T.; Ding, D.Z.; Fan, Z.H.; Chen, R.S. Nonlinear analysis of microwave limiter using field-circuit coupling algorithm based on time-domain volume-surface integral method. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 864–866. [Google Scholar] [CrossRef]
- Han, R.D.; Wang, T.Z.; Wang, Q.; Li, X.J. Research on circuit model of shunts based on field-circuit coupling method. In Proceedings of the 2016 IEEE International Conference on Computational Electromagnetics (ICCEM), Guangzhou, China, 23–25 February 2016; pp. 95–97. [Google Scholar]
- State Grid Corporation of China Control Centre; China Electric Power Research Institute; North China Electric Power Research Institute. Guide on Leading Power Factor Operation Test of Synchronous Generator: Q/GDW746-2012; Electric Power Press: Beijing, China, 2012. [Google Scholar]

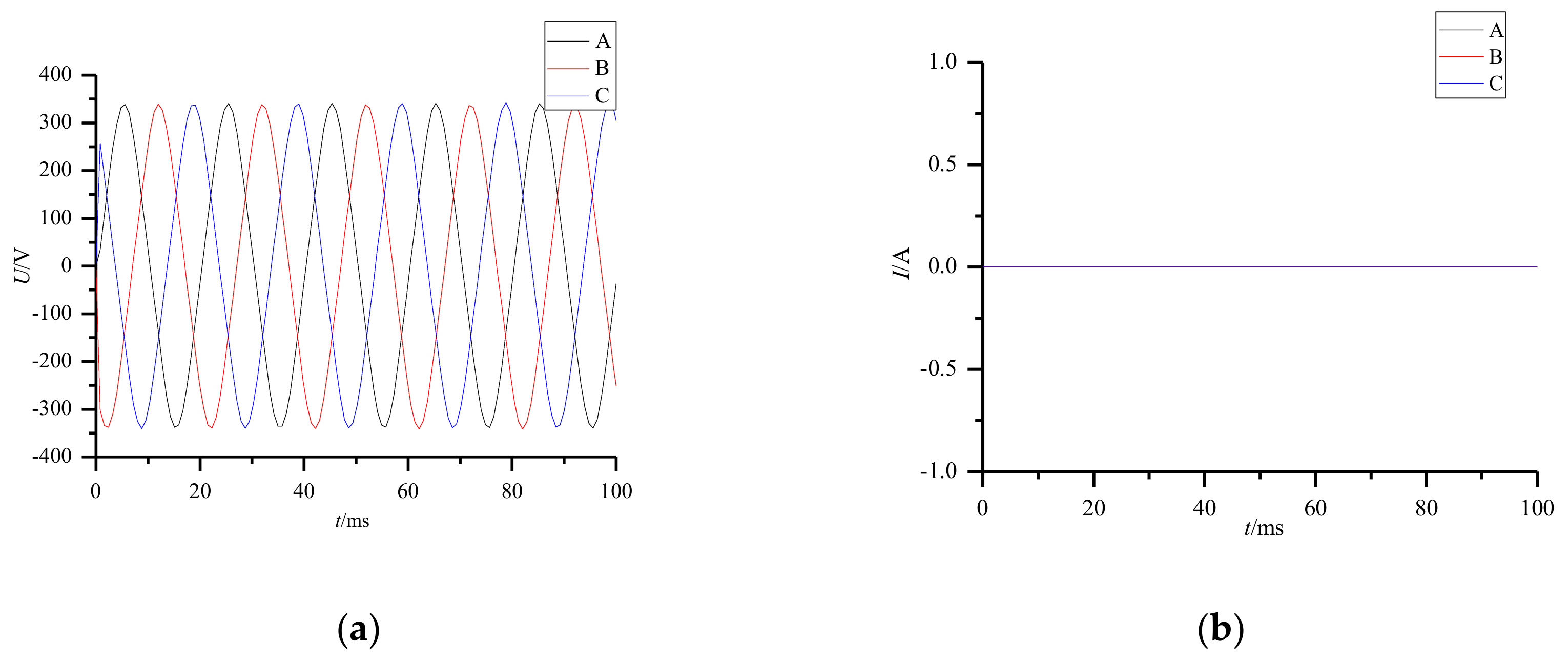
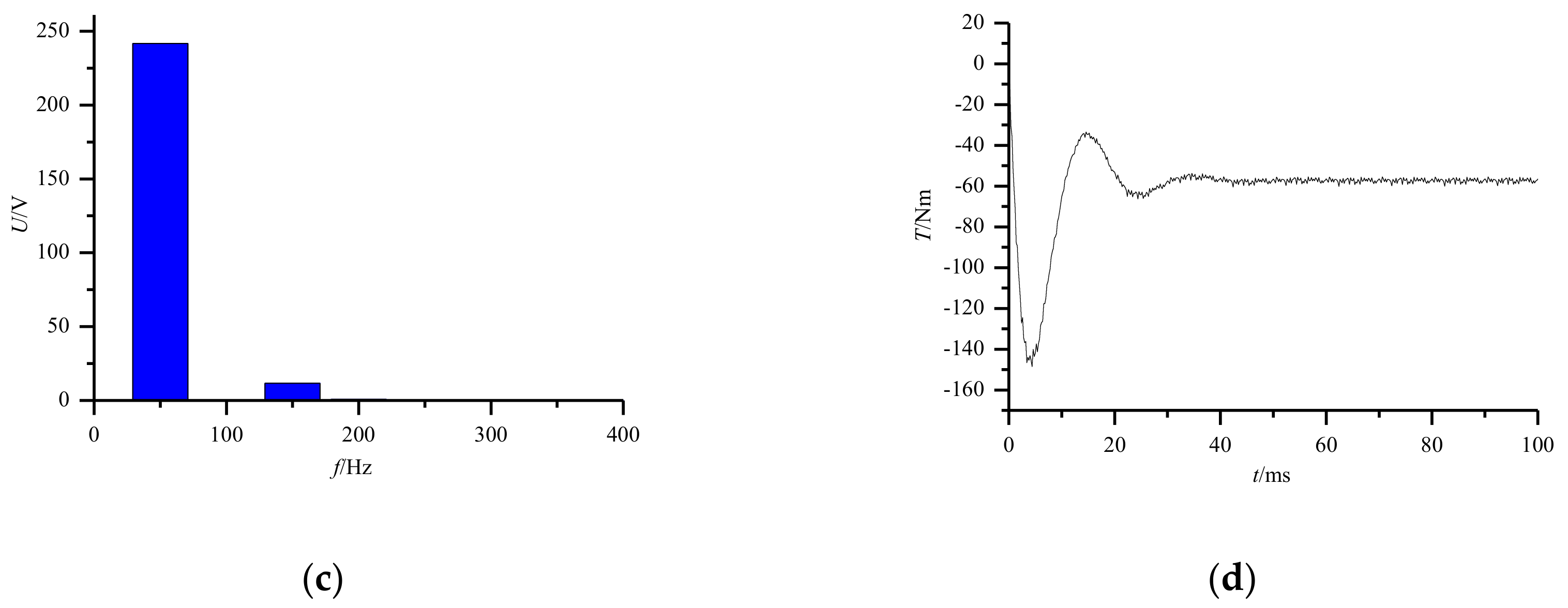
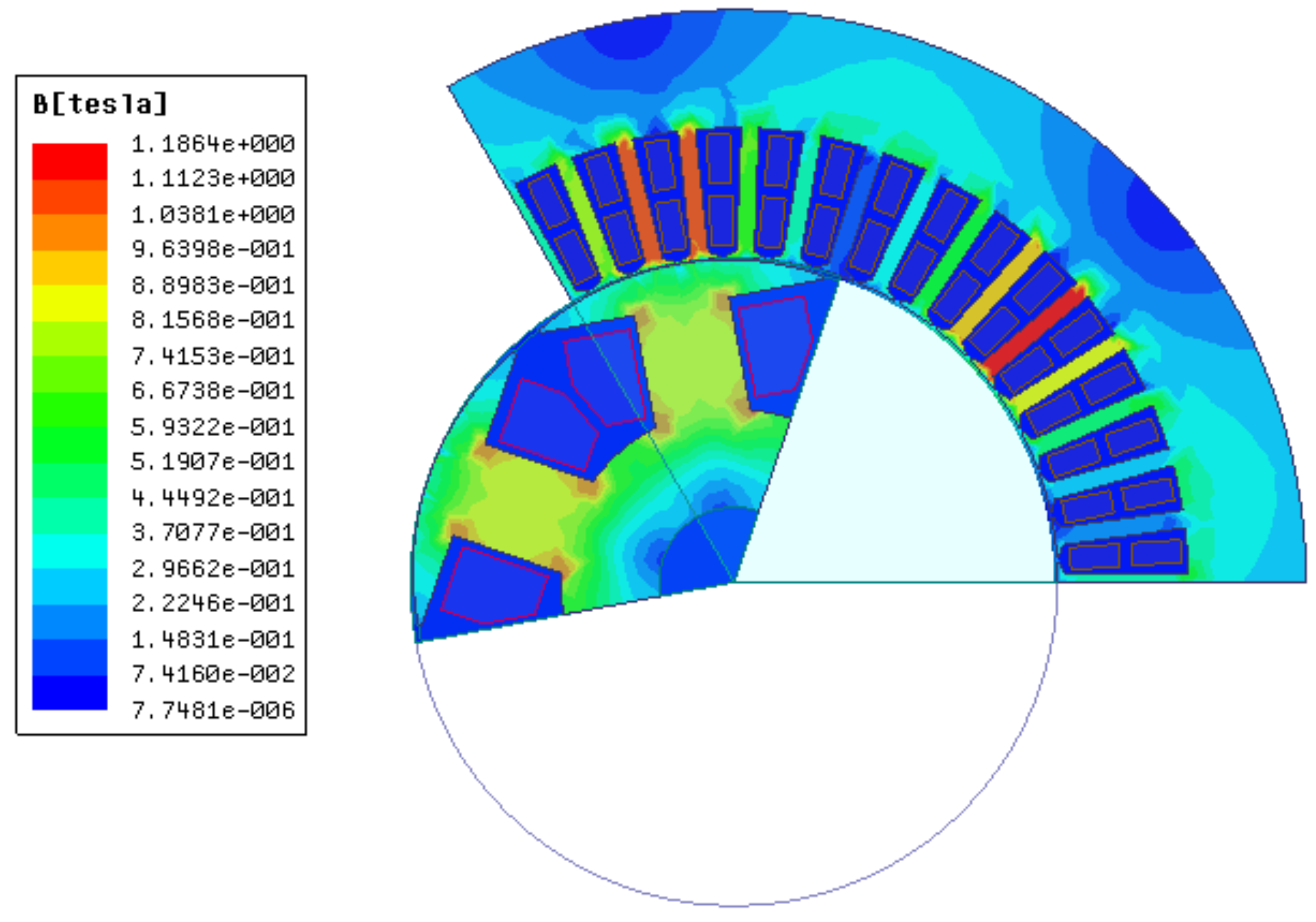
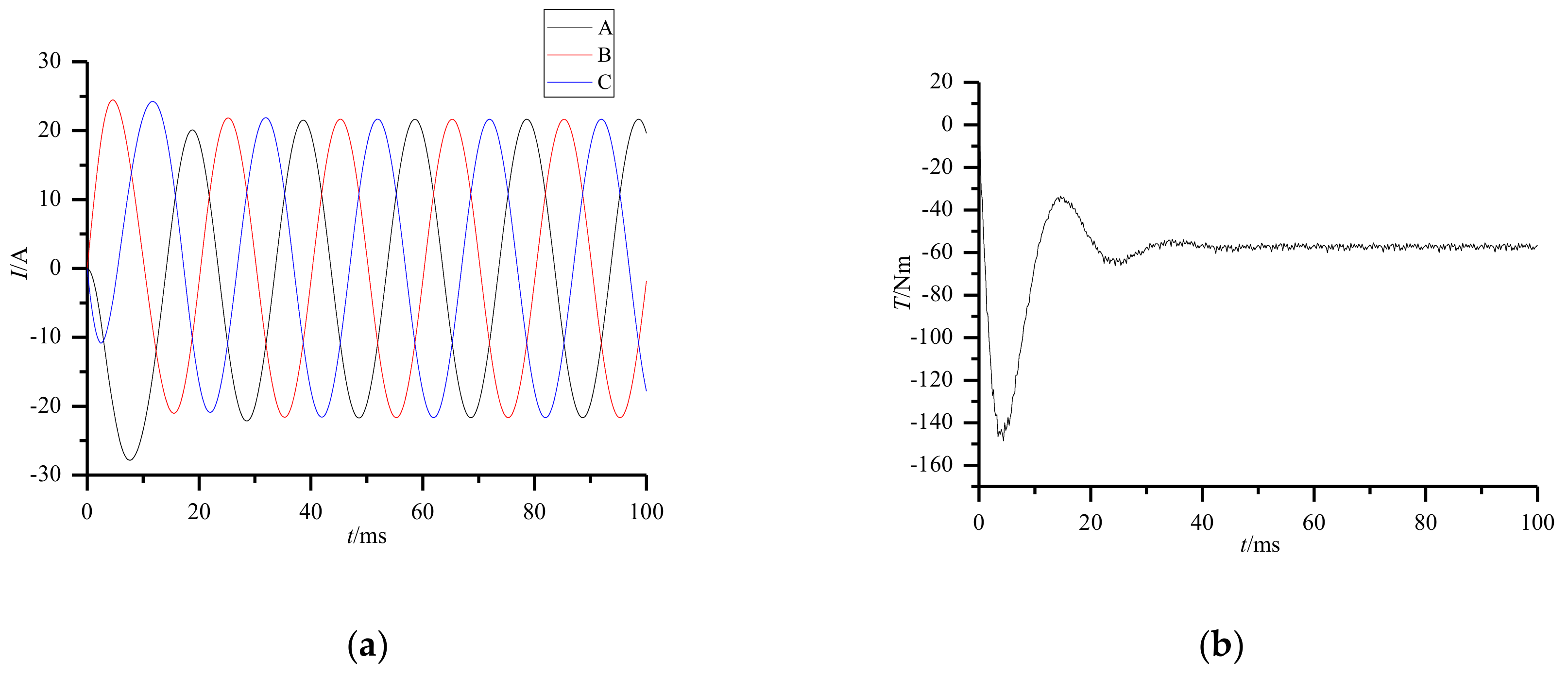
| Motor Parameter | Data | Motor Parameter | Data |
|---|---|---|---|
| Rated voltage | 380 V | Rated current | 22.8 A |
| Rated speed | 1000 r/min | Rated power | 12 kW |
| Rated frequency | 50 Hz | Capacity | 15 kVA |
| Pole number | 6 | Main size ratio | 1.57 |
| Pole-arc coefficient | 0.85 | Stator core outer diameter | 650 mm |
| Core length | 302 mm | Stator core inner diameter | 368 mm |
| Electromagnetism load | 67.5 A/cm | Polar distance | 192.68 mm |
| Total slot number | 45 | Length of pole arc | 163.78 mm |
| Minimum air gap | 1 mm | Maximum air gap | 1.5 mm |
| Winding pitch ratio | 7/7.5 | Number of parallel branches | 3 |
| Winding pitch | 7 | Number of series turns per phase | 40 |
| Winding short-distance coefficient | 0.9945 | Number of conductors per slot | 16 |
| Winding distribution coefficient | 0.9619 | Number of series conductors per phase | 80 |
| Winding coefficient | 0.9566 | Per phase magnetic flux per pole | 2.71 × 10−2 Wb |
| Contrast Parameters | Test Data | Simulation Results |
|---|---|---|
| Rated voltage (V) | 380.0 | 350.25 |
| Excitation current (A) | 1.96 | 1.96 |
| Average air-gap flux density (T) | 0.55 | 0.53 |
| Contrast Parameters | Test Data | Simulation Results |
|---|---|---|
| Rated voltage (V) | 380.0 | 360.6 |
| Excitation current (A) | 2.36 | 2.36 |
| Average air-gap flux density (T) | 0.74 | 0.69 |
| Power Factor | Air Gap Near The Rotor | Air Gap | Air Gap Near The Stator |
|---|---|---|---|
| 0.949 | 0.74 | 0.61 | 0.94 |
| −0.984 | 0.87 | 0.78 | 1.04 |
| 0.951 | 0.71 | 0.63 | 0.98 |
| −0.834 | 0.94 | 0.86 | 1.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Y.; Du, Y.; Liu, Q.; Hou, S.; Zhang, J. Study and Stability Analysis of Leading Phase Operation of a Large Synchronous Generator. Energies 2019, 12, 1047. https://doi.org/10.3390/en12061047
Lv Y, Du Y, Liu Q, Hou S, Zhang J. Study and Stability Analysis of Leading Phase Operation of a Large Synchronous Generator. Energies. 2019; 12(6):1047. https://doi.org/10.3390/en12061047
Chicago/Turabian StyleLv, Yanling, Yizhi Du, Qi Liu, Shiqiang Hou, and Jie Zhang. 2019. "Study and Stability Analysis of Leading Phase Operation of a Large Synchronous Generator" Energies 12, no. 6: 1047. https://doi.org/10.3390/en12061047
APA StyleLv, Y., Du, Y., Liu, Q., Hou, S., & Zhang, J. (2019). Study and Stability Analysis of Leading Phase Operation of a Large Synchronous Generator. Energies, 12(6), 1047. https://doi.org/10.3390/en12061047





