Optimal Placement of Remote-Controlled Switches in Distribution Networks in the Presence of Distributed Generators

Abstract

A two-level optimization method is presented to find the optimal number and location of conventional protective devices to be upgraded to remote-controlled switches (RCSs) for an existing distribution network (DN). The effect of distributed generation (DG) on this problem is considered. In the first level, a nonlinear binary program is proposed to maximize the restored customers subject to technical and topological constraints. All feasible interchanges between protective devices and ties involved in the restoration, when a fault occurs at all possible locations are found considering switching dependencies. In the second level, a nonlinear cost function, combining the expected cost of interruptions (ECOST) and the switch cost, is minimized with respect to the location of RCSs. The expected cost function is computed based on the optimum restoration policies obtained from the first level. The optimum placement of RCSs using the proposed algorithm is tested on a 4-feeder 1069-node test system and compared to the solution obtained with a genetic algorithm (GA) on the same system.

1. Introduction

The reliability of an existing distribution network (DN) can be significantly improved by upgrading existing manual protection devices to remote-controlled switches (RCSs) that have communication capability and can achieve quicker system restoration following a permanent outage (e.g., longer than 5 min) [1,2]. RCSs can reduce both the number and the duration of interruptions; however, they are relatively more expensive than manual protective devices. Thus, the problem of which and how many of the existing manual devices should be replaced with RCSs can help utility companies to gain greater benefit with less cost [3,4,5,6,7,8,9,10,11,12,13,14,15,16]. The most commonly used objective function for determining the optimum location of RCSs includes the reliability of the system and the total cost of installed switches [4,5,6,7,8,9]. However, in [10], the criteria were power loss minimization and load equalization. The problem becomes more involved, if the islanded mode of distributed generation (DG) is considered [4,5,6,11].

The customer-oriented reliability indices, such as system average interruption frequency index (SAIFI), system average interruption duration index (SAIDI), and customer or energy not supplied (ENS), have been used to find the optimal placement and number of automatic switches in DNs in the presence of DG [6,7,8,17,18]. These indices do not represent the outage cost. The expected cost of interruptions (ECOST) considers all permanent outages in the system with a duration of over 5 min, the network configuration, the interruption duration, and all load unavailability rates. ECOST is suitable for adding to the switch cost and transforming a multi-objective problem into a single objective problem [12].

Different optimization methods are utilized to select the optimum placement of switches. Heuristic algorithms like alliance algorithm (AA) [6], particle swarm optimization (PSO) [7], minimum spanning tree (MST) [8], genetic algorithm (GA) [13], simulated annealing [14], ant colony system (ACS) algorithm [15], and fuzzy logic [16] have been used widely to solve the placement problem. In [6], for each fault, the AA solved the placement problem considering the islanded mode of operation for DGs. The algorithm started with the random creation of tribes. The optimum solution was that alliance which corresponds to the minimum cost of the energy unavailability and switches. In [7], PSO was used to find a set of optimal solutions instead of a single solution for switch placement problem. This method helps utility companies to have the adaptable solution to different circumstances and eases the decision making. In [8], a greedy algorithm was used to upgrade the interrupting devices. For any fault in DN, the algorithm minimized the interrupted loads with the minimum number of switching operations considering no more than one load transfer in a restoration scheme. The switches involved in the restoration scheme were upgraded.

Optimal placement problems can be formulated using both linear and nonlinear programming [5,9,10,17,18,19,20,21,22]. In [17], a nonlinear binary programming was presented to find the type and location of protective devices that should be installed. The partial restoration was not considered in problem formulation, and the optimal number of switches was not reflected in the objective function. In [18], a similar method considered the system restoration after fault analysis. However, the optimum islanded mode for DGs was not considered, and the dependency of the restoration steps was not discussed. The mixed integer linear programming (MILP) method was proposed to find the optimum placement of sectionalizing switches in DN [5,19,20,21,22]. In [5], the objective function contained ECOST plus the cost of switches. The faults were categorized into restorable and unreturnable during the repair time. In [9], the same approach also considered the presence of DGs. In [10], to obtain a more accurate result, the dispersed nature of customer interruption costs at a specified failure duration was reflected in ECOST function. In [5,9,10], binary decision variables were assigned to sectionalizing switches. In [19], one interchange was considered to restore the interrupted loads. In [20,21], the problem of placement was discussed in different scenarios. In [22], the relocation of the RCSs and the cost of DGs are also considered. Then, the criterion to obtain the outage cost was the existence of at least one sectionalizing switch between the normally open (NO) switch and the faulted section, rather than deriving the optimum location of the NO switches. Therefore, ECOST was formulated as a linear function of the defined decision variables. However, in a complex DN, having more than one step of restoration is expected, and some of the partial restoration steps might be dependent on the previous switching operations. The switching dependencies and the contribution of NO switches in restoring the interrupted loads make the ECOST function non-linear.

In this paper, the DN is represented by its graph. The problem is defined as how many and which interrupting devices should be upgraded to RCSs to have a more reliable network with minimum cost. A two-level method is introduced to formulate and solve the problem in the presence of DG. For each outage in DN, the switches which are involved in minimizing ENS subject to operational and topological constraints are obtained. The optimum island operation of DG is considered. There may be more than one interchanging operation in the reconfiguration. In this case, the dependencies of the restoration actions are reflected in the cost function. Therefore, the outage cost for each fault is a non-linear function of decision variables. The optimum replacement of the manual switches with RCSs is a multi-objective problem. The final objective function includes ECOST when the failure occurs in all possible fault locations and the switch cost. The main contributions of the paper are: the feasible solutions of restoration policies are first determined, and the optimum one is selected from the feasible set by solving a mathematical program that is formed with the assistance of the fundamental cut-set matrix of DN; the dependencies of switching operations to restore the interrupted loads are considered by obtaining the sequence of switching actions; elite genes (EG) are defined efficiently based on independent switching actions to solve the final objective function; and both normally closed (NC) and NO switches are reflected in the optimization problem; therefore, the optimum upgrading of NO switches can be determined as well.

The remainder of this paper is organized as follows: the system modeling is discussed in Section 2; Section 3 introduces the problem formulation; Section 4 presents the results of testing the proposed algorithm on a case study; finally, the conclusions are drawn in Section 5.

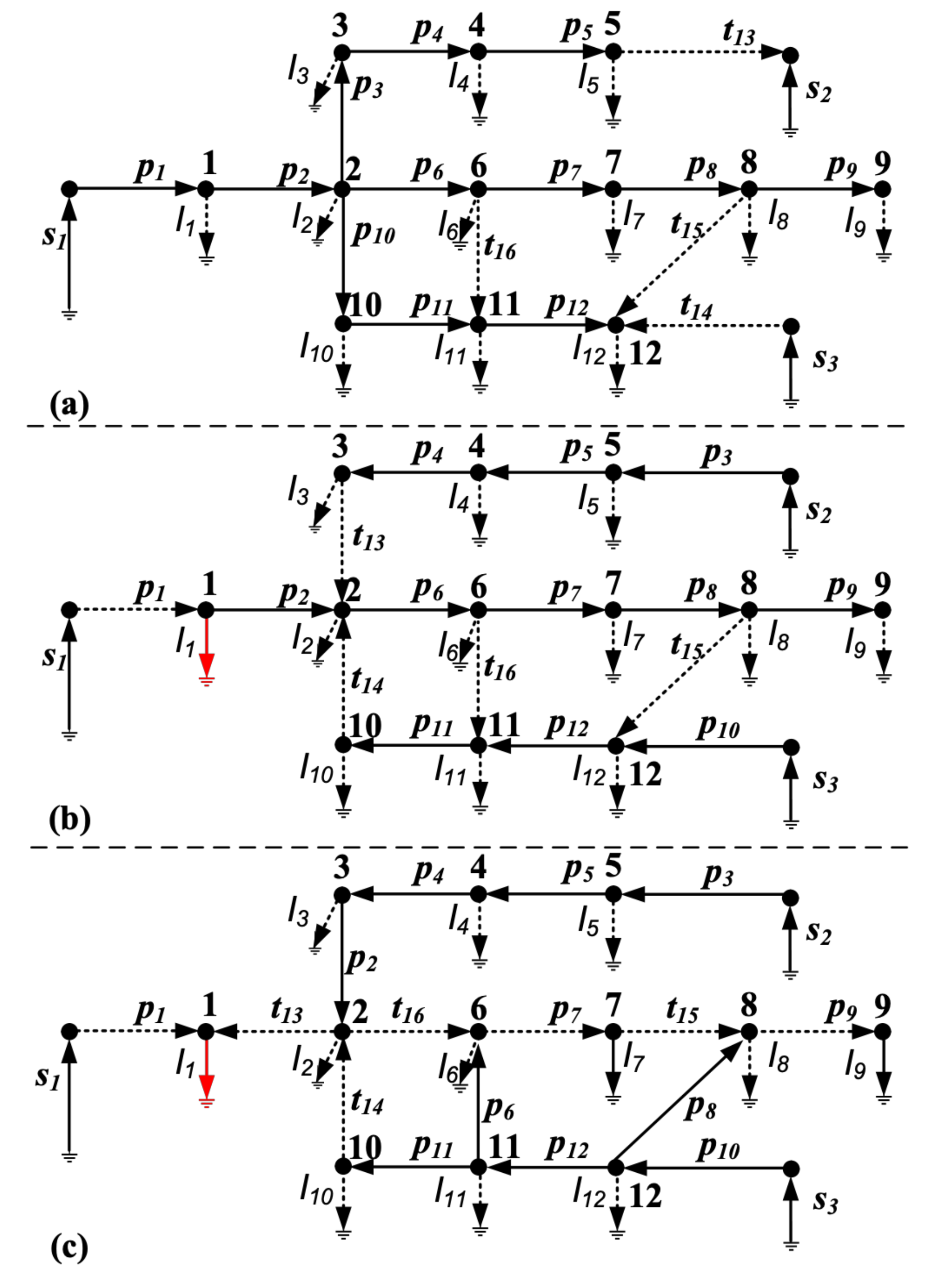
2. System Modeling

A DN can be shown by a properly ordered directed graph containing as its edges the NC interrupting devices, NO switches, sources, and load (connected customers) between the nodes and the ground, and as vertices (nodes) all electrical components including feeder sections between any adjacent interrupting devices [18,23,24]. The main benefit of the graph representation of the DNs is providing a tool to validate certain topological constraints. The DNs are radial and during the restoration should remain radial. The graph representation of the system can guarantee that after any restoration step the network remain radial [25,26,27]. NO switches connect either two nodes within the network or DGs (alternative sources) to network nodes. A properly ordered graph is defined here as one where nodes are numbered such that the first node is connected to the primary source node, and any child node has a number greater than that of its parent node. With respect to the DN graph, a proper tree is defined as containing all sources and NC devices in the branches and all NO devices and loads in the links. Figure 1a shows an example of the graph representation of a DN, where $s$ and $p$ are NC interrupting devices, $t$ are NO ties, and $l$ are the connected loads.

The tree branches are indexed by the number of the arrival node (for example, $p_2$ arrives at node 2 in Figure 1a). The NC protective devices, thus, have indices from $1$ to $M$ corresponding to the total number of NC protective devices. To have the unique index for NC and NO switches, the indices of NO switches are between $M+1$ and $M+N$ where $N$ is the total number of NO switches. Loads are modeled as links which are connected to the nodes, and their indices are the same as the identification number of the respective node ($l_2$ is connected to node $2$ in Figure 1a).

The fundamental cut-set matrix corresponding to the proper tree is partitioned as follows:

(1)

where, $\mathbf{0}$ and $I$ are zero and identity matrices, $D_{SC}$ and $D_{ST}$ relate source cut-sets to customer links and NO ties, respectively, and $D_{PC}$ and $D_{PT}$ relate NC protecting-device cut-sets to customer links and NO tie-links, respectively.

A small radial network and its fundamental cut-set matrix is shown in Figure 1a where $s_1$ is the primary source and $s_2$ is the alternative source. The load of source $s$ can be computed as:

$$S{L}_s=D_{\mathbf{S}\mathbf{C}}(s,:)\cdot L$$

(2)

As it can be seen in Figure 1a the loads are supplied by the primary source, and the loading of DG in the normal situation is zero. Similarly, the load of NC device $j$ is calculated as:

$$C{L}_j=D_{\mathbf{P}\mathbf{C}}(j,:)\cdot L$$

(3)

In the following, three states have been considered for the DN based on [28].

Up or Fully Restored State: there is no failure in the DN, and all loads are supplied by the primary source as in Figure 1a.

Down-State: In this state, a single-node failure has occurred before any restoration. If $a$ is the outage node, it is assumed that all interrupting devices are reliable, and then the isolating device is $p_a$. The loads downstream of node $a$ are interrupted. The cut-set matrix can be used as a guide to accomplish the isolation systematically. Isolation of the faulted node in the down-state is reflected by interchanging tree branch $p_a$ with the load link $l_a$. The new cut-set matrix, denoted as $D^0$, can be derived from the original $D$ by interchange the columns corresponding to $p_a$ and $l_a$ in $D$ matrix. This implies $co{l}_{a+g}\left(I\right)\leftrightarrow co{l}_a\left(D_L\right)$ where $g$ is the number of source nodes in the graph. In Figure 1, a fault occurs at node $1$, and thus, the bold columns of $D$ matrix in Figure 1a (3rd and 8th columns) are interchanged. The bold row corresponding to the tree branch $p_1$ is considered as a pivot to convert the matrix into a reduced row echelon form (RREF) as in (1). The updated cut-set matrix corresponding to the isolated state is shown in Figure 1b.

Partially Restored State: some of the interrupted loads are rerouted. The restoration can be achieved by interchanging the

NC and NO switches as in Figure 1c. An NC device, $p_j$, and a NO tie, $t_k$, can, under certain conditions, form an interchange pair denoted as $\left(j,k\right)$. If $r$ is the restoration iteration following the fault at a node $a$, for the $r$-th restoration iteration, the $\left(j,k\right)$ interchange is reflected in the $D^{r-1}$ matrix applying the necessary column operation $co{l}_{j+g}\left(I\right)\leftrightarrow co{l}_k\left(D_L^{r-1}\right)$ and row operations as described in isolation state. The updated cut-set matrix derived from a number of these operations will be denoted as $D^r$. For example, in Figure 1b, NO switch $t_6$ is the interchangeable link with NC switch $p_4$. To reflect this switching operation in the fundamental cut-set matrix, the bold 6th and 13th columns of $D^0$ matrix are interchanged. The new configuration of the network after this interchange and considering the bold row $p_4$ as the pivot for converting the matrix to RREF is obtained and shown in Figure 1c.

3. Problem Formulation

3.1. Global Objective Function

The objective is to find the optimal number and locations of those switches that should be upgraded in the DN to minimize the cumulative outage cost. For this purpose, we introduce an $\left(M+N\right)\times 1$ binary decision array, $x$, such that $x\left(q\right)$ is $1$ if interrupting device $q\left(1\le q\le M+N\right)$ is selected to be upgraded, and zero otherwise. Then for any choice of $x$, the expected cost of the outage at node $i$ is given as:

$$ECOS{T}_i={\lambda }_i\cdot \left[CD{F}_i(t_r)\cdot I{L}_i-\left(CD{F}_i(t_r)-CD{F}_i(t_s)\right)\right.\left.\cdot R{L}_i(\mathbf{x})\right]$$

(4)

where $CD{F}_i$ is the customer damage function for customers connected to node $i$ expressing the interruption cost per kW [29] and $R{L}_i\left(x\right)$ is the restored load resulting from a restoration policy applied on $x$. The optimization problem is stated as:

$$\underset{x\in {\left\{0,1\right\}}^{M+N}}{\min }CF={\displaystyle \sum _{i=1}^{M}ECOS{T}_i}+sc\cdot {\mathbf{x}}^T\mathbf{x}$$

(5)

To obtain $R{L}_i\left(x\right)$, first, a restoration policy that maximizes the restored load after an outage at node $i$ should be found. For this purpose, a greedy search algorithm is applied. The restoration process may involve several steps, and each step uses the updated cut-set matrix of the previous step starting at $D^0$ for step $r=1$.

At step $r$, the following sets can be readily obtained with the assistance of $D^{r-1}:$ the cut-set of tree branch $n$, ${\mathcal{C}}_n=\left\{m:D^{r-1}\left(n,m\right)\ne 0\right\}$, and similarly the link-set of link $m$, ${\mathcal{L}}_m=\left\{n:D_L^{r-1}\left(n,m\right)\ne 0\right\}$, in which, the pair $\left(j,k\right)$ represents an interchange so that the first and second arguments are the indices of NC and NO switches, respectively. For example, in Figure 1a the links $l_4$, $l_5$, and $t_6$ are in the cut-set of tree branch $p_4$, and the link-set of $t_6$ contains $s_1$, $s_2$, $p_1$, $p_4$, and $p_5$.

An interchanging pair $\left(j,k\right)$ is a feasible switching operation at the $r$-th restoration step if:

1)

The NC switch $j$ is down-stream from the outage node, $i$. For a properly ordered graph, this implies $j>i$.

2)

The NO switch $k$ is in the cut-set of NC switch $j$.

The set of all feasible interchange pairs satisfying conditions $1$ and $2$ at $r$-th iteration is denoted as $I^r$. Note that the feasible set at the $r$-th step can be obtained with the assistance of the cut-set matrix at the $r-1$ step, $D^{r-1}$, since $D^r$ is not yet available.

An illustrative example is solved to describe the proposed algorithm. For the DN shown in Figure 2a, it is assumed that the failure has occurred at node $1$. Therefore, the isolating device is $p_1$. The updated cut-set matrix after isolation step can be used to find the candidate interchanging pairs in the first restoration iteration. It is also assumed that loads of all nodes are $1$ unit except for nodes $6$ and $7$, where the loads are 0.5 and 2 units, respectively. The generation capacities of sources $2$ and $3$ are 4 and 4.5 units, respectively.

Considering conditions 1 and 2 above, in the first iteration of the restoration, $I^1=\left\{\left(2,13\right),\left(3,13\right),\left(4,13\right),\left(5,13\right),\left(2,14\right),\left(10,14\right),\left(11,14\right),\left(12,14\right)\right\}$, affecting sources 2 and 3.

3.2. Local Objective Function

To determine the optimum interchange pairs in $I^r$ considering the optimal islanded mode of operation for DGs, local decision variable, $d_{j,k}\in \left\{0,1\right\}$, is defined for each pair $\left(j,k\right)\in I^r$ such that $d_{j,k}=1$ if the $\left(j,k\right)$ interchange pair is chosen, else is zero. Next, the local optimization problem:

$$\begin{array}{l}\underset{d_{j,k}}{\max }\hspace{1em}TS{L}^r={\displaystyle \sum _{s\in S}S{L}_s^r}\\ \mathrm{Subject} \mathrm{to}:\\ \left(\mathrm{a}\right) d_{j,k}\in \left\{0,1\right\} \left(\forall \left(j,k\right)\in I^r\right),\\ \left(\mathrm{b}\right) S{L}_s^r\left(\left[d_{j,k}\right]\right)\le C{P}_s \left(\forall s\in S\right),\\ \left(\mathrm{c}\right) \mathrm{Interchange} \mathrm{Constraints},\\ \left(\mathrm{d}\right) V_i^{min}\le V_i\le V_i^{max}\end{array}$$

(6)

that maximizes the total source loading, is solved, where $S$ is the set of the indices of the sources. In this paper, the existing DN is to be upgraded. Thus, the protection coordination rules are considered at the normal situation. In the restoration state, it is assumed that the relay protection function can be disabled during the repair time [22].

3.2.1. Interchange Constraints

The interchange constraints in Equation (6) resolve conflicting interchanges, that is, those that interrupt the same path of the graph. We denote ${\mathcal{P}}_{jk}=\left\{m:m\in {\mathcal{L}}_k \mathrm{and} m\ge j\right\}$ as the set of tree branches included in the path from $j \mathrm{to} k$ including $j \mathrm{and} k$. Then, $\left(j,k\right),\left(j^{\prime },k^{\prime }\right)$ are conflicting interchanges if $P_{jk}\cap P_{j^{\prime }{k}^{\prime }}\ne \varnothing$. For each conflicting pair of interchanges, we introduce into the constraint group (c) in Equation (6) the constraint:

$$d_{jk}+d_{j^{\prime }{k}^{\prime }}\le 1$$

(7)

implying mutual exclusion. Examples for this constraint are interchanging pairs $\left(j,k\right),\left(j,k^{\prime }\right)$ and $\left(j,k\right),\left(j^{\prime },k\right)$ in the set $I^r$.

3.2.2. Source Loading

The loading of all sources should not violate their capacity (e.g., the capacity of the system circuits should be considered). For a given $\left(j,k\right)\in I^r$, let $\left(m,n\right)\in I^r$ denote an interchange non-conflicting with $\left(j,k\right)$ and such that $n\in {\mathcal{C}}_j$, then the load transferred by $\left(j,k\right)$ onto source $s$ under all such $\left(m,n\right)$ is written as:

$$T{L}_{j,k,s}^r=d_{j,k}\cdot \left(p_{j,k,s}\cdot C{L}_j^{r-1}-{\displaystyle \sum _{(m,n)}{d}_{m,n}\cdot p_{j,n,s}\cdot C{L}_m^{r-1}}\right)$$

(8)

where:

$$p_{j,k,s}={\mathbf{D}}_{\mathbf{P}\mathbf{T}}^{r-1}\left(j,k\right)\cdot {\mathbf{D}}_{\mathbf{S}\mathbf{T}}^{r-1}\left(s,k\right)$$

(9)

$$p_{j,n,s}={\mathbf{D}}_{\mathbf{P}\mathbf{T}}^{r-1}\left(j,n\right)\cdot {\mathbf{D}}_{\mathbf{S}\mathbf{T}}^{r-1}\left(s,n\right)$$

(10)

are pivoting coefficients from the ${\mathbf{D}}^{r-1}$ matrix. Then, the source load at the $r$-th step can be written as:

$$S{L}_s^r=S{L}_s^{r-1}-{\displaystyle \sum _{(j,k)\in I^r}T{L}_{j,k,s}^r}$$

(11)

Equation (11) is implicitly expressed in terms of the optimization variables $d_{j,k}$ and can be used in Equation (6), where $C{L}_j^{r-1}$ and $S{L}_s^{r-1}$ appearing in Equations (8) and (11) are constants that can be computed from Equations (2) and (3), respectively. By maximizing Equation (6), the switching actions corresponding to the optimum islanded mode of operation for DG can be found. It is worth noting that, at each iteration, having more than one interchange is allowed.

For the illustrative example, the first step of restoration is formulated as below:

$$\begin{array}{ll}\underset{d_{j,k}}{\max }& 11.5d_{2,13}+\left(11.5-3d_{10,14}-2d_{11,14}-d_{12,14}\right)d_{2,13}+3d_{3,13}+2d_{4,13}+d_{5,13}+\\ & 11.5d_{2,14}+\left(11.5-3d_{3,13}-2d_{4,13}-d_{5,13}\right)d_{2,14}+3d_{10,14}+2d_{11,14}+d_{12,14}\end{array}$$

(12)

where the interchange constraints are:

$$\begin{array}{l}{d}_{2,13}+d_{3,13}+d_{4,13}+d_{5,13}\le 1\\ d_{2,14}+d_{10,14}+d_{11,14}+d_{12,14}\le 1\\ d_{2,13}+d_{2,14}\le 1\end{array}$$

(13)

and the loading of the sources by assuming the zero initial load is:

$$\begin{array}{l}11.5d_{2,13}+\left(11.5-3d_{10,14}-2d_{11,14}-d_{12,14}\right)d_{2,13}+3d_{3,13}+2d_{4,13}+d_{5,13}\le 4\\ 11.5d_{2,14}+\left(11.5-3d_{3,13}-2d_{4,13}-d_{5,13}\right)d_{2,14}+3d_{10,14}+2d_{11,14}+d_{12,14}\le 4.5\end{array}$$

(14)

The selected interchanging pairs for the illustrative example are $\left(3,13\right)$ and $\left(10,14\right)$. The restored customers for both interchanges are three. Figure 2b shows the new configuration of the DN.

After finding the candidate optimum interchanging pairs, the cut-set matrix is updated as explained in Section 2. The voltages of all nodes are computed to check the constraint group (d) in the program in Equation (6). The updated cut-set matrix is used to find the current of branches and subsequently the voltage of every node. If the voltage constraints are violated, a constraint will be added to the program in Equation (6) such that the selected interchanges cannot occur simultaneously, and the program should be run again. For instance, let $\left(j,k\right)$ and $\left(m,n\right)$ be the solution of program in Equation (6) in which the voltage constraints are violated in the respective reconfigured network, therefore, $d_{j,k}+d_{m,n}\le 1$ is added to the program as an additional constraint for re-running the program.

3.2.3. Source Relaxation

When, due to generation capacity of the sources, no switching operation is found to restore the interrupted loads, there may be other solutions by removing some of the nodes to meet the source capacity limitation. In this study, the same priority is assigned to all loads. An effective method can be applied through the proposed algorithm, whereby some terminal nodes in the circuit graph of the DN are grounded through a fictitious NC tie, and the corresponding lateral root is replaced with a NO tie. The interchanging pairs are obtained as part of the feasible interchanges.

In Figure 2b, the source relaxation can be considered for node $9$ in the second iteration of the example. The restoration process continues until all DGs are filled out, or no more interchanging pairs are found to improve the load restoration. Figure 2c shows the final configuration of the DN.

Figure 3 shows the flowchart of the first level of the proposed algorithm.

3.3. $R{L}_i\left(\mathit{x}\right)$ Computation

For every $\left(j,k\right)\in I^r$ such that $d_{j,k}=1$, the load restored is:

$$G_{j,k}(\mathbf{x})=C{L}_j^r\cdot {\pi }_j\cdot \mathbf{x}(k)$$

(15)

where ${\pi }_j$ contains products of members of $x$ and it is computed after considering dependencies in the selected switching operations. Dependency occurs if a certain sequence of switching operations to restore the interrupted loads cannot take place until some other switching action has been completed. An interchange $\left(j,k\right)$ on step $r$ can be dependent upon at most one other interchange $\left(m,n\right)$ on step $\nu$ ($1\le \nu \le r-1)$, where $d_{m,n}=1$, if it satisfies the following dependency condition:

$$(j,n),(m,k)\in I^{\nu } \mathrm{and} d_{j,n}=d_{m,k}=0$$

(16)

There can be at most one such $\left(m,n\right)$ with $d_{m,n}=1$ at any step, since if there is another $\left(m^{\prime },n^{\prime }\right)$ in the same step satisfying the above condition, then $\left(j,n\right),\left(j,n^{\prime }\right)\in I^v$ and $\left(m,n\right),\left(m^{\prime },n^{\prime }\right)$ will be conflicting and therefore mutually exclusive. It is likewise for the pair $\left(m,k\right),\left(m^{\prime },k\right)$ (as per previous conditions of conflict). Let $p$ equal the maximum of all $\nu$, $1\le \nu \le r-1$, for which the dependency condition holds or $p=0$ if it does not hold for any $1\le \nu \le r-1$, then:

$${\pi }_j=\left\{\begin{array}{cc}\mathbf{x}(j)& if p=0\\ \mathbf{x}(j)\cdot {\pi }_m& if p\ne 0\end{array}\right.$$

(17)

where the unique NC switch $m$ in interchanging pair $\left(m,n\right)\in I^p$ satisfies the dependency condition. Equation (17) is a recursive formula that always terminates since each new dependency $\left(m,n\right)$ is found in a previous step.

The restored load after an outage at node $i$ can be computed considering all restorations $G_{j,k}\left(x\right)$ that are downstream from $i$, that $i$ is in the path between the source and $j$, and provided that the other NC devices between $i$ and $j$ are not selected. That is:

$$R{L}_i(\mathbf{x})={\displaystyle \sum _{j>i}{G}_{j,k}(\mathbf{x}){\displaystyle \prod _{i\le q\le j}(1-\mathbf{x}(q))}}$$

(18)

3.4. Numerical Implementation

Those interchange pairs that do not resupply the interrupted loads will not be selected. Therefore, ignoring the ineffectual pairs make the algorithm more efficient. With this assumption, a backward search technique is proposed to construct the dependency tree for the DN.

• The switching operations at $r=1$ are independent.
• The selected interchanging pair at $r$-th iteration $\left(j,k\right)$ depends on switching operation of iteration $r-1$ if it is in the cut-set of the previous switching operation. Otherwise, a backward search technique with stop criteria as the following is done to check the dependency of the switching at $r$-th iteration:

  1)

  Finding the switching operation that satisfies the condition of dependent switching.

  2)

  All iterations are checked, and there is no dependency on switching, therefore, the $r$th switching is independent.

• The dependencies can be illustrated graphically by a tree whose branches represent the interchanges at each restoration step and nodes represent the restoration number. If there is an edge between two nodes $p$ and $q$ such that $q>p$, then the switching operation of $q$-th iteration depends on the switching operation of $p$-th iteration. The independent nodes are connected to a reference node.

Figure 4 depicts a dependency tree for the illustrative example. Source relaxation is applied to the 2nd and 3rd iterations, yielding respectively:

$$G_{6,16}=0.5\cdot \mathbf{x}(6)\cdot \mathbf{x}(7)\cdot \mathbf{x}(10)\cdot \mathbf{x}(16)$$

(19)

In Equation (19), the interchanging pair $\left(6,16\right)$ is dependent on the interchanging pairs $\left(7,6\right)$—due to source relaxation—and $\left(10,14\right)$. $G_{6,16}$ implies an independent switching operation that corresponds to interchanging pair $\left(6,16\right)$ and the operation of the NC switches $7$ and $10$.

For every interchanging pair, $\left(j,k\right)$, a set which contains the indices of the term $G_{i,j}$ is defined as the elite gene such that its first and last elements are $j$ and $k$, respectively, and the elements in between are the indices of those NC switches that satisfy Equation (16). In the illustrative example, the elite gene corresponding to interchanging pair $\left(6,16\right)$ is $\left\{6,7,10,16\right\}$.

4. Case Study

A 4-feeder 1069-node test system is studied. This test system is based on the Taxonomy “R3-12.47-2” developed by Pacific Northwest National Laboratory [30]. Figure 5 shows the circuit graph of the test system’s protection tree. The load on each feeder is 4.652 MVA. In this paper, it is assumed that the overloading of feeders can be an additional 25% of their nominal load, the voltage of the substation is regulated to 1.02 per unit, the impedances of all sections are equal to $z=0.244+j0.35 \mathrm{ohm}$, the power factor of all loads is unit, and that loads are distributed equally through the feeders. The generation capacities of DG 1 to 4 are 2.559, 1.279, 2.675, and 1.163 MVA, respectively. It is assumed that the failure rate for all nodes is 0.02 failure/year, the switching time of RCSs is ten minutes, and the repair time for all failures is two hours. It is also assumed that the type of all customers is small-user, then $CDF$ is obtained from [9]. The total cost of a sectionalizing switch including capital investment, installation cost, annual operation, and maintenance costs for a life period of 15 years is $4794 in U.S. dollars [9]. The branch and bound, and the Branch and Reduced Optimization Navigator (BARON) methods are used to solve the nonlinear programs in Equations (5) and (6), respectively. In this paper, a computer with a 3.4-GHz CPU and 8 GB RAM is used to do all the computations. The computation time for the program in Equation (6) for all feeders is 567.38 seconds, and for the program in Equation (5) is 8.86 s.

4.1. Outage Analysis and Optimum Restoration Policies

An outage analysis is performed for the entire system. For each outage, the optimum restoration policy is obtained by solving the program in Equation (6).

Table 1. The elite genes (EG) of the case study.

Feeder 1	Feeder 2	Feeder 3	Feeder 4
$\left\{31,170\right\}$, $\left\{32,170\right\}$, $\left\{38,170\right\}$, and $\left\{40,170\right\}$	$\left\{78,171\right\}$ and $\left\{79,171\right\}$	$\left\{113,169\right\}$ and $\left\{114,169\right\}$	$\left\{158,170\right\}$
$\left\{9,31,161\right\}$, $\left\{10,31,161\right\}$, $\left\{13,31,161\right\}$, $\left\{14,31,161\right\}$, $\left\{18,31,161\right\}$, $\left\{19,31,161\right\}$, $\left\{24,31,161\right\}$, and $\left\{25,161\right\}$	$\left\{59,65,70,166\right\}$, $\left\{64,70,166\right\}$, $\left\{66,70,166\right\}$, $\left\{67,70,166\right\}$, $\left\{68,70,166\right\}$, and $\left\{69,166\right\}$	$\left\{98,163\right\}$, $\left\{99,163\right\}$, $\left\{104,163\right\}$, $\left\{106,163\right\}$,$\left\{107,163\right\}$, $\left\{108,163\right\}$, $\left\{110,163\right\}$, $\left\{111,163\right\}$, $\left\{112,163\right\}$, $\left\{118,163\right\}$, and $\left\{119,163\right\}$	$\left\{129,139,168\right\}$,$\left\{130,140,168\right\}$, and $\left\{131,168\right\}$
$\left\{2,9,165\right\}$, $\left\{4,9,165\right\}$, $\left\{5,9,165\right\}$, $\left\{7,165\right\}$, and $\left\{8,165\right\}$	$\left\{42,52,53,165\right\}$,$\left\{44,53,165\right\}$, $\left\{45,53,165\right\}$, $\left\{49,59,165\right\}$, $\left\{50,59,165\right\}$, and $\left\{51,165\right\}$	$\left\{82,88,93,168\right\}$, $\left\{84,94,168\right\}$, $\left\{85,94,168\right\}$, $\left\{89,98,168\right\}$, and $\left\{90,98,168\right\}$	$\left\{151,164\right\}$, $\left\{152,164\right\}$, $\left\{155,164\right\}$, and $\left\{156,164\right\}$
-	$\left\{70,162\right\}$, $\left\{71,162\right\}$, $\left\{72,162\right\}$, $\left\{75,162\right\}$, and $\left\{76,162\right\}$	-	$\left\{144,151,169\right\}$, $\left\{146,151,169\right\}$,$\left\{147,151,169\right\}$,$\left\{148,151,169\right\}$,$\left\{150,151,169\right\}$,$\left\{139,145,149,151,169\right\}$
-	$\left\{54,64,167\right\}$ and $\left\{53,59,167\right\}$	-	-

shows the EG for all feeders. For instance, if we assume an outage at node 1, the restoration sequence is $\left(31,170\right)$, $\left(9,161\right)$, and $\left(2,165\right)$, respectively. Therefore, the EG corresponding to the independent switching are $\left\{31,170\right\}$, $\left\{19,31,161\right\}$, and $\left\{2,9,165\right\}$. The load flow is done to validate all restoration policies. In this example, the maximum voltage drop is at nodes $34$ and $36$ after the first restoration iteration, and the voltage of these nodes is $0.95$ p.u.

In Table 1, the different EG in each column corresponding to the feeders 1 to 4 are arranged in groups that are separated by lines. Each group corresponds to exactly one NO switch.

4.2. Optimum Switch Location

The restored load function, $R{L}_i\left(x\right)$, was computed from Equation (17). In order to limit the complexity of the function, only two sets from each group in Table 1 were allowed simultaneously. Subsequently, the program in Equation (5) was run, and the solution yielded fourteen switches including NC switches $10$, $19$, $31$, $70$, $99$, $112$, $144$, and $151$, and NO switches $161$, $162$, $163$, $164$, $169$, and $170$ to be upgraded was found.

Table 2. Solutions of the proposed algorithm.

Description	Feeder 1	Feeder 2	Feeder 3	Feeder 4
Upgraded switches	10, 19, 31, 161, and 170	70 and 162	99, 112, and 163	144, 151, 169, and 164
Exp. restored energy (kWh)	704.78	358.2	607.09	511.72
Total cost (U.S.$)	5841.0	6326.9	5609.1	6326.2

shows the optimum selection of devices. The expected energy resupplied is defined as the total energy (kWh) restored in the network in a year. The selected switches for all feeders are shown by the gray lines and the respective indices are inside the circles in Figure 5. Total annual cost of the interruptions for each feeder is $7180.9 in U.S. dollars. Utilizing the mentioned switches reduces the outage cost of the system. The reduction in total annual cost after upgrading to RCSs for feeders 1, 2, 3, and 4 is 18.7%, 11.9%, 21.9%, and 11.9%, respectively.

4.3. A Comparative Study of the Use of Genetic Algorithm and the Proposed Algorithm

The results from the proposed method were compared with the solution obtained from GA. Two GA methods were considered: the traditional GA (TGA) and the optimized GA based on elite genes (EG/GA). The chromosome in TGA is the binary array, $x$, containing the placement of all switches, while the EG/GA uses the EG (shown in Table 1) in its chromosomes. The number of generations, mutation rate, crossover fraction for both two GA methods are set on 40, 2, 0.8, respectively, while the number of generations varies from 10 to 200.

Table 3. Comparison of traditional genetic algorithm (TGA) and EG for Feeder 1.

Population Size	Number of switches		Ex. energy restored (kWh)		Total cost ($)		No. of generations
	TGA	EG/GA	TGA	EG/GA	TGA	EG/GA	TGA	EG/GA
10	14	7	730.36	695.47	8610.8	6519.0	5	11
20	4	6	348.9	690.82	7004.9	6218.8	19	12
50	6	5	683.4	683.84	6247.9	5928.3	22	17
100	2	5	460.55	704.78	5900.3	5841.0	22	19
200	5	5	704.78	704.78	5841.0	5841.0	29	22

,

Table 4. Comparison of TGA and EG for Feeder 2.

Population size	Number of switches		Ex. energy restored (kWh)		Total cost ($)		No. of generations
	TGA	EG/GA	TGA	EG/GA	TGA	EG/GA	TGA	EG/GA
10	16	17	516.37	779.21	10,142.0	9366.0	15	6
20	10	7	530.33	702.45	8166.2	6489.9	25	14
50	3	2	348.90	348.90	6685.3	6365.7	22	15
100	2	2	334.94	358.20	6423.9	6326.9	20	17
200	2	2	358.20	358.20	6326.9	6326.9	25	19

,

Table 5. Comparison of TGA and EG for Feeder 3.

Population size	Number of switches		Ex. energy restored (kWh)		Total cost ($)		No. of generations
	TGA	EG/GA	TGA	EG/GA	TGA	EG/GA	TGA	EG/GA
10	12	6	553.59	579.17	8708.5	6684.2	17	13
20	7	4	530.33	590.80	7207.4	5996.5	22	14
50	3	3	590.80	607.09	5676.9	5609.1	23	17
100	3	3	600.11	607.09	5638.2	5609.1	23	19
200	3	3	600.11	607.09	5638.2	5609.1	27	20

and

Table 6. Comparison of TGA and EG for Feeder 4.

Population size	Number of switches		Ex. energy restored (kWh)		Total cost ($)		No. of generations
	TGA	EG/GA	TGA	EG/GA	TGA	EG/GA	TGA	EG/GA
10	11	5	334.94	518.67	9300.3	6616.7	22	10
20	5	2	341.92	334.94	7353.6	6423.9	20	12
50	3	4	362.86	511.72	6946.7	6326.2	19	11
100	2	4	348.90	511.72	6365.7	6326.2	22	13
200	2	4	348.90	511.72	6365.7	6326.2	25	16

compare the solutions of TGA and the EG/GA in all feeders for different population sizes. The mutation rate is set to 2 for all feeders.

The results obtained by the proposed algorithm in Table 2 are verified by the EG/GA. As can be seen in Figure 5 and the tables, the total cost and the expected energy restored are different when the generation capacity of DGs are not equal. The number and the location of RCSs are a function of DGs’ capacities and the topology of the network. EG/GA tends to generate a better solution in fewer generations. In other words, the convergence speed of the EG/GA for even a better solution is higher than TGA. The solution of the proposed algorithm is comparable with the optimized EG/GA when the population size is relatively high. An increase in population size is equivalent to an increase in computational time.

The cost of switches affects the optimum number of switches. Here, it is assumed that the CDF is fixed, and we increased the switch cost incrementally by 10% from 10% to 300% of the initial switch cost. Figure 6 shows the total annual cost and the optimum number of switches versus the different annual cost of switches. In this figure, the number of switches decreases by increasing the switch cost. However, there are certain upgrading schemes (flat parts in Figure 6) that are robust towards the switch cost. For example, by increasing the switch cost from $351.56 to $607.24, the optimum switches 32, 70, 99, 112, 151, 162, 163, 164, and 170 remained the same, which means that the benefit gained by these switches is great enough to compensate for the increase in the switch cost. Transitioning schemes when there is a high correlation between the switch cost and the optimum number of switches are recognized. For example, in the switch cost interval between $287.64 and $351.56, the number of optimum switches decreases by 55% while the change in the switch cost is only 20%.

Since the location of NO switches and the generation capacity of the DGs for different feeders are not the same, different feeders have different responses to the change in the switch cost. For example, for an increase in the switch cost from $287.64 to $351.56, the selected switches for feeder 3 remained the same which means that the benefit gained by those RCSs exceeded the switch cost for two cases. In feeder 1, both the number and the location of the switches changed by increasing the cost of switches. Five switches 161, 170, 10, 19, and 31 were chosen when the switch was cheaper while the switches 170 and 32 were the selected switches when the switches were more expensive. This change was even more dramatic in feeder 2 where eight switches, 162, 166, 167, 171, 54, 64, 70, and 78 were selected when the annual cost of each switch is $287.64 versus two selected switches 162 and 75 when the annual cost is $351.56. In feeder 4, the number of switches decreased from four to two by increasing the annual switch cost.

The expected energy not served (EENS) is computed in two scenarios; before and after upgrading the network with RCSs. In this study, it is assumed that before upgrading the system, all branches were manual interrupting switches in which the switching time was 90 min.

Table 7. System average interruption frequency index (SAIFI) and system average interruption duration index (SAIDI) before and after upgrading the test system. EENS: expected energy not served.

EENS (kWh/year)	Feeder 1	Feeder 2	Feeder 3	Feeder 4
Before	1620.1	1617.73	1631.69	1659.60
After	680.35	1143.64	822.31	993.55
Improvement	58%	29.31%	49.6%	40.13%

shows the improvement in EENS gained by upgrading the system. It can be seen that the capacity of the DGs and the number of RCSs within feeders are effective on the EENS. For instance, in feeder 1 where there are five RCSs and the generation capacity of the DG1 is relatively high, the improvement is remarkable comparing to the other feeders.

For a given outage restoration, $i$, the solutions for $d_{j,k}$ may not be unique and multiple restoration interchanges may be available that result in the same restored load. The choice affects the combination of $x\left(q\right)\left(1\le q\le M+N\right)$ product terms in $G_{j,k}\left(x\right)$ but it does not affect the total restored load. The alternative interchanges may result in equivalent optimal locations of the RCSs. This can be seen in feeder 4 where the generation capacity of the DG 4 is equal to the restoration capability of the tie switch 170. The NO switches 164 and 170 have the same performance in the restoration schemes and can be selected alternatively.

5. Conclusions

This paper has presented a two-level optimization algorithm to find the optimal number and location of those switches that should be upgraded to RCSs in a given DN. In the first level, a greedy algorithm is used to find the optimum restoration of the network after all possible outages. The power flow is done after any restoration scheme to validate the feasibility of the interchanging actions. The ECOST is constructed based on the interchanging switches including both NC and NO switches involved in the optimum restoration scheme. Here, forming the optimum self-supplied islands is considered, and switching conflicts and dependencies are identified and resolved. To consider the dependency in the switching, a recursive equation giving the restored load is introduced and reflected in the ECOST. In the second optimization level, the global cost-based objective function including the ECOST and the annual cost of switches is formulated and minimized with respect to the location of selected switches.

The proposed method has been successfully tested on a 4-feeder 1069-node test system with 160 protection nodes. To show the effectiveness of the proposed optimization algorithm, TGA and EG/GA are employed to solve the same problem, and the results are compared to the results obtained from the proposed method. It is shown that the proposed method produces better results than TGA. It is also shown that GA using the EG found from the restoration analysis in the first level, produces equivalent results with the proposed method while it has a better convergence speed than TGA. The effect of switch cost on the optimum number of switches was studied. The selected switches that were robust toward the change in the switch cost revealed the strategic locations of the switches that should be considered for upgrading.