Multistage Expansion Co-Planning of Integrated Natural Gas and Electricity Distribution Systems
Abstract
:1. Introduction
- Developing a MILP model for co-expansion planning of EHs, natural gas and electricity distribution grids
- Modelling the impacts of autonomous DG units on natural gas and electricity distribution networks using the EH concept
- Deriving a novel mixed-integer linear formulation for natural gas distribution system expansion planning
- Taking into account the effect of recovered heat from gas-fired DG units on heat demand reduction.
2. Methodology
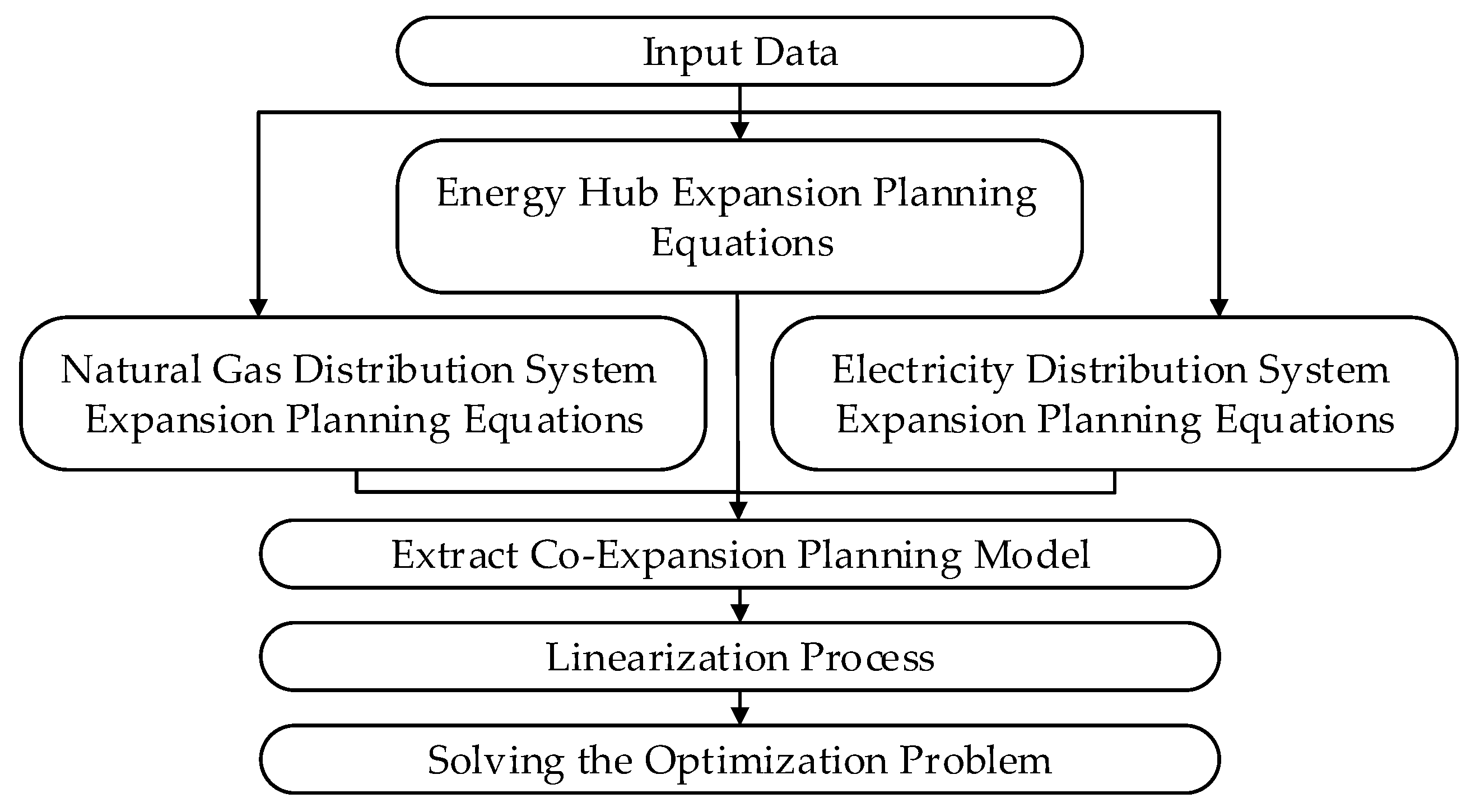
2.1. General Structure of the Proposed Framework
2.2. Problem Formulation
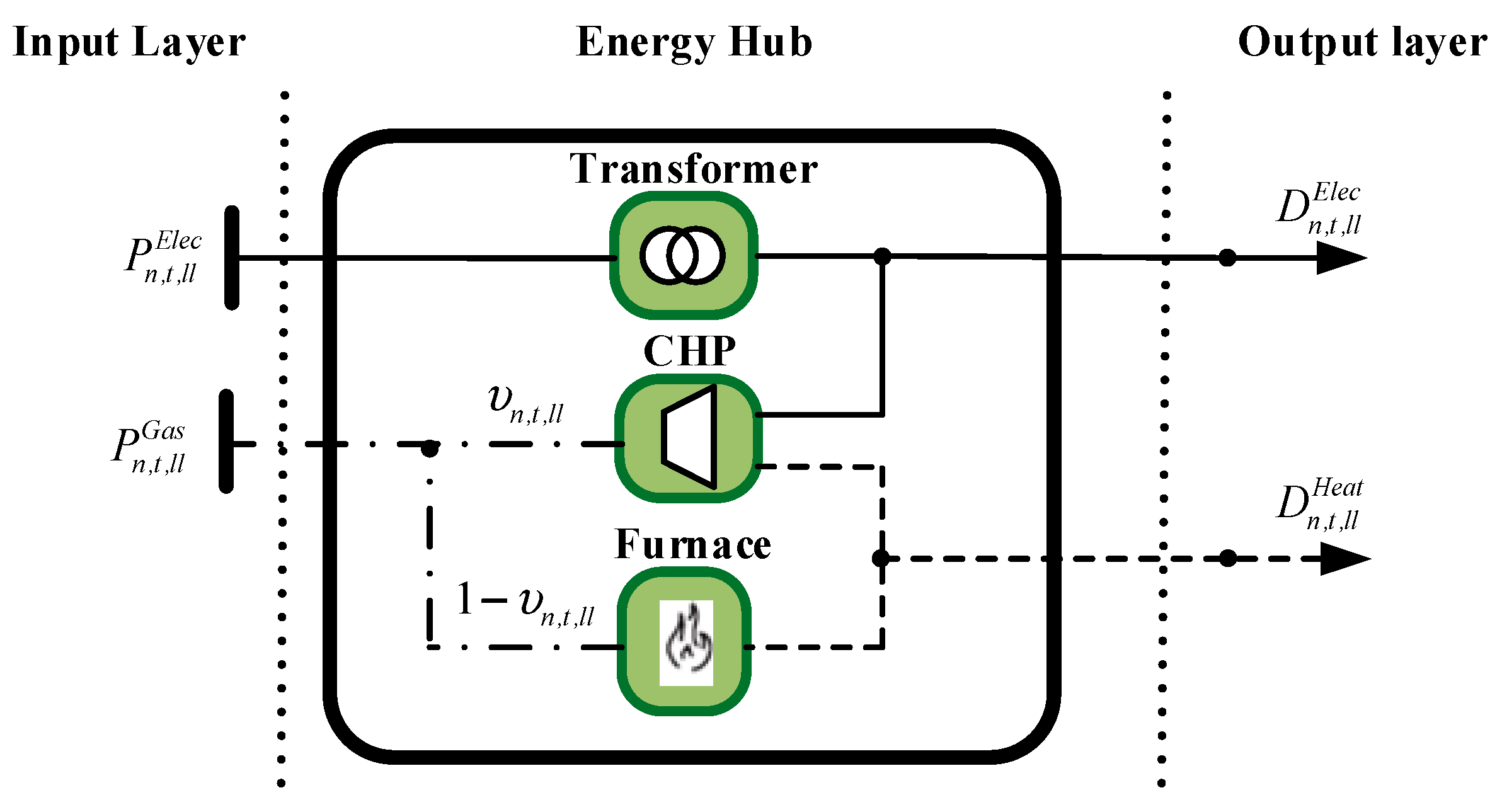
2.2.1. Expansion Planning of Energy Hubs
2.2.2. Electricity Distribution Network Expansion Planning
2.2.3. Natural Gas Distribution Network Expansion Planning
2.2.4. Co-Expansion Formulation
3. Linearization of the Proposed Optimization Model
3.1. Linearization of EHs Planning Model
3.2. Linearization of Electricity Distribution Planning Model
3.3. Linearization of Natural Gas Distribution Network Expansion Planning
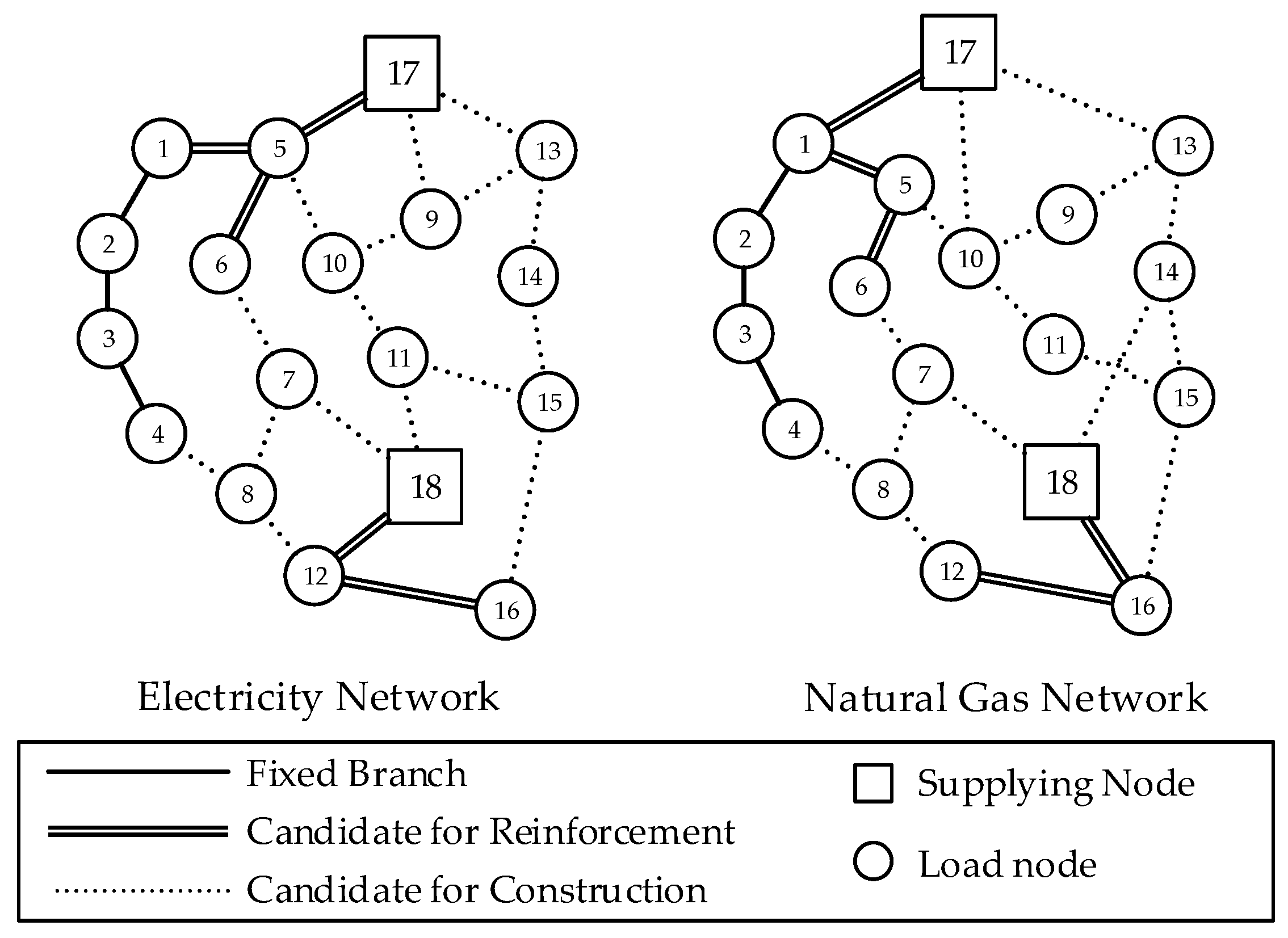
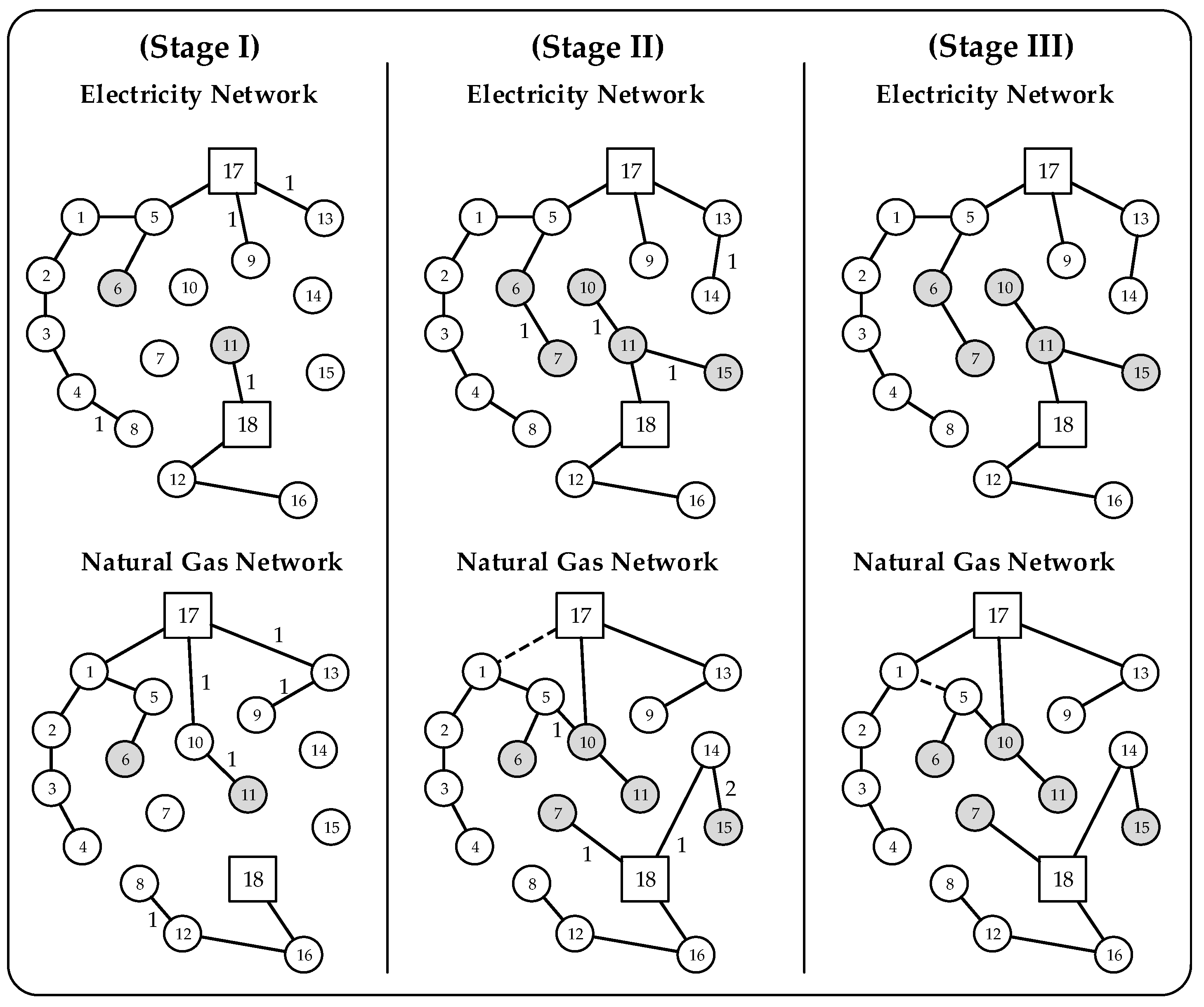
4. Case Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Sets | |
| T | Set of time stages of planning horizon. |
| Candidate alternatives for reinforcement of the existing feeder in the path of branch b. | |
| Candidate alternatives for reinforcement of the existing pipeline in the path of branch b. | |
| Candidate alternatives for reinforcement of city gate c. | |
| Candidate alternatives for reinforcement of substation s. | |
| Set of gas network branches. where are sets of candidate branches for construction of new pipelines, branches with fixed pipelines and candidate branches for reinforcement of existing pipelines, respectively. | |
| Set of city gates. where are sets of candidate new city gates which can be constructed, fixed city gates and existing ones which can be reinforced, respectively. | |
| Set of electricity network branches. where are sets of candidate branches for construction of new feeders, branches with fixed feeders and candidate branches for reinforcement of existing feeders, respectively. | |
| Set of substations. where are sets of candidate new substations which can be constructed, fixed substations and existing ones which can be reinforced, respectively. | |
| Candidate alternatives for construction of a new feeder in the path of branch b. | |
| Candidate alternatives for construction of a new pipeline in the path of branch b. | |
| Candidate alternatives for construction of city gate c. | |
| Candidate alternatives for construction of substation s. | |
| Set of gas network nodes. where are sets of demand and city gate nodes. | |
| Set of electricity network nodes. where are sets of demand and substation nodes. | |
| Ψlp, Zlp | Set of branches connected to load point lp of electricity and gas distribution networks, respectively. |
| Parameters | |
| Construction cost. | |
| Electricity and heat demand of the nth EH at load level ll of stage t. | |
| Dut,ll | Duration of load level ll of stage t (Hours). |
| Maximum capacity of substations. | |
| Maximum flow capacity of pipelines. | |
| Maximum capacity of city gates. | |
| Maximum current capacity of feeders. | |
| IC(.) | Investment cost coefficient of CHP units, furnaces and transformers ($/kW). |
| M | A big number. |
| Maximum allowable total capacity of CHP units within electricity distribution network. | |
| OC(.) | Operating cost coefficient of CHP units, furnaces and transformers ($/kWh). |
| Operating cost. | |
| pfn,t,ll | Power factor. |
| Grid electricity and natural gas prices ($/kWh) | |
| Reinforcement cost. | |
| Vmin, Vmax | Lower and upper bounds of nodal voltages. |
| Vr | Rated voltage of distribution network. |
| Zb, Zb,k | Absolute value of branch impedance. |
| , | Branch impedance. |
| α | Power-to-natural gas flow conversion factor. |
| βb, βb,k | Weymouth constant of gas pipelines. |
| , | Element of node-branch incidence matrix for electricity and gas networks which is −1 or +1 if branch b is connected to load point lp and the predetermined current or flow direction is toward or away from node lp, respectively and is 0 otherwise. |
| , | Present value factors for investment and operating costs. |
| , | Slope and width of block i of piecewise linear pipeline flow function. |
| , | Gas to electricity and gas to heat efficiency of CHP units. |
| , | Efficiency of furnaces and transformers. |
| λmin, λmax | Lower and upper bounds of nodal gas pressures. |
| , | A binary parameter, which is 1 if substation s or city gate c is at load point lp and is 0 otherwise. |
| Variables | |
| Capacity of CHP, furnace and transformer of nth EH at stage t. | |
| CF(.) | Cost functions. |
| GDlp,t,ll, GGc,t,ll | Gas demand at load point lp and injected gas power from city gate c. |
| fb,t,ll | Natural gas flow. |
| , | Positive variables associated with natural gas flow of branch b in predetermined direction and the opposite direction. |
| , | Electricity demand at load point lp and injected electricity power from substation s. |
| Fictitious power injection of substation s. | |
| , | Magnitudes of branch currents and nodal voltages. |
| , | Branch current and nodal voltage phasors. |
| Fictitious current of branch b at time stage t. | |
| Investment cost at stage t. | |
| LPMlp,t | A binary variable associated with the load point mode, which is 1 when load point lp is in service at stage t and is 0 otherwise. |
| Newly installed capacity of CHP, furnace and transformer in nth EH at stage t. | |
| Operating cost at stage t. | |
| , | Electricity and natural gas power input of the nth EH at load level ll of stage t. |
| Δπb,t,ll | Square pressure loss for branch b. |
| Square pressure loss in block i of piecewise linear pipeline flow function. | |
| Binary utilization variables. | |
| λb,k,t | Nodal gas pressures. |
| Binary investment variables for construction of new feeders, substations, pipelines and city gates. | |
| Binary investment variables for reinforcement of existing feeders, substations, pipelines and city gates. | |
| Dispatch factor of the nth EH at load level ll of stage t. | |
| Abbreviations | |
| CHP | Combined heat and power |
| Cig | City gate |
| EDN | Electricity distribution network |
| EH | Energy hub |
| Elec | Electricity |
| Fe | Feeder |
| Fi | Fixed |
| GDN | Gas distribution network |
| Ne | New |
| Pi | Pipeline |
| Re | Reinforcement |
| Sub | Substation |
References
- Zhang, Y.; He, Y.; Yan, M.; Guo, C.; Ding, Y. Linearized Stochastic Scheduling of Interconnected Energy Hubs Considering Integrated Demand Response and Wind Uncertainty. Energies 2018, 11, 2448. [Google Scholar] [CrossRef]
- Chaudry, M.; Jenkins, N.; Strbac, G. Multi-time period combined gas and electricity network optimization. Electr. Power Syst. Res. 2008, 78, 1265–1279. [Google Scholar] [CrossRef]
- Zhang, X.; Che, L.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Electricity-natural gas operation planning with hourly demand response for deployment of flexible ramp. IEEE Trans. Sustain. Energy 2016, 7, 996–1004. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.; Sun, G.; Cheung, K.W.; Sun, Y. Multi-linear probabilistic energy flow analysis of integrated electrical and natural-gas systems. IEEE Trans. Power Syst. 2017, 32, 1970–1979. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.; Sun, G.; Wang, D.; Zhang, Y.; Ma, Z. Stochastic look-ahead dispatch for coupled electricity and natural-gas networks. Electr. Power Syst. Res. 2018, 164, 159–166. [Google Scholar] [CrossRef]
- Costa, D.C.; Nunes, M.V.; Vieira, J.P.; Bezerra, U.H. Decision tree-based security dispatch application in integrated electric power and natural-gas networks. Electr. Power Syst. Res. 2016, 141, 442–449. [Google Scholar] [CrossRef]
- Unsihuay-Vila, C.; Marangon-Lima, J.W.; de Souza, A.C.Z.; Perez-Arriaga, I.J.; Balestrassi, P.P. A model to long-term, multiarea, multistage, and integrated expansion planning of electricity and natural gas systems. IEEE Trans. Power Syst. 2010, 25, 1154–1168. [Google Scholar] [CrossRef]
- Qiu, J.; Dong, Z.Y.; Zhao, J.H.; Xu, Y.; Zheng, Y.; Li, C.; Wong, K.P. Multi-stage flexible expansion co-planning under uncertainties in a combined electricity and gas market. IEEE Trans. Power Syst. 2015, 30, 2119–2129. [Google Scholar] [CrossRef]
- He, C.; Wu, L.; Liu, T.; Shahidehpour, M. Robust co-optimization scheduling of electricity and natural gas systems via ADMM. IEEE Trans. Sustain. Energy 2017, 8, 658–670. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.; Sun, G.; Cheung, K.W.; Wang, D. Identifying optimal energy flow solvability in electricity-gas integrated energy systems. IEEE Trans. Sustain. Energy 2017, 8, 846–854. [Google Scholar] [CrossRef]
- Zhang, X.; Che, L.; Shahidehpour, M.; Alabdulwahab, A.S.; Abusorrah, A. Reliability-based optimal planning of electricity and natural gas interconnections for multiple energy hubs. IEEE Trans. Smart Grid 2017, 8, 1658–1667. [Google Scholar] [CrossRef]
- Zhang, X.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Optimal expansion planning of energy hub with multiple energy infrastructures. IEEE Trans. Smart Grid 2015, 6, 2302–2311. [Google Scholar] [CrossRef]
- Dongxiao, W.; Jing, Q.; Ke, M.; Xiaodan, G.; Zhaoyang, D. Coordinated expansion co-planning of integrated gas and power systems. J. Mod. Power Syst. Clean Energy 2017, 5, 314–325. [Google Scholar]
- Saldarriaga, C.A.; Hincapié, R.A.; Salazar, H. A holistic approach for planning natural gas and electricity distribution networks. IEEE Trans. Power Syst. 2013, 28, 4052–4063. [Google Scholar] [CrossRef]
- Odetayo, B.; MacCormack, J.; Rosehart, W.D.; Zareipour, H. A chance constrained programming approach to integrated planning of distributed power generation and natural gas network. Electr. Power Syst. Res. 2017, 151, 197–207. [Google Scholar] [CrossRef]
- Pazouki, S.; Mohsenzadeh, A.; Ardalan, S.; Haghifam, M.R. Optimal place, size, and operation of combined heat and power in multi carrier energy networks considering network reliability, power loss, and voltage profile. IET Gener. Trans. Distrib. 2016, 10, 1615–1621. [Google Scholar] [CrossRef]
- Geidl, M.; Koeppel, G.; Favre-Perrod, P.; Klockl, B.; Andersson, G.; Frohlich, K. Energy hubs for the future. IEEE Power Energy Mag. 2007, 5, 24–30. [Google Scholar] [CrossRef]
- Parisio, A.; Del Vecchio, C.; Vaccaro, A. A robust optimization approach to energy hub management. Int. J. Electr. Power Energy Syst. 2012, 42, 98–104. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Farzin, H.; Fotuhi-Firuzabad, M.; Amrollahi, R. Generalized analytical approach to assess reliability of renewable-based energy hubs. IEEE Trans. Power Syst. 2017, 32, 368–377. [Google Scholar] [CrossRef]
- Barmayoon, M.H.; Fotuhi-Firuzabad, M.; Rajabi-Ghahnavieh, A.; Moeini-Aghtaie, M. Energy storage in renewable-based residential energy hubs. IET Gener. Trans. Distrib. 2016, 10, 3127–3134. [Google Scholar] [CrossRef]
- Wong, S.; Bhattacharya, K.; Fuller, J.D. Electric power distribution system design and planning in a deregulated environment. IET Gener. Trans. Distrib. 2009, 3, 1061–1078. [Google Scholar] [CrossRef]
- Jooshaki, M.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M.; Lehtonen, M. Incorporating the effects of service quality regulation in decision-making framework of distribution companies. IET Gener. Trans. Distrib. 2018, 12, 4172–4181. [Google Scholar] [CrossRef]
- Humayd, A.S.B.; Bhattacharya, K. Distribution system planning to accommodate distributed energy resources and PEVs. Electr. Power Syst. Res. 2017, 145, 1–11. [Google Scholar] [CrossRef]
- Muñoz-Delgado, G.; Contreras, J.; Arroyo, J.M. Joint expansion planning of distributed generation and distribution networks. IEEE Trans. Power Syst. 2015, 30, 2579–2590. [Google Scholar] [CrossRef]
- Li, R.; Wang, W.; Chen, Z.; Jiang, J.; Zhang, W. A review of optimal planning active distribution system: Models, methods, and future researches. Energies 2017, 10, 1715. [Google Scholar] [CrossRef]
- Kazmi, S.; Shahzad, M.; Shin, D. Multi-objective planning techniques in distribution networks: A composite review. Energies 2017, 10, 208. [Google Scholar] [CrossRef]
- Lotero, R.C.; Contreras, J. Distribution system planning with reliability. IEEE Trans. Power Deliv. 2011, 26, 2552–2562. [Google Scholar] [CrossRef]
- Haffner, S.; Pereira, L.F.A.; Pereira, L.A.; Barreto, L.S. Multistage model for distribution expansion planning with distributed generation—Part I: Problem formulation. IEEE Trans. Power Deliv. 2008, 23, 915–923. [Google Scholar] [CrossRef]
- Pereira Junior, B.R.; Cossi, A.M.; Contreras, J.; Sanches Mantovani, J.R. Multiobjective multistage distribution system planning using tabu search. IET Gener. Trans. Distrib. 2014, 8, 35–45. [Google Scholar] [CrossRef]
- Bollobás, B. Modern Graph Theory; Springer Science & Business Media: New York, NY, USA, 2013; pp. 8–14. [Google Scholar]
- Heidari, S.; Fotuhi-Firuzabad, M.; Kazemi, S. Power distribution network expansion planning considering distribution automation. IEEE Trans. Power Syst. 2015, 30, 1261–1269. [Google Scholar] [CrossRef]
- Lavorato, M.; Franco, J.F.; Rider, M.J.; Romero, R. Imposing radiality constraints in distribution system optimization problems. IEEE Trans. Power Syst. 2012, 27, 172–180. [Google Scholar] [CrossRef]
- Input Data and Results. Available online: https://drive.google.com/open?id=1eaqZSbXYtvWJbeS2Qcg7XmUeW0CU7brs. (accessed on 15 January 2019).
| Simulation Outcome | Case I | Case II | |
|---|---|---|---|
| (M$) | Inv. | 0.686 | 0.689 |
| Op. | 20.576 | 20.509 | |
| (M$) | Inv. | 5.928 | 7.066 |
| Op. | 0.002 | 0.002 | |
| (M$) | Inv. | 8.339 | 8.737 |
| Op. | 0.002 | 0.002 | |
| Total Cost (M$) | 35,533 | 37,005 | |
| Total Installed CHP Capacity (MW) | 1 | 1 | |
| Total Electricity Served by CHPs (GWh) | 21.191 | 27.039 | |
| Total Electricity Energy from the Grid (GWh) | 161.760 | 155.790 | |
| Total Gas from the Grid (Mm3) | 31.610 | 32.441 | |
| Electricity Network Peak Demand (MW) | 8.036 | 8.036 | |
| Natural Gas Network Peak Demand (m3/h) | 1554.396 | 1554.396 | |
| CHP Nodes | 6-7-10-11-15 | 1-4-5-6-8-13-16 | |
| Simulation Time (s) | 477.64 | 74.69 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jooshaki, M.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M.; Lehtonen, M. Multistage Expansion Co-Planning of Integrated Natural Gas and Electricity Distribution Systems. Energies 2019, 12, 1020. https://doi.org/10.3390/en12061020
Jooshaki M, Abbaspour A, Fotuhi-Firuzabad M, Moeini-Aghtaie M, Lehtonen M. Multistage Expansion Co-Planning of Integrated Natural Gas and Electricity Distribution Systems. Energies. 2019; 12(6):1020. https://doi.org/10.3390/en12061020
Chicago/Turabian StyleJooshaki, Mohammad, Ali Abbaspour, Mahmud Fotuhi-Firuzabad, Moein Moeini-Aghtaie, and Matti Lehtonen. 2019. "Multistage Expansion Co-Planning of Integrated Natural Gas and Electricity Distribution Systems" Energies 12, no. 6: 1020. https://doi.org/10.3390/en12061020
APA StyleJooshaki, M., Abbaspour, A., Fotuhi-Firuzabad, M., Moeini-Aghtaie, M., & Lehtonen, M. (2019). Multistage Expansion Co-Planning of Integrated Natural Gas and Electricity Distribution Systems. Energies, 12(6), 1020. https://doi.org/10.3390/en12061020






