Distributed State Estimation of Multi-region Power System based on Consensus Theory
Abstract
1. Introduction
2. Traditional State Estimation Model
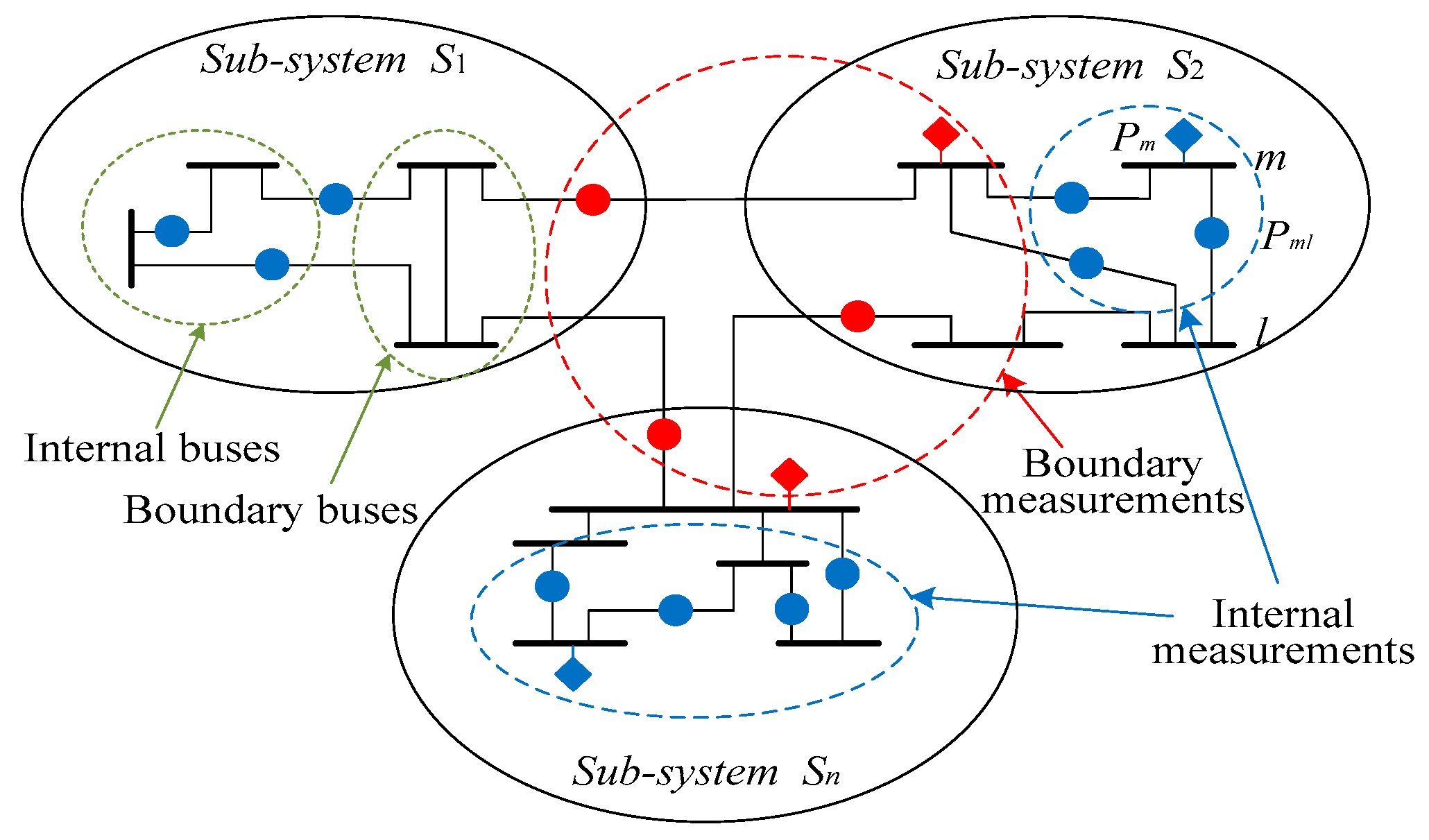
3. Multi-Area State Estimation Model
4. Consensus Algorithm Based Distributed State Estimation Approach
4.1. Graph Description and Consensus Algorithm
4.1.1. Graph Description
4.1.2. Consensus Algorithm
4.2. Propose Distributed State Estimation Method
4.2.1. Distributed Solution Process
4.2.2. Main Steps of Proposed Algorithm
5. Simulation Results
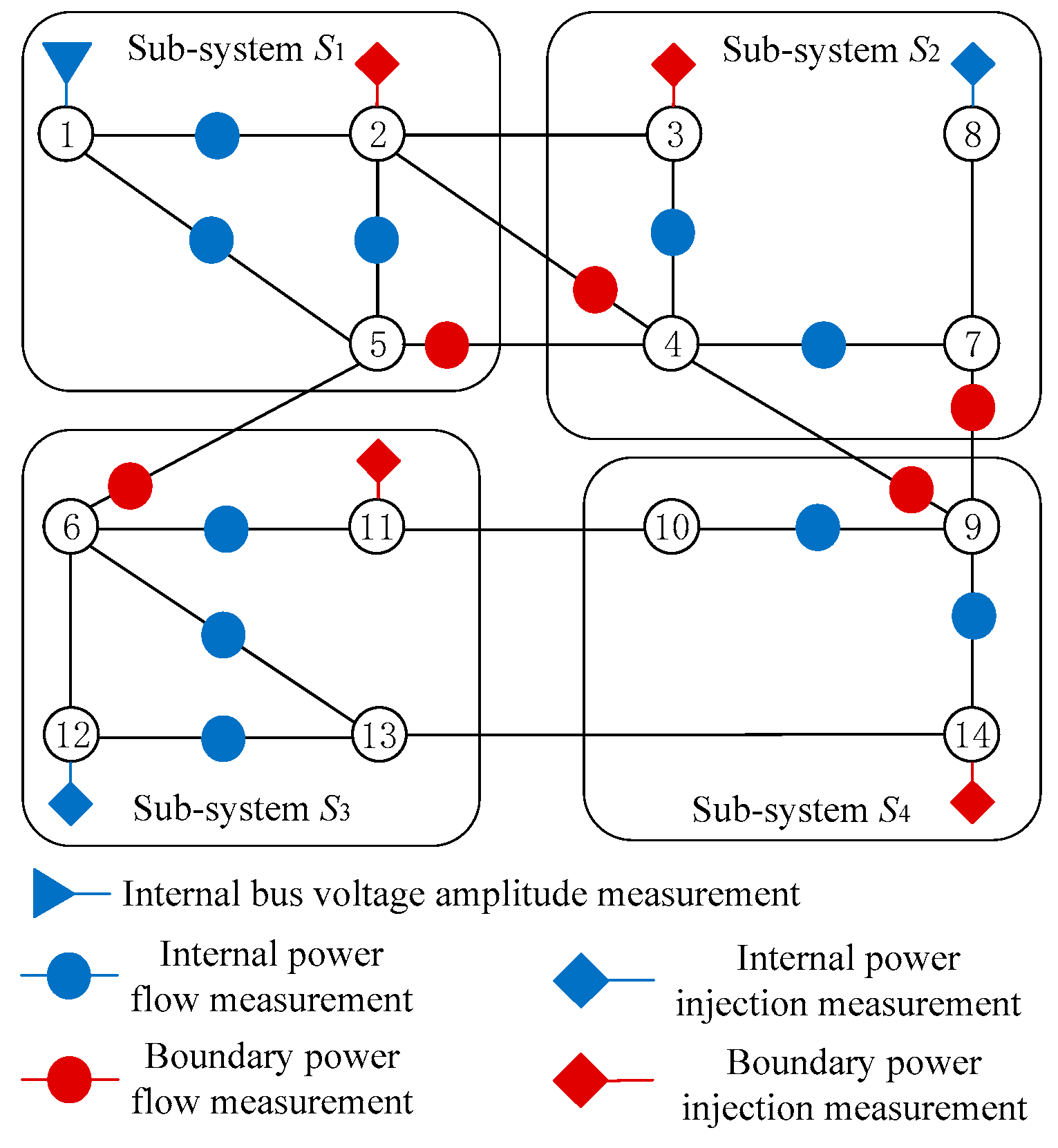
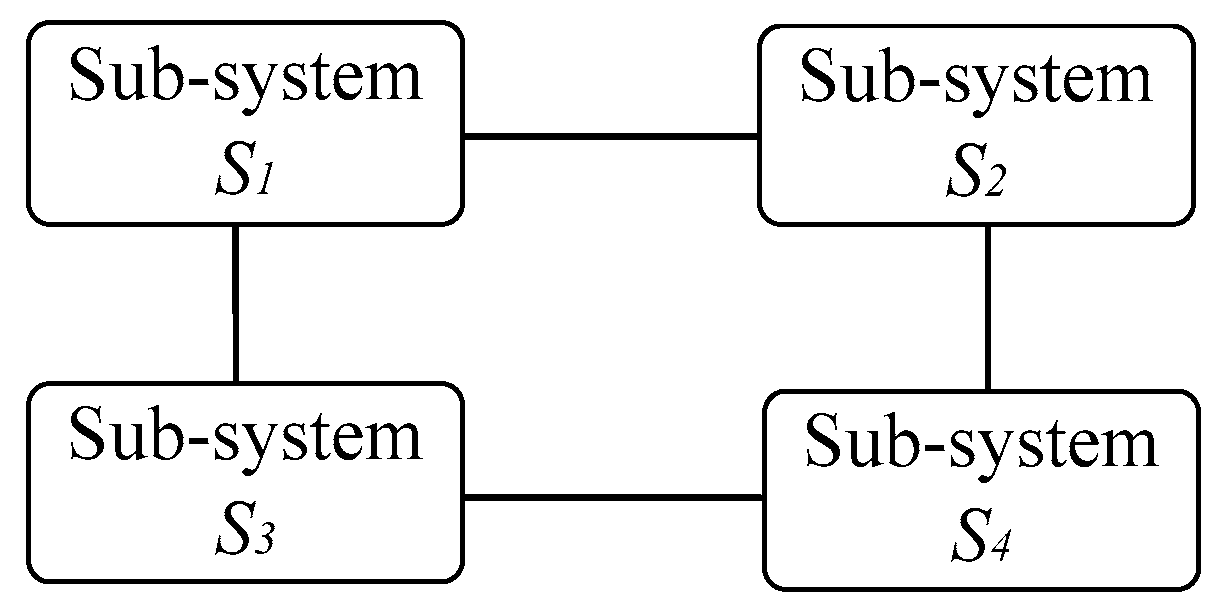
5.1. Case 1: IEEE 14-bus System
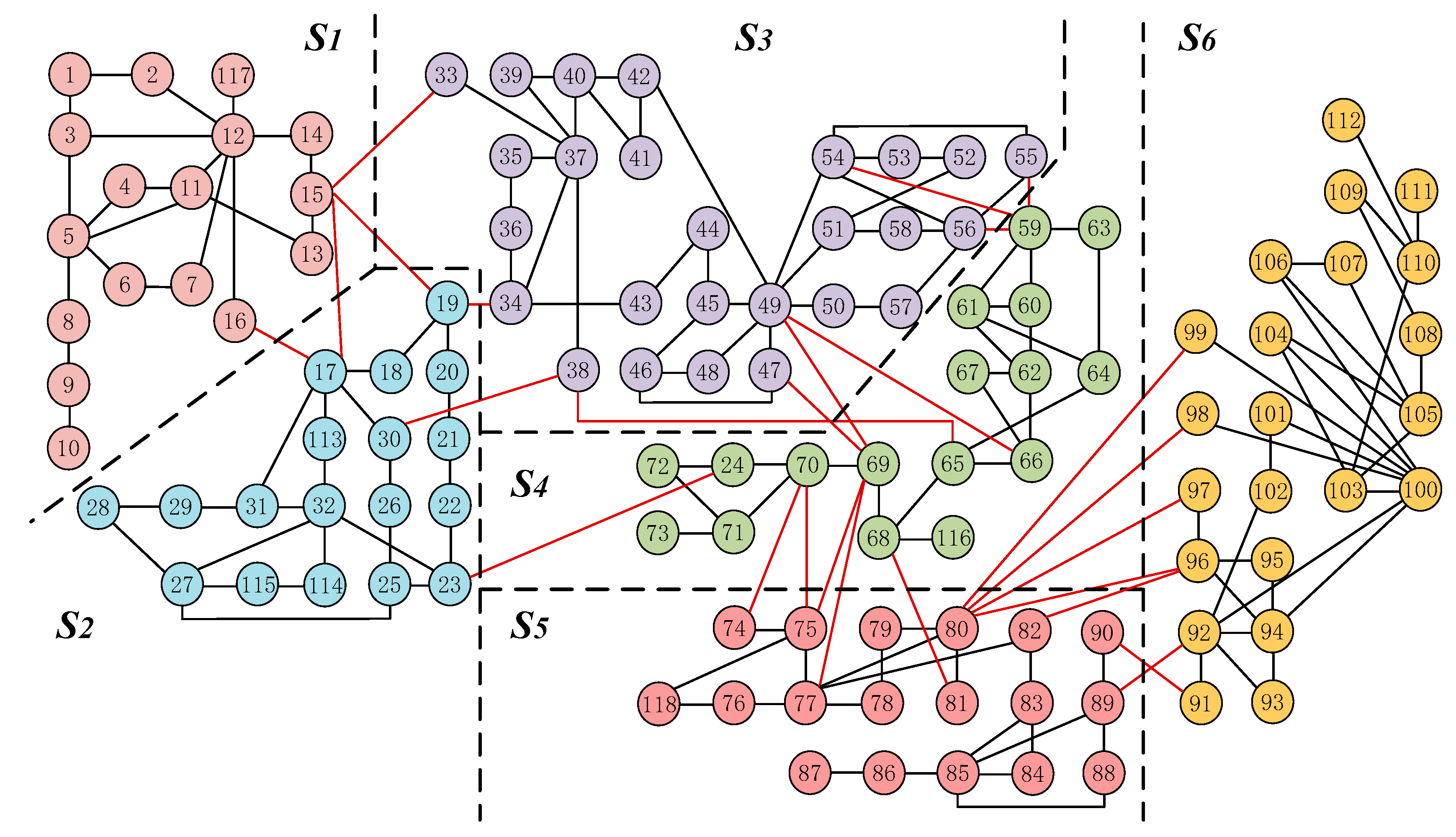
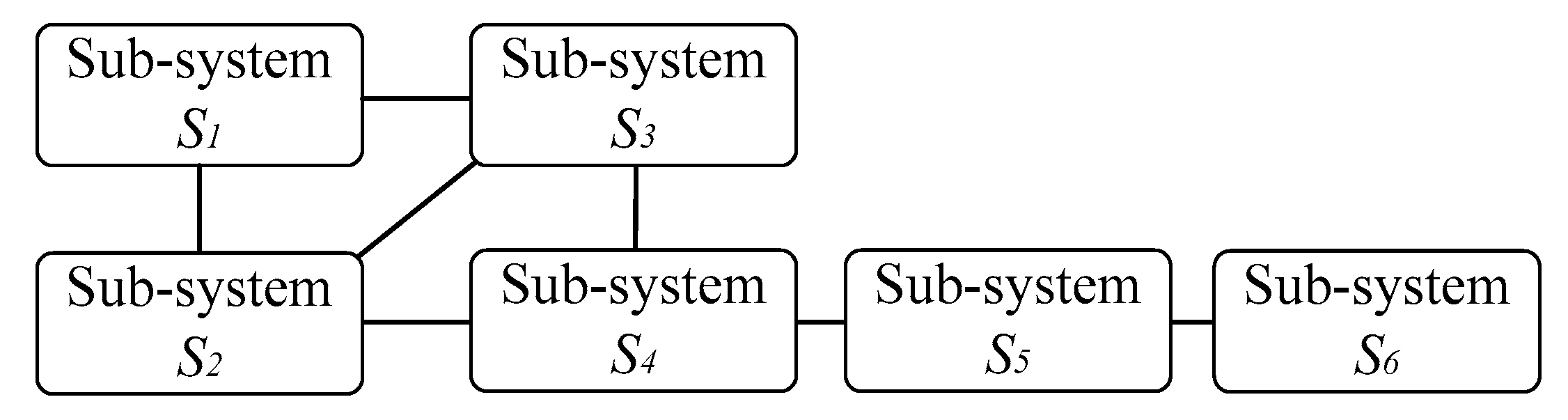
5.2. Case 2: IEEE 118-bus System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gomez-Exposito, A.; Abur, A. Power System State Estimation: Theory and Implementation; CRC Press: Boca Raton, FL, USA, 2004; Volume 17, pp. 213–256. [Google Scholar]
- Rana, M.M.; Li, L.; Su, S. Distributed state estimation using RSC coded smart grid communications. IEEE Access 2015, 3, 1340–1349. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Zhou, D.; Shen, X. Minimum-variance unbiased unknown input and state estimation for multi-agent systems by distributed cooperative filters. IEEE Access 2018, 6, 18128–18141. [Google Scholar] [CrossRef]
- Rana, M.M.; Li, L.; Su, S.W.; Choi, B.J. Modelling the interconnected synchronous generators and its state estimations. IEEE Access 2018, 6, 36198–36207. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, B.; Bose, A.; Sun, H. A distributed multi-control-center dynamic power flow algorithm based on asynchronous iteration scheme. IEEE Trans. Power Syst. 2018, 33, 1716–1727. [Google Scholar] [CrossRef]
- Van Cutsem, T.; Horward, J.L.; Ribbens-Pavella, M. A two-level static state estimator for electric power systems. IEEE Trans. Power Appl. Syst. 1981, 100, 3722–3732. [Google Scholar] [CrossRef]
- Marelli, D.E.; Fu, M. Distributed weighted least-square estimation with fast convergence for large-scale systems. Automatica 2015, 51, 27–39. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.W.; Choi, D.H. Distributed multi-area WLS state estimation integrating measurements weight update. IET Gen. Transm. Distrib. 2017, 11, 2552–2561. [Google Scholar] [CrossRef]
- Ebrahimian, R.; Baldick, R. State estimation distributed processing [for power systems]. IEEE Trans. Power Syst. 2000, 15, 1240–1246. [Google Scholar] [CrossRef]
- Korres, G.N. A distributed multiarea state estimation. IEEE Trans. Power Syst. 2011, 26, 73–84. [Google Scholar] [CrossRef]
- Kar, S.; Hug, G.; Mohammadi, J.; Moura, J.M. Distributed State Estimation and Energy Management in Smart Grids: A Consensus+Innovations Approach. IEEE J. Sel. Top. Signal Process. 2014, 8, 1022–1038. [Google Scholar] [CrossRef]
- Liu, P.; Tian, Y.P.; Zhang, Y. Distributed Kalman filtering with finite-time max-consensus protocol. IEEE Access 2018, 6, 10795–10802. [Google Scholar] [CrossRef]
- Huang, Q.; Schulz, N.N.; Srivastava, A.K.; Haupt, T. Distributed state estimation with PMU using grid computing. In Proceedings of the IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Xie, L.; Choi, D.H.; Kar, S.; Poor, H.V. Fully distributed state estimation for wide-area monitoring systems. IEEE Trans. Smart Grid 2012, 3, 1154–1169. [Google Scholar] [CrossRef]
- Du, J.; Ma, S.; Wu, Y.C.; Poor, H.V. Distributed hybrid power state estimation under PMU sampling phase errors. IEEE Trans. Signal Process. 2018, 62, 4052–4063. [Google Scholar] [CrossRef]
- Yang, Y.; Guan, X.; Zhou, Y.; Wu, J.; Liu, T. Impact of information security on PMU-based distributed state estimation. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Tianjin, China, 21–24 May 2012. [Google Scholar]
- Guo, Y.; Wu, W.; Zhang, B.; Sun, H. A distributed state estimation method for power systems incorporating linear and nonlinear models. Int. J. Electr. Power Energy Syst. 2015, 64, 608–616. [Google Scholar] [CrossRef]
- Minot, A.; Li, N. A fully distributed state estimation using matrix splitting methods. In Proceedings of the 2015 American Control Conference, Chicago, IL, USA, 1–3 July 2015. [Google Scholar]
- Carli, R.; Dotoli, M. Using the distributed proximal alternating direction method of multipliers for smart grid monitoring. In Proceedings of the 13th IEEE Conference on Automation Science & Engineering, Xi’an, China, 20–23 August 2017. [Google Scholar]
- Stuart, T.A.; Herczet, C.J. A sensitivity analysis of weighted least squares state estimation for power systems. IEEE Trans. Power Appar. Syst. 1973, 92, 1696–1701. [Google Scholar] [CrossRef]
- Zhang, Z.; Chow, M.Y. Convergence analysis of the incremental cost consensus algorithm under different communication network topologies in a smart grid. IEEE Trans. Power Syst. 2012, 27, 1761–1768. [Google Scholar] [CrossRef]
- Xia, S.; Bu, S.Q.; Luo, X.; Chan, K.W.; Lu, X. An autonomous real time charging strategy for plug-in electric vehicles to regulate frequency of distribution system with fluctuating wind generation. IEEE Trans. Sustain. Energy 2018, 9, 511–524. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z. Distributed Optimal Resource Management Based on the Consensus Algorithm in a Microgrid. IEEE Trans. Ind. Electron. 2015, 64, 2584–2592. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and Cooperation in Networked Multi-Agent Systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Manitara, N.E.; Hadjicostis, C.N. Distributed Stopping for Average Consensus in Digraphs. IEEE Trans. Control. Netw. Syst. 2018, 5, 957–967. [Google Scholar] [CrossRef]
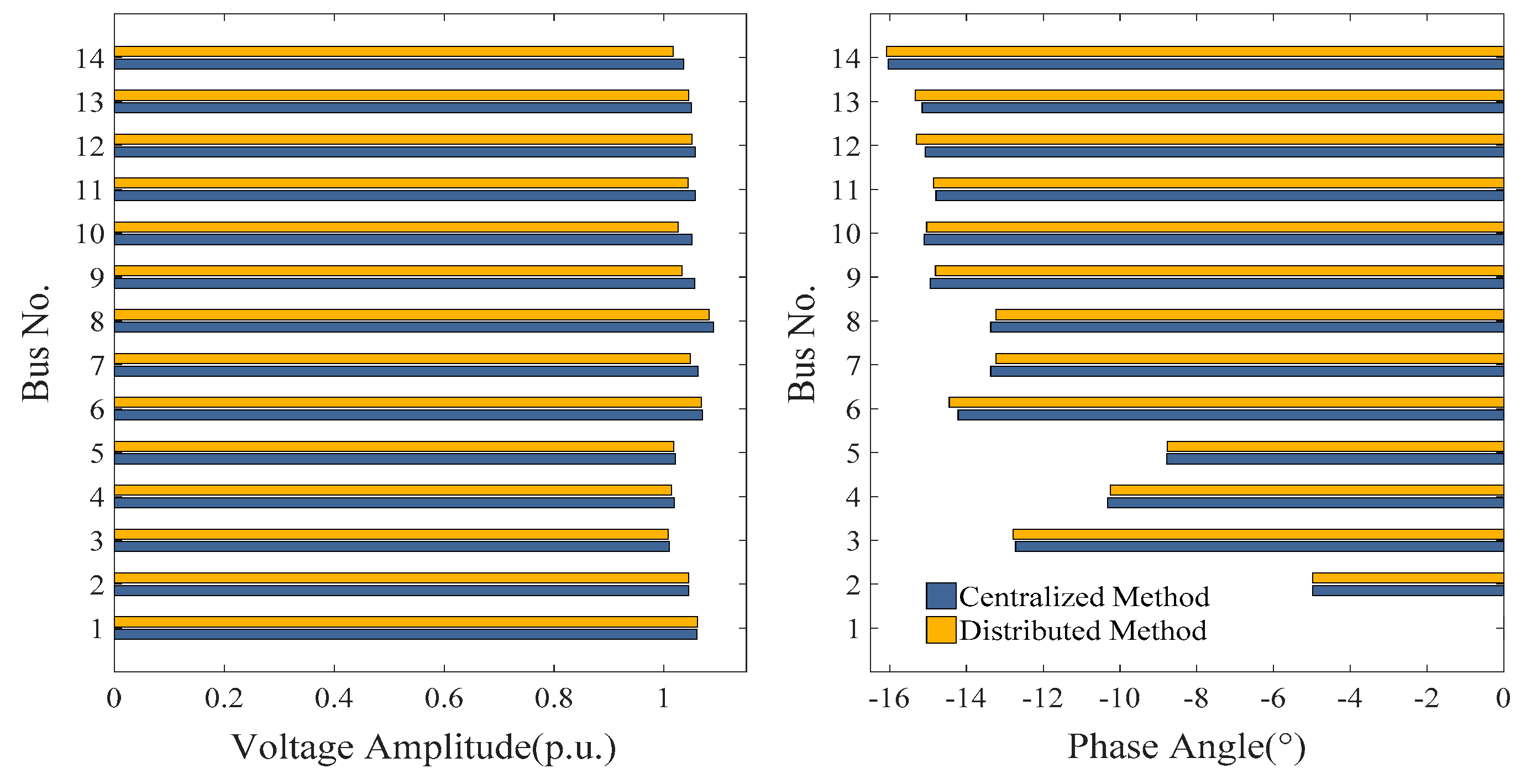
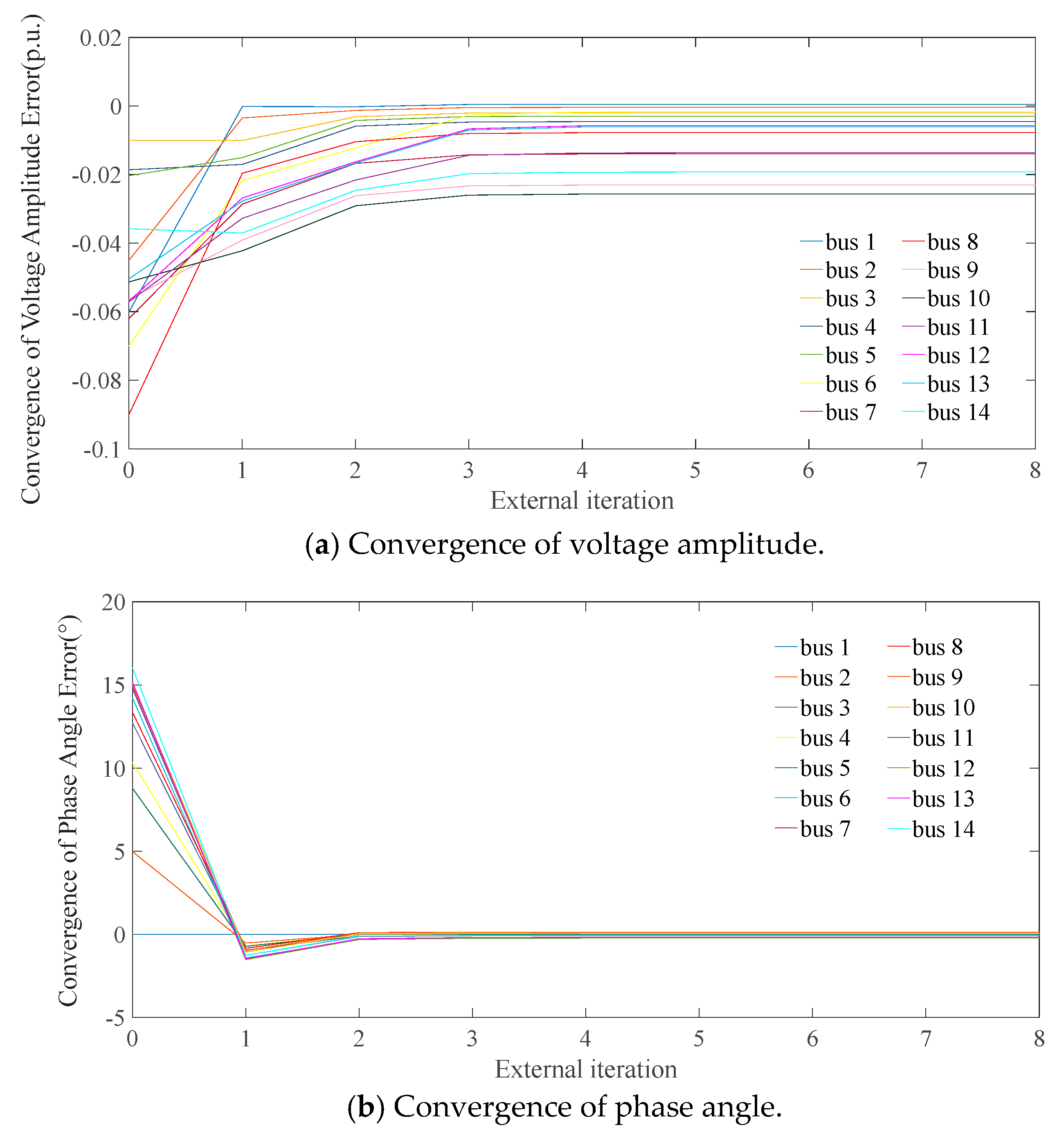
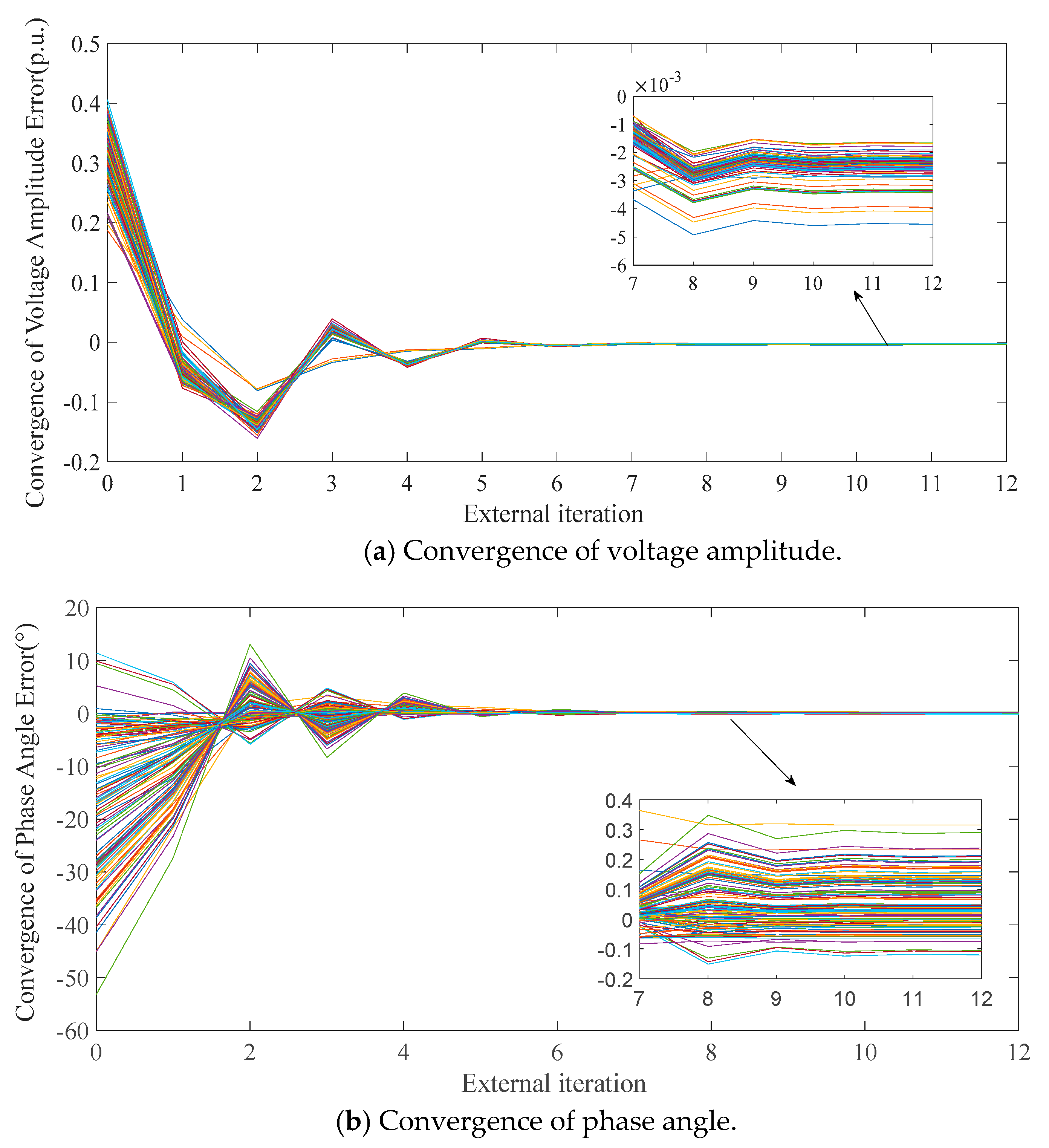
| State Variable | Centralized Method (°) | Distributed Method (°) | State Variable | Centralized Method (p.u.) | Distributed Method (p.u.) |
|---|---|---|---|---|---|
| θ1 | 0 | 0 | V1 | 1.0600 | 1.0605 |
| θ2 | −4.9808 | −4.9816 | V2 | 1.0450 | 1.0446 |
| θ3 | −12.7176 | −12.7860 | V3 | 1.0100 | 1.0080 |
| θ4 | −10.3241 | −10.2464 | V4 | 1.0186 | 1.0140 |
| θ5 | −8.7825 | −8.7684 | V5 | 1.0203 | 1.0174 |
| θ6 | −14.2223 | −14.4500 | V6 | 1.0700 | 1.0683 |
| θ7 | −13.3680 | −13.2353 | V7 | 1.0620 | 1.0480 |
| θ8 | −13.3680 | −13.2353 | V8 | 1.0900 | 1.0822 |
| θ9 | −14.9462 | −14.8114 | V9 | 1.0563 | 1.0333 |
| θ10 | −15.1039 | −15.0375 | V10 | 1.0513 | 1.0256 |
| θ11 | −14.7949 | −14.8601 | V11 | 1.0571 | 1.0435 |
| θ12 | −15.0771 | −15.3064 | V12 | 1.0569 | 1.0512 |
| θ13 | −15.1586 | −15.3386 | V13 | 1.0504 | 1.0444 |
| θ14 | −16.0386 | −16.0839 | V14 | 1.0358 | 1.0166 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, S.; Zhang, Q.; Jing, J.; Ding, Z.; Yu, J.; Chen, B.; Wu, H. Distributed State Estimation of Multi-region Power System based on Consensus Theory. Energies 2019, 12, 900. https://doi.org/10.3390/en12050900
Xia S, Zhang Q, Jing J, Ding Z, Yu J, Chen B, Wu H. Distributed State Estimation of Multi-region Power System based on Consensus Theory. Energies. 2019; 12(5):900. https://doi.org/10.3390/en12050900
Chicago/Turabian StyleXia, Shiwei, Qian Zhang, Jiangping Jing, Zhaohao Ding, Jing Yu, Bing Chen, and Haiwei Wu. 2019. "Distributed State Estimation of Multi-region Power System based on Consensus Theory" Energies 12, no. 5: 900. https://doi.org/10.3390/en12050900
APA StyleXia, S., Zhang, Q., Jing, J., Ding, Z., Yu, J., Chen, B., & Wu, H. (2019). Distributed State Estimation of Multi-region Power System based on Consensus Theory. Energies, 12(5), 900. https://doi.org/10.3390/en12050900






