Stabilization Method Considering Disturbance Mitigation for DC Microgrids with Constant Power Loads
Abstract
1. Introduction
2. Problem Formulation and Stabilization Method
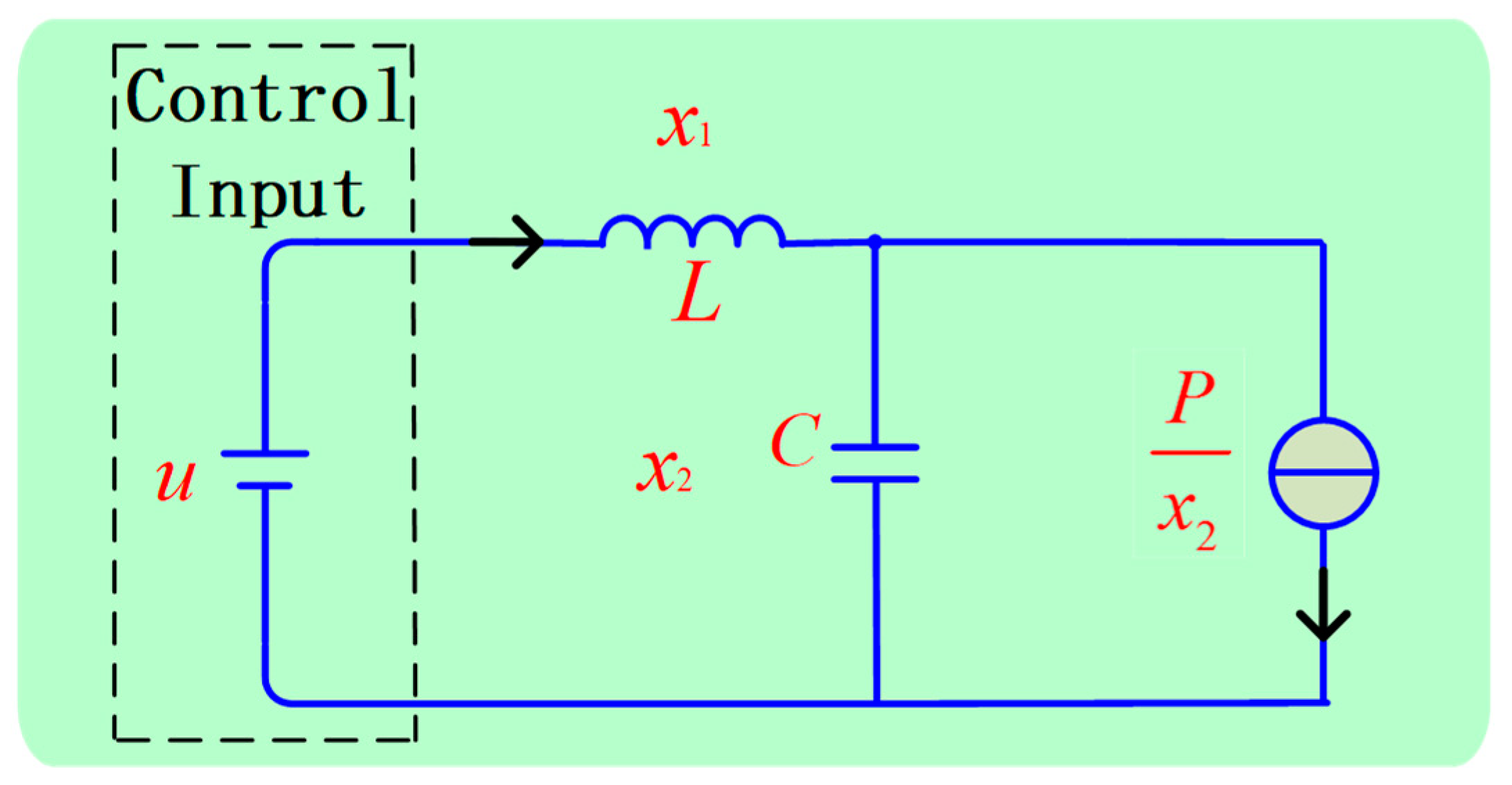
2.1. Problem Formulation
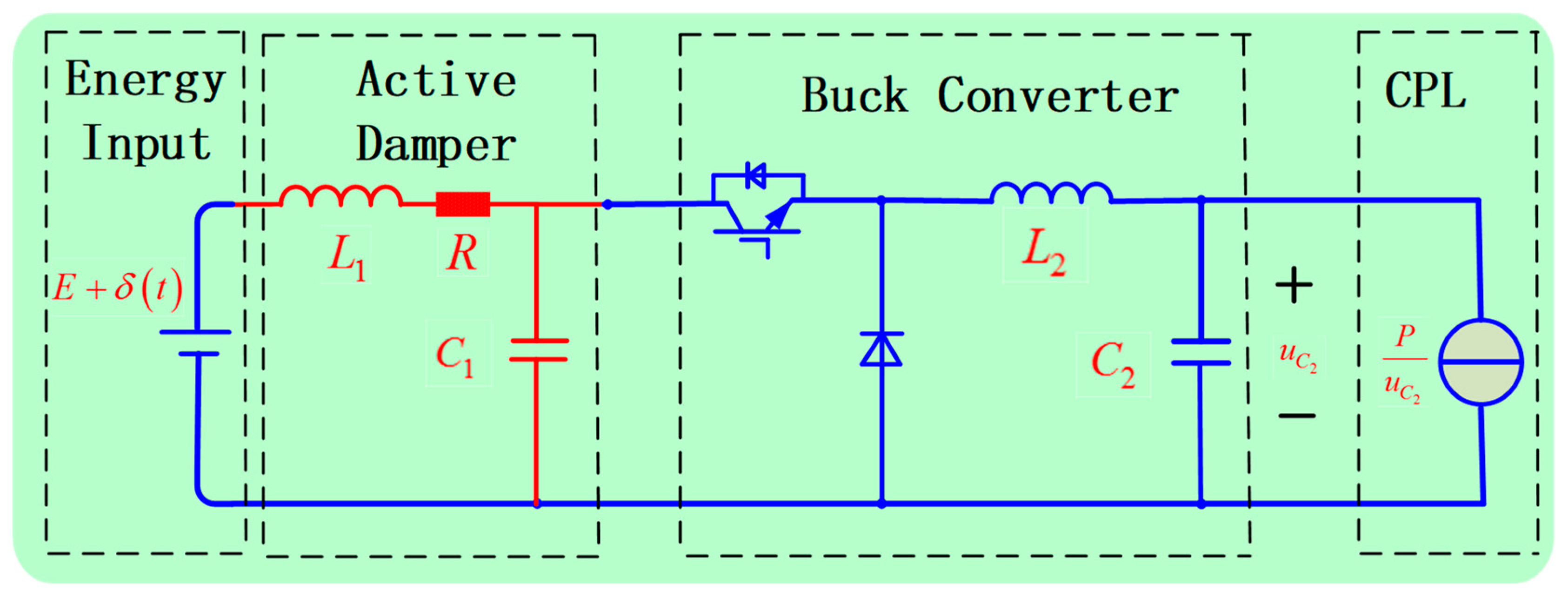
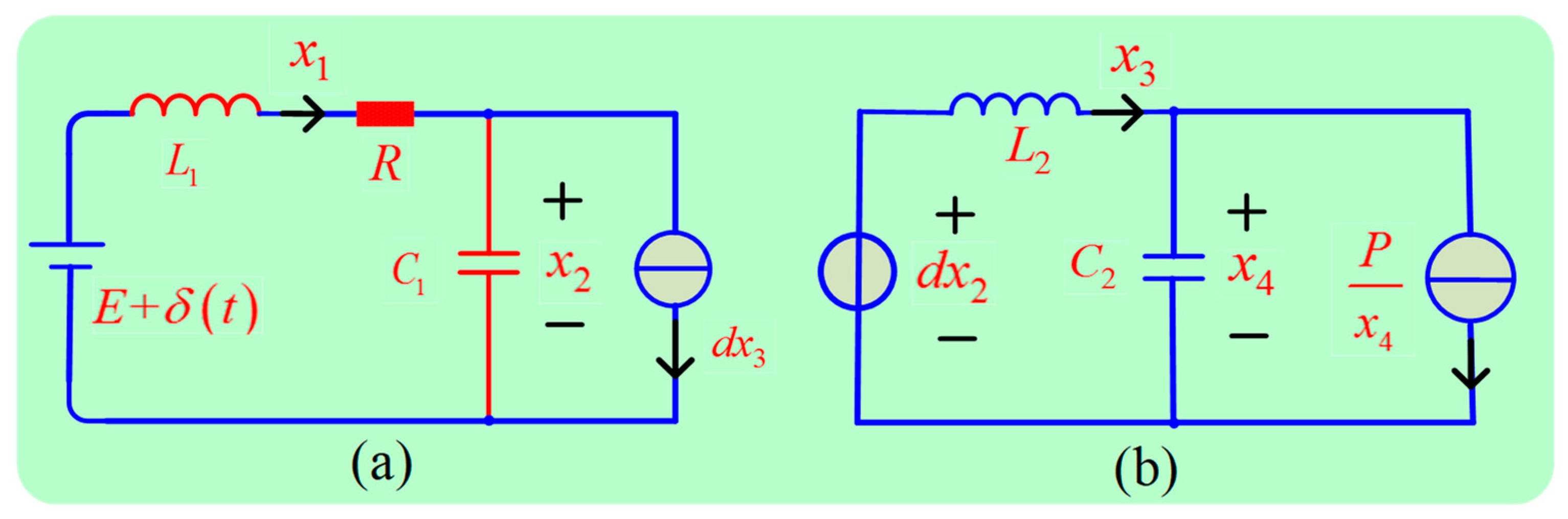
2.2. Proposed Stabilization Method
3. Stability Analysis
3.1. Recent Related Results
3.2. Small-Signal Stability Conditions
3.3. Large-Signal Stability Analysis and DOA Estimation
3.4. Transfer Function of the Disturbance
4. Generalizability of the Proposed Stabilization Method
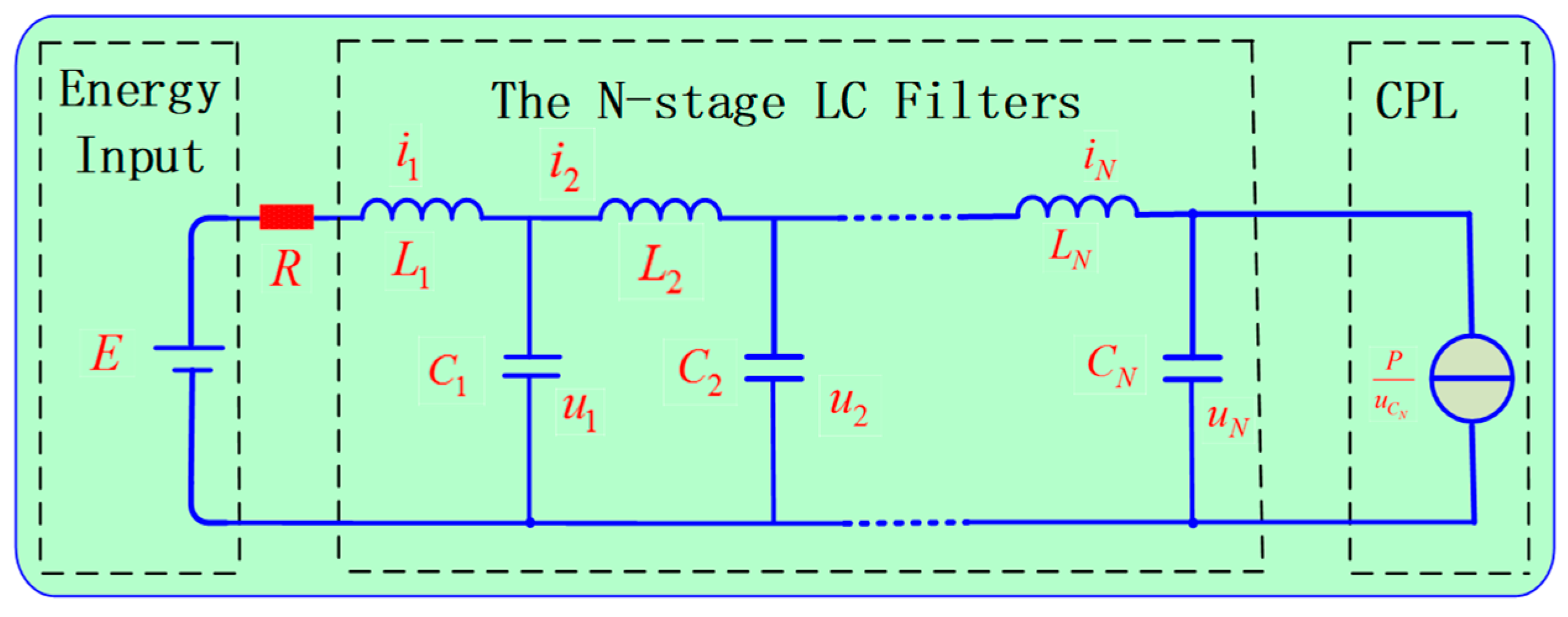
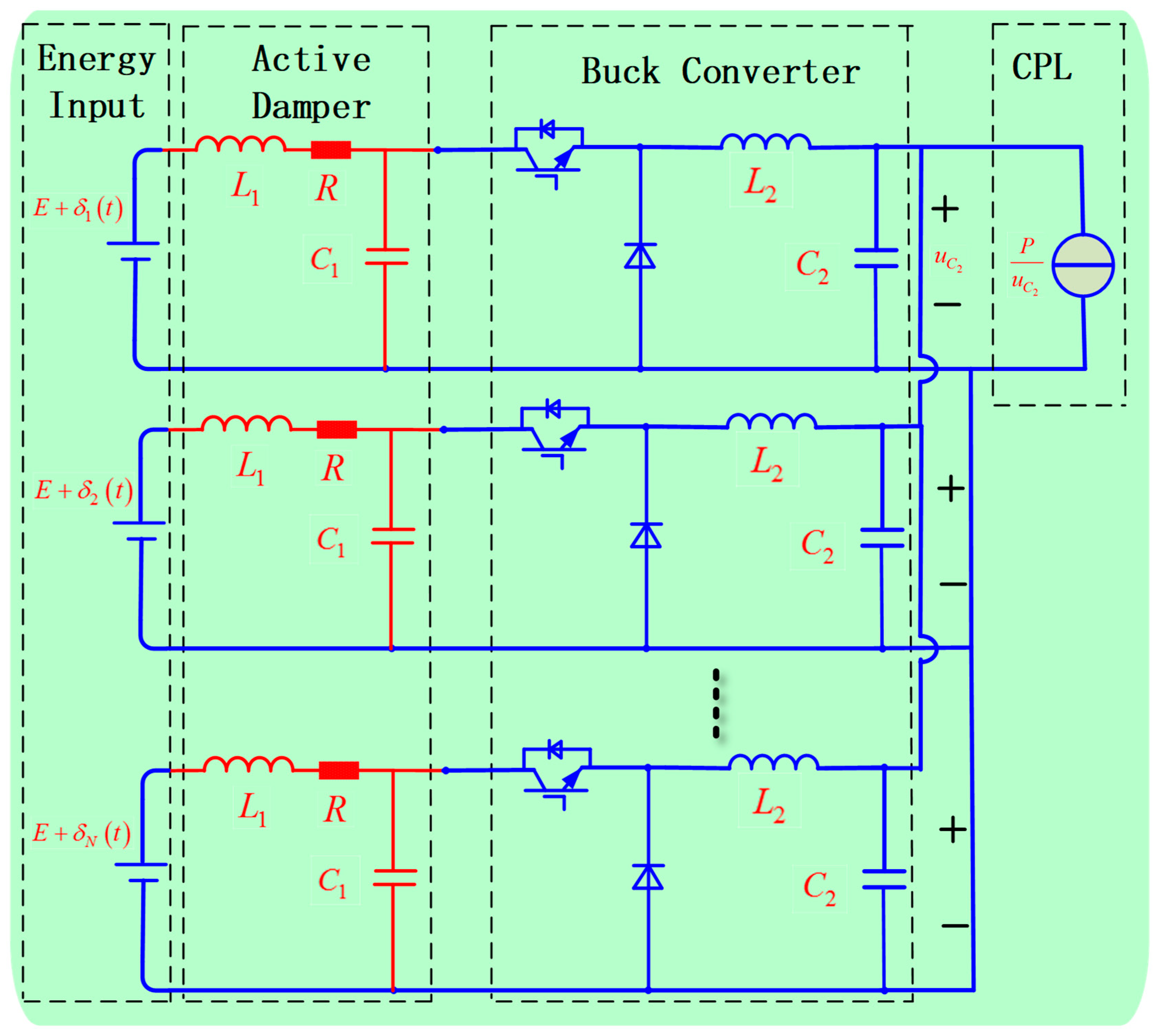
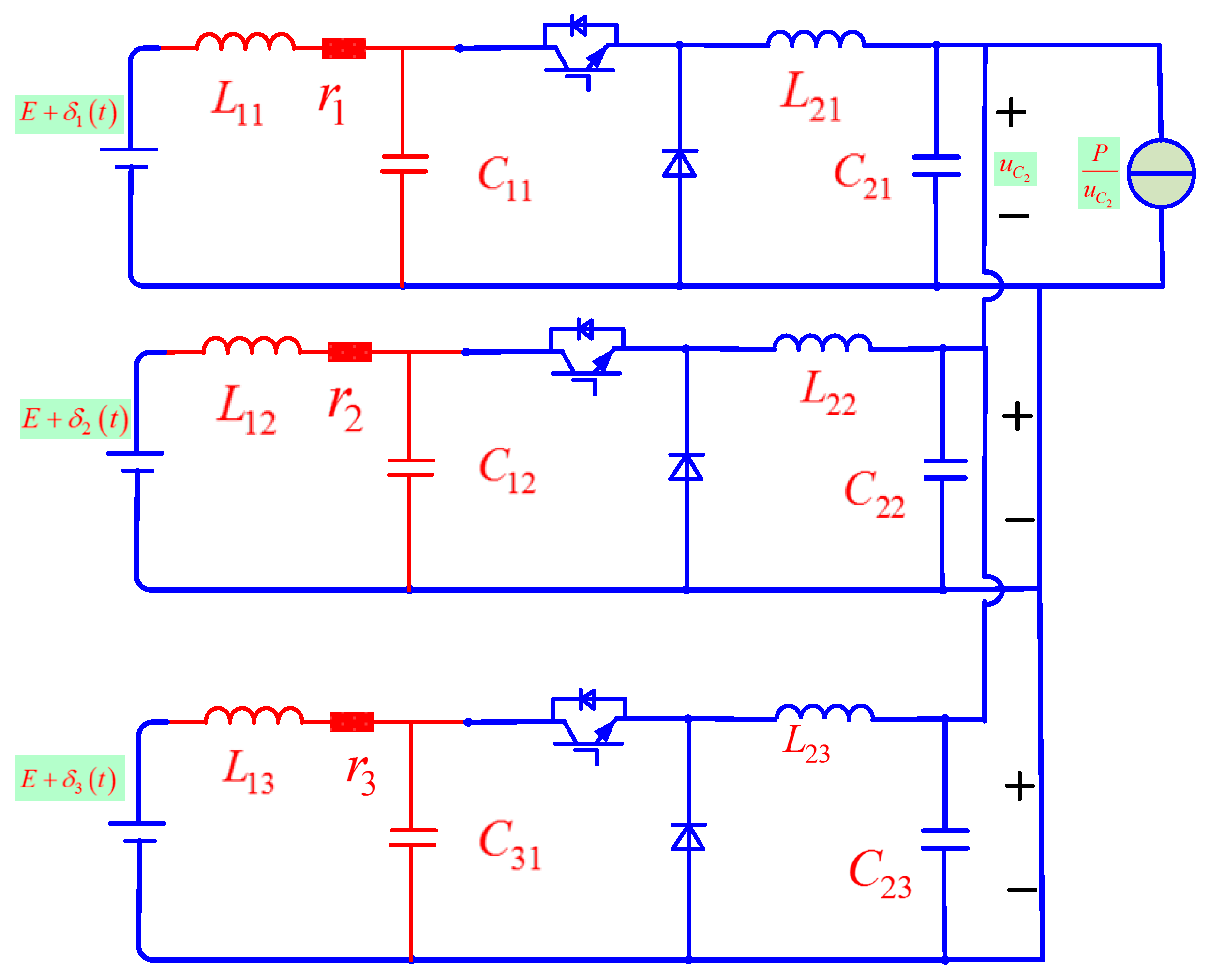
4.1. Stability Analysis of the DC Microgrid with Multiple Identical Converters
4.2. Stability Analysis of the DC Microgrid with Multiple Non-identical Converters
5. Simulation
5.1. Small-Signal Stability Conditions
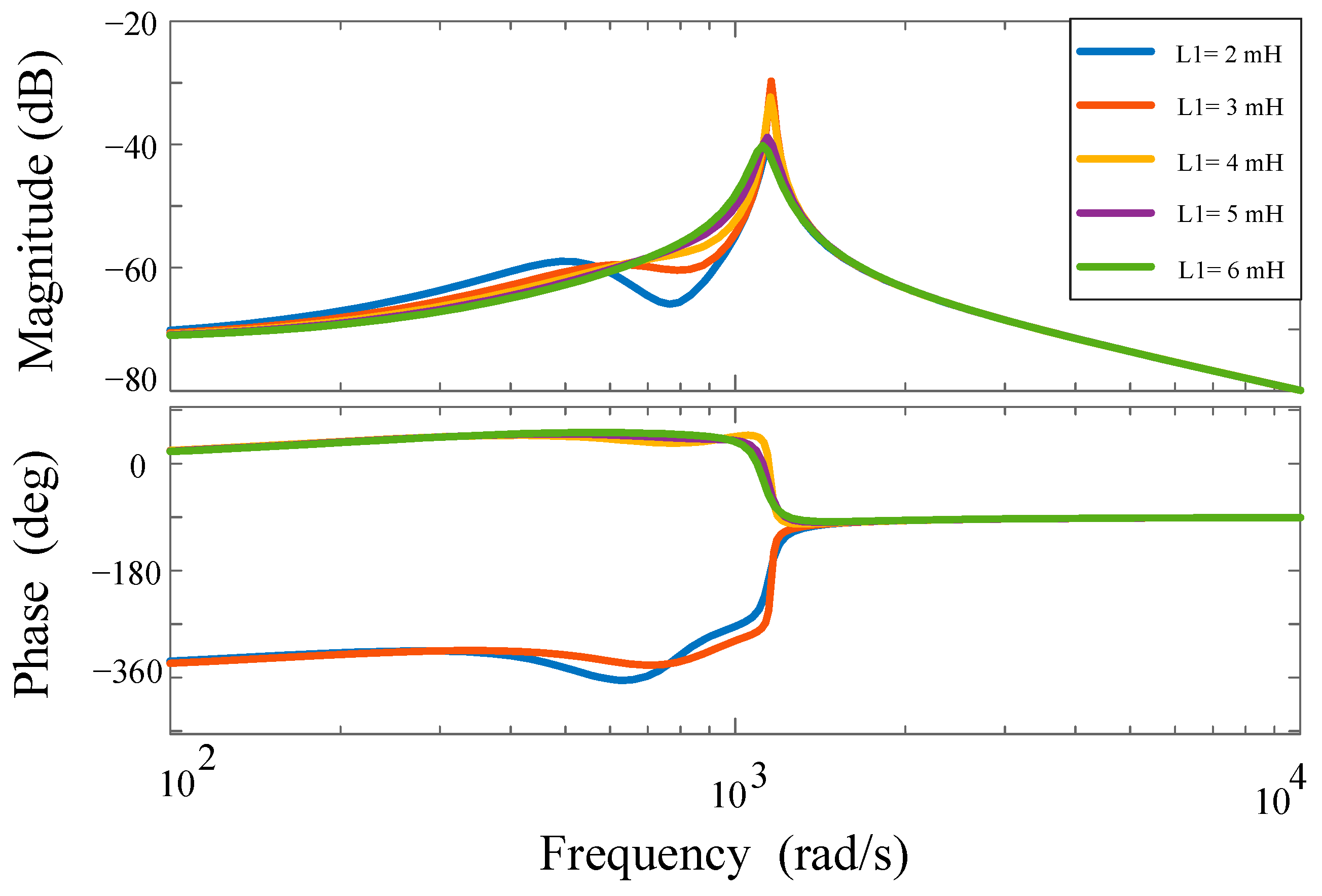
5.2. Transfer Function of the Disturbance
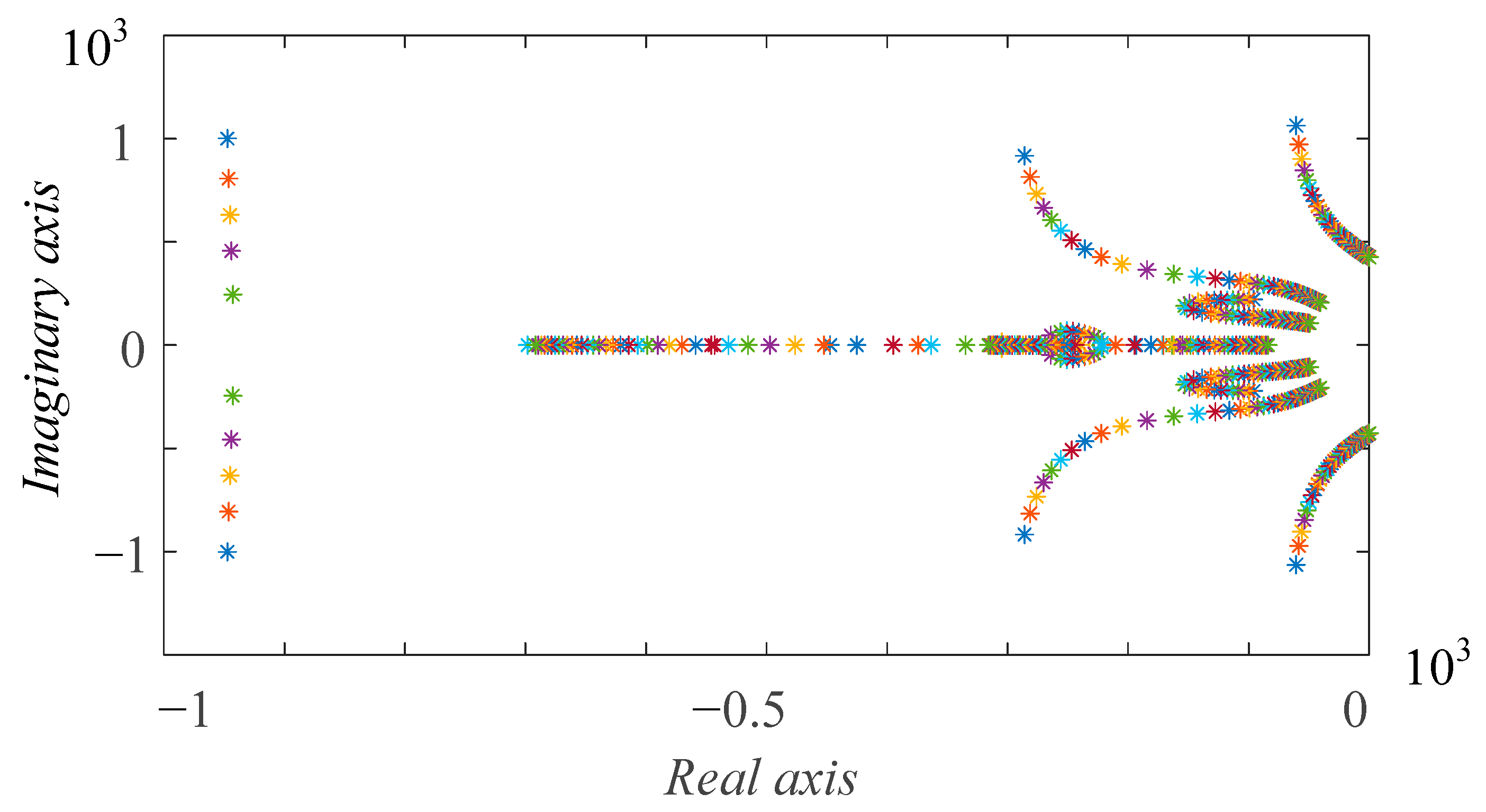
5.3. DOA of the Operation Point
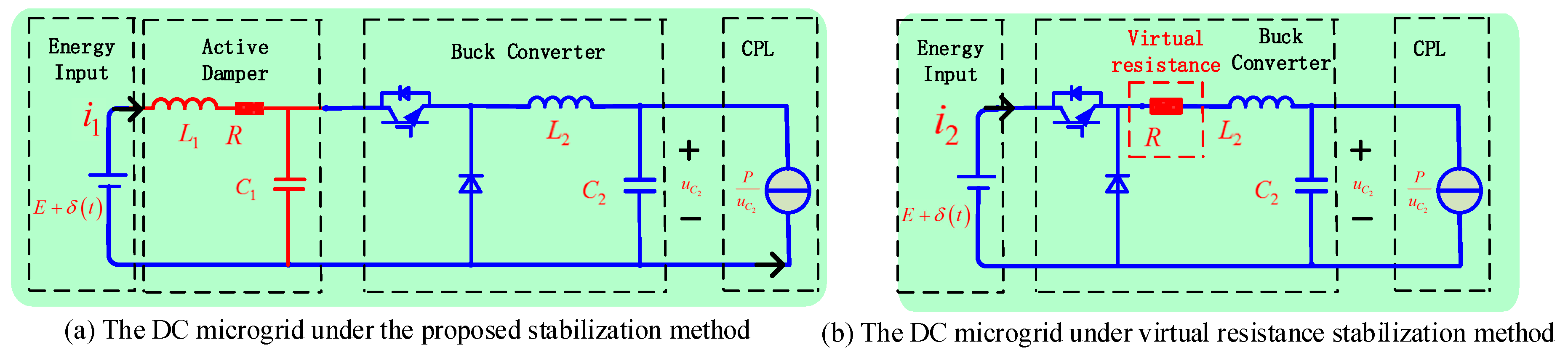
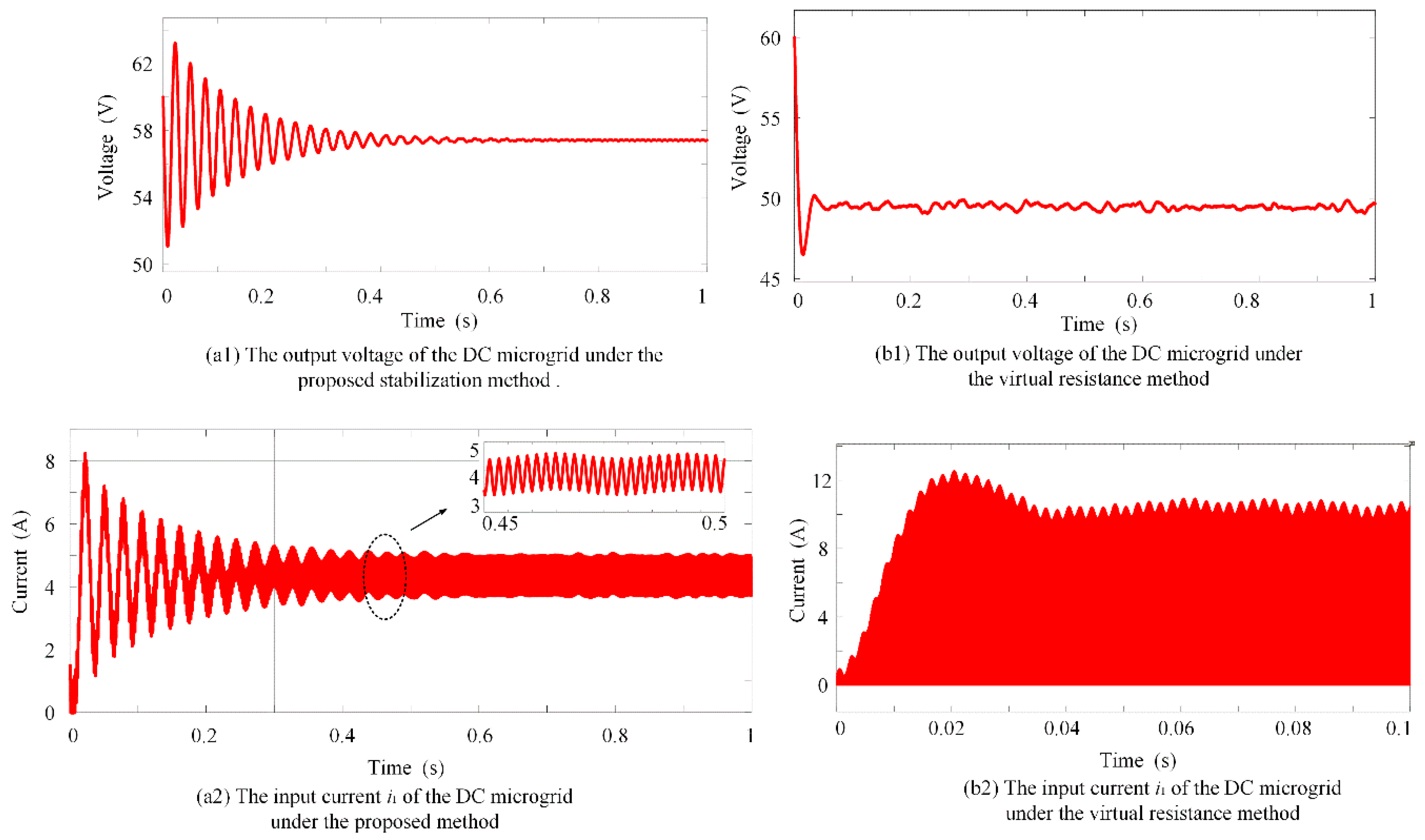
5.4. Compared with Virtual Resistance Method
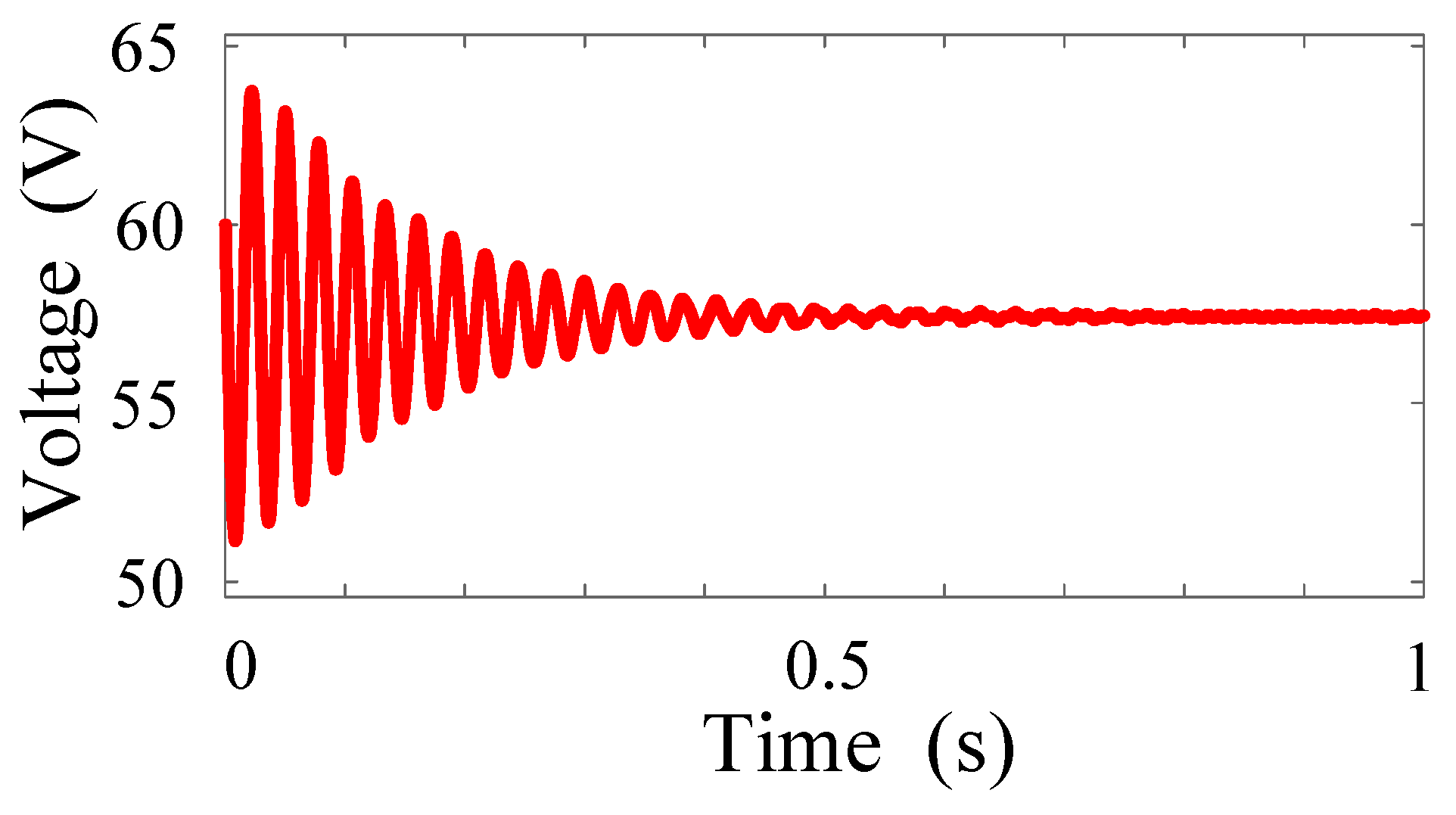
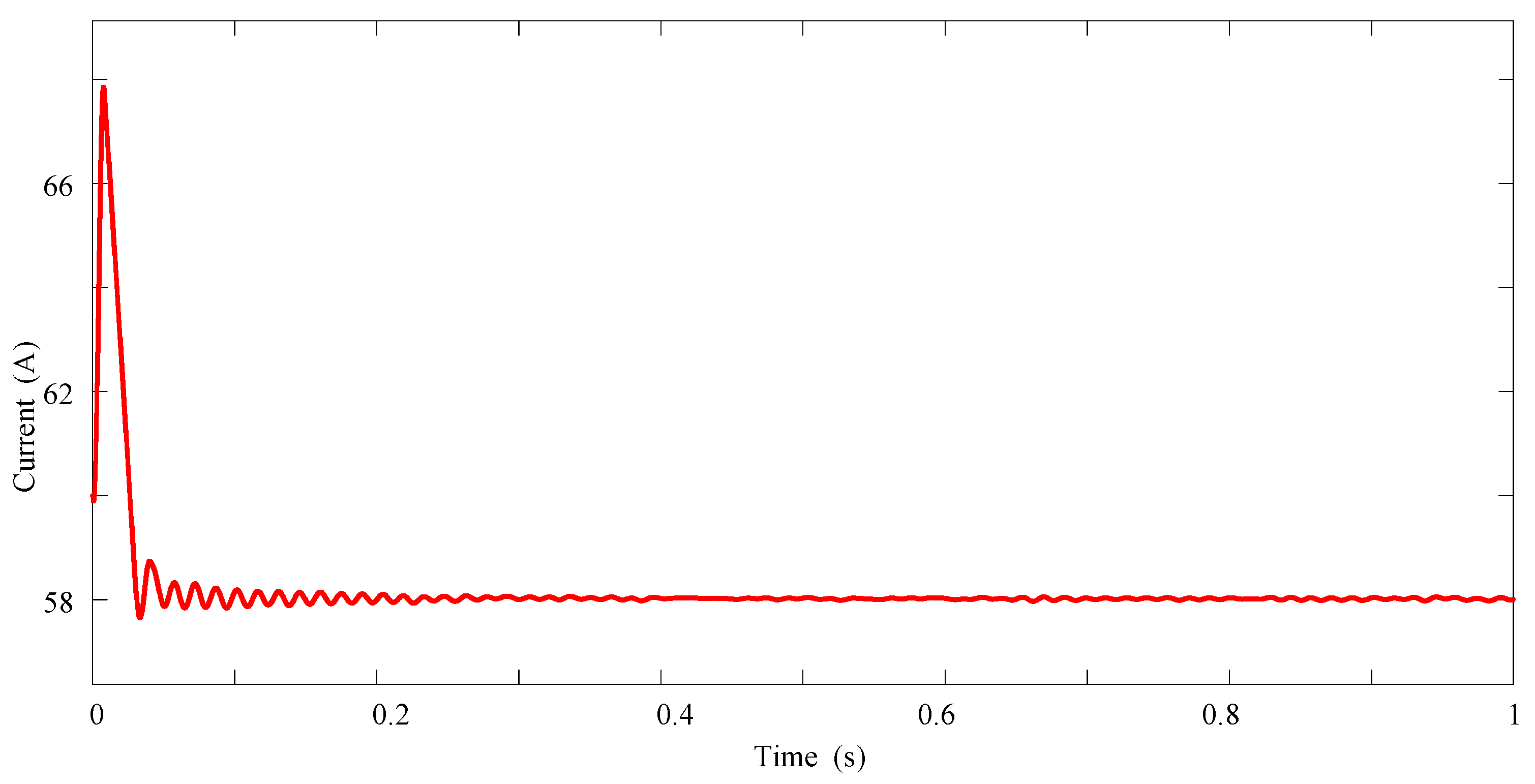
5.5. Simulation Results
5.6. The DC Microgrid with Multiple Identical Converters
5.7. The DC Microgrid with Multiple Identical Converters
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cagnano, A.; de Tuglie, E.; Cicognani, L. Prince—Electrical Energy Systems Lab: A pilot project for smart microgrids. Electr. Power Syst. Res. 2017, 148, 117–148. [Google Scholar] [CrossRef]
- Song, D.; Li, Q.; Cai, Z.; Li, L.; Yang, J.; Su, M.; Joo, Y.H. Model predictive control using multi-step prediction model for electrical yaw system of horizontal-axis wind turbines. IEEE Trans. Sustain. Energy 2018. [Google Scholar] [CrossRef]
- Song, D.; Fan, X.; Yang, J.; Liu, A.; Chen, S.; Joo, Y.H. Power extraction efficiency optimization of horizontal-axis wind turbines through optimizing control parameters of yaw control systems using an intelligent method. Appl. Energy 2018, 224, 224–279. [Google Scholar] [CrossRef]
- Rodríguez-Licea, M.A.; Pérez-Pinal, F.J.; Nuñez-Perez, J.C.; Herrera-Ramirez, C.A. Nonlinear Robust Control for Low Voltage Direct-Current Residential Microgrids with Constant Power Loads. Energies 2018, 11, 1130. [Google Scholar] [CrossRef]
- Hossain, E.; Perez, R.; Padmanaban, S.; Siano, P. Investigation on the Development of a Sliding Mode Controller for Constant Power Loads in Microgrids. Energies 2017, 10, 1086. [Google Scholar] [CrossRef]
- Shuai, Z.; Peng, Y.; Liu, X.; Li, Z.; Guerrero, J.M.; Shen, Z.J. Dynamic Equivalent Modeling for Multi-Microgrid Based on Structure Preservation Method. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Chen, Z.; Blaabjerg, F. Small-signal stability analysis of inverter-fed power systems using component connection method. IEEE Trans. Smart Grid 2018, 9, 5310–5390. [Google Scholar] [CrossRef]
- Shuai, Z.; Peng, Y.; Guerrero, J.M.; Li, Y.; Shen, Z.J. Transient Response Analysis of Inverter-Based Microgrids Under Unbalanced Conditions Using a Dynamic Phasor Model. IEEE Trans. Ind. Electron. 2019, 66, 2866–2879. [Google Scholar] [CrossRef]
- Sun, Y.; Hou, X.; Yang, J.; Han, H.; Su, M.; Guerrero, J.M. New perspectives on droop control in AC microgrid. IEEE Trans. Ind. Electron. 2017, 64, 5741–5745. [Google Scholar] [CrossRef]
- Han, H.; Li, L.; Wang, L.; Su, M.; Zhao, Y.; Guerrero, J.M. A Novel Decentralized Economic Operation in Islanded AC Microgrids. Energies 2017, 10, 804. [Google Scholar] [CrossRef]
- Rana, M.M.; Li, L.; Su, S.W. Controlling the renewable microgrid using semidefinite programming technique. Int. J. Electr. Power Energy Syst. 2017, 84, 231–284. [Google Scholar] [CrossRef]
- Liu, Z.; Su, M.; Sun, Y.; Li, L.; Han, H.; Zhang, X.; Zheng, M. Optimal criterion and global/sub-optimal control schemes of decentralized economical dispatch for AC microgrid. Int. J. Electr. Power Energy Syst. 2019, 104, 104–142. [Google Scholar] [CrossRef]
- Han, H.; Hou, X.; Yang, J.; Wu, J.; Su, M.; Guerrero, J.M. Review of power sharing control strategies for islanding operation of AC microgrids. IEEE Trans. Smart Grid 2016, 7, 215–217. [Google Scholar] [CrossRef]
- Li, L.; Sun, Y.; Liu, Z.; Hou, X.; Shi, G.; Su, M. A Decentralized Control with Unique Equilibrium Point for Cascaded-type Microgrid. IEEE Trans. Sustain. Energy 2019, 10, 310–326. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Han, H.; Liu, Z.; Yuan, W.; Su, M. A fully decentralized control of grid-connected cascaded inverters. IEEE Trans. Sustain. Energy 2019, 10, 310–317. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Zhang, X.; Zhang, G.; Lu, J.; Blaabjerg, F. A Self-Synchronized Decentralized Control for Series-Connected H-bridge Rectifiers. IEEE Trans. Power Electron. 2019. [Google Scholar] [CrossRef]
- Sun, Y.; Shi, G.; Li, X.; Yuan, W.; Su, M.; Han, H.; Hou, X. An f-P/Q droop control in cascaded-type microgrid. IEEE Trans. Power Electron. 2018, 33, 1133–1138. [Google Scholar]
- Masud, R.; Li, L.; Steven, S. Design of Distributed Controllers for Microgrids. Int. J. Innov. Comput. Inf. Control 2017, 13, 1–12. [Google Scholar]
- Masud, R.; Li, L. An overview of distributed microgrid state estimation and control for smart grids. Sensors 2015, 15, 4315–4325. [Google Scholar]
- Cagnano, A.; Bugliari, A.C.; de Tuglie, E. A cooperative control for the reserve management of isolated microgrids. Appl. Energy 2018, 218, 218–265. [Google Scholar] [CrossRef]
- Guo, F.; Wen, C.; Song, Y.-D. Distributed Control and Optimization Technologies in Smart Grid Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wang, Y.; Wang, X.; Chen, Z.; Blaabjerg, F. Distributed optimal control of reactive power and voltage in islanded microgrids. IEEE Trans. Ind. Appl. 2017, 53, 349–353. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Lu, J.; Zhang, X.; Hai, K.L.; Su, M.; Guerrero, J.M. Distributed Hierarchical Control of AC Microgrid Operating in Grid-Connected, Islanded and Their Transition Modes. IEEE Access 2018. [Google Scholar] [CrossRef]
- Guo, F.; Xu, Q.; Wen, C.; Wang, L.; Wang, P. Distributed Secondary Control for Power Allocation and Voltage Restoration in Islanded DC Microgrids. IEEE Trans. Sustain. Energy 2018, 9, 1869–1900. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Wang, X.; Tian, Y.; Tan, Y.; Yang, C. An estimator-based distributed voltage predictive control strategy for AC islanded microgrids. IEEE Trans. Power Electron. 2015, 30, 2930–3951. [Google Scholar] [CrossRef]
- Guo, F.; Wen, C.; Mao, J.; Song, Y. Distributed economic dispatch for smart grids with random wind power. IEEE Trans. Smart Grid 2016, 7, 1583–1587. [Google Scholar] [CrossRef]
- Yang, J.; Yuan, W.; Sun, Y.; Han, H.; Hou, X.; Guerrero, J.M. A novel quasi-master-slave control frame for PV-storage independent microgrid. Int. J. Electr. Power Energy Syst. 2017, 97, 274–297. [Google Scholar] [CrossRef]
- Kwasinski, A.; Onwuchekwa, C.N. Dynamic Behavior and Stabilization of DC Microgrids with Instantaneous Constant-Power Loads. IEEE Trans. Power Electron. 2011, 26, 822–834. [Google Scholar] [CrossRef]
- Gu, Y.; Li, W.; He, X. Passivity-Based Control of DC Microgrid for Self-Disciplined Stabilization. IEEE Trans. Power Electron. 2015, 30, 2630–2632. [Google Scholar]
- Kwasinski, A.; Krein, P.T. Stabilization of constant power loads in dc-dc converters using passivity based control. In Proceedings of the 29th International Telecommunications Energy Conference, Rome, Italy, 30 September–4 October 2007; pp. 867–874. [Google Scholar]
- Magne, P.; Mobarakeh, B.N.; Pierfederici, S. Dynamic Consideration of DC Microgrids With Constant Power Loads and Active Damping System—A Design Method for Fault-Tolerant Stabilizing System. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 570–572. [Google Scholar] [CrossRef]
- Chang, X.; Li, Y.; Li, X.; Chen, X. An Active Damping Method Based on a Supercapacitor Energy Storage System to Overcome the Destabilizing Effect of Instantaneous Constant Power Loads in DC Microgrids. IEEE Trans. Energy Convers. 2017, 32, 32–47. [Google Scholar] [CrossRef]
- Wu, M.; Lu, D.D. An active damping method for stabilization of cascaded connected two stage converter systems with constant power loads in DC microgrids. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems, Melbourne, VIC, Australia, 1–5 June 2014; pp. 2664–2667. [Google Scholar]
- Zhang, X.; Zhong, Q.; Ming, W. Stabilization of Cascaded DC/DC Converters via Adaptive Series-Virtual-Impedance Control of the Load Converter. IEEE Trans. Power Electron. 2016, 31, 6031–6063. [Google Scholar] [CrossRef]
- Lu, X.; Sun, K.; Guerrero, J.M.; Vasquez, J.C.; Huang, L.; Wang, J. Stability Enhancement Based on Virtual Impedance for DC Microgrids with Constant Power Loads. IEEE Trans. Smart Grid 2015, 6, 2783–2786. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, Q.; Ming, W. Stabilization of a Cascaded DC Converter System via Adding a Virtual Adaptive Parallel Impedance to the Input of the Load Converter. IEEE Trans. Power Electron. 2016, 31, 1831–1832. [Google Scholar] [CrossRef]
- Herrera, L.; Zhang, W.; Wang, J. Stability Analysis and Controller Design of DC Microgrids with Constant Power Loads. IEEE Trans. Smart Grid 2017, 8, 800–888. [Google Scholar]
- Marx, D.; Magne, P.; Nahid-Mobarakeh, B.; Pierfederici, S.; Davat, B. Large signal stability analysis tools in DC power systems with constant power loads and variable power loads—A review. IEEE Trans. Power Electron. 2012, 27, 1727–1787. [Google Scholar] [CrossRef]
- Brayton, R.K.; Moser, J.K. A theory of nonlinear Networks I. Q. Appl. Math. 1964, 22, 22–33. [Google Scholar]
- Liu, X.; Zhou, Y.; Zhang, W.; Ma, S. Stability Criteria for Constant Power Loads With Multistage LC Filters. IEEE Trans. Veh. Technol. 2011, 60, 2049–2060. [Google Scholar] [CrossRef]
- Karimipour, D.; Salmasi, F.R. Stability Analysis of AC Microgrids With Constant Power Loads Based on Popov’s Absolute Stability Criterion. IEEE Trans. Circuits Syst. II 2015, 62, 700–760. [Google Scholar] [CrossRef]
- Rahimi, A.M.; Williamson, G.A.; Emadi, A. Loop-Cancellation Technique: A Novel Nonlinear Feedback to Overcome the Destabilizing Effect of Constant-Power Loads. IEEE Trans. Veh. Technol. 2010, 59, 659–661. [Google Scholar] [CrossRef]
- Sulligoi, G.; Bosich, D.; Giadrossi, G.; Zhu, L.; Cupelli, M.; Monti, A. Multiconverter Medium Voltage DC Power Systems on Ships: Constant-Power Loads Instability Solution Using Linearization via State Feedback Control. IEEE Trans. Smart Grid 2014, 5, 2552–2555. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiao, W.; Ha, D. A Sliding-Mode Duty-Ratio Controller for DC/DC Buck Converters With Constant Power Loads. IEEE Trans. Ind. Appl. 2014, 50, 1448–1458. [Google Scholar] [CrossRef]
- Su, M.; Liu, Z.; Sun, Y.; Han, H.; Hou, X. Stability Analysis and Stabilization methods of DC Microgrid with Multiple Parallel-Connected DC-DC Converters loaded by CPLs. IEEE Trans. Smart Grid 2018, 9, 142–149. [Google Scholar] [CrossRef]
- Anand, S.; Fernandes, B.G. Reduced-Order Model and Stability Analysis of Low-Voltage DC Microgrid. IEEE Trans. Ind. Electron. 2013, 60, 5040–5049. [Google Scholar] [CrossRef]
- Tahim, A.P.N.; Pagano, D.J.; Lenz, E.; Stramosk, V. Modeling and Stability Analysis of Islanded DC Microgrids Under Droop Control. IEEE Trans. Power Electron. 2015, 30, 4607–4630. [Google Scholar] [CrossRef]
- Liu, Z.; Su, M.; Sun, Y.; Han, H.; Hou, X.; Guerrero, J.M. Stability analysis of DC microgrids with constant power load under distributed control methods. Automatica 2018, 90, 72–90. [Google Scholar] [CrossRef]
- Liu, Z.; Su, M.; Sun, Y.; Yuan, W.; Han, H. Existence and Stability of Equilibrium of DC Microgrid with Constant Power Loads. IEEE Trans. Power Syst. 2018, 33, 7011–7033. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, H.; Liu, Z.; Liu, H. Stabilization Method Considering Disturbance Mitigation for DC Microgrids with Constant Power Loads. Energies 2019, 12, 873. https://doi.org/10.3390/en12050873
Liang H, Liu Z, Liu H. Stabilization Method Considering Disturbance Mitigation for DC Microgrids with Constant Power Loads. Energies. 2019; 12(5):873. https://doi.org/10.3390/en12050873
Chicago/Turabian StyleLiang, Haolan, Zhangjie Liu, and Hua Liu. 2019. "Stabilization Method Considering Disturbance Mitigation for DC Microgrids with Constant Power Loads" Energies 12, no. 5: 873. https://doi.org/10.3390/en12050873
APA StyleLiang, H., Liu, Z., & Liu, H. (2019). Stabilization Method Considering Disturbance Mitigation for DC Microgrids with Constant Power Loads. Energies, 12(5), 873. https://doi.org/10.3390/en12050873



