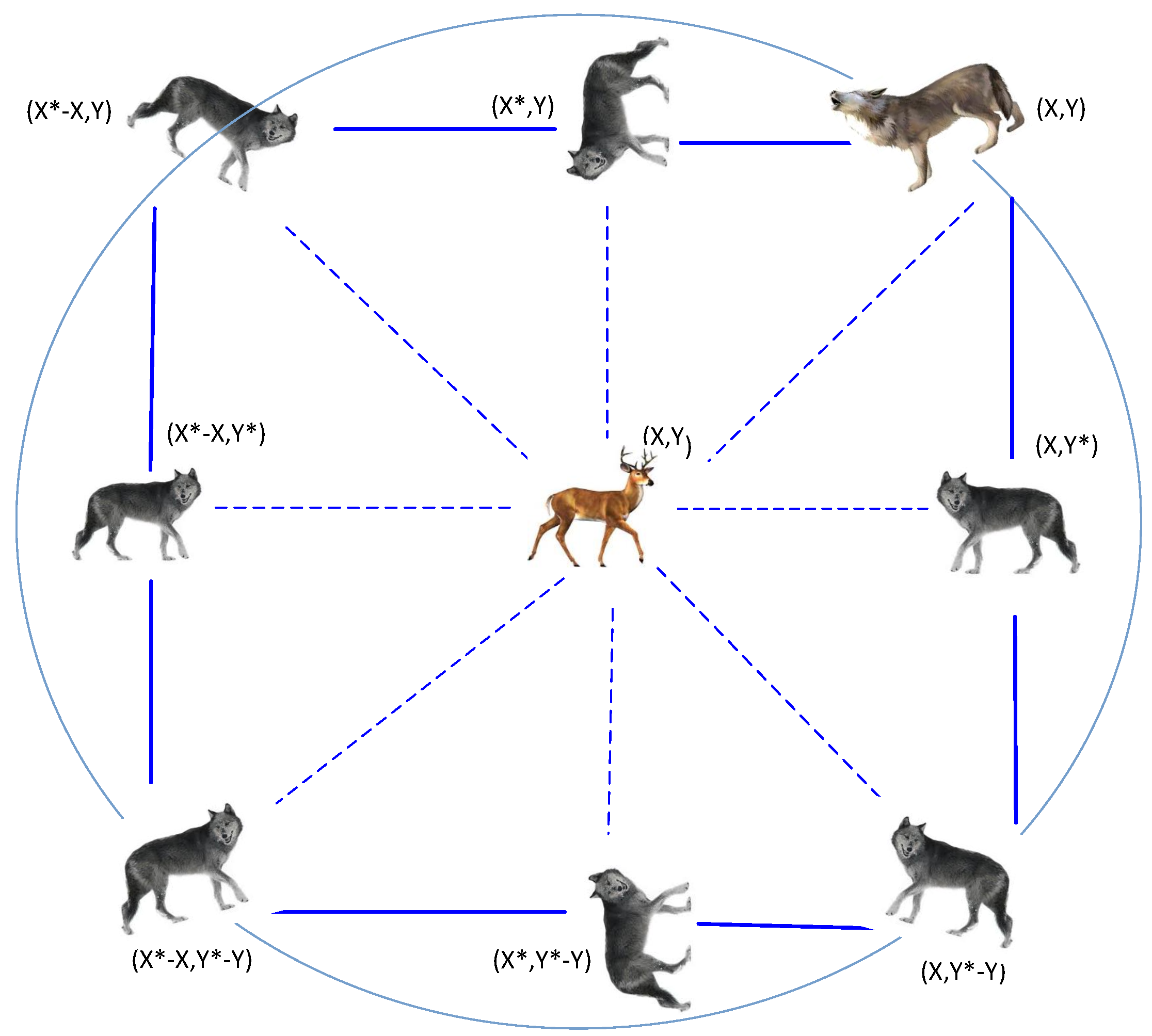
Figure 1.
Grey wolf social hierarchy.
Figure 1.
Grey wolf social hierarchy.
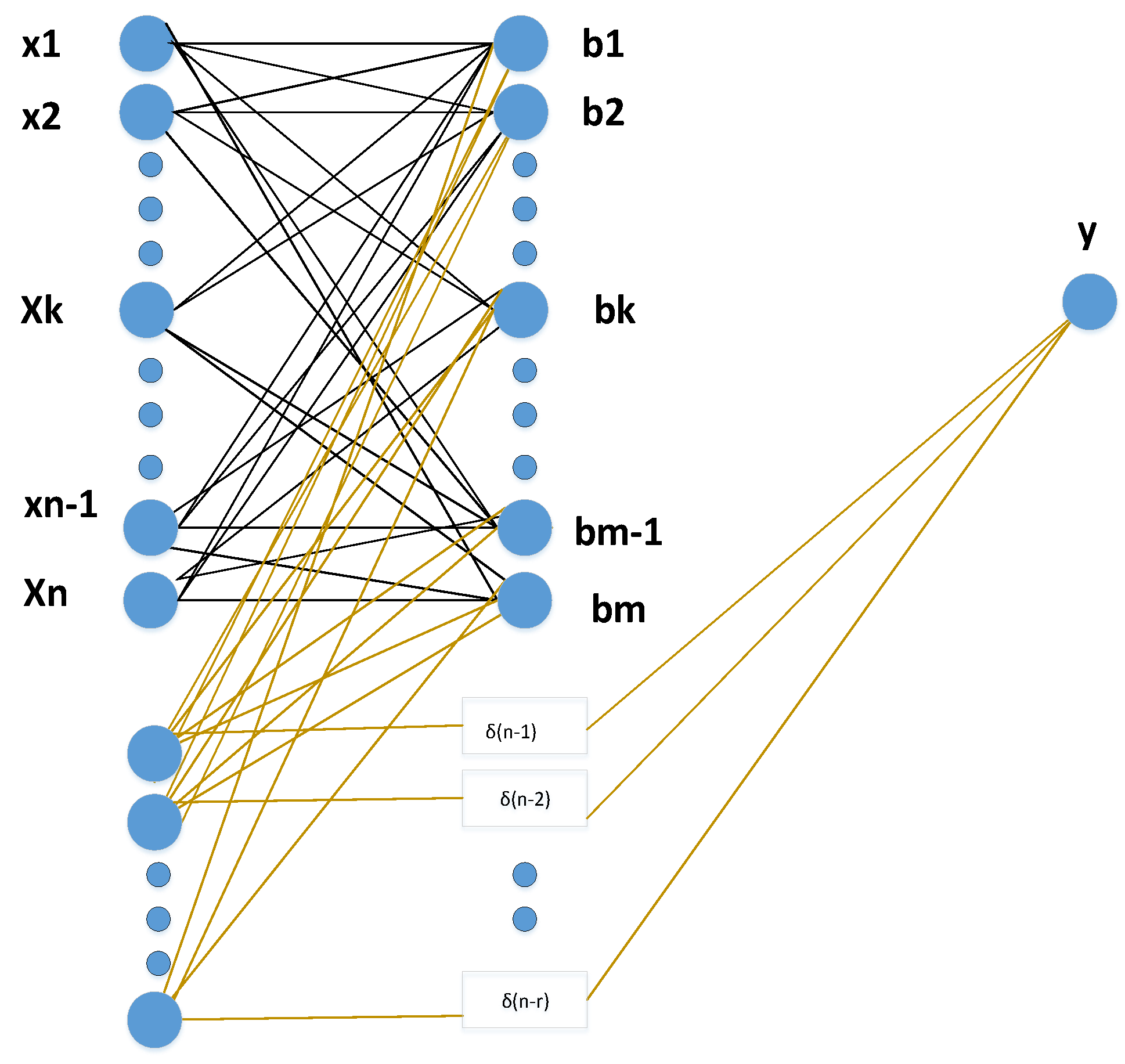
Figure 2.
Functioning of RELM.
Figure 2.
Functioning of RELM.
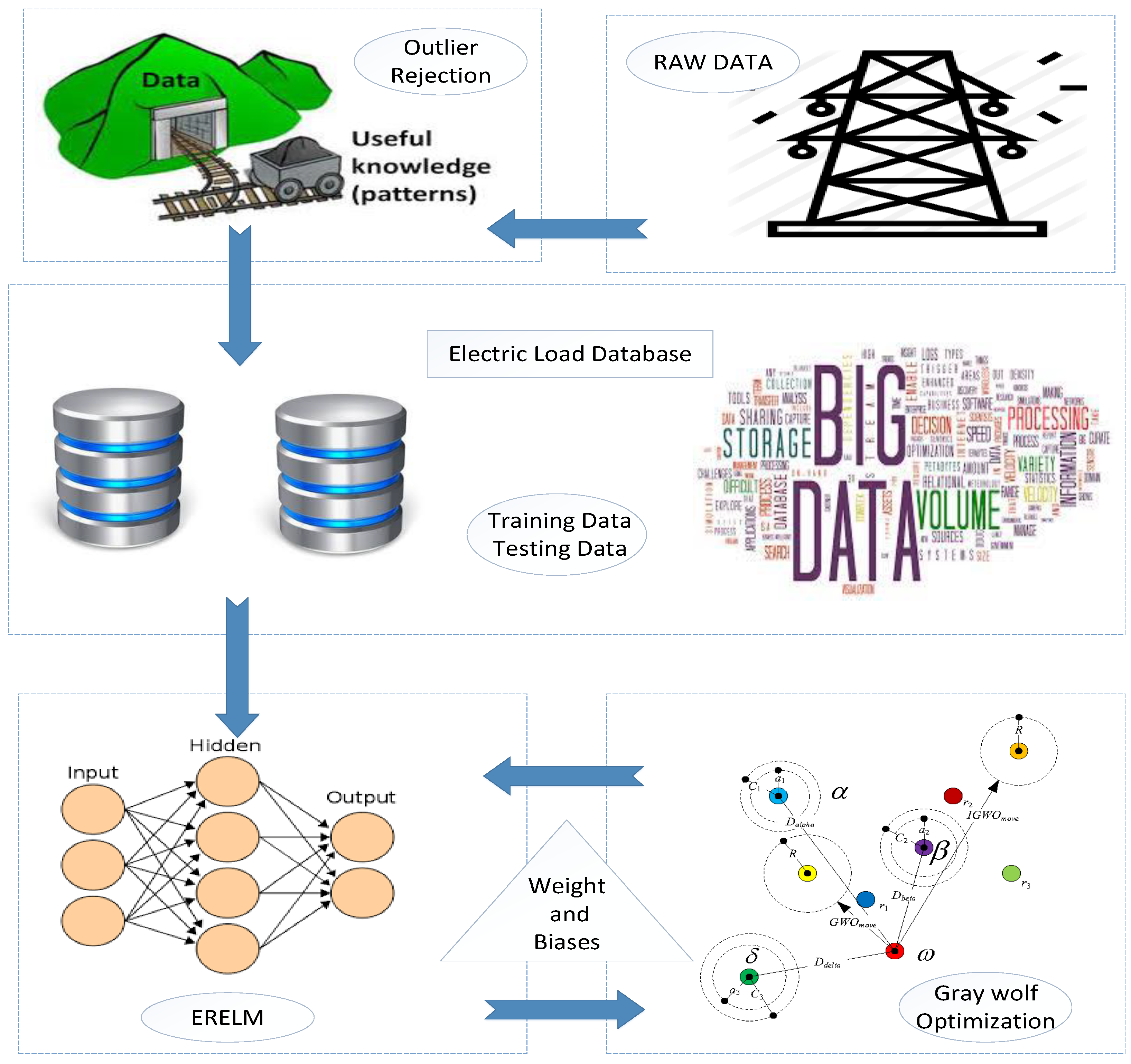
Figure 3.
Proposed system model 1.
Figure 3.
Proposed system model 1.
Figure 4.
Proposed system model 2.
Figure 4.
Proposed system model 2.
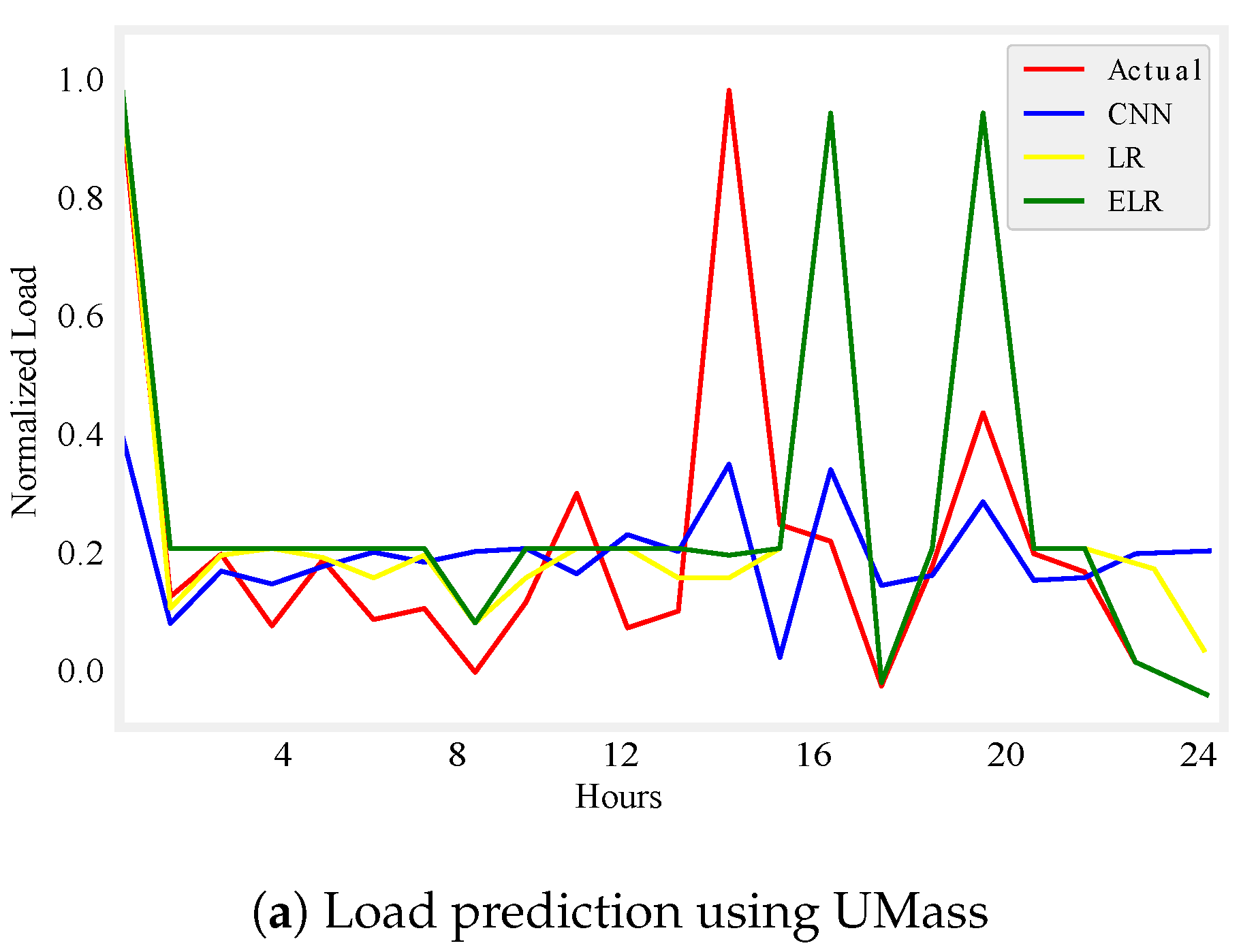
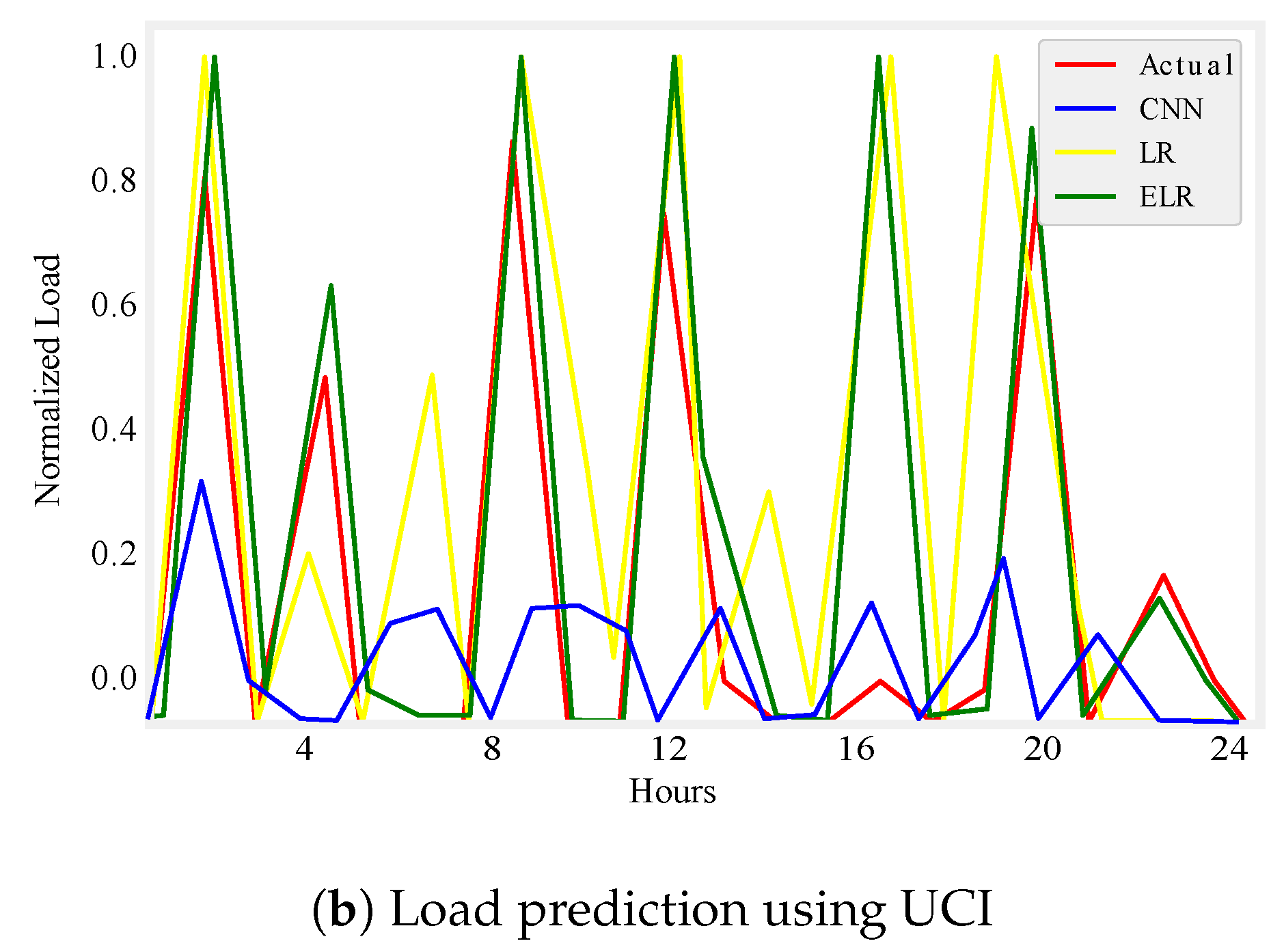
Figure 5.
One day load prediction.
Figure 5.
One day load prediction.
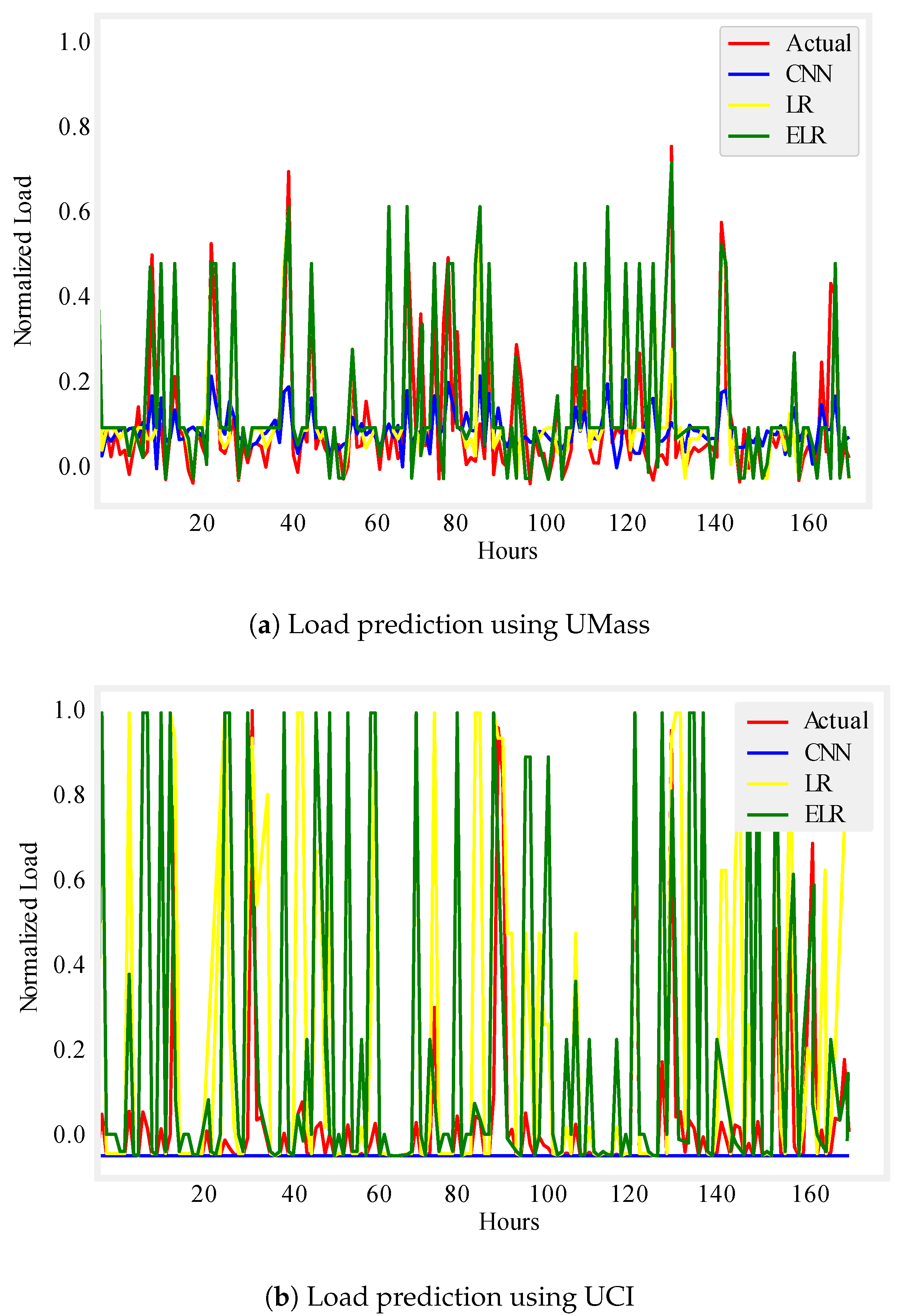
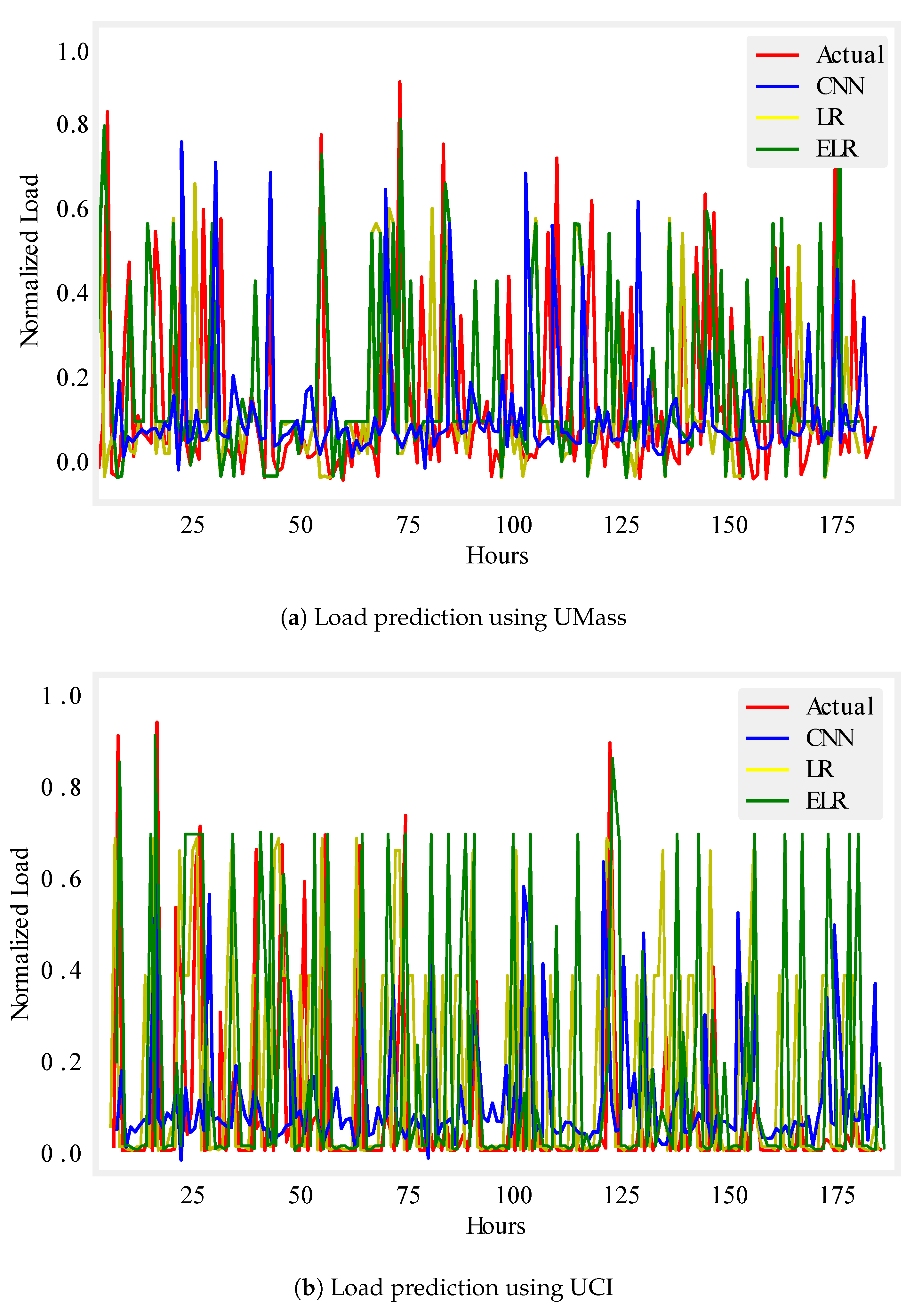
Figure 6.
One week load prediction.
Figure 6.
One week load prediction.
Figure 7.
One month load prediction.
Figure 7.
One month load prediction.
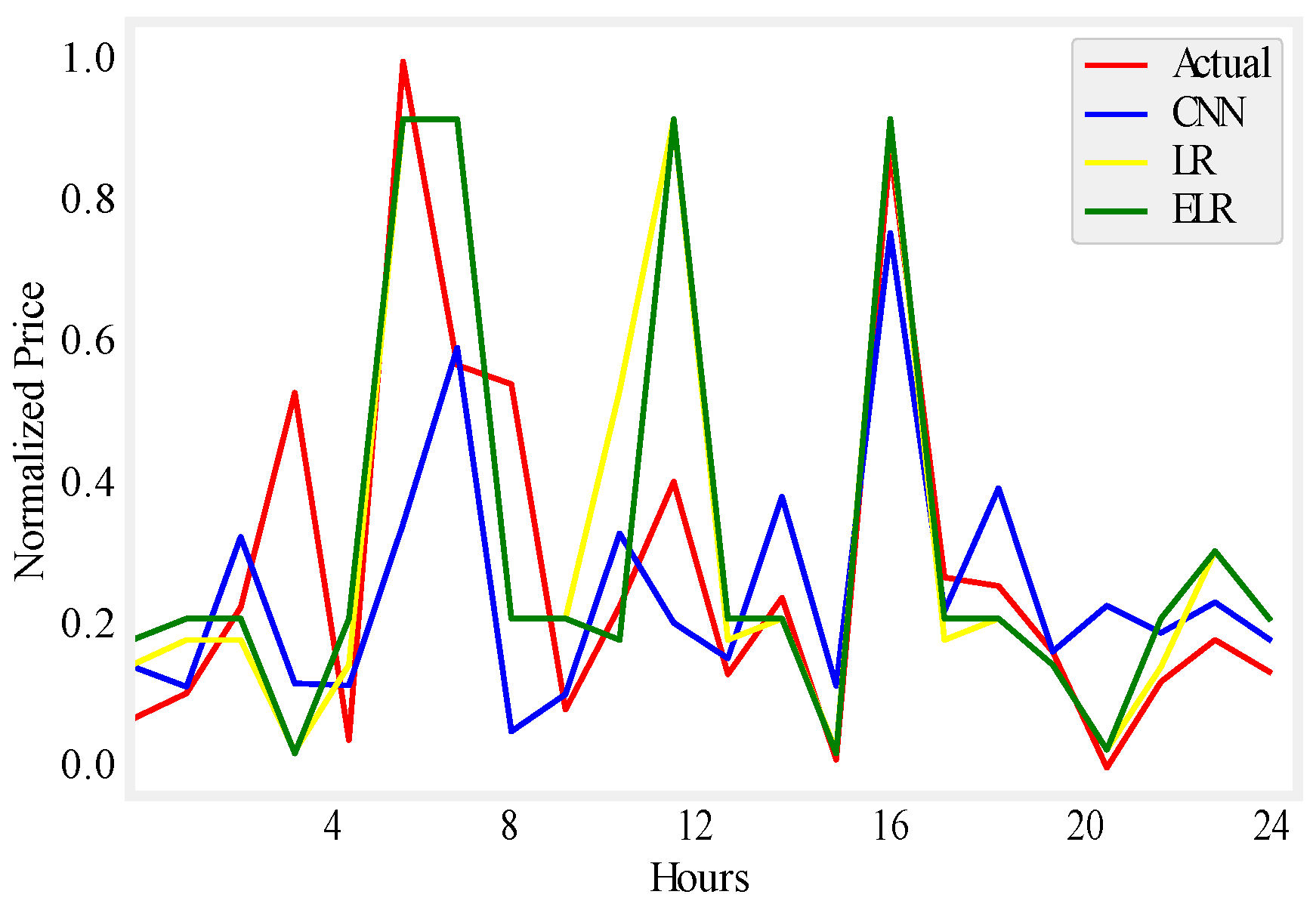
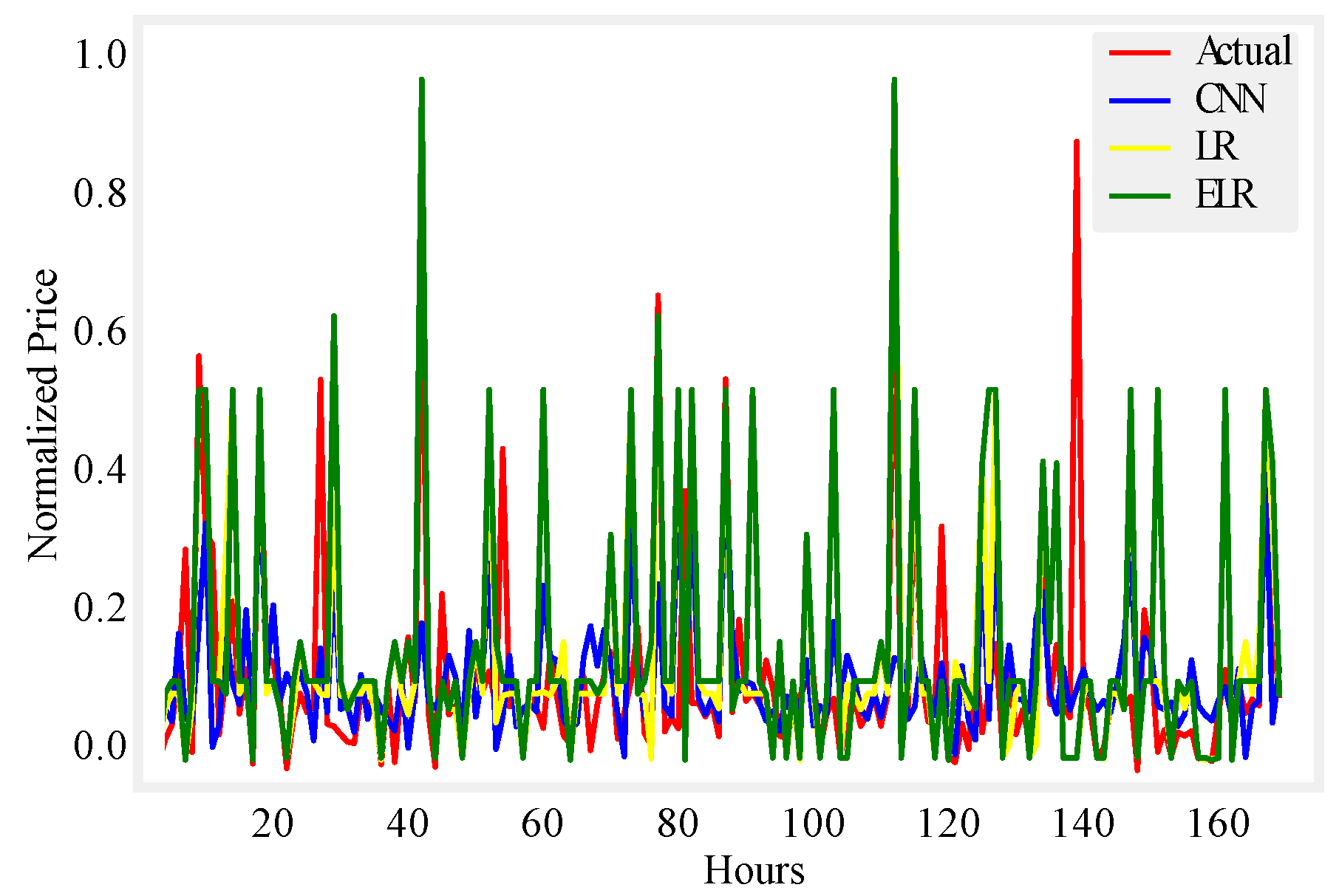
Figure 8.
One day price prediction using UMass.
Figure 8.
One day price prediction using UMass.
Figure 9.
One week price prediction using UMass.
Figure 9.
One week price prediction using UMass.
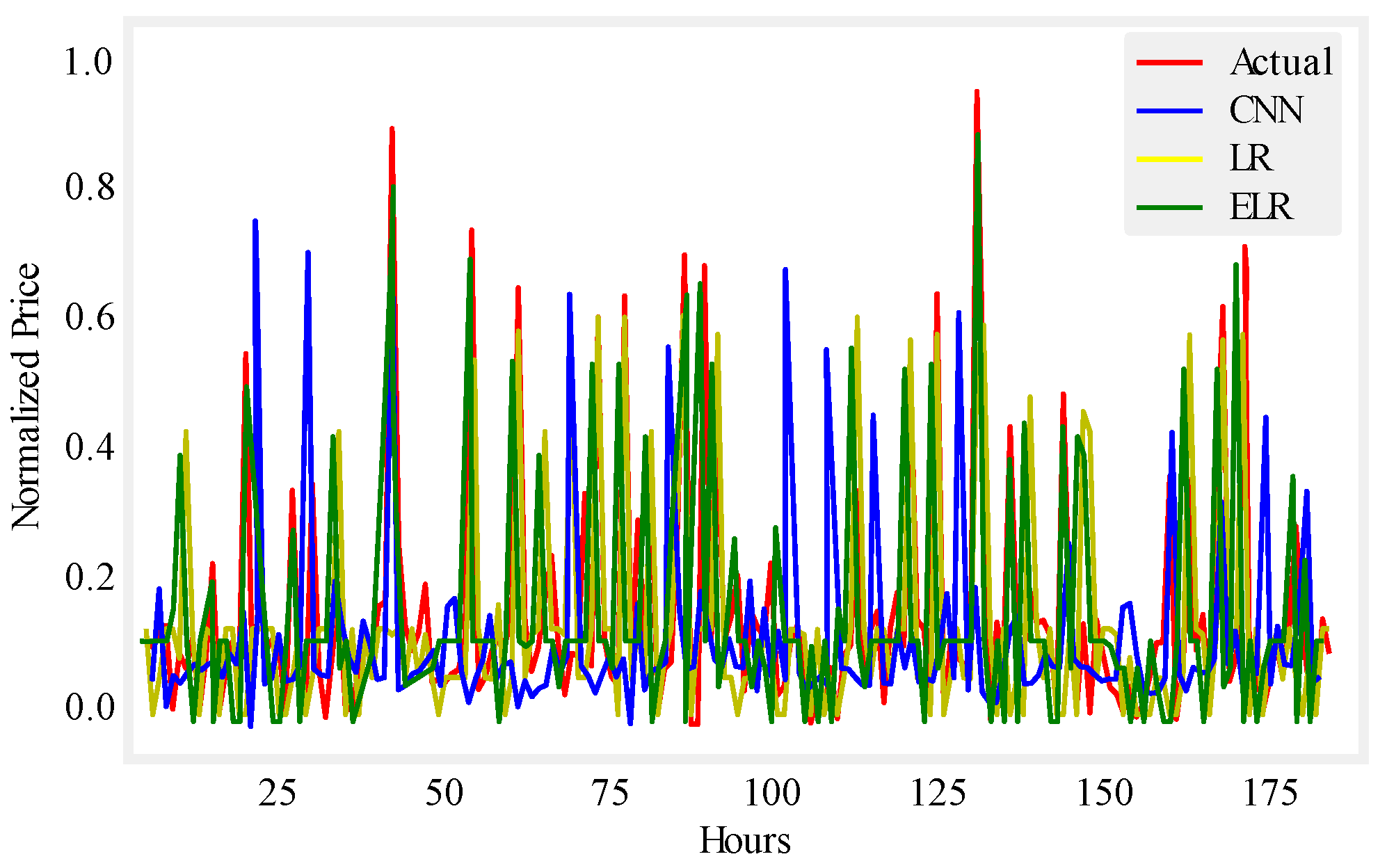
Figure 10.
One month price prediction using UMass.
Figure 10.
One month price prediction using UMass.
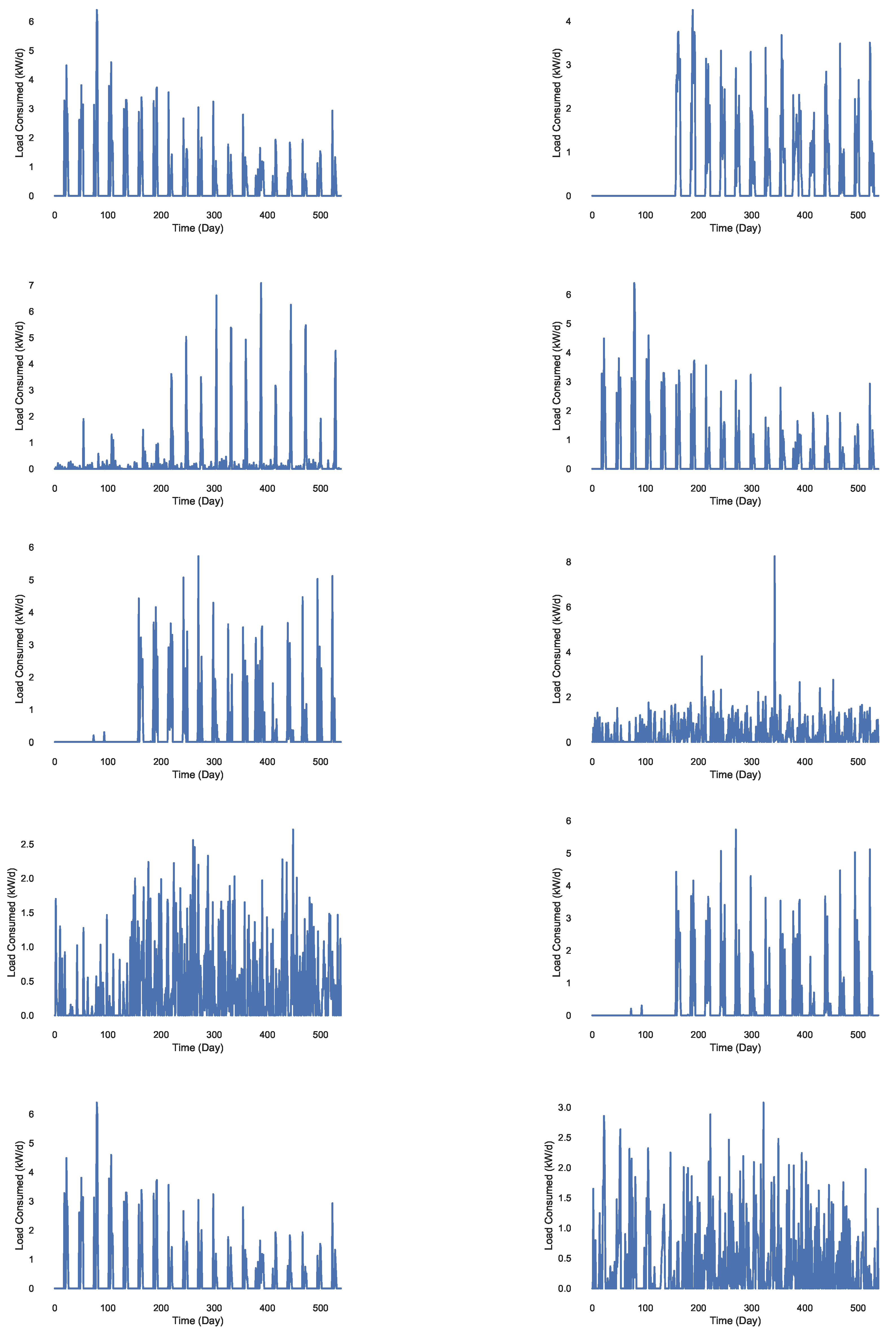
Figure 11.
Daily load consumption of 10 different substations.
Figure 11.
Daily load consumption of 10 different substations.
Figure 12.
Regression line plots using ELM.
Figure 12.
Regression line plots using ELM.
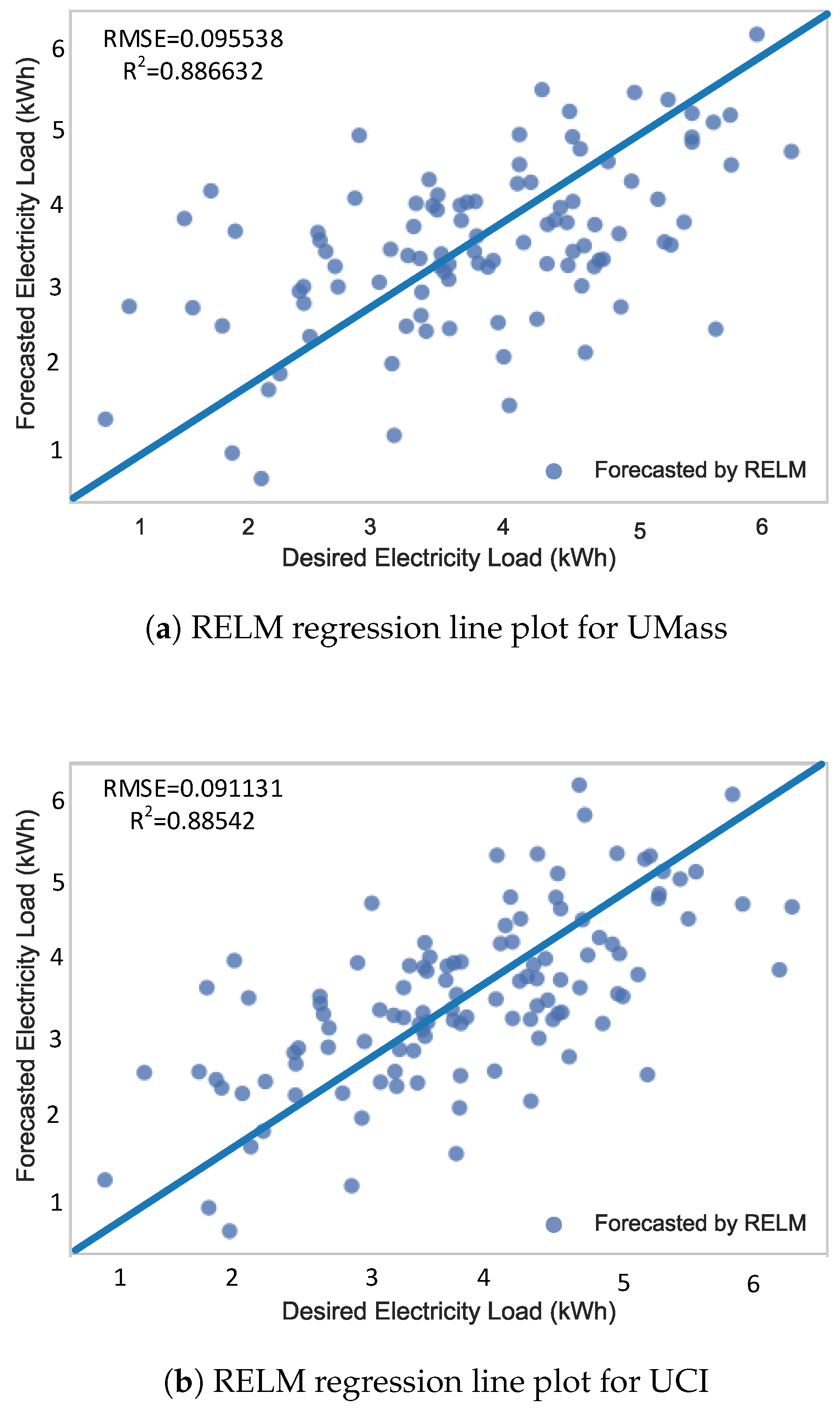
Figure 13.
Regression line plots using RELM.
Figure 13.
Regression line plots using RELM.
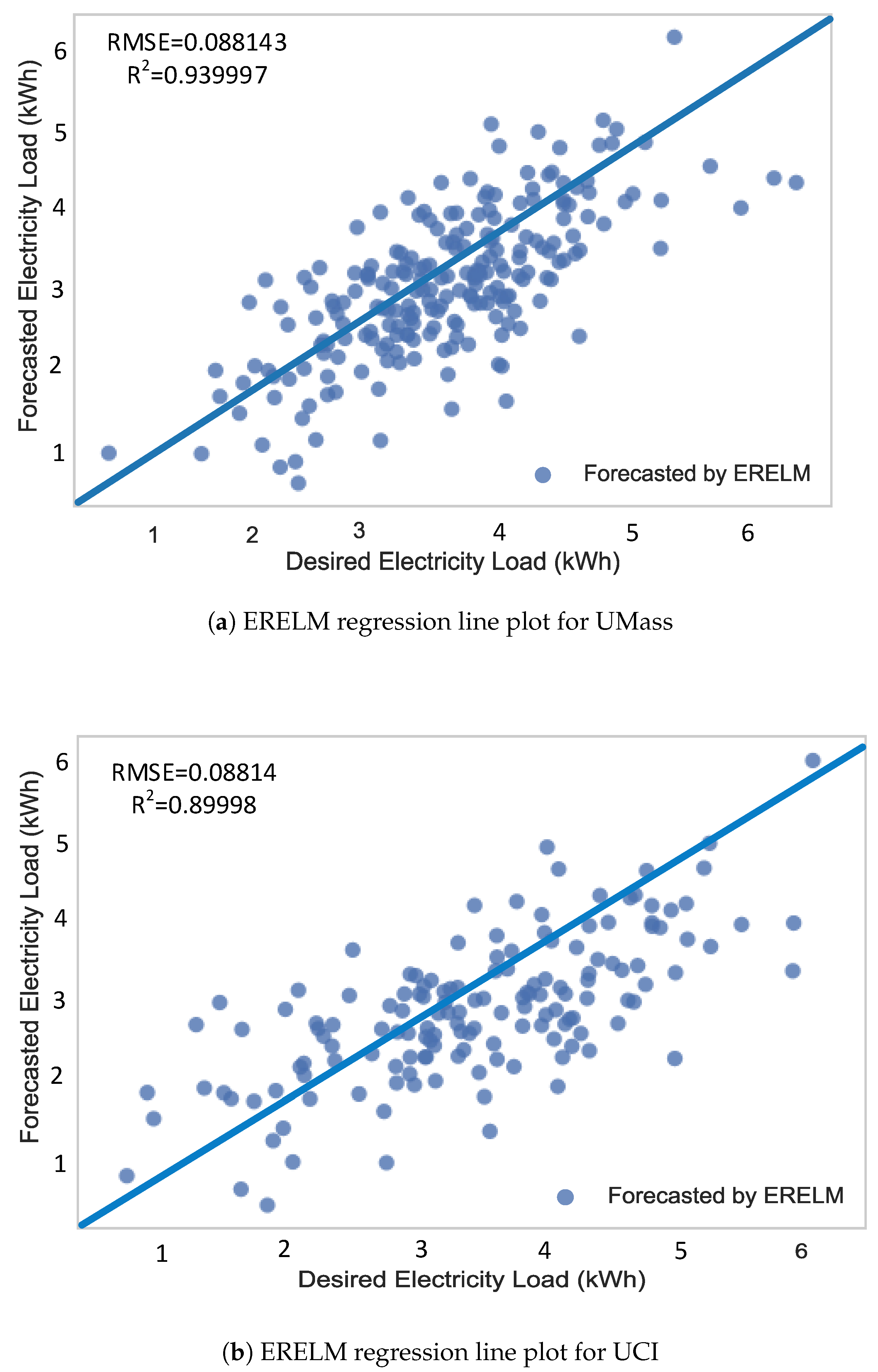
Figure 14.
Regression line plots using ERELM.
Figure 14.
Regression line plots using ERELM.
Table 1.
Differences between TG and SG.
Table 1.
Differences between TG and SG.
| TG | SG |
|---|
| Analogue | Digital |
| One way communication | Two way communication |
| Centralized power generation | Distributed power generation |
| Small number of sensors | Large number of sensors |
| Manual monitoring | Automatic monitoring |
| Difficult to locate failures | Easy to locate failures |
Table 2.
List of abbreviations.
Table 2.
List of abbreviations.
| Abbreviation | Full Form |
|---|
| AEMO | Australia Electricity Market Operators |
| AI | Artificially Intelligent |
| ANN | Artificial Neural Network |
| ARIMA | Auto Regressive Integrated Moving Average |
| ARMAX | Auto Regressive Moving Average with Exogenous variables |
| BP | Back Propagation |
| CART | Classification and Regression Technique |
| CNN | Convolutional Neural Network |
| DAE | Deep Auto Encoders |
| DE-SVM | Differential Evolution Support Vector Machine |
| DNN | Deep Neural Network |
| DRN | Deep Residual Network |
| DSM | Demand Side Management |
| DWT | Discrete Wavelet Transform |
| ELM | Extreme Learning Machine |
| EPEX | European Power Exchange |
| ELR | Enhanced Logistic Regression |
| ERELM | Enhanced Recurrent Extreme Learning Machine |
| FFNN | Feed Forward Neural Network |
| GCA | Gray Correlation Analysis |
| GWO | Grey Wolf Optimization |
| GRU | Gated Recurrent Unit |
| ISO NECA | Independent System Operator New England Control Area |
| KELM | Kernel Extreme Learning Machine |
| KPCA | Kernel Principal Component Analysis |
| LR | Logistic Regression |
| LSTM | Long Short Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MISO | Midcontinent Independent System Operator |
| MLP | Multi Layer Perceptron |
| MLR | Multi Linear Regression |
| MSE | Mean Square Error |
| NLS-SVM | Nonlinear Least Square Support Vector Machine |
| NN | Neural Network |
| NYISO | New York Independent System Operator |
| OS-ELM7 | Online Sequential Extreme Learning Machine |
| PJM | Pennsylvania–New Jersey–Maryland |
| PSO | Particle Swarm Optimization |
| RBM | Restricted Boltzmann Machine |
| RELM | Recurrent Extreme Learning Machne |
| ReLU | Rectified Linear Unit |
| RES | Renewable Energy Sources |
| RFE | Recursive Feature Elimination |
| RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
| SARIMA | Seasonal Auto Regressive Integrated Moving Average |
| SBELM | Sparse Bayesian Extreme Learning Machine |
| SDA | Stacked De-noising Autoencoders |
| SG | Smart Grid |
| SLFN | Single Layer Feedforward Network |
| SM | Smart Meters |
| TG | Traditional Grid |
| TVC-ABC | Time Varying Coefficients Artificial Bee Colony |
Table 3.
List of symbols.
Table 3.
List of symbols.
| Symbol | Description |
|---|
| x | Actual value |
| x’ | Predicted value |
| t | Time slot |
| y | Output |
| h | Step size |
| m | Mean |
| Actual value |
| Forecasted value |
| T | Total time duration |
| N | Total number of samples |
| Fittest wolf 1 |
| Fittest wolf 2 |
| Fittest wolf 3 |
| Remaining wolves |
Table 4.
Summary of related work.
Table 4.
Summary of related work.
| Technique | Features/DataSet | Region | Contributions | Limitations |
|---|
| Bayesian, MLP [8] | Load/UKDale | UK | Forecasting done using behavioural analytic | Requires intensive training |
| MLR, BaggedT, NN [9] | Load and weather/Beijing | Beijing, China | Comparison between techniques done to overcome the limitations | Not suitable for long term forecasting |
| DRN [10] | Load and weather/ISO-NE | New England | Load forecasting done using weather data | Over fitting |
| RBM, ReLU [11] | Load/Korea Electric Company | Korea | Two stage forecasting performed | Long-term forecasting not supported |
| DWT-IR, SVM, SWA [12] | Load/NYISO, AEMO | Australia, US | Dimensionality reduction and paramater optimization done | Time complexity |
| Modified MI, ANN [13] | Load/PJM | US | Two stage forecasting is done | Time complexity |
| DAE [14] | Load/Hong Kong | Hong Kong | Cooling load prediction done | Time and space consuming |
| Pooling Deep RNN [15] | Load/IRISH | Ireland | Pooling of consumers done for aggregated prediction | Difficult to train |
| ELM [16,17] | Load/USF | US | Long, medium and short term forecasting done | Over fitting |
| SLFN [18,19] | Load/Marine Resources Division | Australia | Optimization of weights | Overfitting by using moore-penrose inverse |
| Sparse Bayesian ELM [20] | Electricity Load/Harvard medical college | USA | Optimization of weights and biases using BP | Require intensive training |
| PSO, DPSO [21] | Load/US | USA | Compact ANNs are produced | Large computational time |
| GWO with NN [22] | | USA | Weights and biases optimization | Time complexity |
| RELM [6,23] | Electricity Load/Bench mark UCI machine | Portugal | Use of context neurons | Computationally expensive |
| LSTM, DNN, GRU [24] | Load and price/EPEX | Belgium | Comparison between different models | Over fitting |
| Hilbertian, ARMAX [25] | Price/EPEX | Spain, Germany | Optimization of functional parameters for price forecasting | Non linearity |
| CNN, LSTM [26] | Price/PJM | US | Two NNs are used for price forecasting | Computationally expensive |
| DNN [27] | Price/EPEX | Belgium | Complex patterns are extracted for prediction | Space complexity |
| GCA, KPCA, DE-SVM [28] | Price/ISO NE-CA | New England | Dimensionality reduction is removed using hybrid of KPCA and GCA | Over fitting |
| SDA [29] | Price/MISO | Arkansas, Texas and Indiana | Variant of autoencoder used | Computationally expensive |
| ARIMA, TVC-ABC, NLS-SVM [30] | Price/PJM, NYISO, AEMO | Australia, US | Parameter tuning of SVM done using TV-ABC | Computationally expensive |
| ANN with meta heuristics optimization methods [31] | Load and price/Commercial load of building in China, Taiwan regional electricity load | Taiwan | Various paramater calculations done for accuracy | Accuracy of models depend on nature of dataset |
| OS-ELM with kernel [32] | Load and price/Sylva bench mark | US | Comparison of different algorithms done | Restrict to the computation of streamed data |
| ELM in multi class scenario [33] | Load and price/University of California Irvine | Canada | Robust classification | Computational cost overhead |
| Enhanced Logistic Regression | Load and Price/UMass Electric Dataset | USA | ELR beats conventional techniques | Large computational time |
| RELM enhanced using GWO | Load and Price/UCI Dataset | USA | Optimized weights and biases leads to better prediction | Large computational time is required for weight optimization |
Table 5.
Features in UMass Electric Dataset.
Table 5.
Features in UMass Electric Dataset.
| Original Features |
|---|
| Air Conditioner (AC), Furnace, Cellar lights, Washer, First floor lights, Utility room + Basement, Garage outlets, Master bed + Kids bed, Dryer, Panels, Home office, Dining room, Microwave, Fridge |
Table 6.
Results of CART for UMass Electric Dataset.
Table 6.
Results of CART for UMass Electric Dataset.
| Features | Load Values | Price Values |
|---|
| AC | 0.6653 | 0.6633 |
| Furnace | 0.0103 | 0.0101 |
| Cellar lights | 0.0018 | 0.0011 |
| Washer | 0.0029 | 0.0029 |
| First floor | 0.0032 | 0.0026 |
| Utility + Basement | 0.0615 | 0.0670 |
| Garage | 0.0036 | 0.0070 |
| M. bed + K. bed | 0.0080 | 0.0059 |
| Dryer | 0.1890 | 0.1927 |
| Panels | 0.0033 | 0.0030 |
| Home office | 0.0826 | 0.0083 |
| Dining room | 0.0079 | 0.0084 |
| Microwave | 0.0296 | 0.0262 |
Table 7.
RFE features for a UMass Electric Dataset.
Table 7.
RFE features for a UMass Electric Dataset.
| Type | Number of Features |
|---|
| Original | 16 |
| Selected | 8 |
| Rejected | 8 |
Table 8.
Relief-F features for UMass Electric Dataset.
Table 8.
Relief-F features for UMass Electric Dataset.
| Parameters | Values |
|---|
| Threshold | 10 |
| Selected features | 5 |
| Nearest Neighbors | 3 |
Table 9.
Obtained RMSE using ELM, RELM and ERELM.
Table 9.
Obtained RMSE using ELM, RELM and ERELM.
| Transfer Function | Forecasting Approach | Training | Testing |
|---|
| | ELM | 0.0532 | 0.0535 |
| Hard Limit | RELM | 0.0412 | 0.0423 |
| | ERELM | 0.0332 | 0.0345 |
| | ELM | 0.0513 | 0.0525 |
| Sin | RELM | 0.0352 | 0.362 |
| | ERELM | 0.0321 | 0.0523 |
| | ELM | 0.0634 | 0.0673 |
| Tanh | RELM | 0.0453 | 0.0463 |
| | ERELM | 0.0341 | 0.0321 |
| | ELM | 0.0423 | 0.473 |
| Sigmoid | RELM | 0.0341 | 0.0381 |
| | ERELM | 0.0214 | 0.0235 |
Table 10.
Obtained RMSE for half-yearly testing data using ELM, RELM and ERELM by Monte Carlo and K-Fold cross validation.
Table 10.
Obtained RMSE for half-yearly testing data using ELM, RELM and ERELM by Monte Carlo and K-Fold cross validation.
| Datasets | ERELM | RELM | ELM | RNN | LR |
|---|
| Monte Carlo | K-Fold | Monte Carlo | K-Fold | Monte Carlo | K-Fold | Monte Carlo | K-Fold | Monte Carlo | K-Fold |
|---|
| MT166 | 0.0235 | 0.0265 | 0.0734 | 0.0788 | 0.0824 | 0.0883 | 0.08234 | 0.0852 | 0.0853 | 0.0873 |
| MT168 | 0.0134 | 0.0162 | 0.0421 | 0.0462 | 0.0524 | 0.0423 | 0.0854 | 0.0862 | 0.0756 | 0.0763 |
| MT169 | 0.0153 | 0.02352 | 0.0531 | 0.0353 | 0.0382 | 0.0463 | 0.0853 | 0.0873 | 0.0735 | 0.0762 |
| MT171 | 0.0354 | 0.0423 | 0.0524 | 0.0552 | 0.0634 | 0.0643 | 0.0854 | 0.0852 | 0.072 | 0.0712 |
| MT182 | 0.0242 | 0.0353 | 0.0252 | 0.0352 | 0.0835 | 0.0952 | 0.0753 | 0.0776 | 0.0934 | 0.0952 |
| MT235 | 0.0153 | 0.0142 | 0.0344 | 0.0397 | 0.0634 | 0.0643 | 0.0865 | 0.934 | 0.981 | 0.0991 |
| MT237 | 0.0243 | 0.0297 | 0.0534 | 0.0535 | 0.0752 | 0.0795 | 0.0756 | 0.0762 | 0.0795 | 0.08255 |
| MT249 | 0.0143 | 0.0163 | 0.0524 | 0.0532 | 0.0624 | 0.0693 | 0.0862 | 0.0891 | 0.0753 | 0.0778 |
| MT250 | 0.0342 | 0.0452 | 0.0535 | 0.0562 | 0.0853 | 0.0873 | 0.0764 | 0.0784 | 0.0874 | 0.0894 |
| MT257 | 0.0242 | 0.0215 | 0.0413 | 0.0413 | 0.0642 | 0.0683 | 0.0753 | 0.0794 | 0.0893 | 0.0934 |
| UMass Electric | 0.0398 | 0.0315 | 0.0534 | 0.0563 | 0.0681 | 0.0685 | 0.0712 | 0.0891 | 0.0888 | 0.0913 |
Table 11.
Obtained RMSE for yearly testing data using ELM, RELM and ERELM by Monte Carlo and K-Fold cross validation.
Table 11.
Obtained RMSE for yearly testing data using ELM, RELM and ERELM by Monte Carlo and K-Fold cross validation.
| Datasets | ERELM | RELM | ELM | RNN | LR |
|---|
| Monte Carlo | K-Fold | Monte Carlo | K-Fold | Monte Carlo | K-Fold | Monte Carlo | K-Fold | Monte Carlo | K-Fold |
|---|
| MT166 | 0.0224 | 0.0242 | 0.0651 | 0.0665 | 0.0756 | 0.0801 | 0.08732 | 0.0792 | 0.0862 | 0.0851 |
| MT168 | 0.0124 | 0.0151 | 0.0634 | 0.0732 | 0.0521 | 0.0410 | 0.0831 | 0.0731 | 0.0701 | 0.0678 |
| MT169 | 0.0144 | 0.0224 | 0.0501 | 0.0553 | 0.0424 | 0.0431 | 0.0812 | 0.0912 | 0.0741 | 0.0872 |
| MT171 | 0.0142 | 0.0401 | 0.0421 | 0.0538 | 0.0512 | 0.0682 | 0.0781 | 0.0792 | 0.0712 | 0.0882 |
| MT182 | 0.0182 | 0.0200 | 0.0242 | 0.0250 | 0.0743 | 0.0791 | 0.0824 | 0.0701 | 0.0892 | 0.0822 |
| MT235 | 0.0142 | 0.0152 | 0.0301 | 0.0362 | 0.0582 | 0.0602 | 0.0852 | 0.0892 | 0.0889 | 0.0986 |
| MT237 | 0.0224 | 0.0267 | 0.0513 | 0.0521 | 0.0623 | 0.0632 | 0.0701 | 0.0789 | 0.0862 | 0.0813 |
| MT249 | 0.0132 | 0.0157 | 0.0421 | 0.0613 | 0.0523 | 0.0623 | 0.0782 | 0.0802 | 0.0671 | 0.0742 |
| MT250 | 0.0242 | 0.0273 | 0.0412 | 0.0501 | 0.0602 | 0.0692 | 0.0682 | 0.0772 | 0.0785 | 0.0864 |
| MT257 | 0.0324 | 0.0472 | 0.0401 | 0.0513 | 0.0602 | 0.0744 | 0.0623 | 0.0702 | 0.0876 | 0.0882 |
| UMass Electric | 0.0332 | 0.0412 | 0.0542 | 0.0552 | 0.0582 | 0.0603 | 0.0701 | 0.0771 | 0.0821 | 0.0891 |
Table 12.
Computational time comparison of ERELM, RELM and ELM execution.
Table 12.
Computational time comparison of ERELM, RELM and ELM execution.
| Forecasting Technique | Training Time (s) | Testing Time (s) |
|---|
| ERELM | 0.653 | 0.0346 |
| RELM | 0.0043 | 0.0012 |
| ELM | 0.00124 | 0.001076 |
Table 13.
Load performance metrics comparison for one day using the UMass Electric Dataset.
Table 13.
Load performance metrics comparison for one day using the UMass Electric Dataset.
| Metrics | Half-Yearly Data | Yearly Data |
|---|
| CNN | LR | ELR | CNN | LR | ELR |
|---|
| MSE (abs. val) | 8.84 | 5.84 | 4.77 | 10.2 | 8.97 | 6.8 |
| MAE (abs. val) | 9.24 | 5.25 | 4.34 | 8.75 | 6.25 | 4.24 |
| RMSE (abs. val) | 10.62 | 7.64 | 6.18 | 10.4 | 6.6 | 5.2 |
| MAPE (%) | 25.44 | 22.45 | 18.48 | 36.3 | 33.3 | 30.5 |
| Accuracy (%) | 89.38 | 92.35 | 93.82 | 89.6 | 93.4 | 94.8 |
Table 14.
Load performance metrics comparison for one week using the UMass Electric Dataset.
Table 14.
Load performance metrics comparison for one week using the UMass Electric Dataset.
| Metrics | Half-Yearly Data | Yearly Data |
|---|
| CNN | LR | ELR | CNN | LR | ELR |
|---|
| MSE (abs. val) | 20.2 | 17.97 | 12.97 | 18.9 | 16.5 | 11.3 |
| MAE (abs. val) | 8.82 | 6.87 | 5.28 | 8.75 | 6.25 | 5.19 |
| RMSE (abs. val) | 16.25 | 13.12 | 10.18 | 15.76 | 12.98 | 9.64 |
| MAPE (%) | 25.65 | 22.19 | 17.41 | 33.2 | 25.9 | 22.8 |
| Accuracy (%) | 83.75 | 86.88 | 89.81 | 84.24 | 87.02 | 91.36 |
Table 15.
Load performance metrics comparison for one month using the UMass Electric Dataset.
Table 15.
Load performance metrics comparison for one month using the UMass Electric Dataset.
| Metrics | Half-Yearly Data | Yearly Data |
|---|
| CNN | LR | ELR | CNN | LR | ELR |
|---|
| MSE (abs. val) | 25.82 | 21.82 | 17.37 | 24.02 | 20.56 | 14.25 |
| MAE (abs. val) | 10.55 | 8.23 | 6.79 | 10.35 | 8.15 | 5.33 |
| RMSE (abs. val) | 17.85 | 14.77 | 11.79 | 12.55 | 9.98 | 6.52 |
| MAPE (%) | 29.13 | 27.13 | 23.39 | 25.45 | 21.2 | 20.6 |
| Accuracy (%) | 82.15 | 85.72 | 88.21 | 87.45 | 90.02 | 93.48 |
Table 16.
Price performance metrics comparison for one day using the UMass Electric Dataset.
Table 16.
Price performance metrics comparison for one day using the UMass Electric Dataset.
| Metrics | Half-Yearly Data | Yearly Data |
|---|
| CNN | LR | ELR | CNN | LR | ELR |
|---|
| MSE (abs. val) | 15.08 | 14.39 | 10.09 | 12.58 | 10.85 | 8.6 |
| MAE (abs. val) | 8.25 | 7.65 | 6.01 | 7.85 | 7.05 | 5.88 |
| RMSE (abs. val) | 16.63 | 14.99 | 12.98 | 15.05 | 11.52 | 9.85 |
| MAPE (%) | 19.02 | 18.59 | 17.11 | 20.05 | 18.85 | 15.55 |
| Accuracy (%) | 83.37 | 85.01 | 87.02 | 84.95 | 88.48 | 90.15 |
Table 17.
Price performance metrics comparison for one week using the UMass Electric Dataset.
Table 17.
Price performance metrics comparison for one week using the UMass Electric Dataset.
| Metrics | Half-Yearly Data | Yearly Data |
|---|
| CNN | LR | ELR | CNN | LR | ELR |
|---|
| MSE (abs. val) | 14.05 | 12.80 | 11.22 | 15.02 | 13.45 | 11.25 |
| MAE (abs. val) | 7.55 | 6.04 | 5.03 | 8.02 | 7.05 | 5.25 |
| RMSE (abs. val) | 13.05 | 11.30 | 9.47 | 12.55 | 10.45 | 8.64 |
| MAPE (%) | 14.25 | 13.71 | 13.03 | 16.45 | 15.75 | 15.25 |
| Accuracy (%) | 86.95 | 88.70 | 90.53 | 87.45 | 89.55 | 91.36 |
Table 18.
Price performance metrics comparison for one month using the UMass Electric Dataset.
Table 18.
Price performance metrics comparison for one month using the UMass Electric Dataset.
| Metrics | Half-Yearly Data | Yearly Data |
|---|
| CNN | LR | ELR | CNN | LR | ELR |
|---|
| MSE (abs. val) | 19.45 | 18.91 | 16.47 | 20.05 | 18.54 | 13.35 |
| MAE (abs. val) | 8.95 | 7.70 | 6.44 | 9.35 | 8.15 | 6.42 |
| RMSE (abs. val) | 14.78 | 13.75 | 11.48 | 12.44 | 11.02 | 9.45 |
| MAPE (%) | 21.44 | 20.54 | 18.89 | 23.36 | 22.55 | 19.45 |
| Accuracy (%) | 85.22 | 86.25 | 88.52 | 87.56 | 88.98 | 90.55 |
Table 19.
Load performance metrics comparison for one day using the UCI Dataset.
Table 19.
Load performance metrics comparison for one day using the UCI Dataset.
| Metrics | Half-Yearly Data | Yearly Data |
|---|
| CNN | LR | ELR | CNN | LR | ELR |
|---|
| MSE (abs. val) | 15.05 | 12.47 | 10.56 | 18.20 | 14.3 | 10.4 |
| MAE (abs. val) | 12.45 | 10.34 | 8.56 | 21.47 | 18.37 | 16.61 |
| RMSE (abs. val) | 18.52 | 15.54 | 13.45 | 16.22 | 13.78 | 10.16 |
| MAPE (%) | 28.24 | 25.34 | 20.45 | 27.05 | 23.25 | 20.05 |
| Accuracy (%) | 81.48 | 84.46 | 86.55 | 83.78 | 86.22 | 89.84 |
Table 20.
Load performance metrics comparison for one week using the UCI Dataset.
Table 20.
Load performance metrics comparison for one week using the UCI Dataset.
| Metrics | Half-Yearly Data | Yearly Data |
|---|
| CNN | LR | ELR | CNN | LR | ELR |
|---|
| MSE (abs. val) | 25.20 | 19.66 | 15.77 | 13.25 | 8.34 | 7.2 |
| MAE (abs. val) | 11.35 | 10.01 | 8.24 | 13.98 | 12.47 | 11.39 |
| RMSE (abs. val) | 22.45 | 19.25 | 16.45 | 20.25 | 17.80 | 13.11 |
| MAPE (%) | 28.56 | 25.45 | 19.63 | 30.50 | 25.45 | 18.52 |
| Accuracy (%) | 77.55 | 80.75 | 83.55 | 79.75 | 82.20 | 86.89 |
Table 21.
Load performance metrics comparison for one month using the UCI Dataset.
Table 21.
Load performance metrics comparison for one month using the UCI Dataset.
| Metrics | Half-Yearly Data | Yearly Data |
|---|
| CNN | LR | ELR | CNN | LR | ELR |
|---|
| MSE (abs. val) | 28.35 | 25.55 | 21.68 | 15.50 | 13.8 | 5.47 |
| MAE (abs. val) | 15.35 | 10.34 | 8.95 | 23.46 | 19.3 | 17.7 |
| RMSE (abs. val) | 23.97 | 20.87 | 17.69 | 20.02 | 17.17 | 14.49 |
| MAPE (%) | 31.23 | 29.43 | 25.67 | 27.45 | 25.35 | 20.02 |
| Accuracy (%) | 76.03 | 79.13 | 82.31 | 79.98 | 82.23 | 85.51 |
Table 22.
Accuracy of ERELM using RMSE, MSE and MAE for half-yearly data.
Table 22.
Accuracy of ERELM using RMSE, MSE and MAE for half-yearly data.
| Datasets | RMSE | MSE | MAE |
|---|
| MT166 | 0.0235 | 0.00055 | 0.0243 |
| MT168 | 0.0134 | 0.00017 | 0.0135 |
| MT169 | 0.0153 | 0.00023 | 0.0174 |
| MT171 | 0.0354 | 0.00125 | 0.0352 |
| MT182 | 0.0242 | 0.00058 | 0.0252 |
| MT235 | 0.0153 | 0.00023 | 0.0253 |
| MT237 | 0.0243 | 0.00059 | 0.0254 |
| MT249 | 0.0143 | 0.00020 | 0.0153 |
| MT250 | 0.0342 | 0.001169 | 0.0342 |
| MT257 | 0.0242 | 0.00058 | 0.0253 |
| UMass Electric | 0.0256 | 0.00071 | 0.0623 |
| Arithmetic Mean | 0.0227 | 0.00055 | 0.024218 |
| Standard Deviation | 0.00600 | 0.000350 | 0.006515 |
Table 23.
Accuracy of ERELM using RMSE, MSE and MAE for yearly data.
Table 23.
Accuracy of ERELM using RMSE, MSE and MAE for yearly data.
| Datasets | RMSE | MSE | MAE |
|---|
| MT166 | 0.0224 | 0.00041 | 0.0215 |
| MT168 | 0.0124 | 0.00016 | 0.0142 |
| MT169 | 0.0144 | 0.00015 | 0.0162 |
| MT171 | 0.0142 | 0.00124 | 0.0221 |
| MT182 | 0.0200 | 0.00042 | 0.0224 |
| MT235 | 0.0142 | 0.00047 | 0.0201 |
| MT237 | 0.0224 | 0.00015 | 0.0241 |
| MT249 | 0.0132 | 0.00012 | 0.0142 |
| MT250 | 0.0242 | 0.00102 | 0.0163 |
| MT257 | 0.0324 | 0.00045 | 0.0177 |
| UMass Electric | 0.0332 | 0.00061 | 0.0546 |
| Arithmetic Mean | 0.02027 | 0.00047 | 0.02212 |
| Standard Deviation | 0.00712 | 0.00034 | 0.01077 |