Cost-Optimal Heat Exchanger Network Synthesis Based on a Flexible Cost Functions Framework
Abstract
:1. Introduction
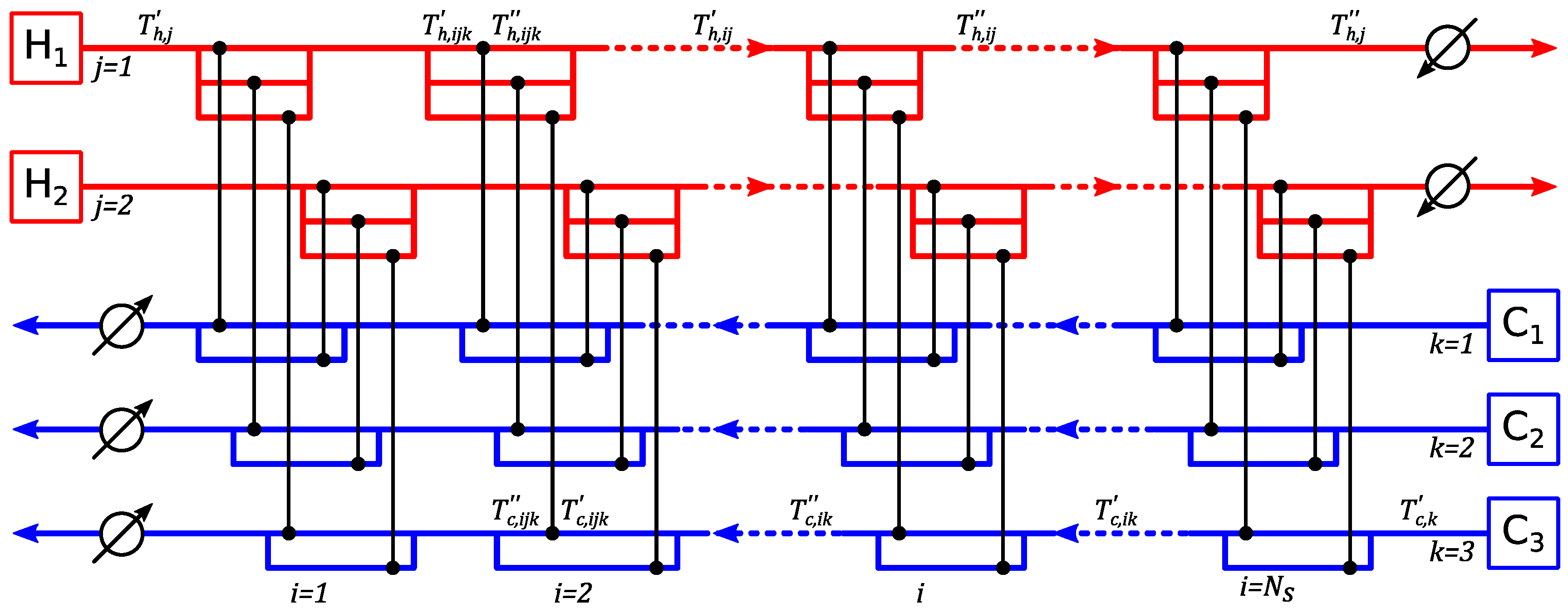
2. Methodology
2.1. Fundamentals
2.2. Objective Function
2.3. Genetic Algorithm
2.4. Local Optimization
3. Examples and Results
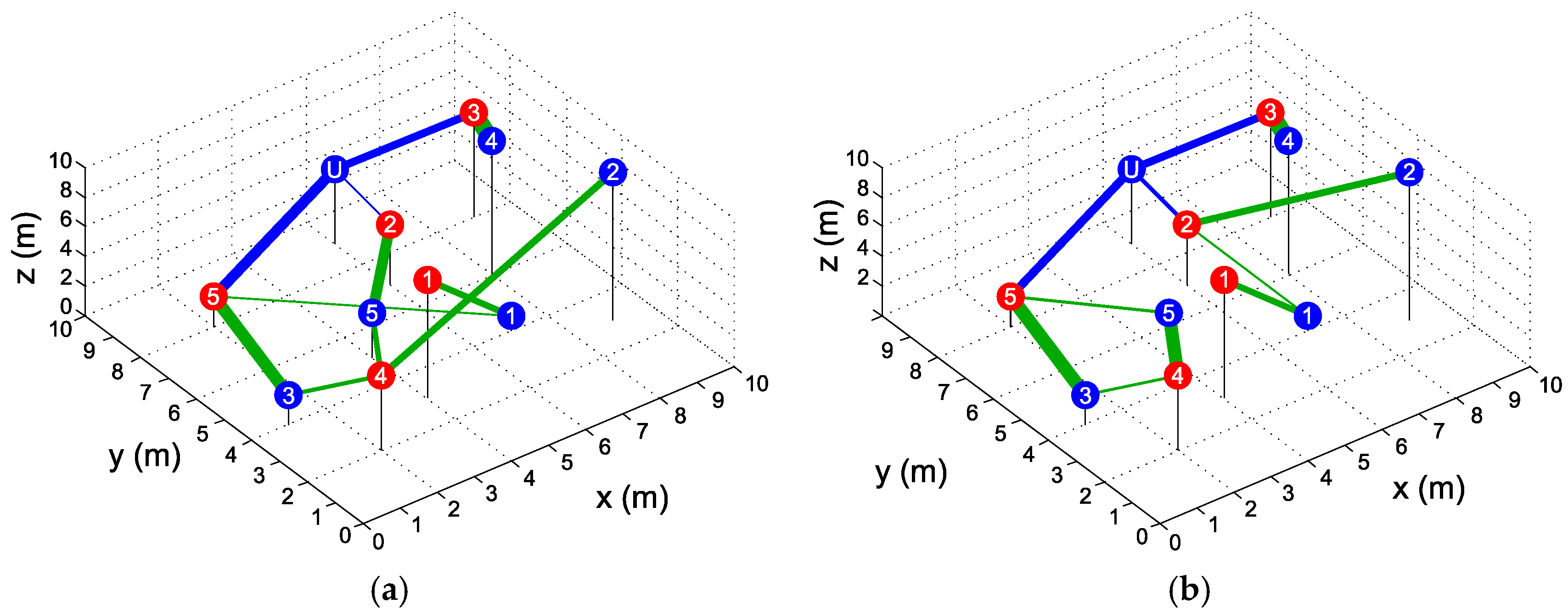
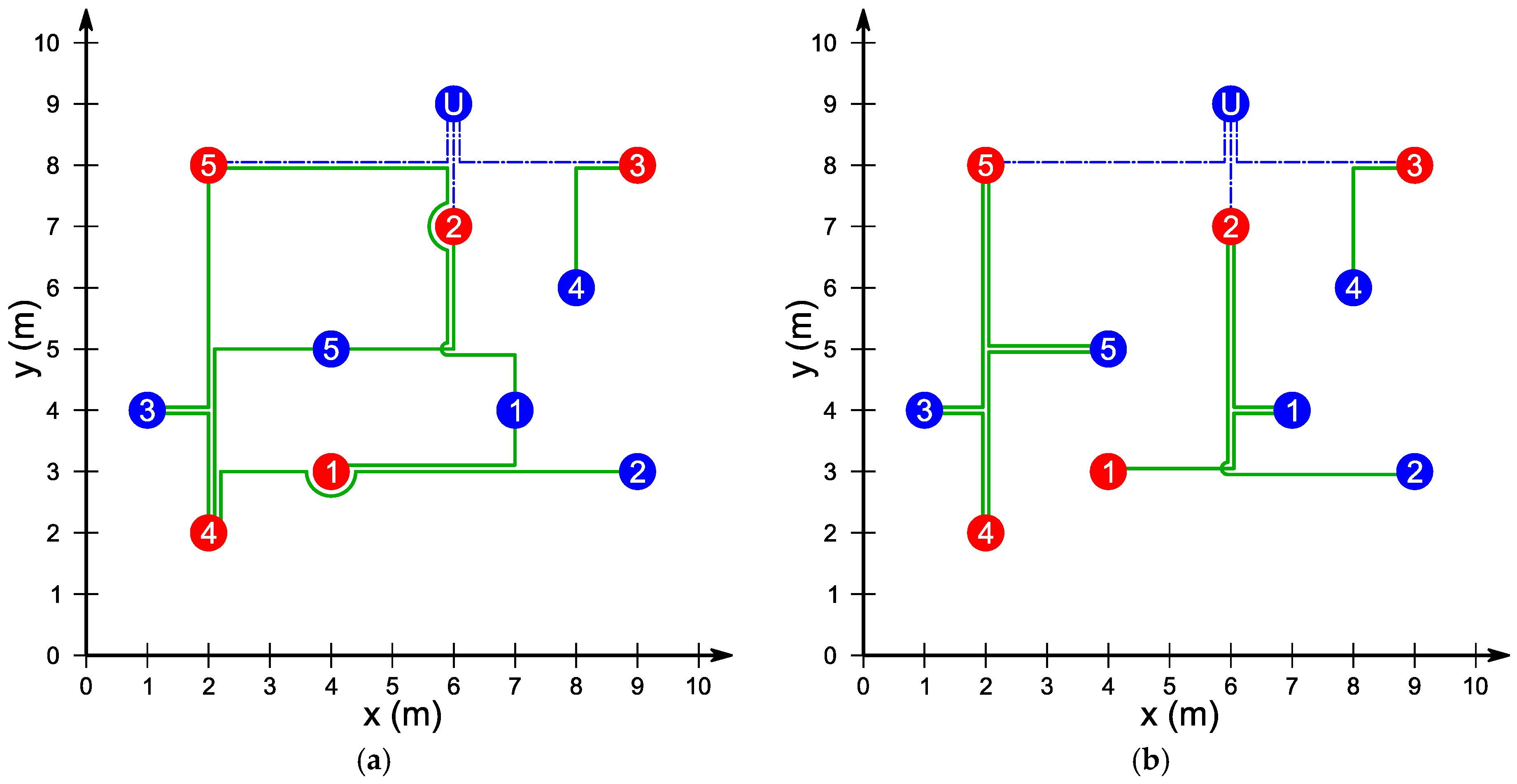
3.1. Example 1
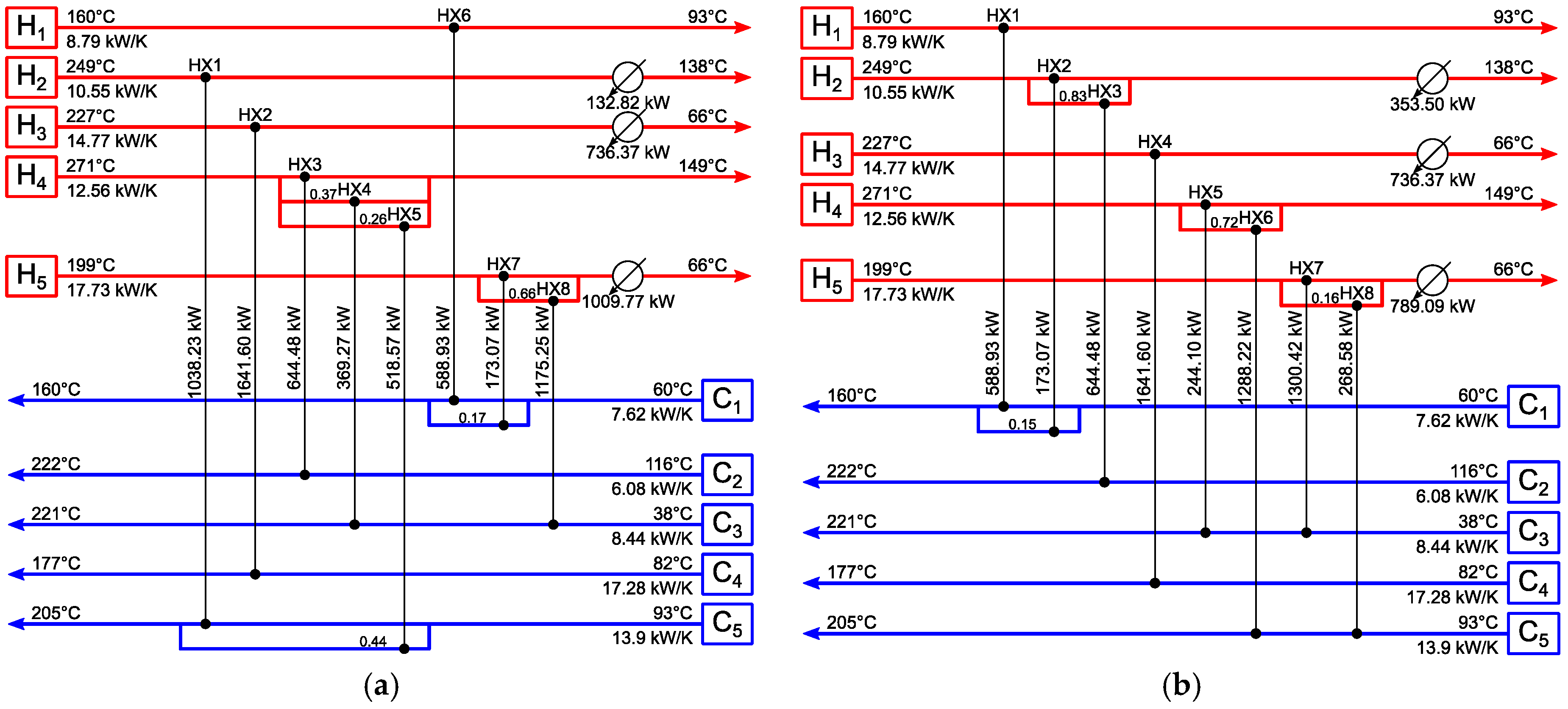
3.1.1. Example 1a
3.1.2. Example 1b
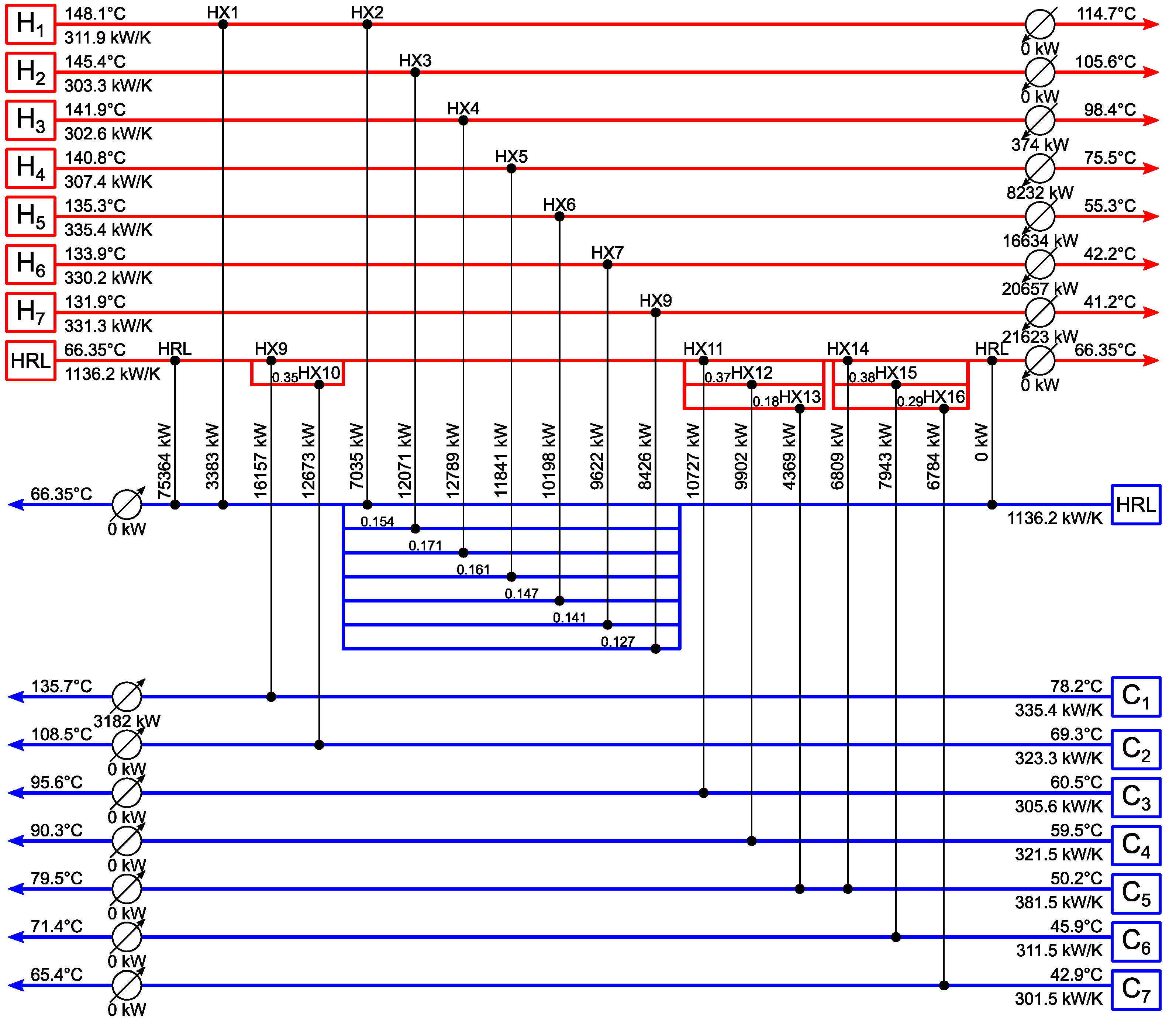
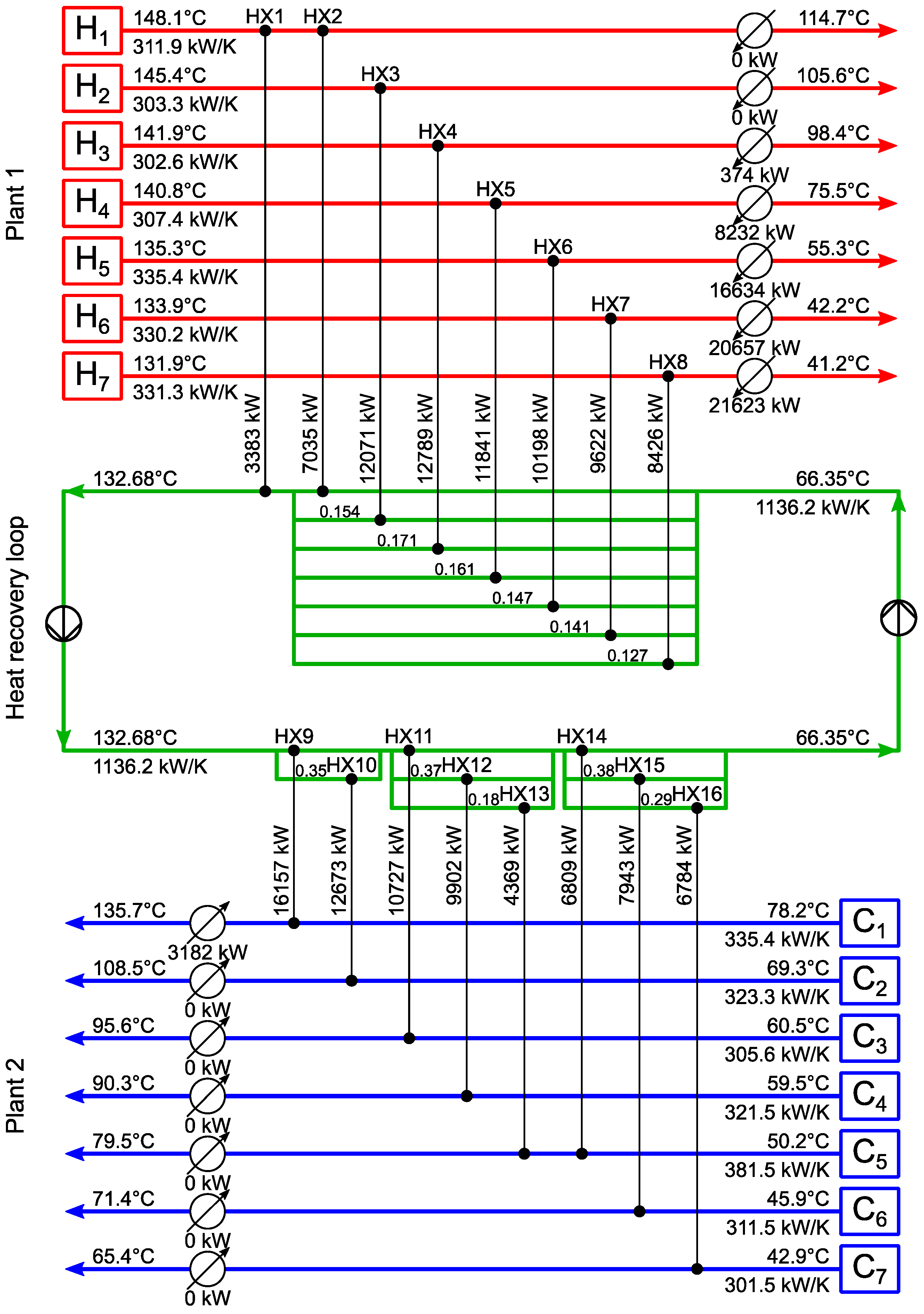
3.2. Example 2
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| HEN | Heat exchanger network | |
| HRL | Heat recovery loop | |
| MER | Maximum energy recovery | |
| MINLP | Mixed integer nonlinear programming | |
| TAC | Total annual costs | |
| Pressure drop (Pa) | ||
| Logarithmic mean temperature difference (LMTD) (K) | ||
| Pump efficiency | ||
| Dynamic viscosity (Pa s) | ||
| Density (kg m−3) | ||
| Heat transfer area of heat exchanger (m2) | ||
| Annualization factor (yr−1) | ||
| Cold utility cost per unit duty ($ kW−1 yr−1) | ||
| Electricity costs ($ kW−1 h−1) | ||
| Hot utility cost per unit duty ($ kW−1 yr−1) | ||
| Heat exchanger capital costs ($) | ||
| Specific heat capacity flow rate (kJ kg−1 K−1) | ||
| Capital costs for piping ($) | ||
| Capital costs for pumps ($) | ||
| Pump operating costs ($ yr−1) | ||
| Total annual costs ($ yr−1) | ||
| Inner diameter (m) | ||
| Outer diameter (m) | ||
| Fanning friction factor | ||
| Relative fitness value | ||
| Heat transfer coefficient (kW m−2 K−1) | ||
| mass flow rate (kg s−1) | ||
| Number of cold process streams | ||
| Number of hot process streams | ||
| Number of stages of a stage-wise superstructure | ||
| Number of transfer units | ||
| Pipe capital costs ($ m−1) | ||
| Heat load (kW) | ||
| Ratio of stream heat capacity flow rates | ||
| Reynolds number | ||
| t | Plant operation duration (h yr−1) | |
| Stream temperature (°C) | ||
| Upper bounds of target temperature (°C) | ||
| Lower bounds of target temperature (°C) | ||
| Velocity (m s−1) | ||
| Overall heat transfer coefficient (kW m−2 K−1) | ||
| Volumetric flow rate (m3 s−1) | ||
| Heat capacity flow rate (kW K−1) | ||
| Specific pipe weight (kg/m) | ||
| Match-based costs ($ yr−1) | ||
| Binary variable | ||
| Cold stream | ||
| Cold utility | ||
| Hot stream | ||
| Hot utility | ||
| Stage index | ||
| Index of heat exchanger in superstructure | ||
| Hot stream index | ||
| Cold stream index | ||
| Maximum | ||
| Minimum | ||
| Inlet temperature | ||
| Outlet temperature |
Appendix A
References
- Rathjens, M.; Fieg, G. Design of cost-optimal heat exchanger networks considering individual, match-dependent cost functions. Chem. Eng. Tran. 2018, 70, 601–606. [Google Scholar] [CrossRef]
- Linnhoff, B.; Hindmarsh, E. The pinch design method for heat exchanger networks. Chem. Eng. Sci. 1983, 38, 745–763. [Google Scholar] [CrossRef]
- Papoulias, S.A.; Grossmann, I.E. A structural optimization approach in process synthesis—II. Heat recovery networks. Comput. Chem. Eng. 1983, 7, 707–721. [Google Scholar] [CrossRef]
- Klemeš, J.J.; Kravanja, Z. Forty years of Heat Integration: Pinch Analysis (PA) and Mathematical Programming (MP). Curr. Opin. Chem. Eng. 2013, 2, 461–474. [Google Scholar] [CrossRef]
- Dhole, V.R.; Linnhoff, B. Total site targets for fuel, co-generation, emissions, and cooling. Comput. Chem. Eng. 1993, 17, S101–S109. [Google Scholar] [CrossRef]
- Chew, K.H.; Klemeš, J.J.; Wan Alwi, S.R.; Abdul Manan, Z. Industrial implementation issues of Total Site Heat Integration. Appl. Therm. Eng. 2013, 61, 17–25. [Google Scholar] [CrossRef]
- Liu, X.; Klemeš, J.J.; Varbanov, P.S.; Qian, Y.; Yang, S.; Liu, X.; Varbanov, P.S.; Klemes, J.J.; Wan Alwi, S.R.; Yong, J.Y. Safety issues consideration for direct and indirect heat transfer on total sites. Chem. Eng. Trans. 2015, 45, 151–156. [Google Scholar] [CrossRef]
- Nemet, A.; Klemeš, J.J.; Moon, I.; Kravanja, Z. Safety Analysis Embedded in Heat Exchanger Network Synthesis. Comput. Chem. Eng. 2017, 107, 357–380. [Google Scholar] [CrossRef]
- Nemet, A.; Klemeš, J.J.; Kravanja, Z. Process synthesis with simultaneous consideration of inherent safety-inherent risk footprint. Front. Chem. Sci. Eng. 2018, 12, 745–762. [Google Scholar] [CrossRef]
- Escobar, M.; Trierweiler, J.O.; Grossmann, I.E. Simultaneous synthesis of heat exchanger networks with operability considerations: Flexibility and controllability. Comput. Chem. Eng. 2013, 55, 158–180. [Google Scholar] [CrossRef]
- Rathjens, M.; Bohnenstädt, T.; Fieg, G.; Engel, O. Synthesis of heat exchanger networks taking into account cost and dynamic considerations. Procedia Eng. 2016, 157, 341–348. [Google Scholar] [CrossRef]
- Pavão, L.V.; Miranda, C.B.; Costa, C.B.B.; Ravagnani, M.A.S.S. Efficient multiperiod heat exchanger network synthesis using a meta-heuristic approach. Energy 2018, 142, 356–372. [Google Scholar] [CrossRef]
- Chang, C.; Chen, X.; Wang, Y.; Feng, X. An efficient optimization algorithm for waste Heat Integration using a heat recovery loop between two plants. Appl. Therm. Eng. 2016, 105, 799–806. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Feng, X. Heat integration across plants considering distance factor. Chem. Eng. Trans. 2013, 35, 25–30. [Google Scholar] [CrossRef]
- Wang, Y.; Chang, C.; Feng, X. A systematic framework for multi-plants Heat Integration combining Direct and Indirect Heat Integration methods. Energy 2015, 90, 56–67. [Google Scholar] [CrossRef]
- Chang, C.; Chen, X.; Wang, Y.; Feng, X. Simultaneous optimization of multi-plant heat integration using intermediate fluid circles. Energy 2017, 121, 306–317. [Google Scholar] [CrossRef]
- Liew, P.Y.; Wan Alwi, S.R.; Klemeš, J.J. Total Site Heat Integration Targeting Algorithm Incorporating Plant Layout Issues. In 24th European Symposium on Computer Aided Process Engineering; Klemes, J., Varbanov, P.S., Liew, P.Y., Eds.; Elsevier Science: Burlington, NJ, USA, 2014; pp. 1801–1806. [Google Scholar]
- Pouransari, N.; Maréchal, F. Heat exchanger network design of large-scale industrial site with layout inspired constraints. Comput. Chem. Eng. 2014, 71, 426–445. [Google Scholar] [CrossRef]
- Souza, R.D.; Khanam, S.; Mohanty, B. Synthesis of heat exchanger network considering pressure drop and layout of equipment exchanging heat. Energy 2016, 101, 484–495. [Google Scholar] [CrossRef]
- Luo, X.; Wen, Q.-Y.; Fieg, G. A hybrid genetic algorithm for synthesis of heat exchanger networks. Comput. Chem. Eng. 2009, 33, 1169–1181. [Google Scholar] [CrossRef]
- Yee, T.F.; Grossmann, I.E.; Kravanja, Z. Simultaneous optimization models for heat integration—I. Area and energy targeting and modeling of multi-stream exchangers. Comput. Chem. Eng. 1990, 14, 1151–1164. [Google Scholar] [CrossRef]
- Fieg, G.; Luo, X.; Jeżowski, J. A monogenetic algorithm for optimal design of large-scale heat exchanger networks. Chem. Eng. Process. Process Intensif. 2009, 48, 1506–1516. [Google Scholar] [CrossRef]
- Brandt, C. Entwicklung und Implementierung Eines Hybriden Genetischen Algorithmus für die Automatisierte Auslegung von Kostenoptimalen Wärmeübertragernetzwerken; Shaker: Herzogenrath, Germany, 2018. [Google Scholar]
- Lewin, D.R.; Wang, H.; Shalev, O. A generalized method for HEN synthesis using stochastic optimization—I. General framework and MER optimal synthesis. Comput. Chem. Eng. 1998, 22, 1503–1513. [Google Scholar] [CrossRef]
- Stegner, C.; Brandt, C.; Fieg, G. EVHE—A new method for the synthesis of HEN. Comput. Chem. Eng. 2014, 64, 95–102. [Google Scholar] [CrossRef]
- Brandt, C.; Fieg, G.; Luo, X. Efficient synthesis of heat exchanger networks combining heuristic approaches with a genetic algorithm. Heat Mass Transf. 2011, 47, 1019–1026. [Google Scholar] [CrossRef]
- Pho, T.K.; Lapidus, L. Topics in computer-aided design: Part II. Synthesis of optimal heat exchanger networks by tree searching algorithms. Aiche J. 1973, 19, 1182–1189. [Google Scholar] [CrossRef]
- Nishida, N.; Liu, Y.A.; Lapidus, L. Studies in chemical process design and synthesis: III. A Simple and practical approach to the optimal synthesis of heat exchanger networks. Aiche J. 1977, 23, 77–93. [Google Scholar] [CrossRef]
- Linnhoff, B.; Flower, J.R. Synthesis of heat exchanger networks: II. Evolutionary generation of networks with various criteria of optimality. Aiche J. 1978, 24, 642–654. [Google Scholar] [CrossRef]
- Lewin, D.R. A generalized method for HEN synthesis using stochastic optimization—II. The synthesis of cost-optimal networks. Comput. Chem. Eng. 1998, 22, 1387–1405. [Google Scholar] [CrossRef]
- Lin, B.; Miller, D.C. Solving heat exchanger network synthesis problems with Tabu Search. Comput. Chem. Eng. 2004, 28, 1451–1464. [Google Scholar] [CrossRef]
- Pariyani, A.; Gupta, A.; Ghosh, P. Design of heat exchanger networks using randomized algorithm. Comput. Chem. Eng. 2006, 30, 1046–1053. [Google Scholar] [CrossRef]
- Chakraborty, S.; Ghosh, P. Heat exchanger network synthesis: The possibility of randomization. Chem. Eng. J. 1999, 72, 209–216. [Google Scholar] [CrossRef]
- Yerramsetty, K.M.; Murty, C.V.S. Synthesis of cost-optimal heat exchanger networks using differential evolution. Comput. Chem. Eng. 2008, 32, 1861–1876. [Google Scholar] [CrossRef]
- Peng, F.; Cui, G. Efficient simultaneous synthesis for heat exchanger network with simulated annealing algorithm. Appl. Therm. Eng. 2015, 78, 136–149. [Google Scholar] [CrossRef]
- Aguitoni, M.C.; Pavão, L.V.; Siqueira, P.H.; Jiménez, L.; Ravagnani, M.A.S.S. Synthesis of a cost-optimal heat exchanger network using genetic algorithm and differential evolution. Chem. Eng. Trans. 2018, 70, 979–984. [Google Scholar] [CrossRef]
- Peters, M.S.; Timmerhaus, K.D.; West, R.E. Plant Design and Economics for Chemical Engineers, 5th ed.; McGraw-Hill: Boston, MA, USA, 2003. [Google Scholar]
- Hipólito-Valencia, B.J.; Rubio-Castro, E.; Ponce-Ortega, J.M.; Serna-González, M.; Nápoles-Rivera, F.; El-Halwagi, M.M. Optimal design of inter-plant waste energy integration. App. Therm. Eng. 2014, 62, 633–652. [Google Scholar] [CrossRef]
- Stijepovic, M.Z.; Linke, P. Optimal waste heat recovery and reuse in industrial zones. Energy 2011. [Google Scholar] [CrossRef]
- Jabbari, B.; Tahouni, N.; Ataei, A.; Panjeshahi, M.H. Design and optimization of CCHP system incorporated into kraft process, using Pinch Analysis with pressure drop consideration. App. Therm. Eng. 2013, 61, 88–97. [Google Scholar] [CrossRef]
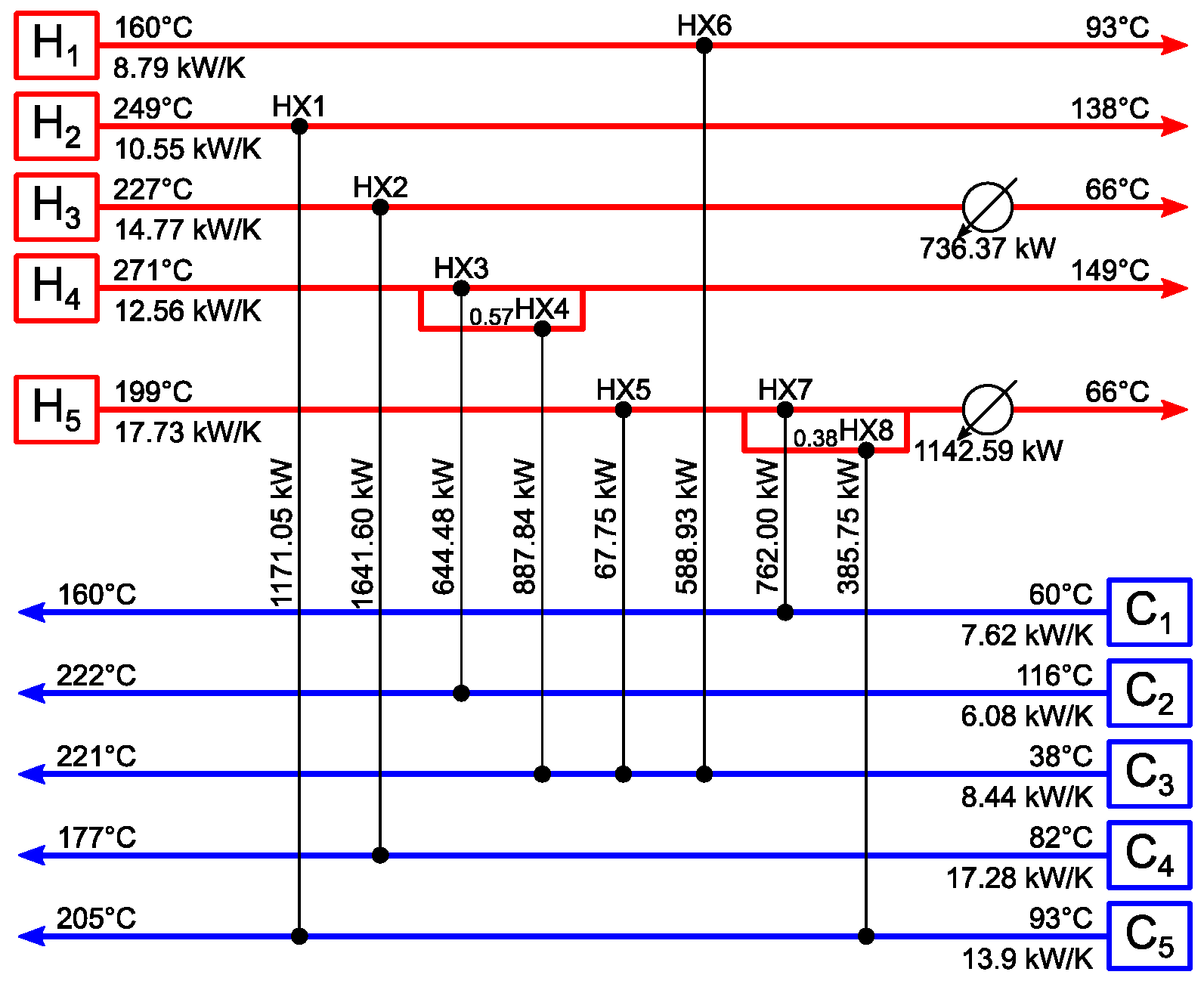
| Stream | ((kW/(m2K) | (kW/K) | ($/(kWyr)) | ||
|---|---|---|---|---|---|
| H1 | 160 | 93 | 1.704 | 8.79 | - |
| H2 | 249 | 138 | 1.704 | 10.55 | - |
| H3 | 227 | 66 | 1.704 | 14.77 | - |
| H4 | 271 | 149 | 1.704 | 12.56 | - |
| H5 | 199 | 66 | 1.704 | 17.73 | - |
| C1 | 60 | 160 | 1.704 | 7.62 | - |
| C2 | 116 | 222 | 1.704 | 6.08 | - |
| C3 | 38 | 221 | 1.704 | 8.44 | - |
| C4 | 82 | 177 | 1.704 | 17.28 | - |
| C5 | 93 | 205 | 1.704 | 13.90 | - |
| HU | 236 | 236 | 3.408 | - | 37.64 |
| CU | 38 | 82 | 1.704 | - | 18.12 |
| Sources | Reported TAC ($/yr) | |
|---|---|---|
| Cost Formulation 1 | Cost Formulation 2 | |
| Lewin et al. 1998 [24] | - | 43,452 1 (43,752 1,3) |
| Lewin 1998 [30] | - | 43,799 1 |
| Lin and Miller 2004 [31] | 43,329 2 | - |
| Pariyani et al. 2006 [32] | - | 43,439 1 (43,611 2) |
| Yerramsetty and Murty 2008 [34] | - | 43,538 1 |
| Peng and Cui 2015 [35] | - | 43,411 1 |
| Aguitoni et al. 2018 [36] | 43,227 2 | 43,596 2 |
| This work | 42,963 2 | 43,321 2 |
| Stream | (m) | (m) | (m) |
|---|---|---|---|
| H1 | 4 | 3 | 8 |
| H2 | 6 | 7 | 4 |
| H3 | 9 | 8 | 7 |
| H4 | 2 | 2 | 5 |
| H5 | 2 | 8 | 2 |
| C1 | 7 | 4 | 1 |
| C2 | 9 | 3 | 10 |
| C3 | 1 | 4 | 2 |
| C4 | 8 | 6 | 9 |
| C5 | 4 | 5 | 3 |
| HU | 5 | 5 | 0 |
| CU | 6 | 9 | 5 |
| Stream | ((kW/(m2K) | (kW/K) | ||
|---|---|---|---|---|
| H1 (plant1) | 148.1 | 114.7 | 1.642 | 311.9 |
| H2 (plant1) | 145.4 | 105.6 | 1.451 | 303.3 |
| H3 (plant1) | 141.9 | 98.4 | 1.754 | 302.6 |
| H4 (plant1) | 140.8 | 75.5 | 1.411 | 307.4 |
| H5 (plant1) | 135.3 | 55.3 | 1.531 | 335.4 |
| H6 (plant1) | 133.9 | 42.2 | 1.721 | 330.2 |
| H7 (plant1) | 131.9 | 41.2 | 1.713 | 331.3 |
| C1 (plant2) | 78.2 | 135.7 | 1.518 | 335.4 |
| C2 (plant2) | 69.3 | 108.5 | 1.631 | 323.3 |
| C3 (plant2) | 60.5 | 95.6 | 1.108 | 305.6 |
| C4 (plant2) | 59.5 | 90.3 | 1.501 | 321.5 |
| C5 (plant2) | 50.2 | 79.5 | 1.203 | 381.5 |
| C6 (plant2) | 45.9 | 71.4 | 1.102 | 311.5 |
| C7 (plant2) | 42.9 | 65.4 | 1.102 | 301.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rathjens, M.; Fieg, G. Cost-Optimal Heat Exchanger Network Synthesis Based on a Flexible Cost Functions Framework. Energies 2019, 12, 784. https://doi.org/10.3390/en12050784
Rathjens M, Fieg G. Cost-Optimal Heat Exchanger Network Synthesis Based on a Flexible Cost Functions Framework. Energies. 2019; 12(5):784. https://doi.org/10.3390/en12050784
Chicago/Turabian StyleRathjens, Matthias, and Georg Fieg. 2019. "Cost-Optimal Heat Exchanger Network Synthesis Based on a Flexible Cost Functions Framework" Energies 12, no. 5: 784. https://doi.org/10.3390/en12050784
APA StyleRathjens, M., & Fieg, G. (2019). Cost-Optimal Heat Exchanger Network Synthesis Based on a Flexible Cost Functions Framework. Energies, 12(5), 784. https://doi.org/10.3390/en12050784




