Optimal Control for Hybrid Energy Storage Electric Vehicle to Achieve Energy Saving Using Dynamic Programming Approach
Abstract
:1. Introduction
2. Materials and Methods
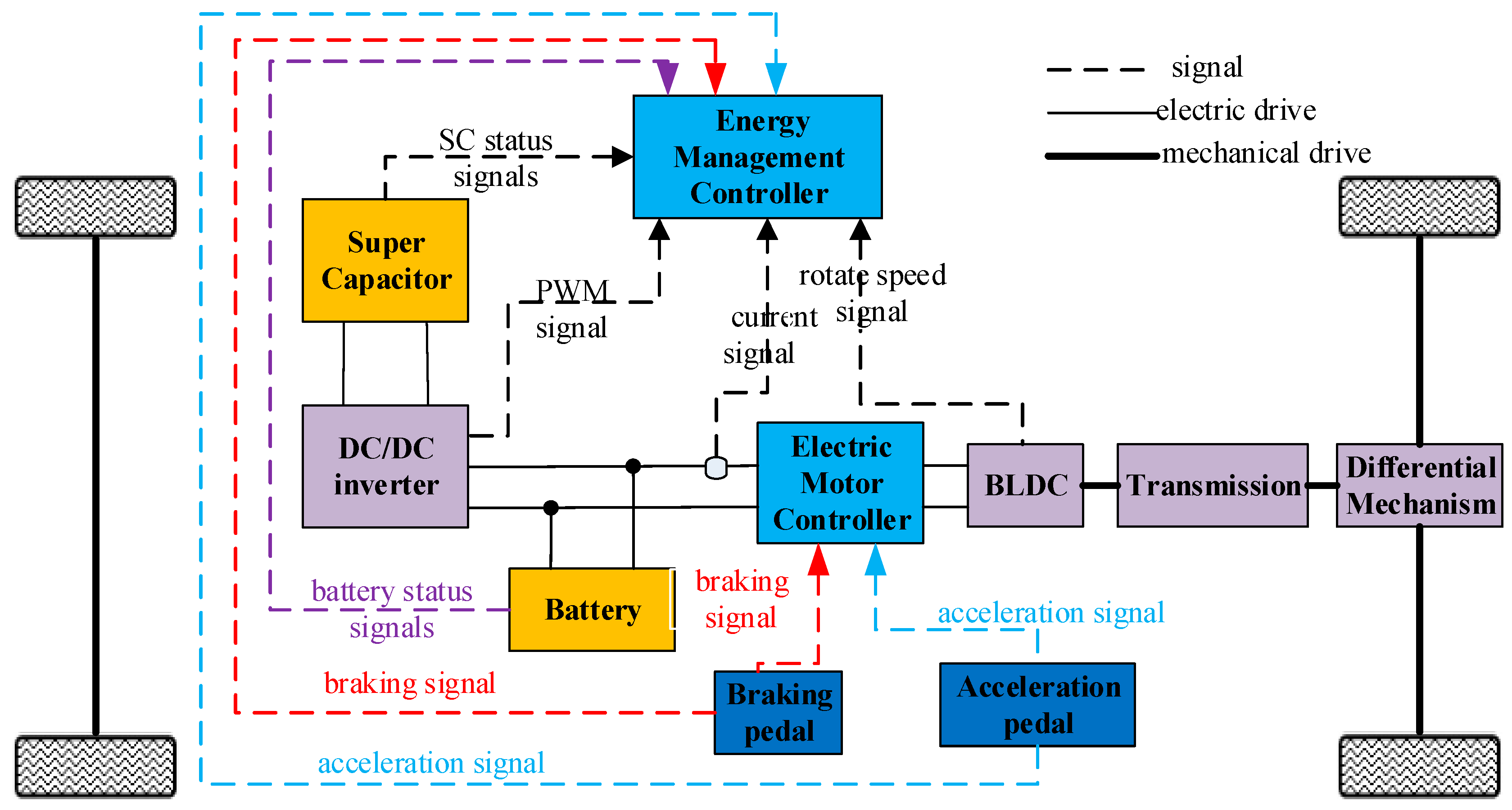
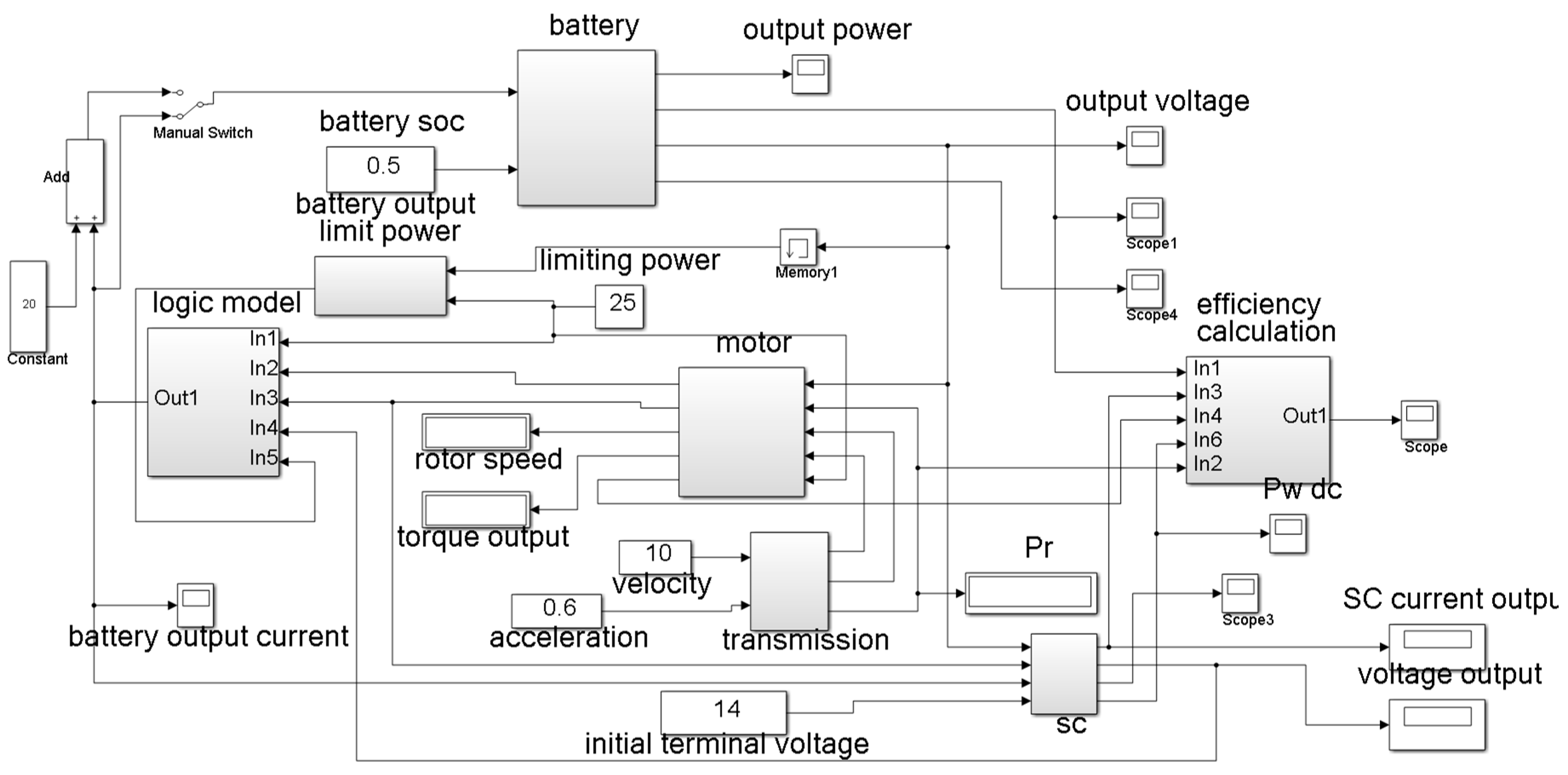
2.1. Description of the Hybrid Power System
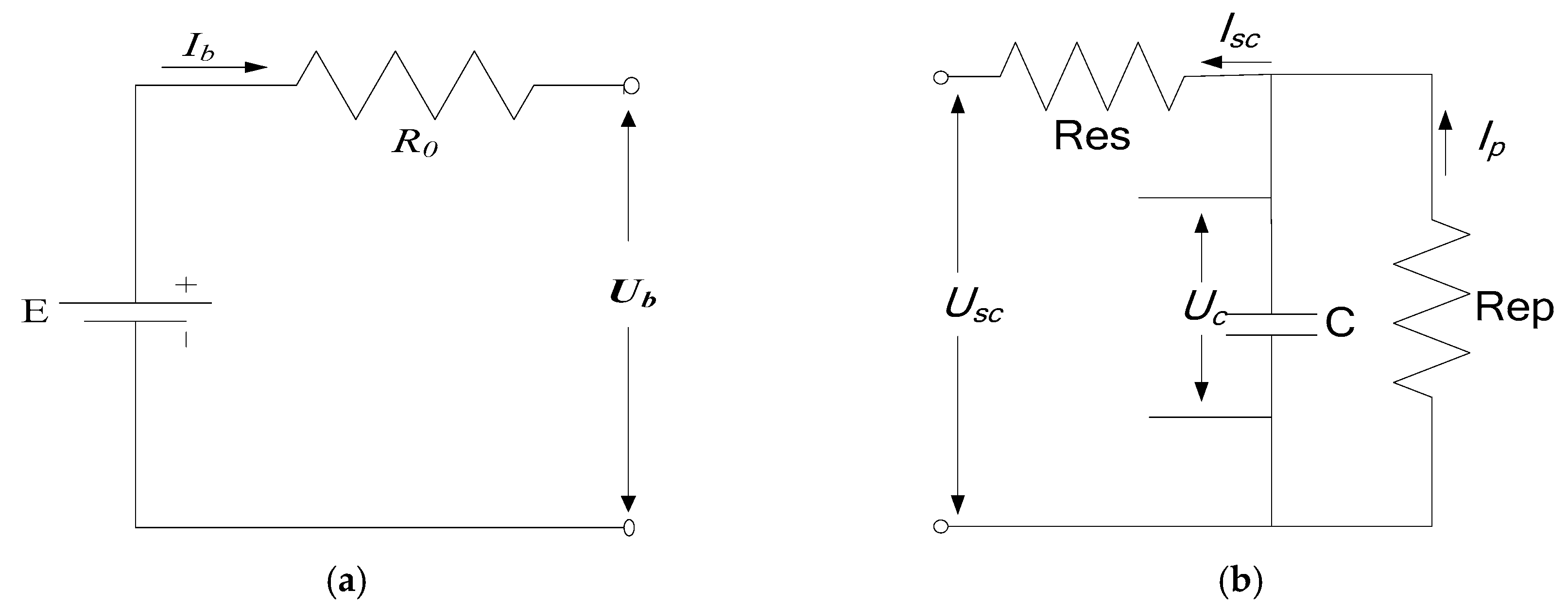
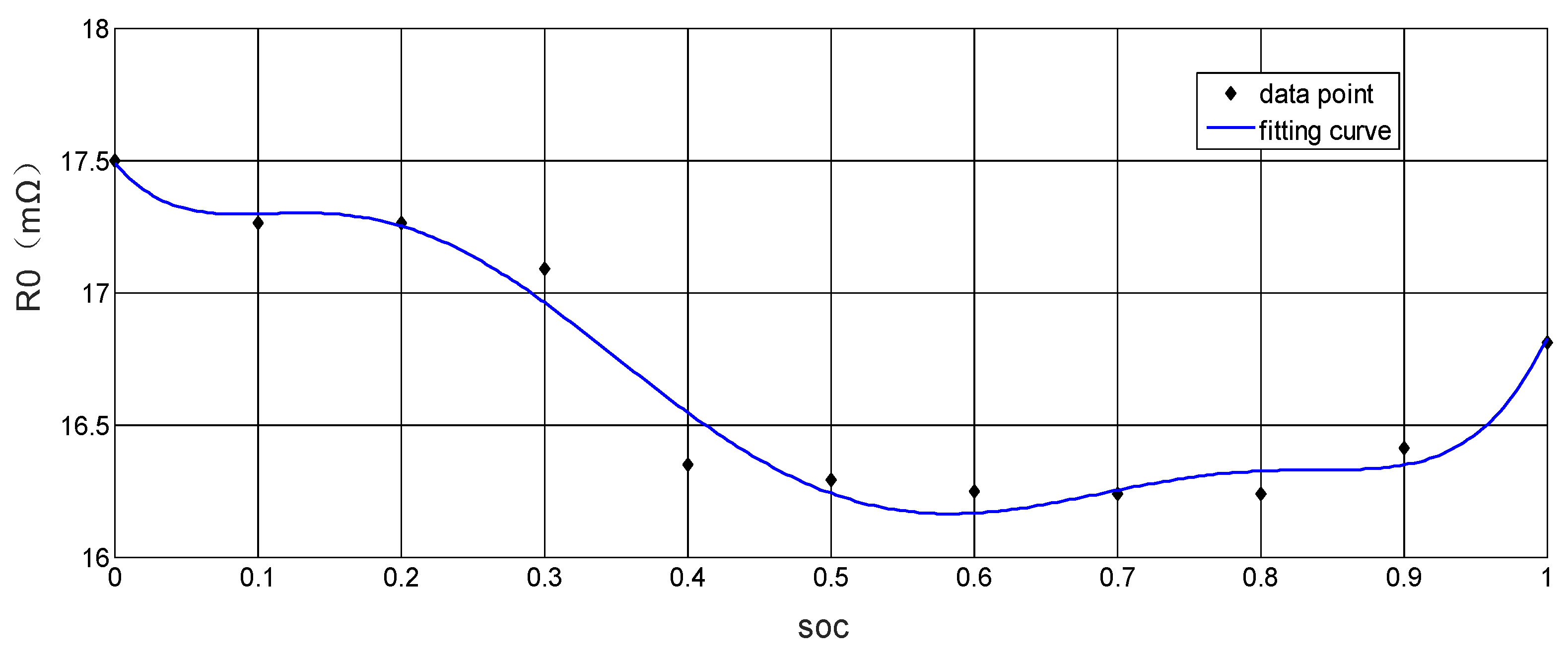
2.2. Battery Model
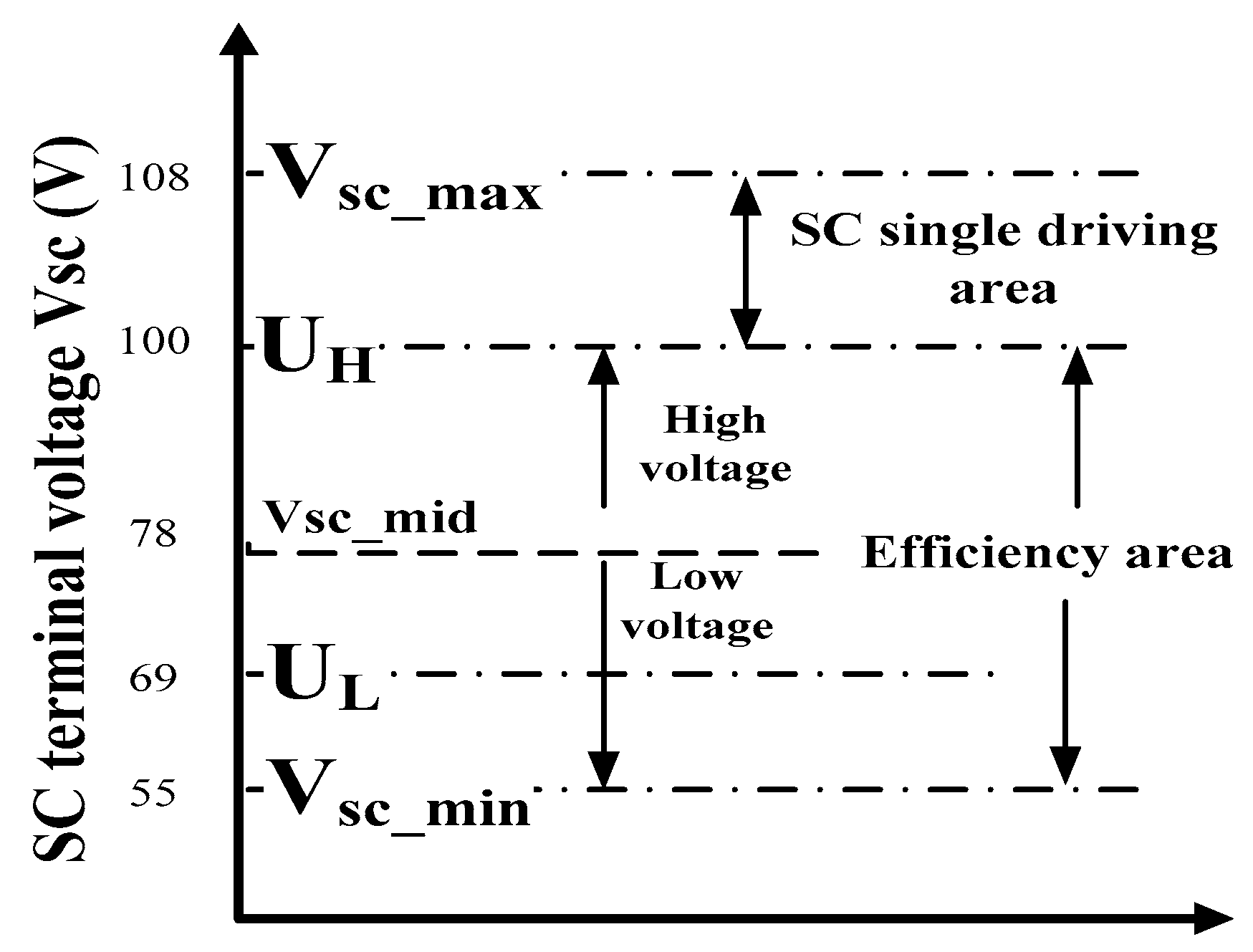
2.3. SC Model
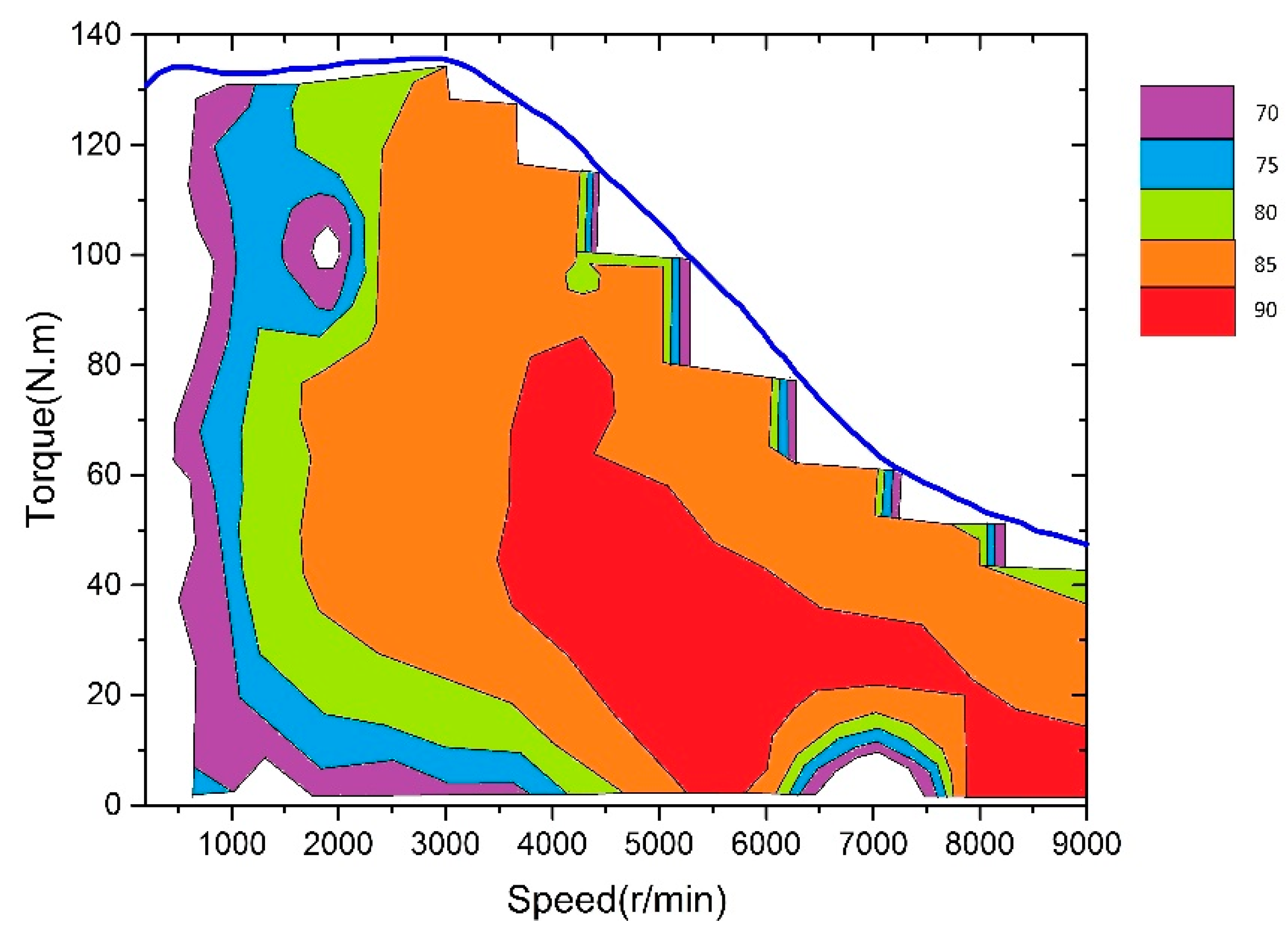
2.4. Electric Motor
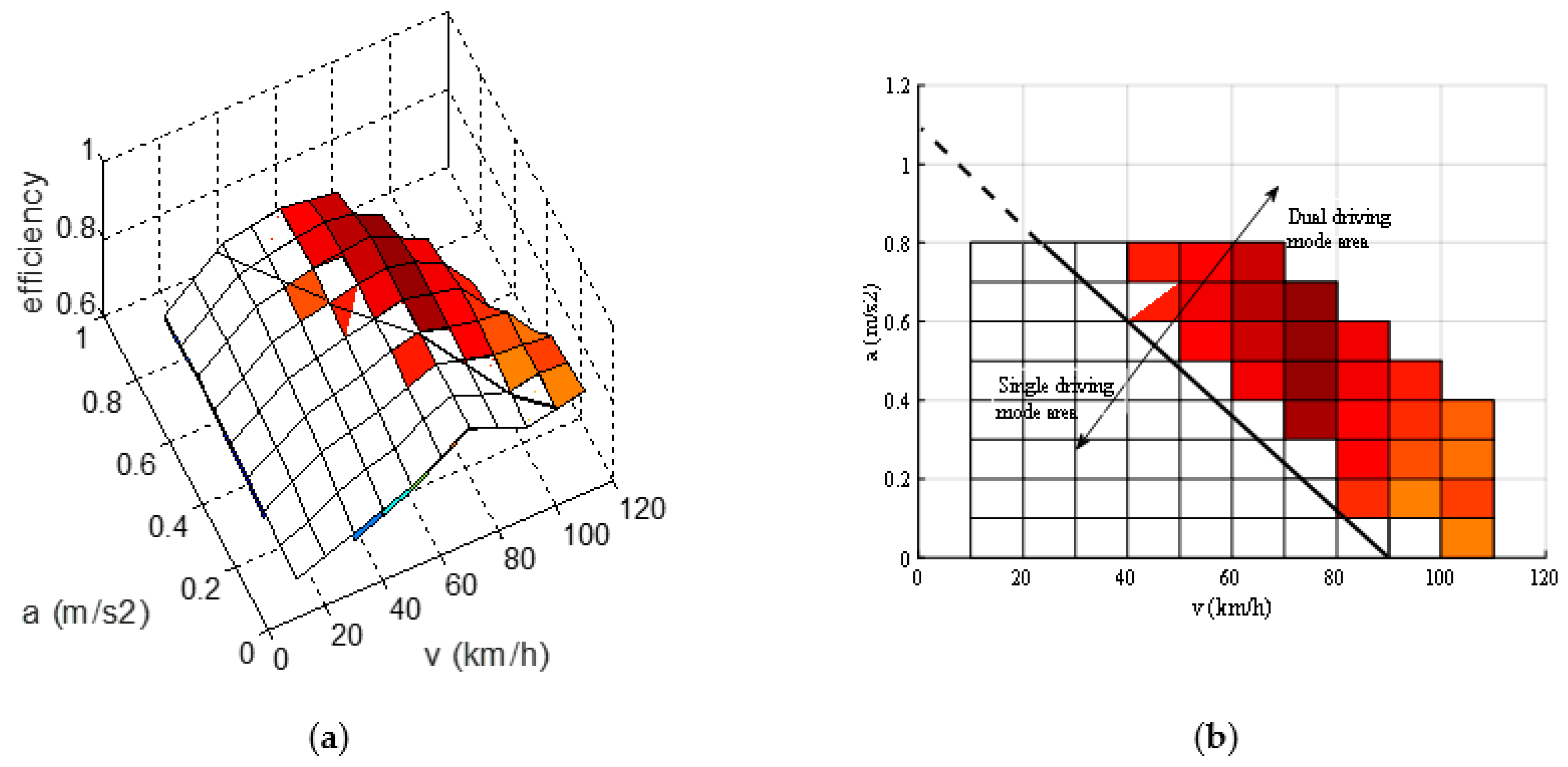
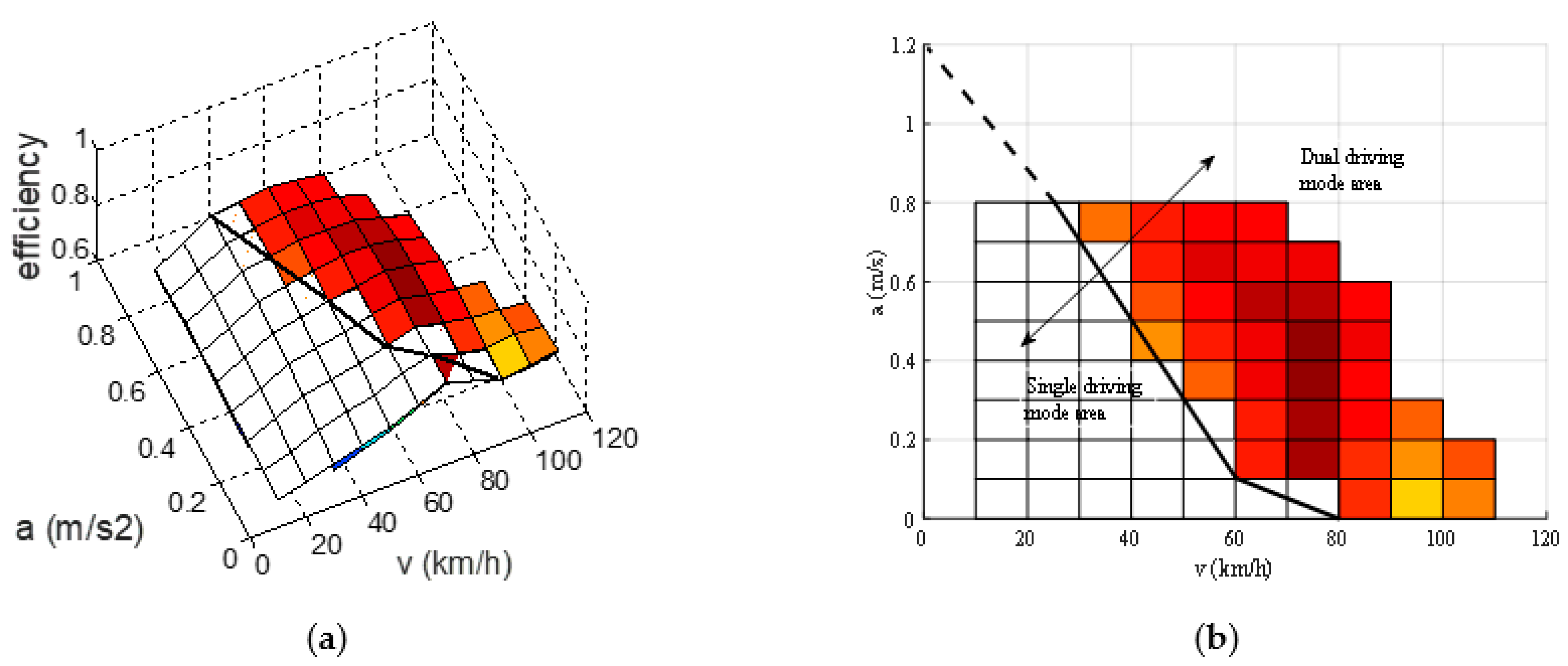
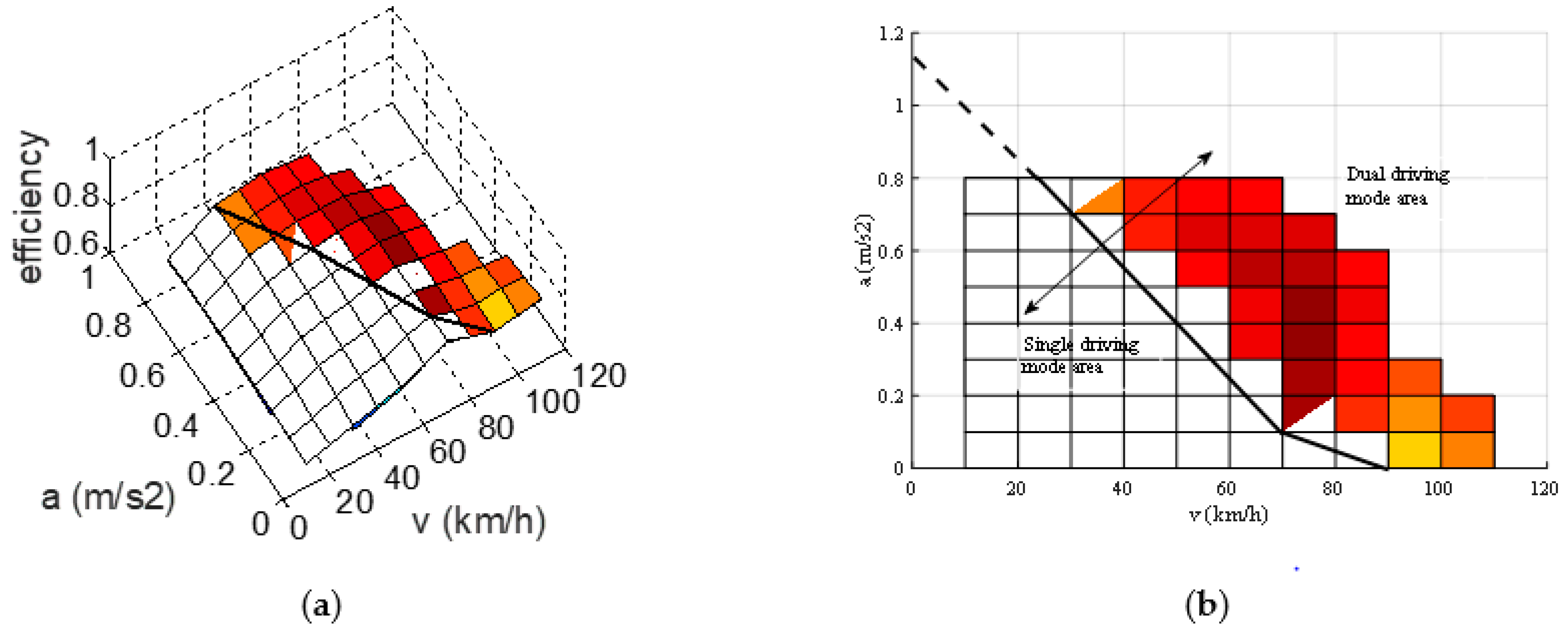
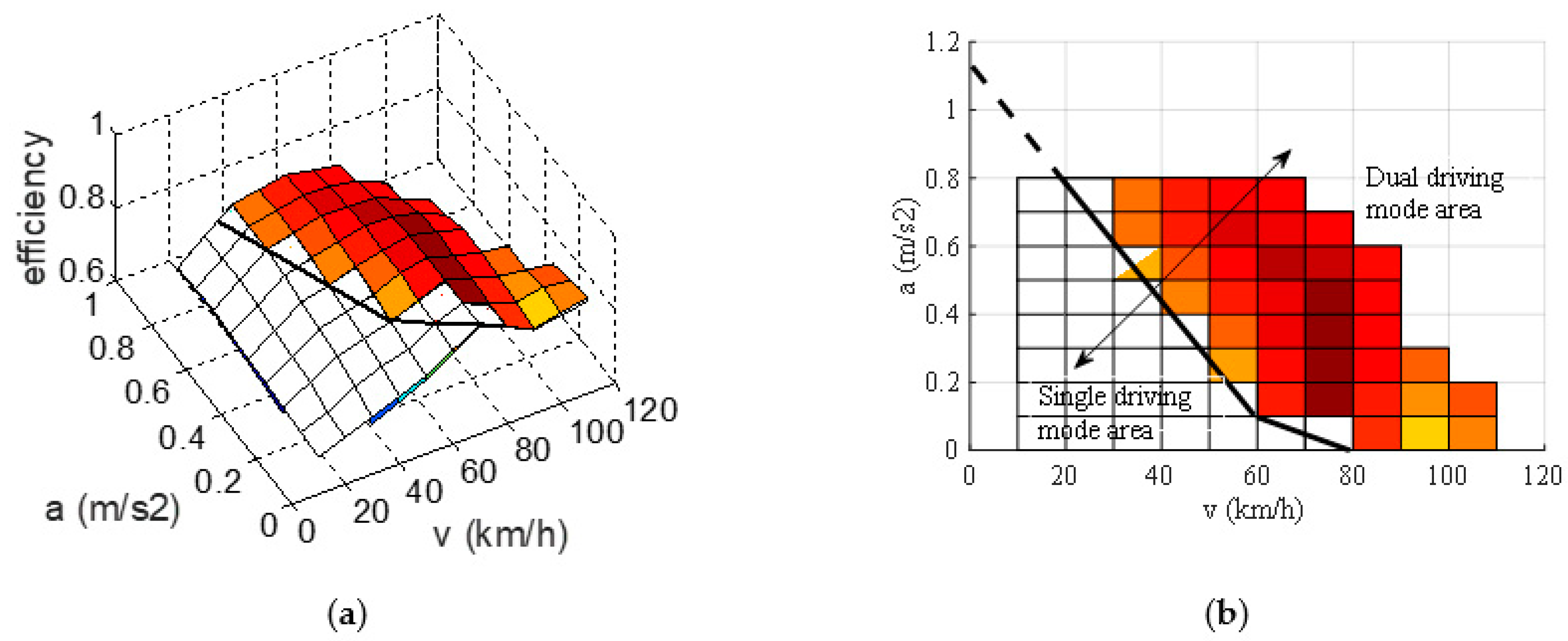
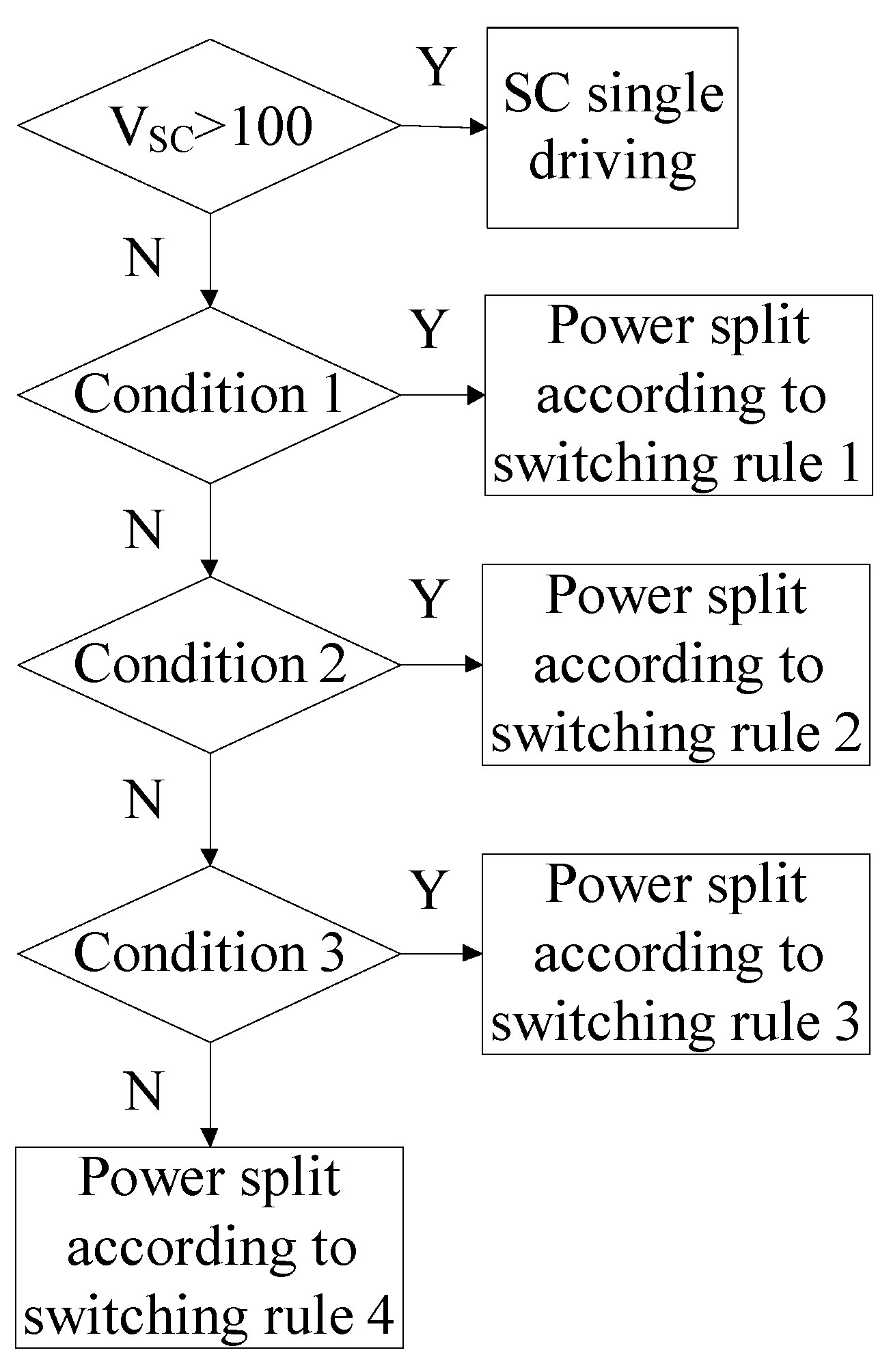
2.5. Rule-Based Energy Management Strategy
2.6. Energy Management Optimal Strategy Derived from DP Approach
3. Results and Discussion
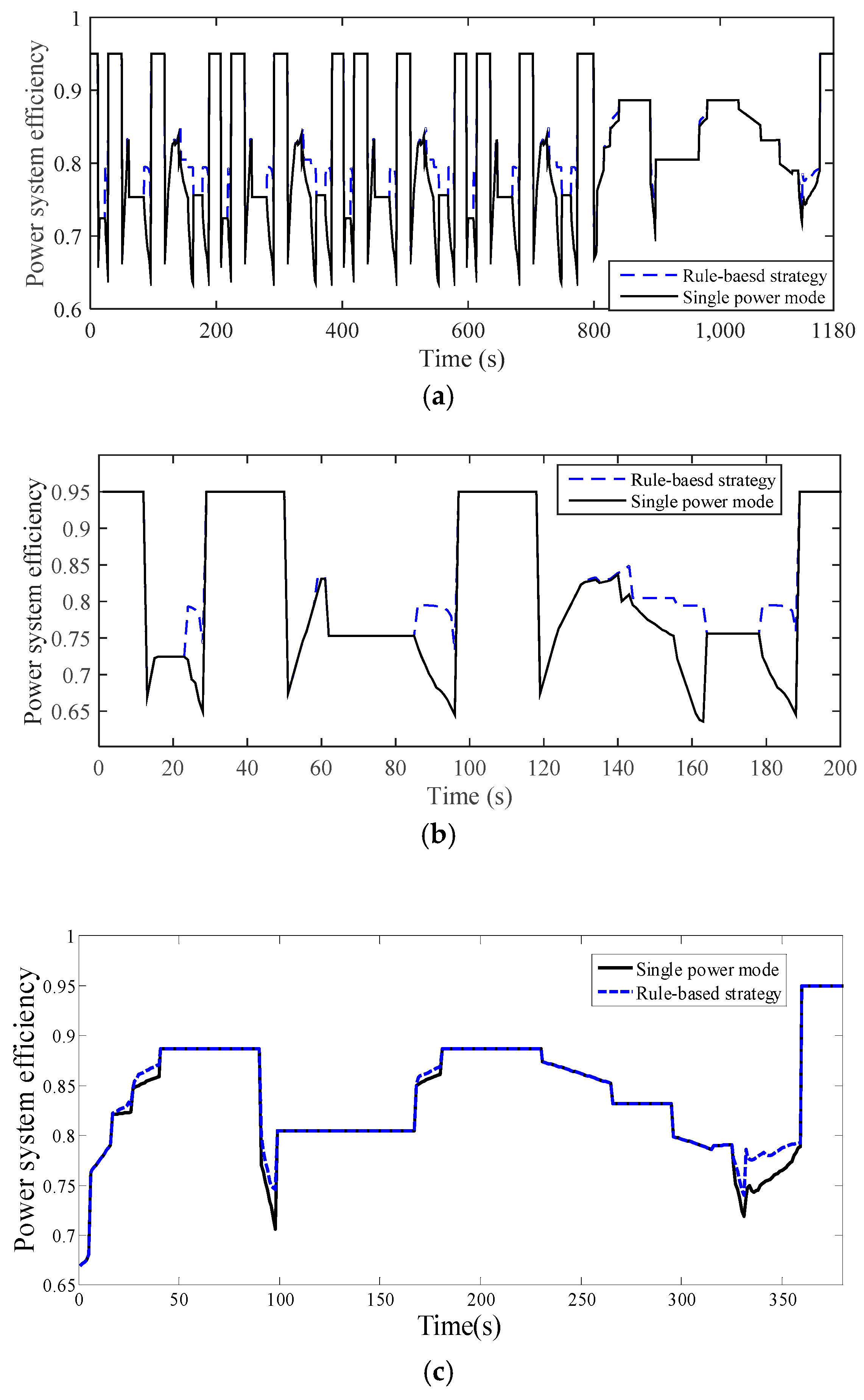
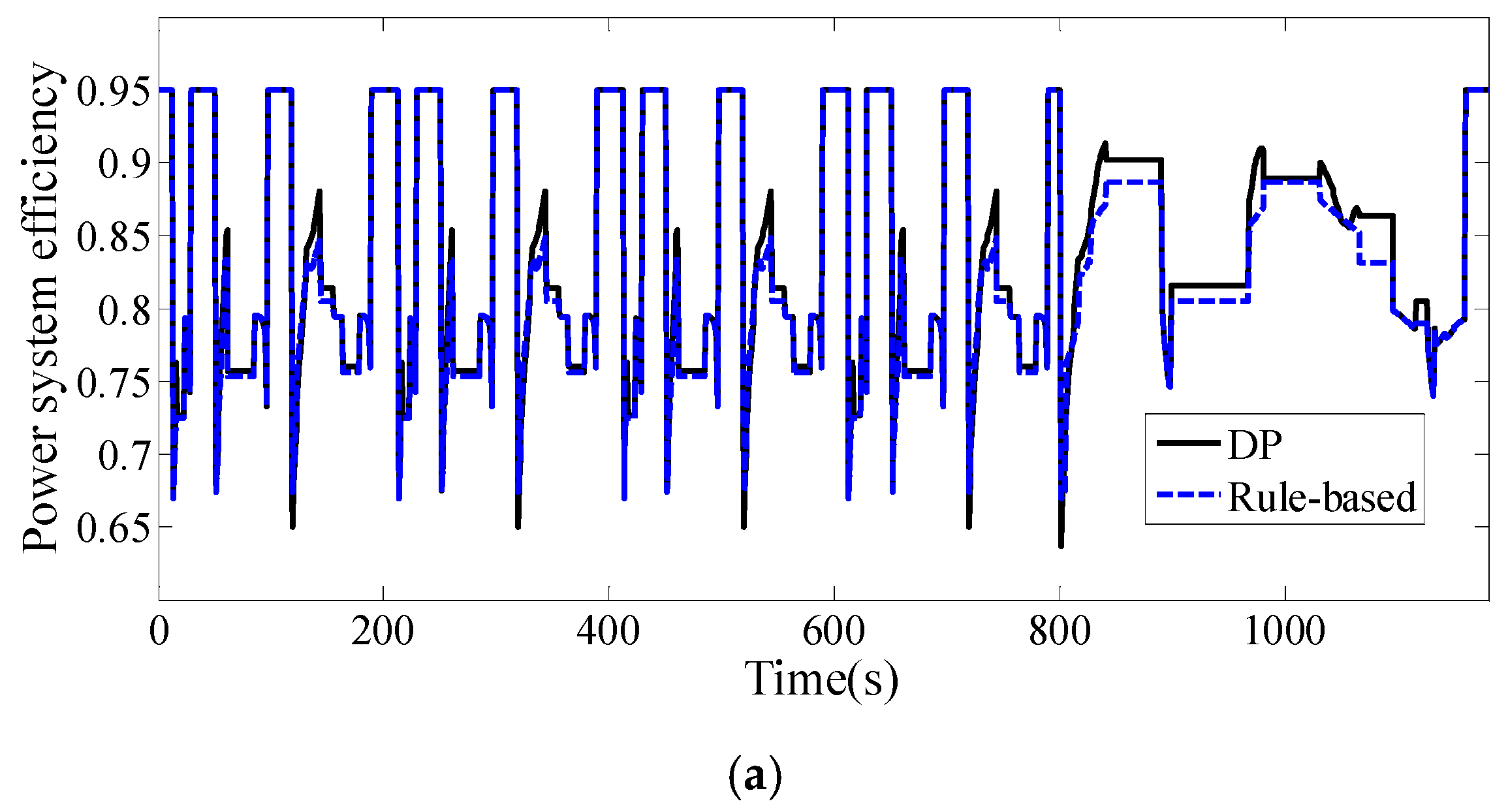
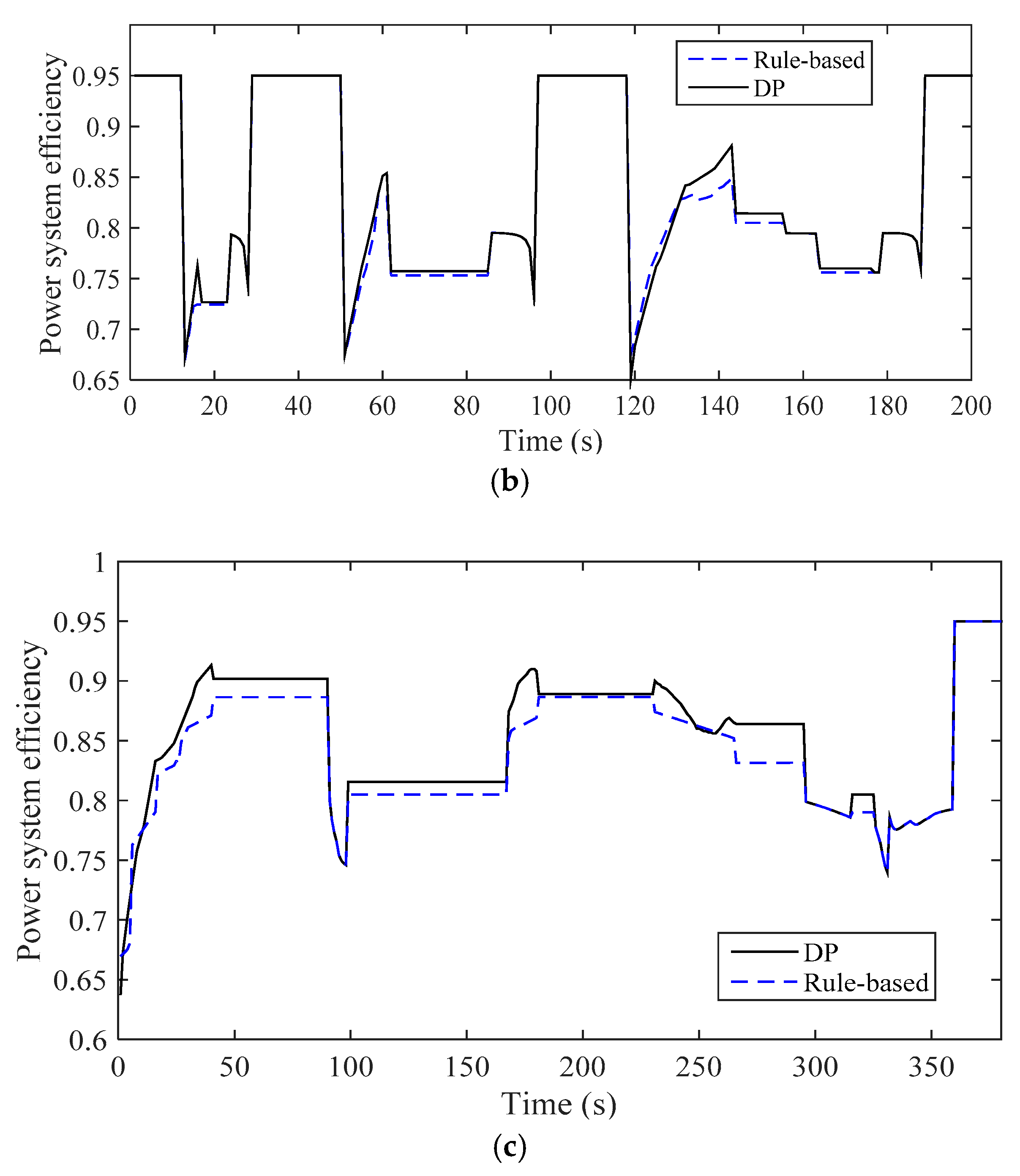
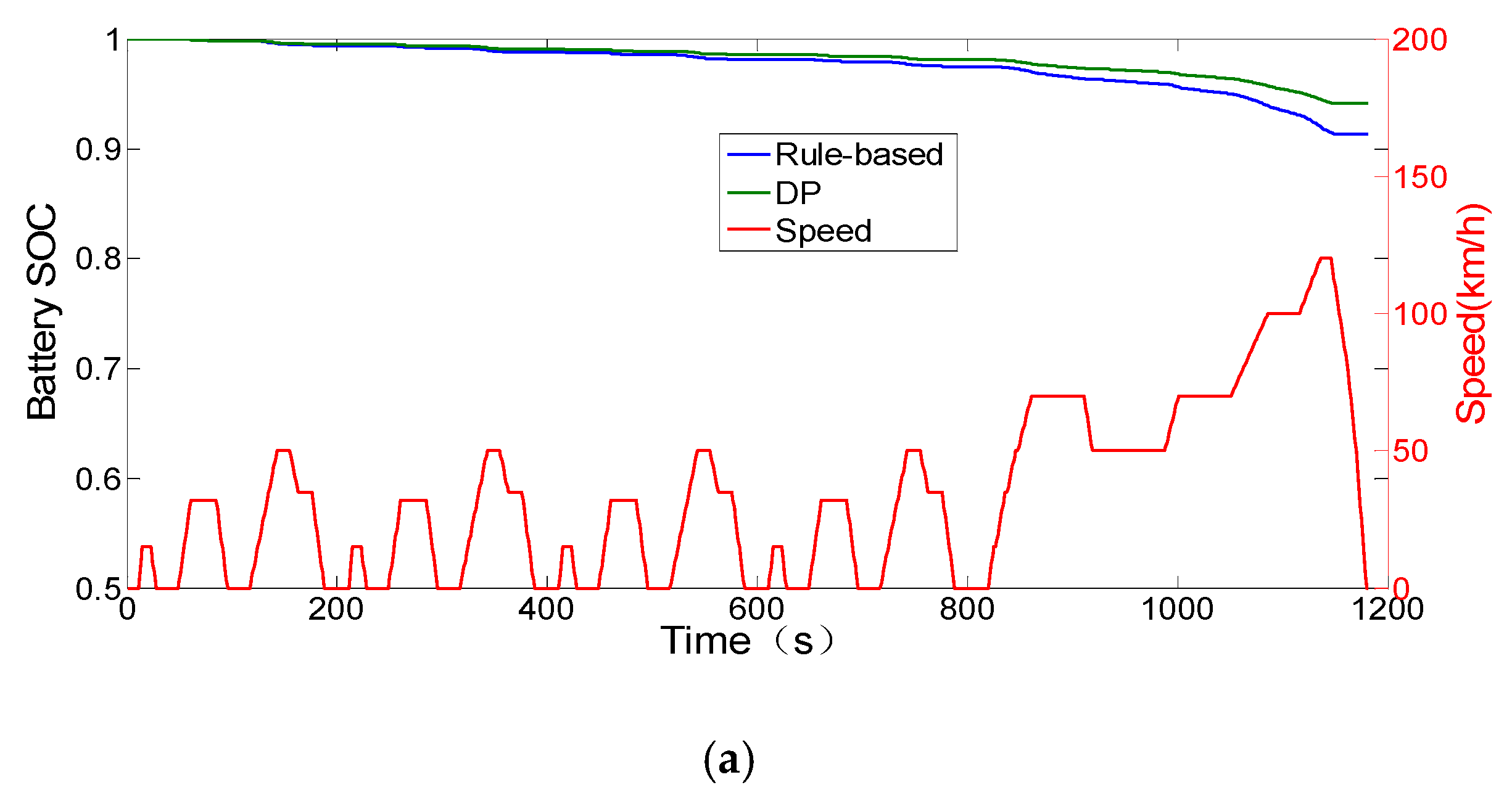
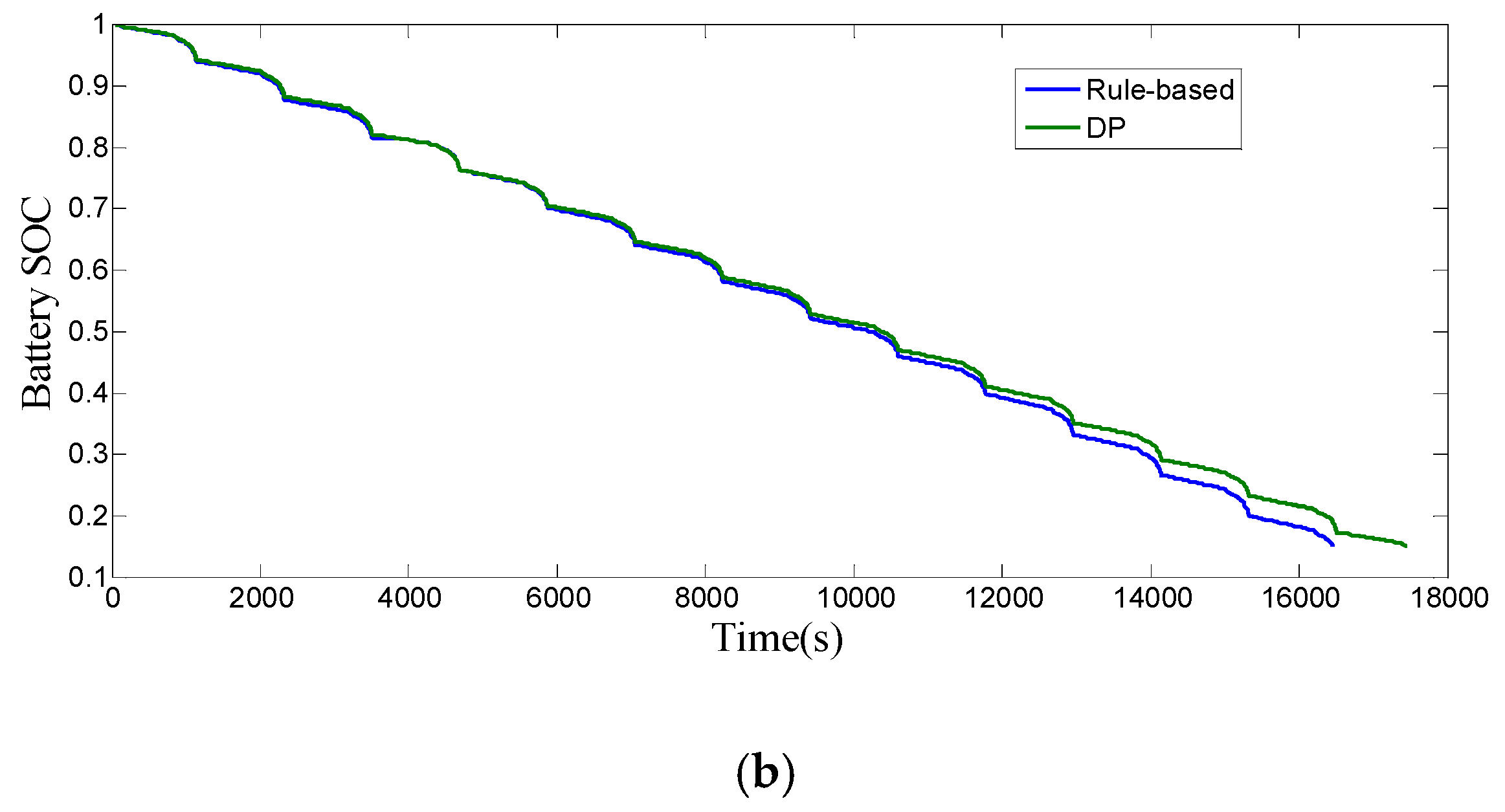
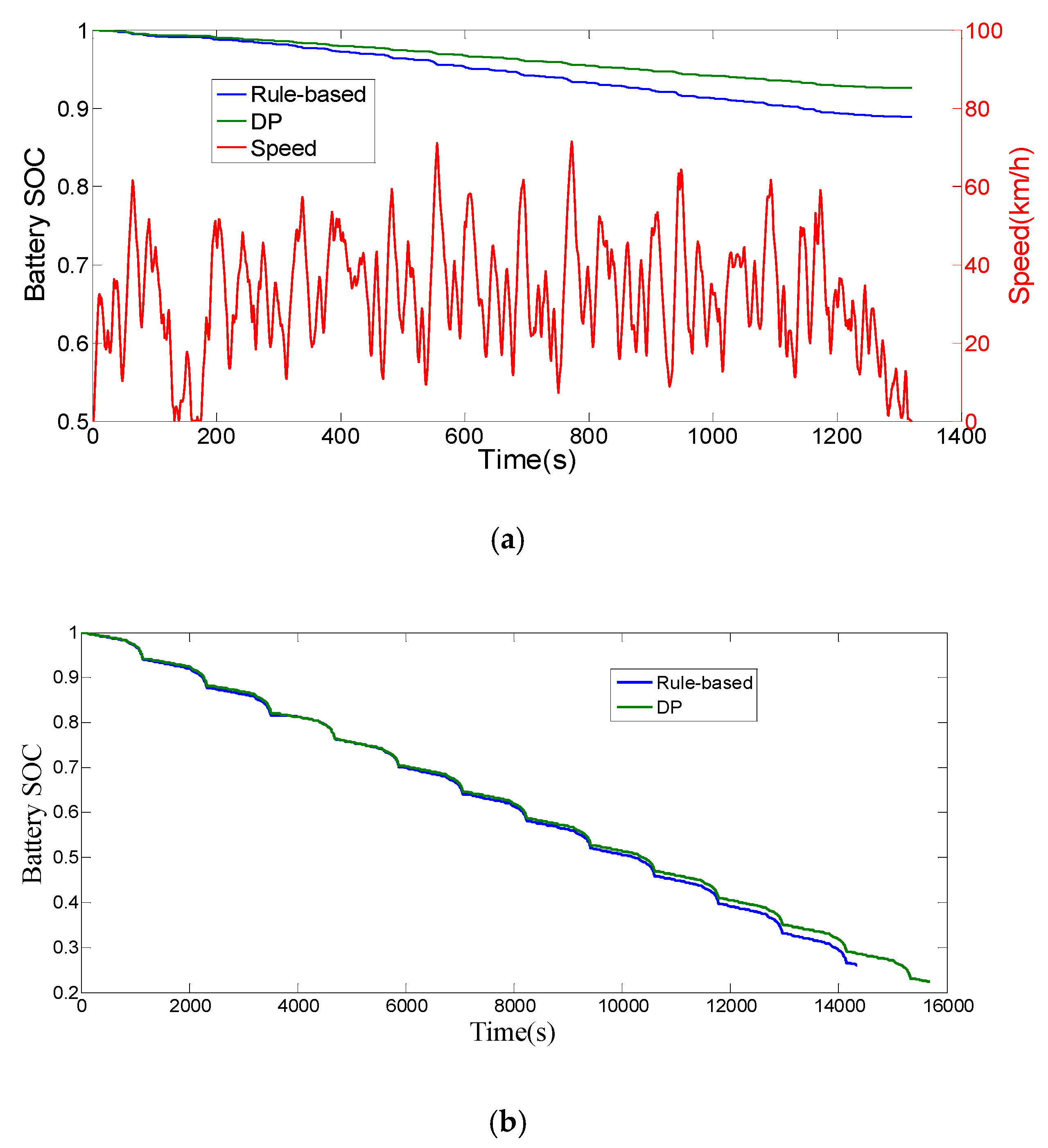
3.1. The Results of Rule-based Strategy
3.2. The Results of DP Strategy
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, M.; Wei, L.; Wen, J. The Parameters Matching and Simulation of Pure Electric Vehicle Composite Power Supply Based on CRUISE. Appl. Mech. Mater. 2014, 602, 2836–2839. [Google Scholar] [CrossRef]
- Griffo, A.; Wang, J. Modeling and Stability Analysis of Hybrid Power Systems for the More Electric Aircraft. Electr. Power Syst. Res. 2012, 82, 59–67. [Google Scholar] [CrossRef]
- Salah, I.B.; Bayoudhi, B.; Diallo, D. EV energy management strategy based on a single converter fed by a hybrid battery/supercapacitor power source. In Proceedings of the IEEE International Conference on Green Energy (ICGE), Sfax, Tunisia, 25 March 2014; pp. 246–250. [Google Scholar]
- Mastragostino, M.; Soavi, F. Strategies for high-Performance supercapacitors for HEV. J. Power Sources. 2007, 174, 89–93. [Google Scholar] [CrossRef]
- Yi, H.; Ma, F. Simulation Study of Compound Power Supply System for Electric Vehicles. Power World 2013, 1, 30–33. [Google Scholar]
- Xu, R.; Wang, Y. Simulation of composite electric power for electric vehicles. In Proceedings of the IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Kagawa, Japan, 6–9 August 2017; pp. 967–972. [Google Scholar]
- Cezar, B.; Onea, A. A rule-based energy management strategy for parallel hybrid vehicles with supercapacitors. In Proceedings of the International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 14–16 October 2011; pp. 1–6. [Google Scholar]
- Shi, Q.; Zhang, C.; Cui, N. Optimal Control of Energy Management Problems for a New Dual Energy Source Pure Electric Vehicle. Trans. China Electrotechnical Soc. 2008, 23, 137–142. [Google Scholar]
- Trovão, J.P.; Antunes, C.H. A comparative analysis of meta-heuristic methods for power management of a dual energy storage system for electric vehicles. Energy Convers. Manage. 2015, 95, 281–296. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Xiong, R.; Xu, J.; You, C. Energy management of a power-split plug-in hybrid electric vehicle based on genetic algorithm and quadratic programming. J. Power Sources 2014, 248, 416–426. [Google Scholar] [CrossRef] [Green Version]
- Padmarajan, B.V.; Mcgordon, A.; Jennings, P.A. Blended Rule-Based Energy Management for PHEV: System Structure and Strategy. IEEE Trans. Veh. Technol. 2016, 65, 8757–8762. [Google Scholar] [CrossRef]
- Banvait, H.; Anwar, S.; Chen, Y. A rule-based energy management strategy for plug-in hybrid electric vehicle (PHEV). In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3938–3943. [Google Scholar]
- Hemi, H.; Ghouili, J.; Cheriti, A. A real time energy management for electrical vehicle using combination of rule-based and ECMS. In Proceedings of the IEEE Electrical Power and Energy Conference (EPEC), Halifax, NS, Canada, 21–23 August 2013; pp. 1–6. [Google Scholar]
- Hung, Y.-H.; Wu, C.-H. An integrated optimization approach for a hybrid energy system in electric vehicles. Appl. Energy 2012, 98, 479–490. [Google Scholar] [CrossRef]
- Hu, X.; Johannesson, L.; Murgovski, N.; Egardt, B. Longevity-conscious dimensioning and power management of the hybrid energy storage system in a fuel cell hybrid electric bus. Appl. Energy 2015, 137, 913–924. [Google Scholar] [CrossRef]
- Laura, V.P.; Guillermo, R.B.; Diego, M.; Guillermo, O.G. Optimization of power management in an hybrid electric vehicle using dynamic programming. Math. Comput. Simul. 2006, 73, 244–254. [Google Scholar]
- Chen, B.-C.; Wu, Y.-Y.; Tsai, H.-C. Design and analysis of power management strategy for range extended electric vehicle using dynamic programming. Appl. Energy 2014, 113, 1764–1774. [Google Scholar] [CrossRef]
- Ansarey, M.; Panahi, M.S.; Ziarati, H.; Mahjoob, M. Optimal energy management in a dual-storage fuel-cell hybrid vehicle using multi-dimensional dynamic programming. J. Power Sources 2014, 250, 359–371. [Google Scholar] [CrossRef]
- Zou, Y.; Chen, R.; Hou, S.; Hu, X. Energy Management Strategy for Hybrid Electric Tracked Vehicle Based on Stochastic Dynamic Programming. J. Mech. Eng. 2012, 48, 91–96. [Google Scholar] [CrossRef]
- Hou, C.; Ouyang, M.; Xu, L.; Wang, H. Approximate Pontryagin’s minimum principle applied to the energy management of plug-in hybrid electric vehicles. Appl. Energy 2014, 115, 174–189. [Google Scholar] [CrossRef]
- Kim, N.; Cha, S.; Peng, H. Optimal Control of Hybrid Electric Vehicles Based on Pontryagin’s Minimum Principle. IEEE Trans. Control Syst. Technol. 2011, 19, 1279–1287. [Google Scholar]
- Song, Z.; Hofmann, H.; Li, J.; Han, X.; Ouyang, M. Optimization for a hybrid energy storage system in electric vehicles using dynamic programming approach. Appl. Energy 2015, 139, 151–162. [Google Scholar] [CrossRef]
- Xu, L.; Ouyang, M.; Li, J.; Yang, F.; Lu, L.; Hua, J. Optimal sizing of plug-in fuel cell electric vehicles using models of vehicle performance and system cost. Appl. Energy 2013, 103, 477–487. [Google Scholar] [CrossRef]
- Bai, Z.; Cao, L.; Yang, J. Study on the Performance Evaluation Method of Power Batteries for Pure Electric Vehicles. J. Hunan Univ.: Nat. Sci. Ed. 2006, 33, 48–51. [Google Scholar]
- Pan, C.; Chen, L.; Chen, L.; Huang, C.; Xie, M. Research on energy management of dual energy storage system based on the simulation of urban driving schedules. Int. J. Electr. Power Energy Syst. 2013, 44, 37–42. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| m, Vehicle mass (kg) | 1360 |
| R, Wheel radius (m) | 0.277 |
| CD, Air drag coefficient | 0.35 |
| A, Front area (m2) | 2.3 |
| ρ, Air density (kg/m3) | 1.29 |
| i0, Transmission ratio | 7.881 |
| ηT, Transmission efficiency (%) | 95 |
| ηr, Regenerative braking efficiency (%) | 65 |
| ηDC, DC/DC converter efficiency (%) | 92 |
| DC bus voltage (V) | 260–350 |
| Parameter | Value |
|---|---|
| Nominal voltage (V) | 3.65 |
| Capacity (Ah) | 42 |
| Stored energy (kWh) | 21 |
| R0 (mΩ) | 16.8 |
| SOC | 1 | 0.9 | 0.8 | 0.7 | 0.6 |
|---|---|---|---|---|---|
| R0/mΩ | 16.81 | 16.41 | 16.24 | 16.24 | 16.25 |
| SOC | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 |
| R0/mΩ | 16.29 | 16.35 | 17.09 | 17.26 | 17.26 |
| Parameter | Value |
|---|---|
| Maximum voltage (V) | 2.7 |
| Capacity (F) | 350 |
| Stored energy (Wh) | 0.35 |
| Maximum discharge current (A) | 170 |
| Resistance (mΩ) | 3.2 |
| Type | Nominal Power (kW) | Maximum Power (kW) | Maximum Speed (r/min) |
|---|---|---|---|
| BLDC | 29 | 40 | 9000 |
| Strategy | Driving Range (km) | Energy Consumption (Wh/km) |
|---|---|---|
| Single battery system | 120 | 104.82 |
| Rule-based | 131 | 90.73 |
| DP approach | 138 | 86.41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.; Liang, Y.; Chen, L.; Chen, L. Optimal Control for Hybrid Energy Storage Electric Vehicle to Achieve Energy Saving Using Dynamic Programming Approach. Energies 2019, 12, 588. https://doi.org/10.3390/en12040588
Pan C, Liang Y, Chen L, Chen L. Optimal Control for Hybrid Energy Storage Electric Vehicle to Achieve Energy Saving Using Dynamic Programming Approach. Energies. 2019; 12(4):588. https://doi.org/10.3390/en12040588
Chicago/Turabian StylePan, Chaofeng, Yanyan Liang, Long Chen, and Liao Chen. 2019. "Optimal Control for Hybrid Energy Storage Electric Vehicle to Achieve Energy Saving Using Dynamic Programming Approach" Energies 12, no. 4: 588. https://doi.org/10.3390/en12040588
APA StylePan, C., Liang, Y., Chen, L., & Chen, L. (2019). Optimal Control for Hybrid Energy Storage Electric Vehicle to Achieve Energy Saving Using Dynamic Programming Approach. Energies, 12(4), 588. https://doi.org/10.3390/en12040588




