In this section, the obtained expressions are verified, using the existing analytical solutions and the finite element method (FEM). All the analytical calculations were implemented using Mathematica [
30]. The FEM results were obtained using CST EM Studio software. In the FEM, the electrical boundary conditions (
) were applied and the distance from the boundary to the coil model was about
times the model height. Annealed copper was used as the coil material, and the current ports were utilized as the excitation sources. Tetrahedral mesh generation for the model was performed automatically, on the commencement of the magnetostatic solver. During the solver run, several mesh refinement passes were performed automatically, until the deviation of the energy value did not exceed the criterion, 2 × 10
−2, between two subsequent passes.
6.1. Comparison with Respect to Finite-Length Coaxial Helical Filaments
Four different calculation methods are utilized in the following comparisons: Equation (21) of this paper, Equation (24) of [
20], FEM, and Equation (38) of [
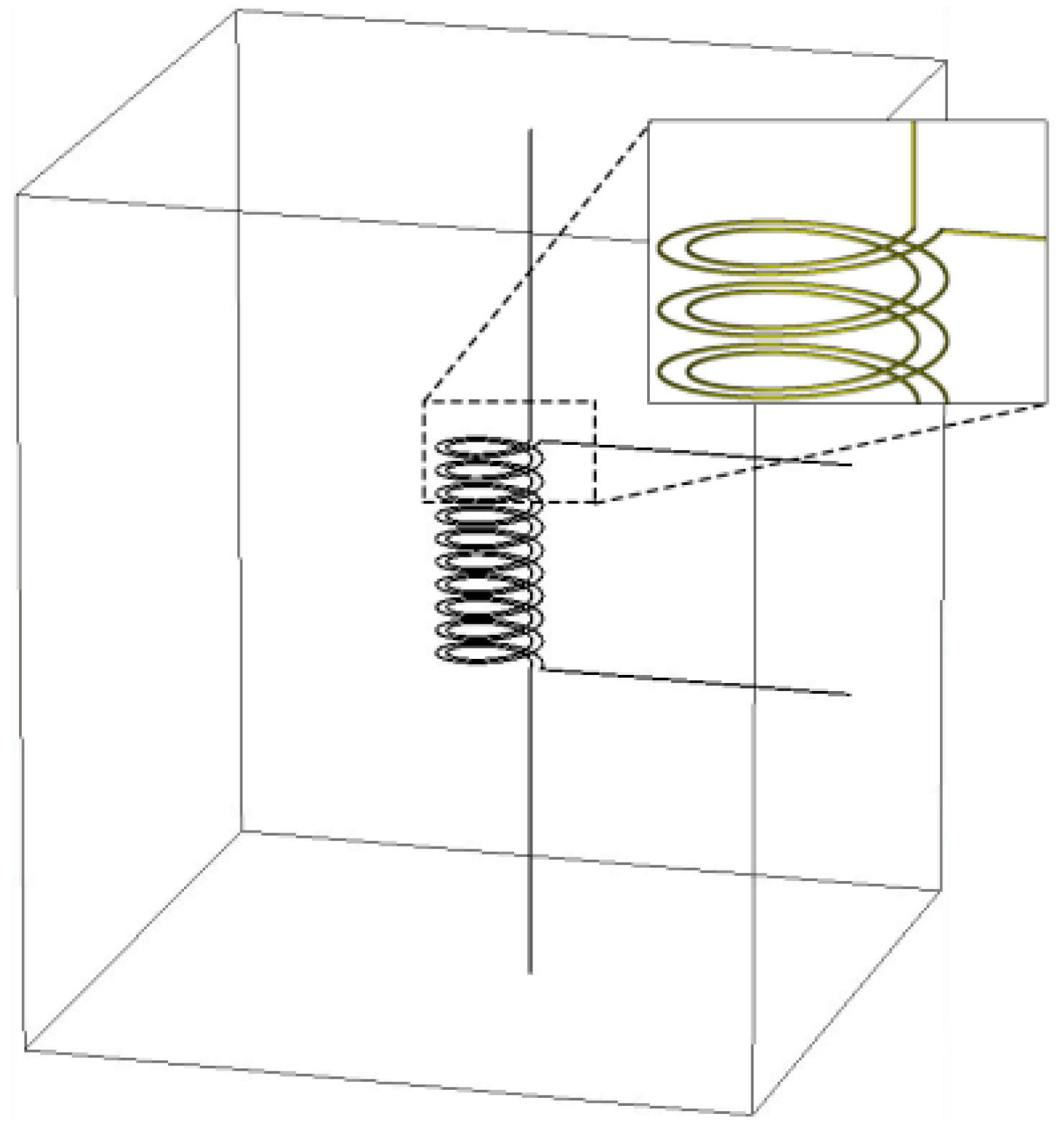
13]. As it is impossible to establish an infinite thin conductor model for calculating the apparent inductance matrix in FEM, the filaments were approximately replaced by coils with small square cross-sections. The edge length of the square was 10 mm and the center point of the square was located on the original filament. Furthermore, as the helical coil is an open-circuit, instead of a closed circuit like the circular coil, in order to avoid error report in the FEM program, the terminal leads were assembled on the model to connect the end of the coil with the boundary, as shown in
Figure 7. The cross-section of the terminal lead was also a square with an edge length of 10 mm. The terminal leads of coils- 1 and 2 were perpendicular to each other. All these above measures were undertaken to guarantee that the FEM program is solvable and to minimize the errors in calculation, when the computing power of the computer is limited. Equation (38) of [
13] was used for the approximate calculation of the mutual inductance. The helical coils were reduced to finite continuous solenoids (circular coils), with the same height and number of turns as the helical coils.
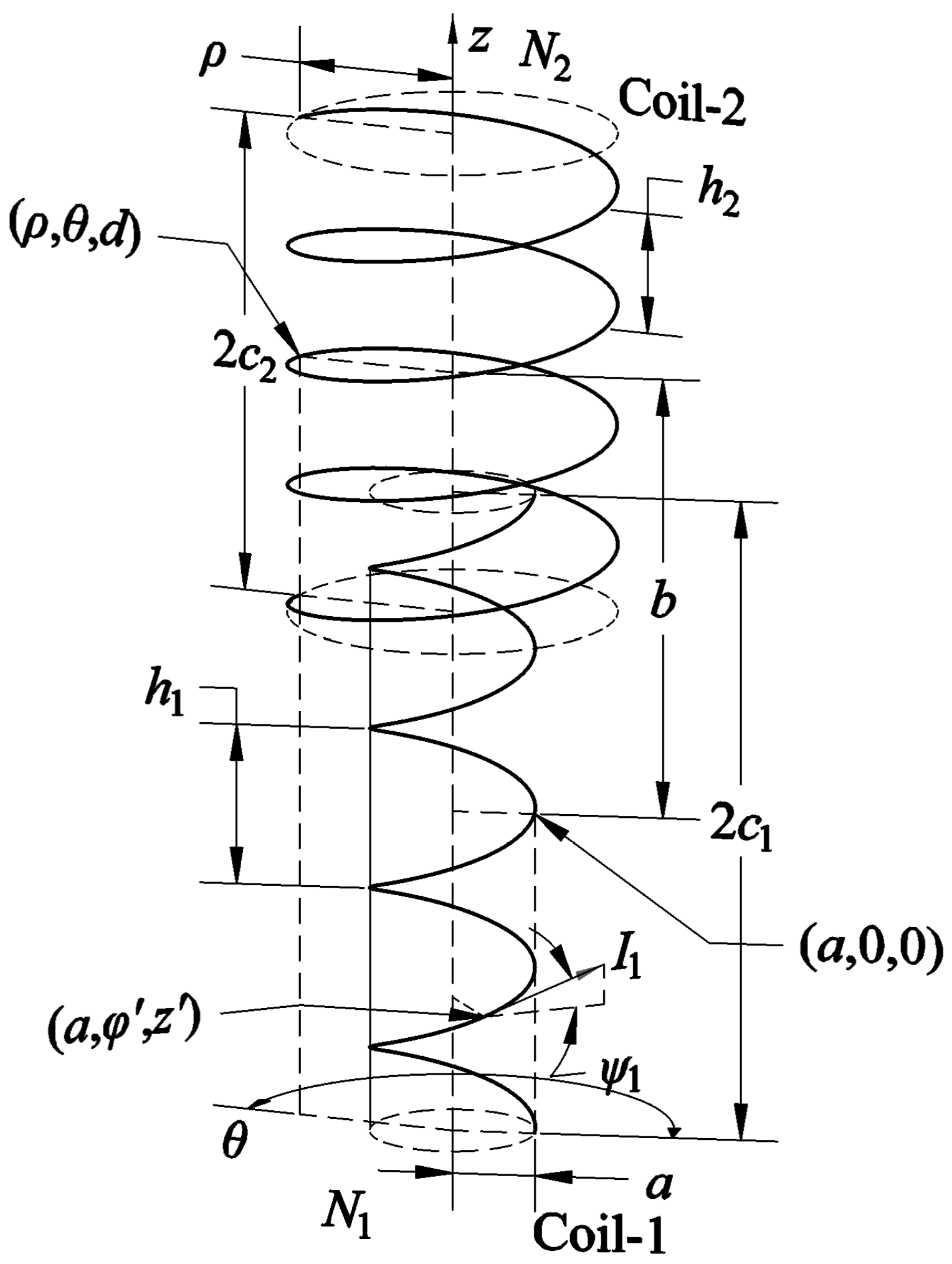
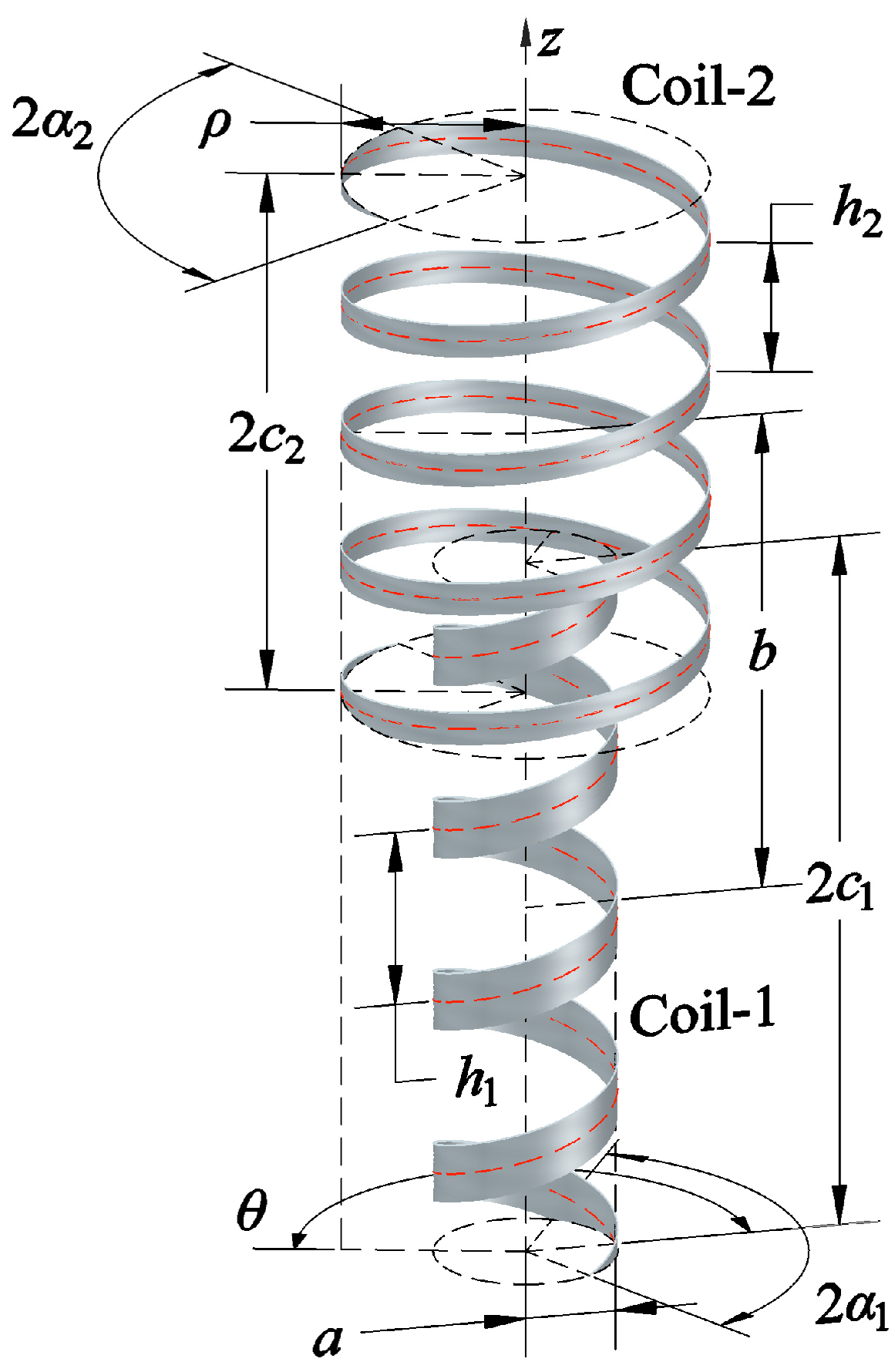
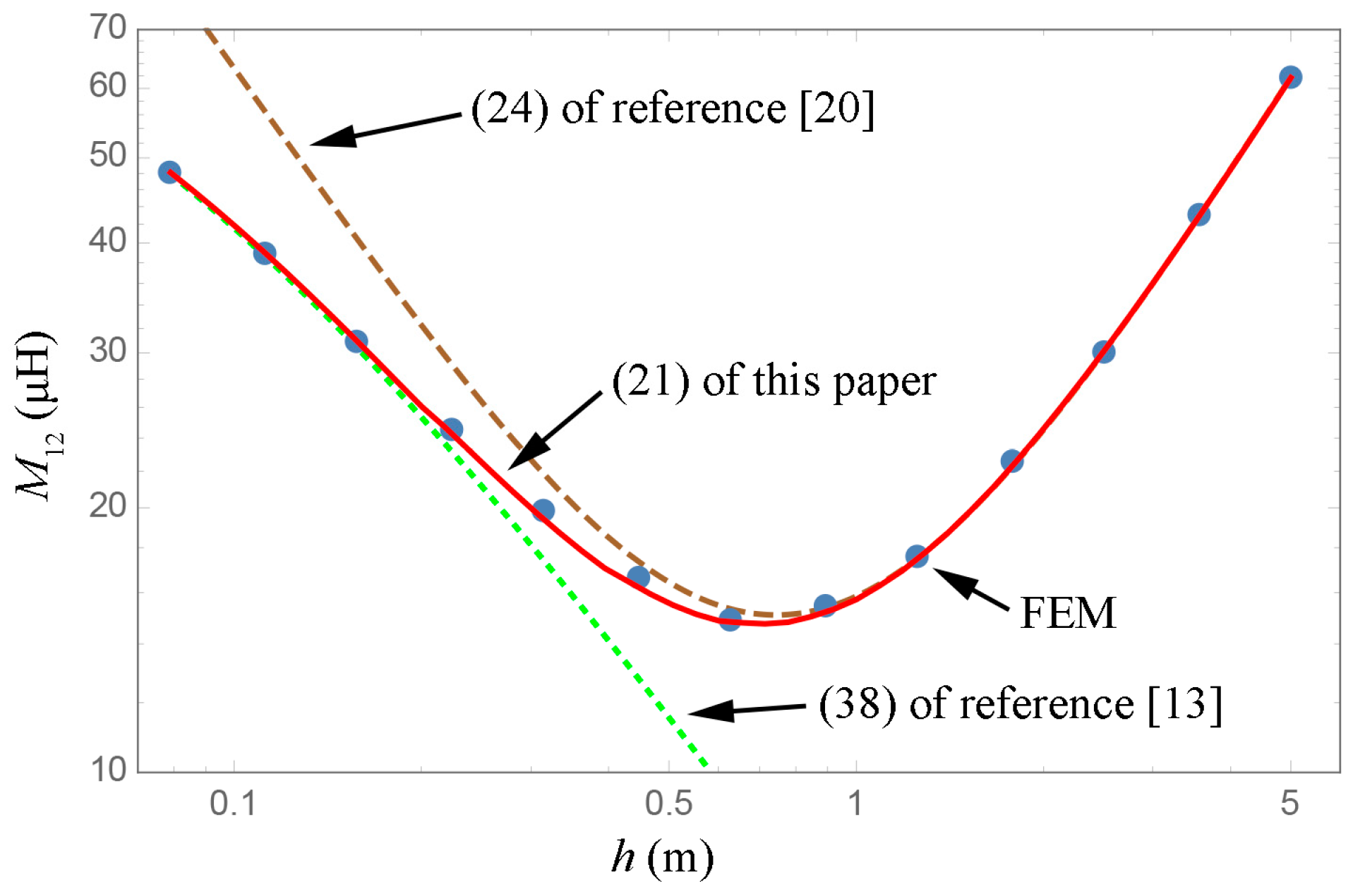
The geometric parameters are listed in
Table 2, for the first comparison, in which
and the two coils are aligned at the ends. The pitch-length (
h) dependence of the mutual inductance is presented in
Figure 8.
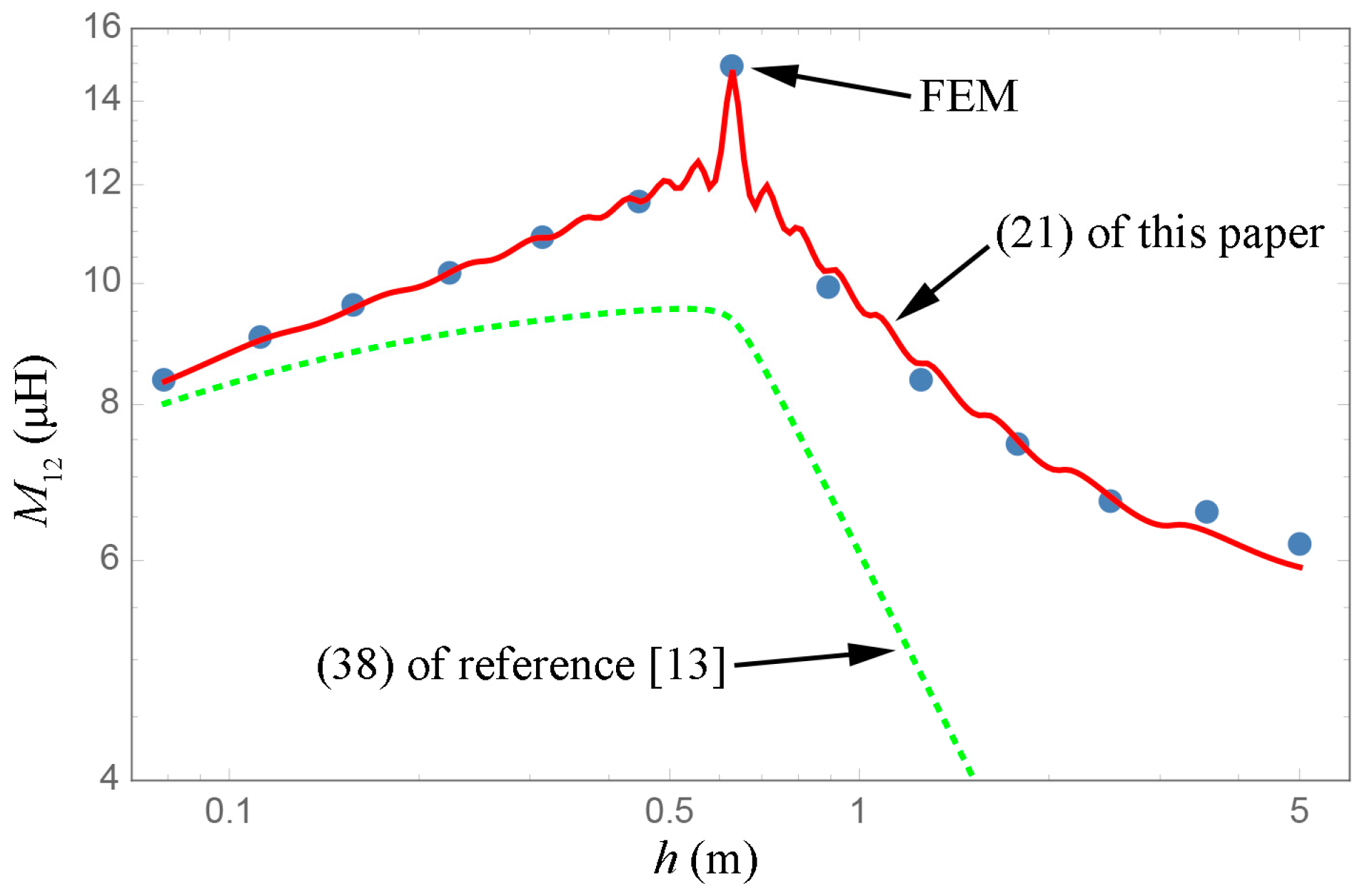
From
Figure 8, it is seen that Equation (21) of this paper is in good agreement with the FEM, for each pitch length (
h). Equation (38) of [
13] is only valid for a small pitch-length, whereas, Equation (24) of [
20] is more suitable for long coils.
Maintaining the alignment of the coils and
, the angular coordinate (
θ) dependence of the mutual inductance is presented in
Figure 9. The geometric parameters are listed in
Table 3, for a fixed pitch length (0.629 m).
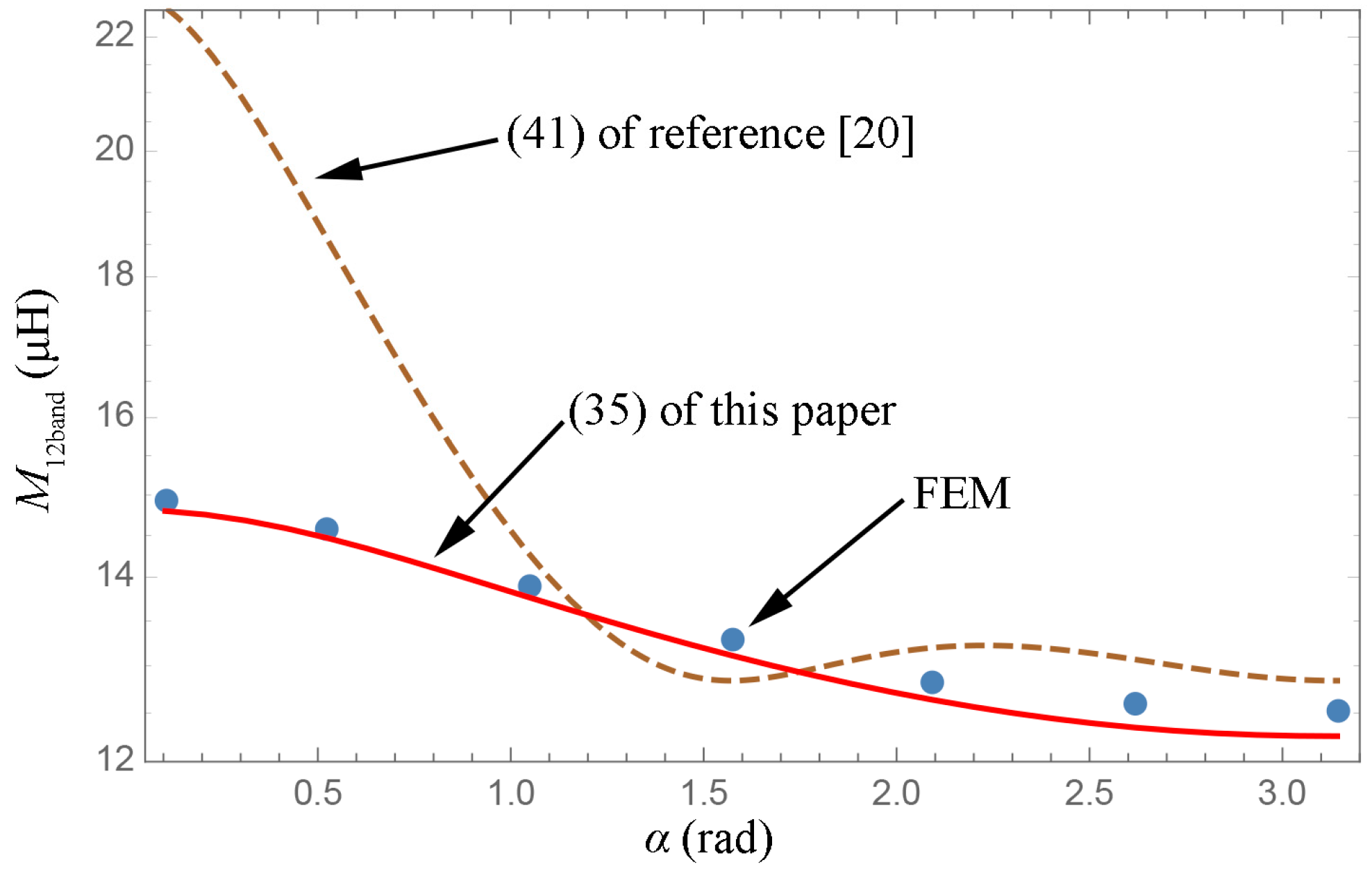
From
Figure 9, it is observed that Equation (21) in this paper is consistent with the FEM result; Equation (24) of [
20] is similar to the other two, but some errors continue to exist. Equation (38) of [
13] is not suitable for this comparison because it is unaffected by the variation in
θ.
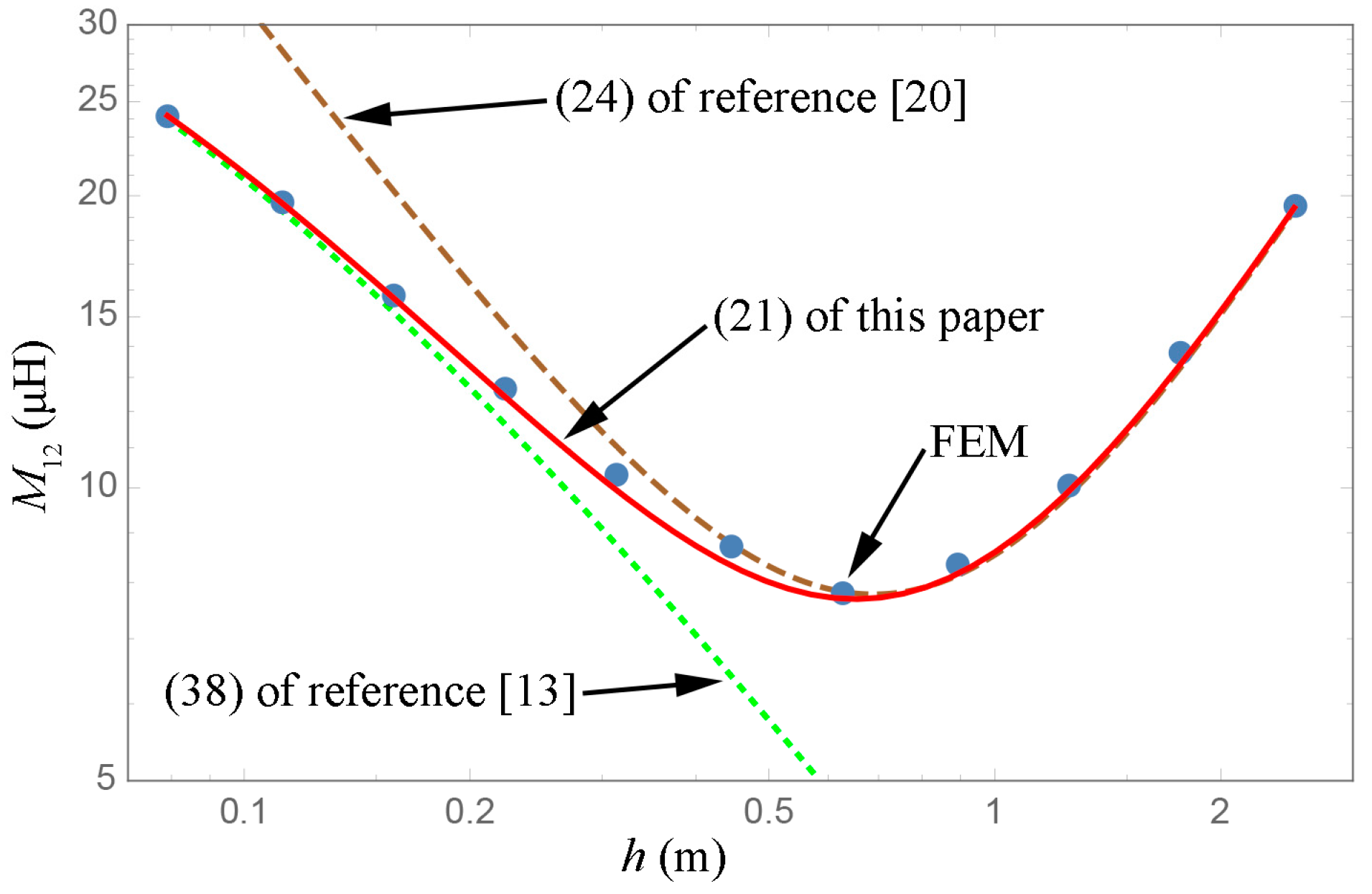
The geometric parameters of coils of the third comparison are shown in
Table 4. The ends of the both coils are aligned and the radii are the same. The angular coordinates (
θ) of the midpoints of conductor center lines are 0 and
π, respectively, and the wires are arranged in a similar manner to the twisted pairs which are common in practice. The pitch-length (
h) dependence of the mutual inductance is presented in
Figure 10.
When the two coil radii are the same, Equation (38) of [
18] cannot be used because the coils are approximated as two overlapping solenoids when using this equation, which leads to calculation program error. It can be seen from
Figure 10 that the results of Equation (21) of this paper and FEM are basically the same, and the Equation (24) of [
20] is only applicable to the case where the pitch length (
h) is large. It is worth noting that the numerical integration of Equation (21) in this comparison converges slowly, which is determined by the intrinsic properties of the modified Bessel functions (
and
).
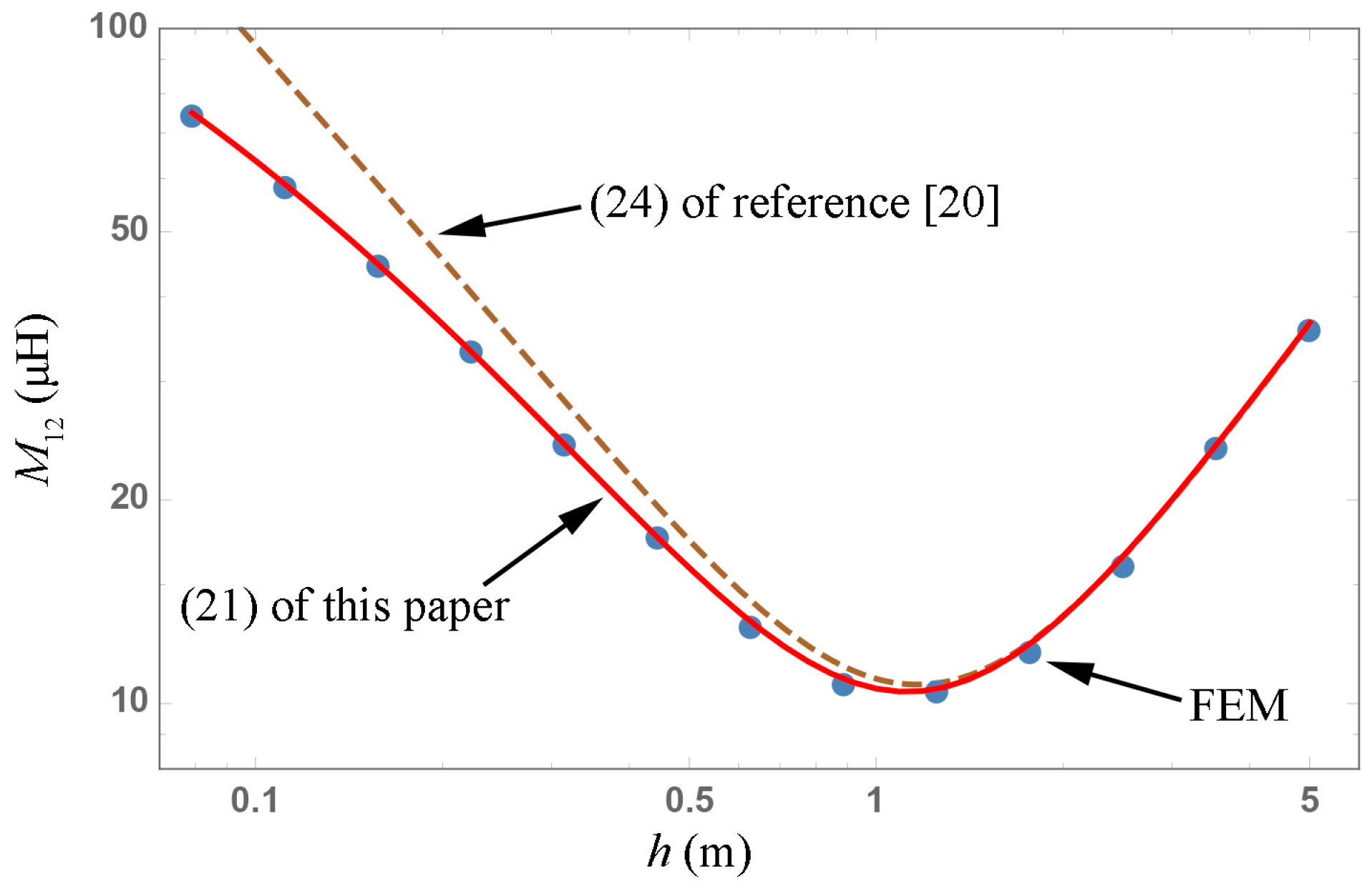
In the fourth comparison,
and the coils remain aligned at the ends. The pitch-length of coil-2 is twice that of coil-1, as specified in
Table 5. The mutual inductances are shown in
Figure 11, on varying
h.
In the case of unequal pitch lengths, the expressions related to the angular coordinates in Equation (24) of [
20] are eliminated. When
h is large and the angular coordinates of the midpoint of the conductors are
(coil-1) and
(coil-2), as shown in
Table 5, the result of Equation (24) in [
20] is similar to those obtained from Equation (21) of this paper and the FEM. However, if coil-2 is rotated by a certain angle around the
z-axis, different from
Figure 9, the result of Equation (24) in [
20] will not change with
θ. The general applicability of this formula is lesser than Equation (21) of this paper. Equation (38) of [
13] is valid, only when
h is small.
Finally, we consider filaments with different heights. One end of each coil is aligned at plane,
, and
. The other geometric parameters are listed in
Table 6. The pitch- length (
h) dependence of the mutual inductance is presented in
Figure 12.
When the heights of the coils are different, Equation (24) of [
20] cannot be used. From the other results, it can be observed that Equation (21) of this paper is in good agreement with the FEM results, and Equation (38) of [
13] is valid, only when
h is small. The curve of Equation (21) of this paper is not smooth, which is an interesting phenomenon. This is because the helical conductors approach and move away, in turn, from each other, as coil-2 is lengthened. The validity of Equation (21) of this paper is verified from the above five comparisons, demonstrating that this equation is suitable for the mutual inductance calculation of finite-length coaxial helical filaments for any geometrical parameter.
6.2. Comparison with Respect to Finite-Length Coaxial Helical Tape Coils and the Effect of the Inverse Mellin Transform
The geometric parameters of the coils in
Figure 3 are listed in
Table 7, for comparison between Equation (35) of this paper, Equation (41) of [
20], and the FEM. The ends of the coils are aligned, and the angles related to the width of the tape are equal (
). The tape-width (
) dependence of the mutual inductance is presented in
Figure 13. Similar to the FEM model in
Section 6.1, the radial thickness of the coil model for the tape coils is 10 mm, and the radial mid-points of the model are located on the tape conductors, which are treated by analytical calculations. Moreover, as shown in
Figure 14, the terminal leads are connected to the ends of the coil center lines.
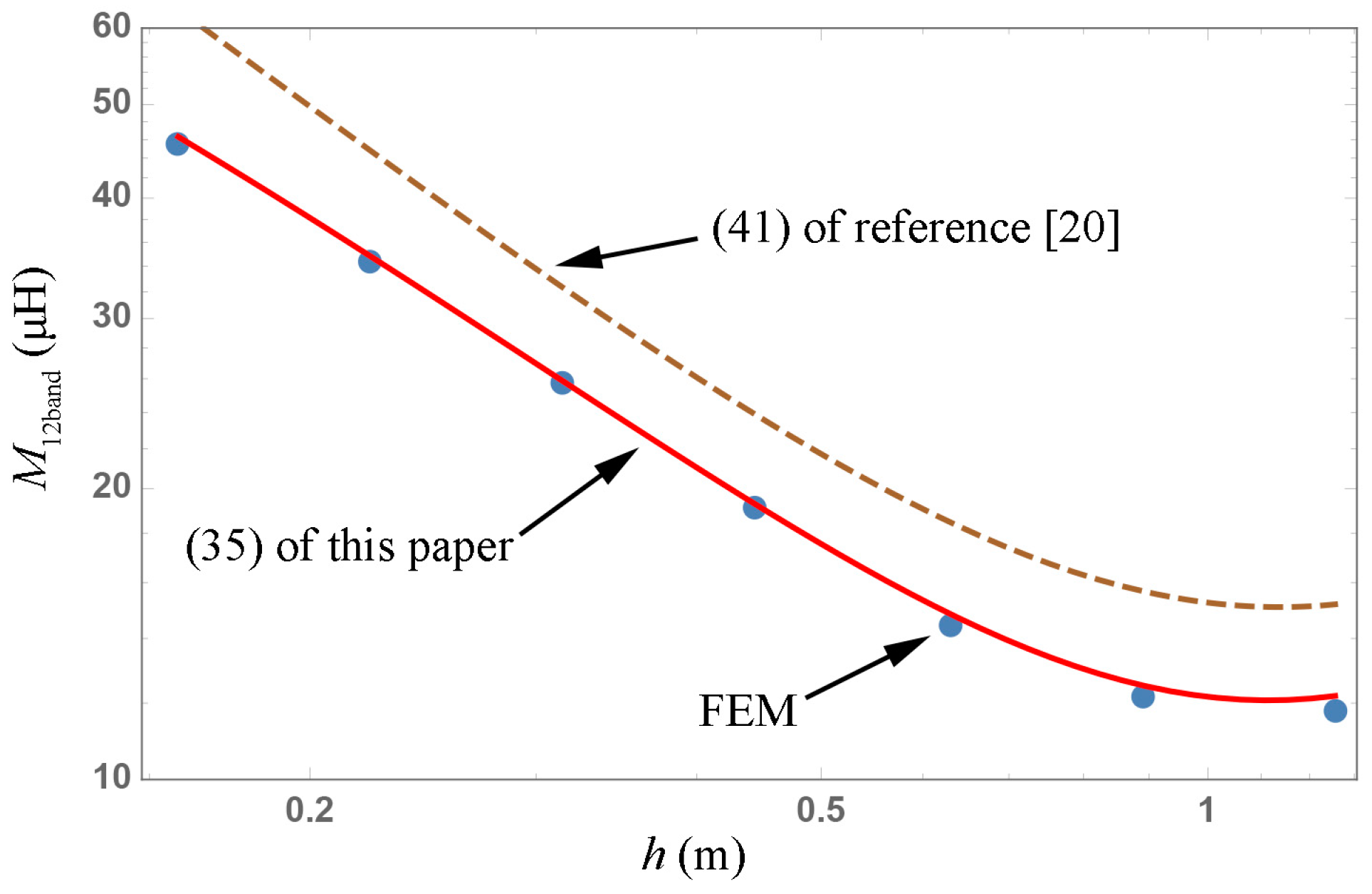
From
Figure 13, it can be observed that Equation (35) of this paper is in good agreement with the FEM; however, there are still certain deviations between Equation (41) of [
20] and the above-mentioned two methods. It is worth noting that, when
approaches zero, the calculation result should approach the mutual inductance (
) of the filaments, with
, in
Figure 8. However, Equation (41) in [
20] does not exhibit this property. In addition, when the mutual inductance of the helical tape coils was derived by integrating the rotation angle of the expression for the mutual inductance of helical filaments, the applicability of the latter Equation (21) to the coil’s geometric parameters was inherited by the former Equation (35); therefore, from the comparisons in
Section 6.1, we can see that Equation (35) of this paper has the most general applicability for different geometric parameters, similar to Equation (21).
For twisted pairs of tape conductors which are common in practice, let both coils of
Figure 3 have the same radius and the ends aligned, the angles related to the width of the wires are equal to
(
). All the geometric parameters are shown in
Table 8. Similar to the third comparison in 6.1, the angular coordinates (
θ) of the midpoints of the centerlines are 0 and π, respectively, then the coils are closely wound together. The pitch-length (
h) dependence of the mutual inductance are presented in
Figure 15.
For the same reason as the third comparison in
Section 6.1, Equation (38) of [
13] cannot be used. It can be seen from
Figure 15 that Equation (35) in this paper is also consistent with the FEM result. The results of Equation (41) in [
20] have some deviation from the former two in all cases in
Figure 15. Since both coils have the same radius, the numerical integration convergence of Equation (35) is also a bit slow.
When the tape conductors in
Figure 3 are closely wound, the inverse Mellin transform can be used for accelerating the calculation speed of the mutual inductance. The geometric parameters are listed in
Table 9, with angles of
, for the following comparison. The ends of the coils are also aligned. The pitch-length (
) dependence of the mutual inductance are presented in
Figure 16. Equation (38) of [
13] is used, as in
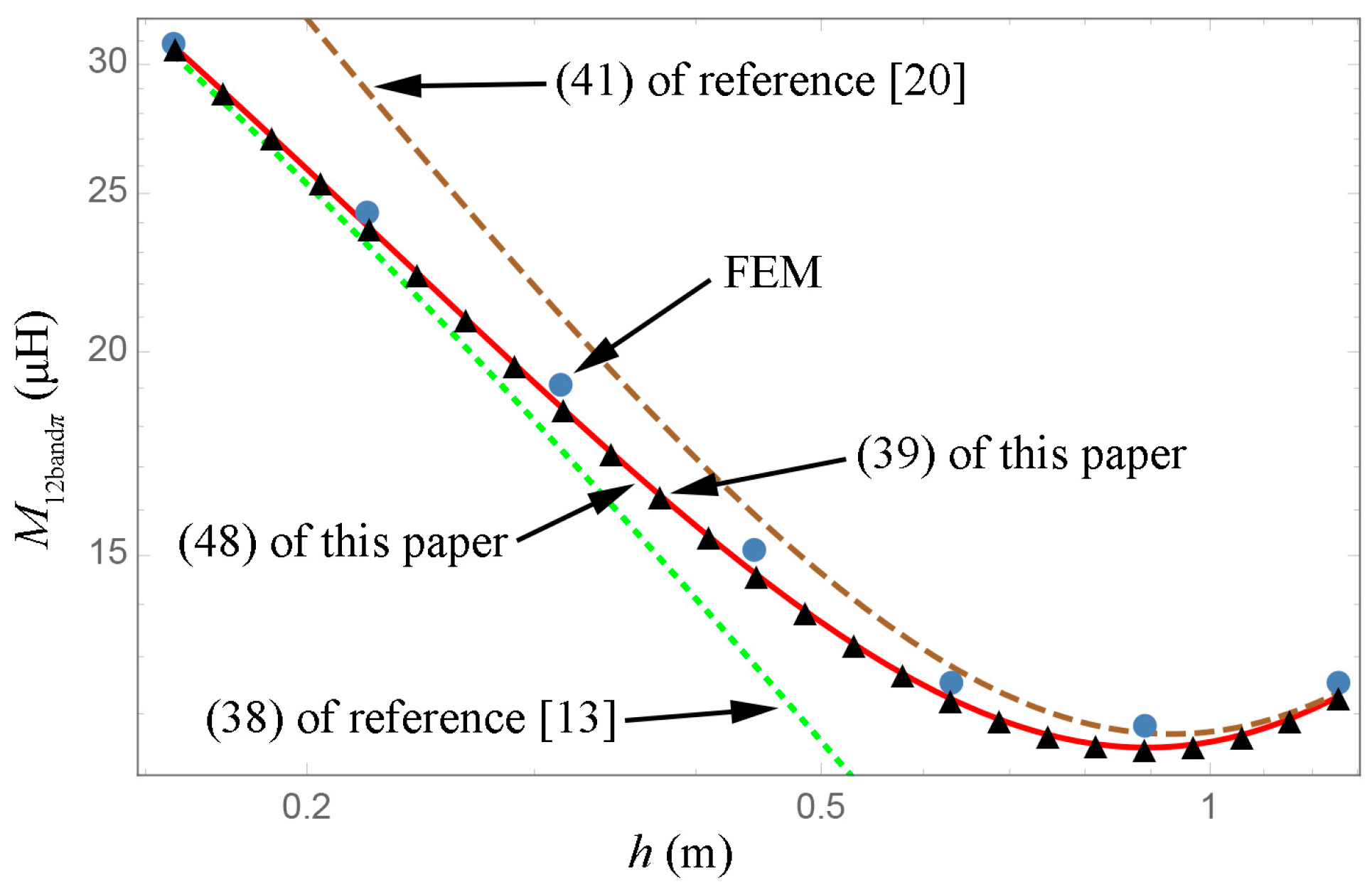
Section 6.1. It can be seen from
Figure 16 that the calculation results are the same for Equations (39) and (48) of this paper. Equation (41) of [
20] is in good agreement only with the FEM, for large
; on the contrary, Equation (38) of [
13] is suitable for small pitch lengths alone. FEM verifies the analytical expressions of this paper, in
Figure 16.
In order to demonstrate the characteristics of the series obtained by inverse Mellin transform,
Table 10 gives the calculation results and time consumption of Equations (39) and (48) at some typical points in
Figure 16. Among them, the “AccuracyGoal” of the numerical integration was set to 10 in Mathematica, and the series terms selected for sums are: only the first term, the 3 first terms, the 5 first terms and the 10 first terms, all the mutual inductance results were rounded to 10 significant figures. The computer running the analytical calculations has an Intel
® Core™ i5-5257U processor with 1866-MHz DDR3 memory (MacBook Pro, Apple Inc., Cupertino, California, U.S.). From
Table 10, we can see that the series in Equation (48) only needs to take the 10 first terms to achieve the same as the first 9 or 10 digits of the numerical integration result, and when the
is large, only 3 terms of the series are required to provide a number which is consistent with the first 10 significant digits of the numerical integration result. It is worth noting that, in most cases, only the first term of the series can lead to a result which fulfills the accuracy requirements of the practical engineering application. The reason why Equation (48) has such a characteristic is that this equation is an asymptotic series with extremely fast convergence. In aspects of time consumption, although the numerical integration has a very high calculation speed (about 200 ms), the series with the same accuracy is faster (about 5 ms) owing to the intrinsic property of itself. Compared to the first two analytical calculation methods, as shown in
Table 11, FEM is extremely time consuming, especially when the coil length is long. The FEM was running on a workstation configured as an Intel
® Xeon
® Silver 4110 processor and 2666-MHz DDR4 memory (Precision 7820, Dell Inc., Round Rock, Texas, U.S.), however, the solution time was greater than 25 h and computing resources were considerably occupied.