A Multi-objective Scheduling Optimization Model for Hybrid Energy System Connected with Wind-Photovoltaic-Conventional Gas Turbines, CHP Considering Heating Storage Mechanism
Abstract
:1. Introduction
- We design a HES including WT, PV, conventional gas turbine (CGT), IBDR, RE and CHP. RE can convert electric energy into heating energy for thermal–electrical synergy supply. A multi-objective thermal–electrical scheduling model and an output model of power and heat sources are proposed.
- Based on the HES maximum operating income and minimum load fluctuation as the objective function, a multi-objective optimization model for HES thermoelectric scheduling is constructed according to the heating storage mechanism under the objective functions. Then, a model solution algorithm is proposed that comprises two steps: linearization of the objective functions and constraints and determination of the optimal weight coefficients of the objective functions.
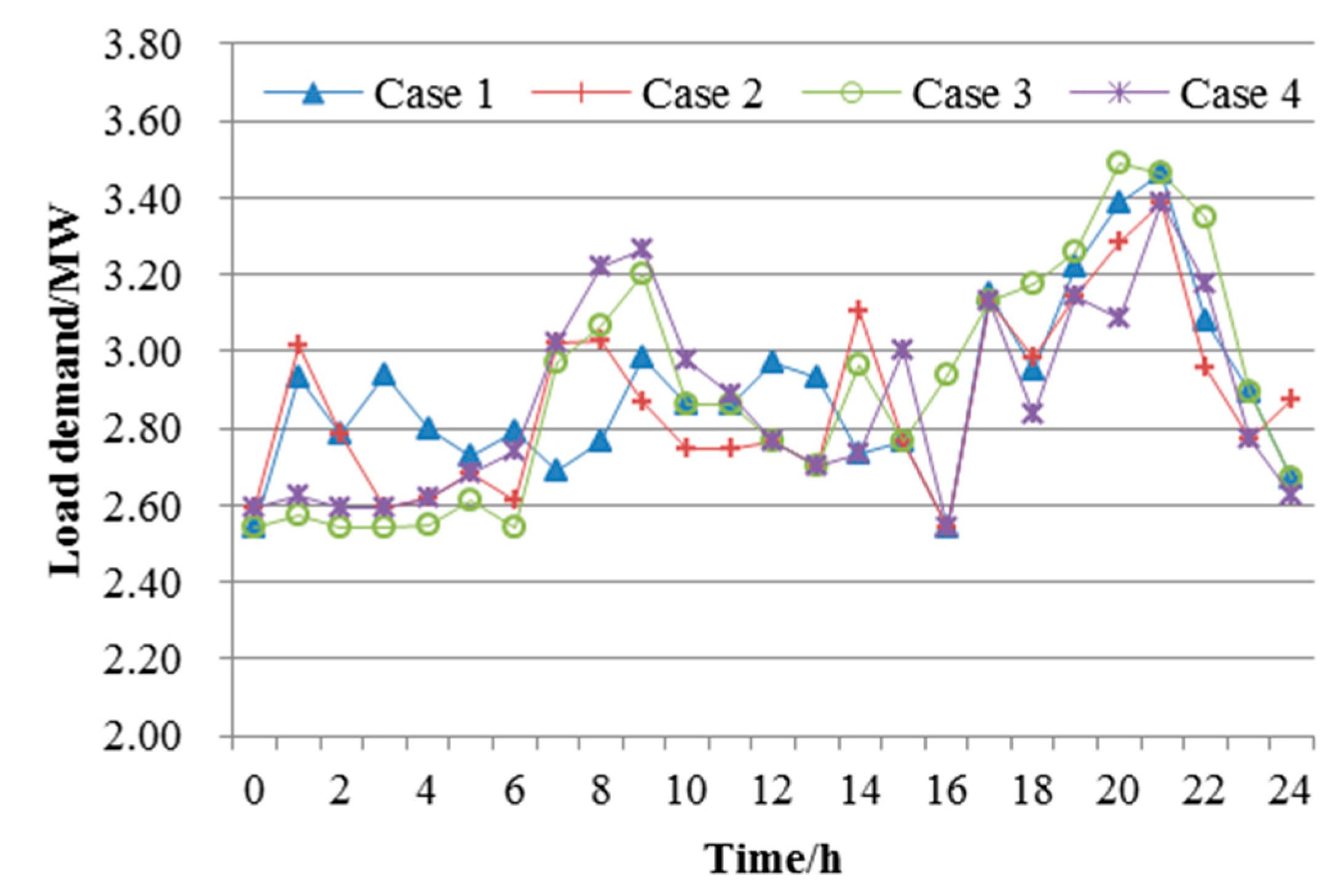
- Four HES operation cases are set and the selected simulation system is a microgrid on an eastern island of China, validating the effects of the proposed models and algorithms. First, the four cases are set by considering the system without and with RE-HS and PBDR to analyze their combined optimization effect. Then, calculate the results of HES scheduling under various conditions, and compare and analyze the calculation results.
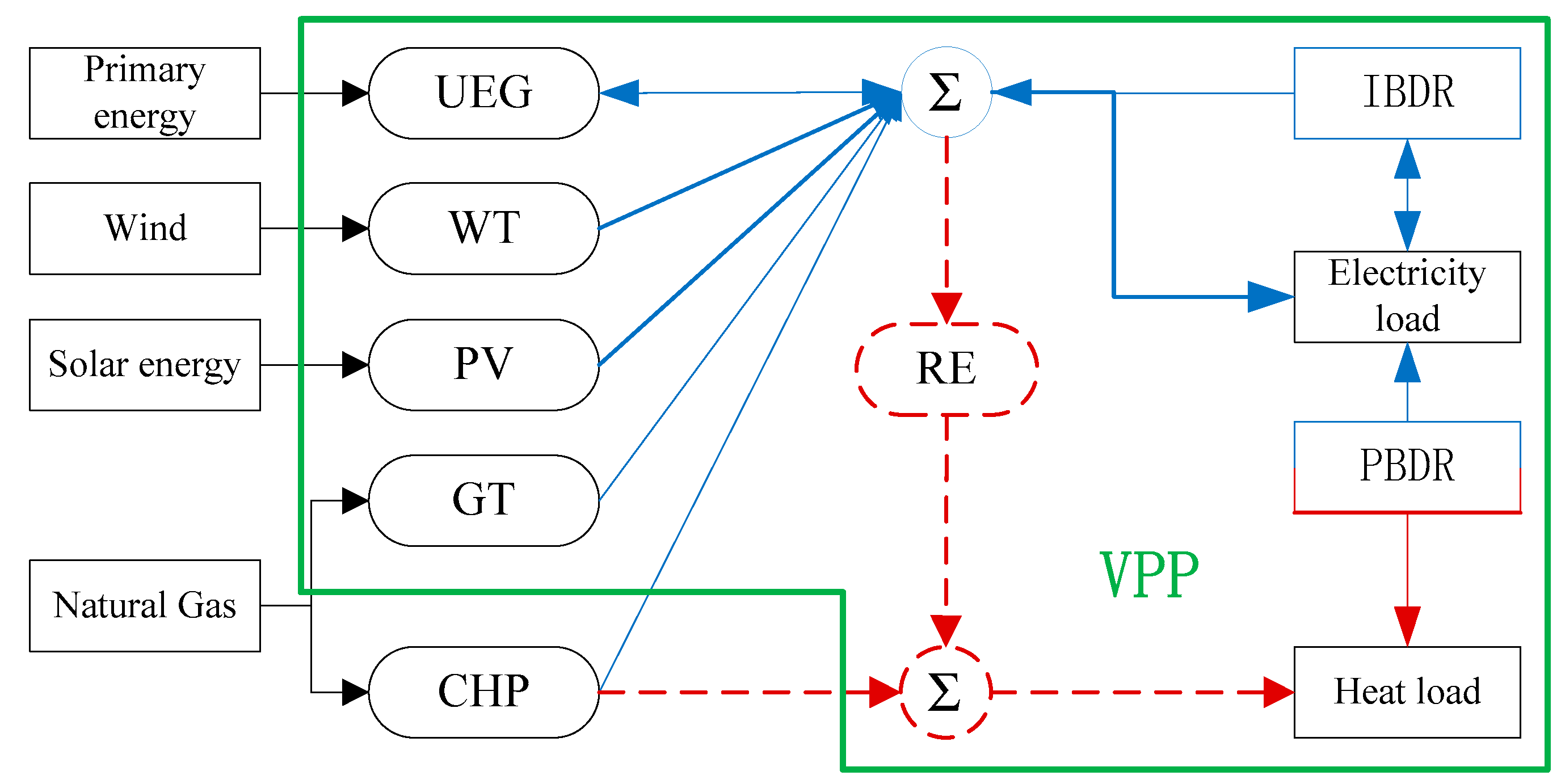
2. Hybrid Energy System Structure Description
2.1. Basic Structure
2.2. Electricity Power Output Model
2.2.1. WT Output
2.2.2. PV Output
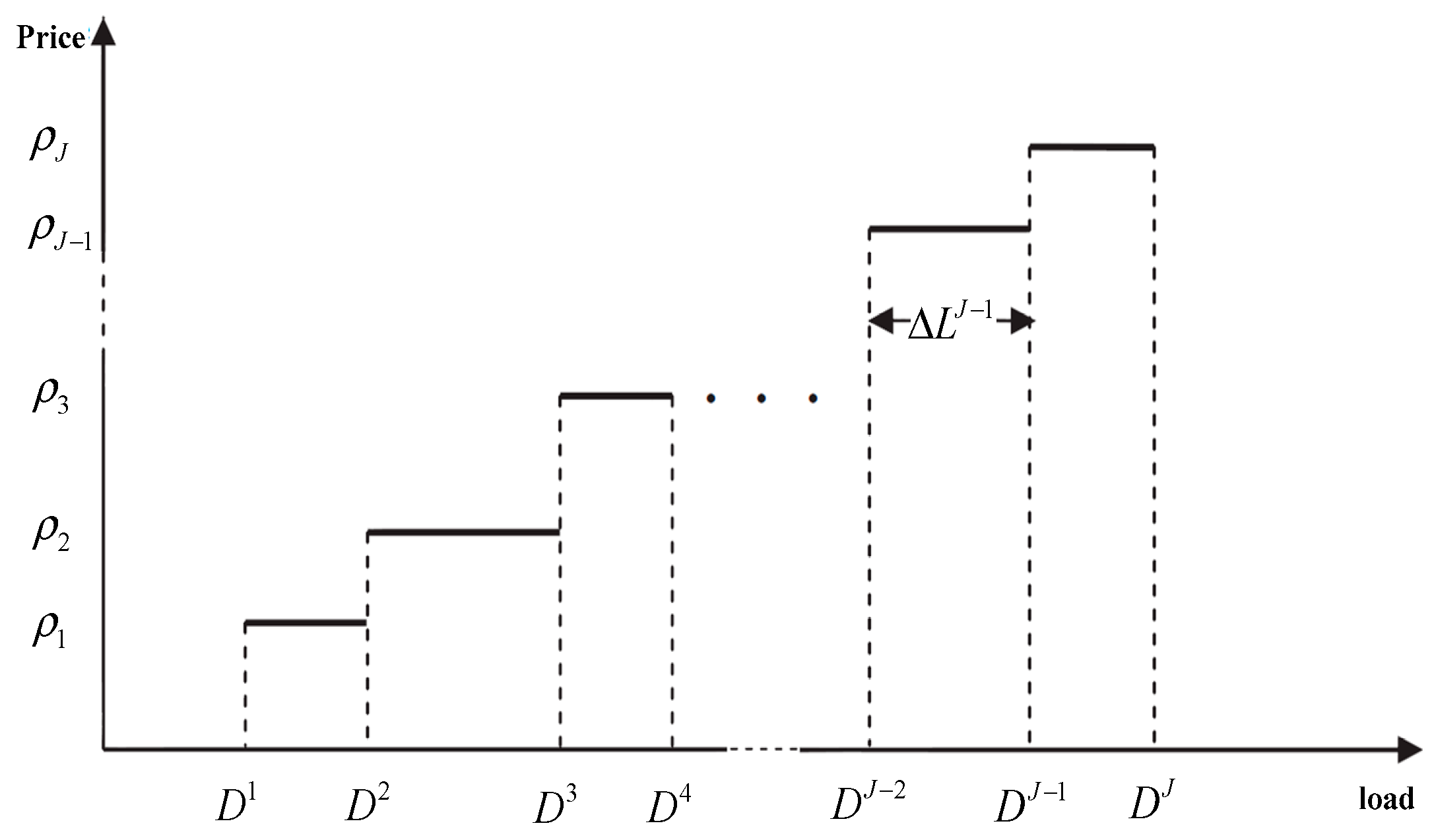
2.2.3. Incentive-Based DR Output Model
2.3. Heating Output Model
2.3.1. CHP Output Model
2.3.2. RE Output Model
3. Multi-Objective Scheduling Optimization Model
3.1. Objective Functions
3.1.1. The Maximum Operation Revenue Objective
3.1.2. The Minimum Load Fluctuation Objective
3.2. Constraint Conditions
3.2.1. Energy Balance Constraints
3.2.2. Power Source Operation Constraints
3.2.3. Heating Power Operation Constraints
3.2.4. System Reserve Constraints
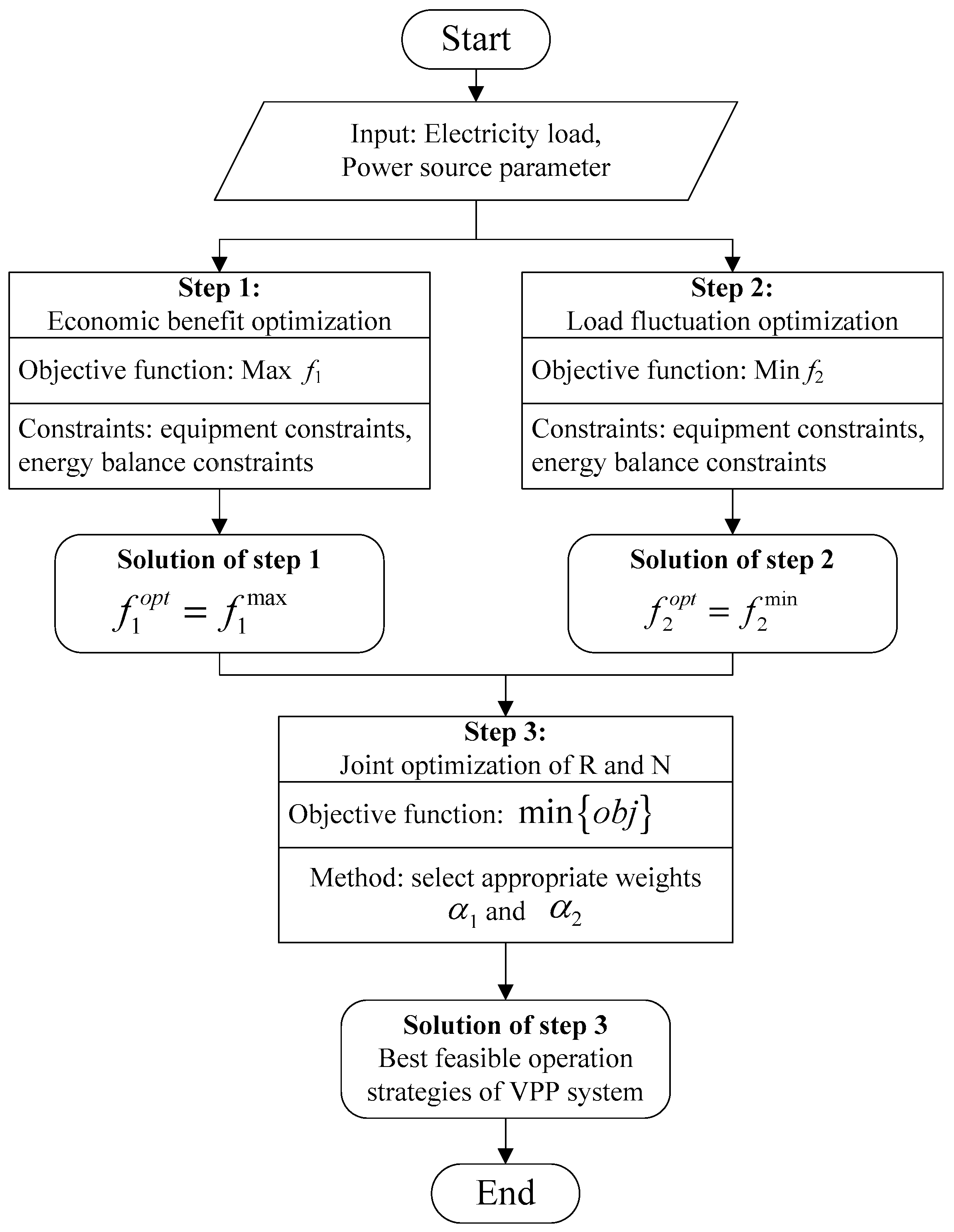
4. Solution Methodology for Multi-Objective Model
4.1. Linearization
4.1.1. Linearization of Objective Functions
4.1.2. Linearization of Constraint Conditions
4.2. Comprehensive Objective Function
5. HES Simulation Scenarios
6. Simulation Analysis
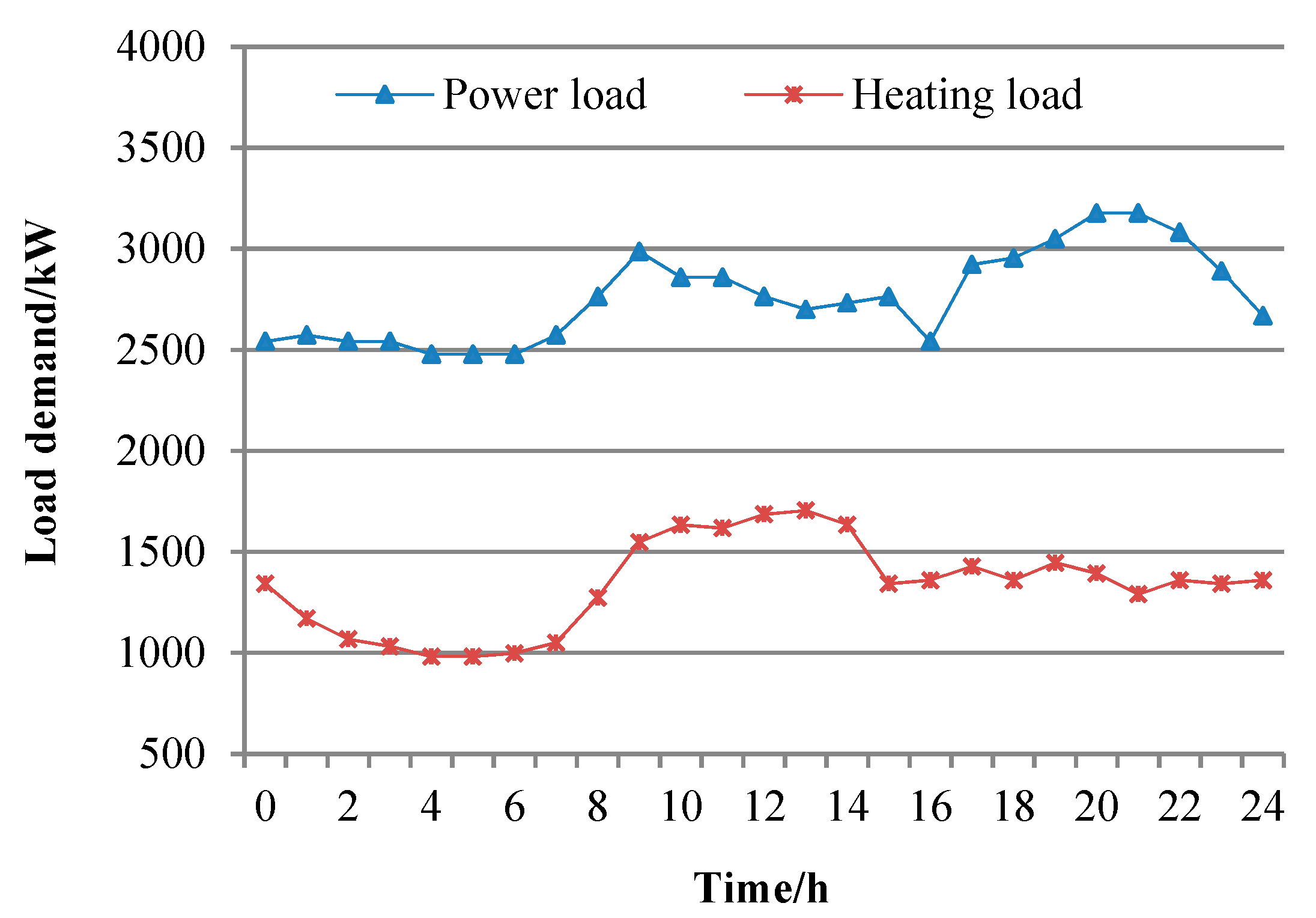
6.1. Basic Data
6.2. Scheduling Operation Results
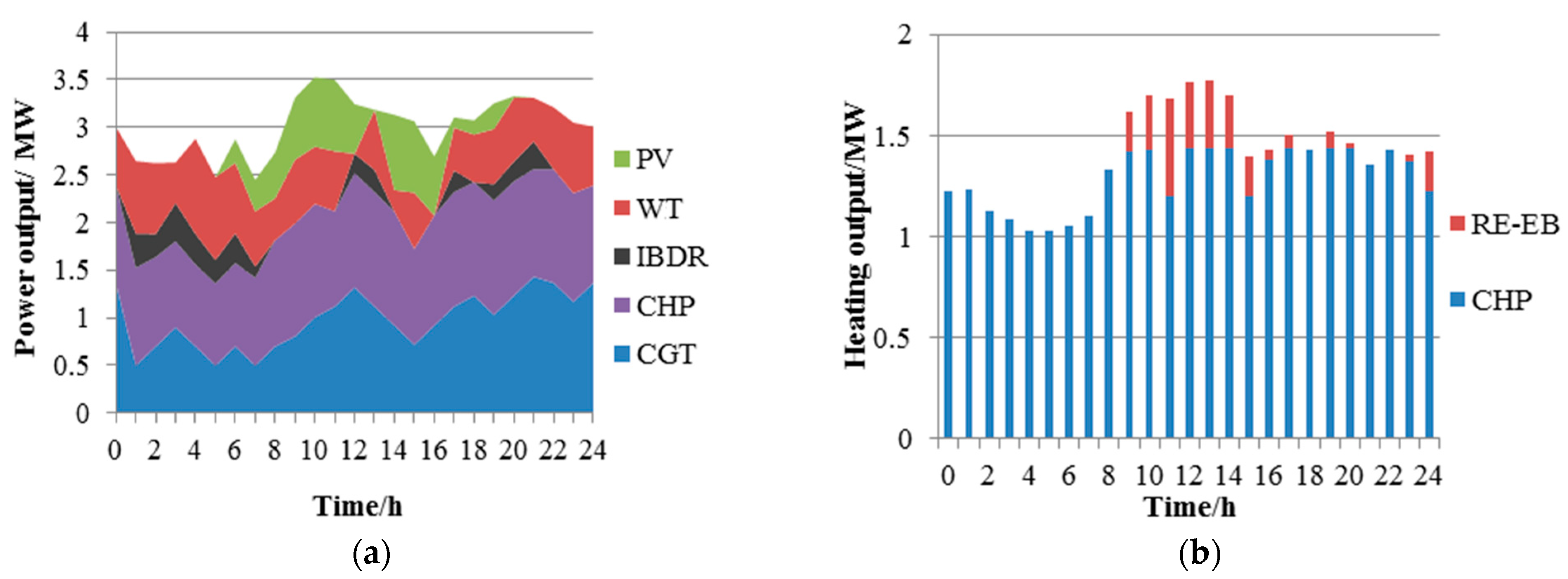
6.2.1. Self-Scheduling of HES Operation in Case 1
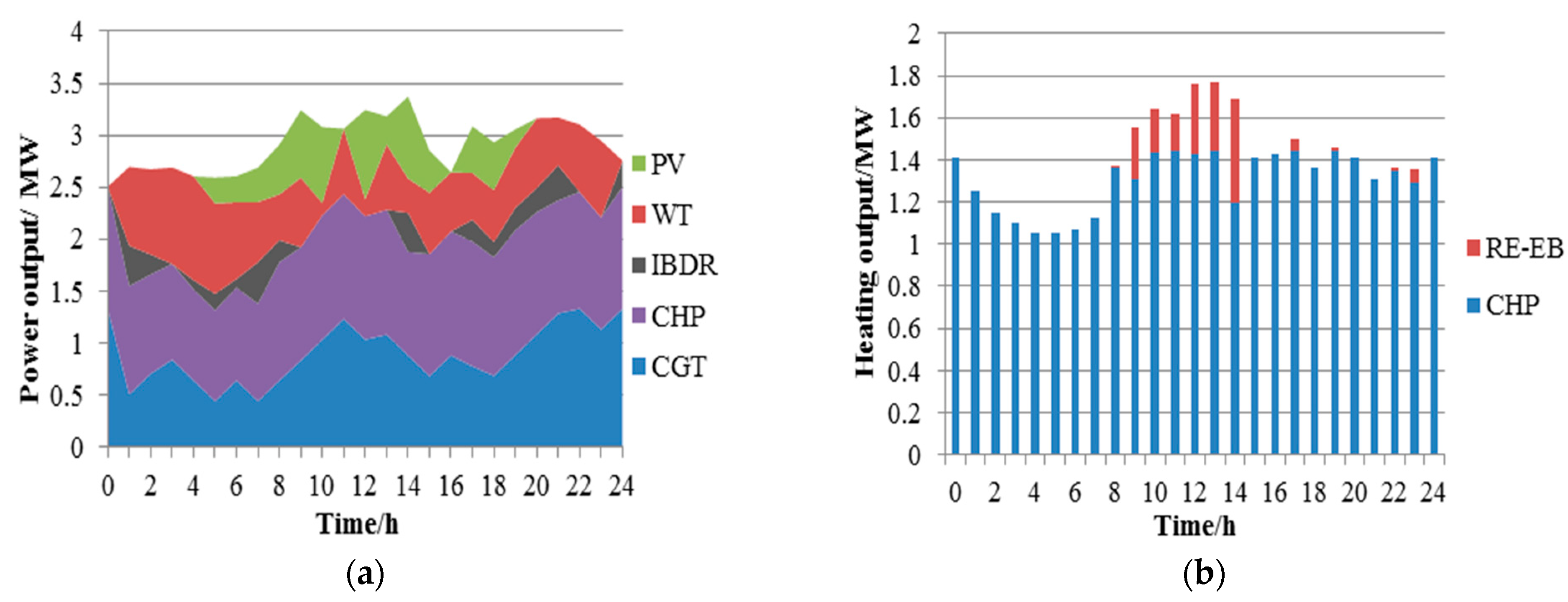
6.2.2. Self-Scheduling of HES Operation in Case 2
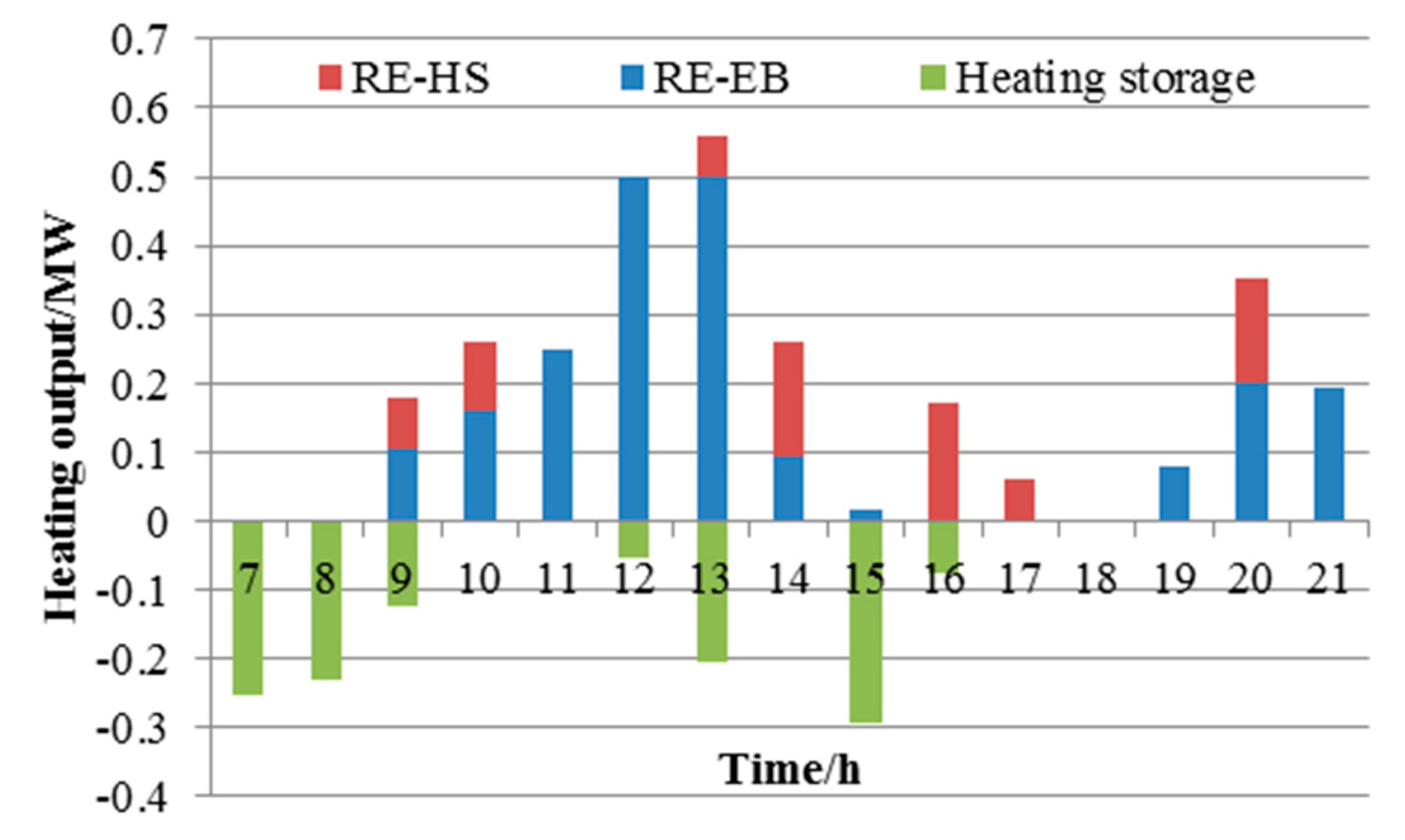
6.2.3. Self-Scheduling of HES in Case 3
6.2.4. Self-Scheduling of HES in Case 4
6.3. Results Analysis
7. Conclusions
- (1)
- HES can meet the load demand by making full use of DER. RE can not only convert the waste energy of WT and PV in the load valley period into heat energy, but also cooperate with CHP to meet the heating needs. In FTL mode, the main heat source is CHP, the main power source is CHP, WT and PV.WT and PV reserve IBDR and CGT can be provided. The difference is that IBDR is mainly concentrated in the period of load peak, and CGT is in the period of load valley.
- (2)
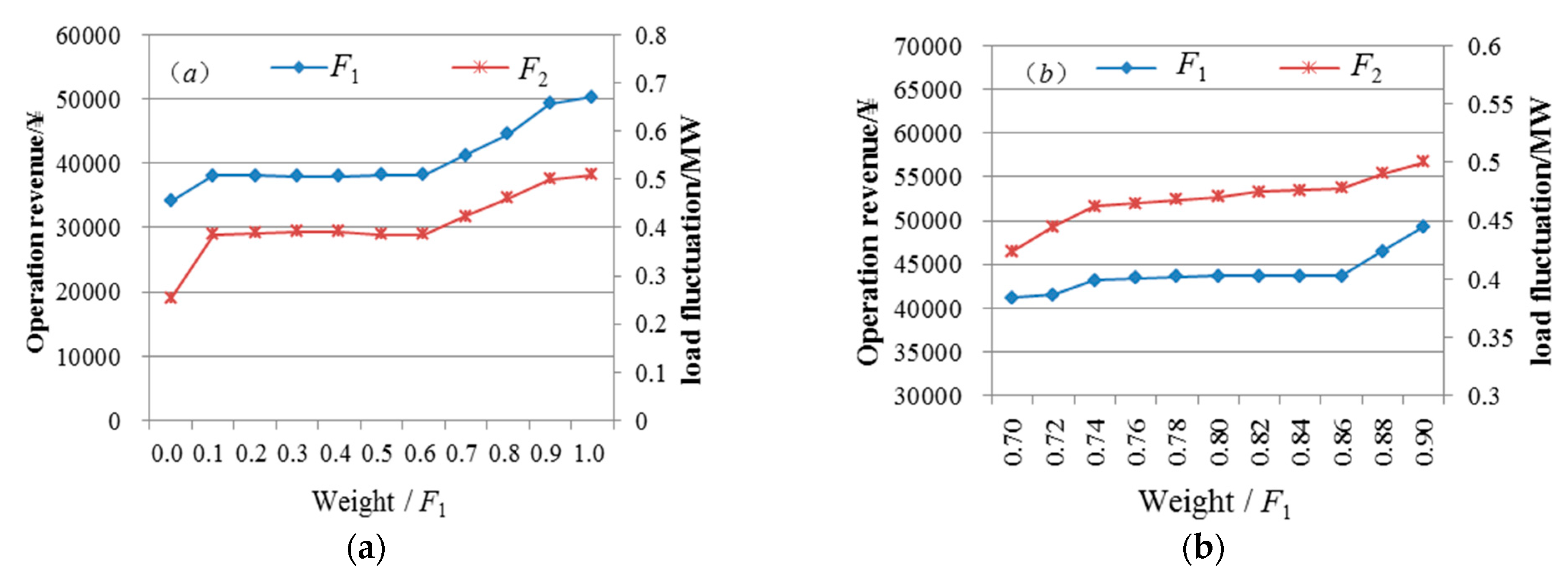
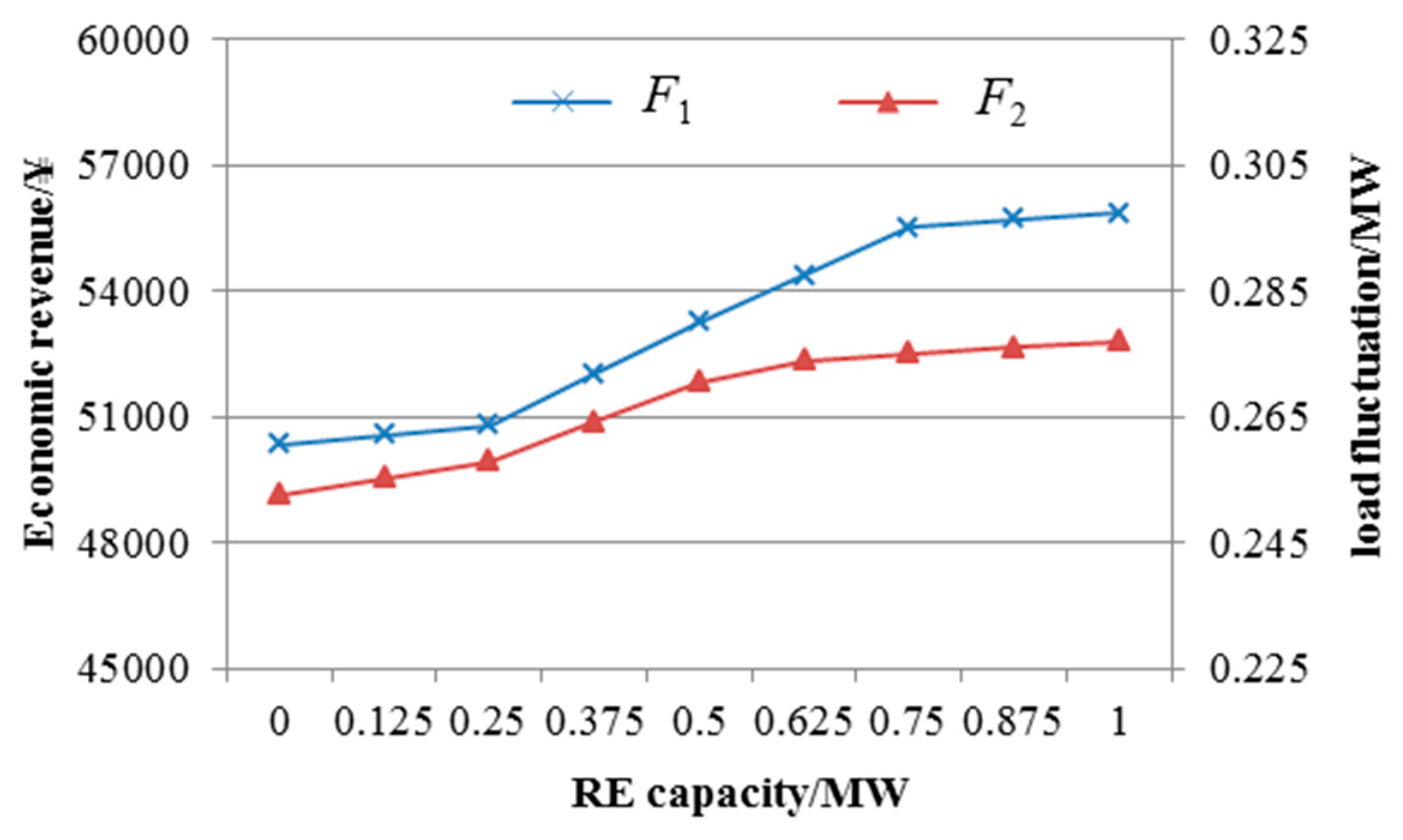
- The proposed HES operation multi-objective scheduling model can maximize operational benefits and minimize load fluctuations. Under the optimal operation revenue mode, the values of F1 and F2 are 50837.03 ¥ and 0.275 × 103 kW, respectively. Under the optimal load fluctuation mode, the values of F1 and F2 are 49852.45 ¥ and 0.246 × 103 kW, respectively. Under the integrated optimization mode, the values of F1 and F2 are 50337.03 ¥ and 0.253 × 103 kW. In comparison with the single-objective optimization mode, the objective function value of the integrated optimization mode can better consider the two optimization models and achieve optimal equilibrium HES operation.
- (3)
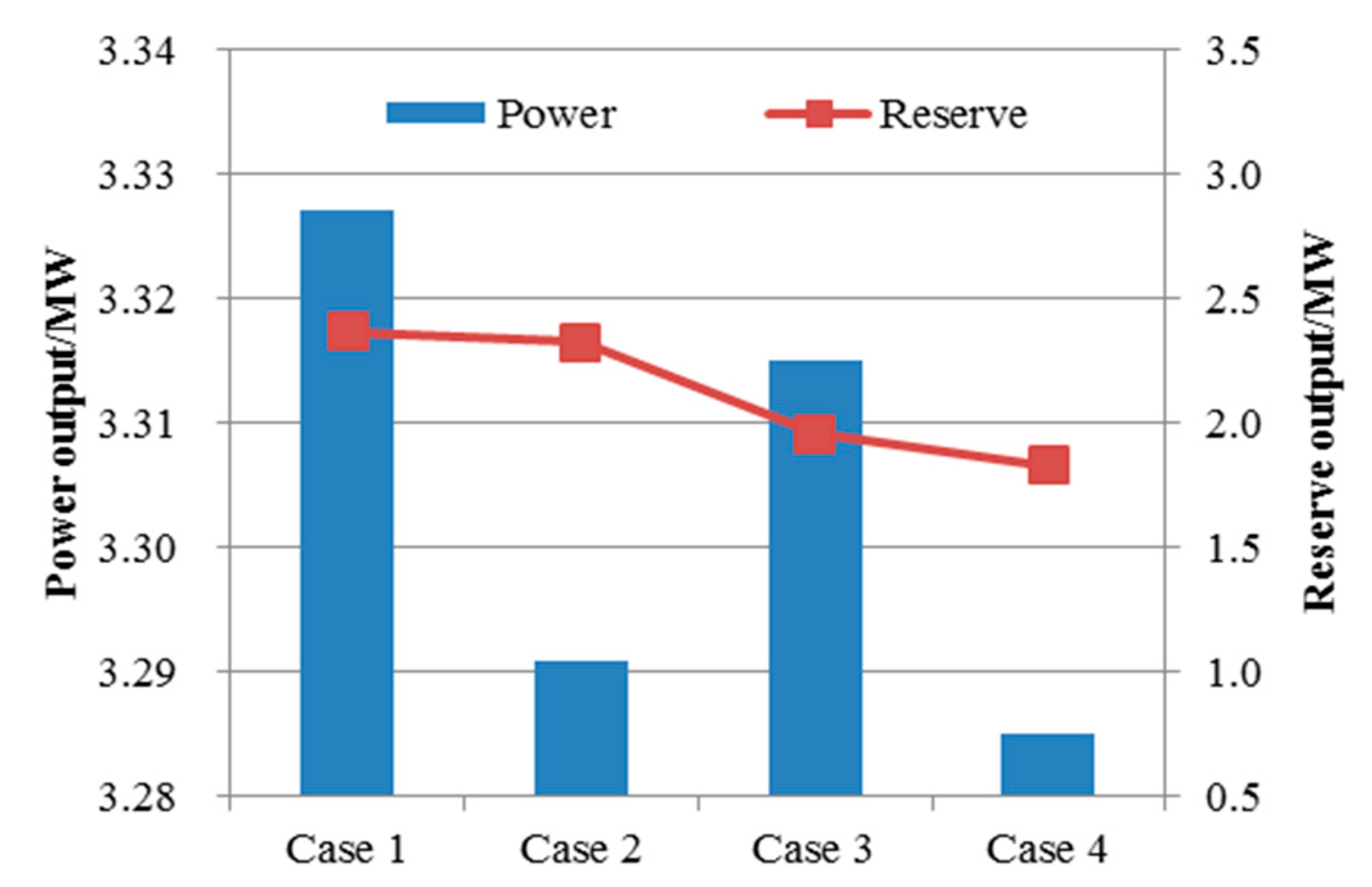
- RE-HS and PBDR have a synergistic optimization effect and can achieve optimal results of HES operation. Compared with the cases of HES scheduling with RE-HS or PBDR alone, when both of them are applied, the values of F1 and F2 in Case 1 increase from 50337.03 ¥ and 0.253 × 103 kW to 53311.05 ¥ and 0.268 × 103 kW in Case 4. The power output values of WT and PV increase from 13.575 × 103 kWh and 6.417 × 103 kWh in Case 1 to 15.172 × 103 kWh and 7.403 × 103 kW. The peak-to-valley ratio reaches the minimum, 1.333. Correspondingly, the power output of IBDR reaches the minimum in Case 4.
- (4)
- This paper focused on the aggregation utilization problem of WT, PV, CGT, and other distributed power sources with CHP, a multi-objective scheduling model and its corresponding algorithm are proposed. The simulation results also prove that the proposed model and algorithm are effective. However, the strong uncertainty of WT and PV directly influence the optimal decisions for HES operation. This problem should be investigated further and will be the focus of our future research.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| DERs | distributed energy |
| RE | regenerative electric |
| CHP | combined heat and power |
| VPP | virtual power plant |
| HES | hybrid energy system |
| IBDR | incentive demand response |
| FTL | follow-up electrical load |
| TOU | time-of use |
| MGs | micro-grids |
| WTs | wind turbine |
| PV | photovoltaic |
| the real-time wind speed | |
| the form factor | |
| the scale factor | |
| the maximum output of the WT | |
| the WT rated output | |
| the real-time wind velocity | |
| t | time |
| the solar radiation intensity | |
| , | the shape parameters of the beta distribution |
| the expected value of the PV radiation intensity | |
| the standard deviations of the PV radiation intensity | |
| output power | |
| efficiency | |
| S | total area |
| radiation intensity | |
| the minimum demand response | |
| the largest demand response | |
| actual load reduction | |
| j | the step |
| available load reduction | |
| the output power provided by IBDR | |
| the supply of heating power of CHP at time t | |
| the supply of electricity power of CHP at time t | |
| the maximum heating power supply | |
| the minimum values of CHP power supply under pure condensation conditions | |
| the minimum values of CHP power supply under pure condensation conditions | |
| the minimum heating power of CHP corresponding to the minimum electricity power | |
| , | the linear supply slopes of heating power and electric power of CHP |
| the minimum electricity power of CHP | |
| the heating power of CHP when the electric power reaches the minimum value | |
| the electric power for the heating supply of RE-EB | |
| the heating power supply of RE-EB | |
| the efficiency of thermal–electrical conversion | |
| the storage capacity for RE-HS | |
| the heat dissipation loss rate of HS | |
| the heating power used for RE-HS | |
| the exothermic power for RE-HS | |
| , | the endothermic and exothermic efficiency |
| the objective function of HES operation net revenue | |
| R | the operating income |
| the price of buying electricity from the grid | |
| the amount of electricity purchased | |
| the cost of power generation | |
| start | |
| ss | close |
| , , | the cost coefficients |
| the operation status | |
| and | the CGT cold and hot startup costs |
| the operating time | |
| the output price | |
| the cost function | |
| the cost of power generation | |
| startup–shutdown | |
| , | the indexes for time |
| the grid-prices | |
| power | |
| heating | |
| the output | |
| the thermal–electricity conversion coefficient of CHP | |
| the prices for power | |
| the prices for heating | |
| the heating output of RE | |
| the power input of RE | |
| the objective of HES load fluctuation | |
| the average load fluctuation for the HES throughout the entire scheduling period | |
| the net output of IBDR | |
| , , and | the power loss rates |
| the electricity purchased from the grid | |
| the input electricity of RE-EB | |
| the input electricity of RE-HS | |
| the status variables of IBDR | |
| the status variables of PBDR | |
| the amount of change after adding PBDR | |
| the demand | |
| the price | |
| the load demand before PBDR | |
| the load demand after PBDR | |
| the electricity price before PBDR | |
| the electricity price after PBDR | |
| the elasticity of price and demand | |
| the heating demand of terminal customers | |
| the heating output | |
| the status variable of implementing PBDR for the heating load | |
| the amount of load change before and after adding PBDR | |
| , | the upper limits of CGT |
| , | the lower limits of CGT |
| , | the maximum and minimum reserve outputs of IBDR in the reserve market |
| , | the maximum and minimum output of IBDR |
| the output of NE | |
| the revised output of NE | |
| the output of CHP under the working condition of the pure condensing condition | |
| the maximum output of RE | |
| , | the storage heating by the HS at the beginning and end of the schedule |
| , | the minimum and maximum capacities of HS under stable operation condition |
| the rated capacity of HS | |
| , | the maximum and minimum values of the HES output |
| ,, and | the upper reserve factors of power load, WT, and PV |
| , | the lower reserve factors of WT and PV |
| , | the upper and lower reserve coefficients of the heating load |
| the time period of CGT operation at the start of the scheduling period | |
| , | set |
References
- Mashhour, M.; Golkar, M.A.; Moghaddas-Tafreshi, S.M. Extending Market Activities for a Distribution Company in Hourly-ahead Energy and Reserve Markets–Part I: Problem Formulation. Energy Convers. Manag. 2011, 52, 477–486. [Google Scholar] [CrossRef]
- David, S.; Arturs, P.; Ioulia, P. Benefits and Cost Implications from Integrating Small Flexible Nuclear Reactors with Off-shore Wind Farms in a Virtual Power Plant. Energy Policy 2012, 46, 558–573. [Google Scholar]
- Wei, H.K.; Liu, J.; Yang, B. Cost-benefit Comparison Between Domestic Solar Water Heater (DSHW) and Building Integrated Photovoltaic (BIPV) Systems for Households in Urban China. Appl. Energy 2014, 126, 47–55. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, C.Y.; Ding, Y. Review of Real-time Electricity Markets for Integrating Distributed Energy Resources and Demand Response. Appl. Energy 2015, 138, 695–706. [Google Scholar] [CrossRef]
- European Virtual Fuel Cell Power Plant Management Summary Report [EB/OL]. 2012-08-13. Available online: http:ec.europa.eu/energy/efficiency/industry/doc/euvpp.pdf/ (accessed on 13 August 2012).
- Rossi, F.; Velazquez, D. A Methodology for Energy Savings Verification in Industry with Application for a CHP (Combined Heat and Power) plant. Energy 2015, 89, 528–544. [Google Scholar] [CrossRef]
- Ju, L.; Tan, Z.; Yuan, J.; Tan, Q.; Li, H.; Dong, F. A Bi-level Stochastic Scheduling Optimization Model for a Virtual Power Plant Connected to a Wind–Photovoltaic–Energy Storage System Considering the Uncertainty and Demand Response. Appl. Energy 2016, 171, 184–199. [Google Scholar] [CrossRef]
- Tan, Z.F.; Wang, G.; Ju, L.W.; Tan, Q.K.; Yang, W.H. Application of CVaR Risk Aversion Approach in the Dynamical Scheduling Optimization Model for Virtual Power Plant Connected with Wind-Photovoltaic-Energy Storage System with Uncertainties and Demand Response. Energy 2017, 124, 198–213. [Google Scholar] [CrossRef]
- Tan, Z.F.; Zhang, H.J.; Shi, Q.S.; Song, Y.H.; Ju, L.W. Multi-objective Operation Optimization and Evaluation of Large-scale NG Distributed Energy System Driven by Gas-steam Combined Cycle in China. Energy Build. 2014, 76, 572–587. [Google Scholar] [CrossRef]
- Yu, S.; Wei, Z.; Sun, G.Q.; Sun, Y.; Wang, D. A Bidding Model for a Virtual Power Plant Considering Uncertainties. Autom. Electric Power Syst. 2014, 38, 44–49. [Google Scholar]
- Project Interim Report[R/OL]. 20 February 2013. Available online: http://www.web2energy.com/ (accessed on 20 February 2013).
- Zapata, J.; Vandewalle, J.; D’haeseleer, W. A Comparative Study of Imbalance Reduction Strategies for Virtual Power Plant Operation. Appl. Thermal Eng. 2014, 71, 847–857. [Google Scholar] [CrossRef]
- Saeed, R.D.; Mohammad, K.S. Risk-based Profit Allocation to DERs Integrated with a Virtual Power Plant Using Cooperative Game Theory. Electrical Power Syst. Res. 2015, 121, 368–378. [Google Scholar]
- Moghaddam, I.G.; Nick, M.; Fallahi, F.; Sanei, M.; Mortazavi, S. Risk-averse Profitbased Optimal Operation Strategy of a Combined Wind Farm-Cascade Hydro System in an Electricity Market. Renew. Energy 2013, 55, 252–259. [Google Scholar] [CrossRef]
- Pandzic, H.; Kuzle, I.; Capuder, T. Virtual Power Plant Mid-term Dispatch Optimization. Appl. Energy 2013, 101, 134–141. [Google Scholar] [CrossRef]
- Wang, Y.; Ai, X.; Tan, Z.; Yan, L.; Liu, S. Interactive Dispatch Modes and Bidding Strategy of Multiple Virtual Power Plants Based on Demand Response and Game Theory. IEEE Trans. Smart Grid 2015, 9, 1–10. [Google Scholar] [CrossRef]
- Carrion, M.; Arroyo, J.M. A Computationally Efficient Mixed-integer Linear Formulation for the Thermal Unit Commitment Problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Erdinc, O. Economic Impacts of Small-scale Own Generating and Storage Units and Electric Vehicles Under Different Demand Response Strategies for Smart Households. Appl. Energy 2014, 126, 142–150. [Google Scholar] [CrossRef]
- Aboelsood, Z.; Hossam, A.G.; Ahmed, E. Optimal Planning of Combined Heat and Power Systems within Microgrids. Energy 2015, 93, 235–244. [Google Scholar]
- Zhang, N.; Wang, Z.F.; Noam, L.; Wei, H. Advancement of Distributed Energy Methods by a Novel High Efficiency Solar-Assisted Combined Cooling, Heating and Power System. Appl. Energy 2019, 218, 179–186. [Google Scholar] [CrossRef]
- Aluisio, B.; Dicorato, M.; Forte, G.; Trovato, M. An Optimization Procedure for Microgrid Day-Ahead Operation in the Presence of CHP facilities. Sustain. Energy Grids Netw. 2017, 11, 34–45. [Google Scholar] [CrossRef]
- Taher, N.; Rasoul, A.A.; Alireza, R.; Babak, A. A New Multi-objective Reserve Constrained Combined Heat and Power Dynamic Economic Emission Dispatch. Energy 2012, 42, 530–545. [Google Scholar]
- Mohammad, R.R.; Mohsen, M.; Saied, E. Economic Analysis of Hybrid System Consists of Fuel Cell and Wind Based CHP System for Supplying Grid-Parallel Residential Load. Energy Build. 2014, 68, 476–487. [Google Scholar]
- Wille, H.B.; Erge, T.; Wittwer, C. Decentralised Optimisation of Cogeneration in Virtual Power Plants. Solar Energy 2010, 84, 604–611. [Google Scholar] [CrossRef]
- Giuntoli, M.; Poli, D. Optimized Thermal and Electrical Scheduling of a Large Scale Virtual Power Plant in the Presence of Energy Storages. IEEE Trans. Smart Grid 2013, 4, 942–955. [Google Scholar] [CrossRef]
- Manijeh, A.; Kazem, Z.; Heresh, S. A Multi-follower Bilevel Stochastic Programming Approach for Energy Management of Combined Heat and Power Micro-Grids. Energy 2018, 149, 135–146. [Google Scholar]
- Aalami, H.A.; Pashaei-Didani, H.; Nojavan, S. Deriving nonlinear models for incentive-based demand response programs. Int. J. Electrical Power Energy Syst. 2019, 106, 223–231. [Google Scholar] [CrossRef]
- Eissa, M.M. First time real time incentive demand response program in smart grid with “i-Energy” management system with different resources. Appl. Energy 2018, 212, 607–621. [Google Scholar] [CrossRef]
- Eissa, M.M. Developing incentive demand response with commercial energy management system (CEMS) based on diffusion model, smart meters and new communication protocol. Appl. Energy 2019, 236, 273–292. [Google Scholar] [CrossRef]
- Guo, Y.H.; Hu, B.; Wan, L.Y.; Xie, K.G.; Yang, H.J.; Shen, Y.M. Optimal Economic Short-term Scheduling of CHP Microgrid Incorporating Heat Pump. Autom. Electric Power Syst. 2015, 39, 16–22. [Google Scholar]
- Ju, L.W.; Li, H.H.; Zhao, J.W. The Multi-objective Stochastic Scheduling Optimization Model for Connecting a Virtual Power Plant with Wind-Photovoltaic-Electric Vehicles Considering Uncertainties and Demand Response. Energy Convers. Manag. 2016, 128, 160–177. [Google Scholar] [CrossRef]

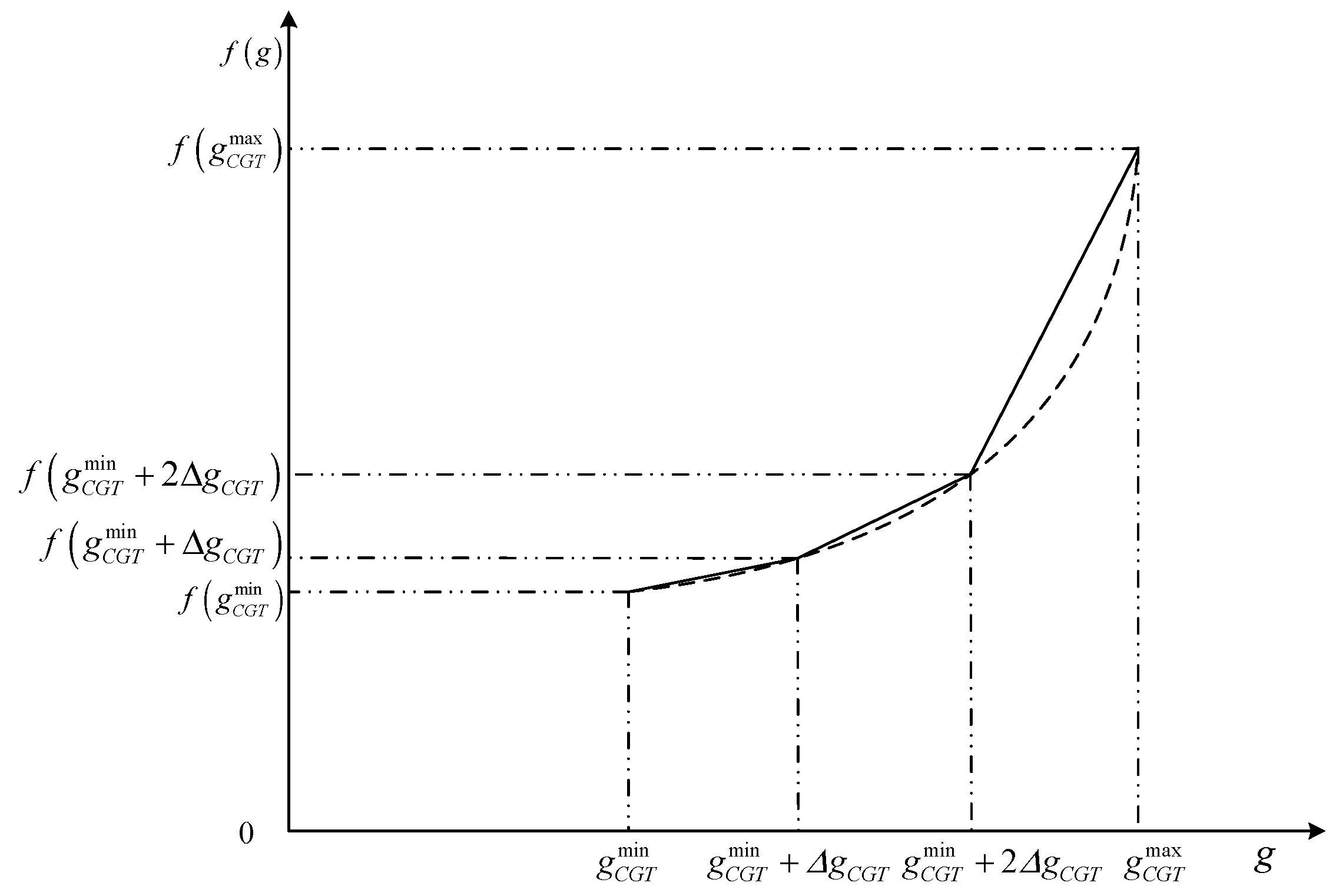



| Objective | Objective Value | CGT | WT | PV | IBDR | CHP | RE-EB | Waste Energy | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1/¥ | F2/× 103 kW | Power | Heating | WT | PV | ||||||
| F1 | 50837.03 | 0.275 | 26.61 | 11.13 | 5.39 | 3.285 | 25.857 | 31.028 | 2.54 | 4.835 | 3.31 |
| F2 | 49852.45 | 0.246 | 36.90 | 3.71 | 2.11 | 3.435 | 26.132 | 31.358 | 2.21 | 12.25 | 6.60 |
| Scenario | Power Load × 103 kW | Heating Load × 103 kW | Peak–Valley Ratio | |||||
|---|---|---|---|---|---|---|---|---|
| Peak | Float | Valley | Peak | Float | Valley | Power | Heating | |
| Before PBDR | 24.141 | 24.522 | 20.425 | 11.646 | 13.198 | 8.551 | 1.282 | 1.737 |
| After PBDR | 23.176 | 24.414 | 20.833 | 11.180 | 13.149 | 8.722 | 1.207 | 1.703 |
| Difference | −0.966 | −0.108 | 0.408 | −0.466 | −0.049 | 0.171 | −0.075 | −0.034 |
| Scenario | Heating Output/× 103 kW | Heating Storage/× 103 kWh | Waste Energy/× 103 kWh | RE Revenue/¥ | ||||
|---|---|---|---|---|---|---|---|---|
| RE-EB | EB-HS | Peak Load | Float Load | Valley Load | WT | PV | ||
| Case 3 | 2.105 | 0.784 | 0.154 | 0.355 | 0.504 | 1.118 | 2.180 | 686.71 |
| Case 4 | 1.932 | 0.767 | 0 | 0.425 | 0.584 | 0.798 | 1.30 | 642.37 |
| Scenario | Weight | Power Output/× 103 kWh | Heating Output/× 103 kWh | Objective Value | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | F2 | CGT | WT | PV | CHP | IBDR | CHP | RE-EB | RE-HS | F1/¥ | F2/× 103 kW | |
| Case 1 | 0.78 | 0.22 | 23.077 | 13.575 | 6.417 | 25.897 | 5.694 | 31.074 | 2.499 | - | 50337.03 | 0.253 |
| Case 2 | 0.72 | 0.28 | 21.044 | 13.894 | 6.503 | 26.046 | 5.616 | 31.256 | 1.958 | - | 52474.01 | 0.269 |
| Case 3 | 0.76 | 0.24 | 23.492 | 14.853 | 6.530 | 25.555 | 5.285 | 30.663 | 2.105 | 0.784 | 53259.95 | 0.273 |
| Case 4 | 0.75 | 0.25 | 20.085 | 15.172 | 7.403 | 25.394 | 5.122 | 30.476 | 1.932 | 0.767 | 53311.05 | 0.268 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Lu, Y.; Ju, L.; Wang, T.; Tan, Q.; Wang, J.; Tan, Z. A Multi-objective Scheduling Optimization Model for Hybrid Energy System Connected with Wind-Photovoltaic-Conventional Gas Turbines, CHP Considering Heating Storage Mechanism. Energies 2019, 12, 425. https://doi.org/10.3390/en12030425
Wang Y, Lu Y, Ju L, Wang T, Tan Q, Wang J, Tan Z. A Multi-objective Scheduling Optimization Model for Hybrid Energy System Connected with Wind-Photovoltaic-Conventional Gas Turbines, CHP Considering Heating Storage Mechanism. Energies. 2019; 12(3):425. https://doi.org/10.3390/en12030425
Chicago/Turabian StyleWang, Yao, Yan Lu, Liwei Ju, Ting Wang, Qingkun Tan, Jiawei Wang, and Zhongfu Tan. 2019. "A Multi-objective Scheduling Optimization Model for Hybrid Energy System Connected with Wind-Photovoltaic-Conventional Gas Turbines, CHP Considering Heating Storage Mechanism" Energies 12, no. 3: 425. https://doi.org/10.3390/en12030425
APA StyleWang, Y., Lu, Y., Ju, L., Wang, T., Tan, Q., Wang, J., & Tan, Z. (2019). A Multi-objective Scheduling Optimization Model for Hybrid Energy System Connected with Wind-Photovoltaic-Conventional Gas Turbines, CHP Considering Heating Storage Mechanism. Energies, 12(3), 425. https://doi.org/10.3390/en12030425





