Geomechanical Upscaling Methods: Comparison and Verification via 3D Printing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Artificial Rock by 3D Printing
2.2. Nanoindentation
2.2.1. Sample Preparation and Test
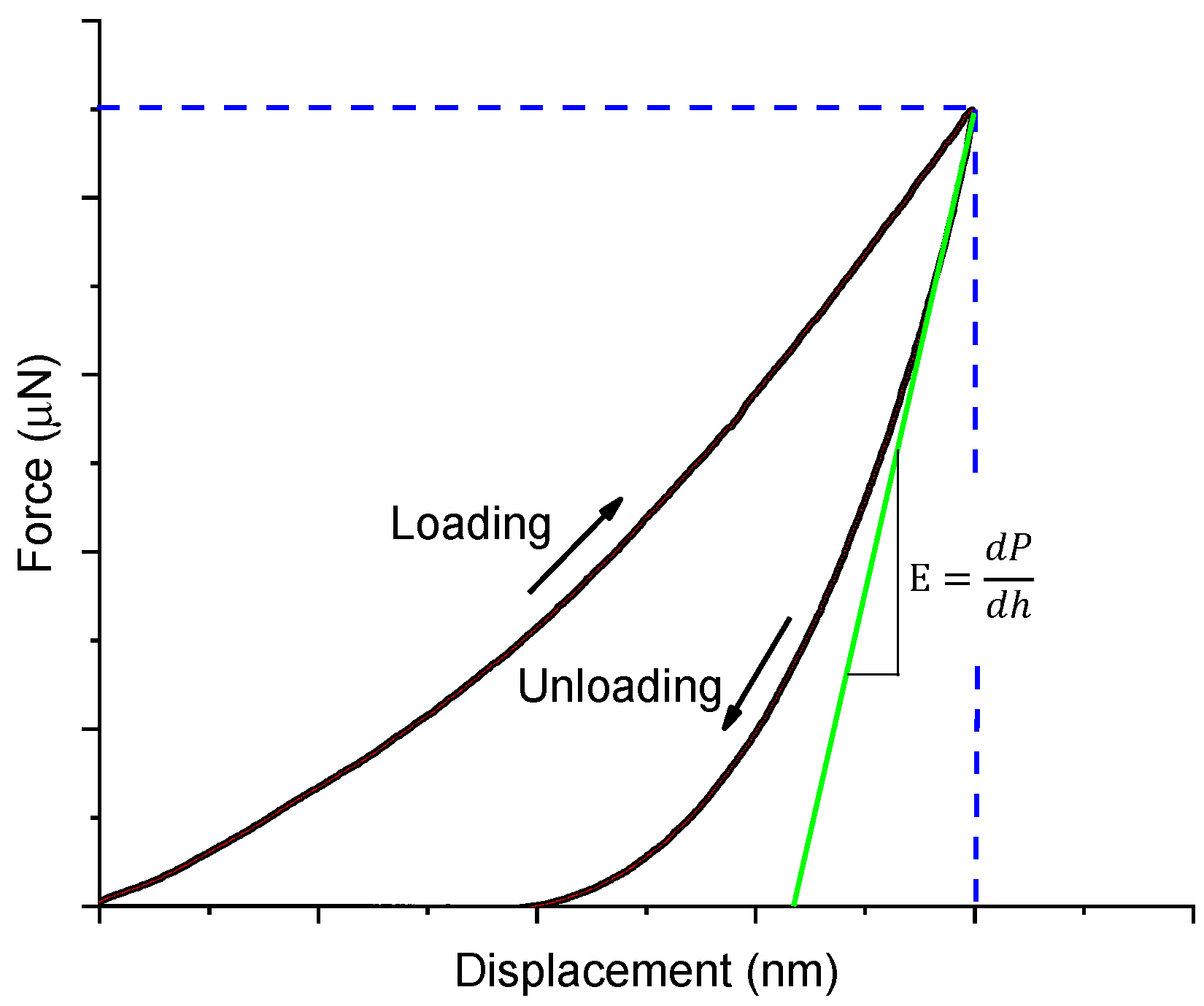
2.2.2. Nanoindentation Theory
2.2.3. Deconvolution Method
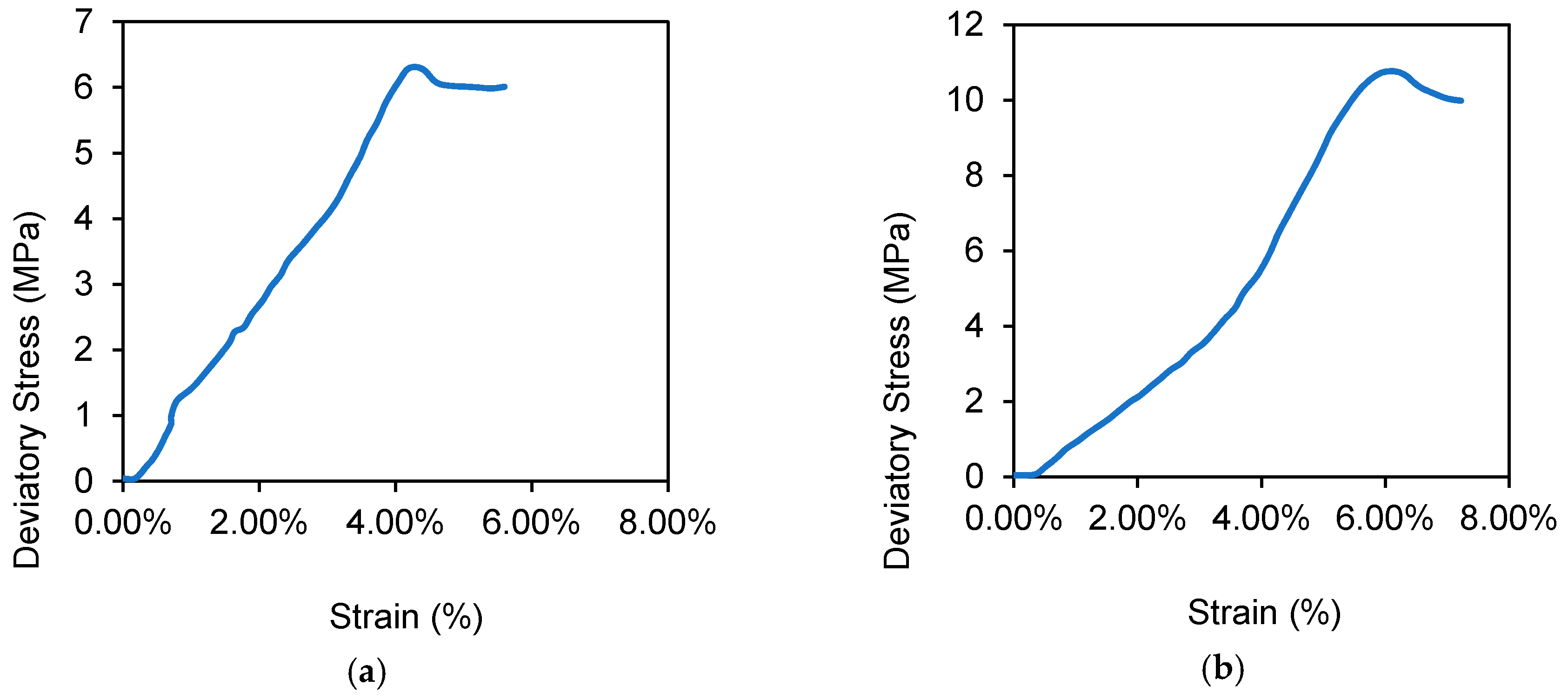
2.3. Triaxial Compression Test
2.4. Upscaling Method
2.4.1. Differential Effective Medium Method
2.4.2. M-T Method
2.4.3. Self-Consistent Method
3. Results
3.1. Nanoscale Geomechanical Properties
3.2. Core Scale Geomechanical Properties
4. Validation and Comparison of Upscaling Methods
4.1. Mori-Tanaka Method
4.2. Self-Consistent Scheme (SCS) Method
4.3. Differential Effective Medium Method
5. Discussion
5.1. The Comparison of Upscaling Methods
5.2. Rock Physics and 3D Printing Technology
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Stiffness tensor | |
| C | Stiffness coefficient |
| c | Multi-variate Gaussian normal density |
| E | Young’s modulus |
| Volume fraction | |
| G | Shear modulus |
| hmax | Maximum displacement |
| K | Bulk modulus |
| N | quantity of all components |
| Hill tensor | |
| Probability density function | |
| Pmax | Peak load |
| S | Contact stiffness |
| T | Total parameters |
| Us | Absolute energy |
| Ue | Elastic energy |
| vE | Elastic energy ratio |
| X | Multi-dimensional array |
| Mean matrices of phase j. | |
| Posterior probability | |
| Fractional difference between horizontal () and vertical () P-wave | |
| Fractional difference between horizontally polarized () and vertically polarized () shear wave |
References
- Guo, Y.; Deng, P.; Yang, C.; Chang, X.; Wang, L.; Zhou, J. Experimental Investigation on Hydraulic Fracture Propagation of Carbonate Rocks under Different Fracturing Fluids. Energies 2018, 11, 3502. [Google Scholar] [CrossRef]
- Peng, J.; Yang, S.-Q. Comparison of mechanical behavior and acoustic emission characteristics of three thermally-damaged rocks. Energies 2018, 11, 2350. [Google Scholar] [CrossRef]
- Chang, X.; Guo, Y.; Zhou, J.; Song, X.; Yang, C. Numerical and Experimental Investigations of the Interactions between Hydraulic and Natural Fractures in Shale Formations. Energies 2018, 11, 2541. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Liu, L.; Sun, J.; Liu, H.; Meng, Q. Experimental study on evolution behaviors of triaxial-shearing parameters for hydrate-bearing intermediate fine sediment. Adv. Geo-Energy Res. 2018, 2, 43–52. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, Y.; Huang, N.; Sugimoto, S. Hydraulic properties of 3D crossed rock fractures by considering anisotropic aperture distributions. Adv. Geo-Energy Res. 2018, 2, 113–121. [Google Scholar] [CrossRef]
- Wanniarachchi, A.; Pathegama Gamage, R.; Lyu, Q.; Perera, S.; Wickramarathne, H.; Rathnaweera, T. Mechanical Characterization of Low Permeable Siltstone under Different Reservoir Saturation Conditions: An Experimental Study. Energies 2019, 12, 14. [Google Scholar] [CrossRef]
- Ulm, F.-J.; Abousleiman, Y. The nanogranular nature of shale. Acta Geotech. 2006, 1, 77–88. [Google Scholar] [CrossRef]
- Bobko, C.P. Assessing the Mechanical Microstructure of Shale by Nanoindentation: The Link between Mineral Composition and Mechanical Properties. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2008. [Google Scholar]
- Deirieh, A.; Ortega, J.; Ulm, F.-J.; Abousleiman, Y. Nanochemomechanical assessment of shale: a coupled WDS-indentation analysis. Acta Geotech. 2012, 7, 271–295. [Google Scholar] [CrossRef]
- Rassouli, F.; Ross, C.; Zoback, M.; Andrew, M. Shale Rock Characterization Using Multi-Scale Imaging. In Proceedings of the 51st US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017. [Google Scholar]
- Dubey, V.; Abedi, S.; Noshadravan, A. Multiscale Modelling of Microcrack-Induced Mechanical Properties in Shales. In Proceedings of the 52nd US Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018. [Google Scholar]
- Li, C.; Ostadhassan, M.; Guo, S.; Gentzis, T.; Kong, L. Application of PeakForce tapping mode of atomic force microscope to characterize nanomechanical properties of organic matter of the Bakken Shale. Fuel 2018, 233, 894–910. [Google Scholar] [CrossRef]
- Li, C.; Ostadhassan, M.; Gentzis, T.; Kong, L.; Carvajal-Ortiz, H.; Bubach, B. Nanomechanical characterization of organic matter in the Bakken formation by microscopy-based method. Mar. Pet. Geol. 2018, 96, 128–138. [Google Scholar] [CrossRef]
- Li, C.; Ostadhassan, M.; Abarghani, A.; Fogden, A.; Kong, L. Multi-scale evaluation of mechanical properties of the Bakken shale. J. Mater. Sci. 2019, 54, 2133–2151. [Google Scholar] [CrossRef]
- Shukla, P.; Kumar, V.; Curtis, M.; Sondergeld, C.H.; Rai, C.S. Nanoindentation studies on shales. In Proceedings of the 47th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 23–26 June 2013. [Google Scholar]
- Mighani, S.; Taneja, S.; Sondergeld, C.; Rai, C. Nanoindentation creep measurements on shale. In Proceedings of the 49th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015. [Google Scholar]
- Vialle, S.; Lebedev, M. Heterogeneities in the elastic properties of microporous carbonate rocks at the microscale from nanoindentation tests. In SEG Technical Program Expanded Abstracts 2015; Society of Exploration Geophysicists: Tulsa, OK, USA, 2015; pp. 3279–3284. [Google Scholar]
- Françis, D.; Pineau, A.; Zaoui, A. Mechanical Behaviour of Materials; Kluwer academic publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Constantinides, G.; Ulm, F.-J. The effect of two types of CSH on the elasticity of cement-based materials: Results from nanoindentation and micromechanical modeling. Cement Concr. Res. 2004, 34, 67–80. [Google Scholar] [CrossRef]
- Levin, V.; Markov, M.; Kanaun, S. Effective field method for seismic properties of cracked rocks. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Nguyen, N.; Giraud, A.; Grgic, D. A composite sphere assemblage model for porous oolitic rocks. Int. J. Rock Mech. Min. Sci. 2011, 48, 909–921. [Google Scholar] [CrossRef]
- Peng, J.; Rong, G.; Cai, M.; Zhou, C.-B. A model for characterizing crack closure effect of rocks. Eng. Geol. 2015, 189, 48–57. [Google Scholar] [CrossRef]
- Zhu, Q.; Shao, J.-F. A refined micromechanical damage–friction model with strength prediction for rock-like materials under compression. Int. J. Solids Struct. 2015, 60, 75–83. [Google Scholar] [CrossRef]
- Campbell, T.; Williams, C.; Ivanova, O.; Garrett, B. Could 3D printing change the world. In Technologies, Potential, and Implications of Additive Manufacturing; Atlantic Council: Washington, DC, USA, 2011. [Google Scholar]
- Espalin, D.; Muse, D.W.; MacDonald, E.; Wicker, R.B. 3D Printing multifunctionality: structures with electronics. Int. J. Adv. Manuf. Technol. 2014, 72, 963–978. [Google Scholar] [CrossRef]
- Mitsouras, D.; Liacouras, P.; Imanzadeh, A.; Giannopoulos, A.A.; Cai, T.; Kumamaru, K.K.; George, E.; Wake, N.; Caterson, E.J.; Pomahac, B.; et al. Medical 3D printing for the radiologist. Radiographics 2015, 35, 1965–1988. [Google Scholar] [CrossRef]
- Chia, H.N.; Wu, B.M. Recent advances in 3D printing of biomaterials. J. Biol. Eng. 2015, 9, 4. [Google Scholar] [CrossRef]
- Mozafari, H.; Dong, P.; Hadidi, H.; Sealy, M.; Gu, L. Mechanical Characterizations of 3D-printed PLLA/Steel Particle Composites. Materials 2019, 12, 1. [Google Scholar] [CrossRef]
- Ishutov, S.; Jobe, T.D.; Zhang, S.; Gonzalez, M.; Agar, S.M.; Hasiuk, F.J.; Watson, F.; Geiger, S.; Mackay, E.; Chalaturnyk, R. Three-dimensional printing for geoscience: Fundamental research, education, and applications for the petroleum industry. AAPG Bull. 2018, 102, 1–26. [Google Scholar] [CrossRef]
- Jiang, C.; Zhao, G.-F.; Zhu, J.; Zhao, Y.-X.; Shen, L. Investigation of dynamic crack coalescence using a gypsum-like 3D printing material. Rock Mech. Rock Eng. 2016, 49, 3983–3998. [Google Scholar] [CrossRef]
- Fereshtenejad, S.; Song, J.-J. Fundamental study on applicability of powder-based 3D printer for physical modeling in rock mechanics. Rock Mech. Rock Eng. 2016, 49, 2065–2074. [Google Scholar] [CrossRef]
- Kong, L.; Ostadhassan, M.; Li, C.; Tamimi, N. Can 3-D Printed Gypsum Samples Replicate Natural Rocks? An Experimental Study. Rock Mech. Rock Eng. 2018, 51, 3061–3074. [Google Scholar] [CrossRef]
- Primkulov, B.; Chalaturnyk, J.; Chalaturnyk, R.; Zambrano Narvaez, G. 3D Printed Sandstone Strength: Curing of Furfuryl Alcohol Resin-Based Sandstones. 3D Print. Addit. Manuf. 2017, 4, 149–156. [Google Scholar] [CrossRef]
- Kong, L.; Ostadhassan, M.; Liu, B.; Li, C.; Liu, K. Multifractal Characteristics of MIP-Based Pore Size Distribution of 3D-Printed Powder-Based Rocks: A Study of Post-Processing Effect. Transp. Porous Media 2018. [Google Scholar] [CrossRef]
- Hainsworth, S.; Page, T. Nanoindentation studies of the chemomechanical effect in sapphire. J. Mater. Sci. 1994, 29, 5529–5540. [Google Scholar] [CrossRef]
- Wilkinson, T.M.; Zargari, S.; Prasad, M.; Packard, C.E. Optimizing nano-dynamic mechanical analysis for high-resolution, elastic modulus mapping in organic-rich shales. J. Mater. Sci. 2015, 50, 1041–1049. [Google Scholar] [CrossRef]
- Rohbeck, N.; Tsivoulas, D.; Shapiro, I.P.; Xiao, P.; Knol, S.; Escleine, J.-M.; Perez, M.; Liu, B. Comparison study of silicon carbide coatings produced at different deposition conditions with use of high temperature nanoindentation. J. Mater. Sci. 2017, 52, 1868–1882. [Google Scholar] [CrossRef]
- Jha, K.K.; Suksawang, N.; Lahiri, D.; Agarwal, A. Energy-Based Analysis of Nanoindentation Curves for Cementitious Materials. ACI Mater. J. 2012, 109. [Google Scholar]
- Vandamme, M.; Ulm, F.-J. Nanogranular origin of concrete creep. Proc. Natl. Acad. Sci. USA 2009, 106, 10552–10557. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Ostadhassan, M.; Xu, X.; Bubach, B. Abnormal behavior during nanoindentation holding stage: Characterization and explanation. J. Pet. Sci. Eng. 2019, 173, 733–747. [Google Scholar] [CrossRef]
- Cheng, Y.-T.; Cheng, C.-M. Scaling approach to conical indentation in elastic-plastic solids with work hardening. J. Appl. Phys. 1998, 84, 1284–1291. [Google Scholar] [CrossRef]
- Jha, K.K.; Suksawang, N.; Lahiri, D.; Agarwal, A. A novel energy-based method to evaluate indentation modulus and hardness of cementitious materials from nanoindentation load–displacement data. Mater. Struct. 2015, 48, 2915–2927. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Basford, K.E. Mixture Models: Inference and Applications to Clustering; Marcel Dekker: New York, NY, USA, 1988; Volume 84. [Google Scholar]
- Moon, T.K. The expectation-maximization algorithm. IEEE Signal Process. Mag. 1996, 13, 47–60. [Google Scholar] [CrossRef]
- Bhat, H.S.; Kumar, N. On the Derivation of the Bayesian Information Criterion; School of Natural Sciences, University of California: Oakland, CA, USA, 2010. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Yang, K.-H.; Yalew, W.M.; Nguyen, M.D. Behavior of geotextile-reinforced clay with a coarse material sandwich technique under unconsolidated-undrained triaxial compression. Int. J. Geomech. 2015, 16, 04015083. [Google Scholar] [CrossRef]
- Hunsche, U. Uniaxial and triaxial creep and failure tests on rock: experimental technique and interpretation. In Visco-Plastic Behaviour of Geomaterials; Springer: Vienna, Austria, 1994; pp. 1–53. [Google Scholar]
- Chen, Y.; Joffre, D.; Avitabile, P. Underwater Dynamic Response at Limited Points Expanded to Full-Field Strain Response. J. Vib. Acoust. 2018, 140, 051016. [Google Scholar] [CrossRef]
- Fjar, E.; Holt, R.M.; Raaen, A.; Risnes, R.; Horsrud, P. Petroleum Related Rock Mechanics; Elsevier: Amsterdam, The Netherlands, 2008; Volume 53. [Google Scholar]
- Mukerji, T.; Berryman, J.; Mavko, G.; Berge, P. Differential effective medium modeling of rock elastic moduli with critical porosity constraints. Geophys. Res. Lett. 1995, 22, 555–558. [Google Scholar] [CrossRef]
- Berryman, J.G. Effective medium theories for multicomponent poroelastic composites. J. Eng. Mech. 2006, 132, 519–531. [Google Scholar] [CrossRef]
- Choy, T.C. Effective Medium Theory: Principles and Applications; Oxford University Press: Oxford, UK, 2015; Volume 165. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Benveniste, Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Miled, K.; Sab, K.; Le Roy, R. Effective elastic properties of porous materials: Homogenization schemes vs experimental data. Mech. Res. Commun. 2011, 38, 131–135. [Google Scholar] [CrossRef]
- Giraud, A.; Nguyen, N.; Grgic, D. Effective poroelastic coefficients of isotropic oolitic rocks with micro and meso porosities. Int. J. Eng. Sci. 2012, 58, 57–77. [Google Scholar] [CrossRef]
- Gercek, H. Poisson’s ratio values for rocks. Int. J. Rock Mech. Min. Sci. 2007, 44, 1–13. [Google Scholar] [CrossRef]
- Berryman, J.G. Mixture theories for rock properties. Rock Phys. Phase Relat. Handb. Phys. Constants 1995, 3, 205–228. [Google Scholar]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Berryman, J.G. Long-wavelength propagation in composite elastic media II. Ellipsoidal inclusions. J. Acoust. Soc. Am. 1980, 68, 1820–1831. [Google Scholar] [CrossRef]
- Dey, A.; Mukhopadhyay, A.K. Nanoindentation of Brittle Solids; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Kong, L.; Ostadhassan, M.; Li, C.; Tamimi, N. Pore characterization of 3D-printed gypsum rocks: A comprehensive approach. J. Mater. Sci. 2018, 53, 5063–5078. [Google Scholar] [CrossRef]
- Tavallali, A.; Vervoort, A. Failure of layered sandstone under Brazilian test conditions: effect of micro-scale parameters on macro-scale behaviour. Rock Mech. Rock Eng. 2010, 43, 641–653. [Google Scholar] [CrossRef]
- Dutta, P.; Mavko, G. Effect of micro-scale anisotropy on solid substitution in macro-scale isotropic composites. In Proceedings of the 2015 SEG Annual Meeting, New Orleans, LA, USA, 18–23 October 2015. [Google Scholar]
- Sharfeddin, A.; Volinsky, A.A.; Mohan, G.; Gallant, N.D. Comparison of the macroscale and microscale tests for measuring elastic properties of polydimethylsiloxane. J. Appl. Polym. Sci. 2015, 132. [Google Scholar] [CrossRef]
- Keller, L.M.; Schwiedrzik, J.J.; Gasser, P.; Michler, J. Understanding Anisotropic Mechanical Properties of Shales at Different Length Scales: In-Situ Micropillar Compression Combined with Finite Element Calculations. J. Geophys. Res. Solid Earth 2017, 122, 5945–5955. [Google Scholar] [CrossRef]
- Zhang, Y.; Lebedev, M.; Al-Yaseri, A.; Yu, H.; Xu, X.; Iglauer, S. Characterization of nanoscale rockmechanical properties and microstructures of a Chinese sub-bituminous coal. J. Nat. Gas Sci. Eng. 2018, 52, 106–116. [Google Scholar] [CrossRef]
- Yang, H.; Luo, S.; Zhang, G.; Song, J. Elasticity of Clay Shale Characterized by Nanoindentation. In Proceedings of the 51st US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017. [Google Scholar]
- Sanahuja, J.; Dormieux, L.; Meille, S.; Hellmich, C.; Fritsch, A. Micromechanical explanation of elasticity and strength of gypsum: from elongated anisotropic crystals to isotropic porous polycrystals. J. Eng. Mech. 2009, 136, 239–253. [Google Scholar] [CrossRef]
- Coon, C.; Pretzel, B.; Lomax, T.; Strlič, M. Preserving rapid prototypes: A review. Herit. Sci. 2016, 4, 40. [Google Scholar] [CrossRef]
- Gardan, J. Method for characterization and enhancement of 3D printing by binder jetting applied to the textures quality. Assem. Autom. 2017, 37, 162–169. [Google Scholar] [CrossRef]
- Dowling, N.E. Mechanical Behavior of Materials; Pearson: London, UK, 2012. [Google Scholar]
- Amann, F.; Kaiser, P.; Button, E.A. Experimental study of brittle behavior of clay shale in rapid triaxial compression. Rock Mech. Rock Eng. 2012, 45, 21–33. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Jing, H.-W.; Wang, S.-Y. Experimental investigation on the strength, deformability, failure behavior and acoustic emission locations of red sandstone under triaxial compression. Rock Mech. Rock Eng. 2012, 45, 583–606. [Google Scholar] [CrossRef]
- Yoneda, J.; Masui, A.; Konno, Y.; Jin, Y.; Egawa, K.; Kida, M.; Ito, T.; Nagao, J.; Tenma, N. Mechanical behavior of hydrate-bearing pressure-core sediments visualized under triaxial compression. Mar. Pet. Geol. 2015, 66, 451–459. [Google Scholar] [CrossRef]
- Goodman, R.E. Introduction to Rock Mechanics; Wiley: New York, NY, USA, 1989; Volume 2. [Google Scholar]
- Ishutov, S.; Hasiuk, F.J.; Fullmer, S.M.; Buono, A.S.; Gray, J.N.; Harding, C. Resurrection of a reservoir sandstone from tomographic data using three-dimensional printing. AAPG Bull. 2017, 101, 1425–1443. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, Y.; Chai, W.; Zhang, Y.; Chen, X. Molecular dynamics simulation and experimental study of the bonding properties of polymer binders in 3D powder printed hydroxyapatite bioceramic bone scaffolds. Ceram. Int. 2017, 43, 13702–13709. [Google Scholar] [CrossRef]
- Higgins, S.M.; Goodwin, S.A.; Bratton, T.R.; Tracy, G.W. Anisotropic stress models improve completion design in the Baxter Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008. [Google Scholar]
- Thomsen, L. Weak elastic anisotropy. Geophysics 1986, 51, 1954–1966. [Google Scholar] [CrossRef]
- Ostadhassan, M.; Zeng, Z.; Jabbari, H. Anisotropy analysis in shale using advanced sonic data-Bakken Case Study. In Proceedings of the American Association of Petroleum Geologists (AAPG) Annual Convention, Long Beach, CA, USA, 22–25 April 2012. [Google Scholar]
- Scholtès, L.; Donzé, F.-V. Modelling progressive failure in fractured rock masses using a 3D discrete element method. Int. J. Rock Mech. Min. Sci. 2012, 52, 18–30. [Google Scholar] [CrossRef]
- Mahabadi, O.K.; Lisjak, A.; Munjiza, A.; Grasselli, G. Y-Geo: New combined finite-discrete element numerical code for geomechanical applications. Int. J. Geomech. 2012, 12, 676–688. [Google Scholar] [CrossRef]
- Nikolic, M.; Ibrahimbegovic, A. Rock mechanics model capable of representing initial heterogeneities and full set of 3D failure mechanisms. Comput. Methods Appl. Mech. Eng. 2015, 290, 209–227. [Google Scholar] [CrossRef]
- Nikolic, M.; Ibrahimbegovic, A.; Miscevic, P. Brittle and ductile failure of rocks: embedded discontinuity approach for representing mode I and mode II failure mechanisms. Int. J. Numer. Methods Eng. 2015, 102, 1507–1526. [Google Scholar] [CrossRef]


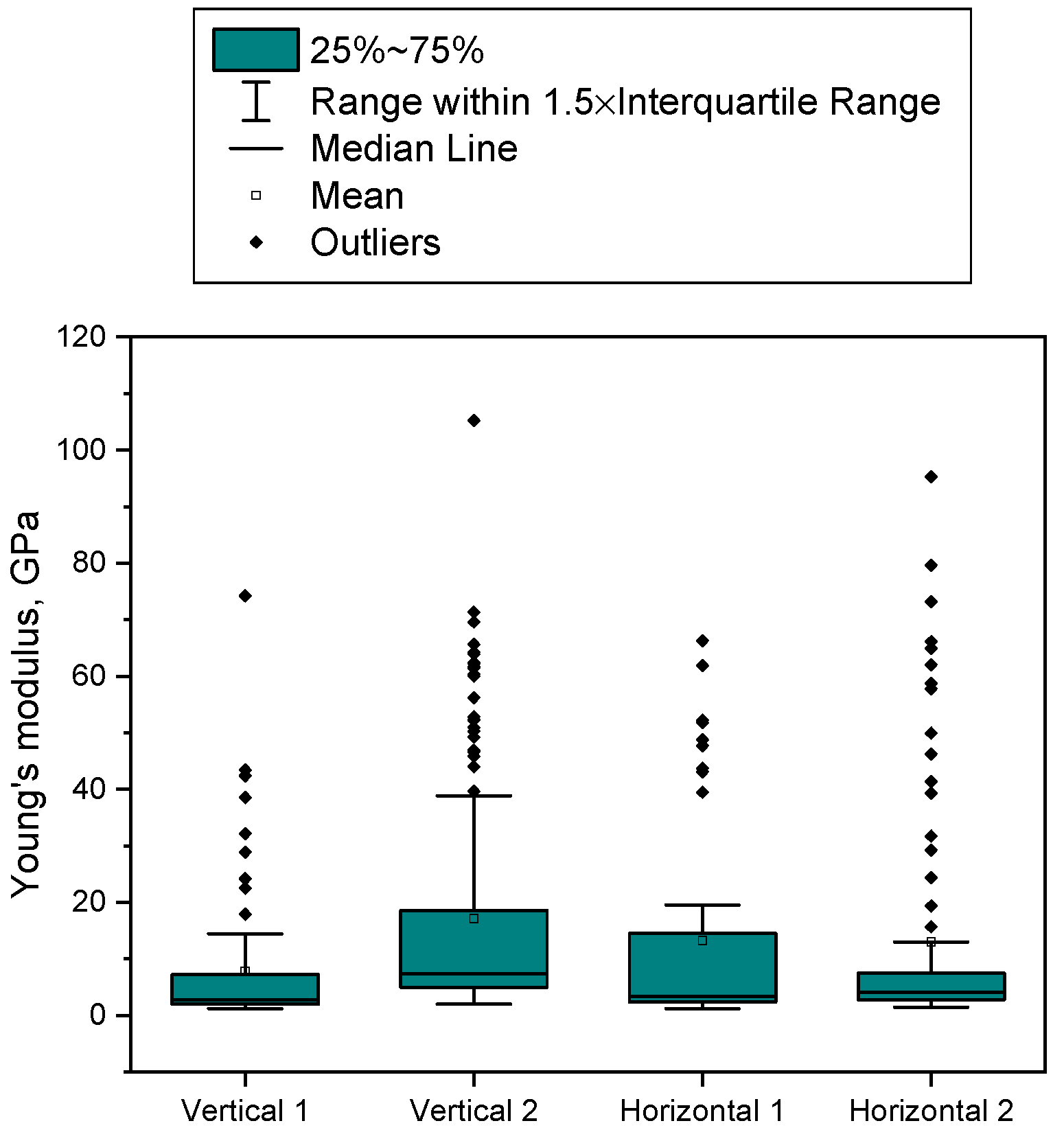
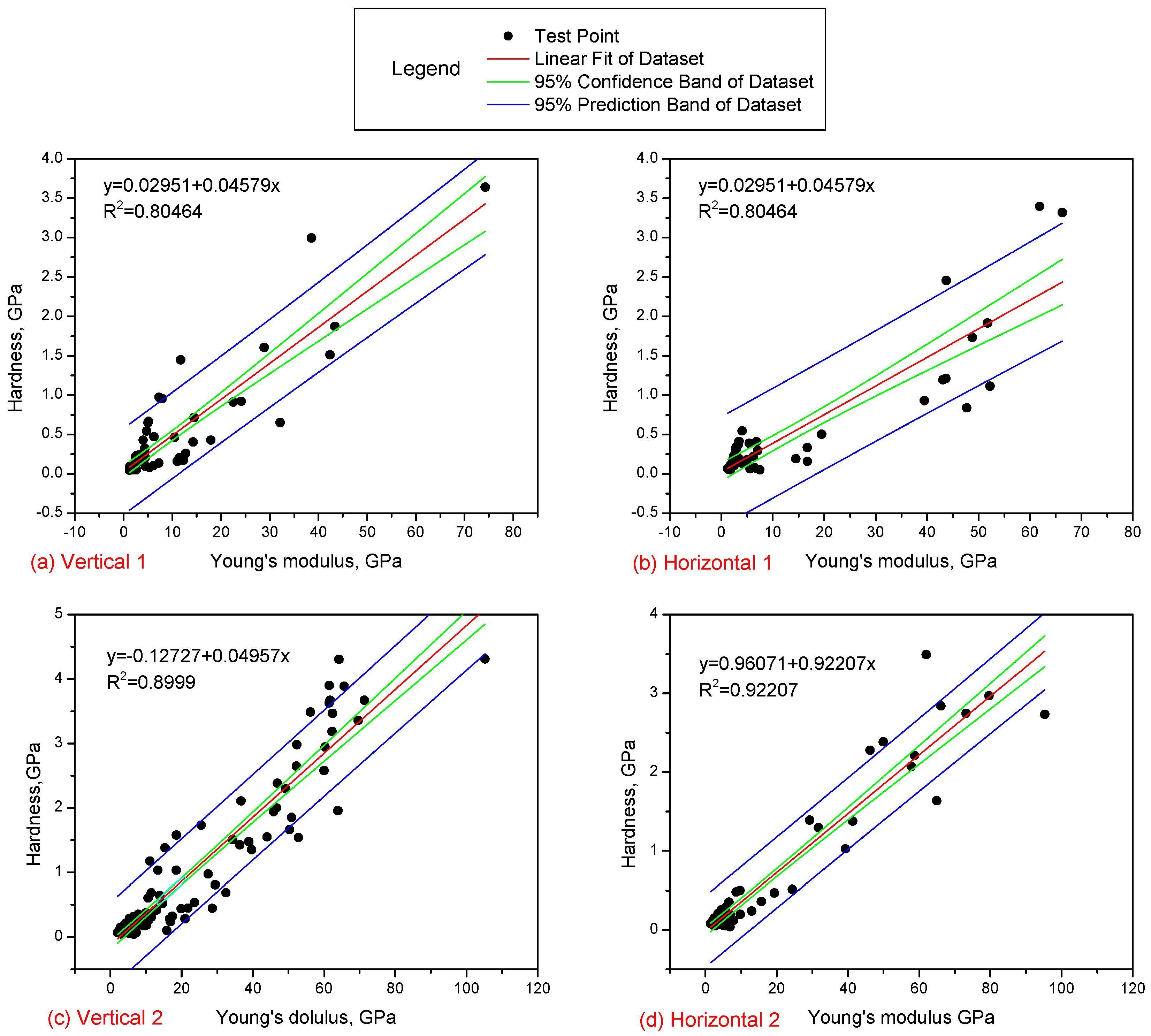

| Sample ID | Phase | Probability | Mean Young’s Modulus (GPa) | Standard Deviation (GPa) |
|---|---|---|---|---|
| V1 | binder | 0.70 | 2.67 | 1.14 |
| gypsum | 0.30 | 19.68 | 16.48 | |
| H1 | binder | 0.73 | 3.39 | 1.77 |
| gypsum | 0.27 | 39.36 | 17.29 | |
| V2 | binder | 0.73 | 5.86 | 2.30 |
| gypsum | 0.27 | 24.06 | 12.73 | |
| H2 | binder | 0.77 | 3.36 | 0.95 |
| gypsum | 0.23 | 8.27 | 4.23 |
| Sample | Gypsum (%) | Binder (%) | Porosity | Young’s Modulus (GPa) | ||
|---|---|---|---|---|---|---|
| Vertical 1 | 0.20 | 0.48 | 0.32 | 2.74 | 1.05 | –0.03 |
| Horizontal 1 | 0.18 | 0.50 | 0.32 | 3.54 | 1.08 | –0.03 |
| Vertical 2 | 0.18 | 0.50 | 0.32 | 5.19 | 1.98 | –0.02 |
| Horizontal 2 | 0.16 | 0.52 | 0.32 | 2.57 | 0.73 | –0.01 |
| Sample | Gypsum (%) | Binder (%) | Porosity | Young’s Modulus (GPa) | ||
|---|---|---|---|---|---|---|
| Vertical 1 | 0.20 | 0.48 | 0.32 | 2.81 | 0.86 | –0.02 |
| Horizontal 1 | 0.18 | 0.50 | 0.32 | 3.67 | 1.16 | –0.03 |
| Vertical 2 | 0.18 | 0.50 | 0.32 | 4.98 | 0.80 | –0.02 |
| Horizontal 2 | 0.16 | 0.52 | 0.32 | 2.40 | 0.77 | –0.01 |
| Sample | Porosity for Upscaling (Dimensionless) | Bulk Modulus (GPa) | Shear Modulus (GPa) | Young’s Modulus (GPa) |
|---|---|---|---|---|
| Vertical 1 | 0.32 | 1.66 | 0.86 | 1.49 |
| Horizontal 1 | 0.32 | 2.22 | 1.17 | 2.00 |
| Vertical 2 | 0.32 | 3.01 | 1.52 | 2.71 |
| Horizontal 2 | 0.32 | 1.48 | 0.73 | 1.33 |
| Cylindrical Sample * | Length (mm) | Diameter (mm) | Young’s Modulus (Gpa) |
|---|---|---|---|
| 1 | 89 | 36 | 0.20 |
| 2 | 89 | 36 | 0.31 |
| 3 | 120 | 50 | 0.32 |
| 4 | 60 | 25 | 0.75 |
| 5 | 100 | 50 | 2.39 |
| 6 | 100 | 50 | 2.43 |
| 7 | 100 | 50 | 3.62 |
| 8 | 100 | 50 | 4.59 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Ostadhassan, M.; Zamiran, S.; Liu, B.; Li, C.; Marino, G.G. Geomechanical Upscaling Methods: Comparison and Verification via 3D Printing. Energies 2019, 12, 382. https://doi.org/10.3390/en12030382
Kong L, Ostadhassan M, Zamiran S, Liu B, Li C, Marino GG. Geomechanical Upscaling Methods: Comparison and Verification via 3D Printing. Energies. 2019; 12(3):382. https://doi.org/10.3390/en12030382
Chicago/Turabian StyleKong, Lingyun, Mehdi Ostadhassan, Siavash Zamiran, Bo Liu, Chunxiao Li, and Gennaro G. Marino. 2019. "Geomechanical Upscaling Methods: Comparison and Verification via 3D Printing" Energies 12, no. 3: 382. https://doi.org/10.3390/en12030382
APA StyleKong, L., Ostadhassan, M., Zamiran, S., Liu, B., Li, C., & Marino, G. G. (2019). Geomechanical Upscaling Methods: Comparison and Verification via 3D Printing. Energies, 12(3), 382. https://doi.org/10.3390/en12030382






