An SNA-DEA Prioritization Framework to Identify Critical Nodes of Gas Networks: The Case of the US Interstate Gas Infrastructure
Abstract
1. Introduction
2. Literature
3. Method
3.1. SNA Metrics
- In-degree. This metric is measured by the sum of the number of ties incoming to a node.
- Out-degree. This metric is measured by the sum of the number of ties outgoing from a node.In a direct weighted network, two further degree metrics can be measured:
- Emission degree. This index is calculated by the sum of all values corresponding to the ties that point from the current node to other nodes.
- Reception degree. This index can be calculated by summing all values corresponding to ties that point to the current node from other nodes.
- Betweenness centrality. This index counts the number of times a node lies on the shortest path (or geodesic path) between other nodes. The normalized flow betweenness centrality of a node is calculated by dividing its flow betweenness by the total flow through all pairs of nodes where it is not a source or target. In particular, the flow betweenness centrality index measures the centrality of a node as a function of the flow through it rather than with respect to the shortest paths [52,53]. Thus, the flow betweenness gives an indication of the contribution of a node to all possible maximum flows, as a global measure. Differently from the basic betweenness centrality index, the flow betweenness centrality measurement allows the relevance of important interactions between nodes in networks having a greater substructure to be captured, where interactions between some groups of nodes have an important weight.
- Sociometric status. This index measures the connectivity of a node (considering both the inputs and outputs) relative to the total number of nodes in the network [54,55]. It is computed by the sum of input and output ties. The sociometric status gives an indication of the relative relevance an individual node has in the transport of natural gas to other nodes in the network.
3.2. DEA Cross-Efficiency
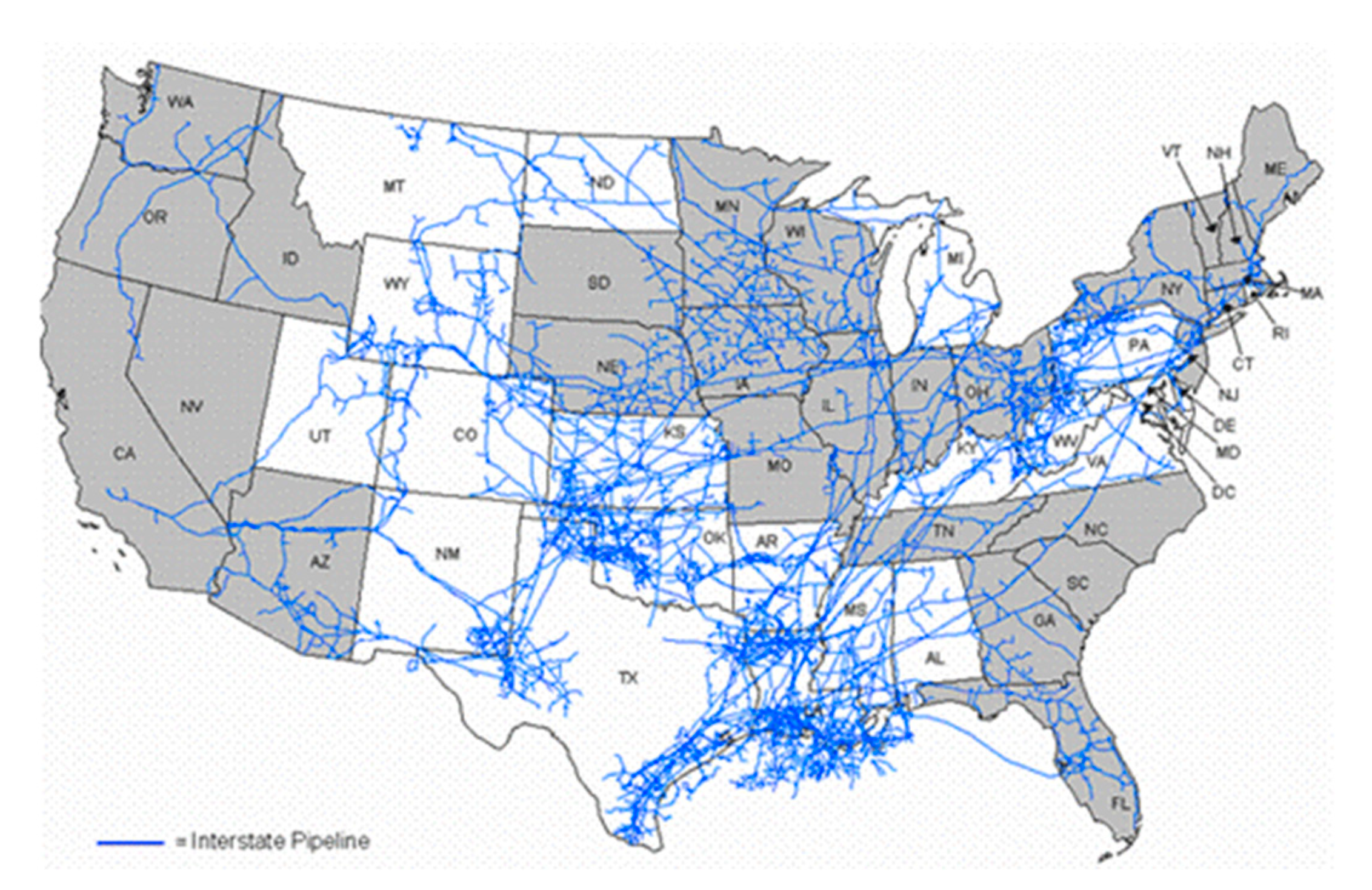
4. Illustrative Case
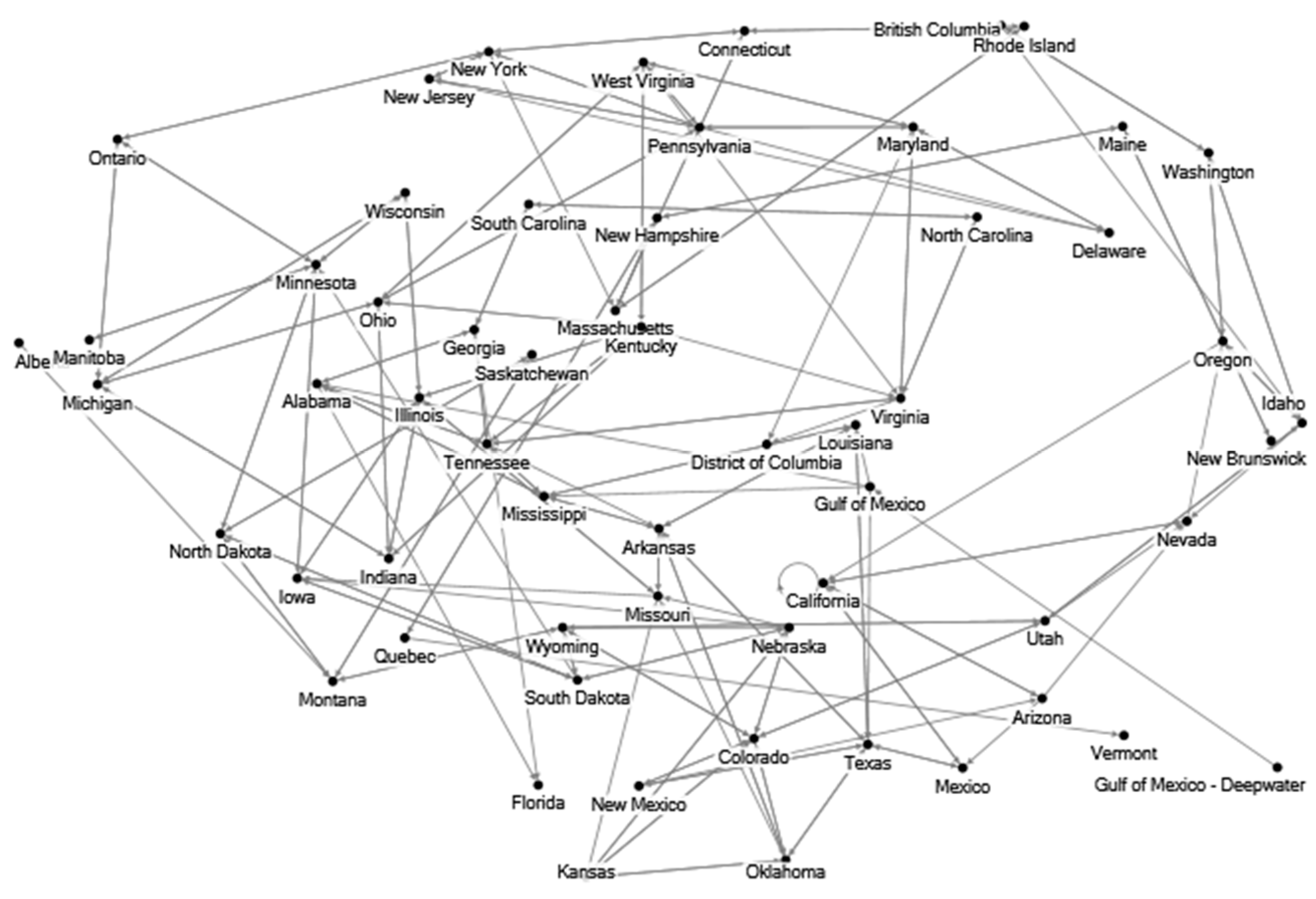
4.1. Data and Variables
4.2. Cross-Efficiency DEA Model Specification
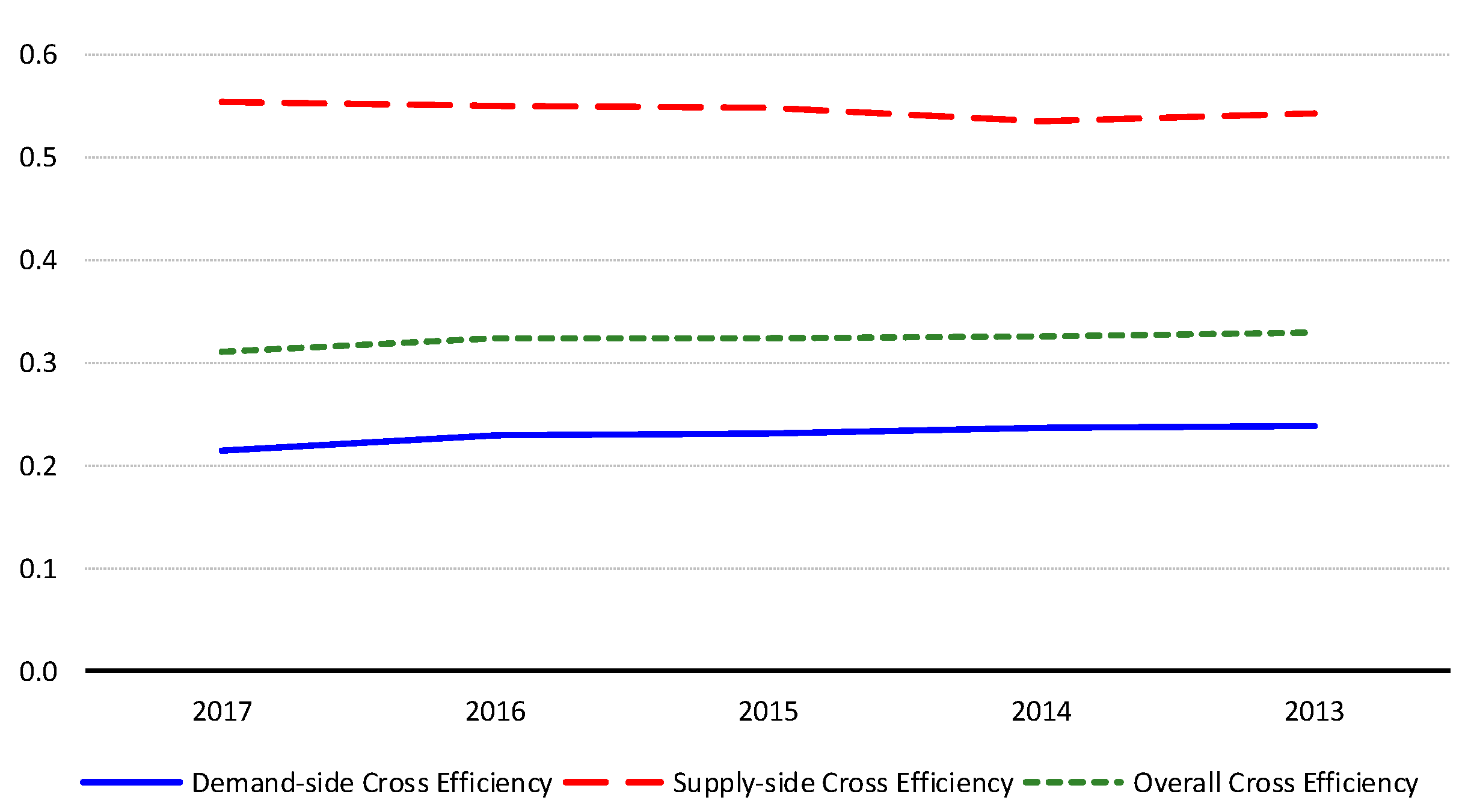
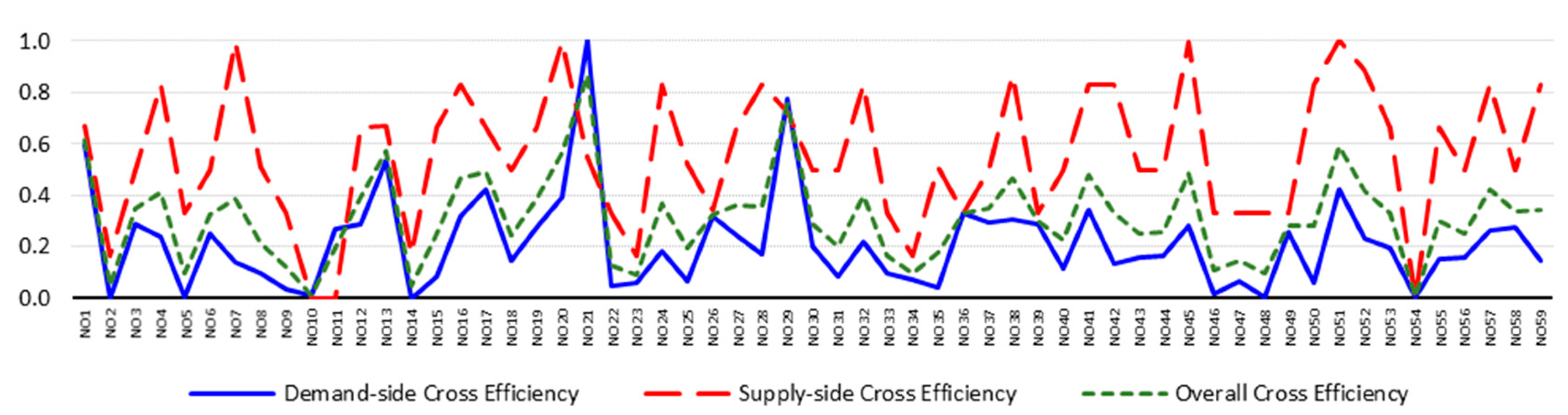
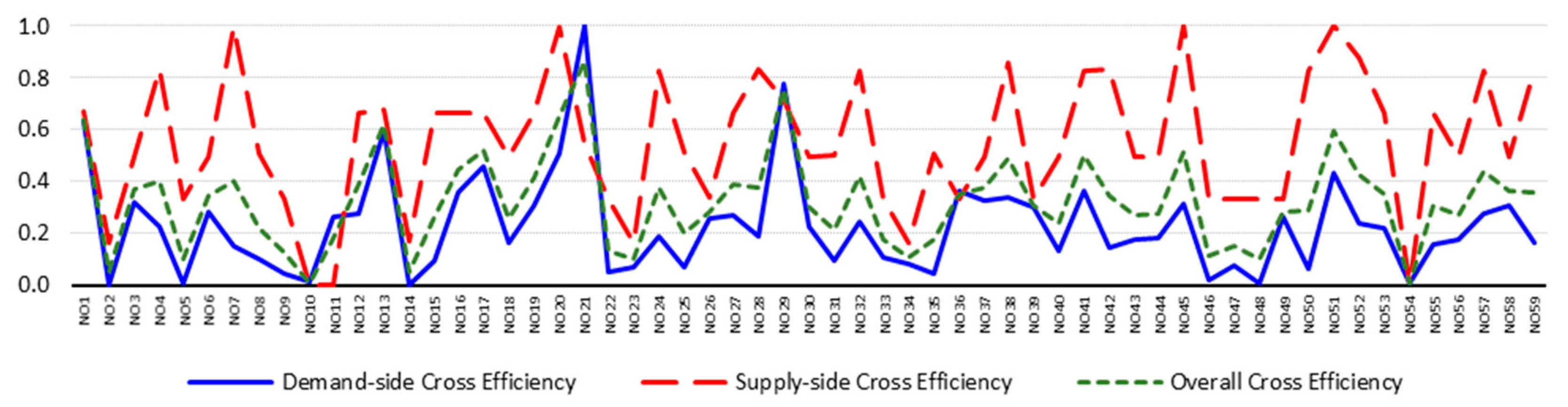
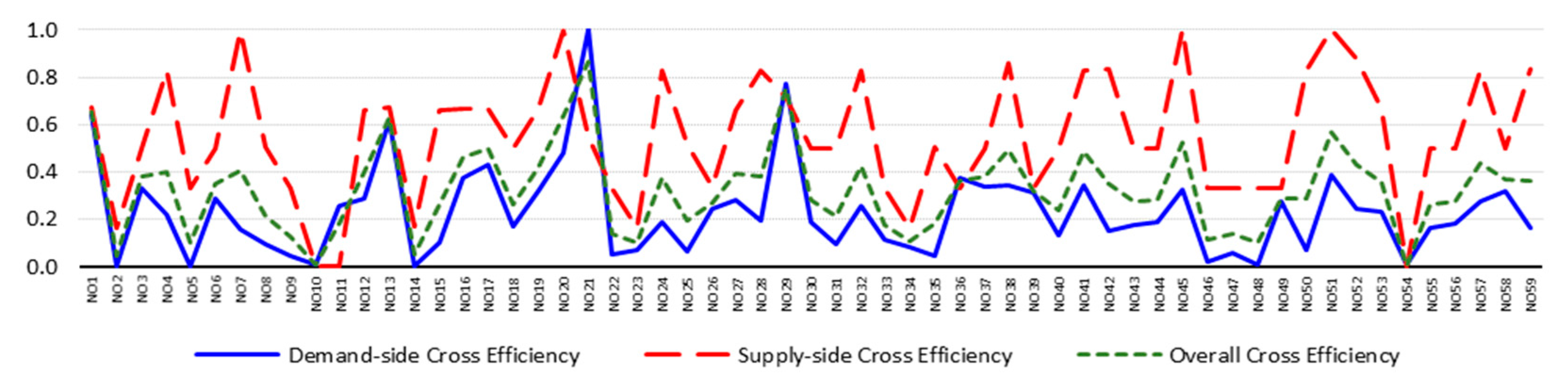
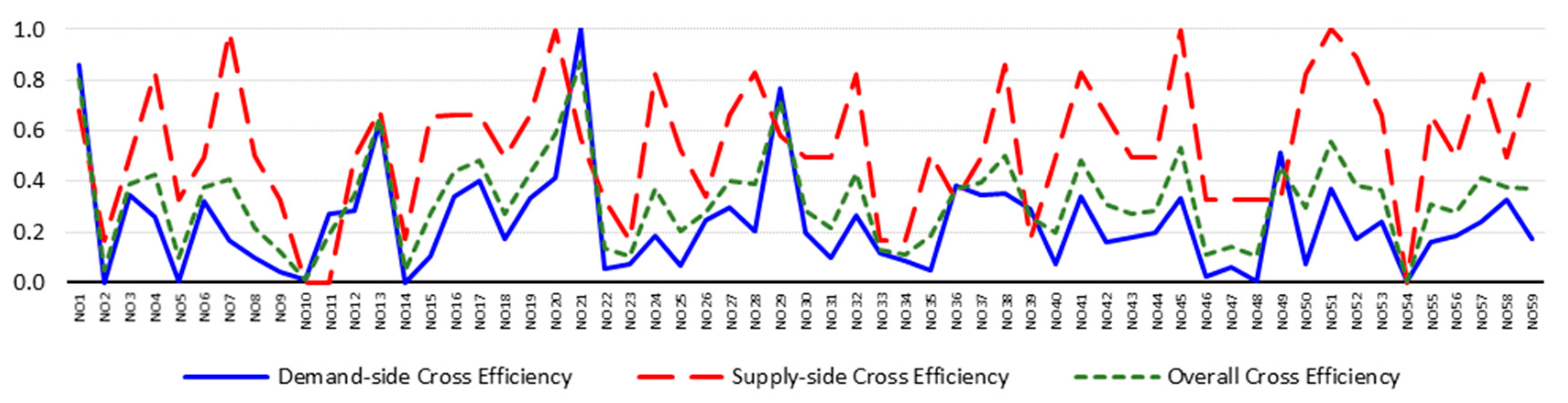
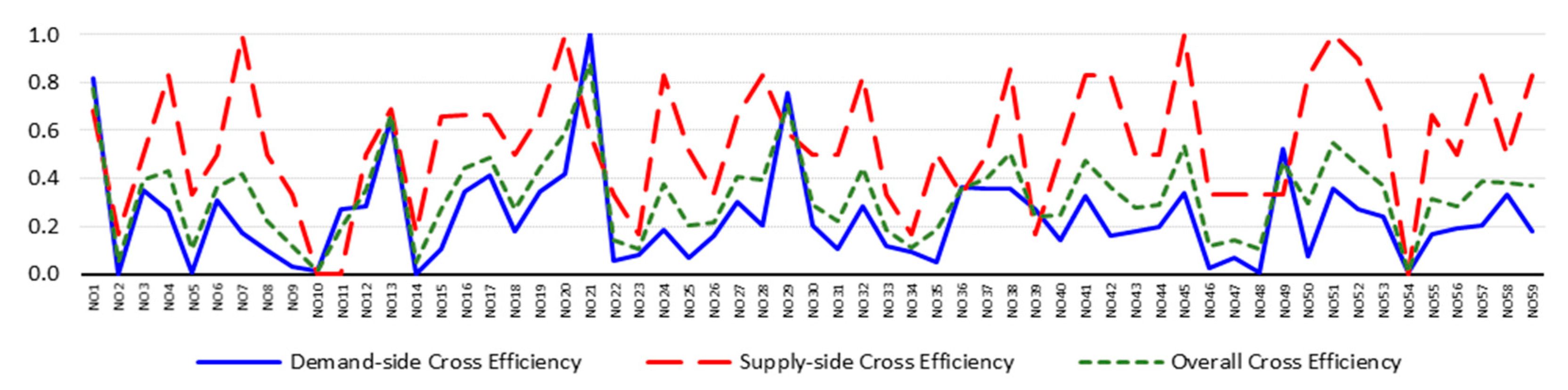
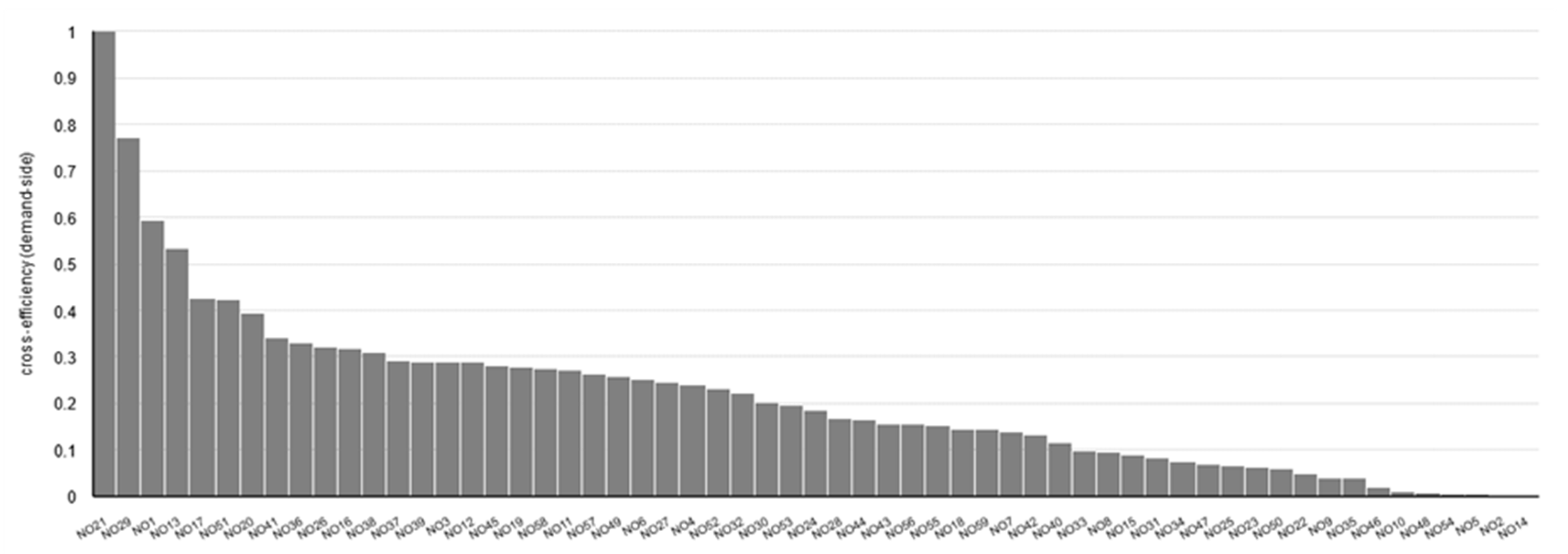
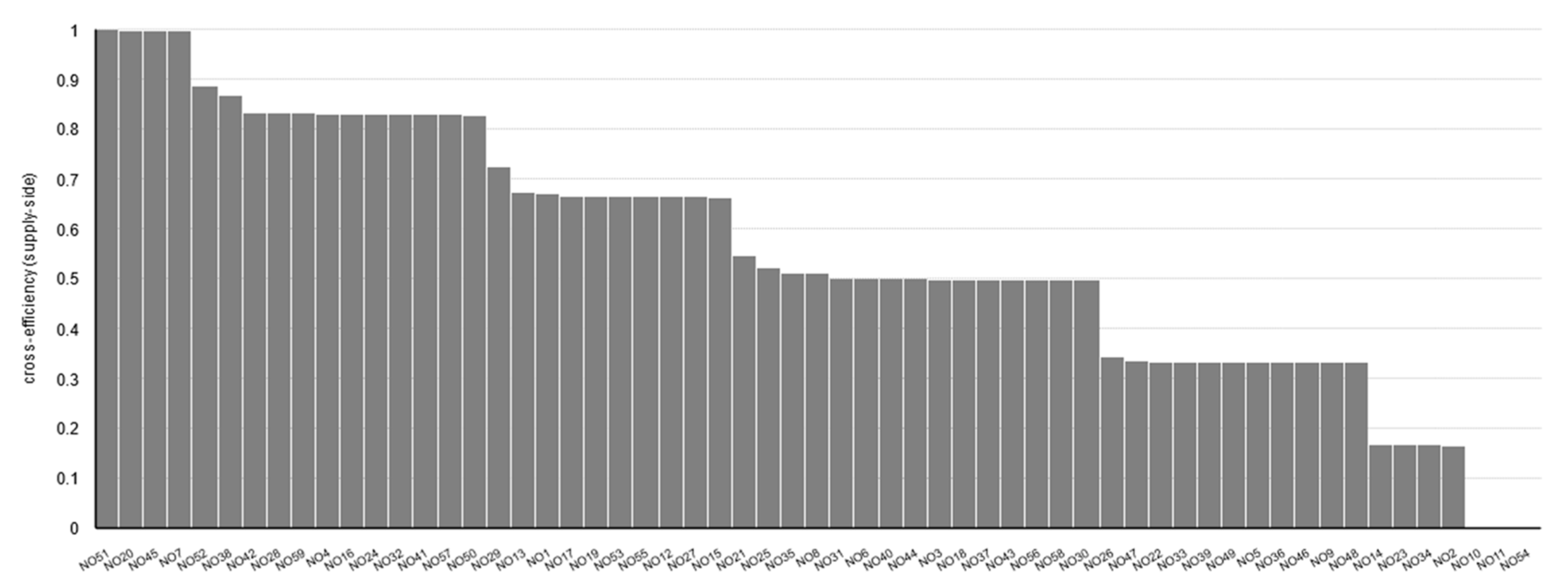
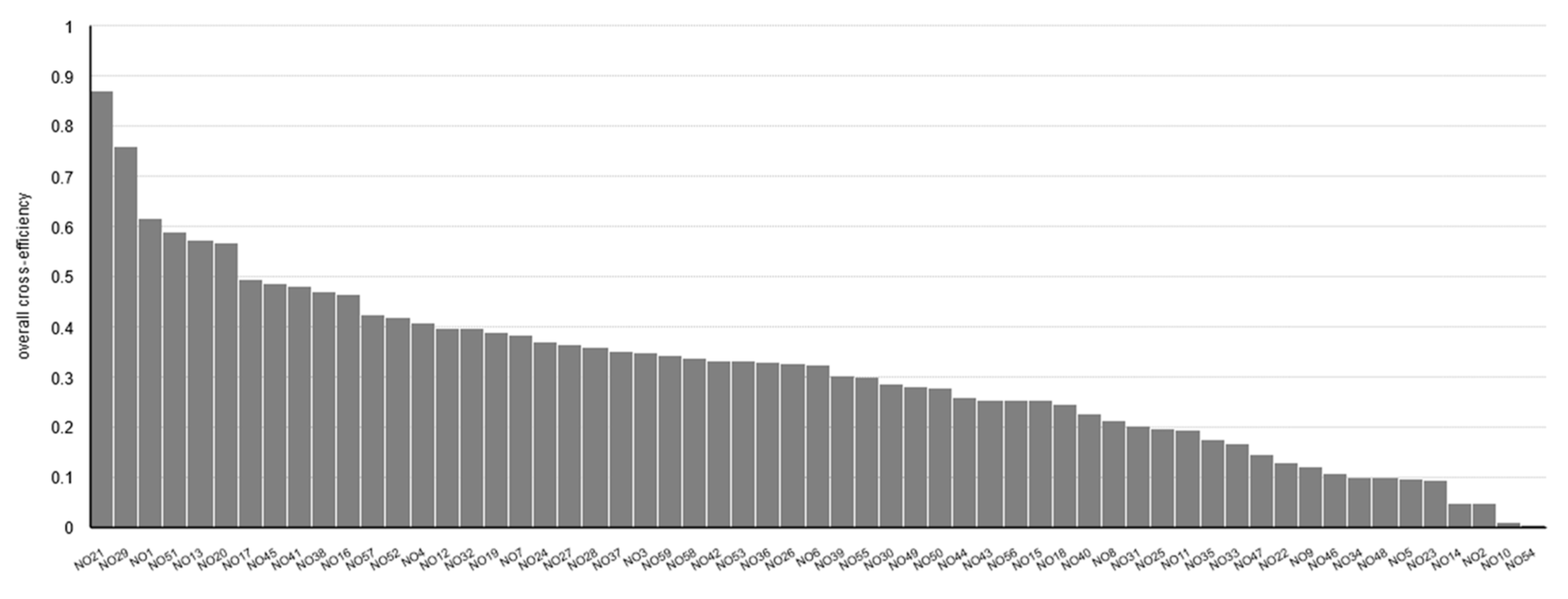
4.3. Results
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Node | State | 2017 | 2016 | 2015 | 2014 | 2013 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | S | OE | D | S | OE | D | S | OE | D | S | OE | D | S | OE | ||
| NO1 | Alabama | 0.595 | 0.670 | 0.616 | 0.631 | 0.670 | 0.643 | 0.644 | 0.672 | 0.652 | 0.860 | 0.680 | 0.807 | 0.815 | 0.680 | 0.775 |
| NO2 | Alberta | 0.000 | 0.165 | 0.047 | 0.000 | 0.166 | 0.048 | 0.000 | 0.166 | 0.049 | 0.000 | 0.164 | 0.049 | 0.000 | 0.165 | 0.049 |
| NO3 | Arizona | 0.289 | 0.498 | 0.349 | 0.322 | 0.498 | 0.373 | 0.333 | 0.498 | 0.381 | 0.347 | 0.495 | 0.391 | 0.352 | 0.497 | 0.395 |
| NO4 | Arkansas | 0.240 | 0.831 | 0.409 | 0.228 | 0.831 | 0.404 | 0.223 | 0.831 | 0.401 | 0.262 | 0.827 | 0.430 | 0.266 | 0.829 | 0.433 |
| NO5 | British Columbia | 0.005 | 0.332 | 0.098 | 0.005 | 0.332 | 0.100 | 0.005 | 0.332 | 0.101 | 0.005 | 0.330 | 0.102 | 0.006 | 0.331 | 0.102 |
| NO6 | California | 0.252 | 0.500 | 0.323 | 0.280 | 0.499 | 0.344 | 0.289 | 0.499 | 0.351 | 0.324 | 0.497 | 0.375 | 0.306 | 0.497 | 0.363 |
| NO7 | Colorado | 0.138 | 0.997 | 0.384 | 0.154 | 0.997 | 0.400 | 0.159 | 0.997 | 0.405 | 0.165 | 0.992 | 0.411 | 0.172 | 0.995 | 0.417 |
| NO8 | Connecticut | 0.096 | 0.510 | 0.214 | 0.104 | 0.506 | 0.222 | 0.096 | 0.506 | 0.216 | 0.100 | 0.501 | 0.219 | 0.101 | 0.501 | 0.220 |
| NO9 | Delaware | 0.039 | 0.331 | 0.122 | 0.043 | 0.331 | 0.127 | 0.045 | 0.331 | 0.129 | 0.041 | 0.328 | 0.126 | 0.028 | 0.329 | 0.118 |
| NO10 | District of Columbia | 0.012 | 0.001 | 0.009 | 0.013 | 0.001 | 0.009 | 0.008 | 0.001 | 0.006 | 0.014 | 0.001 | 0.010 | 0.014 | 0.001 | 0.010 |
| NO11 | Florida | 0.272 | 0.001 | 0.195 | 0.262 | 0.001 | 0.186 | 0.259 | 0.001 | 0.183 | 0.270 | 0.001 | 0.190 | 0.274 | 0.001 | 0.193 |
| NO12 | Georgia | 0.289 | 0.664 | 0.396 | 0.279 | 0.664 | 0.391 | 0.288 | 0.664 | 0.398 | 0.282 | 0.495 | 0.345 | 0.286 | 0.497 | 0.349 |
| NO13 | Gulf of Mexico | 0.534 | 0.672 | 0.574 | 0.595 | 0.675 | 0.618 | 0.615 | 0.676 | 0.633 | 0.640 | 0.680 | 0.652 | 0.650 | 0.691 | 0.662 |
| NO14 | Gulf of Mexico Deepwater | 0.000 | 0.168 | 0.048 | 0.000 | 0.169 | 0.049 | 0.000 | 0.169 | 0.050 | 0.000 | 0.170 | 0.051 | 0.000 | 0.173 | 0.051 |
| NO15 | Idaho | 0.088 | 0.663 | 0.253 | 0.098 | 0.663 | 0.263 | 0.101 | 0.663 | 0.266 | 0.105 | 0.659 | 0.270 | 0.107 | 0.661 | 0.271 |
| NO16 | Illinois | 0.320 | 0.831 | 0.466 | 0.356 | 0.666 | 0.447 | 0.377 | 0.665 | 0.461 | 0.341 | 0.662 | 0.436 | 0.346 | 0.666 | 0.441 |
| NO17 | Indiana | 0.425 | 0.666 | 0.494 | 0.459 | 0.666 | 0.520 | 0.434 | 0.666 | 0.502 | 0.405 | 0.662 | 0.481 | 0.411 | 0.664 | 0.486 |
| NO18 | Iowa | 0.146 | 0.498 | 0.247 | 0.162 | 0.498 | 0.261 | 0.168 | 0.498 | 0.265 | 0.175 | 0.496 | 0.270 | 0.177 | 0.498 | 0.272 |
| NO19 | Kansas | 0.278 | 0.666 | 0.389 | 0.309 | 0.665 | 0.413 | 0.320 | 0.665 | 0.421 | 0.333 | 0.662 | 0.431 | 0.347 | 0.663 | 0.441 |
| NO20 | Kentucky | 0.393 | 0.999 | 0.567 | 0.505 | 0.999 | 0.650 | 0.483 | 0.999 | 0.634 | 0.412 | 0.997 | 0.586 | 0.418 | 0.998 | 0.590 |
| NO21 | Louisiana | 1.000 | 0.545 | 0.870 | 1.000 | 0.547 | 0.868 | 1.000 | 0.549 | 0.868 | 1.000 | 0.571 | 0.873 | 1.000 | 0.584 | 0.877 |
| NO22 | Maine | 0.048 | 0.333 | 0.129 | 0.053 | 0.332 | 0.135 | 0.055 | 0.332 | 0.136 | 0.058 | 0.331 | 0.139 | 0.058 | 0.331 | 0.139 |
| NO23 | Manitoba | 0.063 | 0.166 | 0.093 | 0.071 | 0.166 | 0.098 | 0.073 | 0.166 | 0.100 | 0.076 | 0.165 | 0.102 | 0.077 | 0.166 | 0.103 |
| NO24 | Maryland | 0.185 | 0.830 | 0.369 | 0.189 | 0.830 | 0.376 | 0.187 | 0.830 | 0.376 | 0.183 | 0.826 | 0.374 | 0.186 | 0.827 | 0.376 |
| NO25 | Massachusetts | 0.065 | 0.522 | 0.196 | 0.072 | 0.517 | 0.202 | 0.066 | 0.517 | 0.198 | 0.069 | 0.524 | 0.204 | 0.070 | 0.519 | 0.203 |
| NO26 | Mexico | 0.322 | 0.342 | 0.328 | 0.256 | 0.339 | 0.280 | 0.245 | 0.339 | 0.272 | 0.250 | 0.337 | 0.276 | 0.163 | 0.338 | 0.215 |
| NO27 | Michigan | 0.245 | 0.664 | 0.365 | 0.273 | 0.664 | 0.387 | 0.282 | 0.664 | 0.394 | 0.294 | 0.660 | 0.403 | 0.299 | 0.662 | 0.407 |
| NO28 | Minnesota | 0.169 | 0.832 | 0.359 | 0.188 | 0.831 | 0.376 | 0.195 | 0.832 | 0.382 | 0.203 | 0.827 | 0.388 | 0.206 | 0.830 | 0.391 |
| NO29 | Mississippi | 0.772 | 0.726 | 0.759 | 0.776 | 0.717 | 0.759 | 0.771 | 0.715 | 0.755 | 0.770 | 0.584 | 0.715 | 0.758 | 0.593 | 0.709 |
| NO30 | Missouri | 0.202 | 0.497 | 0.287 | 0.225 | 0.498 | 0.305 | 0.192 | 0.498 | 0.281 | 0.199 | 0.495 | 0.287 | 0.202 | 0.497 | 0.290 |
| NO31 | Montana | 0.084 | 0.501 | 0.203 | 0.093 | 0.499 | 0.212 | 0.096 | 0.499 | 0.215 | 0.100 | 0.496 | 0.218 | 0.102 | 0.498 | 0.219 |
| NO32 | Nebraska | 0.222 | 0.830 | 0.396 | 0.248 | 0.830 | 0.418 | 0.256 | 0.830 | 0.424 | 0.267 | 0.825 | 0.432 | 0.284 | 0.827 | 0.445 |
| NO33 | Nevada | 0.099 | 0.333 | 0.166 | 0.110 | 0.332 | 0.175 | 0.113 | 0.333 | 0.178 | 0.118 | 0.167 | 0.133 | 0.120 | 0.332 | 0.183 |
| NO34 | New Brunswick | 0.074 | 0.166 | 0.100 | 0.082 | 0.166 | 0.107 | 0.085 | 0.166 | 0.109 | 0.089 | 0.164 | 0.111 | 0.090 | 0.165 | 0.112 |
| NO35 | New Hampshire | 0.039 | 0.512 | 0.175 | 0.044 | 0.508 | 0.179 | 0.045 | 0.508 | 0.181 | 0.047 | 0.505 | 0.183 | 0.048 | 0.504 | 0.183 |
| NO36 | New Jersey | 0.329 | 0.332 | 0.330 | 0.362 | 0.333 | 0.354 | 0.375 | 0.332 | 0.362 | 0.384 | 0.331 | 0.368 | 0.365 | 0.332 | 0.355 |
| NO37 | New Mexico | 0.292 | 0.498 | 0.351 | 0.325 | 0.498 | 0.375 | 0.336 | 0.498 | 0.383 | 0.350 | 0.496 | 0.393 | 0.355 | 0.497 | 0.397 |
| NO38 | New York | 0.310 | 0.867 | 0.469 | 0.339 | 0.858 | 0.491 | 0.342 | 0.858 | 0.493 | 0.352 | 0.861 | 0.503 | 0.354 | 0.856 | 0.503 |
| NO39 | North Carolina | 0.291 | 0.333 | 0.303 | 0.302 | 0.332 | 0.311 | 0.312 | 0.332 | 0.318 | 0.292 | 0.175 | 0.257 | 0.272 | 0.168 | 0.241 |
| NO40 | North Dakota | 0.117 | 0.499 | 0.226 | 0.131 | 0.498 | 0.238 | 0.135 | 0.499 | 0.242 | 0.074 | 0.495 | 0.199 | 0.143 | 0.497 | 0.248 |
| NO41 | Ohio | 0.341 | 0.830 | 0.481 | 0.367 | 0.830 | 0.502 | 0.347 | 0.830 | 0.489 | 0.340 | 0.828 | 0.485 | 0.325 | 0.828 | 0.475 |
| NO42 | Oklahoma | 0.133 | 0.833 | 0.333 | 0.148 | 0.832 | 0.347 | 0.153 | 0.832 | 0.352 | 0.159 | 0.662 | 0.308 | 0.161 | 0.831 | 0.360 |
| NO43 | Ontario | 0.156 | 0.498 | 0.254 | 0.174 | 0.498 | 0.269 | 0.180 | 0.498 | 0.273 | 0.177 | 0.495 | 0.272 | 0.180 | 0.496 | 0.274 |
| NO44 | Oregon | 0.165 | 0.499 | 0.260 | 0.183 | 0.499 | 0.275 | 0.189 | 0.499 | 0.280 | 0.197 | 0.498 | 0.286 | 0.200 | 0.497 | 0.288 |
| NO45 | Pennsylvania | 0.281 | 0.999 | 0.486 | 0.312 | 1.000 | 0.513 | 0.323 | 1.000 | 0.521 | 0.336 | 0.997 | 0.533 | 0.337 | 0.998 | 0.533 |
| NO46 | Quebec | 0.019 | 0.332 | 0.109 | 0.021 | 0.331 | 0.112 | 0.022 | 0.331 | 0.113 | 0.023 | 0.329 | 0.114 | 0.023 | 0.330 | 0.114 |
| NO47 | Rhode Island | 0.069 | 0.334 | 0.145 | 0.077 | 0.333 | 0.151 | 0.062 | 0.333 | 0.141 | 0.064 | 0.331 | 0.144 | 0.065 | 0.331 | 0.144 |
| NO48 | Saskatchewan | 0.007 | 0.331 | 0.100 | 0.008 | 0.332 | 0.103 | 0.008 | 0.332 | 0.103 | 0.009 | 0.330 | 0.104 | 0.009 | 0.331 | 0.104 |
| NO49 | South Carolina | 0.259 | 0.333 | 0.280 | 0.266 | 0.332 | 0.285 | 0.275 | 0.333 | 0.292 | 0.516 | 0.331 | 0.461 | 0.524 | 0.332 | 0.467 |
| NO50 | South Dakota | 0.060 | 0.828 | 0.279 | 0.066 | 0.828 | 0.289 | 0.068 | 0.828 | 0.291 | 0.071 | 0.822 | 0.294 | 0.072 | 0.825 | 0.296 |
| NO51 | Tennessee | 0.424 | 1.000 | 0.589 | 0.432 | 1.000 | 0.598 | 0.390 | 1.000 | 0.569 | 0.373 | 1.000 | 0.559 | 0.359 | 1.000 | 0.550 |
| NO52 | Texas | 0.233 | 0.888 | 0.420 | 0.238 | 0.879 | 0.425 | 0.246 | 0.879 | 0.431 | 0.171 | 0.892 | 0.385 | 0.268 | 0.896 | 0.455 |
| NO53 | Utah | 0.198 | 0.665 | 0.332 | 0.222 | 0.665 | 0.352 | 0.230 | 0.665 | 0.357 | 0.239 | 0.662 | 0.365 | 0.243 | 0.663 | 0.368 |
| NO54 | Vermont | 0.006 | 0.001 | 0.004 | 0.006 | 0.001 | 0.005 | 0.006 | 0.001 | 0.005 | 0.007 | 0.001 | 0.005 | 0.007 | 0.001 | 0.005 |
| NO55 | Virginia | 0.152 | 0.665 | 0.299 | 0.159 | 0.665 | 0.306 | 0.164 | 0.499 | 0.262 | 0.162 | 0.663 | 0.310 | 0.164 | 0.663 | 0.312 |
| NO56 | Washington | 0.156 | 0.498 | 0.254 | 0.174 | 0.498 | 0.269 | 0.180 | 0.498 | 0.273 | 0.187 | 0.495 | 0.279 | 0.190 | 0.496 | 0.281 |
| NO57 | West Virginia | 0.263 | 0.830 | 0.425 | 0.277 | 0.831 | 0.438 | 0.277 | 0.830 | 0.439 | 0.239 | 0.825 | 0.413 | 0.206 | 0.828 | 0.390 |
| NO58 | Wisconsin | 0.275 | 0.498 | 0.339 | 0.307 | 0.498 | 0.362 | 0.317 | 0.498 | 0.370 | 0.330 | 0.495 | 0.379 | 0.335 | 0.496 | 0.383 |
| NO59 | Wyoming | 0.145 | 0.832 | 0.342 | 0.162 | 0.832 | 0.357 | 0.167 | 0.832 | 0.362 | 0.174 | 0.828 | 0.368 | 0.176 | 0.831 | 0.371 |
References
- US Energy Information Administration. Monthly Energy Review. June 2019. Available online: https://www.eia.gov/totalenergy/data/monthly/archive/00351906.pdf (accessed on 15 October 2019).
- US Energy Information Administration. International Energy Outlook 2016. Available online: https://www.eia.gov/outlooks/ieo/pdf/0484(2016).pdf (accessed on 15 October 2019).
- Koç, Y.; Warnier, M.; Kooij, R.; Brazier, F. Structural vulnerability assessment of electric power grids. In Proceedings of the 11th IEEE International Conference on Networking, Sensing and Control (ICNSC), Miami, FL, USA, 7–9 April 2014; pp. 386–391. Available online: https://ieeexplore.ieee.org/document/6819657 (accessed on 17 October 2019).
- Fichera, A.; Frasca, M.; Volpe, R. Complex networks for the integration of distributed energy systems in urban areas. Appl. Energy 2017, 193, 336–345. [Google Scholar] [CrossRef]
- Qiao, Z.; Guo, Q.; Sun, H.; Pan, Z.; Liu, Y.; Xiong, W. An interval gas flow analysis in natural gas and electricity coupled networks considering the uncertainty of wind power. Appl. Energy 2017, 201, 343–353. [Google Scholar] [CrossRef]
- Chertikov, M.; Backhaus, S.; Lebedev, V. Cascading of fluctuations in interdependent energy infrastructures: Gas-grid coupling. Appl. Energy 2016, 160, 541–551. [Google Scholar] [CrossRef]
- Su, H.; Zhang, J.; Zio, E.; Yang, N.; Li, X.; Zhang, Z. An integrated system method for supply reliability assessment of natural gas pipeline networks. Appl. Energy 2018, 209, 489–501. [Google Scholar] [CrossRef]
- Ouyang, M. Review on modeling and simulation of interdependent critical infrastructure systems. Reliab. Eng. Syst. Saf. 2014, 121, 43–60. [Google Scholar] [CrossRef]
- Kizhakkedath, A.; Tai, K.; Sim, M.S.; Tiong, R.L.K.; Lin, J. An Agent-Based Modeling and Evolutionary Optimization Approach for Vulnerability Analysis of Critical Infrastructure Networks. In AsiaSim 2013. Communications in Computer and Information Science; Tan, G., Yeo, G.K., Turner, S.J., Teo, Y.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 402. [Google Scholar]
- Subramanian, A.S.R.; Gundersen, T.; Adams, T.A., II. Modeling and Simulation of Energy Systems: A Review. Processes 2018, 6, 238. [Google Scholar] [CrossRef]
- Behrooz, H.A.; Boozarjomehry, R.B. Dynamic optimization of natural gas networks under customer demand uncertainties. Energy 2017, 134, 968–983. [Google Scholar] [CrossRef]
- Fu, X.; Guo, Q.; Sun, H.; Zhang, X.; Wang, L. Estimation of the failure probability of an integrated energy system based on the first order reliability method. Energy 2017, 134, 1068–1078. [Google Scholar] [CrossRef]
- Correa-Posada, C.M.; Sanchez-Martin, P.; Lumbreras, S. Security-constrained model for integrated power and natural-gas system. J. Modeling Power Syst. Clean Energy 2017, 5, 326–336. [Google Scholar] [CrossRef]
- Rehak, D.; Senovsky, P.; Hromada, M.; Lovecek, T. Complex approach to assessing resilience of critical infrastructure elements. Int. J. Crit. Infrastruct. Prot. 2019, 25, 125–138. [Google Scholar] [CrossRef]
- Monforti, F.; Szikszai, A. A Monte-Carlo approach for assessing the adequacy of the European gas transmission system under supply crisis conditions. Energy Policy 2010, 38, 2486–2498. [Google Scholar] [CrossRef]
- Chaudry, M.; Wu, J.; Jenkins, N. A sequential Monte Carlo model of the combined GB gas and electricity network. Energy Policy 2013, 62, 473–483. [Google Scholar] [CrossRef]
- Nan, C.; Sansavini, G. A quantitative method for assessing resilience of interdependent infrastructures. Reliab. Eng. Syst. Saf. 2017, 157, 35–53. [Google Scholar] [CrossRef]
- Voropai, N.I.; Senderov, S.M.; Edelev, A.V. Detection of “bottlenecks” and ways to overcome emergency situations in gas transportation networks on the example of the European gas pipeline network. Energy 2012, 42, 3–9. [Google Scholar] [CrossRef]
- Ouyang, M. Critical location identification and vulnerability analysis of interdependent infrastructure systems under spatially localized attacks. Reliab. Eng. Syst. Saf. 2016, 154, 106–116. [Google Scholar] [CrossRef]
- Shaikh, F.; Ji, Q.; Ying, F. Evaluating China’s natural gas supply security based on ecological network analysis. J. Clean. Prod. 2016, 139, 1196–1206. [Google Scholar] [CrossRef]
- Cetinay, H.; Devriendt, K.; Van Mieghem, P. Nodal vulnerability to targeted attacks in power grids. Appl. Netw. Sci. 2018, 3, 34. [Google Scholar] [CrossRef]
- Beyza, J.; Garcia-Paricio, E.; Yusta, J.M. Applying Complex Network Theory to the Vulnerability Assessment of Interdependent Energy Infrastructures. Energies 2019, 12, 421. [Google Scholar] [CrossRef]
- Beyza, J.; Rui-Paredes, H.F.; Garcia-Paricio, E.; Yusta, J.M. Assessing the criticality of interdependent power and gas systems using complex networks and load flow techniques. Phys. A Stat. Mech. Appl. 2020, 540, 123169. [Google Scholar] [CrossRef]
- Zio, E. Challenges in the vulnerability and risk analysis of critical infrastructures. Reliab. Eng. Syst. Saf. 2016, 152, 137–150. [Google Scholar] [CrossRef]
- Han, F.; Zio, E. A multi-perspective framework of analysis of critical infrastructures with respect to supply service, controllability and topology. Int. J. Crit. Infrastruct. Prot. 2019, 24, 1–13. [Google Scholar] [CrossRef]
- Alipour, Z.; Monfared, M.A.S.; Enrico Zio, E. Comparing topological and reliability-based vulnerability analysis of Iran power transmission network. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2014, 228, 139–151. [Google Scholar] [CrossRef]
- Praks, P.; Kopustinskas, V.; Masera, M. Probabilistic modelling of security of supply in gas networks and evaluation of new infrastructure. Reliab. Eng. Syst. Saf. 2015, 144, 254–264. [Google Scholar] [CrossRef]
- Su, H.; Zio, E.; Zhang, J.; Xueyi, L. A systematic framework of vulnerability analysis of a natural gas pipeline network. Reliab. Eng. Syst. Saf. 2018, 175, 79–91. [Google Scholar] [CrossRef]
- Hanneman, R.A.; Riddle, M. Introduction to Social Network Methods; University of California: Riverside, CA, USA, 2005. [Google Scholar]
- Wasserman, S.; Faust, K. Social Network Analysis; Cambridge University Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Watts, D.J. The “New” science of networks. Annu. Rev. Sociol. 2004, 30, 243–270. [Google Scholar] [CrossRef]
- Willging, P.A. Using Social Network Analysis Techniques to Examine Online Interactions. US China Educ. Rev. 2005, 2, 46–56. [Google Scholar]
- Barabasi, A.L.; Albert, R.; Jeong, H.; Bianconi, G. Power-Law distribution of the World Wide Web. Science 2000, 287, 2115. [Google Scholar]
- lo Storto, C. Investigating information flows across complex product development stages by using social network analysis (SNA). In Proceedings of the COMPENG 2010, Rome, Italy, 22–24 February 2010; ISBN 978-0-7695-3974-4. [Google Scholar]
- lo Storto, C. A four-stage framework for the identification of information flow inefficiencies in the manufacturing environment. Appl. Mech. Mater. 2013, 309, 335–341. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001, 86, 3200–3203. [Google Scholar] [CrossRef]
- Newman, M.E.J. The Structure and Function of Complex Networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Allen, J.; James, A.D.; Gamlen, P. Formal versus informal knowledge networks in R&D: A case study using social network analysis. R D Manag. 2007, 37, 179–196. [Google Scholar]
- Weiwei, L.; Yuan, T.; Zhile, Y.; Kexin, B. Exploring and Visualizing the Patent Collaboration Network: A Case Study of Smart Grid Field in China. Sustainability 2019, 11, 465. [Google Scholar]
- Uzzi, B.; Spiro, J. Collaboration and Creativity: The Small World Problem. Am. J. Sociol. 2005, 111, 447–504. [Google Scholar] [CrossRef]
- Zanin, M.; Lillo, F. Modelling the air transport with complex networks: A short review. Eur. Phys. J. Spec. Top. 2013, 215, 5–21. [Google Scholar] [CrossRef]
- Son, M.G.; Yeo, G.T. Analysis of the Air Transport Network Characteristics of Major Airports. Asian J. Shipp. Logist. 2017, 33, 117–125. [Google Scholar]
- Barrat, A.; Barthélemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. PNAS 2004, 101, 3747–3752. [Google Scholar] [CrossRef]
- Iyengar, D.; Rao, S.; Goldsby, T.J. The Power and Centrality of the Transportation and Warehousing Sector within the US Economy: A Longitudinal Exploration Using Social Network Analysis. Transp. J. 2012, 51, 373–398. [Google Scholar] [CrossRef]
- Saleh, M.; Esa, Y.; Mohamed, A. Applications of Complex Network Analysis in Electric Power Systems. Energies 2018, 11, 1381. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of “small-world” networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, H.; Chen, B.; Li, P. Research on the structural characteristics of transmission grid based on complex network theory. J. Appl. Math. 2014, 2014. [Google Scholar] [CrossRef][Green Version]
- Piccinelli, R.; Krausmann, E. An Analysis of the Vulnerability of Power Grids to Extreme Space Weather Using Complex Network Theory; Technical Report, European Commission Joint Research Center; Institute for the Protection and Security of the Citizen: Ispra, Italy, 2015; Available online: http://publications.jrc.ec.europa.eu/repository/handle/JRC91072 (accessed on 18 October 2019).
- Bonacich, P. Power and Centrality: A family of measures. Am. J. Sociol. 1987, 92, 1170–1182. [Google Scholar] [CrossRef]
- Borgatti, S.P. Centrality and network flow. Soc. Netw. 2005, 27, 55–71. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Newman, M.E.J. A measure of betweenness centrality based on random walks. Soc. Netw. 2005, 27, 39–54. [Google Scholar] [CrossRef]
- Freeman, L.C.; Borgatti, S.P.; White, D.R. Centrality in valued graphs: A measure of betweenness based on network flow. Soc. Netw. 1991, 13, 141–154. [Google Scholar] [CrossRef]
- Houghton, R.J.; Baber, C.; McMaster, R.; Stanton, N.A.; Salmon, P.; Stewart, R.; Walker, G.H. Command and control in emergency services operations: A social network analysis. Ergonomics 2006, 49, 1204–1225. [Google Scholar] [CrossRef]
- Tapiero, C.S.; Lewin, A.Y. The Concept and Measurement of Centrality–An Information Approach. Decis. Sci. 1973, 4, 314–328. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision-making units. Eur. J. Oper. Res. 1989, 2, 429–444. [Google Scholar] [CrossRef]
- Noorizadeh, A.; Mahdiloo, M.; Saen, R.F. Using DEA Cross-efficiency Evaluation for Suppliers Ranking in the Presence of Non-discretionary Inputs. Int. J. Shipp. Transp. Logist. 2013, 5, 95–111. [Google Scholar] [CrossRef]
- Sexton, T.R.; Silkman, R.H.; Hogan, A.J. Data envelopment analysis: Critique and extensions. In Measuring Efficiency: An Assessment of Data Envelopment Analysis; Silkman, R.H., Ed.; Jossey-Bass: New York, NY, USA, 1986; pp. 73–105. [Google Scholar]
- Doyle, J.R.; Green, R.H. Efficiency and cross-efficiency in DEA: Derivations, meanings and uses. J. Oper. Res. Soc. 1994, 45, 567–578. [Google Scholar] [CrossRef]
- lo Storto, C. A double-DEA framework to support decision-making in the choice of advanced manufacturing technologies. Manag. Decis. 2018, 56, 488–507. [Google Scholar] [CrossRef]
- Liang, L.; Wu, J.; Cook, W.D.; Zhu, J. The DEA game cross-efficiency model and its Nash equilibrium. Oper. Res. 2008, 56, 1278–1288. [Google Scholar] [CrossRef]
- Cook, W.D.; Zhu, J. DEA cross efficiency. In Data Envelopment Analysis: A Handbook of Models and Methods; Zhu, J., Ed.; Springer: Boston, MA, USA, 2015; pp. 23–43. [Google Scholar]
- U.S. Energy Information Administration. About U.S. Natural Gas Pipelines – Transporting Natural Gas. Available online: https://www.eia.gov/naturalgas/archive/analysis_publications/ngpipeline/interstate.html (accessed on 17 October 2019).
- U.S. Energy Information Administration. Natural Gas data. Available online: https://www.eia.gov/naturalgas/data.cfm#pipelines (accessed on 17 October 2019).
- Bian, Y.; Yang, F. Resource and environment efficiency analysis of provinces in China: A DEA approach based on Shannon’s entropy. Energy Policy 2010, 38, 1909–1917. [Google Scholar] [CrossRef]
- lo Storto, C. Ecological efficiency-based ranking of cities: A combined DEA Cross-efficiency and Shannon’s entropy method. Sustainability 2016, 8, 124. [Google Scholar] [CrossRef]
- Soleimani-damaneh, M.; Zarepisheh, M. Shannon’s entropy for combining the efficiency results of different DEA models: Method and application. Expert Syst. Appl. 2009, 36, 5146–5150. [Google Scholar] [CrossRef]
- Fang, Y.; Zio, E. Application of Topological Network Measures to Identify Critical Gas Transmission Network Components; Research Report 2018. Available online: https://hal.archives-ouvertes.fr/hal-01924426 (accessed on 9 November 2019).
- Kim, H.; Anderson, R. Temporal node centrality in complex networks. Phys. Rev. E 2012, 85, 026107. [Google Scholar] [CrossRef]
- Huang, D.-W.; Yu, Z.-G. Dynamic-Sensitive centrality of nodes in temporal networks. Sci. Rep. 2017, 7, 41454. [Google Scholar] [CrossRef]
| Index | Equation | Index | Equation |
|---|---|---|---|
| In-degree | Out-degree | ||
| Reception degree | Emission degree | ||
| Flow betweenness centrality | Sociometric status |
| Statistics | Year | ||||
|---|---|---|---|---|---|
| 2017 | 2016 | 2015 | 2014 | 2013 | |
| Number of nodes | 59 | 59 | 59 | 59 | 59 |
| Number of edges | 195 | 194 | 193 | 189 | 191 |
| Index | 2017 | 2016 | 2015 | 2014 | 2013 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Max | Mean | Max | Mean | Max | Mean | Max | Mean | Max | |
| Emission degree | 440.28 | 1896.64 | 418.17 | 1746.64 | 404.97 | 1719.06 | 381.97 | 1716.02 | 381.94 | 1603.75 |
| Reception degree | 440.28 | 2176.57 | 418.17 | 1955.53 | 404.97 | 1891.80 | 381.97 | 1820.33 | 381.94 | 1793.66 |
| Out-degree | 0.06 | 0.10 | 0.06 | 0.10 | 0.06 | 0.10 | 0.05 | 0.10 | 0.05 | 0.10 |
| In-degree | 0.06 | 0.10 | 0.06 | 0.10 | 0.06 | 0.10 | 0.05 | 0.10 | 0.05 | 0.10 |
| Flow betweenness | 174.65 | 887.98 | 175.55 | 871.38 | 176.83 | 872.24 | 184.86 | 811.52 | 178.59 | 835.76 |
| Perspective | Emission Degree | Reception Degree | Out-Degree | In-Degree | Flow Betweenness |
|---|---|---|---|---|---|
| Demand-side | - | Output | - | Input | - |
| Supply-side | Output | - | Output | - | Output |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
lo Storto, C. An SNA-DEA Prioritization Framework to Identify Critical Nodes of Gas Networks: The Case of the US Interstate Gas Infrastructure. Energies 2019, 12, 4597. https://doi.org/10.3390/en12234597
lo Storto C. An SNA-DEA Prioritization Framework to Identify Critical Nodes of Gas Networks: The Case of the US Interstate Gas Infrastructure. Energies. 2019; 12(23):4597. https://doi.org/10.3390/en12234597
Chicago/Turabian Stylelo Storto, Corrado. 2019. "An SNA-DEA Prioritization Framework to Identify Critical Nodes of Gas Networks: The Case of the US Interstate Gas Infrastructure" Energies 12, no. 23: 4597. https://doi.org/10.3390/en12234597
APA Stylelo Storto, C. (2019). An SNA-DEA Prioritization Framework to Identify Critical Nodes of Gas Networks: The Case of the US Interstate Gas Infrastructure. Energies, 12(23), 4597. https://doi.org/10.3390/en12234597





