Modeling and Simulation Performance Evaluation of a Proposed Calorimeter for Testing a Heat Pump System
Abstract
:1. Introduction
2. Materials and Methods
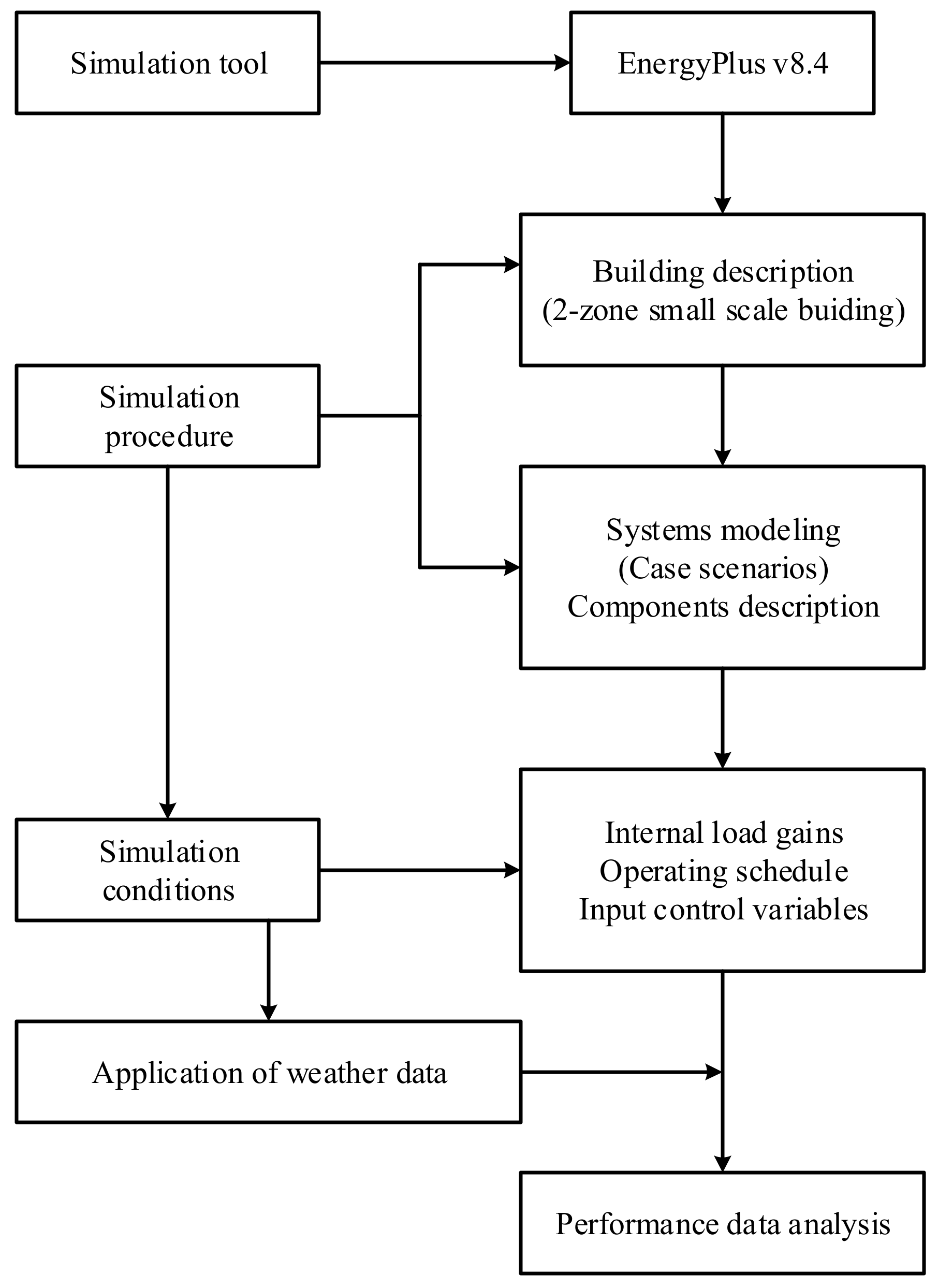
2.1. Simulation Software
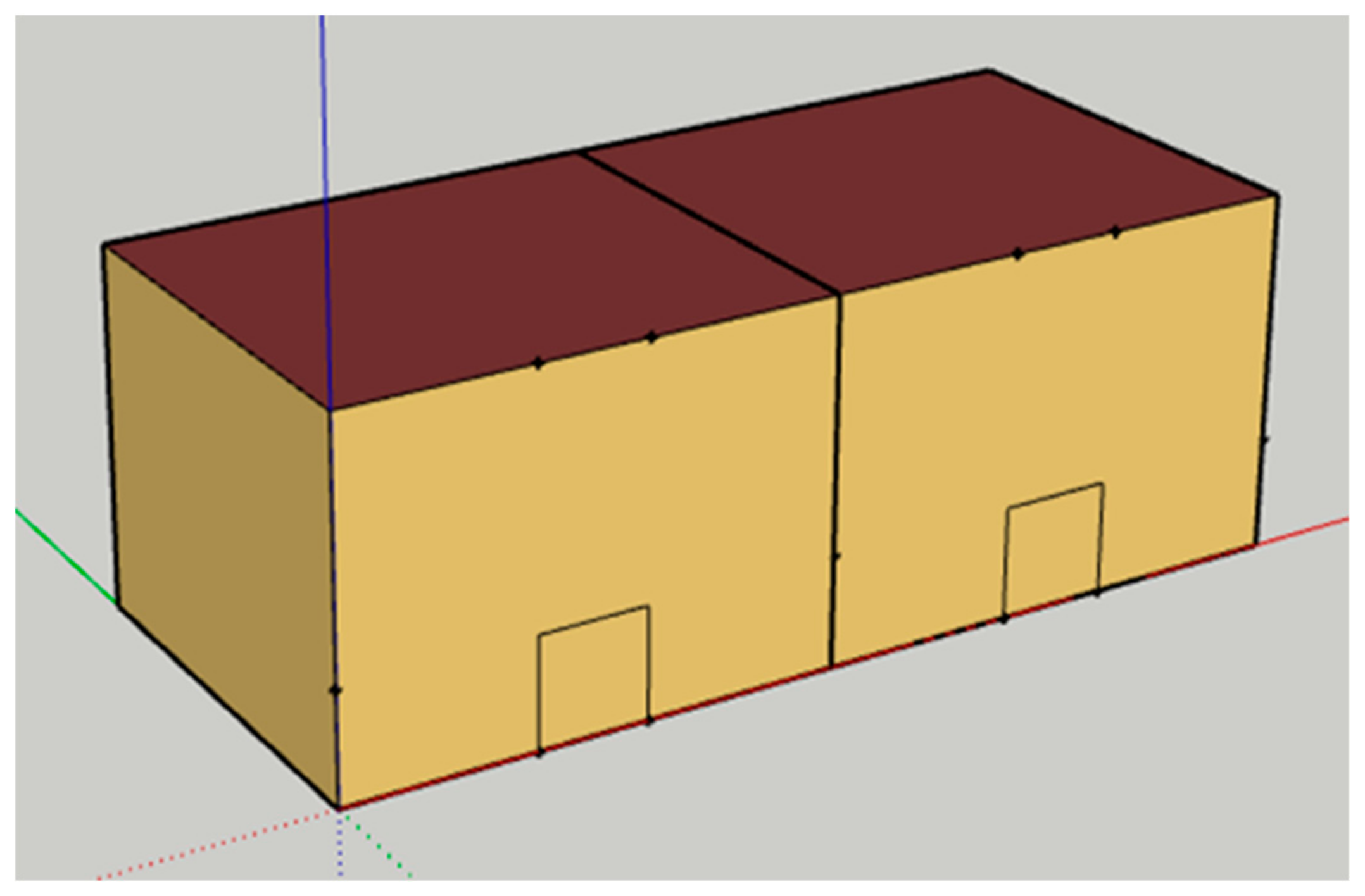
2.2. Building Description
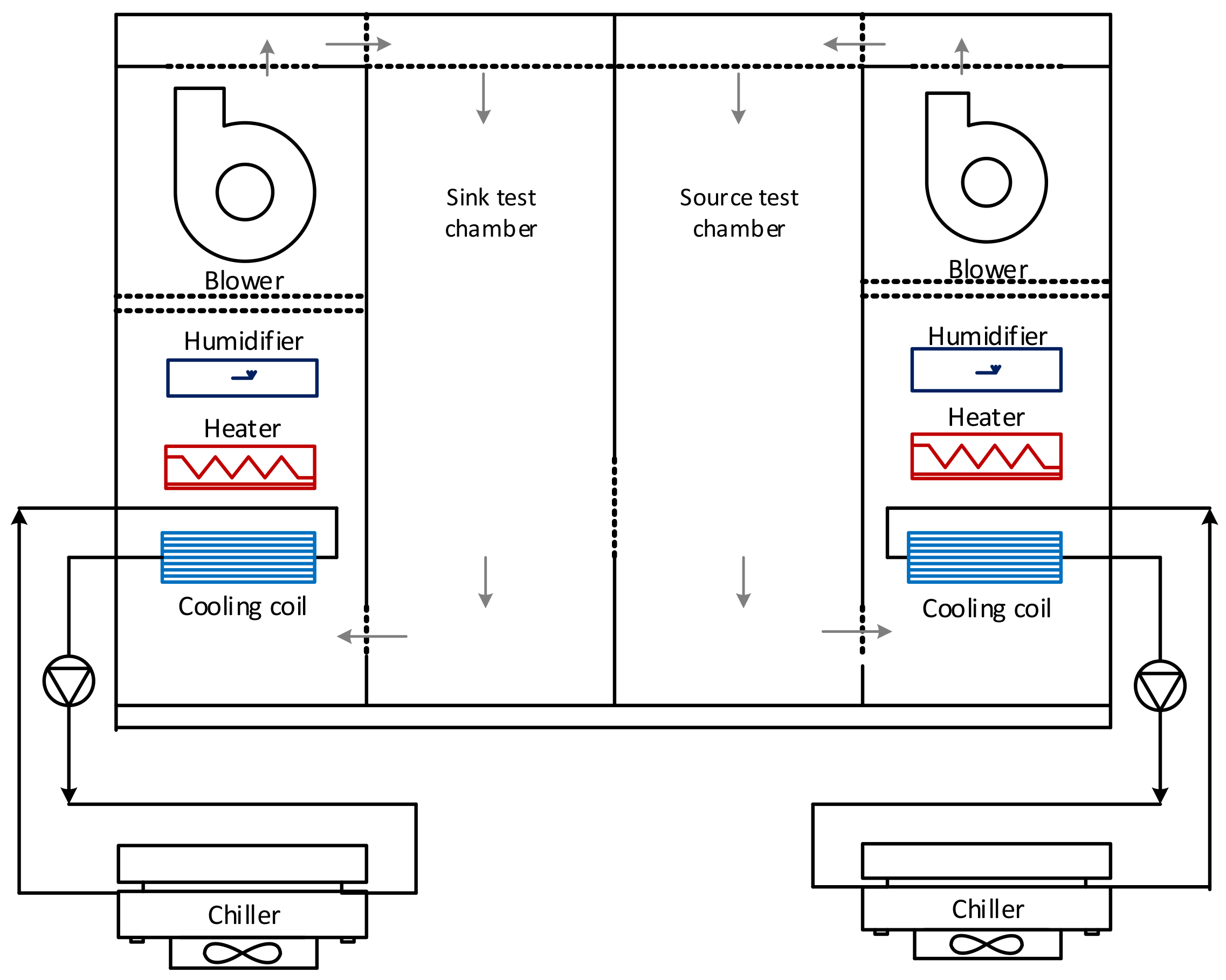
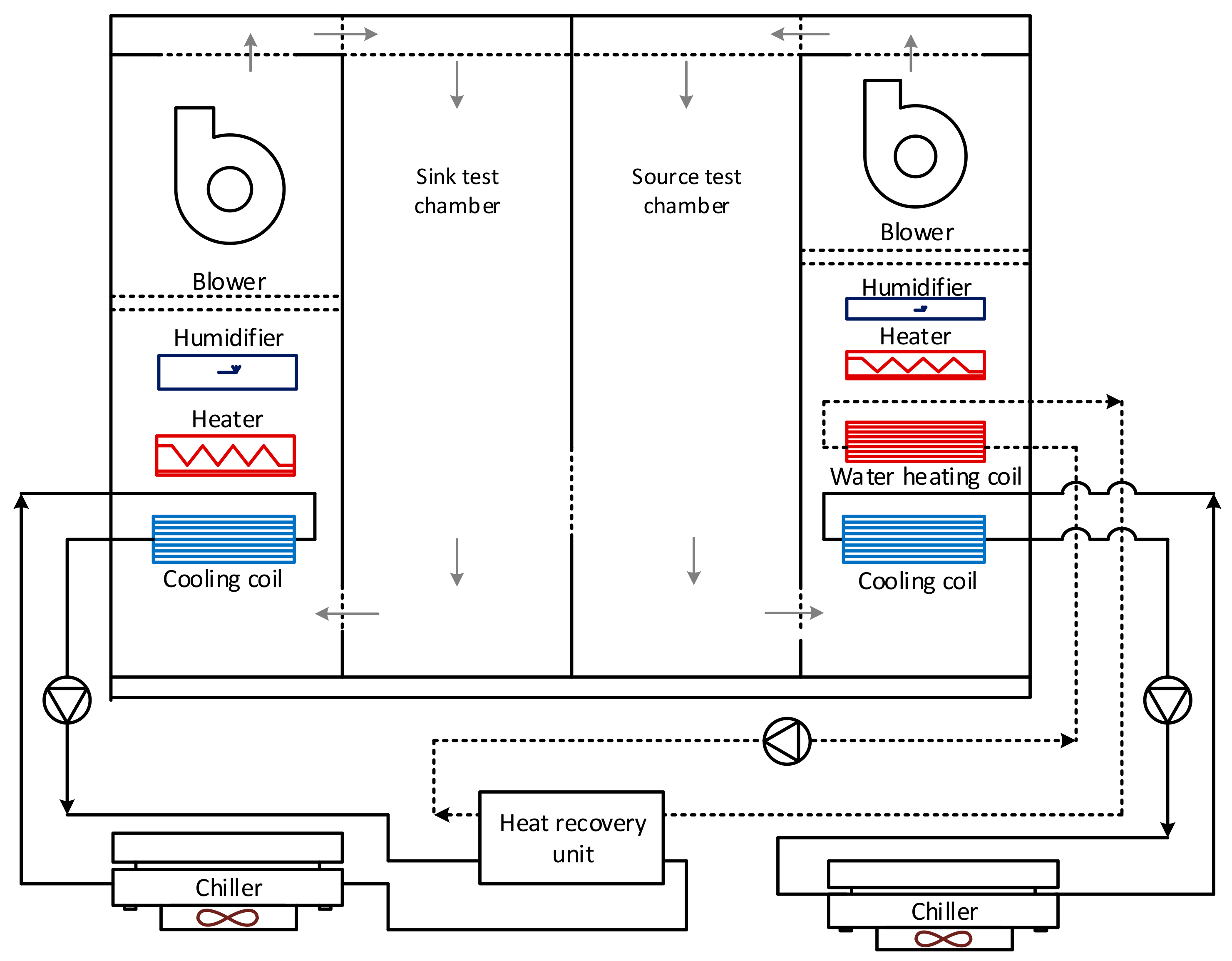
2.3. Description of System Modeling and Simulation Conditions
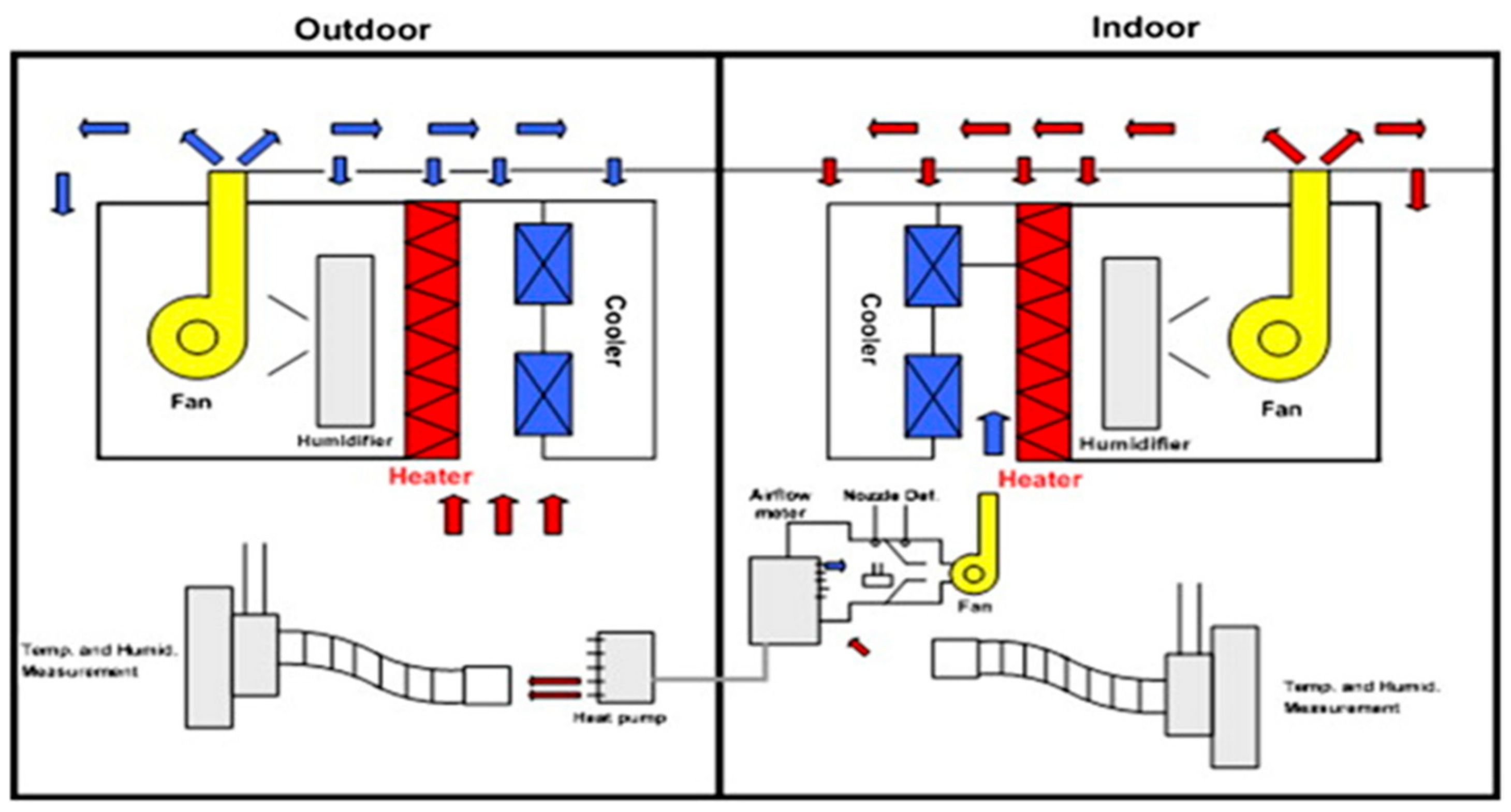
2.4. Description of Component Modeling
2.4.1. Refrigeration Unit Modeling
2.4.2. Heater Modeling
2.4.3. Heat Recovery Unit Modeling
2.4.4. Humidifier Modeling
2.4.5. Pump Modeling
2.4.6. Fan Modeling
3. Analysis of Simulation Results
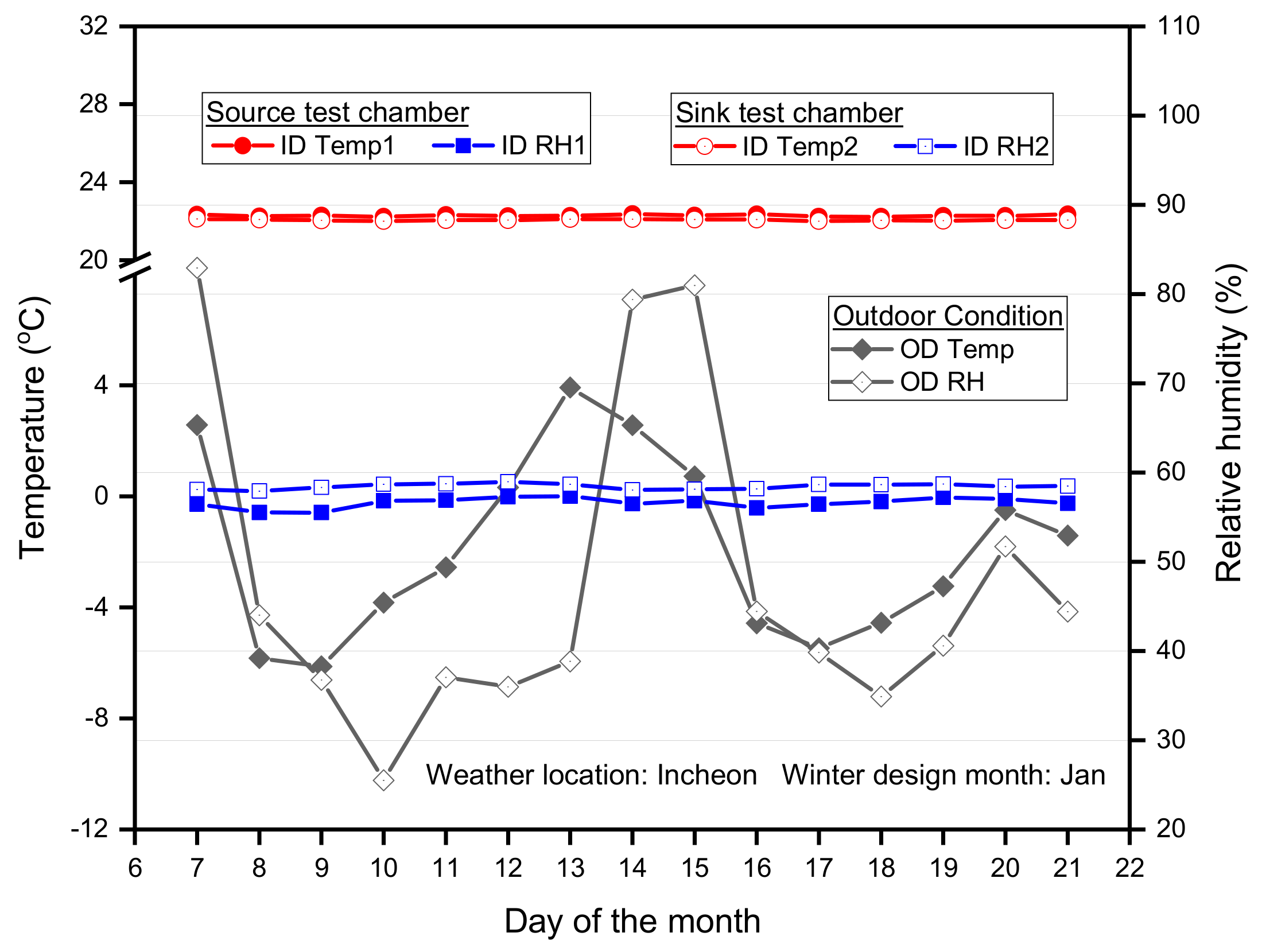
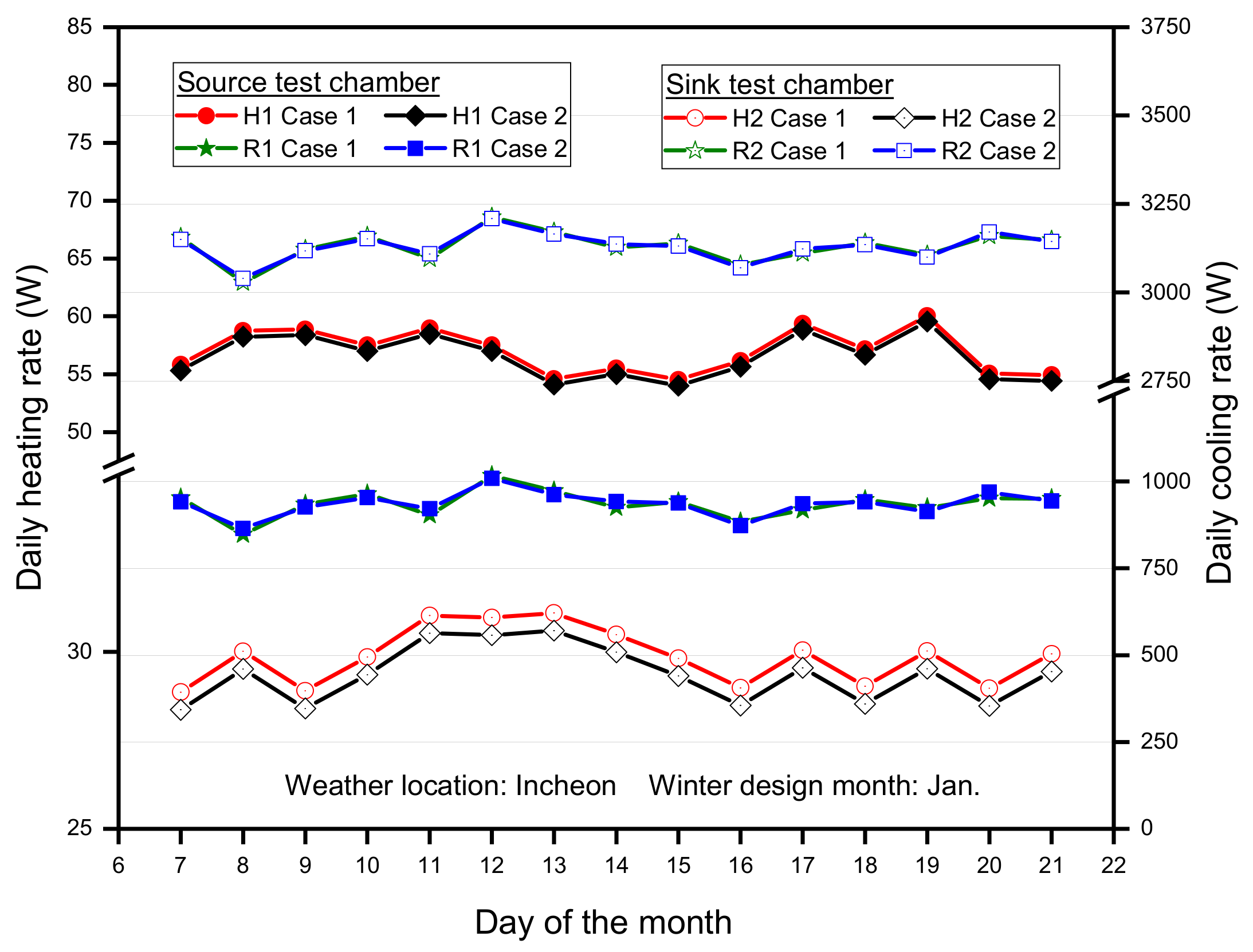
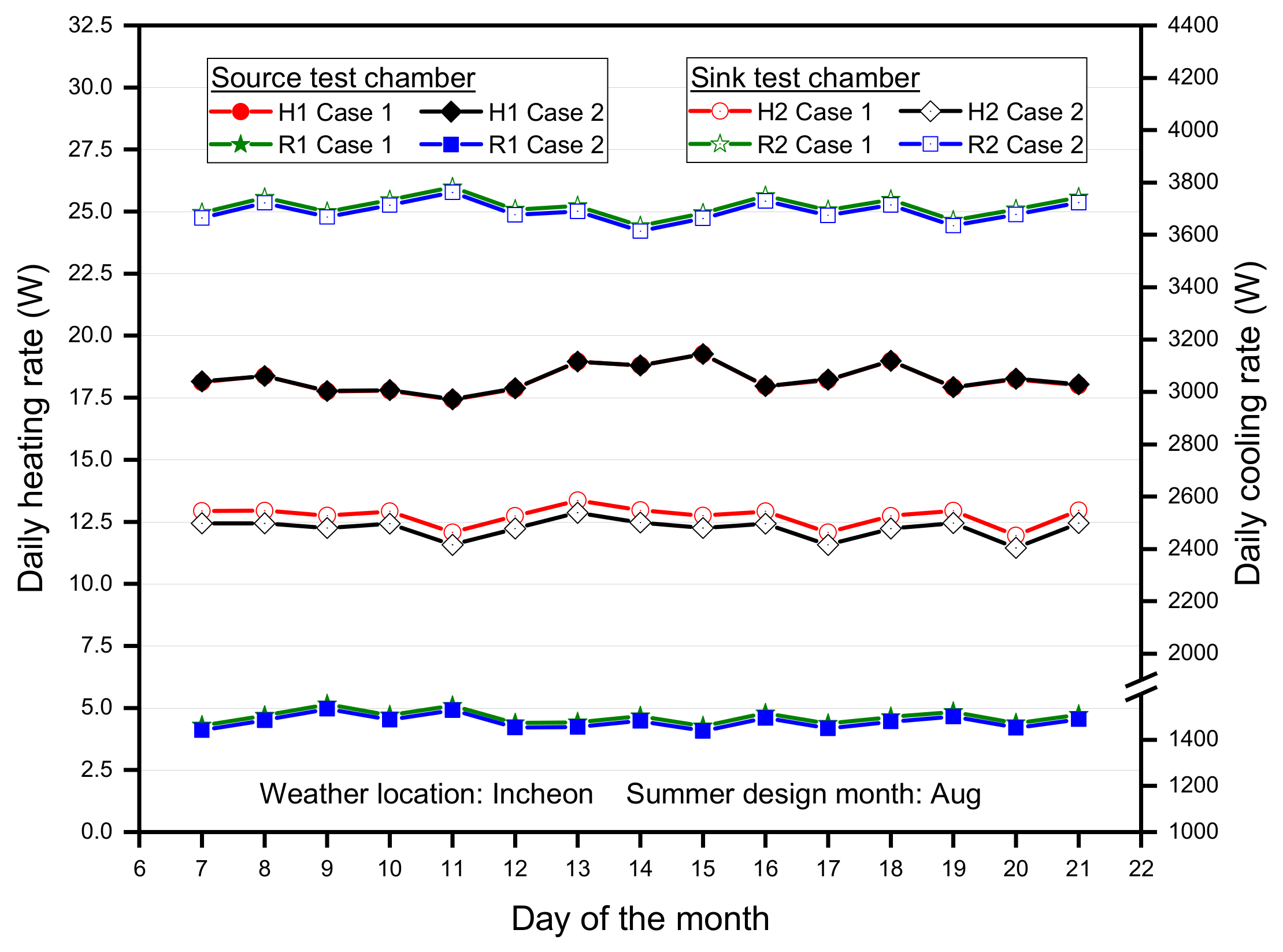
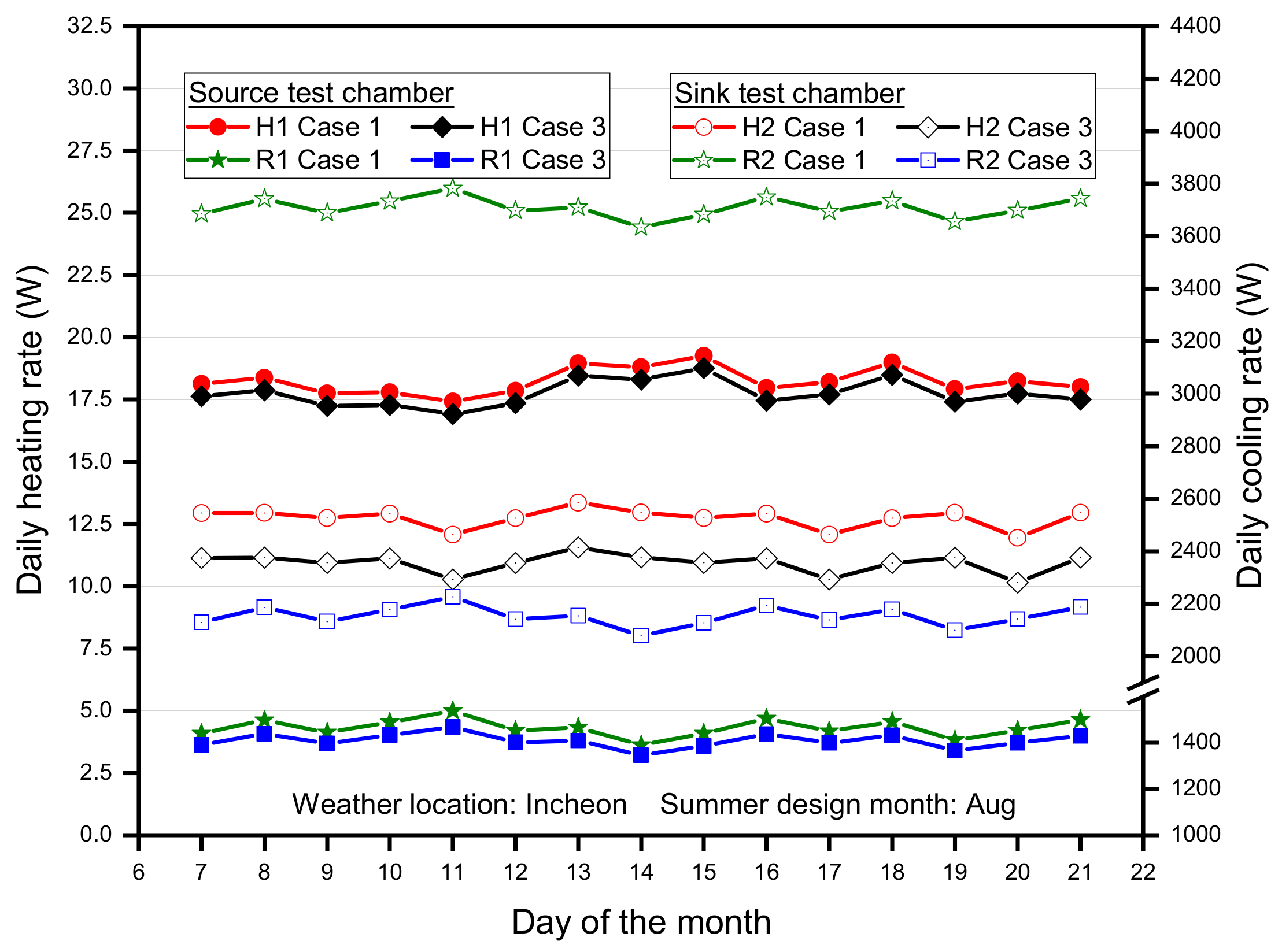
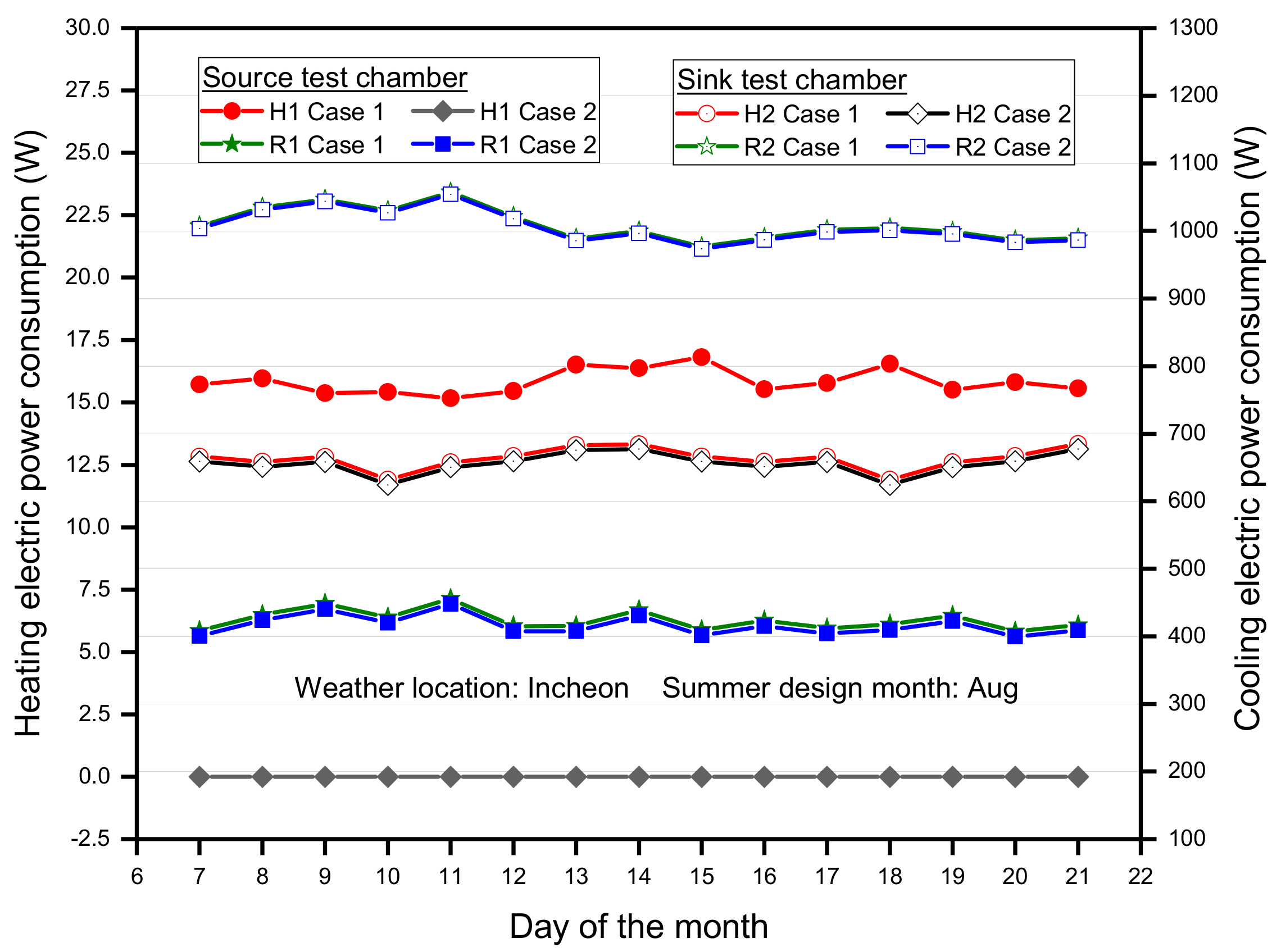
3.1. Performance Analysis of Modeling Cases in Winter Condition
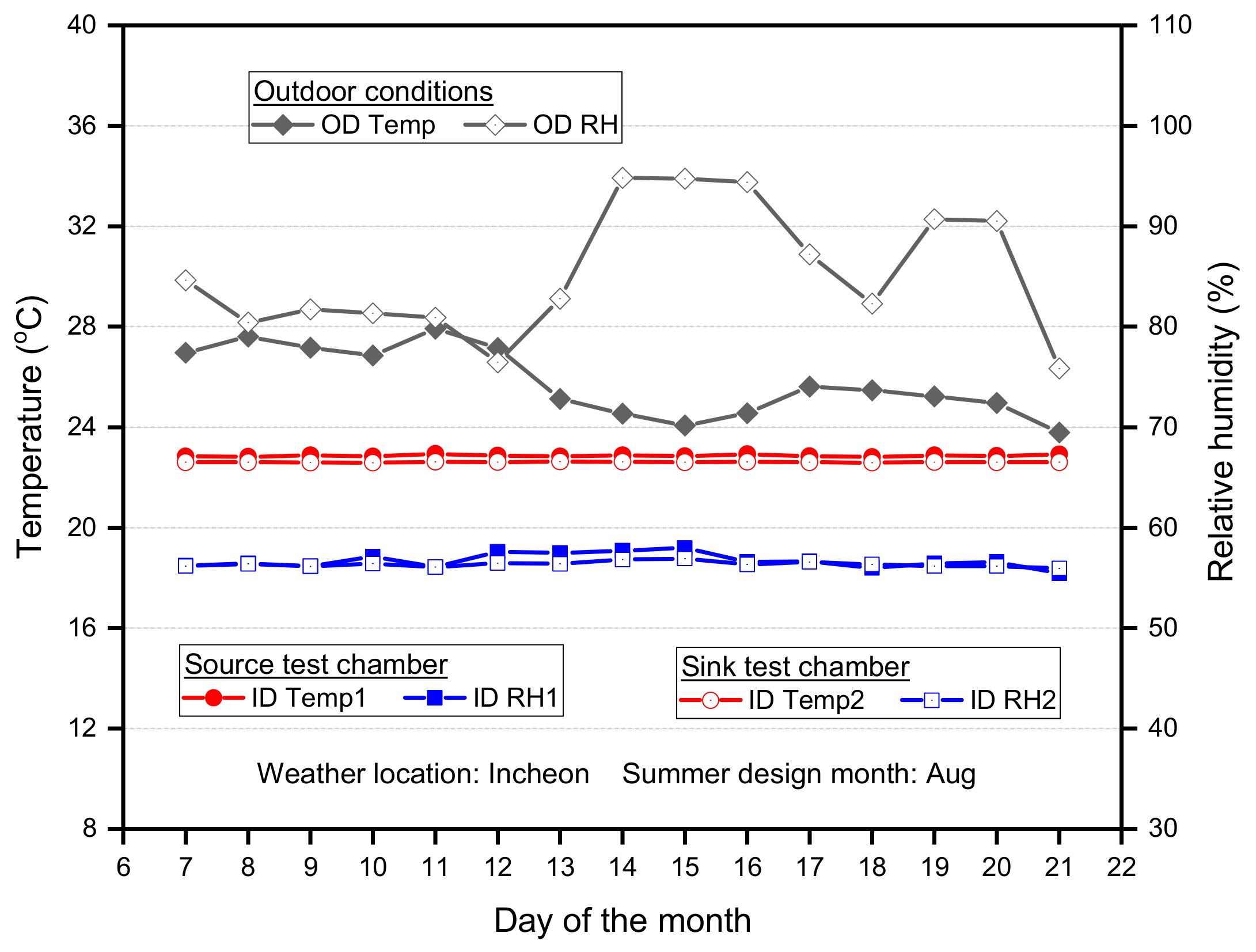
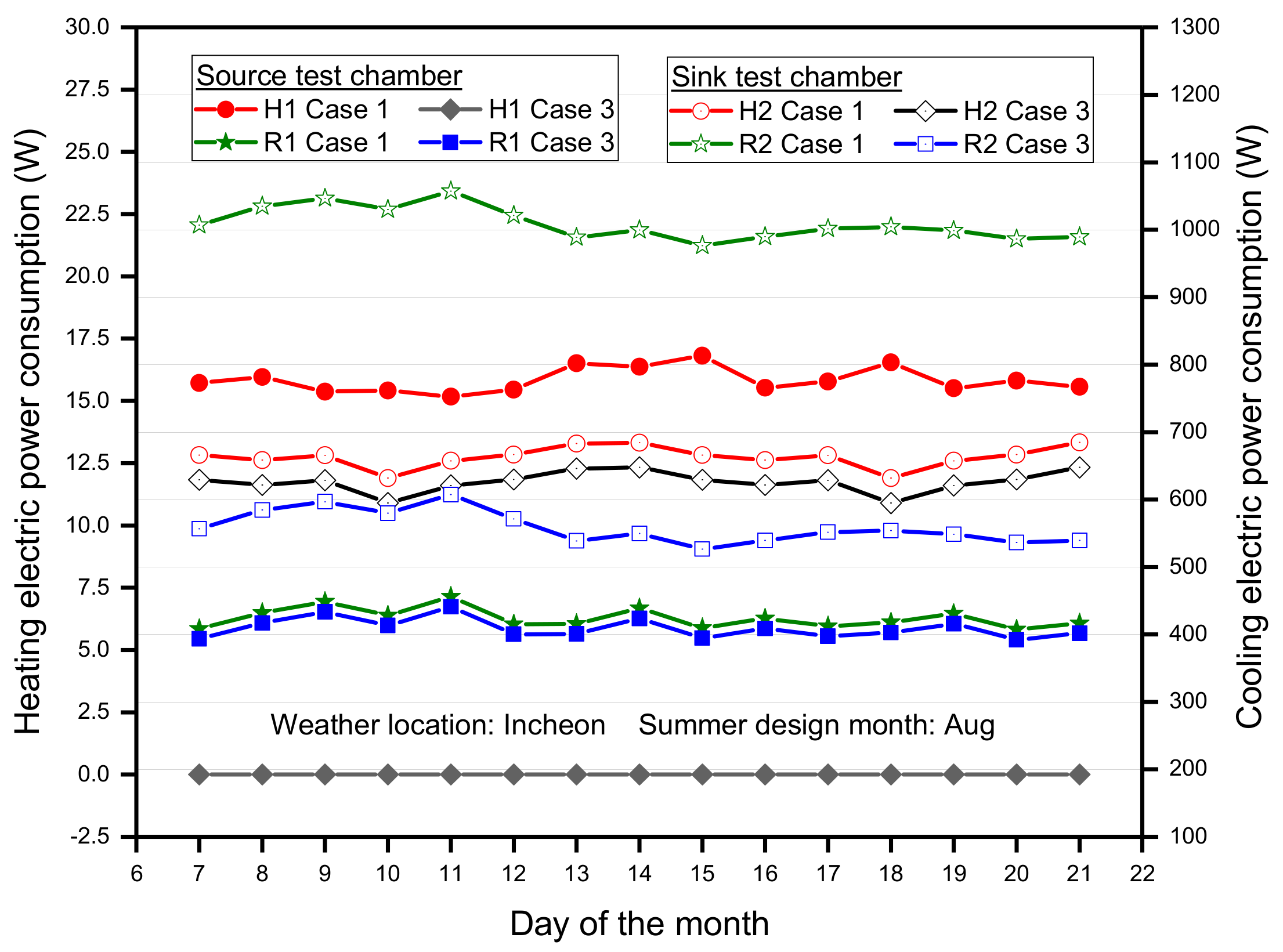
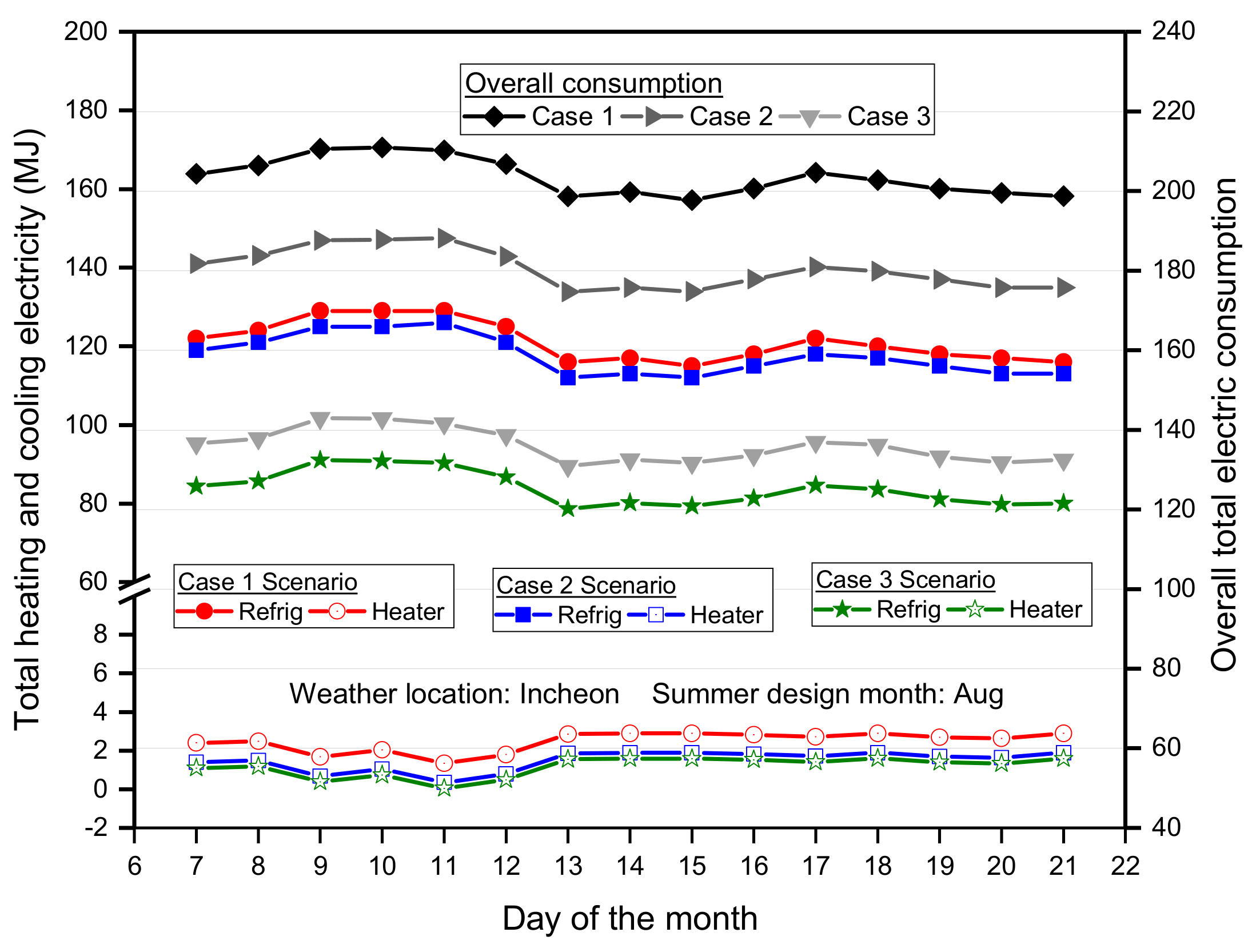
3.2. Performance Analysis of Modeling Cases in Summer Condition
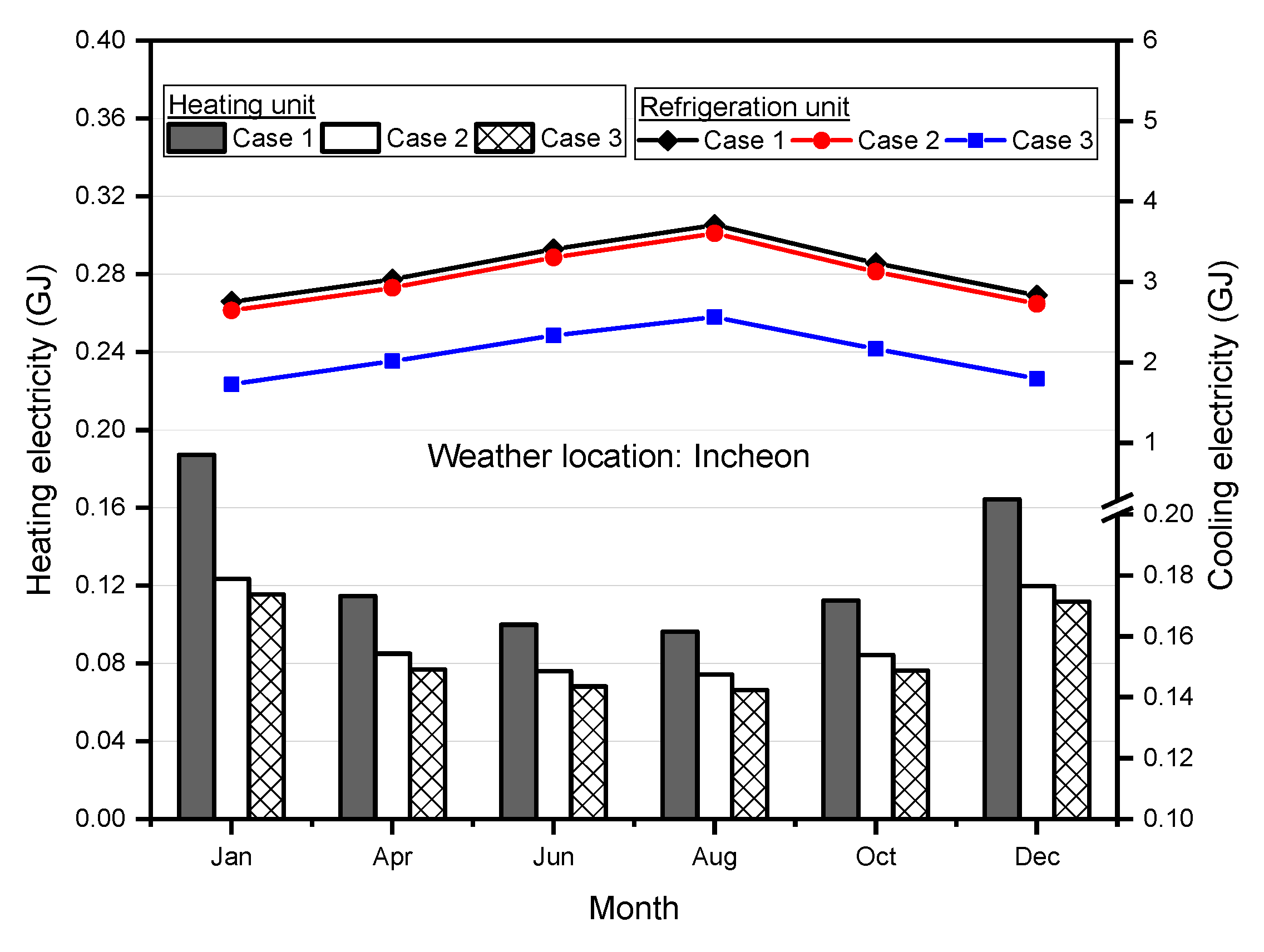
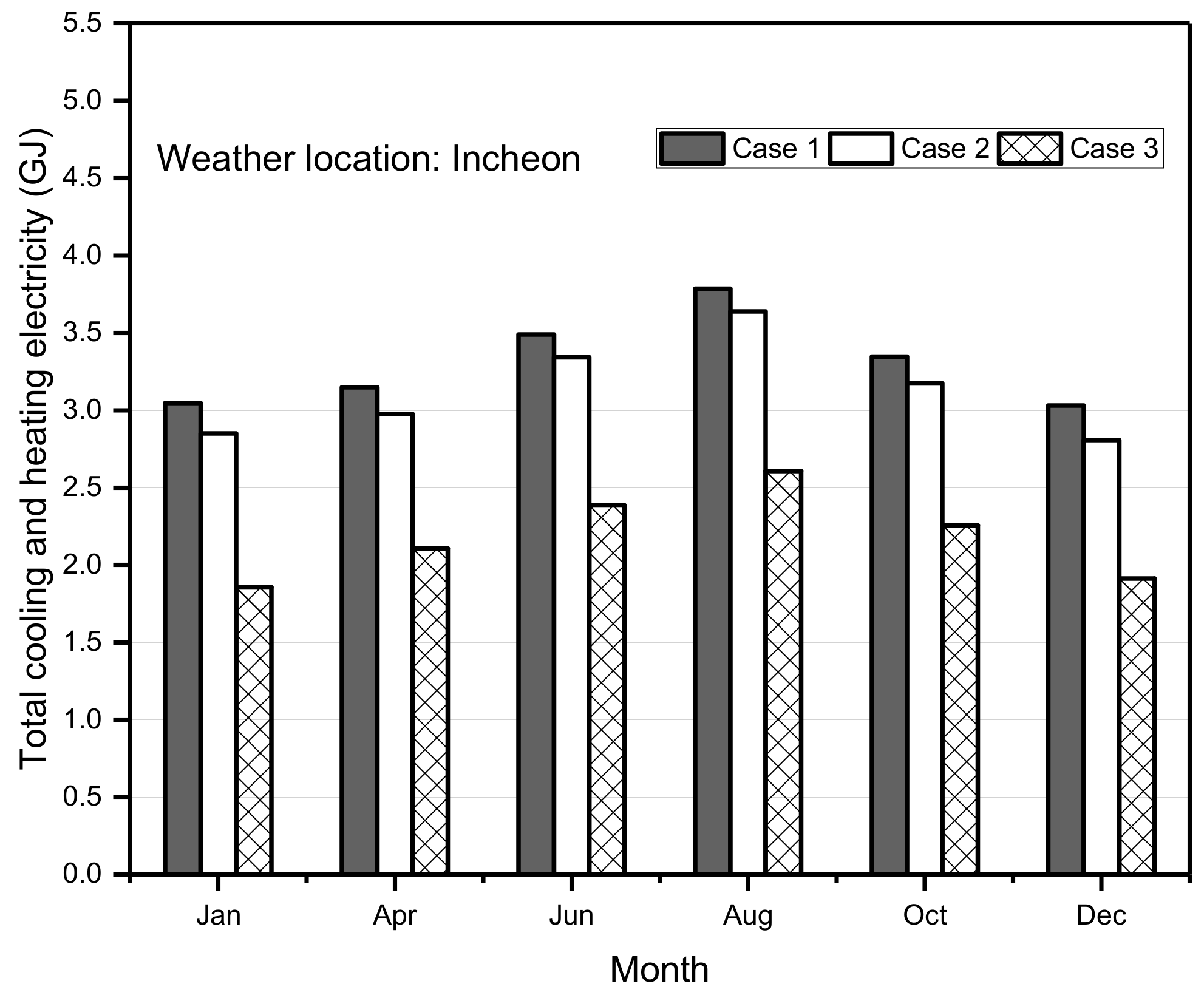
3.3. Monthly Energy Performance Evaluation of Case Scenarios
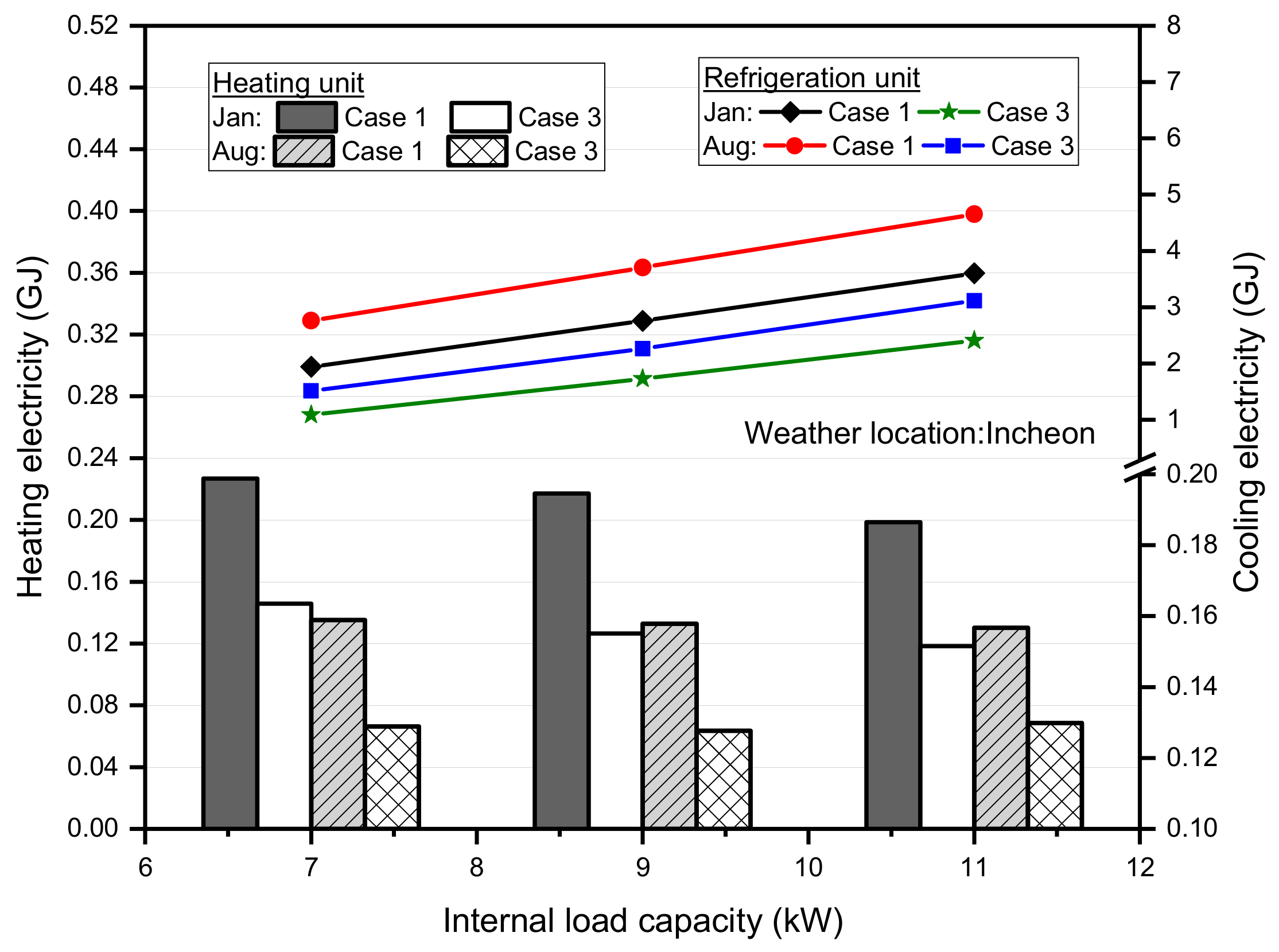
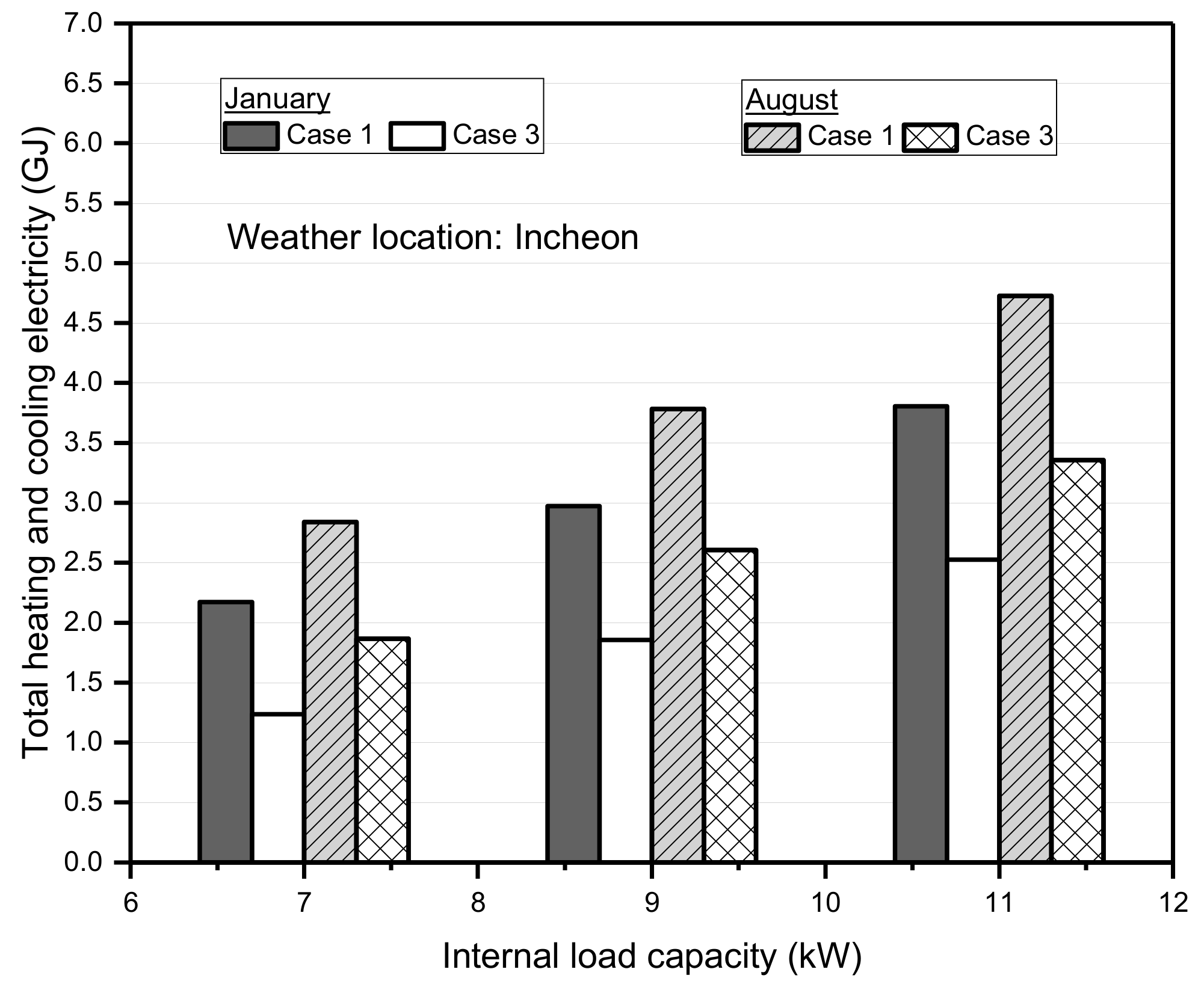
3.4. Energy Performance Analysis with Variation in Test Chamber Load Capacity
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| AHU | air handling unit |
| COP | coefficient of performance |
| COPnom | nominal COP of the chiller |
| cp,cd,w | specific heat of water at condenser inlet temperature, kJ/kg. °C |
| cp,cdwe | specific heat of water at condenser exit temperature, kJ/kg. °C |
| cp,w | specific heat capacity of water at 5 °C, kJ/kg. °C |
| cp,wavg | specific heat of water at average temperature of 60.0 °C, J/kg. °C |
| DB | dry bulb temperature. °C |
| ∆Tc,loop,des | condenser water loop design temperature rise, °C |
| ∆Tloop,des | chilled water loop design temperature rise, °C |
| ∆Tw | sensible temperature rise of water, °C |
| fc,s | component sizing factor |
| Fs | scaling factor, W/ m3/s-Pa |
| H | heater |
| hfg | latent heat of vaporization of water at 100 °C, J/kg |
| Hnom | nominal head or pressure rise across the pump, Pa |
| ID | indoor |
| OD | outdoor |
| ηmotor | motor efficiency |
| p | pressure, Pa |
| Ppump | design power consumption of the pump, W |
| Prated | rated power of the humidifier, W |
| ρw | density of water at standard conditions (5.05 °C), kg/m3 |
| Qdc,nom | loop design nominal capacity of dry cooler, kW |
| Qfan,nom | nominal fan power of the dry cooler, kW; |
| Qnom | nominal cooling capacity of the chiller, kW |
| Qw,a | heat transferred from water to the air, W |
| R | refrigerator |
| RH | relative humidity. % |
| Ta,avg | average air temperature, °C |
| Tw,avg | average water temperature, °C |
| UA | overall thermal conductance, W/°C |
| Vhru | volumetric water flow rate through heat recovery unit, m3/s |
| Vloop,des | loop design volumetric flow rate, m3/s |
| Vnom | nominal design volumetric flow rate, m3/s |
| Vrated | rated capacity of humidifier in volumetric flow rate, m3/s |
| Z | altitude, m |
References
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Mardiana-Idayua, A.; Riffat, S.B.; Zhang, S. Review of heat recovery technologies for building applications. Renew. Sustain. Energy Rev. 2012, 16, 1241–1255. [Google Scholar] [CrossRef]
- Arteconi, A.; Brandoni, C.; Rossi, G.; Polonara, F. Experimental evaluation and dynamic simulation of a ground coupled heat pump for a commercial building. Int. J. Energy Res. 2013, 37, 1971–1980. [Google Scholar] [CrossRef]
- Self, S.J.; Reddy, B.V.; Rosen, M.A. Geothermal heat pump systems: Status review and comparison with other heating options. Appl. Energy 2013, 101, 341–348. [Google Scholar] [CrossRef]
- ASHRAE. Standard 37: Methods of Testing for Rating Electrically Driven Unitary Air Conditioners and Heat Pumps; American Society of Heating, Refrigeration and Air-Conditioning Engineers (ASHRAE): Atlanta, GA, USA, 2009. [Google Scholar]
- ISO. Standard 5151: Non-Ducted Air Conditioners and Heat Pumps-Testing and Rating for Performance; International Standard Organization (ISO): Geneva, Switzerland, 2010. [Google Scholar]
- ASHRAE. Standard 116: Testing Methods for Seasonal Efficiency of Unit Air Conditioners and Heat Pumps; American Society of Heating, Refrigerating and Air Conditioning Engineers (ASHRAE): Atlanta, GA, USA, 1983. [Google Scholar]
- Byuna, J.S.; Lee, J.; Jeon, C.D. Frost retardation of an air-source heat pump by the hot gas bypass method. Int. J. Refrig. 2008, 31, 328–334. [Google Scholar] [CrossRef]
- Jang, J.Y.; Bae, H.H.; Lee, S.J.; Ha, M.Y. Continuous heating of an air-source heat pump during defrosting and improvement of energy efficiency. Appl. Energy 2013, 110, 9–16. [Google Scholar] [CrossRef]
- Ko, Y.; Park, S.; Jin, S.; Kim, B.; Jeong, J.H. The selection of volume ratio of two-stage rotary compressor and its effects on air-to-water heat pump with flash tank cycle. Appl. Energy 2013, 104, 187–196. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, C.; Wang, Y.; Chen, J.; Xu, K.; Li, F.; Wang, N. Experimental investigation of the performance of microchannel heat exchangers with a new type of fin under wet and frosting conditions. Appl. Therm. Eng. 2015, 89, 444–458. [Google Scholar] [CrossRef]
- Choi, H.J.; Kim, B.S.; Kang, D.; Kim, K.C. Defrosting method adopting dual hot gas bypass for an air-to-air heat pump. Appl. Energy 2011, 88, 4544–4555. [Google Scholar] [CrossRef]
- Park, Y.S.; Jeong, J.H.; Ahn, B.H. Heat pump control method based on direct measurement of evaporation pressure to improve energy efficiency and indoor air temperature stability at a low cooling load condition. Appl. Energy 2014, 132, 99–107. [Google Scholar] [CrossRef]
- Fan, H.; Shao, S.; Tian, C. Performance investigation on a multi-unit heat pump for simultaneous temperature and humidity control. Appl. Energy 2014, 113, 883–890. [Google Scholar] [CrossRef]
- Amoabeng, O.K.; Choi, J.M.; Lee, K.H. A study on the performance characteristics of a testing facility for a water-to-water heat pump. Int. J. Refrig. 2018, 86, 113–126. [Google Scholar] [CrossRef]
- Xu, Q.; Riffat, S.; Zhang, S. Review of heat recovery technologies for building applications. Energies 2019, 12, 22. [Google Scholar] [CrossRef]
- Cuce, P.M.; Riffat, S.B. A comprehensive review of heat recovery systems for building applications. Renew. Sustain. Energy Rev. 2015, 47, 665–682. [Google Scholar] [CrossRef]
- Yau, Y.H.; Ahmadzadehtalatapeh, M.A. Review on the application of horizontal heat pipe heat exchangers in air conditioning systems in the tropics. Appl. Therm. Eng. 2010, 30, 77–84. [Google Scholar] [CrossRef]
- Mardiana-Idayu, A.; Riffat, S.B. An experimental study on the performance of enthalpy recovery system for building applications. Energy Build. 2011, 43, 2533–2538. [Google Scholar] [CrossRef]
- Nguyen, A.; Kim, Y.; Shin, Y. Experimental study of sensible heat recovery of heat pump during heating and ventilation. Int. J. Refrig. 2005, 28, 242–252. [Google Scholar] [CrossRef]
- Nasif, M.; Al-Waked, R.; Morrison, G.; Behnia, M. Membrane heat exchanger in HVAC energy recovery systems, systems energy analysis. Energy Build. 2010, 42, 1833–1840. [Google Scholar] [CrossRef]
- Riffat, S.B.; Gillott, M.C. Performance of a novel mechanical ventilation heat recovery heat pump system. Appl. Therm. Eng. 2002, 22, 839–845. [Google Scholar] [CrossRef]
- Gong, G.; Zeng, W.; Wang, L.; Wu, C. A new heat recovery technique for air conditioning/heat pump system. Appl. Therm. Eng. 2008, 28, 2360–2370. [Google Scholar] [CrossRef]
- Gu, Z.; Liu, H.; Li, Y. Thermal energy recovery of air conditioning system and heat recovery system calculation and phase change materials development. Appl. Therm. Eng. 2004, 24, 2511–2526. [Google Scholar] [CrossRef]
- Sukamongkol, Y.; Chungpaibulpatana, S.; Limmeechokchai, B.; Sripadungtham, P. Condenser heat recovery with a PV/T air heating collector to regenerate desiccant for reducing energy use of air conditioning room. Energy Build. 2010, 42, 315–325. [Google Scholar] [CrossRef]
- U.S. Department of Energy. EnergyPlus Building Technologies Program, Energy Efficiency and Renewable Energy; Trimble Inc.: Sunnyvale, CA, USA, 2017. [Google Scholar]
- U.S. Department of Energy. EnergyPlus Simulation Software Version 8.4. In The Encyclopedic Reference to EnergyPlus Input and Output; U.S. Department of Energy: Washington, DC, USA, 2016; Available online: https://energyplus.net/downloads (accessed on 2 December 2019).
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, H.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: Creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- ASHRAE. The Handbook of Heating, Ventilation and Air Conditioning (HVAC); Applications, SI Edition; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2011. [Google Scholar]
- Harmathy, N.; Murgul, V. Heat pump system simulation towards energy performance estimation in office buildings. Procedia Eng. 2016, 165, 1845–1852. [Google Scholar] [CrossRef]
- Kim, S.U. Technology of Energy Simulation. Int. J. Air-Cond Refrig. 2014, 43, 23–38. [Google Scholar]
- Parsons, R. Handbook of Fundamentals: SI Edition; American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE): Atlanta, GA, USA, 2005. [Google Scholar]
- Duan, Z.; Zhao, X.; Liu, J.; Zhang, Q. Dynamic simulation of a hybrid dew point evaporative cooler and vapour compression refrigerated system for a building using EnergyPlus. J. Build. Eng. 2019, 21, 287–301. [Google Scholar] [CrossRef]
- Aikins, K.A.; Choi, J.M. Current status of the performance of ground source heat pump (GSHP) units in the Republic of Korea. Energy 2012, 47, 77–82. [Google Scholar] [CrossRef]
- Boyanoa, A.; Hernandez, P.; Wolfa, O. Energy demands and potential savings in European office buildings: Case studies based on EnergyPlus simulations. Energy Build. 2013, 65, 19–28. [Google Scholar] [CrossRef]
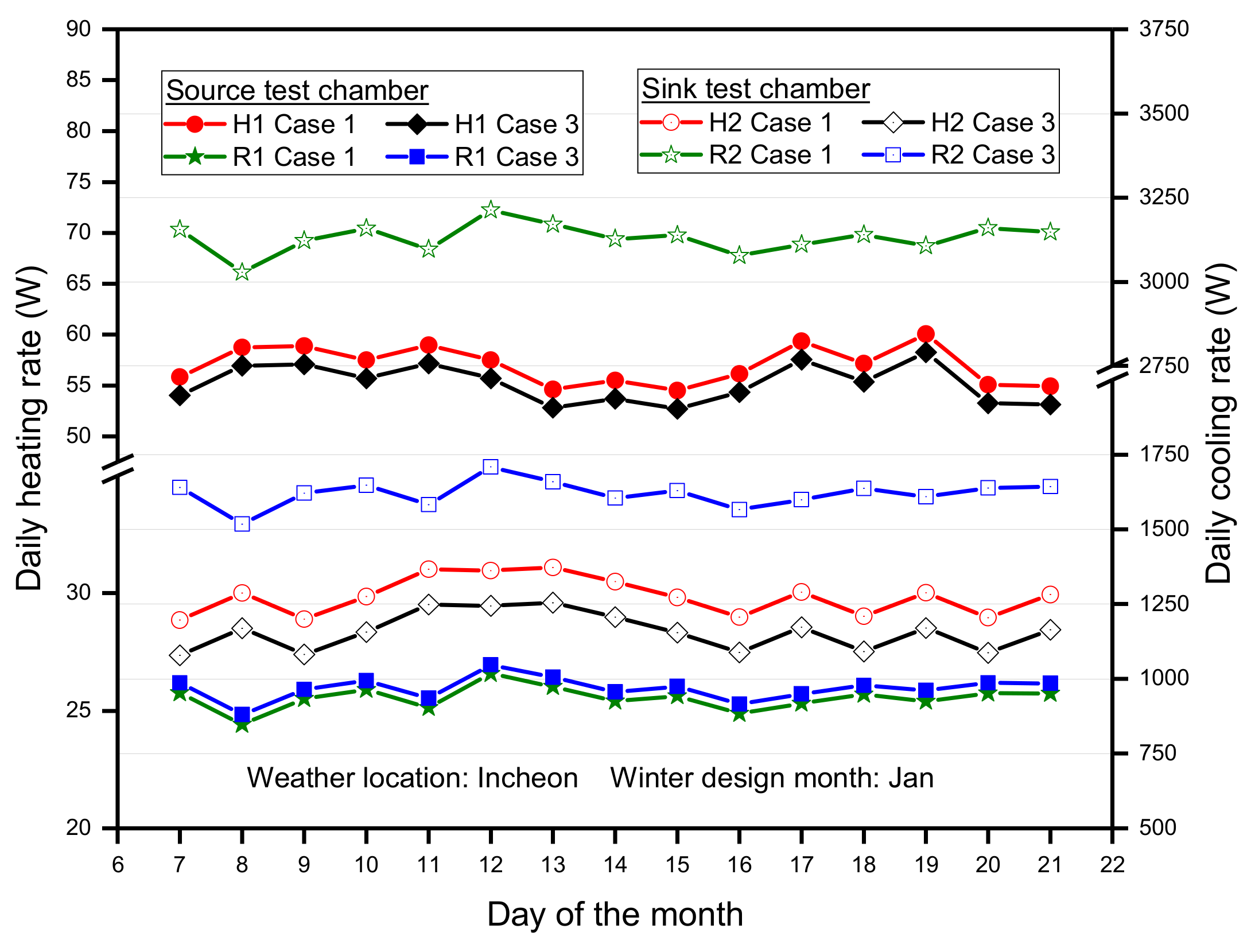
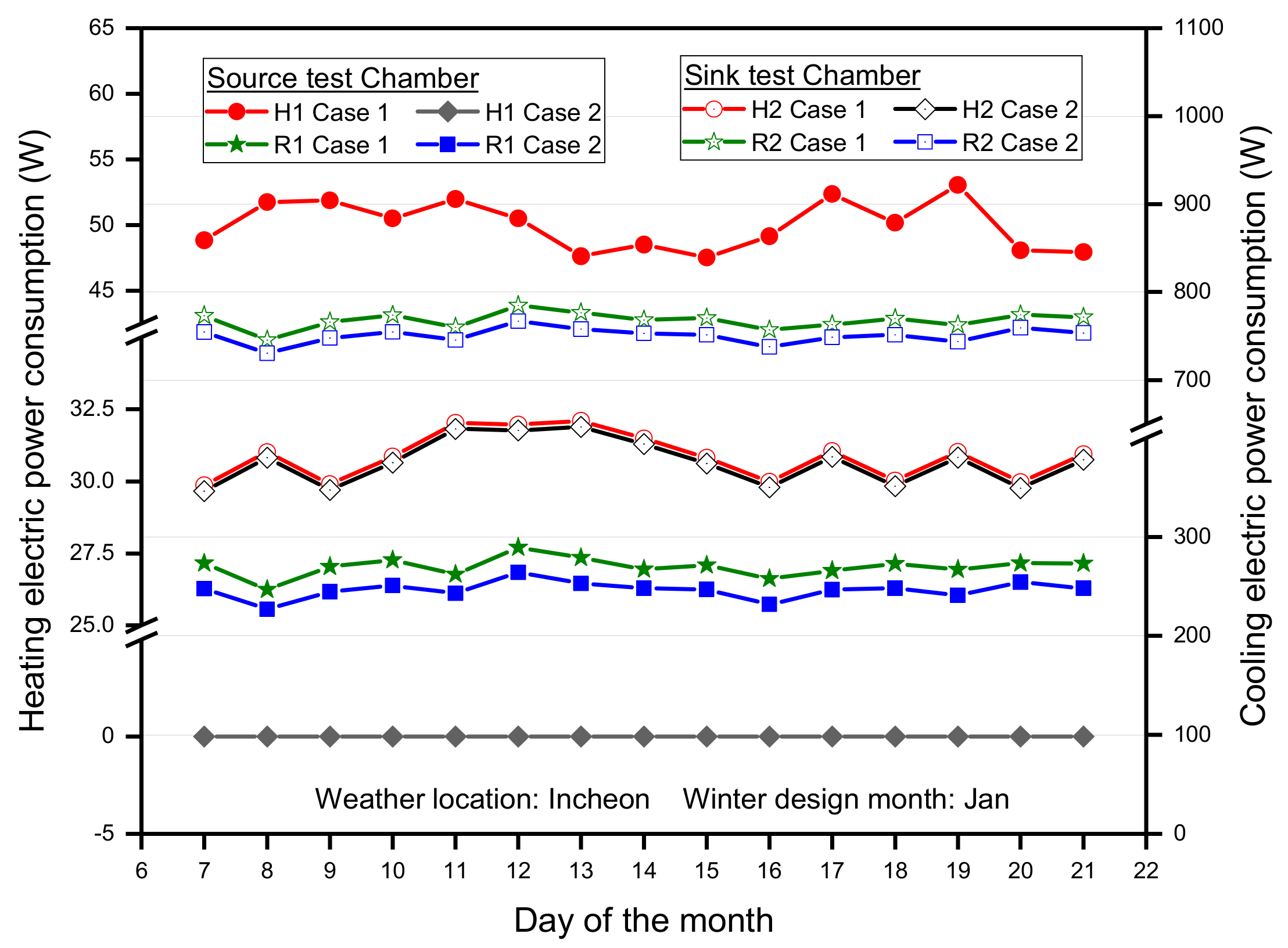
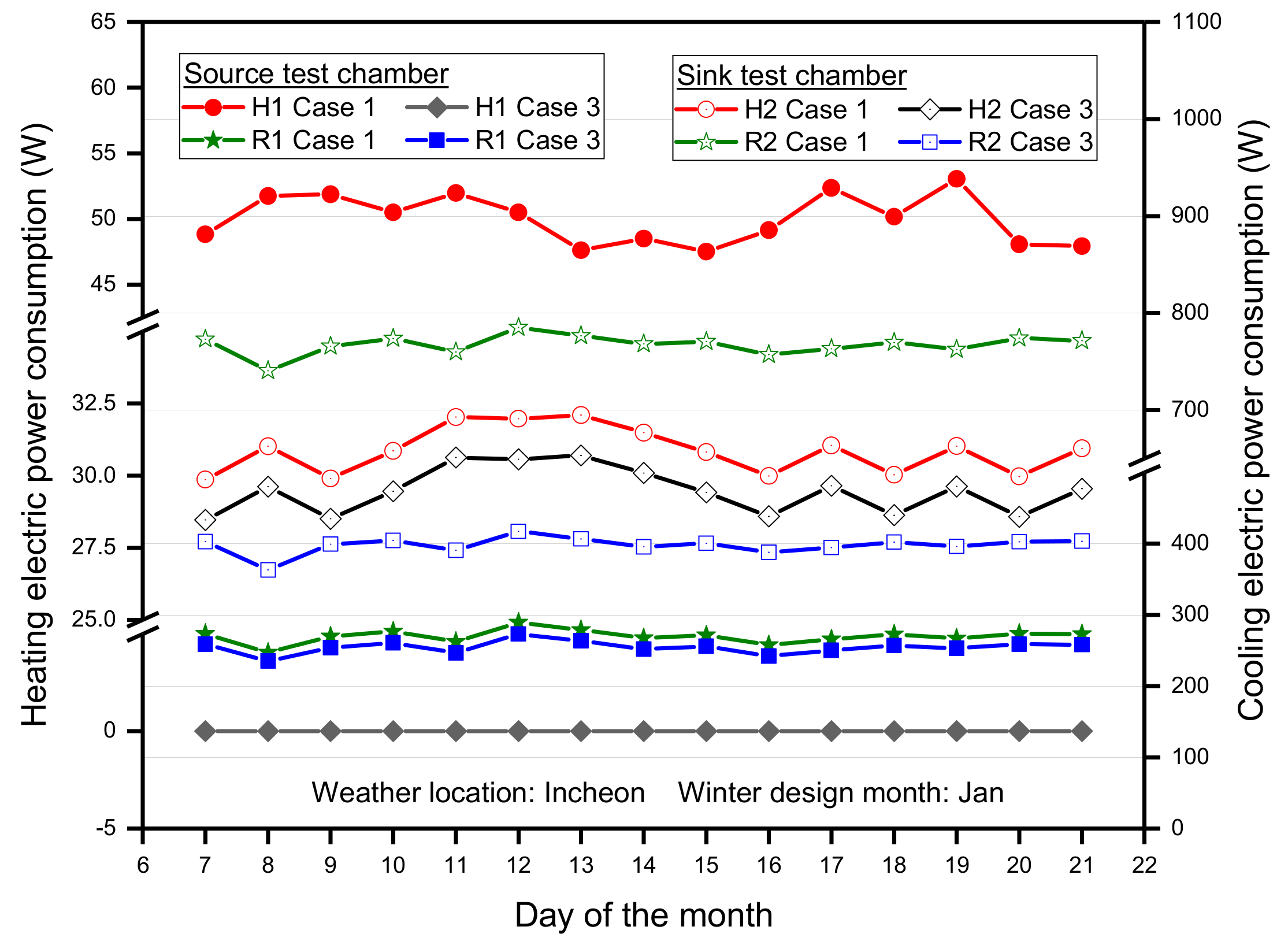
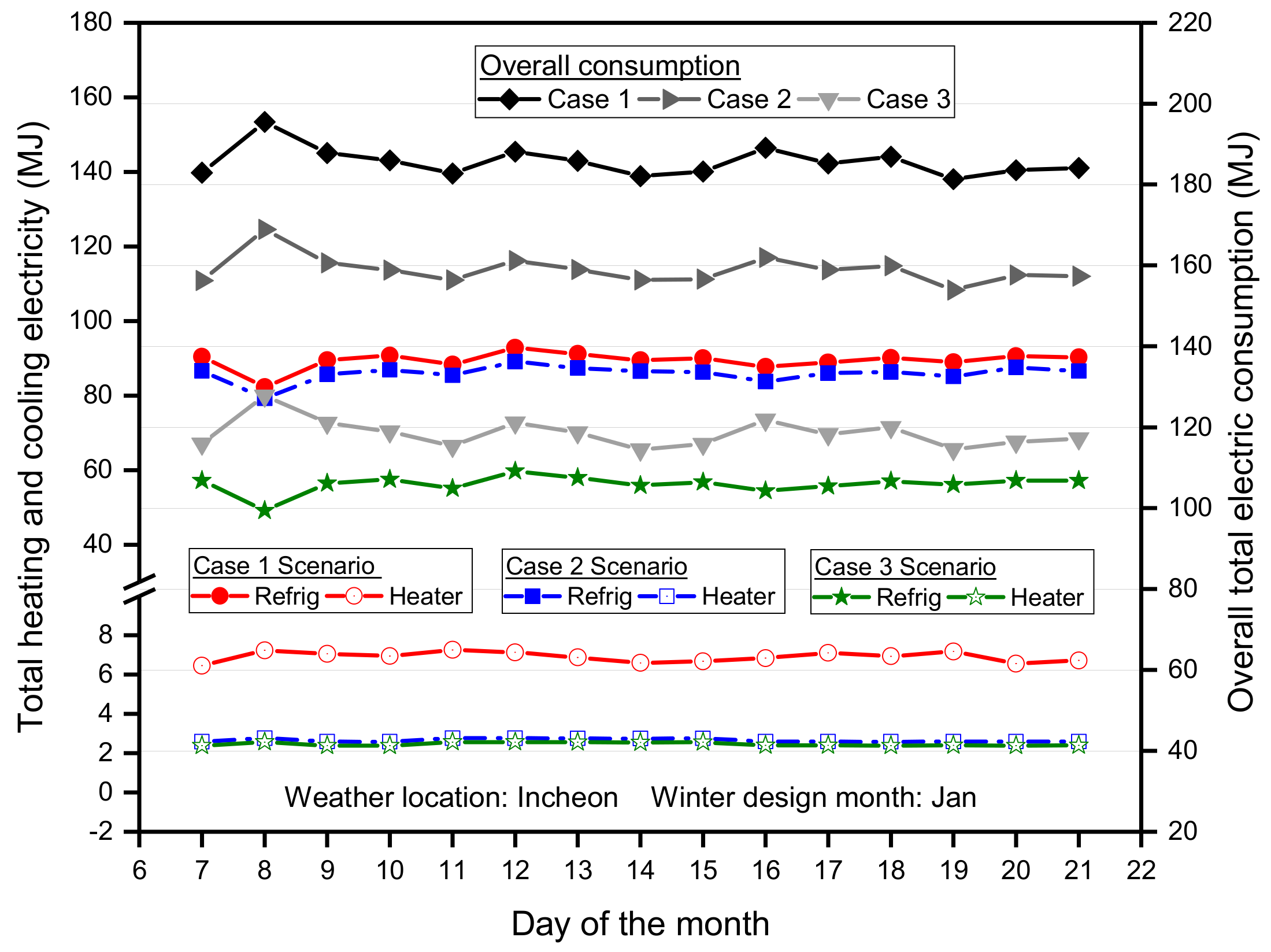
| Item | Unit | Internal Heat Load Capacity | |
|---|---|---|---|
| Sink Chamber | Source Chamber | ||
| Equipment (test unit) | kW | 7 | 5.25 |
| 9 | 6.75 | ||
| 11 | 8.25 | ||
| Item | Specification |
|---|---|
| Software program | EnergyPlus v8.4 |
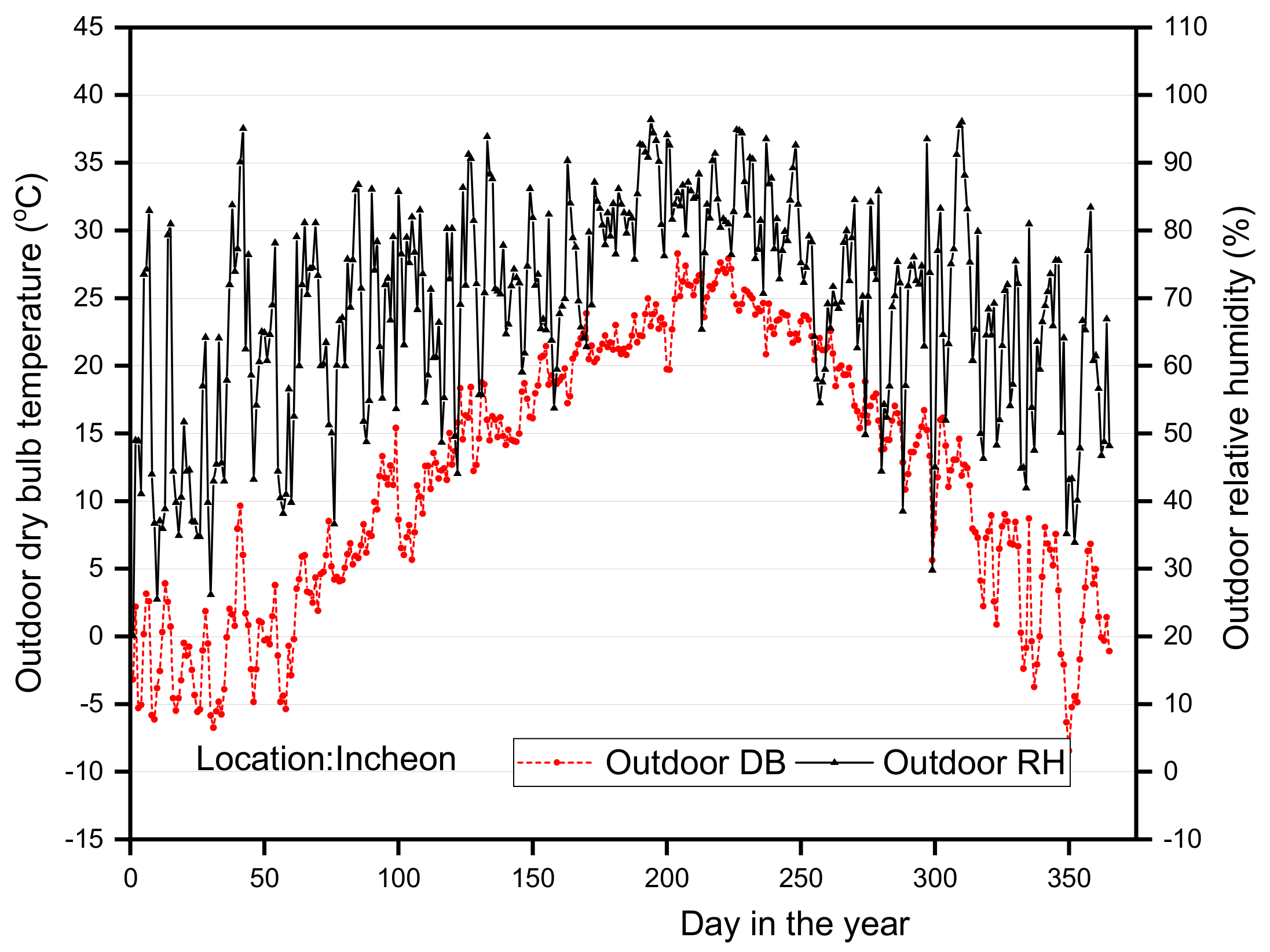
| City/weather location | Incheon (South Korea) |
| System operating schedule | From 10:00 Until 21:00 |
| Indoor heating/cooling setpoint | 21 °C/25 °C |
| Monthly analysis period | Jan., Apr., Jun., Aug., Oct., Dec. |
| Representative days | 7th to 21st (Jan. and Aug.) |
| Lighting internal heat gain | 3.3 W/m2 |
| Equipment (test unit) COP | 4.0 |
| Test operating mode | Heating |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amoabeng, K.O.; Lee, K.H.; Choi, J.M. Modeling and Simulation Performance Evaluation of a Proposed Calorimeter for Testing a Heat Pump System. Energies 2019, 12, 4589. https://doi.org/10.3390/en12234589
Amoabeng KO, Lee KH, Choi JM. Modeling and Simulation Performance Evaluation of a Proposed Calorimeter for Testing a Heat Pump System. Energies. 2019; 12(23):4589. https://doi.org/10.3390/en12234589
Chicago/Turabian StyleAmoabeng, Kofi Owura, Kwang Ho Lee, and Jong Min Choi. 2019. "Modeling and Simulation Performance Evaluation of a Proposed Calorimeter for Testing a Heat Pump System" Energies 12, no. 23: 4589. https://doi.org/10.3390/en12234589
APA StyleAmoabeng, K. O., Lee, K. H., & Choi, J. M. (2019). Modeling and Simulation Performance Evaluation of a Proposed Calorimeter for Testing a Heat Pump System. Energies, 12(23), 4589. https://doi.org/10.3390/en12234589




