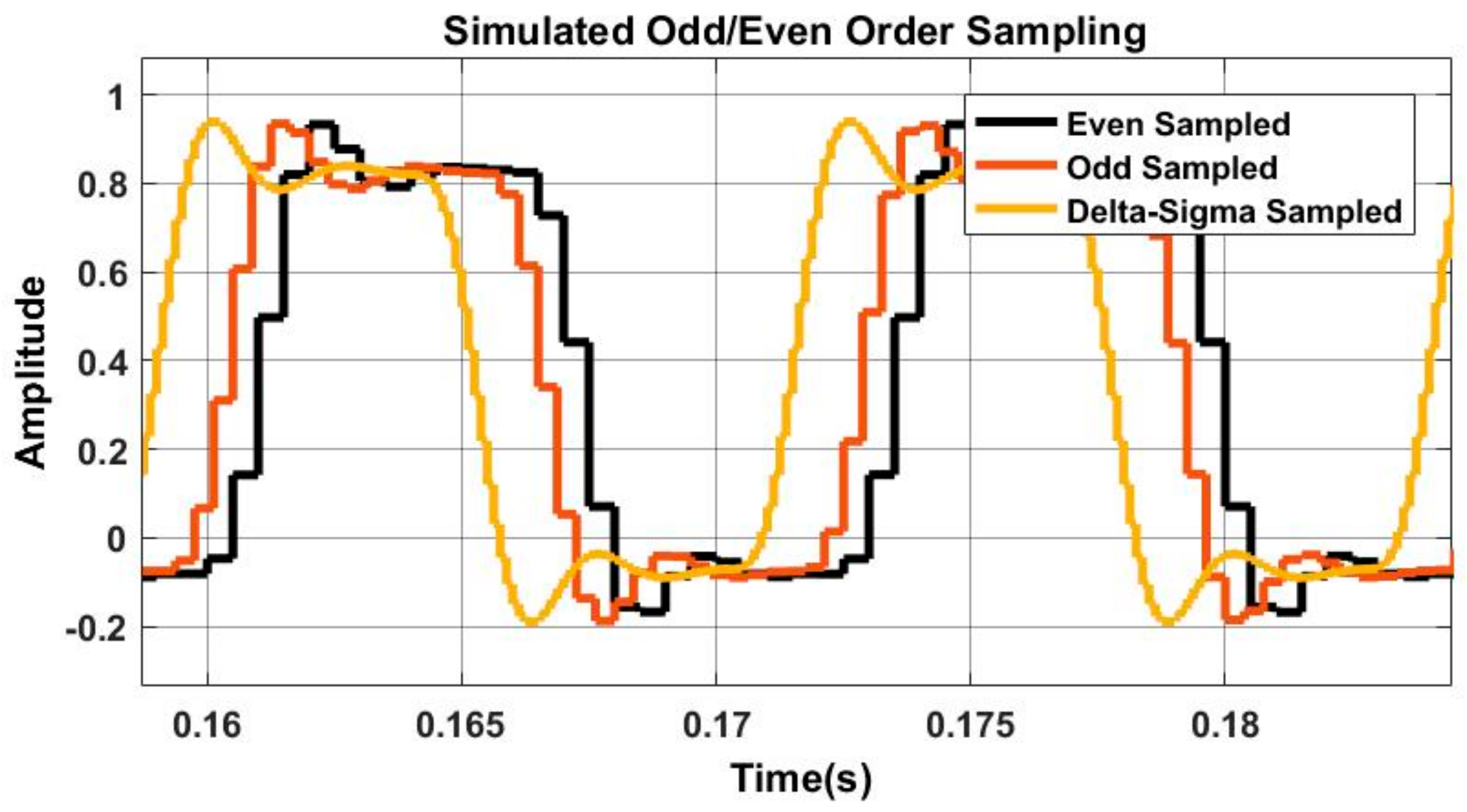
Figure 1.
This portrays the phase performance between 1st order delta-sigma and odd/even order sampling. The phase difference between 1st order delta-sigma and odd/even sampling was created for the design by the transport delay between the signals, and should be ignored for analysis. 1st delta-sigma is indicated by the yellow, odd order sampling by red and even order sampling by black. It should be noted there is a (n−1) phase lag between even order sampling (black) and odd order sampling (red).
Figure 1.
This portrays the phase performance between 1st order delta-sigma and odd/even order sampling. The phase difference between 1st order delta-sigma and odd/even sampling was created for the design by the transport delay between the signals, and should be ignored for analysis. 1st delta-sigma is indicated by the yellow, odd order sampling by red and even order sampling by black. It should be noted there is a (n−1) phase lag between even order sampling (black) and odd order sampling (red).
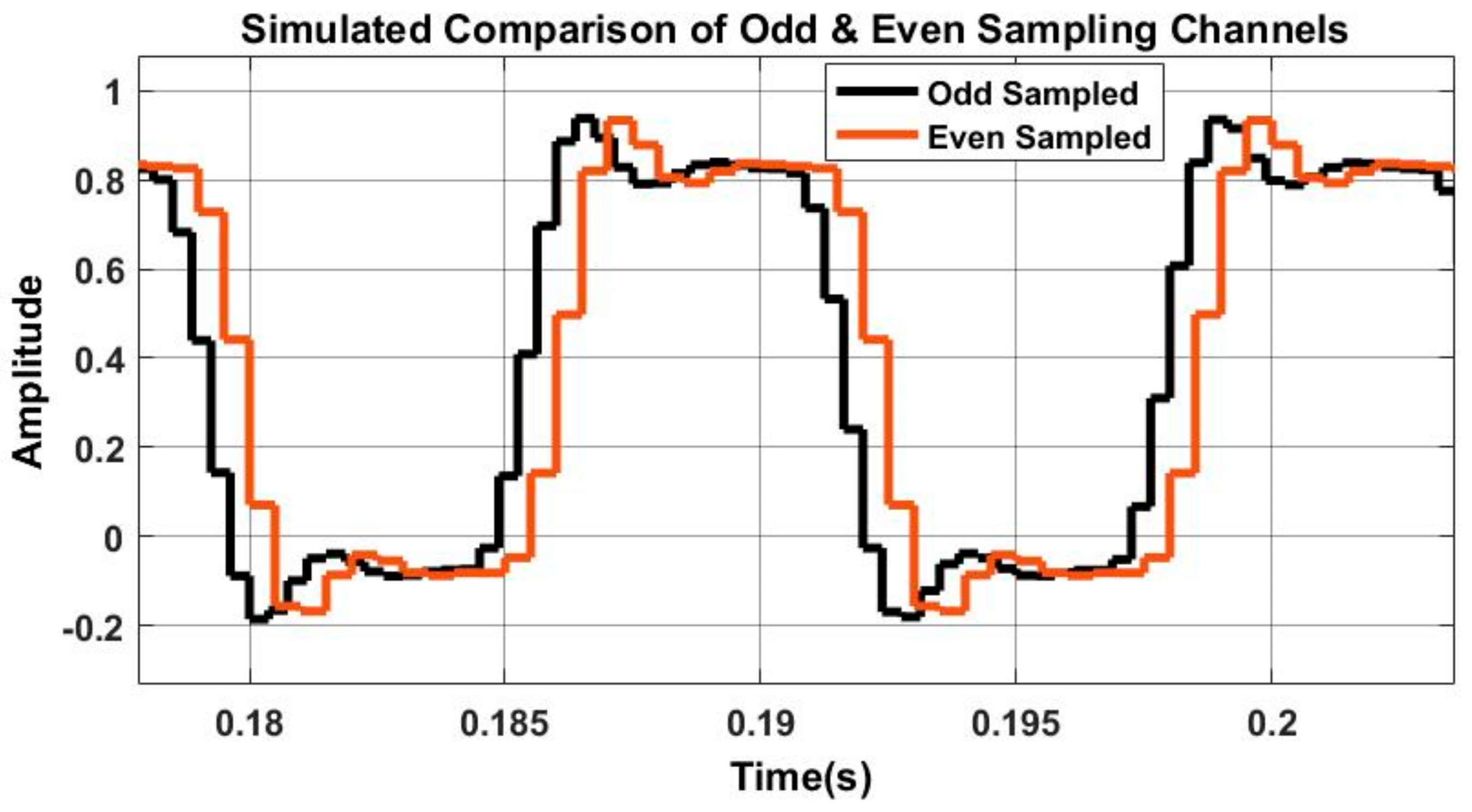
Figure 2.
This portrays the phase lag performance between odd and even order sampling. Odd order sampling is marked by black and even order sampling is marked by red. It should be noted that the (n−1) phase lag between even order sampling (red) and odd order sampling (black) varies per period interval.
Figure 2.
This portrays the phase lag performance between odd and even order sampling. Odd order sampling is marked by black and even order sampling is marked by red. It should be noted that the (n−1) phase lag between even order sampling (red) and odd order sampling (black) varies per period interval.
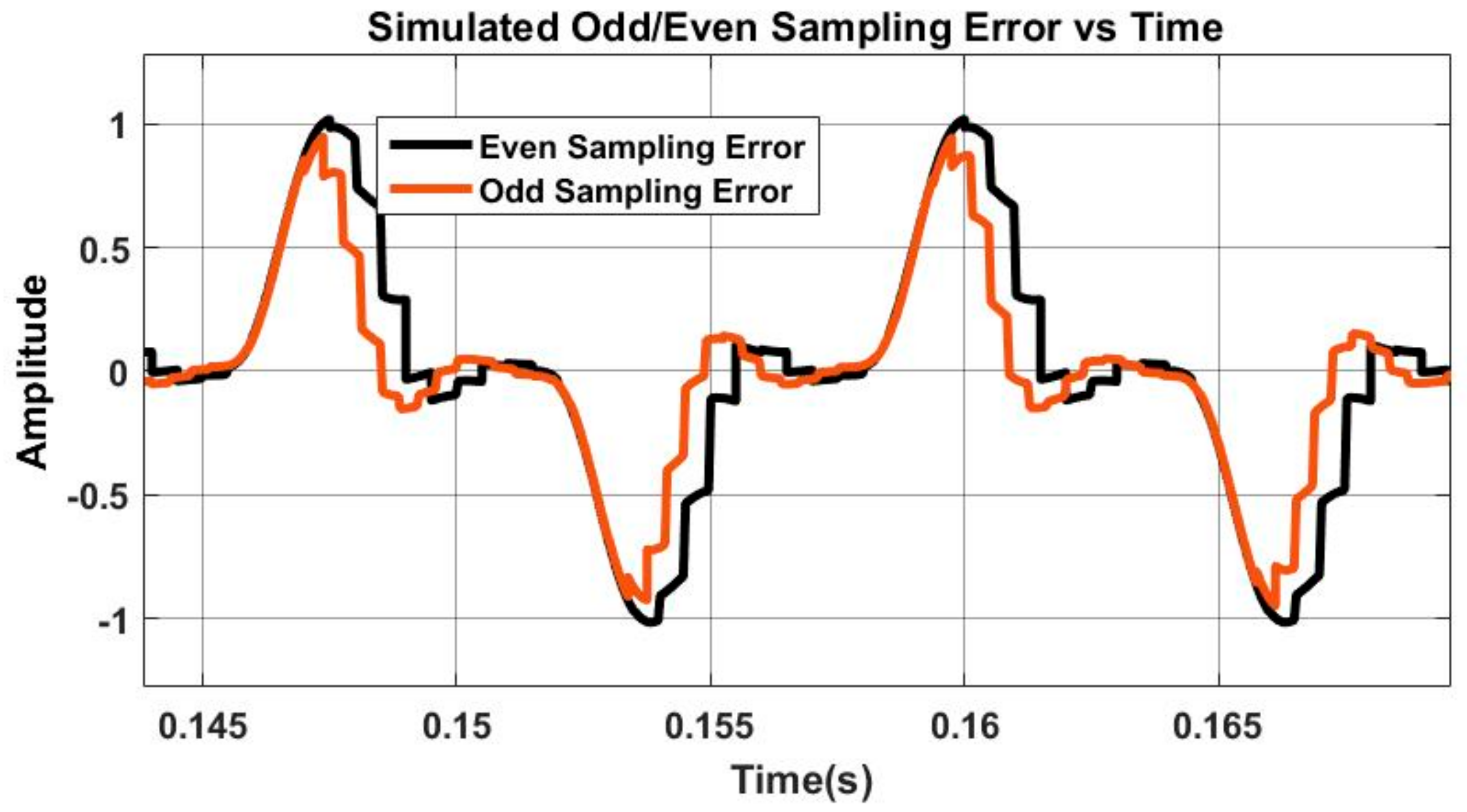
Figure 3.
This portrays the phase lag performance between odd and even order sampling. Odd order sampling was marked by black and even order sampling was by red. It should be noted that the (n−1) phase lag between even order sampling (red) and odd order sampling (black) varies per period interval.
Figure 3.
This portrays the phase lag performance between odd and even order sampling. Odd order sampling was marked by black and even order sampling was by red. It should be noted that the (n−1) phase lag between even order sampling (red) and odd order sampling (black) varies per period interval.
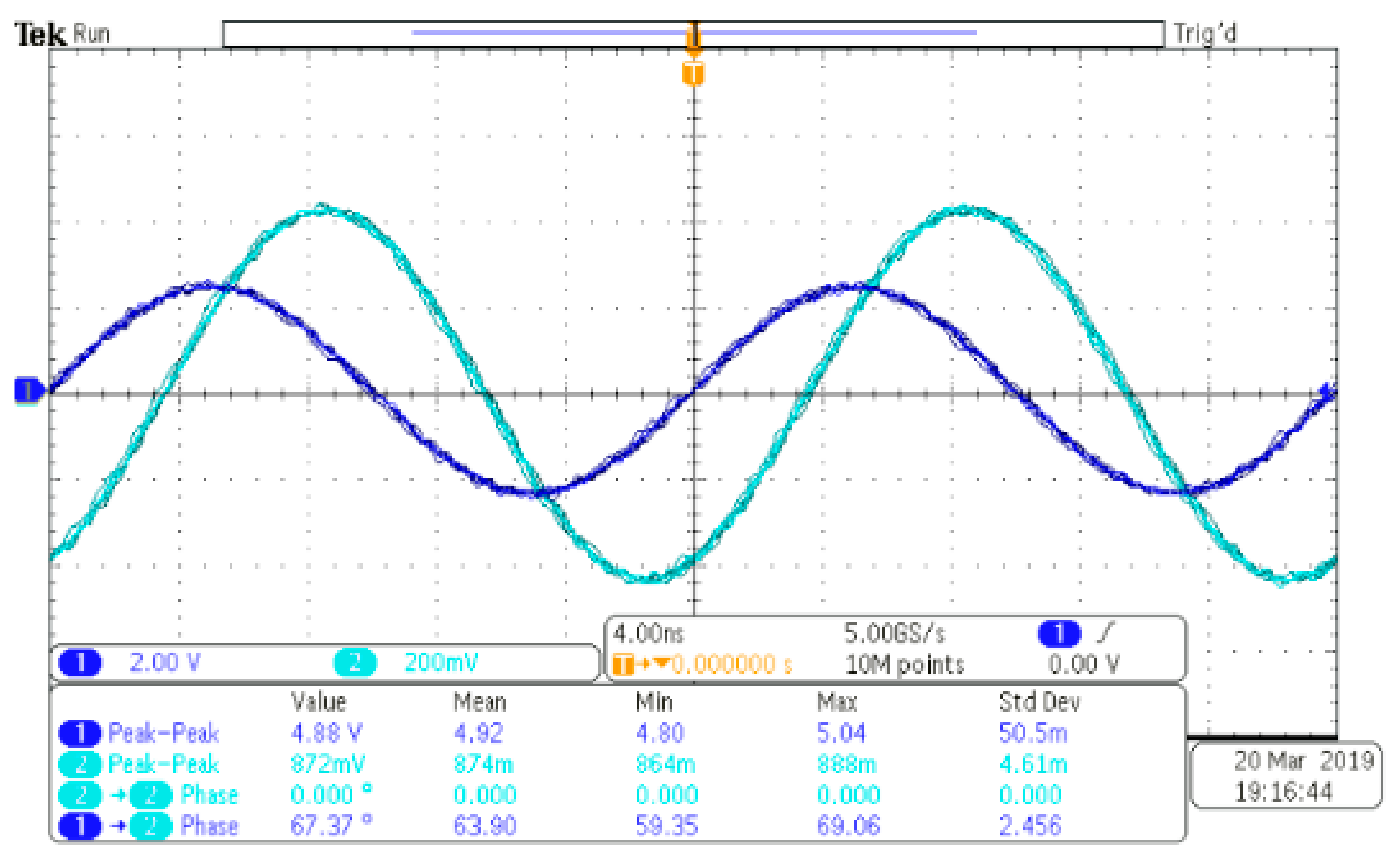
Figure 4.
The oscilloscope output performance of I/Q demodulator with I component connected to Channel 1 and Q connected to Channel 2.
Figure 4.
The oscilloscope output performance of I/Q demodulator with I component connected to Channel 1 and Q connected to Channel 2.
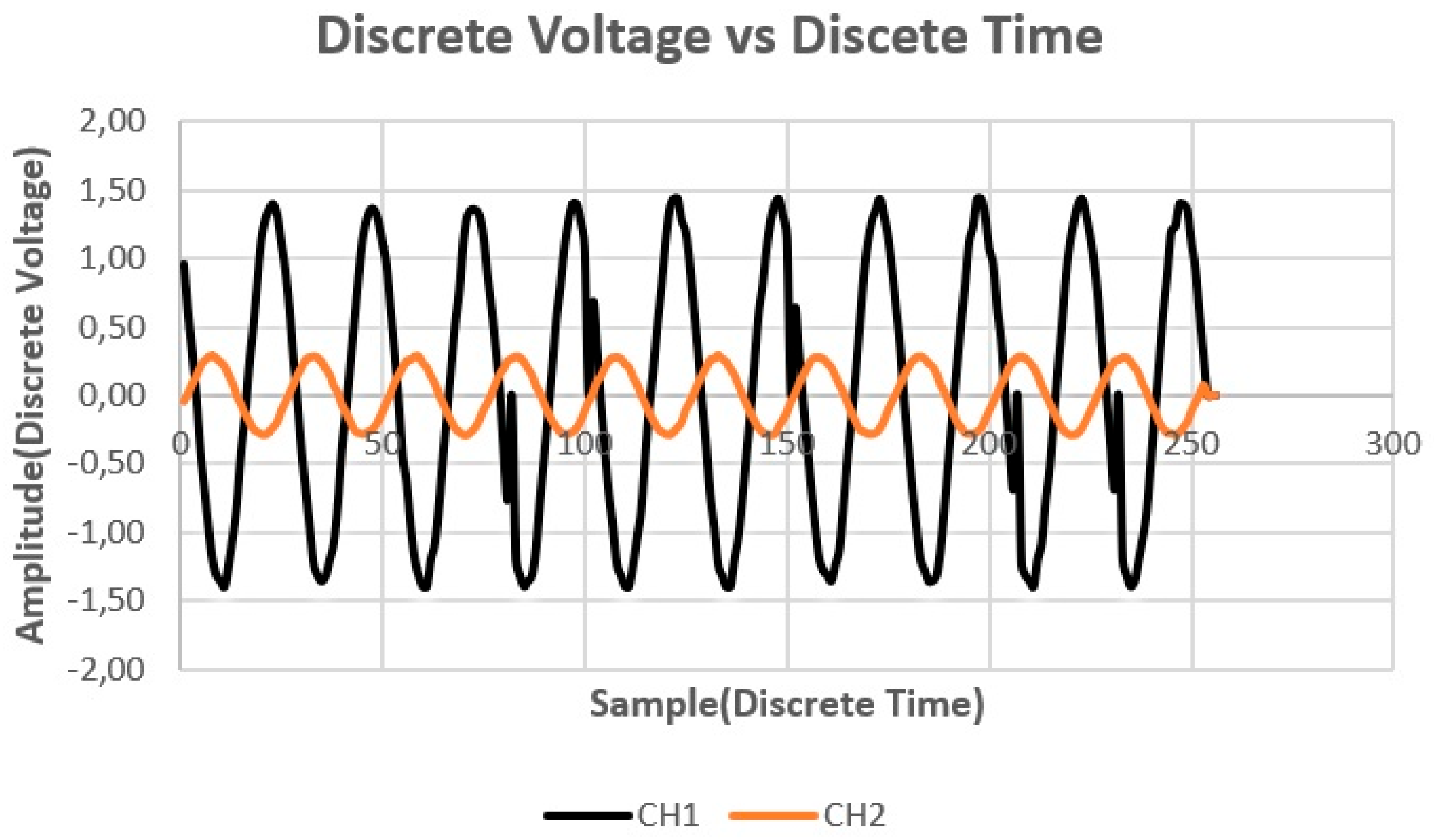
Figure 5.
The Excel reproduced acquired I/Q demodulator samples.
Figure 5.
The Excel reproduced acquired I/Q demodulator samples.
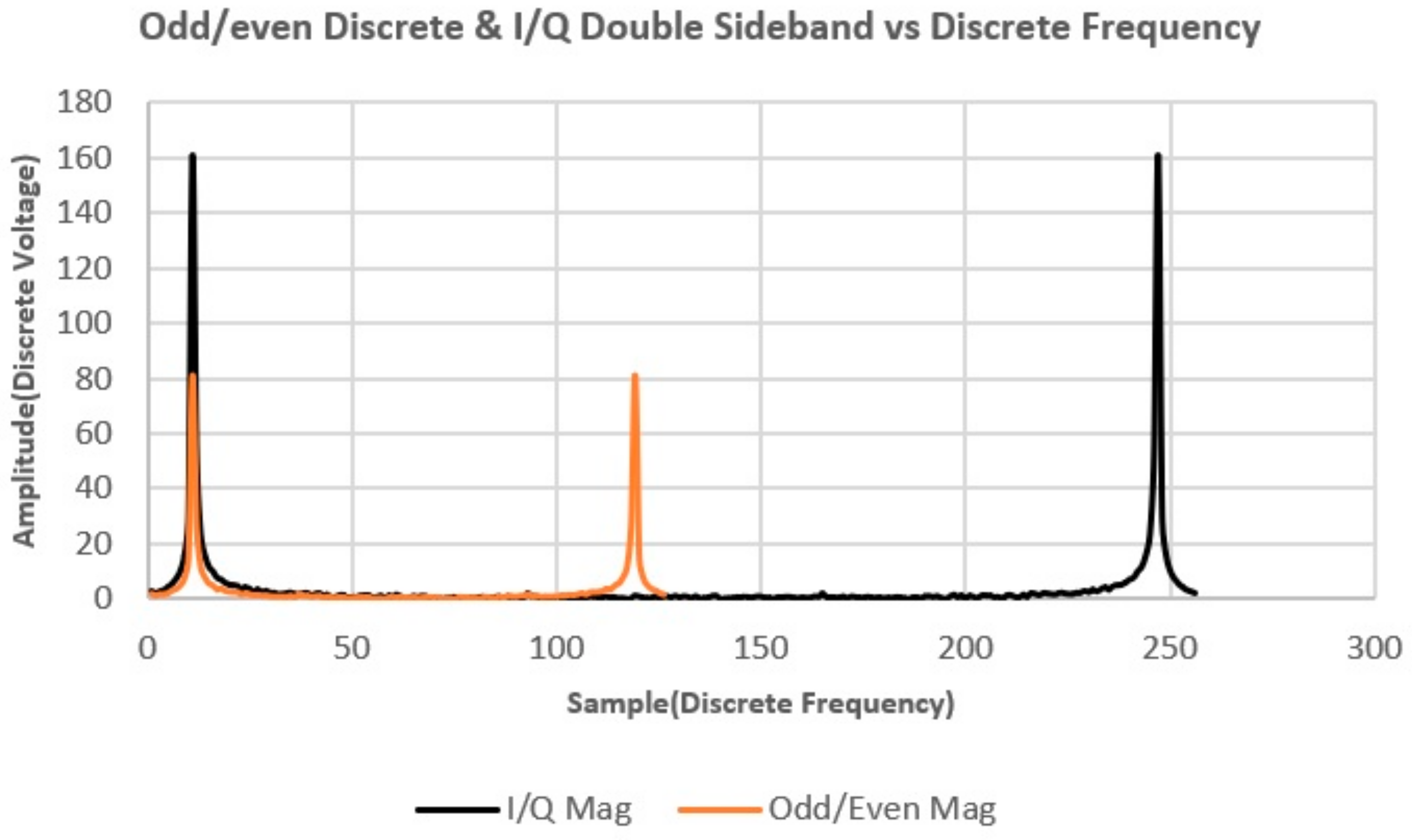
Figure 6.
New odd/even order sample frequency behavior.
Figure 6.
New odd/even order sample frequency behavior.
Figure 7.
The phase error behavior of the new odd/even order sampling.
Figure 7.
The phase error behavior of the new odd/even order sampling.
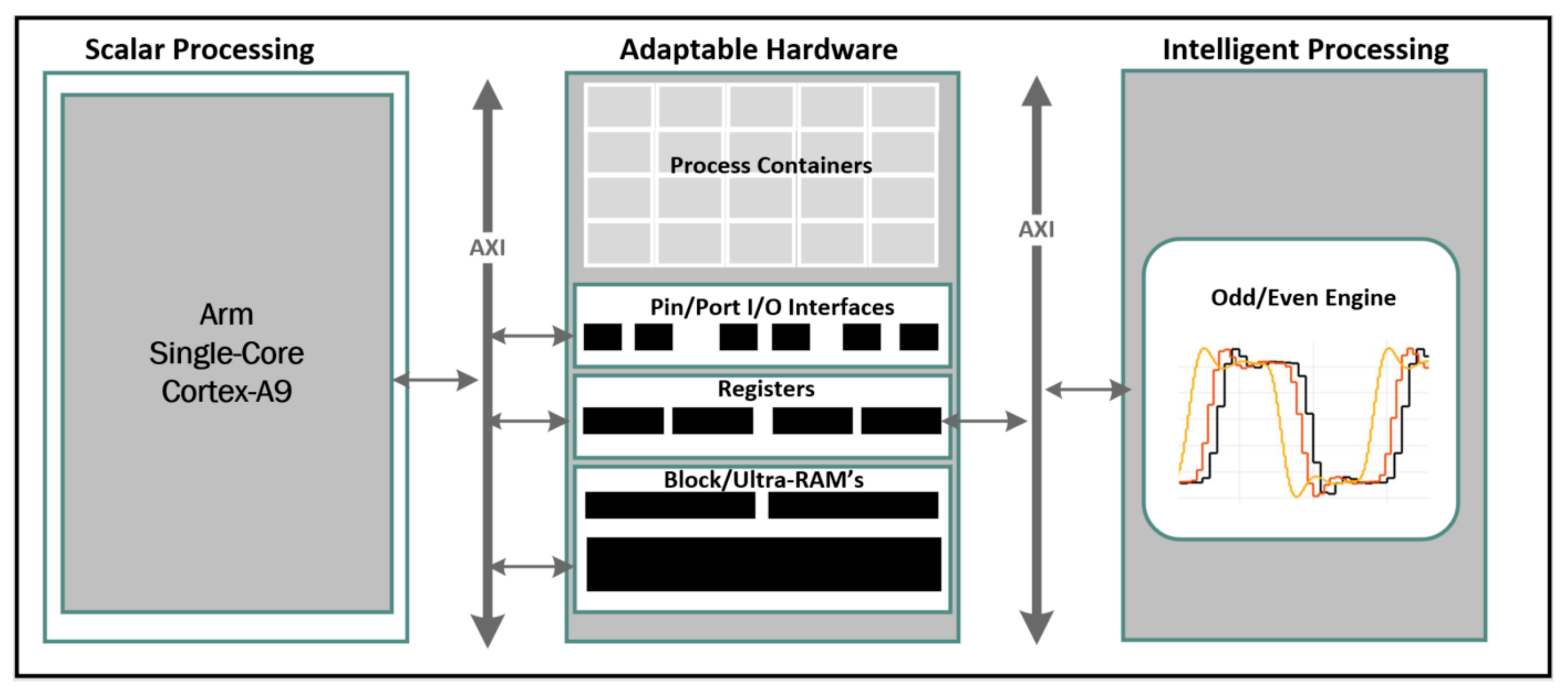
Figure 8.
This presents the proposed new odd/even order sampling architecture block diagram.
Figure 8.
This presents the proposed new odd/even order sampling architecture block diagram.
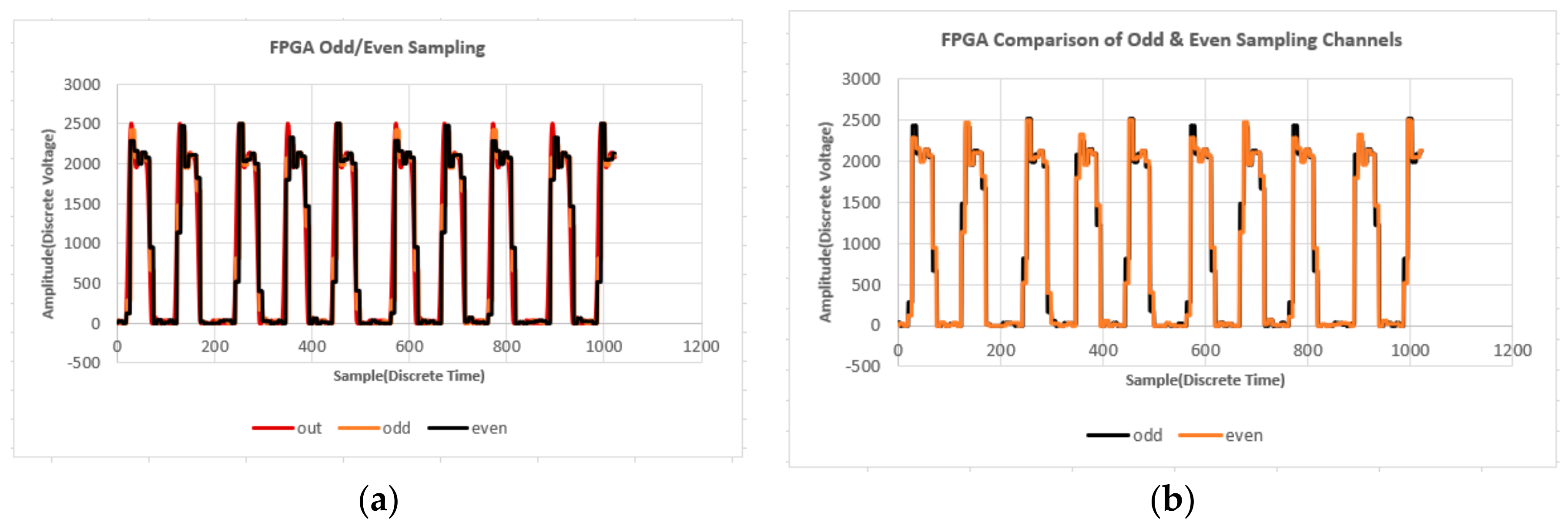
Figure 9.
FPGA architecture implementation results: (a) Source signal which is in phase with I and odd/even order sampling results; (b) Odd and even order sampling results with Vivado integrated logic analyzer (ILA) window configured to 1 kilobyte.
Figure 9.
FPGA architecture implementation results: (a) Source signal which is in phase with I and odd/even order sampling results; (b) Odd and even order sampling results with Vivado integrated logic analyzer (ILA) window configured to 1 kilobyte.
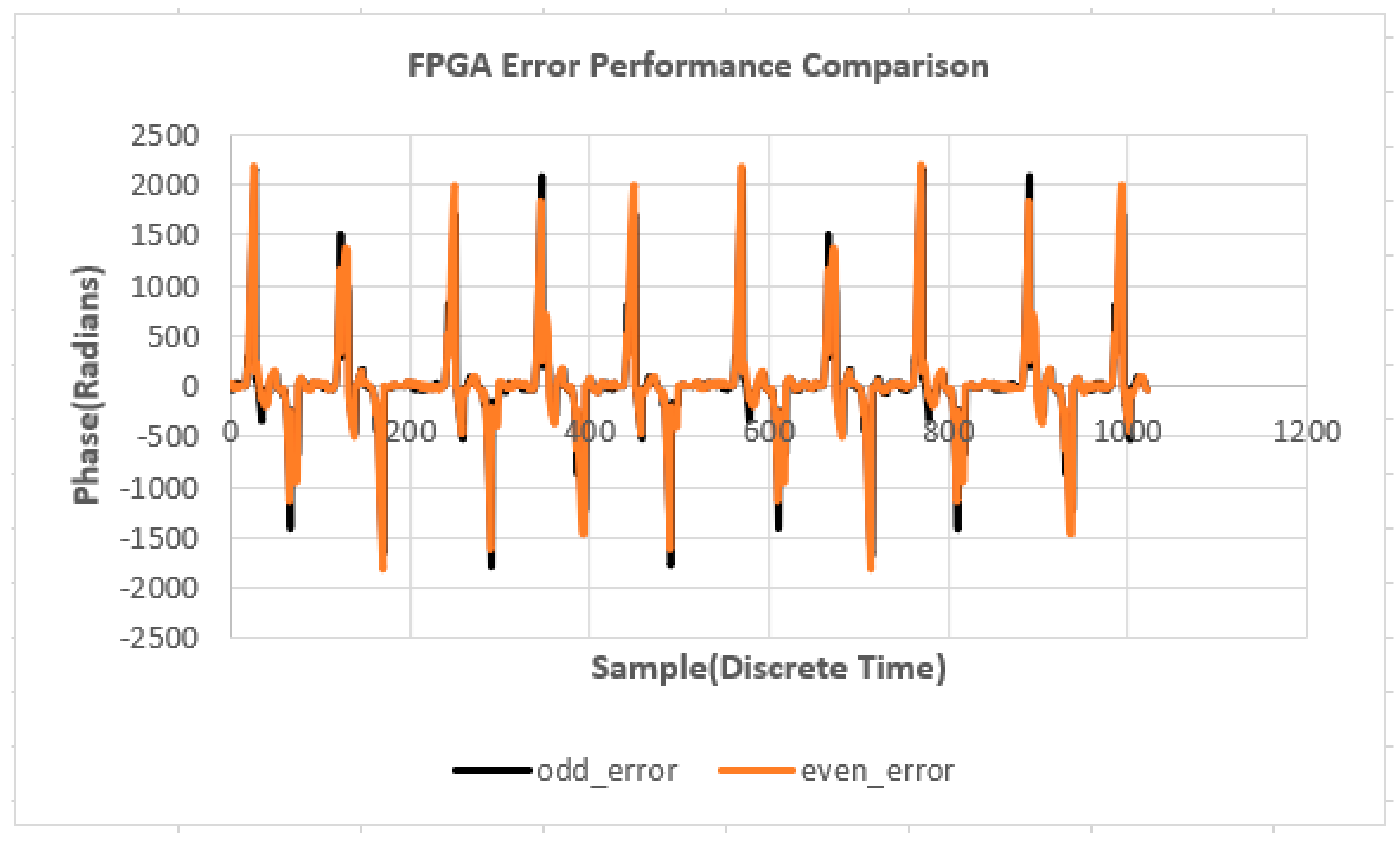
Figure 10.
This figure presents error performance for odd/even order sampling.
Figure 10.
This figure presents error performance for odd/even order sampling.
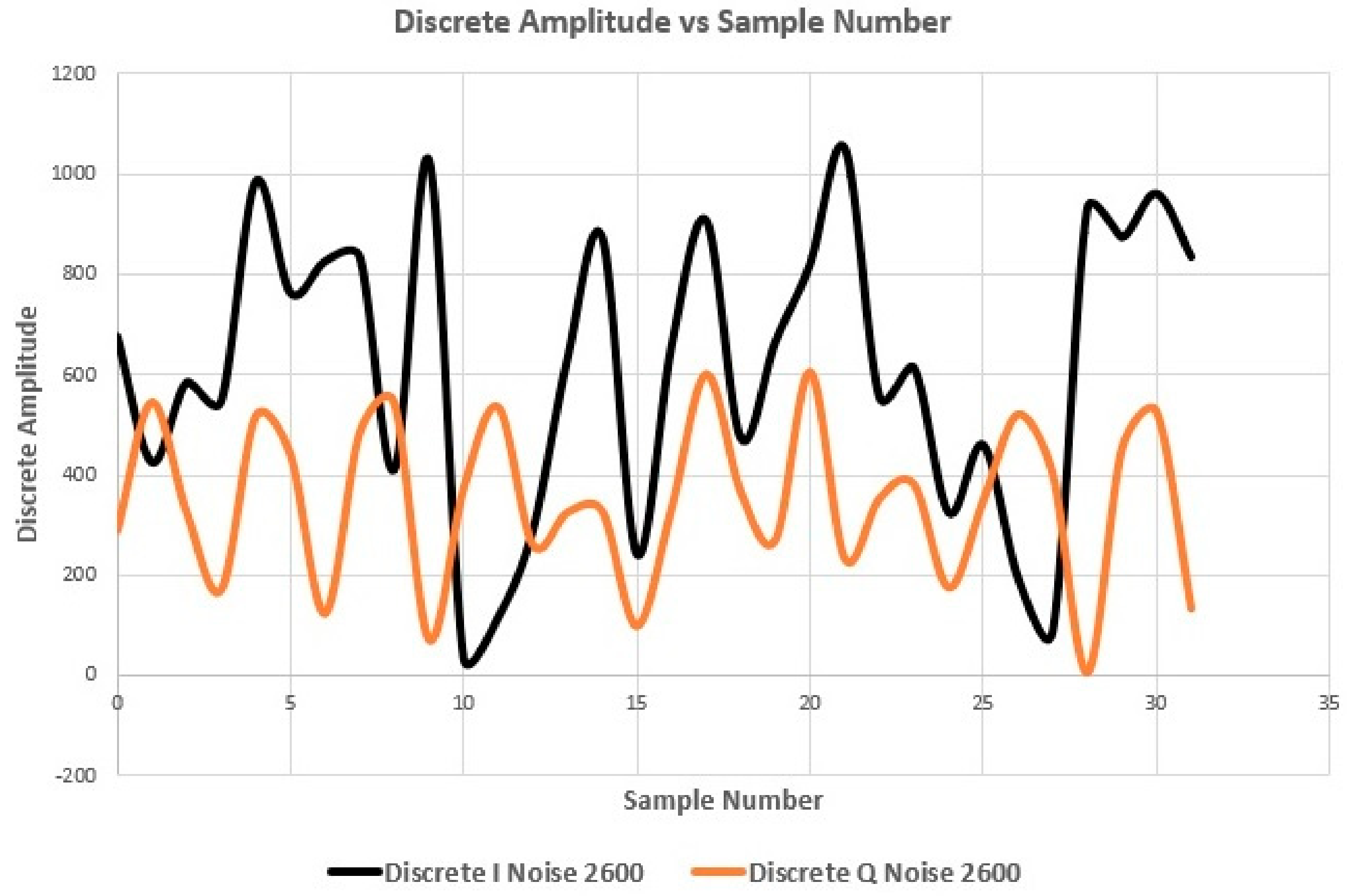
Figure 11.
The noise captured from Radar source on a field test.
Figure 11.
The noise captured from Radar source on a field test.
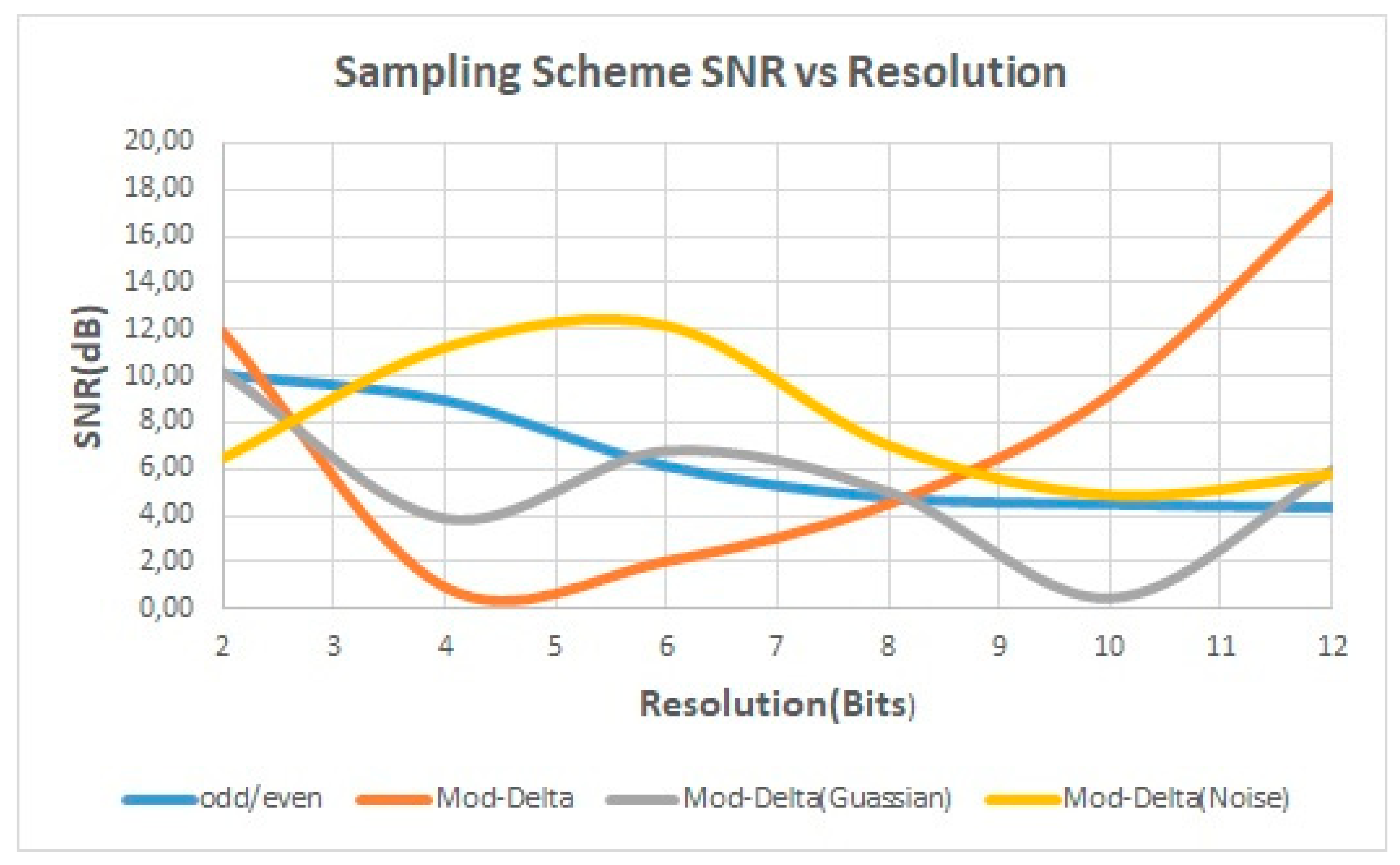
Figure 12.
This figure presents SNR performance between the new odd/even order, Mod-∆, Mod-∆ (Gaussian) and Mod-∆ (Noise) sampling.
Figure 12.
This figure presents SNR performance between the new odd/even order, Mod-∆, Mod-∆ (Gaussian) and Mod-∆ (Noise) sampling.
Table 1.
Variable description for Equation (1).
Table 1.
Variable description for Equation (1).
| Variable | Description |
|---|
| s(t) | Complex signal |
| I(t) | Inphase component |
| Q(t) | Quadrature component |
| WIF | Intermediate Freq |
Table 2.
Variable description for Equations (2) and (3).
Table 2.
Variable description for Equations (2) and (3).
| Variable | Description |
|---|
| Iraw(t) | Demodulated I component |
| Qraw(t) | Demodulated Q component |
| am(t) | Demodulated amplitude |
| φm(t) | Demodulated phase |
Table 3.
I/Q demodulator odd 4th order digital mixing [
2].
Table 3.
I/Q demodulator odd 4th order digital mixing [
2].
| Sample No: (n) | 0 | 1 | 2 | 3 | 4 |
|---|
| I-coefficients | 0 | 1 | 0 | −1 | 0 |
| Q-coefficients 1 | 0 | 0 | −1 | 0 | 1 |
Table 4.
Variable description for Equations (4) and (5).
Table 4.
Variable description for Equations (4) and (5).
| Variable | Description |
|---|
| Iodd(t) | Odd sampled I component |
| Qeven(t) | Even sampled Q component |
| T1,3(t) | Odd sampling time |
| C1,3 | FIR coefficients |
| T2,4(t) | Even sampling time |
| ∆ | Quantization error |
Table 5.
A 4th order FIR filtering I/Q demodulator odd order digital mixing pattern [
2].
Table 5.
A 4th order FIR filtering I/Q demodulator odd order digital mixing pattern [
2].
| Sample No: (n) | 0 | 1 | 2 | 3 | 4 |
|---|
| I-coefficients | 0 | 1 | 0 | −3 | 0 |
| Q-coefficients 1 | 0 | 0 | −3 | 0 | 1 |
Table 6.
I/Q demodulator for even 7th order digital mixing [
1].
Table 6.
I/Q demodulator for even 7th order digital mixing [
1].
| Sample No: (n) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
| I-coefficients | 1 | 0 | −1 | 0 | 1 | 0 | −1 | 0 |
| Q-coefficients 1 | 0 | 1 | 0 | −1 | 0 | 1 | 0 | −1 |
Table 7.
I/Q demodulator for odd 7th order digital mixing [
1].
Table 7.
I/Q demodulator for odd 7th order digital mixing [
1].
| Sample No: (n) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
| I-coefficients | 1 | 0 | −11 | 0 | 15 | 0 | −5 | 0 |
| Q-coefficients 1 | 0 | 5 | 0 | −15 | 0 | 11 | 0 | −1 |
Table 8.
Odd/even order sampling proposed memory mapping.
Table 8.
Odd/even order sampling proposed memory mapping.
| Input Addr | Dual-Port Mem | Output Addr |
|---|
| 0x00 | I (0) | 0x00 |
| … | … | … |
| 0xFF | I (i) | 0xFF |
| Reserved to guard data leak + 2-bit strobe |
| 0x109 | Q (0) | 0x109 |
| … | … | … |
| 0x208 | Q (i) | 0x208 |
Table 9.
Bit arrangement at memory located 0x104.
Table 9.
Bit arrangement at memory located 0x104.
| Bit No | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
| Bit Function | Strobe | Reserved | Reserved | Reserved | Reserved | Flag |
Table 10.
Variable descriptions for Equations (12) and (13).
Table 10.
Variable descriptions for Equations (12) and (13).
| Variable | Description |
| dRM | Dual-port memory |
| wrs | Memory write |
| rds | Memory read |
| Si | Sample number |
| s | Memory strobe |
Table 11.
The 1st order delta-sigma simulation measurements results.
Table 11.
The 1st order delta-sigma simulation measurements results.
| Quantization Step Parameter | Simulation Measurement |
|---|
| ∆T | 124.687 us |
| ∆Y | 0.1477 volts |
| ∆F | 8.020 kHz |
| ∆Y/∆T | 1.185 (Volts/ms) |
Table 12.
Odd/even order simulation measurements results.
Table 12.
Odd/even order simulation measurements results.
| Quantization Step Parameter | Simulation Measurement |
|---|
| ∆T | 378.747 us |
| ∆Y | 0.4120 volts |
| ∆F | 2.640 kHz |
| ∆Y/∆T | 1.088 (Volts/ms) |
Table 13.
Measurement equipment available for the experimental setup.
Table 13.
Measurement equipment available for the experimental setup.
| Experimental Equipment | Equipment Range |
|---|
| Anritsu Signal Generator | 1 Hz to 20 GHz |
| Tektronix Oscilloscope | 1 Hz to 1 GHz |
| Tektronix Spectral Analyzer | 1 Hz to 26 GHz |
Table 14.
ADL5380-EVALZ-ND I/Q Demodulator Electrical Connection Schedule.
Table 14.
ADL5380-EVALZ-ND I/Q Demodulator Electrical Connection Schedule.
| Connector Schedule | Electrical Schedule |
|---|
| RF_p | SMA to Waveguide from Signal Gen |
| RF_n | No SMA connector PCB terminated |
| I_p | SMA to Waveguide to Oscilloscope |
| I_n | No SMA connector PCB terminated |
| Q_p | SMA to Waveguide to Oscilloscope |
| Q_n | No SMA connector PCB terminated |
| V_cc | Croc Clips to Power Supply |
| Ground | Croc Clips to Power Supply |
Table 15.
Spectrogram measurements results.
Table 15.
Spectrogram measurements results.
| Measurements | Settings |
|---|
| ∆ Overlap | Freq | Time/Div | Span |
|---|
| 19% | 1.004649 GHz | | |
| | | 450 us | 24.40 MHz |
Table 16.
High-end wave front frequency spectrum measurements results.
Table 16.
High-end wave front frequency spectrum measurements results.
| Measurements | Settings |
|---|
| Amplitude | Freq | Time/Div | Span |
|---|
| −72.56 dBm | 1.004649 GHz | | |
| | | 10 dB | 24.40 MHz |
Table 17.
I/Q demodulator performance measurements results.
Table 17.
I/Q demodulator performance measurements results.
| Type | Measurements | Settings |
|---|
| | Ch1 | Ch2 | Ch1 | Ch2 |
| Amplitude (P-P) | 4.92 V | 874 mV | 2 V/div | 200 mV/div |
| Phase | 63.90° | 0.00° | 4 ns/div | 4 ns/div |
Table 18.
Proposed new odd/even order sampling architecture breakdown.
Table 18.
Proposed new odd/even order sampling architecture breakdown.
| Sub Block | Functionality |
|---|
| Scalar Processing | Access to Registers as Datatype for Software |
| Adaptable Hardware | Process Container access to Digital Logic(LUT), Pin/Ports, Registers, Block RAM |
| Intelligent Processing | Access to a ground of DSP Slices for equation manipulation |
Table 19.
FPGA resource utilization for the new odd/even order sampling.
Table 19.
FPGA resource utilization for the new odd/even order sampling.
| Description | Used | Available | Utilization |
|---|
| SliceUtilization |
| Slice LUTs | 2044 | 14,400 | 14.19% |
| LUT as Logic | 1828 | 14,400 | 12.69% |
| LUT as Memory | 216 | 6000 | 3.60% |
| SliceRegUtilization |
| Reg as Flip Flop | 3158 | 28,800 | 10.97% |
| Reg as Latch | 0 | 28,800 | 0.00% |
| MultiplexerUtilization |
| F7 Muxes | 52 | 8800 | 0.59% |
| F8 Muxes | 5 | 4400 | 0.11% |
| MemoryUtilization |
| Black RAM | 1.5 | 50 | 3.00% |
| DSPUtilization |
| DSPs | 2 | 66 | 3.03% |
| SpecificFeatureUtilization |
| XADC | 0 | 1 | 0.00% |
| Total Utilization | 48.15% |
Table 20.
FPGA resource utilization for the existing Mod-∆ sampling.
Table 20.
FPGA resource utilization for the existing Mod-∆ sampling.
| Description | Used | Available | Utilization |
|---|
| SliceUtilization |
| Slice LUTs | 2044 | 14,400 | 14.19% |
| LUT as Logic | 1828 | 14,400 | 12.69% |
| LUT as Memory | 216 | 6000 | 3.60% |
| SliceRegUtilization |
| Reg as Flip Flop | 3158 | 28,800 | 10.97% |
| Reg as Latch | 0 | 28,800 | 0.00% |
| MultiplexerUtilization |
| F7 Muxes | 52 | 8800 | 0.59% |
| F8 Muxes | 5 | 4400 | 0.11% |
| MemoryUtilization |
| Black RAM | 1.5 | 50 | 3.00% |
| DSPUtilization |
| DSPs | 20 | 66 | 30.30% |
| SpecificFeatureUtilization |
| XADC | 0 | 1 | 0.00% |
| Total Utilization | 75.45% |
Table 21.
FPGA resource utilization for the existing Mod-∆(Gaussian) sampling.
Table 21.
FPGA resource utilization for the existing Mod-∆(Gaussian) sampling.
| Description | Used | Available | Utilization |
|---|
| SliceUtilization |
| Slice LUTs | 2044 | 14,400 | 14.19% |
| LUT as Logic | 1828 | 14,400 | 12.69% |
| LUT as Memory | 216 | 6000 | 3.60% |
| SliceRegUtilization |
| Reg as Flip Flop | 3158 | 28,800 | 10.97% |
| Reg as Latch | 0 | 28,800 | 0.00% |
| MultiplexerUtilization |
| F7 Muxes | 52 | 8800 | 0.59% |
| F8 Muxes | 5 | 4400 | 0.11% |
| MemoryUtilization |
| Black RAM | 1.5 | 50 | 3.00% |
| DSPUtilization |
| DSPs | 22 | 66 | 33.33% |
| SpecificFeatureUtilization |
| XADC | 0 | 1 | 0.00% |
| Total Utilization | 78.48% |
Table 22.
FPGA resource utilization for the existing Mod-∆(Noise) sampling.
Table 22.
FPGA resource utilization for the existing Mod-∆(Noise) sampling.
| Description | Used | Available | Utilization |
|---|
| SliceUtilization |
| Slice LUTs | 2044 | 14,400 | 14.19% |
| LUT as Logic | 1828 | 14,400 | 12.69% |
| LUT as Memory | 216 | 6000 | 3.60% |
| SliceRegUtilization |
| Reg as Flip Flop | 3158 | 28,800 | 10.97% |
| Reg as Latch | 0 | 28,800 | 0.00% |
| MultiplexerUtilization |
| F7 Muxes | 52 | 8800 | 0.59% |
| F8 Muxes | 5 | 4400 | 0.11% |
| MemoryUtilization |
| Black RAM | 1.5 | 50 | 3.00% |
| DSPUtilization |
| DSPs | 27 | 66 | 40.91% |
| SpecificFeatureUtilization |
| XADC | 0 | 1 | 0.00% |
| Total Utilization | 86.06% |