1. Introduction
In recent years, among renewable energy sources, solar photovoltaic (PV) has experienced rapid growth. According to the most recent survey by the IEA [
1], by the end of 2017, the total PV power capacity installed worldwide amounted to
, leading to the generation of over
of energy (around
of global power output). Utility-scale projects account for about
of total PV installed capacity, with the rest in distributed applications (residential, commercial, and off-grid) [
1]. It is well established that one of the main challenges posed by the massive integration of renewable energy sources, such as PV or wind power in the national grids is their inherently non-programmable nature. Therefore, the capability to forecast the energy produced by a PV plant in a given time frame with good accuracy is a key ingredient in overcoming this challenge [
2], and is also often connected with economic benefits [
3]. The recent evolution of microgrid and smart grid concepts is also a significant driving force for the development of accurate forecasting techniques [
4].
In this paper, we will compare several data-driven techniques, such as machine learning and deep learning, for intra-hour forecasting of the output power of an industrial-scale PV plant (1 MW nominal capacity) at 5 min temporal resolution. Meteorological data acquired from sensors in the field will be used as input data to perform the predictions. This framing of the problem belongs to the class of approaches referred to as
nowcasting [
2,
5].
From an operational point of view, short forecast horizons are relevant for AC power quality and grid stability issues. At these time scales the main source of variability in the power output is cloud movement and generation on a local scale [
6]. Although these phenomena could be modeled from a physical point of view, their complex and turbulent behavior is a challenge that can be tackled effectively with data-driven techniques. Some approaches make use of imaging techniques, either from ground-based [
6] or satellite [
7] cameras, while others only make use of endogenous data [
8] (i.e., the power output is used as the only input feature to the forecasting). The advantages of a data-driven approach for solar power forecasting lies in its ability to learn, from historical data, the complex patterns that are difficult to model (for instance shading phenomena). No knowledge of the specifications of the plant such as the orientation and electrical characteristics of the panels are required.
The predictive performance of machine learning-based methods has been shown to be superior to physical modeling in several cases [
2,
9,
10]. In particular, our comparison includes several well-known regression algorithms that were tested on an extensive range of parameters.
The paper is structured as follows:
Section 2 describes the available dataset and the performed preprocessing,
Section 3 contains the description of the applied methods and the definition of the applied error metrics. The results are collected in
Section 4, and the concluding remarks are drawn in
Section 5.
3. Methods
To apply machine learning techniques, forecasting was framed as a regression problem as follows:
where
is a vector containing the set of selected input features.
In the present case, and . Discrete time steps are defined so that , and a similar notation is adopted for the output of the model .
We have introduced the parameter
B, which controls how far back in time the regressor will look to perform the prediction. This
lookback time, denoted as
, was varied between 2, 4, and 8 h, corresponding to
at 5 min time resolution (see
Figure 3). Generally, the goal of a regression problem is to find the function
which minimizes a suitable definition of the error between the predicted output
and the actual value
.
To this end, a set of pairs of input-output variables on which to
train the parameters (if any) of
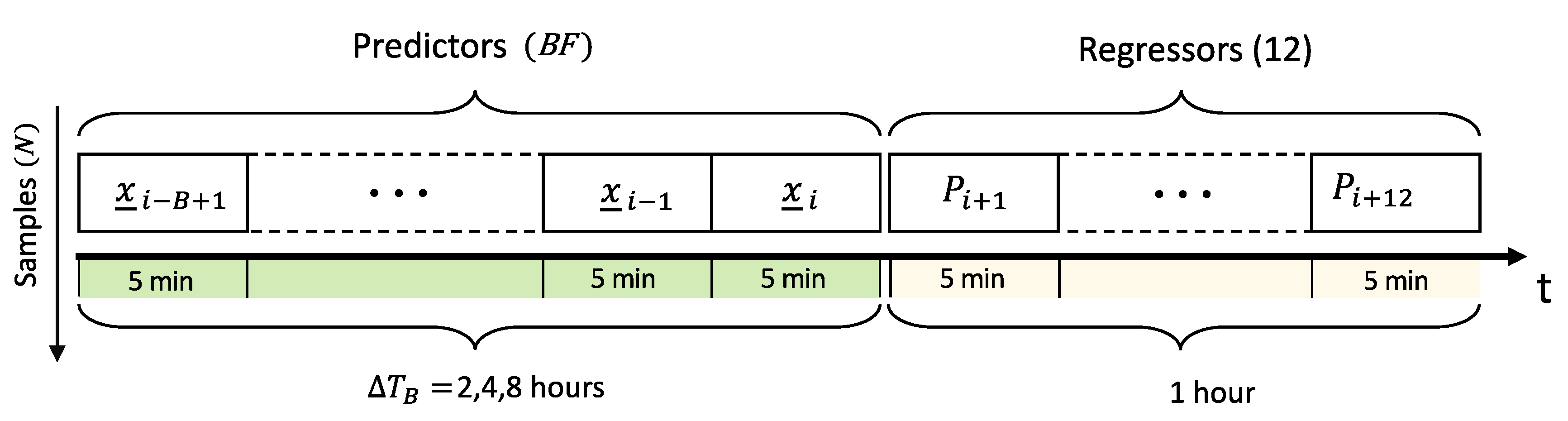
f was constructed and arranged as shown in
Figure 3.
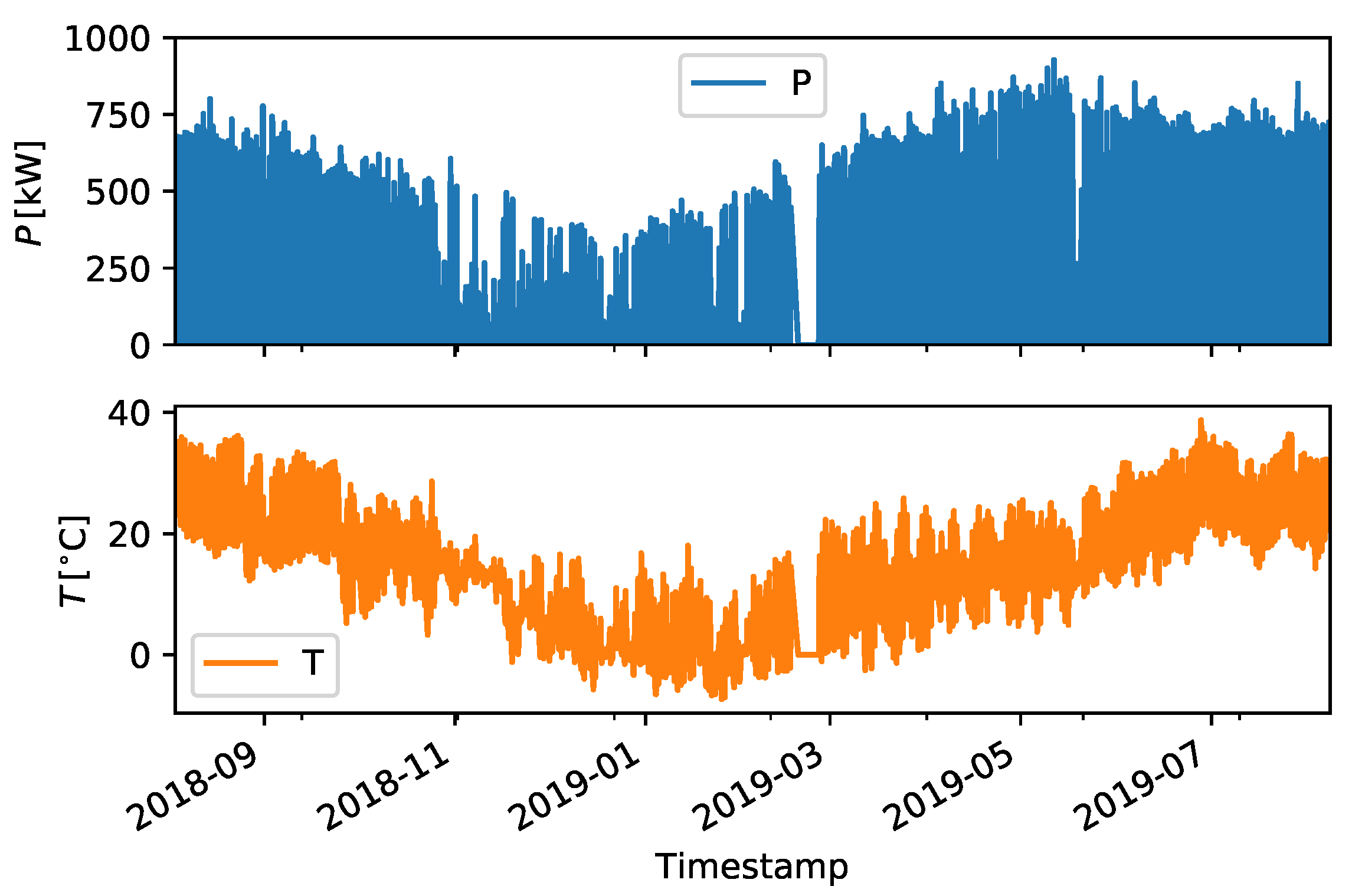
The dataset adopted is affected by some gaps (missing data) and some invalid data in the time series. The missing data have managed to split the dataset into subsets containing only consecutive observations: data within each subset were then cast in the desired form by constructing the time-lagged time series.
On the other hand, a first statistical analysis on the time series shows the inconsistent data are a negligible percentage of the entire dataset, and the machine learning methods analyzed in this study are able to automatically detect and ignore these invalid data. However, IEC 61724 recommendations for PV data monitoring and recording have been carefully followed even if the performance ratio of the considered PV plant has been shown here for non-disclosure reasons.
The final resulting dataset comprised = 103,740 samples: the first samples were used as a training set, with a dimension of = 82,992, while the last constituted a test set of 20,748 samples.
Many regression algorithms to implement the function
f exist and have been applied to solar irradiance or photovoltaic power forecasting: artificial neural networks [
19], tree-based methods [
20], and more recently deep learning approaches [
21]. The algorithms tested in this study are summarized in
Table 4 and
Figure 4 shows the flow-chart, which has been followed in the current analysis of the above-listed algorithms. A detailed description of the working principles of each algorithm is out of the scope of this work and we refer the interested reader to the references provided. For this reason, we now provide only a minimum of details that are useful to motivate the choice of algorithms listed in
Table 4. Linear regression was included as a representative example of a robust and computationally inexpensive algorithm. The Lasso regressor [
22] implements variable selection [
23] by penalizing the importance of features which have little impact on the prediction error. Therefore, it should represent an improvement in the performance of simple linear regression, with a comparable computational cost. The Random Forest [
24] algorithm is based on an ensemble of decision trees aggregated together following the principle of
bagging [
18,
23]. The multilayer perceptron (MLP) [
23] is a type of artificial neural network with multiple
hidden neural layers. The number of layers and the number of neurons in each layer are the main parameters that control the flexibility of the network, that is its capability to learn complex patterns. Training of the MLP is based on the feed-forward and back-propagation paradigm.
In k-nearest-neighbor (KNN) regression [
25], the output
y for an input
x is estimated as the average value of the
k training outputs whose corresponding inputs are the first
k nearest to input
x. An appropriate notion of distance in the space of inputs must be defined, the choice of which impacts regression performance.
Long short-term memory [
26] (LSTM) neural networks belong to the category of recurrent neural networks. The LSTM network structure can be described in terms of units communicating through input and output gates and endowed with a
forget gate that regulates the flow of information between successive units. This enables the network to remember such information for long time intervals. This architecture is well suited to process data that have a sequential nature, as is the case of time series data. This is reflected in how the input data has to be structured (see
Figure 5), either for training or to perform a prediction with an LSTM.
Given a set of
N samples,
F physical features and
B lookback time steps, each sample is a two-dimensional array of dimension
, therefore a portion of the time series comprising
B sequential steps is used to perform the prediction. On the contrary, each input sample to other algorithms is a flat array of
predictors (see
Figure 1), which are all considered equally and independently. For instance, the order in which they are provided is completely irrelevant. The effectiveness of LSTM for time series forecasting has been demonstrated in several studies targeting different types of data [
21,
29].
All the algorithms listed in
Table 4 (except for linear regression) have several parameters that can be tuned. An example is the number and size of the hidden layers in the MLP network. We refer to such variables as
training parameters (especially in the context of deep learning, these are also often referred to as
hyperparameters).
These can have a significant impact on the performance of the algorithm. A robust strategy to find the optimal configuration is to couple a search in training parameter space with k-fold cross-validation (CV). The latter consists of splitting the training set in k subsets (folds) of the same size, then over the course of k iterations, select one of the folds as the test set, while the remaining constitute the training set. At the end, k performance scores are obtained, for instance, the determination coefficient () on the fold acting as the test set. An overall cross-validation score is then built as the average of the k scores. This procedure can, in turn, be iterated on a grid of possible values of the training parameters to find the combination yielding the highest cross-validation score. If m combinations of training parameters are tested, a total of fits of the model is performed. In this study, the general machine learning workflow used for all algorithms except for the LSTM was the following, for each value of the lookback time :
Three-fold cross-validation and hyperparameter search on the training set () samples: training parameters yielding the best cross-validation score were selected. This should select the algorithm with the best generalization performance, which is the one which most likely performs best on new, previously unseen, input data.
Evaluation of the performance of the algorithm on the test set, using common error metrics, after reconstruction of the actual power from the predicted stochastic component.
All algorithms were tested on the same CPU-based hardware. The training time of the LSTM network was considerably longer than the other algorithms. The full cross-validation and hyperparameter search for the MLP, totaling 2400 fits required about 200 min for
h, whereas one single fit of the LSTM required 400 min. Both computations were parallelized to make use of all the threads available on the machine. For this reason, it was not feasible to apply the same hyperparameter tuning approach to the LSTM. Hence, we restricted the search to a family of networks known as encoder-decoder models [
30]. In particular, two architectures were tested, one with a fixed number of units, the other with network size proportional to the lookback times steps
B. We will label the two models LSTM and LSTM2, respectively.
Training of the LSTM networks consists of finding the optimal weights of the neural connection that minimize a suitable error metric on the training set, for instance, the mean square error (
). This was performed using the Adam [
31] algorithm, a standard approach for deep neural networks. Training consists of several successive steps (
epochs). The train
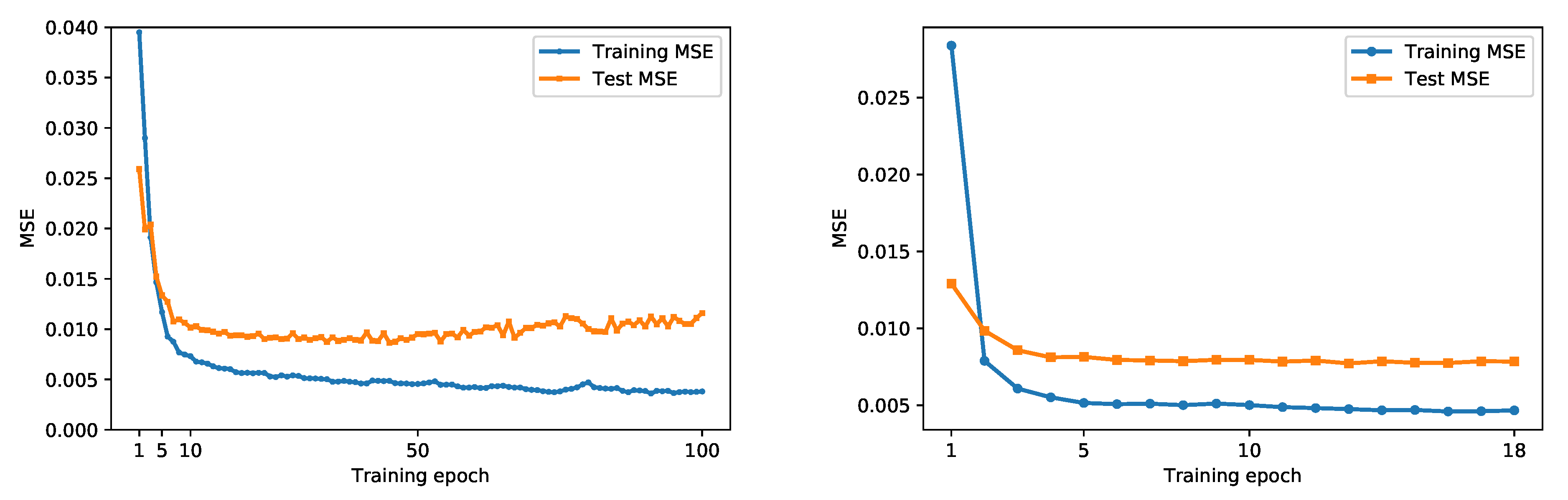
, being the target of the optimization, is by design expected to decrease through the epochs. This does not guarantee that the error on unseen data, for instance on the test set, will decrease as well. This is the well-known issue of overfitting [
23], an example of which is shown in
Figure 6. To prevent this occurrence, an
early stopping strategy was implemented, keeping track of the
on the test set during training and halting the process when the test
stops decreasing. Early stopping was also enabled in the scikit-learn library for the MLP regressor. More technical details on the choice of parameters for all the algorithms are provided in
Appendix A.
Error Metrics
We introduce the main error metrics that will be used in
Section 4. Since the output of our intra-hour forecast is the 12-dimensional vector of the predicted power for each 5-min time step, we will define an error metric for each forecast horizon. That is, for
:
where the index
i spans over the samples.
The performance metrics defined in Equations (
4) to (
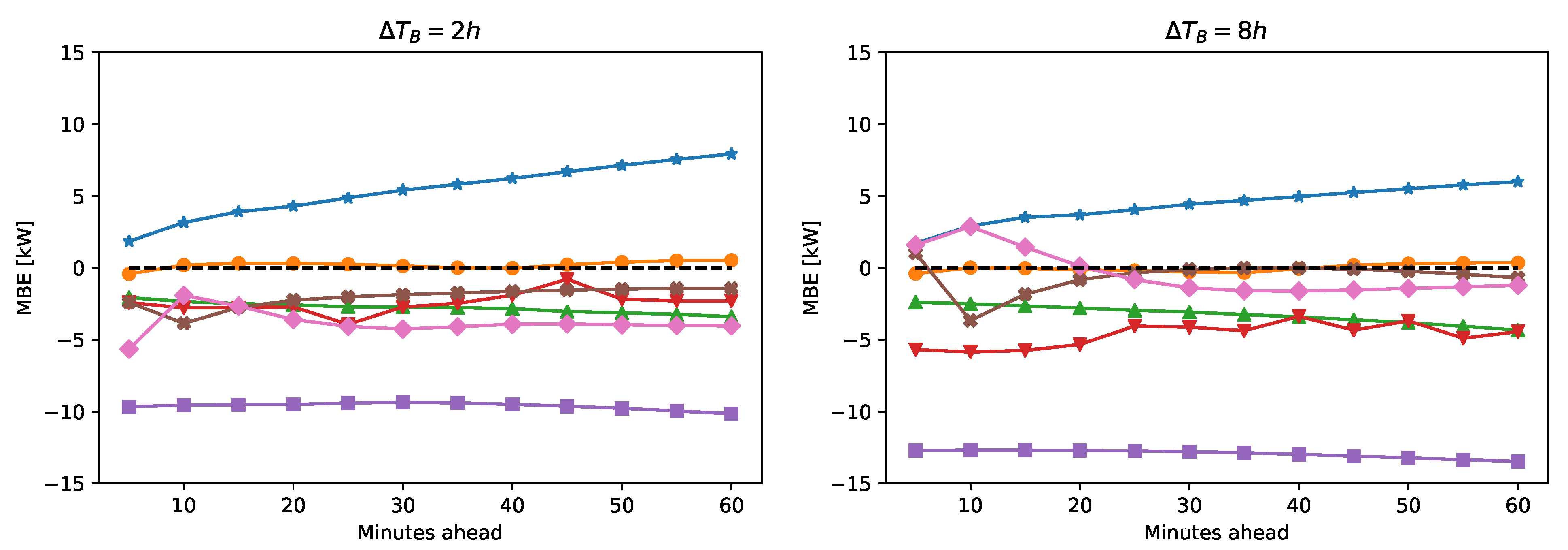
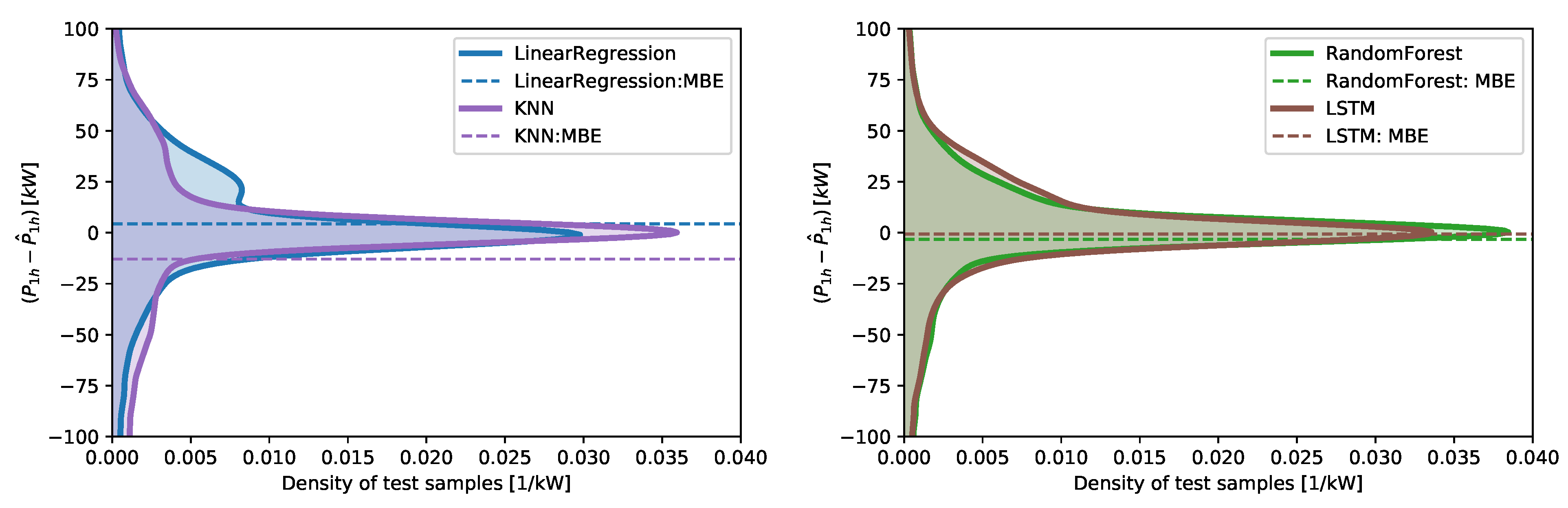
7) are commonly referred to as the mean absolute error (MAE), the root mean square error (RMSE), mean bias error (MBE), and the coefficient of determination (
), respectively.
It is also interesting to evaluate the mean performance of the algorithm in the forecasted hour with a single representative indicator. Several indicators could be built to characterize different qualitative aspects of the prediction. A possible choice is to define the average power in the hour as . With a similar definition for the predicted power (), standard definitions of the performance metrics (MAE, RMSE, ) can be applied to the hourly average power. We will label these metrics as , and .
A persistence forecast was defined as
where the 12 predicted time steps of
are equal to the measured values
observed in the previous 12 time intervals.
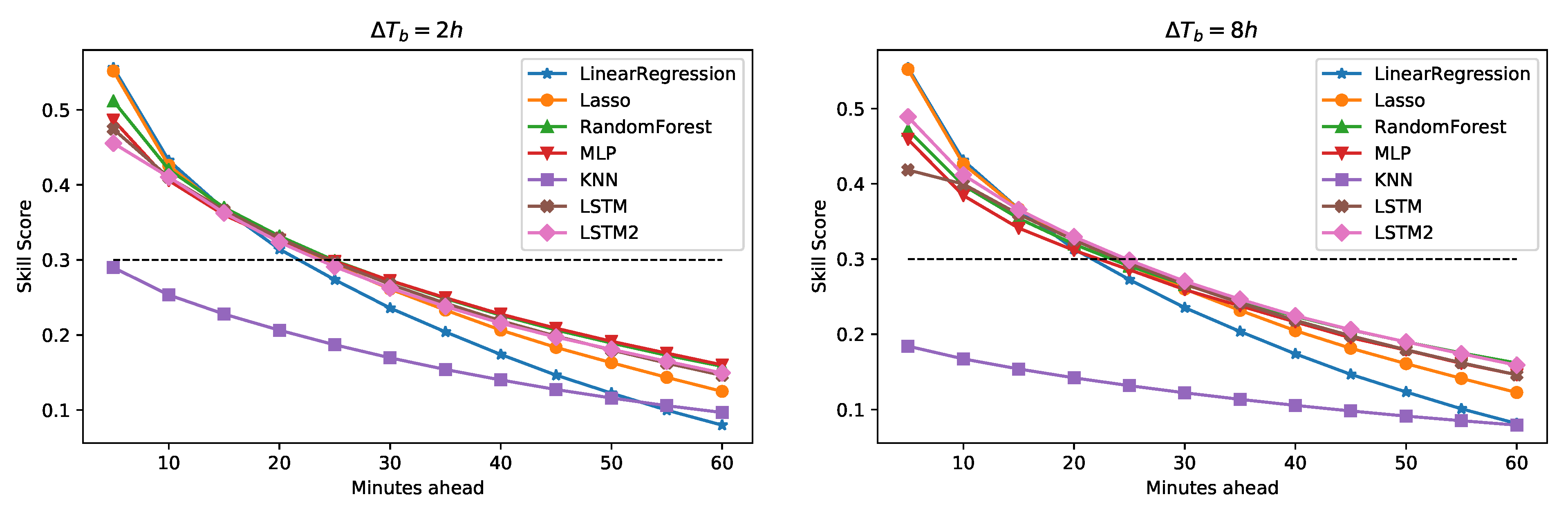
The last error metric introduced in the skill scores (
) [
32], that compares the prediction of the analyzed model with the error made by a persistence method on the same forecast horizon:
5. Conclusions
In this study, several well-know machine learning and deep learning algorithms were compared for the purpose of intra-hour forecasting of the power output of a 1 MW industrial-scale photovoltaic plant; the dataset implemented cover 1 year of measurements.
Each algorithm was tested over a large set of training parameters and standard machine learning practices, such as cross-validation were applied. We maintain that this is approach was required for a fair assessment of the performance.
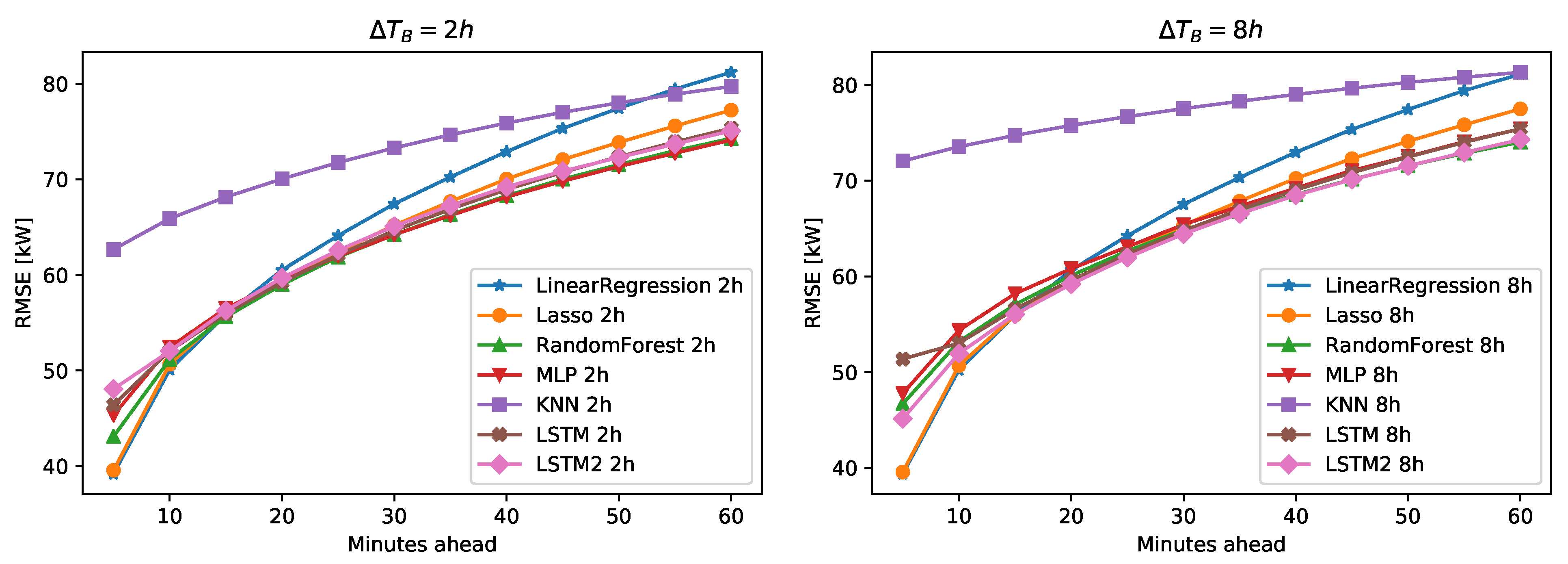
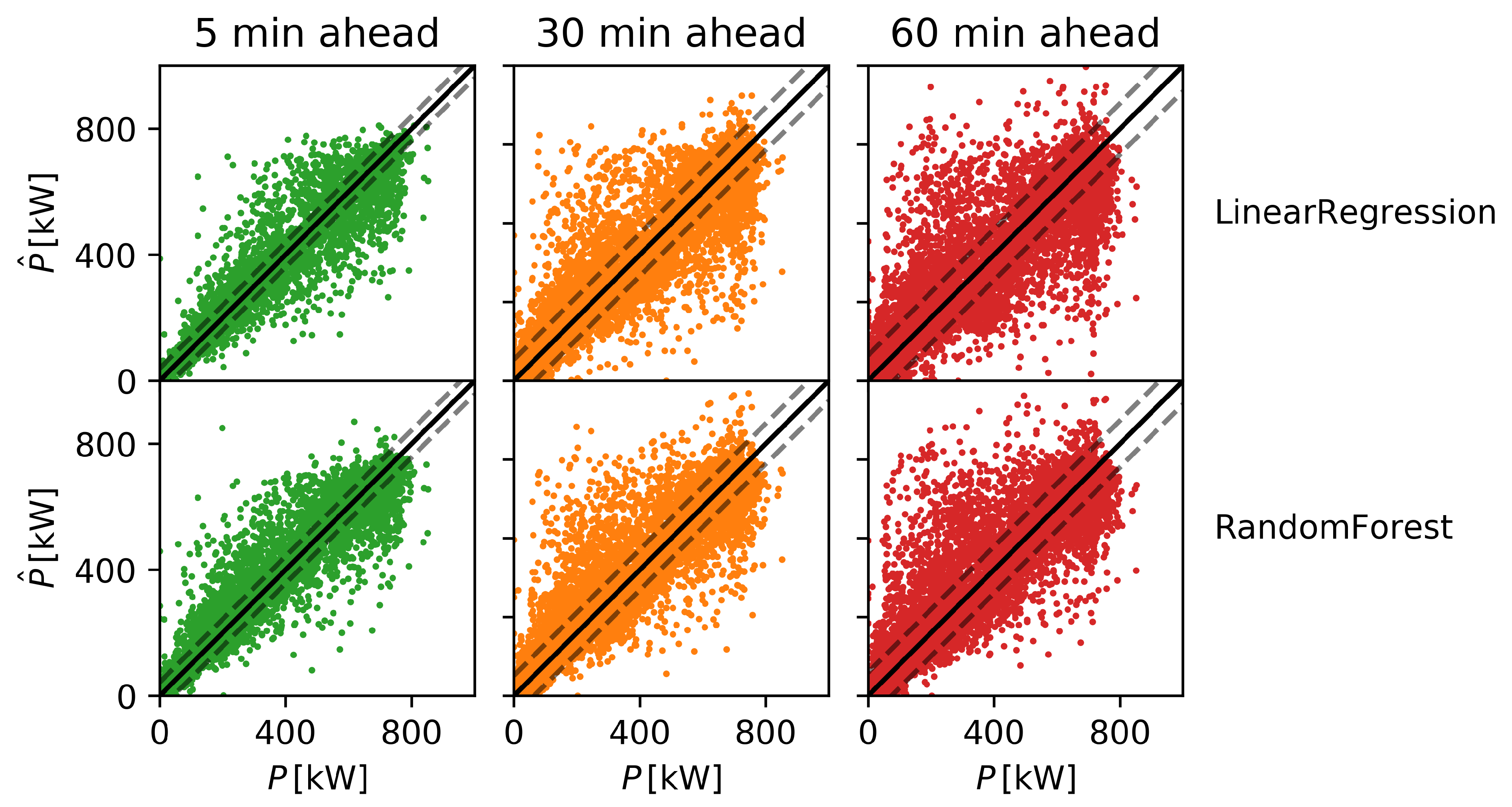
The results highlighted some peculiar features of each regression technique: the Random Forest algorithm, with appropriate selection of the lookback time, was generally the best performing according to all the figures of merit we considered. The strength of this algorithm also lies in its robustness with respect to tuning of the training parameters. This is a particularly desirable feature for industrial applications, where the greater variability of the MLP would require fine-tuning of the parameters for each application on which the algorithm has to be deployed. On the other hand, the ultimate predictive performance of the two algorithms were similar. It must also be highlighted that for short forecast horizons Lasso and Linear regression tend to match or outperform the more flexible algorithms, thus, a hybrid solution for prediction could be a promising development. For the case in hand, we did not find significant benefits in LSTM networks, although they were the only algorithms to show an improvement when increasing the lookback time. This suggests that more complex LSTM architectures could be able to outperform conventional algorithms, provided that suitable hardware to handle very deep neural networks are available in the target application. There are many variables characterizing PV power forecasting efforts [
2]: forecast horizon, forecast interval, type of input data, time resolution, size of the target plant, and geographical region. Therefore, it is often impossible to find a benchmark that shares all these characteristics against which new results can be compared directly [
32,
34].
The results achieved in this paper are related to a single dataset; to reduce the site-dependence of the obtained results, a comparison across different datasets should be performed. Future work will extend the here-exposed analysis to datasets belonging to different site conditions.
Nevertheless, we have identified several studies relevant to contextualize our findings in the present state of the art. For instance LSTM and CNN algorithms were shown to outperform MLP on nowcasting (
min) using sky images as additional input. The maximum reported skill score was 0.21 against persistence [
35]. Using sky camera features, prediction of 10 to 30 min ahead was reported with a forecast skill up to 0.43 [
36]. A skill score of
was reported for up to 30 min-ahead forecasting of PV power using only spatio-temporal correlation between neighboring PV plants [
37]. A recent study [
38] investigated several nowcasting algorithms in a microgrid setting (750 W PV power), finding the Random Forest as the best performing. Other studies aim at the forecasting of solar irradiance rather than the PV power directly. In this setting, forecast skills up to 0.3 [
39] and 0.15 [
40] were reported for intra-hour predictions.
Our approach to data preprocessing prioritized simplicity in the implementation and the identification of the smallest possible set of useful predictors. This is motivated by the need of minimizing the number of sensors to be installed and monitored for effective forecasting. For example, it is remarkable that quality predictions were obtained for a solar-tracking plant by making use of only the global horizontal irradiance. The capability to learn complex patterns without resorting to physical modeling is the main features of data-driven approaches, and was achieved by all the tested algorithms. Naturally, more complex regressors, such as Random Forest should always be preferred for optimal performance. Deep learning tools such as LSTM networks are very promising but might require dedicated hardware (GPUs) or larger training datasets to show significant performance advantage when deployed in industrial applications. This study suggests an effective data-driven workflow for intra-hour PV power forecasting, covering from feature selection to the identification of the best performing algorithms. Such an approach could be of interest for practical applications.