Study on the Evolution Law of Overburden Breaking Angle under Repeated Mining and the Application of Roof Pressure Relief
Abstract
:1. Introduction
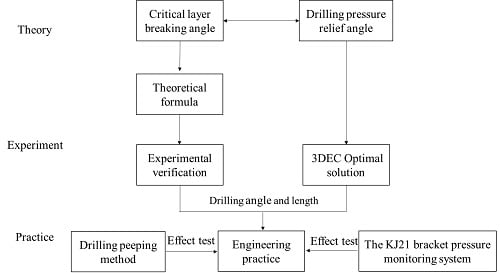
2. Materials and Methods
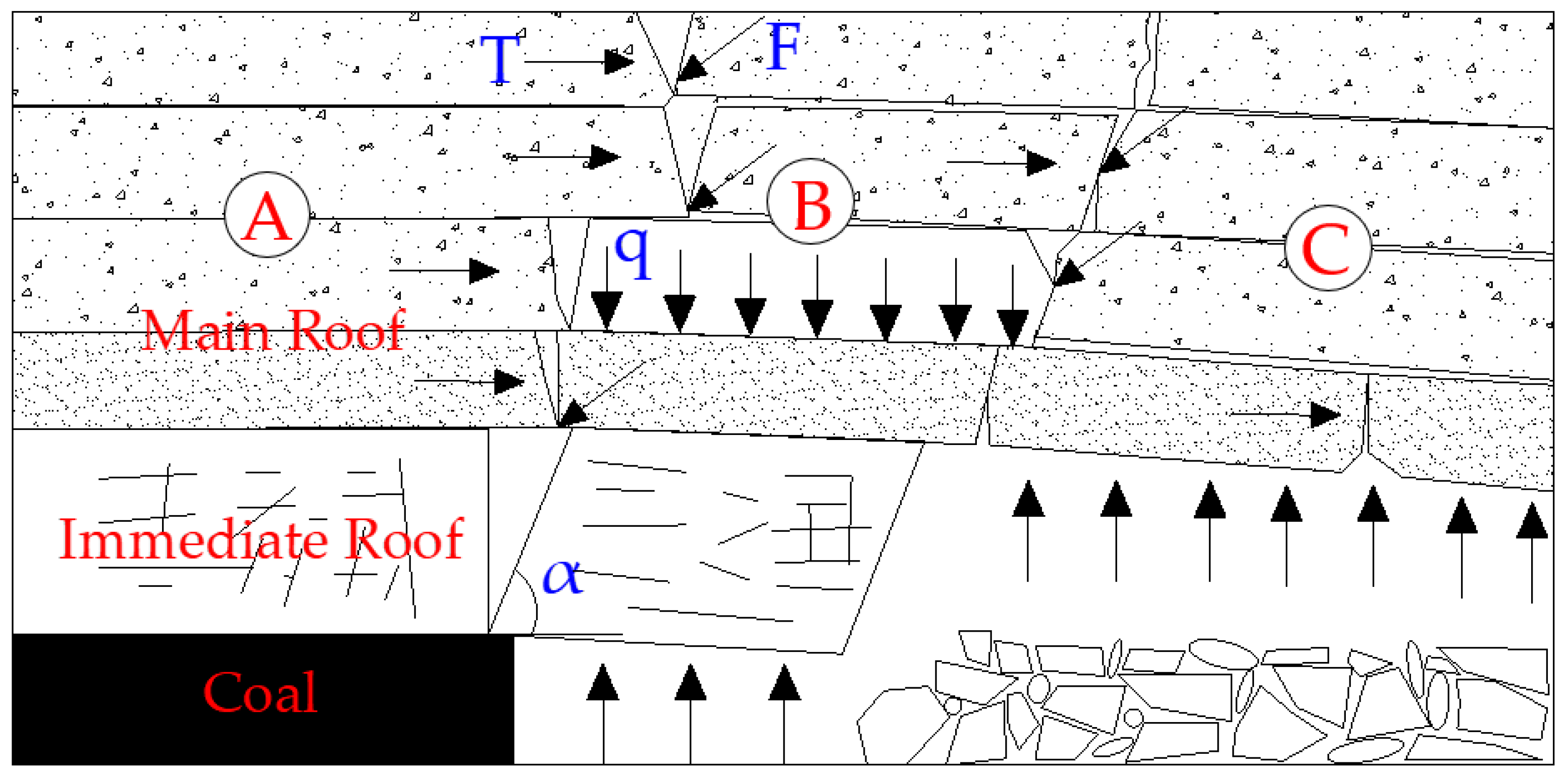
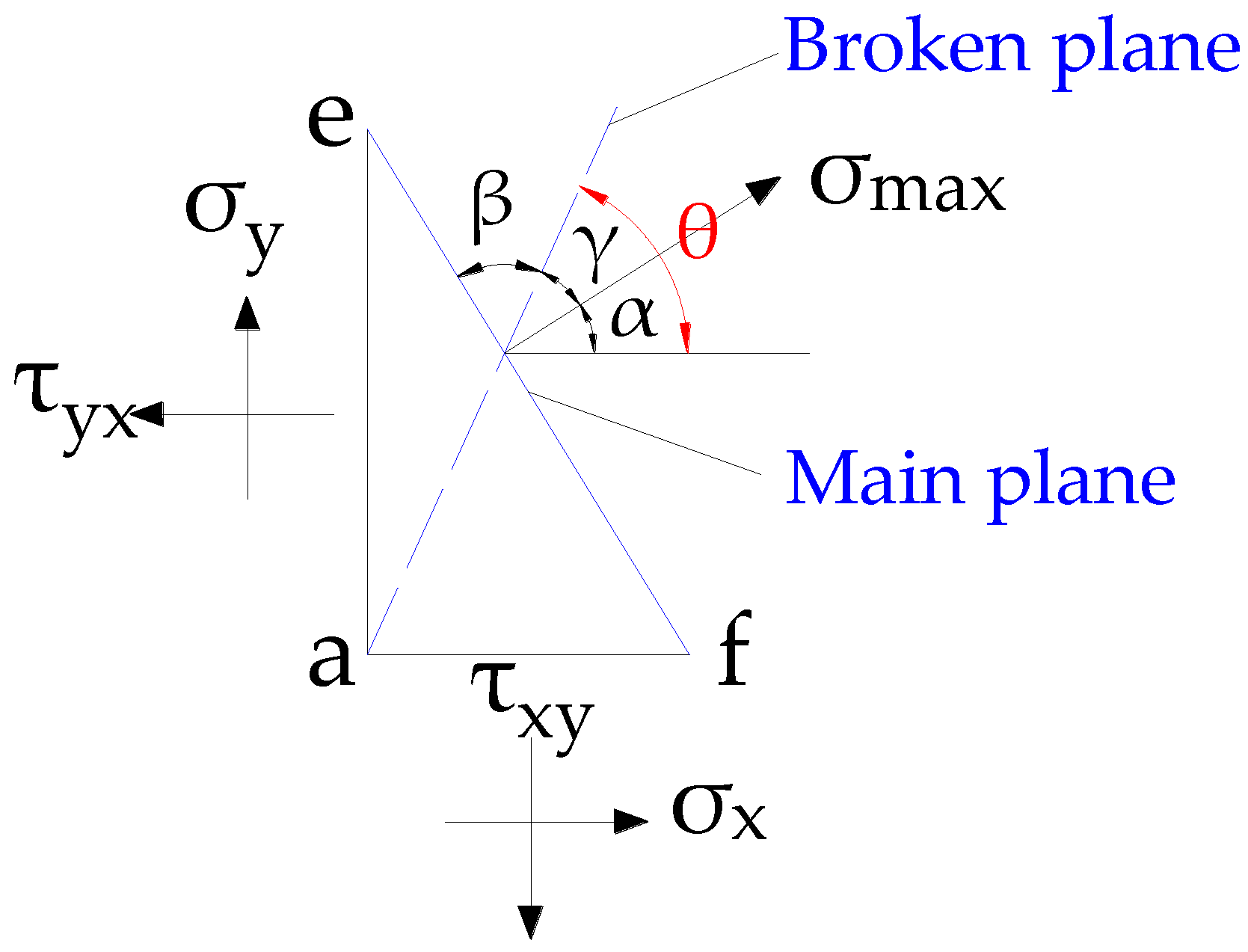
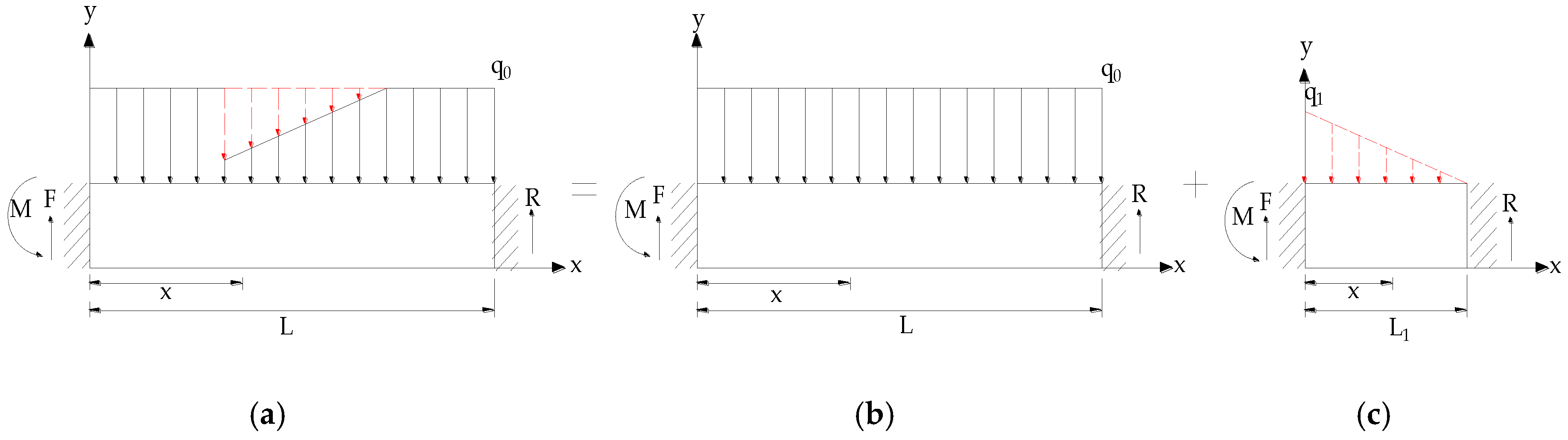
3. Derivation of Breaking Angle Mechanics of Key Layers under Repeated Mining
4. Experimental Verification of Similar Materials for Breaking Angle Calculation Formula
4.1. Verification of Breaking Angle of Key Layer in Single Coal Seam
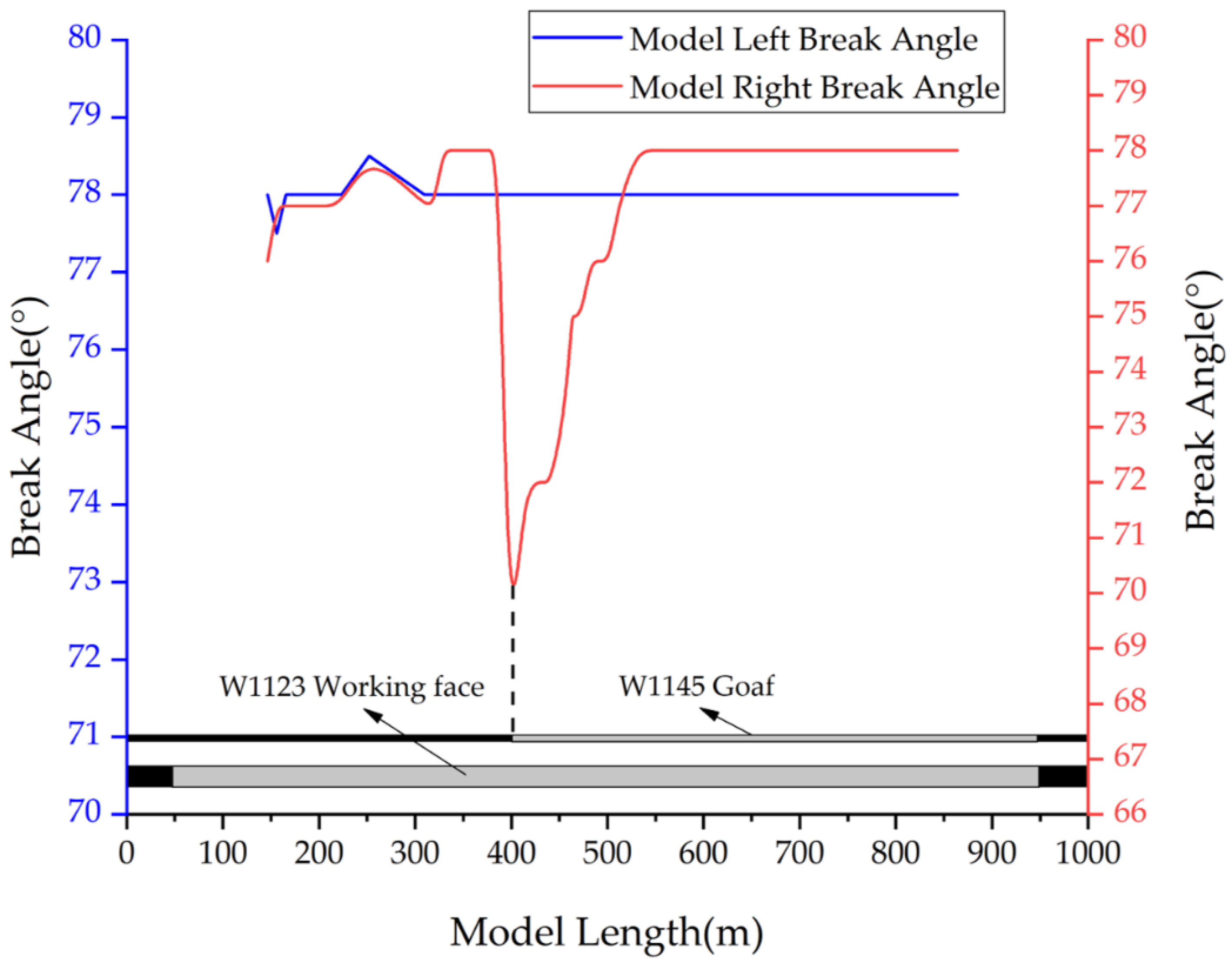
4.2. Key Layer Breaking Angle Verification under Repeated Mining
5. Simulation Analysis of Influence of Elevation Angle of Hard Roof Pressure Relief Drilling on Pressure Relief Effect
5.1. Numerical Model Construction and Calculation Parameters of Pressure Relief Drilling Elevation Angle
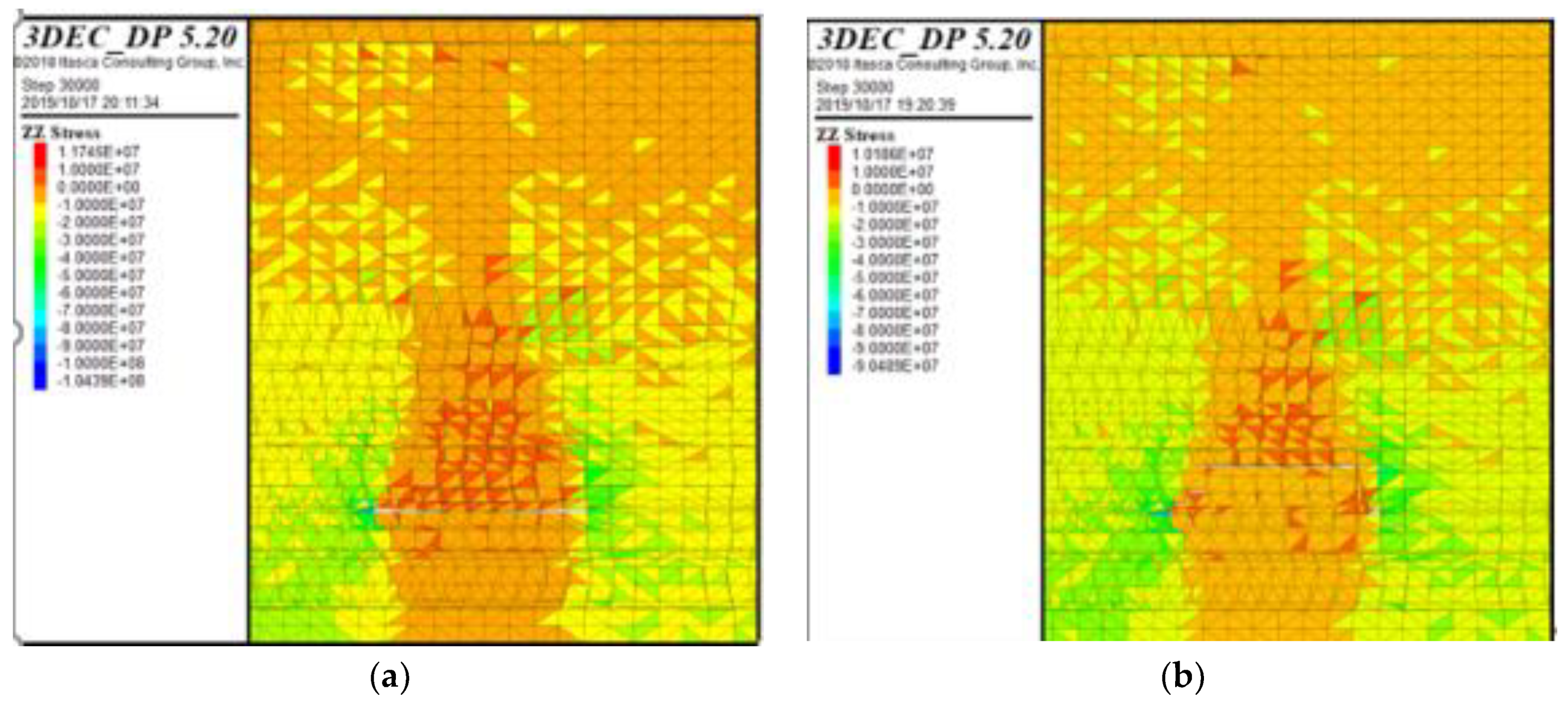
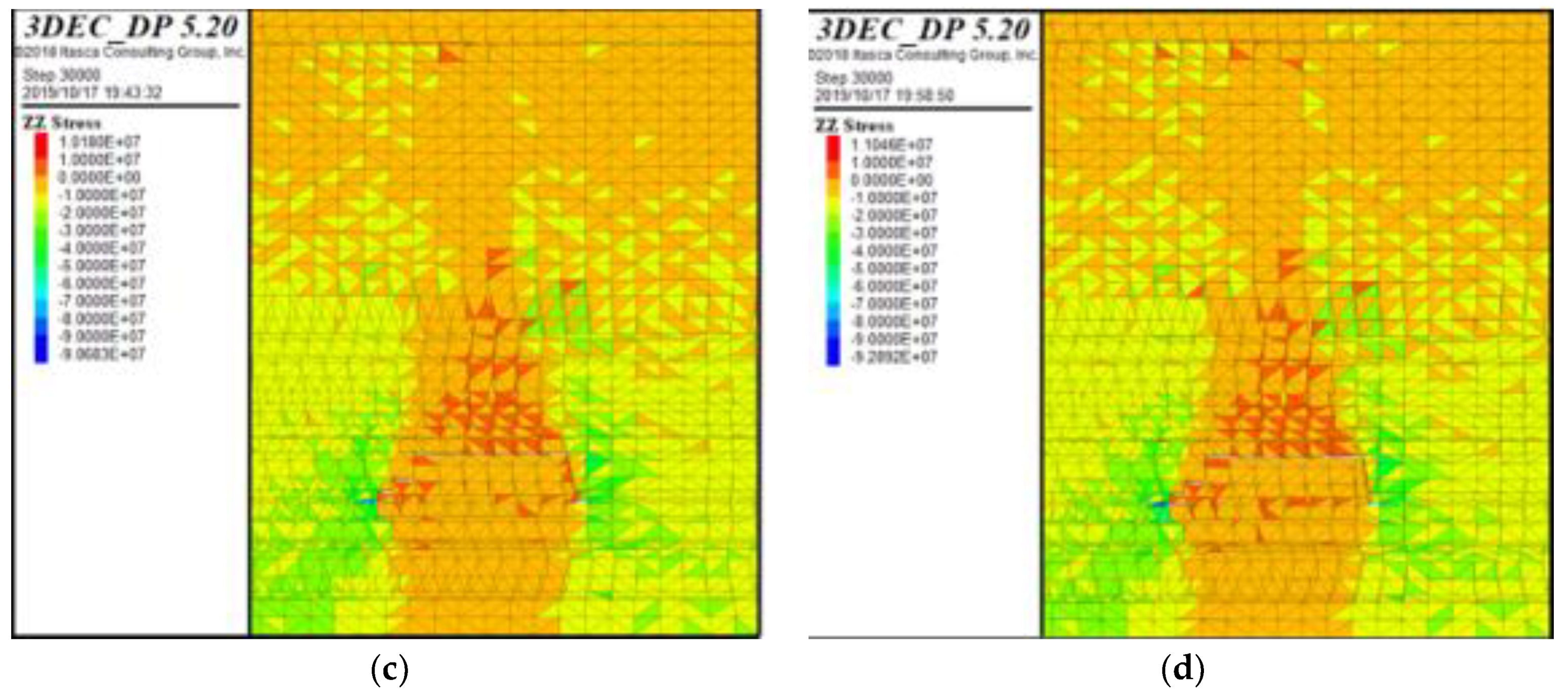
5.2. Falling Form of Roof When Different Pressure Relief Drillings Are at Elevation Angle
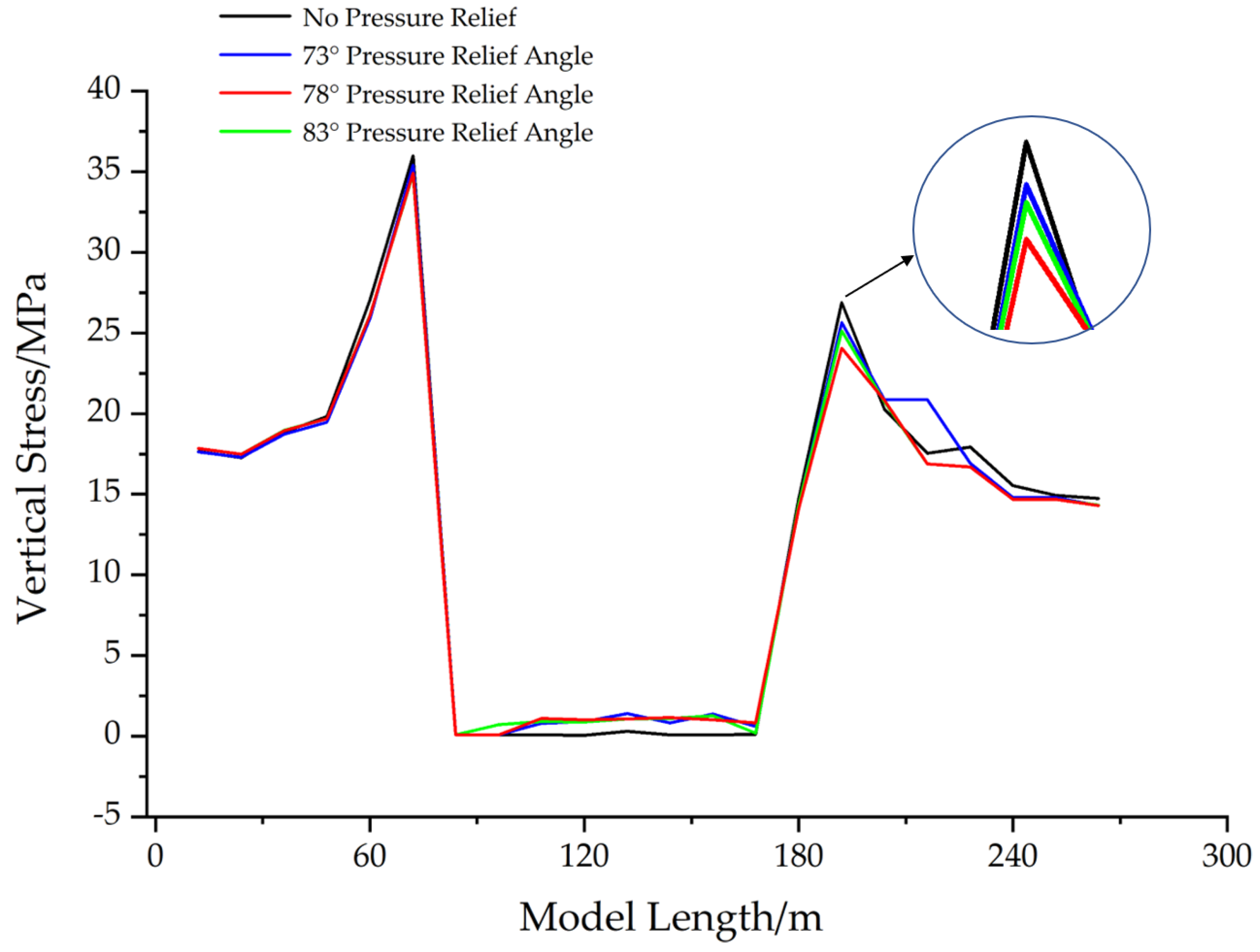
5.3. Stress Distribution Law of Different Pressure Relief Drillings at Elevation Angle
6. Application of Pressure Relief Drilling in Engineering Practice
6.1. Kuangou Coal Mine Engineering Background
6.2. Effect of Scale Effect on Drilling Length
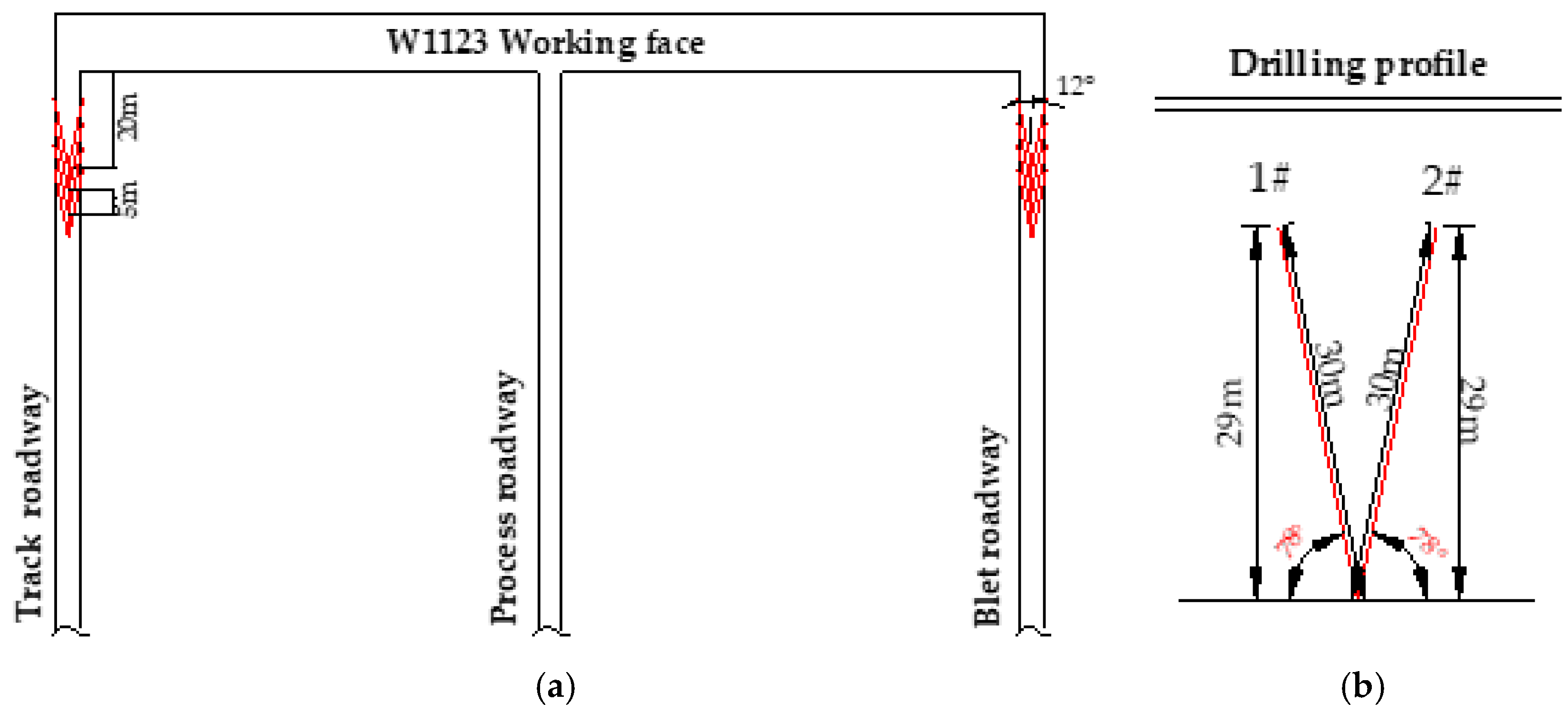
6.3. Design of Pressure Relief Drilling Parameters for Working Face
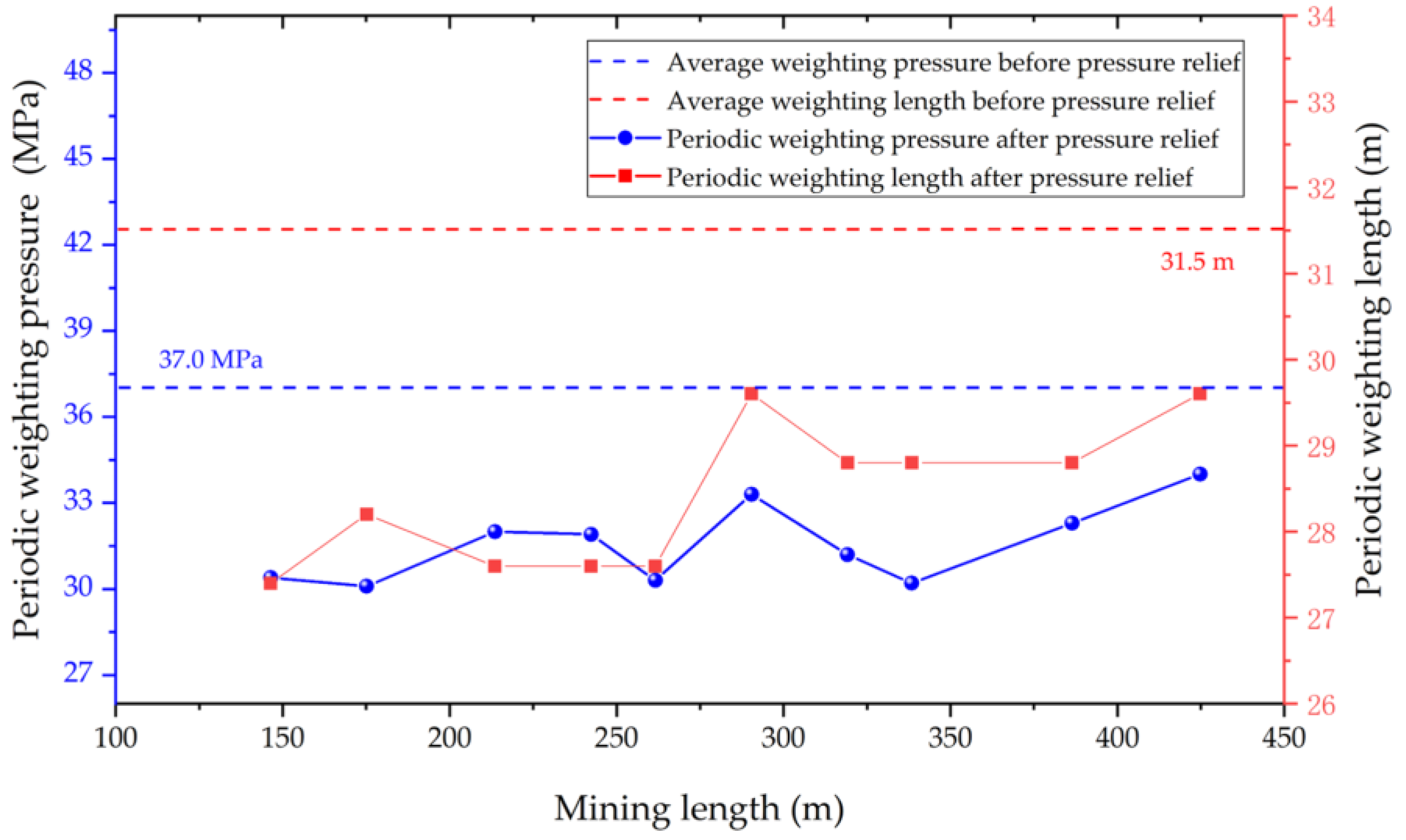
6.4. Pressure Relief Effect Test
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, Y.G.; Qian, M.G. Strata Control Around Coal Face in China; China University of Mining and Technology Press: Xuzhou, China, 1994; pp. 137–143. [Google Scholar]
- Düzgün, H.S.B. Analysis of roof fall hazards and risk assessment for Zonguldak coal basin underground mines. Int. J. Coal Geol. 2005, 64, 104–115. [Google Scholar] [CrossRef]
- Kong, P.; Jiang, L.; Shu, J.; Wang, L. Mining Stress Distribution and Fault-Slip Behavior: A Case Study of Fault-Influenced Longwall Coal Mining. Energies 2019, 12, 2494. [Google Scholar] [CrossRef]
- Wang, G.F.; Gong, S.Y.; Dou, L.M.; Cai, W.; Yuan, X.Y.; Fan, C.J. Rockburst mechanism and control in coalseam with both syncline and hard strata. Saf. Sci. 2019, 115, 320–328. [Google Scholar] [CrossRef]
- Kong, P.; Jiang, L.H.; Jiang, J.Q.; Wu, Y.N.; Chen, L.J.; Ning, J.G. Numerical Analysis of Roadway Rock-Burst Hazard under Superposed Dynamic and Static Loads. Energies 2019, 12, 3761. [Google Scholar] [CrossRef]
- Skrzypkowski, K. Compressibility of materials and backfilling mixtures with addition of solid wastes from flue-gas treatment and fly ashes. E3S Web Conf. 2018, 71, 7. [Google Scholar] [CrossRef]
- Skrzypkowski, K.; Korzeniowski, W.; Poborska-Mlynarska, K. Binding capability of ashes and dusts from municipal solid waste incineration with salt brine and geotechnical parameters of the cemented samples. Arch. Min. Sci. 2018, 63, 903–918. [Google Scholar]
- Brodny, J. Tests of friction joints in mining yielding supports under dynamic load. Arch. Min. Sci. 2011, 56, 303–318. [Google Scholar]
- Brodny, J. Determining the working characteristic of a friction joint in a yielding support. Arch. Min. Sci. 2010, 55, 733–746. [Google Scholar]
- Li, S.B. Borehole Drilling and Pressure Releasing Technology Applied to Mining Gateway Support in Three Soft Seam. Coal Sci. Technol. 2012, 40, 29–32. [Google Scholar]
- Gao, M.S.; Zhang, N.; Guo, C.S.; Dou, L.M. Mechanics and practice of combined supporting technology of 3D anchor-cable and unloading technology of wall of roadway. Chin. J. Geotech. Eng. 2005, 27, 587–590. [Google Scholar]
- Liu, H.G.; He, Y.N.; Xu, J.H.; Han, L.J. Numerical simulation and industrial test of boreholes destressing technology in deep coal tunnel. J. China Coal Soc. 2007, 32, 29–32. [Google Scholar]
- Xie, S.R.; Chen, D.D.; Sun, Y.D. Analysis on thin plate model of basic roof at elastic foundation boundary (I): First breaking. J. China Coal Soc. 2016, 41, 1360–1368. [Google Scholar]
- Moon, J.S. Representativeness of jointed rock mass hydraulic conductivity obtained from packer tests for tunnel inflow rate estimate. Int. J. Rock Mech. Min. Sci. 2011, 48, 836–844. [Google Scholar] [CrossRef]
- Xu, B.; Jiang, J.Q.; Dai, J.; Zheng, P.Q. Mechanical derivation and experimental simulation of breaking angle of key strata in overlying strata. J. China Coal Soc. 2018, 43, 299–606. [Google Scholar]
- Yang, P.J.; He, Y.; Guo, W.B. Disaster-causing mechanism and control measures of extremely thick and hard magmatic rock above working face. J. China Coal Soc. 2013, 38, 2106–2112. [Google Scholar]
- Wang, J.; Ning, J.G.; Qiu, P.Q.; Yang, S.; Shang, H.F. Microseismic monitoring and its precursory parameter of hard roof collapse in longwall faces: A case study. Geomech. Eng. 2019, 17, 375–383. [Google Scholar]
- Sainoki, A.; Mitri, H.S. Simulating intense shock pulses due to asperities during fault-slip. Appl. Geophys. 2014, 103, 71–81. [Google Scholar] [CrossRef]
- Jiang, J.Q.; Zhang, P.P.; Qin, G.P. Analysisof destabilized fracture and microseismic activity of highlocated main key strata. Rock Soil Mech. 2015, 36, 3567–3575. [Google Scholar]
- Chen, P.; Gu, S.C.; Zhang, Y.Z. Study on site measurement of surface movement law under shallow depth coal and vertically repeated mining. Coal Sci. Technol. 2016, 44, 173–177. [Google Scholar]
- Qian, M.G.; Miao, X.X.; He, F.L. Analysis of key block in the structure of voussoir beam in longwall minging. J. China Coal Soc. 1994, 19, 557–563. [Google Scholar]
- Qian, M.G.; Miao, X.X. Theoretical analysis on the structural form and stability of overlying strata in longwall mining. Chin. J. Rock Mech. Eng. 1995, 14, 97–106. [Google Scholar]
- Liu, H.W. Mechanics of Materials, 5th ed.; China Higher Education Press: Beijing, China, 2011; pp. 210–240. [Google Scholar]
- Cai, M.F.; He, M.C.; Liu, D.Y. Rock Mechanics and Engineering, 2rd ed.; China Science Press: Beijing, China, 2013; pp. 210–220. [Google Scholar]
- Li, X.L. The Broken and Instability Law of Hard Roof of Fully-Mechanized Top Coal Caving Mining in Extra-Thick Coal Seam. Master’s Thesis, Chongqing University, Chongqing, China, 2016. [Google Scholar]
- Huang, Q.X.; He, Y.P.; Cao, J. Experimental Investigation on Crack Development Characteristics in Shallow Coal Seam Mining in China. Energies 2019, 12, 1302. [Google Scholar] [CrossRef]
- Shan, P.F.; Lai, X.P. Numerical Simulation of the Fluid-Solid Coupling Process During the Failure of a Fractured Coal-Rock Mass Based on the Regional Geostress Characteristics. Transp. Porous Media 2018, 124, 1061–1079. [Google Scholar] [CrossRef]
- Shan, P.F.; Lai, X.P. Influence of CT scanning parameters on rock and soil images. J. Vis. Commun. Image Represent. 2019, 58, 642–650. [Google Scholar] [CrossRef]
- Shan, P.F.; Lai, X.P. Correlational analytical characterisation of energy dissipation-liberation and acoustic emission during coal-rock mass fracture inducing by coal excavation. Energies 2019, 12, 2382. [Google Scholar] [CrossRef]
- Huang, Q.X.; Cao, J. Research on Coal Pillar Malposition Distance Based on Coupling Control of Three-Field in Shallow Buried Closely Spaced Multi-Seam Mining, China. Energies 2018, 12, 462. [Google Scholar] [CrossRef]
- Wang, X.T.; Li, S.C.; Xu, Z.H.; Xue, Y.G.; Hu, J.; Li, Z.Q.; Zhang, B. An interval fuzzy comprehensive assessment method for rock burst in underground caverns and its engineering application. Bull. Eng. Geol. Environ. 2019, 78, 5161–5176. [Google Scholar] [CrossRef]
- Liu, H.; Yu, B.; Liu, J.N.; Wang, T.X. Investigation of impact rock burst induced by energy released from hard rock fractures Arabian. J. Geosci. 2019, 12, 1–12. [Google Scholar]
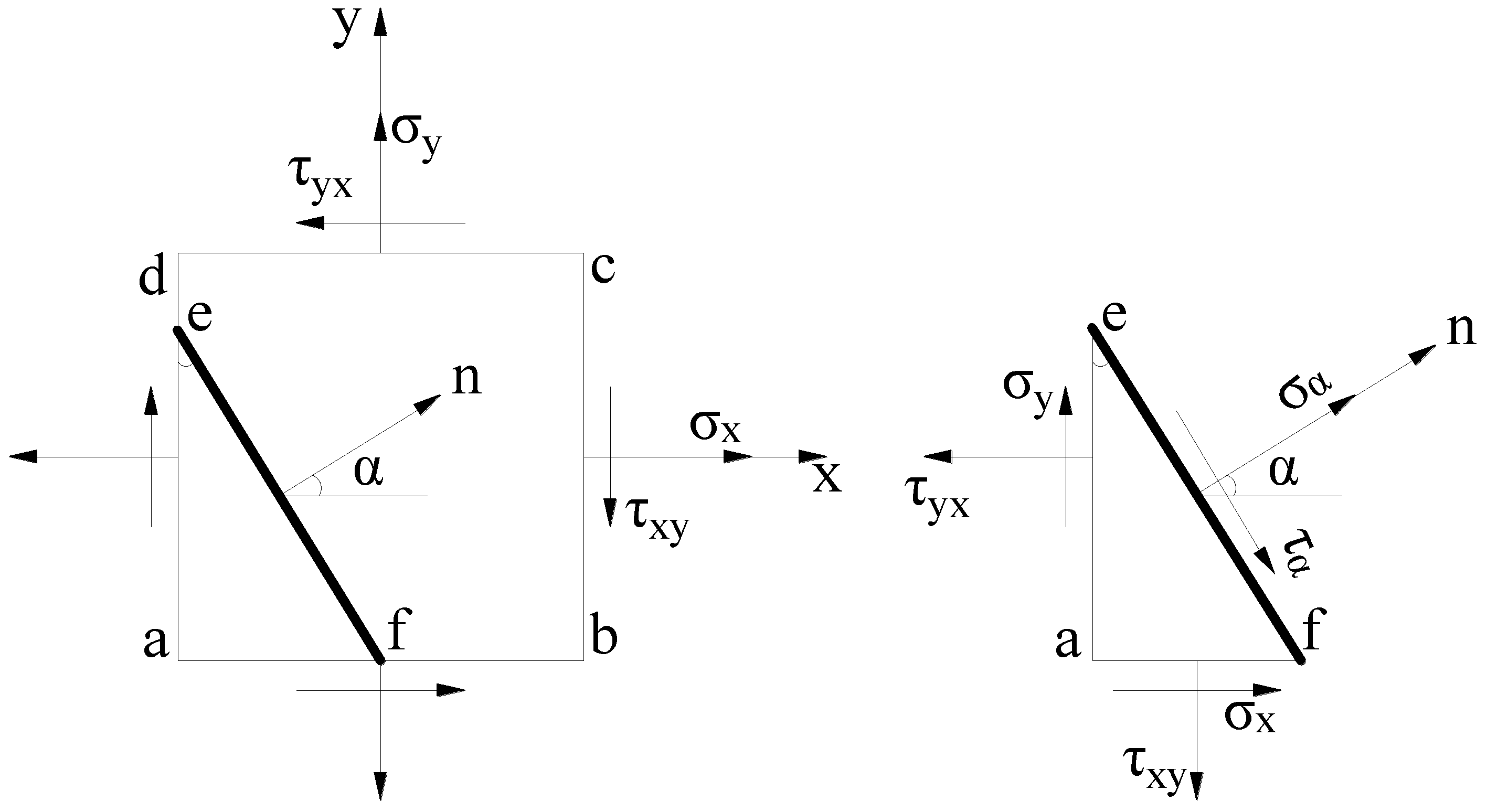







| Layer | Lithology | Thickness/m | Tensile Strength/MPa | qk/MPa | Key Layer |
|---|---|---|---|---|---|
| 28 | Medium Sandstone | 12.3 | 5.87 | 5.41 | / |
| 27 | Mudstone | 10.3 | 2.53 | 5.11 | / |
| 26 | Sandstone | 11.5 | 4.87 | 4.85 | / |
| 25 | Mudstone | 29.2 | 2.47 | 4.59 | / |
| 24 | Fine Sandstone | 11.0 | 7.21 | 3.87 | / |
| 23 | Mudstone | 141.2 | 2.51 | 3.59 | / |
| 22 | Sandy Mudstone | 13.3 | 2.34 | 1.28 | / |
| 21 | Mudstone | 9.5 | 2.43 | 1.20 | / |
| 20 | Sandy Mudstone | 13.5 | 2.54 | 1.10 | / |
| 19 | Sandstone | 13.2 | 4.58 | 1.01 | / |
| 18 | Sandy Mudstone | 7.5 | 2.36 | 0.97 | |
| 17 | Fine Sandstone | 7.3 | 6.87 | 0.83 | |
| 16 | Mudstone | 5.9 | 2.41 | 0.71 | |
| 15 | Sandy Mudstone | 7.6 | 2.42 | 0.57 | |
| 14 | Coarse Sandstone | 15.9 | 7.58 | 0.41 | Main key layer |
| 13 | B4-2 coal | 1.3 | 1.97 | 0.93 | |
| 12 | Sandy Mudstone | 7.7 | 2.33 | 0.92 | |
| 11 | Mudstone | 7.9 | 2.12 | 0.80 | |
| 10 | Coarse Sandstone | 5.0 | 4.48 | 0.67 | |
| 9 | B4-1 Coal | 3.0 | 2.02 | 0.57 | |
| 8 | Mudstone | 8.0 | 2.35 | 0.53 | |
| 7 | Coarse Sandstone | 14.0 | 5.31 | 0.36 | Subcritical key layer |
| 6 | B3 Coal | 1.8 | 2.21 | 0.54 | |
| 5 | Mudstone | 4.0 | 2.43 | 0.51 | |
| 4 | Fine Sandstone | 16.0 | 6.24 | 0.42 | |
| 3 | B2 Coal | 9.5 | 2.15 | / | |
| 2 | Mudstone | 3.9 | 2.54 | / | |
| 1 | Fine Sandstone | 21.9 | 6.12 | / |
| Layer | Lithology | Thickness/m | Normal Stiffness (MPa) | Tangential Stiffness (MPa) | Cohesion (MPa) | Internal Friction Angle (°) | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|---|
| 27 | Mudstone | 10.3 | 7900 | 8100 | 0.12 | 20.0 | 2.53 |
| 26 | Sandstone | 11.5 | 8200 | 6700 | 0.47 | 20.8 | 4.87 |
| 25 | Mudstone | 29.2 | 7900 | 8100 | 0.12 | 20.0 | 2.47 |
| 24 | Fine Sandstone | 11.0 | 4200 | 3900 | 0.93 | 6.0 | 7.21 |
| 23 | Mudstone | 141.2 | 7900 | 8100 | 0.12 | 20.0 | 2.51 |
| 22 | Sandy Mudstone | 13.3 | 8200 | 6700 | 0.47 | 20.8 | 2.34 |
| 21 | Mudstone | 9.5 | 7900 | 8100 | 0.12 | 20.0 | 2.43 |
| 20 | Sandy Mudstone | 13.5 | 8200 | 6700 | 0.47 | 20.8 | 2.54 |
| 19 | Sandstone | 4.58 | 4100 | 3900 | 0.84 | 12.8 | 4.58 |
| 18 | Sandy Mudstone | 2.36 | 8200 | 6700 | 0.47 | 20.8 | 2.36 |
| 17 | Fine Sandstone | 7.3 | 4200 | 3900 | 0.93 | 6.0 | 6.87 |
| 16 | Mudstone | 5.9 | 7900 | 8100 | 0.12 | 20.0 | 2.41 |
| 15 | Sandy Mudstone | 7.6 | 8200 | 6700 | 0.47 | 20.8 | 2.42 |
| 14 | Coarse Sandstone | 15.9 | 7100 | 5900 | 0.35 | 20.0 | 7.58 |
| 13 | B4-2 coal | 1.3 | 7100 | 5900 | 0.14 | 10.0 | 1.97 |
| 12 | Sandy Mudstone | 7.7 | 8200 | 6700 | 0.47 | 20.8 | 2.33 |
| 11 | Mudstone | 7.9 | 7900 | 8100 | 0.12 | 20.0 | 2.12 |
| 10 | Coarse Sandstone | 5.0 | 7100 | 5900 | 0.35 | 20.0 | 4.48 |
| 9 | B4-1 Coal | 3.0 | 3300 | 1100 | 0.14 | 10.0 | 2.02 |
| 8 | Mudstone | 8.0 | 7900 | 8100 | 0.12 | 20.0 | 2.35 |
| 7 | Coarse Sandstone | 14.0 | 7100 | 5900 | 0.35 | 20.0 | 5.31 |
| 6 | B3 Coal | 1.8 | 3300 | 1100 | 0.14 | 10.0 | 2.21 |
| 5 | Mudstone | 4.0 | 7900 | 8100 | 0.12 | 20.0 | 2.43 |
| 4 | Fine Sandstone | 16.0 | 4200 | 3900 | 0.93 | 6.0 | 6.24 |
| 3 | B2 Coal | 9.5 | 3300 | 1100 | 0.14 | 10.0 | 2.15 |
| 2 | Mudstone | 3.9 | 7900 | 8100 | 0.12 | 20.0 | 2.54 |
| 1 | Fine Sandstone | 21.9 | 4200 | 3900 | 0.93 | 6.0 | 6.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, F.; Zhang, T.; Lai, X.; Cao, J.; Shan, P. Study on the Evolution Law of Overburden Breaking Angle under Repeated Mining and the Application of Roof Pressure Relief. Energies 2019, 12, 4513. https://doi.org/10.3390/en12234513
Cui F, Zhang T, Lai X, Cao J, Shan P. Study on the Evolution Law of Overburden Breaking Angle under Repeated Mining and the Application of Roof Pressure Relief. Energies. 2019; 12(23):4513. https://doi.org/10.3390/en12234513
Chicago/Turabian StyleCui, Feng, Tinghui Zhang, Xingping Lai, Jiantao Cao, and Pengfei Shan. 2019. "Study on the Evolution Law of Overburden Breaking Angle under Repeated Mining and the Application of Roof Pressure Relief" Energies 12, no. 23: 4513. https://doi.org/10.3390/en12234513
APA StyleCui, F., Zhang, T., Lai, X., Cao, J., & Shan, P. (2019). Study on the Evolution Law of Overburden Breaking Angle under Repeated Mining and the Application of Roof Pressure Relief. Energies, 12(23), 4513. https://doi.org/10.3390/en12234513