Abstract
Unexpected detonation of granular solid energetic materials is a key safety issue in the propellants manufacturing industry. In this work, a model developed for the characterization of the early stages of the detonation process of granular solid energetic materials is presented. The model relies on a two-phase approach which considers the conservation equations of mass, momentum, and energy and constitutive relations for mass generation, gas-solid particle interaction, interphase heat transfer, and particle-particle stress. The work considers an extension of approximated Riemann solvers and Total Variation Diminishing (TVD) schemes to the solid phase for the numerical integration of the problem. The results obtained with this model show a good agreement with data available in the literature and confirm the potential of the numerical schemes applied to this type of model. The results also permit to assess the effectiveness of different numerical schemes to predict the early stages of this transient combustion process.
1. Introduction
Unexpected detonation of granular solid propellants is a key safety issue. Gun tubes experience pressure build-up during unstable burning in the chamber leading to high mechanical stresses which act on the grains leading to an increase of the chamber pressure, causing the explosion of the gun tube [1]. Moreover, ignition and subsequent combustion of granular solid propellants are also complex mechanisms of high importance in the manufacturing process of many energetic materials, not only because of already mentioned safety issues, but also due to the design of propulsion systems. The penetration of the hot gases into the voids promotes the convective heating of the granules as well as the granule compaction and the rapid pressurization of the system. In case the ignition is not correctly controlled, the process can generate compressive waves which compact the un-reacting region of the grain bed. Under strong pressure waves, the propellant bed might rapidly collapse, leading to a compressive reaction and an explosion. Therefore, it is of major importance to properly understand and model this problem.
The theoretical modeling of this problem has focused on the interests of many studies in the last decades and different approaches can be found in the literature. Some of the first researchers facing the theoretical modeling of this kind of problem were Kuo et al. [2] who developed in their work a fixed-bed model, usually referred to as the KVS (Kuo, Vichenevetsky, Summerfield) model, to describe the transient problem of flame propagation in a packed fixed-bed of granular energetic materials. They used a combination of an explicit finite difference scheme and the method of characteristics to numerically solve the problems. Koo and Kuo [3] compared the model predictions with experimental firing tests with satisfactory results.
On the other hand, Markatos [4] proposed a different approach based on the previous work of Spalding [5]. In that case, the description of the problem considered the governing equations on the basis that mass, momentum, and energy fluxes are balanced over control volumes occupied by space-sharing interspersed continua. According to that concept, distinct phases are present within the same space, their shares of space being measured by their volume fractions. The approach was used to simulate the accelerating flame front for beds of granulated solid energetic materials fixed in a rigid enclosure with satisfactory results [4].
Another type of approach is that developed by Gough [6] and adopted by Oton-Martinez et al. [7] among others, which is based on the formal averaging of the solid propellant and the surrounding gas in the spatial domain considered. This approach relies on the conservation equations of the solid and gas phases where the phases are considered to be a homogeneous continuum. This means that both the gas and the propellant grains are defined to have a uniform value of density and porosity within each fundamental volume cell. Thus, the heterogeneous flow composed of two interacting continua can be described by appropriately defined averages of flow properties.
Regarding the experimental data to feed numerical models, Sandusky [8] provided constitutive relations of compaction obtained from quasi-static compaction experiments with bed diameters approaching that of gun breeches performed on five cannon propellants. The granular materials tested were single-base, double-base, triple-base propellants as well as a nitramine-composite propellant. They found that the dominant compaction mechanism was plastic deformation with the virtual absence of fracture. Kooker et al. [9] experimentally studied the convective ignition process of granular solid propellant beds with the help of a previously built apparatus that transformed a confined bed to a planar hot gas ignition wave. The investigation examined convective ignition behavior of five different granular solid propellants with the same flow conditions: single-base, double-base, triple-base, and nitramine composites.
As for the numerical methods used in the modeling of detonation of granular solid energetic materials, most of the authors used finite-difference schemes [10] although with distinct approaches. Hoffman and Krier [11] and Krier and Kezerle [12] used the MacCormack method [13] with a predictor-corrector scheme. Sheu et al. [14,15,16] and Krier et al. [17] also used a finite-different scheme with the Lax–Wendroff approach [18] whereas Baer and Nunziato [19] and Butler [20] applied the method of lines [21,22]. Markatos [4] used an implicit finite difference algorithm called IPSA (interphase slip algorithm) which anticipates the effects of a change in the local property of one phase on the properties of the other phase at the same location.
To the author’s knowledge, finite-volume approximate Riemann solvers [23] or Total Variation Diminishing (TVD) schemes [24] have not been previously applied to the resolution of problems describing the detonation process of the granular solid energetic materials or explosives. Notwithstanding, these numerical methods are widely used in other types of fluid mechanic problems with good results. Among others, approximate Riemann solvers are heavily used in transient transonic or supersonic problems as well as in the case of transient contact discontinuity problems [25,26], whereas TVD schemes have shown good results in incompressible fluid flow problems [27].
In this work, a predictive model is developed as a tool for the characterization of the detonation process of granular solid energetic materials under shock tube conditions. The tool relies on a two-phase model, which considers a set of equations of continuity, momentum, and energy for the solid and the gas phase, to describe the transient behavior of this combustion process. Regarding the numerical methods, the tool considers the use of approximate Riemann solvers and TVD schemes to face the resolution of the system of partial differential equations of the model. The article is structured as follows: firstly, the physical model and the considered constitutive relations are presented. In the next section, the numerical schemes used for the integration of the model are described. Afterwards, the results provided by the model are compared with data available in the literature and the validation of the model is discussed. The effectiveness of different numerical schemes when facing the description of the early stages of the detonation of granular solid energetic materials is also discussed. Finally, some conclusions are drawn, and future research lines are outlined.
2. Physical Model Description
The approach proposed in this work relies on the conservation equations of mass, energy, and momentum of both gas phase and solid phase to model the physical problem of combustion of granulated solid energetic materials. In this case, the solid phase is considered as incompressible. In the present work, the model is generalized in order to be applied to different solid granulated energetic materials. The basic guidelines proposed by Hoffman and Krier [11] together with the considerations described by Gidaspow [28] are included in this model. Gidaspow [28] suggests including the time derivative of the porosity into the energy equation in order to satisfy the inequality of Clausius-Duhem. However, all space and time derivatives of the porosity, which are present in the momentum and energy equations, respectively, are non-conservative terms that cannot be solved with an explicit numerical method for hyperbolic systems. Thus, in the present work, an alternative model is presented where some constitutive laws are modified, and a re-organization of the conservation equations is performed to obtain a conservative form of the system of equations. That allows the use of numerical schemes for conservative fluxes with a finite-volume approach. This way, updated numerical methods for compressible flow can be applied for the numerical resolution [7]. Moreover, an extension of approximated Riemann solvers to the solid phase was considered for the numerical integration of the problem. Another key aspect in these models is the inclusion of a pressure into the solid, which is defined as the addition of the gas pressure and the inter-granular stress, which introduces an important stiffness from the numerical point of view. All in all, the differential equation system considered in this work can be expressed as:
where is the density, is the gas porosity, is the velocity vector, is the identity vector, is the mass generation, is the pressure, is the intergranular stress, is the drag force, and is the interfacial heat transfer. The chemical energy of the gas phase is defined as,
where and stand for the gas and the particle, respectively.
According to Hoffman and Krier [11], intergranular stress formulation does not prevent particle compaction below minimum compaction. To consider that limitation, they proposed a modification of the momentum equation of particles, so they cannot be accelerated once they have reached that porosity value. If that limitation is imposed, the Equation (5) can be rewritten to:
The term is defined as,
where is a constant value that considers the properties of the particle’s framework, and are the minimum and critical porosity respectively.
Several correlations were chosen to close the proposed model. Among them, drag force, used in momentum and energy conservation equations of gas and solid phases, is defined as:
where is the particle diameter, is the drag coefficient presented by Butler et al. [29] in their study,
This correlation (Equation (11)) is a function of the Reynolds number and gas viscosity :
where is the temperature, is the value of viscosity at 2000 K, and is 2000 K [12].
As for the interfacial heat transfer coefficient, the heat expression form, in the case of having spherical particles , is:
The convective heat transfer coefficient depends on the Nusselt number () with the following expression:
The convective heat transfer coefficient is a function of the Prandtl Number, , and the gas conductivity defined as:
where is the specific heat of the gas at constant volume, is the universal constant of gases, and is the molecular weight of the gas phase.
The correlation of the Nusselt number proposed by Hoffman and Krier [11], Butler et al. [29], and Butler and Krier [20] has the following form:
The gas mass generation equation assuming that particles are spheres is related to the combustion velocity and has the following form:
The combustion law is given by:
where and are vales that depend on the propellant.
As for the gas equation of state, the equation of Noble-Abel is considered,
As previously said, in this model the solid is considered incompressible. However, as presented in Equation (7), there is a solid pressure defined as the addition of gas pressure and the intergranular stress (), understood as the resistance of the particles to be compacted under the critical porosity. In this study, the authors consider the expressions proposed in several works, such as the ones from Krier and Kezerle [12], Hoffman and Krier [11], and Gokhale and Krier [30]:
where K is the bulk modulus.
3. Numerical Method
The physical model includes non-conservative terms. In order to handle this issue, a reconversion of the system was performed in order to have a conservative form of the system of partial differential equations. In particular, the momentum and energy equations for both gas and solid phase are re-organized so that the terms containing partial derivatives of are resolved separately by including them in the source terms. The final system of equations in a homogenous form (without source terms) could be presented in the conservative form and remains hyperbolic. This way, a finite volume approach with an approximate Riemann solver can be used to numerically solve the problem. In this case, an extension of approximated Riemann solvers to the solid phase was considered for the numerical integration of the problem. Therefore, the multi-dimensional Euler equations used in this work for modeling and describing the physical problem of combustion of energetic materials can be written with the following general conservative form,
where is the conserved variables vector, is the tensor of fluxes and is the vector that includes the non-conservative terms and the source terms, which may or not include non-conservative terms and can be defined as:
In our case, the conserved variables vector U, the flux tensor and the source terms vector are
The integration of the homogeneous part of the equation system (Equation (22)) in a control volume yields
where A is the boundary of Ω and is the normal vector to surface A. Considering the first integral as a time-rate of change of the averaging of the conserved variables and the boundary A formed by N surfaces so that , Equation (25) can be written as,
The time derivative of the conserved variables is defined as . Therefore, making use of the Rotational property and considering that the surface integral of the flux is approached by , a finite volume scheme for multiple dimensions in unstructured grids is obtained. Considering the source terms of the nonhomogeneous system,
where is the rotation matrix, its inverse, and is the area of the surface bounding volume Ω.
The time step to solve the equation system is calculated as,
where stands for a Courant–Friedichs–Lewy-like constant, is the speed of sound of the gas phase,
and is the speed of sound of the solid phase,
where is the initial bulk modulus, whose value was taken from Hoffman and Krier [11], and is the density of the propellant.
In order to evaluate the fluxes, several approximations such as the first-order upwind method of Godunov, Lax–Friedrichs scheme, and Lax–Wendroff scheme can be found in the existing literature.
These methods require the solution of the Riemann problem which can be highly demanding. Therefore, approximate Riemann solvers are used in this work. Among the numerical schemes found in literature, Rusanov and MacCormack numerical schemes were chosen to solve the problem of energetic material combustion.
3.1. Rusanov Scheme
Rusanov scheme [31] is a particular case of HLL (Harten Lax and van Leer) Riemann solver [23]. In this approach, an approximation for the intercell numerical flux is obtained directly. The approximation consists of finding, for each interface between two cells, the approximate numerical flow that will be an average value of the numerical flows computed for each cell in the previous step time, corrected with a factor. This factor is proportional to the difference of conservative variables of each cell in the previous step time and a positive speed value , so the numerical flux at each interface is computed as:
being the flux at the interface, the convective flow in the left cell in the previous time step, , the convective flow in the right cell, and a positive value of speed calculated by,
where R and L stand for right and left respectively.
3.2. MacCormack-TVD Scheme
The MacCormack numerical method of second-order in both time and space is presented to solve Navier–Stokes equations developed by Robert MacCormack [13]. According to Lee and Kim [32], the scheme can be written as a variation of the two steps Lax–Wendroff scheme [18], one predictor and one corrector. According to Liang et al. [27], the use of a total variation diminishing (TVD) of the MacCormack scheme will accurately reproduce all flow regimes. Thus, the solution of the system of Equation (22) is obtained by solving three 1-D problems in sequence as proposed in [21],
The TVD-MacCormack scheme is used to solve consecutively the three 1D hyperbolic equations in each time step. Following [21] and taking Equation (33) as an example the discretization scheme is given by
where the superscripts p and c denote the predictor and corrector steps respectively, ∆x and ∆t are the spatial and time steps, and is a function defined as,
with a flow-limiting function such as,
and a variable defined as,
Vectors and are defined as,
and the values of and ,
In this work, this numerical scheme was also extended to the solid phase.
4. Results and Discussion
This section is structured in two parts. Firstly, the validation of the presented model is faced and discussed. Then, the capabilities of different numerical schemes to deal with the physical problem under study are analyzed.
4.1. Model Validation
In the case of detonation of granulated solid propellants, the experimental data available in the open literature are scarce and some key parameters are not often provided. In this study, the validation of the model was carried out in two stages. Firstly, a theoretical two-phase shock tube problem was faced in order to ensure that the model considered was able to characterize the discontinuities linked to shock compressions when friction, interphase heat transfer, and combustion terms were considered. Secondly, an additional validation test was performed by comparing the prediction of the present approach with the data provided by Hoffman and Krier [11] for cyclotetramethylenetetranitramine (HMX).
In the first case, the problem considered a straight tube of 2 m length and 0.1 m height in which there were two distinct zones (left and right) separated by a membrane. At the left side, the initial pressure of the gas was Pa whereas at the right side the initial gas pressure was Pa. Regarding the rest of the variables, the initial conditions on both sides of the tube were the same: , . The ignition temperature was considered to be 300 K, whereas the chemical energy provided for the ignition was J/kg. Particle density and particle diameter considered in this problem were, respectively, 1910 kg/m3 and 0.2 x m. Finally, and . The results obtained are gathered in Figure 1 in terms of the spatial distribution of gas density, porosity, velocities and temperatures of the gas and particle phases as well as gas pressure. As shown, the numerical scheme used ensures an efficient resolution of the shock wave and the subsequent rarefaction waves. Besides, the results suggest that the numerical approach proposed works well with the constitutive laws implemented.
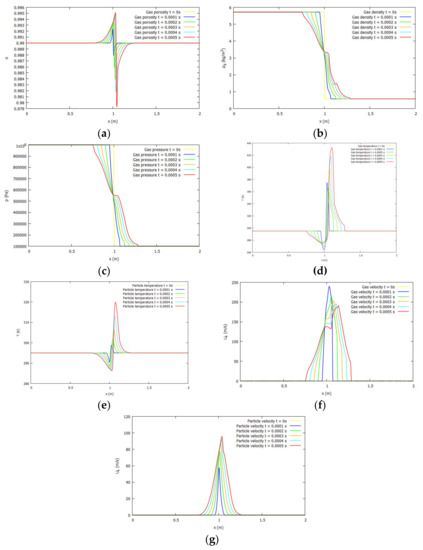
Figure 1.
Numerical results of a combustion shock tube problem obtained for (a) porosity (b) gas density (c) gas pressure (d) gas temperature (e) particle temperature (f) gas velocity and (g) particle velocity.
The second validation problem faced considered the data provided in [11] and permitted to discuss different physical approaches used in the modeling of the initial stages of the detonation of energetic materials. To perform this analysis, a closed and insulated tube of 0.08 m length was chosen. Therefore, there is no transfer of mass and heat through the walls of the tube with the boundary conditions being zero gradient for all variables despite velocity, which is assumed to be zero at the right and left walls.
The necessary input data for the calculation was obtained from the existing bibliography and it is written in Table 1. Although all authors consider a small zone of the control volume already initiated, each one applies different values of pressure and temperature as initial conditions of the test. High differences in the results can be obtained depending on the initial values assumed for the variables.

Table 1.
Input data.
Therefore, and in order to validate the model with literature values, the distributions of pressure, porosity, and gas and particle temperatures provided by Hoffman and Krier [11] at 20 μs, were used as initial conditions for the calculations performed. Simulations were carried out using Rusanov and MacCormack-TVD numerical schemes and their results are compared in the following pages.
Figure 2 shows a comparison of the present model with flame front solution provided by Hoffman and Krier [11] for two cases: the case of the model that includes a modification of the momentum equation (i.e., model formed by the Equations (1)–(4), (6), (7), and (9), Figure 2a) and the case of the model that includes a porosity limiter (Figure 2b). In addition, Figure 3 shows a comparison of the time evolution of porosity distributions with the spatial domain for momentum equation modification. All in all, the results obtained are qualitatively similar to those obtained by Hoffman and Krier [11] with a good agreement between Rusanov and MacCormack numerical schemes. In the case of flame front propagation, the present model with a porosity limiter slightly overestimates this value, as a result, the results of porosity and temperature are displaced in the x-direction with respect the ones provided by Hoffman and Krier [11]. Notwithstanding, this slight overestimation is on the “safe side” as in the case of an accident simulation the code would provide a more adverse scenario than the actual one.
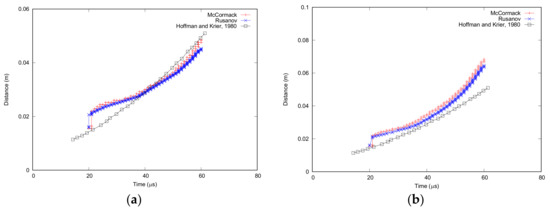
Figure 2.
Comparison of Rusanov and MacCormack Total Variation Diminishing (TVD) results obtained with literature data in Flame front propagation for (a) the model with momentum equation modification and (b) the model with the porosity limiter.
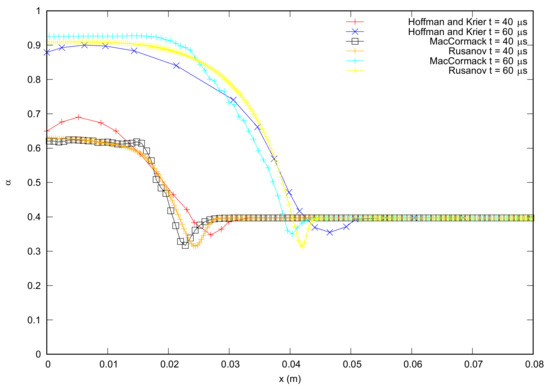
Figure 3.
Comparison of Rusanov and MacCormack TVD results obtained with literature data in porosity for the model with momentum equation modification for 40 and 60 μs.
A grid convergence study was performed in order to assess the sensitivity of the mesh size in the results of the numerical model. Figure 4 shows the results of the numerical model of the case of the flame front propagation (similar to that in Figure 2) as a function of number of cells used in the discretization with Rusanov and TVD schemes. As shown, as the number of cells increases, the numerical solution tends to converge towards the reference data of Hoffman and Krier [11].
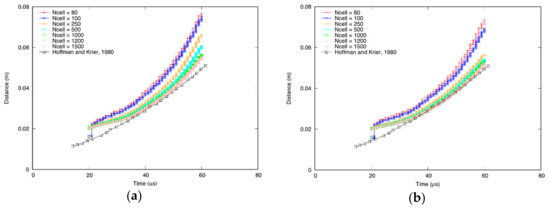
Figure 4.
Grid convergence analysis where the results for flame front propagation are shown for different mesh resolutions (from 80 to 1500 elements). Convergence is observed both with alpha-limited (a) Rusanov and (b) MacCormack TVD.
4.2. Evaluation of the Numerical Strategies Proposed for the Physical Model
This section is structured in two parts depending on how the limitation of the porosity variable is performed. Firstly, Hoffman and Krier [11] system of equations together with the modification of the momentum conservation equation are applied. Afterwards, the calculation is performed limiting the porosity directly in the code in order to prevent this variable reaching values under the minimum accepted.
4.2.1. Modification of Momentum Conservation Equation
The system to be considered is formed by the Equations (1)–(4), (6), (7), and (9) and the solutions are plotted in Figure 5. The results obtained with Rusanov and MacCormack agree well at 40 μs and present slight but not relevant differences at 60 μs for porosity, pressure, and gas temperature. The frame front distributions obtained with both numerical schemes are also very similar to those provided by Hoffman and Krier [11] in their work. However, the modification of the momentum equation provides a solution in which the porosity value is below the minimum physically possible one. Besides, the particle temperature has an unrealistic value. Therefore, a different restriction of some physical variables should be considered.
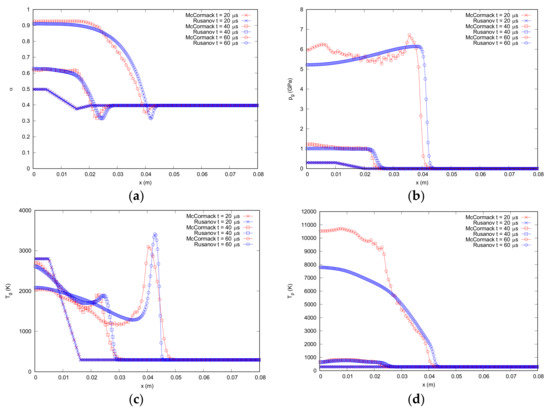
Figure 5.
Comparison of Rusanov and MacCormack TVD results obtained for (a) porosity distribution, (b) pressure distribution, (c) gas temperature distribution, and (d) particle temperature distribution for 20, 40, and 60 μs with the modification of the momentum conservation equation.
4.2.2. Porosity Direct Limiter
The minimum value for porosity should be that for which particles are completely packed and thus, they cannot be further compacted. As seen in Section 4.2.1., the modification of the momentum equation provides a solution in which not only the porosity reaches values under the minimum physical value, but also the particle temperature has an unrealistic value. In order to avoid these drawbacks, a different restriction was tested. In this case, the porosity was limited during the calculation directly in the code by preventing the porosity reaching values under a minimum threshold, which was fixed based on the minimum physical value that the solid particles could occupy in the volume of the domain.
The results obtained for porosity, pressure, and gas and particle temperatures are presented in Figure 6. As already discussed in the previous section, the results obtained are qualitatively similar to those obtained by Hoffman and Krier [11] with a good agreement between Rusanov and MacCormack numerical schemes. Besides, the distribution of particle temperature takes physical values. It is worth noting that the application of the MacCormack scheme to the solid phase provided good results. These show that MacCormack-TVD is an appropriate numerical scheme to be used when integrating the solid phase of this kind of problem.
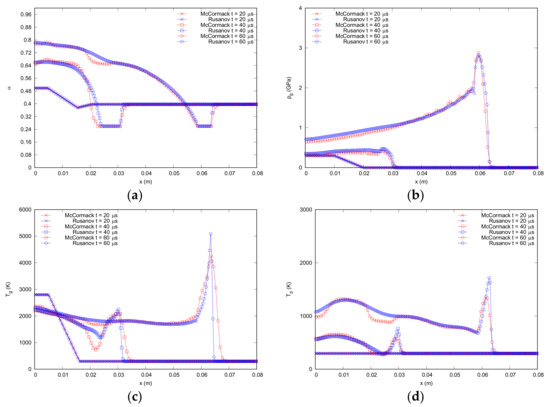
Figure 6.
Comparison of Rusanov and MacCormack TVD results obtained for (a) porosity distribution, (b) pressure distribution, (c) gas temperature distribution, and (d) particle temperature distribution for 20, 40, and 60 μs with the porosity direct limiter.
However, the x-locations of the peak of pressure and temperatures at 60 μs show a displacement compared with those presented by Hoffman and Krier [11]. This phenomenon can be seen in the flame front propagation results represented in Figure 2b. The figure shows a good agreement of both numerical schemes with the result of the bibliography [11] up to 50 μs, increasing the difference between the calculation and the results from literature from this time on. These differences could be due, on the one hand, to the initial values of the parameters chosen as initial conditions, which highly determine the x-location of the peak values for all variables. On the other hand, these could rely on the inconsistency of some input parameters obtained from different sources in the literature.
5. Conclusions
A model was developed to study the early stages of the detonation process of granular energetic materials. To solve the system of differential equations for both gas and solid phases, Rusanov and MacCormack-TVD numerical schemes were used. Besides, the first-order Euler method was used to solve the source terms. Two different models were used to calculate pressure, temperature, and porosity distributions. The first model studied considered the modification of the particle momentum governing equation done by Hoffman and Krier [11]. According to the authors, this modification prevents the porosity from reaching values below the minimum value of compaction that packed beds of spherical particles can reach. However, when this model is applied, the temperature of the particle phase increases and reaches values up to 8000 K and the porosity takes values below the minimum. In order to control the particle temperature, the limitation of the porosity is performed directly in the code by preventing the porosity reaching values below the possible minimum. The magnitude of the values obtained for the main variables of interest when applying this model is similar to those found in the literature. Moreover, the results obtained using Rusanov scheme agree well with those resulting from applying MacCormack-TVD numerical scheme. However, in some cases, the distributions of the variables are displaced in the x-direction with respect to those from the literature. This behavior can be seen by observing the x-coordinate position of the peak values obtained for pressure, temperature, and porosity variables. These differences could be due to the initial values of the parameters chosen as initial conditions, which highly determine the x-location of the peak values for all variables or, on the other hand, to the inconsistency of input data spread in many different sources from the literature.
All in all, the results show that MacCormack-TVD is an appropriate numerical scheme to be used when integrating the solid phase of this kind of physical problem. The extension of the numerical scheme will permit to apply this strategy to different solid propellant problems in future work. Finally, it can be concluded that the last model considered represents, with reasonable accuracy, the physical behavior of the propellant combustion for all variables of interest becoming a predictive tool for the characterization of the early stages of the detonation process of granular solid propellants.
Finally, it is worth commenting on the limitations found in the physical model considered in this work. These limitations can be improved in future work. On one hand, the model adopts the Equation of State (EOS) of Nobel-Abel for the gas phase. It would be advisable to use more complex real gas EOS to improve model accuracy. Moreover, the use of the Jones–Wilkins–Lee (JWL) EOS for both the solid and products could be also considered. However, there is an important limitation to obtain the coefficients for this kind of EOS for the reaction products of HMX and other explosives and/or propellants. On the other hand, turbulence is not considered in the present work. This is an improvement the authors plan to undertake in future work as turbulence can enhance the transport processes between phases.
Author Contributions
Literature survey, F.J.S.V.; Model development, C.L.-M. and J.R.G.-C.; Numerical schemes, C.L.-M. and J.R.G.-C.; Programming and code development, C.L.-M. and J.R.G.-C.; Two phase flow modelling, F.J.S.V.; Analysis of the results and writing, C.L.-M.; Analysis of results and discussion, R.A.O.-M.; Revision of results, F.J.S.V.; Revision of modelling detonation, R.A.O.-M.; Coordination, J.R.G.-C.
Funding
This research was funded by [the Spanish Ministry of Economy and Competitiveness and the European Regional Development Fund] grant number [RTC-2016-5194-8].
Acknowledgments
The research was performed thanks to the financial support of the Spanish Ministry of Economy and Competitiveness and the European Regional Development Fund throughout project RTC-2016-5194-8.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| c | Speed of sound. |
| CFL | Courant–Friedichs–Lewy constant. |
| cv | Specific heat capacity at constant volume. |
| dp | Particle diameter. |
| e | Internal energy. |
| E | Total energy (internal, mechanical) by unit mass. |
| Echem | Chemical reaction energy. |
| EOS | Equation of State |
| g | (Subindex) Relative to gas phase. |
| FD | Drag force source term. |
| fpg | Drag coefficient. |
| Tensor of convective fluxes. | |
| hc | Convection heat transfer coefficient. |
| Identity vector. | |
| k | Thermal conductivity. |
| K | Bulk modulus of solid phase. |
| Mg | Molecular weight of the gas phase. |
| Vector normal to surface. | |
| u | Nusselt number |
| p | (Subindex) Relative to solid (particle) phase. |
| P | Pressure. |
| Pr | Prandtl number. |
| Interfacial heat transfer. | |
| r | Combustion rate |
| Re | Reynolds number. |
| Ru | Universal constant of gases |
| S | Vector of source terms. |
| Sp | Surface area of particle. |
| t | Time. |
| T | Temperature. |
| Rotation matrix. | |
| TVD | Total Variation Diminishing |
| u | Velocity. |
| U | Vector of conserved variables. |
| Vp | Volume of particle. |
| α | Gas porosity (void fraction). |
| αc | Critical porosity. |
| γ | Ratio of the specific heats. |
| Mass generation rate. | |
| ηg | Covolume. |
| µ | Dynamic viscosity. |
| ρ | Density. |
| Tp | Intergranular stress of particles. |
| Ω | Control volume. |
References
- Kubota, N. Propellants and Explosives. Thermochemical Apects of Combustion; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Kuo, K.K.; Vichnevetsky, R.; Summerfield, M. Theory of flame front propagation in porous propellant charges under confinement. AIAA J. 1973, 11, 444–451. [Google Scholar] [CrossRef]
- Koo, J.H.; Kuo, K.K. Transient Combustion in Granular Propellant Beds. Part I. Theoretical Modeling and Numerical Solution of Transient Combustion Processes in Mobile Granular Propellant Beds; Pennsylvania State University Park Department of Mechanical Engineering: State College, PA, USA, 1977. [Google Scholar]
- Markatos, N.C. Modelling of two-phase transient flow and combustion of granular propellants. Int. J. Multiph. Flow 1986, 12, 913–933. [Google Scholar] [CrossRef]
- Spalding, D.B. Numerical computation of multi-phase fluid flow and heat transfer. In Recent Advances in Numerical Methods in Fluids; Pineridge Press: New York, NY, USA, 1980; pp. 139–167. [Google Scholar]
- Gough, P.S.; Zwarts, F.J. Modeling heterogeneous two-phase reacting flow. AIAA J. 1979, 17, 17–25. [Google Scholar] [CrossRef]
- Oton-Martinez, R.A.; Monreal-Gonzalez, G.; Garcia-Cascales, J.R.; Vera-Garcia, F.; Velasco, F.J.S.; Ramirez-Fernandez, F.J. An approach formulated in terms of conserved variables for the characterisation of propellant combustion in internal ballistics. Int. J. Numer. Methods Fluids 2015, 79, 394–415. [Google Scholar] [CrossRef]
- Sandusky, H.W.; Elban, W.L. Quasi-static compaction of porous propellant beds. II. Experiments and application of lattice compaction model to cannon propellants. Powder Technol. 1996, 89, 219–229. [Google Scholar] [CrossRef]
- Kooker, D.E.; Howard, S.L.; Chang, L.M. Convective ignition of a granular solid propellant bed: Influence of propellant composition. Symp. Int. Combust. 1996, 26, 2033–2040. [Google Scholar] [CrossRef]
- John, F. Partial Differential Equations, 4th ed.; Applied Mathematical Sciences; Springer-Verlag: New York, NY, USA, 1982; ISBN 978-0-387-90609-6. [Google Scholar]
- Hoffman, S.J.; Krier, H. Fluid Mechanical Processes of Deflagration to Detonation Transition in Beds of Porous Reactive Solids; Aeronautical and Astronautical Engineering Department, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1980; Technical Report AAE-80_2. [Google Scholar]
- Krier, H.; Kezerle, J.A. A separated two-phase flow analysis to study deflagration-to-detonation transition (DDT) in granulated propellant. Symp. Int. Combust. 1979, 17, 23–34. [Google Scholar] [CrossRef]
- MacCormack, R. The effect of viscosity in hypervelocity impact cratering. In Proceedings of the 4th Aerodynamic Testing Conference, Cincinnati, OH, USA, 28 April 1969—30 April 1969; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1969. [Google Scholar]
- Sheu, T.W.H.; Lee, S.M.; Chen, M.Y.; Yang, V. Analysis of combustion processes in a mobile granular propellant bed. Dynamic Aspects of Explosion Phenomena. 1993, 154, 477–490. [Google Scholar]
- Sheu, T.W.H.; Lee, S.-M. Numerical study of two-dimensional solid-gas combustion through granulated propellants. Numer. Heat Transf. Part Appl. 1995, 27, 395–415. [Google Scholar] [CrossRef]
- Sheu, T.W.H.; Lee, S.-M. Analysis of combustion processes in a gun interior ballistics. Int. J. Comput. Fluid Dyn. 1995, 4, 57–71. [Google Scholar] [CrossRef]
- Krier, H.; Rajan, S.; Van Tassell, W.F. Flame-spreading and combustion in packed beds of propellant grains. AIAA J. 1976, 14, 301–309. [Google Scholar] [CrossRef]
- Lax, P.; Wendroff, B. Systems of conservation laws. Commun. Pure Appl. Math. 1969, 13, 217–237. [Google Scholar] [CrossRef]
- Baer, M.R.; Nunziato, J.W. A two-phase mixture theory for the deflagration-to-detonation transition (ddt) in reactive granular materials. Int. J. Multiph. Flow 1986, 12, 861–889. [Google Scholar] [CrossRef]
- Butler, P.B.; Krier, H. Analysis of deflagration to detonation transition in high-energy solid propellants. Combust. Flame 1986, 63, 31–48. [Google Scholar] [CrossRef]
- Verwer, J.G.; Sanz-Serna, J.M. Convergence of method of lines approximations to partial differential equations. Computing 1984, 33, 297–313. [Google Scholar] [CrossRef]
- Schiesser, W.E.; Griffiths, G.W. A Compendium of Partial Differential Equation Models: Method of Lines Analysis with Matlab; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-0-521-51986-1. [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics—A Practical Introduction; Springer: Berlin, Germany, 2009. [Google Scholar]
- Harten, A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 1983, 49, 357–393. [Google Scholar] [CrossRef]
- García-Cascales, J.R.; Otón-Martínez, R.A.; Velasco, F.J.S.; Vera-García, F.; Bentaib, A.; Meynet, N. Advances in the characterisation of reactive gas and solid mixtures under low pressure conditions. Comput. Fluids 2014, 101, 64–87. [Google Scholar] [CrossRef]
- Velasco, F.J.S.; Otón-Martínez, R.A.; García-Cascales, J.R.; Espín, S.; Meynet, N.; Bentaib, A. Modelling detonation of H2–O2–N2 mixtures in presence of solid particles in 3D scenarios. Int. J. Hydrogen Energy 2016, 41, 17154–17168. [Google Scholar] [CrossRef]
- Liang, D.; Falconer, R.A.; Lin, B. Comparison between TVD-MacCormack and ADI-type solvers of the shallow water equations. Adv. Water Resour. 2006, 29, 1833–1845. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Butler, P.B.; Lembeck, M.F.; Krier, H. Modeling of shock development and transition to detonation initiated by burning in porous propellant beds. Combust. Flame 1982, 46, 75–93. [Google Scholar] [CrossRef]
- Gokhale, S.S.; Krier, H. Modeling of unsteady two-phase reactive flow in porous beds of propellant. Prog. Energy Combust. Sci. 1982, 8, 1–39. [Google Scholar] [CrossRef]
- Rusanov, V.V. Calculation of Interaction of Non-Steady Shockwaves with Obstacles; National Research Council of Canada: Ottawa, ON, Canada, 1962. [Google Scholar]
- Lee, J.K.; Kim, T.K. Application of TVD-McCormack scheme to analysis of dam-break problems. J. Korea Water Resour. Assoc. 2003, 36, 365–374. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).