Energy-Efficient Torque Distribution Optimization for an Omnidirectional Mobile Robot with Powered Caster Wheels
Abstract
:1. Introduction
2. Design and Modelling of the OMR
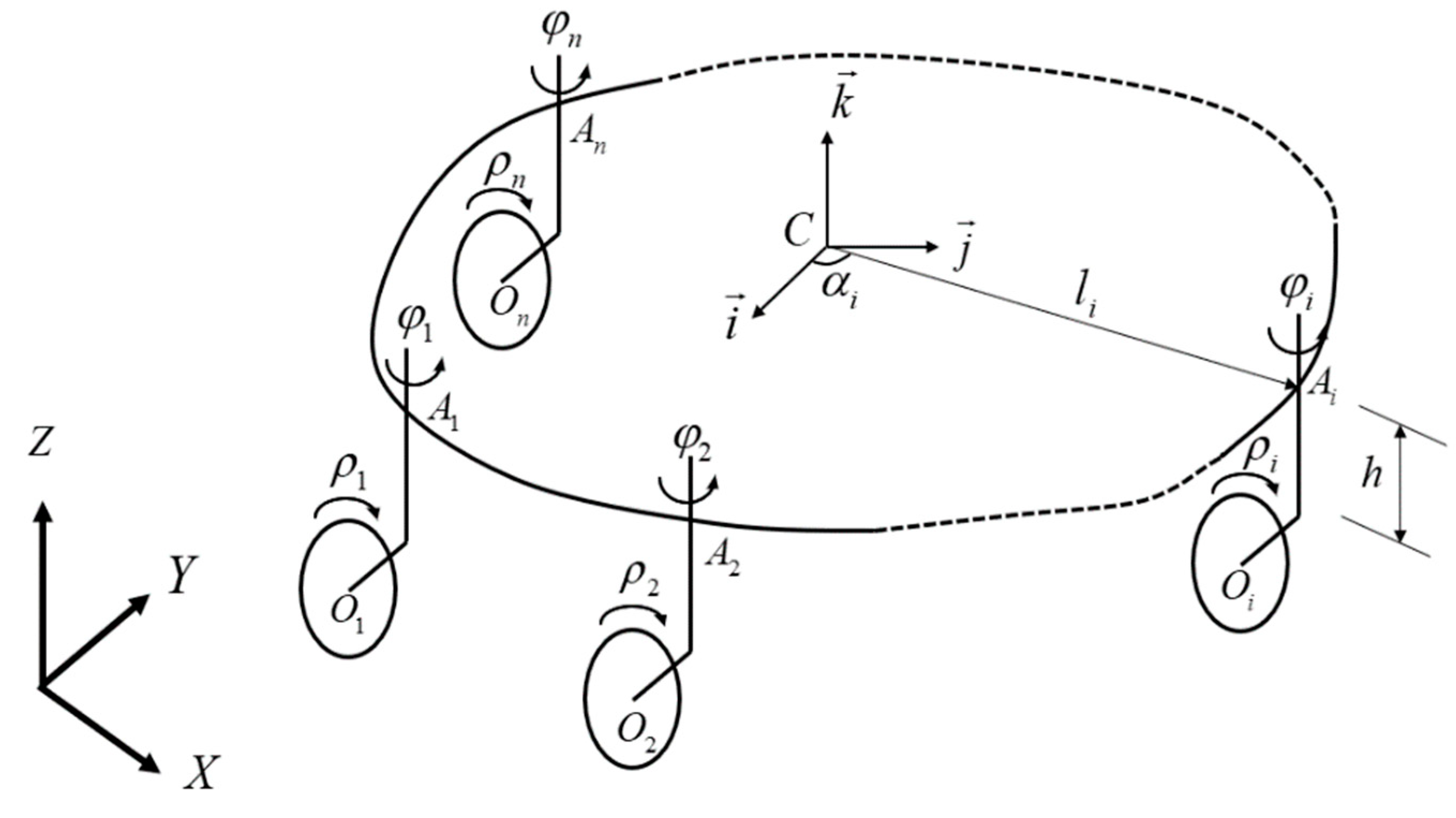
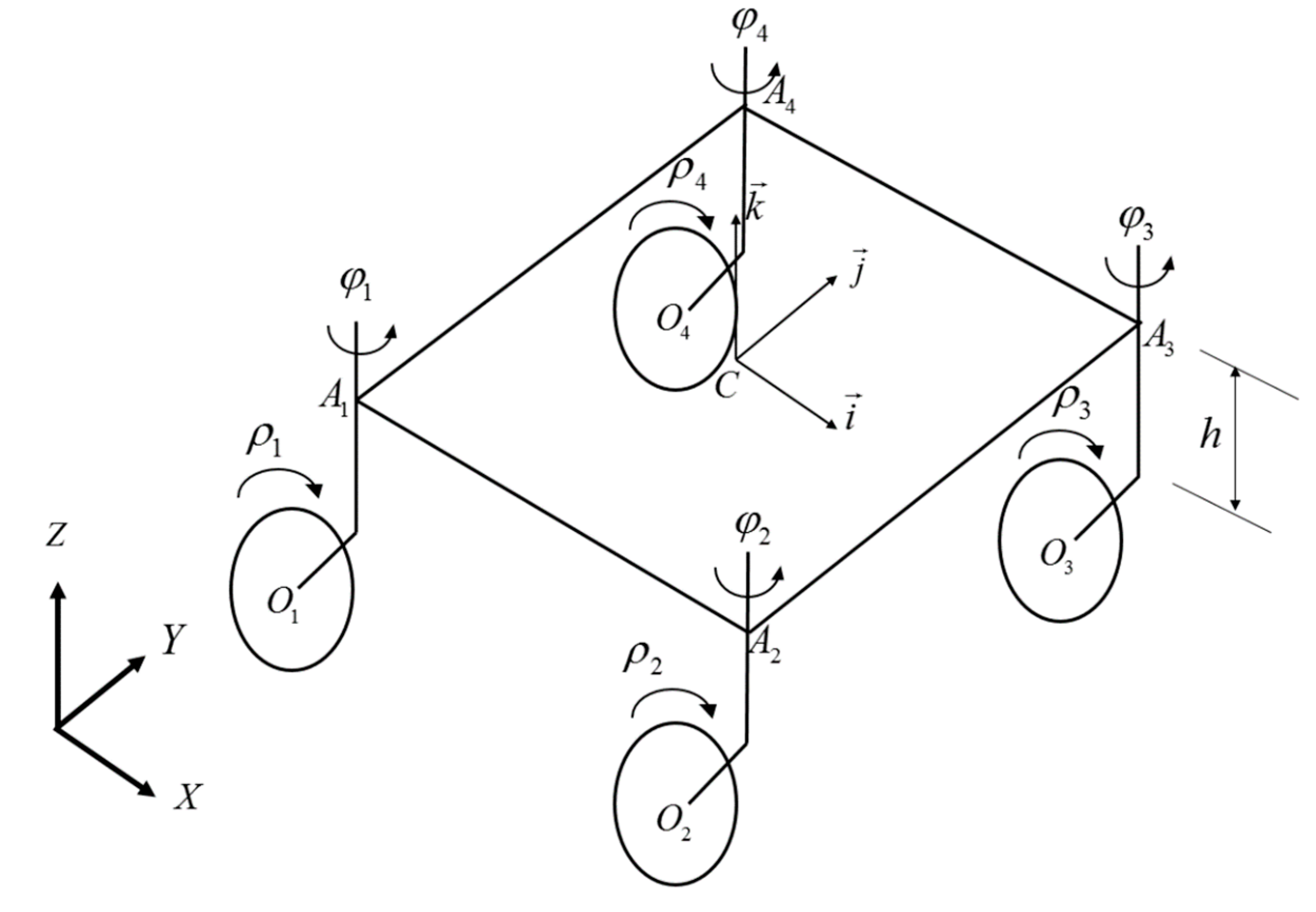
2.1. Kinematic Model of the OMR
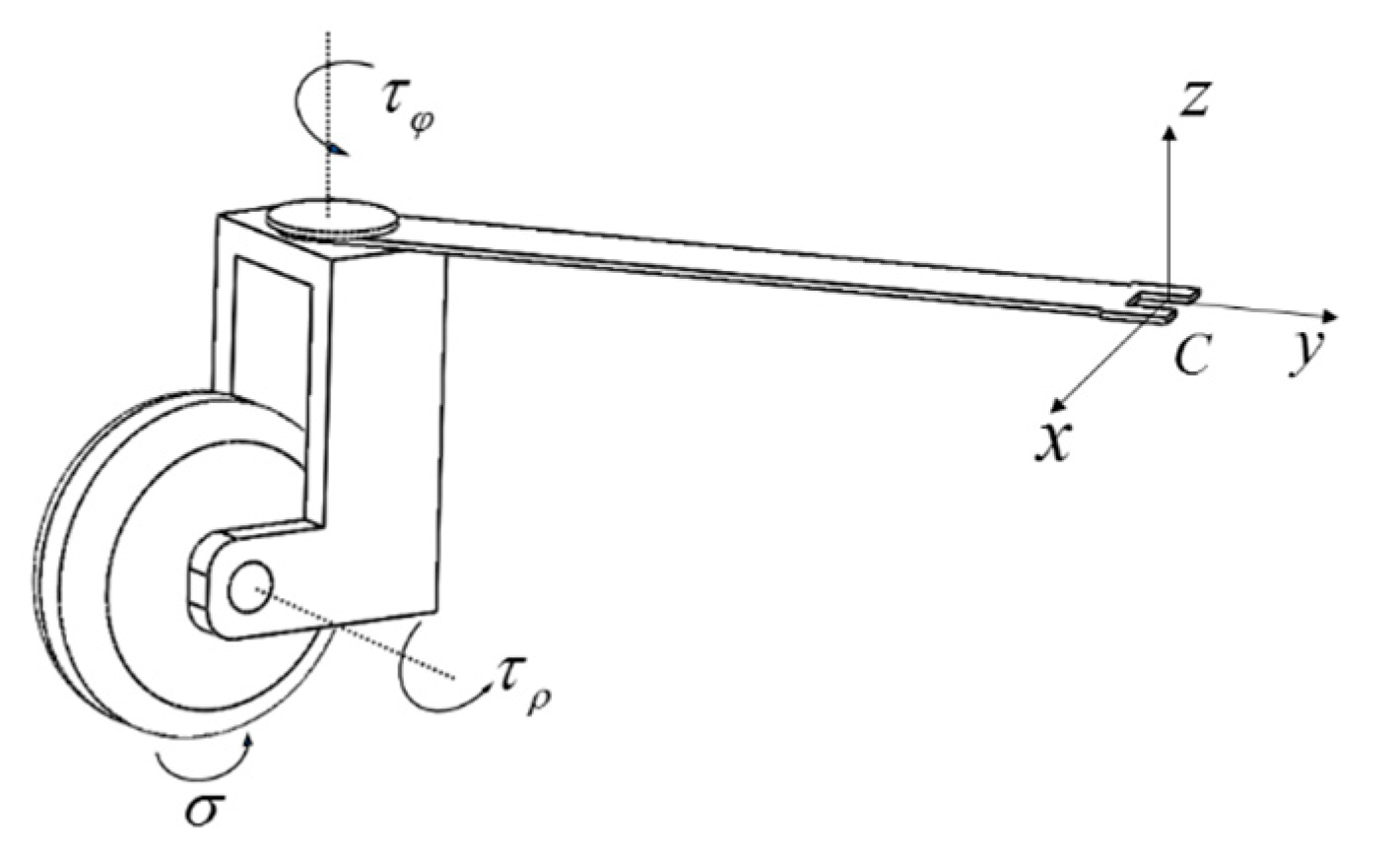
2.2. Joint Space Dynamic Model of the OMR
2.3. Operational Space Dynamic Model of the OMR
3. Energy Consumption Model of the OMR
4. Torque Distribution Schemes for the OMR
4.1. Torque Distribution Schemes Resulting from the Generalized Inverse of the Jacobian
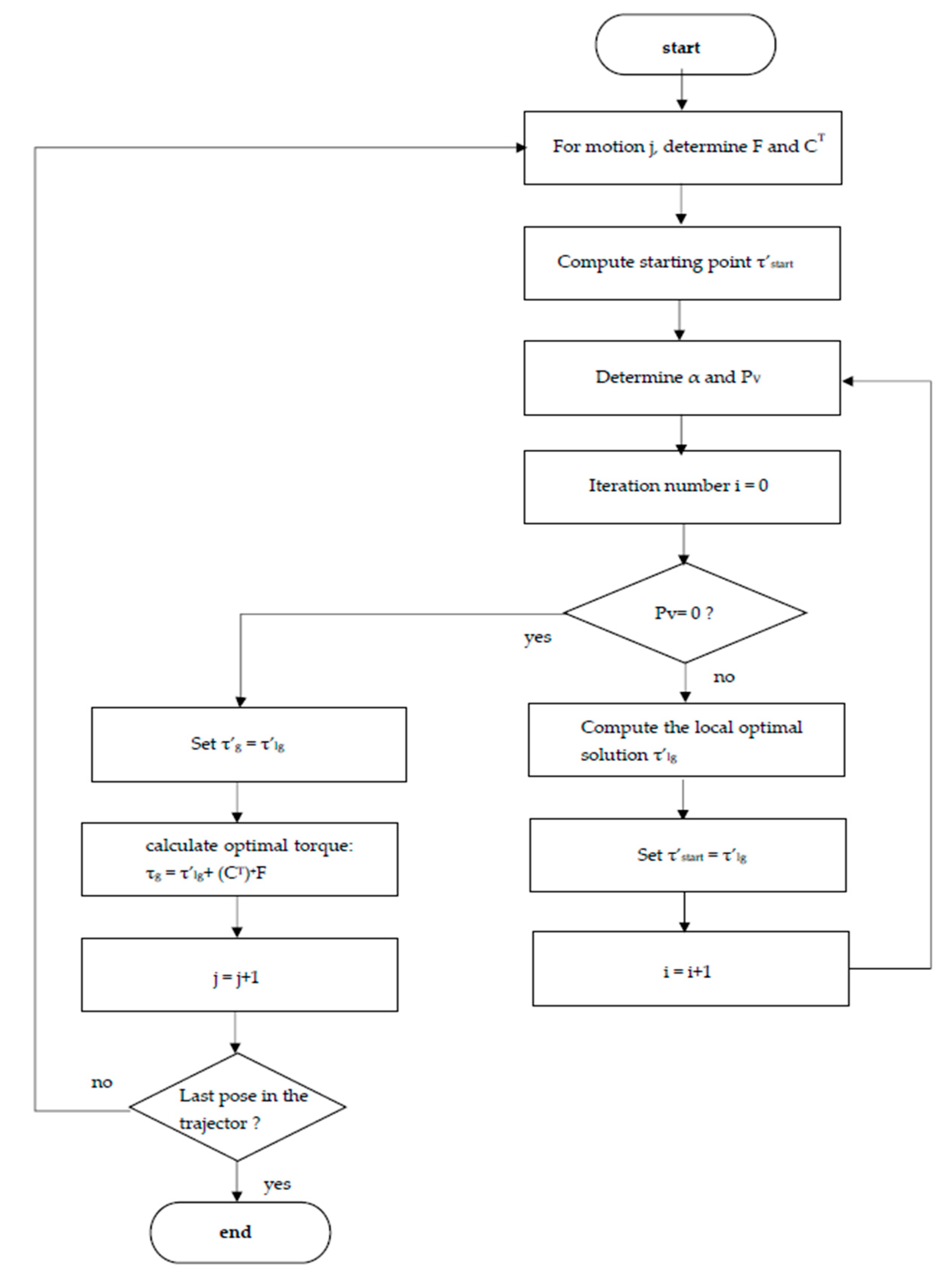
4.2. Gradient Projection-Based Torque Optimization
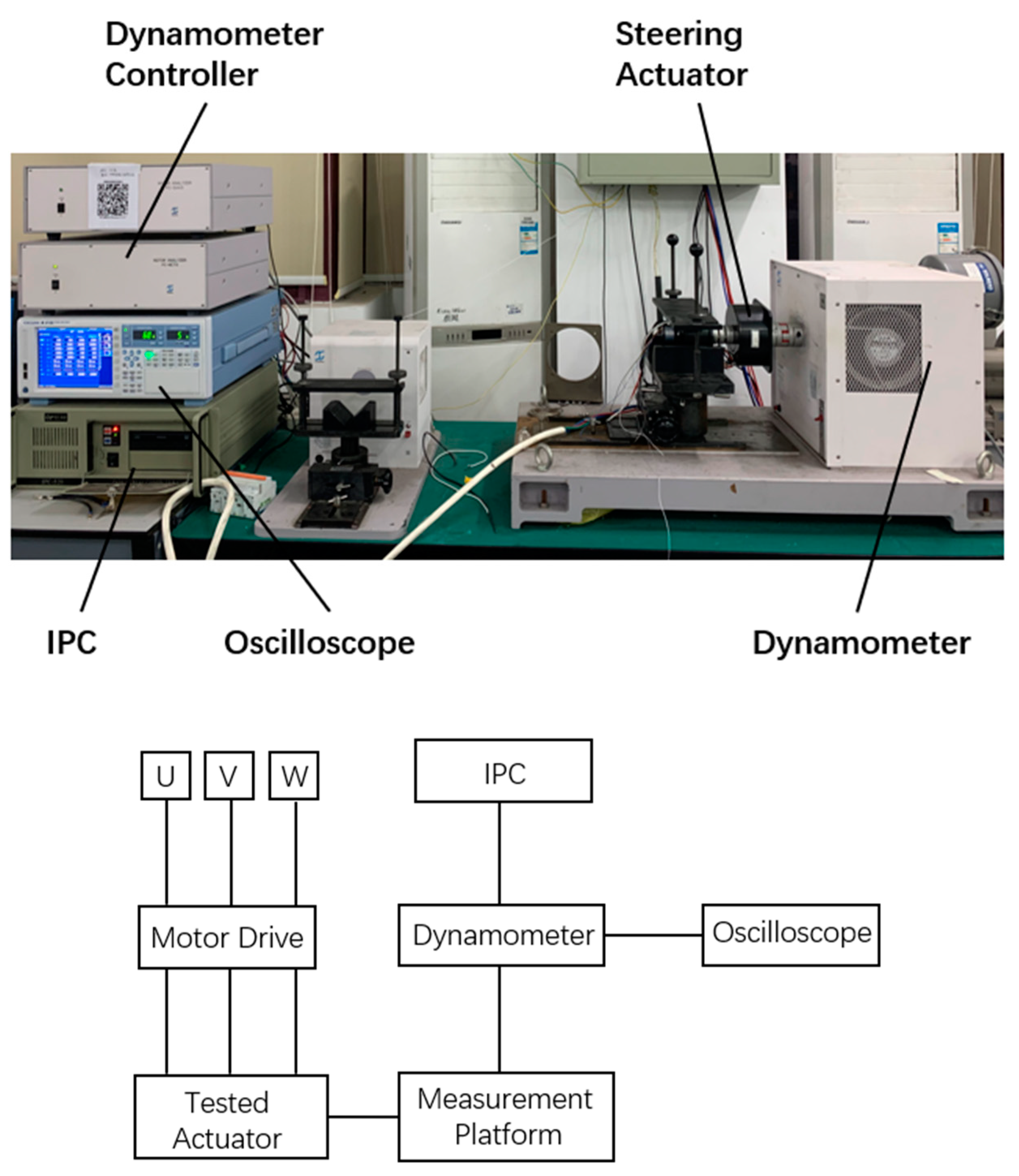
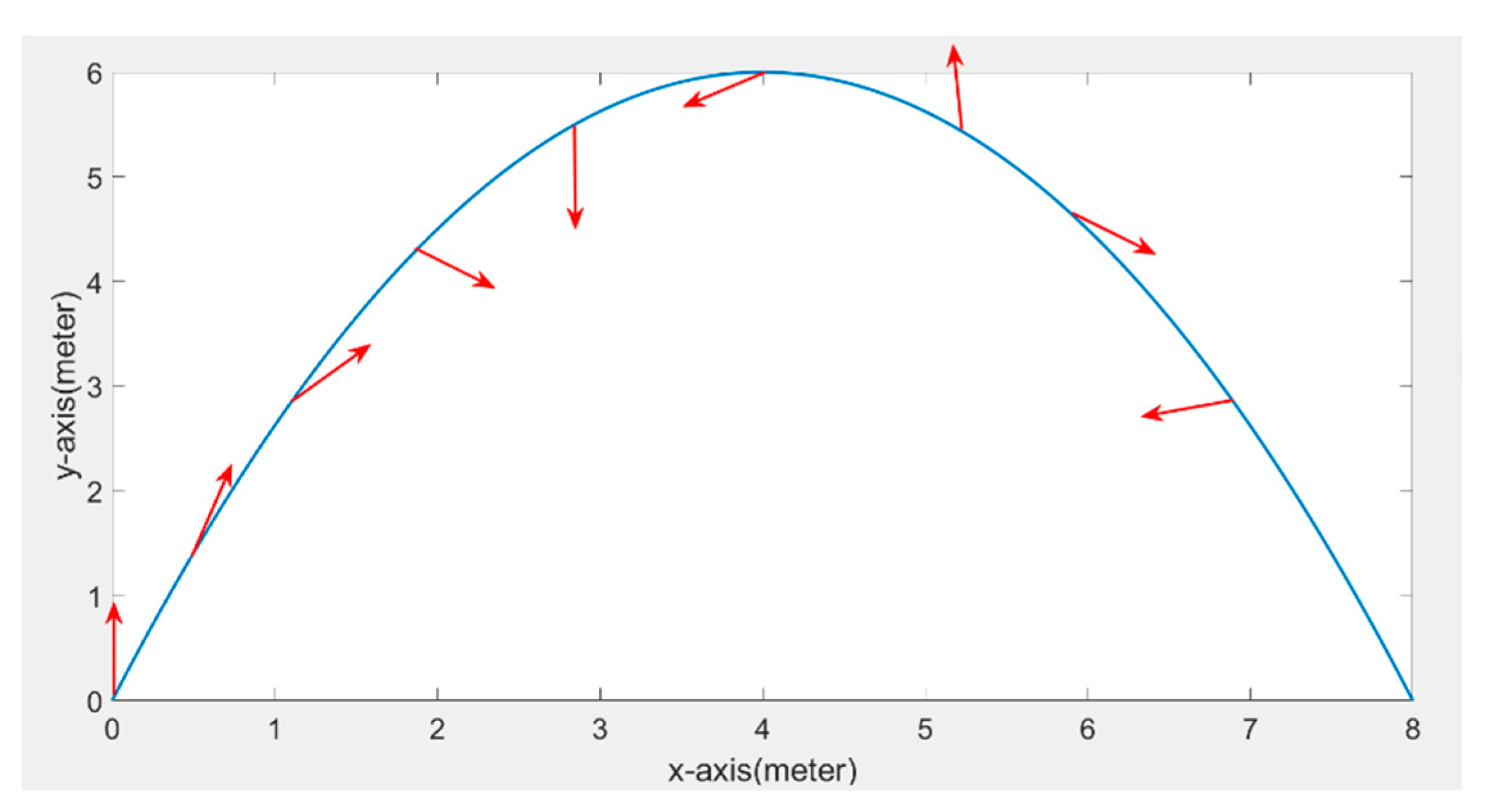
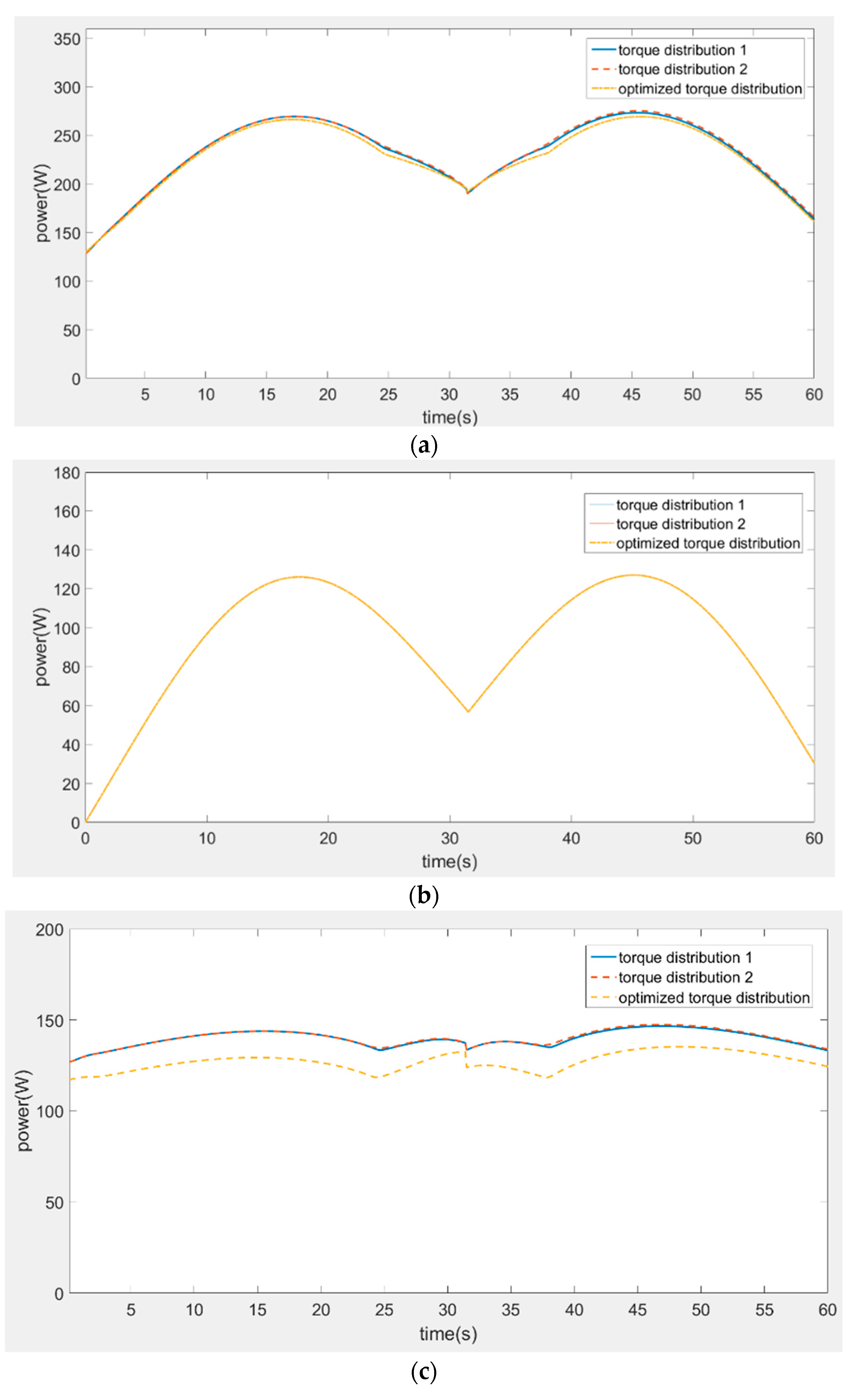
5. Simulation Examples and Results Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Yang, G.; Li, Y.; Lim, T.M.; Lim, C.W. Decoupled powered caster wheel for omnidirectional mobile platforms. In Proceedings of the 2014 IEEE 9th Conference on Industrial Electronics and Applications (ICIEA), Hangzhou, China, 9–11 June 2014; pp. 954–959. [Google Scholar]
- Holmberg, R.; Khatib, O. A powered-caster holonomic robotic vehicle for mobile manipulation tasks. In Romansy 13; Springer: Berlin, Germany, 2000; pp. 157–167. [Google Scholar]
- Canfield, S.L.; Hill, T.W.; Zuccaro, S.G. Prediction and Experimental Validation of Power Consumption of Skid-Steer Mobile Robots in Manufacturing Environments. J. Intell. Robot. Syst. 2018, 94, 1–15. [Google Scholar] [CrossRef]
- Shen, P.; Zhang, X.; Fang, Y. Complete and Time-Optimal Path-Constrained Trajectory Planning with Torque and Velocity Constraints: Theory and Applications. IEEE/ASME Trans. Mechatron. 2018, 23, 735–746. [Google Scholar] [CrossRef]
- Shuang, L.; Dong, S. Minimizing Energy Consumption of Wheeled Mobile Robots via Optimal Motion Planning. IEEE/ASME Trans. Mechatron. 2014, 19, 401–411. [Google Scholar]
- Xie, L.; Henkel, C.; Stol, K.; Xu, W. Power-minimization and energy-reduction autonomous navigation of an omnidirectional Mecanum robot via the dynamic window approach local trajectory planning. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418754563. [Google Scholar] [CrossRef]
- Haidegger, T.; Kovács, L.; Precup, R.-E.; Benyó, B.; Benyó, Z.; Preitl, S. Simulation and control for telerobots in space medicine. Acta Astronaut. 2012, 81, 390–402. [Google Scholar] [CrossRef]
- Kim, H.; Kim, B.K. Minimum-energy trajectory planning and control on a straight line with rotation for three-wheeled omni-directional mobile robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots & Systems, Vilamoura, Portugal, 7–12 October 2012. [Google Scholar]
- Seok, S.; Wang, A.; Chuah, M.Y.; Hyun, D.J.; Lee, J.; Otten, D.M.; Lang, J.H.; Kim, S.; Chuah, M.Y.M. Design Principles for Energy-Efficient Legged Locomotion and Implementation on the MIT Cheetah Robot. IEEE/ASME Trans. Mechatron. 2015, 20, 1117–1129. [Google Scholar] [CrossRef]
- Hou, L.; Zhang, L.; Kim, J. Energy Modeling and Power Measurement for Mobile Robots. Energies 2018, 12, 27. [Google Scholar] [CrossRef]
- Xu, W.; Liu, H.; Liu, J.; Zhou, Z.; Pham, D.T. A Practical Energy Modeling Method for Industrial Robots in Manufacturing. 2016. Available online: https://link.springer.com/chapter/10.1007%2F978-3-319-61994-1_3 (accessed on 15 August 2019).
- Verstraten, T.; Furnemont, R.; Mathijssen, G.; Vanderborght, B.; Lefeber, D. Energy Consumption of Geared DC Motors in Dynamic Applications: Comparing Modeling Approaches. IEEE Robot. Autom. Lett. 2017, 1, 524–530. [Google Scholar] [CrossRef]
- Laopoulos, T.; Neofotistos, P.; Kosmatopoulos, C.; Nikolaidis, S. Measurement of current variations for the estimation of software-related power consumption [embedded processing circuits]. IEEE Trans. Instrum. Meas. 2003, 52, 1206–1212. [Google Scholar] [CrossRef]
- Roennau, A.; Sutter, F.; Kerscher, T.; Dillmann, R. On-Board Energy Consumption Estimation for a Six-Legged Walking Robot. 2015. Available online: https://www.worldscientific.com/doi/abs/10.1142/9789814374286_0064 (accessed on 15 August 2019).
- Holmberg, R. Design and Development of Powered-Caster Holonomic Mobile Robots; Stanford University: Stanford, CA, USA, 2000. [Google Scholar]
- Holmberg, R.; Khatib, O. Development and control of a holonomic mobile robot for mobile manipulation tasks. Int. J. Robot. Res. 2000, 19, 1066–1074. [Google Scholar] [CrossRef]
- Li, Y.P.; Oetomo, D.; Ang, M.H.; Lim, C.W. Torque distribution and slip minimization in an omnidirectional mobile base. In Proceedings of the International Conference on Advanced Robotics, Seattle, WA, USA, 18–20 July 2005. [Google Scholar]
- Yong, L.; Jia, Y.; Ning, X. Dynamic model and adaptive tracking controller for 4-Powered Caster Vehicle. In Proceedings of the IEEE International Conference on Robotics & Automation, Anchorage, AK, USA, 3–8 May 2010. [Google Scholar]
- Zhao, D.; Deng, X.; Yi, J. Motion and internal force control for omnidirectional wheeled mobile robots. IEEE/ASME Trans. Mechatron. 2009, 14, 382–387. [Google Scholar] [CrossRef]
- Campion, G.; Dandrea-Novel, B.; Bastin, G. Structural properties and classification of kinematic and dynamic models of wheeled mobile robots. IEEE Trans. Robot. Autom. 1996, 12, 47–62. [Google Scholar] [CrossRef]
- Chang, K.-S.; Holmberg, R.; Khatib, O. The augmented object model: Cooperative manipulation and parallel mechanism dynamics. In Proceedings of the 2000 IEEE International Conference on Robotics and Automation (ICRA′00), San Francisco, CA, USA, 24–28 April 2000; Volume 1, pp. 470–475. [Google Scholar]
- Halevi, Y.; Carpanzano, E.; Montalbano, G.; Koren, Y. Minimum energy control of redundant actuation machine tools. CIRP Ann. 2011, 60, 433–436. [Google Scholar] [CrossRef]
- Martin, B.; Bobrow, J. Minimum-Effort Motions for Open-Chain Manipulators with Task-Dependent End-Effector Constraints. Int. J. Robot. Res. 1999, 18, 213–224. [Google Scholar] [CrossRef]
- Lee, G.; Park, S.; Lee, D.; Park, F.C.; Jeong, J.I.; Kim, J. Minimizing Energy Consumption of Parallel Mechanisms via Redundant Actuation. IEEE/ASME Trans. Mechatron. 2015, 20, 2805–2812. [Google Scholar] [CrossRef]
- Drofenik, U.; Kolar, J.W. A general scheme for calculating switching-and conduction-losses of power semiconductors in numerical circuit simulations of power electronic systems. In Proceedings of the IPEC, Toki Messe, Japan, 4–8 April 2005; Volume 5, pp. 4–8. [Google Scholar]
- Dubey, R.V.; Euler, J.A.; Babcock, S.M. Real-time implementation of an optimization scheme for seven-degree-of-freedom redundant manipulators. IEEE Trans. Robot. Autom. 1991, 7, 579–588. [Google Scholar] [CrossRef]
- Li, L.; Gruver, W.A.; Zhang, Q.; Yang, Z. Kinematic control of redundant robots and the motion optimizability measure. IEEE Trans. Syst. Man Cybern. Part B. 2001, 31, 155–160. [Google Scholar] [CrossRef] [PubMed]


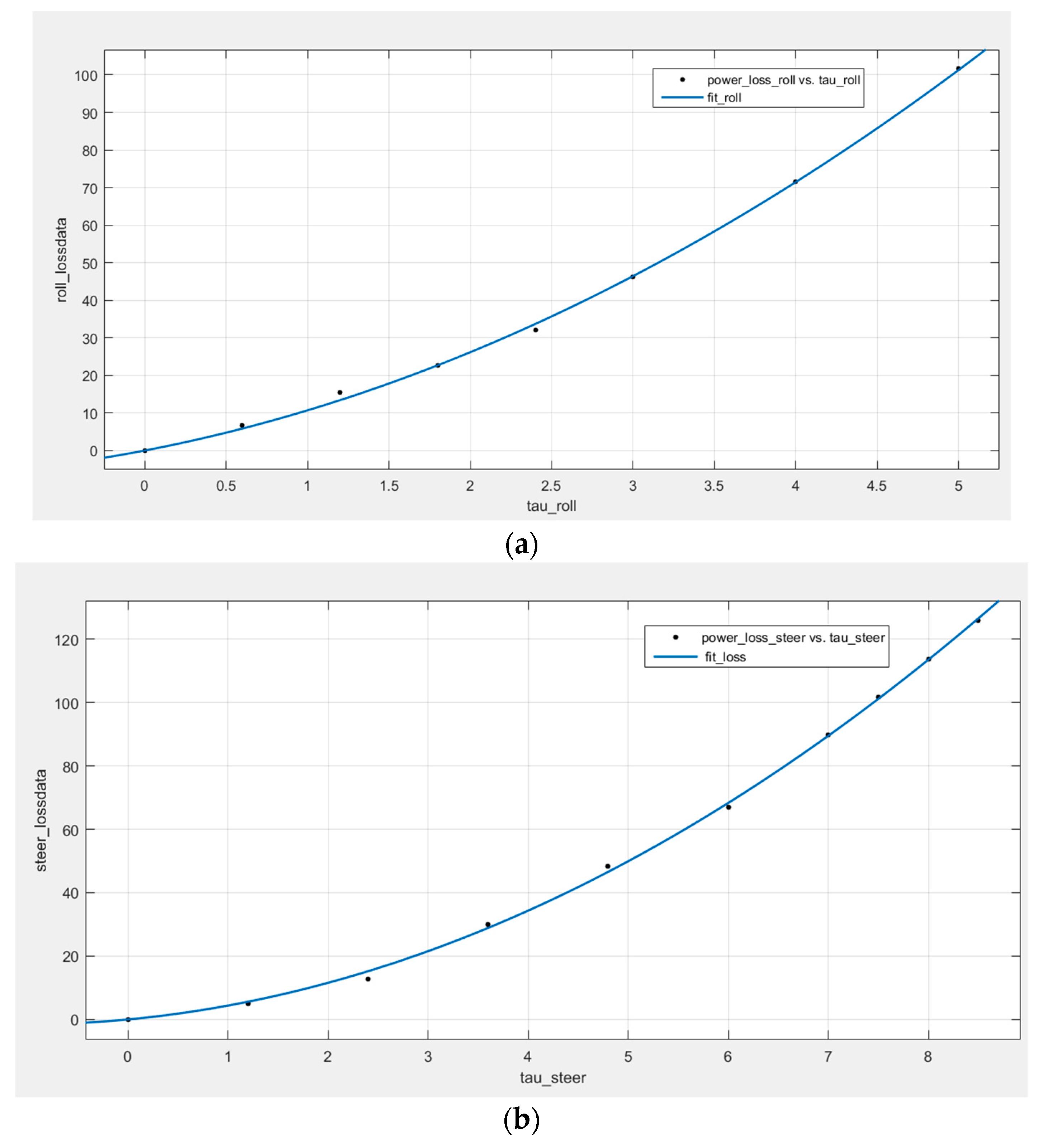

| Class of Actuators | ||
|---|---|---|
| Steering actuator | 2.98 | 1.40 |
| Rolling actuator | 3.39 | 2.31 |
| Torque Distribution Scheme | Energy Loss (Joule) | Energy Consumption (Joule) |
|---|---|---|
| Optimized torque distribution | 7.24 × 103 | 1.26 × 104 |
| Torque distribution 1 | 8.37 × 103 | 1.38 × 104 |
| Torque distribution 2 | 8.39 × 103 | 1.39 × 104 |
| Starting Point | [1,1,1,1,1,1,1,1]T (An Arbitrary Choice) | Pseudo-Inverse Solution | Proposed Method |
|---|---|---|---|
| Average number of iterations per step | 79.24 | 19.57 | 4.86 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, W.; Yang, G.; Wang, C.; Zhang, C.; Chen, C.; Fang, Z. Energy-Efficient Torque Distribution Optimization for an Omnidirectional Mobile Robot with Powered Caster Wheels. Energies 2019, 12, 4417. https://doi.org/10.3390/en12234417
Jia W, Yang G, Wang C, Zhang C, Chen C, Fang Z. Energy-Efficient Torque Distribution Optimization for an Omnidirectional Mobile Robot with Powered Caster Wheels. Energies. 2019; 12(23):4417. https://doi.org/10.3390/en12234417
Chicago/Turabian StyleJia, Wenji, Guilin Yang, Chongchong Wang, Chi Zhang, Chinyin Chen, and Zaojun Fang. 2019. "Energy-Efficient Torque Distribution Optimization for an Omnidirectional Mobile Robot with Powered Caster Wheels" Energies 12, no. 23: 4417. https://doi.org/10.3390/en12234417
APA StyleJia, W., Yang, G., Wang, C., Zhang, C., Chen, C., & Fang, Z. (2019). Energy-Efficient Torque Distribution Optimization for an Omnidirectional Mobile Robot with Powered Caster Wheels. Energies, 12(23), 4417. https://doi.org/10.3390/en12234417






