Robust Design Optimization of Electromagnetic Actuators for Renewable Energy Systems Considering the Manufacturing Cost
Abstract
:1. Introduction
2. Models of Robust Design Optimization
2.1. Average Total Loss Model
2.2. Fluctuation Contribution Rate Model
2.3. Cost Contribution Rate Model
2.4. Robust Optimization Model
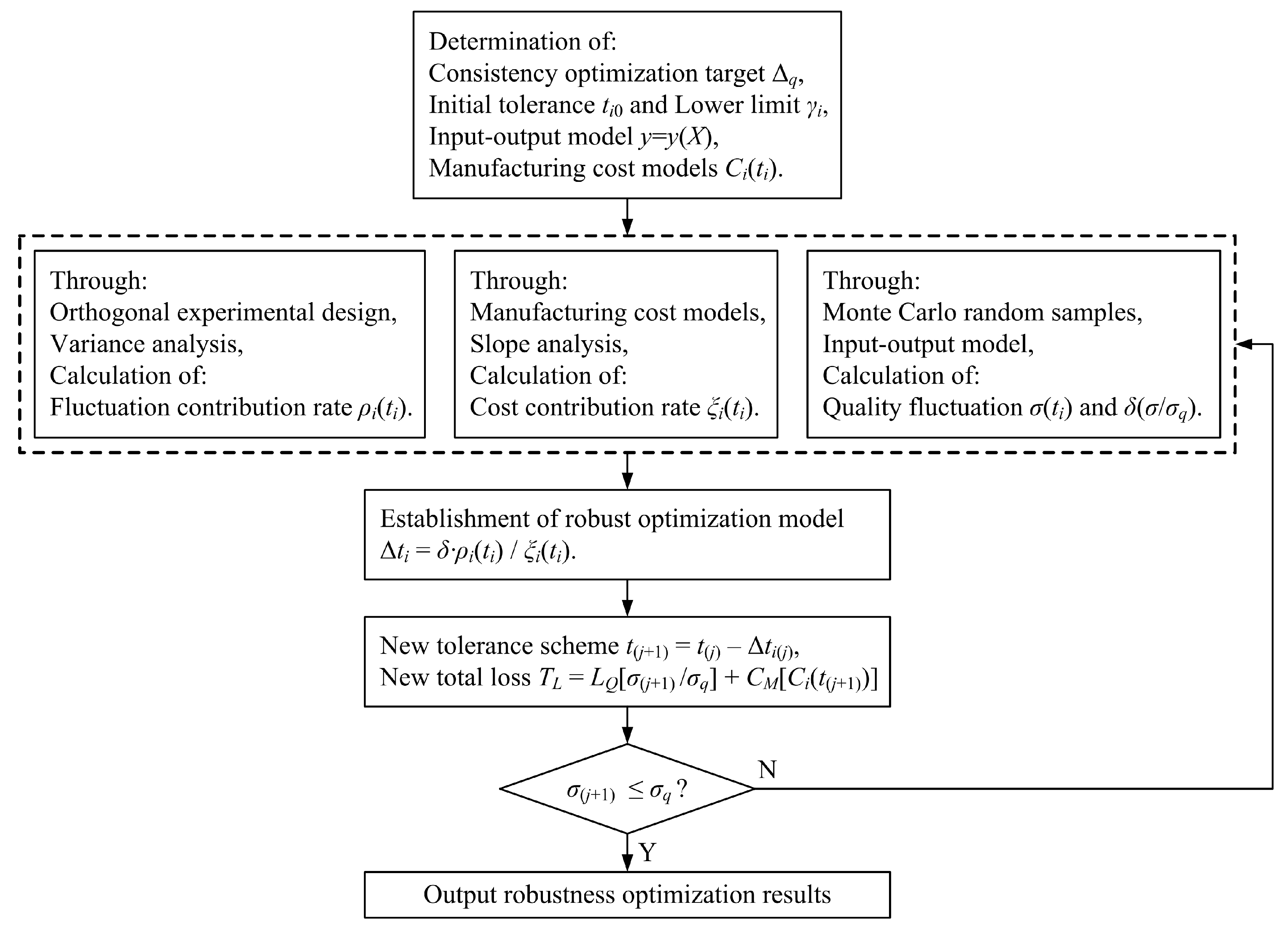
3. Procedure of Robust Design Optimization
4. Case Study
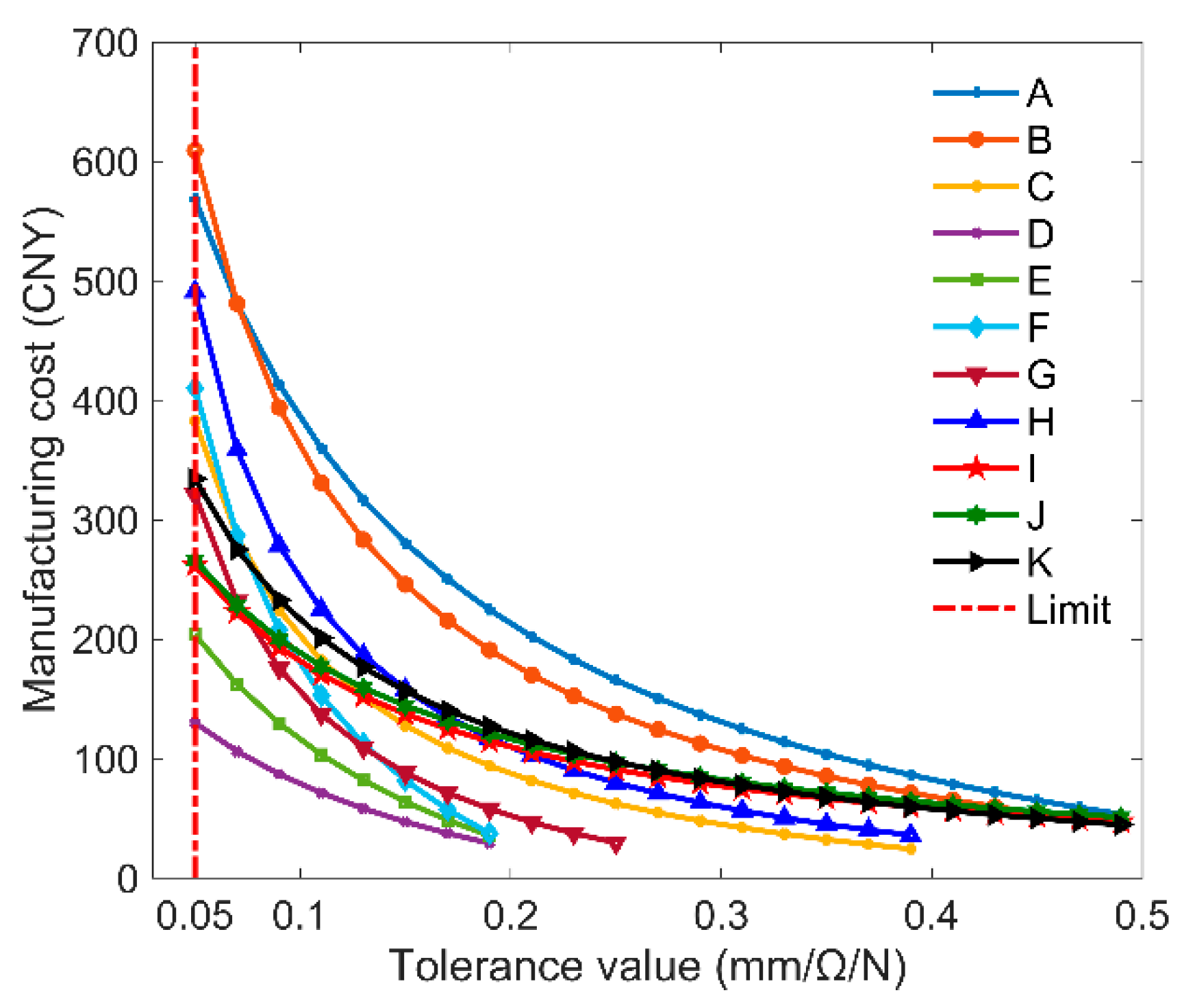
4.1. Manufacturing Cost Models
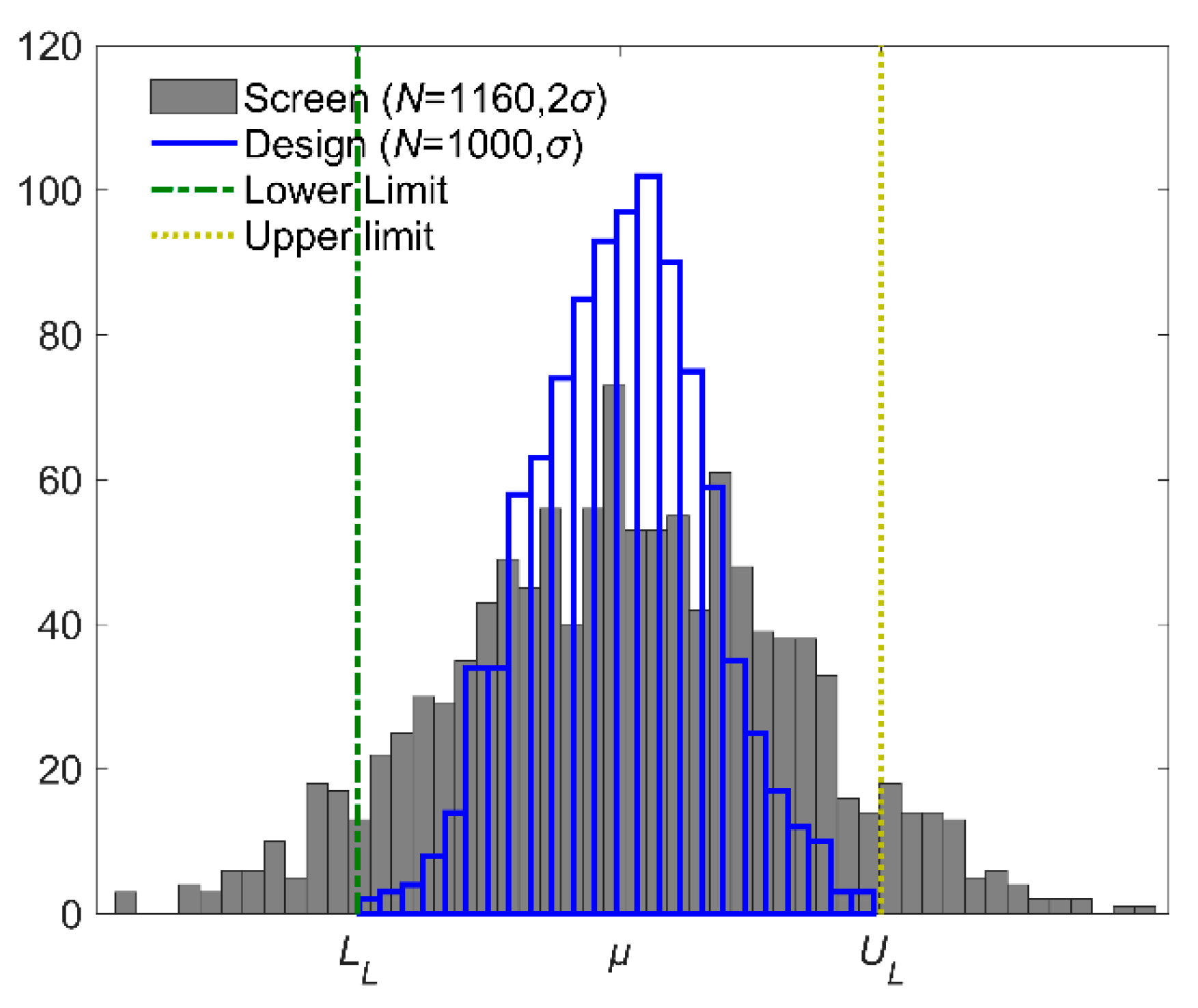
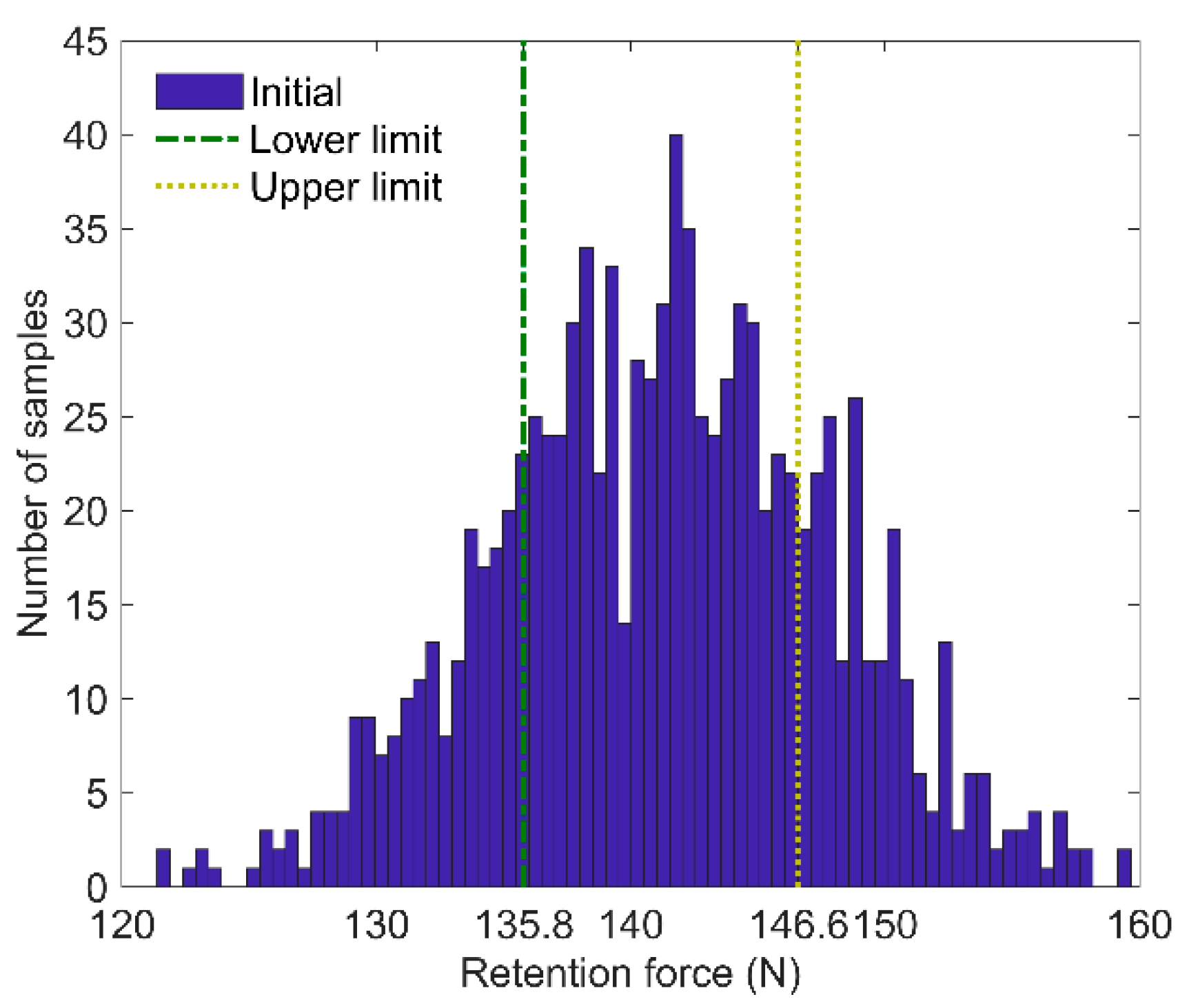
4.2. Initial Total Lost
4.3. Robust Optimization Model
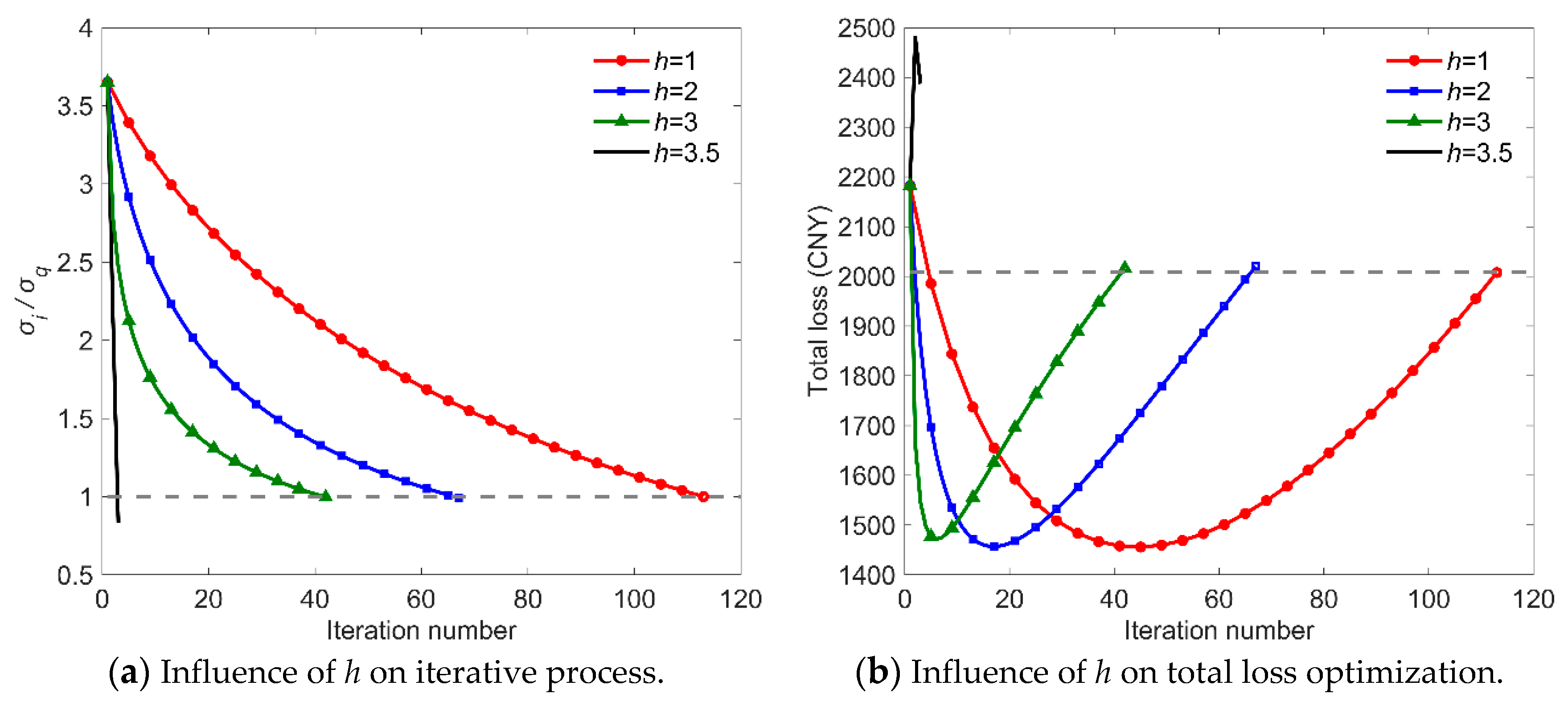
4.4. Consistency Optimization Results
5. Conclusions
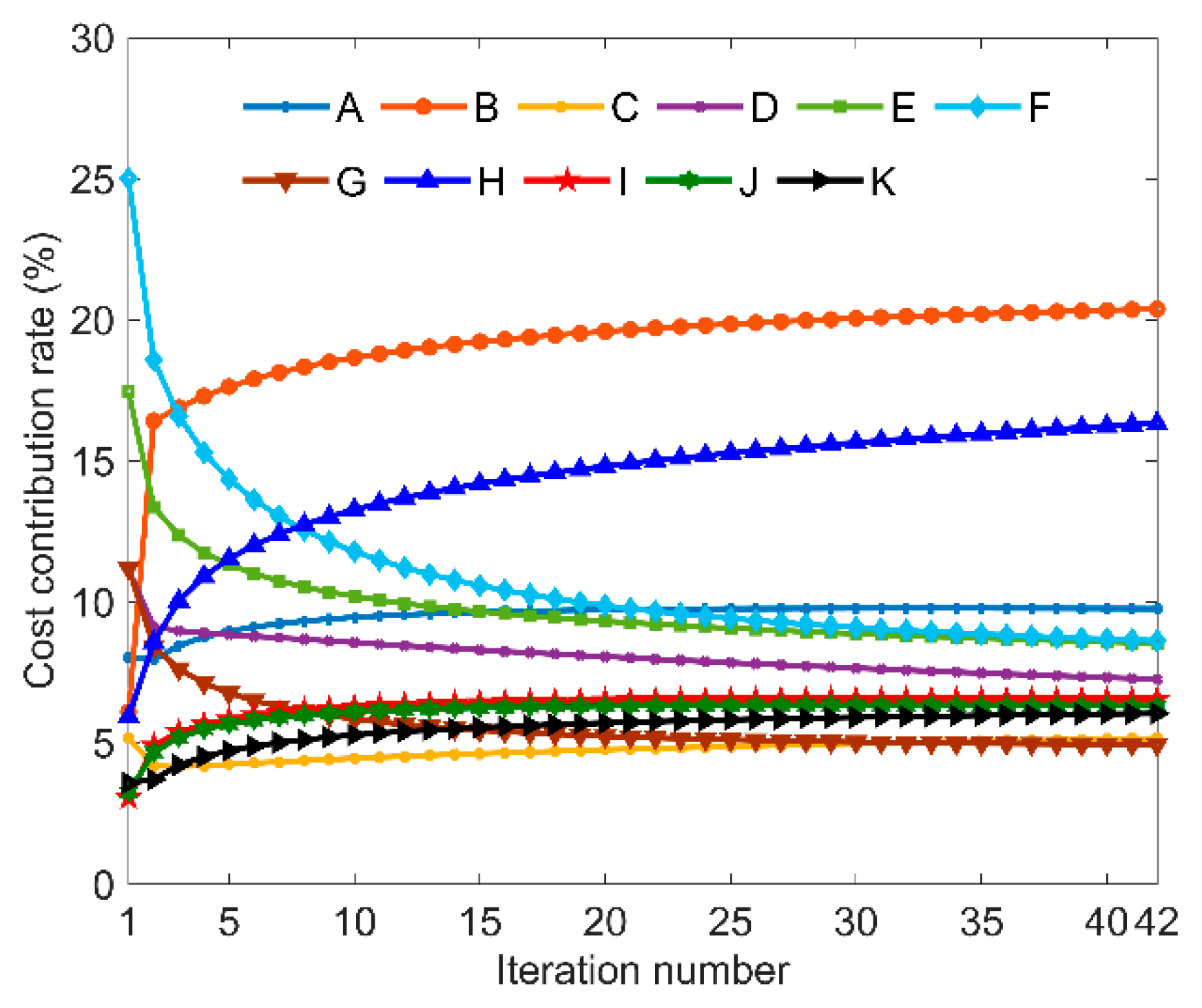
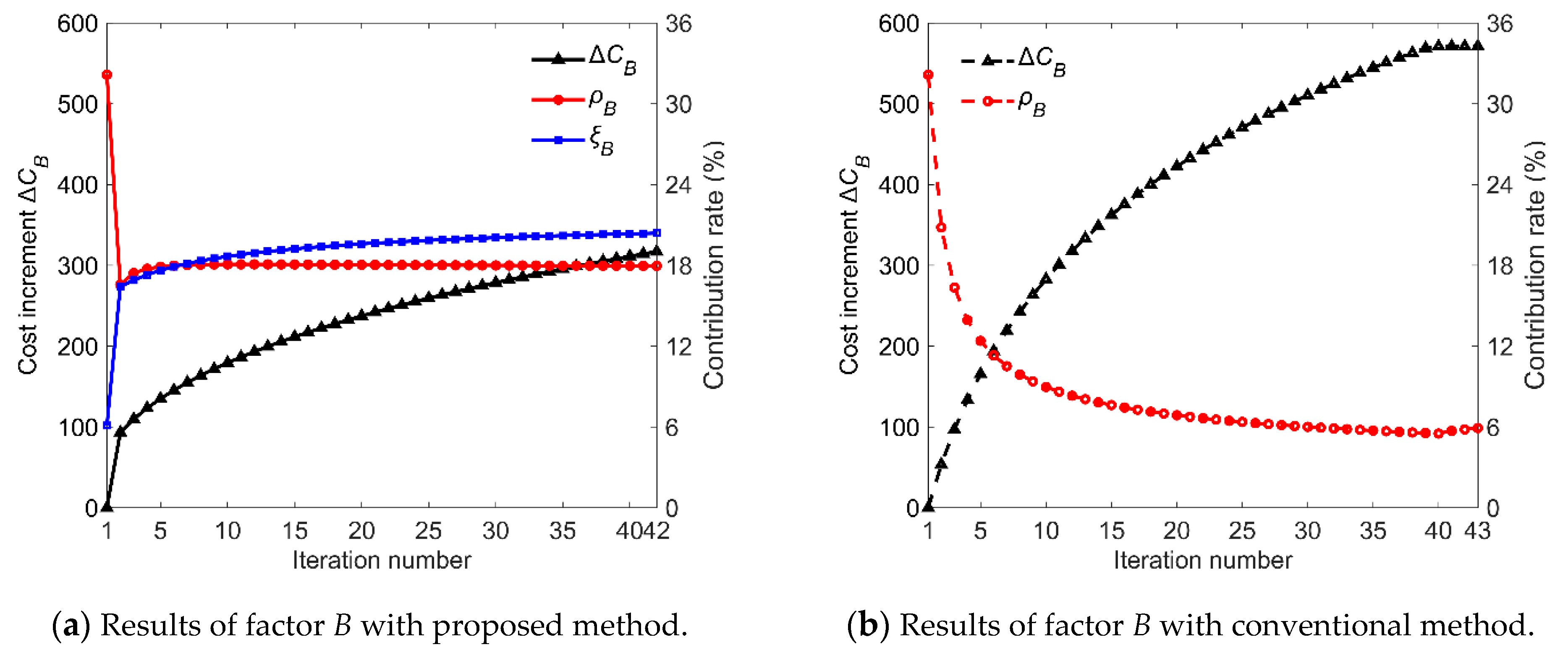
- By using the established robust optimization model combining fluctuation contribution rate and cost contribution rate, the impact of tolerance values on quality loss and manufacturing cost can be considered simultaneously to guide the tolerance optimization process. The downward trend of fluctuation contribution rate of factor B is limited effectively by its rapid increase of cost contribution rate, so the cost increment of this factor has been reduced by 254 (80%). Meanwhile, the cost of factor C is only increased by 13.8 (11%) to reduce the quality loss.
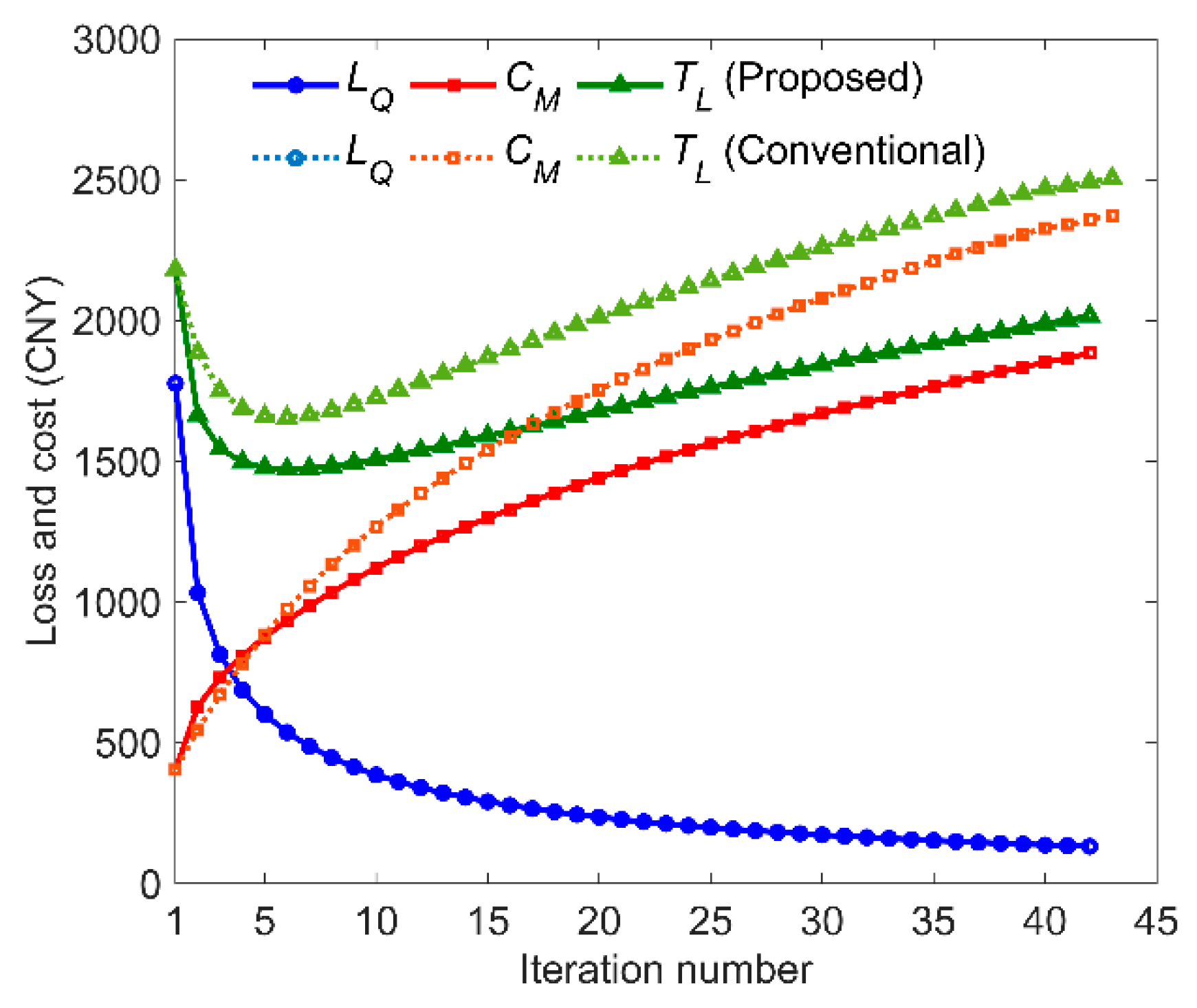
- It is easy to find an effective solution for singly reducing the total loss, but it is a complicated optimization problem to reduce the total loss while improving the consistency to achieve the optimization objective. Through the novel optimization procedure for robust design, the quality loss LQ is reduced accurately to the optimization target, while the increment of manufacturing cost ΔCM is 33% less than that of conventional method.
- After the robust design with proposed method, the error of consistency optimization is 0.3%, and the inherent reliability of contactor is increased from 0.5889 to 0.9973(increased by 69.35%), thereby greatly improving the application reliability of the product in the renewable energy system.
- The method proposed in this paper is based on experimental design, and the input–output relationship model is not necessary, so it is universal for non-linear and high-order explicit/implicit functions in many fields. It should be noted that the form of robust optimization model and its coefficient are all based on experience. Meanwhile, when establishing the manufacturing cost models, a unified model is adopted for all the factors to simplify the optimization process. The above assumption and simplification may affect the efficiency and accuracy when applying this method to other optimization problems, but the error can be reduced through further research and improved according to practical applications.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| List of Symbols | Description |
| TL | Average total loss (CNY) |
| LQ | Average quality loss (CNY) |
| CM | Average manufacturing cost (CNY) |
| y | Output response |
| m | Central value of design |
| X = {x1, …, xn} | Input variables |
| Τ = {t1, …, tn} | Tolerance values of input variables |
| L(y) | Quality loss |
| k | Coefficient in quality loss function |
| ±Δq | Qualified threshold |
| A | Economic loss of unqualified product (CNY) |
| N | Number of samples of batch products |
| σ | Standard deviation of output response distribution |
| σq | Standard deviation of consistency optimization objective |
| Ci | Manufacturing cost corresponding to each input tolerance ti (CNY) |
| αi1~αi3 | Constant coefficients in manufacturing cost model |
| ρi | Fluctuation contribution rate (%) |
| Li | Quality loss caused by input tolerance ti (CNY) |
| e | Noise or error observed in the output response y |
| ρe | Fluctuation contribution rate of error (%) |
| ρil | Monomial contribution rate of input tolerance ti (%) |
| ρiq | Quadratic contribution rate of input tolerance ti (%) |
| ST | Sum of the total deviation square of output response y |
| Ve | Error variance |
| T1i, T2i, T3i | The sub-sum of the experiment results y corresponding to 3 levels of xi |
| r | Repetition number of the same level of xi |
| ξi | Cost contribution rate (%) |
| ΔCi | Cost increment corresponding to each input tolerance ti (CNY) |
| Δti | Tolerance reduction of ti |
| ΔCM | Total increment of manufacturing cost (CNY) |
| κi | Slope of the manufacturing cost function at the tolerance value ti |
| δ | Coefficient in robust optimization model |
| γi | Lower tolerance limit of ti |
| ti0 | Initial tolerance value of ti |
| σ0 | Initial standard deviation of output response y |
| LQ0 | Initial average quality loss (CNY) |
| CM0 | Initial average manufacturing cost (CNY) |
| TL0 | Initial total loss average total loss (CNY) |
| T0 | Initial tolerance values |
| j | Iteration number |
| T(j + 1) | Tolerance values in the (j + 1)th iteration |
| Δti(j) | Tolerance reduction of ti in the jth iteration |
| TL(j + 1) | Average total loss in the (j + 1)th iteration (CNY) |
| σ(j + 1) | Standard deviation of output response in the (j + 1)th iteration |
References
- Astaneh, M.; Roshandel, R.; Dufo-Lopez, R.; Bernal-Agustin, J.L. A novel framework for optimization of size and control strategy of lithium-ion battery based off-grid renewable energy systems. Energy Convers. Manag. 2018, 175, 99–111. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Ma, H.; Zhang, J.; Peng, Q. Multi-objective optimization of charging patterns for lithium-ion battery management. Energy Convers. Manag. 2018, 159, 151–162. [Google Scholar] [CrossRef]
- Chen, K.D.; Zhao, F.Q.; Hao, H.; Liu, Z.W. Synergistic impacts of China’s subsidy policy and new energy vehicle credit regulation on the technological development of battery electric vehicles. Energies 2018, 11, 3193. [Google Scholar] [CrossRef]
- Yao, J.W.; Zhang, Y.M.; Yan, Z.; Li, L. A group approach of smart hybrid poles with renewable energy, street lighting and EV charging based on DC micro-grid. Energies 2018, 11, 3445. [Google Scholar] [CrossRef]
- Da Luz, C.M.A.; Tofoli, F.L.; Vicente, P.D.S.; Vicente, E.M. Assessment of the ideality factor on the performance of photovoltaic modules. Energy Convers. Manag. 2018, 167, 63–69. [Google Scholar] [CrossRef]
- Merchaoui, M.; Sakly, A.; Mimouni, M.F. Particle swarm optimisation with adaptive mutation strategy for photovoltaic solar cell/module parameter extraction. Energy Convers. Manag. 2018, 175, 151–163. [Google Scholar] [CrossRef]
- Schuëller, G.I.; Jensen, H.A. Computational methods in optimization considering uncertainties—An overview. Comput. Methods Appl. Mech. Energy 2008, 198, 2–13. [Google Scholar] [CrossRef]
- Tang, L.C.; Goh, T.N.; Lam, S.W.; Zhang, C.W. Fortification of six sigma: Expanding the DMAIC toolset. Qual. Reliab. Eng. Int. 2007, 23, 3–18. [Google Scholar] [CrossRef]
- Nilsen, T.; Aven, T. Models and model uncertainty in the context of risk analysis. Reliab. Eng. Syst. Saf. 2003, 79, 309–317. [Google Scholar] [CrossRef]
- Pedersen, S.N.; Christensen, M.E.; Howard, T.J. Robust design requirements specification: A quantitative method for requirements development using quality loss functions. J. Eng. Des. 2016, 27, 544–567. [Google Scholar] [CrossRef]
- Liu, M.Z.; Liu, C.H.; Xing, L.L.; Mei, F.D.; Zhang, X. Study on a tolerance grading allocation method under uncertainty and quality oriented for remanufactured parts. Int. J. Adv. Manuf. Technol. 2016, 87, 1265–1272. [Google Scholar] [CrossRef]
- Taguchi, G. Quality engineering in Japan. Bull. Jpn. Soc. Precis. Eng. 1985, 19, 237–242. [Google Scholar] [CrossRef]
- Sfantsikopoulos, M.M. A cost-tolerance analytical approach for design and manufacturing. Int. J. Adv. Manuf. Technol. 1990, 5, 126–134. [Google Scholar] [CrossRef]
- Liang, H.M.; Ren, W.B.; Ye, X.R.; Zhai, G.F. Research on the reliability tolerance analysis method of electromagnetic relay in aerospace. Chin. J. Aeronaut. 2005, 18, 65–71. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, T.; Yang, J. A comprehensive review of tolerance analysis models. Int. J. Adv. Manuf. Technol. 2018, 97, 3055–3085. [Google Scholar] [CrossRef]
- Lee, S.; Kim, K.; Cho, S.; Jang, J.; Lee, T.; Hong, J. Optimal design of interior permanent magnet synchronous motor considering the manufacturing tolerances using Taguchi robust design. IET Electr. Power Appl. 2014, 8, 23–28. [Google Scholar] [CrossRef]
- Gao, R.X.K.; Hoefer, W.J.R.; Li, E.P. Quality synthesis based robust optimization for electromagnetic wave absorbers using Taguchi’s tolerance design method. IEEE Trans. Antenn. Propag. 2014, 62, 2102–2108. [Google Scholar] [CrossRef]
- Liang, H.M.; Ye, X.R.; Zhai, G.F. Research on the tolerance distribution of sealed electromagnetic relay with reliability index. IEICE Trans. Electron. 2006, E89-C, 1164–1172. [Google Scholar] [CrossRef]
- Zhai, G.F.; Liang, H.M.; Xu, F.; Liu, M.K. New method of tolerance design of electromagnetic relay reliability. J. Eng. Des. 2004, 15, 425–431. [Google Scholar]
- Shi, J.; Zhong, Z.; Zhu, X. Robust design and optimization for autonomous PV-wind hybrid power systems. J. Zhejiang Univ. Sci. A 2008, 9, 401–409. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.; Hartman, N.W.; Sutherland, J.W. Allocation of assembly tolerances to minimize costs. Cirp. Ann. Manuf. Technol. 2019, 68, 13–16. [Google Scholar] [CrossRef]
- Tsai, J.T. Robust optimal-parameter design approach for tolerance design problems. Eng. Optim. 2010, 42, 1079–1093. [Google Scholar] [CrossRef]
- Douglas, C.M. Stu Hunter’s contributions to experimental design and quality engineering. Qual. Eng. 2014, 26, 5–15. [Google Scholar]
- Deng, J.; Yu, H.D.; Ye, X.R.; Zhai, G.F. Consistency optimization for batch product of electromagnetic relay with improved robust tolerance design method. In Proceedings of the 1st International Conference on Reliability Systems Engineering, Beijing, China, 21–23 October 2015. [Google Scholar]
- Tang, L.C.; Xu, K. A unified approach for dual response surface optimization. J. Qual. Technol. 2002, 34, 437–447. [Google Scholar] [CrossRef]
- Ma, B.; Lei, G.; Zhu, J.G.; Guo, Y.G.; Liu, C.C. Application-oriented robust design optimization method for batch production of permanent-magnet motors. IEEE Trans. Ind. Electron. 2018, 65, 1728–1739. [Google Scholar] [CrossRef]
- Ma, B.; Lei, G.; Liu, C.C.; Zhu, J.G.; Guo, Y.G. Robust tolerance design optimization of a PM claw pole motor with soft magnetic composite cores. IEEE Trans. Magn. 2018, 54, 8102404. [Google Scholar] [CrossRef]
- Jeang, A. Tolerance chart balancing with a complete inspection plan taking account of manufacturing and quality costs. Int. J. Adv. Manuf. Technol. 2011, 55, 675–687. [Google Scholar] [CrossRef]
- Terán, A.; Pratt, D.B.; Case, K.E. Present worth of external quality losses for symmetric nominal-is-better quality characteristics. Eng. Econ. 1996, 42, 39–52. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Liu, D.S.; Wen, Z.J.; Liu, T. Modeling present worth of product quality loss of SIB characteristic based on service life distribution. Appl. Mech. Mater. 2013, 397, 846–851. [Google Scholar] [CrossRef]
- Khodaygan, S. A multiple objective framework for optimal asymmetric tolerance synthesis of mechanical assemblies with degrading components. Int. J. Adv. Manuf. Technol. 2019, 100, 2177–2205. [Google Scholar] [CrossRef]
- Robles, N.; Roy, U. Optimal tolerance allocation and process-sequence selection incorporating manufacturing capacities and quality issues. J. Manuf. Syst. 2004, 23, 127–133. [Google Scholar] [CrossRef]
- Cheng, B.W.; Maghsoodloo, S. Optimization of mechanical assembly tolerances by incorporating Taguchi’s quality loss function. J. Manuf. Syst. 1995, 14, 264–276. [Google Scholar] [CrossRef]
- Wu, Z.; Elmaraghy, W.H.; Elmaraghy, H.A. Evaluation of cost tolerance algorithms for design tolerance analysis and synthesis. Manuf. Rev. 1988, 1, 168–179. [Google Scholar]
- Deng, J.; Ye, X.R.; Lin, Y.G.; Li, Q.Y.; Zhai, G.F. A new robust tolerance design method for electromechanical device based on variable contribution rate coefficients. J. Eng. Des. 2017, 28, 532–548. [Google Scholar] [CrossRef]
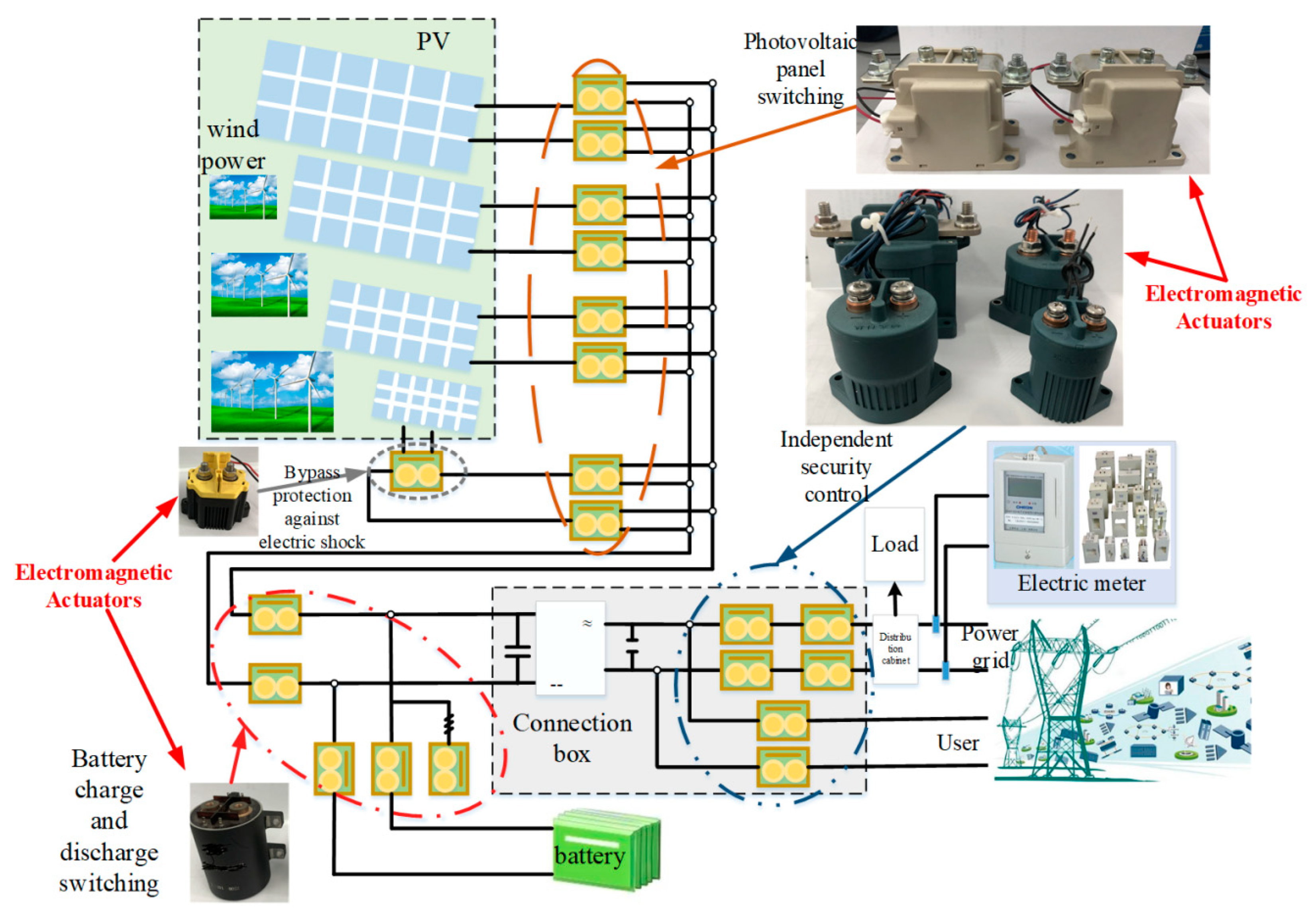


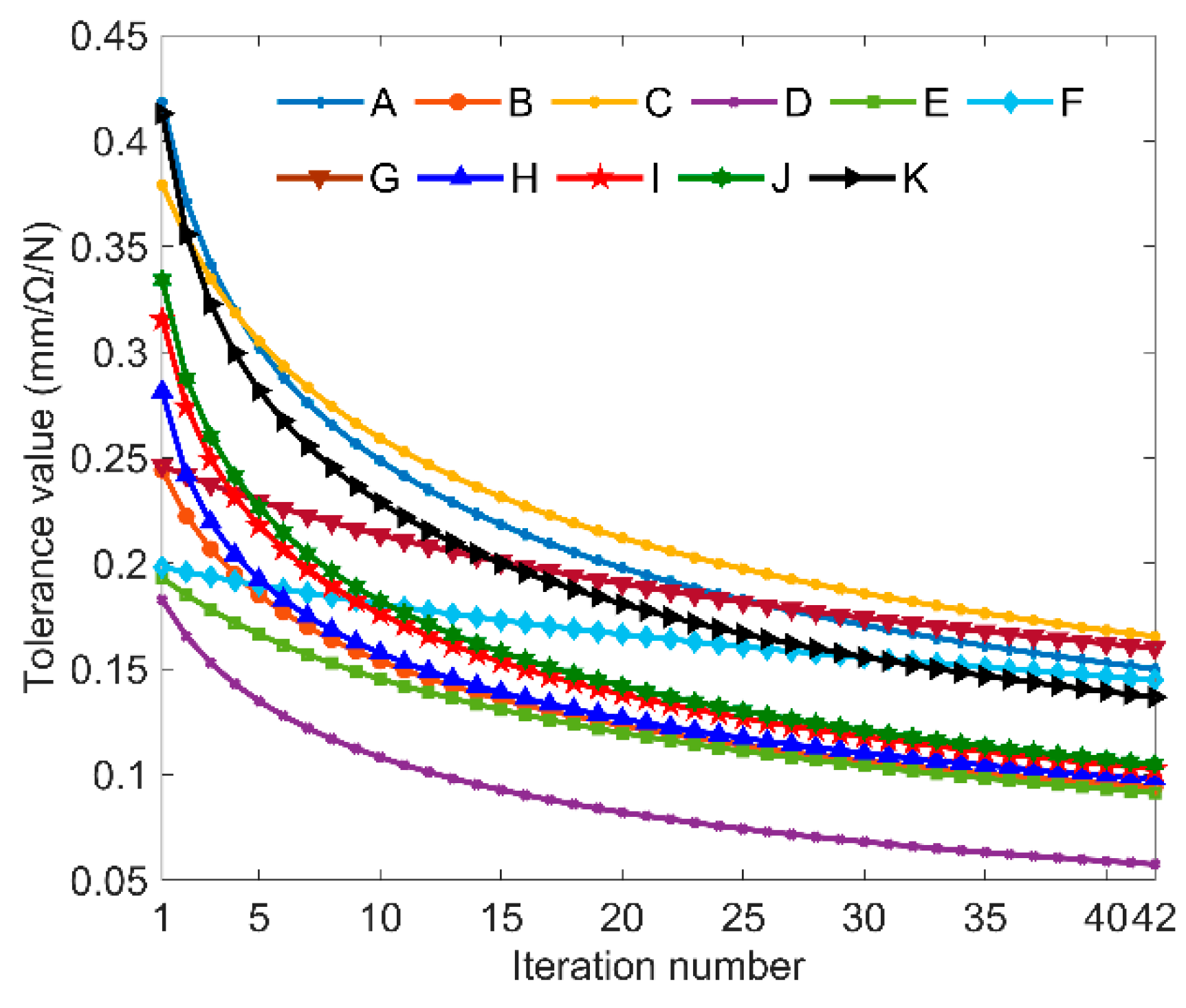


| Input Variables | Initial Tolerances | Lower Limits |
|---|---|---|
| A—Yoke assembly position (mm) | ±0.5 | ±0.05 |
| B—Armature assembly position (mm) | ±0.5 | ±0.05 |
| C—Yoke polar diameter (mm) | ±0.4 | ±0.05 |
| D—Armature polar diameter (mm) | ±0.2 | ±0.05 |
| E—Armature outer diameter (mm) | ±0.2 | ±0.05 |
| F—Core diameter (mm) | ±0.2 | ±0.05 |
| G—Iron core outer diameter (mm) | ±0.25 | ±0.05 |
| H—Coil resistance/10* (Ω) | ±0.4 | ±0.05 |
| I—Reaction spring preload/2* (N) | ±0.5 | ±0.05 |
| J—Rebound spring preload/2* (N) | ±0.5 | ±0.05 |
| K—Contact pressure/2* (N) | ±0.5 | ±0.05 |
| Coefficients | αi1 | αi2 | αi3 | Ci0 (CNY) |
|---|---|---|---|---|
| A | –102.13 | 89.20 | 0.083 | 50.87 |
| B | –63.00 | 57.13 | 0.035 | 43.79 |
| C | –48.20 | 29.73 | 0.019 | 22.76 |
| D | –88.73 | 35.87 | 0.114 | 25.49 |
| E | –137.73 | 49.20 | 0.094 | 29.61 |
| F | –151.40 | 39.87 | 0.021 | 28.99 |
| G | –68.00 | 26.07 | 0.017 | 29.63 |
| H | –45.53 | 32.73 | 0.011 | 34.11 |
| I | –10.87 | 32.47 | 0.069 | 46.19 |
| J | –11.47 | 35.53 | 0.078 | 50.01 |
| K | –21.00 | 35.53 | 0.050 | 43.61 |
| Input Variables | ρi (%) | ξi (%) | Δti |
|---|---|---|---|
| A | 13.52 | 8.04 | 0.0818 |
| B | 32.16 | 6.12 | 0.2557 |
| C | 2.21 | 5.18 | 0.0208 |
| D | 3.94 | 11.14 | 0.0172 |
| E | 2.48 | 17.44 | 0.0069 |
| F | 0.93 | 25.01 | 0.0018 |
| G | 0.87 | 11.20 | 0.0038 |
| H | 14.48 | 5.94 | 0.1186 |
| I | 11.65 | 3.07 | 0.1847 |
| J | 11.10 | 3.26 | 0.1657 |
| K | 6.44 | 3.60 | 0.0871 |
| Input Variables | Initial Values | Optimal Values | Normalized Values |
|---|---|---|---|
| A—Yoke assembly position (mm) | ±0.5 | ±0.150 | ±0.15 |
| B—Armature assembly position (mm) | ±0.5 | ±0.094 | ±0.09 |
| C—Yoke polar diameter (mm) | ±0.4 | ±0.166 | ±0.17 |
| D—Armature polar diameter (mm) | ±0.2 | ±0.058 | ±0.06 |
| E—Armature outer diameter (mm) | ±0.2 | ±0.091 | ±0.09 |
| F—Core diameter (mm) | ±0.2 | ±0.145 | ±0.15 |
| G—Iron core outer diameter (mm) | ±0.25 | ±0.160 | ±0.16 |
| H—Coil resistance/10* (Ω) | ±0.4 | ±0.098 | ±0.10 |
| I—Reaction spring preload/2* (N) | ±0.5 | ±0.103 | ±0.10 |
| J—Rebound spring preload/2* (N) | ±0.5 | ±0.105 | ±0.11 |
| K—Contact pressure/2* (N) | ±0.5 | ±0.137 | ±0.14 |
| Method | Initial | Conventional | Proposed |
|---|---|---|---|
| Standard deviation | 6.57 | 1.79 | 1.79 |
| Quality loss | 1777.2 | 132.0 | 132.6 |
| Manufacturing cost | 405.1 | 2373.1 | 1883.5 |
| Total loss | 2182.3 | 2505.1 | 2016.1 |
| Inherent reliability | 0.5889 | 0.9973 | 0.9973 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, J.; Liu, X.; Zhai, G. Robust Design Optimization of Electromagnetic Actuators for Renewable Energy Systems Considering the Manufacturing Cost. Energies 2019, 12, 4353. https://doi.org/10.3390/en12224353
Deng J, Liu X, Zhai G. Robust Design Optimization of Electromagnetic Actuators for Renewable Energy Systems Considering the Manufacturing Cost. Energies. 2019; 12(22):4353. https://doi.org/10.3390/en12224353
Chicago/Turabian StyleDeng, Jie, Xiaohan Liu, and Guofu Zhai. 2019. "Robust Design Optimization of Electromagnetic Actuators for Renewable Energy Systems Considering the Manufacturing Cost" Energies 12, no. 22: 4353. https://doi.org/10.3390/en12224353
APA StyleDeng, J., Liu, X., & Zhai, G. (2019). Robust Design Optimization of Electromagnetic Actuators for Renewable Energy Systems Considering the Manufacturing Cost. Energies, 12(22), 4353. https://doi.org/10.3390/en12224353





