e4clim 1.0: The Energy for a Climate Integrated Model: Description and Application to Italy
Abstract
1. Introduction
- 1.
- Design and analyse mixes with high shares of VREs,
- 2.
- Evaluate the benefits of spatial and technological diversification,
- 3.
- Assess different optimization strategies taking the variability of both the generation and the demand into account,
- 4.
- Choose between optimal mixes representing different trade-offs,
- 5.
- Assess the impact of climate variability on energy mixes on a broad range of time scales (from hours to decades),
- 6.
- Take the impact of climate change into account,
- 7.
- Integrate new technologies for which little data is available,
- 8.
- Track uncertainties and evaluate the robustness of results to input data and modeling approaches using observations, statistical models and multiple input data sources,
- 9.
- Use a fully open-source tool available to the research, engineering and education communities, helping access and manage open-data, relying on free third-party libraries, and covering the whole chain of operations, from downloading input data to representing results,
- 10.
- Perform sensitivity analyses which are computationally tractable,
- 11.
- Easily configure and extend the model to new applications and research questions.
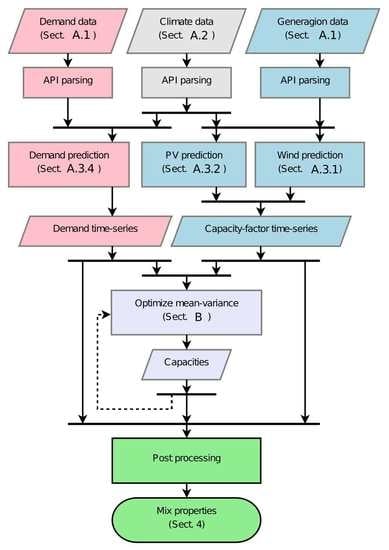
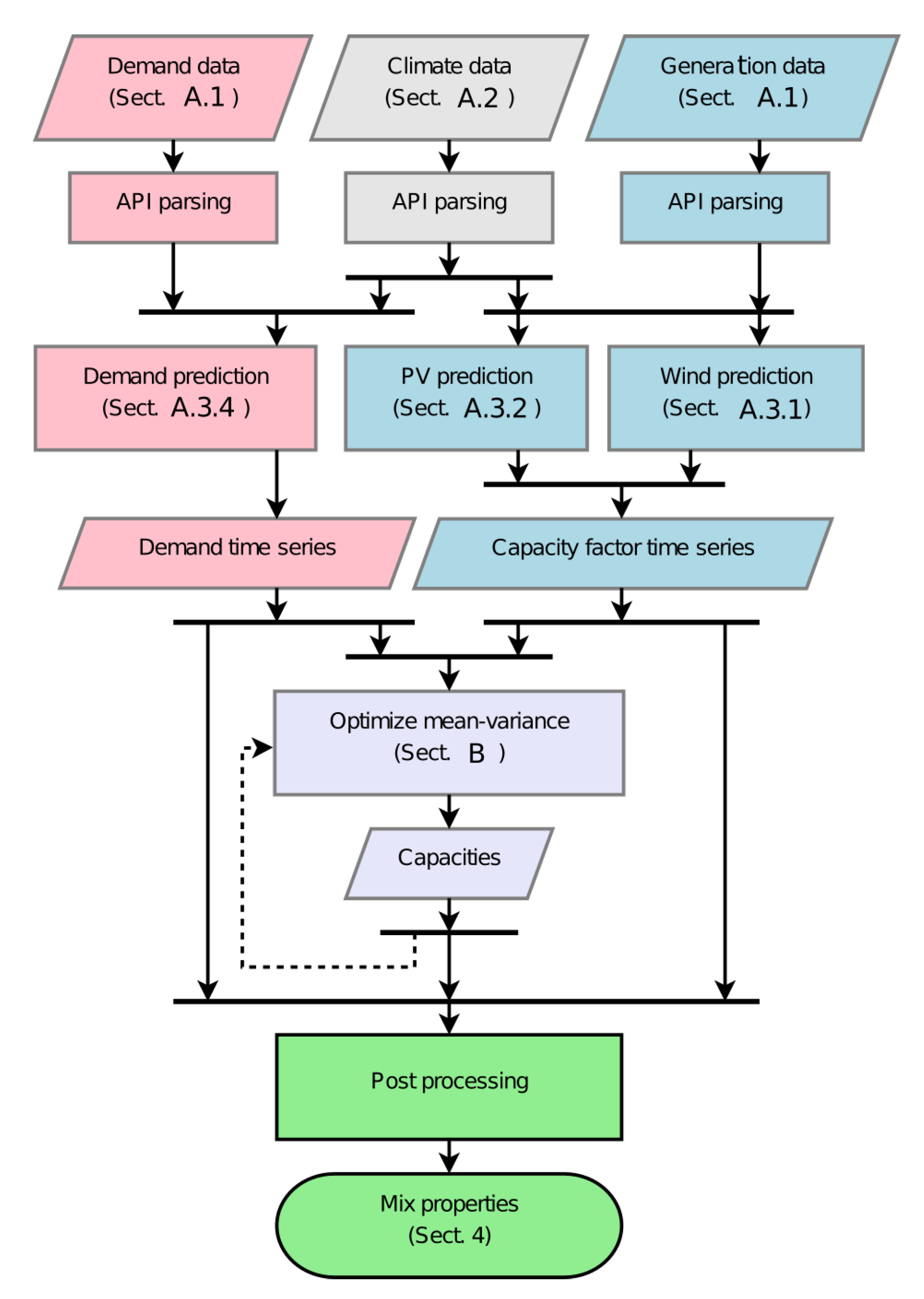
2. Methodology and Software Design
- Computing georeferenced energy time series from historic or climate data,
- Distributing capacities spatially and technologically,
- Post-processing and analyzing the resulting mixes.
3. A Concrete Implementation for Mean-Variance Analyses
3.1. Mix Analysis
3.2. Mix Optimization
3.3. Energy Models
- the “wind” production is “predicted” from wind data fed to a power curve at each grid point of the climate data (Appendix A.3.1), summed over each zone, and bias corrected against wind production observations (Appendix A.3.3),
- the “PV” production is computed from surface irradiance and temperature data fed to an electric model (Appendix A.3.2), summed over each zone, and bias corrected against PV production observations (Appendix A.3.3),
- the “demand” is estimated via a linear Bayesian regression model taking as input warming and cooling degree days averaged over each zone and fitted to demand observations (Appendix A.3.4).
3.4. Energy, Climate and Geographic Data
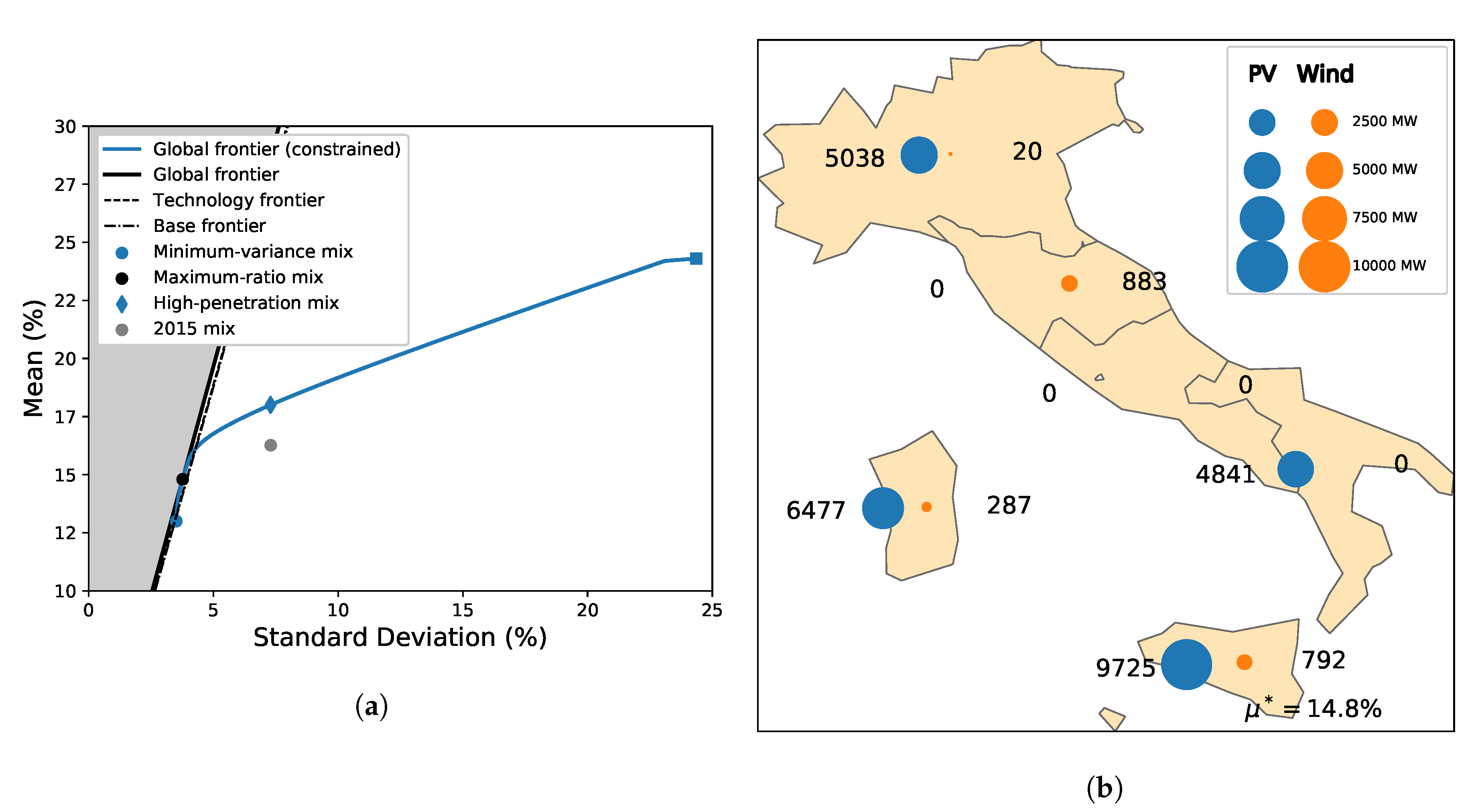
4. Application: Italian PV-Wind Optimal Recommissioning
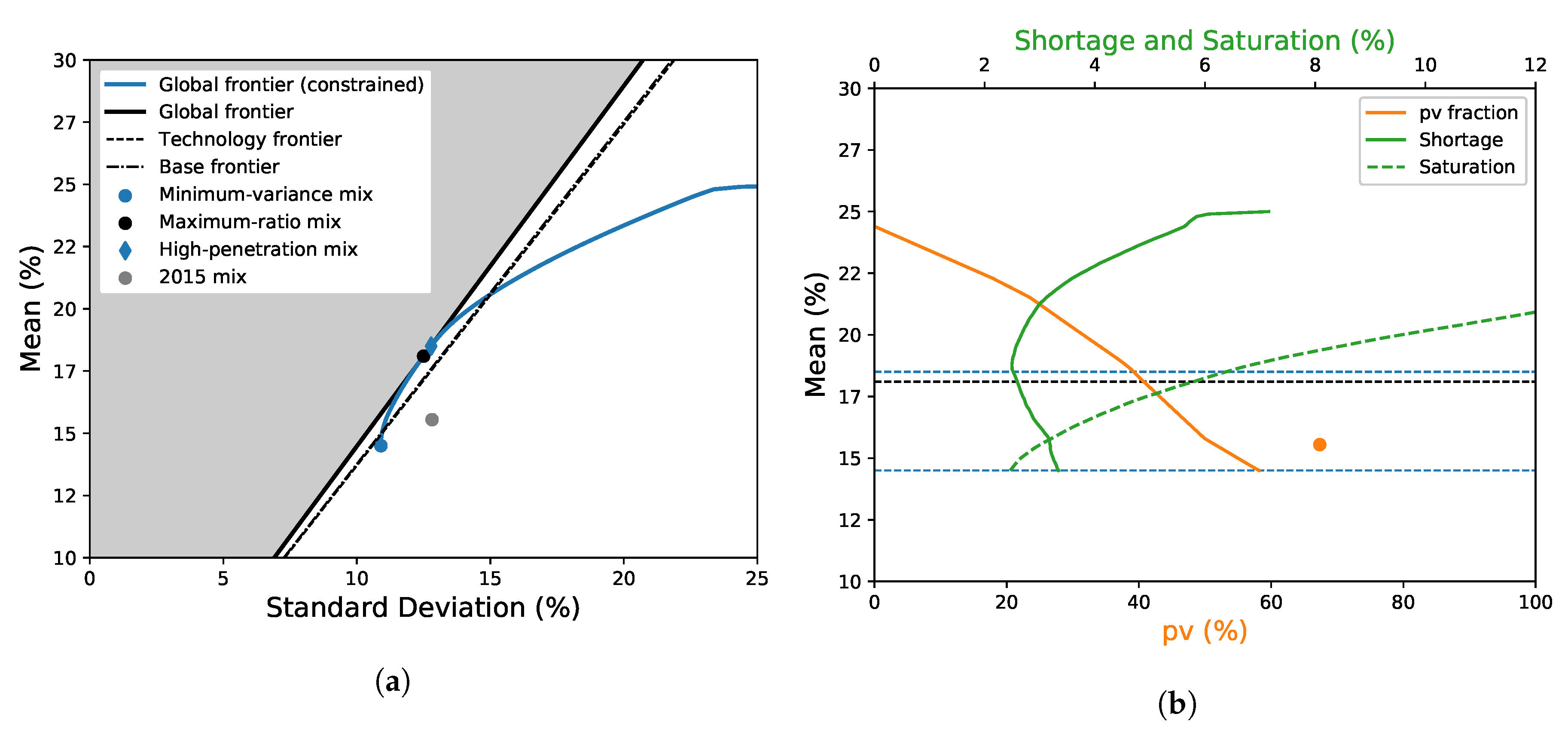
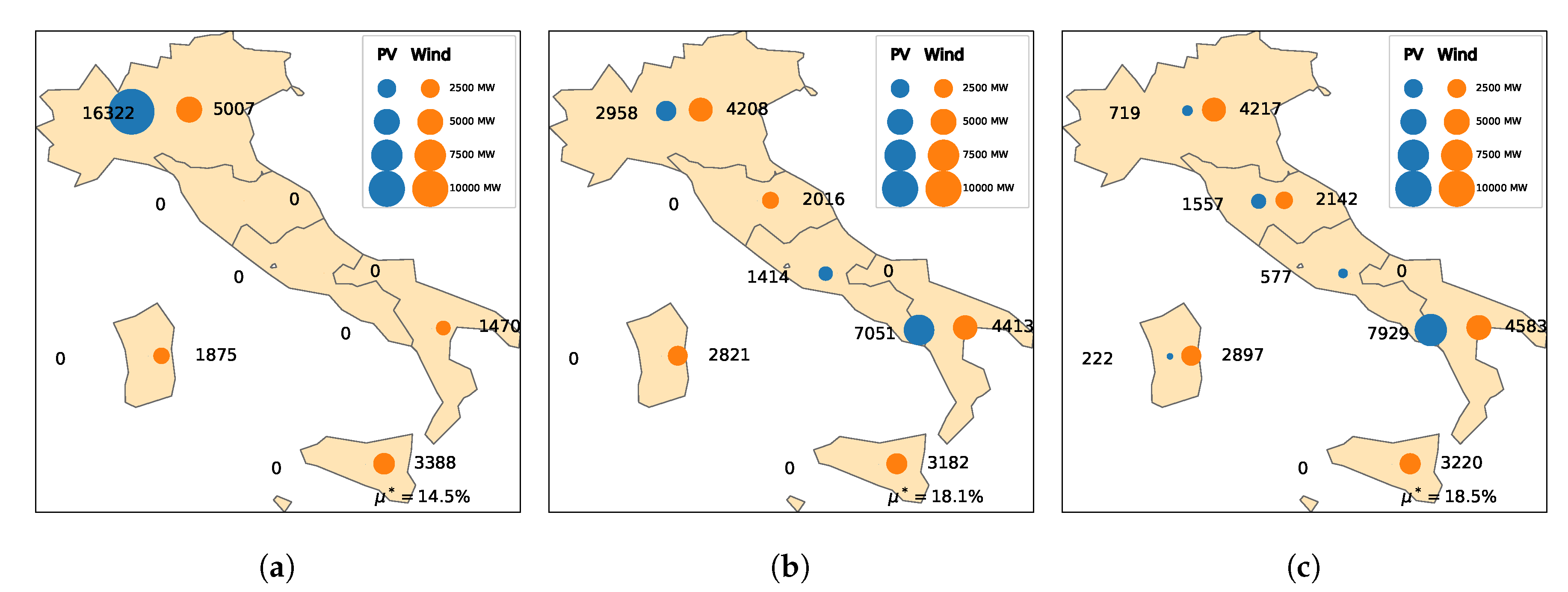
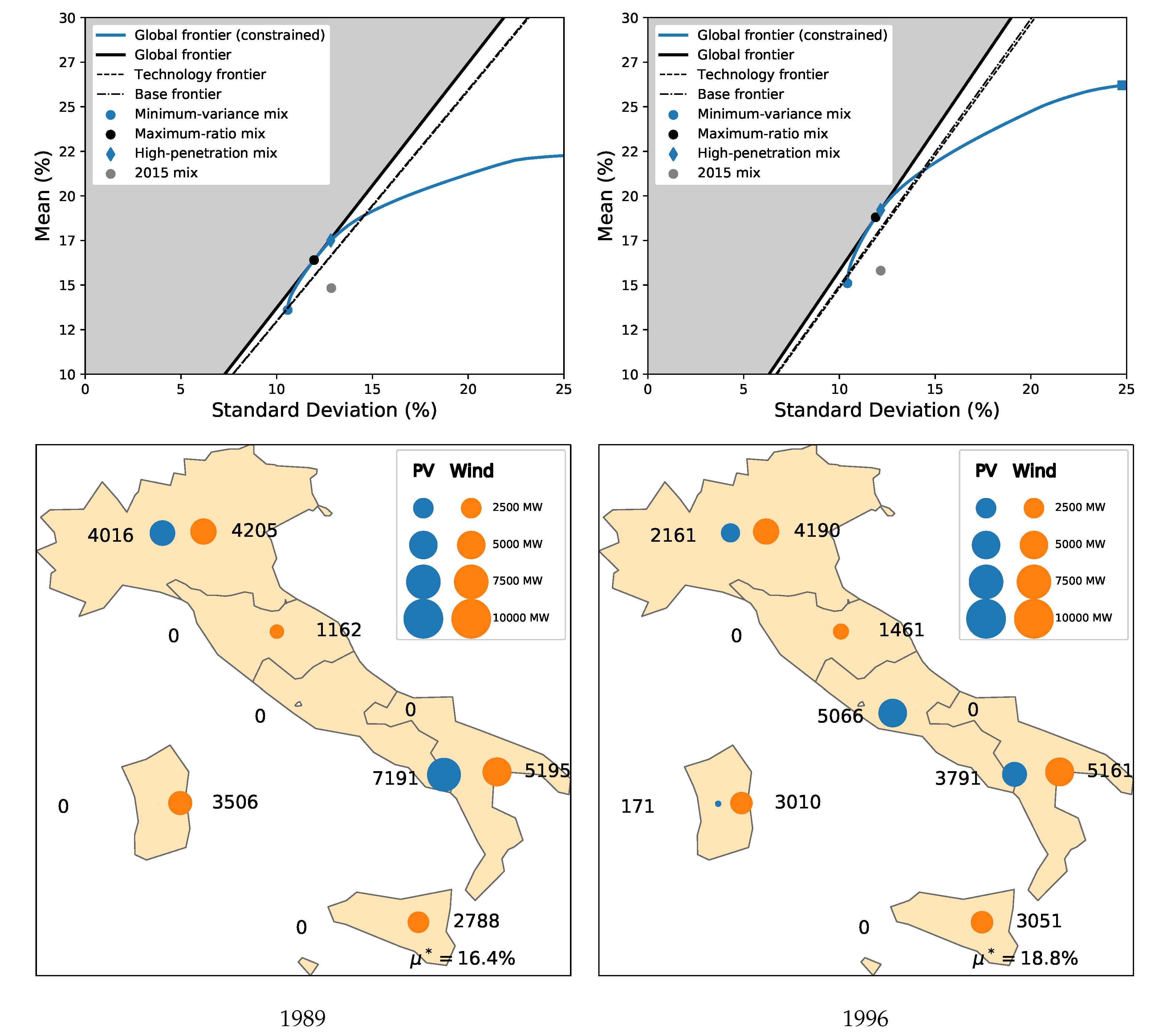
4.1. General Results
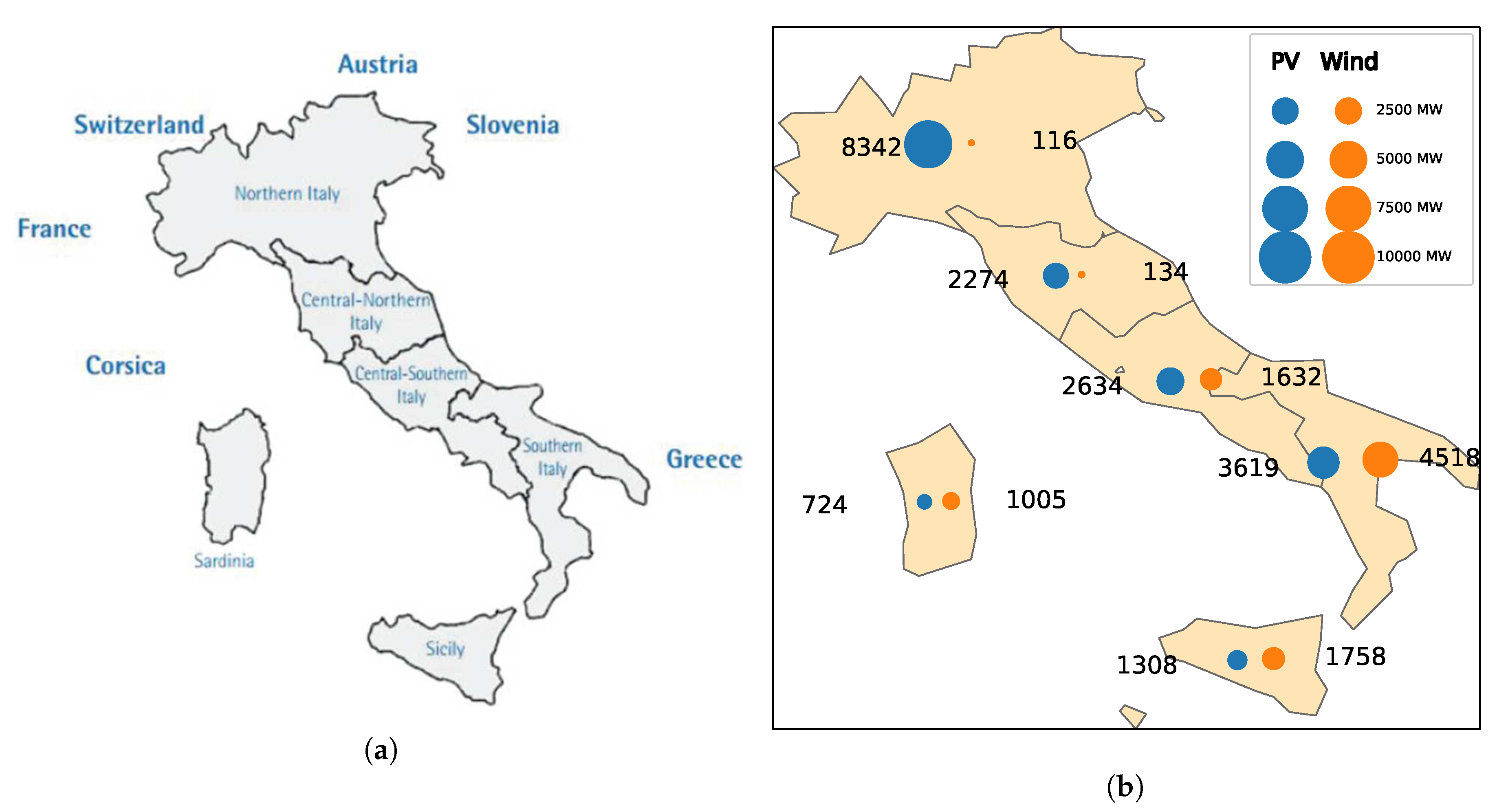
4.2. Comparison with the 2015 Italian Mix
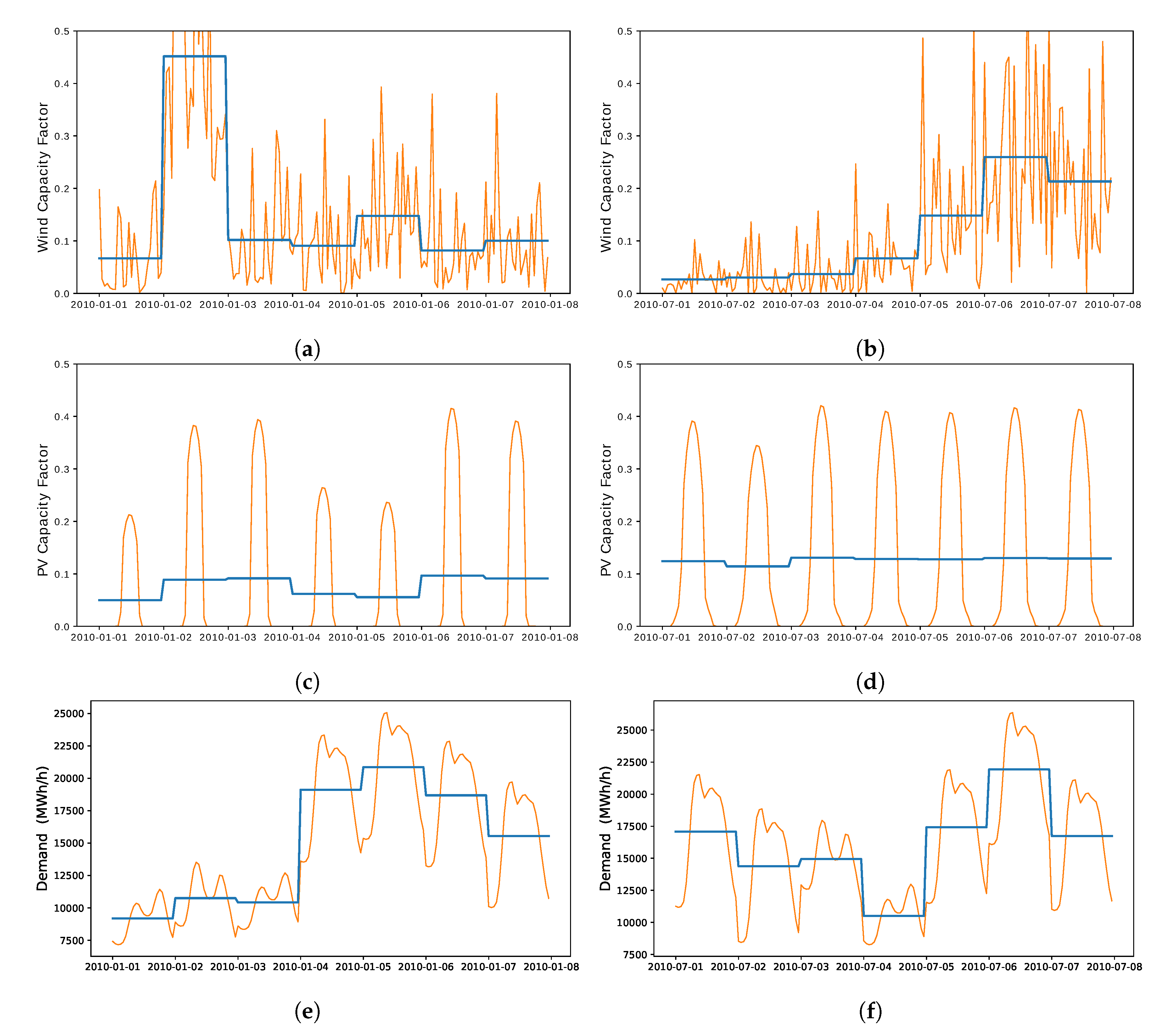
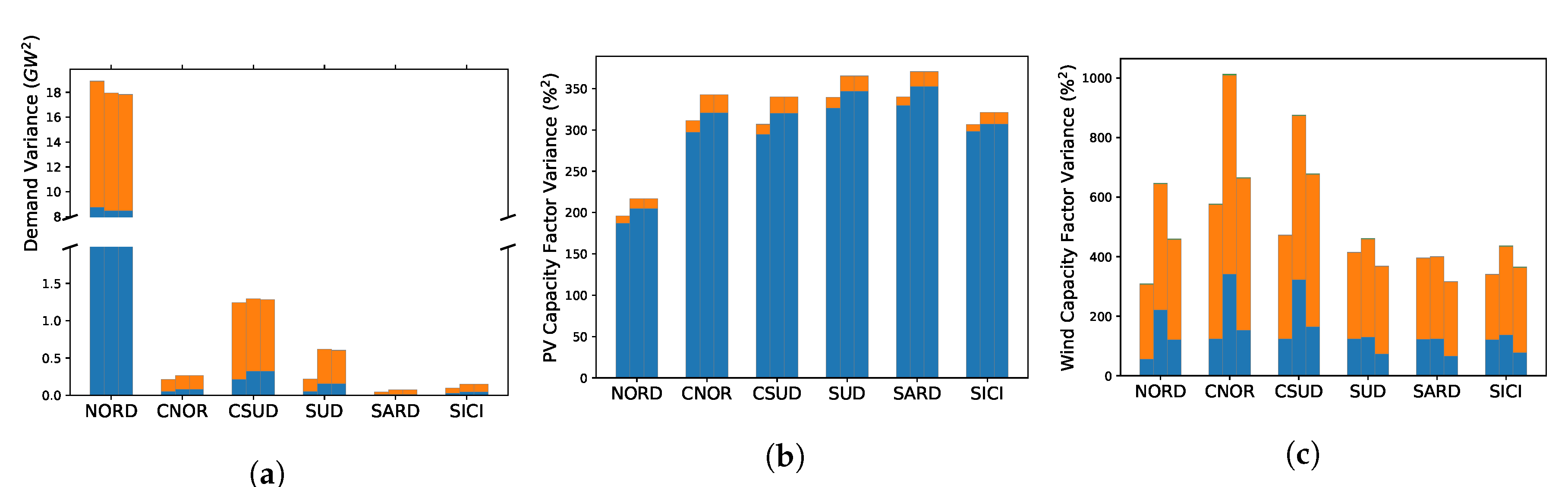
4.3. Choice of the Climate Data and Climate Variability
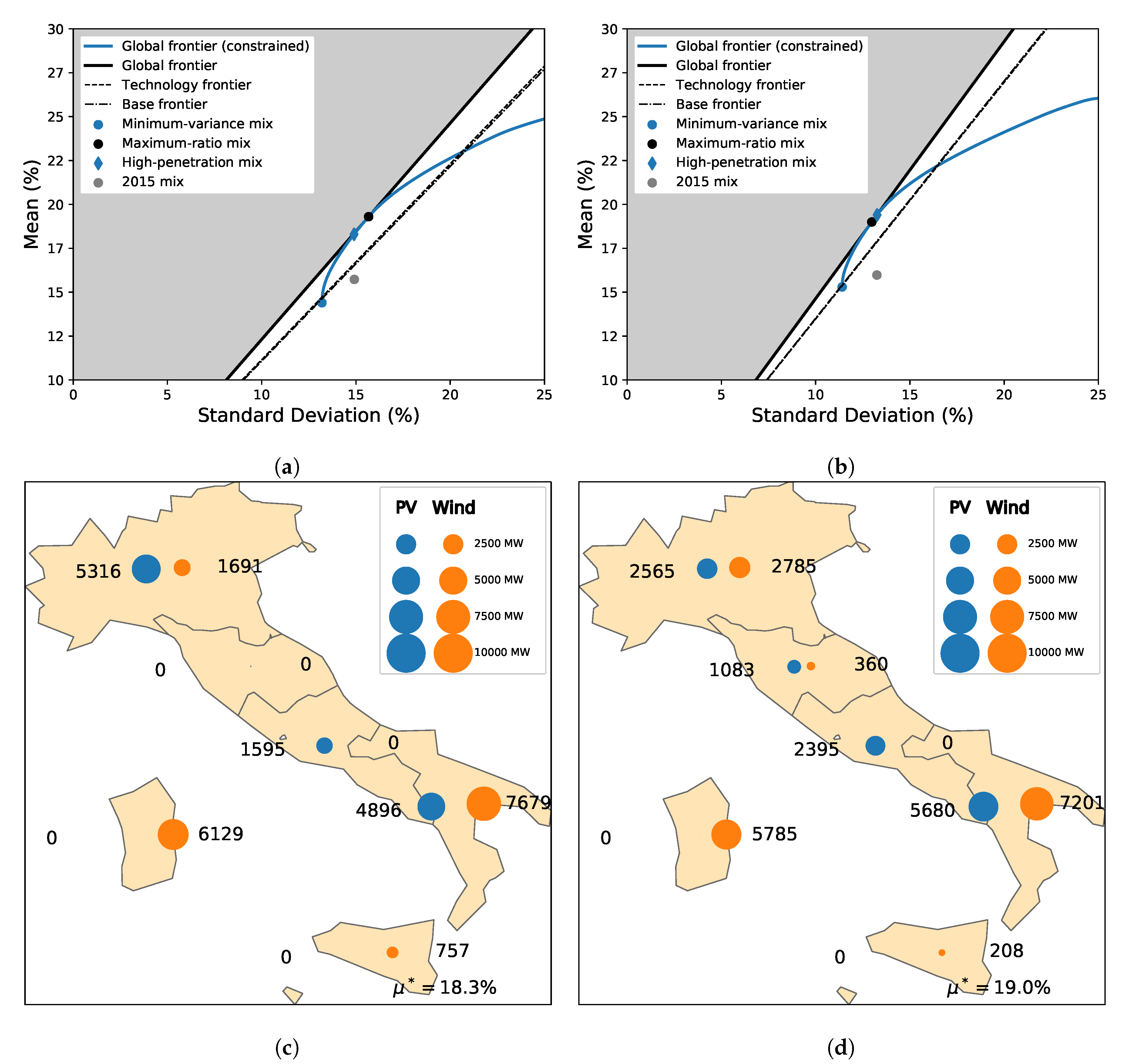
4.3.1. Dependence on the Climate Data
4.3.2. Interannual to Decadal Variability
4.3.3. Intraday Variability
5. Conclusions
6. Known Limitations of the Software and Methodology
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Data and Model Description
Appendix A.1. Energy Data: GME and Terna Databases
| Zone | Electrical Demand | Capacity Factor (%) | ||
|---|---|---|---|---|
| (TWh/y) | (%) | PV | Wind | |
| NORD | 121 | 58 | 11.7 | 20.0 |
| CNOR | 19.4 | 9.2 | 13.4 | 19.5 |
| CSUD | 30.3 | 14 | 13.9 | 18.9 |
| SUD | 15.0 | 7.1 | 15.0 | 21.0 |
| SARD | 10.8 | 5.1 | 14.4 | 18.5 |
| SICI | 13.5 | 6.4 | 15.2 | 18.6 |
Appendix A.2. Climate Data
Appendix A.2.1. CORDEX Regional Simulations
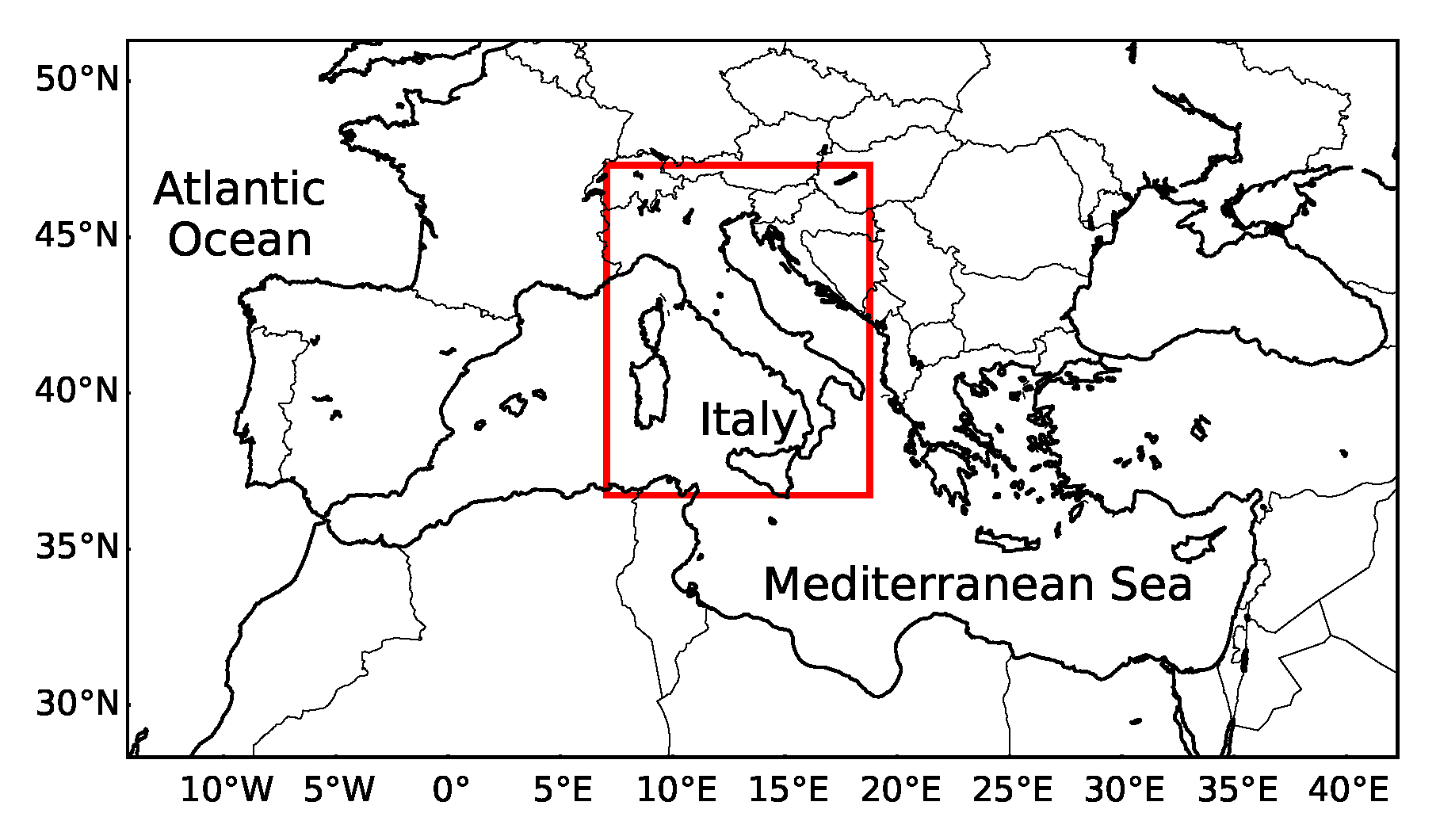
Appendix A.2.2. MERRA-2 Reanalysis
Appendix A.3. Model Description
Appendix A.3.1. Wind Model
Appendix A.3.2. PV Model
Appendix A.3.3. Aggregation and Bias Correction
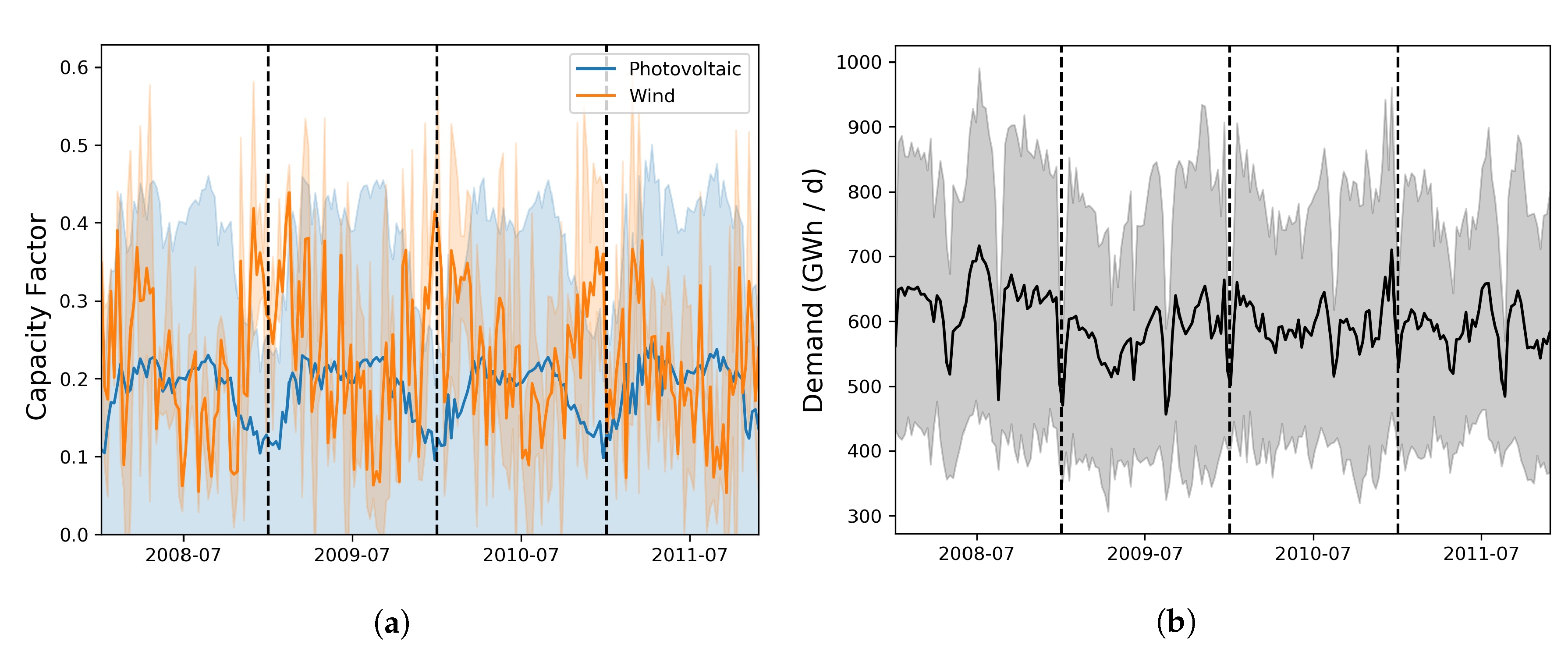
Appendix A.3.4. Electricity-Demand Model
- applications: assessments, forecasting [116],
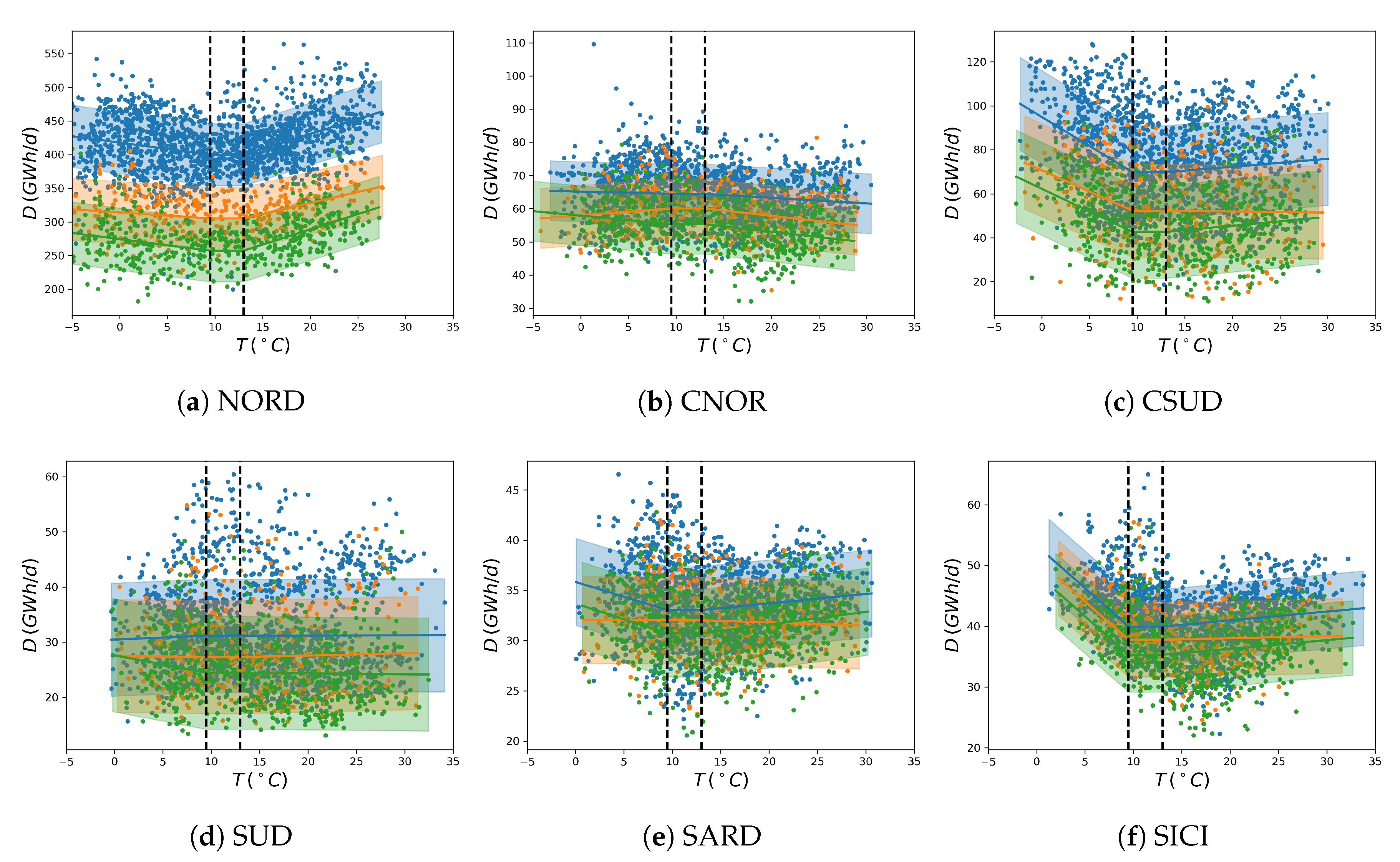
Appendix B. Mean-Variance Analysis
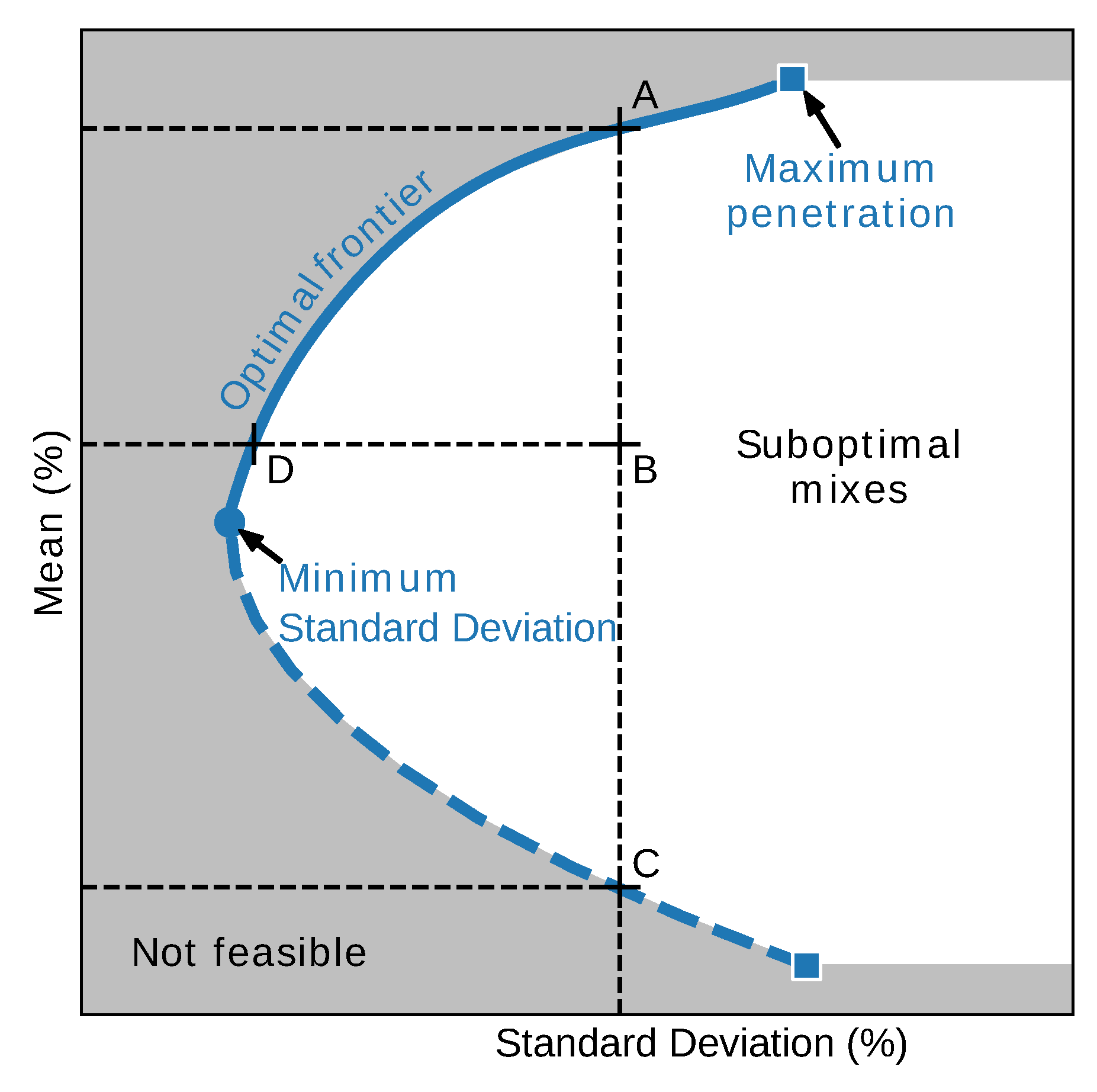
Appendix B.1. Mean-Variance Optimization Problem
Appendix B.2. Method to Find an Approximation of the Optimal Frontier
Appendix B.2.1. The Biobjective Algorithm
Appendix B.2.2. How to Find the Bound on the RHS of (A9) and (A13)
Appendix B.2.3. Algorithm to Solve the Single-Objective Problems
References
- International Energy Agency (IEA). World Energy Outlook 2018; Technical Report; IEA: Paris, France, 2018. [Google Scholar]
- Labussière, O.; Nadaï, A. (Eds.) Energy Transitions: A Socio-Technical Inquiry; Palgrave Macmillan: London, UK, 2018. [Google Scholar] [CrossRef]
- Ueckerdt, F.; Brecha, R.; Luderer, G. Analyzing Major Challenges of Wind and Solar Variability in Power Systems. Renew. Energy 2015, 81, 1–10. [Google Scholar] [CrossRef]
- Hirth, L.; Ueckerdt, F.; Edenhofer, O. Integration Costs Revisited—An Economic Framework for Wind and Solar Variability. Renew. Energy 2015, 74, 925–939. [Google Scholar] [CrossRef]
- Giebel, G. Wind Power Has a Capacity Credit. A Catalogue of 50+ Supporting Studies. e-WINDENG J. 2005, 1, 13. [Google Scholar]
- Stoft, S. Power System Economics: Designing Markets for Electricity; Wiley-IEEE Press: Hoboken, NJ, USA, 2002. [Google Scholar]
- Apt, J. The Spectrum of Power from Wind Turbines. J. Power Sources 2007, 169, 369–374. [Google Scholar] [CrossRef]
- Frunt, J.; Kling, W.L.; van den Bosch, P.P.J. Classification and Quantification of Reserve Requirements for Balancing. Electr. Power Syst. Res. 2010, 80, 1528–1534. [Google Scholar] [CrossRef]
- Huber, M.; Dimkova, D.; Hamacher, T. Integration of Wind and Solar Power in Europe: Assessment of Flexibility Requirements. Energy 2014, 69, 236–246. [Google Scholar] [CrossRef]
- Van Stiphout, A.; Vos, K.D.; Deconinck, G. The Impact of Operating Reserves on Investment Planning of Renewable Power Systems. IEEE Trans. Power Syst. 2017, 32, 378–388. [Google Scholar] [CrossRef]
- Spiecker, S.; Weber, C. The Future of the European Electricity System and the Impact of Fluctuating Renewable Energy—A Scenario Analysis. Energy Policy 2014, 65, 185–197. [Google Scholar] [CrossRef]
- Heard, B.P.; Brook, B.W.; Wigley, T.M.L.; Bradshaw, C.J.A. Burden of Proof: A Comprehensive Review of the Feasibility of 100% Renewable-Electricity Systems. Renew. Sustain. Energy Rev. 2017, 76, 1122–1133. [Google Scholar] [CrossRef]
- Hansen, K.; Breyer, C.; Lund, H. Status and Perspectives on 100% Renewable Energy Systems. Energy 2019, 175, 471–480. [Google Scholar] [CrossRef]
- Widén, J.; Carpman, N.; Castellucci, V.; Lingfors, D.; Olauson, J.; Remouit, F.; Bergkvist, M.; Grabbe, M.; Waters, R. Variability Assessment and Forecasting of Renewables: A Review for Solar, Wind, Wave and Tidal Resources. Renew. Sustain. Energy Rev. 2015, 44, 356–375. [Google Scholar] [CrossRef]
- Graabak, I.; Korpås, M. Variability Characteristics of European Wind and Solar Power Resources—A Review. Energies 2016, 9, 449. [Google Scholar] [CrossRef]
- James, I.N. Introduction to Circulating Atmospheres; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Holton, J.R. An Introduction to Dynamic Meteorology, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Duffie, J.; Beckman, W. Solar Engineering of Thermal Processes, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Holttinen, H. Hourly Wind Power Variations in the Nordic Countries. Wind Energy 2005, 8, 173–195. [Google Scholar] [CrossRef]
- Katzenstein, W.; Fertig, E.; Apt, J. The Variability of Interconnected Wind Plants. Energy Policy 2010, 38, 4400–4410. [Google Scholar] [CrossRef]
- Tarroja, B.; Mueller, F.; Eichman, J.D.; Brouwer, J.; Samuelsen, S. Spatial and Temporal Analysis of Electric Wind Generation Intermittency and Dynamics. Renew. Energy 2011, 36, 3424–3432. [Google Scholar] [CrossRef]
- Giebel, G. A Variance Analysis of the Capacity Displaced by Wind Energy in Europe. Wind Energy 2007, 10, 69–79. [Google Scholar] [CrossRef]
- Kempton, W.; Pimenta, F.M.; Veron, D.E.; Colle, B.A. Electric Power from Offshore Wind via Synoptic-Scale Interconnection. Proc. Natl. Acad. Sci. USA 2010, 107, 7240–7245. [Google Scholar] [CrossRef] [PubMed]
- Gueymard, C.A.; Wilcox, S.M. Assessment of Spatial and Temporal Variability in the US Solar Resource from Radiometric Measurements and Predictions from Models Using Ground-Based or Satellite Data. Sol. Energy 2011, 85, 1068–1084. [Google Scholar] [CrossRef]
- Marcos, J.; Marroyo, L.; Lorenzo, E.; García, M. Smoothing of PV Power Fluctuations by Geographical Dispersion. Prog. Photovolt. Res. Appl. 2012, 20, 226–237. [Google Scholar] [CrossRef]
- Buttler, A.; Dinkel, F.; Franz, S.; Spliethoff, H. Variability of Wind and Solar Power—An Assessment of the Current Situation in the European Union Based on the Year 2014. Energy 2016, 106, 147–161. [Google Scholar] [CrossRef]
- Heide, D.; von Bremen, L.; Greiner, M.; Hoffmann, C.; Speckmann, M.; Bofinger, S. Seasonal Optimal Mix of Wind and Solar Power in a Future, Highly Renewable Europe. Renew. Energy 2010, 35, 2483–2489. [Google Scholar] [CrossRef]
- Holttinen, H. Impact of Hourly Wind Power Variations on the System Operation in the Nordic Countries. Wind Energy 2005, 8, 197–218. [Google Scholar] [CrossRef]
- Sinden, G. Characteristics of the UK Wind Resource: Long-Term Patterns and Relationship to Electricity Demand. Energy Policy 2007, 35, 112–127. [Google Scholar] [CrossRef]
- Bett, P.E.; Thornton, H.E. The Climatological Relationships between Wind and Solar Energy Supply in Britain. Renew. Energy 2016, 87, 96–110. [Google Scholar] [CrossRef]
- Coker, P.; Barlow, J.; Cockerill, T.; Shipworth, D. Measuring Significant Variability Characteristics: An Assessment of Three UK Renewables. Renew. Energy 2013, 53, 111–120. [Google Scholar] [CrossRef]
- Widén, J. Correlations between Large-Scale Solar and Wind Power in a Future Scenario for Sweden. IEEE Trans. Sustain. Energy 2011, 2, 177–184. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Huld, T.; Monforti-Ferrario, F. Local Complementarity of Wind and Solar Energy Resources over Europe: An Assessment Study from a Meteorological Perspective. J. Appl. Meteorol. Climatol. 2016, 56, 217–234. [Google Scholar] [CrossRef]
- Santos-Alamillos, F.J.; Pozo-Vázquez, D.; Ruiz-Arias, J.A.; Lara-Fanego, V.; Tovar-Pescador, J. Analysis of Spatiotemporal Balancing between Wind and Solar Energy Resources in the Southern Iberian Peninsula. J. Appl. Meteorol. Climatol. 2012, 51, 2005–2024. [Google Scholar] [CrossRef]
- Hirth, L. The Market Value of Variable Renewables. The Effect of Solar Wind Power Variability on Their Relative Price. Energy Econ. 2013, 38, 218–236. [Google Scholar] [CrossRef]
- Hirth, L. The Optimal Share of Variable Renewables: How the Variability of Wind and Solar Power Affects Their Welfare-Optimal Deployment. Energy J. 2015, 36, 149–184. [Google Scholar] [CrossRef]
- Shirizadeh, B.; Perrier, Q.; Quirion, P. How Sensitive Are Optimal Fully Renewable Power Systems to Technology Cost Uncertainty? FAERE Policy Paper; CIRED: Paris, France, 2019. [Google Scholar]
- Heide, D.; Greiner, M.; von Bremen, L.; Hoffmann, C. Reduced Storage and Balancing Needs in a Fully Renewable European Power System with Excess Wind and Solar Power Generation. Renew. Energy 2011, 36, 2515–2523. [Google Scholar] [CrossRef]
- Rodríguez, R.A.; Becker, S.; Andresen, G.B.; Heide, D.; Greiner, M. Transmission Needs across a Fully Renewable European Power System. Renew. Energy 2014, 63, 467–476. [Google Scholar] [CrossRef]
- Becker, S.; Rodriguez, R.A.; Andresen, G.B.; Schramm, S.; Greiner, M. Transmission Grid Extensions during the Build-up of a Fully Renewable Pan-European Electricity Supply. Energy 2014, 64, 404–418. [Google Scholar] [CrossRef]
- Becker, S.; Frew, B.A.; Andresen, G.B.; Zeyer, T.; Schramm, S.; Greiner, M.; Jacobson, M.Z. Features of a Fully Renewable US Electricity System: Optimized Mixes of Wind and Solar PV and Transmission Grid Extensions. Energy 2014, 72, 443–458. [Google Scholar] [CrossRef]
- Nelson, J.; Johnston, J.; Mileva, A.; Fripp, M.; Hoffman, I.; Petros-Good, A.; Blanco, C.; Kammen, D.M. High-Resolution Modeling of the Western North American Power System Demonstrates Low-Cost and Low-Carbon Futures. Energy Policy 2012, 43, 436–447. [Google Scholar] [CrossRef]
- Lund, H.; Mathiesen, B.V. Energy System Analysis of 100% Renewable Energy Systems-The Case of Denmark in Years 2030 and 2050. Energy 2009, 34, 524–531. [Google Scholar] [CrossRef]
- François, B.; Borga, M.; Creutin, J.D.; Hingray, B.; Raynaud, D.; Sauterleute, J.F. Complementarity between Solar and Hydro Power: Sensitivity Study to Climate Characteristics in Northern-Italy. Renew. Energy 2016, 86, 543–553. [Google Scholar] [CrossRef]
- Raynaud, D.; Hingray, B.; François, B.; Creutin, J.D. Energy Droughts from Variable Renewable Energy Sources in European Climates. Renew. Energy 2018, 125, 578–589. [Google Scholar] [CrossRef]
- Perera, A.T.D.; Nik, V.M.; Wickramasinghe, P.U.; Scartezzini, J.L. Redefining Energy System Flexibility for Distributed Energy System Design. Appl. Energy 2019, 253, 113572. [Google Scholar] [CrossRef]
- Siraganyan, K.; Perera, A.T.D.; Scartezzini, J.L.; Mauree, D. Eco-Sim: A Parametric Tool to Evaluate the Environmental and Economic Feasibility of Decentralized Energy Systems. Energies 2019, 12, 776. [Google Scholar] [CrossRef]
- Del Río, P.; Calvo Silvosa, A.; Iglesias Gómez, G. Policies and Design Elements for the Repowering of Wind Farms: A Qualitative Analysis of Different Options. Energy Policy 2011, 39, 1897–1908. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Brazilian, M.; Roques, F. Analytical Methods for Energy Diversity and Security: Portfolio Optimization in the Energy Sector: A Tribute to the Work of Dr. Shimon Awerbuch; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Beltran, H. Modern Portfolio Theory Applied To Electricity Generation Planning. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign County, IL, USA, 2009. [Google Scholar]
- Roques, F.; Hiroux, C.; Saguan, M. Optimal Wind Power Deployment in Europe-A Portfolio Approach. Energy Policy 2010, 38, 3245–3256. [Google Scholar] [CrossRef]
- Thomaidis, N.S.; Santos-Alamillos, F.J.; Pozo-Vázquez, D.; Usaola-García, J. Optimal Management of Wind and Solar Energy Resources. Comput. Oper. Res. 2016, 66, 284–291. [Google Scholar] [CrossRef]
- Santos-Alamillos, F.J.; Thomaidis, N.S.; Usaola-García, J.; Ruiz-Arias, J.A.; Pozo-Vázquez, D. Exploring the Mean-Variance Portfolio Optimization Approach for Planning Wind Repowering Actions in Spain. Renew. Energy 2017, 106, 335–342. [Google Scholar] [CrossRef]
- Pryor, S.C.; Barthelmie, R.J.; Schoof, J.T. Inter-Annual Variability of Wind Indices across Europe. Wind Energy 2006, 9, 27–38. [Google Scholar] [CrossRef]
- Papadimas, C.D.; Fotiadi, A.K.; Hatzianastassiou, N.; Vardavas, I.; Bartzokas, A. Regional Co-Variability and Teleconnection Patterns in Surface Solar Radiation on a Planetary Scale. Int. J. Climatol. 2010, 30, 2314–2329. [Google Scholar] [CrossRef]
- Andresen, G.B.; Søndergaard, A.A.; Greiner, M. Validation of Danish Wind Time Series from a New Global Renewable Energy Atlas for Energy System Analysis. Energy 2015, 93, 1074–1088. [Google Scholar] [CrossRef]
- Zeyringer, M.; Price, J.; Fais, B.; Li, P.H.; Sharp, E. Designing Low-Carbon Power Systems for Great Britain in 2050 That Are Robust to the Spatiotemporal and Inter-Annual Variability of Weather. Nat. Energy 2018, 3, 395–403. [Google Scholar] [CrossRef]
- Pozo-Vazquez, D.; Santos-Alamillos, F.J.; Lara-Fanego, V.; Ruiz-Arias, J.A.; Tovar-Pescador, J. The Impact of the NAO on the Solar and Wind Energy Resources in the Mediterranean Area. In Hydrological, Socioeconomic and Ecological Impacts of the North Atlantic Oscillation in the Mediterranean Region; Vicente-Serrano, S.M., Trigo, R.M., Eds.; Advances in Global Change Research; Springer: Dordrecht, The Netherlands, 2011; pp. 213–231. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Kushnir, Y.; Ottersen, G.; Visbeck, M. The North Atlantic Oscillation Climatic Significance and Environmental Impact; American Geophysical Union: Washington, DC, USA, 2003. [Google Scholar]
- Thornton, H.E.; Scaife, A.A.; Hoskins, B.J.; Brayshaw, D.J. The Relationship between Wind Power, Electricity Demand and Winter Weather Patterns in Great Britain. Environ. Res. Lett. 2017, 12, 064017. [Google Scholar] [CrossRef]
- Collins, S.; Deane, P.; Gallachóir, B.Ó.; Pfenninger, S.; Staffell, I. Impacts of Inter-Annual Wind and Solar Variations on the European Power System. Joule 2018, 2, 2076–2090. [Google Scholar] [CrossRef] [PubMed]
- Bett, P.E.; Thornton, H.E.; Clark, R.T. European Wind Variability over 140 Yr. Adv. Sci. Res. 2013, 10, 51–58. [Google Scholar] [CrossRef]
- Vautard, R.; Cattiaux, J.; Yiou, P.; Thépaut, J.N.; Ciais, P. Northern Hemisphere Atmospheric Stilling Partly Attributed to an Increase in Surface Roughness. Nat. Geosci. 2010, 3, 756–761. [Google Scholar] [CrossRef]
- Bakker, A.M.R.; den Hurk, B.J.J.M.V.; Coelingh, J.P. Decomposition of the Windiness Index in the Netherlands for the Assessment of Future Long-Term Wind Supply. Wind Energy 2013, 16, 927–938. [Google Scholar] [CrossRef]
- Tobin, I.; Vautard, R.; Balog, I.; Bréon, F.M.; Jerez, S.; Ruti, P.M.; Thais, F.; Vrac, M.; Yiou, P. Assessing Climate Change Impacts on European Wind Energy from ENSEMBLES High-Resolution Climate Projections. Clim. Chang. 2015, 128, 99–112. [Google Scholar] [CrossRef]
- Barstad, I.; Sorteberg, A.; dos Santos Mesquita, M. Present and Future Offshore Wind Power Potential in Northern Europe Based on Downscaled Global Climate Runs with Adjusted SST and Sea Ice Cover. Renew. Energy 2012, 44, 398–405. [Google Scholar] [CrossRef]
- Jerez, S.; Tobin, I.; Vautard, R.; Montávez, J.P.; López-Romero, J.M.; Thais, F.; Bartok, B.; Christensen, O.B.; Colette, A.; Déqué, M.; et al. The Impact of Climate Change on Photovoltaic Power Generation in Europe. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Isaac, M.; van Vuuren, D.P. Modeling Global Residential Sector Energy Demand for Heating and Air Conditioning in the Context of Climate Change. Energy Policy 2009, 37, 507–521. [Google Scholar] [CrossRef]
- Eskeland, G.S.; Mideksa, T.K. Electricity Demand in a Changing Climate. Mitig. Adapt. Strategies Glob. Chang. 2010, 15, 877–897. [Google Scholar] [CrossRef]
- Jourdier, B. Wind Resource in Metropolitan France: Assessment Methods, Variability and Trends. Ph.D. Thesis, Ecole Polytechnique, Palaiseau, France, 2015. [Google Scholar]
- Bremen, L.V. Large-Scale Variability of Weather Dependent Renewable Energy Sources. In Management of Weather and Climate Risk in the Energy Industry; Troccoli, A., Ed.; NATO Science for Peace and Security Series C: Environmental Security; Springer: Dordrecht, The Netherlands, 2010; pp. 189–206. [Google Scholar]
- Staffell, I.; Pfenninger, S. Using Bias-Corrected Reanalysis to Simulate Current and Future Wind Power Output. Energy 2016, 114, 1224–1239. [Google Scholar] [CrossRef]
- Pfenninger, S.; Staffell, I. Long-Term Patterns of European PV Output Using 30 Years of Validated Hourly Reanalysis and Satellite Data. Energy 2016, 114, 1251–1265. [Google Scholar] [CrossRef]
- Moraes, L.; Bussar, C.; Stoecker, P.; Jacqué, K.; Chang, M.; Sauer, D.U. Comparison of Long-Term Wind and Photovoltaic Power Capacity Factor Datasets with Open-License. Appl. Energy 2018, 225, 209–220. [Google Scholar] [CrossRef]
- Schlachtberger, D.P.; Brown, T.; Schäfer, M.; Schramm, S.; Greiner, M. Cost Optimal Scenarios of a Future Highly Renewable European Electricity System: Exploring the Influence of Weather Data, Cost Parameters and Policy Constraints. Energy 2018, 163, 100–114. [Google Scholar] [CrossRef]
- Weijermars, R.; Taylor, P.; Bahn, O.; Das, S.R.; Wei, Y.M. Review of Models and Actors in Energy Mix Optimization—Can Leader Visions and Decisions Align with Optimum Model Strategies for Our Future Energy Systems? Energy Strategy Rev. 2012, 1, 5–18. [Google Scholar] [CrossRef]
- Ringkjøb, H.K.; Haugan, P.M.; Solbrekke, I.M. A Review of Modelling Tools for Energy and Electricity Systems with Large Shares of Variable Renewables. Renew. Sustain. Energy Rev. 2018, 96, 440–459. [Google Scholar] [CrossRef]
- Pfenninger, S.; DeCarolis, J.; Hirth, L.; Quoilin, S.; Staffell, I. The Importance of Open Data and Software: Is Energy Research Lagging Behind? Energy Policy 2017, 101, 211–215. [Google Scholar] [CrossRef]
- Feser, F.; Rockel, B.; von Storch, H.; Winterfeldt, J.; Zahn, M. Regional Climate Models Add Value to Global Model Data: A Review and Selected Examples. Bull. Am. Meteorol. Soc. 2011, 92, 1181–1192. [Google Scholar] [CrossRef]
- Monforti, F.; Huld, T.; Bódis, K.; Vitali, L.; D’Isidoro, M.; Lacal-Arántegui, R. Assessing Complementarity of Wind and Solar Resources for Energy Production in Italy. A Monte Carlo Approach. Renew. Energy 2014, 63, 576–586. [Google Scholar] [CrossRef]
- Von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Miettinen, K.M. Nonlinear Multiobjective Optimization; Springer: New York, NY, USA, 1999. [Google Scholar]
- Hartmann, D.L. Global Physical Climatology; Academic Press: San Diego, CA, USA, 1994. [Google Scholar] [CrossRef]
- Boccard, N. Capacity Factor of Wind Power Realized Values vs. Estimates. Energy Policy 2009, 37, 2679–2688. [Google Scholar] [CrossRef]
- GSE. Rapporto Statistico 2015: Energia Da Fonti Rinnovabili in Italia; Technical Report; GSE: Roma, Italy, 2015. [Google Scholar]
- Ruti, P.M.; Somot, S.; Giorgi, F.; Dubois, C.; Flaounas, E.; Obermann, A.; Dell’Aquila, A.; Pisacane, G.; Harzallah, A.; Lombardi, E.; et al. Med-CORDEX Initiative for Mediterranean Climate Studies. Bull. Am. Meteorol. Soc. 2016, 97, 1187–1208. [Google Scholar] [CrossRef]
- Long, C.S.; Fujiwara, M.; Davis, S.; Mitchell, D.M.; Wright, C.J. Climatology and Interannual Variability of Dynamic Variables in Multiple Reanalyses Evaluated by the SPARC Reanalysis Intercomparison Project (S-RIP). Atmos. Chem. Phys. 2017, 17, 14593–14629. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 2; Technical Report NCAR/TN-468+STR; NCAR: Boulder, CO, USA, 2005. [Google Scholar]
- Drobinski, P.; Ducrocq, V.; Alpert, P.; Anagnostou, E.; Béranger, K.; Borga, M.; Braud, I.; Chanzy, A.; Davolio, S.; Delrieu, G.; et al. HyMeX A 10-Year Multidisciplinary Program on the Mediterranean Water Cycle. Bull. Am. Meteorol. Soc. 2014, 95, 1063–1082. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Salameh, T.; Drobinski, P.; Dubos, T. The Effect of Indiscriminate Nudging Time on Large and Small Scales in Regional Climate Modelling: Application to the Mediterranean Basin. Q. J. R. Meteorol. Soc. 2010, 136, 170–182. [Google Scholar] [CrossRef]
- Omrani, H.; Drobinski, P.; Dubos, T. Optimal Nudging Strategies in Regional Climate Modelling: Investigation in a Big-Brother Experiment over the European and Mediterranean Regions. Clim. Dyn. 2013, 41, 2451–2470. [Google Scholar] [CrossRef]
- Omrani, H.; Drobinski, P.; Dubos, T. Using Nudging to Improve Global-Regional Dynamic Consistency in Limited-Area Climate Modeling: What Should We Nudge? Clim. Dyn. 2015, 44, 1627–1644. [Google Scholar] [CrossRef]
- Flaounas, E.; Drobinski, P.; Vrac, M.; Bastin, S.; Lebeaupin-Brossier, C.; Stéfanon, M.; Borga, M.; Calvet, J.C. Precipitation and Temperature Space–Time Variability and Extremes in the Mediterranean Region: Evaluation of Dynamical and Statistical Downscaling Methods. Clim. Dyn. 2013, 40, 2687–2705. [Google Scholar] [CrossRef]
- Stéfanon, M.; Drobinski, P.; D’Andrea, F.; Lebeaupin-Brossier, C.; Bastin, S. Soil Moisture-Temperature Feedbacks at Meso-Scale during Summer Heat Waves over Western Europe. Clim. Dyn. 2014, 42, 1309–1324. [Google Scholar] [CrossRef]
- Chiriaco, M.; Bastin, S.; Yiou, P.; Haeffelin, M.; Dupont, J.C.; Stéfanon, M. European Heatwave in July 2006: Observations and Modeling Showing How Local Processes Amplify Conducive Large-Scale Conditions. Geophys. Res. Lett. 2014, 41, 5644–5652. [Google Scholar] [CrossRef]
- Lebeaupin Brossier, C.L.; Drobinski, P.; Béranger, K.; Bastin, S.; Orain, F. Ocean Memory Effect on the Dynamics of Coastal Heavy Precipitation Preceded by a Mistral Event in the Northwestern Mediterranean. Q. J. R. Meteorol. Soc. 2013, 139, 1583–1597. [Google Scholar] [CrossRef]
- Lebeaupin Brossier, C.L.; Bastin, S.; Béranger, K.; Drobinski, P. Regional Mesoscale Air–Sea Coupling Impacts and Extreme Meteorological Events Role on the Mediterranean Sea Water Budget. Clim. Dyn. 2015, 44, 1029–1051. [Google Scholar] [CrossRef]
- Berthou, S.; Mailler, S.; Drobinski, P.; Arsouze, T.; Bastin, S.; Béranger, K.; Lebeaupin-Brossier, C. Prior History of Mistral and Tramontane Winds Modulates Heavy Precipitation Events in Southern France. Tellus A Dyn. Meteorol. Oceanogr. 2014, 66, 24064. [Google Scholar] [CrossRef]
- Berthou, S.; Mailler, S.; Drobinski, P.; Arsouze, T.; Bastin, S.; Béranger, K.; Lebeaupin-Brossier, C. Sensitivity of an Intense Rain Event between Atmosphere-Only and Atmosphere–Ocean Regional Coupled Models: 19 September 1996. Q. J. R. Meteorol. Soc. 2015, 141, 258–271. [Google Scholar] [CrossRef]
- Berthou, S.; Mailler, S.; Drobinski, P.; Arsouze, T.; Bastin, S.; Béranger, K.; Flaounas, E.; Brossier, C.L.; Somot, S.; Stéfanon, M. Influence of Submonthly Air–Sea Coupling on Heavy Precipitation Events in the Western Mediterranean Basin. Q. J. R. Meteorol. Soc. 2016, 142, 453–471. [Google Scholar] [CrossRef]
- Omrani, H.; Drobinski, P.; Arsouze, T.; Bastin, S.; Lebeaupin-Brossier, C.; Mailler, S. Spatial and Temporal Variability of Wind Energy Resource and Production over the North Western Mediterranean Sea: Sensitivity to Air-Sea Interactions. Renew. Energy 2017, 101, 680–689. [Google Scholar] [CrossRef]
- Drobinski, P.; Anav, A.; Lebeaupin Brossier, C.; Samson, G.; Stéfanon, M.; Bastin, S.; Baklouti, M.; Béranger, K.; Beuvier, J.; Bourdallé-Badie, R.; et al. Model of the Regional Coupled Earth System (MORCE): Application to Process and Climate Studies in Vulnerable Regions. Environ. Model. Softw. 2012, 35, 1–18. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Fujiwara, M.; Wright, J.S.; Manney, G.L.; Gray, L.J.; Anstey, J.; Birner, T.; Davis, S.; Gerber, E.P.; Harvey, V.L.; Hegglin, M.I.; et al. Introduction to the SPARC Reanalysis Intercomparison Project (S-RIP) and Overview of the Reanalysis Systems. Atmos. Chem. Phys. 2017, 17, 1417–1452. [Google Scholar] [CrossRef]
- Jurado, M.; Caridad, J.M.; Ruiz, V. Statistical Distribution of the Clearness Index with Radiation Data Integrated over Five Minute Intervals. Sol. Energy 1995, 55, 469–473. [Google Scholar] [CrossRef]
- Tovar, J.; Olmo, F.J.; Alados-Arboledas, L. One-Minute Global Irradiance Probability Density Distributions Conditioned to the Optical Air Mass. Sol. Energy 1998, 62, 387–393. [Google Scholar] [CrossRef]
- Holttinen, H.; Meibom, P.; Orths, A.; Lange, B.; O’Malley, M.; Tande, J.O.; Estanqueiro, A.; Gomez, E.; Söder, L.; Strbac, G.; et al. Impacts of Large Amounts of Wind Power on Design and Operation of Power Systems, Results of IEA Collaboration. Wind Energy 2011, 14, 179–192. [Google Scholar] [CrossRef]
- Justus, C.G.; Mikhail, A. Height Variation of Wind Speed and Wind Distributions Statistics. Geophys. Res. Lett. 1976, 3, 261–264. [Google Scholar] [CrossRef]
- Villanueva, D.; Feijóo, A.; Pazos, J.L. Multivariate Weibull Distribution for Wind Speed and Wind Power Behavior Assessment. Resources 2013, 2, 370–384. [Google Scholar] [CrossRef]
- Hosenuzzaman, M.; Rahim, N.A.; Selvaraj, J.; Hasanuzzaman, M.; Malek, A.B.M.A.; Nahar, A. Global Prospects, Progress, Policies, and Environmental Impact of Solar Photovoltaic Power Generation. Renew. Sustain. Energy Rev. 2015, 41, 284–297. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J.A. On the Temperature Dependence of Photovoltaic Module Electrical Performance: A Review of Efficiency/Power Correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Diffuse Fraction Correlations. Sol. Energy 1990, 45, 1–7. [Google Scholar] [CrossRef]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Evaluation of Hourly Tilted Surface Radiation Models. Sol. Energy 1990, 45, 9–17. [Google Scholar] [CrossRef]
- Weron, R. Modeling and Forecasting Electricity Loads and Prices; John Wiley & Sons: Chichester, UK, 2006. [Google Scholar]
- Bessec, M.; Fouquau, J. The Non-Linear Link between Electricity Consumption and Temperature in Europe: A Threshold Panel Approach. Energy Econ. 2008, 30, 2705–2721. [Google Scholar] [CrossRef]
- Damm, A.; Köberl, J.; Prettenthaler, F.; Rogler, N.; Töglhofer, C. Impacts of +2 Degree C Global Warming on Electricity Demand in Europe. Clim. Services 2017, 7, 12–30. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Electricity Consumption Forecasting in Italy Using Linear Regression Models. Energy 2009, 34, 1413–1421. [Google Scholar] [CrossRef]
- Apadula, F.; Bassini, A.; Elli, A.; Scapin, S. Relationships between Meteorological Variables and Monthly Electricity Demand. Appl. Energy 2012, 98, 346–356. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Linear Regression Models to Forecast Electricity Consumption in Italy. Energy Sources Part B Econ. Plan. Policy 2013, 8, 86–93. [Google Scholar] [CrossRef]
- De Felice, M.; Alessandri, A.; Ruti, P.M. Electricity Demand Forecasting over Italy: Potential Benefits Using Numerical Weather Prediction Models. Electr. Power Syst. Res. 2013, 104, 71–79. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Terna. Sustainability Report 2016; Technical Report; Terna: Rome, Italy, 2016. [Google Scholar]
- MacKay, D.J.C. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Müller, A.C.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API Design for Machine Learning Software: Experiences from the Scikit-Learn Project. arXiv 2013, arXiv:1309.0238. [Google Scholar]
- Mencarelli, L.; D’Ambrosio, C. Complex Portfolio Selection via Convex Mixed-Integer Quadratic Programming: A Survey. Int. Trans. Oper. Res. 2018, 26, 389–414. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Goldfarb, D.; Idnani, A. A Numerically Stable Dual Method for Solving Strictly Convex Quadratic Programs. Math. Programm. 1983, 27, 1–33. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tantet, A.; Stéfanon, M.; Drobinski, P.; Badosa, J.; Concettini, S.; Cretì, A.; D’Ambrosio, C.; Thomopulos, D.; Tankov, P. e4clim 1.0: The Energy for a Climate Integrated Model: Description and Application to Italy. Energies 2019, 12, 4299. https://doi.org/10.3390/en12224299
Tantet A, Stéfanon M, Drobinski P, Badosa J, Concettini S, Cretì A, D’Ambrosio C, Thomopulos D, Tankov P. e4clim 1.0: The Energy for a Climate Integrated Model: Description and Application to Italy. Energies. 2019; 12(22):4299. https://doi.org/10.3390/en12224299
Chicago/Turabian StyleTantet, Alexis, Marc Stéfanon, Philippe Drobinski, Jordi Badosa, Silvia Concettini, Anna Cretì, Claudia D’Ambrosio, Dimitri Thomopulos, and Peter Tankov. 2019. "e4clim 1.0: The Energy for a Climate Integrated Model: Description and Application to Italy" Energies 12, no. 22: 4299. https://doi.org/10.3390/en12224299
APA StyleTantet, A., Stéfanon, M., Drobinski, P., Badosa, J., Concettini, S., Cretì, A., D’Ambrosio, C., Thomopulos, D., & Tankov, P. (2019). e4clim 1.0: The Energy for a Climate Integrated Model: Description and Application to Italy. Energies, 12(22), 4299. https://doi.org/10.3390/en12224299