Improving Energy Efficiency Fairness of Wireless Networks: A Deep Learning Approach

Abstract

Achieving energy efficiency (EE) fairness among heterogeneous mobile devices will become a crucial issue in future wireless networks. This paper investigates a deep learning (DL) approach for improving EE fairness performance in interference channels (IFCs) where multiple transmitters simultaneously convey data to their corresponding receivers. To improve the EE fairness, we aim to maximize the minimum EE among multiple transmitter–receiver pairs by optimizing the transmit power levels. Due to fractional and max-min formulation, the problem is shown to be non-convex, and, thus, it is difficult to identify the optimal power control policy. Although the EE fairness maximization problem has been recently addressed by the successive convex approximation framework, it requires intensive computations for iterative optimizations and suffers from the sub-optimality incurred by the non-convexity. To tackle these issues, we propose a deep neural network (DNN) where the procedure of optimal solution calculation, which is unknown in general, is accurately approximated by well-designed DNNs. The target of the DNN is to yield an efficient power control solution for the EE fairness maximization problem by accepting the channel state information as an input feature. An unsupervised training algorithm is presented where the DNN learns an effective mapping from the channel to the EE maximizing power control strategy by itself. Numerical results demonstrate that the proposed DNN-based power control method performs better than a conventional optimization approach with much-reduced execution time. This work opens a new possibility of using DL as an alternative optimization tool for the EE maximizing design of the next-generation wireless networks.

1. Introduction

For the last decade, energy efficiency (EE) of wireless communication systems, which measures the effectiveness of the power consumption utilized for the data transmission, has been emerging as an important performance metric for the next-generation networking scenarios including wireless sensor networks, device-to-device communications, and internet-of-things (IoT) systems [1,2,3,4,5,6,7,8,9,10]. The EE metric was introduced in [1], and it is defined as the ratio of achievable data rate to total power consumption. The fractional programming framework was employed in [1,2] to address the EE maximization problems in various configurations. Extending these works, the EE maximizing cooperative communication strategies were investigated in the multi-cell multi-user networks [3,4,5,6,7,8,9,10]. Weighted sum EE metrics was intensively studied in [4,5,6,7]. Zero forcing (ZF)-based coordinated beamforming schemes were proposed in [4], which maximize the sum EE of the multiple heterogeneous networks. To further increase the EE performance, the works in [5,6,7] relaxed the ZF assumption and presented optimization algorithms for identifying efficient precoding solution without the ZF condition. Due to the multi-cell and multi-user interference terms, the weighted sum EE maximization problems are no longer convex and cannot be tackled by the off-the-shelf convex optimization software. Hence, handling the non-convexity of the EE maximization tasks has been an important issue in the multi-cell environment. The authors of [5,6] employed the fractional programming framework for the weighted EE maximization problem in the multi-cell systems and provided alternating optimization algorithms where blocks of the optimization variables are determined in an iterative manner. However, such an alternating calculation loses the globally optimality of the weighted EE maximization problems. This issue was addressed in [7] by applying the branch-and-bound (BnB) method, which iteratively searches lower and upper bounds of the original problem and converges the globally optimal point. However, the iterative bound searches and solution calculations of the BnB algorithm would result in high computational complexity for the fast fading environment where the beamforming solution may not be timely obtained for the real-time communication services.

The sum EE maximization would not be an appropriate design approach since it cannot guarantee the quality of the EE for heterogeneous wireless devices. In particular, in the multi-cell systems, the EE of each cell was defined as the sum EE of all intra-cell users [4,5,6,7]. Obviously, such a design leads to highly unbalanced EE performance among multiple cells and mobile users, and cannot guarantee the EE performance of each wireless devices. To overcome this issue, the EE fairness has been suggested as an alternative performance measure of the sum EE metric [3,8,9,10]. The fairness of the EE can be examined by the minimum EE performance among multiple wireless devices. Thus, the EE fairness optimization has been typically expressed as the maximization task of the minimum EE performance, resulting in the max-min formulations. The max-min nature of the EE fairness formulation ensures that all the wireless devices achieve the same level of EE performance. However, the maximization of the EE fairness would be more difficult than that of the sum EE performance due to the non-smooth and non-convex objective functions. The Dinkelhach method was adopted in [8] along with the alternating optimization process for solving the EE fairness maximization problem in the multi-cell networks. To reduce the computational complexity of the alternating optimization, the successive convex approximation (SCA) framework was applied to maximize the minimum EE performance [3,9,10]. Among those, the conic approximation strategy provided in [3] has been revealed as the most effective solution in terms of both the performance and the computational complexity.

The previous works have mostly focused on the traditional optimization techniques, and thus they relied on the convex optimization software such as the CVX. The optimization approaches are powerful for identifying model-based calculation algorithms with guaranteed convergence. However, the convex optimization software generally requires iterative computations for each channel realization, implying that the algorithms in [3,8,9,10] would not be practical for the fast fading environment in which the channel statistics would change before computing the solution. Hence, the conventional optimization approaches might not be a good solution for handling the EE fairness maximization problems in real-time communication scenarios. In addition, due to the non-convexity of the EE formulation, the optimization algorithms in [3,8,9,10] cannot guarantee the globally optimality for their convergence point. It is thus not easy to identify the globally optimal performance based on the traditional optimization techniques.

To tackle these difficulties, deep learning (DL) techniques [11,12] have recently applied in the design of wireless communication systems [13,14,15,16,17] and resource management algorithms [18,19,20,21,22,23]. The data-driven optimization capability of the DL has been shown to be efficient for addressing model-free and non-convex formulations in the wireless communication networks. The possibility of the DL was investigated in [13,14,15,16,17] for a design of end-to-end physical layer communication modules. Meanwhile, there have been intensive studies on using deep neural networks (DNNs) to solve wireless resource allocation problems [18,19,20,21,22,23]. The authors of [18] proposed a supervised learning method which learns the input–output behavior of an existing power control scheme, the weighted minimum mean square error (WMMSE) algorithm, to maximize the sum rate performance in an interference channel (IFC) setup. The method in [18] achieves a similar performance of the WMMSE algorithm with much reduced time complexity. However, the supervised learning nature in [18] can only produce the DNN simply memorizing the locally optimal solution of the WMMSE algorithm. Hence, it is not easy to handle the non-convexity of the resource allocation problems and the supervised learning approach generally yields the degraded sum rate performance.

Unsupervised learning-based power control schemes have recently been investigated [19,20,21,22,23] to overcome the limitations of the supervised training strategy. The unsupervised learning does not need the training label data, i.e., the solution obtained by the WMMSE as in [18], and finds an effective resource management solution by itself. The DNNs are employed to approximate the unknown optimal solution directly, whose approximation accuracy is guaranteed by the universal approximation theorem. As a result, it is possible to identify the globally optimal resource allocation solution by utilizing well-designed DNNs. In [19], the sum rate and the sum EE maximization problems were tackled via the DNNs trained in an unsupervised manner. It was shown that the unsupervised learning techniques perform better than the WMMSE algorithm which achieves a locally optimal solution for the sum rate maximization problem. In addition, the computational complexity of the DNN-based power control scheme is much lower than that of the WMMSE method requiring the iterative calculations. Similar results have been observed in [20,21,22,23], where the possibilities of the DNN for solving the non-convex sum rate maximization problem in cognitive radio and device-to-device communication setups. However, since these methods are restricted to the sum performance optimization, it is still not clear whether the DL-based approach is valid for the EE fairness maximization task with the fractional and non-smooth objective function.

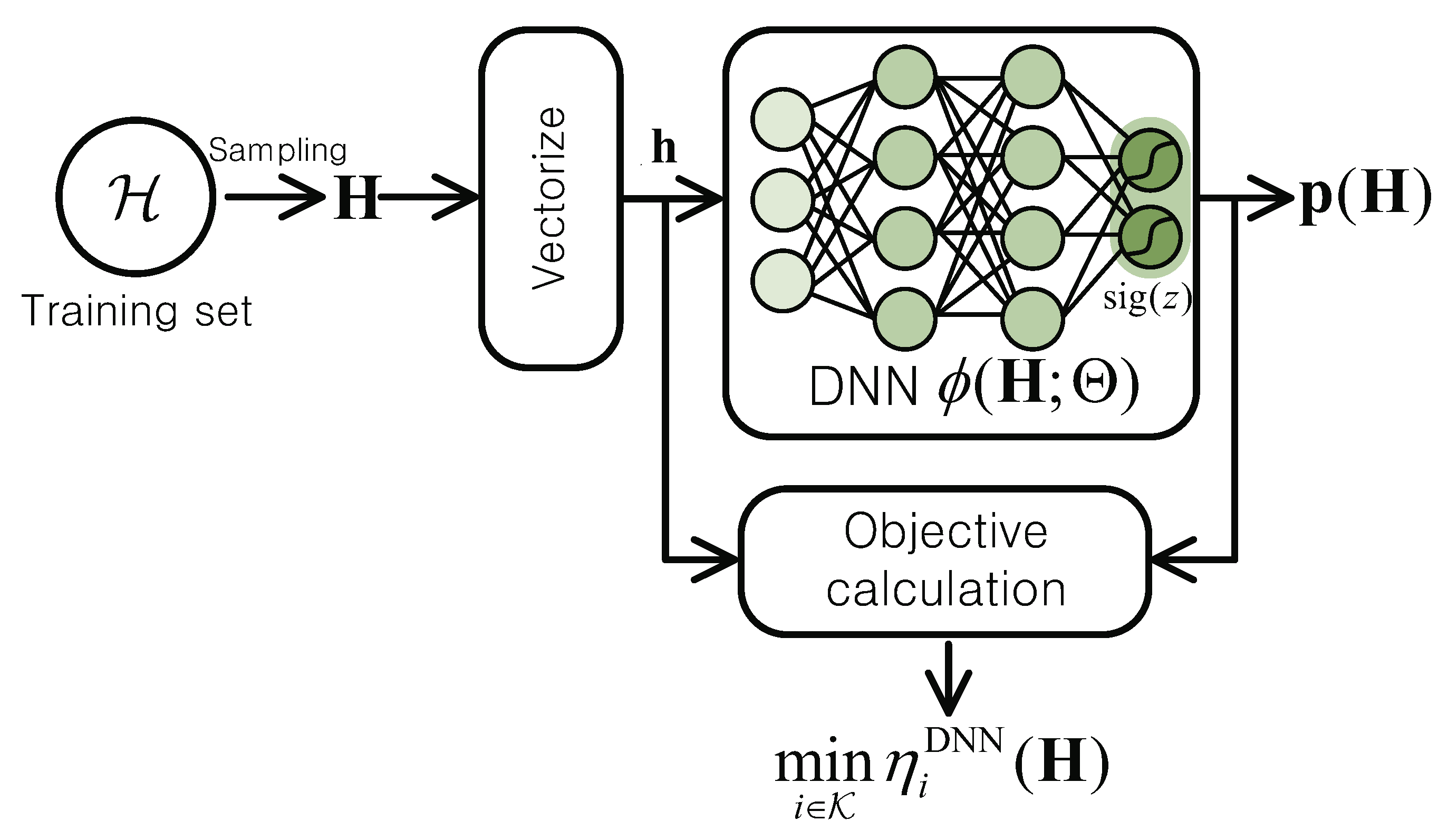
In this paper, we revisit the EE fairness maximization problem for the IFC, where the globally optimal solution is generally not available due to the non-convexity [3]. Our target is to apply the DL technique for improving the EE fairness performance of existing optimization approaches as well as reducing the computational complexity. We introduce a fully-connected DNN structure for approximating a mapping from the channel vector to the optimal power control solution. The original EE fairness maximization problem determining unknown solution computation strategy is reformulated into the training task of the DNN such that it can produce an effective power allocation solution. However, the state-of-the-art DL libraries, which are based on the gradient descent (GD) method, would not be feasible in our formulation due to the non-smooth max-min EE objective function. We thus derive a modification of the GD update rule for the EE fairness maximization problem. An unsupervised training algorithm is proposed which does not require any information regarding the optimal power control policy. The test performance of the trained DNN was examined through intensive numerical simulations. It was verified that the proposed DNN-based power control scheme performs better than the best known performance achieved by the SCA framework [3]. In addition, the numerical results prove that the DNN can significantly reduce the execution time of the conventional SCA method.

This paper is organized as follows. Section 2 describes the system model for the IFC and formulates the EE fairness maximization problem. The proposed DNN approach and the unsupervised training strategy are presented in Section 3. We provide numerical results of the trained DNNs in Section 4 and compare its performance with traditional optimization approaches. Finally, the paper is terminated with conclusions in Section 5.

Throughout this paper, we employ uppercase boldface letters, lowercase boldface letters, and normal letters for matrices, vectors, and scalar quantities, respectively. Sets of m-by-n complex-valued and real-valued matrices are denoted by ${\mathbb{C}}^{m\times n}$ and ${\mathbb{R}}^{m\times n}$, respectively. The expectation operation over random variable X is represented as ${\mathbb{E}}_X[·]$.

2. System Model

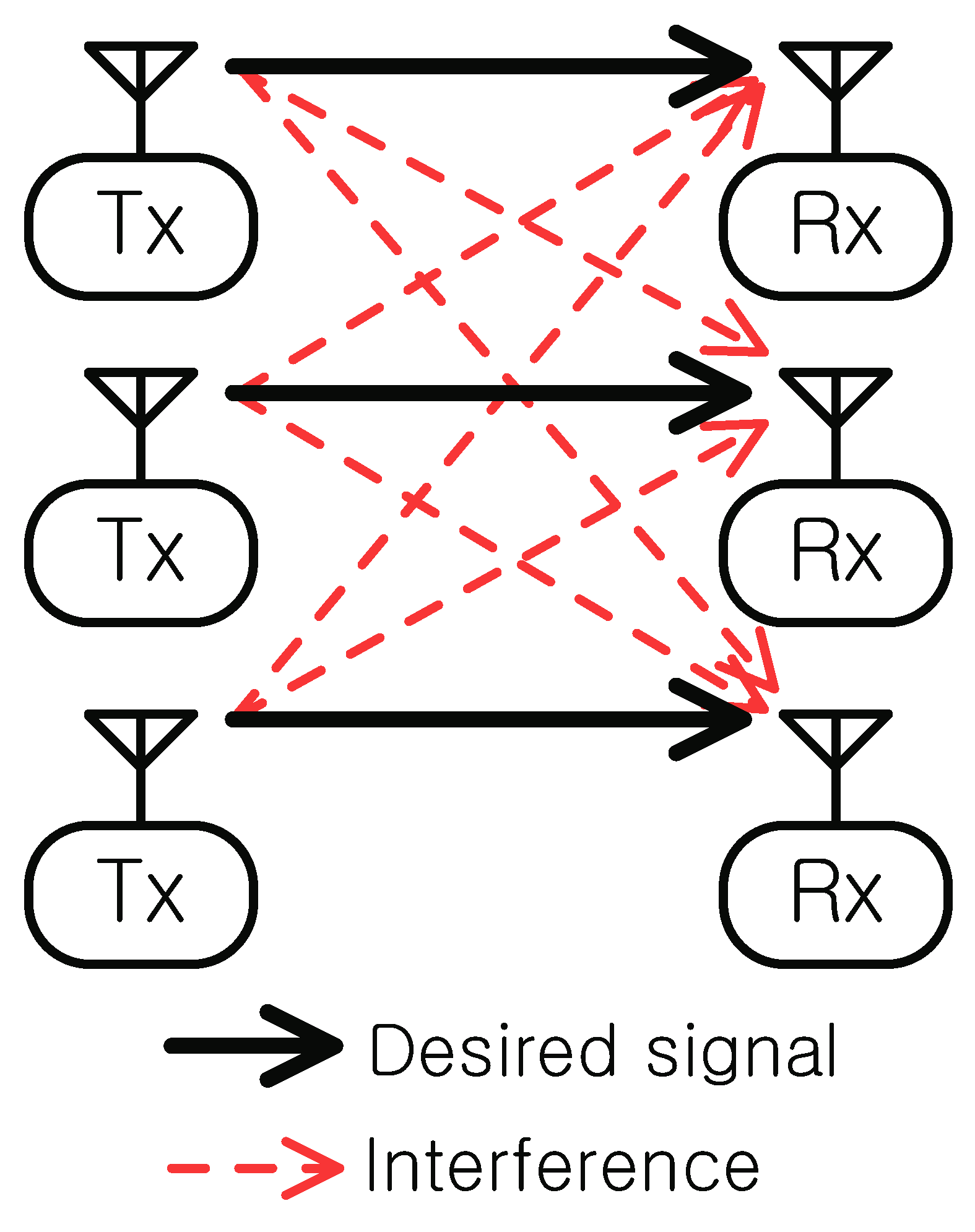
We consider an IFC in Figure 1 in which multiple transmitters convey information to multiple receivers at the same time over the same frequency band. Without loss of the generality, it is assumed that there exist total K transmitter–receiver pairs. Let $\mathcal{K}\triangleq \{1,\cdots ,K\}$ be the set of indices of the transmitters and receivers, i.e., index k can refer to transmitter k or receiver k. Each receiver is supported by its corresponding transmitter, and the signals leaked from each transmitter to other receivers act as interference degrading the communication performance. Such a scenario prevails in practical wireless networks including multi-cell communication systems, IoT, and device-to-device networks.

Throughout the paper, quasi-static frequency-flat fading is assumed, but the channel coefficient would vary at each transmission time block. Denoting $g_{ij}\in \mathbb{C}$ as the complex channel coefficient between transmitter i and receiver j ($i,j\in \mathcal{K}$), the received signal $y_i\in \mathbb{C}$ at receiver i is written by

$$\begin{array}{c}\hfill y_i=\sqrt{p_i}{g}_{ii}{x}_i+\sum _{j\in \mathcal{K}\setminus i}\sqrt{p_j}{g}_{ji}{x}_j+n_i,\end{array}$$

(1)

where $x_i\sim \mathcal{CN}(0,1)$ stands for the transmitted symbol at transmitter i, $n_i\sim \mathcal{CN}(0,1)$ equals the Gaussian noise, and $p_i$ is the transmit power of transmitter i. From  Equation (1), the data rate achieved at receiver i is written by

$$\begin{array}{c}\hfill R_i\left(\mathbf{H}\right)=log\left(1+\frac{h_{ii}{p}_i\left(\mathbf{H}\right)}{1+{\sum }_{j\in \mathcal{K}\setminus i}{h}_{ji}{p}_j\left(\mathbf{H}\right)}\right).\end{array}$$

(2)

where $h_{ij}\triangleq {\left|g_{ij}\right|}^2$ is the channel gain between transmitter i and receiver j, $\mathbf{H}=\{h_{ij},\forall i,j\in \mathcal{K}\}\in {\mathbb{C}}^{K\times K}$ indicates the channel matrix collecting all the channel gains. Here, the transmit power $p_i\left(\mathbf{H}\right)$, $\forall i\in \mathcal{K}$, is now represented as a function of the channel gain matrix $\mathbf{H}$ to be optimized for each channel realization $\mathbf{H}$.

The EE of transmitter i is defined as the ratio of the achievable rate $R_i\left(\mathbf{H}\right)$ to its total power consumption $Q_i\left(\mathbf{H}\right)$ which includes the overall power related to the signal transmission and circuit operations. The total power consumption $Q_i\left(\mathbf{H}\right)$ at transmitter i can be characterized as [3,10]

$$\begin{array}{c}\hfill Q_i\left(\mathbf{H}\right)=\frac{1}{\zeta }{p}_i\left(\mathbf{H}\right)+P_C,\end{array}$$

(3)

where $\zeta \in (0,1]$ accounts for the efficiency of the power amplifier and $P_C$ denotes the static operation power of circuitry such as the mixer, the cooling systems, the power supply, the frequency synthesizer, the digital-to-analog converter, etc. [1]. Then, the EE ${\eta }_i\left(\mathbf{H}\right)$ of transmitter i is expressed as

$$\begin{array}{c}\hfill {\eta }_i\left(\mathbf{H}\right)=\frac{R_i\left(\mathbf{H}\right)}{Q_i\left(\mathbf{H}\right)}=\frac{log\left(1+\frac{h_{ii}{p}_i\left(\mathbf{H}\right)}{1+{\sum }_{j\in \mathcal{K}\setminus i}{h}_{ji}{p}_j\left(\mathbf{H}\right)}\right)}{\frac{1}{\epsilon }{p}_i\left(\mathbf{H}\right)+P_C}.\end{array}$$

(4)

In a practical IFC setup, due to the heterogeneous nature of wireless propagation, the EE performance of multiple transmitter–receiver pairs is highly asymmetric. Hence, we desire to balance the EE performance by maximizing the minimum EE averaged over an arbitrary given fading distribution $\mathbf{H}$. The instantaneous minimum EE ${\eta }_{min}\left(\mathbf{H}\right)$ for a given channel realization $\mathbf{H}$ can be represented as

$$\begin{array}{c}\hfill {\eta }_{min}\left(\mathbf{H}\right)=\underset{i\in \mathcal{K}}{min}{\eta }_i\left(\mathbf{H}\right)=\underset{i\in \mathcal{K}}{min}\frac{log\left(1+\frac{h_{ii}{p}_i\left(\mathbf{H}\right)}{1+{\sum }_{j\in \mathcal{K}\setminus i}{h}_{ji}{p}_j\left(\mathbf{H}\right)}\right)}{\frac{1}{\epsilon }{p}_i\left(\mathbf{H}\right)+P_C}\end{array}$$

(5)

Then, the problem for maximizing the average minimum EE ${\mathbb{E}}_{\mathbf{H}}\left[{\eta }_{min}\left(\mathbf{H}\right)\right]={\mathbb{E}}_{\mathbf{H}}\left[{min}_{i\in \mathcal{K}}{\eta }_i\left(\mathbf{H}\right)\right]$ is formulated as

$$\begin{array}{cc}\hfill & \underset{\mathbf{p}\left(\mathbf{H}\right)}{max}{\mathbb{E}}_{\mathbf{H}}\left[\underset{i\in \mathcal{K}}{min}{\eta }_i\left(\mathbf{H}\right)\right]\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \mathrm{subject}\mathrm{to}0\le p_i\left(\mathbf{H}\right)\le P_i,\forall i\in \mathcal{K},\hfill \end{array}$$

(7)

where $\mathbf{p}\left(\mathbf{H}\right)\triangleq \{p_i\left(\mathbf{H}\right),\forall i\in \mathcal{K}\}\in {\mathbb{R}}^{N\times 1}$ is the concatenation of the transmit power of all the transmitters and the constraint in Equation (7) indicates the transmit power constraint with $P_i$ being the maximum allowable transmit power budget at transmitter i.

In general, Equation (6) is a non-convex problem [24], and it is highly difficult to identify the globally optimal solution ${\mathbf{p}}^{\star }\left(\mathbf{H}\right)$. To address the non-convexity of Equation (6), theoretical optimization techniques have been applied in recent literature [3,10]. In particular, the SCA framework [25] is adapted in [3,10], which tackle a series of convex approximations of Equation (6) in an iterative manner. The monotonic convergence and the complexity analysis of these SCA-based algorithms have been intensively studied. However, the conventional methods [3,10] suffer from several implementation challenges. First, due to the coupled variables in the objective function of Equation (6), the SCA framework cannot guarantee the quality of the convergence points of the SCA algorithms. To be specific, the conventional methods can only satisfy the necessary optimality condition, and, obviously, this limits the performance of the solution since they generally converges to poor local optimum and saddle points. Next, the iterative nature of the SCA framework incurs expensive and repetitive calculations for the algorithms in [3,10], resulting in the expensive computation cost for the transmitters. This becomes severe in the fast fading scenario where the channel coefficients $\mathbf{H}$ changes before computing the solution of Equation (6) through the iterations.

To overcome such limitations of traditional optimization approaches, we propose a DL-based power control scheme for the minimum EE maximization problem in Equation (6). The DL-based resource management techniques have been recently investigated [18,19,20,21,22,23]. Existing studies have mostly focused on the sum rate maximization problem [18,20,21,22,23], which has been known to be simpler than our formulation in Equation (6). Although the sum EE maximization was considered in [19], it is not clear whether the max-min EE formulation can be indeed addressed by the DL algorithms. Therefore, the expression power of the DNNs for solving the EE fairness problem in Equation (6) has not been adequately examined in the literature. It is worth noting that, since the training of DNNs are typically based on the gradient descent method [12,26], it would not be straightforward to verify the feasibility of the state-of-the-art DL libraries for addressing the non-smooth optimization problem in Equation (6). Therefore, maximizing the EE fairness performance is a nontrivial task through the exiting sum metric training rules [18,19,20,21,22,23].

3. Proposed DL-Based Power Control Scheme

In this section, we present a DL approach to solve the non-convex EE fairness problem in Equation (6) efficiently. The basics of the DL are briefly introduced, followed by the proposed DL-based solution.

3.1. DL Basics

As illustrated in Figure 2, we consider a fully-connected DNN with an input layer, L hidden layers, and an output layer. The DNN computes an output vector ${\mathbf{x}}_{L+1}\in {\mathbb{R}}^{N_{L+1}\times 1}$ of length $N_{L+1}$ for a given input feature ${\mathbf{x}}_0\in {\mathbb{R}}^{N_0\times 1}$ of length $N_0$. The input vector ${\mathbf{x}}_0$ is regarded as the training data sampled from the training set $\mathcal{X}\triangleq \left\{{\mathbf{x}}_0\right\}$ collected in advance. When the distribution of ${\mathbf{x}}_0$ is available, e.g., the Rayleigh fading, the training data can be randomly generated from the known probability density function. The end-to-end operation of the DNN is characterized by a mapping $\varphi :{\mathbb{R}}^{N_0\times 1}\to {\mathbb{R}}^{N_{L+1}\times 1}$. For convenience, let us denote layer 0 and $L+1$ as the input and output layers, respectively, whereas hidden layers are represented by layer l for $l=1,\cdots ,L$. Each layer l for $l=1,\cdots ,L,L+1$ produces its output vector ${\mathbf{x}}_l\in {\mathbb{R}}^{N_l\times 1}$ of length $N_l$ from its input ${\mathbf{x}}_{l-1}\in {\mathbb{R}}^{N_{l-1}\times 1}$ of length $N_{l-1}$, which is obtained from the preceding layer $l-1$. To be specific, the output ${\mathbf{x}}_l$ of layer l is given by

$$\begin{array}{c}\hfill {\mathbf{x}}_l={\sigma }_l({\mathbf{W}}_l{\mathbf{x}}_{l-1}+{\mathbf{b}}_l),\end{array}$$

(8)

where ${\sigma }_l(·)$ stands for an activation function at layer l, and ${\mathbf{W}}_l\in {\mathbb{R}}^{N_l\times N_{l-1}}$ and ${\mathbf{b}}_l\in {\mathbb{R}}^{N_l\times 1}$ denote a weight matrix and a bias vector at layer l, respectively. From  Equation (8), it can be seen that the calculation of each layer is expressed as linear matrix multiplication and addition followed by the activation function. The activation function ${\sigma }_l(·)$ is an element-wise function which introduces the non-linearity to the DNN. Possible candidates for the activation functions are the sigmoid function, $\mathrm{sig}\left(z\right)\triangleq \frac{1}{1+e^{-z}}$, rectified linear unit (ReLU) function, $\mathrm{ReLU}\left(z\right)\triangleq max\{0,z\}$, etc. Since the choice of the activation functions is directly related to the expression capability of the DNN, we need to carefully determine efficient functions $\{{\sigma }_l(·),\forall l\}$ by examining the validation performance.

Finally, the output ${\mathbf{x}}_{L+1}$ of the DNN is obtained through $L+1$ successive computations in Equation (8). When $\mathsf{\Theta }\triangleq \{{\mathbf{W}}_l,{\mathbf{b}}_l,\forall l\}$ includes the set of the weight matrices and the bias vectors of the DNN, the end-to-end calculation of the DNN can be written as

$$\begin{array}{cc}\hfill {\mathbf{x}}_{L+1}& ={\sigma }_{L+1}({\mathbf{W}}_{L+1}{\sigma }_L({\mathbf{W}}_L\cdots {\sigma }_1({\mathbf{W}}_1{\mathbf{x}}_0+{\mathbf{b}}_1)\cdots +{\mathbf{b}}_L)+{\mathbf{b}}_{L+1}),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \triangleq \varphi ({\mathbf{x}}_0;\mathsf{\Theta }),\hfill \end{array}$$

(10)

where the mapping ${\mathbf{x}}_{L+1}=\varphi ({\mathbf{x}}_0;\mathsf{\Theta })$ characterizes the end-to-end operation of the DNN. The aim of the DL is to identify the parameter set $\mathsf{\Theta }$ minimizing (or maximizing) a certain objective function $\mathcal{C}\left(\mathsf{\Theta }\right)$ specifying targets and applications of the DNN. The objective function includes the performance of the training samples ${\mathbf{x}}_0$ by measuring the average performance over the training set $\mathcal{X}$. In general, the objective function $\mathcal{C}\left(\mathsf{\Theta }\right)$ can be written by

$$\begin{array}{c}\hfill \mathcal{C}\left(\mathsf{\Theta }\right)={\mathbb{E}}_{\mathcal{X}}\left[c({\mathbf{x}}_0,{\mathbf{x}}_{L+1};\mathsf{\Theta })\right],\end{array}$$

(11)

where the function $c({\mathbf{x}}_0,{\mathbf{x}}_{L+1};\mathsf{\Theta })$ stands for the objective of each training sample ${\mathbf{x}}_0\in \mathcal{X}$. The minimization of $\mathcal{C}\left(\mathsf{\Theta }\right)$ with respect to $\mathsf{\Theta }$ is regarded as the training of the DNN. Due to non-convexity of the activation functions and serial calculations in Equation (8), the solution to minimize $\mathcal{C}\left(\mathsf{\Theta }\right)$ cannot be obtained in a closed-form expression. To this end, the state-of-the-art DL techniques employ the mini-batch stochastic gradient descent (SGD) method for determining an efficient DNN parameter $\mathsf{\Theta }$ [12]. An iterative update rule of the mini-batch SGD at training iteration t is expressed as

$$\begin{array}{cc}\hfill {\mathsf{\Theta }}^{\left[t\right]}& ={\mathsf{\Theta }}^{[t-1]}-\alpha {\nabla }_{\mathsf{\Theta }}\mathcal{C}\left({\mathsf{\Theta }}^{[t-1]}\right),\hfill \\ \hfill & ={\mathsf{\Theta }}^{[t-1]}-\alpha {\mathbb{E}}_{\mathcal{X}}\left[{\nabla }_{\mathsf{\Theta }}c({\mathbf{x}}_0,{\mathbf{x}}_{L+1};{\mathsf{\Theta }}^{[t-1]})\right],\hfill \\ \hfill & \simeq {\mathsf{\Theta }}^{[t-1]}-\alpha \frac{1}{S}\sum _{{\mathbf{x}}_0\in \mathcal{S}}{\nabla }_{\mathsf{\Theta }}c({\mathbf{x}}_0,{\mathbf{x}}_{L+1};{\mathsf{\Theta }}^{[t-1]}),\hfill \end{array}$$

(12)

where ${\mathsf{\Theta }}^{\left[t\right]}$ is the DNN parameter obtained at iteration t, $\alpha >0$ denotes the learning rate, and ${\nabla }_{\mathsf{\Theta }}\mathcal{C}\left({\mathsf{\Theta }}^{\left[t\right]}\right)$ accounts for the gradient of $\mathcal{C}\left(\mathsf{\Theta }\right)$ evaluated at $\mathsf{\Theta }={\mathsf{\Theta }}^{\left[t\right]}$. In  Equation (12), the expected gradient ${\mathbb{E}}_{\mathcal{X}}\left[{\nabla }_{\mathsf{\Theta }}c({\mathbf{x}}_0,{\mathbf{x}}_{L+1};\mathsf{\Theta })\right]$ is approximated by its empirical mean $\frac{1}{S}{\sum }_{{\mathbf{x}}_0\in \mathcal{S}}{\nabla }_{\mathsf{\Theta }}c({\mathbf{x}}_0,{\mathbf{x}}_{L+1};\mathsf{\Theta })$ measured over a mini-batch set $\mathcal{S}\subset \mathcal{X}$ with $S\triangleq \left|\mathcal{S}\right|$ training samples. By using commercial graphics processing unit (GPUs), parallel and fast implementation of Equation (12) is possible. After the training, the generalization performance of the trained DNN $\mathsf{\Theta }$ is examined by using a test set consisting of the unseen data during the training step.

3.2. DL Approach for EE Fairness Maximization

We provide the DL approach for solving the EE fairness problem in Equation (6). A key idea is to approximate unknown optimal solution ${\mathbf{p}}^{\star }\left(\mathbf{H}\right)$ of Equation (6) through a DNN. We construct a DNN-based optimization framework, as shown in Figure 3. We first sample numerous channel realizations $\left\{\mathbf{H}\right\}$ from the training set $\mathcal{H}$ for constructing a mini-batch set $\mathcal{S}$ at each iteration of the SGD algorithm in Equation (12). The training set $\mathcal{H}=\left\{\mathbf{H}\right\}$ consists of real measurement channel values or can be considered as a known probability density function of the fading environment such as the Rayleigh distribution.

The channel gain matrix $\mathbf{H}\in {\mathbb{C}}^{N\times N}$ is first vectorized into $\mathbf{h}\in {\mathbb{C}}^{N^2\times 1}$ to be passed to the fully-connected DNN in Equation (9). The channel gain vector $\mathbf{h}$ is then processed by L-layer DNN $\varphi (\mathbf{H};\mathsf{\Theta })$ by setting ${\mathbf{x}}_0=\mathbf{H}$ in Equation (9). Then, the output of the DNN ${\mathbf{x}}_{L+1}$ is utilized as the transmit power solution, i.e., ${\mathbf{x}}_{L+1}=\mathbf{p}\left(\mathbf{H}\right)$. In other words, the solution computation rule $\mathbf{p}\left(\mathbf{H}\right)$ is alternatively calculated using the DNN as

$$\begin{array}{c}\hfill \mathbf{p}\left(\mathbf{H}\right)\simeq \varphi (\mathbf{H};\mathsf{\Theta }).\end{array}$$

(13)

From Equation (13), we approximate the optimal transmit power ${\mathbf{p}}^{\star }\left(\mathbf{H}\right)$, which is generally unknown and intractable, through the fully-connected DNN $\varphi (\mathbf{H};\mathsf{\Theta })$. However, the expression power of the DNN is still unclear for representing the optimal solution. The following theorem provides rigorous and mathematical basis for the DNN approximation in Equation (13).

Theorem 1.

For a compact set $\mathcal{H}=\left\{\mathbf{H}\right\}$, there exists a L-layer DNN $\varphi (\mathbf{H};\mathsf{\Theta })$, which is realized with sigmoid activation functions and sufficiently large L, can approximate any continuous-valued function $\mathbf{p}\left(\mathbf{H}\right)$ over $\mathbf{H}\in \mathcal{H}$ within an arbitrary small worst-case error $\epsilon >0$. Mathematically, it is given as

$$\begin{array}{c}\hfill \underset{\mathbf{H}\in \mathcal{H}}{sup}\parallel \mathbf{p}\left(\mathbf{H}\right)-\varphi (\mathbf{H};\mathsf{\Theta })\parallel \le \epsilon .\end{array}$$

(14)

The proof of Theorem 1 is given in [18,27]. The above theorem, which is well-known as the universal approximation theorem [27], verifies the existence of the structure and the parameter set of the DNN $\varphi (\mathbf{H};\mathsf{\Theta })$ that can act as a universal approximator for any continuous function $\mathbf{p}\left(\mathbf{H}\right)$. A recent work [28] proved that the universal approximation theorem holds for any Lebesgue-integrable function $\mathbf{p}\left(\mathbf{H}\right)$ with ${\int }_{\mathcal{H}}\left|\mathbf{p}\left(\mathbf{H}\right)\right|\mathrm{d}\mathbf{H}<\infty$ and a fully-connected DNN having the ReLU activation functions. More preciously, the result in [28] can be expressed as

$$\begin{array}{c}\hfill {\int }_{\mathcal{H}}|\mathbf{p}\left(\mathbf{H}\right)-\varphi (\mathbf{H};\mathsf{\Theta })|\mathrm{d}\mathbf{H}<\epsilon .\end{array}$$

(15)

The Lebesgue-integrable property of $\mathbf{p}\left(\mathbf{H}\right)$ along with the universal approximation theorem in Equation (15) reveals that our DNN $\varphi (\mathbf{H};\mathsf{\Theta })$ can successfully approximate non-continuous but Lebesgue-integrable mappings such as the indicator function. Since Equations (14) and (15) hold for any mapping $\mathbf{p}\left(\mathbf{H}\right)$ defined over the compact set $\mathcal{H}$, the universal approximation is also fulfilled for the optimal ${\mathbf{p}}^{\star }\left(\mathbf{H}\right)$. Therefore, the DNN approximation approach in Equation (13) is accurate for the unknown optimal solution $\mathbf{p}\left(\mathbf{H}\right)$ for the EE fairness maximization problem regardless of its continuity.

Although the universal approximation theorem guarantees the quality of the DNN approximation in Equation (13), it does not state how to determine the DNN parameter satisfying Equations (14) and (15). Hence, we need to derive an efficient training strategy determining $\mathsf{\Theta }$ for the EE fairness maximization. To this end, by plugging Equation (13) into Equation (6), the original optimization problem in Equation (6) is first reformulated into

$$\begin{array}{cc}\hfill & \underset{\mathsf{\Theta }}{max}{\mathbb{E}}_{\mathbf{H}}\left[\underset{i\in \mathcal{K}}{min}{\eta }_i^{\mathrm{DNN}}(\mathbf{H};\mathsf{\Theta })\right]\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & \mathrm{subject}\mathrm{to}0\le {\left[\varphi (\mathbf{H};\mathsf{\Theta })\right]}_i\le P_i,\forall i\in \mathcal{K},\hfill \end{array}$$

(17)

where ${\left[\mathbf{z}\right]}_i$ indicates the ith element of a vector $\mathbf{z}$ and ${\eta }_i^{\mathrm{DNN}}(\mathbf{H};\mathsf{\Theta })$ denotes the EE of transmitter i in Equation (4) evaluated via the DNN solution $\mathbf{p}\left(\mathbf{H}\right)=\varphi (\mathbf{H};\mathsf{\Theta })$, which is defined as

$$\begin{array}{c}\hfill {\eta }_i^{DNN}(\mathbf{H};\mathsf{\Theta })=\frac{log\left(1+\frac{h_{ii}{\left[\varphi (\mathbf{H};\mathsf{\Theta })\right]}_i}{1+{\sum }_{j\in \mathcal{K}\setminus i}{h}_{ji}{\left[\varphi (\mathbf{H};\mathsf{\Theta })\right]}_j}\right)}{\frac{1}{\epsilon }{\left[\varphi (\mathbf{H};\mathsf{\Theta })\right]}_i+P_C}.\end{array}$$

(18)

Compared to the original formulation in Equation (6) whose optimization variable is the intractable function $\mathbf{p}\left(\mathbf{H}\right)$, we now optimize the DNN parameter set $\mathsf{\Theta }$ in the DNN training problem in Equation (16), which can be handled by the state-of-the-art DL optimization tool, e.g., the mini-batch SGD algorithm. However, since the SGD method has been typically developed for unconstrained training applications, the transmit power constraint in Equation (17) cannot be straightforwardly tackled by existing DL libraries. To overcome this difficulty, we construct the DNN $\varphi (\mathbf{H};\mathsf{\Theta })$ such that it always produces a feasible solution for Equation (17). We set the activation function of the output layer ${\sigma }_{L+1}\left(\mathbf{z}\right)$ as a scaled sigmoid function as

$$\begin{array}{c}\hfill {\sigma }_{L+1}\left(\mathbf{z}\right)=\mathbf{P}\odot \mathrm{sig}\left(\mathbf{z}\right),\end{array}$$

(19)

where $\mathbf{P}={[P_1,\cdots ,P_K]}^T\in {\mathbb{R}}^{K\times 1}$ denotes the stacked vector of the transmit power budget $P_i$, $\forall i\in \mathcal{K}$, and ⊙ accounts for the element-wise multiplication operator. Thanks to the fact ${\left[\mathrm{sig}\left(\mathbf{z}\right)\right]}_i\in [0,1]$, the output activation in Equation (19) is guaranteed to yield the feasible transmit power solution ${\left[\varphi (\mathbf{H};\mathsf{\Theta })\right]}_i\in [0,P_i]$.

Using the output activation in Equation (19), we can remove the transmit power constraint in Equation (17). Then, the problem in Equation (16) can be simplified into an unconstrained training task as

$$\begin{array}{cc}\hfill & \underset{\mathsf{\Theta }}{max}{\mathbb{E}}_{\mathbf{H}}\left[\underset{i\in \mathcal{K}}{min}{\eta }_i^{\mathrm{DNN}}(\mathbf{H};\mathsf{\Theta })\right].\hfill \end{array}$$

(20)

The unconstrained DL solvers can be applied to address the problem in Equation (20). At the tth iteration, the mini-batch SGD update rule in Equation (12) for Equation (20) is expressed as

$$\begin{array}{c}\hfill {\mathsf{\Theta }}^{\left[t\right]}={\mathsf{\Theta }}^{[t-1]}+\alpha \frac{1}{S}\sum _{\mathbf{H}\in \mathcal{S}}{\nabla }_{\mathsf{\Theta }}\left[\underset{i\in \mathcal{K}}{min}{\eta }_i^{\mathrm{DNN}}(\mathbf{H};{\mathsf{\Theta }}^{[t-1]})\right],\end{array}$$

(21)

where $\mathcal{S}=\left\{\mathbf{H}\right\}$ with $S\triangleq \left|\mathcal{S}\right|$ is the mini-batch set of the channel gain matrix $\mathbf{H}$ and the sign of the update direction of Equation (21) changes since our target is to maximize the minimum EE ${min}_{i\in \mathcal{K}}{\eta }_i\left(\mathbf{H}\right)$. In  Equation (21), the gradient ${\nabla }_{\mathsf{\Theta }}\left[{min}_{i\in \mathcal{K}}{\eta }_i^{\mathrm{DNN}}(\mathbf{H};\mathsf{\Theta })\right]$ would not be available due to the non-smooth minimum operation. This issue can be handled via a simple modification of the update rule based on the sub-gradient method [24] developed for addressing non-differential functions. Let $\widehat{i}$ be the index of the transmitter having the smallest EE performance, i.e.,

$$\begin{array}{c}\hfill \widehat{i}\triangleq arg\underset{i\in \mathcal{K}}{min}{\eta }_i^{\mathrm{DNN}}(\mathbf{H};\mathsf{\Theta }).\end{array}$$

(22)

Then, the sub-gradient ${\partial }_{\mathsf{\Theta }}\left[{min}_{i\in \mathcal{K}}{\eta }_i^{\mathrm{DNN}}(\mathbf{H};\mathsf{\Theta })\right]$ with respect to $\mathsf{\Theta }$ is obtained as [29]

$$\begin{array}{c}\hfill {\partial }_{\mathsf{\Theta }}\left[\underset{i\in \mathcal{K}}{min}{\eta }_i^{\mathrm{DNN}}(\mathbf{H};\mathsf{\Theta })\right]={\nabla }_{\mathsf{\Theta }}{\eta }_{\widehat{i}}^{\mathrm{DNN}}(\mathbf{H};\mathsf{\Theta }).\end{array}$$

(23)

Finally, the proposed training rule can be expressed as

$$\begin{array}{c}\hfill {\mathsf{\Theta }}^{\left[t\right]}={\mathsf{\Theta }}^{[t-1]}+\alpha \frac{1}{S}\sum _{\mathbf{H}\in \mathcal{S}}{\nabla }_{\mathsf{\Theta }}{\eta }_{\widehat{i}}^{\mathrm{DNN}}(\mathbf{H};{\mathsf{\Theta }}^{[t-1]}).\end{array}$$

(24)

3.3. Training and Implementation

A training algorithm for solving Equation (20) is presented in Algorithm 1. Before the training, we need to construct the training set $\mathcal{H}=\left\{\mathbf{H}\right\}$ which contains numerous channel gain matrices. It is worth noting that the training set can be the probability space since the distribution of the channel $\mathbf{H}$ has been well investigated and accurately modeled, e.g., the Rayleigh and the Rician fading. Hence, similar to [13], we can generate infinitely large number of training samples during the iterations of the SGD algorithm. An efficient initialization of the DNN parameter $\mathsf{\Theta }$ can be found by the Xavier initialization strategy [30]. At each training iteration, we sample a random mini-batch set $\mathcal{S}$ from the known distribution of the channel. Then, the DNN parameter is updated based on the mini-batch sub-gradient method in Equation (24). We repeat these iterative updates during the predefined training iteration T. One may apply the early stopping technique [11] by observing validation performance of the DNN evaluated over validation samples which are independently generated with the training data.

Algorithm 1 Mini-batch SGD training algorithm.

Construct the training set $\mathcal{H}$. Initialize $t=0$, the DNN parameter ${\mathsf{\Theta }}^{\left[0\right]}$, and the number of iterations T.   for $t=1:T$ do  Sample a mini-batch channel set $\mathcal{S}\subset \mathcal{H}$.  Update ${\mathsf{\Theta }}^{\left[t\right]}\leftarrow {\mathsf{\Theta }}^{[t-1]}+\alpha \frac{1}{S}{\sum }_{\mathbf{H}\in \mathcal{S}}{\nabla }_{\mathsf{\Theta }}{\eta }_{\widehat{i}}^{\mathrm{DNN}}(\mathbf{H};{\mathsf{\Theta }}^{[t-1]})$. end for Obtain the trained DNN parameter ${\mathsf{\Theta }}^{\left[T\right]}$.

The proposed DL method in Algorithm 1 does not require any knowledge of the optimal solution ${\mathbf{p}}^{\star }\left(\mathbf{H}\right)$ during the training step. Thus, the proposed DL training strategy is regarded as an unsupervised learning policy [19,20,21,22,23]. Notice that the supervised learning approach [18] needs to generate the labeled data, i.e., the solution obtained from existing optimization algorithm, for all the channel samples $\mathbf{H}$ in the training set $\mathcal{H}$. Since the proposed unsupervised learning method does not depend on the solution of the original formulation in Equation (6), the training of the DNN can be done in a much simpler way compared to the supervised training algorithms [18].

The training process might require intensive computations for updating a large number of weights and biases with numerous training samples. However, since we can obtain the training data in advance, the DNN training task can be performed offline before the real-time communication. Once the DNN is trained, its real-time calculations are replaced with the linear matrix multiplications in Equation (8) whose computational complexity is much lower than that of the iterative optimization methods such as the SCA algorithm [3]. Thus, in terms of the real-time execution time, the proposed DNN-based power control scheme would be more efficient than the conventional algorithm. This is further discussed through numerical results in Section 4. The implementation of the proposed DL-based power control scheme can be achieved by means of memory units at the transmitters. Specifically, the trained DNN parameter $\mathsf{\Theta }$, which is a collection of trained weight matrices and bias vectors, is stored to memory units of each transmitter. Then, based on the channel matrix $\mathbf{H}$ each transmitter i can compute its transmit power $p_i\left(\mathbf{H}\right)$ as $p_i\left(\mathbf{H}\right)={\left[\varphi (\mathbf{H};\mathsf{\Theta })\right]}_i$.

The DNN trained over a certain distribution of $\mathbf{H}$ might not be applied to other channel models. To this end, we train multiple DNNs for all possible analytical channel models in advance. For instance, two DNNs are individually trained with the Rayleigh and the Rican fading setups. In the real-time communication, the transmitters, e.g., the eNodeBs in the LTE systems, can determine the channel statistics based on the feedback information of the receivers. Hence, the transmitters can estimate the distribution of $\mathbf{H}$ and can select one DNN that matches with the real-time channel statistics. The transmitters can also check the change in the long-term channel statistics, and the dynamic switching of the DNN is possible in practice. Thanks to the high-speed memory units, the delay incurred by the DNN switching is negligible compared to the overall communication duration. As a result, the proposed DNN approach can be directly applied to a more realistic scenario when the long-term characteristics of the channels vary without retraining processes.

4. Numerical Results

In this section, we present numerical results evaluating the maximized minimum (max-min) EE performance of the proposed DNN scheme. Unless otherwise stated, a DNN with $L=6$ hidden layers was considered. The dimension of the hidden layer was set to $50K$, whereas the output layer dimension was fixed to K to produce K-dimensional transmit power solution $\mathbf{p}\left(\mathbf{H}\right)\in {\mathbb{R}}^{K\times 1}$. The ReLU function $\mathrm{ReLU}\left(z\right)=max\{0,z\}$, which is a popular choice for hidden activation functions [11,12,13,20], was adopted for all hidden layers. We applied the batch normalization technique [31] after each hidden and output layer to accelerate the training process. Unless otherwise stated, the learning rate $\alpha$ and the mini-batch size S were set to $\alpha =0.0003$ and $S=5000$, respectively. The early stopping [11] was employed with $T=25,000$ training iterations and ${10}^6$ validation samples.

We utilized the Adam method [26] for the SGD algorithm. At each iteration t, the update rules of the moving average of the gradient ${\mathbf{m}}^{\left[t\right]}$, the second moment ${\mathbf{v}}^{\left[t\right]}$, and the DNN parameter ${\mathsf{\Theta }}^{\left[t\right]}$ are given, respectively, by [26]

$$\begin{array}{cc}\hfill {\mathbf{m}}^{\left[t\right]}& ={\beta }_1{\mathbf{m}}^{[t-1]}+(1-{\beta }_1){\mathbf{g}}^{[t-1]},\hfill \\ \hfill {\mathbf{v}}^{\left[t\right]}& ={\beta }_2{\mathbf{v}}^{[t-1]}+(1-{\beta }_2){\mathbf{g}}^{[t-1]}\odot {\mathbf{g}}^{[t-1]},\hfill \\ \hfill {\mathsf{\Theta }}^{\left[t\right]}& ={\mathsf{\Theta }}^{[t-1]}-\eta \frac{\sqrt{1-{\beta }_2^t}}{1-{\beta }_1^t}{\mathbf{m}}^{\left[t\right]}\oslash (\sqrt{{\mathbf{v}}^{\left[t\right]}}+\varrho ),\hfill \end{array}$$

where ${\mathbf{g}}^{\left[t\right]}$ is defined as the instantaneous gradient of the cost function, ⊘ denotes the element-wise division, and $\sqrt{{\mathbf{v}}^{\left[t\right]}}$ indicates the element-wise square root of the vector ${\mathbf{v}}^{\left[t\right]}$. Two hyper parameters ${\beta }_1\in [0,1)$ and ${\beta }_2\in [0,1)$ adjust the decaying rates of the moving average of the first and the second momentums of the gradient, respectively. Following [26], we fixed ${\beta }_1=0.9$ and ${\beta }_2=0.999$. A positive parameter $\varrho >0$ was introduced to avoid numerical errors. For the initialization, ${\mathbf{m}}^{\left[0\right]}$ and ${\mathbf{v}}^{\left[0\right]}$ were set to the zero vectors.

All the channel gains for the training, validation, and testing steps were generated with the Rayleigh fading. The transmit power constraint $P_i$ for each transmitter i was fixed as $P_1=\cdots =P_K=P$ and the power amplifier efficiency $\zeta$ was given as $\zeta =0.35$ [3]. The training was implemented in Python with Tensorflow on a PC with Intel Core i7 CPU $@3.60$ GHz, 32 GB of RAM, and GeForce RTX 2080 GPU.

4.1. DNN Validation

In this subsection, we validate our hyper-parameter setting for the DNN training such as the number of hidden layers and the mini-batch size. In Figure 4, we first present the convergence of the training and the validation performance of the proposed DNN with $K=2$ and $P_C=33$ dBm for $P=25$ and 30 dBm. As reference, we consider the following three baselines.

• SCA [3]: The SCA-based iterative optimization algorithm in [3] was implemented with the CVX and MOSEK solver.
• Maximum power: The transmit power was set to it maximum value as $p_i\left(\mathbf{H}\right)=P$, $\forall i\in \mathcal{K}$.
• Random power: A random transmission policy was employed where $p_i\left(\mathbf{H}\right)$ is uniformly distributed over $[0,P]$.

It is shown that the performance of the DNN evaluated over the training and the validation sets converges well, implying that the proposed SGD update (Equation (24)) is effective for the max-min formulation in Equation (6). It is interesting to see that the proposed DNN method performs better than other baselines, especially the conventional SCA-based optimization approach [3]. Due to the non-convex nature of Equation (6), the SCA algorithm developed in [3] cannot guarantee the global optimality and converges to the KKT stationary point of Equation (6). On the contrary, the proposed DL approach is able to identify the global optimum for Equation (6) as discussed in the universal approximation theorem [27,28]. This infers that the DNN could handle the non-convexity of the EE fairness maximization problem with the data-driven SGD update rule in Equation (24).

Figure 5 illustrates the convergence behavior of the validation performance with $K=4$, $P_C=33$ dBm, and $P=30$ dBm for various number of hidden layers L. The convergence performance of a DNN with a single hidden layer, i.e., $L=1$, is worse than other configurations, whereas the performance of DNNs with $L=3$, 5, and 7 hidden layers show similar performance. However, it is observed that the convergence speed of the case with $L=7$ is slower than that of $L=3$ and 5. This is because the DNN with such a large number of hidden layers overfits to its training data [11]. Hence, the validation performance of the DNN with $L=7$ would not that be good compared to other cases. We thus fixed $L=5$ for the rest of the simulation.

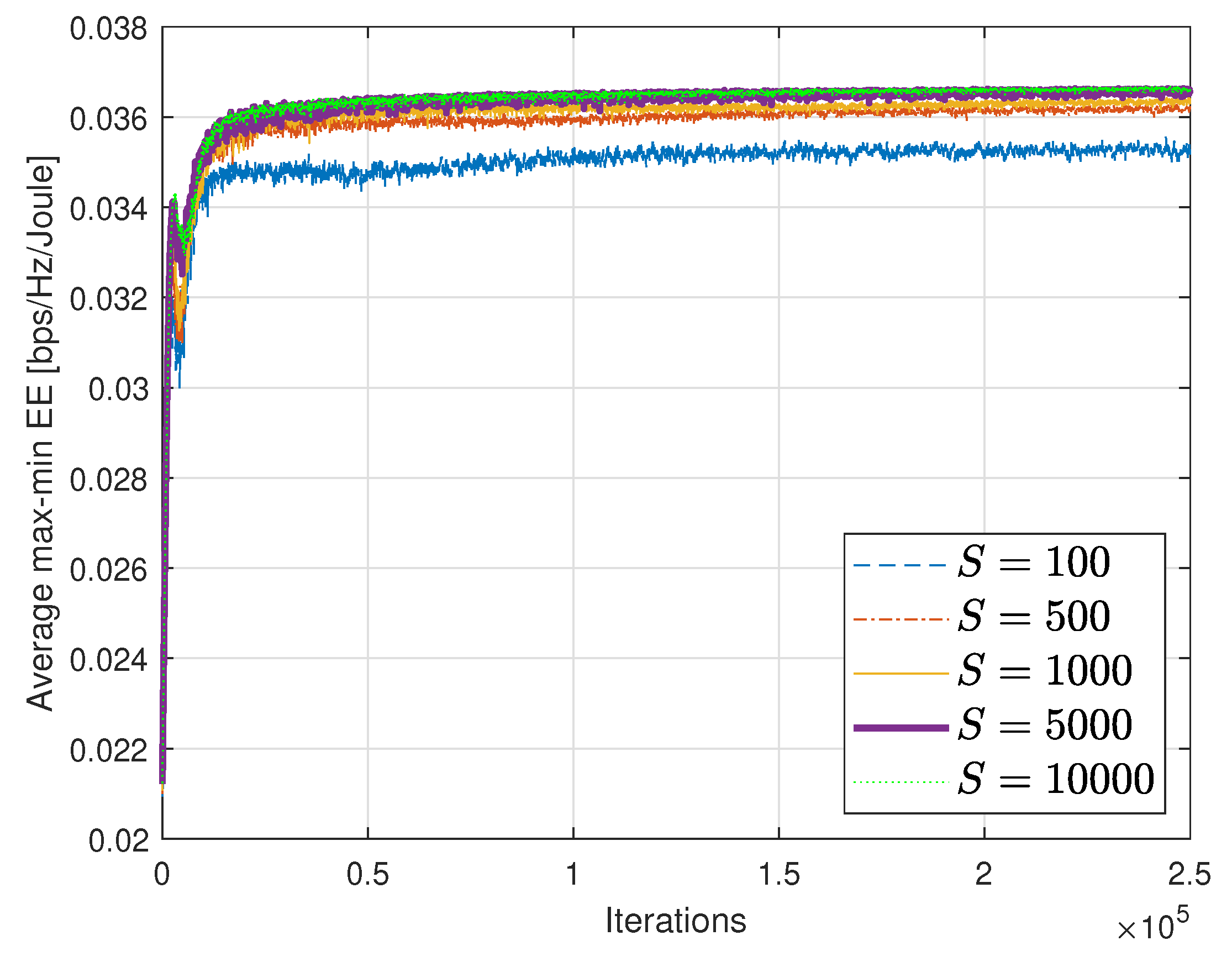
In Figure 6, we plot the convergence performance with different mini-batch size S. The DNN trained with a small mini-batch set ($S=100$ and 500) converges to a poor performance. We can see that increasing the mini-batch size is beneficial to improve the validation performance of the DNN since the empirical expectation of the sub-gradient in Equation (24) becomes more accurate as S grows. However, a large mini-batch size needs intensive SGD computation in the training step. Thus, we need to choose an appropriate S for achieving a good trade-off between the performance and the training complexity. In Figure 6, we can see that $S=5000$ is an efficient choice for our scenario.

4.2. Performance Comparison

In this subsection, we focus on evaluating the test performance of the trained DNN and comparison with the baseline methods. Figure 7 depicts the average max-min EE performance with respect to the transmit power budget P with $P_C=33$ dBm for $K=2$ and 4. It is clear that the proposed DNN-based power control scheme is superior to other baselines. In particular, the proposed DNN method performs better than the conventional optimization approach [3] regardless of K and P.

Table 1. Average CPU Running Time [s].

	SCA [3]		DNN
	$\mathit{P}=10$ dBm	$\mathit{P}=20$ dBm
$K=2$	0.79	1.67	6.00 × 10${}^{-4}$
$K=3$	0.97	2.64	9.85 × 10${}^{-4}$
$K=4$	1.10	3.13	1.24 × 10${}^{-3}$

shows the average CPU running time of the SCA method [3] and the proposed DNN scheme. Notice that the computations of the SCA method are online tasks which should be performed for each channel realization, whereas the training of the DNN can be performed offline with the aid of the training data collected in advance. Since the proposed DL approach does not require any retraining processes, the offline training complexity does not affect the online execution time of the trained DNN. Therefore, for fair comparison, the complexity of the DNN was evaluated only for the online testing step for producing the power control solution via successive linear operations in Equation (9). We implemented the test calculation of the trained DNN using Matlab and CPU and Matlab with CVX carried out the SCA algorithm. The CPU simulation was performed on a PC with Intel Core i5 CPU and 8 GB of RAM. We can see that the proposed DNN remarkably reduces the CPU running time compared to that of the SCA algorithm [3], which iteratively calculates the solution for each channel realization. This is because the real-time computation of the trained DNN is simply realized by the cascaded matrix multiplications and additions in Equation (9). Therefore, the power control solution of the proposed DNN method can be easily obtained compared to the iterative SCA algorithm [3]. It is also worth noting that the complexity of the proposed DL method only depends on the number of receivers K but not the transmit power constraint P since the proposed DNN structure relies only on K. The results in Table 1 infer that the proposed DNN not only improves the EE fairness performance but also reduces the energy required for the optimization tasks at the transmitters. Therefore, the proposed DL-based power control strategy could provide high EE performance in terms of both the communication and the computations.

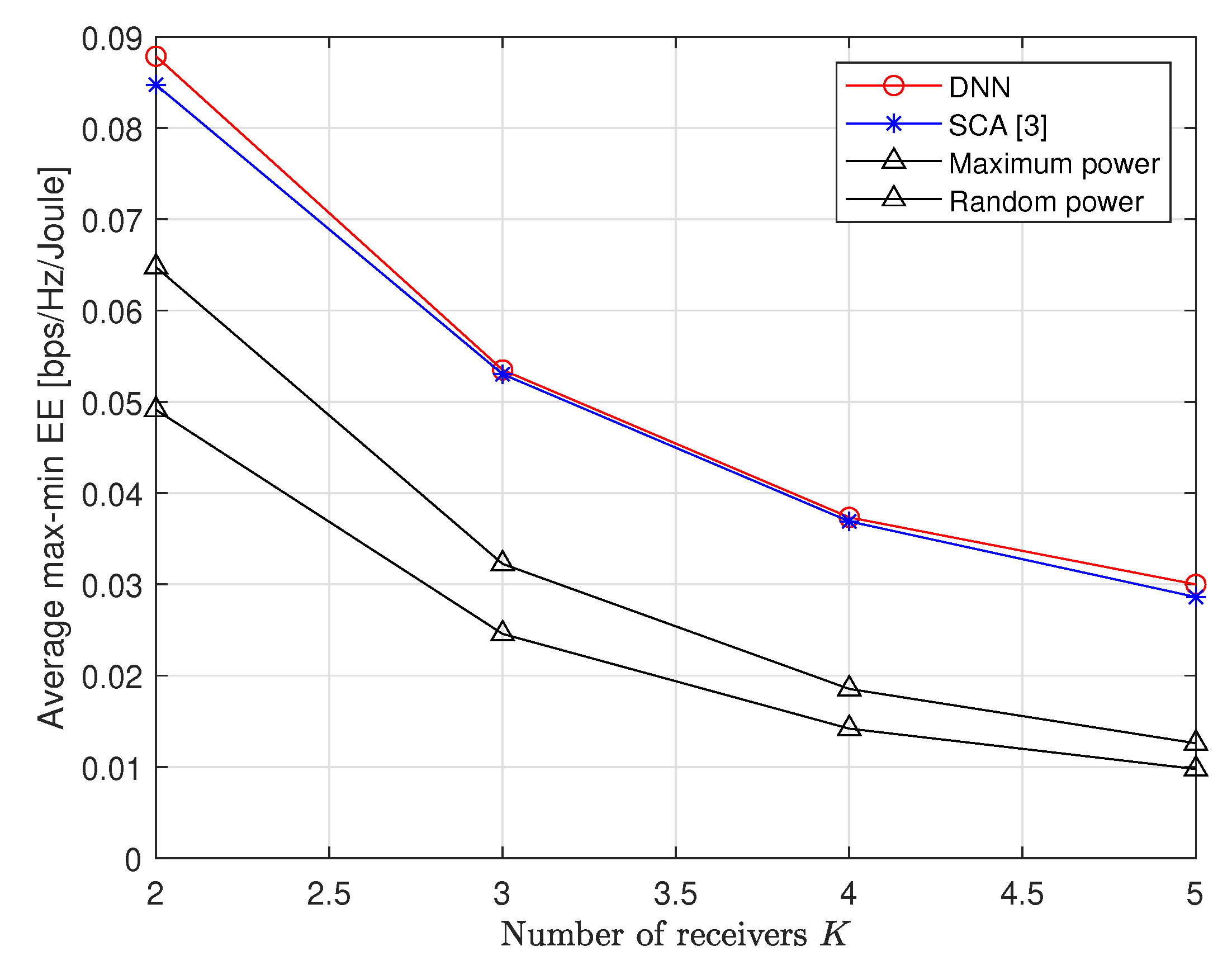
Figure 8 presents the average max-min EE performance with respect to the number of receivers K. Both the proposed DNN scheme and the conventional SCA algorithm show a similar performance for a large K. However, as observed in Table 1, the computational complexity of the DNN is much lower than that of the conventional SCA approach. We thus conclude that the proposed DNN scheme still has advantages over the method in [3] even with a small performance gain.

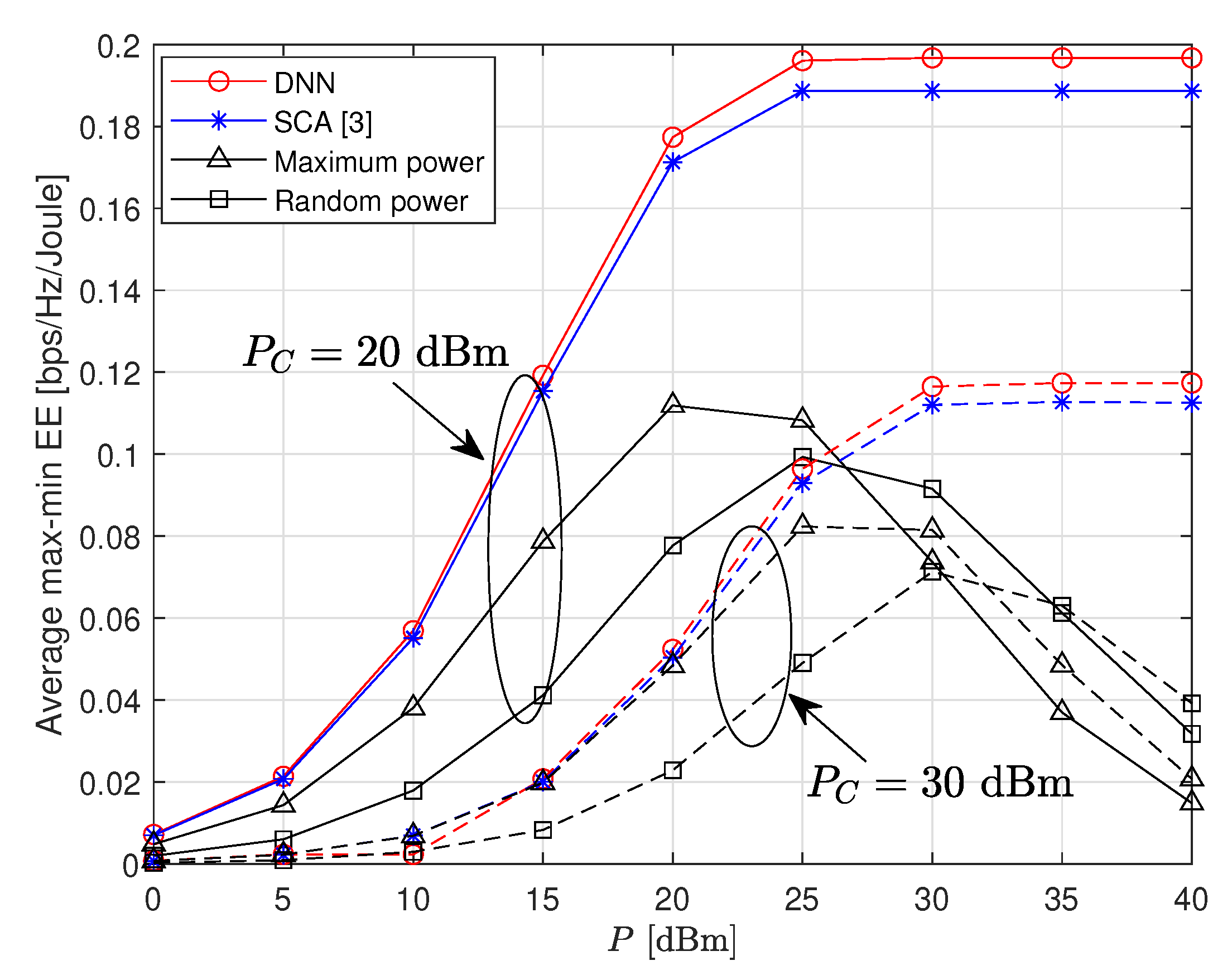
Figure 9 provides the average max-min EE performance by changing P with various circuit power $P_C$. It is revealed that the performance gain achieved by the proposed DNN scheme gets larger as P increases. We can also see that the DNN is still powerful for a large circuit power with $P_C=30$ dBm.

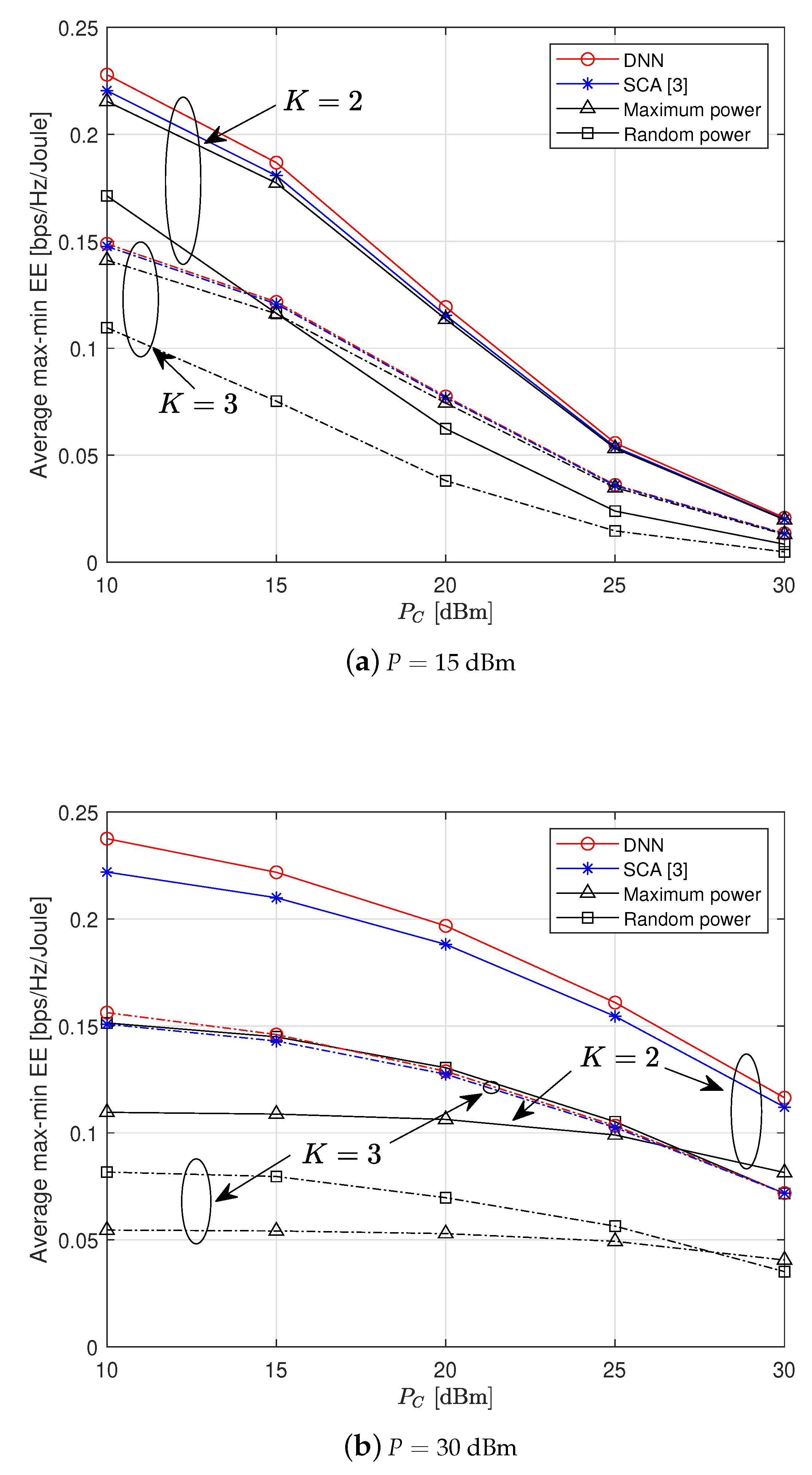
To further examine the impact of the circuit power, we present the average max-min EE performance in Figure 10 for $K=2$ and 3. It is shown that the proposed DL method performs well regardless of the circuit power $P_C$. We observe that the gain achieved by the proposed DL scheme over the conventional SCA algorithm gets larger as $P_C$ decreases. The DNN scheme becomes more powerful in the high regime of $P=30$ dBm (Figure 10b). Such a performance gain obtained by the DL approach is significantly meaningful with much reduced computational complexity.

5. Conclusions

This paper studies a DL method for improving the EE fairness performance in the IFC systems where multiple transmitters simultaneously communicate with their corresponding receivers. In particular, the maximization task of the minimum EE is investigated to determine energy-efficient transmit power control strategy at the transmitters. This results in non-convex, fractional, and non-smooth max-min EE formulations. Although the EE fairness maximization has been recently addressed by using the SCA framework, such a traditional optimization approach suffers from high computational complexity for the iterations and the optimality loss. To tackle these issues, we present a DNN-based power control scheme where the unknown optimal solution is approximated by carefully designed DNNs. The universal approximation theorem guarantees the optimality of the proposed DNN approach; however, it is still unclear how to identify an efficient DNN parameter set for maximizing the EE fairness performance. We propose an unsupervised learning algorithm such that the DNN is trained to directly maximize the minimum EE performance by observing numerous channel samples during the training steps. A careful analysis on the SGD update rule for the non-smooth objective function is presented for the proposed training algorithm. Intensive numerical results verify the effectiveness of the proposed DL-based power control method over the conventional SCA algorithm. It was observed that the EE fairness performance can be improved by the proposed DL method. In addition, it is shown that the DNN can shift the online calculations of the SCA method to its offline training step. As a result, the real-time CPU execution time of the proposed DL scheme is much lower than that of the SCA algorithm.