Data Mining Applications in Understanding Electricity Consumers’ Behavior: A Case Study of Tulkarm District, Palestine
Abstract
1. Introduction
2. Background
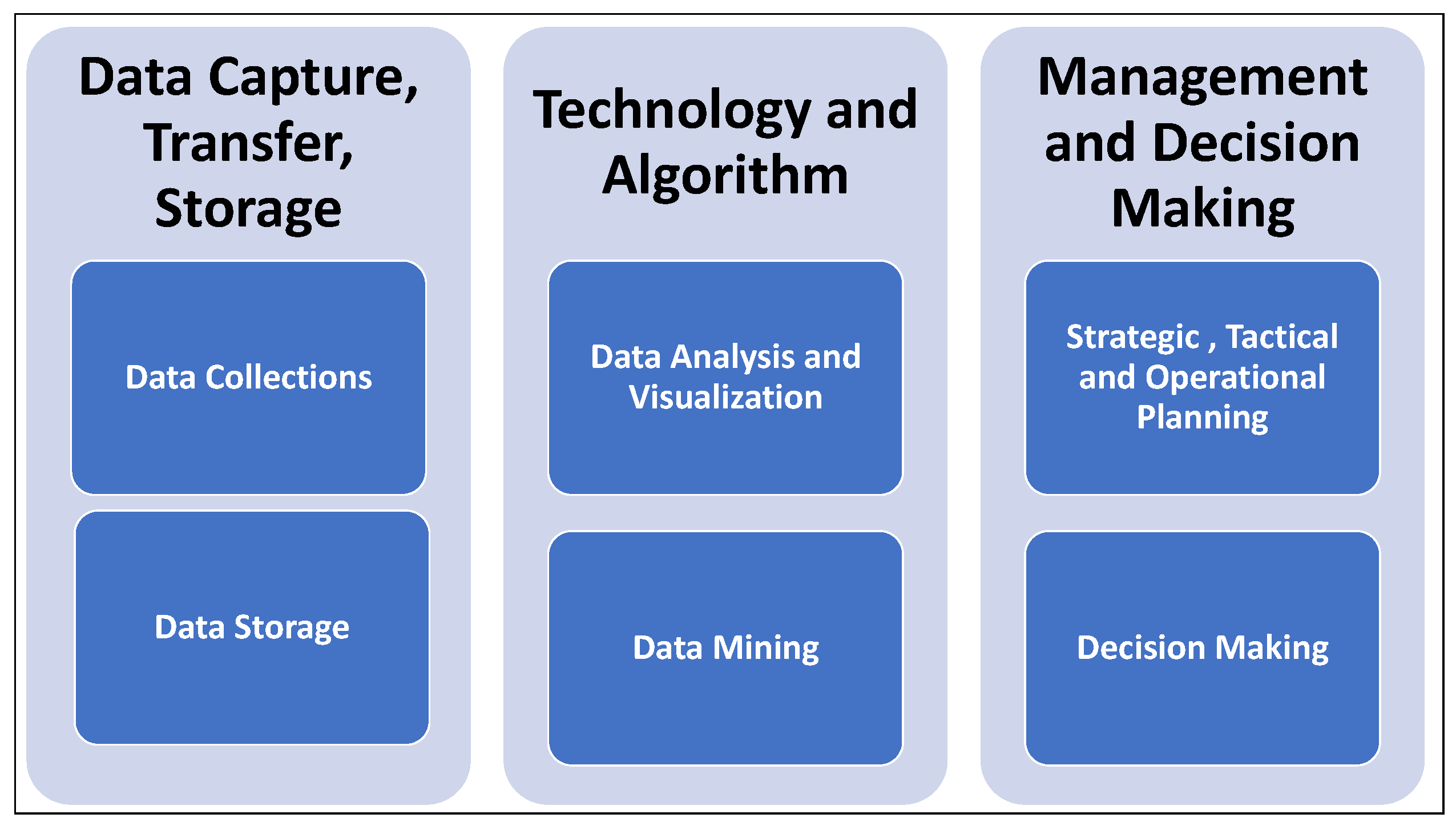
- Data capture, transfer and storage: Electricity data is collected by consumers services centers (Vending Stations), then transferred to System Master Station (SMS), then stored and accumulated in a specific database;
- Data is processed using data analysis, visualization and data mining techniques;
- Management of electricity system will use the result of analysis to support strategic, tactical and operational planning, decision making, and polices drawing of electricity management system at TM.
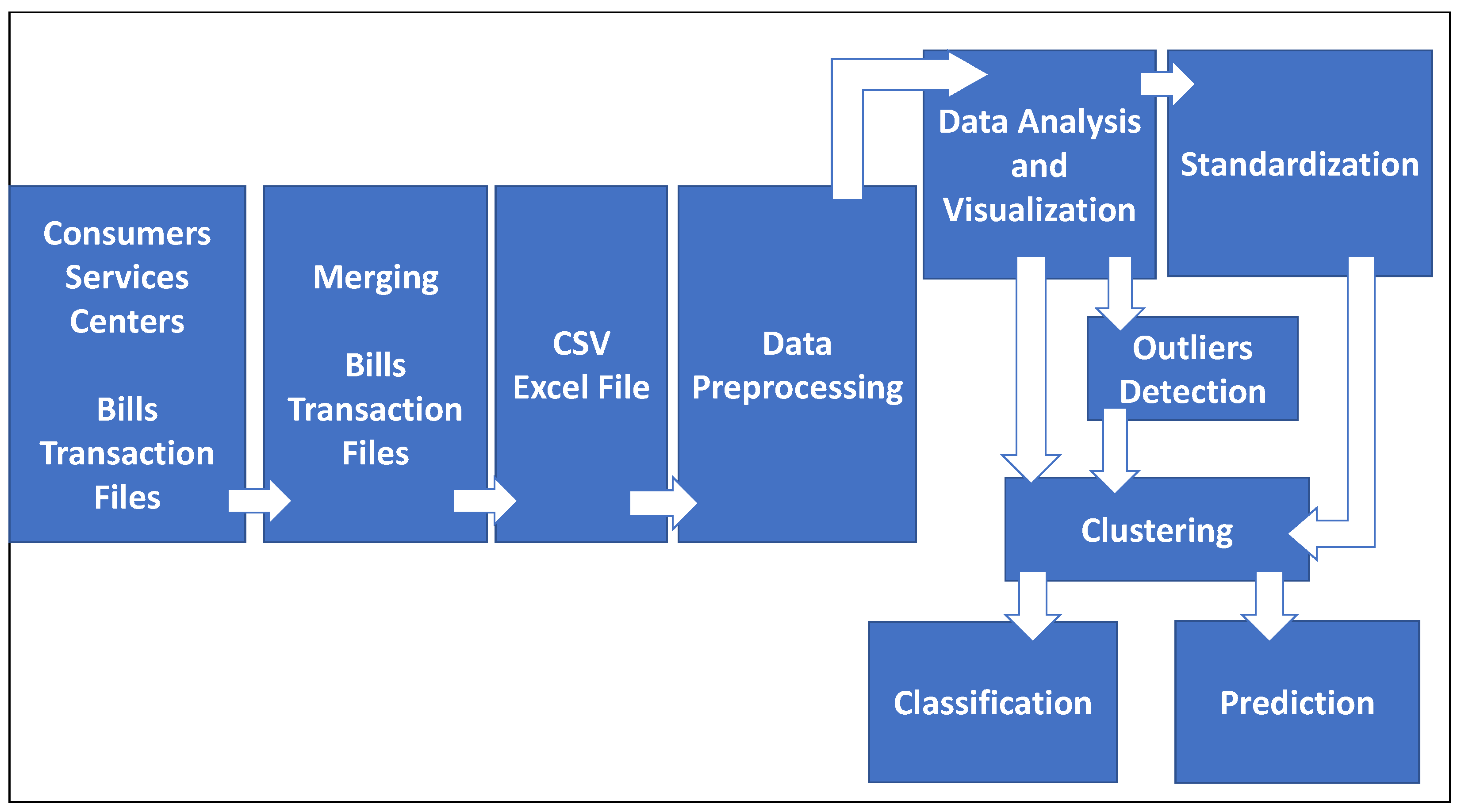
3. Key Components of the Data Analysis Approach
- Step 1
- Data Capture, Transfer, and Storage.
- Data is captured from different consumer service centers (vending stations) distributed in the Tulkarm district.
- Data is transferred to SMS to ensure a common database.
- Data and feature selection. The first step consists of the data definition, which will be applied to the ECPB data analysis process. Typically, the study of load profiling is implemented based on stored historical data and electricity consumers’ commercial information as well [9]. In this step, the types of consumers selected for the analysis is defined. A good understanding and knowledge of the study application area are required at this phase in order to choose calmly the attributes related to the demand objectives, contracted power, time of day, tariff period, peak power value, geographical areas, etc. The definition of the period of time such as season and year, which is intended to analyze is one of the important tasks, as well as the recorded interval cadence specification [9].
- Electricity consumers prepaid bills data is stored in csv format to form ECPB data set.
- Step 2
- Technology and Algorithm.
- Data pre-processing is applied on the data set to have a cleaned data set ready for analysis.
- Many data pre-processing techniques used in the literature. Section 4 discussed these techniques in detail.
- Data standardization (normalization). See Section 4.1.5.
- Data analysis and data visualization. To obtain a summary and data understanding of the data set, descriptive statistical analysis such as means, standard deviations, medians, variances, correlations, and the five number summary like maximum, minimum, first quartile, third quartile, median and mean are applied. This statistical analysis tells the basic idea how the data set is useful or not for further experimentation. More about statistical analysis is shown in Section 4.2
- Data mining techniques. Data mining is defined in [9] “Is the task of discovering patterns in large data sets involving methods of artificial intelligence, machine learning, statistics, and database systems”. In [10] data mining is considered as an intermediate step with KDD process. This process involves the whole procedure of a data set analysis. The steps are as follows. Data warehousing, which includes all the techniques and procedures to process missing values or errors in data in order to be analyzed. Data mining, which is the intermediate step, the main goal of this step is to extract useful relations or information from the data. The final step is the interpretation of the result, an expert is needed to analyze the obtained results from the data mining procedures in order to draw the conclusions.
- The main techniques applied in the data mining process are as follows. Machine learning, which is classified as Supervised and Unsupervised Learning techniques and algorithms. In supervised learning, we have decision trees, artificial neural networks, Bayes classifier, Association rules, case-base reasoning, genetic algorithm, fuzzy sets, and rough sets. In unsupervised learning, we have clustering, and self-organizing maps. Prediction involves regression models, decision trees, artificial neural network, and support vector machine. Evolution analysis involves time-series data mining, and classification of time-related data.
- Step 3
- Management and Decision MakingFindings and results will support executives, department managers and decision-makers of the electricity system to manage the electricity system in an efficient and effective manner. Electricity systems management is concerning the traditional large consumption customers and also the residential user with medium and high energy consumption, whose electricity consumption depicts abnormal or unbalanced patterns, and peak-off areas where the energy demand remains low [10]. Demand-side management (DSM) tools provide end-user a with valuable interface, information and reports to facilitate energy management. DSM or demand response (DR) as defined by the U.S. Department of Energy technical report: “Changes in electric usage by end-user customers from their normal consumption patterns in response to changes in the price of electricity over time, or to incentive payments designed to induce lower electricity use at times of high wholesale market prices or when system reliability is jeopardized [13]”. Financial incentives and awareness are used to address management by DSM, whereas active management of loads in households and appliances is used by DR [10]. Periodical reports about electricity consumption are sent to electricity consumers by electricity management departments in order to adjust their behaviors to reduce energy costs. This is because of the inability of electricity meters to enable consumers directly review their electricity usage. The awareness of all consumers about energy production and consumption let them adapt their electricity usage during high demand periods, high pricing or lower supply. Therefore, more reliable and stable supply, savings and efficiency will be obtained [14].
4. Theoretical Background of Data Mining Techniques
4.1. Data Pre-Processing
4.1.1. Data Cleaning
4.1.2. Data Integration
4.1.3. Data Transformation
4.1.4. Data Reduction
4.1.5. Data Standardization
4.2. Data Analysis and Data Visualization
4.3. Outliers Detection
4.4. Clustering
4.5. Data Classification
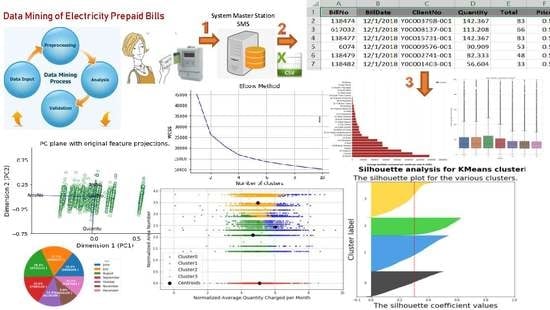
5. Experiment
- Data pre-processing techniques, such as data cleaning, integration, transformation, reduction and discretization are applied on the data set.
- Intensive data analysis is implemented on the ECPB data set. Data is analyzed in order to understand consumers’ electricity consumption behavior and consumers’ smart card charging frequencies over time, areas and tariffs. Monthly, weekly, daily, period (evening, morning, and night), and hourly analysis are applied. Electricity consumption summary per area zone and tariff analysis is applied. This analysis is done using descriptive statistics techniques.
- Outliers detection is applied on the data set. Box plot as a visualization tool is used for this purpose.
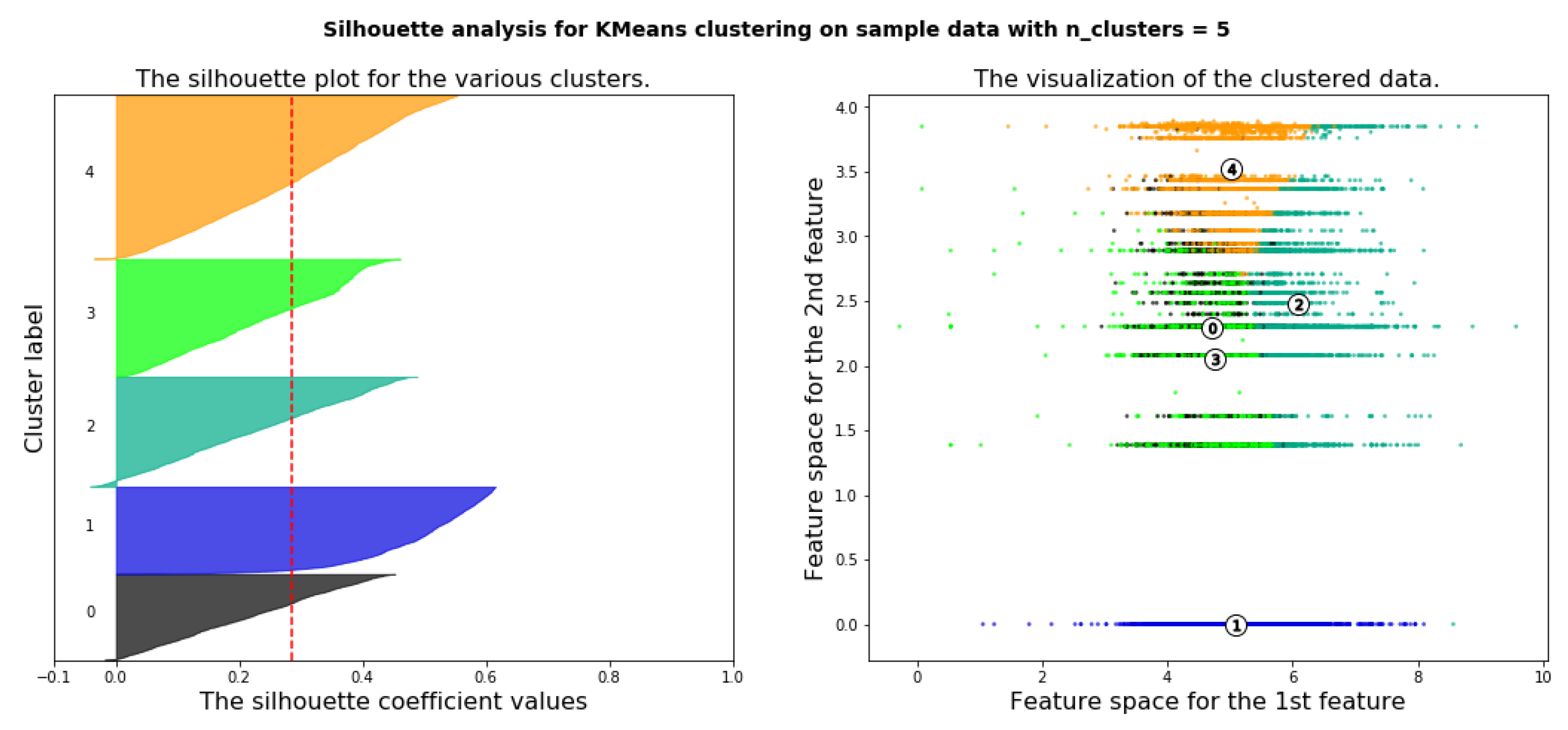
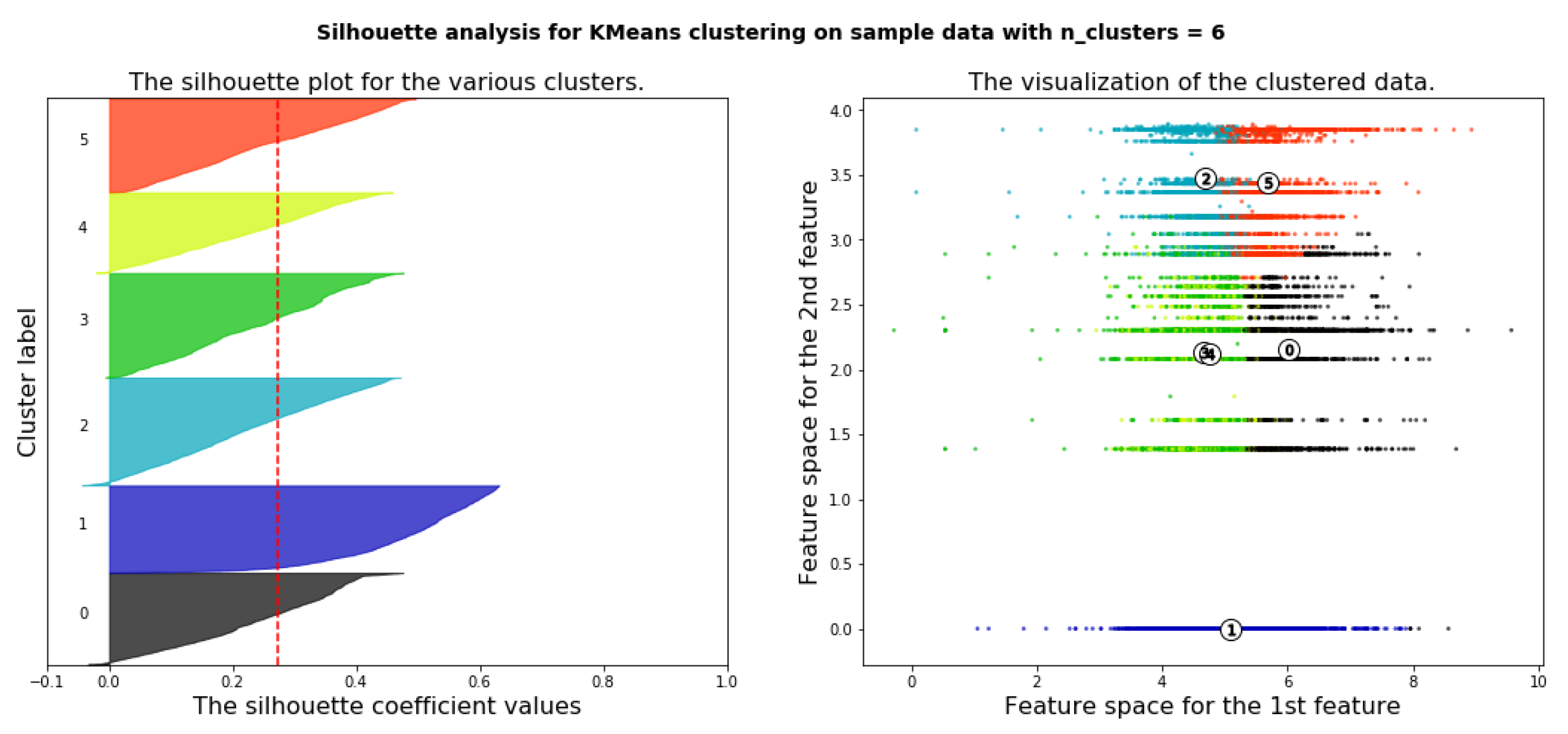
- K-means clustering algorithm is applied to the ECPB data set. Principal components analysis (PCA) for feature dimensions reduction is applied. One of the main goals of PCA is to reduce the dimensions of the data. Therefore, the complexity of the problem is reduced. Elbow method and silhouette analysis are used to determine the optimal number of clusters to run the K-Means clustering algorithm.
- Classification algorithms are applied. As a result of applying K-Means clustering, new consumer segmentation for electricity consumers is obtained. This new feature is added to the data set and used to apply classification algorithm. Support vector machine (SVM) classifiers are used.
- Step 1
- Install Anaconda 3 and its Python libraries to your computer. You can use the following URL link for the installation. https://www.anaconda.com/distribution/
- Step 2
- Download the data sets and codes files to your local drive. You can use the following URL link to download the data sets and codes files. https://github.com/1175maher/Electricity-Data-Mining. There are 10 files. Three Excel data files (.xlsx), three csv files (.csv) and four Jupyter Notebook Python files (.jpynb). These files are:
- Electricity consumers’ prepaid bills data file. Its name is elect-data.xlsx. It contains all the prepaid bills transactions from June to December 2018. Each row represents one transaction. There are about 250,000 row.
- Consumers’ data file. Its name is clients.xlsx. It contains all electricity consumers’ identification data. There are about 18,000 consumers.
- Tariff data file. Its name is tarif.xlsx. It contains data about consumers’ tariff types such as household, industrial, agricultural, etc. They are about 21 different tariff types.
- Data pre-processing code file. Its name is lelect-data-preprocessing.jpynb. This file contains the code required to clean the raw data file in 1.
- An output file produced after running the code file in 4. Its name is elect-data-phase1.csv.
- Data mapping code file. Its name is elect-mapping-data.jpynb. This file contains the code required to map data files in 2 and 3 with file in 5.
- An output file produced after running the code file in 6. Its name is elect-data-final.csv.
- The data analysis and visualization codes file. Its name is elect-data-analysis-visualization.jpynb. This file contains the codes required for data analysis and visualization using the cleaned and pre-processed data set files in 7, 1 and 2.
- The data mining codes file.Its name is elect-datamining.jpynb. This file contains the codes required for data mining techniques using the data set file in 7.
- The elect-datamining.jpynb is use elect-PCA.csv as an input data file.
- Step 3
- Data pre-processing phase. Open elect-data-perprocessing.jpynb file from the jupyter notebook. Modify the code to setup your data path address. The main input file used here is the elect-data.xlsx file. After running the codes the output file produced is elect-data-phase1.csv file. It is a pre-processed cleaned data set for electricity consumers’ prepaid bills.
- Step 4
- Data mapping phase. Open elect-mapping-data.jpynb file from jupyter notebook. Modify the code to set up your data path address. The main input files used here are the clients.xlsx, tarif.xlsx and elect-data-phase1.csv files. After running the codes the clients and tariffs data are mapped to the electricity consumers’ prepaid bills data in elect-data-phase1.csv file.The output file produced is elect-data-final.csv file. It is a final pre-processed electricity data that is ready for data analysis and mining.
- Step 5
- Data analysis and visualization phase. Open elect-data-analysis-visualization.jpynb file from the jupyter notebook. Modify the code to set up your data path address. The main input files used here are the elect-data-final.csv, clients.xlsx, and tarif.xlsx. After running the codes, data analysis and visualization are implemented and produced.
- Step 6
- Data mining phase. Open elect-datamining.jpynb file from the jupyter notebook. Modify the code to set up your data path address. The main input file used here is the elect-PCA.csv. After running the codes, the data mining techniques such as data normalization, principal components analysis (PCA), elbow method, and silhouette analysis. Clustering and classification are implemented on the data sets.
6. Results and Discussion
6.1. Data Pre-Processing Phase
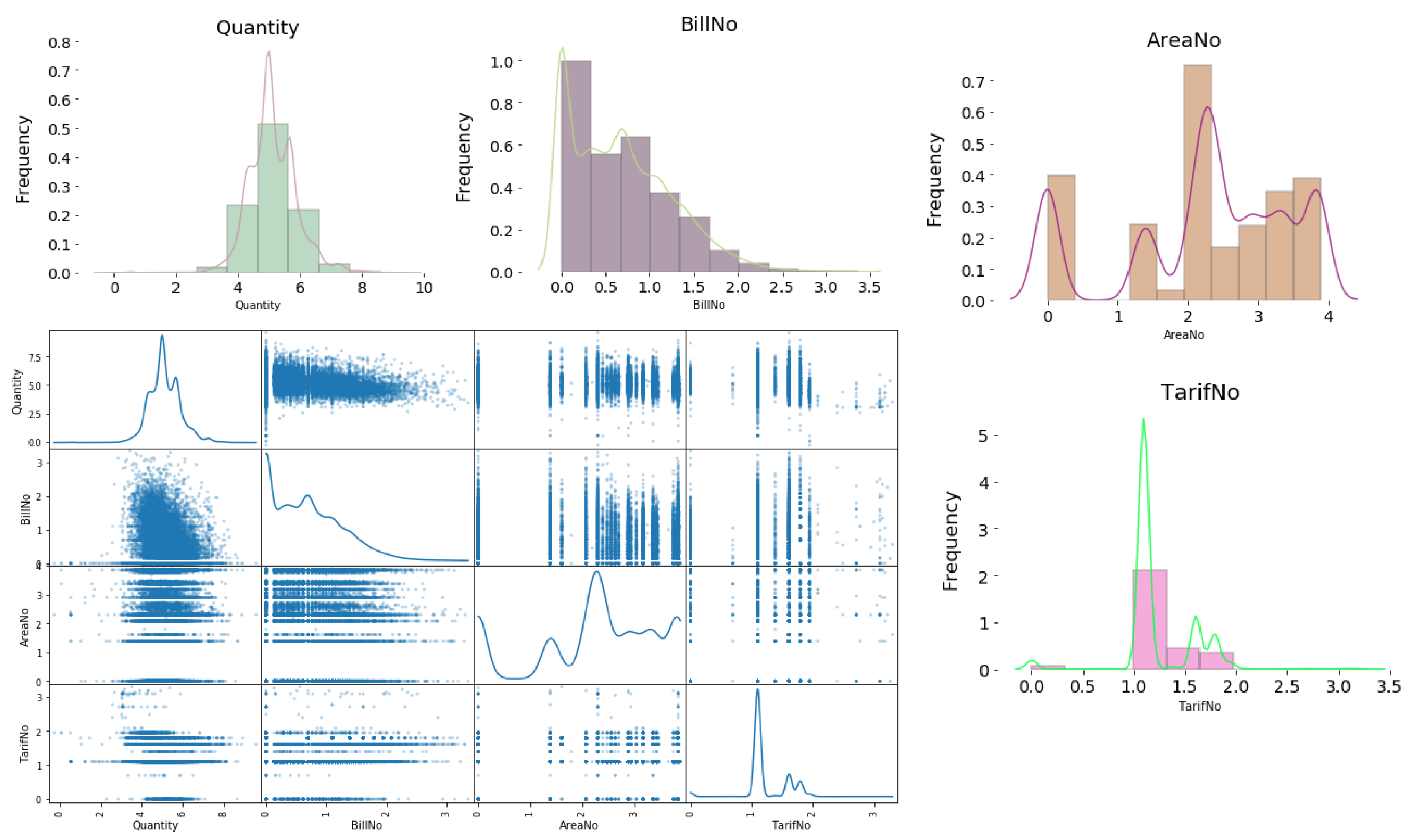
6.2. Data Understanding Phase
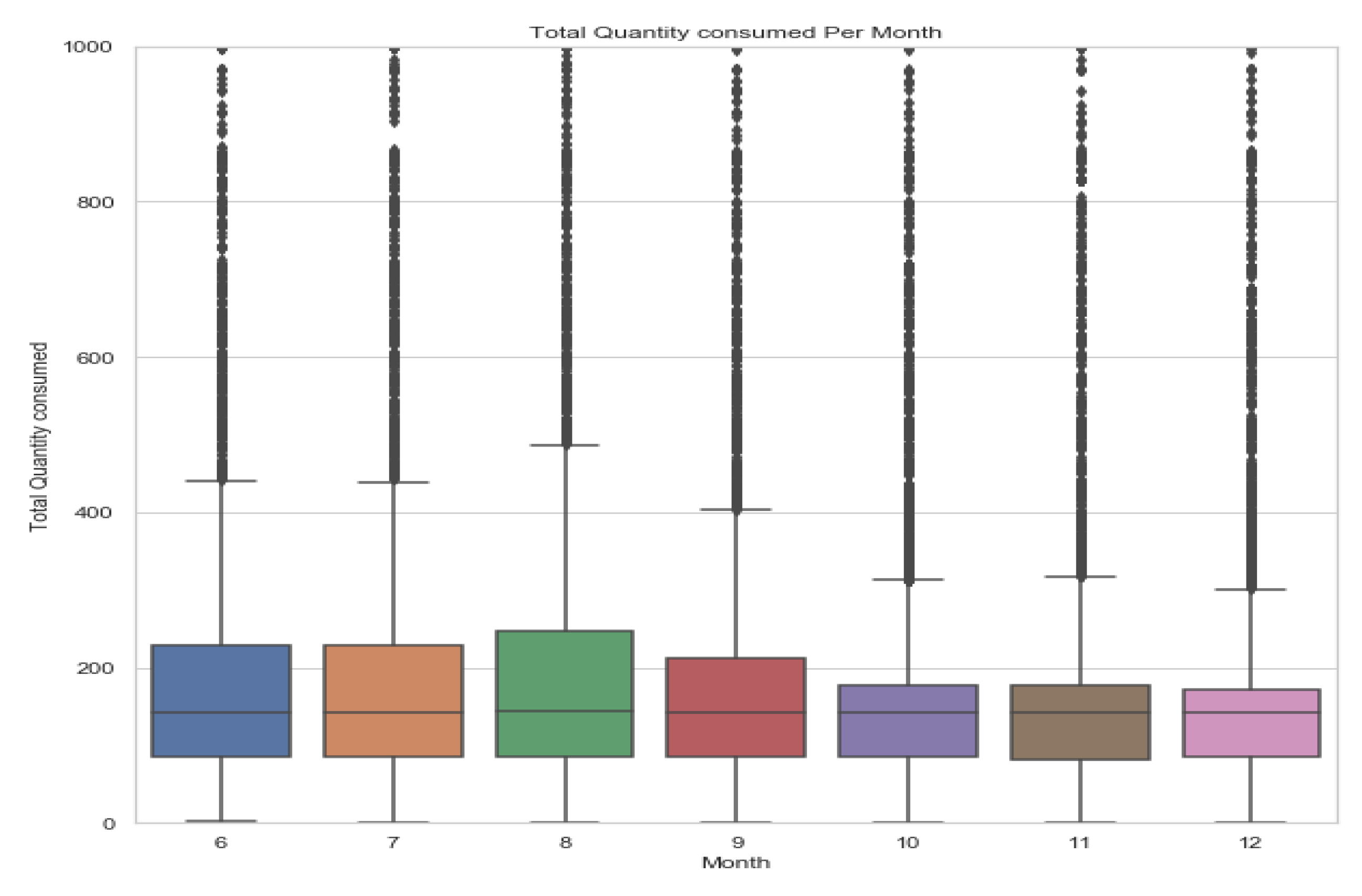
6.2.1. Monthly Analysis
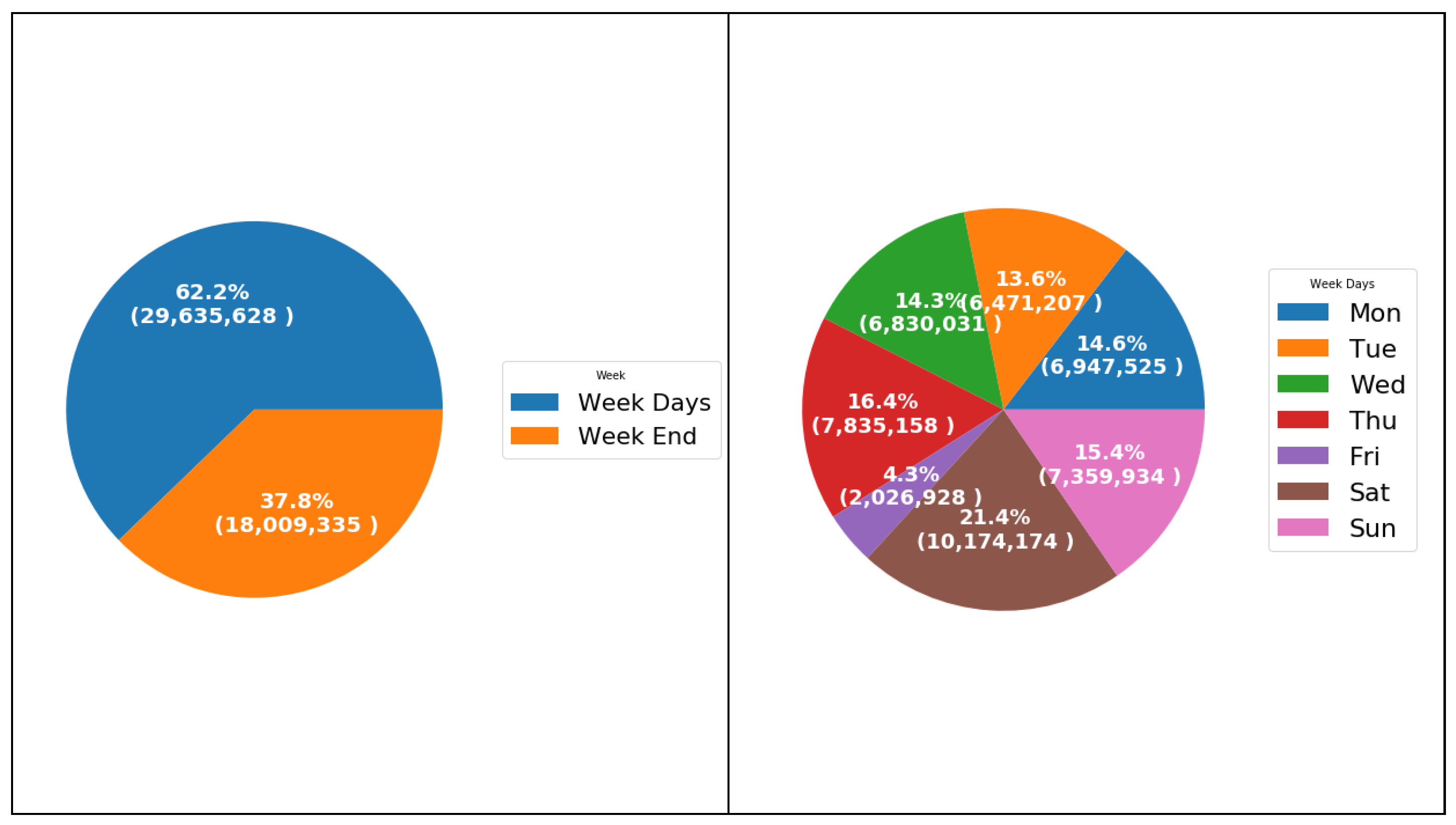
6.2.2. Weekly and Daily Analysis
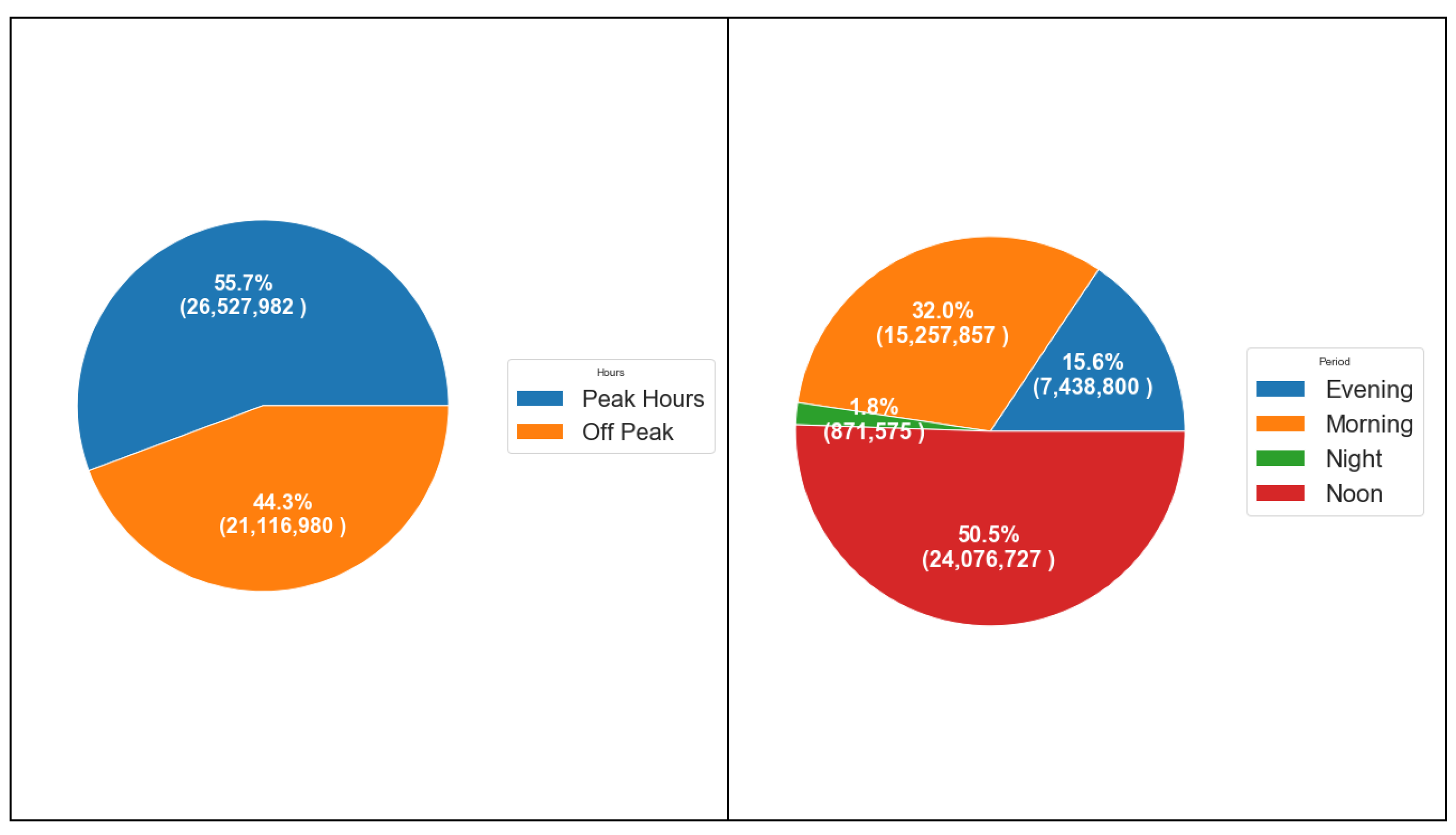
6.2.3. Period and Hourly Analysis
6.2.4. Electricity Consumption Summary per Area Zone
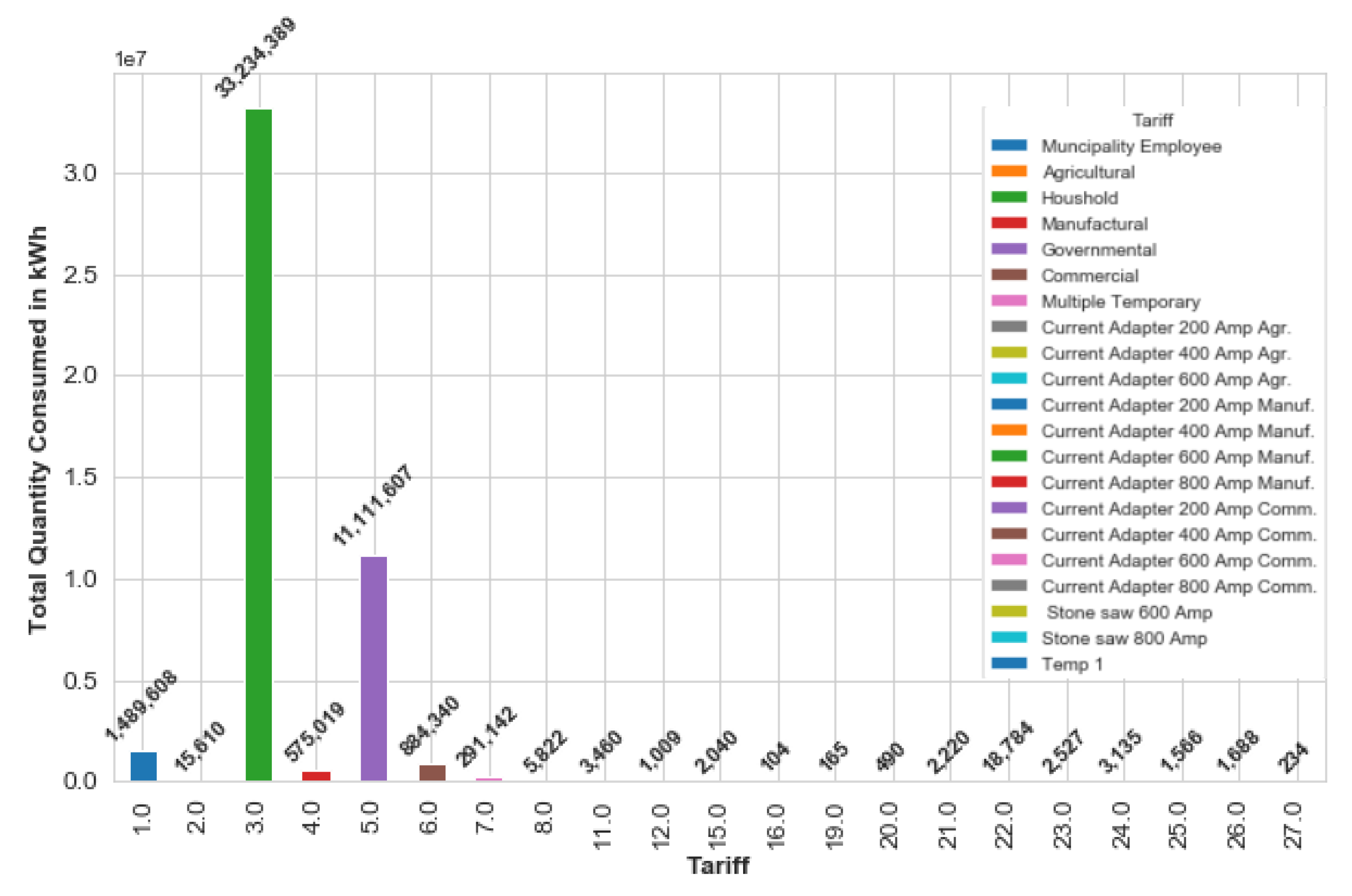
6.2.5. Tariff Analysis
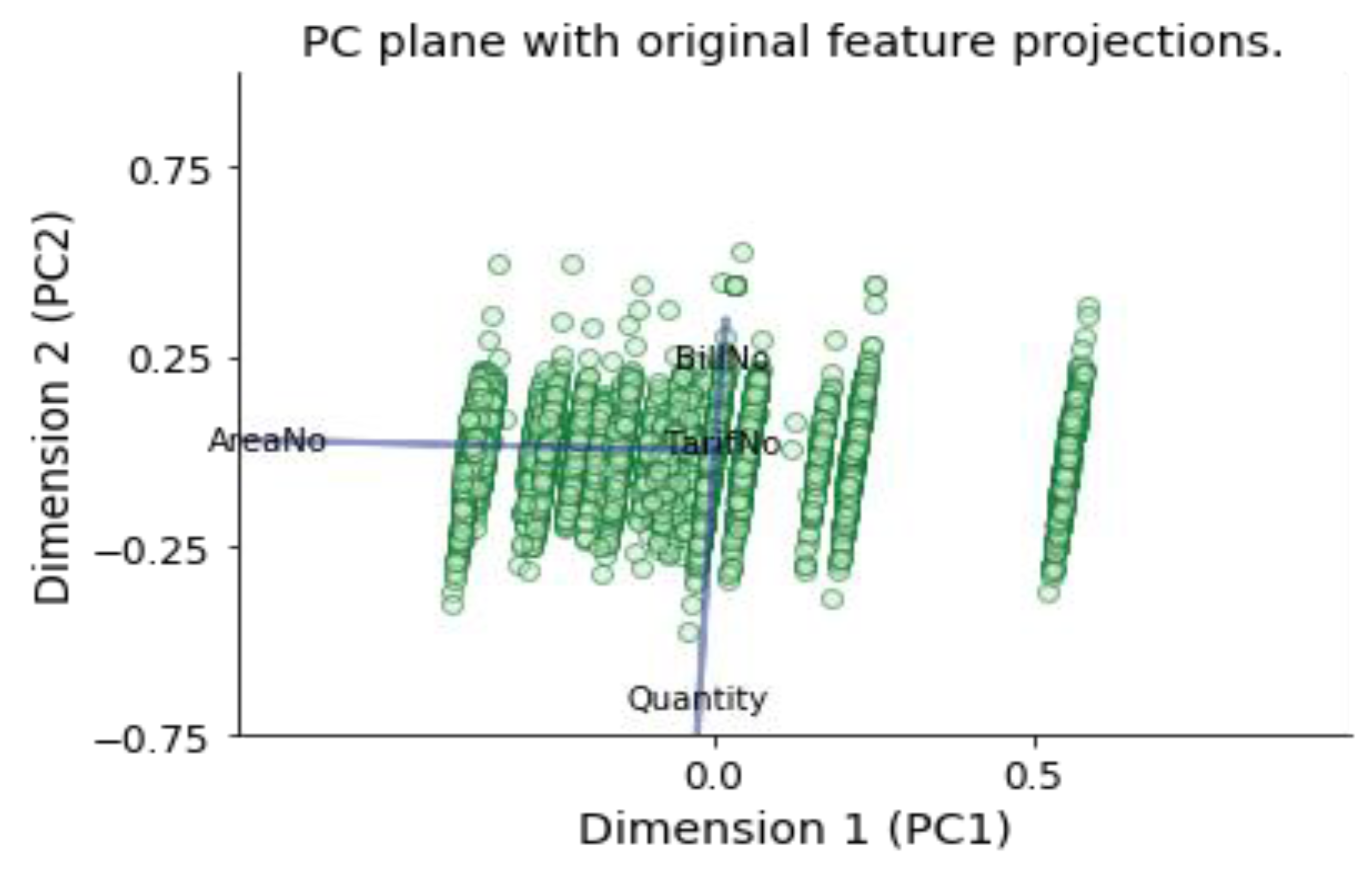
6.2.6. Feature Transformation by Using Principal Component Analysis (PCA)
- Dimension 1 has a high negative weight for AreaNo feature and low negative weight for Quantity feature. This dimension might represent electricity consumers located in areas with high Areano and consume low quantities.
- Dimension 2 has a high negative weight for Quantity feature, and medium positive weight for BillNo feature, and low positive weight for AreaNo feature. This dimension might represent electricity consumers who consume large quantities per month and charge their smart card a moderate number of times per month and located in areas with low Areano.
- Dimension 3 has a high positive weight for BillNo feature, and medium positive weight for Quantity feature, and approximately 0 weight for AreaNo feature, and low negative weight for TariffNo feature. This dimension might represent electricity consumers who charge their smart card large number of times per month, consumes medium quantites, located in one specific AreaNo, and have Tariff Type with low TariffNo.
6.3. Outliers Detection
- The most electricity consumption per month by ConsumerID Y00010828-001105, which belongs to AreaNo 10 (North) and TariffID 5 (Governmental), is a government institution. This is a justifiable consumption.
- Some large quantities of electricity consumption per month by many consumers such as ConsumerID Y00005543-001476 who belong to AreaNo 47 (Tulkarm) and TariffNo 6 (Commercial), it is a commercial economic entity. This is a justifiable consumption.
- Some large quantities of electricity consumption per month by many consumers who belong to TariffNo 3 (Household). This is not justifiable and more investigation should be conducted on them. Table 2 shows a list of consumers who have large quantities of electricity consumption per month.
6.4. Clustering (The Application of K-Means Clustering on The Data Set)
6.4.1. Clustering for Consumers Segmentation
- The shape of cluster: clusters shape is spherical, which means the distribution variance is spherical. We have to have a normally distributed variables with the same variance.
- The size of cluster: the same number of observations for all clusters.
- The correlation between variables: no or little correlation between the variables.
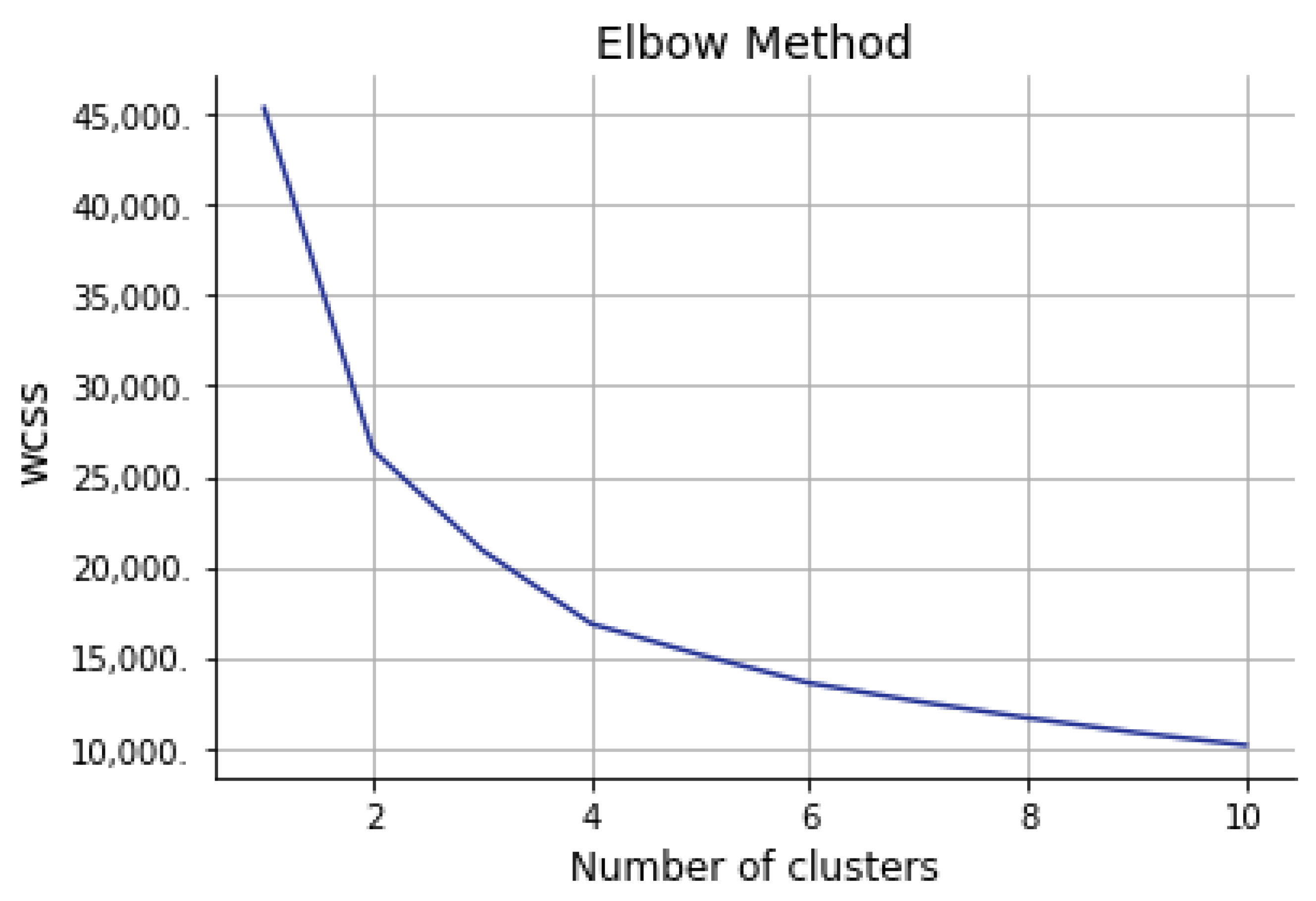
6.4.2. Deciding the Optimal Number of Clusters Using Elbow Method
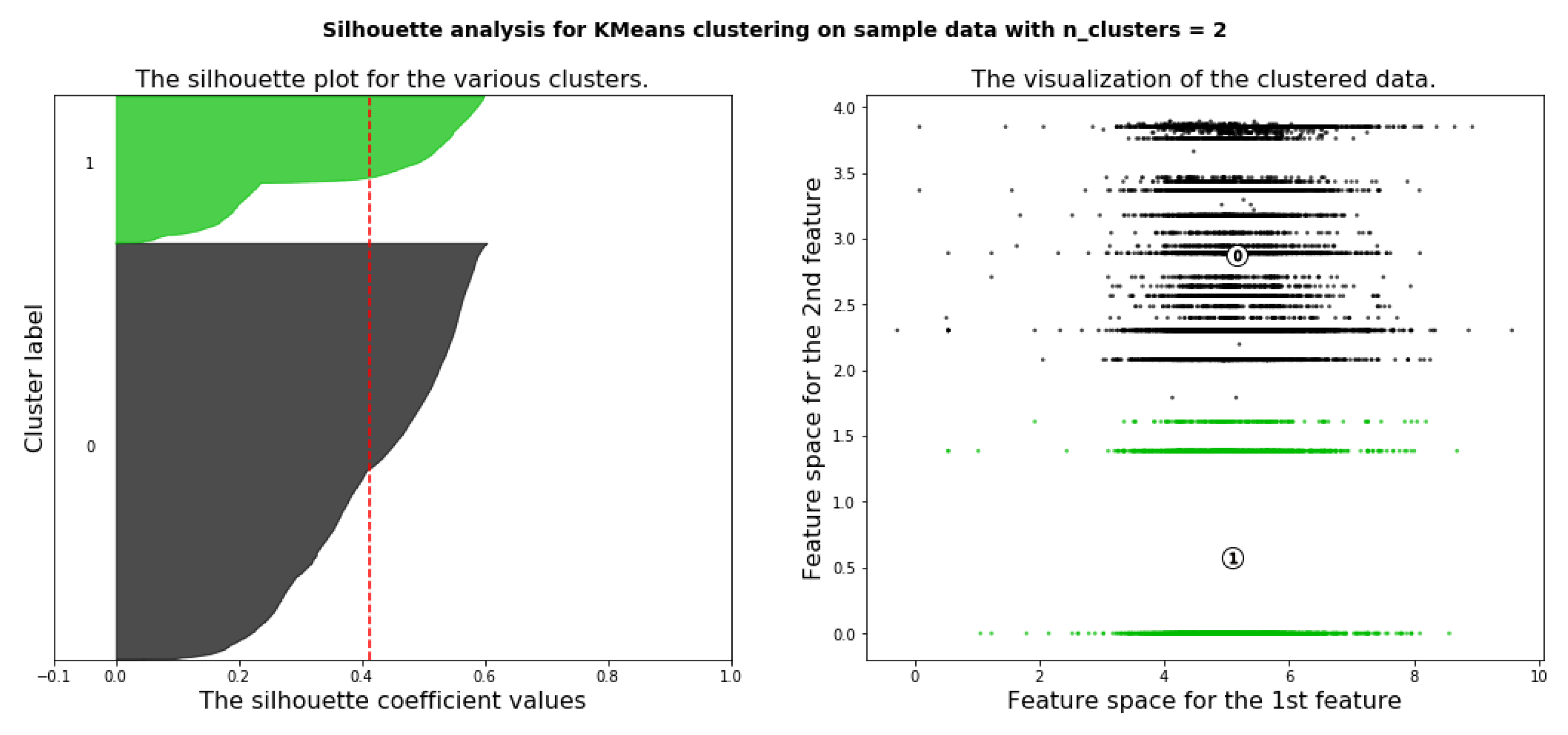
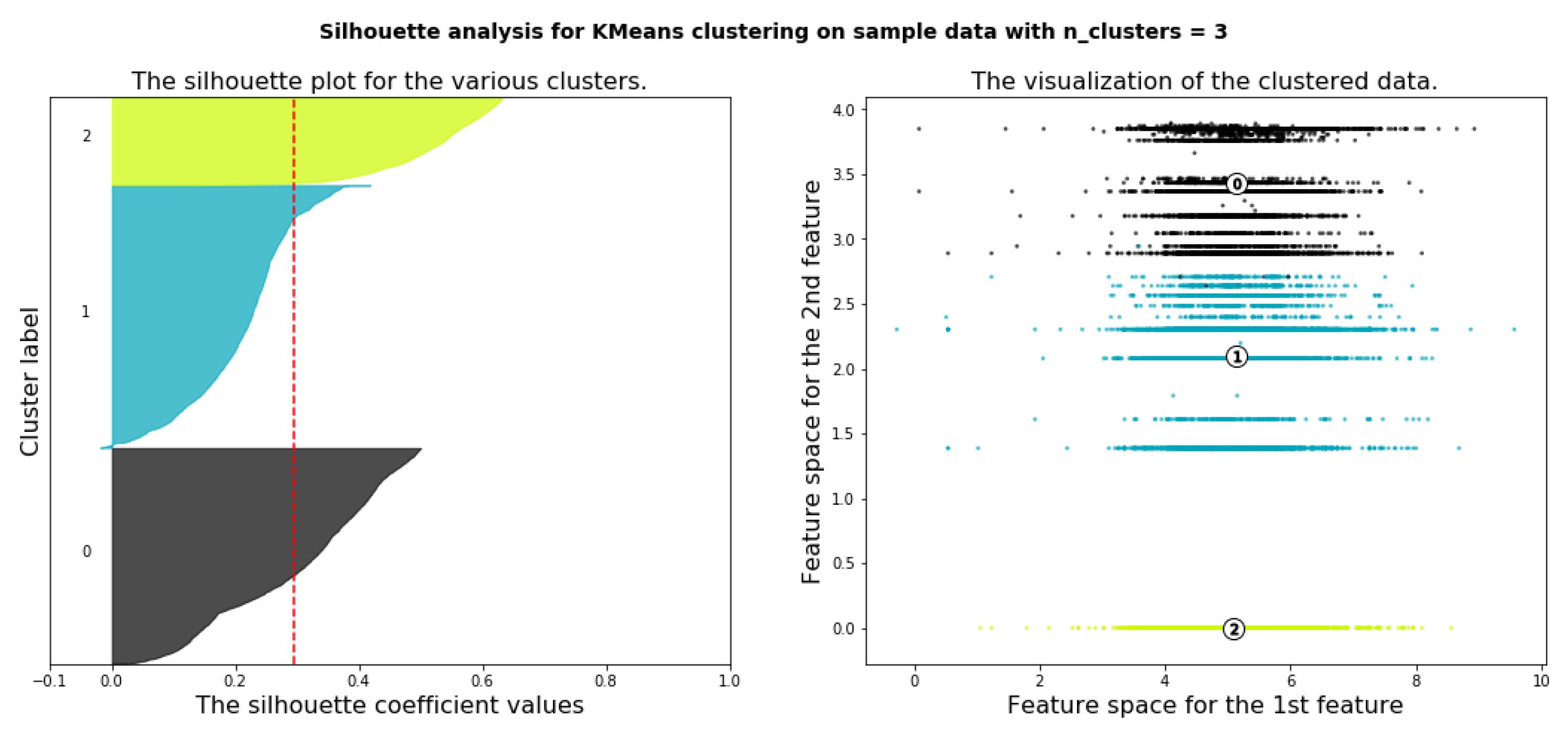
6.4.3. Deciding the Optimal Number of Clusters Using Silhouette Analysis
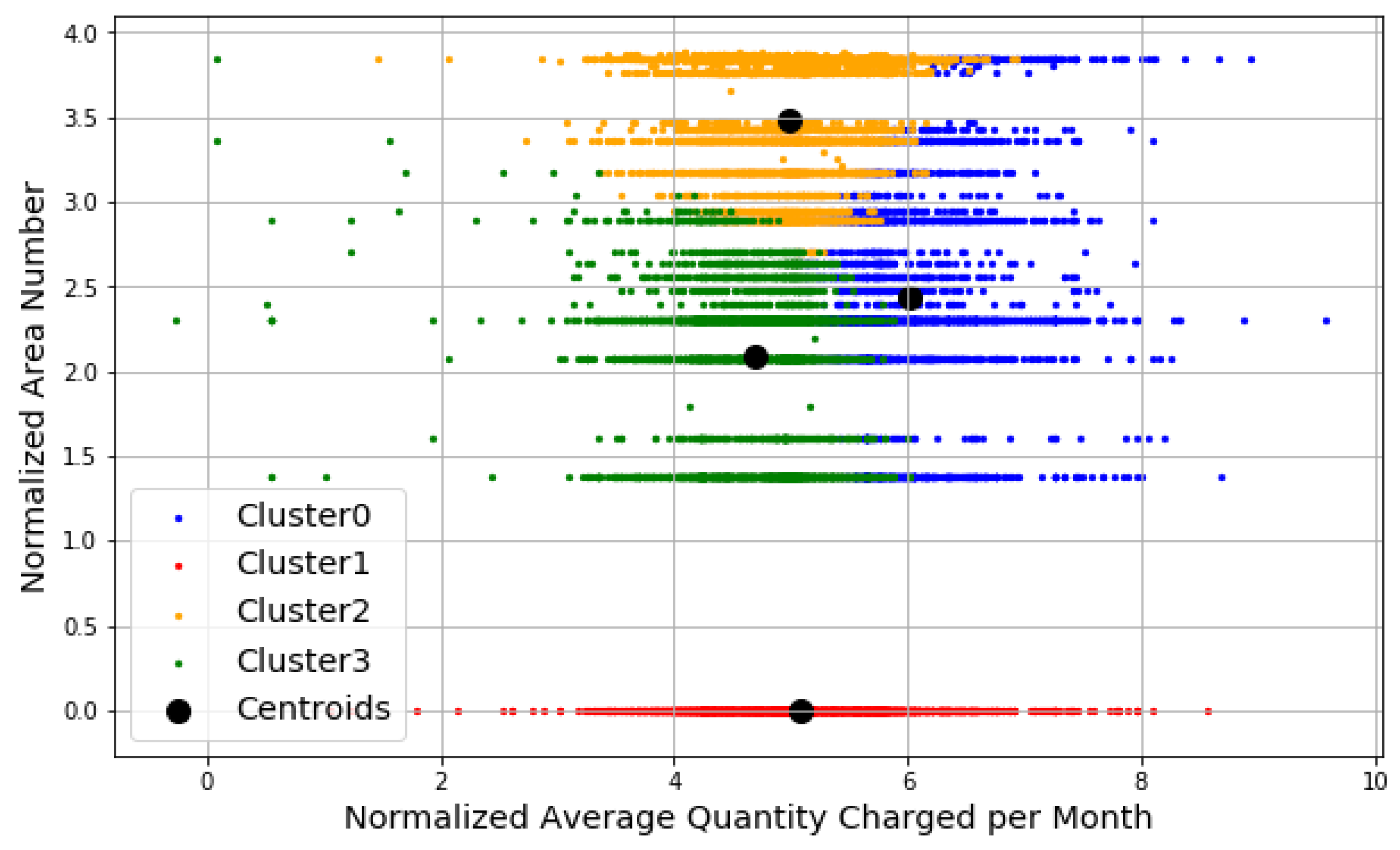
6.4.4. Applying K-means Clustering with Number of Cluster Is Four (k = 4)
- Cluster 0: consumers with quantities between (20 and 1000) kWh and distributed in areas where AreaNo between (14 and 48).
- Cluster 1: consumers with quantities less than 4000 kWh and are located in AreaNo 1.
- Cluster 2: consumers with quantities between (20 and 7500) kWh and distributed in areas where AreaNo between (4 and 47).
- Cluster 3: consumers with quantities less than or equal 400 kWh and distributed in areas where AreaNo between (4 and 29).
- The ability of the management to draw their policies and set their programs that will be suitable for each of its consumer-segment.
- Predicting the electricity consumption associated with each segment and effectively and efficiently manage the forces of demand and supply.
- Unravelling some latent dependencies amongst consumers such that their behavior in electricity consumption, number of times they charge their smart cards per month, etc.
- Management and decision support in terms of risky situations such as shortages in electricity supply in case of electricity cut off.
- Forecasting the growth in demand for electricity for each consumer segment.
- Forecasting of the growth rates in new consumers in the coming months.
- Understanding consumers’ distributions in each area and the number of times each consumer segments charging their smart cards per month to make decisions to open new vending stations and to know the feasibility of their opening.
6.5. Classification
6.5.1. Classification Performance Results
6.5.2. Discussion of Confusion Matrix
7. Conclusions
- Outliers detection. A list of household electricity consumers with huge electricity consumption per month is created in order to do more consumer investigation.
- A new consumer segmentation is proposed by implementing the K-Means clustering algorithm, four consumer clusters or segments are identified and labeled. The advantages of the new consumers segmentation compared with the existing segmentation, that the existing segmentation relies on the consumers’ tariff only (household, agricultural, governmental, manufacturer, etc.), while the new proposed consumers segmentation help electricity management system to understand how electricity is actually consumed for different consumers and obtain the consumers’ load profiles or load patterns, tariff design related to the electricity consumption, consumer scale load forecasting, demand response and energy efficiency targeting, non-technical loss detection and outliers detection. Moreover, the management can benefit from This new consumers segmentation as follows:
- (a)
- Drawing policies and programs that will be suitable for each of its consumer-segment.
- (b)
- Predicting the electricity consumption for each segment and effectively and efficiently manage the forces of demand and supply.
- (c)
- Unravelling some latent dependencies amongst consumers such that their behavior in electricity consumption, number of times they charge their smart cards per month etc.
- (d)
- Managing risky situations such as shortages in electricity supply in case of electricity cut off.
- (e)
- Forecasting the growth in demand of electricity for each consumer segments.
- (f)
- Forecasting of the growth rates in new consumers in the coming months.
- (g)
- Evaluating the feasibility of opening new vending stations for each consumer segment to better serving them.
- A new consumer segmentation feature is added to the data set and then a classification problem is solved by SVM classification method. Confusion matrices are produced to show the accuracy of the classification and prediction.
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| TM | TulKarm Municipality |
| ECPB | Electricity consumers prepaid bills |
| PENRA | Palestinian Energy and Natural Resources Authority |
| PERC | Palestinian Electricity Regulatory Council |
| WBGS | West Bank and Gaza Strip |
| SMS | System master station |
| KDD | Knowledge discovery in database |
| DSM | Demand side management |
| DR | Demand response |
| kWh | Kilo Watt per Hour |
| PCA | Principal components analysis |
| WCSS | Within cluster sum of square |
| SVM | Support vector machine |
References
- Silva, D.; Xinghuo, Y.; Alahakoon, D.; Holmes, G. Data Mining Framework for Electricity Consumption Analysis From Meter Data. IEEE Trans. Ind. Inform. 2011, 7, 399–407. [Google Scholar] [CrossRef]
- CES-MED. Municipality of Tulkarm Sustainable Energy Action Plan (SEAP). 4 January 2016. Available online: https://www.ces-med.eu/sites/default/files/SEAP_Tulkarem_Palestine.pdf (accessed on 14 April 2019).
- Wang, Y.; Chen, Q.; Kang, C.; Xia, Q. Clustering of electricity consumption behavior dynamics toward Big Data applications. IEEE Trans. Smart Grid 2016, 7. [Google Scholar] [CrossRef]
- Granell, R.; Axon, C.; Wallom, D. Impacts of raw data temporal resolution using selected clustering methods on residential electricity load profiles. IEEE Trans. Power Syst. 2015, 30, 3217–3224. [Google Scholar] [CrossRef]
- The World Factbook-Middle East: West Bank. Central Intelligence Agency, 26 September 2018. Available online: https://www.cia.gov/library/publications/the-world-factbook/geos/we.html (accessed on 3 October 2018).
- PCBS (Palestinian Central Bureau of Statistics). Demographic Survey of the West Bank and Gaza Strip; District Report Series. No. 1–9; PCBS: Ramallah, Palestine, 2010.
- Palestinian Electricity Regulatory Council (PERC). Annual Report; PERC: Ramallah, Palestine, 2011. [Google Scholar]
- Bandyopadhyay, K. User acceptance of prepayment metering systems in India. Int. J. Indian Cult. Bus. Manag. 2008, 1, 450–465. [Google Scholar] [CrossRef]
- Ramos, S.; Duarte, J.; Vale, Z. A Data-mining based Methodology to support MV Electricity Customers’ Characterization. Energy Build. 2015. [Google Scholar] [CrossRef]
- Benitez, I.; Quijano, A.; Diez, J.; Delgado, I. Dynamic clustering segmentation applied to load profiles for energy consumption from Spanish customers. Electr. Power Energy Syst. 2014, 437–448. [Google Scholar] [CrossRef]
- Fayyad, U.; Piatetsky-shapiro, G.; Smyth, P. From data science to knowledge discovery in databases. AI Mag. 1996, 17, 37–45. [Google Scholar]
- Vijay, K.; Bala, D. Predictive Analytics and Data Mining Concepts and Practice with Rapidminer; Morgan Kaufmann: Burlington, MA, USA, 2015. [Google Scholar]
- Benefits of Demand Response in Electricity Markets and Recommendations for Achieving Them; Tech. Rep.; U.S. Department of Energy: New York, NY, USA, 2005.
- Alahakoon, D.; Yu, X. Smart electricity meter data intelligence for future energy systems: A survey. IEEE Trans. Ind. Inform. 2015. [Google Scholar] [CrossRef]
- Bhatt, C. Data Visualization and Visual Data Mining. CSI Communications. January 2014. Available online: https://www.researchgate.net/publication/259922079-Data-Visualization-and-Visual-Data-Mining (accessed on 4 April 2019).
- Kumar, K.; Chadrasekaran, R.M. Attribute Correction-Data Cleaning Using Association Rule and Clustering Methods. Int. J. Data Min. Knowl. Manag. Process 2011, 1. [Google Scholar] [CrossRef]
- Chapman, D. Principles and Methods of Data Cleaning: Primary Species and Species-Occurrence Data; Version 1.0.; Global Biodiversity Information Facility: Copenhagen, Denmark, 2005; Available online: http://www.gbif.org/document/80528 (accessed on 3 April 2019).
- Bazeer, A.; Ramkumar, T. Data Integration-Challenges, Techniques and Future Directions: A Comprehensive Study. Indian J. Sci. Technol. 2016, 9. [Google Scholar] [CrossRef]
- Manikandan, S. Preparing to analyze data. J. Pharmacol. Pharmacother. 2010, 1, 64–65. [Google Scholar] [CrossRef]
- Vora, P.; Oza, B. Improved Data Reduction Technique in Data Mining. IJCSMC 2013, 2, 169–174. [Google Scholar]
- Bin Mohamad, I.; Usman, D. Standardization and Its Effects on K-Means Clustering Algorithm. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 3299–3303. [Google Scholar] [CrossRef]
- Aksoy, S.; Haralick, R. Feature normalization and likelihood-based similarity measures for image retrieval. Pattern Recognit. Lett. 2001, 22, 563–582. [Google Scholar] [CrossRef]
- Larose, D. Discovering Knowledge in Data: An Introduction to Data Mining; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Karthikeyani, N.; Thangavel, K. Impact of Normalization in Distributed K-Means Clustering. Int. J. Soft Comput. 2009, 4, 168–172. [Google Scholar]
- Xia, B.; Gong, P. Review of business intelligence through data analysis. Benchmark. Int. J. 2014, 21, 300–311. [Google Scholar] [CrossRef]
- Friendly, M.; Denis, D.; Truman, S. Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization. Project. History of Data Visualization January 2001. Available online: https://www.researchgate.net/project/History-of-Data-Visualization (accessed on 13 April 2019).
- Świgoń, M. Information limits: Definition, typology and types. Aslib Proc. 2011, 63, 364–379. [Google Scholar] [CrossRef]
- Mandinach, E.; Honey, M.; Light, D. A theoretical framework for data-driven decision making. In Proceedings of the Annual Meeting of the American Educational Research Association, San Francisco, CA, USA, 1–5 April 2006. [Google Scholar]
- Siemens, G. Connectivism: A learning theory for the digital age. Int. J. Instruct. Technol. Distance Learn. 2005, 2, 3–10. [Google Scholar]
- Moore, J. Data visualization in support of executive decision making. Interdiscip. J. Inf. Knowl. Manag. 2017, 12, 125–138. [Google Scholar] [CrossRef]
- Aggarwal, C.; Yu, P. An effective and efficient algorithm for high-dimensional outlier detection. VLDB J. 2005, 14, 211–221. [Google Scholar] [CrossRef]
- Breunig, M.; Kriegel, H.; Ng, R.; Sander, J. Lof: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; Volume 29, pp. 93–104. [Google Scholar]
- Krzywinski, M.; Altman, N. Visualizing samples with box plots. Nat. Method 2014, 11, 119–120. [Google Scholar] [CrossRef]
- Zhao, Q.; Franti, P. Centroid Ratio for a Pairwise Random Swap Clustering Algorithm. IEEE Trans. Knowl. Data Eng. 2014, 26. [Google Scholar] [CrossRef]
- Badase, S.; Deshbhratar, G.; Bhagat, A. Classification and Analysis of Clustering Algorithms for Large Datasets. In Proceedings of the International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, 19–20 March 2015. [Google Scholar] [CrossRef]
- Ketchen, D.; Shook, C. The Application of Cluster Analysis in Strategic Management Research: An Analysis and Critique. Strateg. Manag. J. 1996, 17, 441–458. [Google Scholar] [CrossRef]
- Niu, D.; Dy, J.; Jordan, M. Iterative Discovery of Multiple Alternative Clustering Views. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1340–1353. [Google Scholar] [CrossRef]
- Cios, K.; Pedrycz, W.; Swiniarski, R.; Kurgan, L. Data Mining: A Knowledge Discovery Approach; Springer: New York, NY, USA, 2007. [Google Scholar]
- Nyce, C. Predictive Analytics White Paper. In American Institute for CPCU; Insurance Institute of America: Malvern, PA, USA, 2007; pp. 9–10. Available online: https://www.the-digital-insurer.com/wp-content/uploads/2013/12/78-Predictive-Modeling-White-Paper.pdf (accessed on 18 September 2019).
- Gmyzin, D. A Comparison of Supervised Machine Learning Classification Techniques and Theory-Driven Approaches for the Prediction of Subjective Mental Workload. Master’s Thesis, Dublin Institute of Technology, Dublin, Ireland, 2017. [Google Scholar] [CrossRef]
- Kotsiantis, S. Supervised machine learning: A review of classification techniques. Informatica 2007, 31, 249–268. [Google Scholar]
- Ryan Spain, G. Python and R in Big Data and Data Science. 2018 DZone Guide to Big Data: Stream Processing, Statistics, and Scalability. Available online: https://dzone.com/articles/dzone-research-5 (accessed on 4 April 2019).
- Jolliffe, I.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. A Math. Phys. Eng Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Hambrick, D.; Schecter, S. Turnaround strategies for mature industrial-product business units. Acad. Manag. J. 1983, 26, 231–248. [Google Scholar] [CrossRef]
- Aldenderfer, M.; Blashfield, R. Cluster Analysis; Sage: Newbury Park, CA, USA, 1984. [Google Scholar] [CrossRef]




| Attribute | Description | Format |
|---|---|---|
| BillNo | The bill number of the prepaid smart card charging transaction | Numeric |
| BillDate | The bill date of the prepaid smart card charging transaction | Date |
| ConsumerID | Consumer or user unique ID | String |
| Quantity | The quantity charged in kWh | Numeric |
| Price | The price of 1 KWH | Numeric |
| Hour | The hour of charging smart card | Numeric |
| Period | The period in the day, Evening, Morning, Noon, and Night | String (Evening 6 p.m.–8 p.m., Morning 6 a.m.–10 a.m., Noon 11 a.m.–5 p.m., Night otherwise. |
| Peak | The peak hours during the day are 6 a.m.–10 a.m. and 5 p.m.–8 p.m., or off peak hours otherwise | Numeric (peak-hour = 1, off peak = 2) |
| Day | The day in which the transaction is occurred | Numeric |
| DayofWeek | Weekday | Numeric (Mon = 0 and Sun = 6) |
| WeekEnd | Week end in Palestine is Friday and Saturday, here refers to days before and after Friday the weekend i.e., Thursday and Saturday. | Numeric (Weekend = 1 and 0 otherwise) |
| Month | The month in which the transaction is occurred | Numeric |
| Month-Period | There are 3 months periods June-August is period 1, September-November is period 2, and December is period 3. | Numeric |
| AreaNo | The area number where consumer is located | Numeric (from 1 to 48) |
| TariffNo | Consumers’ Tariff | Numaric (from 1 to 27) |
| ConsumerID | Quantity in kWh per Month | AreaID | Area Name |
|---|---|---|---|
| Y00013083-00143 | 8488.851 | 4 | West |
| Y00010603-00113 | 6831.904 | 1 | Sowth |
| Y00006277-001473 | 5145.798 | 47 | Tulkarm |
| Y00005194-001133 | 5145.798 | 13 | Ezbet Al-Jarad |
| Y00013083-00143 | 5116.638 | 4 | West |
| Y00011015-001473 | 5116.638 | 47 | Tulkarm |
| Y00018491-001103 | 4288.165 | 10 | North |
| Y00011015-001473 | 4288.165 | 47 | Tulkarm |
| Y00015645-00183 | 4087.479 | 8 | East |
| Class | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 1351 | 0 | 32 | 26 |
| 1 | 104 | 867 | 0 | 0 |
| 2 | 94 | 0 | 1940 | 9 |
| 3 | 153 | 0 | 11 | 1871 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
AbuBaker, M. Data Mining Applications in Understanding Electricity Consumers’ Behavior: A Case Study of Tulkarm District, Palestine. Energies 2019, 12, 4287. https://doi.org/10.3390/en12224287
AbuBaker M. Data Mining Applications in Understanding Electricity Consumers’ Behavior: A Case Study of Tulkarm District, Palestine. Energies. 2019; 12(22):4287. https://doi.org/10.3390/en12224287
Chicago/Turabian StyleAbuBaker, Maher. 2019. "Data Mining Applications in Understanding Electricity Consumers’ Behavior: A Case Study of Tulkarm District, Palestine" Energies 12, no. 22: 4287. https://doi.org/10.3390/en12224287
APA StyleAbuBaker, M. (2019). Data Mining Applications in Understanding Electricity Consumers’ Behavior: A Case Study of Tulkarm District, Palestine. Energies, 12(22), 4287. https://doi.org/10.3390/en12224287