Luenberger-Sliding Mode Observer Based Backstepping Control for the SCR System in a Diesel Engine

Abstract

In order to keep the ammonia (NH₃) slip of the downstream selective catalytic reduction (SCR) system at a low level and simultaneously achieve a high nitrogen oxide (NO_X) conversion rate, a Luenberger-sliding mode observer based backstepping control method is proposed. Considering that the internal working condition of the catalyst cannot be measured by commercial sensors directly, a Luenberger-sliding mode observer is designed to estimate the ammonia concentration at the middle of the catalyst. In addition, based on the stepped distributed characteristic of the surface ammonia coverage ratio along the SCR axial direction, a backstepping control method is utilized for the SCR system, in which the SCR system is decomposed into two subsystems. Firstly, the Lyapunov function is designed to ensure the convergence of the downstream subsystem, and then the virtual control law is obtained. After that, taking the virtual control law as the tracking target of the upstream subsystem, the Lyapunov function of virtual control law is given. Finally, the actual control law of the whole closed loop system is acquired. Simulations under different conditions are conducted to investigate the effect of the proposed control method. In addition, comparisons with the traditional PID (Proportion Integration Differentiation) control are presented. Results show that the proposed method is much better than the PID control method in overshoot, setting time, and tracking error.

1. Introduction

Diesel engines have attracted more and more attention in recent years due to their high economy, high power, and low CO and HC emissions [1,2,3]. However, owing to the special combustion process, a diesel engine produces much more nitrogen oxide (NO_X) and particulate matter (PM), which is harmful to the environment and human health. Various regulations have been legislated against diesel engine NO_X and PM emissions. In order to meet stringent regulations, devices such as selective catalytic reduction (SCR) systems and diesel particle filters (DPF) are installed in post-processing systems to reduce emissions. SCR refers to the use of reducing agents to selectively react with NOx in flue gas and generate non-toxic and pollution-free N₂ and H₂O under the action of a catalyst. Generally, in SCR systems, 32.5% of aqueous urea solution is injected into the tail gas pipe of the engine; urea is then decomposed into ammonia, which reacts with NOx to generate N₂ and H₂O. However, excessive urea can lead to NH₃ leakage in the tailpipe and increase the usage cost. On the other hand, insufficient NH₃ injection will lead to low NOx conversion and higher tail pipe NOx emissions [3,4]. A great deal of research has been done to minimize NOx emissions and limit NH₃ leaks at the same time, in which a promising method is to control the NH₃ concentration and coverage of NH₃ in the SCR catalyst at the optimum [5]. NH₃ coverage and the ammonia coverage ratio are defined in (1), where $\mathrm{\Theta }$ is NH₃ storage capacity and $M_{N{H}_3}$ is the amount of NH₃ stored inside the SCR catalyst.

$${\theta }_{N{H}_3}=\frac{M_{N{H}_3}}{\mathrm{\Theta }}$$

(1)

Much research has been conducted into SCR control systems [4,5,6]. In general, the SCR control strategy can be divided into non-model-based [7,8] and model-based [9,10,11,12,13,14,15,16,17]. The non-model-based methods include the pulse spectrum-based blue jet control method [7] and the PID control method [8]. Although the non-model-based method is relatively mature, its performance in transient and low temperature conditions makes it increasingly difficult to meet stricter emission regulations due to the problems of time delay, system inertia, and sensor measurement error and system uncertainty. As emission regulations become more and more stringent, model-based methods, such as predictive control [9], are needed urgently. Simulation and test bench results show that, compared to the non-model-based method, the model-based control method has higher accuracy and better environmental adaptability.

It should be mentioned that the values of NH₃ concentration and NH₃ coverage of the catalyst is vital for the SCR control system. Unfortunately, it is inconvenient to measure NH₃ coverage directly through commercial sensors. To address the problem, observer based methods are prospective and widely used. Reference [18] presents an observer for estimating the NH₃ concentration of catalysts in SCR. The observer can be used for NH₃ distribution control of the SCR catalyst and fault diagnosis of the diesel engine. Experiments show that the observer estimates converge to the sensor readings and can track the values well. However, the concentration cannot be estimated well in the first 1100 seconds. In [4], an approach by utilizing two post-selective-catalytic-reduction nitrogen oxide sensors with different ammonia cross-sensitivity factors is proposed to estimate the nitrogen oxide concentration, the ammonia concentration, and the ammonia surface coverage ratio. Experimental results show that the proposed method can be useful in reducing the cost of SCR diagnosis, NH₃ coverage estimation, and advanced SCR controls. In addition, an extended Kalman filter [19] can also be utilized to estimate the NOx sensor cross-sensitivity to ammonia. It is noteworthy that the performance of an urea-SCR system may be related to the NH₃/NO_X ratio and the NO/NO₂ ratio. Studies show that the ratio of NO to NO₂ varies with the reduction rate and conversion efficiency of NO_X [1]. A sliding mode observer is widely used in system state estimation because of its strong robustness [20,21,22,23]. S. Hasan [24] introduced the Luenberger term into the design of the sliding mode observer, which not only improved the robustness of the observer, but also improved the speed of parameter estimation. Based on the above analysis, a Luenberger sliding mode observer is designed to estimate the state of the two-cell SCR catalyst.

Backstepping control is mainly used to deal with robust control systems with nonlinear and parametric uncertainties [25,26]. SCR is a typical nonlinear system with uncertain parameters, which is very suitable for backstepping control. Thus, in [27], the backstepping control is used successfully, but the unmeasurable problem of NH₃ concentration is not mentioned.

In this paper, considering the advantages of the Luenberger-sliding mode observer [24] and backstepping control [25,26], a Luenberger-sliding mode observer based backstepping control method is applied to a nonlinear SCR system. The aims of this work are to simultaneously minimize the NOx emissions and limit the NH₃ slip under a certain input and output constraint. A Luenberger-sliding mode observer is designed to estimate NH₃ concentration and then, based on the Lyapunov stability analysis and the stepped distributed characteristic of the surface NH₃ coverage ratio along the SCR axial direction, a backstepping control method is designed for SCR system adblue dosing. After that, the stability analysis of the proposed control strategy is described. The proposed approach is validated through computer simulations that are compared with the traditional PID control. Simulation results show that the system controlled by the proposed method has promising performance in overshoot, setting time, and tracking error.

2. Selective Catalytic Reduction System

2.1. SCR System Operation Principles

Figure 1 is a schematic diagram of an SCR system, in which temperature, NOx, and NH₃ sensors are located upstream and downstream of the SCR catalyst. In order to monitor the status of the intermediate catalyst, NOx and NH₃ sensors are installed between two SCR batteries. Note that the inlet NOx measurement will not be contaminated by NH₃, while the intermediate and downstream NOx sensors will be affected by the cross sensitivity of NH₃. According to [27], the concentration of NOx is a combination of the NOx and NH₃ concentrations, as shown in (2):

$$C_{N{O}_x,mea}=C_{N{O}_x}+K{C}_{N{H}_3}$$

(2)

where $C_{N{O}_x,mea}$ is the NOx sensor reading, $C_{N{O}_x}$ is the true value of the NOx concentration, $C_{N{H}_3}$ is the NH₃ concentration, and $K$ denotes the cross-sensitivity factor. In this paper, $K$ is considered to be a constant.

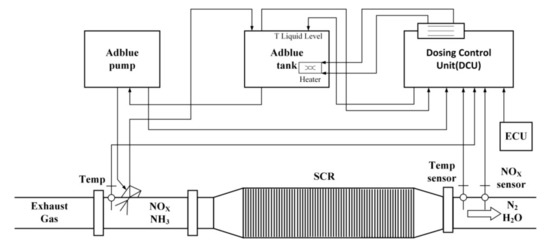
Figure 1. Schematic diagram of a selective catalytic reduction (SCR) system.

The reduction involves three processes. First, the urea solution sprayed into the upstream exhaust pipe is converted into NH₃, which generally consists of three chemical reactions: Urea solution evaporation, urea decomposition, and isocyanic acid hydrolysation. The main chemical reactions are summarized as:

Aqueous urea solution evaporation:

$$(N{H}_2)CO(liquid)\to {(N{H}_2)}_{2}CO(solid)+H_{2}O.$$

(3)

Urea decomposition:

$${(N{H}_2)}_{2}CO\to 2N{H}_3+HNCO.$$

(4)

Isocyanic acid (HNCO) hydrolysation:

$$HNCO+H_{2}O\to N{H}_3+C{O}_2.$$

(5)

Then, the converted NH₃ is adsorbed on the surface of the catalyst matrix. Finally, the NH₃ reacts with NOx to form nitrogen molecules.

It should be noted that that urea can be completely converted in the upstream tailpipe if the catalyst pool has a good geometric design and the exhaust has a suitable temperature [28]. Therefore, it is reasonable to assume that 100% of the urea aqueous solution is converted to gaseous NH₃ before the SCR catalyst unit.

The NH₃ adsorption and desorption reactions can be expressed as [29]:

$$Z+N{H}_3\to ZN{H}_3$$

(6)

$$ZN{H}_3\to Z+N{H}_3$$

(7)

where Z is the active substrate site of the SCR catalyst cell and $ZN{H}_3$ represents NH₃ adsorbed on the SCR substrate. The adsorbed NH₃ is active enough to reduce the NOx in terms of the chemical reactions. The main NOx reduction process can be summarized as follows:

$$4N{H}_3+4NO+O_2\to 4N_2+6H_{2}O$$

(8)

$$4N{H}_3+2NO+2N{O}_2\to 4N_2+6H_{2}O$$

(9)

$$8N{H}_3+6N{O}_2\to 7N_2+12H_{2}O.$$

(10)

In some cases, when the gas temperature is quite high, the adsorbed NH₃ can also be oxidized, as shown in (11):

$$4N{H}_3+5O_2\to 4NO+6H_{2}O.$$

(11)

2.2. SCR Dynamic Model and Analysis of Observability and Controllability

Assuming that the physical variables in the SCR catalyst unit are uniform, a SCR model is developed based on the above reaction. For convenience, the mass transfer and the surface phase concentration of species in the model are neglected. In this paper, the nonlinear model of the SCR model is expressed using the state-space form [29]:

$$\left[\begin{array}{l}{\dot{C}}_{NO}\\ \dot{\theta }\\ {\dot{C}}_{N{H}_3}\end{array}\right]=\left[\begin{array}{l}-C_{NO}(\mathrm{\Theta }{r}_{\mathrm{red}}\theta +\frac{F}{V})+r_{oxi}\mathrm{\Theta }\theta \\ -\theta (r_{\mathrm{ads}}{C}_{N{H}_3}+r_{des}+r_{red}{C}_{NO}+r_{oxi})+r_{ads}{C}_{N{H}_3}\\ -C_{N{H}_3}[\mathrm{\Theta }{r}_{ads}(1-\theta )+\frac{F}{V}]+\mathrm{\Theta }{r}_{\mathrm{des}}\theta \end{array}\right]+\left[\begin{array}{c}0\\ 0\\ \frac{F}{V}\end{array}\right]C_{N{H}_3,in}+\left[\begin{array}{c}\frac{F}{V}\\ 0\\ 0\end{array}\right]C_{NO,in}$$

(12)

where, $C_{NO}$, $C_{N{H}_3}$, $C_{NO,in}$, and $C_{N{H}_3,in}$ are the concentrations of NO, NH₃, inlet NO, and inlet NH₃, respectively. $r_{red}$, $r_{ads}$, $r_{des}$, and $r_{oxi}$ are standard reaction rate, adsorption rate, desorption rate, and oxidation rate, respectively. $F$ is the exhaust flow rate and $V$ is the SCR volume. $\theta$ denotes the ammonia coverage ratio and $R$ is the universal gas constant.

Let

$$x={[x_1 x_2 x_3]}^T$$

(13)

where $x_1=C_{NO}$, $x_2=\theta$, $x_3=C_{N{H}_3}$.

Linearize the nonlinear model with respect to operating points and obtain the linear state space equation:

$$\left\{\begin{array}{l}\dot{x}=Ax+Bu+Dd\\ y=Cx\end{array}\right.$$

(14)

where

$A=\left[\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right], B=\left[\begin{array}{c}0\\ 0\\ \frac{F}{V}\end{array}\right], D=\left[\begin{array}{c}\frac{F}{V}\\ 0\\ 0\end{array}\right], C=\left[\begin{array}{ccc}0& 0& 1\end{array}\right],$

$A_{11}=-\mathrm{\Theta }{r}_{red}{x}_2-\frac{F}{V}, A_{12}=-\mathrm{\Theta }{r}_{red}{x}_1+\mathrm{\Theta }{r}_{oxi},$

$A_{13}=0, A_{21}=-r_{red}{x}_2, A_{23}=r_{ads}(1-x_2),$

$A_{22}=-r_{ads}{x}_3+r_{des}+r_{red}{x}_1+r_{oxi}, A_{31}=0,$

$A_{32}=\mathrm{\Theta }{r}_{ads}{x}_3+\mathrm{\Theta }{r}_{des}$, $A_{33}=-\mathrm{\Theta }{r}_{ads}(1-x_2)-\frac{F}{V}$, $u=C_{N{H}_3,in}$ is the inlet ammonia concentration, $d=C_{NO,in}$ is the inlet NO concentration.

The controllability grammian matrix takes the form:

$$Q_C=\left[\begin{array}{ccc}\begin{array}{l}0\\ 0\\ 1\end{array}& \begin{array}{c}0\\ A_{23}\\ A_{33}\end{array}& \begin{array}{l}{A}_{12}{A}_{23}\\ (A_{22}{A}_{23}+A_{23}{A}_{33})\\ (A_{23}{A}_{32}+A^2{}_{33})\end{array}\end{array}\right].$$

(15)

In most cases, the rank of the controllability grammian matrix is equal to 3. However, it may lose rank under certain operations:

(1)

$A_{23}=0$, $rank(Q_C)=1$; the NH₃ coverage ratio and the NO_X concentration are uncontrollable. At that point, the NH₃ coverage ratio reaches 100%. However, it will not happen in practice.

(2)

$A_{12}=0$, $rank(Q_C)=2$; the NO_X is uncontrollable. In the meantime, $r_{oxi}>r_{red}\times C_{NO}$, the reasonable working temperature, is below 600 °C. Therefore, the loss of controllability due to this condition is not expected operationally.

3. Observer Design and Stability Analysis

3.1. Two-Cell SCR Catalyst Ammonia Concentration Observer Design

According to [8], ammonia storage in SCR catalysts varies along the axis of the catalysts. Moreover, the ammonia storage in the upstream and downstream of the SCR catalysts has a direct impact on the conversion of NOx and the emission of NH₃ in the tail gas. In order to express the internal state of the SCR catalytic converter more accurately, a two-cell SCR catalytic converter system is designed, shown in Figure 2 [18].

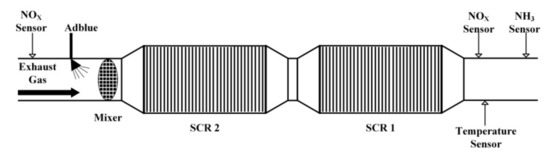
Figure 2. Two-cell SCR catalyst model.

Considering the NH₃ concentration and NH₃ coverage ratio, the dynamic model is presented as follows:

$${\dot{\theta }}_1=-{\theta }_1(r_{\mathrm{ads},1}{C}_{N{H}_3,1}+r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,1})+r_{ads,1}{C}_{N{H}_3,1}$$

(16)

$${\dot{\theta }}_2=-{\theta }_2(r_{\mathrm{ads},2}{C}_{N{H}_3,2}+r_{des,2}+r_{red,2}{C}_{NO,2}+r_{oxi,2})+r_{ads,2}{C}_{N{H}_3,2}$$

(17)

$${\dot{C}}_{N{H}_3,1}=-C_{N{H}_3,1}[{\mathrm{\Theta }}_1{r}_{ads,1}(1-{\theta }_1)+\frac{F_1}{V_1}]+{\mathrm{\Theta }}_1{r}_{\mathrm{des},1}{\theta }_1+\frac{F_1}{V_1}{C}_{N{H}_3,2}$$

(18)

$${\dot{C}}_{N{H}_3,2}=-C_{N{H}_3,2}[{\mathrm{\Theta }}_2{r}_{ads,2}(1-{\theta }_2)+\frac{F_2}{V_2}]+{\mathrm{\Theta }}_2{r}_{\mathrm{des},2}{\theta }_2+\frac{F_2}{V_2}{C}_{N{H}_3,in}.$$

(19)

To estimate the NH₃ coverage ratio, a Luenberger-sliding mode observer is proposed to observe the NH₃ coverage ratio of the upstream cell [20]:

$${\dot{\widehat{C}}}_{N{H}_3,2}=-{\widehat{C}}_{N{H}_3,2}[{\mathrm{\Theta }}_2{r}_{ads,2}(1-{\widehat{\theta }}_2)+\frac{F_2}{V_2}]+{\mathrm{\Theta }}_2{r}_{\mathrm{des},2}{\widehat{\theta }}_2+\frac{F_2}{V_2}{C}_{N{H}_3,in}+l_{2,2}(C_{N{H}_3,1}-{\widehat{C}}_{N{H}_3,2})+k_{2,2}\mathrm{sgn}(C_{N{H}_3,1}-{\widehat{C}}_{N{H}_3,2})$$

(20)

where

$${\dot{\widehat{\theta }}}_2=-{\widehat{\theta }}_2(r_{\mathrm{ads},2}{\widehat{C}}_{N{H}_3,2}+r_{des,2}+r_{red,2}{\widehat{C}}_{NO,2}+r_{oxi,2})+r_{ads,2}{\widehat{C}}_{N{H}_3,2}+l_{1,2}({\widehat{C}}_{N{H}_3,2}-{\widehat{C}}_{N{H}_3,1})+k_{1,2}\mathrm{sgn}({\widehat{C}}_{N{H}_3,2}-{\widehat{C}}_{N{H}_3,1})$$

(21)

$${\dot{\widehat{\theta }}}_1=-{\widehat{\theta }}_1(r_{\mathrm{ads},1}{\widehat{C}}_{N{H}_3,1}+r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,1})+r_{ads,1}{\widehat{C}}_{N{H}_3,1}$$

(22)

$${\dot{\widehat{C}}}_{N{H}_3,1}=-{\widehat{C}}_{N{H}_3,1}[{\mathrm{\Theta }}_1{r}_{ads,1}(1-{\widehat{\theta }}_1)+\frac{F_1}{V_1}]+{\mathrm{\Theta }}_1{r}_{\mathrm{des},1}{\widehat{\theta }}_1+\frac{F_1}{V_1}{C}_{N{H}_3,2}+l_{2,1}(C_{N{H}_3,1}-{\widehat{C}}_{N{H}_3,1})+k_{2,1}\mathrm{sgn}(C_{N{H}_3,1}-{\widehat{C}}_{N{H}_3,1})$$

(23)

$${\dot{\widehat{C}}}_{NO,2}=-{\widehat{C}}_{NO,2}({\mathrm{\Theta }}_2{r}_{\mathrm{red},2}{\widehat{\theta }}_2+\frac{F_2}{V_2})+r_{oxi,2}{\mathrm{\Theta }}_2{\widehat{\theta }}_2+\frac{F_2}{V_2}{C}_{NO,in}$$

(24)

$k_{1,2},k_{2,1},k_{2,2}>0$, $0\le {\widehat{\theta }}_2$, ${\widehat{\theta }}_2\le 1$, $0\le {\widehat{C}}_{N{H}_3,1}<1$, ${\widehat{C}}_{N{H}_3,2}\le {\widehat{C}}_{N{H}_3,\max }<1$.

3.2. Observer Stability Analysis

As mentioned above, the NH₃ coverage ratio is one of the important factors for the NH₃ storage distribution control, and its estimation requires the NH₃ concentration. The observability is demonstrated in the following [28]:

3.2.1. Convergence Analysis of ${\widehat{\theta }}_1$

First, select the Lyapunov function candidate as:

$$V_{{\theta }_1}=\frac{1}{2}{\tilde{\theta }}_1^2.$$

(25)

Then, the differentiate (25), gives:

$${\dot{V}}_{{\theta }_1}={\tilde{\theta }}_1{\dot{\tilde{\theta }}}_1=-{\tilde{\theta }}_1^2(r_{\mathrm{ads},1}{\widehat{C}}_{N{H}_3,1}+r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,1}).$$

(26)

It is apparent that ${\dot{V}}_{{\theta }_1}\le 0$, which means that ${\widehat{\theta }}_1$ converges to ${\theta }_1$ within a finite period of time.

3.2.2. Convergence Analysis of ${\widehat{C}}_{N{H}_3,2}$

Convergence analysis of ${\widehat{C}}_{N{H}_3,2}$

$${\dot{\tilde{C}}}_{N{H}_3,1}=\frac{F_1}{V_1}{\tilde{C}}_{N{H}_3,2}-l_{2,1}({\tilde{C}}_{N{H}_3,1})-k_{2,1}\mathrm{sgn}({\tilde{C}}_{N{H}_3,1})$$

(27)

since $0\le {\tilde{C}}_{N{H}_3,2}\le C_{N{H}_3,\max }$, let $k_{2,1}>\frac{F_{1,\max }}{V_1}{C}_{N{H}_3,\max }$, then ${\widehat{C}}_{N{H}_3,2}$ can converges to $C_{N{H}_3,2}$ in a finite period of time. Once the sliding mode is reached in the short term, there will be ${\dot{\tilde{C}}}_{N{H}_3,1}={\tilde{C}}_{N{H}_3,1}=0$. That means:

$$\frac{F_1}{V_1}{\tilde{C}}_{N{H}_3,2}=k_{2,1}\mathrm{sgn}({\tilde{C}}_{N{H}_3,1})$$

(28)

$$\mathrm{sgn}({\tilde{C}}_{N{H}_3,2})=\mathrm{sgn}({\tilde{C}}_{N{H}_3,1}).$$

(29)

Select the Lyapunov function candidate as:

$$V_{C_{N{H}_3,2}}=\frac{1}{2}{\tilde{C}}_{N{H}_3,2}^2.$$

(30)

Then, differentiate (31) gives:

$$\begin{array}{l}{\dot{V}}_{C_{N{H}_3,2}}={\tilde{C}}_{N{H}_3,2}{\dot{\tilde{C}}}_{N{H}_3,2}=-{\tilde{C}}_{N{H}_3,2}[-{\tilde{C}}_{N{H}_3,2}({\mathrm{\Theta }}_2{r}_{ads,2}+\frac{F_2}{V_2})+\\ C_{N{H}_3,2}{\mathrm{\Theta }}_2{r}_{ads,2}-{\widehat{C}}_{N{H}_3,2}{\mathrm{\Theta }}_2{r}_{ads,2}{\widehat{\theta }}_2+{\mathrm{\Theta }}_2{r}_{ads,2}{\tilde{\theta }}_2-l_{2,2}({\tilde{C}}_{N{H}_3,2})-k_{2,2}\mathrm{sgn}({\tilde{C}}_{N{H}_3,2})]\end{array}.$$

(31)

Let $k_{2,2}>\max |C_{N{H}_3,2}{\mathrm{\Theta }}_2{r}_{ads,2}-{\widehat{C}}_{N{H}_3,2}{\mathrm{\Theta }}_2{r}_{ads,2}{\widehat{\theta }}_2+{\mathrm{\Theta }}_2{r}_{ads,2}{\tilde{\theta }}_2|$,then ${\dot{V}}_{C_{N{H}_3,2}}$ is negative and definite, and ${\widehat{C}}_{N{H}_3,2}$ converges to $C_{N{H}_3,2}$ in a finite period of time.

3.2.3. Convergence Analysis of ${\widehat{\theta }}_2$

Let ${\tilde{C}}_{N{H}_3,2}=0$ as a sliding surface; once the sliding mode is reached, there will be ${\dot{\tilde{C}}}_{N{H}_3,2}={\tilde{C}}_{N{H}_3,2}=0$. Select the Lyapunov function candidate as:

$$V_{{\theta }_2}=\frac{1}{2}{\tilde{\theta }}_2^2.$$

(32)

Then, differentiate (32) gives:

$$\begin{array}{l}{\dot{V}}_{{\theta }_2}={\tilde{\theta }}_2{\dot{\tilde{\theta }}}_2={\tilde{\theta }}_2[-{\tilde{\theta }}_2(r_{des,2}+r_{red,2}{\widehat{C}}_{NO,2}+r_{oxi,2})+{\widehat{\theta }}_2{r}_{\mathrm{ads},2}{\widehat{C}}_{N{H}_3,2}-{\widehat{\theta }}_2{r}_{\mathrm{ads},2}{\widehat{C}}_{N{H}_3,2}\\ +r_{\mathrm{ads},2}{\tilde{C}}_{N{H}_3,2}-l_{1,2}({\tilde{C}}_{N{H}_3,2})-k_{1,2}\mathrm{sgn}({\tilde{C}}_{N{H}_3,2}]\end{array}.$$

(33)

Let $k_{1,2}>|C_{N{H}_3,2}{r}_{ads,2}{|}_{\max }$, then ${\dot{V}}_{{\theta }_2}$ is negative and definite, and ${\widehat{\theta }}_2$ can converge to ${\theta }_2$ in a finite period of time.

4. Backstepping Control Law Design

In order to keep NH₃ leakage of the downstream SCR system at a low level and achieve a high NOx conversion rate at the same time, the controller should keep downstream NH₃ coverage below constraint ${\theta }_1^{*}$ and control upstream NH₃ coverage at the desired target, ${\theta }_2^{*}$. Based on the two-cell SCR system model, the dynamic equations are expressed as [18]:

$${\dot{x}}_1=F_1(x_1,x_3,T,C_{NO})+G_1(x_1,x_3,T,C_{NO})x_3$$

(34)

$${\dot{x}}_2=F_2(x_1,x_2,\mathrm{\Theta },T,F,V)+G_2(x_1,x_2,\mathrm{\Theta },T,F,V)x_4$$

(35)

$${\dot{x}}_3=F_3(x_4,x_3,\mathrm{\Theta },T,F,V)+G_3(x_4,x_3,\mathrm{\Theta },T,F,V)u$$

(36)

$${\dot{x}}_4=F_4(x_3,x_4,T,C_{NO})+G_4(x_3,x_4,T,C_{NO})x_4$$

(37)

where

$${[x_1 x_2 x_3 x_4]}^T={[{\theta }_1 C_{N{H}_3,1} {\theta }_2 C_{N{H}_3,2}]}^T$$

(38)

$${[x_{1,\min } x_{2,\min } x_{3,\min } x_{4,\min }]}^T\le {[x_1 x_2 x_3 x_4]}^T\le {[x_{1,\max } x_{2,\max } x_{3,\max } x_{4,\max }]}^T$$

(39)

$G_1(\cdot )>0$, $G_2(\cdot )>0$, $G_3(\cdot )>0$, $G_4(\cdot )>0$, $F_1(\cdot )<0$, $F_4(\cdot )<0$.

According to the backstepping theory, the control law is designed to let $x_4$ approach ${\theta }_2^{*}$ under the condition $x_1\le {\theta }_1^{*}$.

$$u=\frac{-G_2(x_2-{\xi }_1)-G_4(x_4-{\theta }_2^{*})-K_{3}sign(x_3-{\xi }_2)-F_3+{\dot{\xi }}_2}{G_3}$$

(40)

$${\xi }_1=-K_1\frac{x_1-{\theta }_1^{*}}{1-x_1}$$

(41)

$${\xi }_2=\frac{-K_2\left(x_2-{\xi }_1\right)-F_2+{\dot{\xi }}_2-K_0{G}_1\left(x_1-{\theta }_1^{*}\right)}{G_2}$$

(42)

$$K_1=\frac{C}{2G_4(1-{\theta }_1^{*})}(sign((x_1-{\theta }_1^{*})(x_4-{\theta }_2^{*}))+1),C>0$$

(43)

$$K_2>\frac{{\left|F_2\right|}_{\max }+K_0{G}_{1,\max }}{x_{2,\min }}$$

(44)

$$K_3>G_{4,\max }{\left|x_4-{\theta }_2^{*}\right|}_{\max }$$

(45)

$$sign(x)=\left\{\begin{array}{l}-1,x<0\\ 0,x=0\\ 1,x>0\end{array}\right.$$

(46)

Stability of the backstepping is necessary for the controller design. For this system, two cases should be considered. One is $x_1>{\theta }_1^{*}$; at this time, the downstream ammonia coverage ratio is fairly high, and $x_1$ can converge to ${\theta }_1^{*}$. Another is $x_1\le {\theta }_1^{*}$; the constraint is satisfied, and $x_4$ can converge to ${\theta }_2^{*}$.

4.1. Stability Analysis of Case 1

(1) For Equation (34), the Lyapunov function candidate can be defined as:

$$V_1=\frac{K_0}{2}{\widehat{x}}_1^2>0$$

(47)

where $\widehat{x}=x_1-{\theta }_1^{*}$ and $K_0>0$, and taking the time derivative of $V_1$ gives

$${\dot{V}}_1=K_0{\widehat{x}}_1{\dot{\widehat{x}}}_1=K_0{\widehat{x}}_1{F}_1+K_0{\widehat{x}}_1{G}_1{x}_3.$$

(48)

Combining (34) with (38) obtains:

$${\dot{V}}_1=-K_0{\widehat{x}}_1({\widehat{x}}_1+{\theta }_1^{*})(r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,i})+K_0{r}_{ads,1}{\widehat{x}}_1{x}_2(1-({\widehat{x}}_1+{\theta }_1^{*}))K_0{\widehat{x}}_1{F}_1.$$

(49)

Select the virtual control input $x_2$ as ${\xi }_1$. Combined, (40) and (43), gives

$$x_{2,vir}={\xi }_1=-K_1\frac{x_1-{\theta }_1^{*}}{1-x_1}=\frac{C(x_1-{\theta }_1^{*})}{2G_4(1-{\theta }_1^{*})(1-x_1)}(sign((x_1-{\theta }_1^{*})(x_4-{\theta }_2^{*}))+1).$$

(50)

Then

$${\dot{V}}_1=-K_0{\widehat{x}}_1({\widehat{x}}_1+{\theta }_1^{*})(r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,i})-\frac{C{K}_0{\widehat{x}}_1^2{r}_{ads,1}}{2G_4(1-{\theta }_1^{*})}(sign((x_1-{\theta }_1^{*})(x_4-{\theta }_2^{*}))+1)$$

(51)

bacause ${\widehat{x}}_1>0$

$${\widehat{x}}_1({\widehat{x}}_1+{\theta }_1^{*})(r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,i})>{\widehat{x}}_1^2(r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,i})>0$$

(52)

and

$$\frac{C{K}_0{\widehat{x}}_1^2{r}_{ads,1}}{2G_4(1-{\theta }_1^{*})}(sign((x_1-{\theta }_1^{*})(x_4-{\theta }_2^{*}))+1)\ge 0$$

(53)

$${\dot{V}}_1\le -K_0{\widehat{x}}_1({\widehat{x}}_1+{\theta }_1^{*})(r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,i})\le -K_0{\widehat{x}}_1^2({\widehat{x}}_1+{\theta }_1^{*})(r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,i})=-Q_1<0$$

(54)

where, $Q_1$ is positive and definite. Therefore, $x_1$ can converge to ${\theta }_1^{*}$.

(2) For Equation (35), in order to ensure that the real $x_2$ can converge to the desired value,$x_{2,tar}$, with the action of ${\xi }_2$, the Lyapunov function candidate can be defined as:

$$V_2=V_1+\frac{1}{2}{z}_2^2=\frac{K_0}{2}{\widehat{x}}_1^2+\frac{1}{2}{z}_2^2$$

(55)

where

$$z_2=x_2-{\xi }_1.$$

(56)

Taking the time derivative of $V_2$ gives:

$${\dot{V}}_2=K_0{\widehat{x}}_1{\dot{\widehat{x}}}_1^{}+z_2{\dot{z}}_2^{}.$$

(57)

Because $x_2={\xi }_1+z_2$, according to (48) and (64), we can get:

$$\begin{array}{ll}{\dot{V}}_2& \le -K_0{\widehat{x}}_1^2({\widehat{x}}_1+{\theta }_1^{*})(r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,i})+K_0{\widehat{x}}_1{G}_1{z}_2+z_2({\dot{x}}_2-{\dot{\xi }}_1)\\ & =-Q_1+z_2(K_0{\widehat{x}}_1{G}_1+F_2+G_2{x}_3-{\dot{\xi }}_1)\end{array}.$$

(58)

Letting $x_3={\xi }_2$, as the virtual control signal, gets:

$${\dot{V}}_2\le -K_0{\widehat{x}}_1^2({\widehat{x}}_1+{\theta }_1^{*})(r_{des,1}+r_{red,1}{C}_{NO,1}+r_{oxi,i})-K_2{x}_2^2=-Q_2<0$$

(59)

where, $Q_2$ is positive and definite. Therefore, $x_2$ can converge to $x_{2,tar}$.

(3) For Equation (36), in order to ensure that $x_3$ can converge to the desired value, $x_{3,tar}$, with the action of input signal $u$, the Lyapunov function candidate can be defined as:

$$V_3=V_2+\frac{1}{2}{z}_3^2$$

(60)

where $z_3=x_3-{\xi }_2$. Analogously, according to (59), taking the time derivative of $V_3$ gives:

$${\dot{V}}_3={\dot{V}}_2+z_3{\dot{z}}_3\le -Q_2+G_2{z}_2{z}_3+z_3({\dot{x}}_3-{\dot{\xi }}_2)=-Q_2+z_3(G_2{z}_2+F_3+G_{3}u-{\dot{\xi }}_2).$$

(61)

Based on (40) and (61), it can be achieved by:

$${\dot{V}}_3\le -Q_2-z_3(K_{3}sign(z_3)+g_4(x_4-{\theta }_2^{*}))=-Q_3.$$

(62)

Because $K_3>g_{4,\max }{\left|x_4-{\theta }_2^{*}\right|}_{\max }$, ${\dot{V}}_3<0$, $x_3$ can converge to $x_{3,tar}$.

According to the above mentioned analysis, based on the Lyapunov functions (47), (55), (60), and the control law (39), $x_1$, $x_2$, and $x_3$ can converge to the desired value, respectively.

4.2. Stability Analysis of Case 2

In this case, the NH₃ coverage ratio of the downstream SCR system should be lower than the value $x_{2,tar}$, therefore, the Lyapunov function is design to prove that $x_4$ can converge to ${\theta }_2^{*}$ with the action of ${\xi }_2$.

(1) For Equation (34), select ${\xi }_2$ as the virtual control input of $x_3$; the Lyapunov function candidate can be defined as:

$$V_4=\frac{1}{2}{\widehat{x}}_4^2$$

(63)

where ${\widehat{x}}_4=x_4-{\theta }_2^{*}$.

Taking the time derivative of $V_4$, gives:

$${\dot{V}}_4={\widehat{x}}_4{\dot{\widehat{x}}}_4={\widehat{x}}_4(F_4+G_4{x}_3).$$

(64)

Let $x_{3,tar}={\xi }_2$, then:

$${\dot{V}}_4={\widehat{x}}_4{\dot{\widehat{x}}}_4={\widehat{x}}_4(f_4+g_4{\xi }_2)={\widehat{x}}_4(f_4+\frac{g_4}{g_2}(-K_2(x_2-{\xi }_1)-f_2+{\dot{\xi }}_2-K_0{g}_1(x_1-{\theta }_1^{*}))).$$

(65)

At this moment, there are two different conditions needing consideration.

If $x_1<{\theta }_1^{*}$ and $x_4\ge {\theta }_2^{*}$, then $sign((x_1-{\theta }_1^{*})(x_4-{\theta }_2^{*})+1)=0$, $K_1=0$, and ${\xi }_1={\dot{\xi }}_1=0$. ${\dot{V}}_4$ can be written as:

$${\dot{V}}_4={\widehat{x}}_4(f_4-\frac{g_4}{g_2}(K_2{x}_2+f_2+K_0{g}_1(x_1-{\theta }_1^{*}))).$$

(66)

Based on (44):

$$\begin{array}{ll}{\dot{V}}_4& \le {\widehat{x}}_4(f_{4,\max }-\frac{g_{4,\max }}{g_{2,\max }}(K_2{x}_{2,\min }+f_2-K_0{g}_1))\\ & \le {\widehat{x}}_4(f_{4,\max }-\frac{g_{4,\max }}{g_{2,\max }}({\left|f_2\right|}_{\max }+K_0{g}_{1,\min }+f_2+K_0{g}_1))<0\end{array}.$$

(67)

Since ${\dot{V}}_4$ is negative and definite, $x_4$ can converge to ${\theta }_2^{*}$.

If $x_1<{\theta }_1^{*}$ and $x_4<{\theta }_2^{*}$, in order that ${\dot{V}}_4$ is negative and definite, according to (65), it can be achieved by:

$$F_4+G_4{\xi }_2>0.$$

(68)

Combined, (40), (41), and (43), obtain:

$$F_4+G_4{\xi }_2=F_4+\frac{G_4}{G_2}[-K_2(x_2+K_1\frac{x_1-{\theta }_1^{*}}{1-x_1})-F_2-K_1\frac{(F_1-G_1{x}_2)(1-{\theta }_1^{*})}{{(1-x_1)}^2}-K_0{G}_1(x_1-{\theta }_1^{*}].$$

(69)

Since $x_1<{\theta }_1^{*}$ and $x_4<{\theta }_2^{*}$, (68) can be achieved if the following condition is satisfied:

$$x_1-{\theta }_1^{*}<\frac{G_2(1-x_1)(1-{\theta }_1^{*})}{K_{2}C+G_1{G}_4{K}_0(1-x_1)(1-{\theta }_1^{*})}[F_4-\frac{K_2{G}_4{x}_2}{G_2}-\frac{G_4{F}_2}{G_2}-\frac{C(F_1+G_1{x}_2)(1-{\theta }_1^{*})}{G_2{(1-x_1)}^2}]=\omega .$$

(70)

If $\omega \ge 0$, ${\widehat{x}}_1$ can converge to zero. If $\omega <0$ and $C$ and $K_2$ are large enough, $\omega$ can be very close to zero, which means that $x_4$ can converge to ${\theta }_2^{*}$ when $x_1<{\theta }_1^{*}-\left|\omega \right|$.

(2) For Equation (35), the Lyapunov function candidate can be defined as:

$$V_5=V_4+\frac{1}{2}{z}_3^2.$$

(71)

According to (65) and (39), it can be achieved by:

$$\begin{array}{ll}{\dot{V}}_5& ={\dot{V}}_4+z_3{\dot{z}}_3\le G_4{z}_3{\widehat{x}}_4+z_3({\dot{x}}_3-{\dot{\xi }}_2)\\ & =z_3({\widehat{x}}_4{G}_4+F_3+G_{3}u-{\dot{\xi }}_2)=-z_3(K_{3}sign(z_3)+G_2{z}_2)\end{array}.$$

(72)

Based on (45),${\dot{V}}_5$ is negative, $x_3$ can converge to ${\xi }_2$, and $x_4$ can converge to ${\theta }_2^{*}$.

5. Experiment Results and Analysis

Several studies have reported that the combination of DOC (Diesel Oxidation Catalyst), DPF, and SCR has become one of the most common post-processing applications in heavy diesel engines, which can handle PM and NOx simultaneously [30,31,32]. Normally, DOC, installed upstream of the SCR catalysts, is utilized to convert part of NO into NO₂. At the same time, DPF, installed between the DOC and the SCR, is used for reducing PM emissions. Figure 3 shows a schematic diagram of a SCR after-treatment system. The detail parameters of the parts are listed in Table 1, Table 2, Table 3 and Table 4.

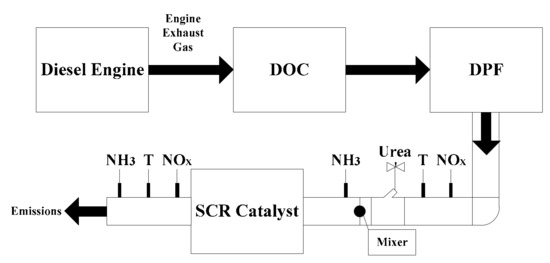
Figure 3. Schematic diagram of SCR after-treatment system for simulation.

Table 1. The detail parameters of the Engine.

Item	Quantity
Engine type	4-cylinder
Bore (mm)	100
Stroke (mm)	110
Connecting rod length (mm)	152
Compression ratio	18
Engine displacement (liter)	3

Table 2. Configuration parameters of SCR in GT power.

Item	Quantity
Cell density (1/inch2)	400
Length (mm)	250
Diamater (mm)	25
Active surface site density (mole/m3)	125

Table 3. Configuration parameters of DOC in GT-power.

Item	Quantity
Channel geometry	square
Front area (mm2)	20000
Cell density (1/inch2)	400
Length (mm)	150

Table 4. Configuration parameters of DPF in GT-power.

Item	Quantity
Trap diameter (mm)	130
Filter wall thickness (inch)	0.014
Channel length (mm)	260
Inlet cell density (1/inch2)	95

According to the proposed algorithm, the schematic diagram of the control system is designed as shown in Figure 4. In the system, the NH₃ concentration is estimated by the Luenberger-sliding mode observer and used as the input of the backstepping control. After that, the SCR is controlled by the controller.

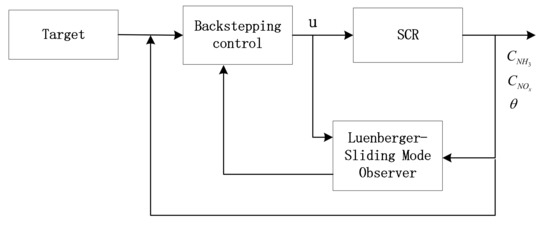
Figure 4. Schematic diagram of the control system.

5.1. Experiment Validation of Luenberger-Sliding Mode Observer

In this section, the effectiveness of the observer will be validated first. Because the main reactions on the catalyst are standard reactions and fast reactions, as shown in (8) and (9), the simple model-based controller is targeting a molar ratio of NH₃/NO_X of 1/1 in order to suppress NH₃ leakage. The observer result of the mid-catalyst NH₃ concentration at three different NO₂/NO ratios and different temperatures are shown in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.

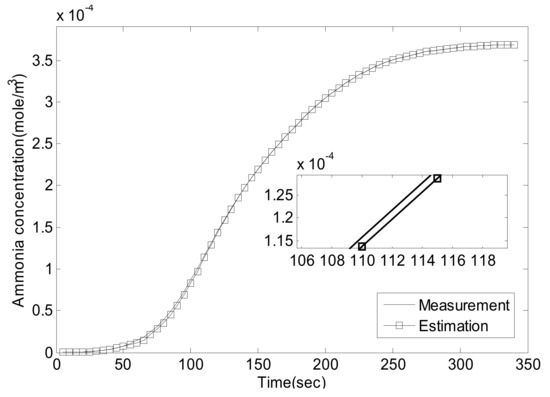
Figure 5. NO₂/NO = 0/1, 30 °C, comparison of $C_{N{H}_3,2}$.

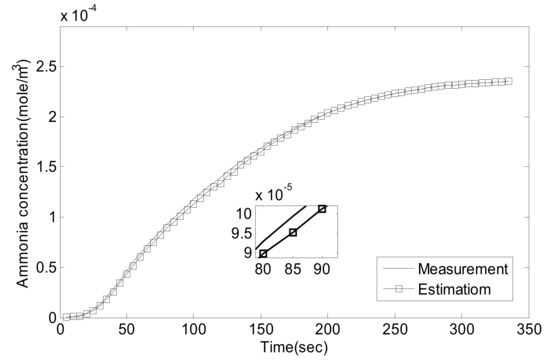
Figure 6. NO₂/NO = 0/1, 350 °C, comparison of $C_{N{H}_3,2}$.

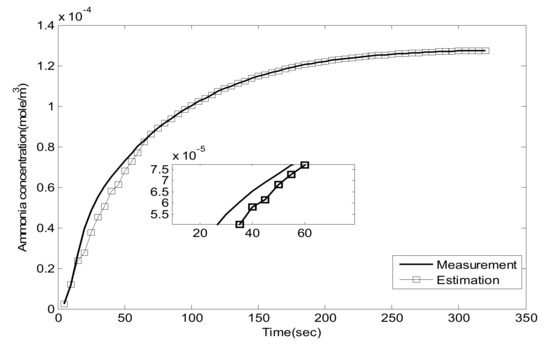
Figure 7. NO₂/NO = 0/1, 400 °C, comparison of $C_{N{H}_3,2}$.

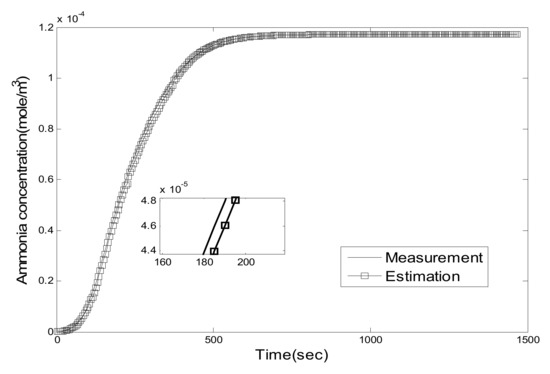
Figure 8. NO₂/NO = 1/2, 300 °C, comparison of $C_{N{H}_3,2}$.

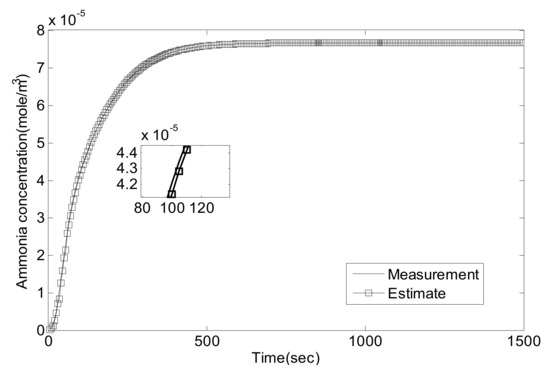
Figure 9. NO₂/NO = 1/2, 350 °C, comparison of $C_{N{H}_3,2}$.

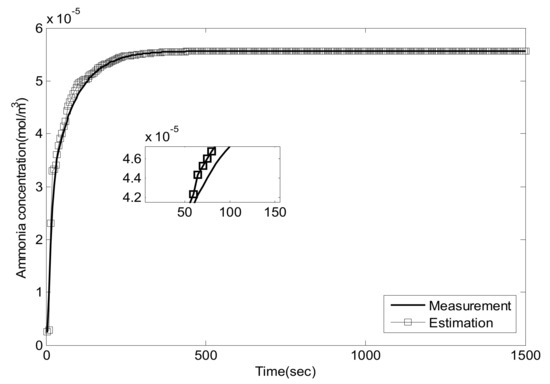
Figure 10. NO₂/NO = 1/2, 400 °C, comparison of $C_{N{H}_3,2}$.

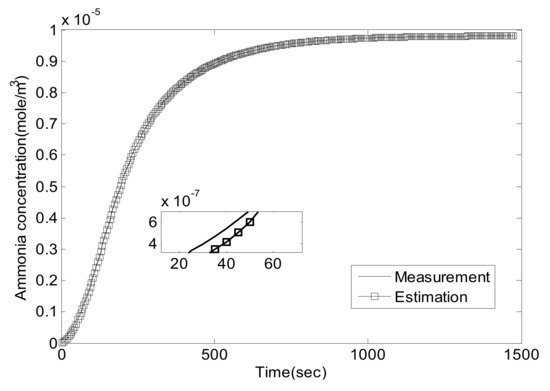
Figure 11. NO₂/NO = 1/1, 300 °C, comparison of $C_{N{H}_3,2}$.

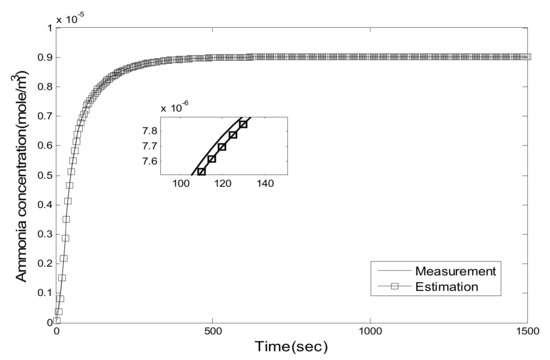
Figure 12. NO₂/NO = 1/1, 350 °C, comparison of $C_{N{H}_3,2}$.

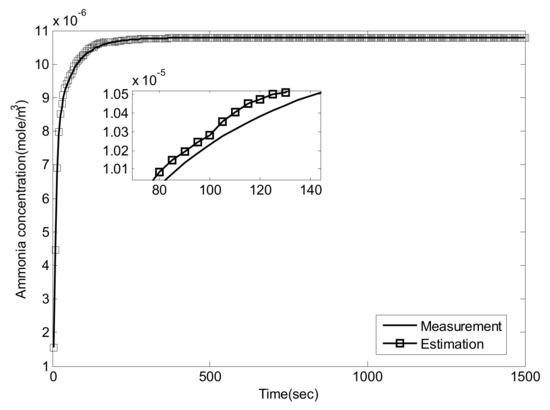
Figure 13. NO₂/NO = 1/1, 400 °C, comparison of $C_{N{H}_3,2}$.

In order to show their performance more intuitively, the mean absolute error is given in Table 5.

Table 5. Mean absolute error for Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.

	NO2/NO = 0/1	NO2/NO = 1/2	NO2/NO = 1/1
300 °C	1.9 × 10−6	1.6 × 10−6	1.1 × 10−7
350 °C	3.1 × 10−6	1.7 × 10−6	0.6 × 10−7
400 °C	4.2 × 10−6	2.1 × 10−6	1.6 × 10−7

As can be seen, the proposed Luenberger-sliding mode observer estimation can converge to sensor measurements very well at different working conditions. The experimental results show that the observation accuracy of mid-catalyst NH₃ concentration can be achieved by using the proposed observer.

5.2. Simulation Validation of the Luenberger-Sliding Mode Observer Based Backstepping Control for SCR System

To illustrate the validity of the Luenberger-sliding mode observer based backstepping control for the after-treatment process, NO_X conversion efficiency and NH₃ leakage are taken as the output, and the injection of urea (concentration of the inlet ammonia) is taken as the input. To show the effectiveness of the proposed control strategy, traditional PID control is used for comparison. The control performance of the proposed Luenberger-sliding mode observer based backstepping control strategy is shown in Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22. The control performance of the two control methods is compared using integrated absolute error (IAE) criteria:

$$IAE={\displaystyle \sum \left|e(t)\right|}dt$$

(73)

where $e(t)$ is the error between the reference value and the actual process output. The value of IAE is enumerated in Table 6.

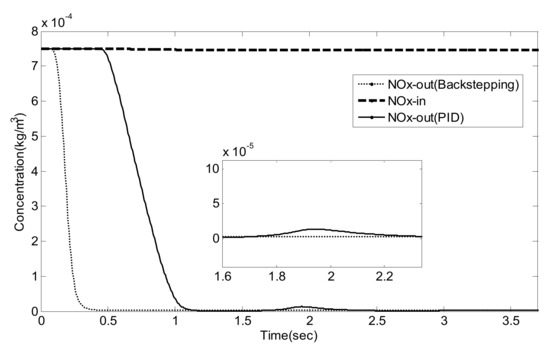
Figure 14. NO/NO₂ = 1/0, NOx concentration before and after the SCR system.

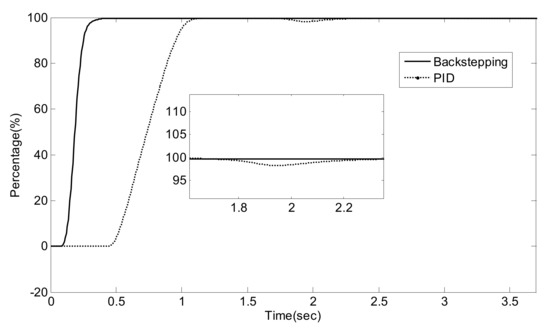
Figure 15. NO/NO₂ = 1/0, NOx conversion efficiency.

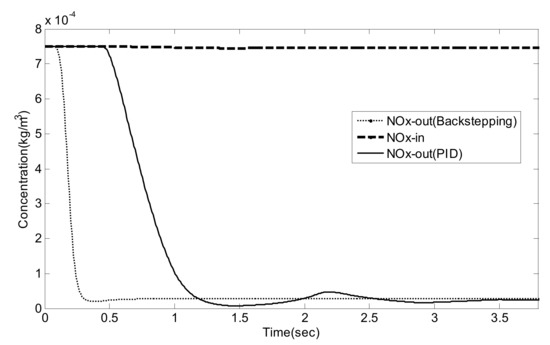
Figure 16. NO/NO₂ = 2/1, NOx concentration before and after the SCR system.

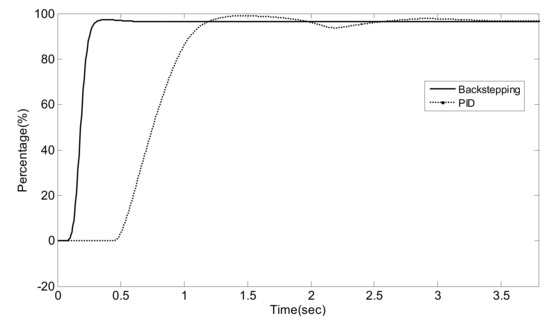
Figure 17. NO/NO₂ = 2/1, NOx conversion efficiency.

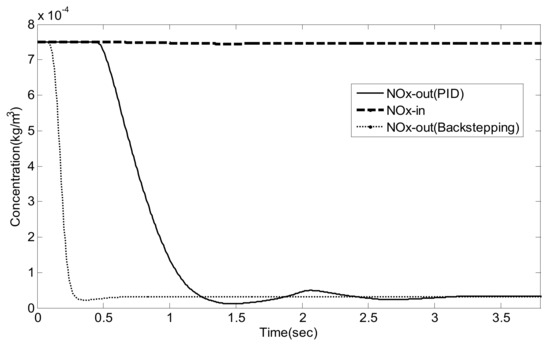
Figure 18. NO/NO₂ = 1/1, NOx concentration before and after the SCR system.

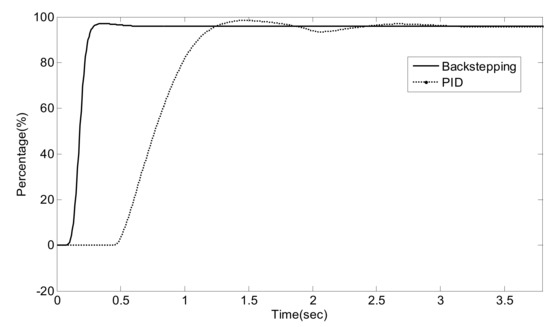
Figure 19. NO/NO₂ = 1/1, NOx conversion efficiency.

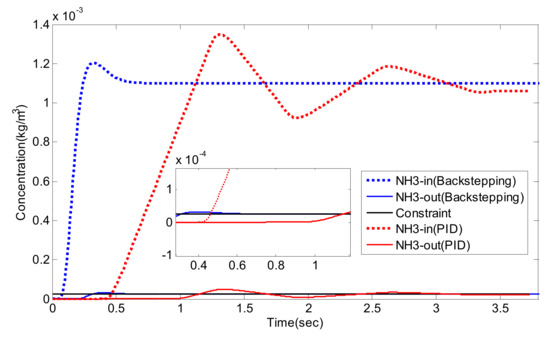
Figure 20. NO/NO₂ = 1/0, NH₃ concentration before and after the SCR system.

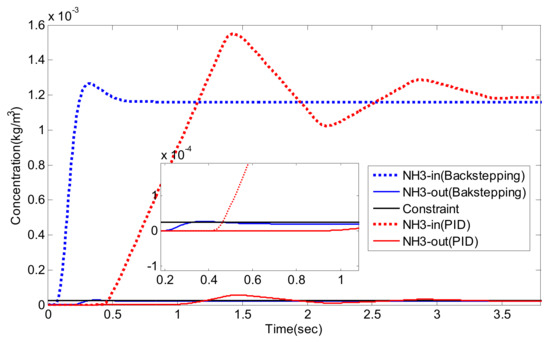
Figure 21. NO/NO₂ = 2/1, NH₃ concentration before and after the SCR system.

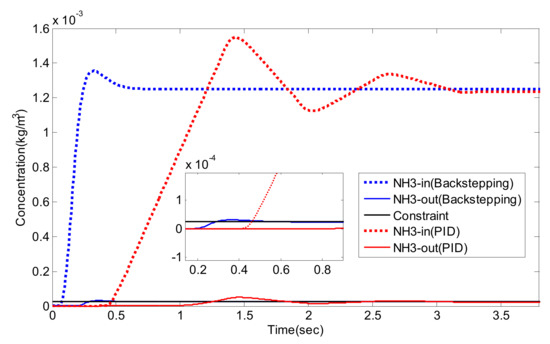
Figure 22. NO/NO₂ = 1/1, NH₃ concentration before and after the SCR system.

Table 6. Control performance of the two control strategies.

	NO/NO2	Settling Time (s)	Overshoot (%)	Integrated Absolute Error (IAE)
PID	1/0	3.2	27.8	0.1482
	2/1	3.3	30.0	0.1784
	1/1	3.1	25.2	0.1649
Luenberger-Sliding Mode Observer Based Backstepping	1/0	0.49	9.3	0.0373
	2/1	0.49	8.9	0.0295
	1/1	0.48	8.3	0.0310

As can be seen from Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 and Table 6, traditional PID control and Luenberger-sliding mode observer based backstepping control can basically meet the control requirements, and both can achieve high NOx conversion rate when the NH₃ leakage in the tail gas exceeds the standard, or when a small amount exceeds the standard. Nevertheless, traditional PID control has a large overshoot, which is when it injects excessive adblue into the engine exhaust in a short time. As can be seen from Figure 14, Figure 16 and Figure 19, NH₃ emission from the SCR catalytic converter outlet fluctuates for a period of time, which does not meet the requirements of emission regulations. The proposed controller reaches better operating points in which about 96.2% of NO_X is reduced while allowing about 24 ppm NH₃ slip past the catalyst. Although the backstepping control method also has a small amount of overshoot, the downstream emission of the SCR catalysts does not exceed the limit, which is in line with the requirements of emission regulations. Moreover, the backstepping control method has a shorter adjustment time. Even in the case of overshoot, NH₃ emissions downstream of the SCR catalyst can quickly return to normal levels, which is conducive to achieving a higher NO_X conversion rate. Furthermore, the control response obtained using the Luenberger-sliding mode observer based backstepping controller has smaller overshoot and relatively shorter settling time. The control responses indicate the efficiency of the proposed controller with excellent set-point tracking properties.

6. Conclusions

In this paper, a Luenberger-sliding mode observer based backstepping control strategy was proposed to estimate the mid-catalyst ammonia concentration and calculate the input of adblue. The dynamics of a SCR system was modeled to represent the actual process in the design study of the Luenberger-sliding mode observer based backstepping control strategy. The Lyapunov technique was used for demonstrating the stability of the observer and the backstepping SCR control method. Through the simulation test, the performance of the Luenberger-sliding mode observer and the proposed approach was verified under the conditions of different intake components and different intake temperatures. The results show that the observer has high estimation accuracy under different conditions, with a maximum average error of less than 4.2 × 10⁻⁶. Furthermore, the Luenberger-sliding mode observer based backstepping control strategy can keep the ammonia slip of the downstream SCR system at a low level and simultaneously achieve a high NO_X conversion rate, which is much better than the popular PID control method in setting time, overshoot, and tracking error.