Forecasting the Price Distribution of Continuous Intraday Electricity Trading
Abstract
1. Introduction
2. Data Set & Data Transformation
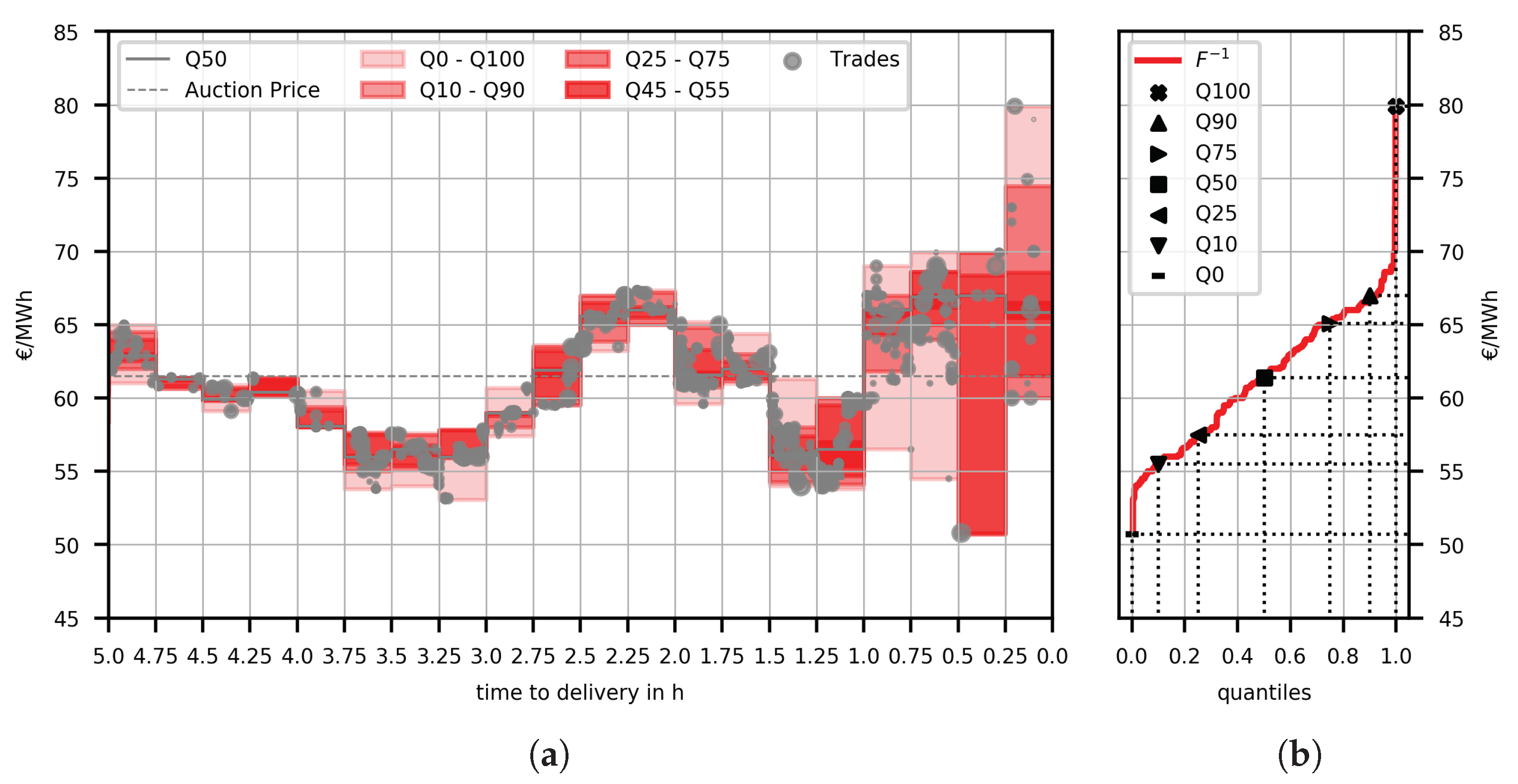
2.1. Constructing Price Distributions from Intraday Trading Data
2.2. Exogenous Data
3. Predicting the Quantiles of the Price Distribution
3.1. Linear Regression Models
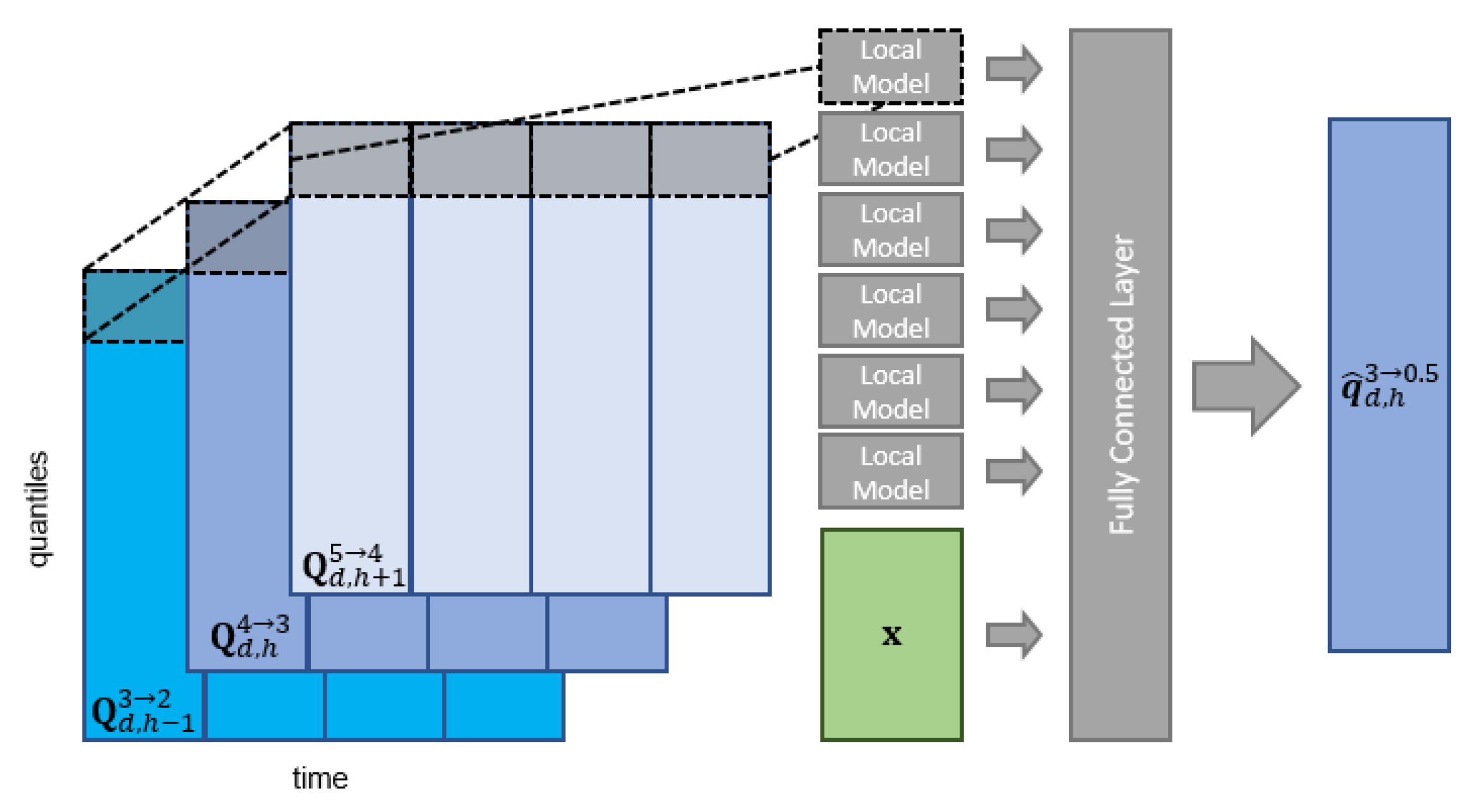
3.2. Neural Network Model
3.3. Naive Benchmark Models
4. Forecasting Study
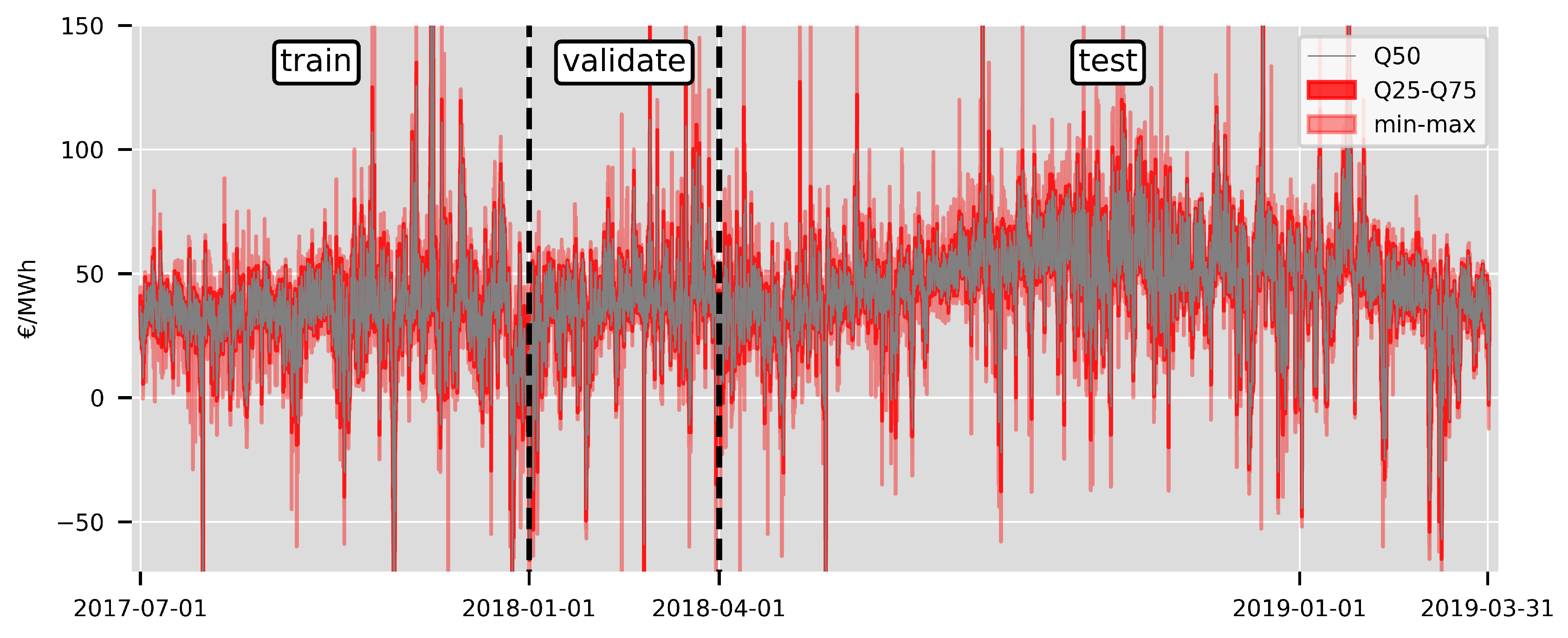
4.1. Forecasting Strategy
4.2. Evaluation
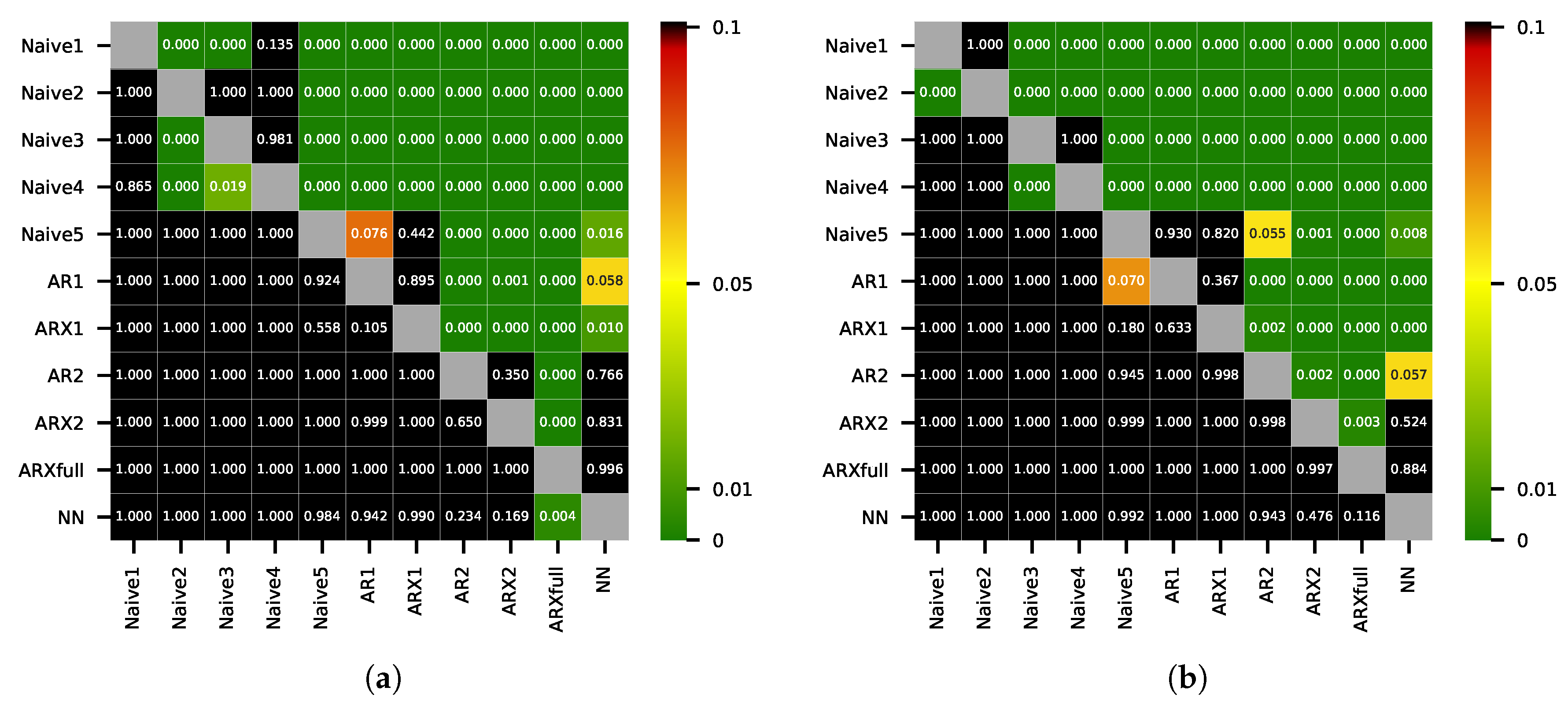
5. Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CDF | cumulative density function |
| DM | Diebold-Mariano |
| MAE | mean absolute error |
| MQD | mean integrated quadratic distance |
| MWD | mean Wasserstein distance |
| QD | integrated quadratic distance |
| RMSE | root mean squared error |
| VWECDF | volume-weighted empirical cumulative density function |
| WD | Wasserstein distance |
References
- Ocker, F.; Ehrhart, K.M. The “German Paradox” in the balancing power markets. Renew. Sustain. Energy Rev. 2017, 67, 892–898. [Google Scholar] [CrossRef]
- Koch, C.; Hirth, L. Short-term electricity trading for system balancing: An empirical analysis of the role of intraday trading in balancing Germany’s electricity system. Renew. Sustain. Energy Rev. 2019, 113, 109–275. [Google Scholar] [CrossRef]
- EPEXSpot. Traded Volumes Soar to an All Time High in 2018. 2018. Available online: https://www.epexspot.com/en/press-media/press/details/press/Traded_volumes_soar_to_an_all-time_high_in_2018 (accessed on 4 November 2019).
- EPEXSpot. Description of Epex Spot Market Indices (May 2019). 2019. Available online: https://www.epexspot.com/document/39669/EPEX%20SPOT%20Indices (accessed on 4 November 2019).
- Viehmann, J. State of the German Short-Term Power Market. Z. Für Energiewirtschaft 2017, 41, 87–103. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Andrade, J.; Filipe, J.; Reis, M.; Bessa, R. Probabilistic price forecasting for day-ahead and intraday markets: Beyond the statistical model. Sustainability 2017, 9, 1990. [Google Scholar] [CrossRef]
- Monteiro, C.; Ramirez-Rosado, I.; Fernandez-Jimenez, L.; Conde, P. Short-term price forecasting models based on artificial neural networks for intraday sessions in the iberian electricity market. Energies 2016, 9, 721. [Google Scholar] [CrossRef]
- Maciejowska, K.; Nitka, W.; Weron, T. Day-Ahead vs. Intraday—Forecasting the Price Spread to Maximize Economic Benefits. Energies 2019, 12, 631. [Google Scholar] [CrossRef]
- Uniejewski, B.; Marcjasz, G.; Weron, R. Understanding intraday electricity markets: Variable selection and very short-term price forecasting using LASSO. Int. J. Forecast. 2019, 35, 1533–1547. [Google Scholar] [CrossRef]
- Narajewski, M.; Ziel, F. Econometric modelling and forecasting of intraday electricity prices. arXiv 2018, arXiv:1812.09081. [Google Scholar] [CrossRef]
- EPEXSpot. Available online: www.epexspot.com (accessed on 4 November 2019).
- ENTSOE-E. transparency Platform. Available online: transparency.entsoe.eu (accessed on 4 November 2019).
- EPEXSpot. Epex Spot Market Rules. 2019. Available online: http://www.epexspot.com/de/extras/download-center (accessed on 4 November 2019).
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 4 November 2019).
- Uniejewski, B.; Weron, R.; Ziel, F. Variance Stabilizing Transformations for Electricity Spot Price Forecasting. IEEE Trans. Power Syst. 2018, 33, 2219–2229. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Statist. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Diebold, F.; Mariano, R. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]
- Harvey, D.; Leybourne, S.; Newbold, P. Testing the equality of prediction mean squared errors. Int. J. Forecast. 1997, 13, 281–291. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 26, 1–22. [Google Scholar]
- Ziel, F.; Weron, R. Day-ahead electricity price forecasting with high-dimensional structures: Univariate vs. multivariate modeling frameworks. Energy Econ. 2018, 70, 396–420. [Google Scholar] [CrossRef]
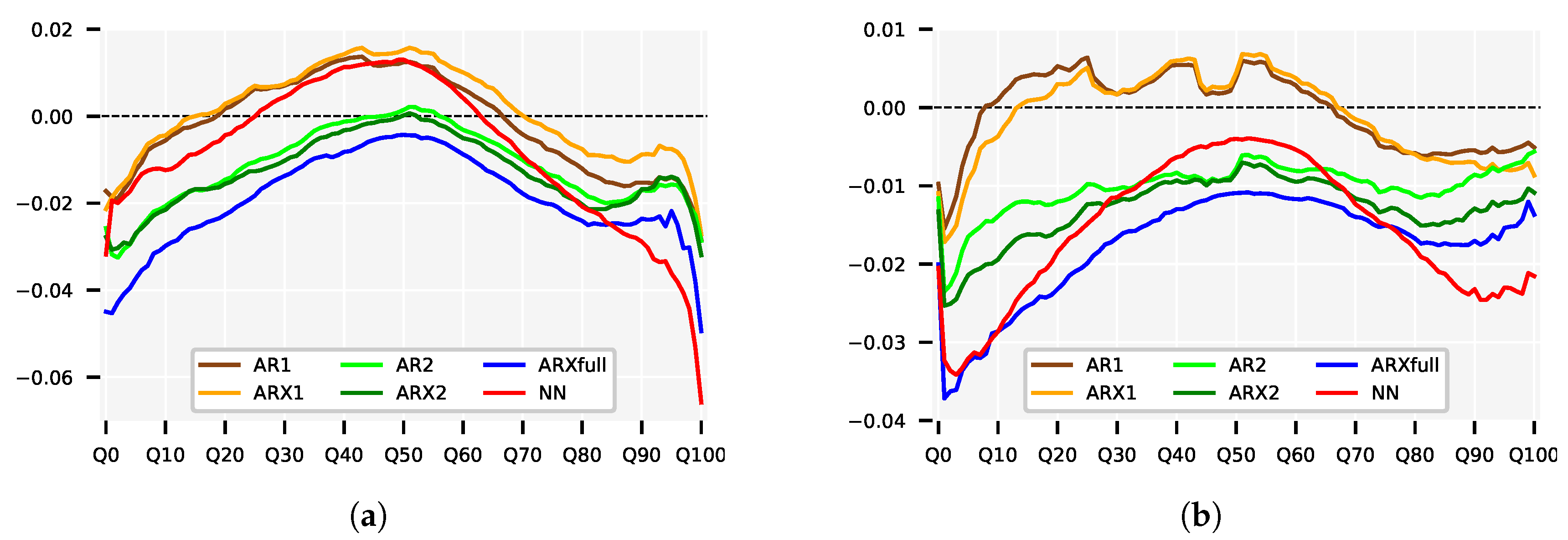
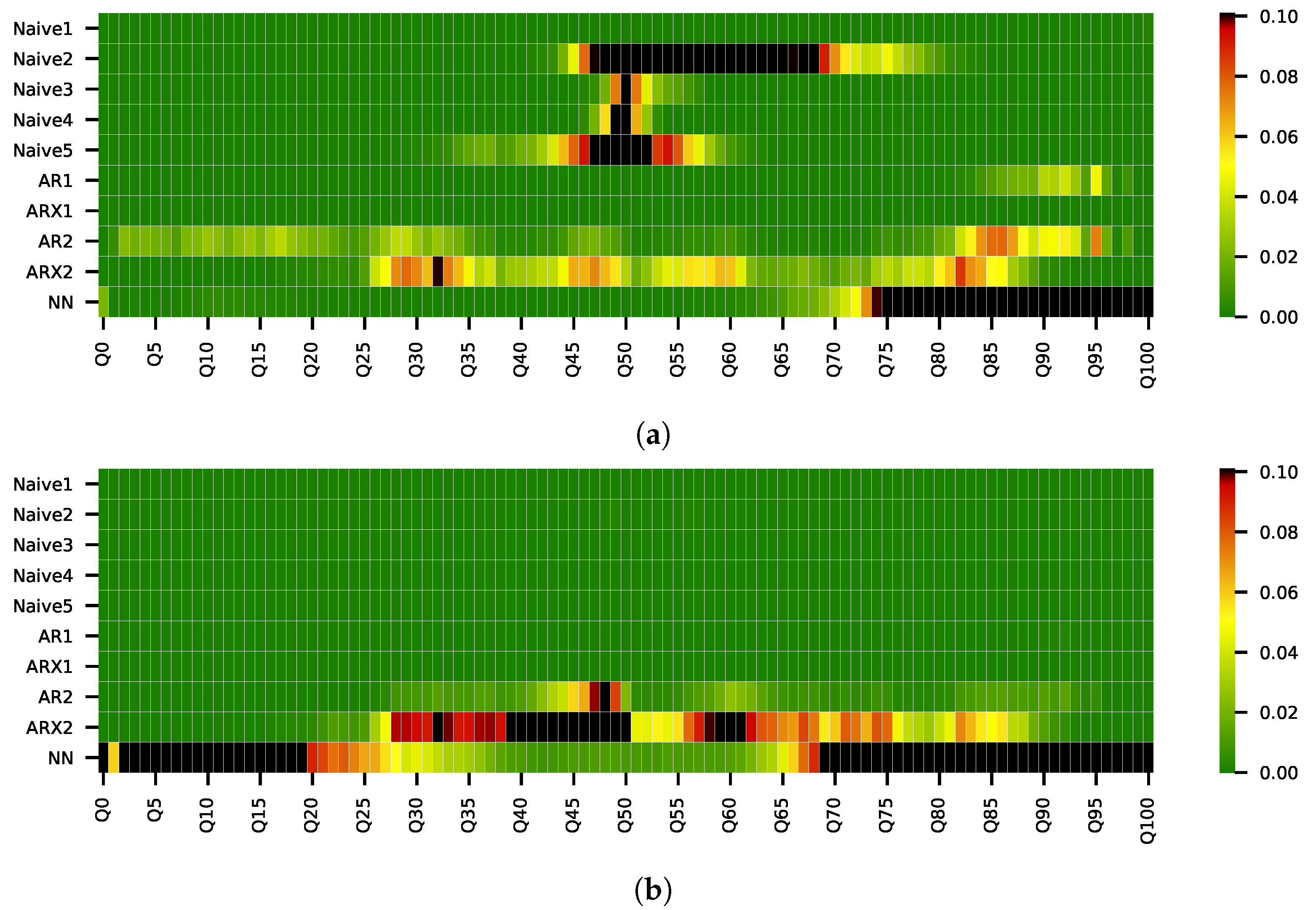
| Naive1 | Naive2 | Naive3 | Naive4 | Naive5 | AR1 | ARX1 | AR2 | ARX2 | ARXfull | NN | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MWD | 4.147 | 3.912 | 4.008 | 4.091 | 3.803 | 3.789 | 3.801 | 3.751 | 3.747 | 3.721 | 3.763 |
| MQD | 1.938 | 2.041 | 1.535 | 1.585 | 1.414 | 1.418 | 1.409 | 1.395 | 1.375 | 1.362 | 1.371 |
| Naive1 | Naive2 | Naive3 | Naive4 | Naive5 | AR1 | ARX1 | AR2 | ARX2 | ARXfull | NN | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q0 | 7.52 | 8.96 | 8.23 | 8.45 | 7.11 | 6.99 | 6.96 | 6.93 | 6.91 | 6.79 | 6.88 |
| Q10 | 4.62 | 4.61 | 4.65 | 4.70 | 4.23 | 4.21 | 4.21 | 4.15 | 4.14 | 4.11 | 4.18 |
| Q20 | 4.10 | 3.85 | 3.97 | 4.00 | 3.71 | 3.71 | 3.72 | 3.65 | 3.65 | 3.62 | 3.69 |
| Q30 | 3.80 | 3.43 | 3.52 | 3.53 | 3.38 | 3.40 | 3.40 | 3.35 | 3.34 | 3.33 | 3.39 |
| Q40 | 3.70 | 3.26 | 3.30 | 3.31 | 3.24 | 3.28 | 3.29 | 3.24 | 3.23 | 3.21 | 3.28 |
| Q50 | 3.68 | 3.21 | 3.21 | 3.21 | 3.21 | 3.25 | 3.25 | 3.21 | 3.21 | 3.19 | 3.25 |
| Q60 | 3.69 | 3.22 | 3.27 | 3.30 | 3.24 | 3.26 | 3.27 | 3.23 | 3.22 | 3.21 | 3.25 |
| Q70 | 3.75 | 3.34 | 3.45 | 3.55 | 3.37 | 3.35 | 3.37 | 3.33 | 3.33 | 3.31 | 3.34 |
| Q80 | 3.99 | 3.69 | 3.88 | 4.02 | 3.70 | 3.65 | 3.67 | 3.63 | 3.62 | 3.61 | 3.62 |
| Q90 | 4.50 | 4.43 | 4.60 | 4.82 | 4.31 | 4.24 | 4.27 | 4.24 | 4.24 | 4.21 | 4.18 |
| Q100 | 7.38 | 8.49 | 8.18 | 8.66 | 7.36 | 7.16 | 7.16 | 7.15 | 7.13 | 7.00 | 6.88 |
| Naive1 | Naive2 | Naive3 | Naive4 | Naive5 | AR1 | ARX1 | AR2 | ARX2 | ARXfull | NN | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q0 | 14.19 | 15.64 | 17.01 | 17.10 | 13.07 | 12.95 | 12.93 | 12.92 | 12.90 | 12.81 | 12.80 |
| Q10 | 7.10 | 7.20 | 6.88 | 7.05 | 6.22 | 6.23 | 6.20 | 6.14 | 6.10 | 6.04 | 6.04 |
| Q20 | 6.30 | 6.05 | 5.95 | 6.03 | 5.54 | 5.57 | 5.56 | 5.48 | 5.46 | 5.42 | 5.44 |
| Q30 | 5.88 | 5.36 | 5.36 | 5.41 | 5.17 | 5.17 | 5.17 | 5.11 | 5.10 | 5.08 | 5.11 |
| Q40 | 5.77 | 5.10 | 5.09 | 5.12 | 5.03 | 5.06 | 5.06 | 4.99 | 4.99 | 4.97 | 5.00 |
| Q50 | 5.79 | 5.04 | 5.04 | 5.04 | 5.04 | 5.06 | 5.06 | 5.00 | 5.00 | 4.98 | 5.02 |
| Q60 | 5.88 | 5.15 | 5.19 | 5.21 | 5.13 | 5.15 | 5.15 | 5.09 | 5.08 | 5.07 | 5.10 |
| Q70 | 6.19 | 5.60 | 5.82 | 5.88 | 5.51 | 5.50 | 5.50 | 5.46 | 5.45 | 5.43 | 5.44 |
| Q80 | 6.88 | 6.56 | 6.91 | 7.09 | 6.27 | 6.23 | 6.23 | 6.20 | 6.18 | 6.16 | 6.15 |
| Q90 | 8.53 | 8.60 | 9.21 | 9.58 | 7.98 | 7.93 | 7.92 | 7.91 | 7.87 | 7.84 | 7.79 |
| Q100 | 19.73 | 20.41 | 24.68 | 25.38 | 18.81 | 18.72 | 18.65 | 18.71 | 18.61 | 18.56 | 18.41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janke, T.; Steinke, F. Forecasting the Price Distribution of Continuous Intraday Electricity Trading. Energies 2019, 12, 4262. https://doi.org/10.3390/en12224262
Janke T, Steinke F. Forecasting the Price Distribution of Continuous Intraday Electricity Trading. Energies. 2019; 12(22):4262. https://doi.org/10.3390/en12224262
Chicago/Turabian StyleJanke, Tim, and Florian Steinke. 2019. "Forecasting the Price Distribution of Continuous Intraday Electricity Trading" Energies 12, no. 22: 4262. https://doi.org/10.3390/en12224262
APA StyleJanke, T., & Steinke, F. (2019). Forecasting the Price Distribution of Continuous Intraday Electricity Trading. Energies, 12(22), 4262. https://doi.org/10.3390/en12224262




