Modelling and Design of Real-Time Energy Management Systems for Fuel Cell/Battery Electric Vehicles
Abstract
:1. Introduction
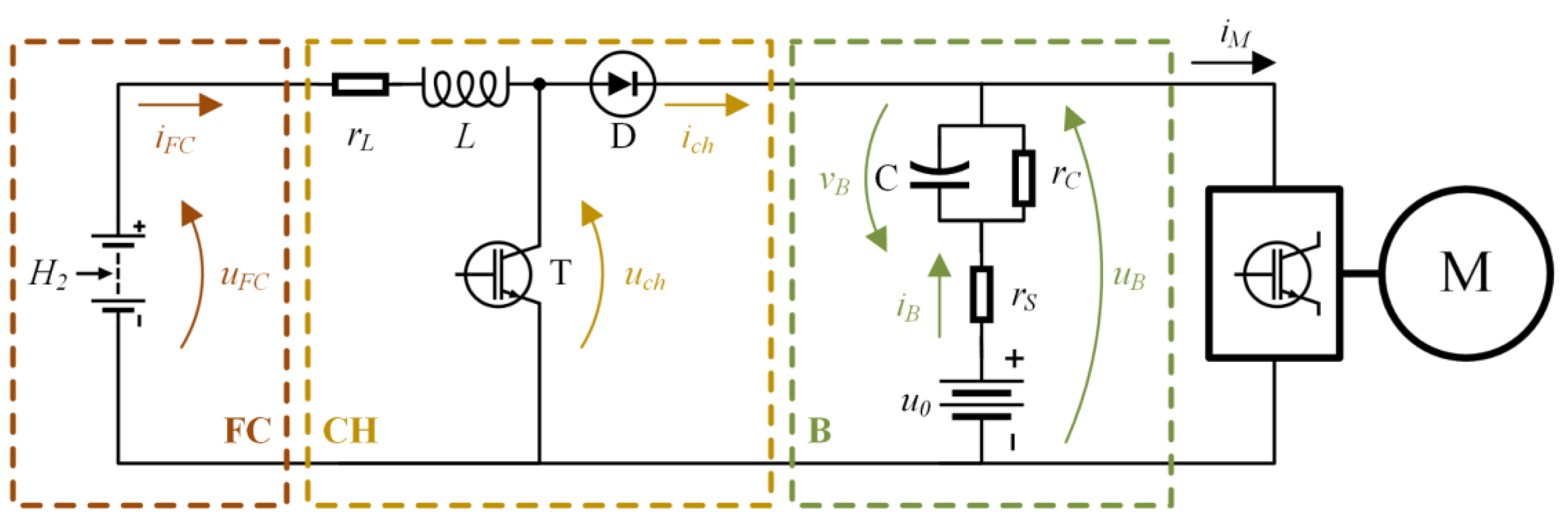
2. Modelling of the FCBEV Propulsion System
2.1. Fuel Cell
2.2. Battery
2.3. Traction Motor
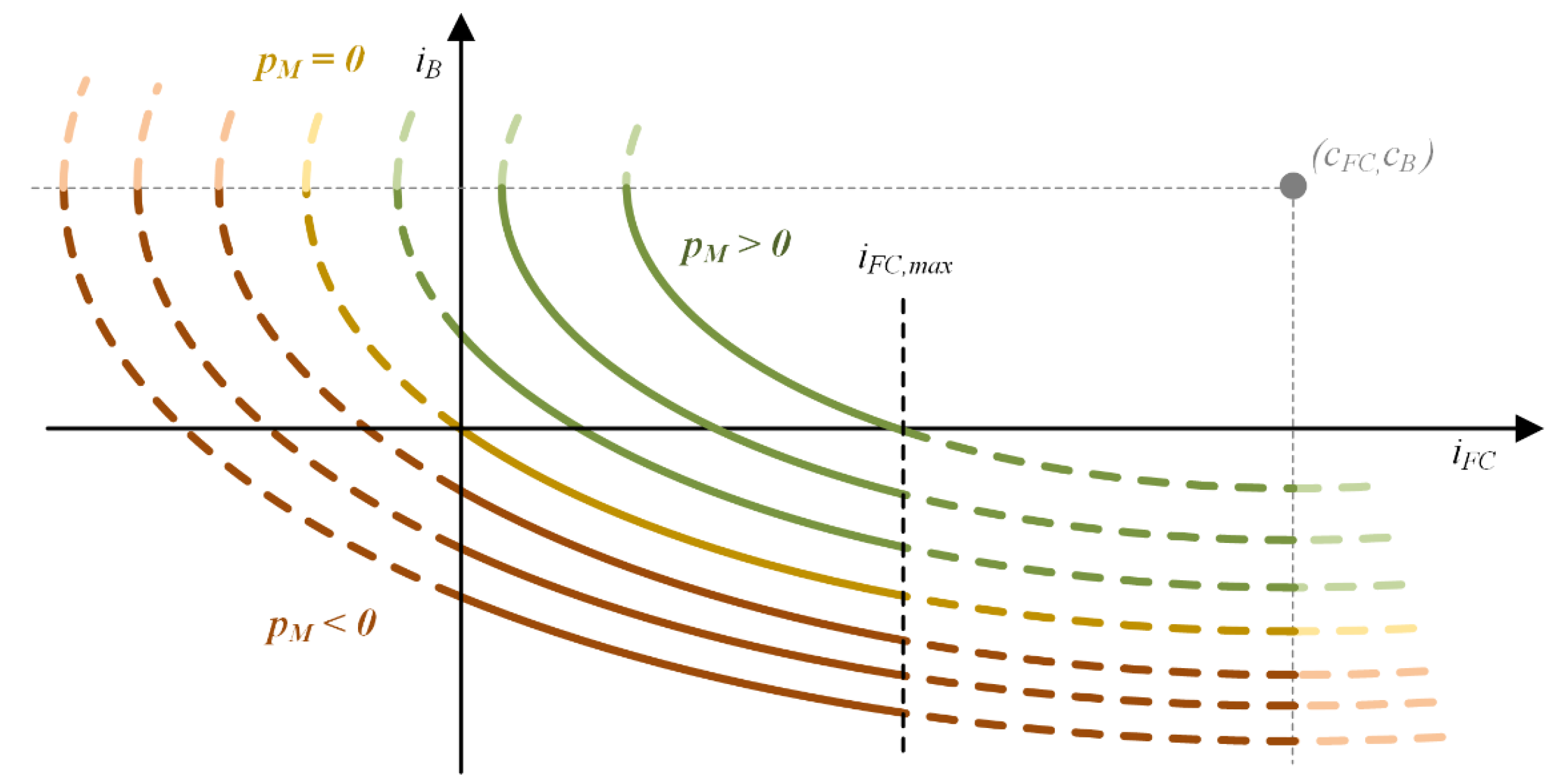
3. FCBEV Cost Function
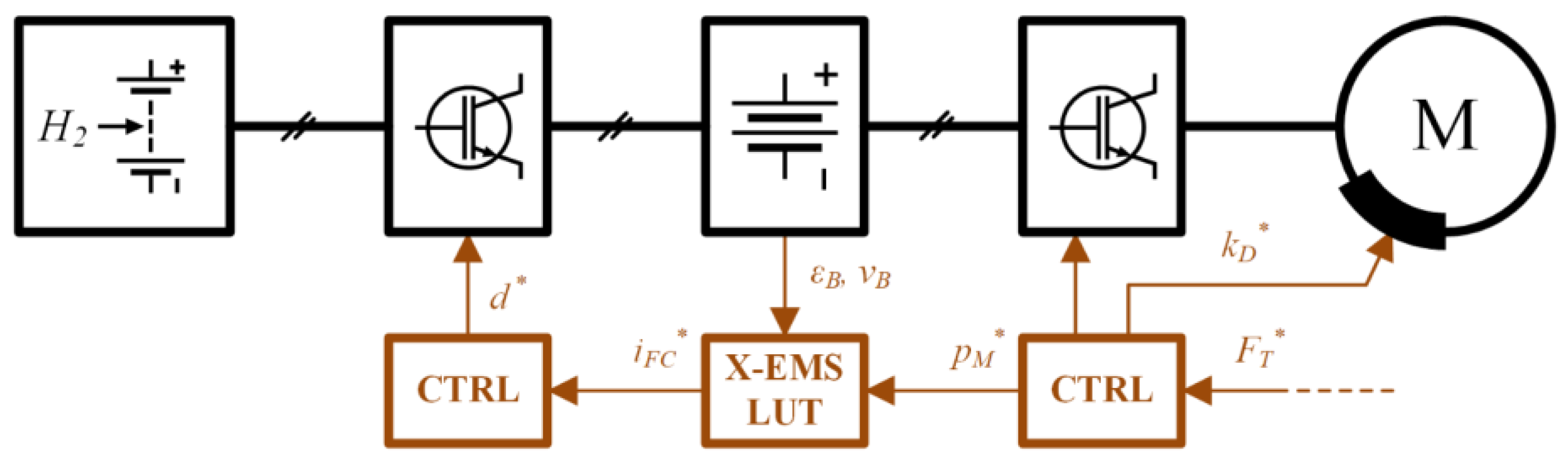
4. Proposed Energy Management Systems
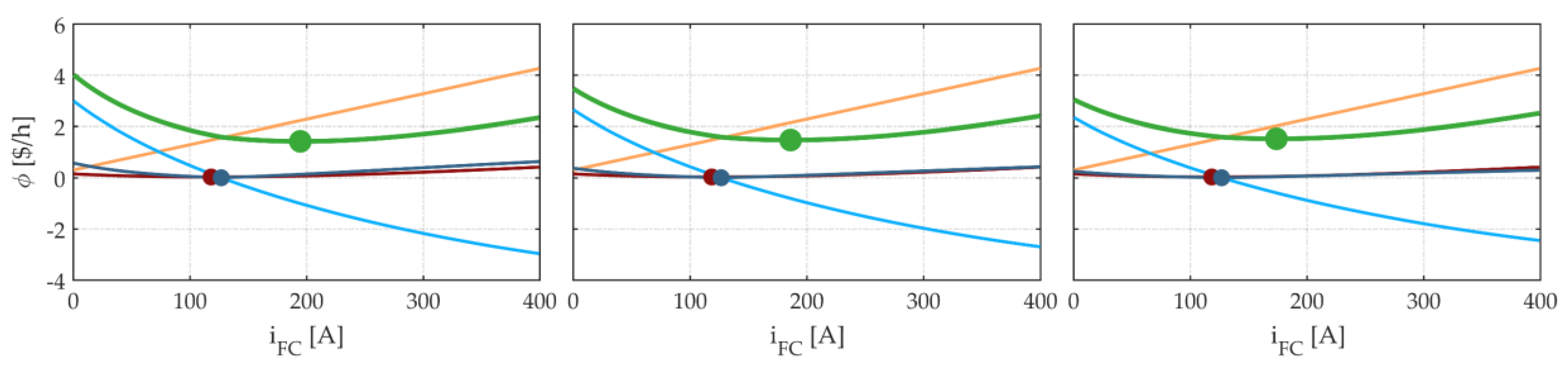
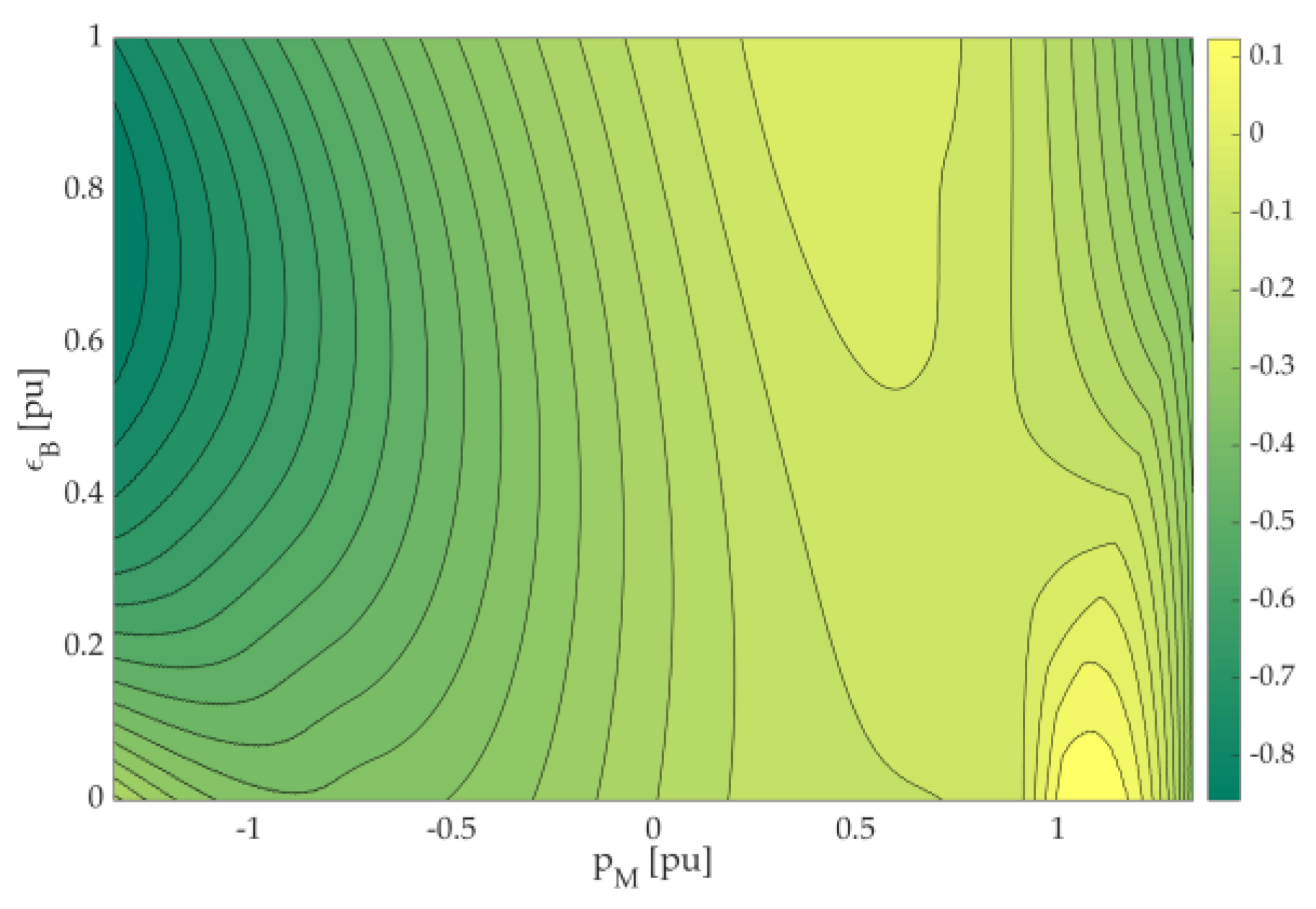
4.1. Simplified EMS
- The FCBEV propulsion system is at steady-state operation and, thus, time derivatives of iFC and vB have been assumed equal to zero in (2) and (10), respectively:
- The FC polarisation curve is approximated by a linear function of iFC:
- εB is considered an input of the EMS, like pM, because it is not possible to plan any εB evolution due to the knowledge of only instantaneous iB values.
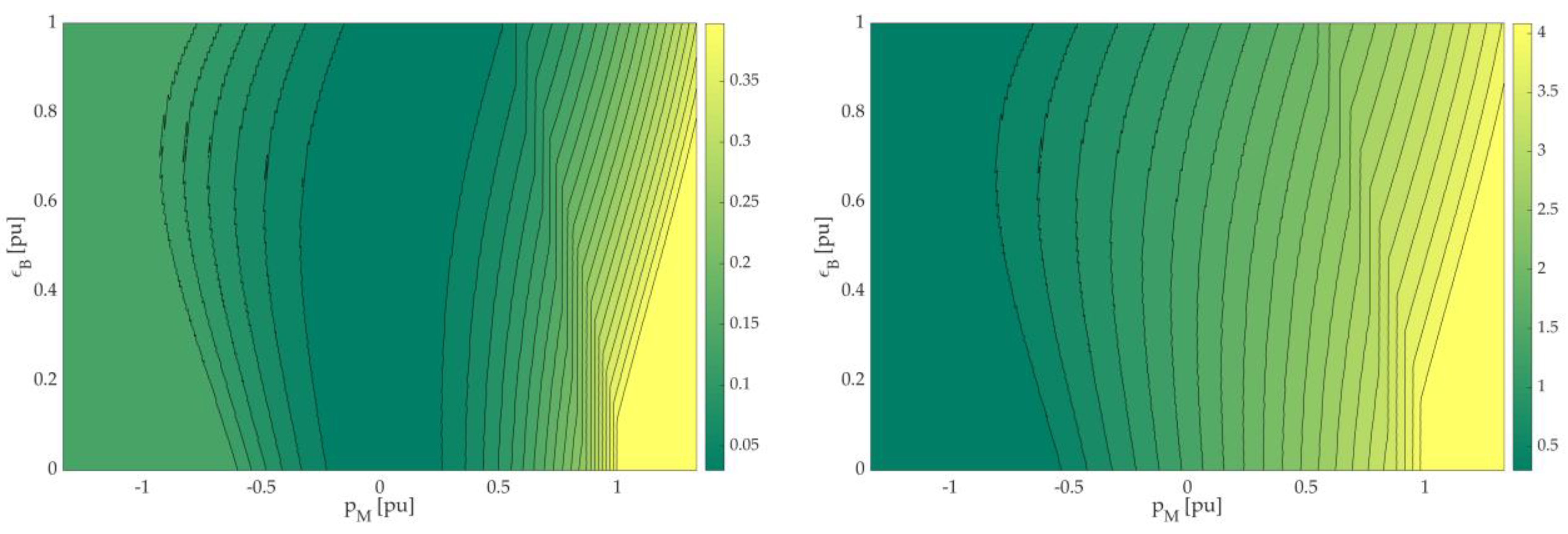
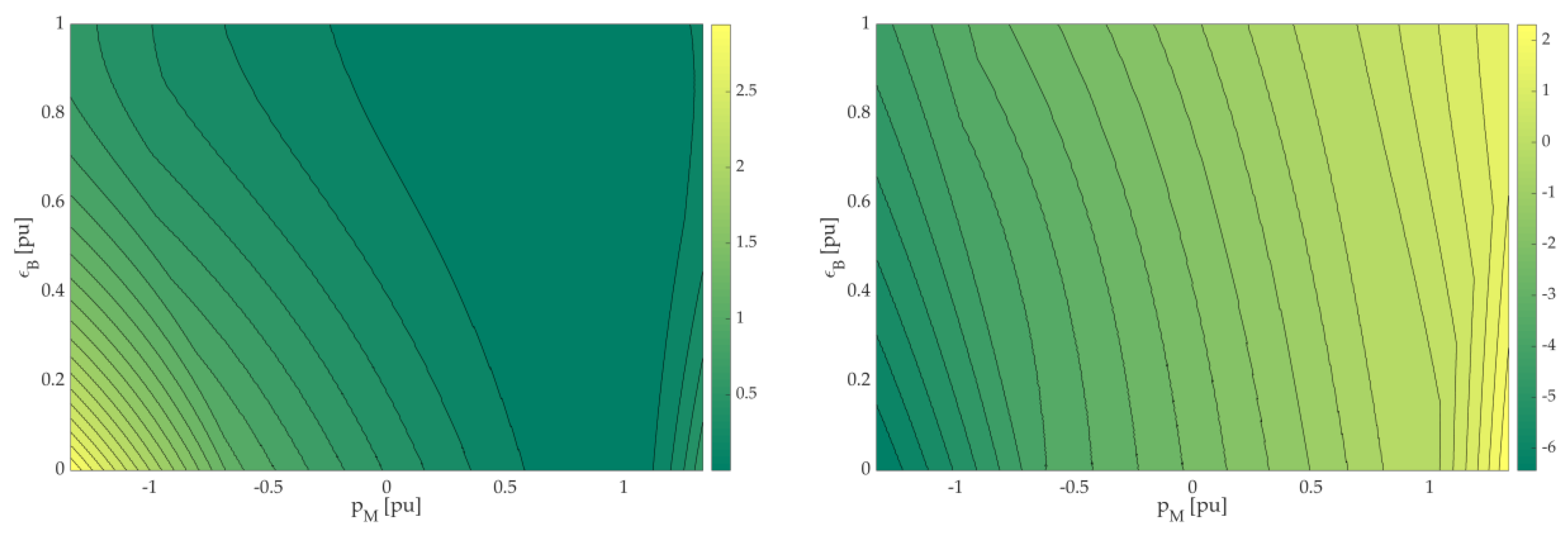
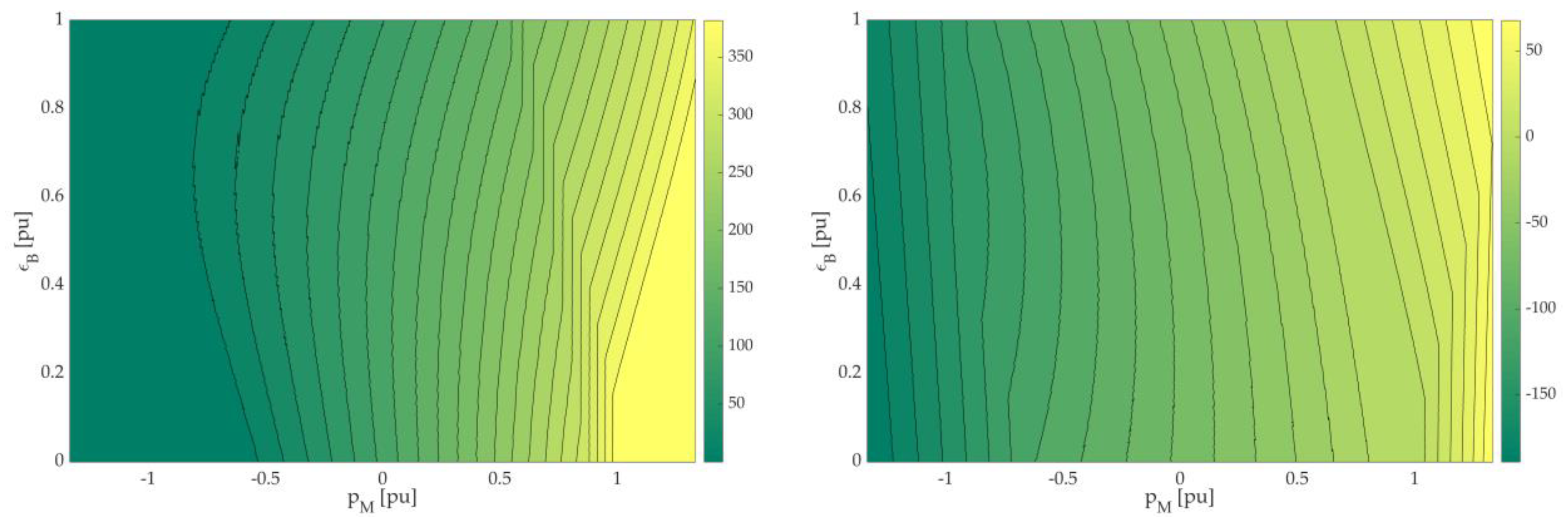
4.2. Advanced EMS
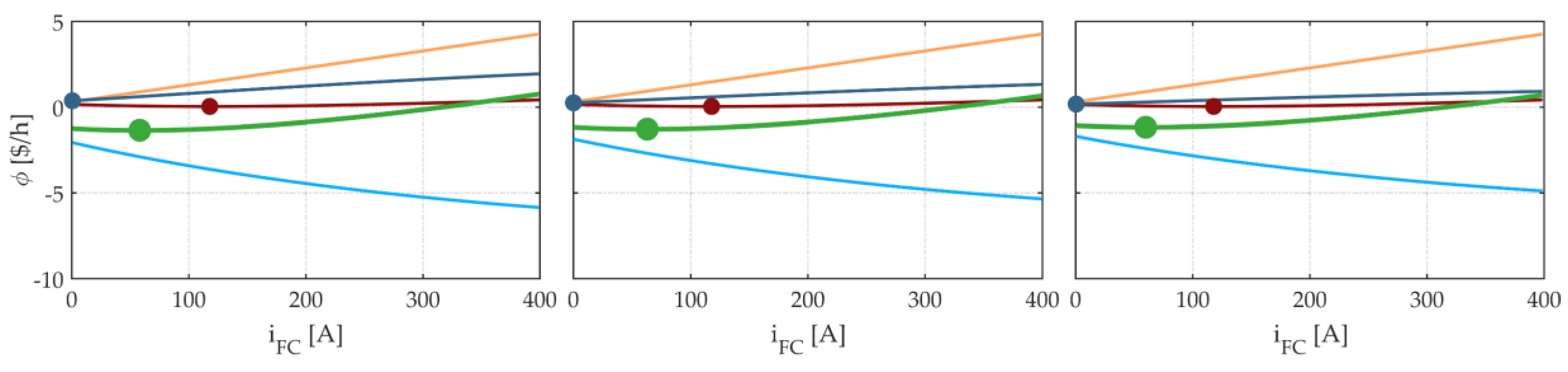
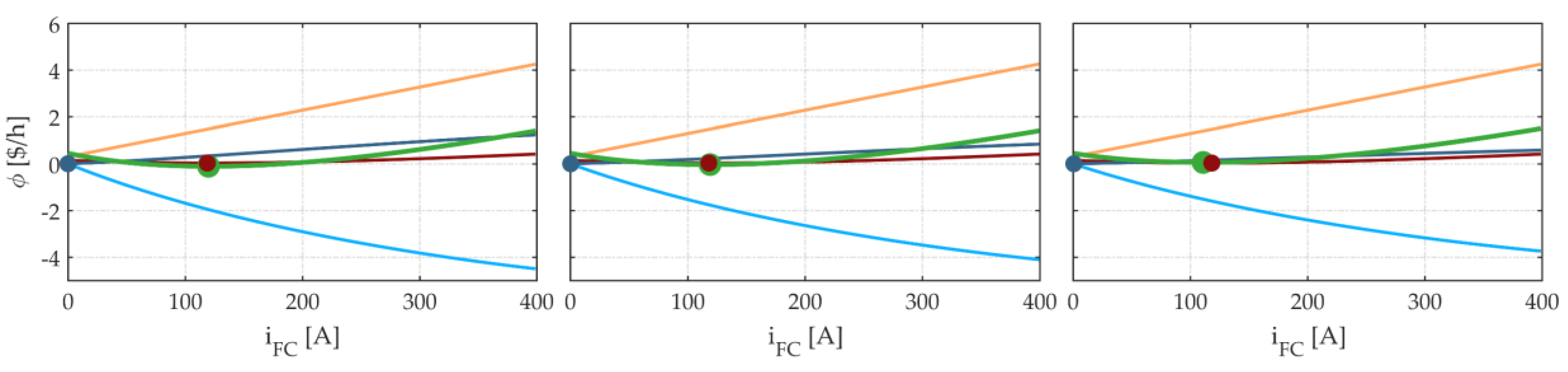
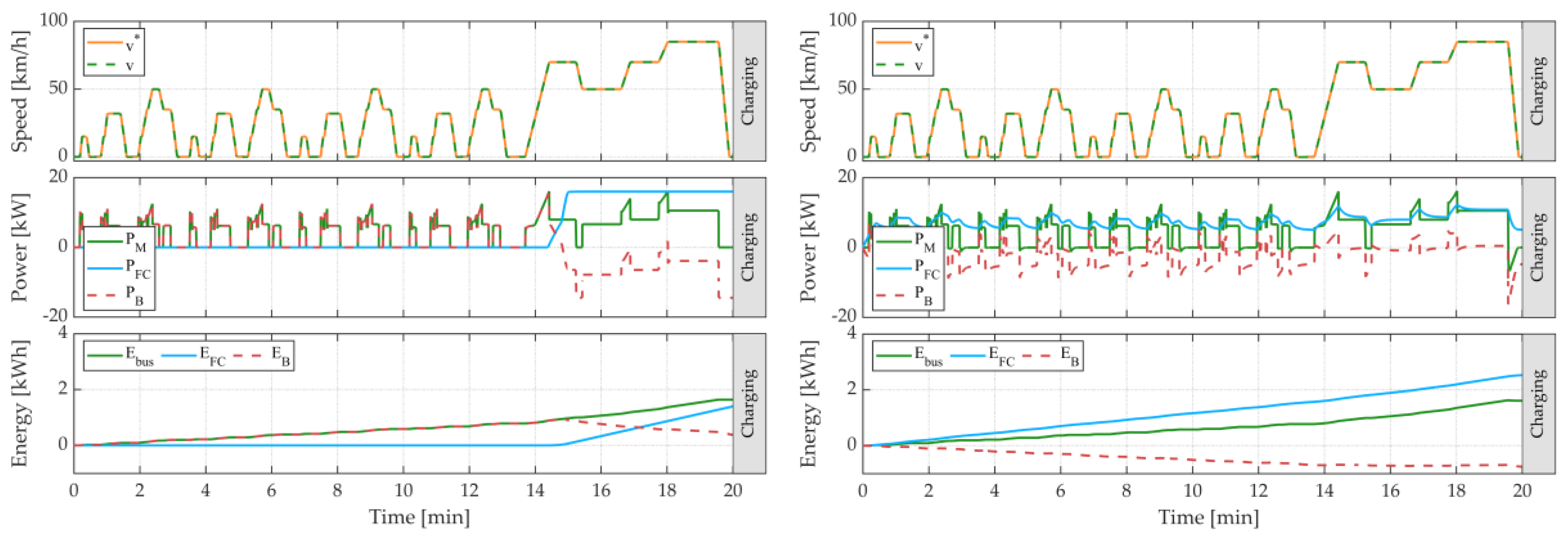
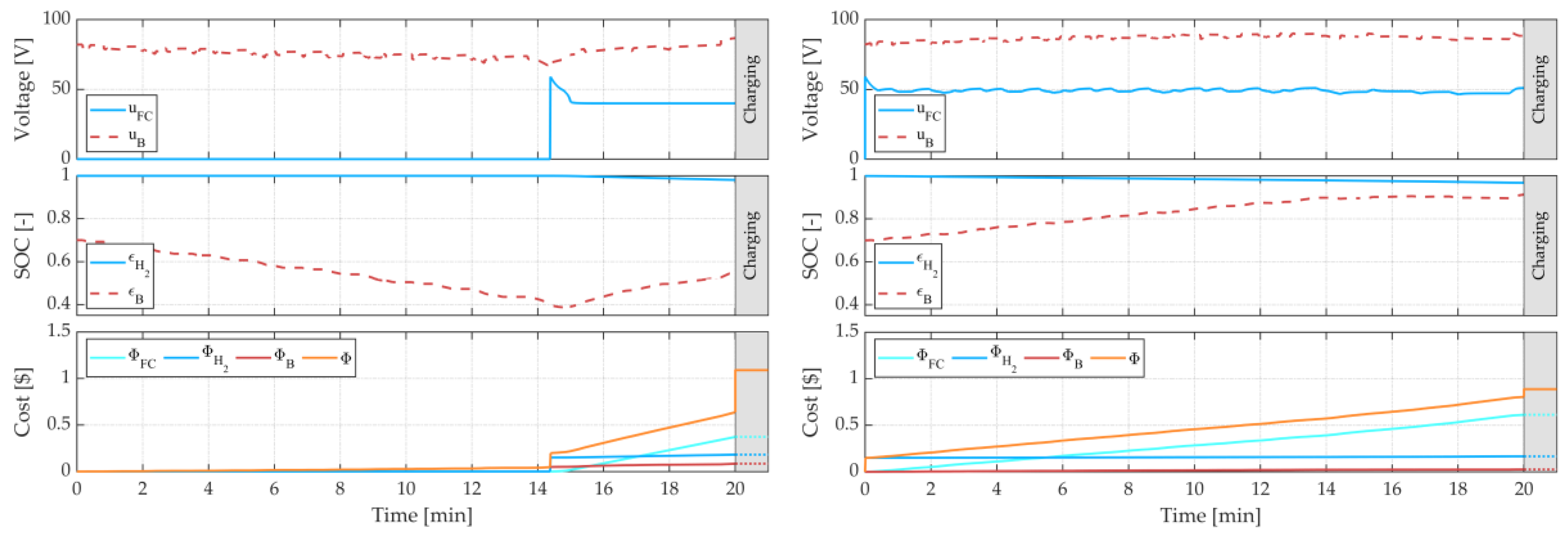
5. Simulation Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Symbol | Meaning | Value | Unit |
|---|---|---|---|
| uFC (iFC) | FC voltage (current) | - | V (A) |
| pFC | FC power | - | W |
| uCH (iCH) | average voltage (current) of the boost converter | - | V (A) |
| pCH | average power of the boost converter | - | W |
| d | duty cycle of the switch T of the boost converter | - | - |
| uB | DC-link voltage | - | V |
| u0 | B voltage source | - | V |
| iB (εB) | B current (state-of-charge) | - | A (-) |
| vB | voltage of the RC branch of B | - | V |
| pM | M power at the DC-link | - | W |
| FM | M traction effort | - | N |
| FT | overall traction effort | - | N |
| Fb | braking force | - | N |
| kD | regenerative braking coefficient | - | - |
| v | vehicle speed | - | m/s |
| n | number of FC starts | - | - |
| Φ | overall cost function | - | $ |
| Φ0 | instantaneous component of Φ | - | $ |
| φ | integrating component of Φ | - | $/s |
| ϕFC | FC cost function | - | $ |
| φFC | integrating component of ϕFC | - | $/s |
| ϕH2 | H2 cost function | - | $ |
| φH2 | integrating component of ϕH2 | - | $/s |
| ϕB | B cost function | - | $ |
| φB | integrating component of ϕB | - | $/s |
| ϕST | “charge sustaining” cost function | - | $ |
| φST | integrating component of ϕST | - | $/s |
| ϑ | polar variable of current ellipse | - | rad |
| ΔT | time interval | - | s |
| ψ | average value of φ within ΔT | - | $/s |
| Symbol | Meaning | Value | Unit |
|---|---|---|---|
| a0 | coefficient of the FC polarization curve | 59.12 | V |
| a1 | coefficient of the FC polarization curve | −0.119 | V/A |
| a2 | coefficient of the FC polarization curve | 0.449 | mV/A2 |
| a3 | coefficient of the FC polarization curve | −0.678 | µV/A3 |
| rL (L) | resistance (inductance) of the boost converter | - | Ω (H) |
| γ0 | coefficient of the H2 consumption curve | 23.7 | g/s |
| γ1 | coefficient of the H2 consumption curve | 0.786 | g/s/A |
| ηch | average efficiency of the boost converter | 0.95 | - |
| µ0 | coefficient of the B voltage source curve | 74.0829 | V |
| µ1 | coefficient of the B voltage source curve | 11.4857 | V |
| rs | B series resistance | 28 | mΩ |
| rC, C | resistance and capacitance of the RC branch of B | 141.7 (3529.4) | mΩ (F) |
| QB | B rated capacity | 40 | Ah |
| ηM | M efficiency | - | - |
| ξM, ςM | efficiency-based M coefficients | - | - |
| cFC | FC specific cost | 600 | $ |
| ΔFC | FC start-stop coefficient | 2.5·10−4 | - |
| kFC | FC load coefficient | 1.3889·10−8 | s−1 |
| α | FC load coefficient | 4 | - |
| PFC | FC rated power | 6 | kW |
| cH2 | Hydrogen cost | 3.5·10−3 | $/g |
| cB | B specific cost | 640 | $ |
| kB | B load coefficient | 4.6296·10−10 | C−1 |
| IB | B rated current | 40 | A |
| p3 | “charge sustaining” coefficient | −0.0286 | $ |
| p2 | “charge sustaining” coefficient | 0.2527 | $ |
| p1 | “charge sustaining” coefficient | −1.3620 | $ |
| p0 | “charge sustaining” coefficient | 1.1376 | $ |
| aFC | gain coefficient of current ellipse | - | Ω½ |
| aB | gain coefficient of current ellipse | - | Ω½ |
| cFC | iFC-axis component of current ellipse center | - | A |
| cB | iB-axis component of current ellipse center | - | A |
| r | equivalent radius of current ellipse | - | A/Ω½ |
| b1 | coefficient of the iB-iFC relationship | - | A |
| b0 | coefficient of the iB-iFC relationship | - | A2 |
References
- Ehsani, M.; Gao, Y.; Emadi, A. Modern Electric, Hybrid. Electric, and Fuel Cell Vehicles: Fundamentals, Theory, and Design, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009; ISBN 978-1-4200-5400-2. [Google Scholar]
- Das, H.S.; Tan, C.W.; Yatim, A.H.M. Fuel cell hybrid electric vehicles: A review on power conditioning units and topologies. Renew. Sustain. Energy Rev. 2017, 76, 268–291. [Google Scholar] [CrossRef]
- Gurz, M.; Baltacioglu, E.; Hames, Y.; Kaya, K. The meeting of hydrogen and automotive: A review. Int. J. Hydrogen Energy 2017, 42, 23334–23346. [Google Scholar] [CrossRef]
- Xun, Q.; Liu, Y.; Holmberg, E. A Comparative Study of Fuel Cell Electric Vehicles Hybridization with Battery or Supercapacitor. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 389–394. [Google Scholar]
- Hemmati, R.; Saboori, H. Emergence of hybrid energy storage systems in renewable energy and transport applications—A review. Renew. Sustain. Energy Rev. 2016, 65, 11–23. [Google Scholar] [CrossRef]
- Sulaiman, N.; Hannan, M.A.; Mohamed, A.; Majlan, E.H.; Wan Daud, W.R. A review on energy management system for fuel cell hybrid electric vehicle: Issues and challenges. Renew. Sustain. Energy Rev. 2015, 52, 802–814. [Google Scholar] [CrossRef]
- Feroldi, D.; Carignano, M. Sizing for fuel cell/supercapacitor hybrid vehicles based on stochastic driving cycles. Appl. Energy 2016, 183, 645–658. [Google Scholar] [CrossRef]
- Xu, L.; Mueller, C.D.; Li, J.; Ouyang, M.; Hu, Z. Multi-objective component sizing based on optimal energy management strategy of fuel cell electric vehicles. Appl. Energy 2015, 157, 664–674. [Google Scholar] [CrossRef]
- Xu, L.; Ouyang, M.; Li, J.; Yang, F.; Lu, L.; Hua, J. Optimal sizing of plug-in fuel cell electric vehicles using models of vehicle performance and system cost. Appl. Energy 2013, 103, 477–487. [Google Scholar] [CrossRef]
- Sampietro, J.L.; Puig, V.; Costa-Castelló, R. Optimal Sizing of Storage Elements for a Vehicle Based on Fuel Cells, Supercapacitors, and Batteries. Energies 2019, 12, 925. [Google Scholar] [CrossRef]
- Wang, L.; Collins, E.G., Jr.; Li, H. Optimal Design and Real-Time Control for Energy Management in Electric Vehicles. IEEE Trans. Veh. Technol. 2011, 60, 1419–1429. [Google Scholar] [CrossRef]
- Livint, G.; Stan, A.G. Control strategies for hybrid electric vehicles with two energy sources on board. In Proceedings of the International Conference and Exposition on Electrical and Power Engineering (EPE 2014), Iasi, Romania, 16–18 October 2014; pp. 142–147. [Google Scholar]
- Zhang, T.; Wang, P.; Chen, H.; Pei, P. A review of automotive proton exchange membrane fuel cell degradation under start-stop operating condition. Appl. Energy 2018, 223, 249–262. [Google Scholar] [CrossRef]
- Sulaiman, N.; Hannan, M.A.; Mohamed, A.; Ker, P.J.; Majlan, E.H.; Wan Daud, W.R. Optimization of energy management system for fuel-cell hybrid electric vehicles: Issues and recommendations. Appl. Energy 2018, 228, 2061–2079. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Xu, L.; Ouyang, M. Power management and economic estimation of fuel cell hybrid vehicle using fuzzy logic. In Proceedings of the 5th IEEE Vehicle Power and Propulsion Conference (VPPC 2009), Dearborn, MI, USA, 7–10 September 2009; pp. 1749–1754. [Google Scholar]
- Ravey, A.; Mohammadi, A.; Bouquain, D. Control strategy of fuel cell electric vehicle including degradation process. In Proceedings of the 41st Annual Conference of the IEEE Industrial Electronics Society (IECON 2015), Yokohama, Japan, 9–12 November 2015; pp. 003508–003513. [Google Scholar]
- Jawadi, S.; Slama, S.B.; Zafar, B.; Cherif, A. An efficient control strategy for hybrid PEMFC/Supercapacitor power source applied for automotive application. In Proceedings of the 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA 2015), Monastir, Tunisia, 21–23 December 2015; pp. 432–437. [Google Scholar]
- Kaya, K.; Hames, Y. Two new control strategies: For hydrogen fuel saving and extend the life cycle in the hydrogen fuel cell vehicles. Int. J. Hydrogen Energy 2019, 44, 18967–18980. [Google Scholar] [CrossRef]
- Weyers, C.; Bocklisch, T. Simulation-based investigation of energy management concepts for fuel cell–battery–hybrid energy storage systems in mobile applications. Energy Procedia 2018, 155, 295–308. [Google Scholar] [CrossRef]
- Marzougui, H.; Kadri, A.; Amari, M.; Bacha, F. Frequency separation based energy management strategy for fuel cell electrical vehicle with super-capacitor storage system. In Proceedings of the 9th International Renewable Energy Congress (IREC 2018), Hammamet, Tunisia, 20–22 March 2018; pp. 1–6. [Google Scholar]
- Tani, A.; Camara, M.B.; Dakyo, B. Energy Management Based on Frequency Approach for Hybrid Electric Vehicle Applications: Fuel-Cell/Lithium-Battery and Ultracapacitors. IEEE Trans. Veh. Technol. 2012, 61, 3375–3386. [Google Scholar] [CrossRef]
- Badji, A.; Abdeslam, D.O.; Becherif, M.; Eltoumi, F.; Benamrouche, N. Analyze and evaluate of energy management system for fuel cell electric vehicle based on frequency splitting. Math. Comput. Simul. 2019, 167, 65–77. [Google Scholar] [CrossRef]
- Ettihir, K.; Boulon, L.; Agbossou, K. Energy management strategy for a fuel cell hybrid vehicle based on maximum efficiency and maximum power identification. IET Electr. Syst. Transp. 2016, 6, 261–268. [Google Scholar] [CrossRef]
- Pregelj, B.; Micor, M.; Dolanc, G.; Petrovčič, J.; Jovan, V. Impact of fuel cell and battery size to overall system performance—A diesel fuel-cell APU case study. Appl. Energy 2016, 182, 365–375. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Liu, X.; Yan, J. Enhancing fuel cell durability for fuel cell plug-in hybrid electric vehicles through strategic power management. Appl. Energy 2019, 241, 483–490. [Google Scholar] [CrossRef]
- Bizon, N. Energy optimization of fuel cell system by using global extremum seeking algorithm. Appl. Energy 2017, 206, 458–474. [Google Scholar] [CrossRef]
- Li, H.; Ravey, A.; N’Diaye, A.; Djerdir, A. A novel equivalent consumption minimization strategy for hybrid electric vehicle powered by fuel cell, battery and supercapacitor. J. Power Sources 2018, 395, 262–270. [Google Scholar] [CrossRef]
- Cheng, G.; Hao, L.; Xinbo, C.; Shaoming, Q. Parameter design of the powertrain of fuel cell electric vehicle and the energy management strategy. In Proceedings of the 34th Chinese Control Conference (CCC 2015), Hangzhou, China, 28–30 July 2015; pp. 8027–8032. [Google Scholar]
- Wang, Y.; Moura, S.J.; Advani, S.G.; Prasad, A.K. Power management system for a fuel cell/battery hybrid vehicle incorporating fuel cell and battery degradation. Int. J. Hydrogen Energy 2019, 44, 8479–8492. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, L.; Li, J.; Hu, Z.; Ouyang, M. Energy management and component sizing for a fuel cell/battery/supercapacitor hybrid powertrain based on two-dimensional optimization algorithms. Energy 2019, 177, 386–396. [Google Scholar] [CrossRef]
- Bambang, R.T.; Rohman, A.S.; Dronkers, C.J.; Ortega, R.; Sasongko, A. Energy Management of Fuel Cell/Battery/Supercapacitor Hybrid Power Sources Using Model Predictive Control. IEEE Trans. Ind. Inform. 2014, 10, 1992–2002. [Google Scholar]
- da Fonseca, R.; Bideaux, E.; Jeanneret, B.; Gerard, M.; Desbois-Renaudin, M.; Sari, A. Energy management strategy for hybrid fuel cell vehicle. In Proceedings of the 12th International Conference on Control, Automation and Systems (ICCAS 2012), Jeju Island, Korea, 17–21 October 2012; pp. 485–490. [Google Scholar]
- Tribioli, L.; Cozzolino, R.; Chiappini, D.; Iora, P. Energy management of a plug-in fuel cell/battery hybrid vehicle with on-board fuel processing. Appl. Energy 2016, 184, 140–154. [Google Scholar] [CrossRef]
- Gaoua, Y.; Caux, S.; Lopez, P.; Raga, C.; Barrado, A.; Lazaro, A. Hybrid Systems Energy Management Using Optimization Method Based on Dynamic Sources Models. In Proceedings of the 10th IEEE Vehicle Power and Propulsion Conference (VPPC 2014), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar]
- Li, H.; Ravey, A.; N’Diaye, A.; Djerdir, A. Equivalent consumption minimization strategy for hybrid electric vehicle powered by fuel cell, battery and supercapacitor. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society (IECON 2016), Florence, Italy, 23–26 October 2016; pp. 4401–4406. [Google Scholar]
- Morales-Morales, J.; Cervantes, I.; Cano-Castillo, U. On the Design of Robust Energy Management Strategies for FCHEV. IEEE Trans. Veh. Technol. 2015, 64, 1716–1728. [Google Scholar] [CrossRef]
- Serpi, A.; Porru, M.; Damiano, A. An Optimal Power and Energy Management by Hybrid Energy Storage Systems in Microgrids. Energies 2017, 10, 1909. [Google Scholar] [CrossRef]
- Weitzel, T.; Glock, C.H. Energy management for stationary electric energy storage systems: A systematic literature review. Eur. J. Oper. Res. 2018, 264, 582–606. [Google Scholar] [CrossRef]
- Agüera-Pérez, A.; Palomares-Salas, J.C.; González de la Rosa, J.J.; Florencias-Oliveros, O. Weather forecasts for microgrid energy management: Review, discussion and recommendations. Appl. Energy 2018, 228, 265–278. [Google Scholar] [CrossRef]
- Serpi, A.; Porru, M. A Real-Time Energy Management System for Operating Cost Minimization of Fuel Cell/Battery Electric Vehicles. In Proceedings of the 13th IEEE Vehicle Power and Propulsion Conference (VPPC 2017), Belfort, France, 11–14 December 2017; pp. 1–5. [Google Scholar]
- Depature, C.; Jemei, S.; Boulon, L.; Bouscayrol, A.; Marx, N.; Morando, S.; Castaings, A. IEEE VTS Motor Vehicles Challenge 2017—Energy Management of a Fuel Cell/Battery Vehicle. In Proceedings of the Proc. of 12nd IEEE Vehicle Power and Propulsion Conference (VPPC 2016), Hangzhou, China, 17–20 October 2016; pp. 1–6. [Google Scholar]
- Depature, C.; Jemei, S.; Boulon, L.; Bouscayrol, A.; Marx, N.; Morando, S.; Castaings, A. Energy Management in Fuel-Cell\/Battery Vehicles: Key Issues Identified in the IEEE Vehicular Technology Society Motor Vehicle Challenge 2017. IEEE Vehicular Technol. Mag. 2018, 13, 144–151. [Google Scholar] [CrossRef]
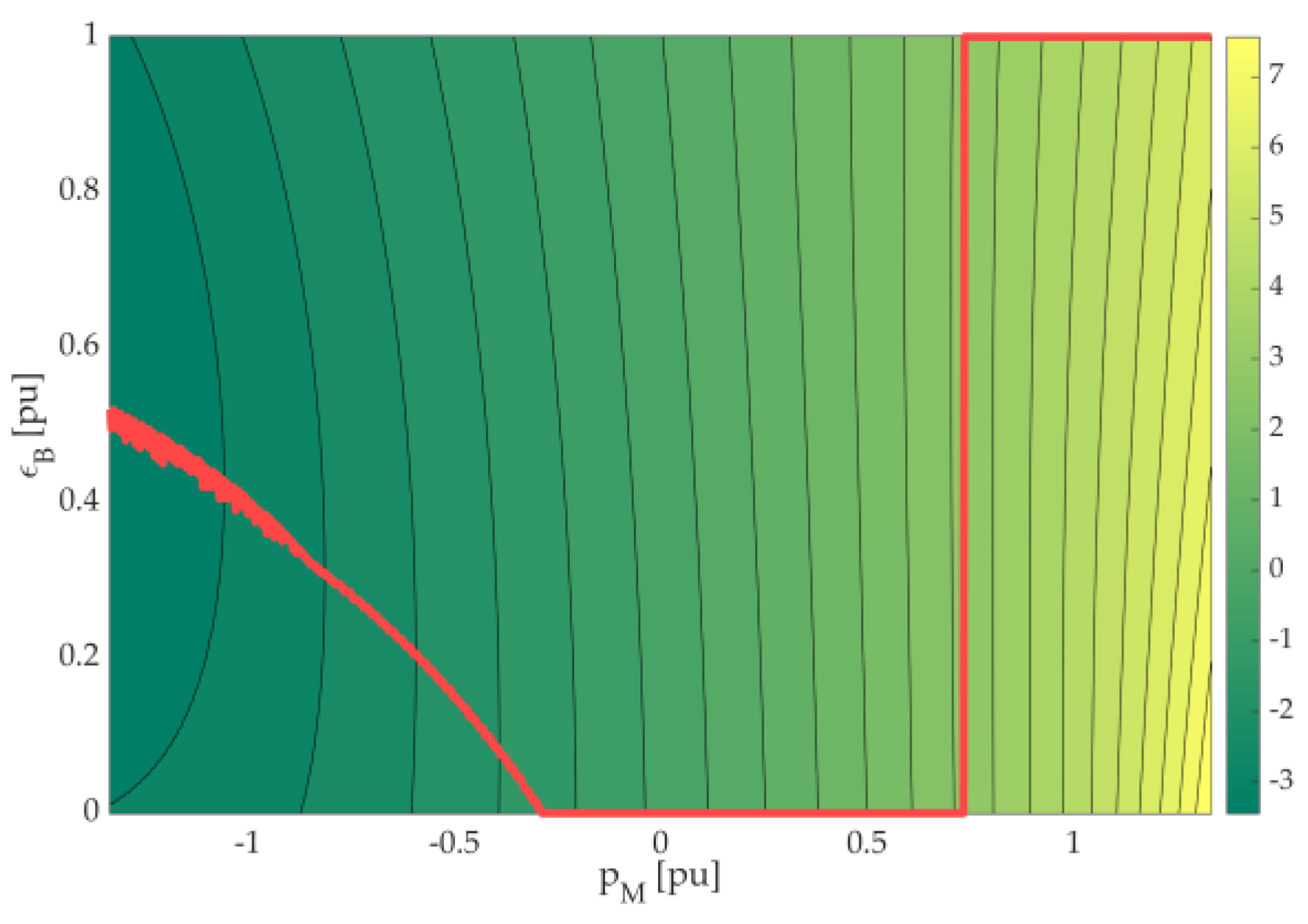
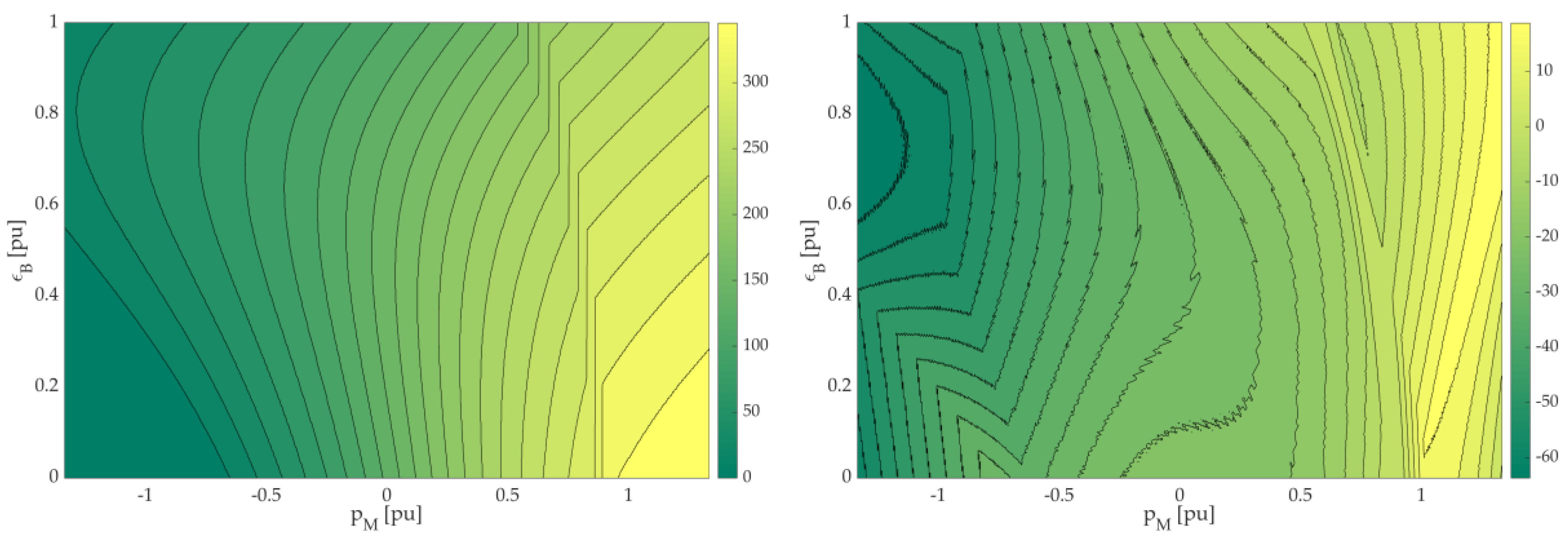
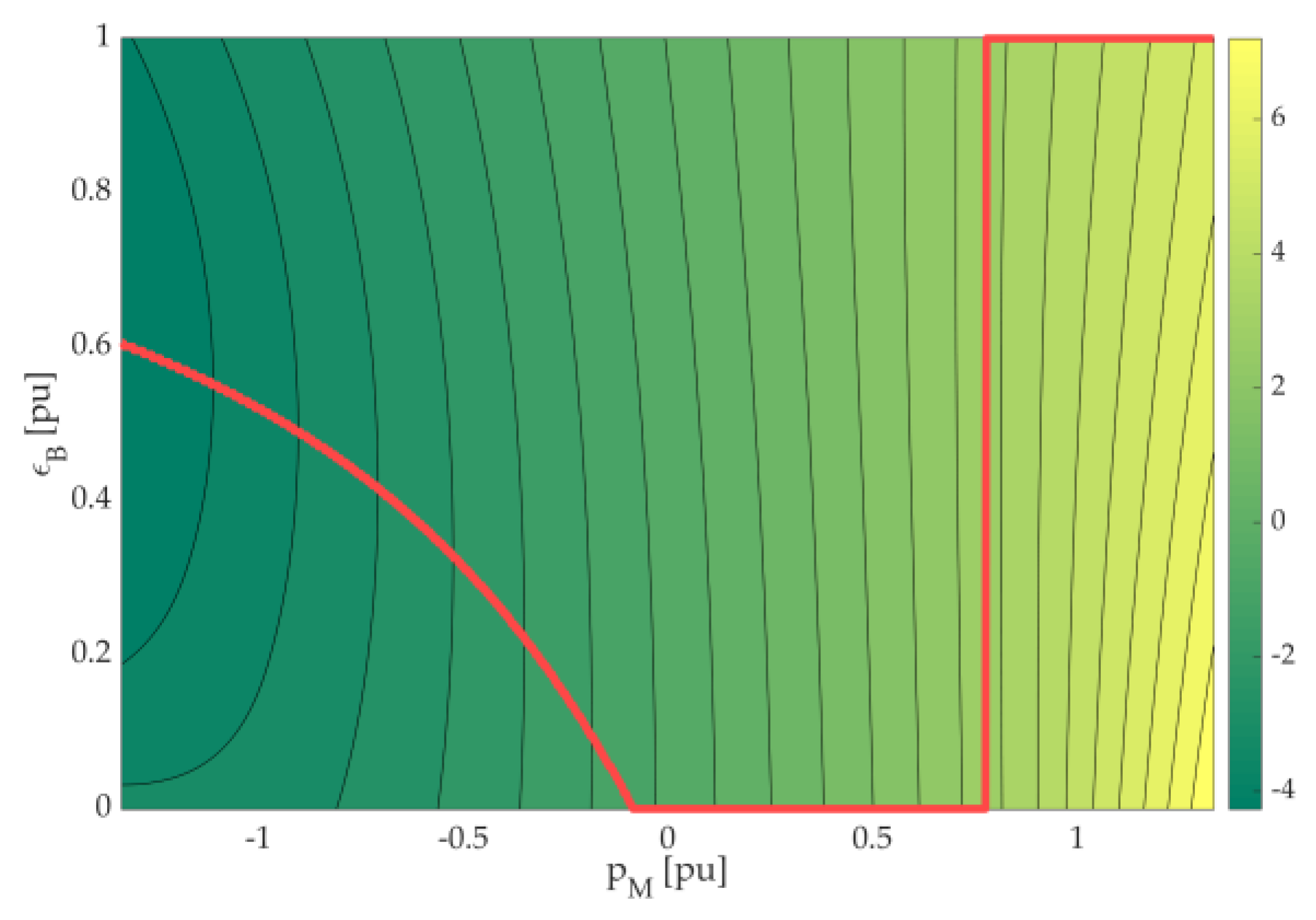
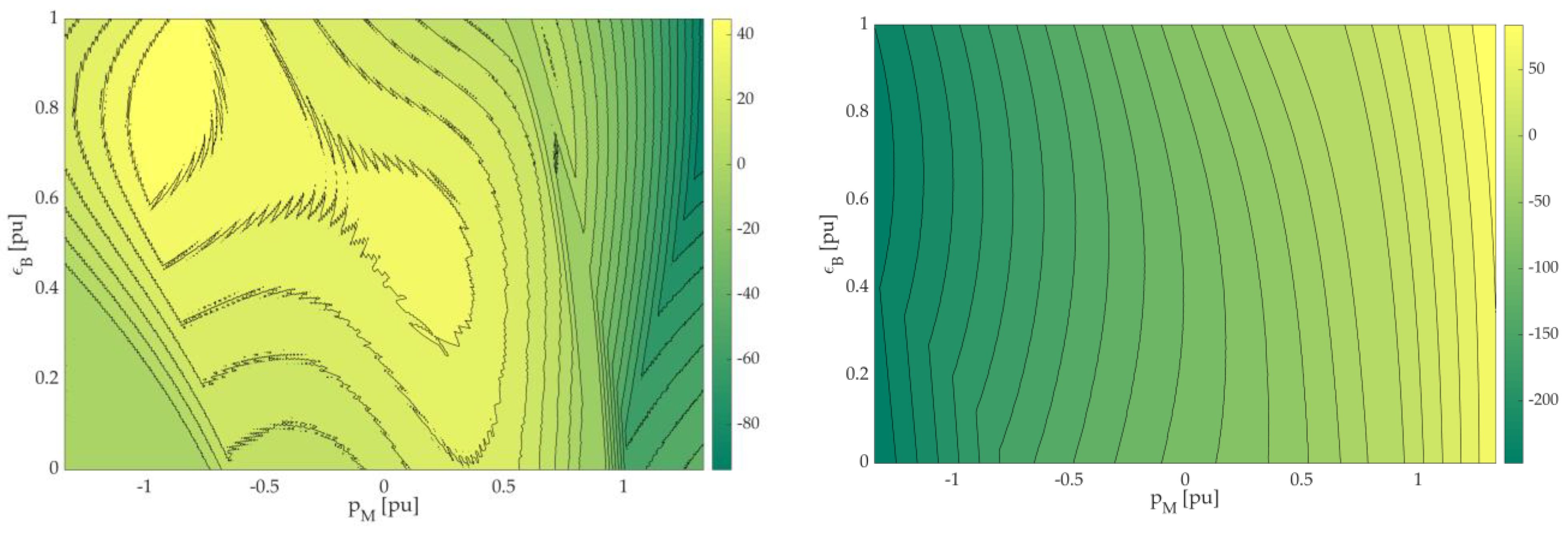
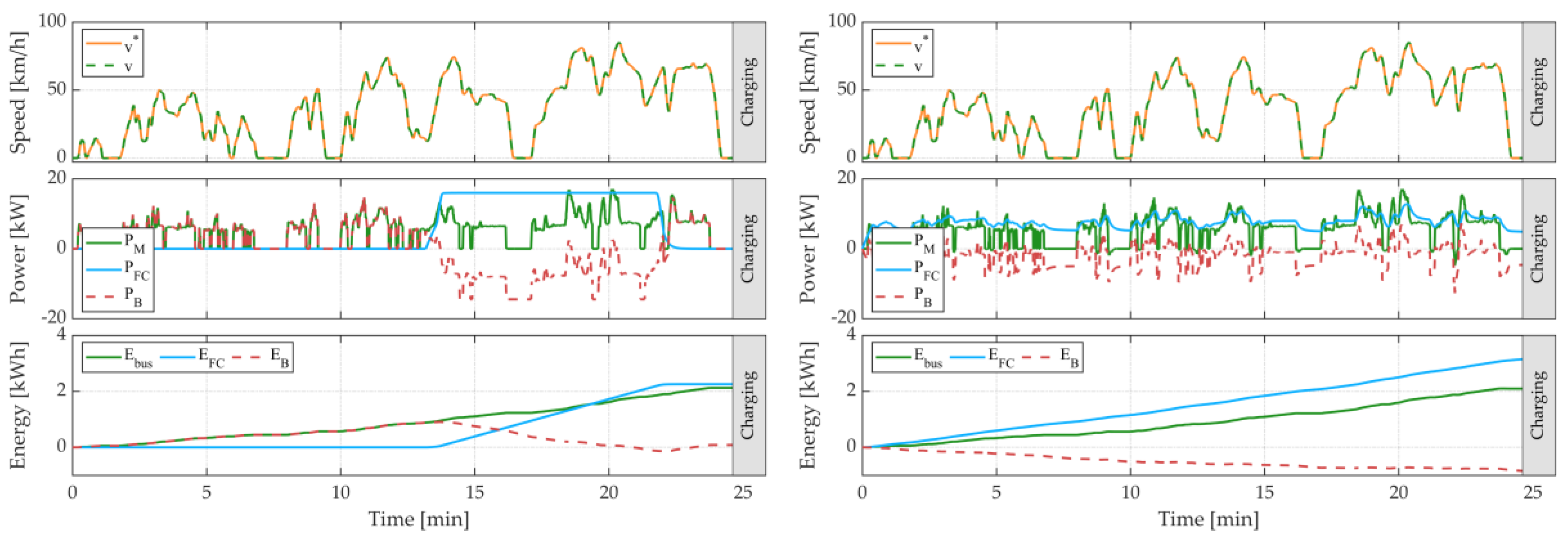
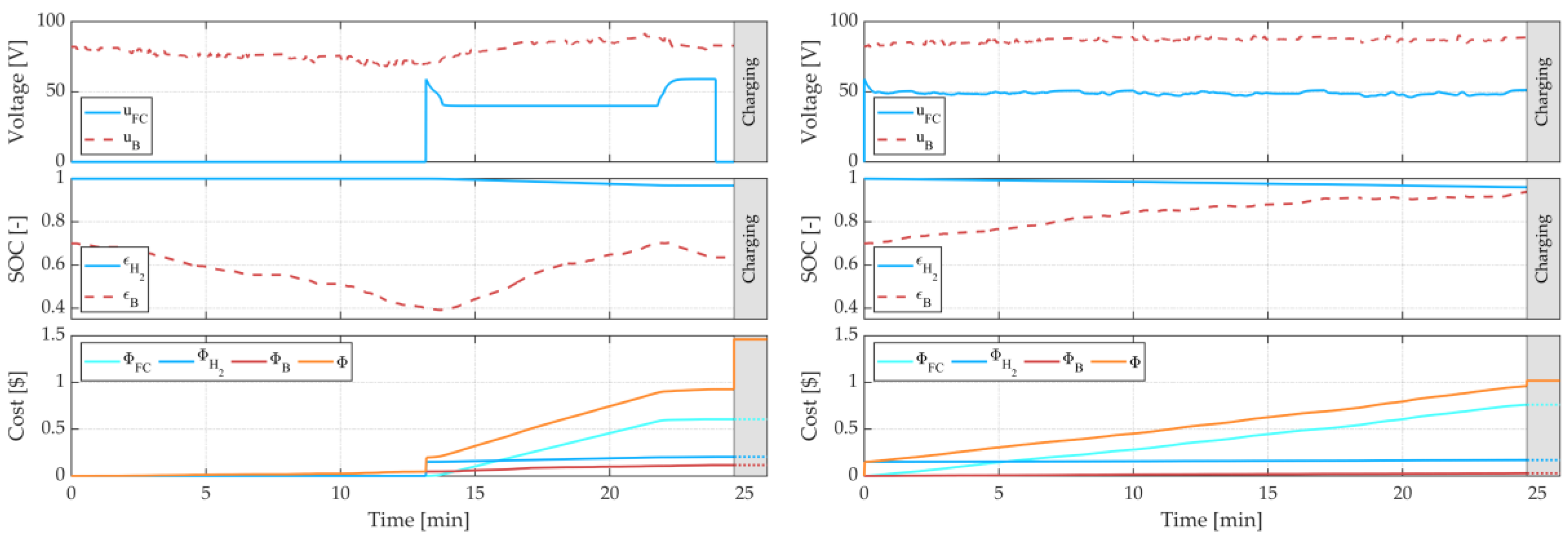
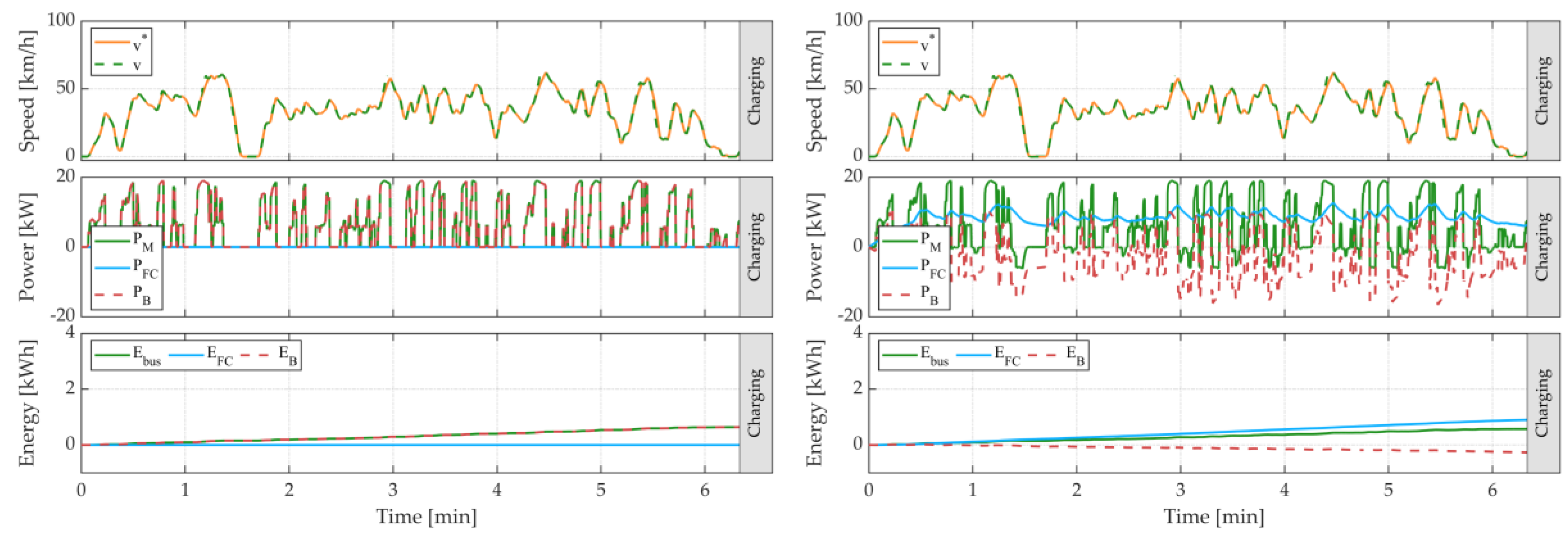
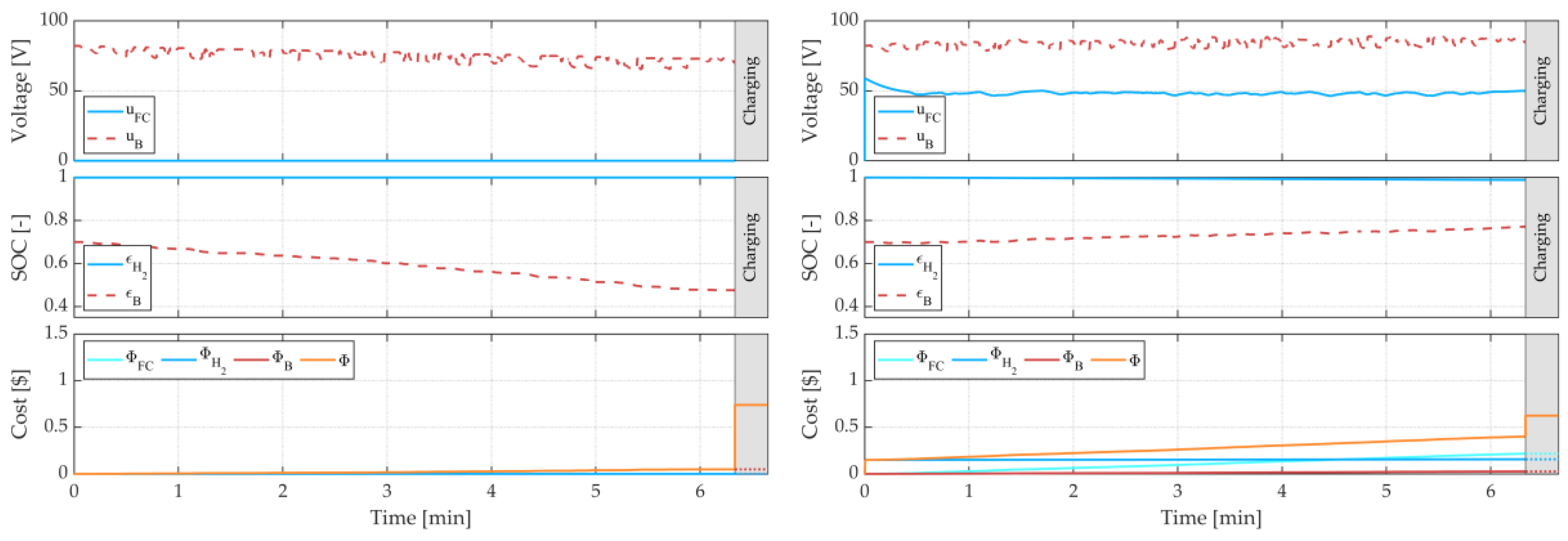
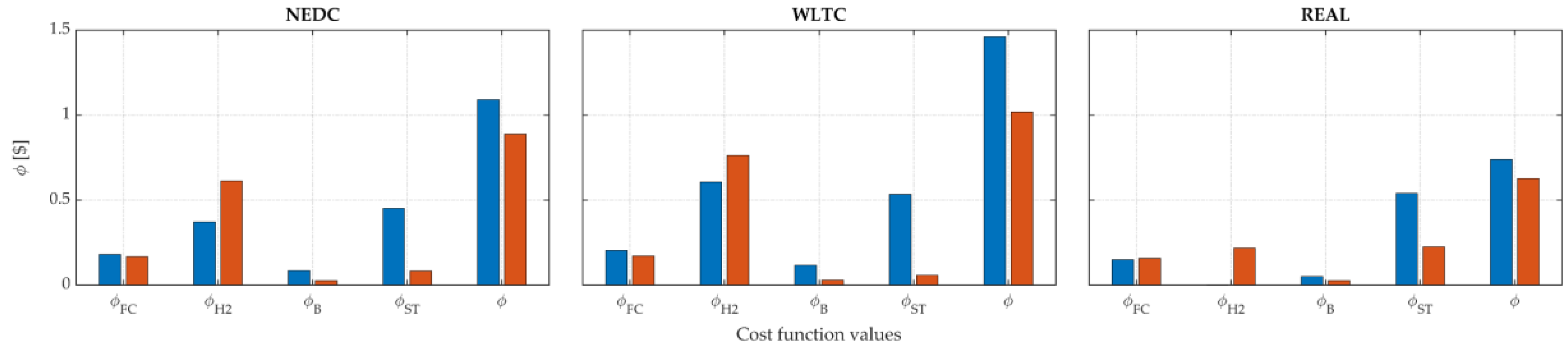
| EMS | NEDC | WLTC | REAL | |
|---|---|---|---|---|
| ϕFC [$] | H-EMS | 0.1812 | 0.2043 | 0.1500 |
| S-EMS | 0.1665 | 0.1702 | 0.1568 | |
| ϕH2 [$] | H-EMS | 0.3720 | 0.6062 | 0.0000 |
| S-EMS | 0.6131 | 0.7625 | 0.2171 | |
| ϕB [$] | H-EMS | 0.0842 | 0.1162 | 0.0493 |
| S-EMS | 0.0259 | 0.0286 | 0.0269 | |
| ϕST [$] | H-EMS | 0.4522 | 0.5338 | 0.5405 |
| S-EMS | 0.0826 | 0.0575 | 0.2240 | |
| Φ [$] | H-EMS | 1.0897 | 1.4605 | 0.7398 |
| S-EMS | 0.8881 | 1.0187 | 0.6248 |
| ΔT [s] | Cycle | S-EMS | A-EMS | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | 0 | 0 | 5 | 20 | 60 | 120 | 180 | 240 | 300 | 360 | 420 | 480 | |
| ϕFC [$] | NEDC | 0.1665 | 0.1669 | 0.1669 | 0.1669 | 0.1668 | 0.1668 | 0.1668 | 0.1669 | 0.1670 | 0.1670 | 0.1671 | 0.1672 |
| WLTC | 0.1702 | 0.1711 | 0.1711 | 0.1710 | 0.1708 | 0.1704 | 0.1704 | 0.1704 | 0.1704 | 0.1705 | 0.1705 | 0.1706 | |
| REAL | 0.1568 | 0.1571 | 0.1571 | 0.1570 | 0.1569 | 0.1567 | 0.1565 | 0.1564 | 0.1562 | 0.1561 | 0.1560 | 0.1558 | |
| ϕH2 [$] | NEDC | 0.6131 | 0.6409 | 0.6405 | 0.6391 | 0.6354 | 0.6301 | 0.6253 | 0.6207 | 0.6162 | 0.6119 | 0.6077 | 0.6037 |
| WLTC | 0.7625 | 0.7827 | 0.7825 | 0.7821 | 0.7807 | 0.7786 | 0.7749 | 0.7698 | 0.7650 | 0.7603 | 0.7558 | 0.7515 | |
| REAL | 0.2171 | 0.2246 | 0.2243 | 0.2237 | 0.2219 | 0.2192 | 0.2167 | 0.2143 | 0.2121 | 0.2099 | 0.2077 | 0.2056 | |
| ϕB [$] | NEDC | 0.0259 | 0.0290 | 0.0290 | 0.0288 | 0.0283 | 0.0276 | 0.0270 | 0.0265 | 0.0260 | 0.0255 | 0.0251 | 0.0247 |
| WLTC | 0.0286 | 0.0312 | 0.0311 | 0.0310 | 0.0308 | 0.0305 | 0.0300 | 0.0293 | 0.0288 | 0.0282 | 0.0278 | 0.0274 | |
| REAL | 0.0269 | 0.0274 | 0.0274 | 0.0274 | 0.0272 | 0.0271 | 0.0269 | 0.0268 | 0.0267 | 0.0266 | 0.0266 | 0.0266 | |
| ϕST [$] | NEDC | 0.0826 | 0.0526 | 0.0531 | 0.0545 | 0.0584 | 0.0641 | 0.0694 | 0.0744 | 0.0794 | 0.0842 | 0.0889 | 0.0935 |
| WLTC | 0.0575 | 0.0382 | 0.0383 | 0.0385 | 0.0391 | 0.0403 | 0.0441 | 0.0496 | 0.0549 | 0.0602 | 0.0652 | 0.0701 | |
| REAL | 0.2240 | 0.2149 | 0.2152 | 0.2160 | 0.2181 | 0.2212 | 0.2242 | 0.2271 | 0.0230 | 0.2326 | 0.2353 | 0.2379 | |
| Φ [$] | NEDC | 0.8881 | 0.8894 | 0.8894 | 0.8892 | 0.8889 | 0.8886 | 0.8885 | 0.8884 | 0.8885 | 0.8886 | 0.8888 | 0.8891 |
| WLTC | 1.0187 | 1.0231 | 1.0230 | 1.0226 | 1.0213 | 1.0198 | 1.0193 | 1.0191 | 1.0191 | 1.0191 | 1.0192 | 1.0195 | |
| REAL | 0.6248 | 0.6240 | 0.6240 | 0.6240 | 0.6241 | 0.6242 | 0.6244 | 0.6246 | 0.6248 | 0.6251 | 0.6255 | 0.6259 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serpi, A.; Porru, M. Modelling and Design of Real-Time Energy Management Systems for Fuel Cell/Battery Electric Vehicles. Energies 2019, 12, 4260. https://doi.org/10.3390/en12224260
Serpi A, Porru M. Modelling and Design of Real-Time Energy Management Systems for Fuel Cell/Battery Electric Vehicles. Energies. 2019; 12(22):4260. https://doi.org/10.3390/en12224260
Chicago/Turabian StyleSerpi, Alessandro, and Mario Porru. 2019. "Modelling and Design of Real-Time Energy Management Systems for Fuel Cell/Battery Electric Vehicles" Energies 12, no. 22: 4260. https://doi.org/10.3390/en12224260
APA StyleSerpi, A., & Porru, M. (2019). Modelling and Design of Real-Time Energy Management Systems for Fuel Cell/Battery Electric Vehicles. Energies, 12(22), 4260. https://doi.org/10.3390/en12224260






