Fluid–Structure Interaction and Flow Redistribution in Membrane-Bounded Channels
Abstract
1. Introduction
1.1. Hydrodynamics in Undeformed Membrane-Bounded Systems
1.2. Motivation and Strategy of the Present Study
- In the ideal case of a uniform (along the whole channel) transmembrane pressure (TMP), a relatively simple chain of effects and consequences would be triggered: (a) Membrane/channel deformation; (b) changes in the friction coefficients in both fluid compartments with respect to those in the undeformed configuration; and, finally, (c) consequent changes in the solutions flow rates for any given inlet-to-outlet imposed pressure drop. Such TMP effects in ED and RED processes were documented in our previous studies [22,23], which revealed a significant influence of membrane deformation on the hydrodynamics and mass transfer in channels equipped with different profiled membranes.
- In the realistic case of a non-uniform TMP, the above chain becomes a closed loop (a two-way fluid–structure interaction, FSI) made up of: (a) Space-dependent membrane/channel deformation; (b) space-dependent changes in the friction coefficients, f, in both fluid compartments; (c) consequent space-dependent changes in the flow rates for any given inlet-to-outlet imposed pressure drop; (d) space-dependent changes in the frictional pressure losses and, thus, in the pressure distribution in both channels; and, finally, (e) changes in the spatial distribution of TMP (leading us back to point a). Once an equilibrium configuration is attained by the system, the flow distribution will generally turn out to be uneven (redistribution), also affecting the concentrations, solute mass transfer rates, and electric current densities.
- At the small scale of the unit cell (periodic domain identified by the membrane profiles), fully three-dimensional structural mechanics simulations were conducted by using the Ansys-Mechanical® code in order to compute the deformation of membranes/channels under different values of the transmembrane pressure, TMP, as discussed in a previous paper [22].
- Still at the unit cell scale, fully three-dimensional CFD simulations were conducted for each deformed configuration using the Ansys-CFX® code; these simulations provided the relation between the flow rate and driving pressure gradient (hydraulic characteristic) as a function of the amount of deformation, and thus of the applied TMP, as discussed in the same paper [22].
- In the present study, focused on the larger cell pair scale, the above results were summarized in the form of a correlation between the apparent hydraulic permeability (itself a function of the flow rate) and the transmembrane pressure, as will be discussed in Section 2.2.
- Finally, the above information was fed to a 2-D simplified model of the cell pair as will be described in Section 2.4 and Section 2.5.
2. Materials and Methods
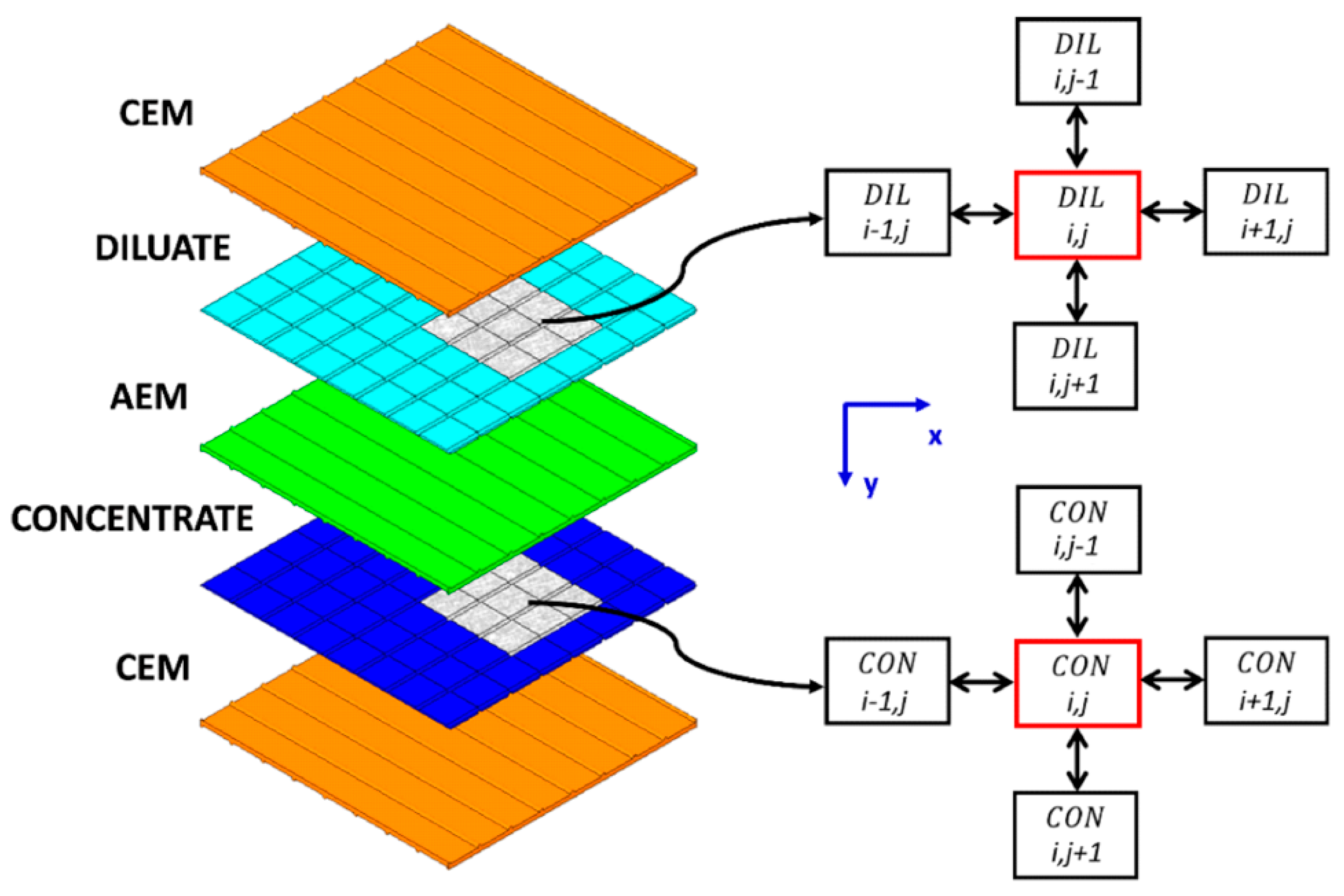
2.1. From a Small- to Large-Scale Description of Membrane-Bounded Channels
2.2. Computational Domain and Modelling Assumptions
- (a)
- The flow field is steady.
- (b)
- The fluid properties are constant and are the same in both the DIL and CON channels (the values ρ = 997 kg/m3 and μ = 8.89·10−4 Pa·s were used in the examples discussed in this paper).
- (c)
- AEM and CEM membranes share the same mechanical properties and profiles geometry, so that the same correlation for the channel apparent permeability applies to both channels.
- (d)
- Transmembrane water transport (due to osmotic flow and electro-osmotic drag) is neglected. Therefore, the inlet flow rate coincides with the outlet flow rate. This assumption is justified by the fact that the transmembrane water flow rate is much less than the main water flow rate along the channels. For example, even in the unrealistically extreme case of ED with a large concentration gradient (seawater–freshwater), a high current density (100 A/m2), large channel length/thickness ratio (3000, e.g., L = 0.6 m, H = 200 μm), low superficial velocity (1 cm/s) in both channels, large membrane osmotic permeability (10 mL/(m2 h bar)), and hydration number of 7 (water molecules/ion), the total transmembrane water flow rate estimated by elementary balances is less than 8% of the axial flow rate of each solution.
- Flow rates exiting a computational block are assumed to be positive, while flow rates entering a block are assumed to be negative.
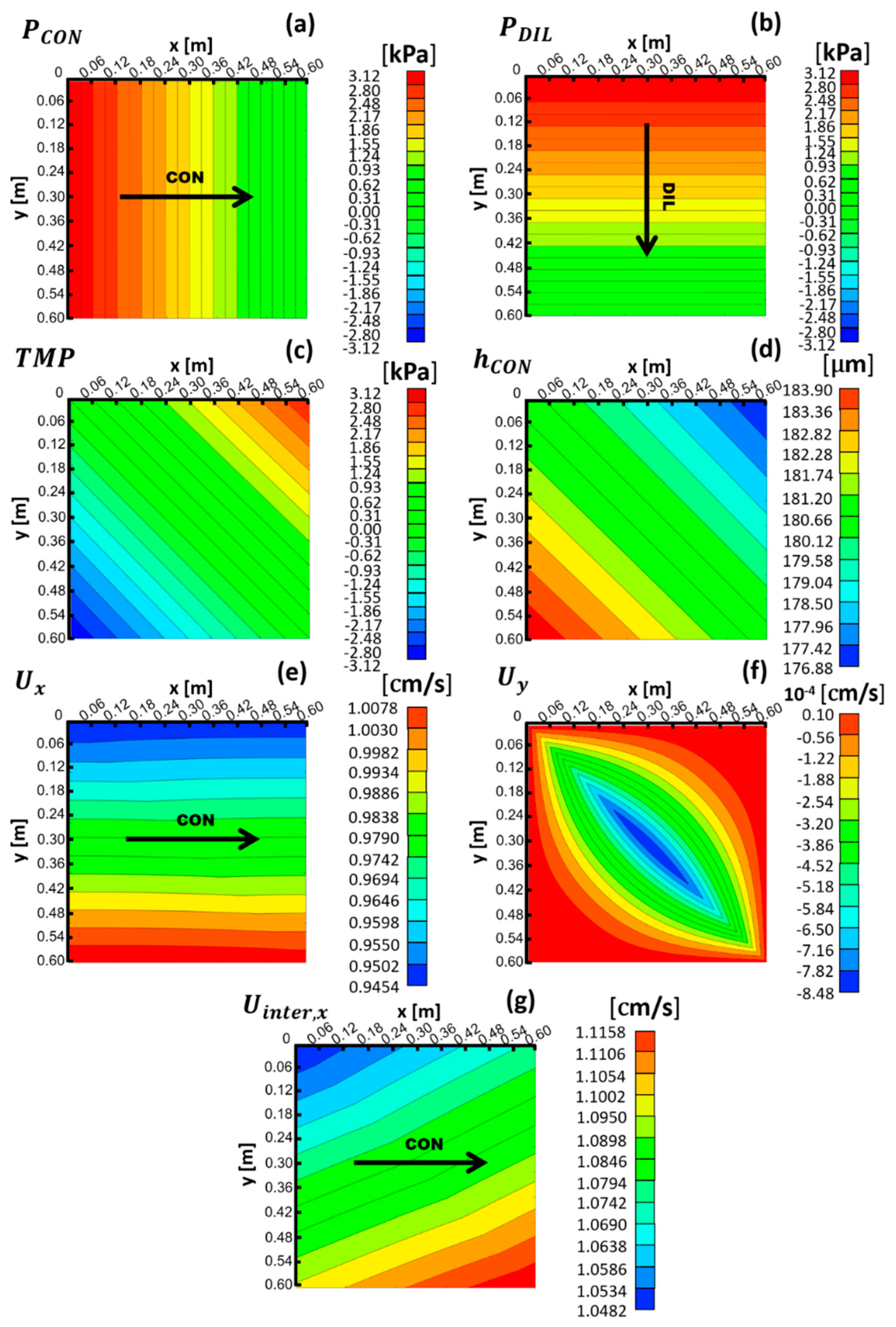
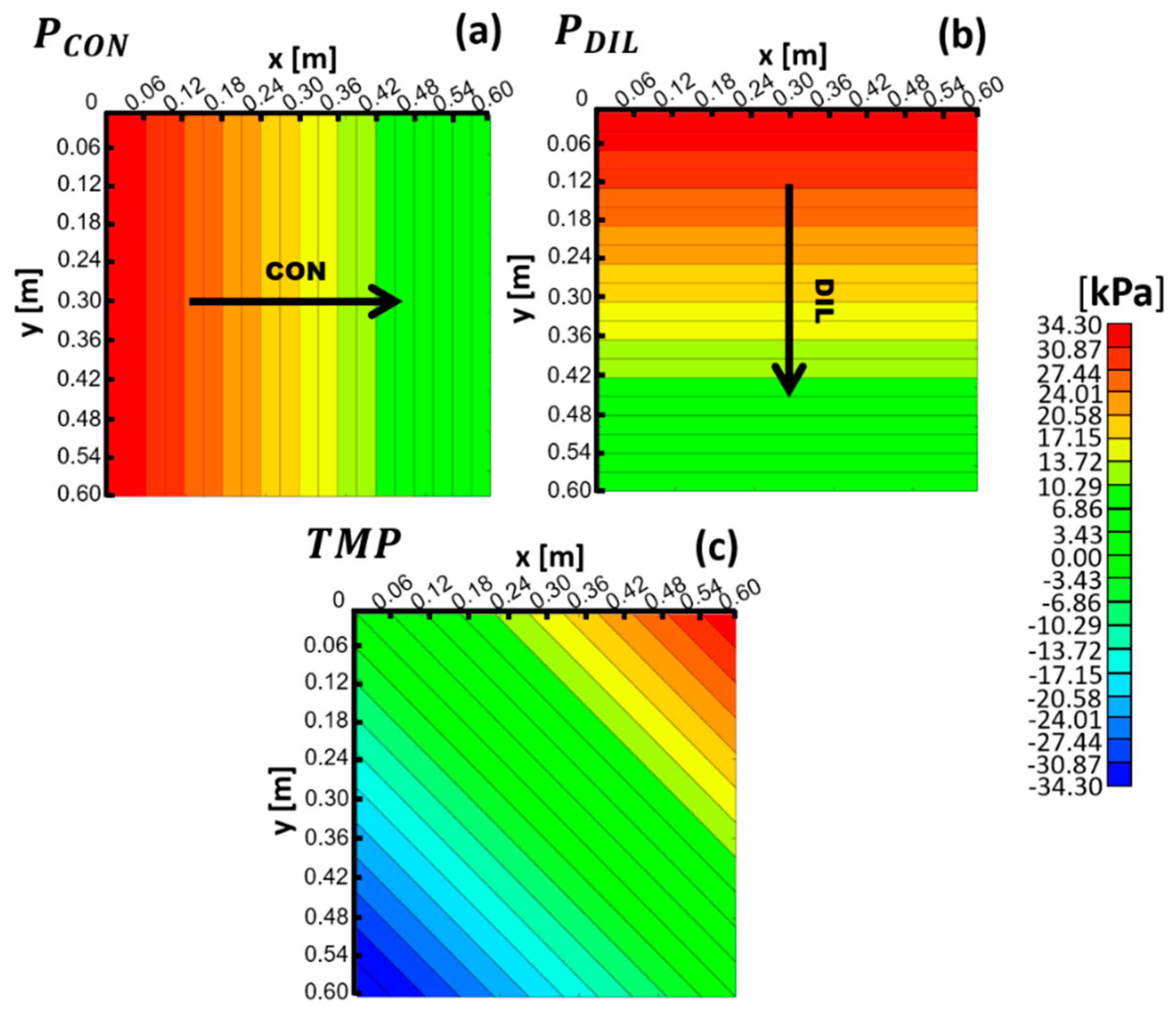
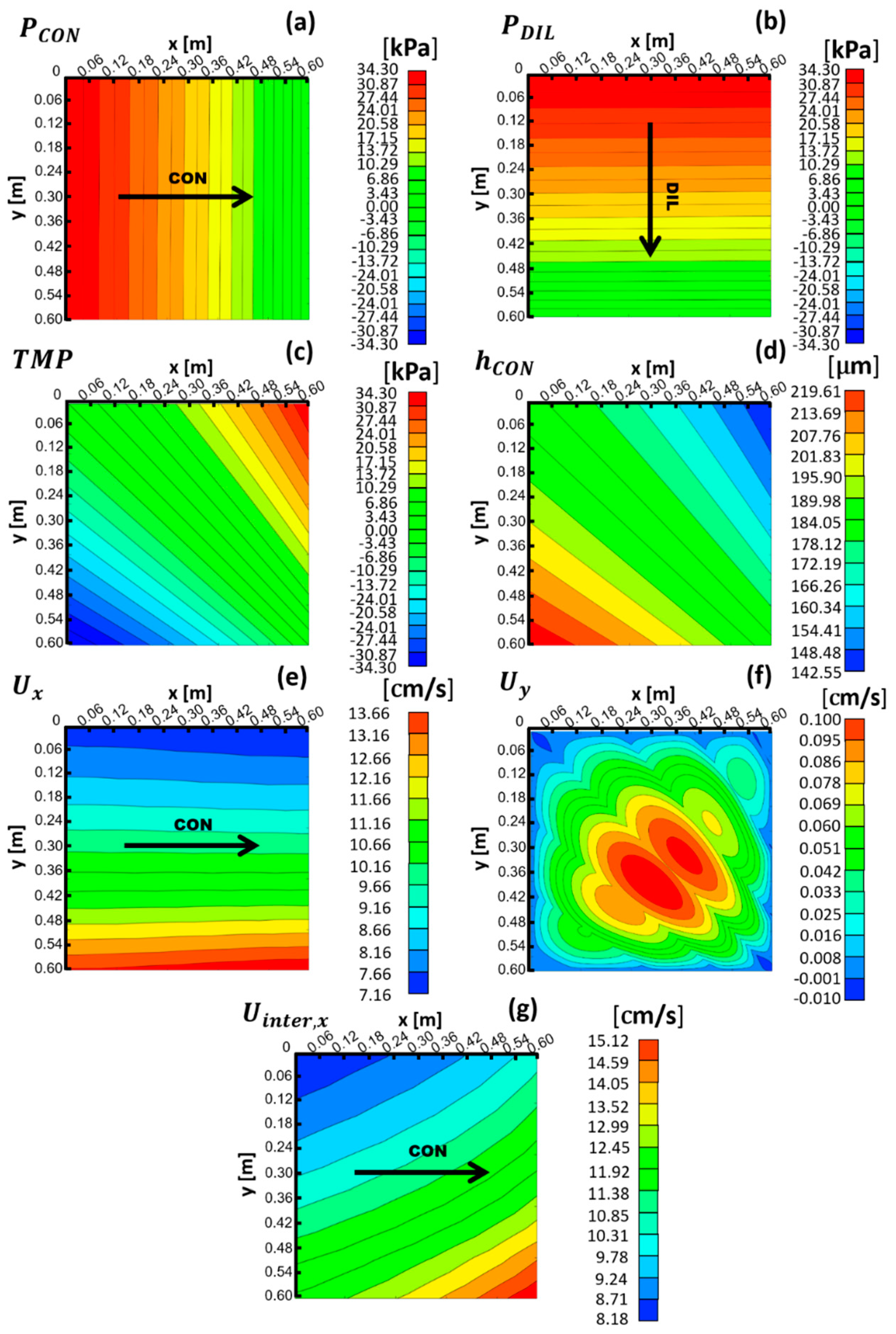
- The TMP is calculated as the difference between the local pressures in the DIL and CON compartments (), so that, as mentioned above, it is positive when DIL is expanded and CON compressed. By definition, if the CON compartment locally experiences a given value of TMP, at the corresponding location, the DIL compartment is subjected to −TMP.
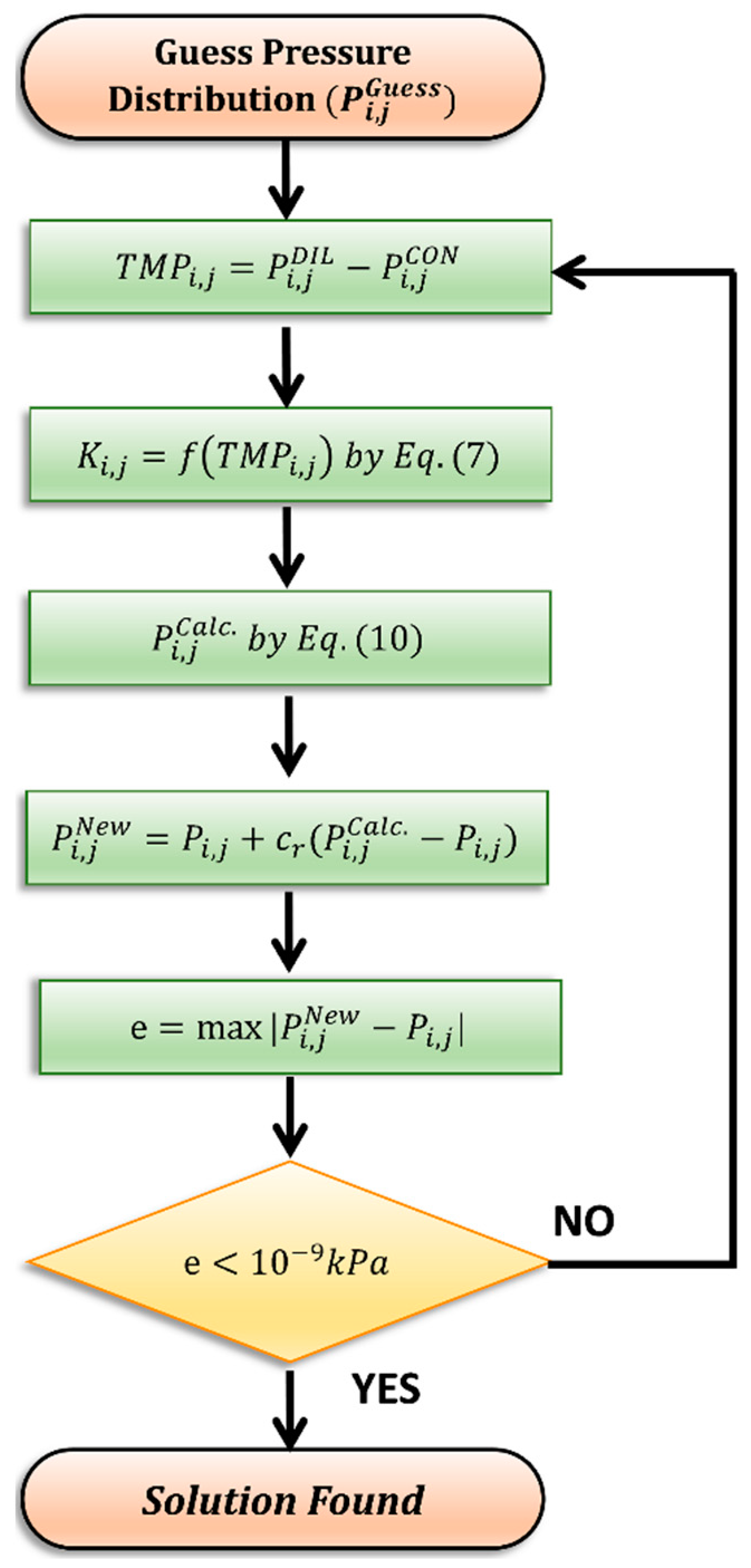
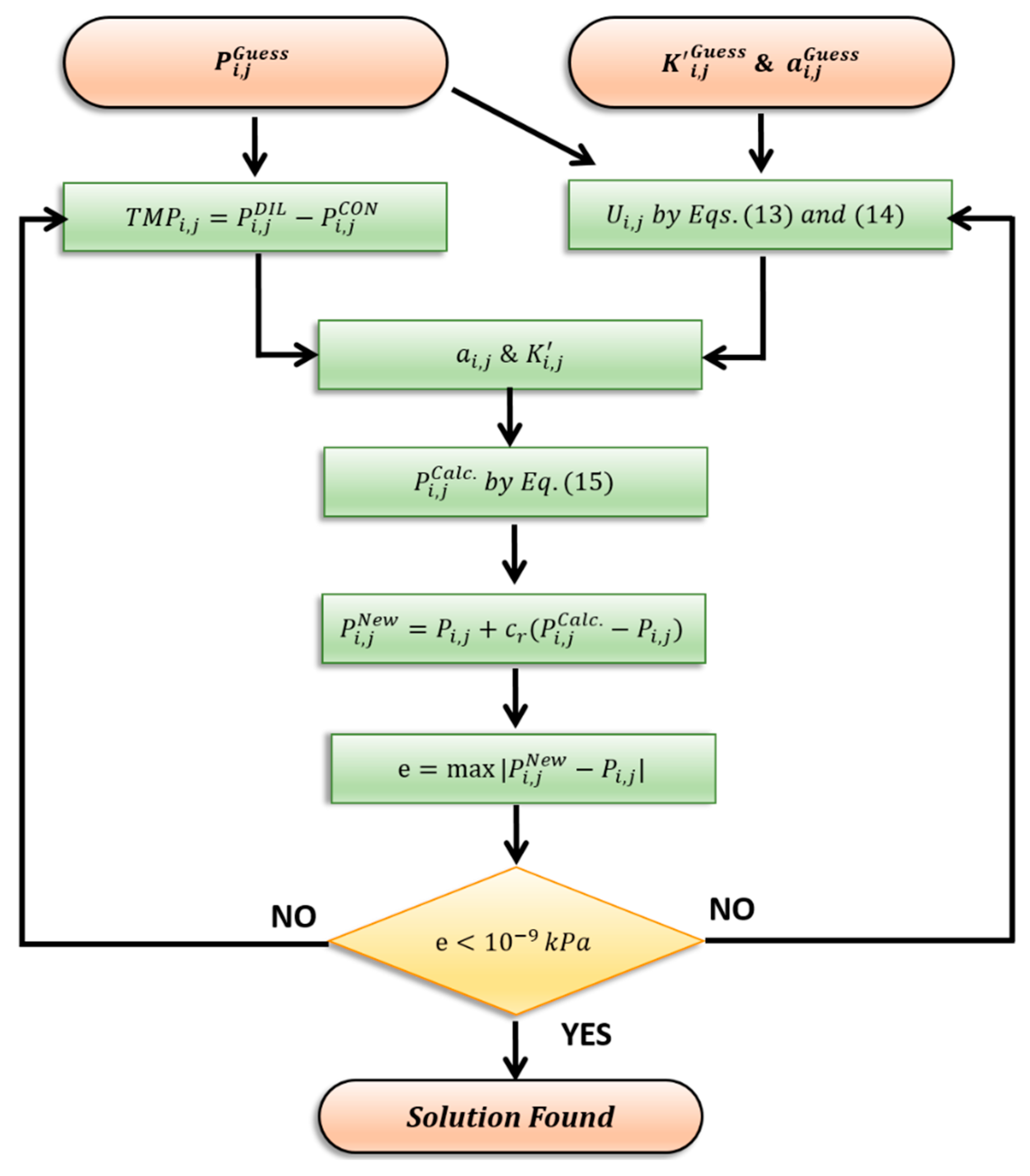
2.3. Discretized Continuity Equation
2.4. Discretized Darcy Equation for the Case of Low Velocity
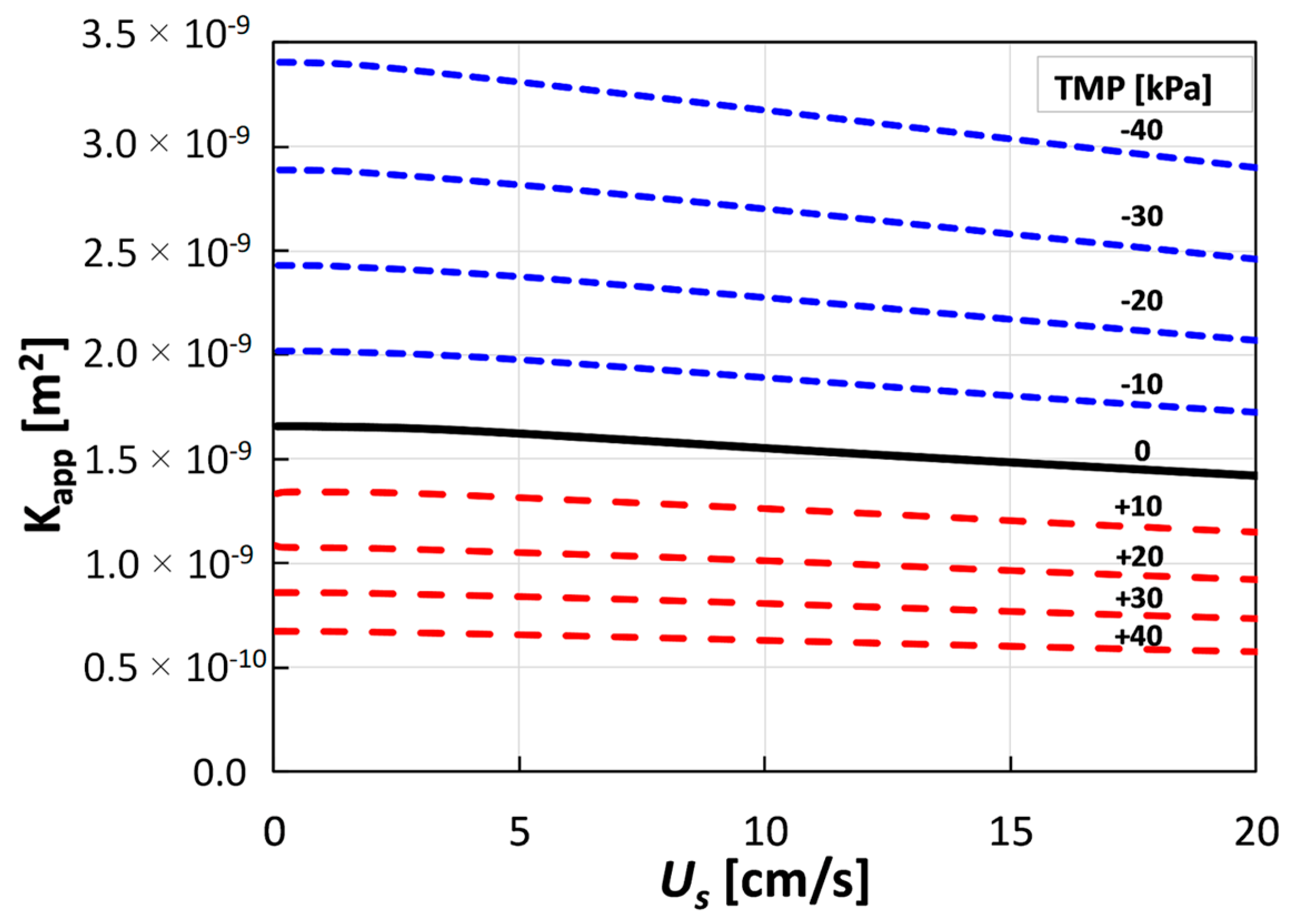
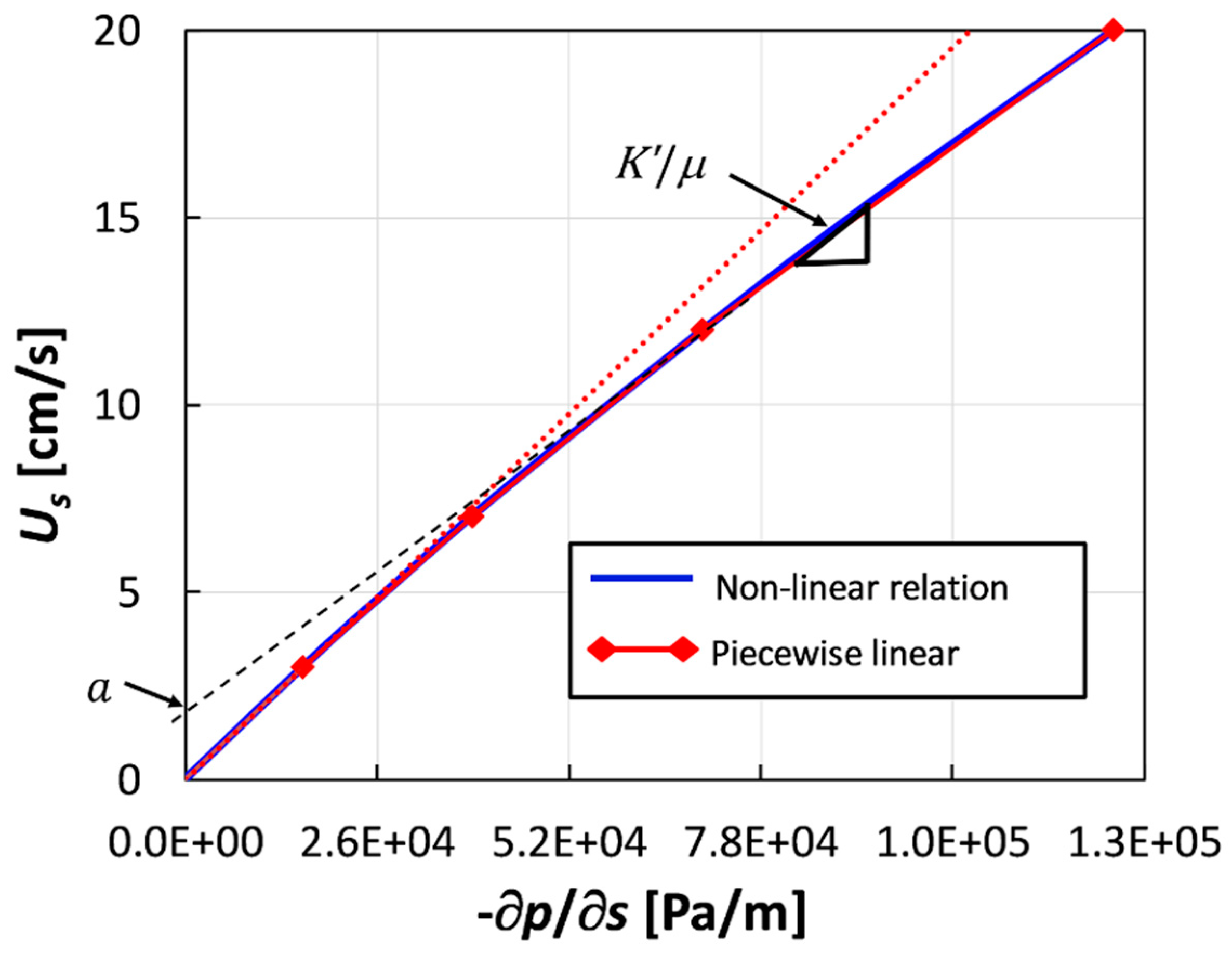
2.5. Model Adjustment for Non-Darcyan Flow Regime
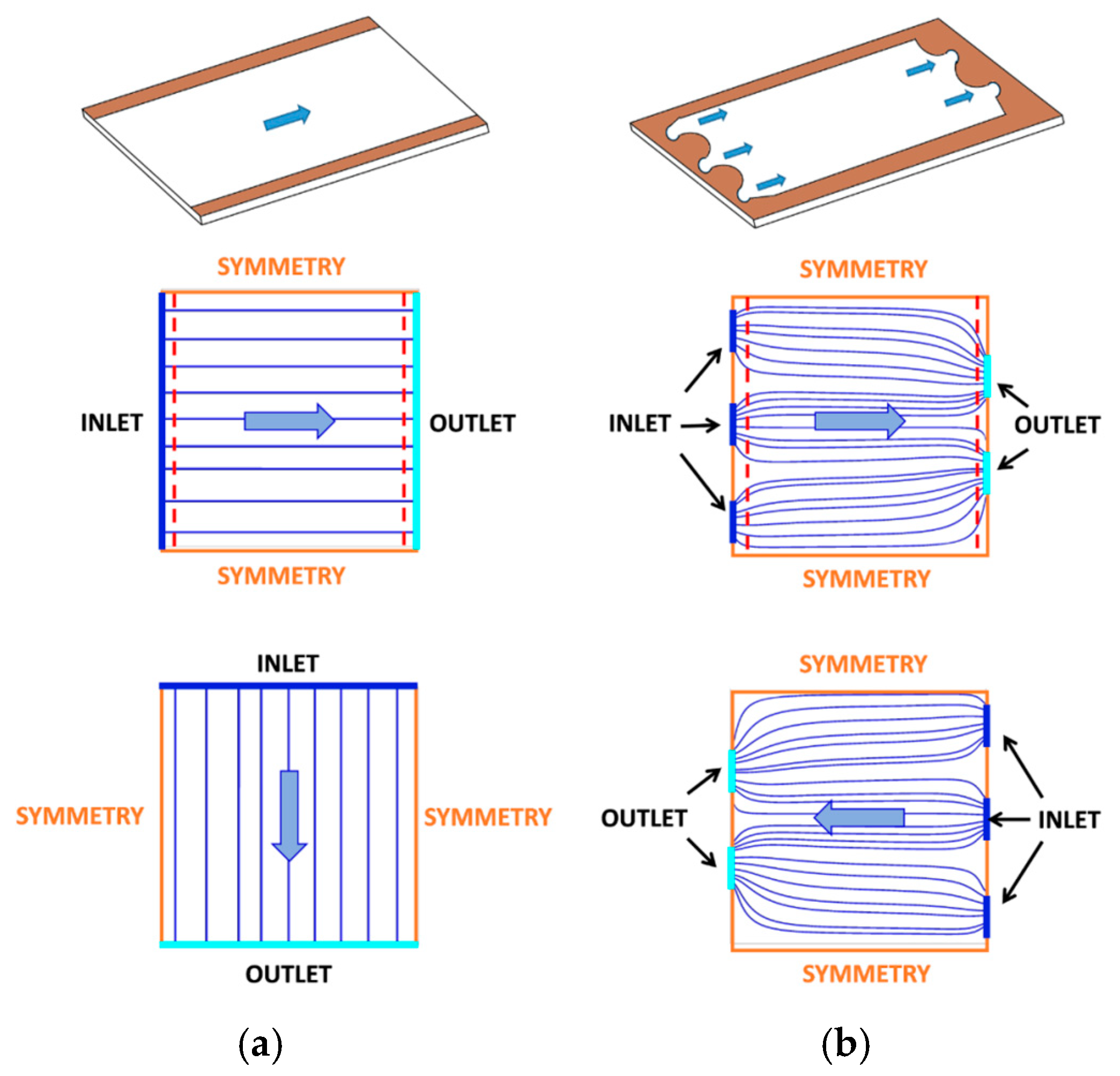
2.6. Flow Arrangement and Boundary Conditions
3. Results and Discussion
3.1. Cross Flow Arrangement
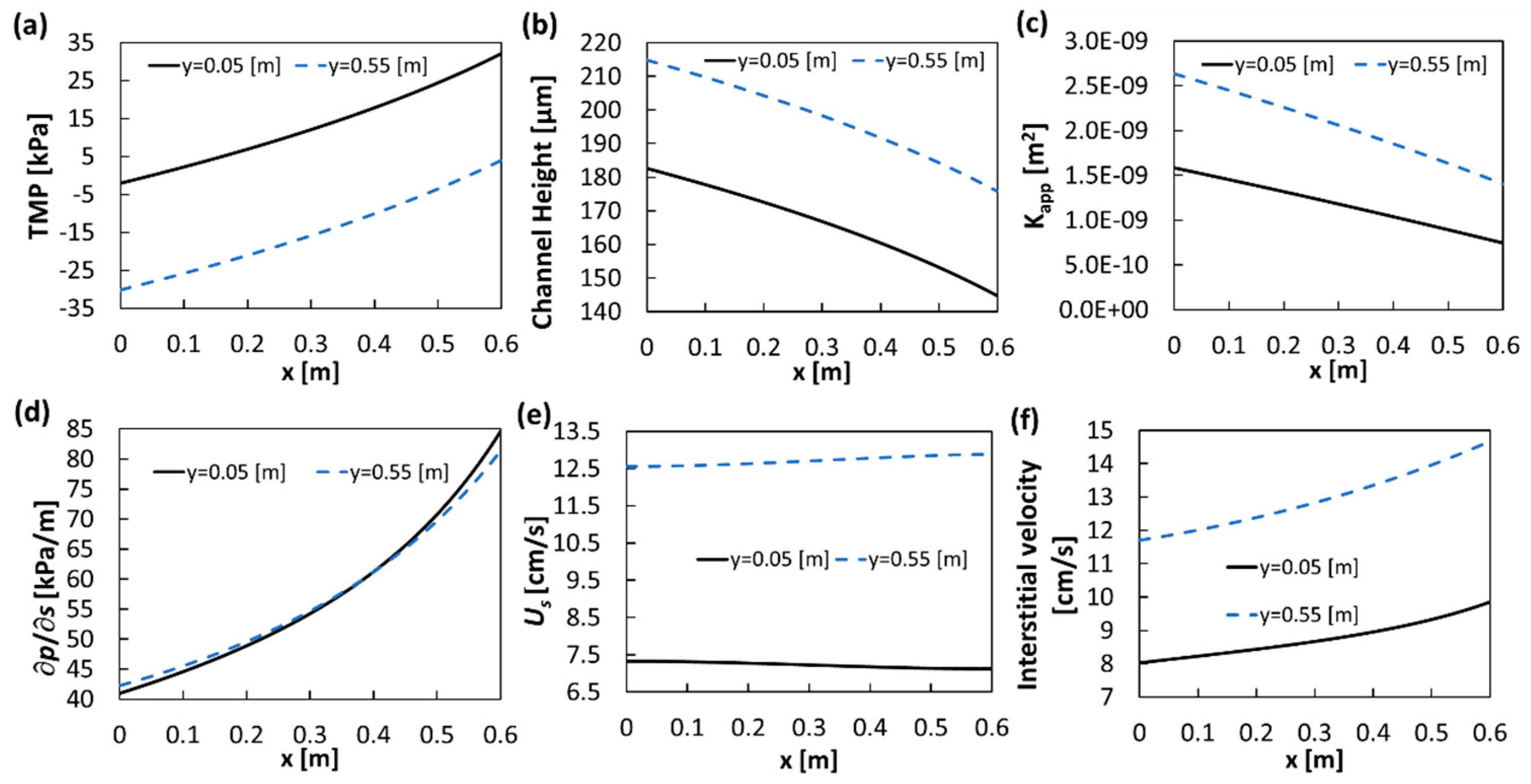
3.1.1. Low Velocity Case (Pin − Pout = 3.12 kPa, Yielding Us ≈ 1 cm/s)
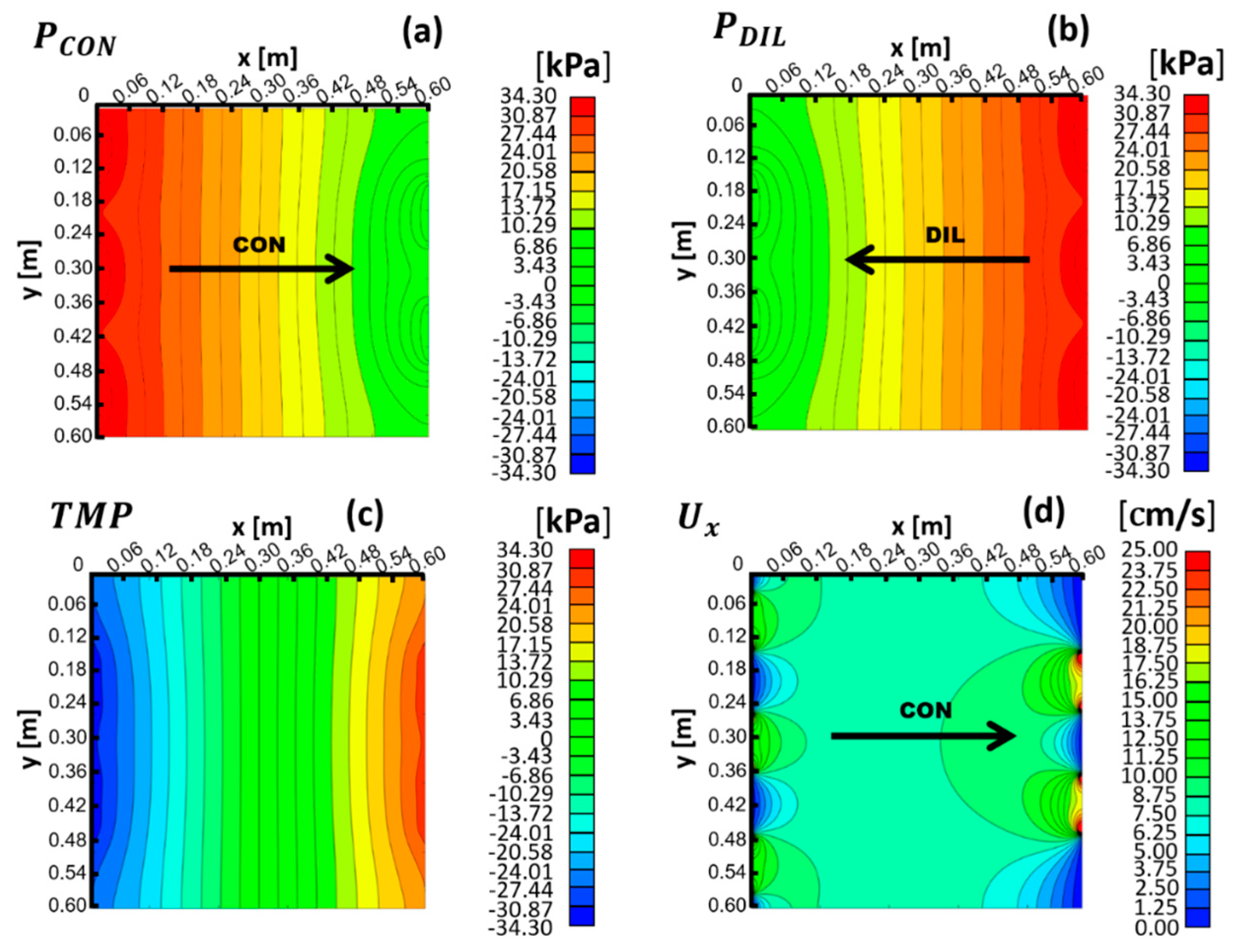
3.1.2. Higher Velocity Case (Pin − Pout = 34.3 kPa, Yielding Us ≈ 10 cm/s)
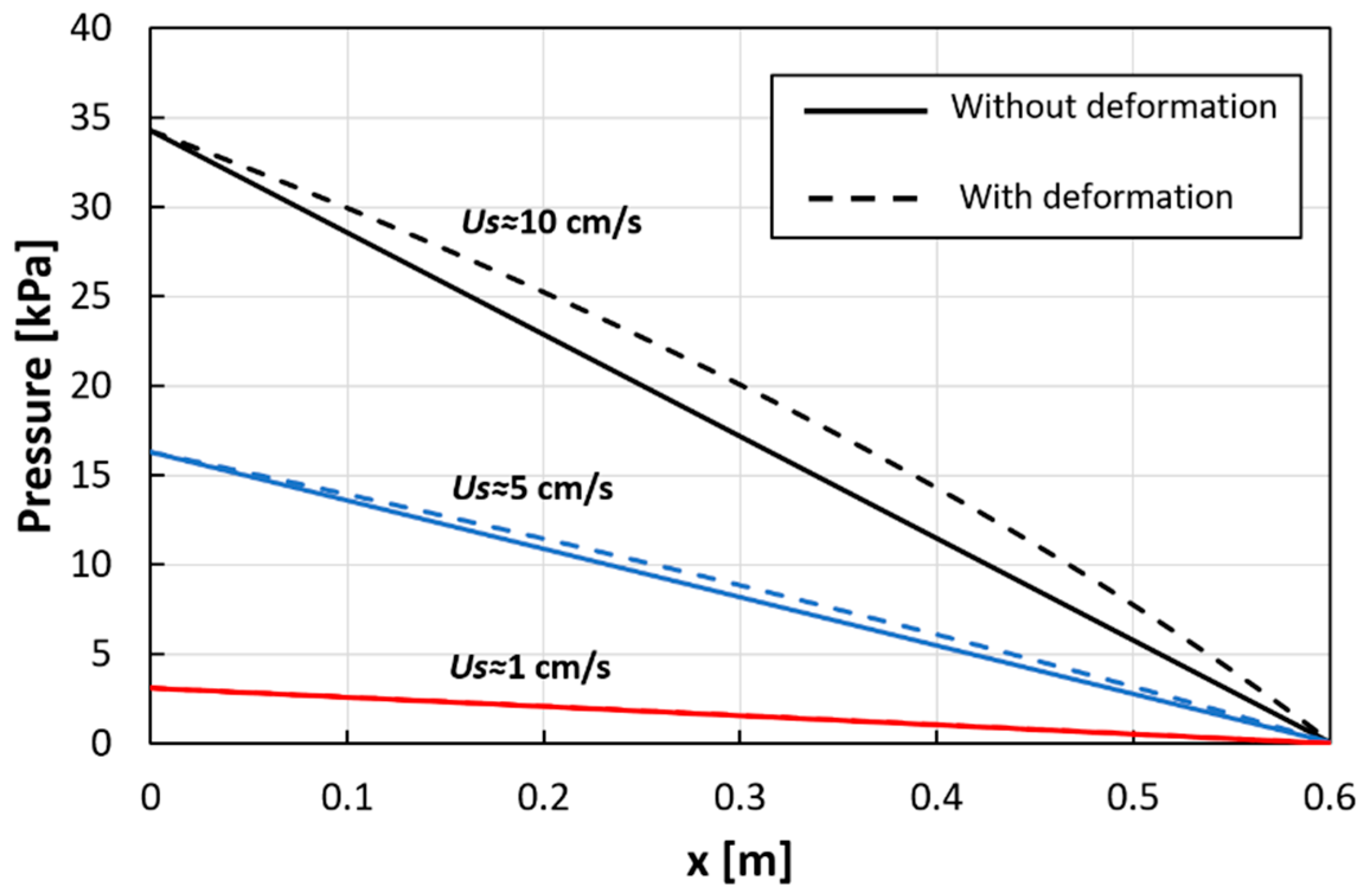
3.1.3. Pressure Profiles for All Cross Flow Cases
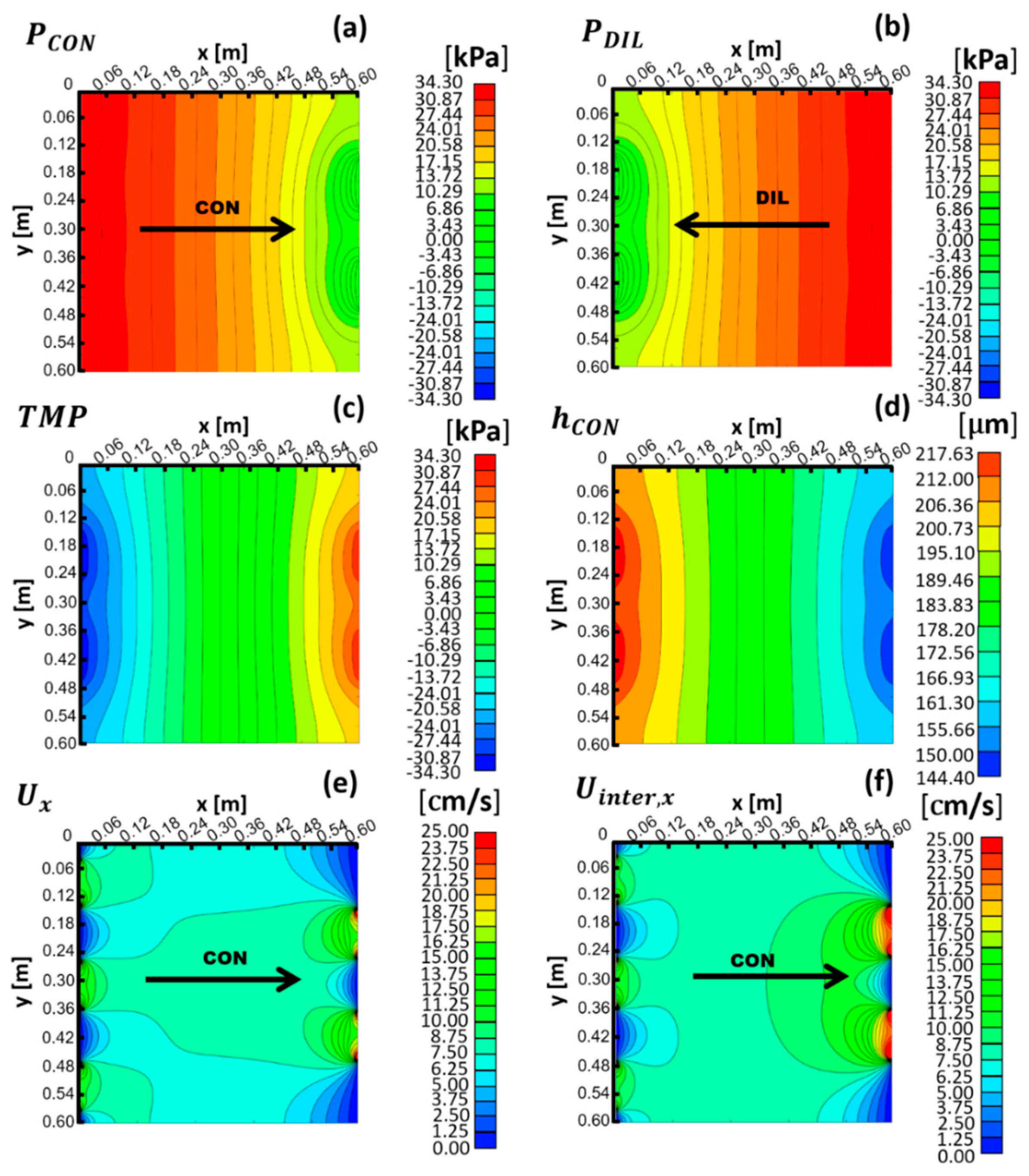
3.2. Counter Flow Arrangement
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
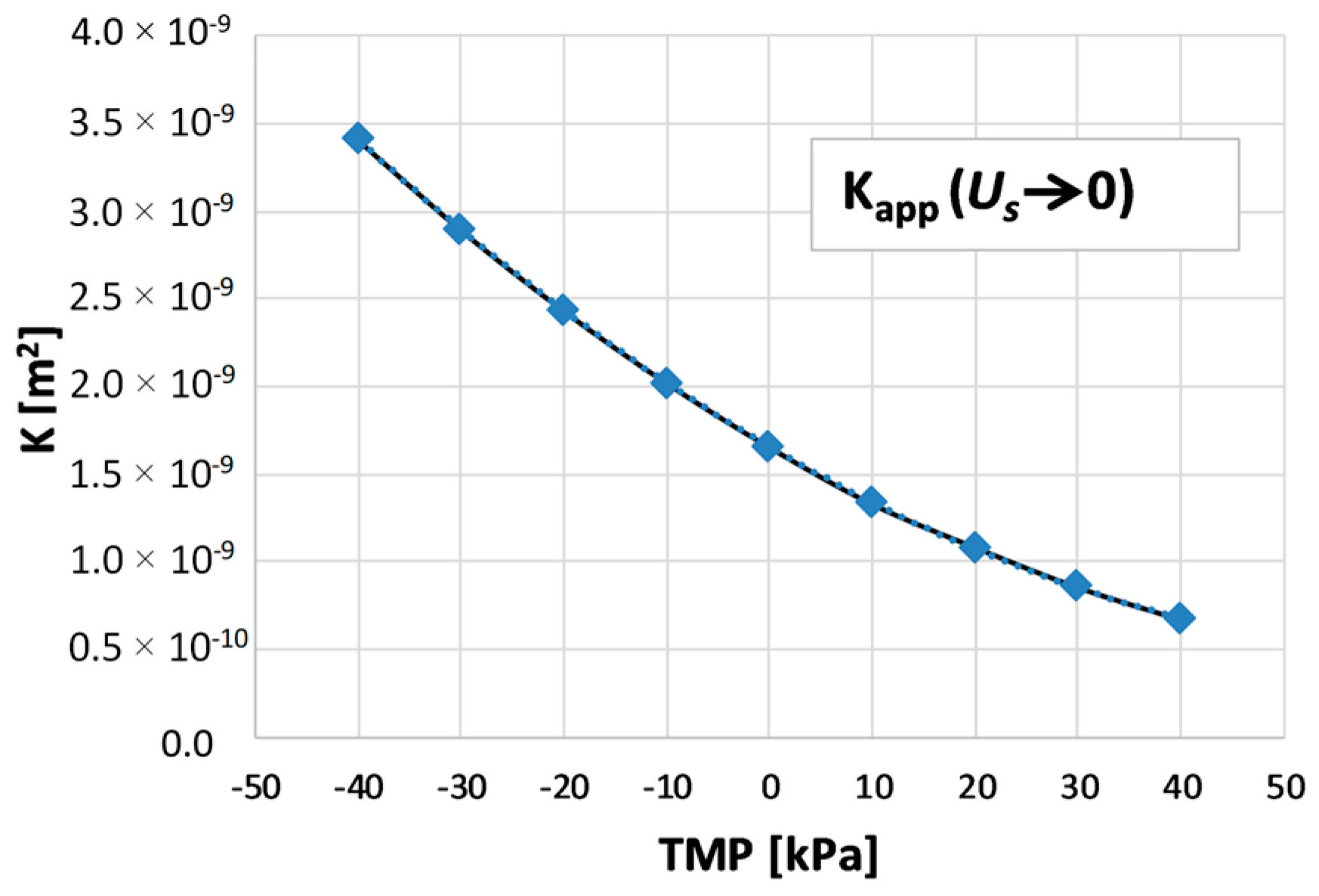
Appendix A. Dependence of Equivalent Channel Height and Channel Hydraulic Permeability on TMP
Appendix A.1. Equivalent Channel Height
| TMP [kPa] | V [mm3] | h [μm] |
|---|---|---|
| 40 | 0.349 | 136 |
| 30 | 0.376 | 147 |
| 20 | 0.404 | 158 |
| 10 | 0.432 | 169 |
| 0 | 0.462 | 180 |
| −10 | 0.491 | 192 |
| −20 | 0.521 | 203 |
| −30 | 0.550 | 215 |
| −40 | 0.579 | 226 |
Appendix A.2. Channel Permeability for Non-Darcyan Flow
| 0 < U < 3 cm/s | 3 < U < 7 cm/s | |||
|---|---|---|---|---|
| TMP [kPa] | K [m2] | a [cm/s] | K′ [m2] | a [cm/s] |
| 40 | 6.754 · 10−10 | 0 | 6.289 · 10−10 | 0.20677 |
| 30 | 8.651 · 10−10 | 0 | 8.052 · 10−10 | 0.20784 |
| 20 | 1.088 · 10−9 | 0 | 1.012 · 10−9 | 0.20885 |
| 10 | 1.356 · 10−9 | 0 | 1.261 · 10−9 | 0.20938 |
| 0 | 1.670 · 10−9 | 0 | 1.553 · 10−9 | 0.20934 |
| −10 | 2.034 · 10−9 | 0 | 1.891 · 10−9 | 0.20973 |
| −20 | 2.439 · 10−9 | 0 | 2.271 · 10−9 | 0.20753 |
| −30 | 2.893 · 10−9 | 0 | 2.693 · 10−9 | 0.20727 |
| −40 | 3.397 · 10−9 | 0 | 3.163 · 10−9 | 0.20678 |
| 7 < U < 12 cm/s | 12 < U < 20 cm/s | |||
|---|---|---|---|---|
| TMP [kPa] | K′ [m2] | a [cm/s] | K′ [m2] | a [cm/s] |
| 40 | 5.777 · 10−10 | 0.7598 | 5.169 · 10−10 | 1.9422 |
| 30 | 7.393 · 10−10 | 0.7634 | 6.612 · 10−10 | 1.9506 |
| 20 | 9.287 · 10−10 | 0.7668 | 8.302 · 10−10 | 1.9584 |
| 10 | 1.158 · 10−9 | 0.7686 | 1.034 · 10−9 | 1.9625 |
| 0 | 1.425 · 10−9 | 0.7684 | 1.274 · 10−9 | 1.9622 |
| −10 | 1.735 · 10−9 | 0.7697 | 1.551 · 10−9 | 1.9651 |
| −20 | 2.085 · 10−9 | 0.7623 | 1.865 · 10−9 | 1.9483 |
| −30 | 2.473 · 10−9 | 0.7615 | 2.213 · 10−9 | 1.9462 |
| −40 | 2.905 · 10−9 | 0.7598 | 2.600 · 10−9 | 1.9425 |
Appendix B. Grid Dependence and Validation Against CFD Results
Appendix B.1. Grid Dependence
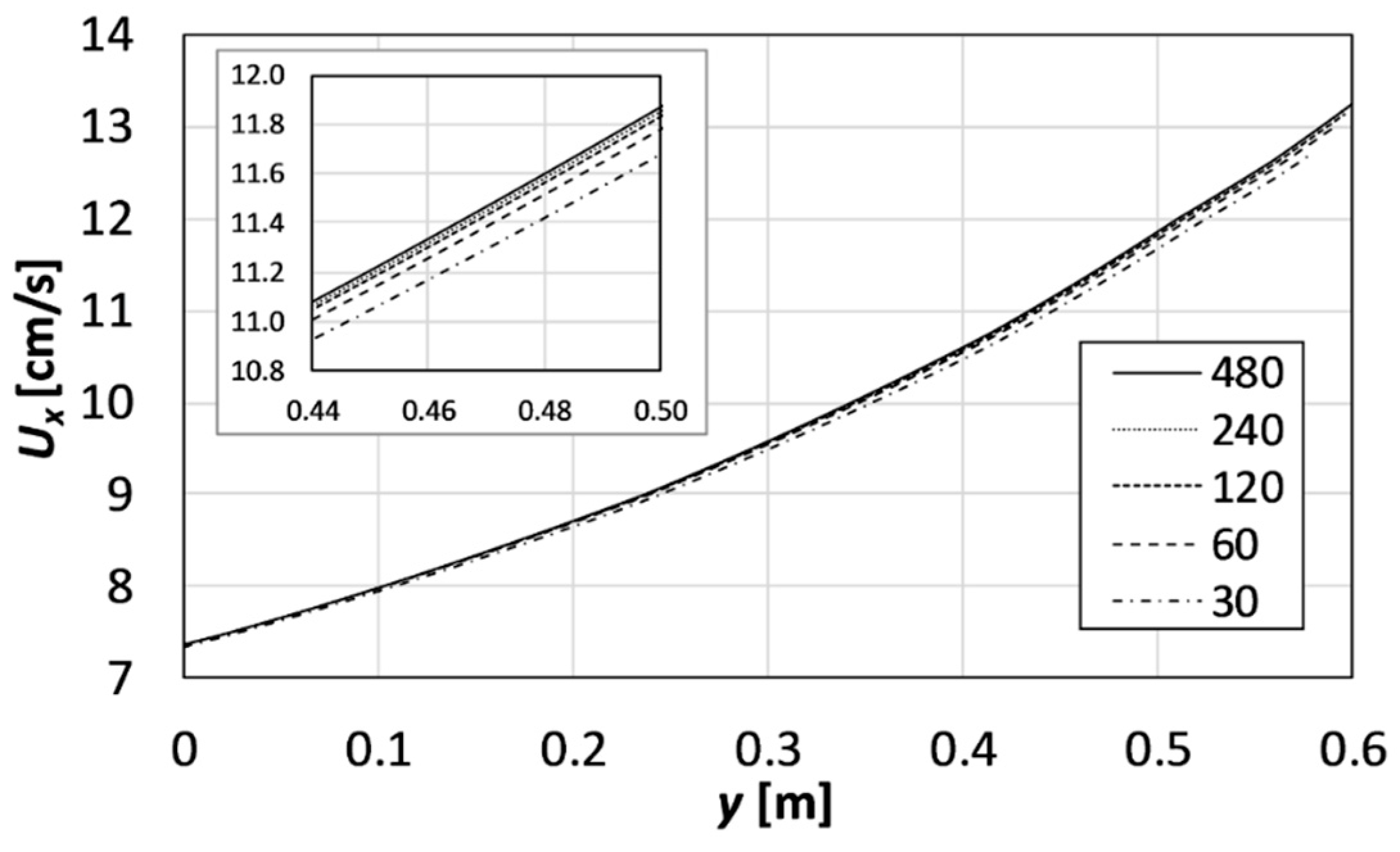
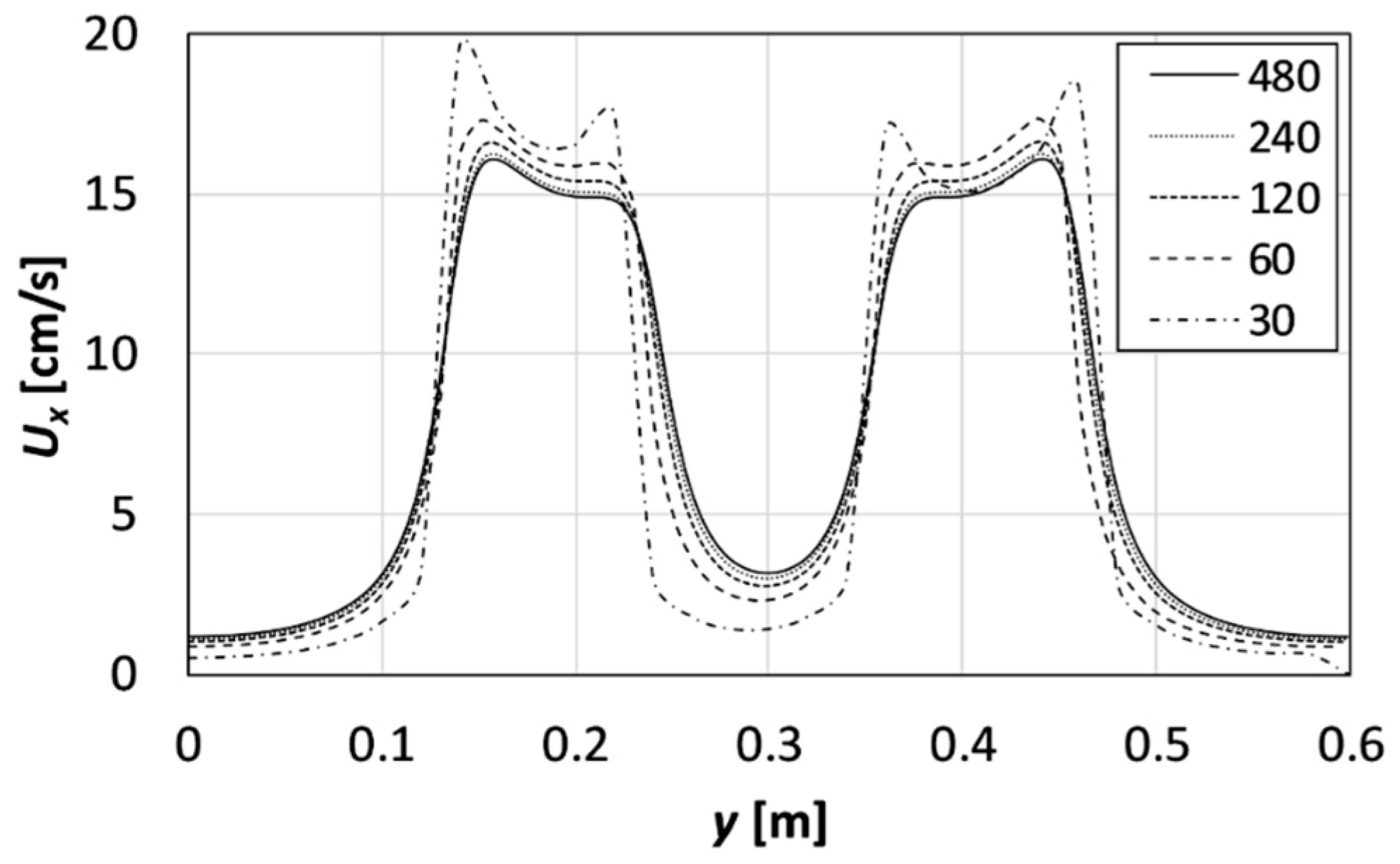
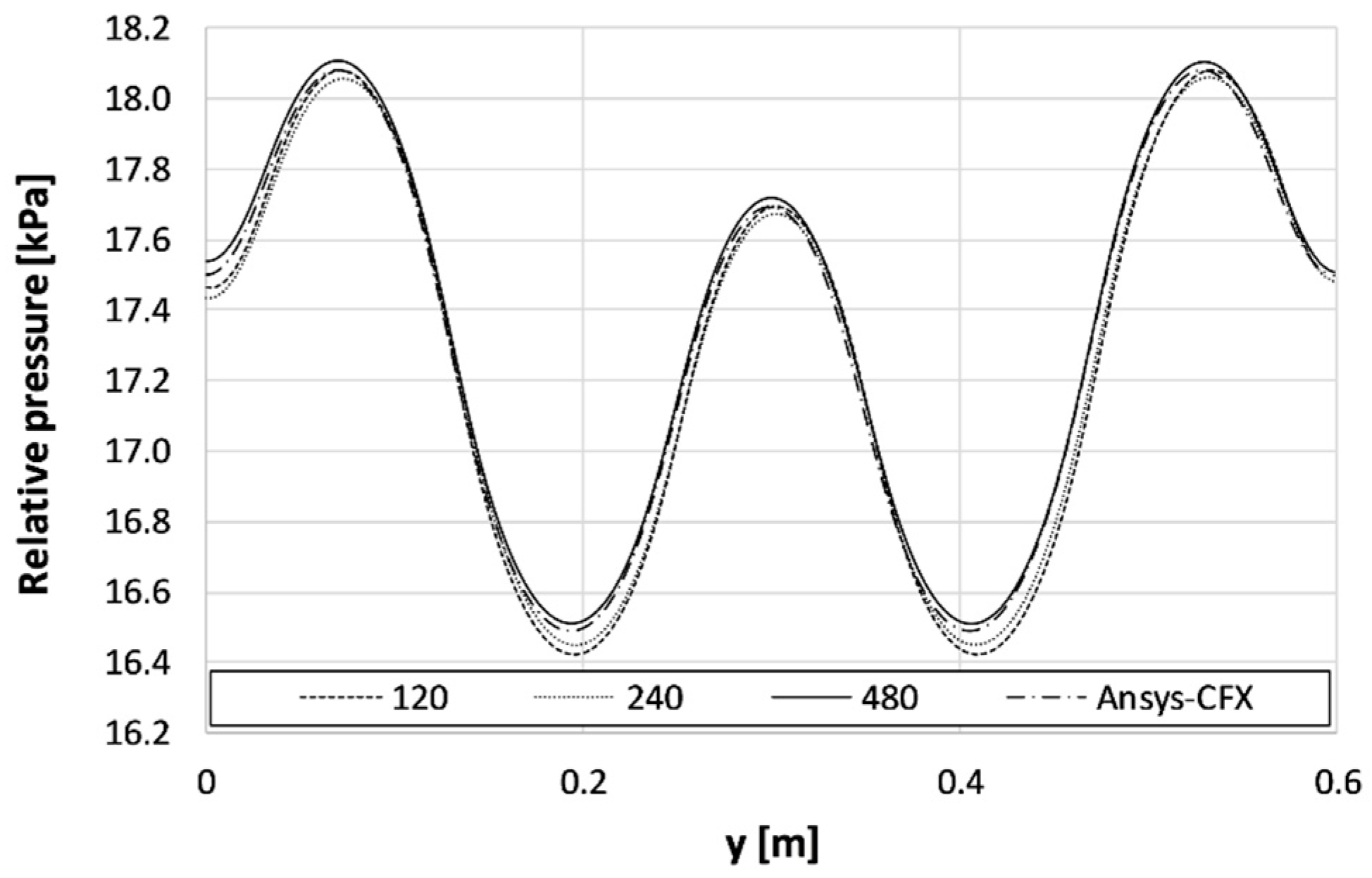
Appendix B.2. Comparison with CFD Results
- The porous media model was assumed, and steady state simulations were performed.
- Values of the permeability and of the resistance loss coefficient were determined by means of a quadratic regression of the undeformed channel characteristics (Figure 6). The permeability was set to 1.65·10−9 m2 and the resistance loss coefficient to 989 m−1.
- Free slip wall boundary conditions were set at the upper and lower walls of the channel (representative of membrane surfaces). The latter condition was imposed to avoid viscous fluid–wall interaction, which would lead to erroneous results; in fact, the friction characteristics of the membrane surfaces and profiles are already taken into account by the permeability and resistance coefficients.
- Symmetry or no slip boundary conditions were imposed at the lateral edges of the domain.
References
- Campione, A.; Gurreri, L.; Ciofalo, M.; Micale, G.; Tamburini, A.; Cipollina, A. Electrodialysis for water desalination: A critical assessment of recent developments on process fundamentals, models and applications. Desalination 2018, 434, 121–160. [Google Scholar] [CrossRef]
- Tufa, R.A.; Pawlowski, S.; Veerman, J.; Bouzek, K.; Fontananova, E.; di Profio, G.; Velizarov, S.; Goulão Crespo, J.; Nijmeijer, K.; Curcio, E. Progress and prospects in reverse electrodialysis for salinity gradient energy conversion and storage. Appl. Energy 2018, 225, 290–331. [Google Scholar] [CrossRef]
- Pawlowski, S.; Crespo, J.G.; Velizarov, S. Pressure drop in reverse electrodialysis: Experimental and modeling studies for stacks with variable number of cell pairs. J. Memb. Sci. 2014, 462, 96–111. [Google Scholar] [CrossRef]
- Pawlowski, S.; Rijnaarts, T.; Saakes, M.; Nijmeijer, K.; Crespo, J.G.; Velizarov, S. Improved fluid mixing and power density in reverse electrodialysis stacks with chevron-profiled membranes. J. Memb. Sci. 2017, 531, 111–121. [Google Scholar] [CrossRef]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G.; Ciofalo, M. CFD prediction of concentration polarization phenomena in spacer-filled channels for reverse electrodialysis. J. Memb. Sci. 2014, 468, 133–148. [Google Scholar] [CrossRef]
- La Cerva, M.; Liberto, M.D.; Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G.; Ciofalo, M. Coupling CFD with a one-dimensional model to predict the performance of reverse electrodialysis stacks. J. Memb. Sci. 2017, 541, 595–610. [Google Scholar] [CrossRef]
- Pawlowski, S.; Geraldes, V.; Crespo, J.G.; Velizarov, S. Computational fluid dynamics (CFD) assisted analysis of profiled membranes performance in reverse electrodialysis. J. Memb. Sci. 2016, 502, 179–190. [Google Scholar] [CrossRef]
- Koutsou, C.P.; Yiantsios, S.G.; Karabelas, A.J. A numerical and experimental study of mass transfer in spacer-filled channels: Effects of spacer geometrical characteristics and Schmidt number. J. Memb. Sci. 2009, 326, 234–251. [Google Scholar] [CrossRef]
- Dirkse, M.H.; van Loon, W.K.P.; Stigter, J.D.; Post, J.W.; Veerman, J.; Bot, G.P.A. Extending potential flow modelling of flat-sheet geometries as applied in membrane-based systems. J. Memb. Sci. 2008, 325, 537–545. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karabelas, A.J. On the fluid mechanics of spiral-wound membrane modules. Ind. Eng. Chem. Res. 2009, 48, 10025–10036. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karabelas, A.J. Mathematical analysis of the meso-scale flow field in spiral-wound membrane modules. Ind. Eng. Chem. Res. 2011, 50, 4653–4666. [Google Scholar] [CrossRef]
- Kodým, R.; Vlasák, F.; Šnita, D.; Černín, A.; Bouzek, K. Spatially two-dimensional mathematical model of the flow hydrodynamics in a channel filled with a net-like spacer. J. Memb. Sci. 2011, 368, 171–183. [Google Scholar] [CrossRef]
- Pánek, P.; Kodým, R.; Šnita, D.; Bouzek, K. Spatially two-dimensional mathematical model of the flow hydrodynamics in a spacer-filled channel—The effect of inertial forces. J. Memb. Sci. 2015, 492, 588–599. [Google Scholar] [CrossRef]
- She, Q.; Hou, D.; Liu, J.; Tan, K.H.; Tang, C.Y. Effect of feed spacer induced membrane deformation on the performance of pressure retarded osmosis (PRO): Implications for PRO process operation. J. Memb. Sci. 2013, 445, 170–182. [Google Scholar] [CrossRef]
- Karabelas, A.J.; Koutsou, C.P.; Sioutopoulos, D.C. Comprehensive performance assessment of spacers in spiral-wound membrane modules accounting for compressibility effects. J. Memb. Sci. 2018, 549, 602–615. [Google Scholar] [CrossRef]
- Hereijgers, J.; Ottevaere, H.; Breugelmans, T.; De Malsche, W. Membrane deflection in a flat membrane microcontactor: Experimental study of spacer features. J. Memb. Sci. 2016, 504, 153–161. [Google Scholar] [CrossRef]
- Moreno, J.; Slouwerhof, E.; Vermaas, D.A.; Saakes, M.; Nijmeijer, K. The Breathing Cell: Cyclic Intermembrane Distance Variation in Reverse Electrodialysis. Environ. Sci. Technol. 2016, 50, 11386–11393. [Google Scholar] [CrossRef]
- Park, S.-M.; Lee, S. Influence of Hydraulic Pressure on Performance Deterioration of Direct Contact Membrane Distillation (DCMD) Process. Membranes 2019, 9, 37. [Google Scholar] [CrossRef]
- Lian, B.; Blandin, G.; Leslie, G.; Le-Clech, P. Impact of module design in forward osmosis and pressure assisted osmosis: An experimental and numerical study. Desalination 2018, 426, 108–117. [Google Scholar] [CrossRef]
- Yuan, Z.; Wei, L.; Afroze, J.D.; Goh, K.; Chen, Y.; Yu, Y.; She, Q.; Chen, Y. Pressure-retarded membrane distillation for low-grade heat recovery: The critical roles of pressure-induced membrane deformation. J. Memb. Sci. 2019, 579, 90–101. [Google Scholar] [CrossRef]
- Hong, S.K.; Kim, C.S.; Hwang, K.S.; Han, J.H.; Kim, H.K.; Jeong, N.J.; Choi, K.S. Experimental and numerical studies on pressure drop in reverse electrodialysis: Effect of unit cell configuration. J. Mech. Sci. Technol. 2016, 30, 5287–5292. [Google Scholar] [CrossRef]
- Battaglia, G.; Gurreri, L.; Airò Farulla, G.; Cipollina, A.; Pirrotta, A.; Micale, G.; Ciofalo, M. Membrane Deformation and Its Effects on Flow and Mass Transfer in the Electromembrane Processes. Int. J. Mol. Sci. 2019, 20, 1840. [Google Scholar] [CrossRef] [PubMed]
- Battaglia, G.; Gurreri, L.; Airò Farulla, G.; Cipollina, A.; Pirrotta, A.; Micale, G.; Ciofalo, M. Pressure-Induced Deformation of Pillar-Type Profiled Membranes and Its Effects on Flow and Mass Transfer. Computation 2019, 7, 32. [Google Scholar] [CrossRef]
- Ciofalo, M.; Ponzio, F.; Tamburini, A.; Cipollina, A.; Micale, G. Unsteadiness and transition to turbulence in woven spacer filled channels for Membrane Distillation. J. Phys. Conf. Ser. 2017, 796, 012003. [Google Scholar] [CrossRef]
- Schock, G.; Miquel, A. Mass transfer and pressure loss in spiral wound modules. Desalination 1987, 64, 339–352. [Google Scholar] [CrossRef]
- Irmay, S. On the theoretical derivation of Darcy and Forchheimer formulas. Eos Trans. Am. Geophys. Union 1958, 39, 702–707. [Google Scholar] [CrossRef]
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Tedesco, M.; Mazzola, P.; Tamburini, A.; Micale, G.; Bogle, I.D.L.; Papapetrou, M.; Cipollina, A. Analysis and simulation of scale-up potentials in reverse electrodialysis. Desalin. Water Treat. 2014, 55, 3391–3403. [Google Scholar] [CrossRef]
- Moreno, J.; Grasman, S.; Van Engelen, R.; Nijmeijer, K. Upscaling Reverse Electrodialysis. Environ. Sci. Technol. 2018, 52, 10856–10863. [Google Scholar] [CrossRef]
- Wright, N.C.; Shah, S.R.; Amrose, S.E.; Winter, A.G. A robust model of brackish water electrodialysis desalination with experimental comparison at different size scales. Desalination 2018, 443, 27–43. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Battaglia, G.; Gurreri, L.; Cipollina, A.; Pirrotta, A.; Velizarov, S.; Ciofalo, M.; Micale, G. Fluid–Structure Interaction and Flow Redistribution in Membrane-Bounded Channels. Energies 2019, 12, 4259. https://doi.org/10.3390/en12224259
Battaglia G, Gurreri L, Cipollina A, Pirrotta A, Velizarov S, Ciofalo M, Micale G. Fluid–Structure Interaction and Flow Redistribution in Membrane-Bounded Channels. Energies. 2019; 12(22):4259. https://doi.org/10.3390/en12224259
Chicago/Turabian StyleBattaglia, Giuseppe, Luigi Gurreri, Andrea Cipollina, Antonina Pirrotta, Svetlozar Velizarov, Michele Ciofalo, and Giorgio Micale. 2019. "Fluid–Structure Interaction and Flow Redistribution in Membrane-Bounded Channels" Energies 12, no. 22: 4259. https://doi.org/10.3390/en12224259
APA StyleBattaglia, G., Gurreri, L., Cipollina, A., Pirrotta, A., Velizarov, S., Ciofalo, M., & Micale, G. (2019). Fluid–Structure Interaction and Flow Redistribution in Membrane-Bounded Channels. Energies, 12(22), 4259. https://doi.org/10.3390/en12224259










