Fractional-Order Modeling and Parameter Identification for Ultracapacitors with a New Hybrid SOA Method
Abstract
1. Introduction
- ⬤
- The model structure is connected to UC dynamic characteristics;
- ⬤
- The using of fractional order reduces the number of parameters;
- ⬤
- The resistance voltage dependence has been taken into account;
- ⬤
- The hybrid optimization algorithm improves recognition accuracy.
2. Fractional-Order Calculus
- ⬤
- Grünwald–Letnikov Definition:
- ⬤
- Riemann–Liouville Definition:
- ⬤
- Caputo definition:
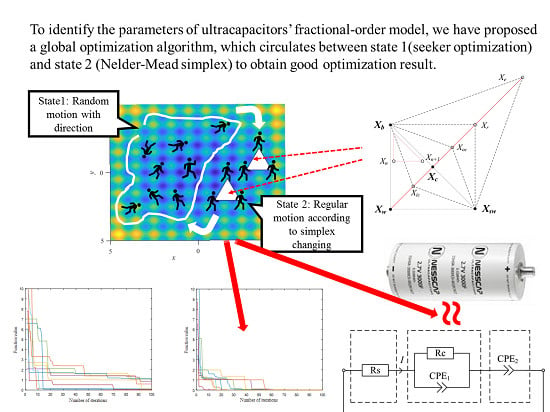
3. A New Hybrid Algorithm: NMSA
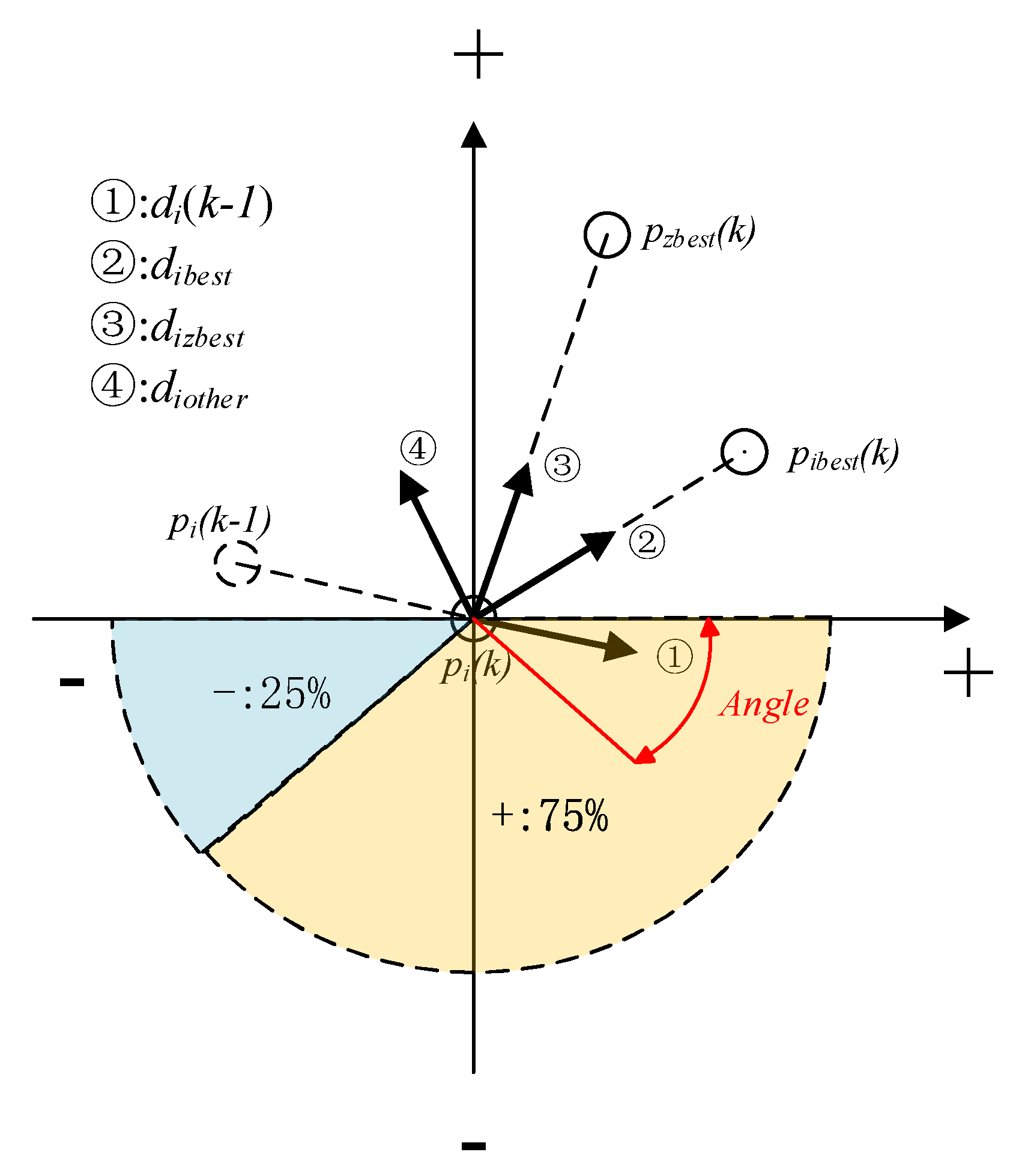
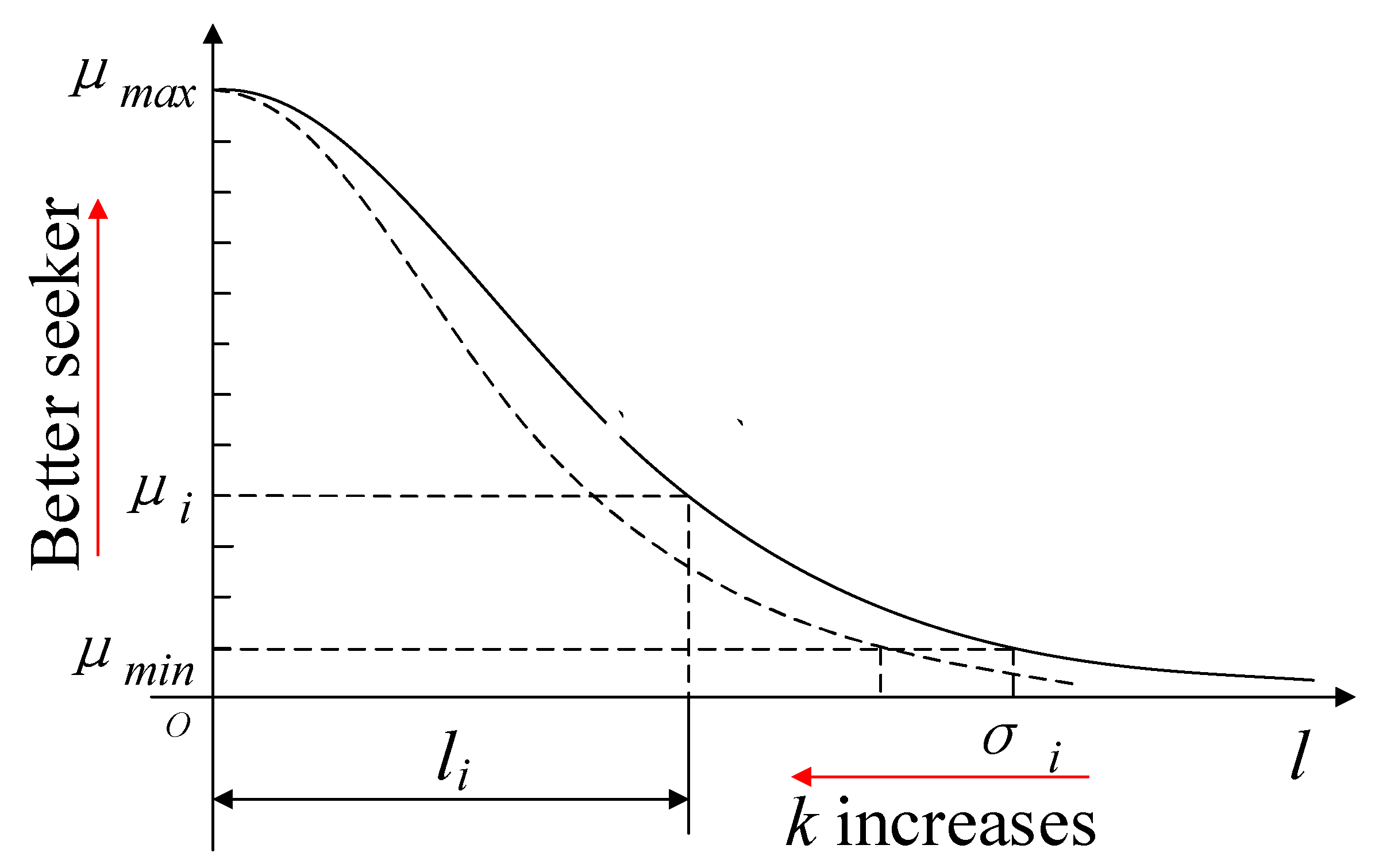
3.1. Seeker Optimization Algorithm (SOA)
3.2. Nelder–Mead Simplex Algorithm
3.3. New Hybrid SOA: NMSA
4. Modeling and Identification of UC
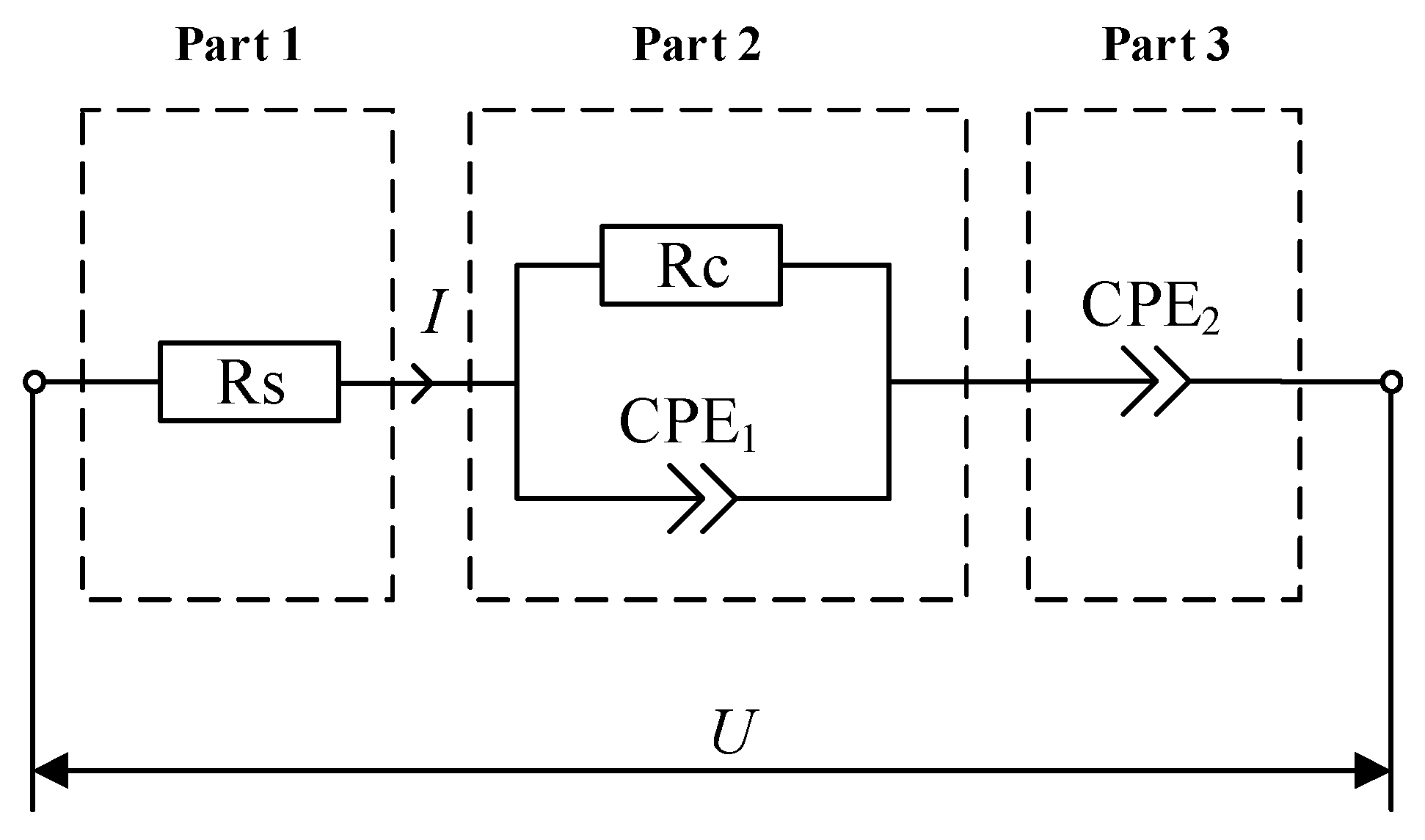
4.1. Fractional Order Modeling of UC
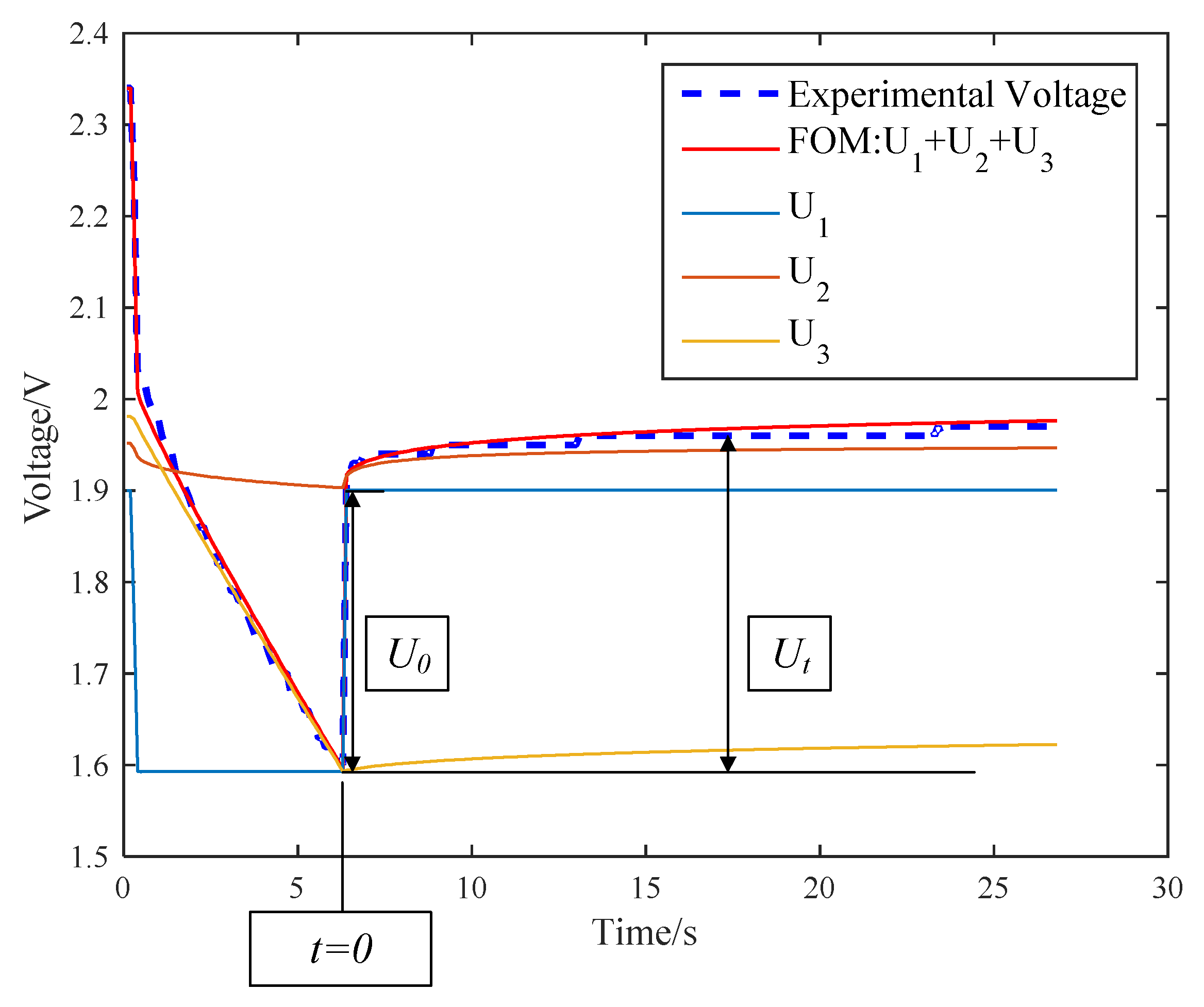
4.2. Time Domain Response Analysis of UC
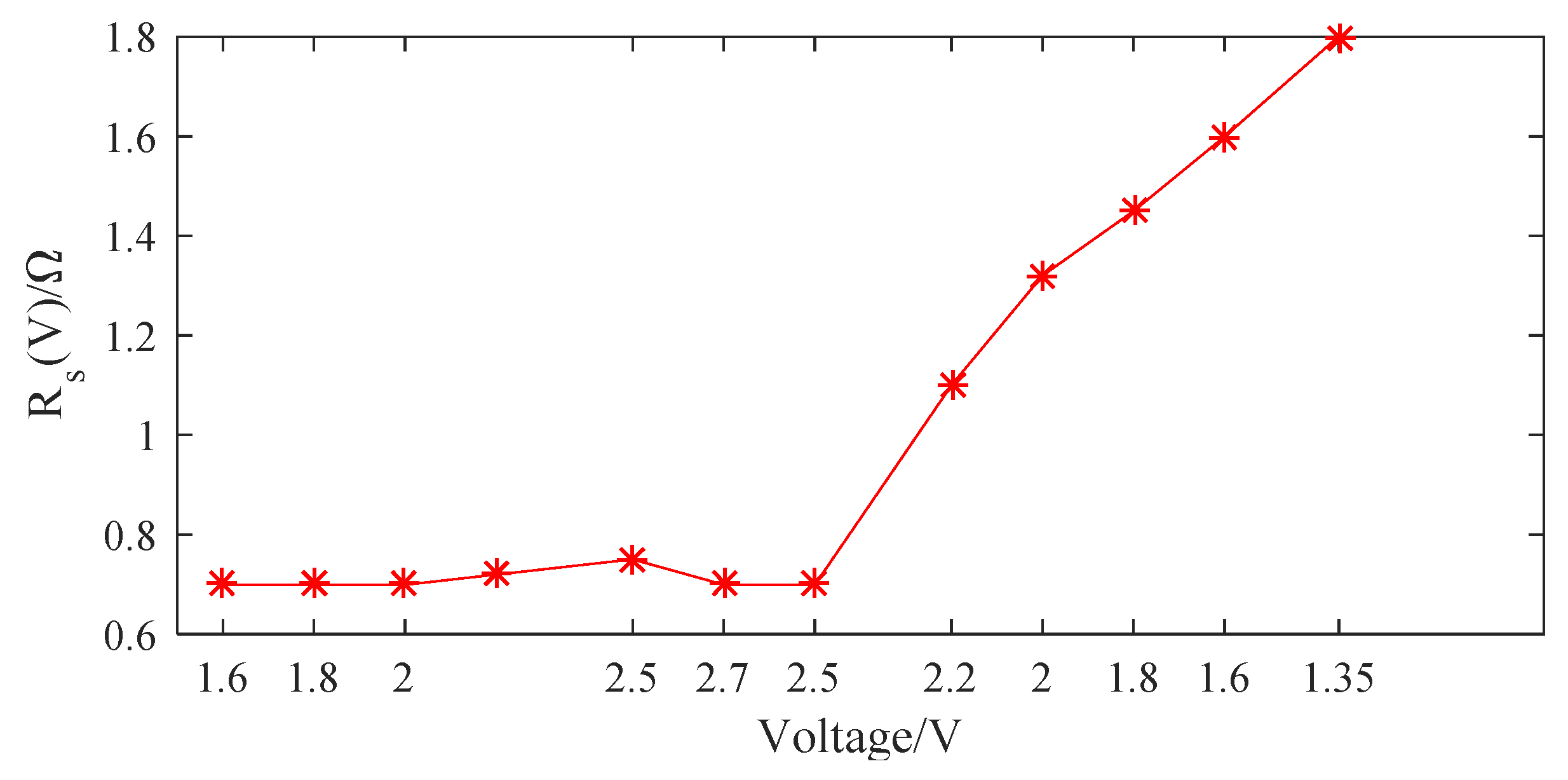
4.3. Parameter Estimation in Time Domain
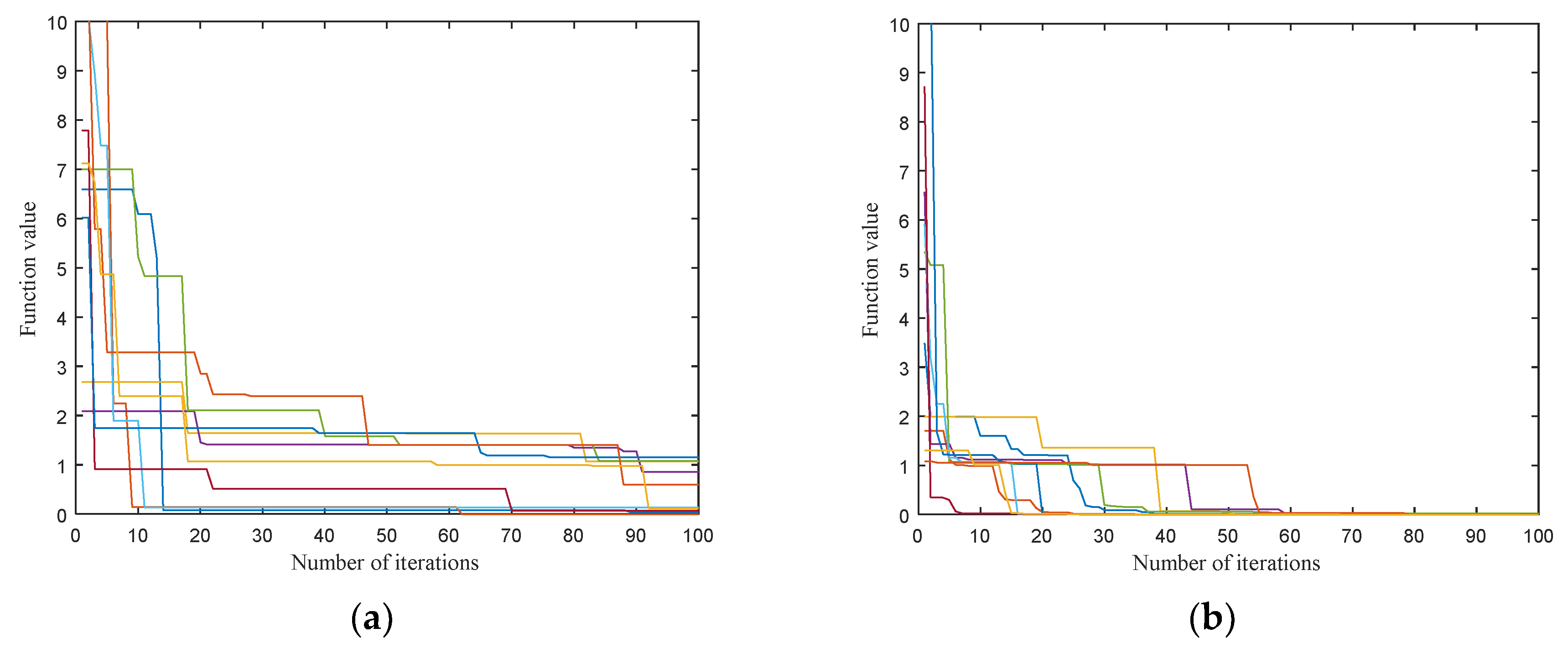
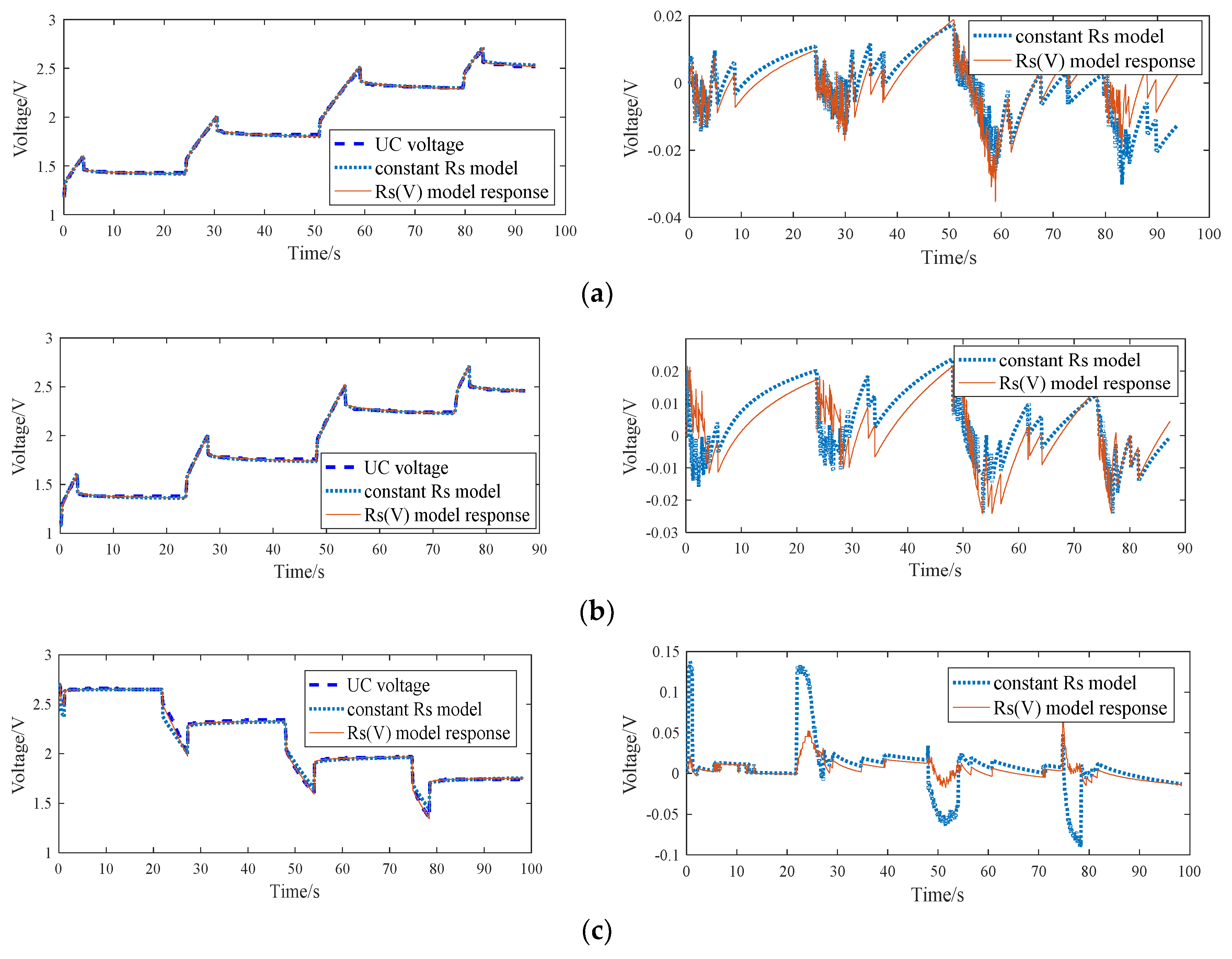
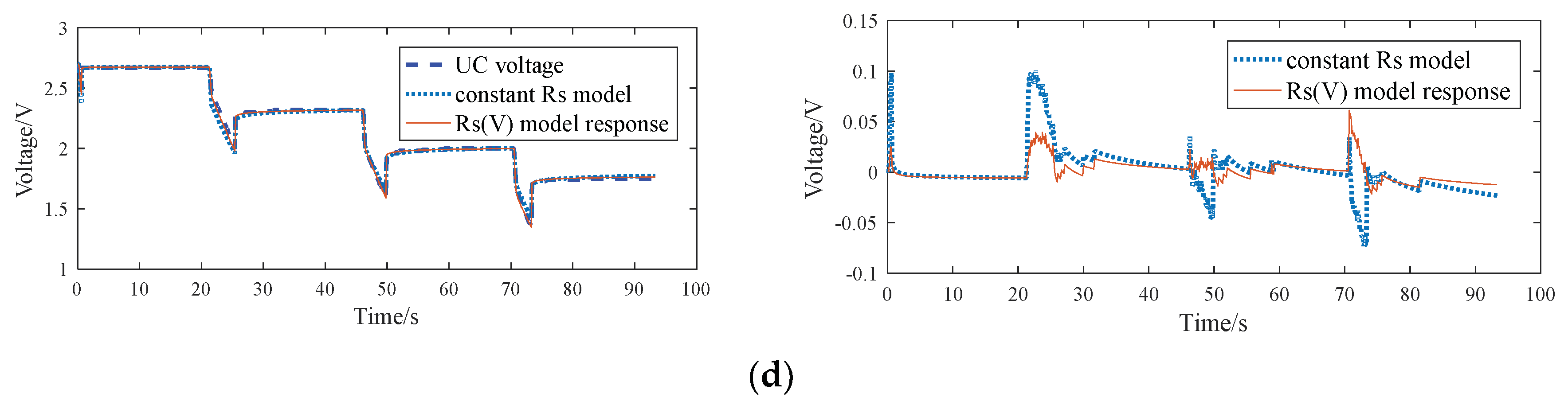
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kurra, N.; Jiang, Q.; Alshareef, H.N. A general strategy for the fabrication of high performance microsupercapacitors. Nano Energy 2015, 16, 1–9. [Google Scholar] [CrossRef]
- Ladrón de Guevara, A.; Boscá, A.; Pedrós, J.; Climent-Pascual, E.; de Andrés, A.; Calle, F.; Martínez, J. Reduced Graphene oxide/polyaniline electrochemical supercapacitors fabricated by laser. Appl. Surf. Sci. 2019, 467, 691–697. [Google Scholar] [CrossRef]
- Conway, B.E. Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications, 1st ed.; Springer Science & Business Media: New York, NY, USA, 2013; pp. 11–31. [Google Scholar]
- Oldham, K.B. A Gouy–Chapman–Stern model of the double layer at a (metal)/(ionic liquid) interface. J. Electroanal. Chem. 2008, 613, 131–138. [Google Scholar] [CrossRef]
- Staser, J.A.; Weidner, J.W. Mathematical modeling of hybrid asymmetric electrochemical capacitors. J. Electrochem. Soc. 2014, 161, E3267–E3275. [Google Scholar] [CrossRef]
- Eddahech, A.; Ayadi, M.; Briat, O.; Vinassa, J.-M. Multilevel neural-network model for supercapacitor module in automotive applications. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 1460–1465. [Google Scholar]
- Zhu, S.; Li, J.; Ma, L.; He, C.; Liu, E.; He, F.; Shi, C.; Zhao, N. Artificial neural network enabled capacitance prediction for carbon-based supercapacitors. Mater. Lett. 2018, 233, 294–297. [Google Scholar] [CrossRef]
- Ma, H.; Wang, B.; Liu, K.R. Distributed Signal Compressive Quantization and Parallel Interference Cancellation for Cloud Radio Access Network. IEEE Trans. Commun. 2018, 66, 4186–4198. [Google Scholar] [CrossRef]
- Spyker, R.L.; Nelms, R.M. Classical equivalent circuit parameters for a double-layer capacitor. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 829–836. [Google Scholar] [CrossRef]
- Zubieta, L.; Bonert, R. Characterization of double-layer capacitors for power electronics applications. IEEE Trans. Ind. Applicat. 2000, 36, 199–205. [Google Scholar] [CrossRef]
- Itagaki, M.; Suzuki, S.; Shitanda, I.; Watanabe, K.; Nakazawa, H. Impedance analysis on electric double layer capacitor with transmission line model. J. Power Sources 2007, 164, 415–424. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Fractional-order models of supercapacitors, batteries and fuel cells: A survey. Mater. Renew. Sustain. Energy 2015, 4, 9. [Google Scholar] [CrossRef]
- Bertrand, N.; Sabatier, J.; Briat, O.; Vinassa, J.-M. Embedded fractional nonlinear supercapacitor model and its parametric estimation method. IEEE Trans. Ind. Electron. 2010, 57, 3991–4000. [Google Scholar]
- Li, M.; Liu, X. The least squares based iterative algorithms for parameter estimation of a bilinear system with autoregressive noise using the data filtering technique. Signal Process. 2018, 147, 23–34. [Google Scholar] [CrossRef]
- Ding, F.; Chen, H.; Xu, L.; Dai, J.; Li, Q.; Hayat, T. A hierarchical least squares identification algorithm for Hammerstein nonlinear systems using the key term separation. J. Frankl. Inst. 2018, 355, 3737–3752. [Google Scholar] [CrossRef]
- Spendley, W.; Hext, G.R.; Himsworth, F.R. Sequential application of simplex designs in optimisation and evolutionary operation. Technometrics 1962, 4, 441–461. [Google Scholar] [CrossRef]
- Nazareth, L.; Tseng, P. Gilding the lily: A variant of the Nelder-Mead algorithm based on golden-section search. Comput. Optim. Appl. 2002, 22, 133–144. [Google Scholar] [CrossRef]
- Sun, J.; Zhao, J.; Wu, X.; Fang, W.; Cai, Y.; Xu, W. Parameter estimation for chaotic systems with a drift particle swarm optimization method. Phys. Lett. A 2010, 374, 2816–2822. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. Fractional-order modeling and State-of-Charge estimation for ultracapacitors. J. Power Sources 2016, 314, 28–34. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Parameter estimation for chaotic systems by hybrid differential evolution algorithm and artificial bee colony algorithm. Nonlinear Dyn. 2014, 77, 61–71. [Google Scholar] [CrossRef]
- Dai, C.; Chen, W.; Cheng, Z.; Li, Q.; Jiang, Z.; Jia, J. Seeker optimization algorithm for global optimization: A case study on optimal modelling of proton exchange membrane fuel cell (PEMFC). J. Electr. Power 2011, 33, 369–376. [Google Scholar] [CrossRef]
- Ketabi, A.; Sheibani, M.R.; Nosratabadi, S.M. Power quality meters placement using seeker optimization algorithm for harmonic state estimation. J. Electr. Power 2012, 43, 141–149. [Google Scholar] [CrossRef]
- Kumar, M.R.; Deepak, V.; Ghosh, S. Fractional-order controller design in frequency domain using an improved nonlinear adaptive seeker optimization algorithm. Turk. J. Electr. Eng. Comput. 2017, 25, 4299–4310. [Google Scholar] [CrossRef]
- Ross, B. A brief history and exposition of the fundamental theory of fractional calculus. In Fractional Calculus and Its Applications, 1st ed.; Ross, B., Ed.; Springer: Berlin, German, 1975; Volume 457, pp. 1–36. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications, 1st ed.; Springer Science & Business Media: London, UK, 2010; pp. 9–34. [Google Scholar]
- Dzieliński, A.; Sierociuk, D.; Sarwas, G. Some applications of fractional order calculus. Bull. Pol. Acad. Sci. Tech. Sci. 2010, 58, 583–592. [Google Scholar] [CrossRef]
- Mühlenbein, H.; Schomisch, M.; Born, J. The parallel genetic algorithm as function optimizer. Parallel Comput. 1991, 17, 619–632. [Google Scholar] [CrossRef]
- Thomas, B. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms, 1st ed.; Oxford University Press: New York, NY, USA, 1996; pp. 137–159. [Google Scholar]
- Xue, D.; Bai, L. Numerical algorithms for Caputo fractional-order differential equations. Int. J. Control 2017, 90, 1201–1211. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, Y.; Burke, A.F. Performance testing of supercapacitors: Important issues and uncertainties. J. Power Sources 2017, 363, 327–340. [Google Scholar] [CrossRef]
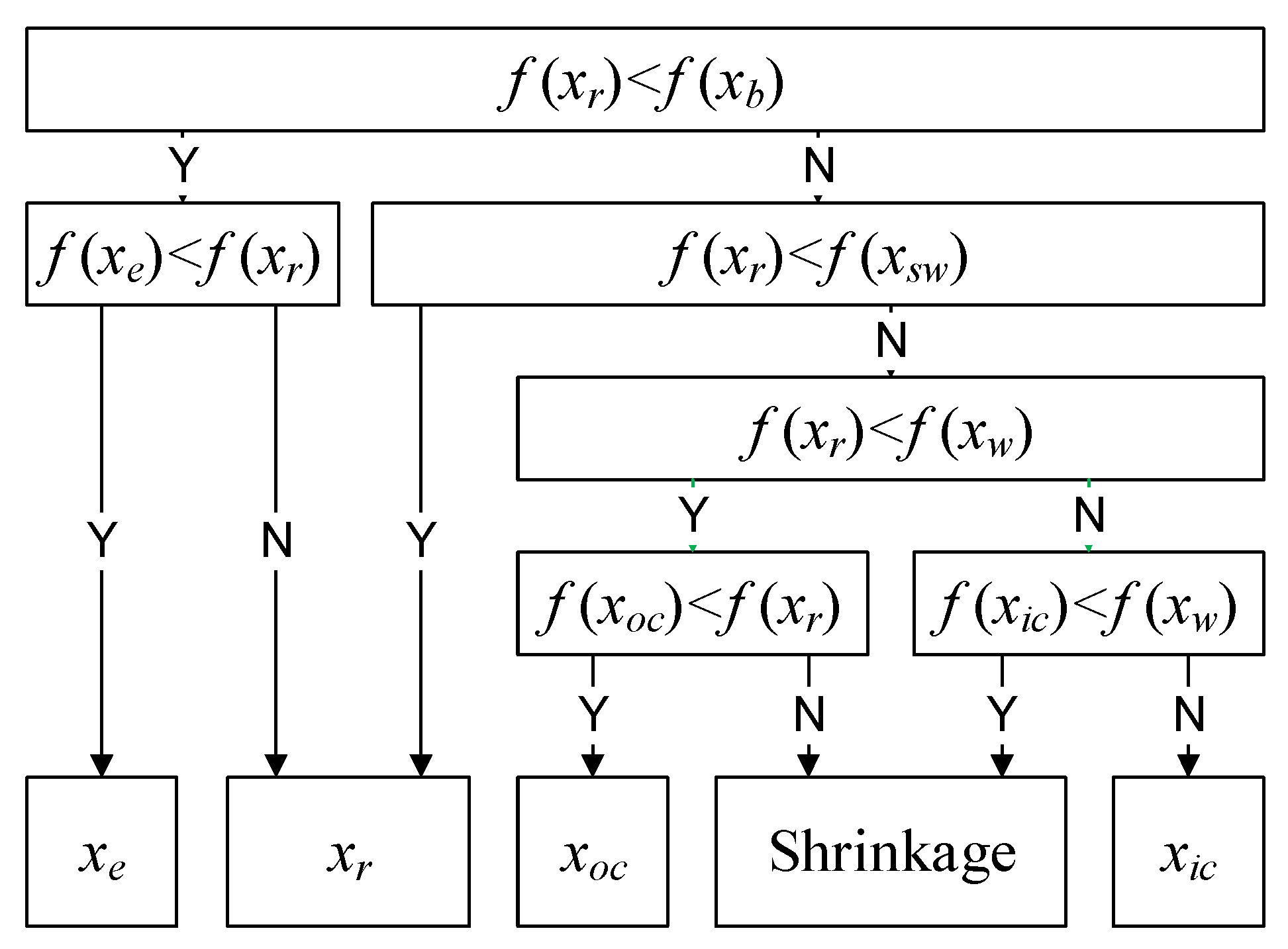
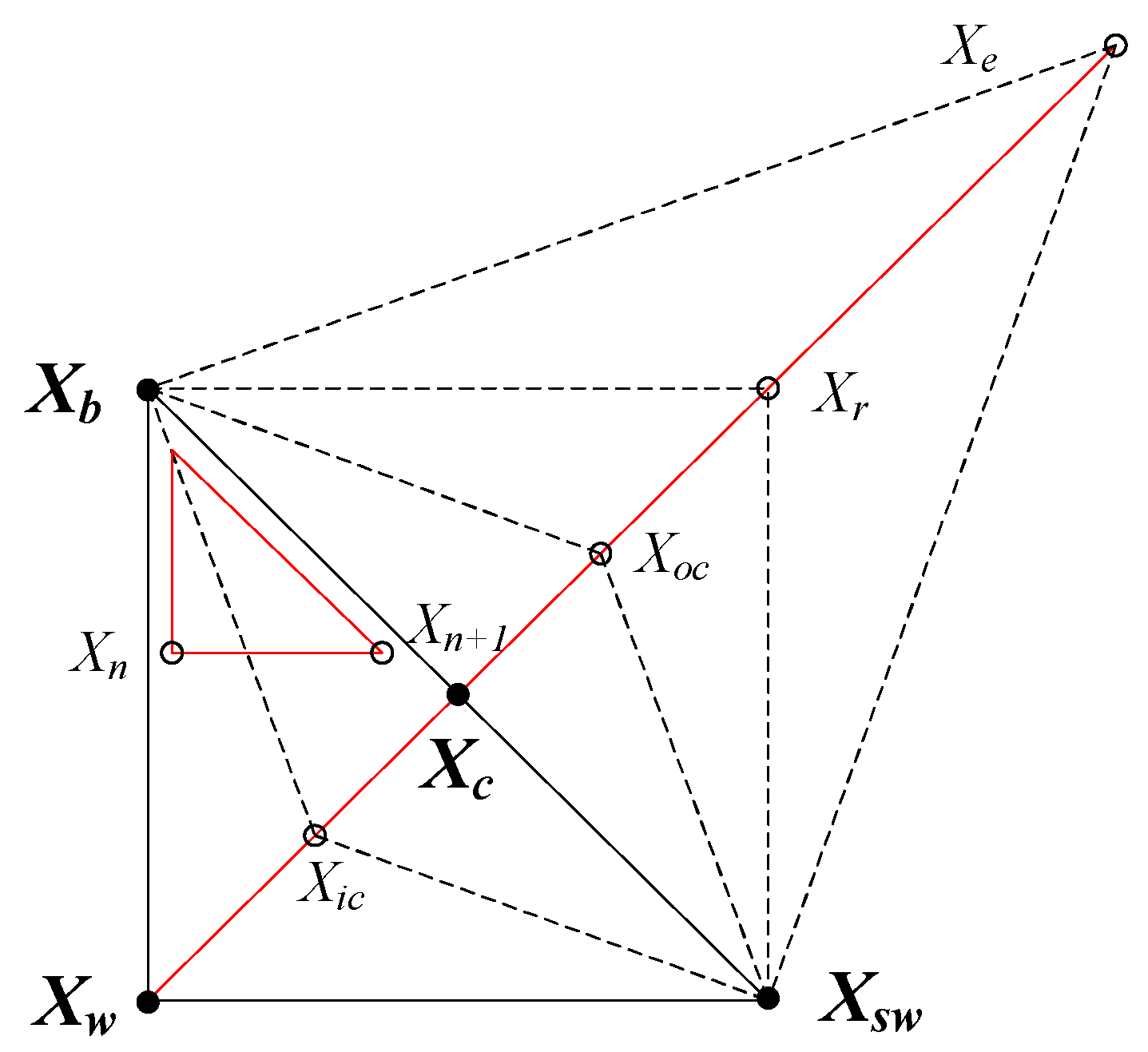
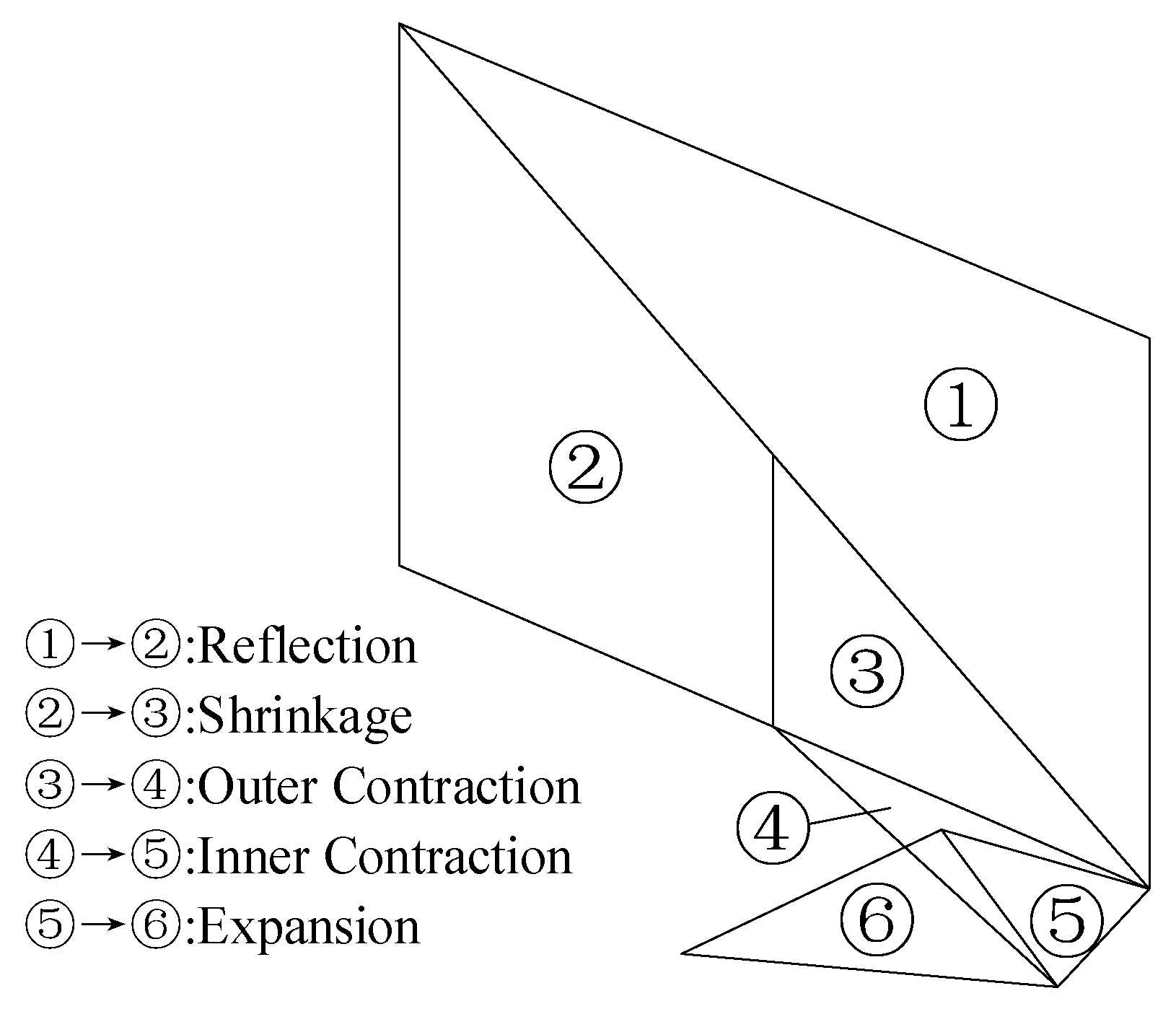
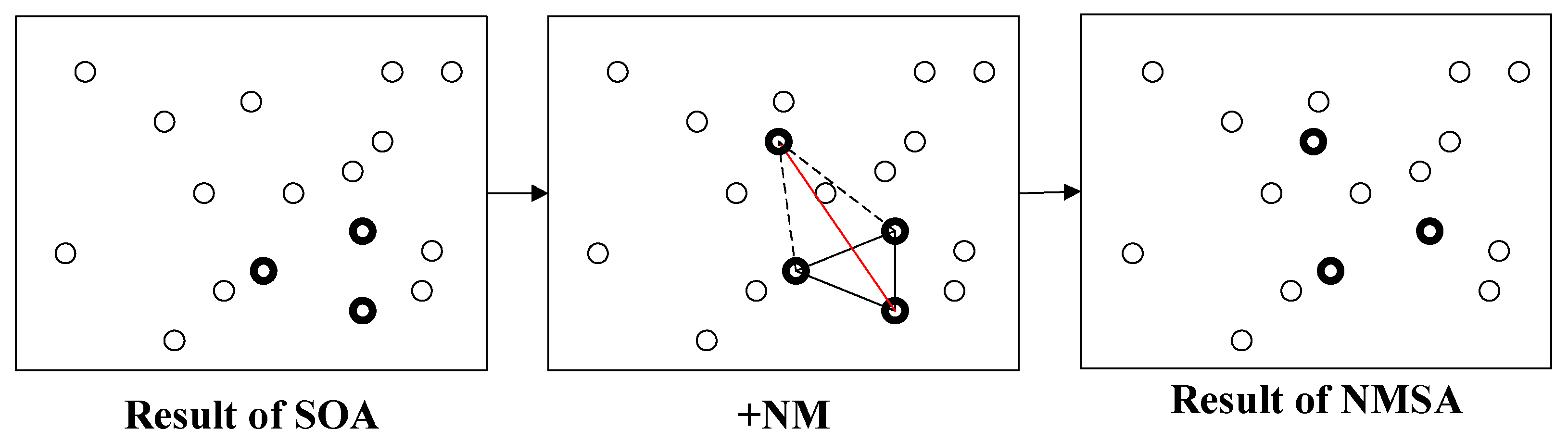
| Basis | Candidate | ||
|---|---|---|---|
| Best vertex | Reflection point | ||
| Second worst vertex | Expansion point | ||
| Worst vertex | Outer contraction point | ||
| Centroid | Inner contraction point | ||
| Shrinkage points | |||
| (+8.8432E−3, −1.1794E−2) | +4.3093E−2 | (+1.1729E−3, +6.7883E−3) | +9.4136E−3 |
| (−2.0045E−3, −2.9132E−3) | +2.4808E−3 | (−4.1521E−3, +3.3201E−5) | +3.4204E−3 |
| (−1.0142E00, −6.2758E−3) | +1.0763E00 | (−4.3177E−4, −1.2294E−3) | +3.3684E−4 |
| (+6.6242E−2, −5.0537E−3) | +8.6317E−1 | (+2.7027E−3, −7.0799E−3) | +1.1392E−2 |
| (+1.0154E00, −6.6096E−3) | +1.0867E00 | (−9.5493E−3, +3.2802E−3) | +2.0220E−2 |
| (+2.1976E−2, −1.4773E−2) | +1.3893E−1 | (+2.2814E−3, +6.8896E−4) | +1.1267E−3 |
| (−1.7572E−2, +8.4259E−3) | +7.5280E−2 | (−2.1941E−3, −2.5050E−2) | +4.4583E−3 |
| (−9.7707E−1, −2.2125E−2) | +1.1553E00 | (−3.0697E−4, +2.6148E−3) | +1.3751E−3 |
| (−2.0418E−2, −5.1174E−2) | +5.9771E−1 | (−5.7813E−4, −1.8963E−3) | +7.7976E−4 |
| (+2.3927E−2, +2.9333E−3) | +1.1507E−1 | (−9.8208E−4, +1.1038E−4) | +1.9376E−4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Liu, W.; Chu, L.; Zhao, J. Fractional-Order Modeling and Parameter Identification for Ultracapacitors with a New Hybrid SOA Method. Energies 2019, 12, 4251. https://doi.org/10.3390/en12224251
Guo J, Liu W, Chu L, Zhao J. Fractional-Order Modeling and Parameter Identification for Ultracapacitors with a New Hybrid SOA Method. Energies. 2019; 12(22):4251. https://doi.org/10.3390/en12224251
Chicago/Turabian StyleGuo, Jianhua, Weilun Liu, Liang Chu, and Jingyuan Zhao. 2019. "Fractional-Order Modeling and Parameter Identification for Ultracapacitors with a New Hybrid SOA Method" Energies 12, no. 22: 4251. https://doi.org/10.3390/en12224251
APA StyleGuo, J., Liu, W., Chu, L., & Zhao, J. (2019). Fractional-Order Modeling and Parameter Identification for Ultracapacitors with a New Hybrid SOA Method. Energies, 12(22), 4251. https://doi.org/10.3390/en12224251