Mobilized Mohr-Coulomb and Hoek-Brown Strength Parameters during Failure of Granite in Alxa Area in China for High-Level Radioactive Waste Disposal

1. Introduction

Granite is considered as one of the most important types of host rock for geological disposal of high-level radioactive waste (HLW) [1,2,3,4,5,6,7,8,9]. An appropriate modelling on the mechanical behavior of granite is of great importance for site selection and design of the repository [9,10,11,12,13]. Specially, it should be noted that the heat induced by the nuclear waste may have considerable influences on the mechanical behavior of the host rock, so the thermal effect cannot be ignored [8,12,14,15,16,17].

There have been extensive studies on the mechanical behaviors of the host rock for HLW disposal [1,9,18,19,20,21,22]. In many studies, simultaneously mobilized Mohr-Coulomb strength parameters (cohesion and friction angle) were used in the modelling of the underground excavation [23,24,25,26,27]. In order to describe the plastic strain softening behavior of the rock, they assumed that both cohesion and friction angle degrade from the initial value to the residual value with the increasing plastic strain, and piecewise linear models were usually adopted [23,24,25,26,27]. However, based on a series of theoretical analyses and laboratory experimental studies on cohesive soil, granite, marble, limestone, etc., it has been found that the geo-materials always show non-simultaneous mobilization of strength components, i.e., cohesion will be degraded and friction angle will be enhanced with the increasing damage or plastic strain during the failure process [26,28,29,30,31,32,33,34,35]. This is owing to the development of cracks inside the rock decreases the cohesive strength, while the induced crack surfaces make the frictional strength increases [26,29,36]. Accordingly, the cohesion weakening friction strengthening (CWFS) model was proposed, and this model with linear equations was used for modelling the failure process of URL Mine-by tunnel [26,29,36]. A comparison study shows that CWFS model can capture the failure extent and depth of failure (DOF) of this circular excavation better than the other widely used models such as elastic model, elastic-perfectly plastic model, elastic-brittle model, etc. [26]. Thereafter, more linear CWFS models are used in the researches and give reasonable simulations on the stability of underground openings, pillars, as well as the process of crack propagation [30,37,38,39]. Nonetheless, it was pointed out that the linear CWFS model may result in a problematic behavior of the stress – strain curves, and a fitted non-linear CWFS model with smooth curves was proposed, which was proved to be able to capture the gradual damage process better [31]. More recently, reference [40] proposed the guidelines for the parameters selection for CWFS modelling analysis of excavations. Up to date, the concept of CWFS analyses has widely been accepted in modelling the failure of brittle rocks.

However, the studies on the mobilization of strength parameters mainly focused on the Mohr-Coulomb criterion. As an actual fact, Hoek-Brown criterion is also widely used in the modelling of field rock engineering [41,42]. There were some studies using piecewise linear models with simultaneous mobilization of Hoek-Brown strength parameters ($m$ and $s$) to analyze rock behaviors [23,24,26,43]. Nevertheless, according to the above-mentioned analyses on the non-simultaneous mobilization of cohesion and friction angle, we should notice whether the Hoek-Brown strength parameters may also be mobilized non-simultaneously during the damage and failure process of rock. If the answer is yes, what is the characteristics of this mobilization? What is the relationship between the mobilized Hoek-Brown strength parameters and the rock damage or plastic strain? This has not been investigated in the published researches, and it is required to conduct a detailed study.

In the recent several decades, extensive field and laboratory researches have been carried out in the site selection of HLW disposal in China [1,2,4,10,15,20,22,44,45]. Alxa candidate area in Inner Mongolia is one of the three candidate areas with large volume of granitic rock. Figure 1 presents the location of Alxa area with two sub-areas (TMS and NRG), as well as the main geological structures around this area. More detailed information about Alxa area has been provided in reference [1]. Field investigations on the outcrops have been conducted and four boreholes (named as TMS01, TMS02, NRG01 and NRG02) with the depth of 600 m have been drilled. Laboratory experiments on the cored samples have also been carried out for studying the mechanical properties of the rock. These researches show that the granite around NRG01 borehole shows the best rock mass quality in Alxa candidate area [1]. Nonetheless, further studies should still be conducted on NRG01 granite samples with coarse grains for a better modelling on the mechanical behaviors. What is the characteristics of the mobilization of cohesion and friction angle for NRG01 granite samples? How will the heat produced by the nuclear waste affect the mechanical behavior of NRG01 granite samples during the damage and failure process? Will the mobilization of Hoek-Brown strength parameters occur for NRG01 granite samples in a simultaneous or non-simultaneous way? Is there any suitable equations to describe this mobilization? What is the mechanism?

Based on a series of systematic uniaxial and tri-axial compression experiments on NRG01 granite samples treated by different temperatures, mobilization of both Mohr-Coulomb and Hoek-Brown strength parameters have been analyzed in details. This paper is organized as follows: In Section 2, the physical and mechanical properties of the samples, the experimental setup and methods will be introduced. The experimental results will be presented in Section 3. Section 4 will provide the systematic data analyses and discussions on both the mobilization of Mohr-Coulomb and Hoek-Brown strength parameters during the failure process of NRG01 granite samples under different heat treatments. Based on the above-mentioned analyses and discussions, some conclusions will be drawn in Section 5.

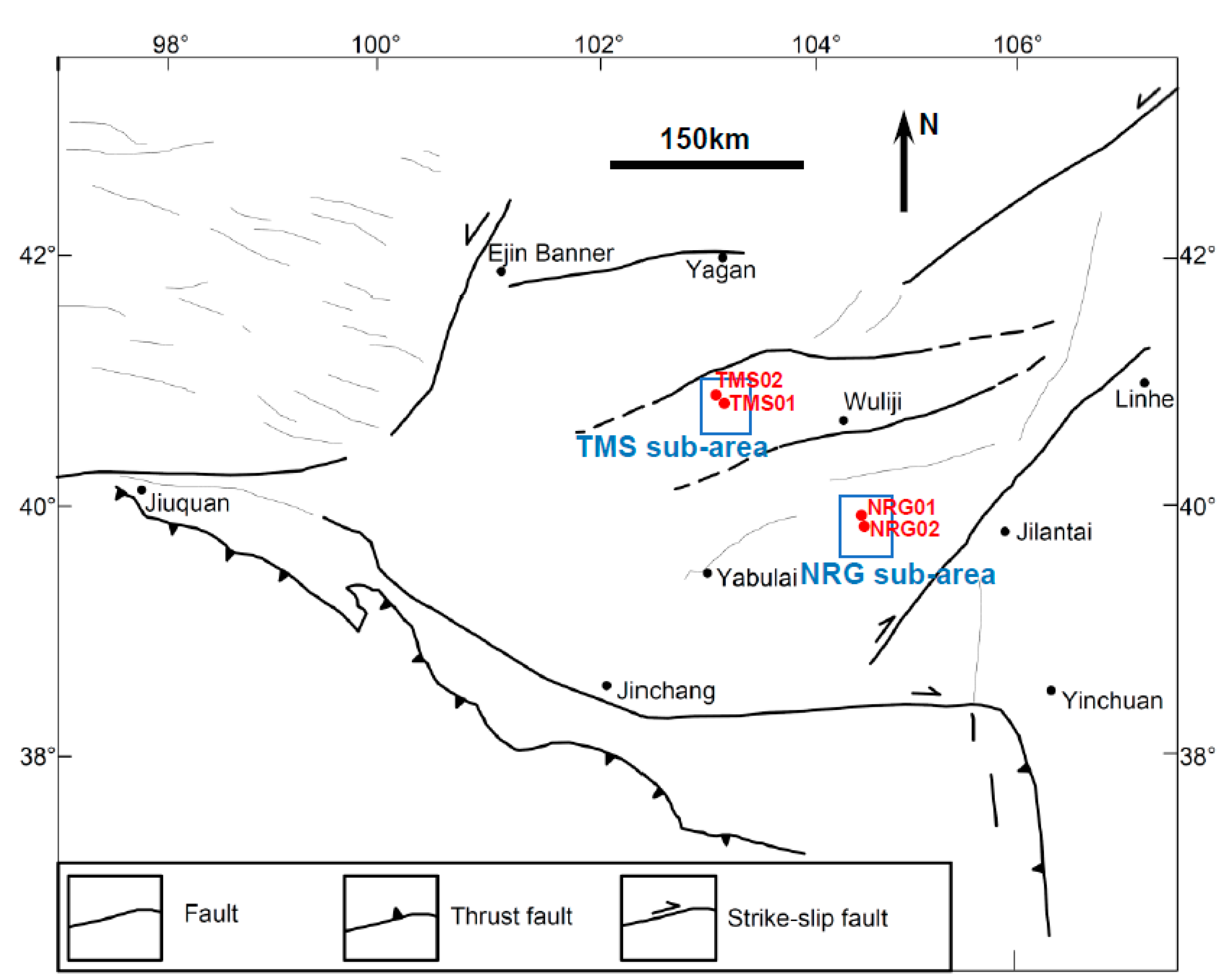
2. Samples and Experimental Methods

NRG01 granite samples treated by different temperatures are used to conduct a series of uniaxial and tri-axial compression tests with various confining pressures. The obtained stress-strain data will be used for analyzing the mobilization of strength components during the brittle failure of granite considering the thermal effect.

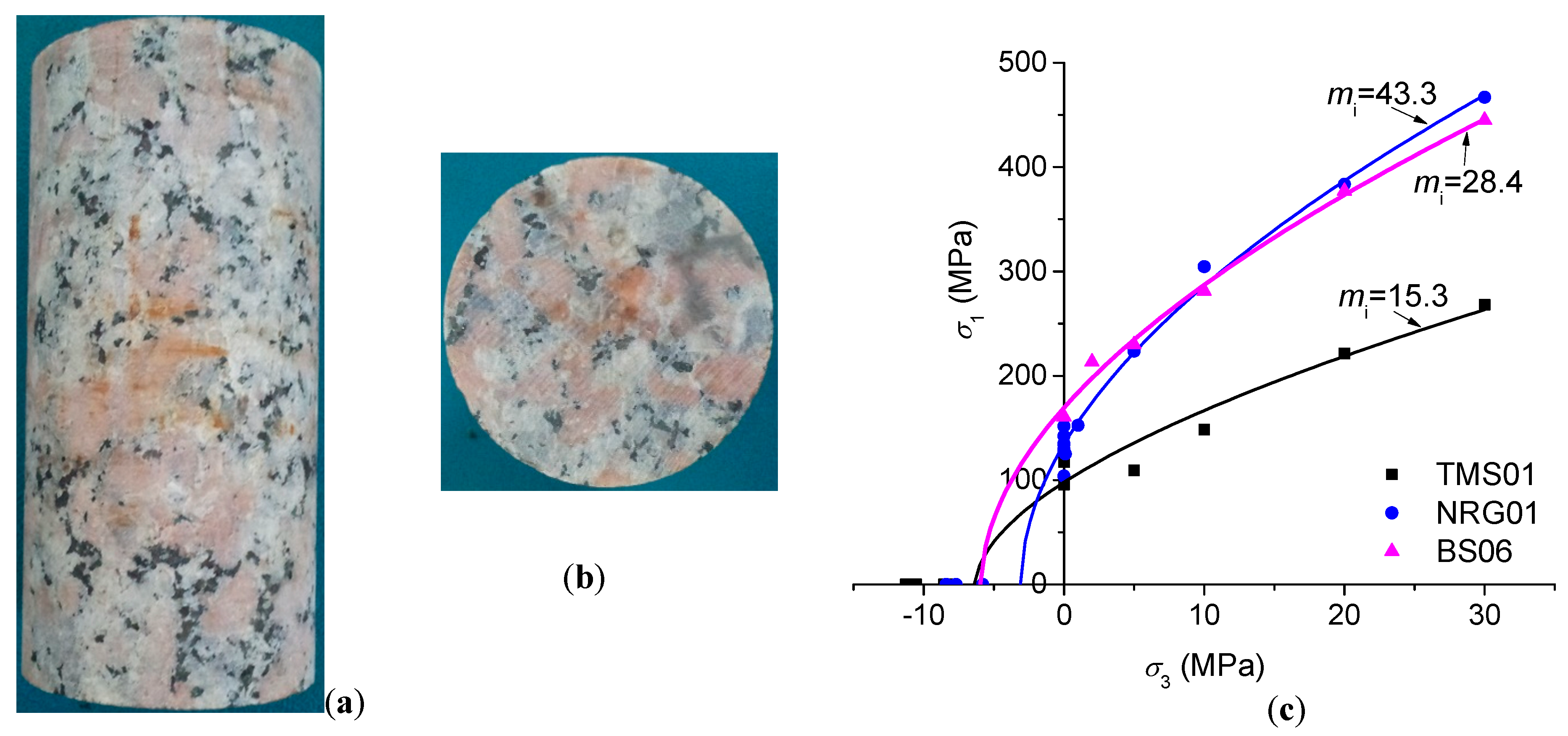
2.1. Samples

The granite samples are cored from NRG01 borehole, which is one of the four 600 m-deep boreholes in Alxa area. According to the field investigations on the corresponding outcrops, RQD analyses on the drilling cores, as well as the mechanical experiments on the cored specimens in laboratory, NRG01 samples show the best structural and strength quality and thus are selected to be used for further studies [1].

The pink samples are cored from the depth of 500–600 m. The typical samples are presented in Figure 2a,b. It can be found that the samples are heterogeneous and have coarse particles. According to the observation on thin sections under polarized microscopy, the mineral contents and the grain sizes of NRG01 granite samples are analyzed and listed in

Table 1. Mineral contents and grain sizes of NRG01 granite samples (based on [47]).

Minerals	Contents	Grain Sizes (mm)
alkali feldspar	45%	2.0–8.0
plagioclase	18%	1.3–3.0
quartz	25%	1.5–4.0
biotite	12%	0.8–1.5

[47]. Based on the mineral components, the samples should be named as biotite syenogranite. Nevertheless, they are still called as granite samples in this paper for simplicity. Figure 2c shows a comparison on the strength values of different granite samples under various confining pressures. Apparently, NRG01 samples have higher strength than TMS01 granite samples cored from TMS01 borehole in TMS sub-area (shown in Figure 1) of Alxa candidate area. Compared with BS06 granite samples cored from Beishan candidate area in Gansu Province [48], NRG01 samples show a little lower strength under lower confinements (σ₃ = 0–10 MPa), while a little higher strength under higher confinements (σ₃ > 10 MPa). Based on peak strength values fitted with linear Mohr-Coulomb criterion, NRG01 granite samples have the cohesion of 20.1 MPa, and internal friction angle of 57.5°. Hoek-Brown criterion is also used to analyze the data, and the non-linear Hoek-Brown fitting curve is shown in Figure 2c.

2.2. Experimental Methods

A series of cylindrical NRG01 granite samples are well prepared (listed in

Table 2. Design for the tests under different confinements and heat treatment.

NO.	Length (mm)	Diameter (mm)	Density (g/mm3)	Confinement (MPa)	Temperature (°C)
N1-20	100.17	49.55	2.64	0	20
N1-14	100.13	49.51	2.65	5	20
N1-29	99.67	49.99	2.63	10	20
N1-7	100.31	49.99	2.65	20	20
N1-23	100.09	49.46	2.64	5	20
N1-77	100.39	50.17	2.63	0	100
N1-83	100.32	50.03	2.63	5	100
N1-85	100.15	50.02	2.65	10	100
N1-88	100.28	50.14	2.64	20	100
N1-92	100.45	50.11	2.64	30	100
N1-79	100.49	50.21	2.65	0	200
N1-82	100.32	49.74	2.64	5	200
N1-87	100.37	50.13	2.63	10	200
N1-89	100.45	49.72	2.64	20	200
N1-93	98.79	50.14	2.65	30	200

) for uniaxial and tri-axial compression experiments under various confining pressures (σ₃ = 0, 5, 10, 20, and 30 MPa). Concerning the heat produced by the high-level radioactive waste during the long-term disposal period, the effect of temperature should also be considered in this study. According to an extensive review on the conceptual design of repositories [7,49,50,51,52], the temperature applied on the host rock will be no higher than 100 °C–120 °C. Consequently, this study focuses on the range from 20 °C (room temperature) to 200 °C.

The specimens are firstly heated in a heating cabinet to the designed temperatures as shown in Table 2. The heating rate is set as 2 °C/min. When the target temperatures are reached, the heat treated samples are used for a series of uniaxial and tri-axial compression experiments with the TAW2000 servo-control tri-axial compression test system in Key Laboratory of Shale Gas and Geoengineeirng, Chinese Academy of Sciences. It should be noted that the rock specimens cannot remain their treatment temperatures as there is not a heating system during the compression tests. The confining pressures are applied to the target values as presented in Table 2, followed by the axial loading at a constant strain rate of 1.0 × 10⁻⁵·s⁻¹. During each test, the axial and lateral strain are both measured with a set of extensometers, and the axial stress is obtained according to the axial load monitored by a force sensor. Consequently, the axial stress – axial strain curve and axial stress—lateral strain curve can be recorded for each test, and the failure characteristics of the specimens will also be observed after the experiments are completed.

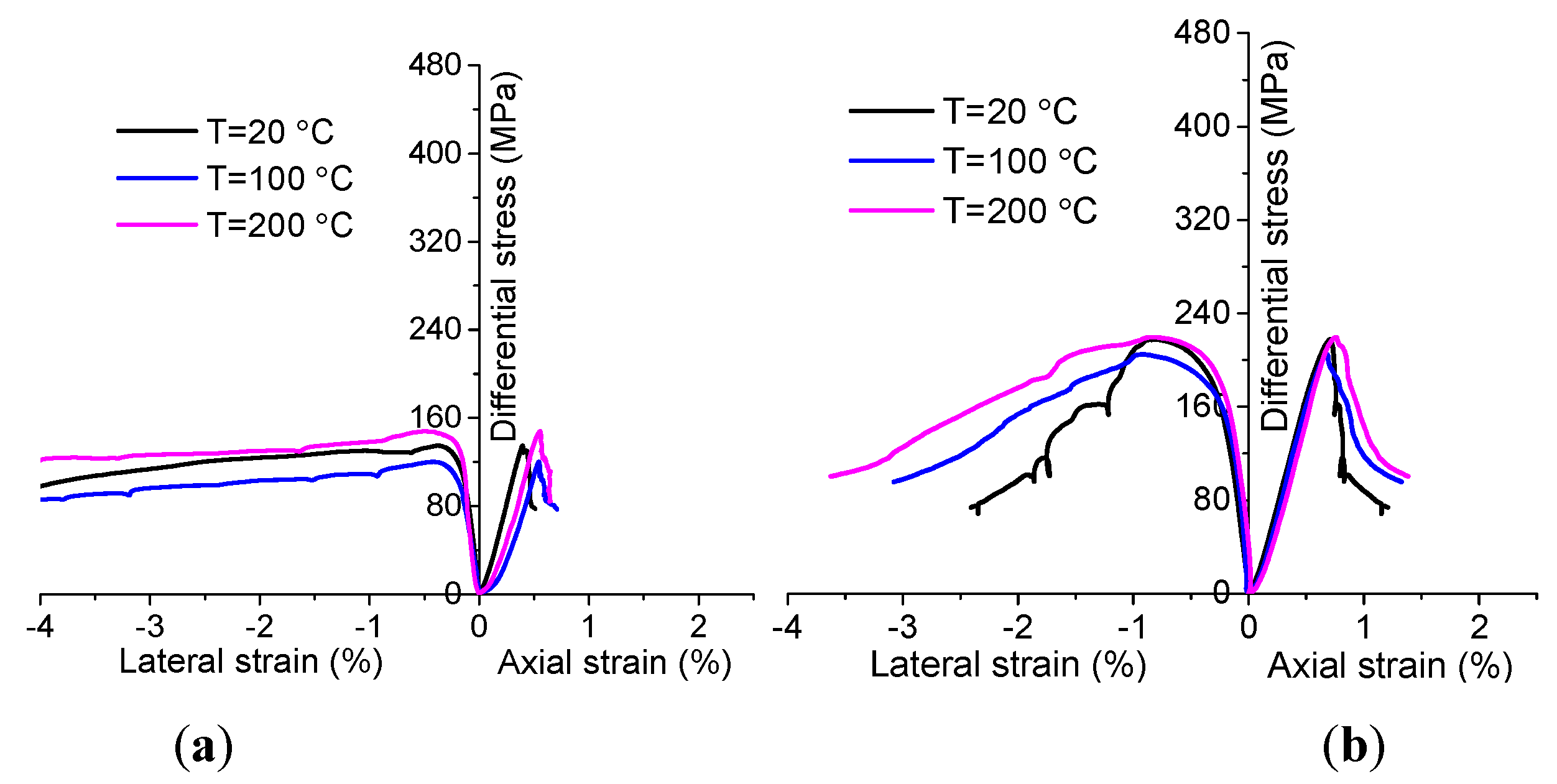
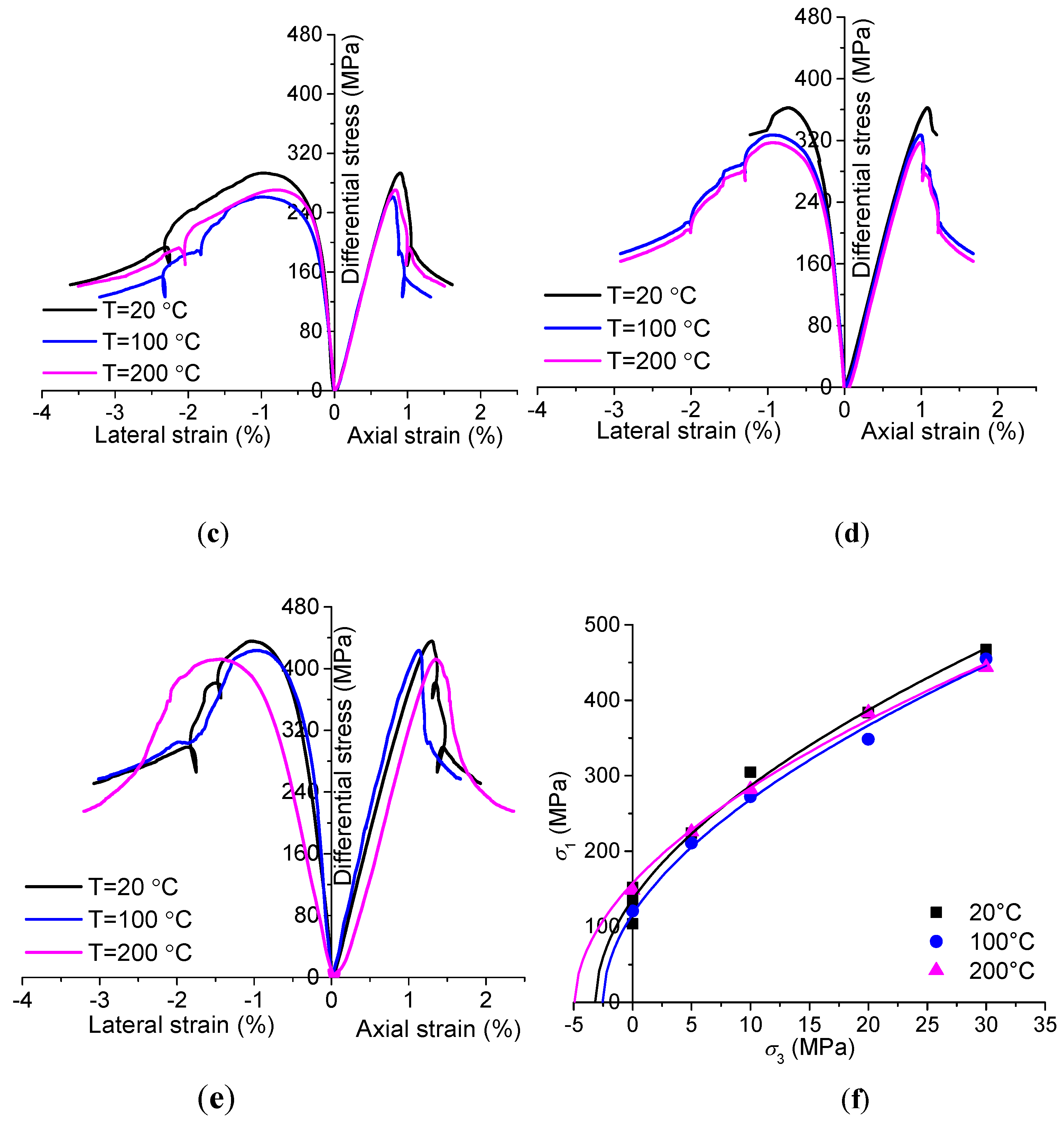
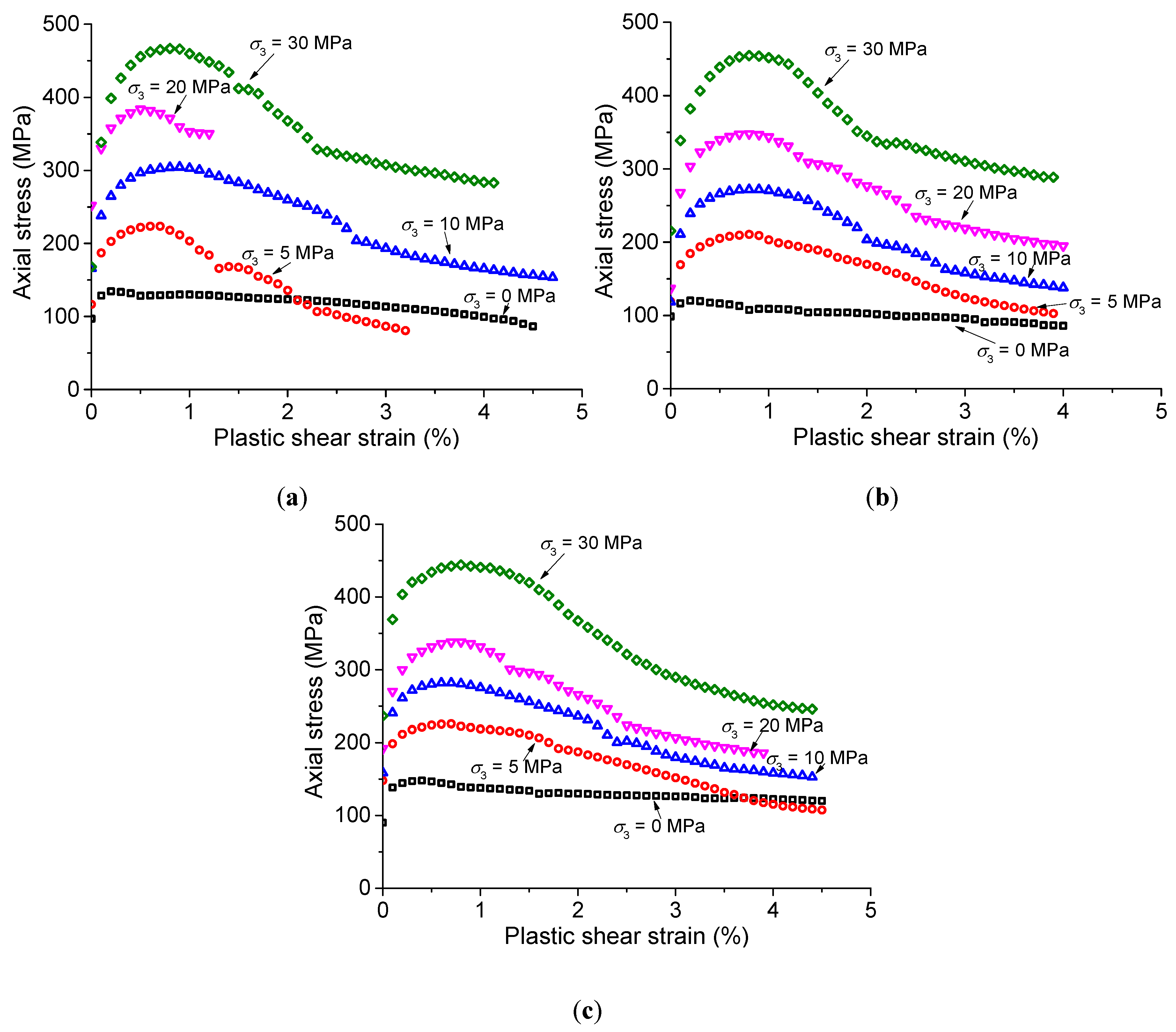
3. Experimental Results

The differential stress—axial strain curves and differential stress—lateral strain curves for all the tests are presented in Figure 3a–e. It should be noted that differential stress (σ₁ − σ₃) is used in these curves in order for a more consistent observation. The peak strength values and the strength envelopes fitted with Hoek-Brown criterion are shown in Figure 3f. Based on these test results, some features can be observed as follows:

(1)

For the NRG01 granite samples treated by different temperatures (T = 20 °C, 100 °C and 200 °C), the differential stress – axial strain curves show the similar brittle – ductile transition behaviors with the increasing confining pressures (σ₃ = 0–30 MPa);

(2)

According to the experimental results, the heat treatment by temperatures no higher than 200 °C does not have very significant influence on the stress – strain curves of the NRG01 granite samples under various confining pressures (σ₃ = 0–30 MPa). However, if we make a more careful observation, it can be found that the samples treated by higher temperature show relatively more ductile behavior during the post-peak stage;

(3)

The peak strength values are also very close for the samples treated by different temperatures. This means that the heat treatment by temperatures no higher than 200 °C does not have very obvious influence on the strength values of the NRG01 granite samples under various confining pressures (σ₃ = 0–30 MPa).

4. Data Analyses and Discussion

4.1. Mobilized Mohr-Coulomb Strength Parameters During Failure of NRG01 Granite

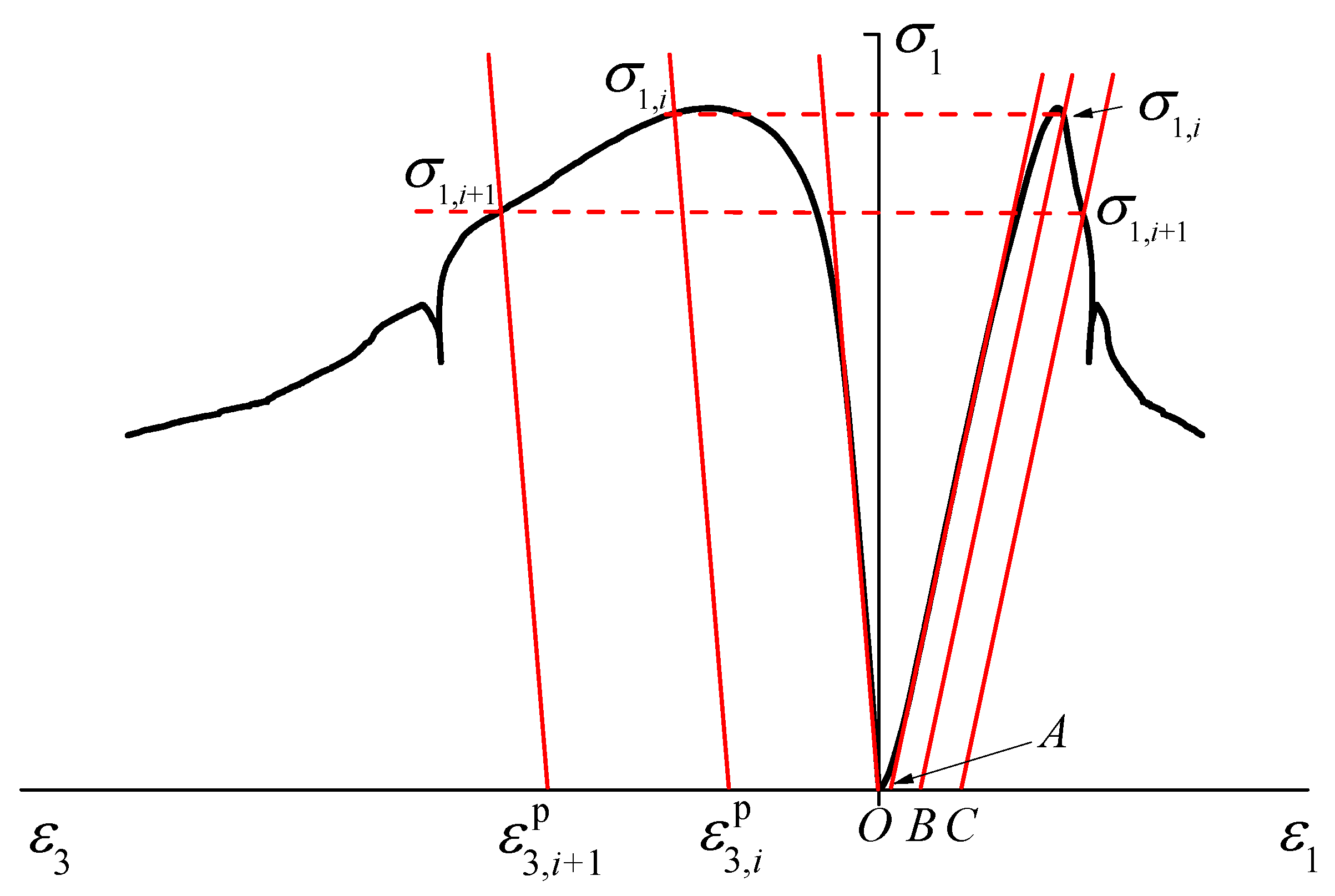
4.1.1. Analytical Method

According to the previous studies [26,28,31,33,53], the Mohr-Coulomb strength parameters (cohesion c and inner frictional angle φ) of rock should be mobilized dependent on rock damage or plastic parameters of geo-materials. The most widely accepted plastic parameter is the plastic shear strain ${\gamma }^{\mathrm{p}}$, which can be obtained as the difference between the maximum and minimum principal plastic strains (${\epsilon }_1^{\mathrm{p}}$ and ${\epsilon }_3^{\mathrm{p}}$, respectively) [27,30,33,54]:

$${\gamma }^{\mathrm{p}}={\epsilon }_1^{\mathrm{p}}-{\epsilon }_3^{\mathrm{p}},$$

(1)

There are usually two methods to obtain the plastic strain values. One method is to differentiate the recoverable and irrecoverable strain by taking cyclic loading-unloading experiments. The plastic strain can be obtained from the irrecoverable strain in each cycle of the tests directly, however, it is quite complicated to control this type of experiment, and the data is limited by the numbers of cycles [27,33,54,55]. Therefore, another method is developed based on the assumption that the unloading curve in each cycle has the same modulus as the initial deformation modulus. In this way, a series of plastic strains can be obtained with a series of assumed loading-unloading cycles by just carrying out conventional uniaxial and tri-axial compression experiments. This method has been widely accepted and used in many studies [27,33,54] and is also employed here in this research. Figure 4 gives a sketch to illustrate this method for determining the plastic axial and lateral strains, as well as the corresponding axial stress values. A series of lines parallel with the tangent lines at the linear elastic stage of the σ₁-ε₁ curves are drawn to determine the plastic axial strain ${\epsilon }_{1,i}^{\mathrm{p}}$ and plastic lateral strain ${\epsilon }_{3,i}^{\mathrm{p}}$, respectively. The symbol i here is a series of positive integers, showing that a series of plastic strain values can be collected with this method. It should be noted that there is a gap $\left|OA\right|$ owing to the crack closure stage of σ₁-₁ curves, so this gap should be removed for determining the plastic axial strain ${\epsilon }_{1,i}^{\mathrm{p}}$:

$${\epsilon }_{1,i}^{\mathrm{p}}=\left|OB\right|-\left|OA\right|, {\epsilon }_{1,i+1}^{\mathrm{p}}=\left|OC\right|-\left|OA\right|,$$

(2)

Then the plastic shear strain can be obtained as:

$${\gamma }_i^{\mathrm{p}}={\epsilon }_{1,i}^{\mathrm{p}}-{\epsilon }_{3,i}^{\mathrm{p}},$$

(3)

For each plastic shear strain, the corresponding maximum principal stress σ₁ is collected under different confining pressures σ₃. Thereafter, cohesion c and internal friction angle $\phi$ can be calculated by drawing Mohr circles or by linear fitting of σ₁ and σ₃ with the following equation:

$${\sigma }_1=\frac{2c\cos \phi }{1-\sin \phi }+\frac{1+\sin \phi }{1-\sin \phi }{\sigma }_3$$

(4)

The values of c and $\phi$ can then be plotted with the increasing plastic shear strain. As the temperature induced by the high-level radioactive waste may affect the mechanical behavior of the host rock, the evolutionary characteristics of c and $\phi$ are also studied for NRG01 granite under different heat treatment (20 °C–200 °C).

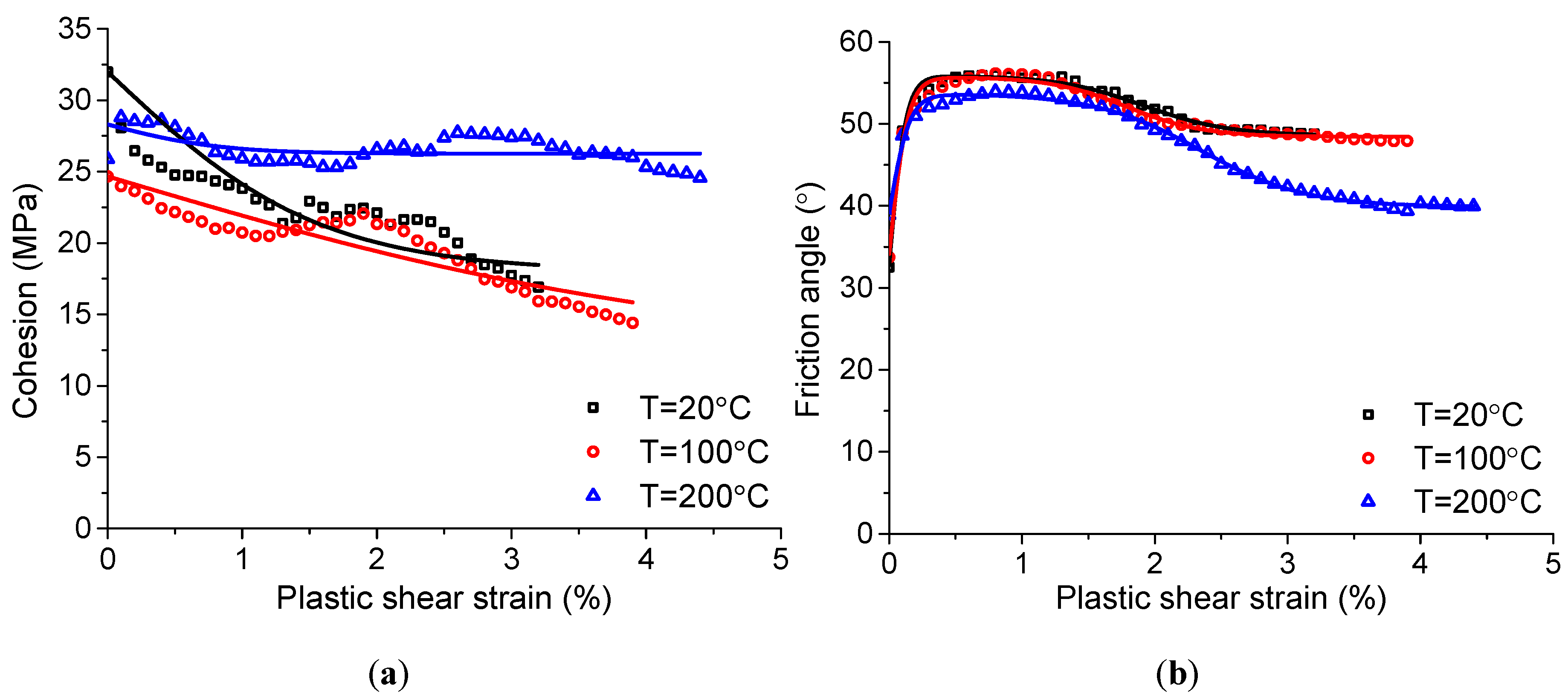
4.1.2. Data Analyses and Discussion

Based on the stress-strain curves of NRG01 granite under different heat treatment and confinements presented in Figure 3, as well as the methodology demonstrated in Section 4.1.1, a series of axial stress at different plastic shear strains can be plotted in Figure 5. For each plastic shear strain, a set of axial stress values under various confining pressures can be obtained to calculate the cohesion and friction angle. These values are shown in Figure 5.

The results obtained in Figure 6 show that NRG01 granite samples have the generally cohesion weakening and friction strengthening (CWFS) behaviors for various treatment temperatures (room temperature to 200 °C). According to the published references [26,29,31,36], the cohesion component should be weakened to the residual value before the full mobilization of friction angle, however, it is not true for NRG01 granite treated by different temperatures. It is shown that cohesion is weakened in a gradual manner with increasing plastic shear strain, nevertheless, the friction angle increases to the peak value more immediately. As an actual fact, the test results similar to this study can also be found in references [30,31,33]. This difference has also been discussed in [29,36], and it is believed that the plastic strain limit at which the cohesion reaches the residual value or the friction angle is fully mobilized is dependent on many factors such as the rock type, grain size, heterogeneity, as well as the hoop effect owing to the cylindrical shape of the specimens, etc. More systematic studies should be carried out to learn more clearly about the exact influencing factors and the mechanism.

Based on the characteristics of the mobilized cohesion and friction angle presented in Figure 6, the generally used linear CWFS model [30,37,38,39] may not be suitable for NRG01 granite. For a better description of the rock behaviors, a non-linear model should be used. With the fitting Equations (5) and (6) proposed in reference [31], the mobilized cohesion and friction angle values can be well fitted as shown in Figure 6. The fitted coefficients are listed in

Table 3. The fitted coefficients determining the mobilized Mohr-Coulomb strength parameters during the failure of NRG01 granite samples under different treatment temperatures.

Temperature (°C)	${\mathit{c}}_{\mathbf{i}}$	${\mathit{c}}_{\mathbf{r}}$	${\mathit{\gamma }}_{\mathit{c},\mathbf{r}}^{\mathbf{p}}$	${\mathit{R}}^2$	${\mathit{\phi }}_{\mathbf{i}}$	${\mathit{\phi }}_{\mathbf{max}}$	${\mathit{\phi }}_{\mathbf{r}}$	${\mathit{\gamma }}_{\mathit{\phi },\mathbf{max}}^{\mathbf{p}}$	${\mathit{\gamma }}_{\mathit{\phi },\mathbf{r}}^{\mathbf{p}}$	${\mathit{R}}^2$
20	31.99	18.00	3.93	0.6696	32.78	55.91	48.58	0.31	3.52	0.9864
100	24.67	12.00	11.35	0.8341	34.14	55.74	48.43	0.35	3.23	0.9746
200	28.31	26.26	2.08	0.2001	39.21	53.70	39.89	0.38	4.3	0.9931

.

$$c=c_{\mathrm{r}}+(c_{\mathrm{i}}-c_{\mathrm{r}})[2-\frac{2}{1+\exp (-5\frac{{\gamma }^{\mathrm{p}}}{{\gamma }_{c,\mathrm{r}}^{\mathrm{p}}})}],$$

(5)

where, $c_{\mathrm{i}}$ and $c_{\mathrm{r}}$ are the initial and residual values of cohesion, respectively. ${\gamma }_{c,\mathrm{r}}^{\mathrm{p}}$ is the plastic shear strain when the cohesion is close to the residual value.

$$\phi ={\phi }_{\mathrm{i}}+({\phi }_{\max }-{\phi }_{\mathrm{i}})[\frac{2}{1+\exp (-5\frac{{\gamma }^{\mathrm{p}}}{{\gamma }_{\phi ,\max }^{\mathrm{p}}})}-1]-({\phi }_{\max }-{\phi }_{\mathrm{r}})\left[\frac{1}{1+\exp (-5\frac{2{\gamma }^{\mathrm{p}}-{\gamma }_{\phi ,\mathrm{r}}^{\mathrm{p}}}{{\gamma }_{\phi ,\mathrm{r}}^{\mathrm{p}}})}\right],$$

(6)

where, ${\phi }_{\mathrm{i}}$ is the initial value of friction angle, while ${\phi }_{\max }$ is the maximum value, and ${\phi }_{\mathrm{r}}$ is the residual value. ${\gamma }_{\phi ,\max }^{\mathrm{p}}$ is the plastic shear strain when the friction angle is close to its peak value, while ${\gamma }_{\phi ,\mathrm{r}}^{\mathrm{p}}$ is the plastic shear strain when the friction angle is close to its residual value.

According to Figure 6, it can also be observed that the different treated temperatures may lead to a few different evolutionary behaviors of cohesion and friction angle for NRG01 granite samples. The more obvious influences are shown for the behaviors of cohesion component, i.e., the sample under room temperature (T = 20 °C) shows an apparently higher initial cohesion value ($c$ = 31.99 MPa), and a more obvious decrease with the increasing plastic shear strain, compared with the samples treated by higher temperatures ($c$ = 24.67 MPa and 25.88 MPa for T = 100 °C and 200 °C, respectively). This should be explained by the more thermally induced cracks in the heat treated samples, which decreased the initial cohesive strength of the specimens. According to Figure 6b, the thermally treated samples by higher temperatures present higher initial friction angles ($\phi$ = 38.87 ° for T = 200 °C, compared with $\phi$ = 32.54 ° and 33.74 ° for T = 20 °C and 100 °C, respectively), which should also be resulted from the more thermally induced crack surfaces treated by higher temperatures. Based on these observations, a general trend can be concluded that higher treatment temperatures may lead to relatively lower initial values of cohesion ($c$) and higher initial values of friction angles ($\phi$) for NRG01 granite samples. This phenomenon should be owing to the different amounts of thermally induced cracks inside the rock under the effects of different temperatures.

This section demonstrates the characteristics of mobilized cohesion and friction angle during the failure process of NRG01 granite samples treated by different temperatures. The non-simultaneous mobilization should be considered in the constitutive models when analyzing the stability of the host rock for site selection or design of a HLW disposal repository.

4.2. Mobilized Hoek-Brown Strength Parameters During Failure of NRG01 Granite

As discussed above, the non-simultaneous mobilization of strength parameters mainly focused on the linear Mohr-Coulomb criterion. For the widely used non-linear Hoek-Brown criterion, only simultaneous mobilization of strength parameters ($m$ and $s$) can be found to be considered in the published studies [23,24,25,26]. It is quite necessary to research the mobilization behaviors of Hoek-Brown strength parameters during the failure process of rock. This section will present such a study based on the laboratory experiments on NRG01 granite samples treated by different temperatures.

4.2.1. Analytical Method

The similar method as illustrated in Figure 4 is used here for determining a series of plastic strain and axial stress values. So the same results presented in Figure 5 can be used in this part of analyses. For each certain plastic shear strain value, the set of stress values under different confining pressures are used to fit the Hoek-Brown criterion [26,42]:

$${\sigma }_1={\sigma }_3+{\sigma }_{\mathrm{ci}}{(m_{\mathrm{b}}\frac{{\sigma }_3}{{\sigma }_{\mathrm{ci}}}+s)}^a,$$

(7)

where, ${\sigma }_1$ and ${\sigma }_3$ are the maximum and minimum principal stresses, respectively; ${\sigma }_{\mathrm{ci}}$ is the uniaxial compression strength of the intact rock; $m_{\mathrm{b}}$, $s$ and $a$ are the constants for the damaged rock specimens.

It should be noted that the parameter $s$ is related to the fracturing degree of the samples. When σ₃ = 0, the uniaxial compression strength of the damaged samples can be obtained as:

$${\sigma }_{\mathrm{c}}={\sigma }_{\mathrm{ci}}{s}^a,$$

(8)

As the constant $a$ is defined as:

$$a=\frac{1}{2}+\frac{1}{6}\left(e^{-GSI/15}-e^{-20/3}\right),$$

(9)

where, GSI is the Geological Strength Index indicating the rock quality with the number ranging from 0 (totally fractured) to 100 (intact) [41,42]. It can be seen that for 25 < GSI < 100, the value of $a$ is very close to 0.5. Therefore, $a$ is reasonable enough to be set as a constant number 0.5 for simplicity in this study. Thereafter, for the damaged samples at each plastic shear strain, $s$ can be identified based on the corresponding uniaxial compression strength values presented in Figure 5 by the following equation:

$$s={({\sigma }_{\mathrm{c}}/{\sigma }_{\mathrm{ci}})}^{0.5},$$

(10)

With the determined $s$ values, a series of $m_{\mathrm{b}}$ values can be obtained by fitting the data in Figure 5 with Equation (7). As a result, the mobilized $m_{\mathrm{b}}$ and $s$ values varying with plastic shear strain for NRG01 granite samples treated by different temperatures are presented in Figure 7a,b, respectively.

4.2.2. Data Analyses and Discussion

According to Figure 7, for NRG01 granite samples treated by different temperatures (T = 20 °C, 100 °C and 200 °C), several features can be observed as follows:

(1)

Similar to the mobilization of cohesion and friction angle, the mobilization of Hoek-Brown strength parameters ($m_{\mathrm{b}}$ and $s$) is also non-simultaneous during the failure process of NRG01 granite treated by different temperatures no higher than 200 °C;

(2)

With increasing plastic shear strain, $m_{\mathrm{b}}$ increases significantly to a maximum value and then decreases until a residual value;

(3)

$s$ decreases gradually with the increasing plastic shear strain. This is related to the damage and fracturing process during the tests.

The mobilization of $m_{\mathrm{b}}$ can be fitted with Equation (11):

$$\begin{array}{c}{m}_{\mathrm{b}}=m_{\mathrm{bi}}+\left(m_{\mathrm{bmax}}-m_{\mathrm{bi}}\right)\left[\frac{2}{1+\exp \left(-5\frac{{\gamma }^{\mathrm{p}}}{{\gamma }_{m\mathrm{b},\max }^{\mathrm{p}}}\right)}-1\right]\\ -\left(m_{\mathrm{bmax}}-m_{\mathrm{br}}\right)\left[\frac{1}{1+\exp \left(-5\frac{2{\gamma }^{\mathrm{p}}-{\gamma }_{m\mathrm{b},\mathrm{r}}^{\mathrm{p}}}{{\gamma }_{m\mathrm{b},\mathrm{r}}^{\mathrm{p}}}\right)}\right],\end{array}$$

(11)

where, $m_{\mathrm{bi}}$ and $m_{\mathrm{br}}$ are the initial and residual value of $m_{\mathrm{b}}$, respectively; $m_{\mathrm{bmax}}$ is the maximum value of $m_{\mathrm{b}}$; ${\gamma }_{m\mathrm{b},\max }^{\mathrm{p}}$ is the plastic shear strain when $m_{\mathrm{b}}$ is close to its peak value, while ${\gamma }_{m\mathrm{b},\mathrm{r}}^{\mathrm{p}}$ is the plastic shear strain when $m_{\mathrm{b}}$ is close to its residual value.

The mobilization of $s$ can be fitted with Equation (12):

$$s=\frac{s_{\mathrm{i}}-s_{\mathrm{r}}}{1+{\left({\gamma }^{\mathrm{p}}/{\gamma }_0^{\mathrm{p}}\right)}^n}+s_{\mathrm{r}},$$

(12)

where, $s_{\mathrm{i}}$ and $s_{\mathrm{r}}$ are the initial and residual value of $s$, respectively. ${\gamma }_0^{\mathrm{p}}$ is the transitional plastic shear strain when the $s$ value turns to decrease in a gradual manner. $n$ is a constant determining the shape of the curve.

The fitted curves are presented in Figure 7, and the fitted coefficients are shown in

Table 4. The fitted coefficients determining the mobilized Hoek-Brown strength parameters during the failure of NRG01 granite samples under different treatment temperatures.

T (°C) 1	${\mathit{m}}_{\mathbf{bi}}$	${\mathit{m}}_{\mathbf{br}}$	${\mathit{m}}_{\mathbf{bmax}}$	${\mathit{\gamma }}_{\mathit{m}\mathbf{b},\mathbf{max}}^{\mathbf{p}}$	${\mathit{\gamma }}_{\mathit{m}\mathbf{b},\mathbf{r}}^{\mathbf{p}}$	${\mathit{R}}^2$	${\mathit{s}}_{\mathbf{i}}$	${\mathit{s}}_{\mathbf{r}}$	${\mathit{\gamma }}_0^{\mathbf{p}}$	$\mathit{n}$	${\mathit{R}}^2$
20	4.64	12.40	43.71	0.56	3.65	0.9947	1.00	−1.00	8.15	1.72	0.9751
100	4.68	13.98	45.64	0.72	3.53	0.9868	1.00	0.45	1.80	2.00	0.9464
200	8.54	4.09	43.08	0.52	4.09	0.9940	1.00	0.63	1.41	1.70	0.9860

¹ T means the treatment temperature.

. According to Figure 7a, it can be observed that the mobilization of $m_{\mathrm{b}}$ value has very similar characteristics with the increasing plastic shear strain, for the NRG01 granite samples treated by different temperatures (T = 20 °C, 100 °C and 200 °C). Based on a more detailed observation on Figure 7a, we can find that for the NRG01 granite samples treated by the temperature T = 200 °C, the initial value of $m_{\mathrm{b}}$ = 7.24. This is apparently higher than the value for the cases of lower temperatures ($m_{\mathrm{b}}$ = 3.54 and 2.59, for T = 20 °C and 100 °C, respectively). It is always believed that $m_{\mathrm{b}}$ value is more related to the frictional strength in Mohr-Coulomb criterion [29,56]. For the case of T = 200 °C, there should be more crack surfaces induced by the heat in the granite samples, and this should be the reason why the initial values of friction angle and $m_{\mathrm{b}}$ are both higher. According to Figure 7b, the mobilization of $s$ value are also quite similar with the increasing plastic shear strain, for the NRG01 granite samples treated by different temperatures (T = 20 °C, 100 °C and 200 °C). There are not enough evidence to prove how heat treatment influence the mobilization of $s$ value based on this study. More systematic experimental studies should be carried out in order to make clear the characteristics of mobilized $s$ during the failure process of granite treated by different temperatures.

5. Conclusions

NRG01 granite samples cored from Alxa candidate area for HLW disposal were treated by different temperatures, and then were used to carry out a series of uniaxial and tri-axial compression experiments under different confining pressures. Complete axial stress—axial strain curves and axial stress—lateral strain curves were recorded. These data were collected to study the mobilization of both Mohr-Coulomb and Hoek-Brown strength parameters during the damage and failure of NRG01 granites samples considering the effect of heat induced by the nuclear waste. According to the analyses in this study, several conclusions can be drawn as follows:

(1)

Cohesion weakening and friction angle strengthening occurs during the damage and failure process of NRG01 granite samples treated by different temperatures. However, compared with the findings in the previous studies, cohesion decreases in a more gradual manner for NRG01 granite samples, and the friction angle increases immediately to its maximum value before the cohesion approaching to the residual value. This may be owing to the grain size, heterogeneity, or even the hoop effect induced by the cylindrical shape of the samples. More systematic studies are required to make clear the exact influencing factors, as well as the mechanism.

(2)

The temperatures of no higher than 200 °C do not have significant influence on the characteristics of mobilized cohesion or friction angle during the damage and failure process of NRG01 granite samples. However, the samples under room temperature (20 °C) have higher initial cohesion than the samples treated by higher temperatures (T=100 °C and 200 °C). In addition, the samples treated by temperature of 200 °C have higher friction angle than the samples treated by lower temperatures. This should be caused by the cracks induced by the heat treatment.

(3)

The Hoek-Brown strength parameters $m_{\mathrm{b}}$ and $s$ are also observed to show non-simultaneous mobilization behaviors during the failure process of NRG01 granite samples treated by different temperatures. It is found that $m_{\mathrm{b}}$ increases significantly to a maximum value and then decreases until a residual value, and $s$ decreases gradually with the increasing plastic shear strain. The general characteristics of the mobilized $m_{\mathrm{b}}$ and $s$ are similar for NRG01 granite samples treated by different temperatures, and the fitted equations for modelling the mobilization of both parameters are proposed. The samples treated by temperature of 200 °C have higher initial $m_{\mathrm{b}}$ value, this should also be caused by the cracks induced by the heat treatment.

These findings on the mobilization of strength parameters provide a better understanding on the strength properties of NRG01 granite samples, and can be used for building a plastic constitutive model in the next step. This study should also be helpful for guiding the selection and design of HLW disposal repository in Alxa area in China. This study put forward the research on non-simultaneous mobilization of strength parameters to Hoek-Brown strength criterion, and more experimental studies are required to consolidate the results. The methods used in this paper can also be used for this kind of analyses in the other candidate areas for HLW disposal.