Estimation of Single-Diode and Two-Diode Solar Cell Parameters by Using a Chaotic Optimization Approach
Abstract
1. Introduction
- (a)
- (b)
- estimation based on experimental data [8].
- (a)
- (b)
- numerical extraction [13] and
- (c)
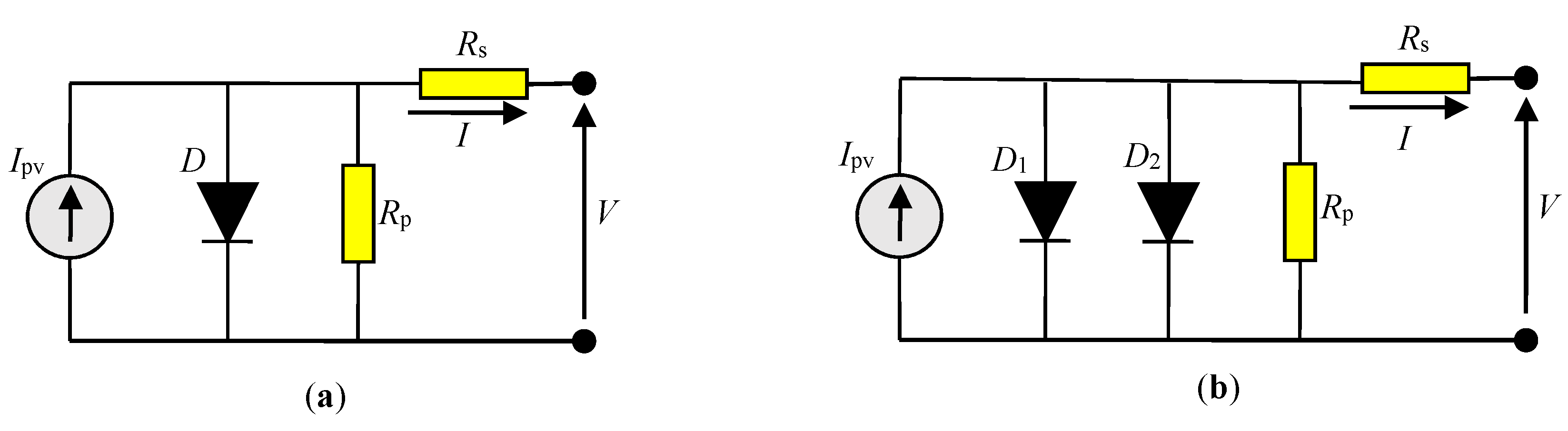
2. Mathematical Modeling of Single and Double Solar Cells
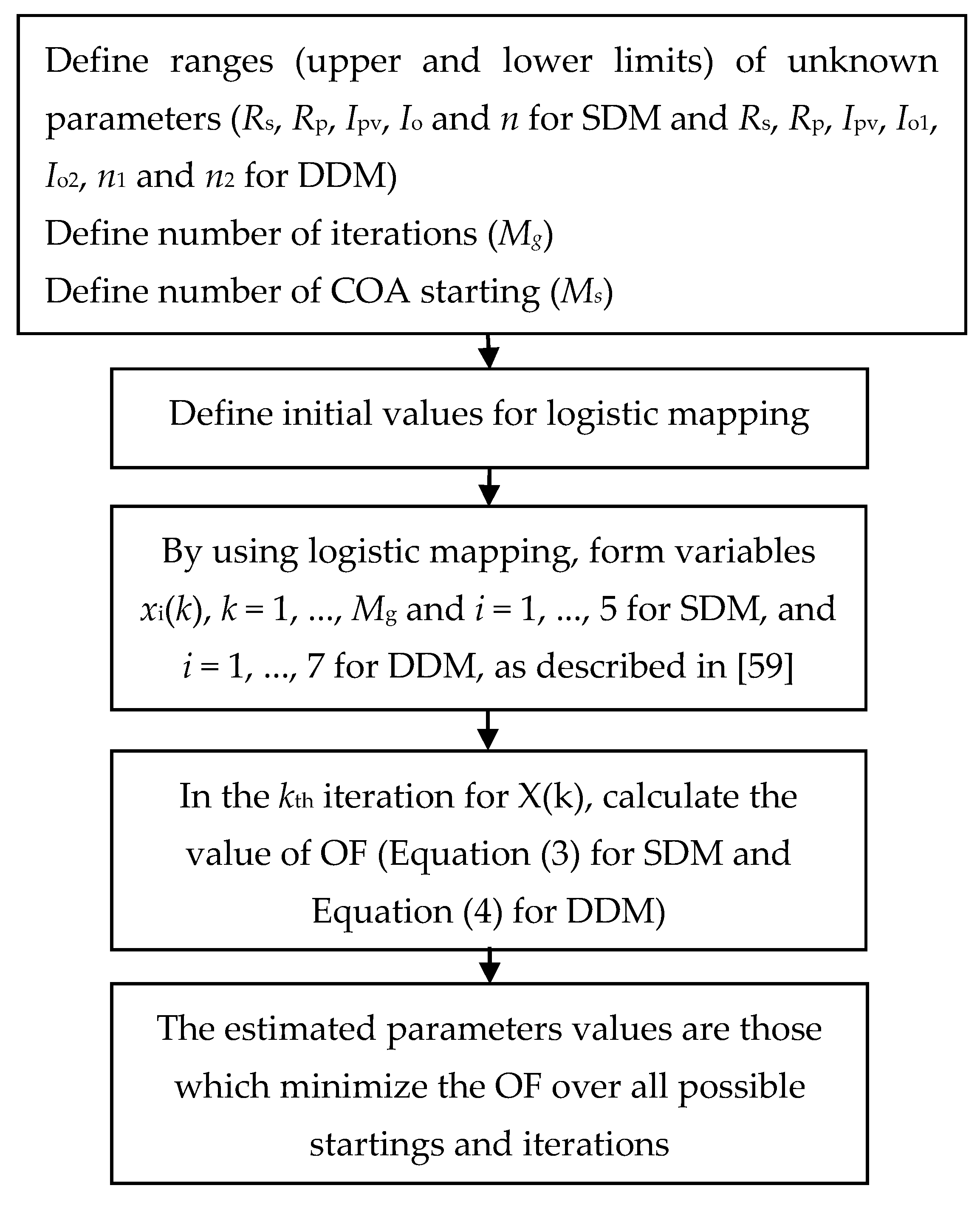
3. COA and Objective Function
4. Simulation Results
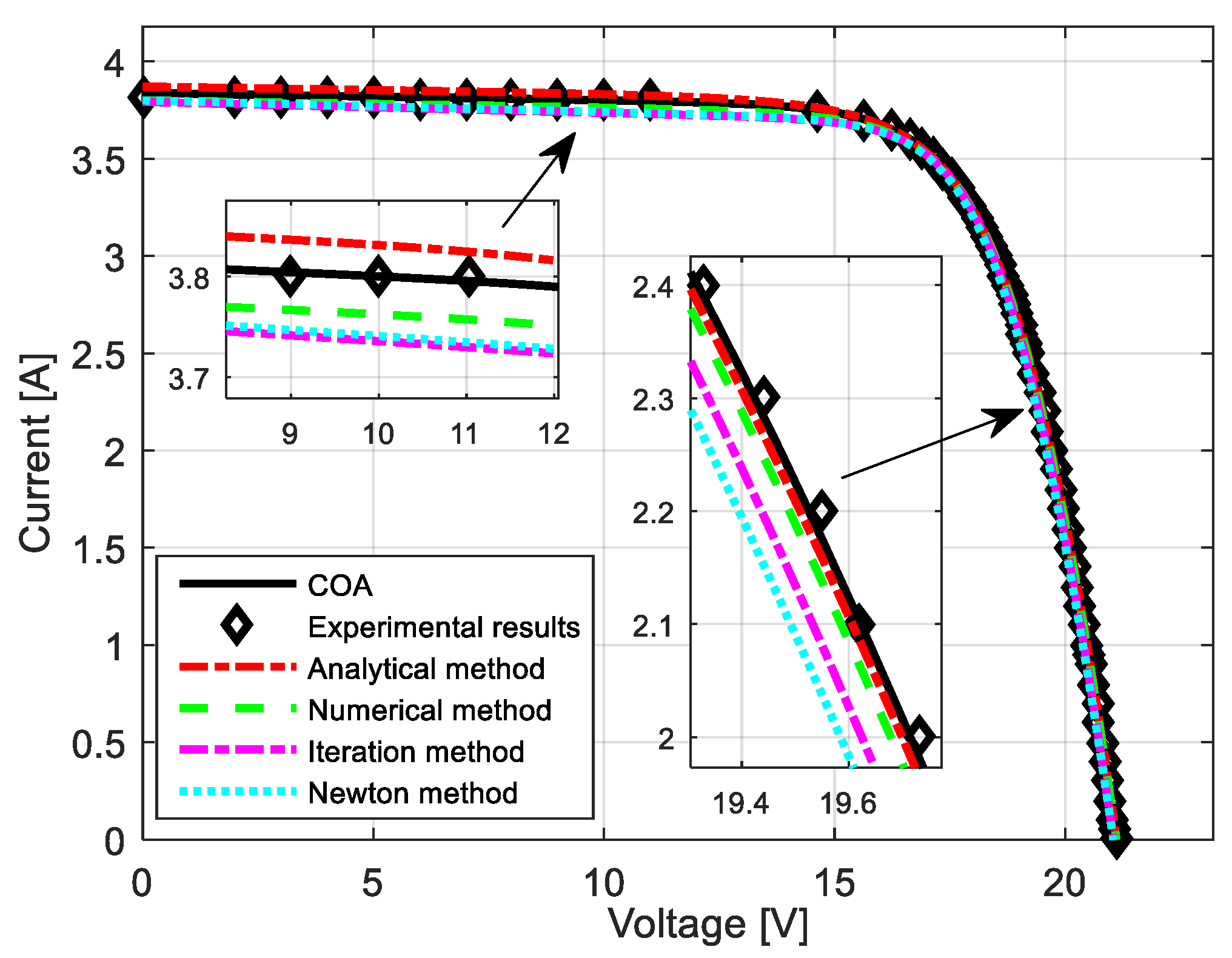
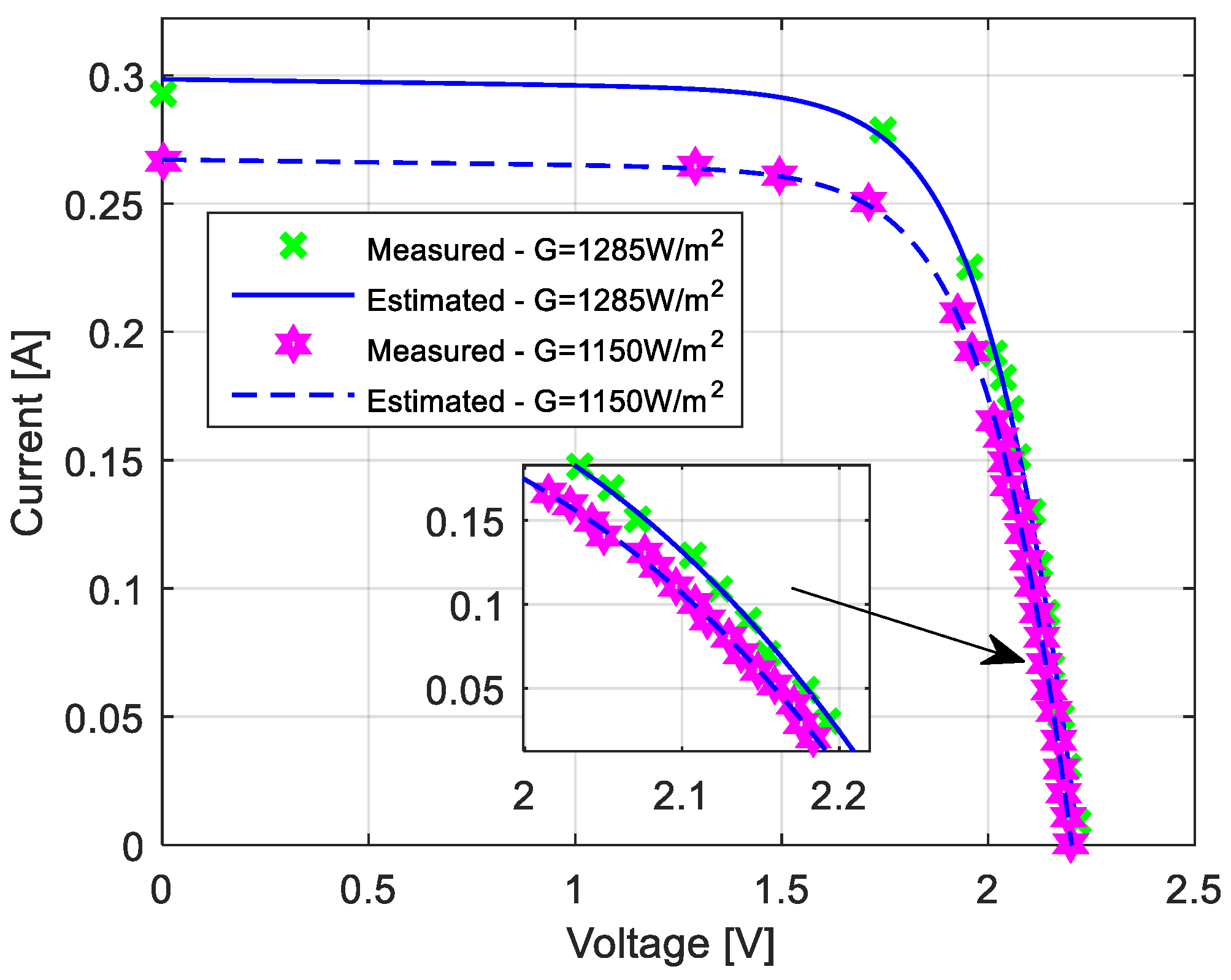
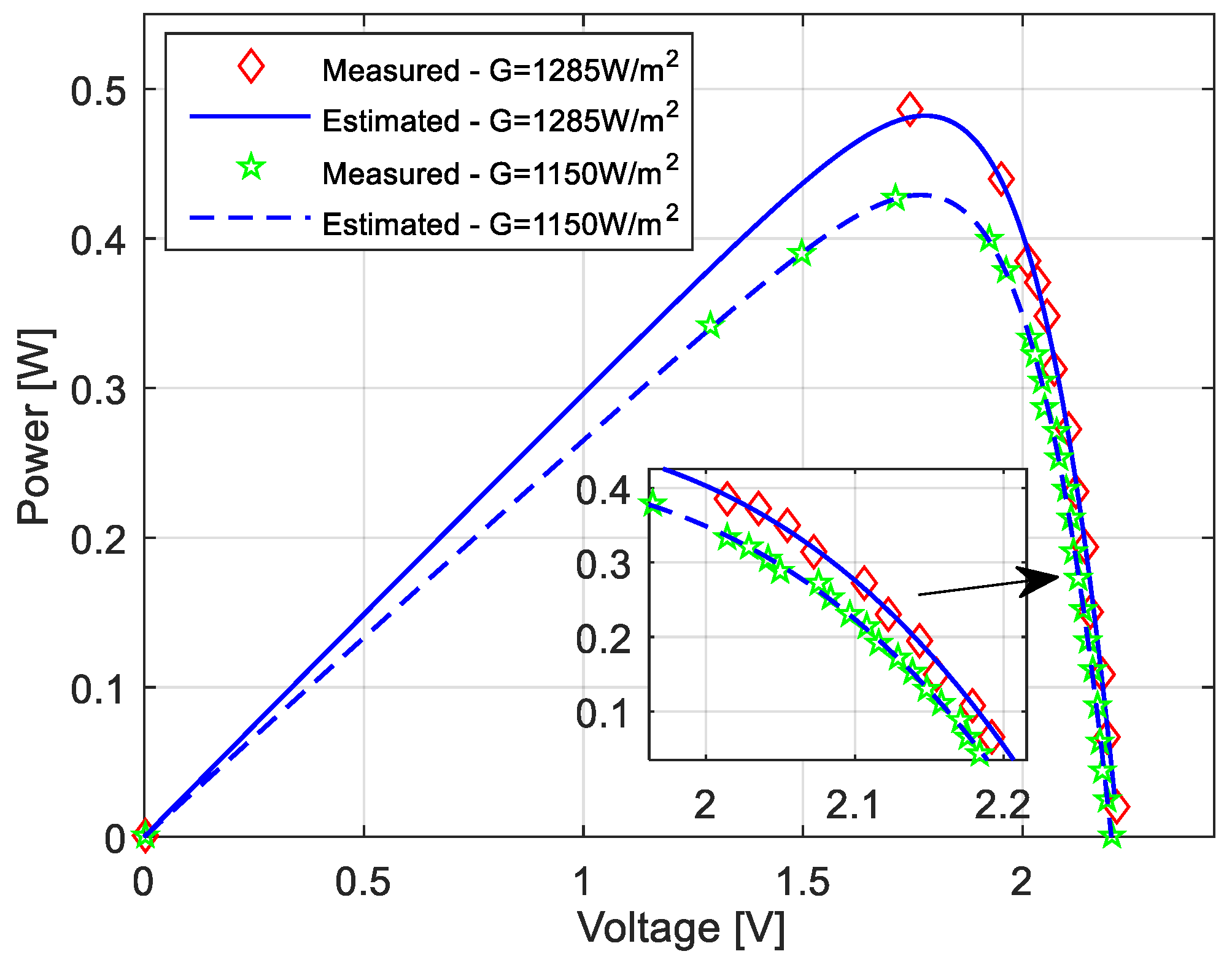
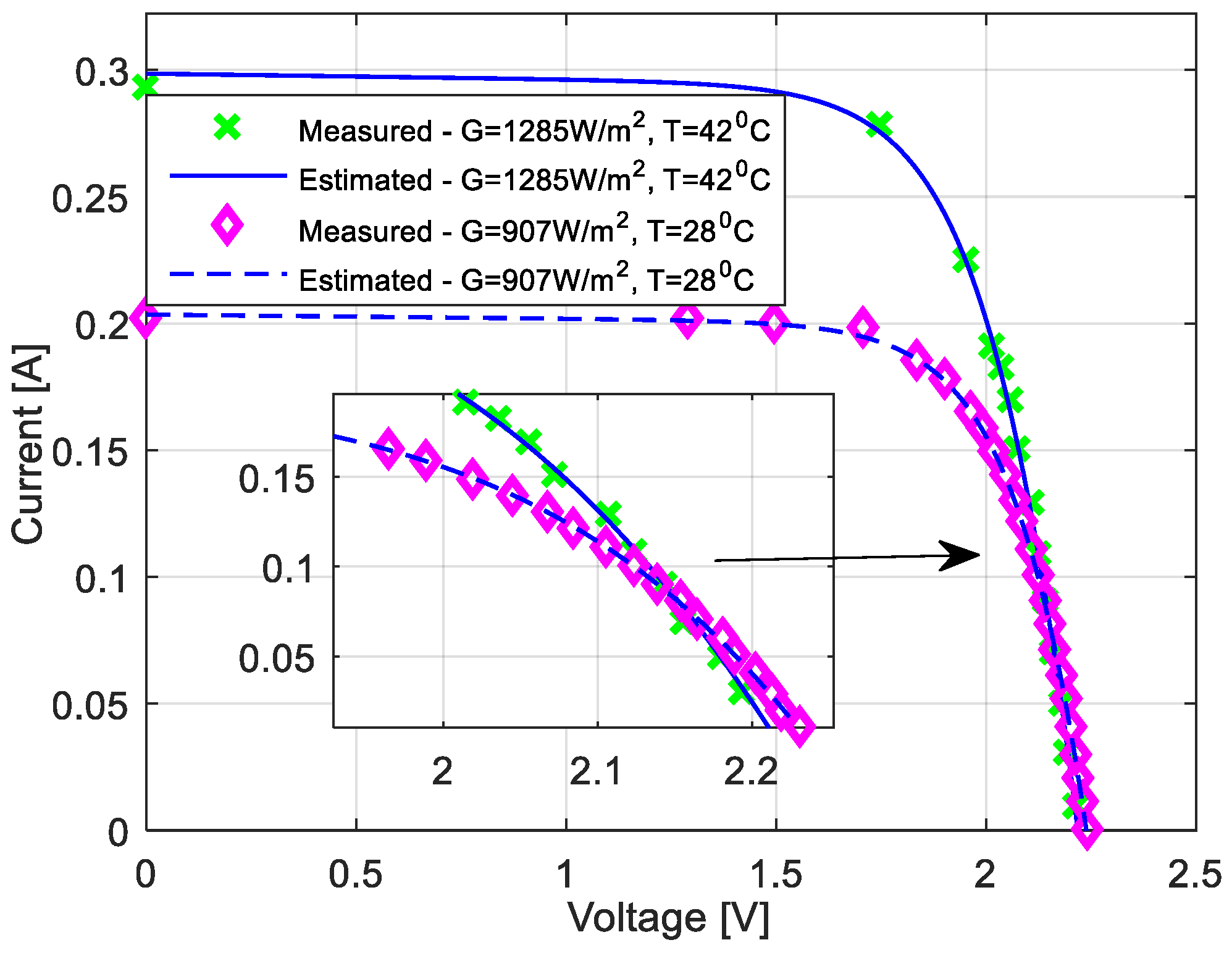
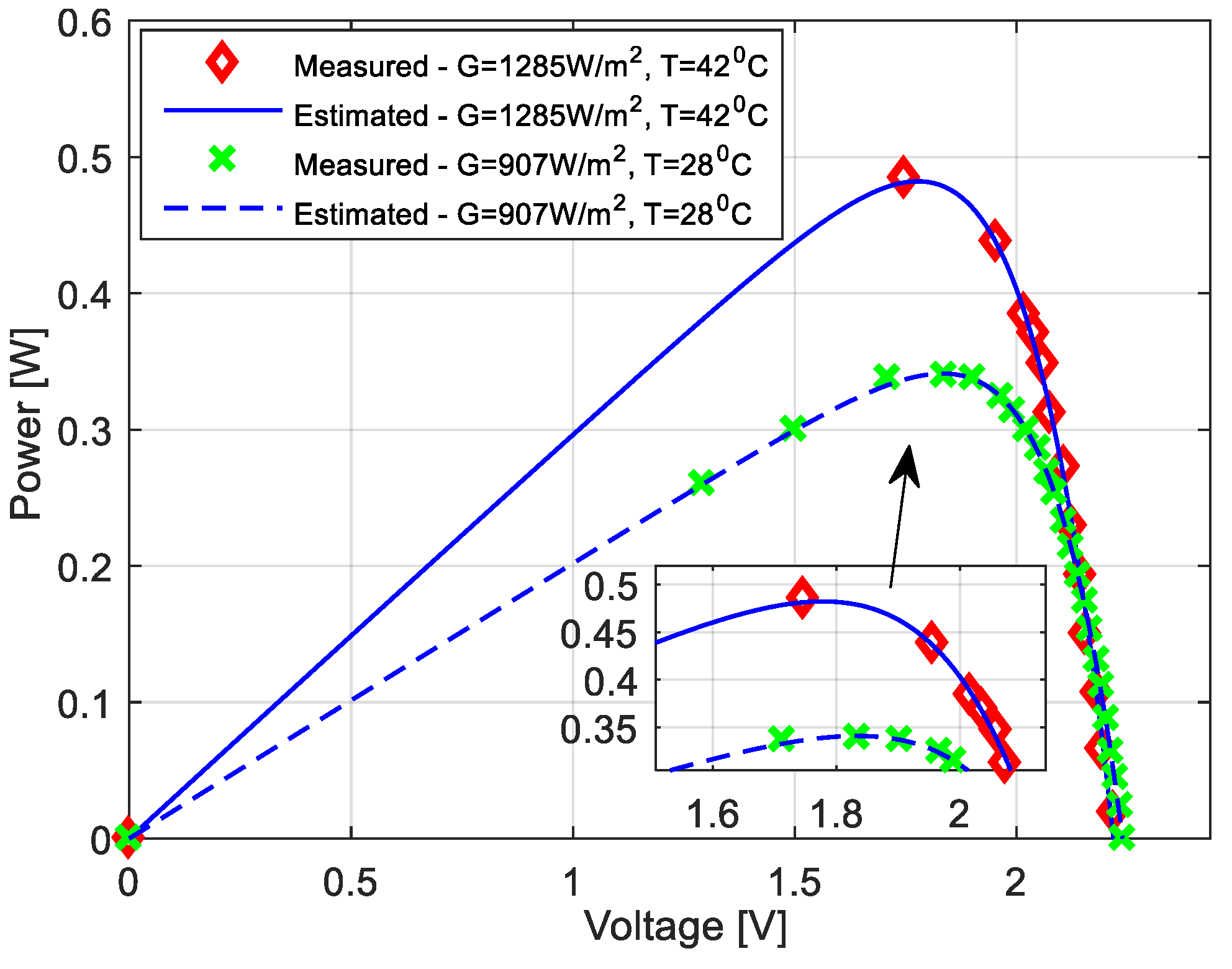
5. Experimental Results and Analysis
- two solar modules and one module: 4 solar cells, 400 mW, 2 V, 0.5 A,
- TES 1333R data logging Solar power meter—instrument with range of 2000 W/m2, high resolution (0.1 W/m2), and wide spectral resolution (400–1100 nm), etc.
- lamp—special double spotlight lamp that simulates sunlight. It provides the optimal light spectrum for the solar module.
- USB Data Monitor—used for data acquisition. Also, it is connected to the computer and software through the USB port.
- load—simulates electric consumer load.
- software—designed to facilitate system control, parameter monitoring, data acquisition and graphical representation of the collected data.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Moshksar, E.; Ghanbari, T. Adaptive Estimation Approach for Parameter Identification of Photovoltaic Modules. IEEE J. Photovolt. 2017, 7, 614–623. [Google Scholar] [CrossRef]
- Ali, H.; Mojgan, H.; Saad, M.; Hussein, H. Solar cell parameters extraction based on single and double-diode models: A review. Renew. Sustain. Energy Rev. 2016, 56, 494–509. [Google Scholar]
- Kashif, I.; Zainal, S.; Hamed, T. Simple, fast and accurate two-diode model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2011, 95, 586–594. [Google Scholar]
- Chitti, B.B.; Suresh, G. A novel simplified two-diode model of photovoltaic (PV) module. IEEE J. Photovolt. 2014, 4, 1156–1161. [Google Scholar]
- Chen, Y.; Sun, Y.; Meng, Z. An improved explicit double-diode model of solar cells: Fitness verification and parameter extraction. Energy Convers. Manag. 2018, 169, 345–358. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Salvini, A. Identification of the one-diode model for photovoltaic modules from datasheet values. Sol. Energy 2014, 108, 432–446. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Wu, G.; Amaratunga, G.A.J. Parameter estimation of solar cells using datasheet information with the application of an adaptive differential evolution algorithm. Renew. Energy 2019, 132, 425–438. [Google Scholar] [CrossRef]
- Laudani, A.; Riganti, F.F.; Salvini, A. High performing extraction procedure for the one-diode model of a photovoltaic panel from experimental I-V curves by using reduced forms. Sol. Energy 2014, 103, 316–326. [Google Scholar] [CrossRef]
- Chatterjee, A.; Keyhani, A.; Kapoor, D. Identification of photovoltaic source models. IEEE Trans. Energy Convers. 2011, 24, 883–889. [Google Scholar] [CrossRef]
- Shongwe, S.; Hanif, M. Comparative analysis of different single-diode PV modeling methods. IEEE J. Photovolt. 2015, 5, 938–946. [Google Scholar] [CrossRef]
- Batzelis, E. Non-Iterative Methods for the Extraction of the Single-Diode Model Parameters of Photovoltaic Modules: A Review and Comparative Assessment. Energies 2019, 12, 358. [Google Scholar] [CrossRef]
- Jordehi, A.R. Parameter estimation of solar photovoltaic (PV) cells: A. review. Renew. Sustain. Energy Rev. 2016, 61, 354–371. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A. An efficient parameters extraction technique of photovoltaic models for performance assessment. Sol. Energy 2017, 158, 192–206. [Google Scholar] [CrossRef]
- Kashif, I.; Salam, Z.; Mekhilef, S.; Shamsudin, A. Parameter extraction of solar photo voltaic modules using penalty based differential evolution. Appl. Energy 2012, 99, 297–308. [Google Scholar]
- Dhruv, K.; Goswami, Y.; Kumar, R.V. A novel approach to parameter estimation of photovoltaic systems using hybridized optimizer. Energy Convers. Manag. 2019, 187, 486–511. [Google Scholar]
- Dalia, Y.; Dalia, A.; Eteiba, M.B.; Ponnuthurai, N.S. Static and dynamic photovoltaic models’ parameters identification using Chaotic Heterogeneous Comprehensive Learning Particle Swarm Optimizer variants. Energy Convers. Manag. 2019, 182, 546–563. [Google Scholar]
- Abd, E.M.; Diego, O. Parameter estimation of solar cells diode models by an improved opposition-based whale optimization algorithm. Energy Convers. Manag. 2018, 171, 1843–1859. [Google Scholar]
- Manel, M.; Anis, S.; Faouzi, M.M. Particle swarm optimisation with adaptive mutation strategy for photovoltaic solar cell/module parameter extraction. Energy Convers. Manag. 2018, 175, 151–163. [Google Scholar]
- Kler, D.; Sharma, P.; Banerjee, A.; Rana, V.; Kumar, K.P.S. PV cell and module efficient parameters estimation using evaporation rate-based water cycle algorithm. Swarm Evolut. Comput. 2017, 35, 93–110. [Google Scholar] [CrossRef]
- Lin, P.; Cheng, S.; Yeh, W.; Chen, Y.; Wu, L. Parameters extraction of solar cell models using a modified simplified swarm optimization algorithm. Sol. Energy 2017, 144, 594–603. [Google Scholar] [CrossRef]
- Ram, J.P.; Babu, T.S.; Dragicevic, T.; Rajasekar, N. A new hybrid bee pollinator flower pollination algorithm for solar PV parameter estimation. Energy Convers. Manag. 2017, 135, 463–476. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. Parameter estimation of photovoltaic system using imperialist competitive algorithm. Renew. Energy 2017, 111, 307–320. [Google Scholar] [CrossRef]
- Chen, X.; Yu, K.; Du, W.; Zhao, W.; Liu, G. Parameters identification of solar cell models using generalized oppositional teaching learning-based optimization. Energy 2016, 99, 170–180. [Google Scholar] [CrossRef]
- Guo, L.; Meng, Z.; Sun, Y.; Wang, L. Parameter identification and sensitivity analysis of solar cell models with cat swarm optimization algorithm. Energy Convers. Manag. 2016, 108, 520–528. [Google Scholar] [CrossRef]
- Hamid, N.F.A.; Rahim, N.A.; Selvaraj, J. Solar cell parameters identification using hybrid Nelder-Mead and modified particle swarm optimization. J. Renew. Sustain. Energy 2016, 8, 1–10. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, P.; Chen, Z.; Cheng, S. A population classification evolution algorithm for the parameter extraction of solar cell models. Int. J. Photoenergy 2016, 2016, 2174573. [Google Scholar] [CrossRef]
- Tong, N.T.; Pora, W. A parameter extraction technique exploiting intrinsic properties of solar cells. Appl. Energy 2016, 176, 104–115. [Google Scholar] [CrossRef]
- Jamadi, M.; Merrikh-Bayat, F.; Bigdeli, M. Very accurate parameter estimation of single- and double-diode solar cell models using a modified artificial bee colony algorithm. Int. J. Energy Environ. Eng. 2016, 7, 13–25. [Google Scholar] [CrossRef]
- Ali, E.E.; El-Hameed, M.A.; El-Fergany, A.A.; El-Arini, M.M. Parameter extraction of photovoltaic generating units using multi-verse optimizer. Sustain. Energy Technol. Assess. 2016, 17, 68–76. [Google Scholar] [CrossRef]
- Chellaswamy, C.; Ramesh, R. Parameter extraction of solar cell models based on adaptive differential evolution algorithm. Renew. Energy 2016, 97, 823–837. [Google Scholar] [CrossRef]
- Jordehi, A.R. Time varying acceleration coefficients particle swarm optimisation (TVACPSO): A new optimisation algorithm for estimating parameters of PV cells and modules. Energy Convers. Manag. 2016, 129, 262–274. [Google Scholar] [CrossRef]
- Ma, J.; Man, K.L.; Guan, S.U.; Ting, T.O.; Wong, P.W. Parameter estimation of photovoltaic model via parallel particle swarm optimization algorithm. Int. J. Energy Res. 2016, 40, 343–352. [Google Scholar] [CrossRef]
- Yuan, X.; He, Y.; Liu, L. Parameter extraction of solar cell models using chaotic asexual reproduction optimization. Neural Comput. Appl. 2015, 26, 227–239. [Google Scholar] [CrossRef]
- Lim, L.H.I.; Ye, Z.; Ye, J.; Yang, D.; Du, H. A linear identification of diode models from single I-V characteristics of PV panels. IEEE Trans. Ind. Electron. 2015, 62, 4181–4193. [Google Scholar] [CrossRef]
- El-Fergany, A. Efficient tool to characterize photovoltaic generating systems using mine blast algorithm. Electr. Power Compon. Syst. 2015, 43, 890–901. [Google Scholar] [CrossRef]
- Alam, D.F.; Yousri, D.A.; Eteiba, M.B. Flower pollination algorithm based solar PV parameter estimation. Energy Convers. Manag. 2015, 101, 410–422. [Google Scholar] [CrossRef]
- Dkhichi, F.; Oukarfi, B.; Fakkar, A.; Belbounaguia, N. Parameter identification of solar cell model using Levenberg–Marquardt algorithm combined with simulated annealing. Sol. Energy 2014, 110, 781–788. [Google Scholar] [CrossRef]
- Niu, Q.; Zhang, L.; Li, K. A biogeography-based optimization algorithm with mutation strategies for model parameter estimation of solar and fuel cells. Energy Convers. Manag. 2014, 86, 1173–1185. [Google Scholar] [CrossRef]
- Niu, Q.; Zhang, H.; Li, K. An improved TLBO with elite strategy for parameters identification of PEM fuel cell and solar cell models. Int. J. Hydrogen Energy 2014, 39, 3837–3854. [Google Scholar] [CrossRef]
- Oliva, D.; Cuevas, E.; Pajares, G. Parameter identification of solar cells using artificial bee colony optimization. Energy 2014, 72, 93–102. [Google Scholar] [CrossRef]
- Yuan, X.; Xiang, Y.; He, Y. Parameter extraction of solar cell models using mutative-scale parallel chaos optimization algorithm. Sol. Energy 2014, 108, 238–251. [Google Scholar] [CrossRef]
- Patel, S.J.; Panchal, A.K.; Kheraj, V. Extraction of solar cell parameters from a single current–voltage characteristic using teaching learning-based optimization algorithm. Appl. Energy 2014, 119, 384–393. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Extraction of maximum power point in solar cells using bird mating optimizer-based parameters identification approach. Sol. Energy 2013, 90, 123–133. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Artificial bee swarm optimization algorithm for parameters identification of solar cell models. Appl. Energy 2013, 102, 943–949. [Google Scholar] [CrossRef]
- Jiang, L.L.; Maskell, D.L.; Patra, J.C. Parameter estimation of solar cells and modules using an improved adaptive differential evolution algorithm. Appl. Energy 2013, 112, 185–193. [Google Scholar] [CrossRef]
- Ma, J.; Ting, T.O.; Man, K.L.; Zhang, N.; Guan, S.-U.; Wong, P.W.H. Parameter estimation of photovoltaic models via cuckoo search. J. Appl. Math. 2013, 2013, 362619. [Google Scholar] [CrossRef]
- Hachana, O.; Hemsas, K.E.; Tina, G.M.; Ventura, C. Comparison of different metaheuristic algorithms for parameter identification of photovoltaic cell/module. J. Renew. Sustain. Energy 2013, 5, 053112. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Parameter identification for solar cell models using harmony search-based algorithms. Sol. Energy 2012, 86, 3241–3249. [Google Scholar] [CrossRef]
- AlHajri, M.F.; El-Naggar, K.M.; AlRashidi, M.R.; Al-Othman, A.K. Optimal extraction of solar cell parameters using pattern search. Renew. Energy 2012, 44, 238–245. [Google Scholar] [CrossRef]
- El-Naggar, K.M.; AlRashidi, M.R.; AlHajri, M.F.; Al-Othman, A.K. Simulated annealing algorithm for photovoltaic parameters identification. Sol. Energy 2012, 86, 266–274. [Google Scholar] [CrossRef]
- AlRashidi, M.R.; AlHajri, M.F.; El-Naggar, K.M.; Al-Othman, A.K. A new estimation approach for determining the I-V characteristics of solar cells. Sol. Energy 2011, 85, 1543–1550. [Google Scholar] [CrossRef]
- Ye, M.; Wang, X.; Xu, Y. Parameter extraction of solar cells using particle swarm optimization. J. Appl. Phys. 2009, 105, 1–8. [Google Scholar] [CrossRef]
- Shuhui, X.; Yong, W. Parameter estimation of photovoltaic modules using a hybrid flower pollination algorithm. Energy Convers. Manag. 2017, 144, 53–68. [Google Scholar]
- Kunjie, Y.; Xu, C.; Xin, W.; Zhenlei, W. Parameters identification of photovoltaic models using self-adaptive teaching-learning-based optimization. Energy Convers. Manag. 2017, 145, 233–246. [Google Scholar]
- Derick, M.; Rani, C.; Rajesh, M.; Farrag, M.E.; Wang, Y.; Busawon, K. An improved optimization technique for estimation of solar photovoltaic parameters. Sol. Energy 2017, 157, 116–124. [Google Scholar] [CrossRef]
- Gnetchejo, P.J.; Essiane, S.N.; Ele, P.; Wamkeue, R.; Wapet, D.M.; Ngoffe, S.P. Important notes on parameter estimation of solar photovoltaic cell. Energy Convers. Manag. 2019, 197, 111870. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H. Accurate MATLAB Simulink PV System Simulator Based on a Two-Diode Model. J. Power Electron. 2011, 11, 179–187. [Google Scholar] [CrossRef]
- Elbaset, A.A.; Ali, H.; Abd-El Sattar, M. Novel seven-parameter model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2014, 130, 442–455. [Google Scholar] [CrossRef]
- Rubežić, V.; Lazović, L.; Jovanović, A. Parameter identification of Jiles-Atherton model using the chaotic optimization method. Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 2067–2080. [Google Scholar] [CrossRef]
- Ćalasan, M.; Mujičić, D.; Rubežić, V.; Radulović, M. Estimation of Equivalent Circuit Parameters of Single-Phase Transformer by Using Chaotic Optimization Approach. Energies 2019, 12, 1697. [Google Scholar] [CrossRef]
- Coelho, L.S. Tuning of PID controller for an automatic regulator voltage system using chaotic optimization approach. Chaos Solitons Fractals 2009, 39, 1504–1514. [Google Scholar] [CrossRef]
- Jovanović, A.; Lazović, L.; Rubežić, V. Adaptive Array Beamforming Using a Chaotic Beamforming Algorithm. Int. J. Antennas Propag. 2016, 2016, 8354204. [Google Scholar] [CrossRef]
- Jovanović, A.; Lazović, L.; Rubežić, V. Radiation pattern synthesis using a Chaotic beamforming algorithm. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 1814–1829. [Google Scholar] [CrossRef]
- Yang, D.; Li, G.; Cheng, G. On the efficiency of chaos optimization algorithms for global optimization. Chaos Solitons Fractals 2007, 34, 1366–1375. [Google Scholar] [CrossRef]
- Valdivia-González, A.; Zaldívar, D.; Cuevas, E.; Pérez-Cisneros, M.; Fausto, F.; González, A. A Chaos-Embedded Gravitational Search Algorithm for the Identification of Electrical Parameters of Photovoltaic Cells. Energies 2017, 10, 1052. [Google Scholar] [CrossRef]
- Oliva, D.; Ewees, A.A.; Aziz, M.A.E.; Hassanien, A.E.; Peréz-Cisneros, M. A Chaotic Improved Artificial Bee Colony for Parameter Estimation of Photovoltaic Cells. Energies 2017, 10, 865. [Google Scholar] [CrossRef]
- Oliva, D.; Aziz, M.A.E.; Hassanien, A.E. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 2017, 200, 141–154. [Google Scholar] [CrossRef]
- Bertuglia, C.S.; Via, F. Nonlinearity, Chaos, and Complexity; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Tress, W. Interpretation and evolution of open-circuit voltage, recombination, ideality factor and subgap defect states during reversible light-soaking and irreversible degradation of perovskite solar cells. Energy Environ. Sci. 2017. [Google Scholar] [CrossRef]
- Wetzelaer, G.A.H.; Kuik, M.; Lenes, M.; Blom, P.W.M. Origin of the dark-current ideality factor in polymer:fullerene bulk heterojunction solar cells. AIP Appl. Phys. Lett. 2011, 99, 153506. [Google Scholar] [CrossRef]
- Perovich, S.M.; Djukanovic, M.; Dlabac, T.; Nikolic, D.; Calasan, M. Concerning a novel mathematical approach to the solar cell junction ideality factor estimation. Appl. Math. Model. 2015, 39, 3248–3264. [Google Scholar] [CrossRef]
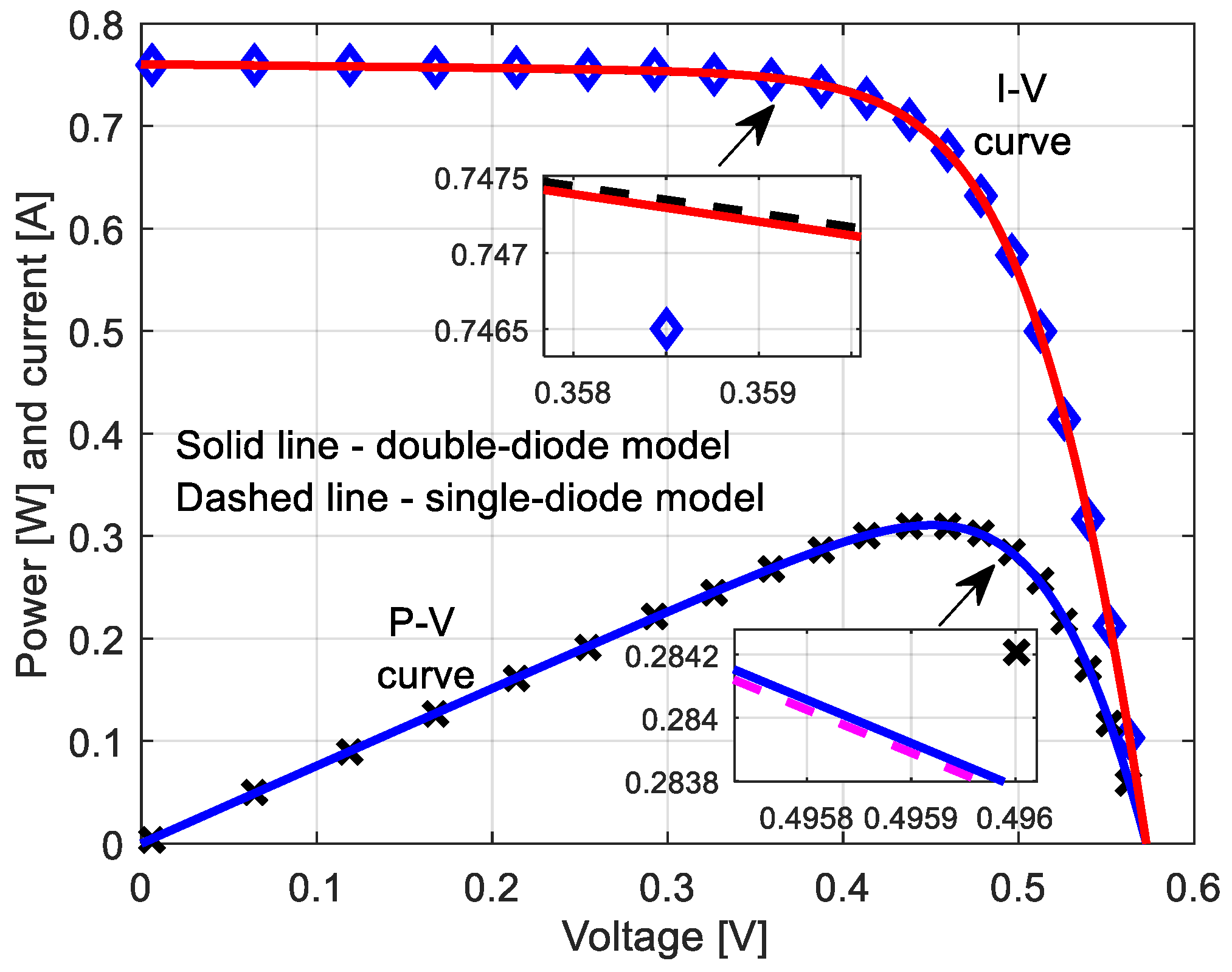

| No. | Algorithm | Reference | First Author, Year | Ipv (A) | I0 (μA) | n | Rs (Ω) | Rp (Ω) | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| Proposed Method—COA | 0.7607745 | 0.3230018 | 1.4811774 | 0.0363775 | 53.73 | 9.860221 × 10−4 | |||
| 1. | HISA * | [15] | Dhruv, 2019 | 0.7607078 | 0.3106845918 | 1.47726778 | 0.03654694 | 52.88979426 | 9.8911 × 10−4 |
| 2. | HCLPSO * | [16] | Dalia, 2019 | 0.76079 | 0.31062 | 1.4771 | 0.036548 | 52.885 | 1.12009 × 10−3 |
| 3. | OBWOA * | [17] | Abd, 2018 | 0.76077 | 0.3232 | 1.5208 | 0.0363 | 53.6836 | 1.1417 × 10−3 |
| 4. | MPSO * | [18] | Manel, 2018 | 0.760787 | 0.310683 | 1.475262 | 0.036546 | 52.88971 | 7.33007 × 10−3 |
| 5. | ER-WCA | [19] | Kler D, 2017 | 0.760776 | 0.322699 | 1.481080 | 0.036381 | 53.69100 | 9.8609 × 10−4 |
| 6 | MSSO | [20] | Lin P, 2017 | 0.760777 | 0.323564 | 1.481244 | 0.036370 | 53.742465 | 1.0599 × 10−3 |
| 7 | BPFPA * | [21] | Ram JP, 2017 | 0.7600 | 0.3106 | 1.4774 | 0.0366 | 57.7151 | 1.2536 × 10−3 |
| 8 | ICA | [22] | Fathy A, 2017 | 0.7603 | 0.14650 | 1.4421 | 0.0389 | 41.1577 | 1.1582 × 10−1 |
| 9 | GOTLBO | [23] | Chen X, 2016 | 0.760780 | 0.331552 | 1.483820 | 0.036265 | 54.115426 | 9.8744 × 10−4 |
| 10 | CSO | [24] | Guo L, 2016 | 0.76078 | 0.3230 | 1.48118 | 0.03638 | 53.7185 | 9.8612 × 10−4 |
| 11. | NM-MPSO | [25] | Hamid N, 2016 | 0.76078 | 0.32306 | 1.48120 | 0.03638 | 53.7222 | 9.8620 × 10−4 |
| 12. | PCE | [26] | Zhang Y, 2016 | 0.760776 | 0.323021 | 1.481074 | 0.036377 | 53.718525 | 1.0606 × 10−3 |
| 13. | TONG | [27] | Tong NT, 2016 | 0.7610 | 0.3635 | 1.4935 | 0.03660 | 62.574 | 2.3859 × 10−3 |
| 14. | MABC | [28] | Jamadi M, 2016 | 0.760779 | 0.321323 | 1.481385 | 0.036389 | 53.39999 | 2.7610 × 10−3 |
| 15. | MVO | [29] | Ali EE, 2016 | 0.7616 | 0.32094 | 1.5252 | 0.0365 | 59.5884 | 1.2680 × 10−1 |
| 16. | DET | [30] | Chellaswamy C, 2016 | 0.751 | 0.315 | 1.487 | 0.036 | 54.532 | 2.4481 × 10−2 |
| 17. | WCA | [31] | Jordehi AR, 2016 | 0.760908 | 0.4135540 | 1.504381 | 0.035363 | 57.669488 | 7.6069 × 10−3 |
| 18. | TLBO | 0.760809 | 0.312244 | 1.47578 | 0.036551 | 52.8405 | 7.2723 × 10−3 | ||
| 19. | GWO | 0.760996 | 0.2430388 | 1.451219 | 0.037732 | 45.116309 | 7.2845 × 10−3 | ||
| 20. | TVACPSO | 0.760788 | 0.3106827 | 1.475258 | 0.036547 | 52.889644 | 7.3438 × 10−3 | ||
| 21. | PPSO | [32] | Ma J, 2016 | 0.7608 | 0.3230 | 1.4812 | 0.0364 | 53.7185 | 9.9161 × 10−4 |
| 22. | CARO | [33] | Yuan X, 2015 | 0.76079 | 0.31724 | 1.48168 | 0.03644 | 53.0893 | 8.1969 × 10−3 |
| 23. | LI | [34] | Lim LHI, 2015 | 0.7609438 | 0.3456572 | 1.48799169 | 0.03614233 | 49.482205 | 1.3462 × 10−3 |
| 24. | MBA | [35] | El-Fergany A. 2015 | 0.7604 | 0.2348 | 1.4890 | 0.0388 | 44.61 | 1.1672 × 10−1 |
| 25. | FPA * | [36] | Alam DF, 2015 | 0.76079 | 0.310677 | 1.47707 | 0.0365466 | 52.8771 | 1.2121 × 10−3 |
| 26. | LMSA | [37] | Dkhichi F, 2014 | 0.76078 | 0.31849 | 1.47976 | 0.03643 | 53.32644 | 9.8649 × 10−4 |
| 27. | DE | [38] | Niu Q, 2014 | 0.76068 | 0.35515 | 1.49080 | 0.03598 | 56.5533 | 1.0035 × 10−3 |
| 28. | BBO | 0.76098 | 0.86100 | 1.58742 | 0.03214 | 78.8555 | 2.3929 × 10−3 | ||
| 29. | BBO-M | 0.76078 | 0.31874 | 1.47984 | 0.03642 | 53.36227 | 9.8656 × 10−4 | ||
| 30. | STLBO | [39] | Niu Q, 2014 | 0.76078 | 0.32302 | 1.48114 | 0.03638 | 53.7187 | 9.9763 × 10−4 |
| 31. | TLBO | 0.76074 | 0.32378 | 1.48136 | 0.03641 | 54.4029 | 1.0016 × 10−3 | ||
| 32. | ABC | [40] | Oliva D, 2014 | 0.7608 | 0.3251 | 1.4817 | 0.0364 | 53.6433 | 1.0967 × 10−3 |
| 33. | HPEPD | [8] | Laudani A, 2014 | 0.7607884 | 0.3102482 | 1.4769641 | 0.03655304 | 52.859056 | 1.1487 × 10−3 |
| 34. | MPCOA | [41] | Yuan X, 2014 | 0.76073 | 0.32655 | 1.48168 | 0.03635 | 54.6328 | 2.3131 × 10−3 |
| 35. | TLBO | [42] | Patel SJ, 2014 | 0.7608 | 0.3223 | 1.4837 | 0.0364 | 53.76027 | 9.6960 × 10−3 |
| 36. | BMO | [43] | Askarzadeh A, 2013 | 0.76077 | 0.32479 | 1.48173 | 0.03636 | 53.8716 | 9.8622 × 10−4 |
| 37. | ABSO | [44] | 0.76080 | 0.30623 | 1.47583 | 0.03659 | 52.2903 | 9.9125 × 10−4 | |
| 38. | IADE | [45] | Jiang LL, 2013 | 0.7607 | 0.33613 | 1.4852 | 0.03621 | 54.7643 | 9.9076 × 10−4 |
| 39. | CS | [46] | Ma J, 2013 | 0.7608 | 0.323 | 1.4812 | 0.0364 | 53.7185 | 9.9161 × 10−4 |
| 40. | ABSO | [47] | Hachana O, 2013 | 0.76080 | 0.30623 | 1.47986 | 0.03659 | 52.2903 | 1.4169 × 10−2 |
| 41. | ABCDE | 0.76077 | 0.32302 | 1.47986 | 0.03637 | 53.7185 | 4.8548 × 10−3 | ||
| 42. | DE | 0.76077 | 0.32302 | 1.48059 | 0.03637 | 53.7185 | 2.3423 × 10−3 | ||
| 43. | MPSO | 0.76077 | 0.32302 | 1.47086 | 0.03637 | 53.7185 | 3.9022 × 10−2 | ||
| 44. | GGHS | [48] | Askarzadeh A, 2012 | 0.76092 | 0.32620 | 1.48217 | 0.03631 | 53.0647 | 9.9089 × 10−4 |
| 45. | HS | 0.76070 | 0.30495 | 1.47538 | 0.03663 | 53.5946 | 9.9515 × 10−4 | ||
| 46. | IGHS | 0.76077 | 0.34351 | 1.48740 | 0.03613 | 53.2845 | 1.0335 × 10−3 | ||
| 47. | PS | [49] | AlHajri MF, 2012 | 0.7617 | 0.9980 | 1.6000 | 0.0313 | 64.10256 | 1.4936 × 10−2 |
| 48. | SA | [50] | El-Naggar KM, 2012 | 0.7620 | 0.4798 | 1.5172 | 0.0345 | 43.10345 | 1.8998 × 10−2 |
| 49. | GA | [51] | AlRashidi MR, 2011 | 0.7619 | 0.8087 | 1.5751 | 0.0299 | 42.37288 | 1.9078 × 10−2 |
| 50. | PSO | [52] | Ye M, 2009 | 0.760798 | 0.322721 | 1.48382 | 0.0363940 | 53.7965 | 9.6545 × 10−3 |
| No. | Algorithm | Ref. | First Author, Year | Ipv(A) | Io1(μA) | Io2(μA) | Rs(Ω) | Rp(Ω) | n1 | n2 | RMSE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Proposed Method—COA | 0.76078105 | 0.2259742 | 0.749346 | 0.03674043 | 55.4854236 | 1.45101673 | 2 | 9.82484852 × 10−4 | |||
| 1. | GOFPANM | [53] | X Shuhui, 2017 | 0.7607811 | 0.7493476 | 0.2259743 | 0.0367404 | 55.485449 | 2 | 1.4510168 | 9.82485 × 10−4 |
| 2. | SATLBO | [54] | Y Kunjie, 2017 | 0.76078 | 0.25093 | 0.545418 | 0.03663 | 55.117 | 1.45982 | 1.99941 | 9.82941 × 10−4 |
| 3. | MSSO | [20] | P Lin, 2017 | 0.760748 | 0.234925 | 0.671593 | 0.036688 | 55.714662 | 1.454255 | 1.995305 | 1.059101 × 10−3 |
| 4. | WDO | [55] | M Derick, 2017 | 0.7606 | 0.2531 | 0.0482 | 0.037433 | 52.6608 | 151.162 | 1.38434 | 1.095213 × 10−3 |
| 5. | CSO | [24] | L Guo, 2016 | 0.76078 | 0.22732 | 0.72785 | 0.036737 | 55.3813 | 1.45151 | 1.99769 | 9.82532 × 10−4 |
| 6. | GOTLBO | [23] | X Chen, 2016 | 0.760752 | 0.800195 | 0.220462 | 0.036783 | 56.0753 | 1.999973 | 1.448974 | 9.83152 × 10−4 |
| 7. | PCE | [26] | Y Zhang, 2016 | 0.760781 | 0.226015 | 0.749340 | 0.03674 | 55.483160 | 1.450.923 | 2 | 9.8248 × 10−4 |
| 8. | MABC | [28] | M Jamadi, 2016 | 0.7607821 | 0.24102992 | 0.6306922 | 0.03671215 | 54.7550094 | 1.4568573 | 2.0000.538 | 9.8276 × 10−4 |
| 9. | FPA | [36] | DF Alam, 2015 | 0.760795 | 0.300088 | 0.166159 | 0.0363342 | 52.3475 | 1.47477 | 2 | 1.24239 × 10−3 |
| 10. | BMO | [43] | A. Askarzadeh, 2013 | 0.76078 | 0.2111 | 0.87688 | 0.03682 | 558.081 | 1.44533 | 1.99.997 | 9.82661 × 10−4 |
| 11. | ABSO | [44] | A. Askarzadeh, 2013 | 0.73078 | 0.26713 | 0.38191 | 0.03657 | 54.6219 | 1.46512 | 1.98152 | 9.8359 × 10−04 |
| 12. | IGHS | [48] | A. Askarzadeh, 2012 | 0.76079 | 0.97310 | 0.16791 | 0.03690 | 56.8368 | 1.92126 | 1.42814 | 9.86572 × 10−4 |
| Algorithm | Mean Value of Requested Time (s) | Maximal Value of Requested Time (s) | Minimal Value of Requested Time (s) |
|---|---|---|---|
| COA | 0.016416 | 0.017023 | 0.015871 |
| ER-WCA [19] | 0.021063 | 0.024145 | 0.019492 |
| CS [46] | 0.029179 | 0.037177 | 0.027130 |
| HS [48] | 0.021103 | 0.023264 | 0.020393 |
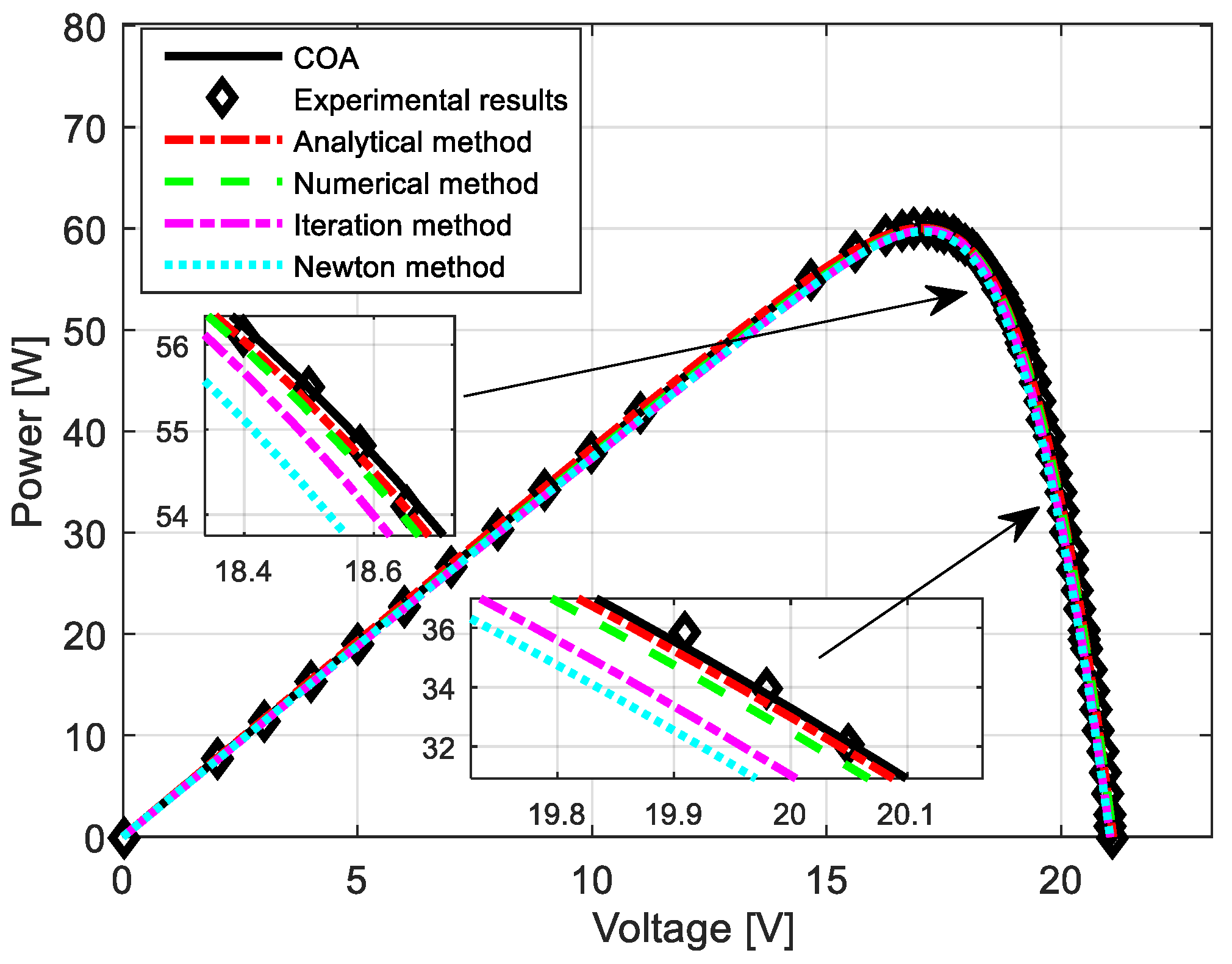
| Parameter | Analytical Method [13] | Numerical Method [13] | Iteration Method [57] | Newton Method [58] | COA |
|---|---|---|---|---|---|
| Ipv (A) | 3.8752 | 3.8046 | 3.8 | 3.8084 | 3.8418 |
| Io1 (A) | 3.6129 × 10−10 | 3.9901 × 10−10 | 4.704 × 10−10 | 4.8723 × 10−10 | 4.95821 × 10−8 |
| Io2 (A) | 9.3773 × 10−6 | 4.033 × 10−6 | 4.704 × 10−10 | 6.1528 × 10−10 | 9.54961 × 10−9 |
| Rs (Ω) | 0.3084 | 0.3397 | 0.35 | 0.3692 | 0.2495 |
| Rp (Ω) | 280.6449 | 280.2171 | 176.4 | 169.0471 | 267.57 |
| n1 | 1 | 0.99859 | 1 | 1.0003 | 1.2569 |
| n2 | 2 | 2.0014 | 1.2 | 1.9997 | 1.9345 |
| RMSE | 0.0358 | 0.0517 | 0.1211 | 0.1636 | 0.0194 |
| SDM | DDM | ||
|---|---|---|---|
| Rs (Ω) | 0.2283 | Rs (Ω) | 0.2513 |
| Rsh (Ω) | 439.55 | Rsh (Ω) | 782.9911 |
| Io (A) | 10.56 × 10−8 | Io1 (A) | 6.8452 × 10−8 |
| Ipv (A) | 0.2987 | n1 | 0.3342 |
| n | 0.3441 | Ipv (A) | 0.2972 |
| RMSE | 4.3418 × 10−4 | Io2 (A) | 6.0643 × 10−8 |
| n2 | 1.9906 | ||
| RMSE | 4.146 × 10−4 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ćalasan, M.; Jovanović, D.; Rubežić, V.; Mujović, S.; Đukanović, S. Estimation of Single-Diode and Two-Diode Solar Cell Parameters by Using a Chaotic Optimization Approach. Energies 2019, 12, 4209. https://doi.org/10.3390/en12214209
Ćalasan M, Jovanović D, Rubežić V, Mujović S, Đukanović S. Estimation of Single-Diode and Two-Diode Solar Cell Parameters by Using a Chaotic Optimization Approach. Energies. 2019; 12(21):4209. https://doi.org/10.3390/en12214209
Chicago/Turabian StyleĆalasan, Martin, Dražen Jovanović, Vesna Rubežić, Saša Mujović, and Slobodan Đukanović. 2019. "Estimation of Single-Diode and Two-Diode Solar Cell Parameters by Using a Chaotic Optimization Approach" Energies 12, no. 21: 4209. https://doi.org/10.3390/en12214209
APA StyleĆalasan, M., Jovanović, D., Rubežić, V., Mujović, S., & Đukanović, S. (2019). Estimation of Single-Diode and Two-Diode Solar Cell Parameters by Using a Chaotic Optimization Approach. Energies, 12(21), 4209. https://doi.org/10.3390/en12214209






