Brazil Offshore Wind Resources and Atmospheric Surface Layer Stability
Abstract
1. Introduction
2. Materials and Methods
2.1. Satellite Wind Data
2.2. Air-Sea Temperature, Humidity, Heat Fluxes and Surface Pressure
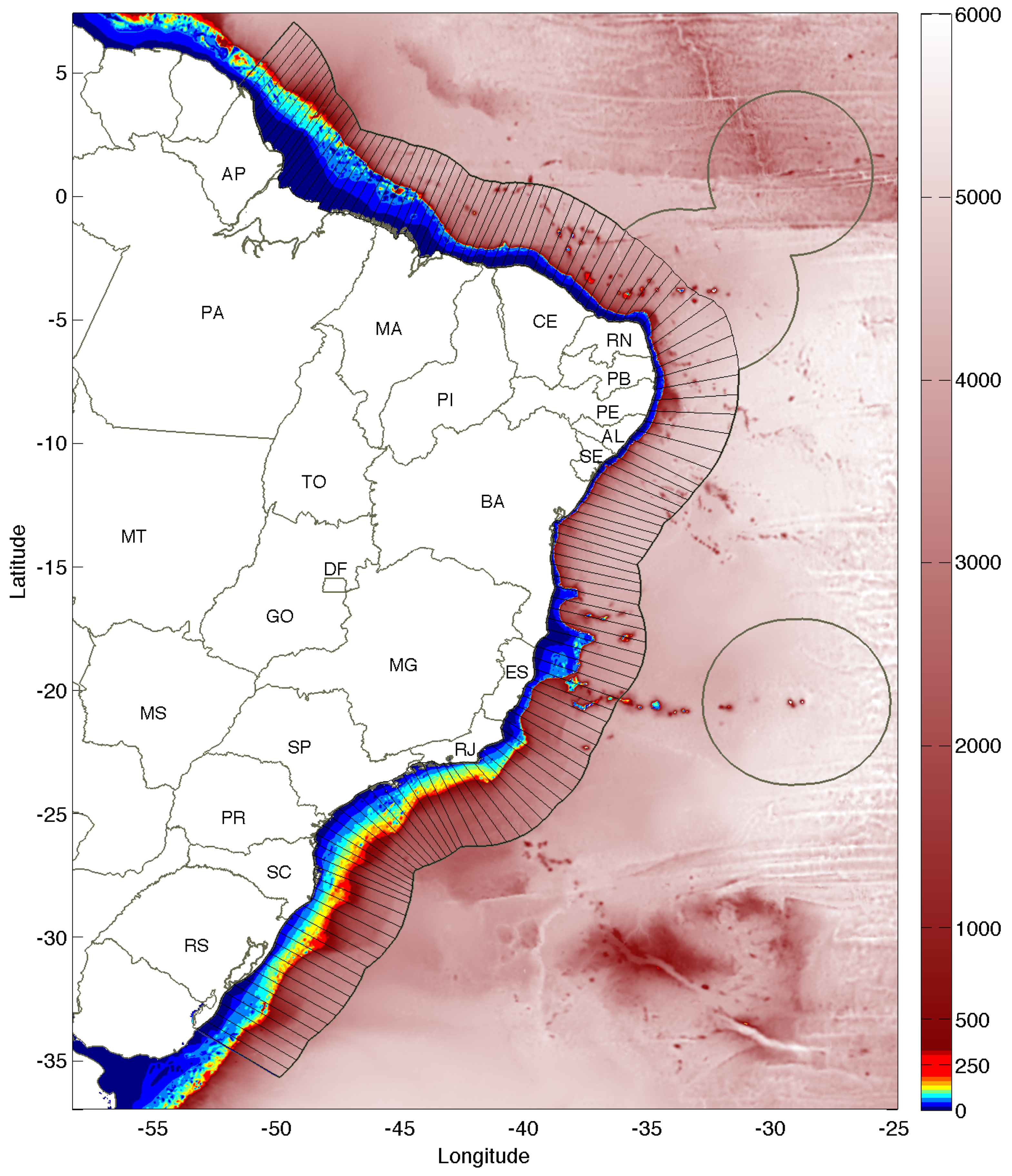
2.3. Bathymetry and ZEE Data
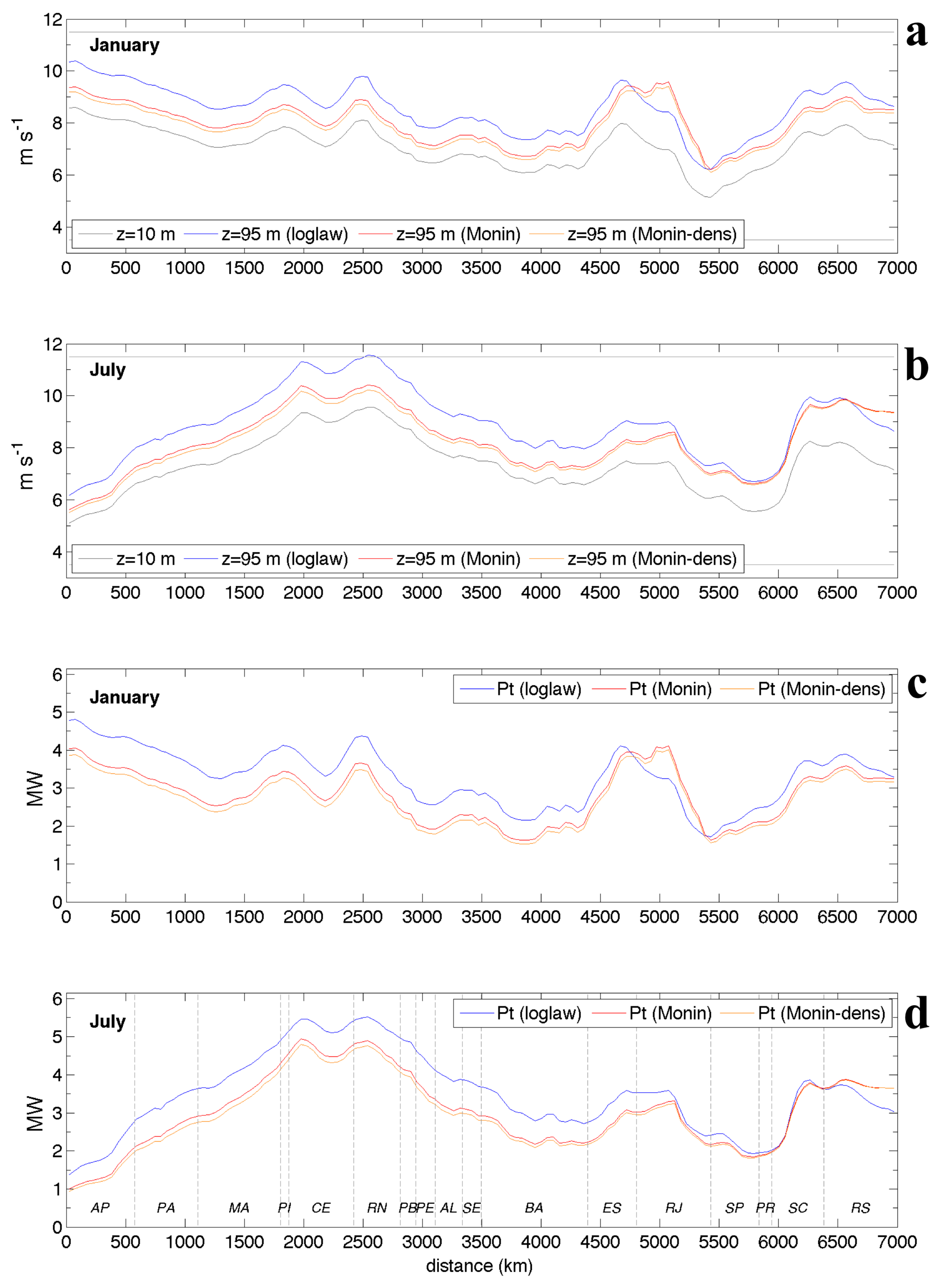
2.4. Wind Data Vertical Extrapolation
2.5. Wind Power and Resource Integration
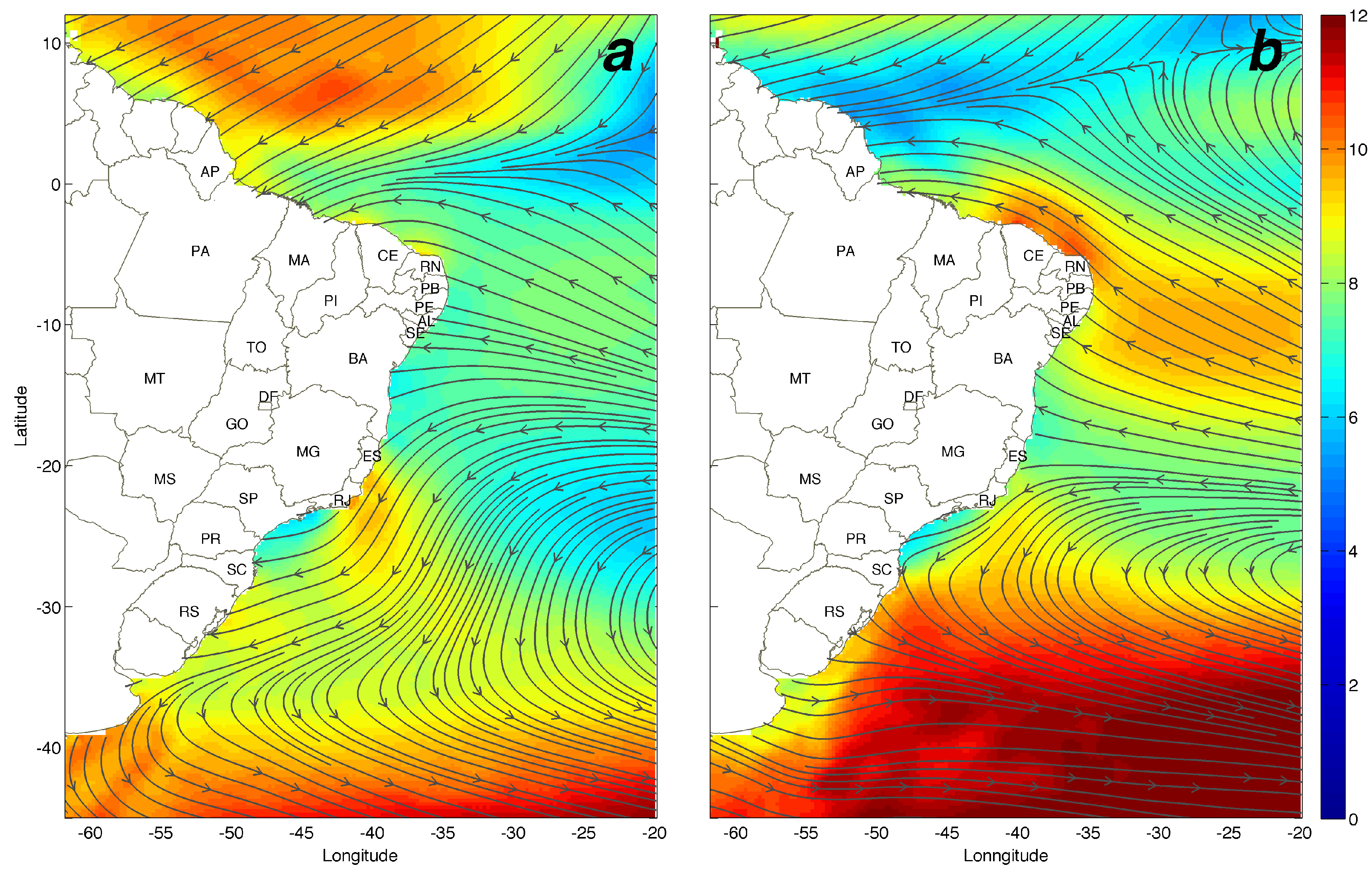
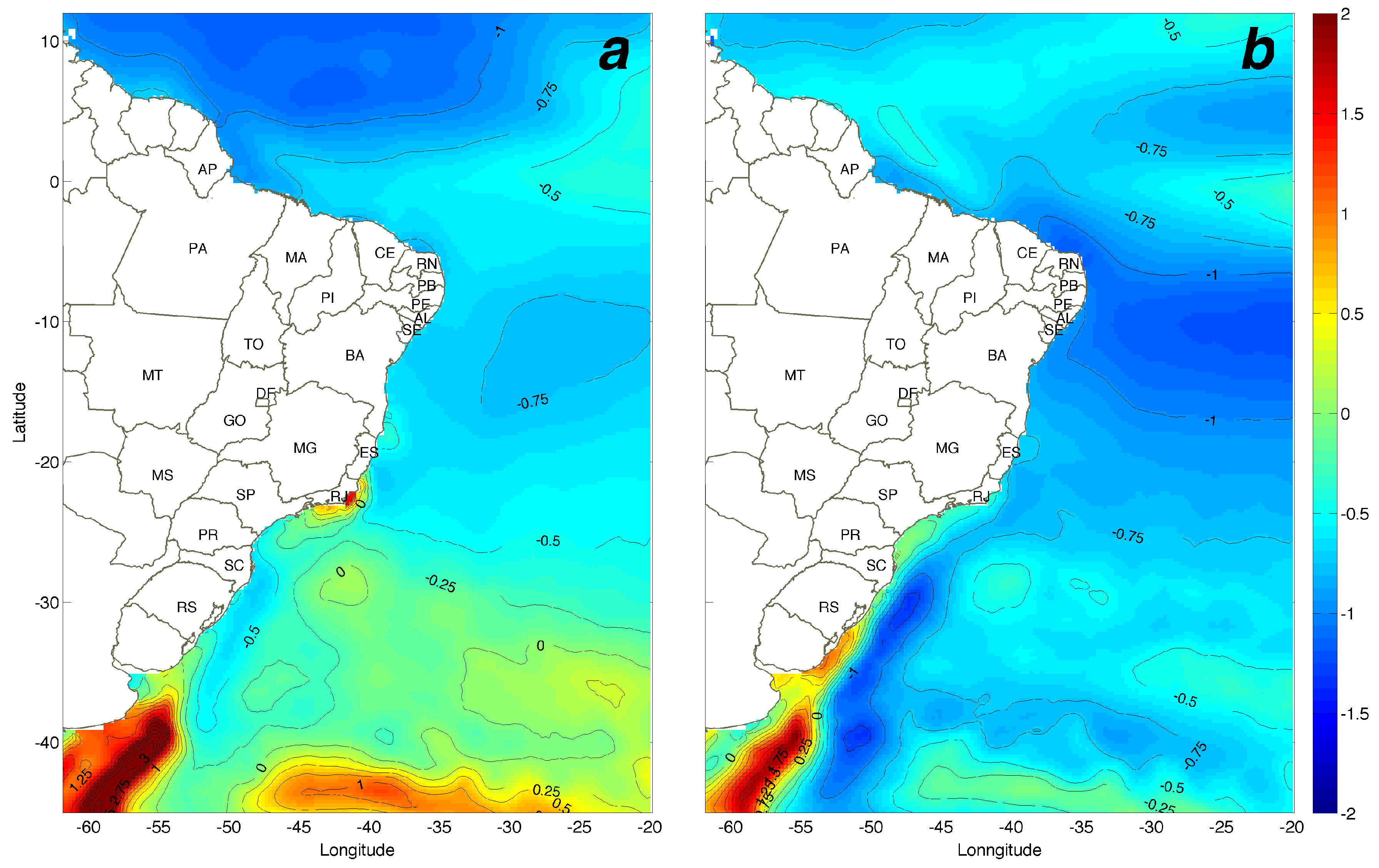
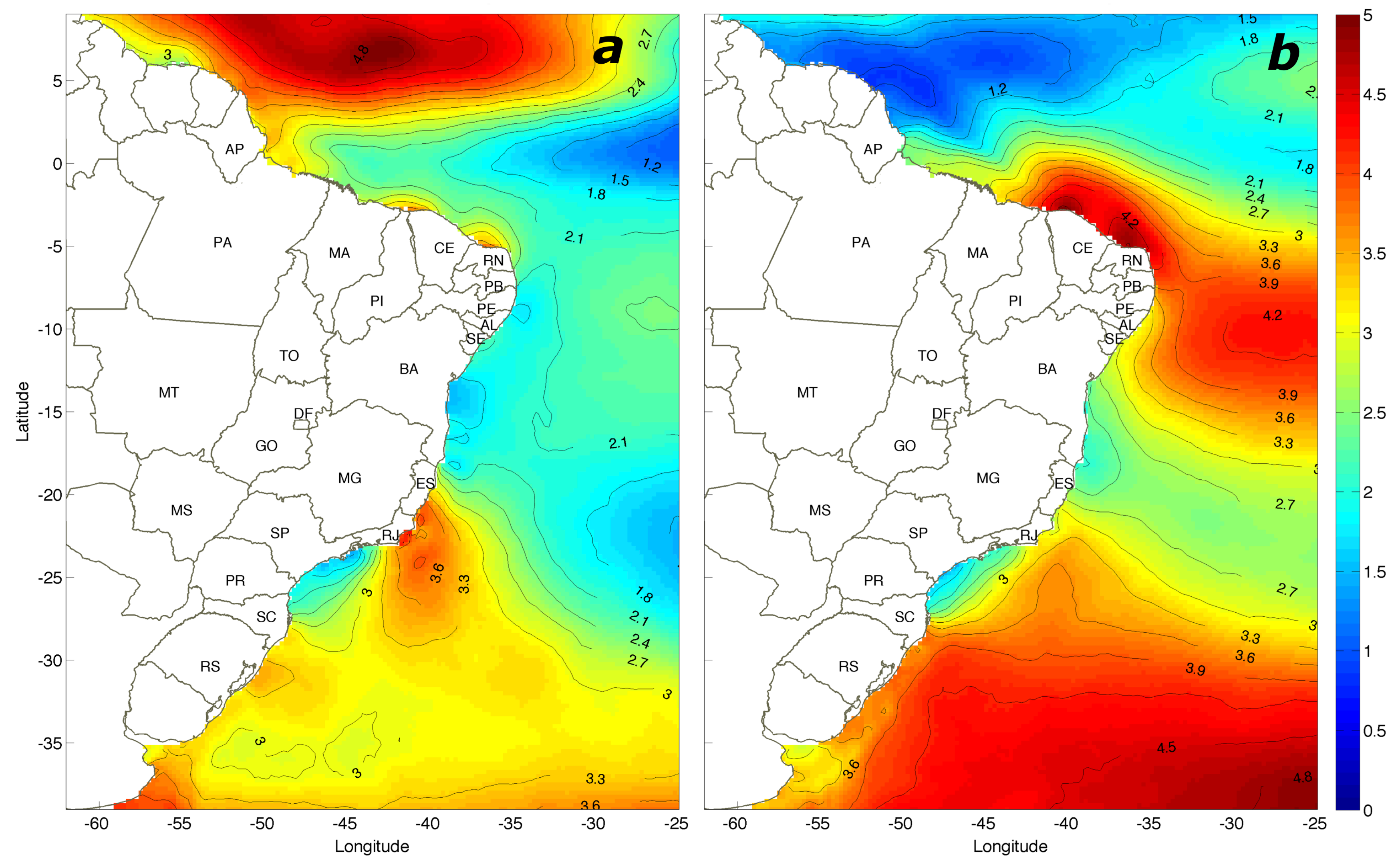
3. Results
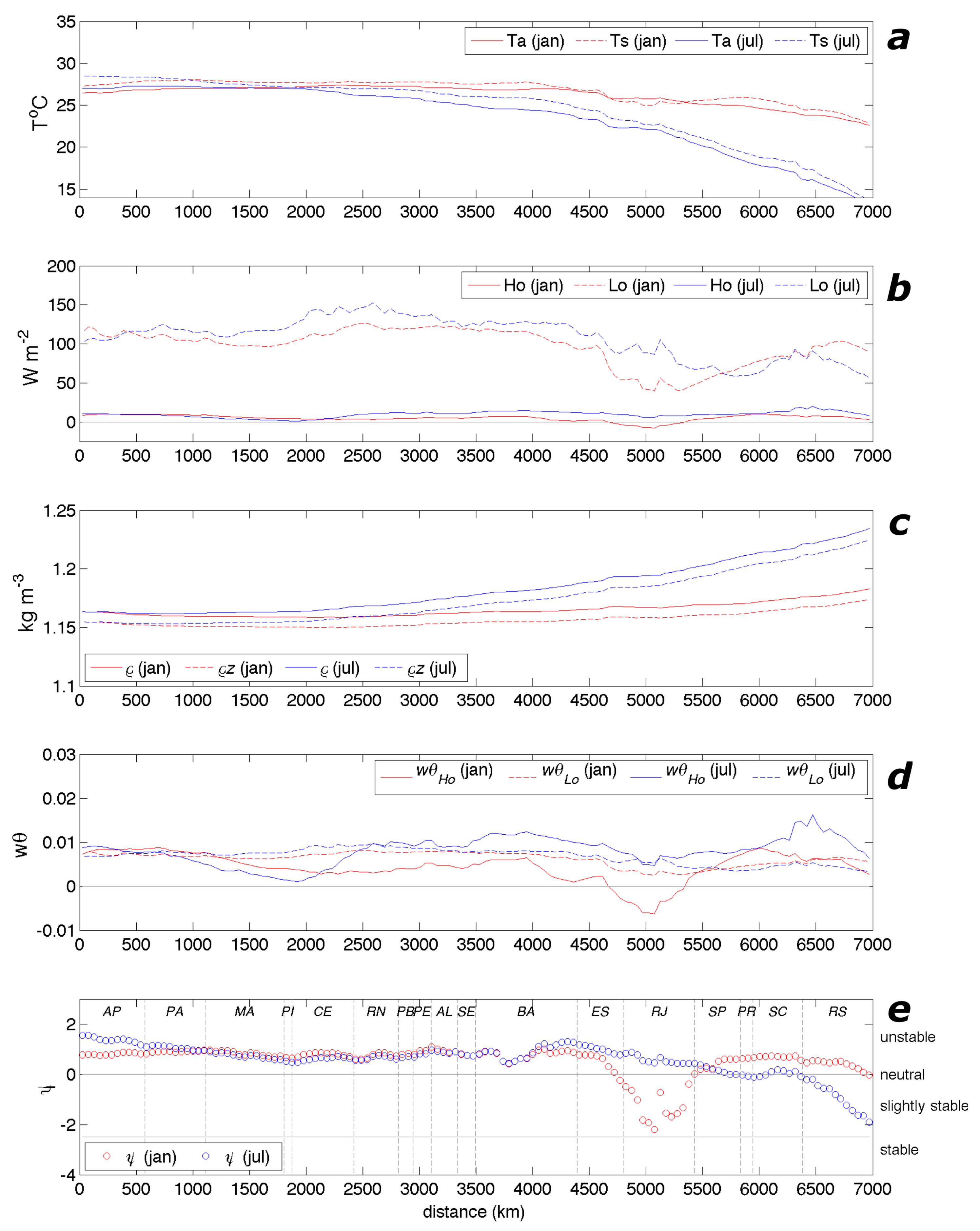
3.1. Air, Sea Surface Temperature and Heat Fluxes
3.2. Surface Layer Stability
3.3. Wind Speed Distributions
3.4. Atmospheric Stability Impact on Wind Estimations
3.5. Turbine Power Fields
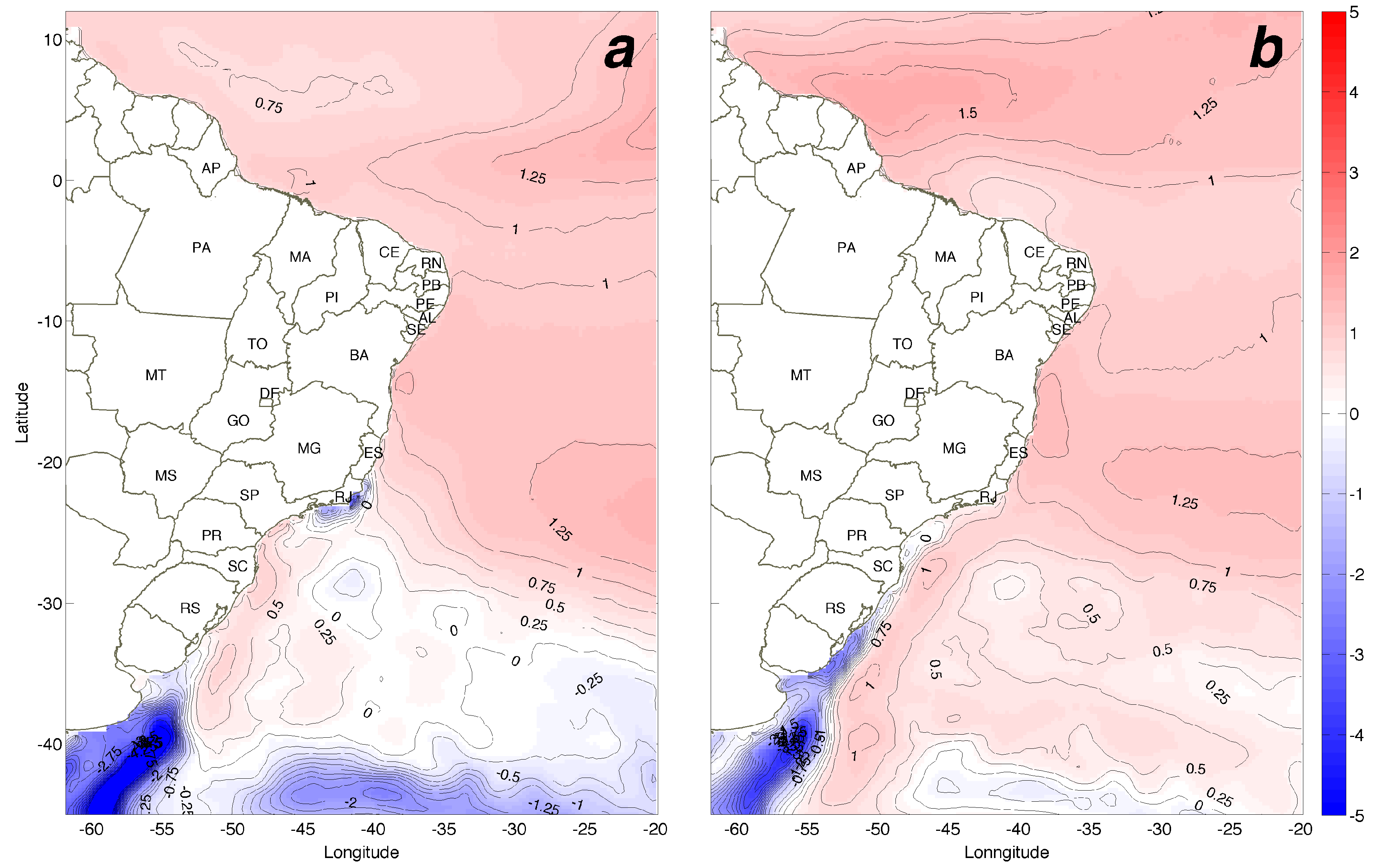
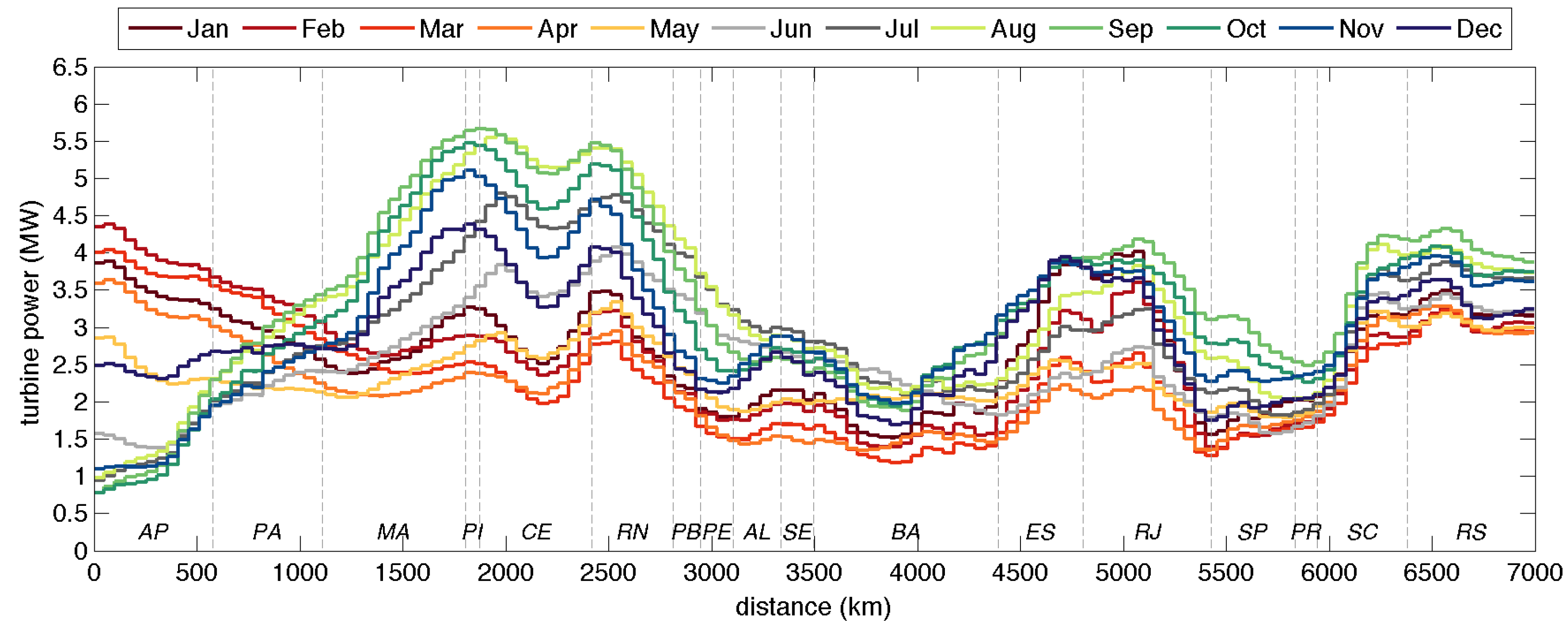
3.6. Seasonal Variability
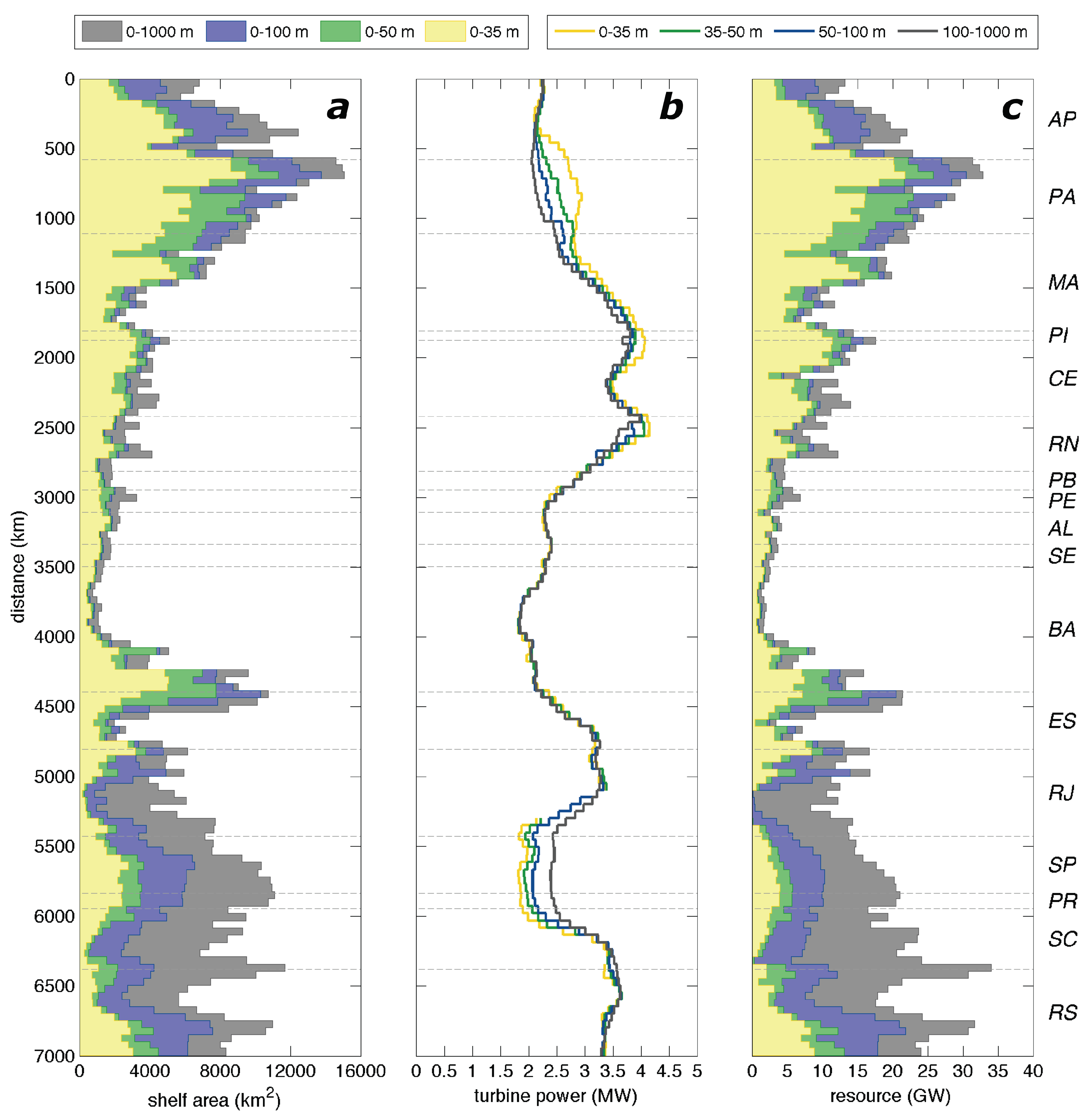
3.7. Resource Distribution
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rodrigues, S.; Restrepo, C.; Kontos, E.; Pinto, R.T.; Bauer, P. Trends of offshore wind projects. Renew. Sustain. Energy Rev. 2015, 49, 1114–1135. [Google Scholar] [CrossRef]
- Wind Europe. Offshore Wind in Europe. Key Trends and Statistics 2018; Technical Report; Wind Europe: Brussels, Belgium, 2018; Available online: https://windeurope.org (accessed on 14 April 2019).
- GWEC. Global Wind 2018 Report; Technical Report; Global Wind Energy Council: Brussels, Belgium, 2018; Available online: http://www.gwec.net (accessed on 14 April 2019).
- Wind Europe. Wind Energy in Europe: Scenarios for 2030; Technical Report; Wind Europe: Brussels, Belgium, 2017; Available online: https://windeurope.org (accessed on 14 April 2019).
- Musial, W.; Butterfield, S.; Ram, B. Energy from Offshore Wind; Technical Report; NREL/CP-500-39450; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2006. [Google Scholar]
- Arshad, M.; O’Kelly, B.C. Offshore wind-turbine structures: A review. Proc. ICE-Energy 2013, 166, 139–152. [Google Scholar] [CrossRef]
- Hywind. Building the World’s First Floating Offshore Wind Farm; Technical Report; Hywind, Statoil: Grampian, UK, 2015; Available online: http://www.statoil.com (accessed on 28 February 2018).
- Hywind. Hywind Scotland Pilot Park; Technical Report; Hywind, Statoil: Grampian, UK, 2016; Available online: http://www.statoil.com (accessed on 27 April 2018).
- Kempton, W.; Pimenta, F.M.; Veron, D.E.; Colle, B.A. Electric power from offshore wind via synoptic-scale interconnection. Proc. Natl. Acad. Sci. USA 2011, 107, 7240–7245. [Google Scholar] [CrossRef]
- Decker, J.D.; Woyte, A. Review of the various proposals for the European offshore grid. Renew. Energy 2013, 49, 58–62. [Google Scholar] [CrossRef]
- Storrer, M.; Garcia, P.; Barbosa, E.E. The Asa Branca offshore wind farm—A change for the creation of a new cluster for the supply of 10 GW of multimegawatt wind turbines in Brazil. In Proceedings of the European Offshore Wind Conference and Exhibition, Stockholm, Sweden, 14–16 September 2009; Wind Europe: Stockholm, Sweden, 2009. [Google Scholar]
- Tenproject. Offshore Wind Energy—Progettazione, studi di fattibilita e studi paesaggistici; Technical Report; Ten Project: San Giorgio del Sannio, Italy, 2015; Available online: https://www.tenproject.it/eolico-offshore (accessed on 27 March 2019).
- Pimenta, F.M.; Kempton, W.; Garvine, R.W. Combining meteorological stations and satellite data to evaluate the offshore wind power resource of Southeastern Brazil. Renew. Energy 2008, 33, 2375–2387. [Google Scholar] [CrossRef]
- Liu, W.T.; Tang, W.; Xie, X. Wind power distribution over the ocean. Geophys. Res. Lett. 2008, 35, L13808. [Google Scholar] [CrossRef]
- Capps, S.B.; Zender, C.S. Estimated global ocean wind power potential from QuikSCAT observations, accounting for turbine characteristics and siting. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Hasager, C.B. Offshore winds mapped from satellite remote sensing. WIREs Energy Environ. 2014, 3, 594–603. [Google Scholar] [CrossRef]
- Hasager, C.B.; Mouche, A.; Badger, M.; Bingol, F.; Karagali, J.; Driesenaar, T.; Stoffelen, A.; Peña, A.; Longépé, N. Offshore wind climatology based on synergetic use of Envisat ASAR, ASCAT and QuikSCAT. Remote Sens. Environ. 2015, 156, 247–263. [Google Scholar] [CrossRef]
- Doubrawa, P.; Barthelmie, R.J.; Pryor, S.C.; Hasager, C.B.; Badger, M.; Karagali, I. Satellite winds as a tool for offshore wind resource assessment: The Great Lakes Wind Atlas. Remote Sens. Environ. 2015, 168, 349–359. [Google Scholar] [CrossRef]
- Silva, A.R.; Pimenta, F.M.; Assireu, A.T.; Spyrides, M.H.C. Complementarity of Brazil’s hydro and offshore wind power. Renew. Sustain. Energy Rev. 2016, 56, 413–427. [Google Scholar] [CrossRef]
- Karagali, I. Scatterometry for wind energy. In Remote Sensing for Wind Energy; Report-0029 (EN); Pena, A., Karagali, I., Eds.; DTU Wind Energy, Riso Campus: Roskilde, Denmark, 2013; pp. 296–308. [Google Scholar]
- Lange, B.; Larsen, S.; Hojstrup, J.; Barthelmie, R. Importance of thermal effects and sea surface roughness for offshore wind resource assessment. J. Wind Eng. Ind. Aerod. 2004, 92, 959–988. [Google Scholar] [CrossRef]
- Barthelmie, R.J. The effects of atmospheric stability on coastal wind climates. Met. Appl. 1999, 6, 39–47. [Google Scholar] [CrossRef]
- Sathe, A.; Gryning, S.E.; Peña, A. Comparison of the atmospheric stability and wind profiles at two wind farm sites over a long marine fetch in the North Sea. Wind Energy 2011, 14, 767–780. [Google Scholar] [CrossRef]
- Archer, C.L.; Colle, B.A.; Veron, D.L.; Veron, F.; Sienkiewicz, M.J. On the predominance of unstable atmospheric conditions in the marine boundary layer offshore of the U.S. northeastern coast. J. Geophys. Res. 2016, 121, 8869–8885. [Google Scholar] [CrossRef]
- Arya, S.P. Introduction to Micrometeorology; International Geophysics Series; Academic Press: San Diego, CA, USA, 2001; p. 420. [Google Scholar]
- Capps, S.B.; Zender, C.S. Global ocean wind power sensitivity to surface layer stability. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Thomas, N.; Seim, H.; Haines, S. An Observational, Spatially Explicit, Stability-Based Estimate of the Wind Resource off the Shore of North Carolina. J. Appl. Meteorol. Climatol. 2015, 54, 2407–2425. [Google Scholar] [CrossRef]
- Badger, M.; Peña, A.; Hahmann, A.N.; Mouche, A.A.; Hasager, C.B. Extrapolating Satellite Winds to Turbine Operating Heights. J. Appl. Meteorol. Climatol. 2016, 55, 975–991. [Google Scholar] [CrossRef]
- Yu, L.; Weller, R.A. Multidecade Global Flux Datasets from the Objectively Analyzed Air-Sea Fluxes (OafLux) Project: Latent and Sensible Fluxes, Ocean Evaporation, and Related Surface Meteorological Variables; Technical Report; OA-2008-01; WHOI, Woods Hole Oceanographic Institute: Woods Hole, MA, USA, 2008. [Google Scholar]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP-DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 1631–1643. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; Technical Memorandum NESDIS NGDC-24; Technical Report; NOAA, National Geophysical Data Center: Boulder, CO, USA, 2009. [Google Scholar] [CrossRef]
- Archer, C.L.; Jacobson, M.Z. Geographical and seasonal variability of the global practical wind resources. Appl. Geogr. 2013, 45, 119–130. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; Wiley: West Sussex, UK, 2004; 577p. [Google Scholar]
- Zhang, H.; Bates, J.J.; Reynolds, R.W. Assessment of composite global sampling: Sea surface wind speed. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Zeng, L.; Levy, G. Space and time aliasing structure in monthly mean polar-orbiting satellite data. J. Geophys. Res. 1995, 100, 5133–5142. [Google Scholar] [CrossRef]
- Zhang, H. Blended and Gridded High Resolution Global Sea Surface Winds from Multiple Satellites; Technical Report; NOAA, NESDIS National Climate Data Center: Asheville, NC, USA, 2006. [Google Scholar]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 15, 571–591. [Google Scholar] [CrossRef]
- IBGE. Mapas temáticos, bases e referenciais; Technical Report; IBGE, Instituto Brasileiro de Geografia e Estatística: Rio de Janeiro, Brasil, 2015. [Google Scholar]
- Large, W.G.; Pond, S. Open ocean momentum flux measurements in moderate to strong winds. J. Phys. Oceanogr. 1981, 11, 324–336. [Google Scholar] [CrossRef]
- Stull, R. An Introduction to Boundary Layer Meteorology; Atmospheric and Oceanographic Sciences Library; Kluwer Academic Publishers: Norwell, MA, USA, 1988; 667p. [Google Scholar]
- Garratt, J.R. The Atmospheric Boundary Layer. Earth-Sci. Rev. 1994, 3, 89–134. [Google Scholar] [CrossRef]
- Holtslag, A.A.M.; De Bruin, H.A.R. Applied modeling of the nighttime surface energy balance over land. J. Appl. Meteorol. 1988, 27, 689–704. [Google Scholar] [CrossRef]
- Lu, X.; McElroy, M.B.; Kiviluoma, J. Global potential for wind-generated electricity. Proc. Natl. Acad. Sci. USA 2009, 106, 10933–10938. [Google Scholar] [CrossRef]
- Silveira, I.C.A.; Shmidt, A.C.K.; Campos, E.J.D.; Godoi, S.S.; Ikeda, Y. A Corrente do Brasil ao largo da costa leste Brasileira. Braz. J. Oceanogr. 2000, 48, 171–183. [Google Scholar] [CrossRef]
- Stramma, L.; England, M. On the water masses and mean circulation of the South Atlantic ocean. J. Geophys. Res. 1999, 104, 20863–20883. [Google Scholar] [CrossRef]
- Rodrigues, R.R.; Lorenzzetti, J.A. A numerical study of the effects of bottom topography and coastline geometry on the Southeast Brazilian coastal upwelling. Cont. Shelf Res. 2001, 21, 371–394. [Google Scholar] [CrossRef]
- Palóczy, A.; da Silveira, I.; Castro, B.; Calado, L. Coastal upwelling off Cape São Tomé (22° S, Brazil): The supporting role of deep ocean processes. Cont. Shelf Res. 2014, 89, 38–50. [Google Scholar] [CrossRef]
- Piola, A.R.; Campos, E.J.D.; Möller, O.O.; Charo, M.; Martinez, C. Subtropical Shelf Front off eastern South America. J. Geophys. Res. 2000, 105, 6565–6578. [Google Scholar] [CrossRef]
- Souza, R.B.; Robinson, I.S. Lagrangian and satellite observations of the Brazilian Coastal Current. Cont. Shelf Res. 2004, 24, 241–262. [Google Scholar] [CrossRef]
- Möller, O.O.; Piola, A.R.; Freitas, A.C.; Campos, E.D. The effects of river discharge and seasonal winds on the shelf off southeastern South America. Cont. Shelf Res. 2008, 28, 1607–1624. [Google Scholar] [CrossRef]
- Pimenta, F.M.; Kirwan, A.D. The response of large outflows to wind forcing. Cont. Shelf Res. 2014, 89, 24–37. [Google Scholar] [CrossRef]
- Pimenta, F.M.; Campos, E.J.D.; Miller, J.; Piola, A. A numerical study of the Plata river plume along the Southeastern South American continental shelf. Braz. J. Oceanogr. 2005, 53, 129–146. [Google Scholar] [CrossRef]
- Piola, A.R.; Matano, R.P.; Palma, E.D.; Möller, O.O.; Campos, E.J.D. The influence of the Plata river discharge on the western South Atlantic shelf. Geophys. Res. Lett. 2005, 32, L01603. [Google Scholar] [CrossRef]
- Campos, E.J.D.; Ikeda, Y.; Castro, B.M.; Gaeta, S.A.; Lorenzzetti, J.A.; Stevenson, M.R. Experiment studies circulation in the Western South Atlantic. In EOS Transaction; Amer. Geophys. Union: Washington, DC, USA, 1996; Volume 77, pp. 253–259. [Google Scholar] [CrossRef]
- Vivier, F.; Provost, C. Volume transport of the Malvinas current: Can the flow be monitored by TOPEX/POSEIDON? J. Geophys. Res. 1999, 104, 21105–21122. [Google Scholar] [CrossRef]
- Satyamurty, P.; Ferreira, C.C.; Gan, M.A. Cyclonic vortices over South America. Tellus 1990, 42, 194–201. [Google Scholar] [CrossRef][Green Version]
- Cavalcanti, I.F.A.; Ferreira, N.J.; Silva, M.G.A.J.; Silva Dias, M.A.F. Tempo e clima no Brasil; Oficina de Textos: São Paulo, Brazil, 2009; 463p. [Google Scholar]
- Ortiz, G.P.; Kampel, M. Potencial da energia eólica offshore na margem do Brasil. In Proceedings of the V Simpósio Brasileiro de Oceanografia, Oceanografia e Políticas Públicas, Santos, SP, Brazil, 17–20 April 2011; pp. 1–4. [Google Scholar]
- Nunes, H.M.P. Avaliação do potencial eólico ao largo da costa nordeste do Brasil. Master’s Thesis, Universidade de Brasília, Brasília, Brazil, 2012. [Google Scholar]
- Souza, A.G.Q.; Pimenta, F.M.; Silva, A.R.; Melo, E.C.S.; Silva, M.P.; Ianniruberto, M.; Nunes, H.M.P. North and Northeast Brazil Offshore Wind Power. In Proceedings of the Thirteenth International Congress of the Brazilian Geophysical Society, SBGf, Rio de Janeiro, RJ, Brazil, 26–29 August 2013; pp. 1–5. [Google Scholar] [CrossRef]
- EWEA. The European Offshore Wind Industry–Key Trends and Statistics 2015; Eur. Wind Energy Assoc.: Brussels, Belgium, 2015; p. 24. [Google Scholar]
- Dhanju, A.; Whitaker, P.; Kempton, W. Assessing offshore wind resources: An accessible methodology. Renew. Energy 2008, 33, 55–64. [Google Scholar] [CrossRef]
- Pimenta, F.M.; Assireu, A.T. Simulating reservoir storage for a wind-hydro hydrid system. Renew. Energy 2015, 76, 757–767. [Google Scholar] [CrossRef]
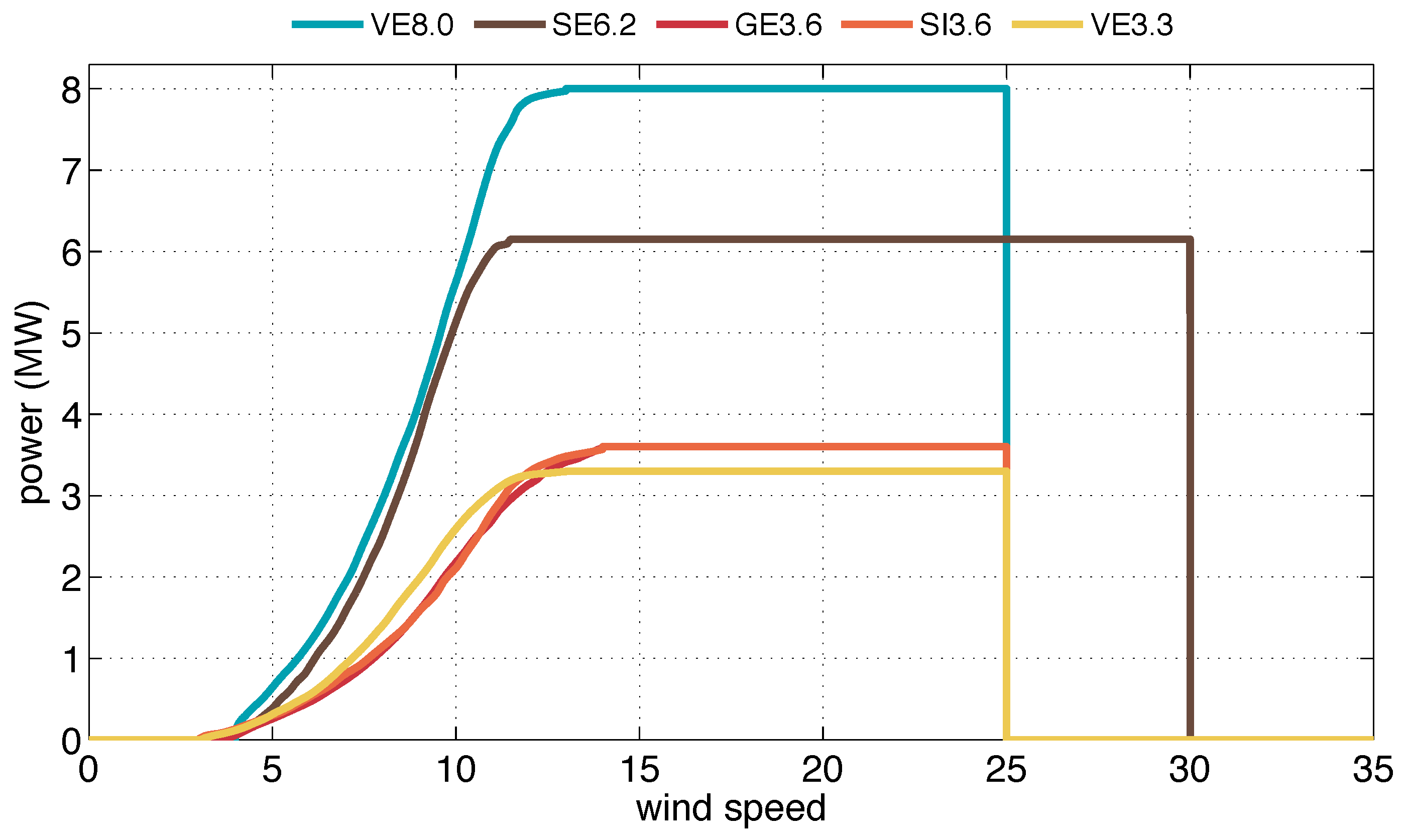
| Turbine Model | |||||
|---|---|---|---|---|---|
| Operating data | VE 3.3 | GE 3.6 | SI 3.6 | SE 6.2 | VE 8.0 |
| Rated capacity (kW) | 3300 | 3600 | 3600 | 6150 | 8000 |
| Cut-in speed (m s) | 3.0 | 3.5 | 3.0 | 3.5 | 4.0 |
| Cut-out speed (m s) | 25 | 25 | 25 | 30 | 25 |
| Rated speed (m s) | 13 | 14 | 14 | 11.5 | 13 |
| Rotor diameter (m) | 112 | 104 | 120 | 152 | 164 |
| Swept area (m) | 9852 | 8495 | 11,300 | 18,146 | 21,124 |
| Bathymetric Interval | Shelf Area (km) | Resource (GW) | VE 3.3 | GE 3.6 | SI 3.6 | SE 6.2 | VE 8.0 |
|---|---|---|---|---|---|---|---|
| 723 | 713 | 548 | 729 | 737 | |||
| 0–35 m | 318,618 | 753 | 747 | 573 | 764 | 771 | |
| 937 | 957 | 734 | 959 | 977 | |||
| 976 | 963 | 741 | 983 | 995 | |||
| 0–50 m | 429,529 | 1017 | 1007 | 774 | 1030 | 1039 | |
| 1248 | 1274 | 977 | 1276 | 1301 | |||
| 1337 | 1326 | 1021 | 1346 | 1366 | |||
| 0–100 m | 589,465 | 1389 | 1383 | 1063 | 1405 | 1423 | |
| 1670 | 1710 | 1312 | 1704 | 1742 | |||
| 7217 | 7114 | 5482 | 7257 | 7346 | |||
| EEZ - Brazil | 3,144,308 | 7509 | 7430 | 5715 | 7577 | 7664 | |
| 8948 | 9119 | 6990 | 9134 | 9308 | |||
| 892 | 866 | 673 | 885 | 899 | |||
| EEZ - Trindade | 468,612 | 924 | 899 | 698 | 920 | 933 | |
| 1137 | 1145 | 883 | 1149 | 1174 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pimenta, F.M.; Silva, A.R.; Assireu, A.T.; Almeida, V.d.S.e.; Saavedra, O.R. Brazil Offshore Wind Resources and Atmospheric Surface Layer Stability. Energies 2019, 12, 4195. https://doi.org/10.3390/en12214195
Pimenta FM, Silva AR, Assireu AT, Almeida VdSe, Saavedra OR. Brazil Offshore Wind Resources and Atmospheric Surface Layer Stability. Energies. 2019; 12(21):4195. https://doi.org/10.3390/en12214195
Chicago/Turabian StylePimenta, Felipe M., Allan R. Silva, Arcilan T. Assireu, Vinicio de S. e Almeida, and Osvaldo R. Saavedra. 2019. "Brazil Offshore Wind Resources and Atmospheric Surface Layer Stability" Energies 12, no. 21: 4195. https://doi.org/10.3390/en12214195
APA StylePimenta, F. M., Silva, A. R., Assireu, A. T., Almeida, V. d. S. e., & Saavedra, O. R. (2019). Brazil Offshore Wind Resources and Atmospheric Surface Layer Stability. Energies, 12(21), 4195. https://doi.org/10.3390/en12214195







