Using True RMS Current Measurements to Estimate Harmonic Impacts of Multiple Nonlinear Loads in Electric Distribution Grids
Abstract
1. Introduction
- (1)
- Validation using the permutation importance as a metric to measure the impact factor for each nonlinear load by comparison with the result obtained by ATP software in a controlled simulation scheme using the IEEE-13 bus system [10].
- (2)
- Applying the methodology to the AMI system installed at the Federal University of Pará campus located in the north of Brazil, so that it is possible to indicate the most representative nonlinear loads in impacting the THDu at the Common Coupling Point (CCP) with the utility electric grid. The result of this test case was also compared to the methodology presented by [10].
2. Related Works
- (1)
- The methodology uses as input the true RMS current, an electric variable that can be easily measured by low-cost meters, making viable for the reality of both distribution utilities and customers. The use of true RMS current in identifying and quantifying the impact of multiple nonlinear loads on voltage total harmonic distortion levels at the CCP as proposed in this article is a novelty.
- (2)
- The methodology can be applied with other input and output variables as long as they are representative to the scope of the problem. True RMS current was chosen because it is the most accessible magnitude with high correlation with voltage total harmonic distortion levels at the point of interest;
- (3)
- It presents an innovative and insightful methodology for solving the problem of identifying and quantifying the impact of multiple loads on the THDu level per phase at the CCP through a metric which is inherent to the regression tree technique. As it is already a step of the computational technique chosen, the estimation of input variables importance in the output variable does not add computational cost.
- (1)
- Understanding that Advanced Metering Infrastructure is a relatively new definition, this article presents some procedures to ensure data reliability during its implementation;
- (2)
- Provides real-time power quality monitoring in all phases of the distribution grid, identifying meters with big contribution to total harmonic distortion;
- (3)
- Allows a wide range of experiments with varying time windows. According to the case to be studied by the grid managers, the combination of the proposed methodology with an AMI is able to investigate the meters contributions at different times per day, week or month, investigating the most impacting loads on the grid power quality seasonally.
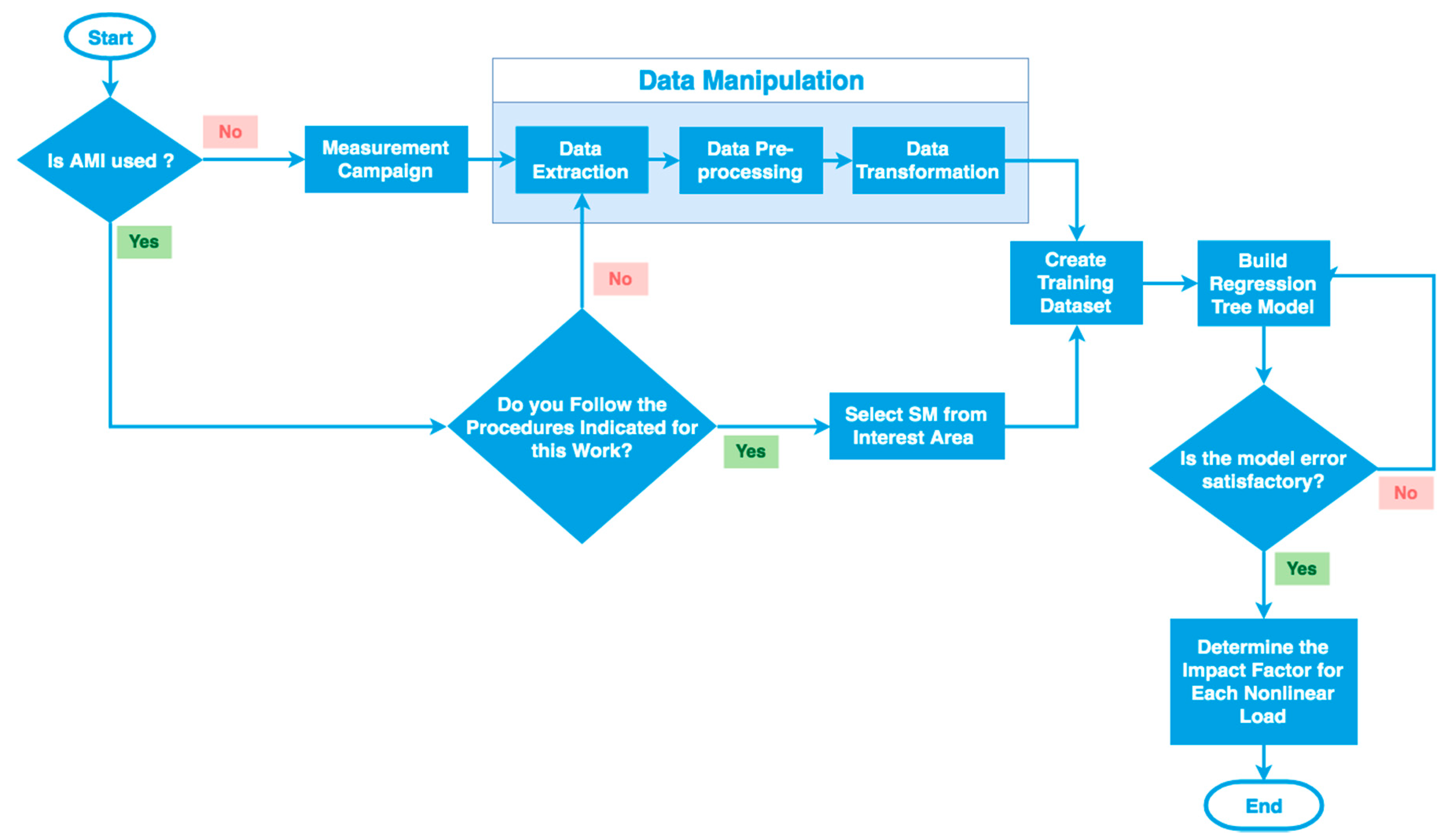
3. Proposed Methodology
Aprocedures for Implementing the Methodology in an Advanced Metering Infrastructure
- End user devices-Smart Meters;
- Communication;
- Meters Data Management System (MDMS).
- Flag communication failures;
- Scan network to check if meter is connected or disconnected to system;
- Identify and flag meter configuration changes;
- Request data and apply checksums CRC (Cyclic Redundancy Check).
| Algorithm 1: CHAUVENET CRITERIA |
 |
4. Results and Discussion
4.1. Permutation Importance Validation
4.1.1. IEEE-13 Bus Industrial Electrical Distribution System
4.1.2. Data Manipulation
4.1.3. Comparison between Techniques and Metrics
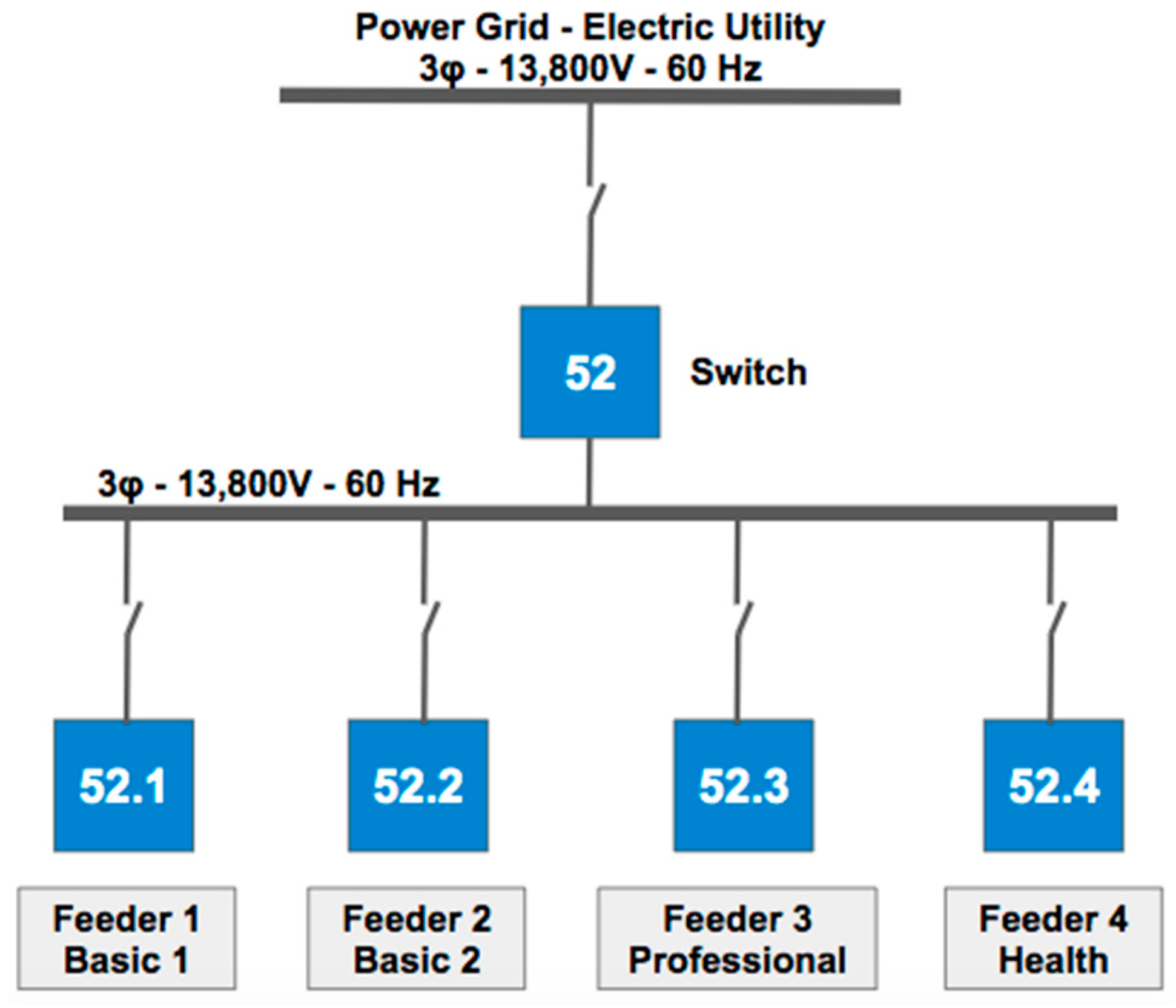
4.2. Test Case in an Advanced Metering Infrastructure Instalation
4.2.1. Brief Description of SISGEE (Electric Management System)
4.2.2. Test Scenario Description
4.2.3. Parameters Definition
4.2.4. Impact Factor Calculation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Harmonics, P.S. Power System Harmonics: An Overview. IEEE Trans. Power Appar. Syst. 1983, 2455–2460. [Google Scholar] [CrossRef]
- Arrillaga, J.; Watson, N.R. Power System Harmonics, 2nd ed.; John Wiley & Sons: Chichester, UK, 2003. [Google Scholar]
- IEEE. IEEE Recomemend Practices and Requirements for Harmonic Control in Electrical Power Systems; IAS—IEEE Industry Applications Society: New York, NY, USA, 2014; pp. 519–1992. [Google Scholar] [CrossRef]
- Variz, A.M. Three-phase Harmonic Load Flow by the Current Injection (Fluxo de carga harmônico trifásico pela injeção de corrente). Master’s Thesis, COPPE/UFRJ—Instituto Alberto Luiz Coimbra de Pós-Graduação e Pesquisa de Engenharia (Coppe/UFRJ), Rio de Janeiro, Brazil, 2006. [Google Scholar]
- Electric Energy Distribution Procedures Guide—PRODIST. Module 8—Power Quality; Electric Energy Brazilian Agency (ANEEL): Brasilia, Brazil, 2017. [Google Scholar]
- Mohassel, R.R.; Fung, A.; Mohammadi, F.; Raahemifar, K. A survey on Advanced Metering Infrastructure. Int. J. Electr. Power Energy Syst. 2014, 63, 473–484. [Google Scholar] [CrossRef]
- Sigle, M.; Bauer, M.; Liu, W.; Dostert, K. Transmission Channel Properties of the Low Voltage Grid for Narrowband Power Line Communication. In Proceedings of the IEEE International Symposium on Power Line Communications and Its Applications, Udine, Italy, April 2011. [Google Scholar]
- Sigle, M.; Dostert, K.; Liu, W. Channel characterization and system verification for narrowband power line communication in smart grid applications. IEEE Commun. Mag. 2011, 49, 28–35. [Google Scholar] [CrossRef]
- Bucci, G.; D’Innocenzo, F.; Dolce, S.; Fiorucci, E.; Ciancetta, F. Power Line Communication, Overview of Standards and Applications. In Proceedings of the XXI IMEKO World Congress Measurement in Research and Industry, Prague, Czech Republic, 30 August–4 September 2015. [Google Scholar]
- Manito, A.; Bezerra, U.; Tostes, M.; Matos, E.; Carvalho, C.; Soares, T. Evaluating Harmonic Distortions on Grid Voltages Due to Multiple Nonlinear Loads Using Artificial Neural Networks. Energies 2018, 11, 3303. [Google Scholar] [CrossRef]
- Xu, W.; Liu, Y. A method for determining customer and utility harmonic contributions at the point of common coupling. IEEE Trans. Power Deliv. 2000, 15, 804–811. [Google Scholar] [CrossRef]
- Pyzalski, T.; Wilkosz, K. Identification of harmonic sources in a power system: A new method. In Proceedings of the 2005 IEEE Russia Power Tech, St. Petersburg, Russia, 27–30 June 2005; pp. 1–6. [Google Scholar]
- Wang, W.; Nino, E.E.; Xu, W. Harmonic impedance measurement using a thyristor-controlled short circuit. IET Gener. Transm. Distrib. 2007, 1, 707–713. [Google Scholar] [CrossRef]
- Srinivasan, D.; Ng, W.S.; Liew, A.C. Neural-network-based signature recognition for harmonic source identification. IEEE Trans. Power Deliv. 2006, 21, 398–405. [Google Scholar] [CrossRef]
- Mazumdar, J.; Harley, R.G.; Lambert, F.C. System and Method for Determining Harmonic Contributions from Non-Linear Loads. U.S. Patent US 7,013,227, 14 March 2006. [Google Scholar]
- Mazumdar, J.; Harley, R.G.; Lambert, F.C.; Venayagamoorthy, G.K. Neural network-based method for predicting nonlinear load harmonics. IEEE Trans. Power Electron. 2007, 22, 1036–1045. [Google Scholar] [CrossRef]
- Mazumdar, J.; Harley, R.G. Recurrent neural networks trained with backpropagation through time algorithm to estimate nonlinear load harmonic currents. IEEE Trans. Ind. Electron. 2008, 55, 3484–3491. [Google Scholar] [CrossRef]
- Yin, Z.; Sun, Y.; Yu, T. New methods exploration for harmonic source identification technologies. In Proceedings of the 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, Shandong, China, 6–9 July 2011; pp. 399–402. [Google Scholar]
- Kandev, N.P.; Chénard, S. Method for determining customer contribution to harmonic variations in a large power network. In Proceedings of the International Conference Harmonics and Quality of Power (ICHQP), Bergamo, Italy, 26–29 September 2010; pp. 1–7. [Google Scholar]
- Matos, O.; Soares, T.M.; Bezerra, U.H.; de Lima Tostes, M.E.; Manito, A.R.A.; Costa, B.C., Jr. Using linear and non-parametric regression models to describe the contribution of non-linear loads on the voltage harmonic distortions in the electrical grid. IET Gener. Transm. Distrib. 2016, 10, 1825–1832. [Google Scholar] [CrossRef]
- Paixao, U.C., Jr.; Manito, A.R.A.; Rocha, G.V.S.; Monteiro, F.P.; Carvalho, C.C.M.M.; Bezerra, U.H.; Tostes, M.E.L. Evaluation of Harmonic Contribution Impacts in the Electric Grid Through Linear Regression, Artificial Neural Networks and Regression tree. In Proceedings of the IEEE PES Transmission & Distribution Conference and Exhibition—Latin America (T&D-LA), Lima, Peru, 18–21 August 2018. [Google Scholar] [CrossRef]
- Moradifar, A.; Akbari Foroud, A.; Gorgani Firouzjah, K. Intelligent localisation of multiple non-linear loads considering impact of harmonic state estimation accuracy. IET Gener. Transm. Distrib. 2017, 11, 1943–1953. [Google Scholar] [CrossRef]
- Mazin, H.E.; Xu, W.; Huang, B. Determining the harmonic impacts of multiple harmonic-producing loads. In Proceedings of the IEEE Power Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1187–1195. [Google Scholar] [CrossRef]
- Ganjisaffar, Y.; Caruana, R.; Lopes, C.V. Bagging gradient boosted trees for high precision, low variance ranking models. In Proceedings of the 34th SIGIR, Beijing, China, 24–28 July 2011; pp. 85–94. [Google Scholar]
- Asadi, N.; Lin, J.; de Vries, A.P. Runtime Optimizations for Tree-Based Machine Learning Models. IEEE Trans. Knowl. Data Eng. 2014, 26, 2281–2292. [Google Scholar] [CrossRef]
- Zhang, B.; Ren, J.; Cheng, Y.; Wang, B.; Wei, Z. Health Data Driven on Continuous Blood Pressure Prediction Based on Gradient Boosting Decision Tree Algorithm. IEEE Access 2019, 7, 32423–32433. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Manual on Setting Up, Using, and Understanding Random Forests; v3.1; Statistics Department University of California Berkeley: Berkeley, CA, USA, 2002. [Google Scholar]
- Warren, H.S. Cyclic Redundancy Check. In Hacker’s Delight, 2nd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2013; pp. 319–323. [Google Scholar]
- Lin, L.; Sherman, P.D. Cleaning data the Chauvenet way. In Proceedings of the South East SAS Users Group—SESUG, Hilton Head, SC, USA, 4–6 November 2007. [Google Scholar]
- Holman, J.P. Experimental Methods for Engineers, 6th ed.; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Louppe, G.; Wehenkel, L.; Sutera, A.; Geurts, P. Understanding variable importances in forests of randomized trees. In Proceedings of the NIPS 2013—Neural Information Processing Systems Conference, Lake Tahoe, NV, USA, 5–10 December 2013. [Google Scholar]
- Nandlall, S.D.; Millard, K. Quantifying the Relative Importance of Variables and Groups of Variables in Remote Sensing Classifiers Using Shapley Values and Game Theory. IEEE Geosci. Remote Sens. Lett. 2019, 1–5. [Google Scholar] [CrossRef]
- Behnamian, A.; Millard, K.; Banks, S.N.; White, L.; Richardson, M.; Pasher, J. A Systematic Approach for Variable Selection with Random Forests: Achieving Stable Variable Importance Values. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1988–1992. [Google Scholar] [CrossRef]
- Alternative Transiente Program—ATP (ATP Draw)—User’s Manual, Version 5.6; Norwegian University of Technology Trondheim: Trondheim, Norway, 2009.
- Abu-Hashim, R.; Burch, R.; Chang, G.; Grady, M.; Gunther, E.; Halpin, M.; Harziadonin, C.; Liu, Y.; Marz, M.; Ortmeyer, T.; et al. Test systems for harmonics modeling and simulation. IEEE Trans. Power Deliv. 1999, 14. [Google Scholar] [CrossRef]
- Test System 3: A 13-Bus Balanced Industrial Distribution System, Harmonics Working Group—Power Quality Subcommittee, IEEE Power and Energy Society. Available online: http://grouper.ieee.org/groups/harmonic/simulate/download.htm (accessed on 8 October 2019).
- Jegadeesan, M.; Venkatesh, N. Estimation and Mitigation of Current and Voltage Harmonics in Distribution System Using Distributed Generation. In Proceedings of the International Conference on Innovations in Engineering and Technology (ICIET’14), Madurai, Tamil Nadu, India, 21–22 March 2014. [Google Scholar]
- El-Mamlouk, W.M.; Mostafa, H.E.; El-Sharkawy, M.A. Active power filter controller for harmonic suppression in industrial distribution system. Ain Shams Eng. J. 2011, 2, 161–172. [Google Scholar] [CrossRef]
- Ayunda, S.W. Harmonics propagation and distortion caused by a nonlinear load in balance distribution network. Afr. J. Phys. 2016, 3, 110–118. [Google Scholar]
- Cano-Plata, E.A.; Jimenez-Lozano, G.; Soto-Marín, O.J.; Ustariz-Farfán, A.J. Hybrid Simulation of Power Quality Assessment: An Application for Power Ground Grid in Arc Furnace Systems. IEEE Trans. Ind. Appl. 2016, 52, 2648–2653. [Google Scholar] [CrossRef]
- Muniz, J.R.S.; Moraes, J.A.A.; Rocha, G.V.S.; Nunes, M.V.A.; Barradas, R.P.S.; Bezerra, U.H.; Brito, A.B.; Monteiro, F.P.; Carvalho, R.L.S. ATP Cards Automatic Generation from an Electrical Network Elements Database Using Python. In Proceedings of the IEEE International Conference on Industry Applications (INDUSCON), São Paulo, Brazil, 11–14 November 2018. [Google Scholar] [CrossRef]
- Tavares, K.A.; Silva, K.M. Evaluation of Power Transformer Differential Protection Using the ATP Software. IEEE Latin Am. Trans. 2014, 12, 161–168. [Google Scholar] [CrossRef]
- Chen, X. A three-phase multi-legged transformer model in ATP using the directly-formed inverse inductance matrix. IEEE Trans. Power Deliv. 1996, 11, 1554–1562. [Google Scholar] [CrossRef]
- Apostolopoulos, C.; Tsakiris, D. Design and Performance Evaluation of a High-Impedance REF Scheme for MV/LV Transformers. IEEE Trans. Ind. Appl. 2015, 51, 5398–5409. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]








| Error | Code |
|---|---|
| Without Error | 0 |
| Communication Error | 1 |
| CRC Error | 2 |
| NaN Error | 3 |
| Date Error | 4 |
| N | AR |
|---|---|
| 3 | 1.38 |
| 5 | 1.65 |
| 6 | 1.73 |
| 7 | 1.8 |
| 10 | 1.96 |
| 50 | 2.57 |
| 100 | 2.87 |
| 300 | 3.14 |
| 500 | 3.29 |
| 1000 | 3.48 |
| Harmonic Sources | HS1 (%) | HS2 (%) | HS3 (%) | HS4 (%) |
|---|---|---|---|---|
| ATP Calculated Impact (Reference Values) | 11.83 Fourth | 51.82 First | 12.68 Third | 23.67 Second |
| GBRT Calculated Impact | 11.43 Fourth | 51.63 First | 12.71 Third | 24.23 Second |
| GBRT Calculated Impact (without pre-processing) | 19.74 Third | 42.36 First | 8.82 Fourth | 29.08 Second |
| ANN Calculated Impact | 13.83 Third | 52.83 First | 12.73 Fourth | 20.61 Second |
| Electrical Characteristics | |
|---|---|
| Feed voltage | 80 to 300 Vac/Vdc |
| Consumption | 10 VA |
| Voltage Measurement | 30 to 300 Vac (phase-neutral) |
| Voltage Accuracy | 0.5% |
| Current Measurement | 60 A to 3000 A (Model TR4000/TI) |
| Current Accuracy | 0.5% |
| Phase Angle Accuracy | <5 degree |
| Power Accuracy | 1.0% |
| Communication | RS-485 MODBUS RTU or Ethernet |
| Memory Autonomy | Up to 60 days |
| Feeder | Name | Main Activity | Power (KVA) |
|---|---|---|---|
| 1 | Language and Communication Institute | Administration | 150 |
| CAPACIT | Administration | 225 | |
| Physics Lab (Research) | Laboratories | 225 | |
| Communications and IT Center | Laboratories | 225 | |
| Department of Material Resources | Administration | 225 | |
| Chemistry Lab (Research) | Laboratories | 300 | |
| Biological Sciences 1 Institute | Class Blocks | 500 | |
| Biological Sciences 2 Institute | Class Blocks | 500 | |
| Biological Sciences 3 Institute | Class Blocks | 500 | |
| 2 | Central Library 1 | Administration | 225 |
| Central Library 2 | Administration | 225 | |
| Geosciences Institute | Class Blocks | 225 | |
| Convention Center Benedito Nunes | Administration | 500 | |
| Administration Building 1 | Administration | 500 | |
| Administration Building 2 | Administration | 750 | |
| 3 | Education Sciences Institute | Administration | 225 |
| Technology Institute | Administration | 225 | |
| Architecture Center | Class Blocks | 225 | |
| Applied Social Sciences Institute | Class Blocks | 225 | |
| Legal Sciences Institute | Class Blocks | 300 | |
| Electrical Engineering Lab | Laboratories | 300 | |
| Electrical Engineering Lab Annex | Laboratories | 500 | |
| 4 | Center of Energy Efficiency in Amazon | Laboratories | 225 |
| Nutrition Center | Laboratories | 225 | |
| Physiotherapy College | Laboratories | 225 | |
| Odontology | Laboratories | 300 | |
| --- | Main Power Cabin | --- | --- |
| Feeder | Location | Nominal Power (kVA) | Measured Power (kVA) | Nominal/Measured (%) |
|---|---|---|---|---|
| 1 | Basic 1 | 5587.5 | 2850 | 51.01% |
| 2 | Basic 2 | 3775 | 2425 | 64.24% |
| 3 | Professional | 5950 | 2000 | 33.61% |
| 4 | Health | 3012.5 | 675 | 22.41% |
| A | B | C | |
|---|---|---|---|
| MAE | 0.1379 (+/− 0.000910) | 0.1262 (+/− 0.000010) | 0.1347 (+/− 0.000047) |
| MAPE | 4.9519 (+/− 0.030815) | 4.4932 (+/− 0.000418) | 3.1215 (+/− 0.001083) |
| MSE | 0.0304 (+/− 0.000174) | 0.0245 (+/− 0.000002) | 0.0301 (+/− 0.000019) |
| Feeder | Name | Phase A (%) | Phase B (%) | Phase C (%) | |||
|---|---|---|---|---|---|---|---|
| Permutation | MAPE | Permutation | MAPE | Permutation | MAPE | ||
| 1 | Chemistry Lab (Research) | 3.37 | 3.71 | 3.45 | 4.29 | 2.62 | 3.65 |
| Biological Sciences Institute 1 | 2.28 | 3.60 | 4.01 | 2.58 | 2.75 | 7.66 | |
| Biological Sciences Institute 2 | 5.67 | 4.45 | 2.45 | 2.99 | 2.32 | 3.60 | |
| Biological Sciences Institute 3 | 1.92 | 1.76 | 1.26 | 1.24 | 1.90 | 1.32 | |
| Language and Communication Institute | 1.56 | 1.59 | 5.10 | 4.31 | 2.08 | 1.41 | |
| Physics Lab (Research) | 2.82 | 3.86 | 6.86 | 9.32 | 2.25 | 3.12 | |
| Total | 17.61 | 18.96 | 23.14 | 24.73 | 13.91 | 2.76 | |
| 2 | Central Library 2 | 4.20 | 2.82 | 8.76 | 10.81 | 2.84 | 2.58 |
| Convention Center Benedito Nunes | 3.02 | 4.15 | 4.60 | 5.81 | 6.40 | 3.92 | |
| Geoscience Institute | 21.25 | 20.85 | 4.26 | 4.28 | 5.42 | 7.44 | |
| Administration Building 1 | 7.11 | 5.82 | 13.05 | 12.25 | 8.69 | 7.23 | |
| Administration Building 2 | 8.81 | 8.27 | 9.89 | 9.61 | 9.63 | 10.72 | |
| Total | 44.38 | 41.91 | 40.55 | 42.76 | 32.98 | 31.90 | |
| 3 | Architecture Center | 6.72 | 6.04 | 2.46 | 2.54 | 2.97 | 3.07 |
| Electrical Engineering Lab | 1.80 | 2.81 | 4.80 | 1.92 | 3.98 | 4.28 | |
| Electrical Engineering Lab Annex | 4.36 | 5.72 | 4.68 | 3.75 | 2.89 | 2.67 | |
| Applied Social Sciences Institute | 3.23 | 2.81 | 5.61 | 7.09 | 3.90 | 2.76 | |
| Education Sciences Institute | 2.89 | 2.80 | 1.97 | 3.92 | 6.89 | 4.23 | |
| Legal Sciences Institute | 2.22 | 3.23 | 3.41 | 2.05 | 10.95 | 12.53 | |
| Technology Institute | 2.26 | 2.10 | 2.35 | 2.81 | 2.08 | 2.13 | |
| Total | 23.48 | 25.51 | 25.28 | 24.08 | 33.65 | 31.67 | |
| 4 | CEAMAZON | 5.25 | 4.22 | 6.48 | 5.90 | 3.17 | 3.94 |
| Nutrition Faculty | 4.47 | 4.78 | 4.55 | 2.53 | 6.68 | 3.54 | |
| Physiotherapy College | 4.82 | 4.62 | - | - | 9.61 | 8.19 | |
| Total | 14.54 | 13.62 | 11.03 | 8.43 | 19.46 | 15.67 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
P. Monteiro, F.; A. Monteiro, S.; Tostes, M.E.; H. Bezerra, U. Using True RMS Current Measurements to Estimate Harmonic Impacts of Multiple Nonlinear Loads in Electric Distribution Grids. Energies 2019, 12, 4132. https://doi.org/10.3390/en12214132
P. Monteiro F, A. Monteiro S, Tostes ME, H. Bezerra U. Using True RMS Current Measurements to Estimate Harmonic Impacts of Multiple Nonlinear Loads in Electric Distribution Grids. Energies. 2019; 12(21):4132. https://doi.org/10.3390/en12214132
Chicago/Turabian StyleP. Monteiro, Flávia, Suzane A. Monteiro, Maria E. Tostes, and Ubiratan H. Bezerra. 2019. "Using True RMS Current Measurements to Estimate Harmonic Impacts of Multiple Nonlinear Loads in Electric Distribution Grids" Energies 12, no. 21: 4132. https://doi.org/10.3390/en12214132
APA StyleP. Monteiro, F., A. Monteiro, S., Tostes, M. E., & H. Bezerra, U. (2019). Using True RMS Current Measurements to Estimate Harmonic Impacts of Multiple Nonlinear Loads in Electric Distribution Grids. Energies, 12(21), 4132. https://doi.org/10.3390/en12214132





