Development of the Availability Concept by Using Fuzzy Theory with AHP Correction, a Case Study: Bulldozers in the Open-Pit Lignite Mine
Abstract
1. Introduction
2. Materials and Methods
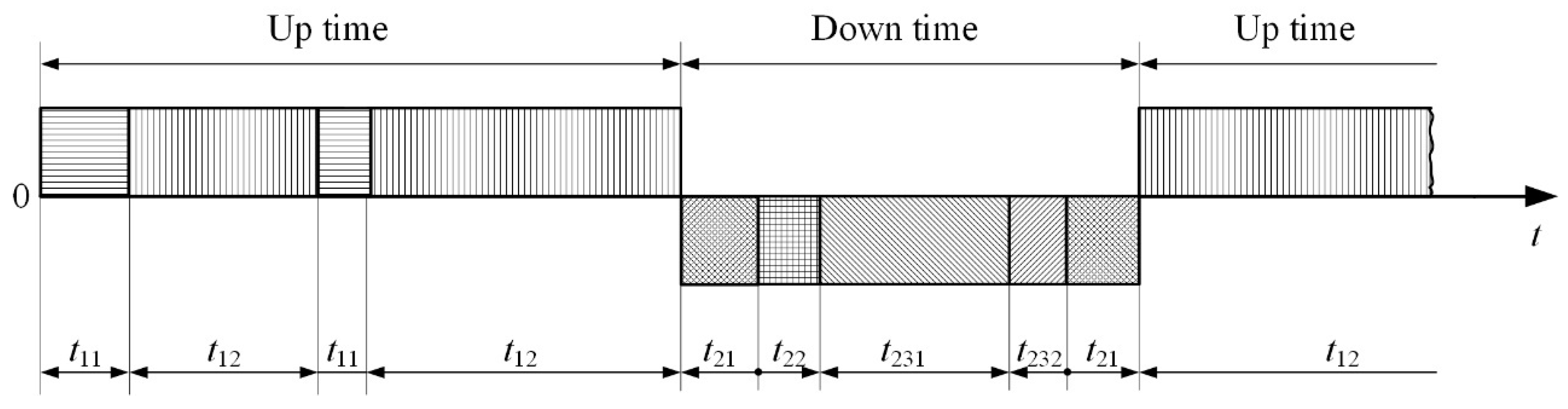
2.1. The Availability Concept in the Technical Systems of Maintenance Engineering
- failure intensity:
- maintenance intensity:
2.2. Expert Fuzzy-AHP Synthesis Model Availability
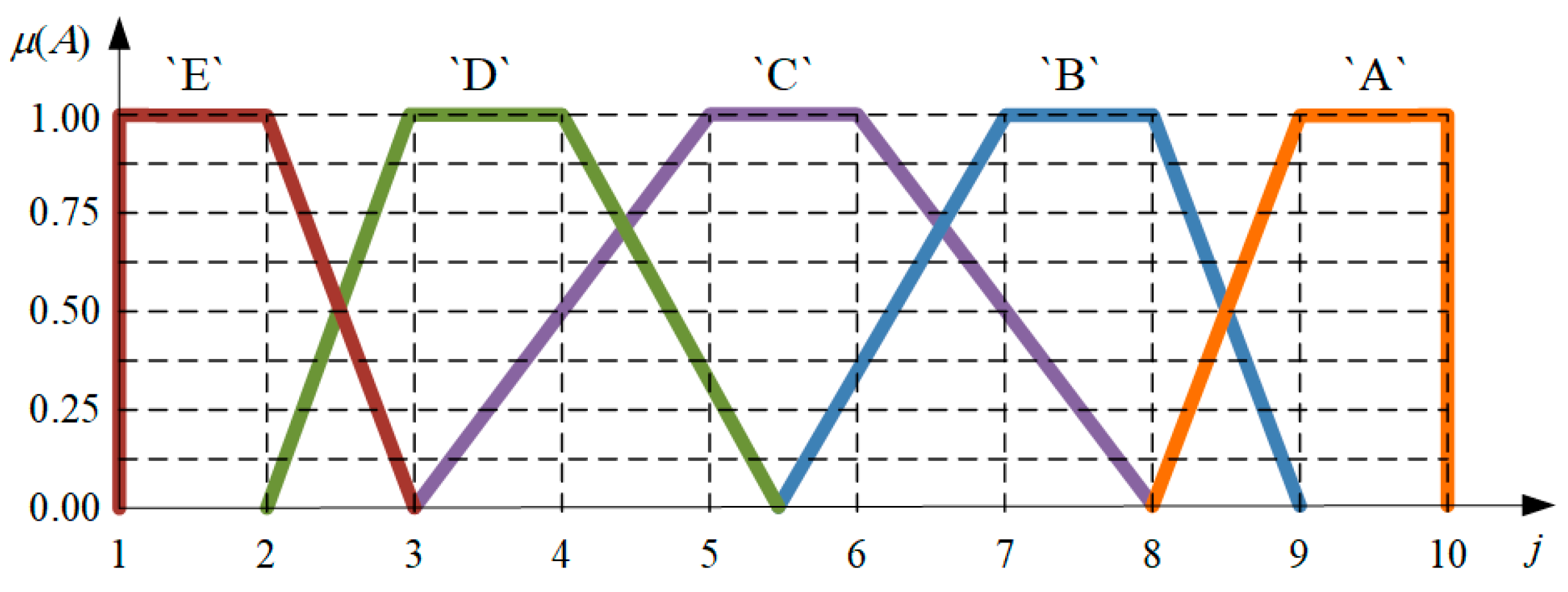
2.2.1. Fuzzy Inference in the Synthesis Model
- ‘A‘(R)—No sudden, unplanned failures were recorded.
- ‘B‘(R)—There are some interruptions in work. Negligible impact on the time state picture of the technical system.
- ‘C’(R)—Failures occur. In most cases, they are expected, and therefore, in some way they can be planned. Failures can be eliminated on the spot.
- ‘D’(R)—Occurrence of failure is frequent. The reliability of the machine is low. Efficiency is reduced.
- ‘E’(R)—Constant breakdowns occur. The machine is not at the required working level.
- ‘A’(M)—Any intervention can be fully planned in terms of time and work organization. Diagnosis is simple. Repairs are quick. No corrosion. Defective parts are not of a large mass. It is possible to plan time and work organization.
- ‘B’(M)—Quick identification of weaknesses is possible (errors, faults …). It is constructively easy to repair. There may be some minor interference errors.
- ‘C’(M)—Possible difficulties during preventive and service maintenance, for reasons of constructive nature, inaccessibility of parts, due to the appearance of corrosion, the mass of the element, and the like.
- ‘D’(M)—It is not possible to plan the duration of the intervention and the organization of work. There are a number of complications during dismantling and assembly.
- ‘E’(M)—The breakdown cannot be remedied in an acceptable time. It is necessary to disconnect the machine from the operating unit for a longer period of time.
- ‘A’(S)—Any work with the machine can be fully planned in terms of time and organization. There are spare parts and tools. There are trained repairmen. The workshop is close. There are no administrative difficulties.
- ‘B’(S)—Administrative and logistical support is at a satisfactory level. Supply of spare parts is fast. Workshop is at a short distance. Possible purchase of necessary paperwork.
- ‘C’(S)—All activities related to maintenance support (spare parts, tools, workshops, employee training, etc.) are at a satisfactory level. Utilization of the machine is correct in most cases.
- ‘D’(S)—There are difficulties in purchasing spare parts. Additional training is necessary. There are administrative difficulties. Utilization of the machine is a little bit harder than expected.
- ‘E’(S)—There are no spare parts. The workers are not trained. There are administrative problems. The workshop is remote. Every utilization of the machine is full of unpredictability due to inadequate training, logistical support, etc. It is not possible to plan activities in the context of time and organization.
- wi is the influential factor of the corresponding partial indicator on availability obtained on the basis of mutual ranking of partial indicators, where wRi + wMi + wSi = 1 (Equation (17));
- jc is a class to which the corresponding fuzzy number (9) belongs for the observed membership function and the given combination c, where jc = 1, …, n;
2.2.2. AHP Ranking Model
3. Results: Case Study Availability of Bulldozers
3.1. Preparation of Questionnaires, Statistical Processing and Fuzzification of Expert Opinions
- with ‘A‘, three out of four analysts (experts):
- with ‘B‘, all four analysts (experts):
- with ‘C‘, only one analyst (expert):
3.2. AHP Ranking
3.3. Max–Min Composition
- For Jc = 6, 14 combinations were recorded: 4-6-6, …, 9-6-6;
- For Jc = 7, 51 combinations were recorded: 4-6-8, …, 10-8-6;
- For Jc = 8, 65 combinations were recorded: 4-6-10, …, 10-10-7;
- For Jc = 9, 39 combinations were recorded: 4-6-8, …, 10-10-9;
- For Jc = 10, 6 combinations were recorded: 7-10-10, …, 10-10-10;
3.4. Identification
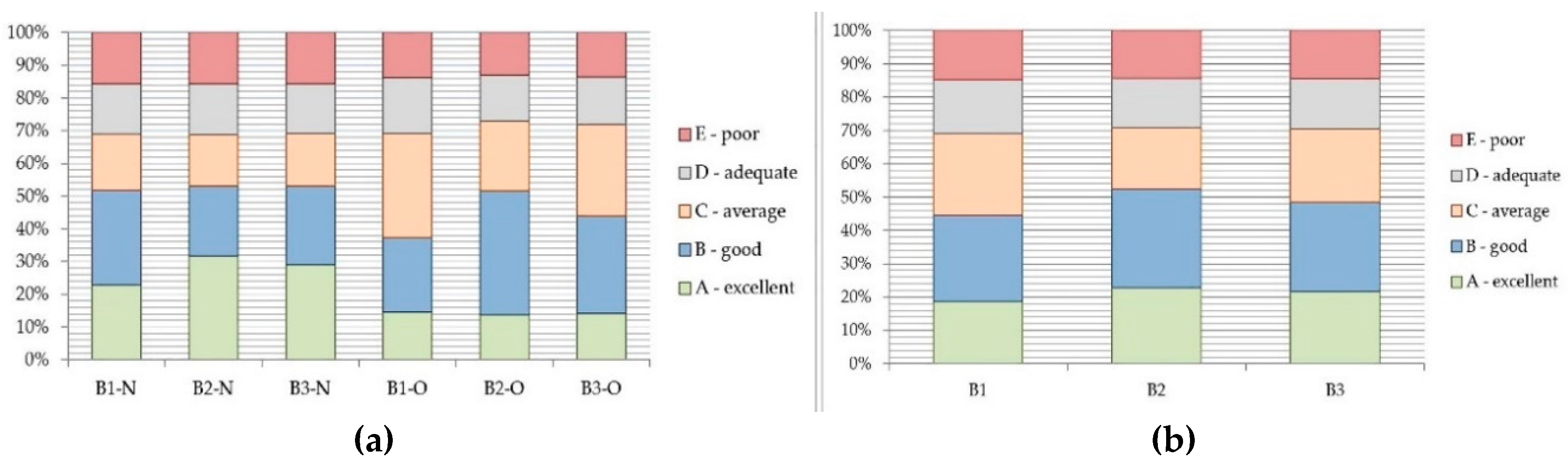
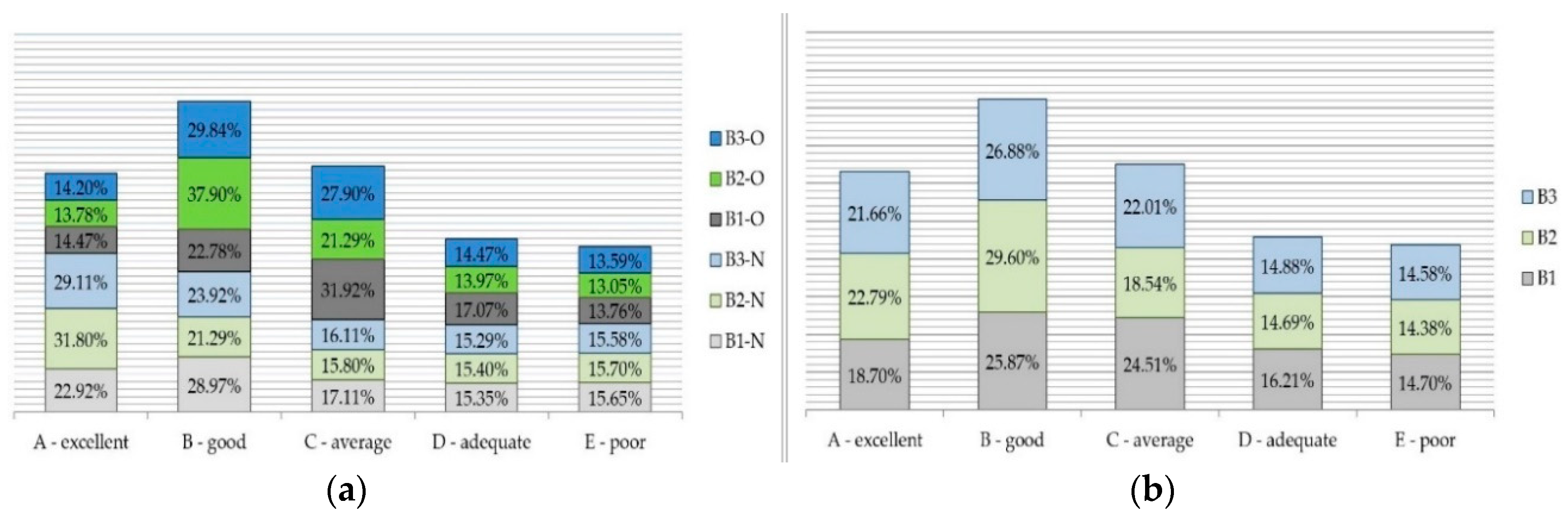
3.5. Results Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Papic, L.; Milovanovic, Z.N. Systems Maintainability and Reliability; The Research Center of Dependability and Quality Management DQM: Prijevor, Serbia, 2007. [Google Scholar]
- Dhillon, B.S. Mining Equipment Reliability, Maintainability and Safety; Springer: London, UK, 2008. [Google Scholar]
- Todorovic, J. Maintainability Engineering; JUMV: Belgrade, Serbia, 1993. [Google Scholar]
- Conlon, J.C.; Lilius, W.A.; Tubbesing, F.H., Jr. Test and Evaluation of System Reliability, Availability and Maintainability, A Primer; No. DOD-3235.1-H; Department of Defense: Washington, DC, USA, 1982. [Google Scholar]
- International Electrotechnical Commission. INTERNATIONAL STANDARD IEC—Dependability Management 60300, 2003–01. Available online: https://webstore.iec.ch/preview/info_iec60300-3-1%7Bed2.0%7Den.pdf (accessed on 16 October 2019).
- Strandberg, K. IEC 300: The Dependability Counterpart of ISO 9000. In Proceedings of the Annual Reliability and Maintainability Symposium, Orlando, FL, USA, 29–31 January 1991; pp. 463–467. [Google Scholar]
- Avizienis, A.; Laprie, J.C.; Randell, B.; Landwehr, C. Basic concept and taxonomy of dependable and secure computing. IEEE Trans. Dependable Secur. Comput. 2004, 1, 11–33. [Google Scholar] [CrossRef]
- Avizienis, A.; Laprie, J.; Randell, B. Dependability and its threats—A taxonomy. In IFIP Congress Topical Sessions; Springer: Boston, MA, USA, 2004; pp. 91–120. [Google Scholar]
- Cai, K.Y. System failure engineering and fuzzy methodology an introductory overview. Fuzzy Sets Syst. 1996, 83, 113–133. [Google Scholar] [CrossRef]
- Miodragovic, R.; Tanasijevic, M.; Mileusnic, Z.; Jovancic, P. Effectiveness assessment of agricultural machinery based on fuzzy sets theory. Expert Syst. Appl. 2012, 39, 8940–8946. [Google Scholar] [CrossRef]
- Ebramhimipour, V.; Suzuki, K. A synergetic approach for assessing and improving equipment performance in offshore industry based on dependability. Reliab. Eng. Syst. Saf. 2006, 91, 10–19. [Google Scholar] [CrossRef]
- Ivezic, D.; Tanasijevic, M.; Ignjatovic, D. Fuzzy Approach to Dependability Performance Evaluation. Qual. Reliab. Eng. Int. 2008, 24, 779–792. [Google Scholar] [CrossRef]
- Tanasijevic, M.; Ivezic, D.; Jovancic, P.; Catic, D.; Zlatanovic, D. Study of Dependability Evaluation for Multi-hierarchical Systems Based on Max–Min Composition. Qual. Reliab. Eng. Int. 2013, 29, 317–326. [Google Scholar] [CrossRef]
- Tanasijevic, M.; Ivezic, D.; Jovancic, P.; Ignjatovic, D.; Bugaric, U. Dependability assessment of open-pit mines equipment—Study on the bases of fuzzy algebra rules. Eksploat. Niezawodn. Maint. Reliab. 2013, 15, 66–74. [Google Scholar]
- Jones, J.V. Supportability Engineering Handbook; Introduction Chapter; McGraw-Hill Education: New York, NY, USA, 2007. [Google Scholar]
- Erkoyuncu, J.A.; Khan, S.; Eiroa, A.L.; Butler, N.; Rushton, K.; Brocklebank, S. Perspectives on trading cost and availability for corrective maintenance at the equipment type level. Reliab. Eng. Syst. Saf. 2017, 168, 53–69. [Google Scholar] [CrossRef][Green Version]
- Klir, G.J.; Yuan, B. Fuzzy Sets and Fuzzy Logic, Theory and Applications; Prentice Hall: New York, NY, USA, 1995; ISBN 0-13-101171-5. [Google Scholar]
- Djuric, R.; Milisavljevic, V. Investigation on the relationship between reliability of track mechanism and dust content in rocks of lignite open pits. Maint. Reliab. 2016, 18, 142–150. [Google Scholar] [CrossRef]
- Tanasijevic, M. A fuzzy-based decision support model for evaluation of mining machinery. In Proceedings of the 48th International October Conference on Mining and Metallurgy, Bor, Serbia, 28 September–1 October 2016; pp. 15–18. [Google Scholar]
- Ivezic, D.; Tanasijevic, M.; Jovancic, P.; Djuric, R. A Fuzzy Expert Model for Availability Evaluation. In Proceedings of the 20th International Carpathian Control Conference (ICCC), Kraków-Wieliczka, Poland, 26–29 May 2019; ISBN 978-1-7281-0701-1. [Google Scholar]
- Saaty, T.L. Decision Making: The Analytical Hierarchy Process; Mc-Graw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Jankovic, I.; Djenadic, S.; Ignjatovic, D.; Jovancic, P.; Subaranovic, T.; Ristovic, I. Multi-Criteria Approach for Selecting Optimal Dozer Type in Open-Cast Coal Mining. Energies 2019, 12, 2245. [Google Scholar] [CrossRef]
- Karimnia, H.; Bagloo, H. Optimum mining method selection using fuzzy analytical hierarchy process-Qapiliq salt mine, Iran. Int. J. Min. Sci. Technol. 2015, 25, 225–230. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making with the analytical hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Djenadic, S.; Miletic, F.; Jovancic, P.; Jankovic, I.; Lazic, M. Analitičko hijerarhijski proces primenjen za selekciju hidrauličnih bagera na površinskim kopovima. In Proceedings of the VIII Međunarodna Konferencija OMC 2018, Zlatibor, Serbia, 17–20 October 2018; Jugoslovenski komitet za površinsku eksploataciju: Belgrade, Serbia; pp. 14–16. [Google Scholar]
- Stevanovic, D.; Lekic, M.; Krzanovic, D.; Ristovic, I. Application of MCDA in selection of different mining methods and solutions. Res. J. 2018, 12, 171–180. [Google Scholar] [CrossRef]
- Milentijevic, G.; Nedeljkovic, B.; Lekic, M.; Nikic, Z.; Ristović, I.; Djokic, J. Application of a Method for Intelligent Multi-Criteria Analysis of the Environmental Impact of Tailing Ponds in Northern Kosovo and Metohija. Energies 2016, 9, 935. [Google Scholar] [CrossRef]
- Saaty, T.L. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process; RWS Publications: Pittsburgh, PA, USA, 2000. [Google Scholar]
- Djenadic, S.; Jovancic, P.; Ignjatovic, D.; Miletic, F.; Jankovic, I. Analiza primene višekriterijumskih metoda u optimizaciji izbora hidrauličnih bagera na površinskim kopovima. Tehnika 2019, 70, 369–377. [Google Scholar] [CrossRef]
- Ignjatovic, D.; Jovancic, P. Optimisation of Operation and Costs of Auxiliary Mechanization in Order to Increase the Utilization of Overburden and Coal Systems on the Open-Cast Mines of Electrical Power Supply of Serbia—Research Study; Faculty of Mining and Geology: Belgrade, Serbia, 2018. [Google Scholar]

| The Level of Importance | Numerical Value | Reciprocal Value |
|---|---|---|
| Extreme importance | 9 | 1/9 (0.111) |
| Very strong to extreme importance | 8 | 1/8 (0.125) |
| Very strong importance | 7 | 1/7 (0.143) |
| Strong to very strong importance | 6 | 1/6 (0.167) |
| Strong importance | 5 | 1/5 (0.200) |
| Moderate to strong importance | 4 | 1/4 (0.250) |
| Moderate importance | 3 | 1/3 (0.333) |
| Equal to moderate importance | 2 | 1/2 (0.500) |
| Equal importance | 1 | 1 (1.000) |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| RI | 0.00 | 0.00 | 0.52 | 0.89 | 1.11 | 1.25 | 1.35 | 1.40 | 1.45 | 1.49 | 1.51 | 1.53 | 1.56 | 1.57 | 1.59 |
| Years of Operation | B1 | B2 | B3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t1, h | t2, h | A(t) | t1, h | t2, h | A(t) | t1, h | t2, h | A(t) | |||||
| N | 1 | 519 | 20 | 0.96 | 0.96 | 934 | 25 | 0.97 | 0.97 | 753 | 37 | 0.95 | 0.94 |
| 2 | 1893 | 92 | 0.95 | 3004 | 128 | 0.96 | 3741 | 290 | 0.93 | ||||
| O | 3 | 3372 | 334 | 0.91 | 0.89 | 3415 | 262 | 0.93 | 0.90 | 3476 | 384 | 0.90 | 0.84 |
| 4 | 4100 | 498 | 0.89 | 3631 | 367 | 0.91 | 3102 | 572 | 0.84 | ||||
| 5 | 4325 | 431 | 0.91 | 4296 | 494 | 0.90 | 2635 | 622 | 0.81 | ||||
| 6 | 3601 | 449 | 0.89 | 4127 | 445 | 0.90 | 2757 | 664 | 0.81 | ||||
| 7 | 1438 | 234 | 0.86 | 2894 | 387 | 0.88 | 2008 | 343 | 0.85 | ||||
| Analyst | B1-N | B2-N | B3-N | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ‘A’ | ‘B’ | ‘C’ | ‘D’ | ‘E’ | ‘A’ | ‘B’ | ‘C’ | ‘D’ | ‘E’ | ‘A’ | ‘B’ | ‘C’ | ‘D’ | ‘E’ | ||
| 1. | R | 0.7 | 0.3 | 0.8 | 0.2 | 0.6 | 0.4 | |||||||||
| M | 0.4 | 0.6 | 0.7 | 0.3 | 0.5 | 0.5 | ||||||||||
| S | 0.3 | 0.7 | 0.6 | 0.4 | 0.6 | 0.4 | ||||||||||
| 2. | R | 0.6 | 0.4 | 0.6 | 0.4 | 0.3 | 0.7 | |||||||||
| M | 0.6 | 0.4 | 0.8 | 0.2 | 0.6 | 0.4 | ||||||||||
| S | 0.5 | 0.5 | 0.4 | 0.6 | 0.5 | 0.5 | ||||||||||
| 3. | R | 0.9 | 0.1 | 1 | 1 | |||||||||||
| M | 0.4 | 0.6 | 0.6 | 0.4 | 0.7 | 0.3 | ||||||||||
| S | 0.2 | 0.8 | 0.6 | 0.4 | 0.7 | 0.3 | ||||||||||
| 4. | R | 0.5 | 0.5 | 0.7 | 0.3 | 0.4 | 0.6 | |||||||||
| M | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | ||||||||||
| S | 1 | 1 | 0.3 | 0.7 | ||||||||||||
| Σ | R | 0.450 | 0.525 | 0.025 | 0 | 0 | 0.525 | 0.475 | 0 | 0 | 0 | 0.325 | 0.675 | 0 | 0 | 0 |
| M | 0.525 | 0.475 | 0 | 0 | 0 | 0.700 | 0.300 | 0 | 0 | 0 | 0.625 | 0.375 | 0 | 0 | 0 | |
| S | 0.250 | 0.750 | 0 | 0 | 0 | 0.650 | 0.350 | 0 | 0 | 0 | 0.525 | 0.475 | 0 | 0 | 0 | |
| Analyst | B1-O | B2-O | B3-O | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ‘A’ | ‘B’ | ‘C’ | ‘D’ | ‘E’ | ‘A’ | ‘B’ | ‘C’ | ‘D’ | ‘E’ | ‘A’ | ‘B’ | ‘C’ | ‘D’ | ‘E’ | ||
| 1. | R | 0.6 | 0.4 | 0.7 | 0.3 | 0.8 | 0.2 | |||||||||
| M | 0.6 | 0.4 | 0.6 | 0.4 | 0.4 | 0.6 | ||||||||||
| S | 0.3 | 0.7 | 0.5 | 0.5 | 0.4 | 0.6 | ||||||||||
| 2. | R | 0.9 | 0.1 | 0.5 | 0.5 | 0.2 | 0.8 | |||||||||
| M | 0.8 | 0.2 | 0.8 | 0.2 | 0.5 | 0.5 | ||||||||||
| S | 0.4 | 0.6 | 0.1 | 0.9 | 0.4 | 0.6 | ||||||||||
| 3. | R | 0.1 | 0.9 | 0.3 | 0.7 | 0.7 | 0.3 | |||||||||
| M | 0.6 | 0.4 | 0.9 | 0.1 | 0.8 | 0.2 | ||||||||||
| S | 0.9 | 0.1 | 0.8 | 0.2 | 1 | |||||||||||
| 4. | R | 0.5 | 0.5 | 0.2 | 0.8 | 1 | ||||||||||
| M | 0.3 | 0.7 | 0.5 | 0.5 | 0.1 | 0.9 | ||||||||||
| S | 0.8 | 0.2 | 0.4 | 0.6 | 0.2 | 0.8 | ||||||||||
| Σ | R | 0 | 0.300 | 0.675 | 0.025 | 0 | 0 | 0.425 | 0.575 | 0 | 0 | 0 | 0.050 | 0.825 | 0.125 | 0 |
| M | 0.150 | 0.375 | 0.375 | 0.100 | 0 | 0.150 | 0.650 | 0.200 | 0 | 0 | 0.150 | 0.650 | 0.200 | 0 | 0 | |
| S | 0.075 | 0.275 | 0.575 | 0.075 | 0 | 0.025 | 0.650 | 0.325 | 0 | 0 | 0.150 | 0.700 | 0.150 | 0 | 0 | |
| AHP Preferences | B1-N (B2-N, B3-N) | B1-O | B2-O | B3-O | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | M | S | R | M | S | R | M | S | R | M | S | |
| R | 1 | 1/2 | 1/3 | 1 | 1 | 1 | 1 | 1/3 | 1/3 | 1 | 2 | 2 |
| M | 2 | 1 | 1/2 | 1 | 1 | 1 | 3 | 1 | 1 | 1/2 | 1 | 1 |
| S | 3 | 2 | 1 | 1 | 1 | 1 | 3 | 1 | 1 | 1/2 | 1 | 1 |
| AHP Ranking | B1-N | B1-O | B2-N | B2-O | B3-N | B3-O |
|---|---|---|---|---|---|---|
| WR | 0.1630 | 0.3333 | 0.1630 | 0.1428 | 0.1630 | 0.5000 |
| WM | 0.2968 | 0.3333 | 0.2968 | 0.4286 | 0.2968 | 0.2500 |
| WS | 0.5401 | 0.3333 | 0.5401 | 0.4286 | 0.5401 | 0.2500 |
| λmax | 3.00921 | 3 | 3.00921 | 3 | 3.00921 | 3 |
| CI | 0.00460 | 0 | 0.00460 | 0 | 0.00460 | 0 |
| CR | 0.00885 | 0 | 0.00885 | 0 | 0.00885 | 0 |
| Machine | ‘A’—Excellent | ‘B’—Good | ‘C’—Average | ‘D’—Adequate | ‘E’—Poor |
|---|---|---|---|---|---|
| B1-N | 0.22922 | 0.28970 | 0.17108 | 0.15354 | 0.15645 |
| B2-N | 0.31801 | 0.21294 | 0.15800 | 0.15400 | 0.15705 |
| B3-N | 0.29108 | 0.23916 | 0.16110 | 0.15290 | 0.15576 |
| B1-O | 0.14472 | 0.22777 | 0.31916 | 0.17073 | 0.13762 |
| B2-O | 0.13784 | 0.37904 | 0.21289 | 0.13971 | 0.13052 |
| B3-O | 0.14204 | 0.29836 | 0.27904 | 0.14466 | 0.13591 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djenadic, S.; Ignjatovic, D.; Tanasijevic, M.; Bugaric, U.; Jankovic, I.; Subaranovic, T. Development of the Availability Concept by Using Fuzzy Theory with AHP Correction, a Case Study: Bulldozers in the Open-Pit Lignite Mine. Energies 2019, 12, 4044. https://doi.org/10.3390/en12214044
Djenadic S, Ignjatovic D, Tanasijevic M, Bugaric U, Jankovic I, Subaranovic T. Development of the Availability Concept by Using Fuzzy Theory with AHP Correction, a Case Study: Bulldozers in the Open-Pit Lignite Mine. Energies. 2019; 12(21):4044. https://doi.org/10.3390/en12214044
Chicago/Turabian StyleDjenadic, Stevan, Dragan Ignjatovic, Milos Tanasijevic, Ugljesa Bugaric, Ivan Jankovic, and Tomislav Subaranovic. 2019. "Development of the Availability Concept by Using Fuzzy Theory with AHP Correction, a Case Study: Bulldozers in the Open-Pit Lignite Mine" Energies 12, no. 21: 4044. https://doi.org/10.3390/en12214044
APA StyleDjenadic, S., Ignjatovic, D., Tanasijevic, M., Bugaric, U., Jankovic, I., & Subaranovic, T. (2019). Development of the Availability Concept by Using Fuzzy Theory with AHP Correction, a Case Study: Bulldozers in the Open-Pit Lignite Mine. Energies, 12(21), 4044. https://doi.org/10.3390/en12214044




