A Stochastic-CVaR Optimization Model for CCHP Micro-Grid Operation with Consideration of Electricity Market, Wind Power Accommodation and Multiple Demand Response Programs
Abstract
1. Introduction
- (1)
- Through considering EM participation, it is further expanded in this paper the theory of CCHP operation optimization.
- (2)
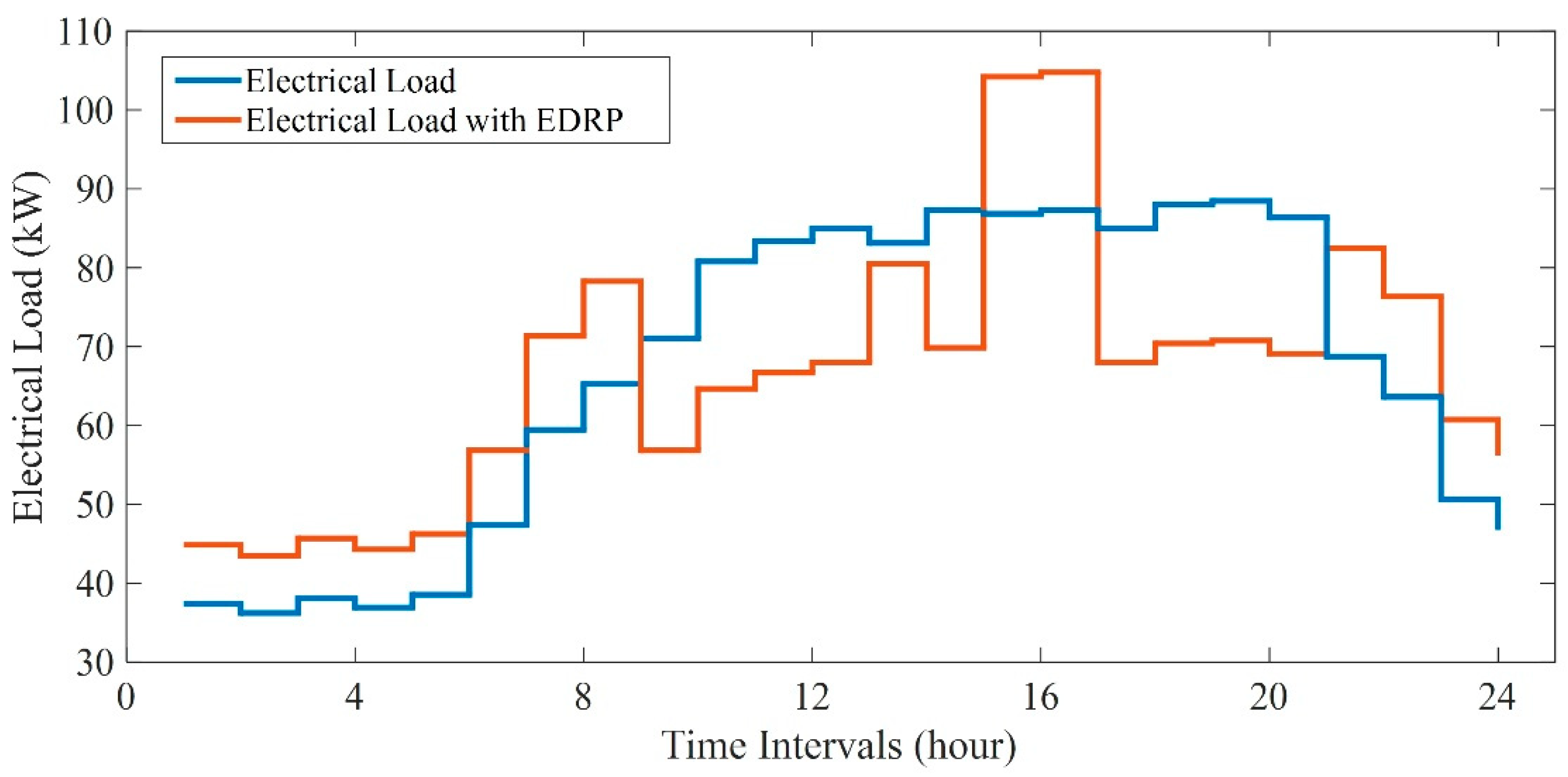
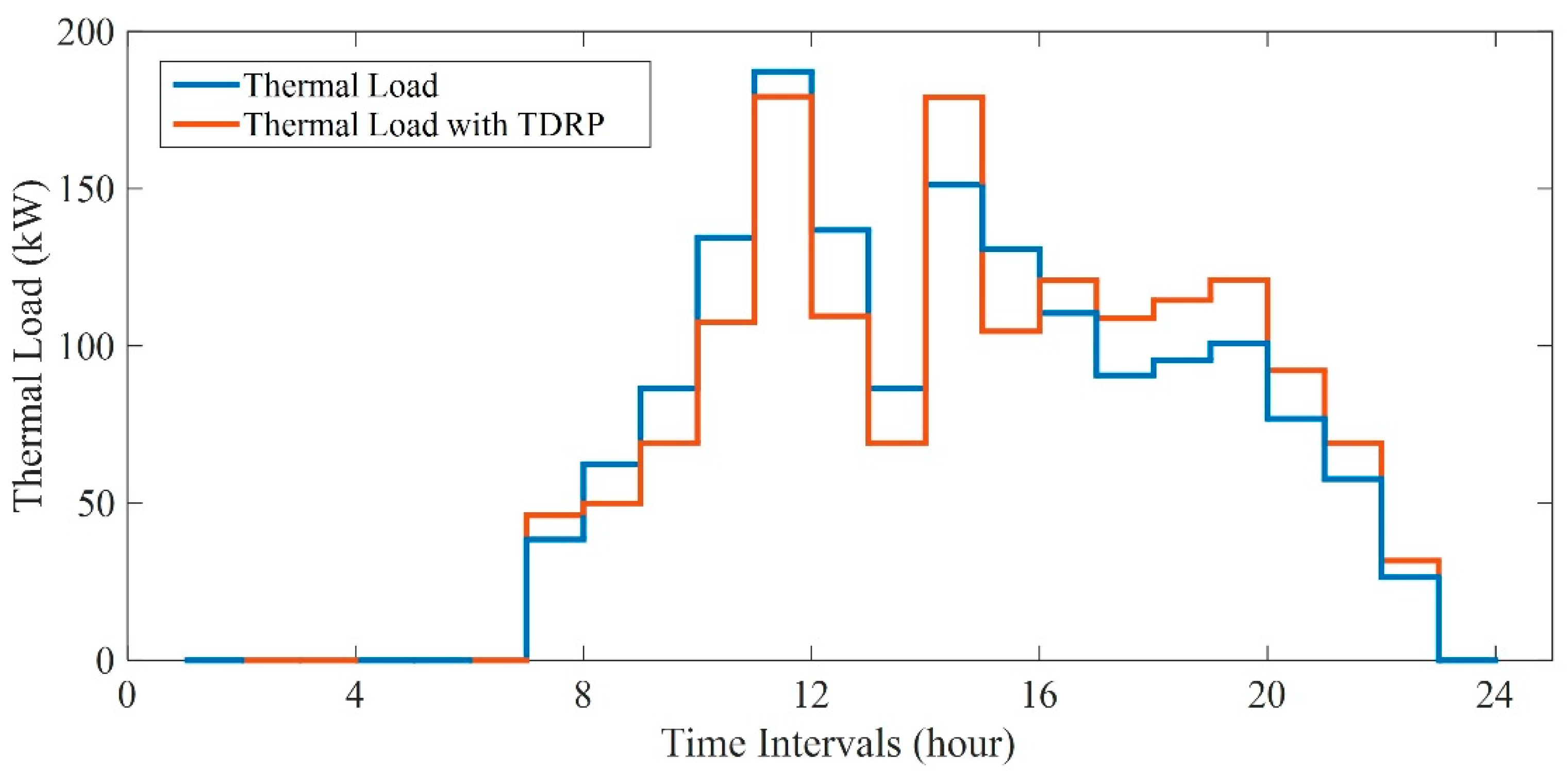
- By introducing multiple DRPs (EDRP, TDRP and CDRP), the electrical, thermal and cooling loads can be transformed as flexible sources for better performance of CCHP micro-grid operation.
- (3)
- The CVaR theory for risk control is involved, which makes CCHP micro-grid reduce the potential risk of operational cost increase under the conditions of stochastic fluctuations of EM clearing prices etc.
- (4)
- By applying the SO method, uncertainties such as EM clearing prices and wind power outputs are depicted using stochastic scenarios. On the one hand, it is feasible to make the operation of CCHP micro-grid achieve operational cost minimization and wind power accommodation etc.; on the other hand, it is feasible to linearize the CVaR formulation, through which our proposed model is converted into a mixed integer linear programming (MILP), thus guaranteeing relatively low computational complexity and the existence of global optimum operation point.
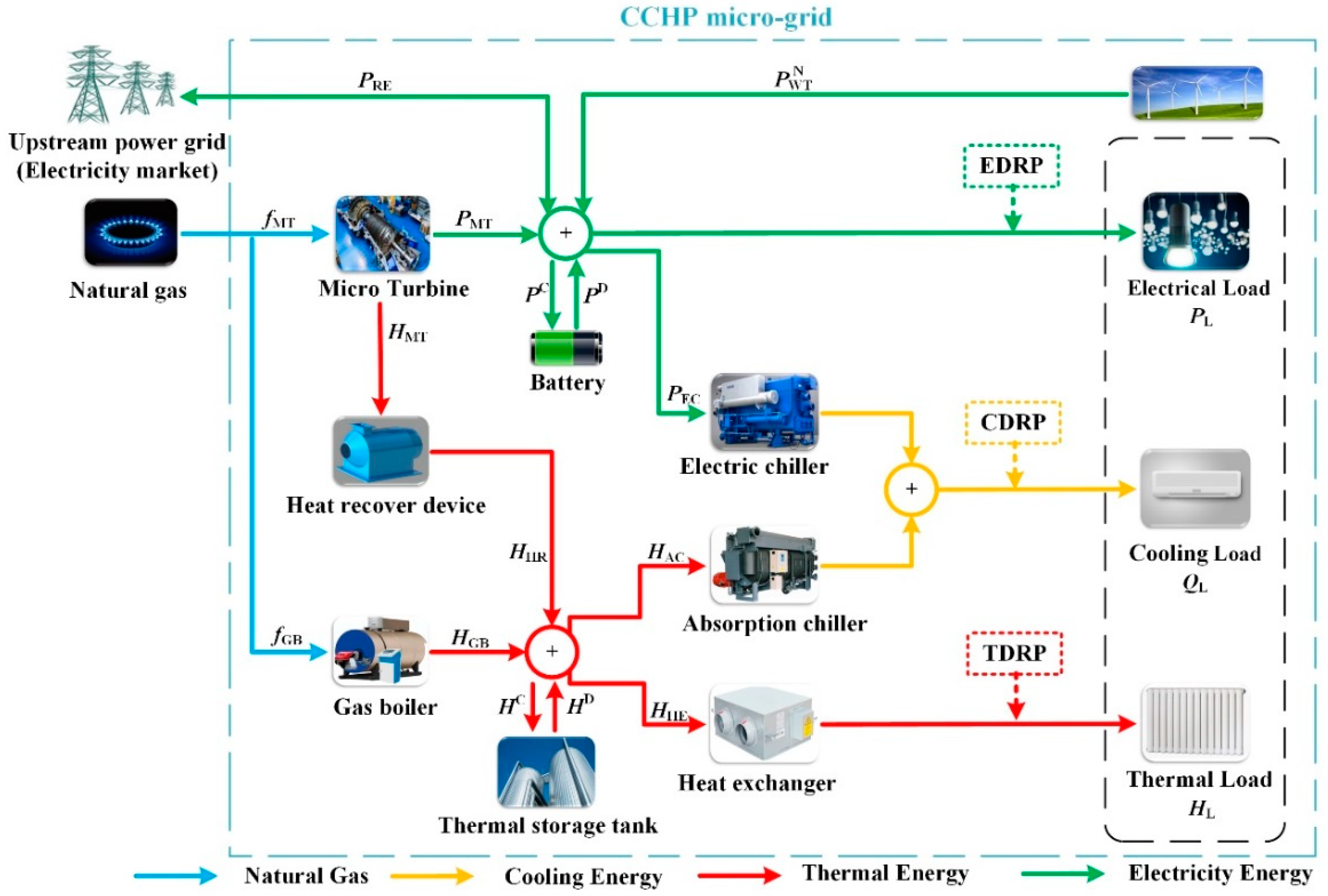
2. CCHP Micro-Gird Description and Modeling
2.1. Micro Turbine
2.2. Wind turbine
2.3. Gas Boiler
2.4. Heat Recovery Unit
2.5. Battery and Thermal Tank
2.6. Electrical and Absorption Chillers
2.7. Electricity exchange with EMs
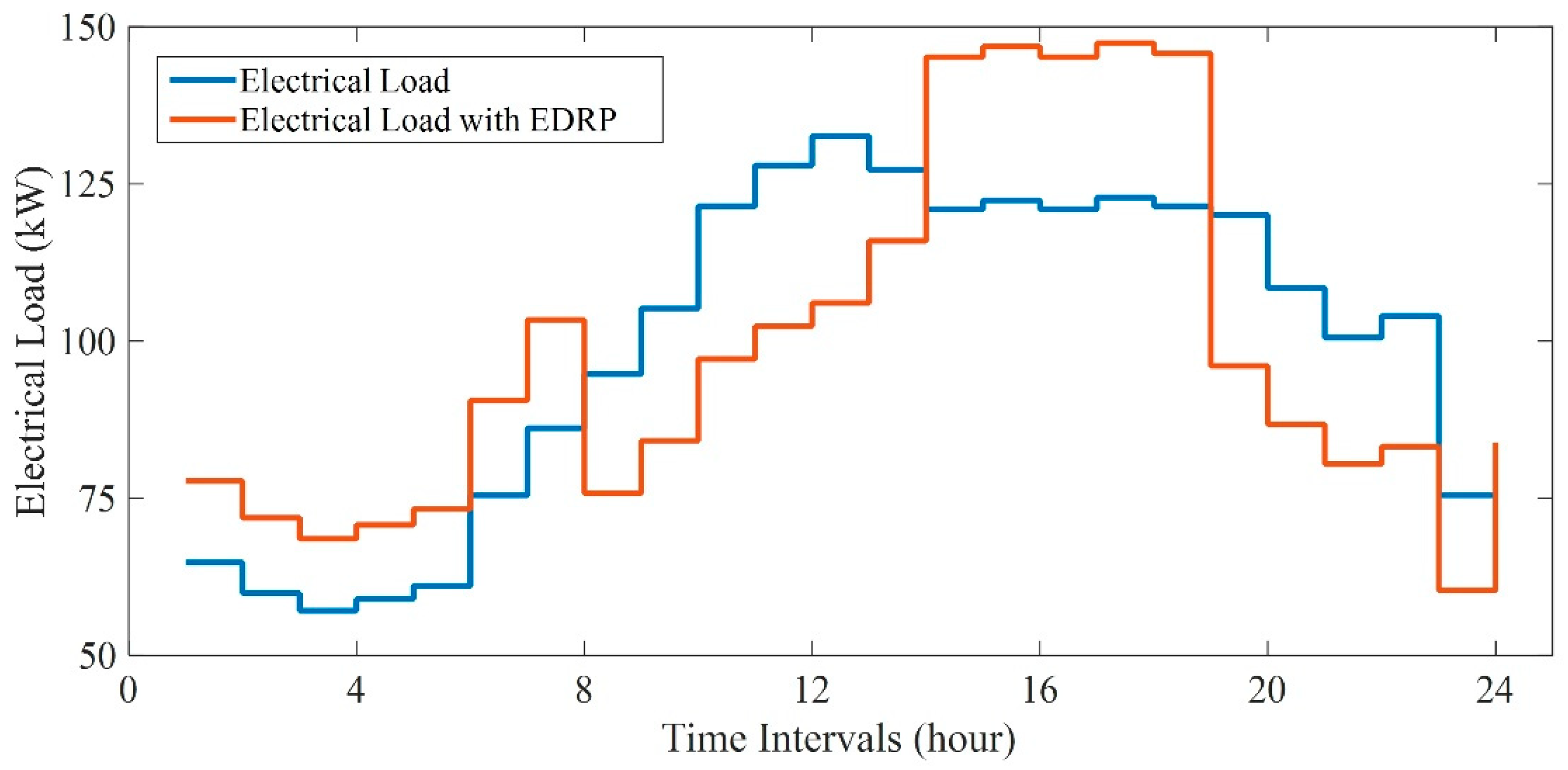
2.8. Multiple DRPs
3. Methodology
3.1. Uncertainties
3.2. Stochastic-CVaR Optimization Model for CCHP Micro-Grid Operation
3.2.1. Objective Function
3.2.2. Operational Constraints
- (1)
- Our proposed model is actually a MILP problem which can guarantee relatively low computational complexity and the existence of global optimum operation point.
- (2)
- Power bidding decisions are obtained along with operational decisions by solving our proposed model, which actually presents a coordinated optimization framework of operation and power bidding for CCHP micro-grid under EM circumstances.
4. Simulation and Discussions
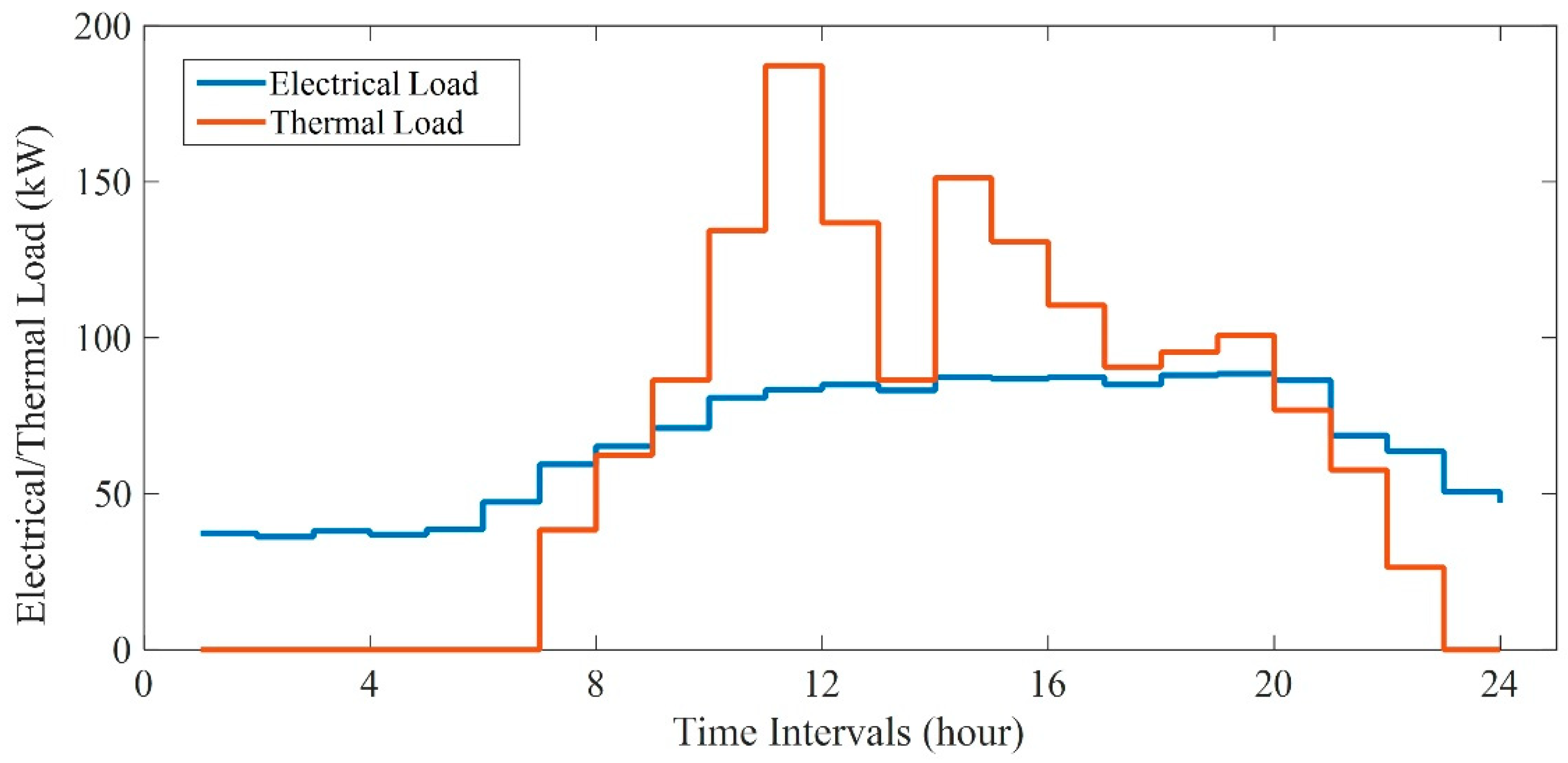
4.1. Data Description
4.2. Case Design
- (1)
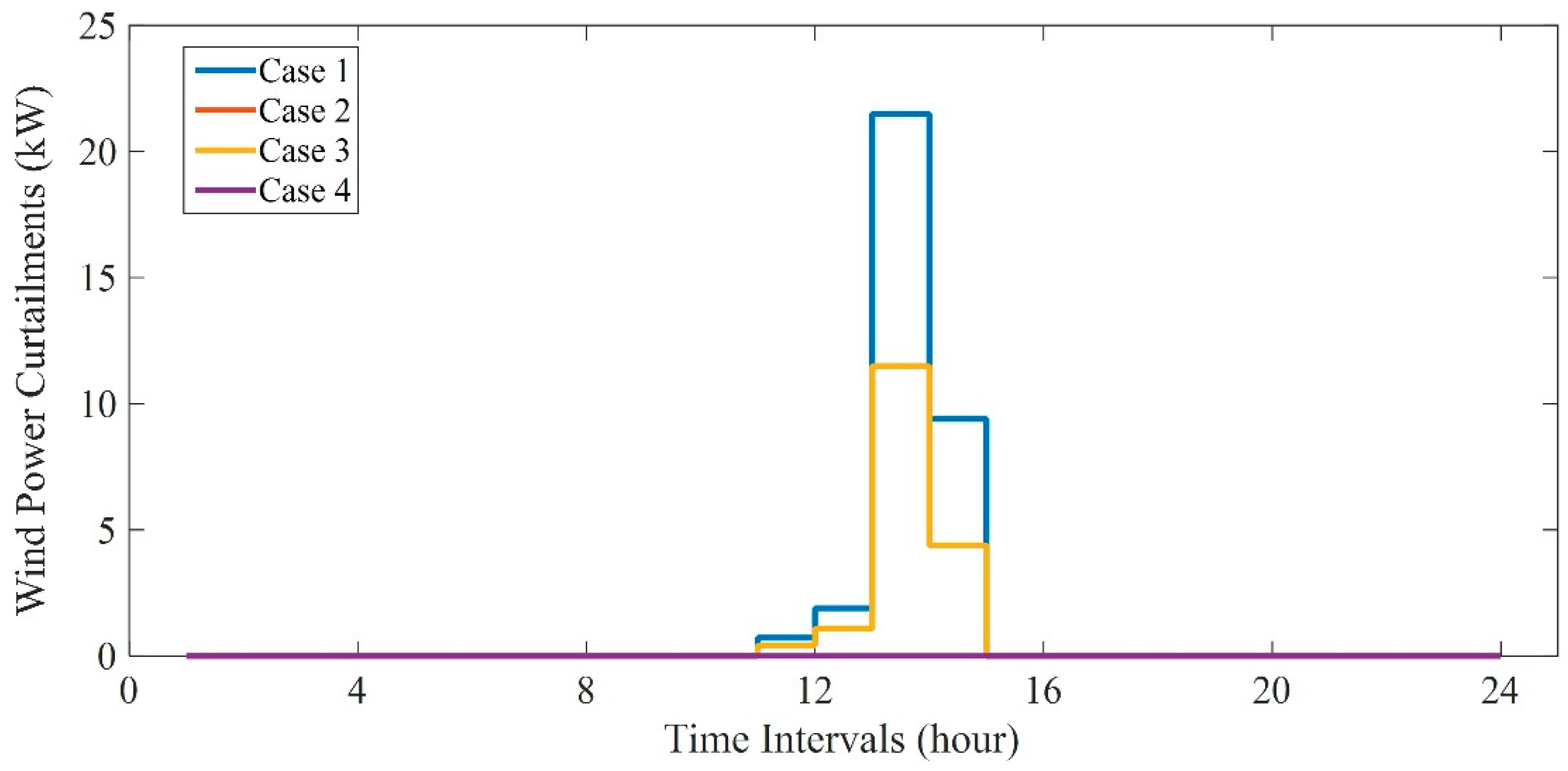
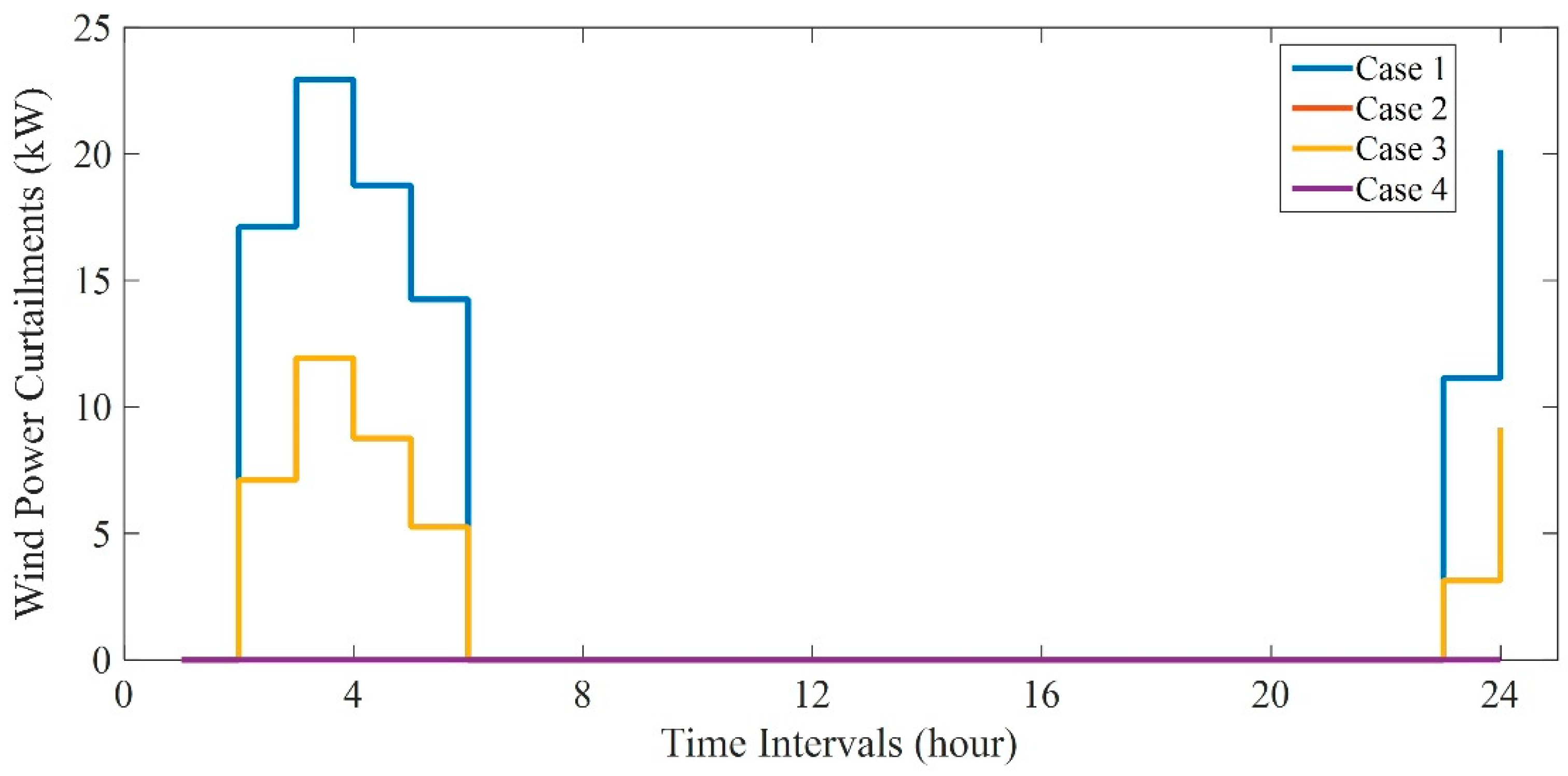
- The comparison between Case 1 and Cases 2–4 is to verify that the introduction of SO method can help CCHP micro-grid realize operational cost reduction, wind power accommodation, as well as secure and stable operation in the face of EM clearing prices and wind power outputs uncertainties.
- (2)
- The comparison between Cases 1–2 and Cases 3–4 is to verify that the introduction of CVaR method can help CCHP micro-grid avoid the potential risk of operational cost increase caused by day-ahead and real-time clearing prices fluctuation.
- (3)
- The comparison between Case 3 and Case 4 is to verify that the introduction of multiple DRPs can achieve electrical, thermal and cooling loads adjustments for further reducing operational cost.
- (4)
- The comparison between Case 4 and Case 5 is to verify that considering EM participation can help CCHP micro-grid achieve relatively higher energy efficiency and lower operational cost.
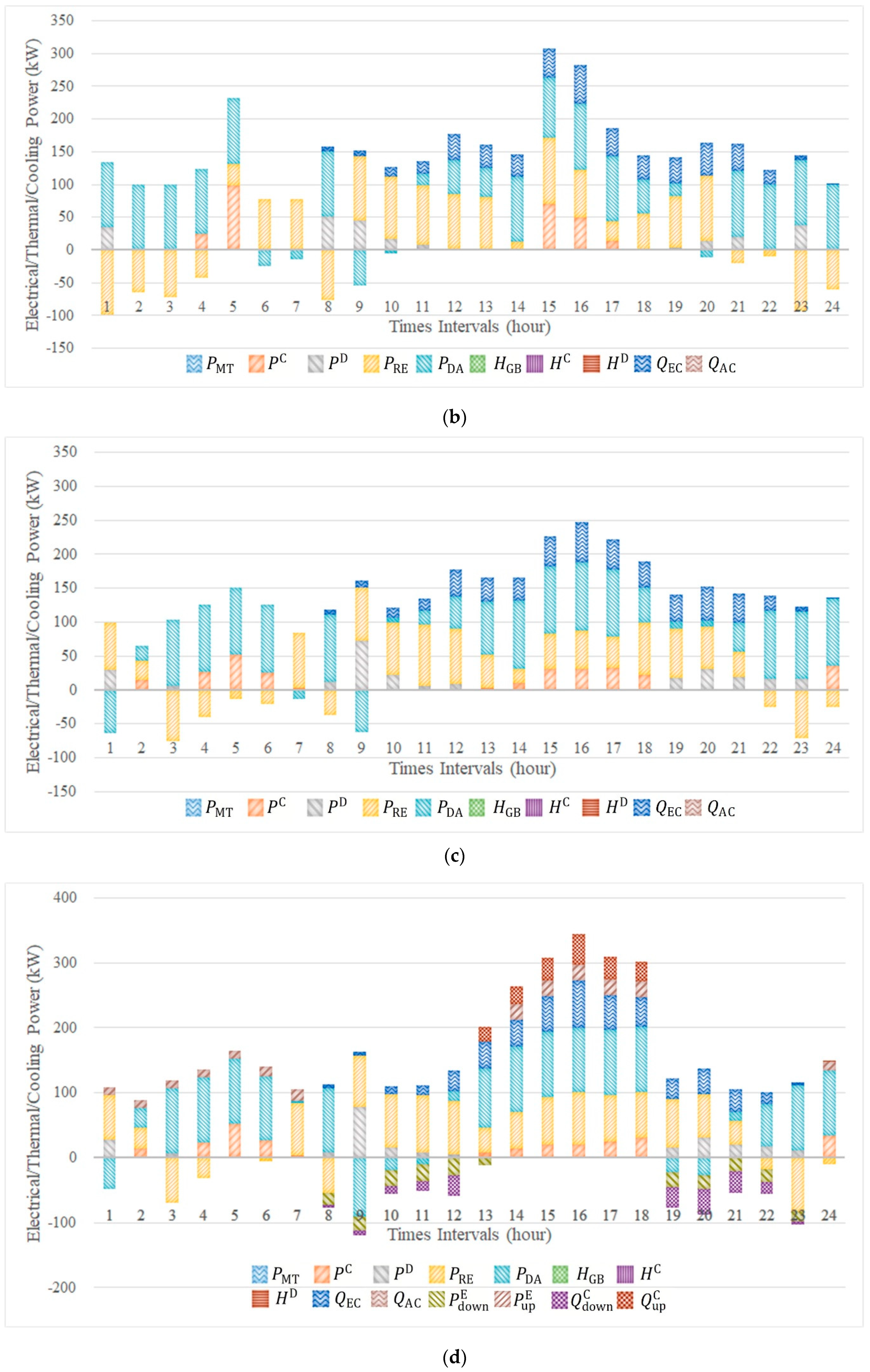
4.3. Simulated Test of the Proposed Stochastic-CVaR Approach and Multiple DRPs
- (5)
- (6)
- when the simulations are completed, the AOCs (average operational cost) and COCs (CVaR value of operational cost) in Table 5 and Table 7 can be calculated based on the optimal operation results. The specific calculation formulas for AOCs and COCs are detailed in Appendix C.
- (7)
- (1)
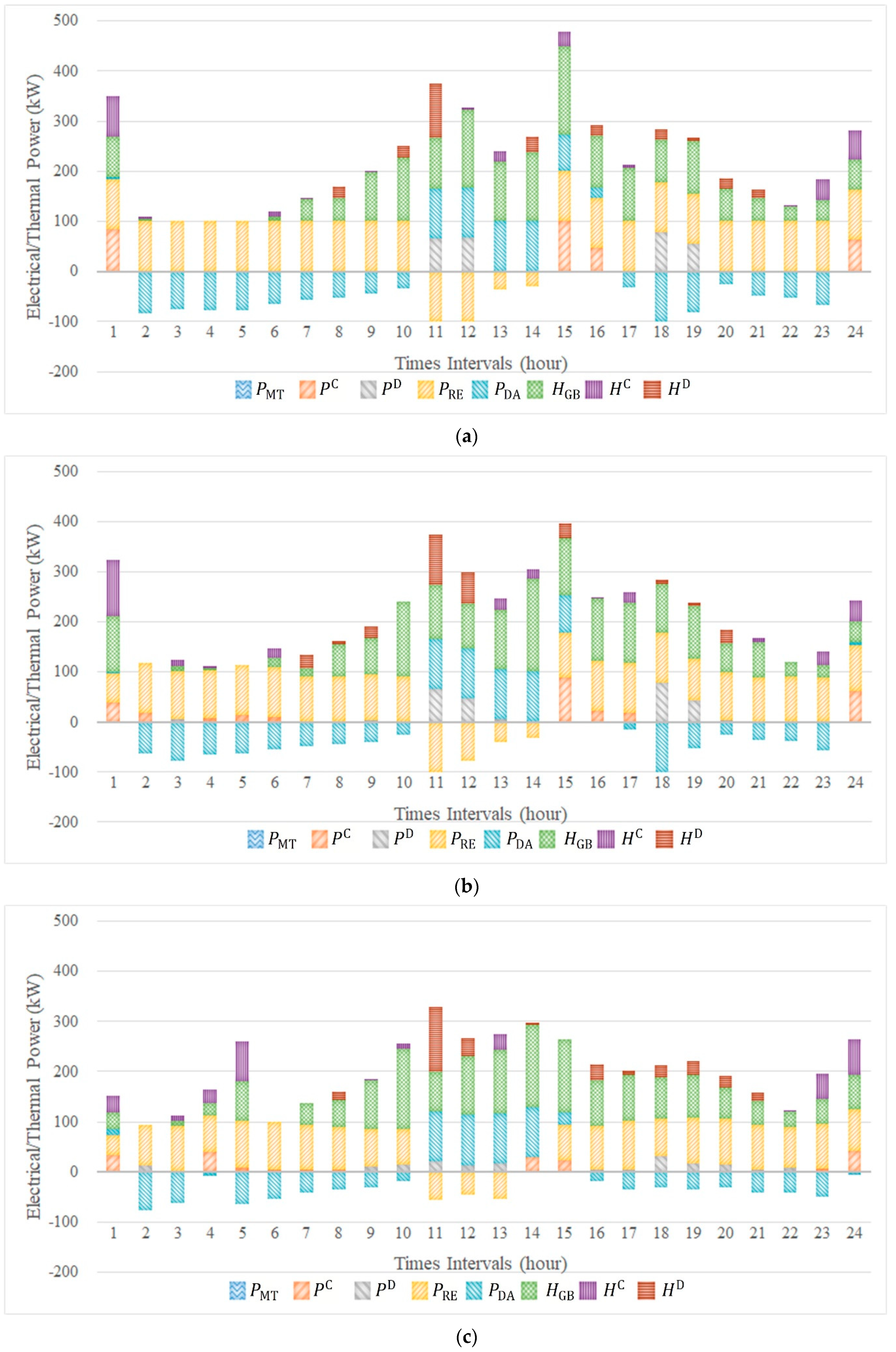
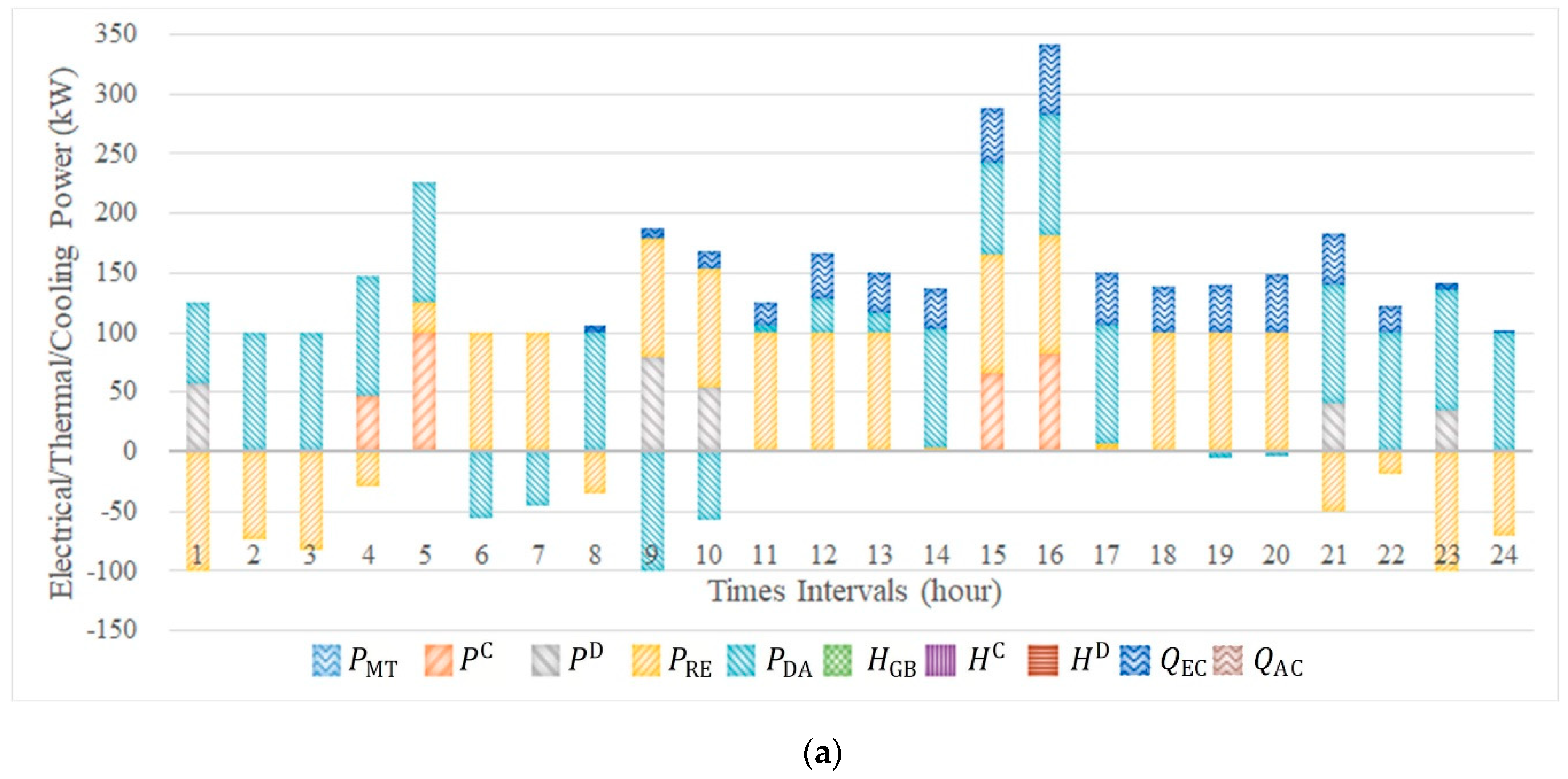
- Compared with Cases 1 and 2, the CCHP micro-grid is inclined to exchange less electrical energy with EMs in Cases 3 and 4 (as reflected in Table 4 and Table 6, both of the average electrical energy purchasing from and selling to EMs in Cases 3 and 4 are less than that in Cases 1 and 2). The main reason is that the introduction of CVaR in Case 3 and 4 makes CCHP micro-grid more willing to avoid the potential risk of operational cost increase caused by day-ahead and real-time clearing prices fluctuation.
- (2)
- Compared with Case 3, CCHP micro-grid is inclined to exchange more electrical energy with EMs in Case 4 (as reflected in Table 4 and Table 6, both of the average electrical energy purchasing from and selling to EMs in Case 4 are less than that in Case 3). This increase is achieved because of the introduction of multiple DRPs in Case 4 to further weaken the potential risk of operational cost increase caused by day-ahead and real-time clearing prices fluctuation.
- (3)
- The AOC in Case 1 is slightly lower than that in Cases 2–4, however, the COC in Case 1 is significantly higher than that in Cases 2–4. The main reason is that the deterministic model in Case 1 only pursues the cost minimization, which ignores the interferences of uncertainties such as clearing prices and wind power outputs etc. Neglecting the interferences of uncertainties may achieve the desired effect in cost minimization, but it often leads to higher potential risk of operational cost increase caused by uncertainties.
- (4)
- The COCs in Cases 3 and 4 are lower than that in Cases 1 and 2. That is to say, by implementing CVaR method, the potential risk of operational cost increase caused by day-ahead and real-time clearing prices fluctuation can be considerably reduced.
- (5)
- Both of the AOCs and COCs in Case 4 are lower than that in Case 3. That is to say, besides the cost reduction effect, the potential risk is further weakened via introducing multiple DRPs.
- (6)
- As listed in Table 8, the computational times of Cases 2–4 are relatively longer than that of Case 1. The main reason is that the introduction of multiple stochastic scenarios makes the number of variables and operational constraints increase accordingly. In addition, the introduction of CVaR method and multiple DRPs makes models in Case 4 consume a bit more time than Cases 2 and 3. It is generally known that the day-ahead market starts at least 12 hours before the delivery day, that is to say, relatively low computational times make our proposed model feasible in practice.
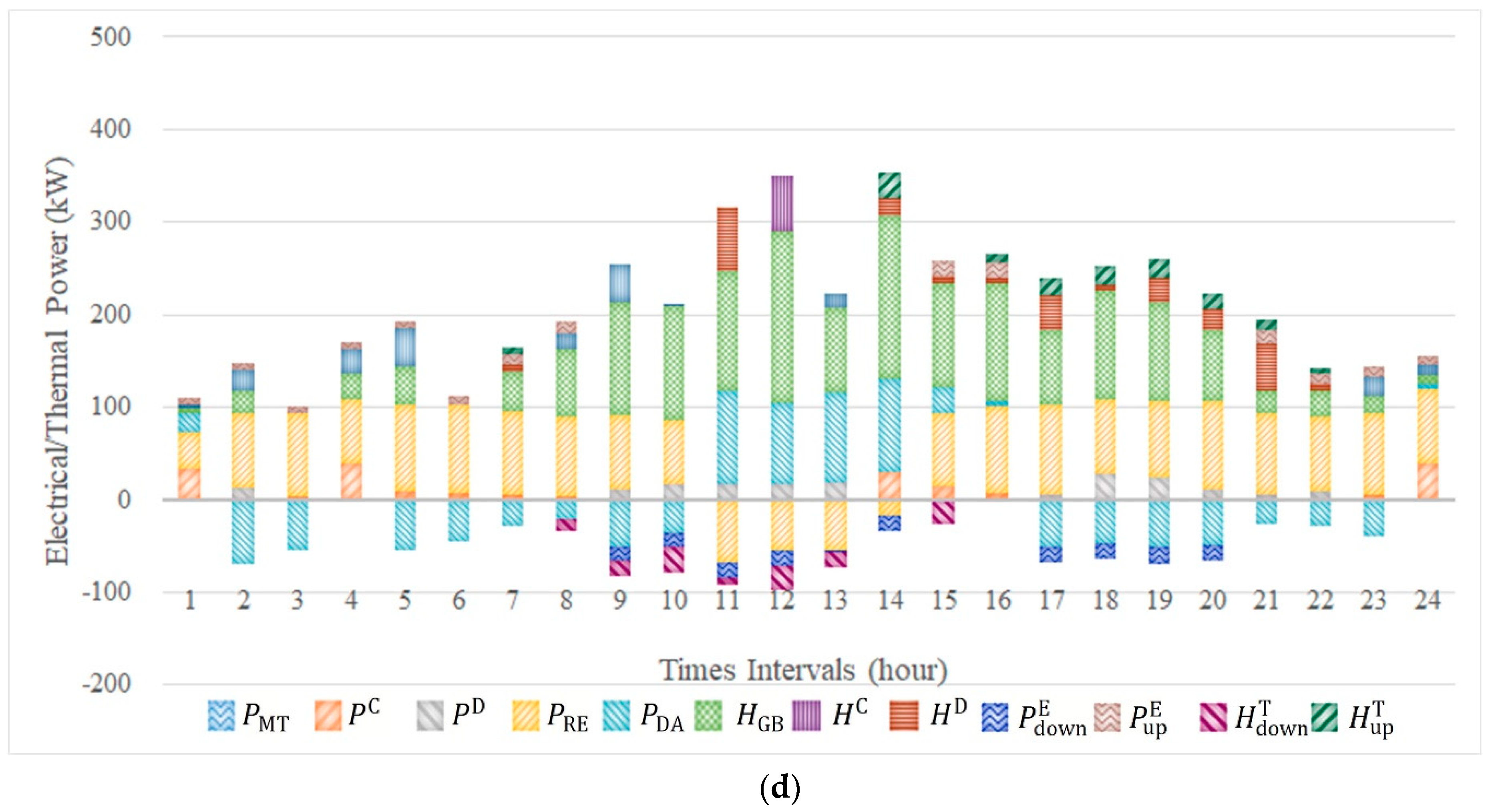
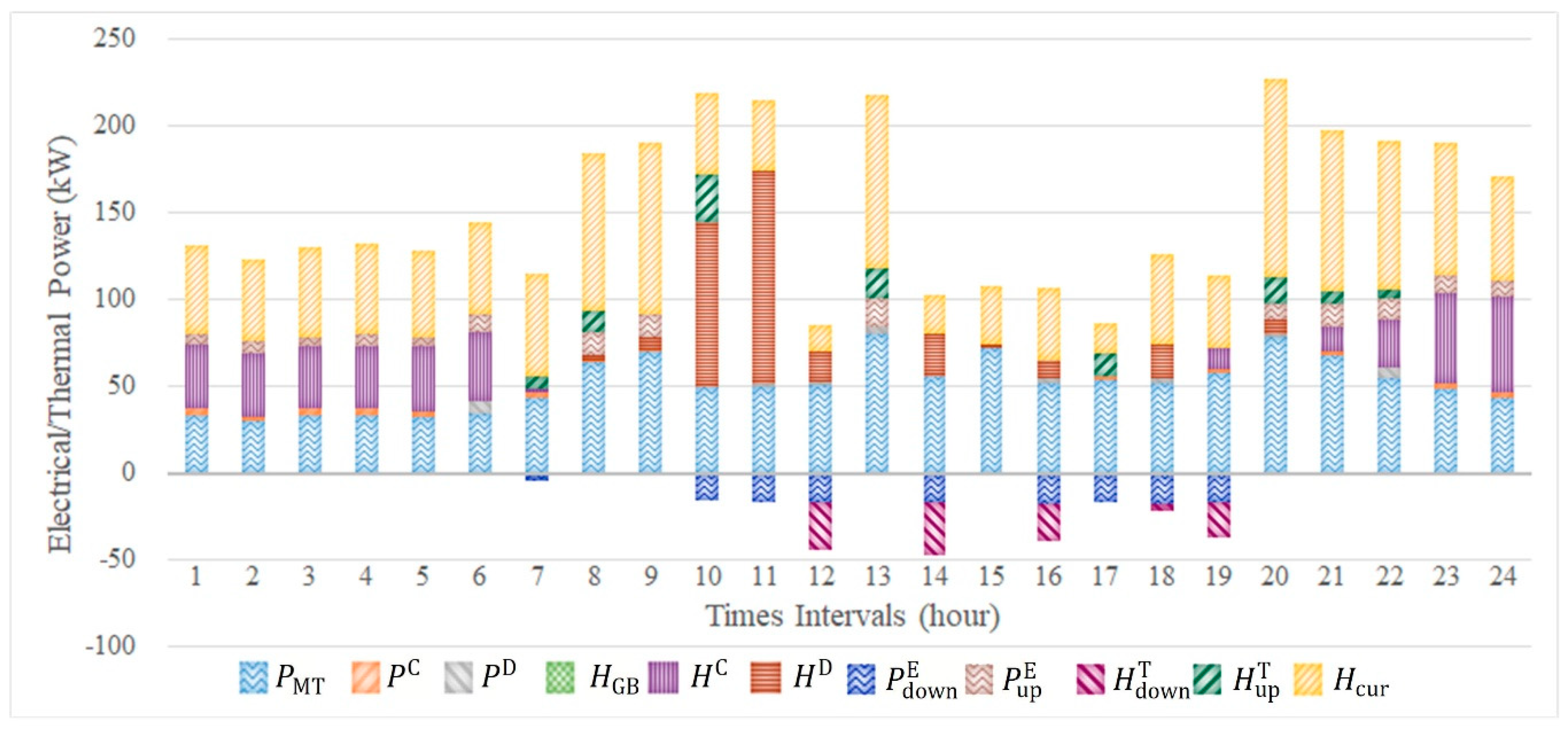
4.4. Simulated Test of Coordinately Optimizing EM Power Biddings
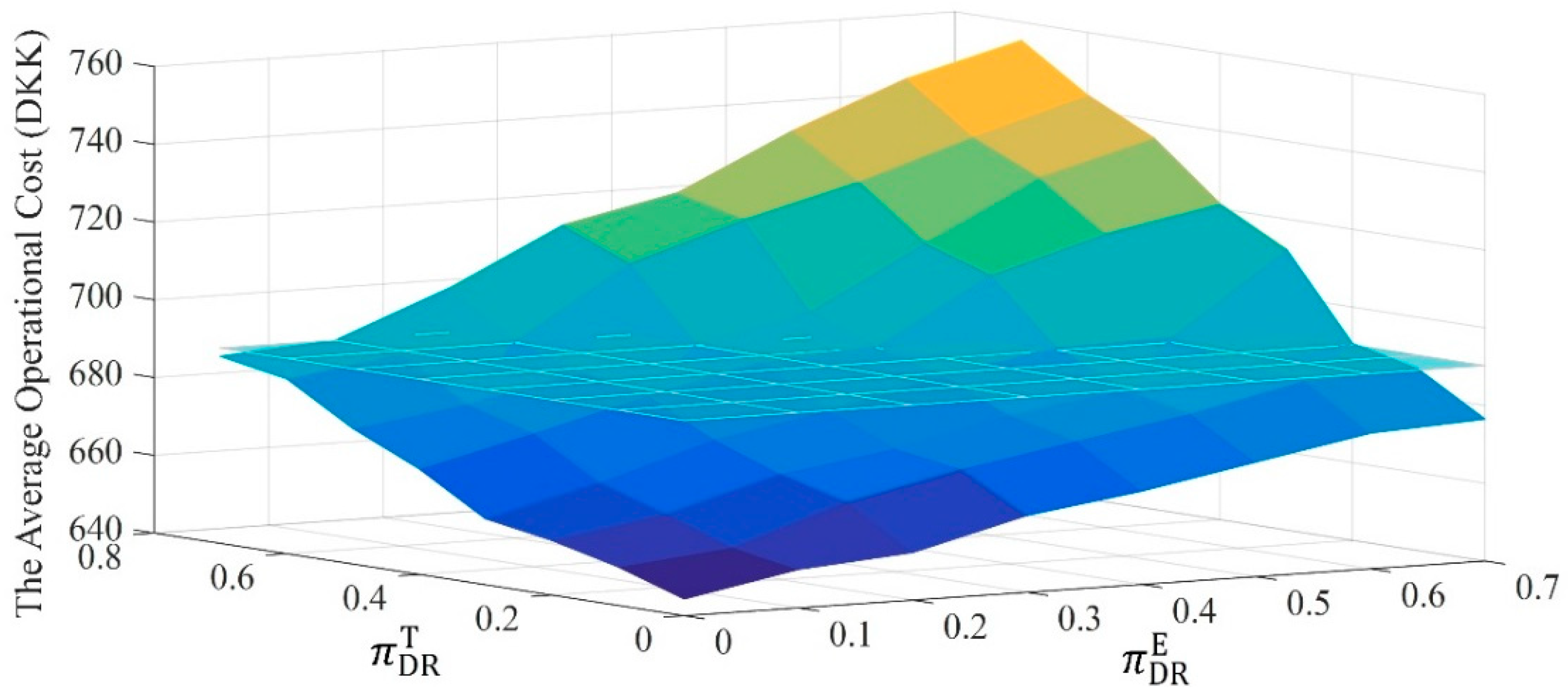
4.5. Sensitivity Studies
5. Conclusions
- (1)
- From Section 4.2, it has been verified that our proposed model is able to help CCHP micro-grid operation reaches better performance under EM circumstances. Specifically, a. by introducing SO method, our proposed model ensures that CCHP micro-grid can realize operational cost reduction, wind power accommodation, as well as secure and stable operation in the face of EM clearing prices and wind power outputs uncertainties; b. by employing the CVaR method, our proposed model helps CCHP micro-grid avoid the potential risk of operational cost increase caused by EM clearing prices fluctuation; c. by implementing multiple DRPs, our proposed model further optimizes the operation of CCHP micro-grid in terms of operational cost, potential risk and wind power accommodation.
- (2)
- In Section 4.3, it has been verified that relatively higher energy efficiency and lower operational cost can be achieved for CCHP micro-grid operation by coordinately optimizing EM power biddings (considering EM participation).
- (3)
- By implementing our simulations, it takes an average of 12.37 s to obtain the optimal operation results by solving our proposed model. That is to say relatively low computational time makes our proposed model feasible in practice.
- (4)
- From sensitivity analysis, it can be found that: a. changing the weighting parameter ω will cause AOC and COC values to change in opposite directions (forming a Pareto efficient frontier); b. different values of the unit compensation expense parameters and will affect the effect of implementing multiple DRPs.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Abbreviations | |
| CCHP | combined cooling, heating and power |
| EM | electrical market |
| CVaR | conditional value at risk |
| DRP | demand response program |
| EDRP | electrical demand response program |
| TDRP | thermal demand response program |
| CDRP | cooling demand response program |
| MT | micro turbine |
| WT | wind turbine |
| GB | gas boiler |
| HR | heat recovery |
| BT | battery |
| TT | thermal tank |
| HE | heat exchanger |
| EC | electrical chiller |
| AC | absorption chiller |
| Indices and Sets | |
| index for time periods | |
| set of stochastic scenarios | |
| index for scenarios | |
| set of scenario index | |
| set of power bidding decisions | |
| set of operational decisions | |
| Parameters and Constants | |
| the minimum/maximum electrical power produced by MT, kW | |
| the ramping rate of MT, kW | |
| the minimum uptime/downtime for MT, h | |
| the capacity of GB/HR, kW | |
| the charging/discharging capacity of BT, kW | |
| the minimum/maximum limitation for residual energy in BT, kW | |
| the charging/discharging capacity of TT, kW | |
| the minimum/maximum limitation for residual energy in TT, kW | |
| the maximum power input of EC/AC, kW | |
| maximum ratios of shifted down and shifted up electrical load | |
| maximum ratios of shifted down and shifted up thermal load | |
| maximum ratios of shifted down and shifted up cooling load | |
| Variables | |
| Binary Variables | |
| means MT is on or off during period t () | |
| means MT is start-up or not during period t () | |
| means MT is shut-down or not during period t () | |
| and | mean BT is in charging status during period t (. ) |
| and | mean BT is in discharging status during period t () |
| and | mean TT is in charging status during period t () |
| and | mean TT is in discharging status during period t () |
| and | mean the electrical load is in shifting down status during period t () |
| and | mean the electrical load is in shifting up status during period t () |
| and | mean the thermal load is in shifting down status during period t () |
| and | mean the thermal load is in shifting up status during period t () |
| and | mean the cooling load is in shifting down status during period t () |
| and | mean the cooling load is in shifting up status during period t () |
| Continuous Variables | |
| the electrical/thermal/cooling load during period t (), kW | |
| the EM clearing prices at day-ahead/real-time stage during period t () under scenario , DKK | |
| the scheduled electrical/thermal power output of MT during time period t () under scenario , kW | |
| the scheduled thermal power output of GB during time period t () under scenario , kW | |
| the scheduled power bid with real-time EM during time period t () under scenario , kW | |
| the wind power output during period t () under scenario , kW | |
| the thermal power recovered by HR during period t () under scenario , kW | |
| the residual energy of BT/TT at the end of period t () under scenario , kW | |
| the charging/discharging power of BT during period t () under scenario , kW | |
| thermal power stored/released by TT during period t () under scenario , kW | |
| the cooling power output of EC/AC during period t () under scenario , kW | |
| the electrical power input of EC during period t () under scenario , kW | |
| the thermal power input of AC during period t () under scenario , kW | |
Appendix A

Appendix B
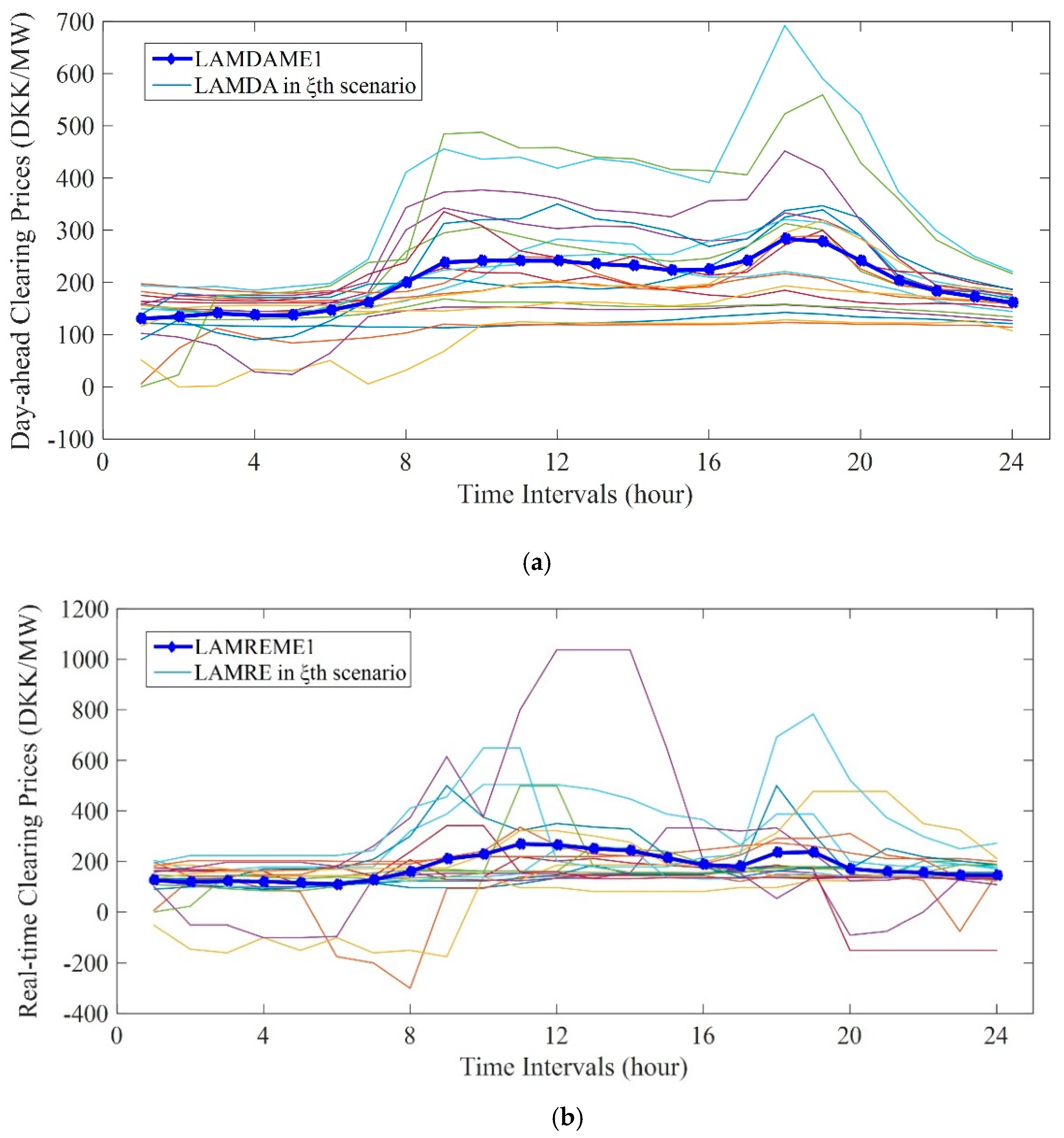
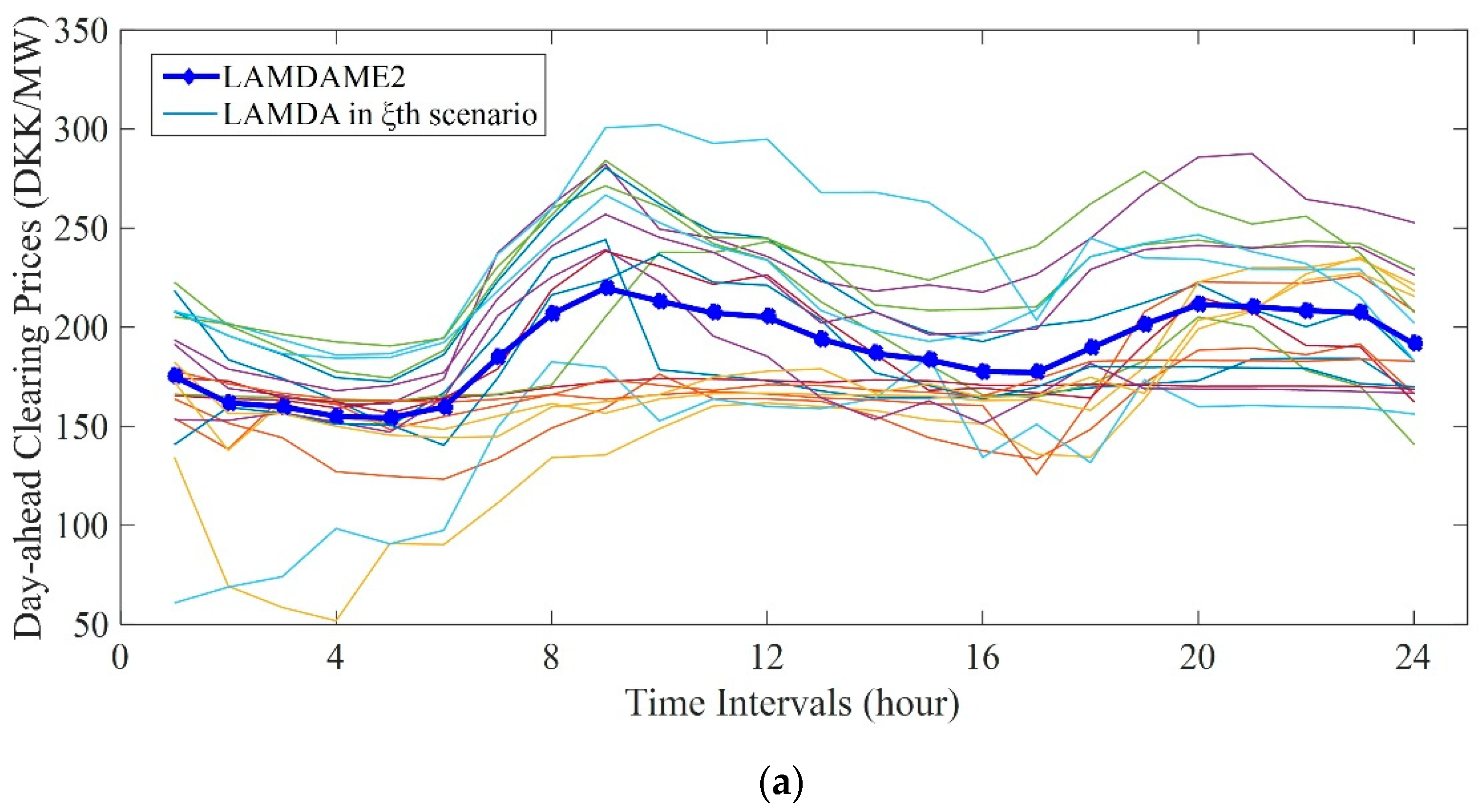

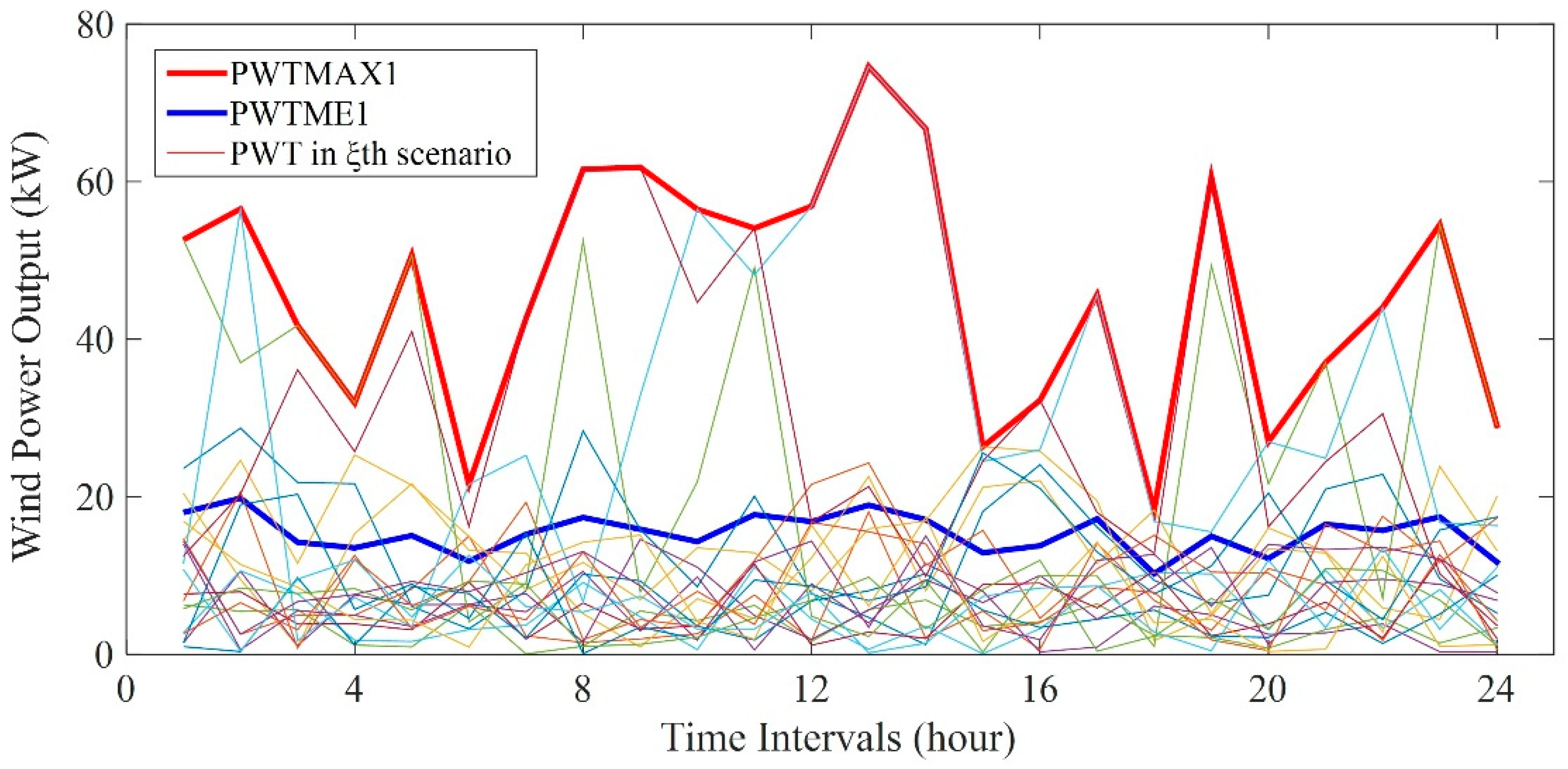
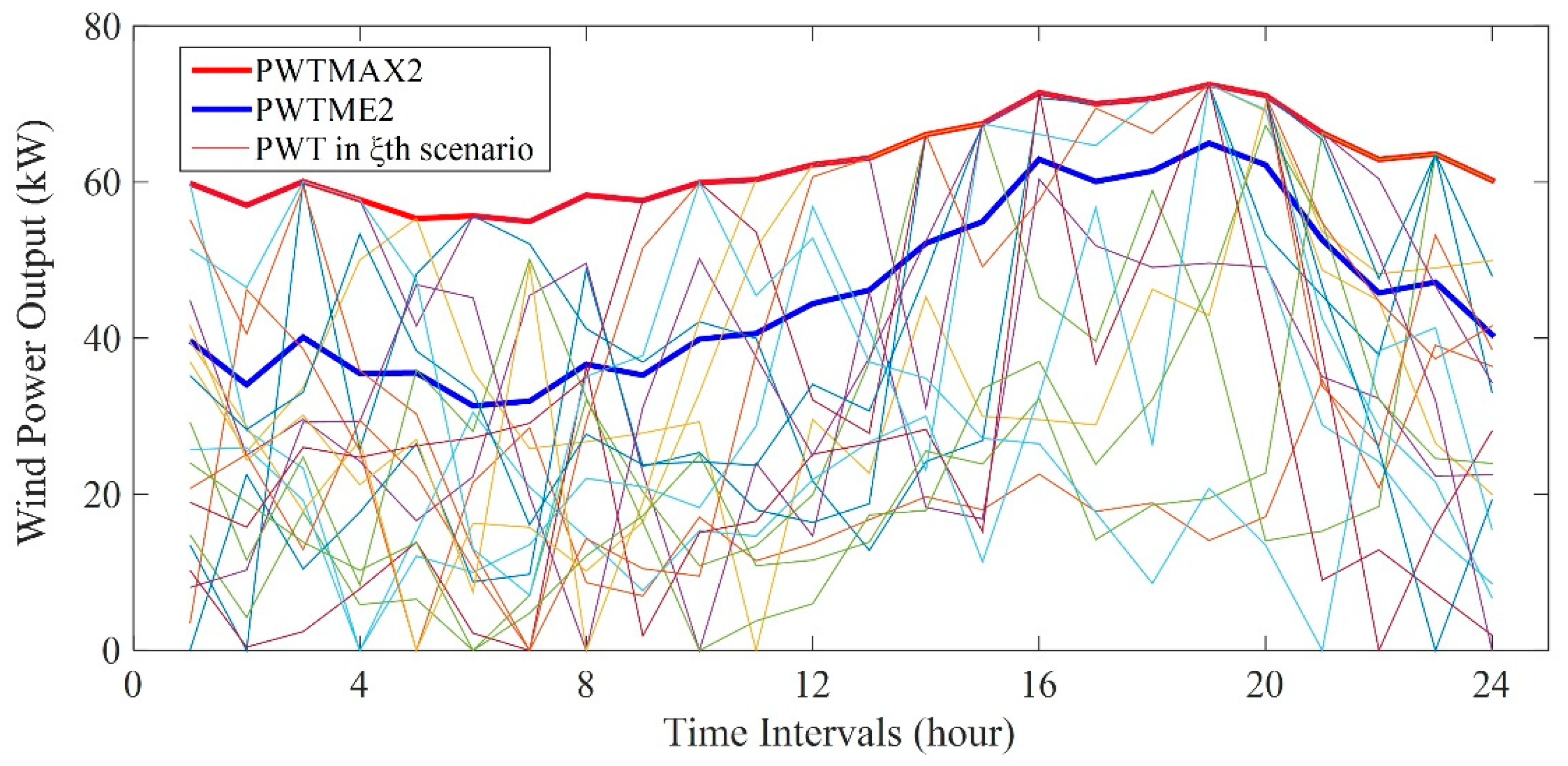

Appendix C
References
- Yan, Y.; Zhang, C.; Li, K.; Wang, Z. An integrated design for hybrid combined cooling, heating and power system with compressed air energy storage. Appl. Energy 2018, 210, 1151–1166. [Google Scholar] [CrossRef]
- Zhou, X.; Ai, Q. Distributed economic and environmental dispatch in two kinds of CCHP microgrid clusters. Int. J. Electr. Power Energy Syst. 2019, 112, 109–126. [Google Scholar] [CrossRef]
- Chahartaghi, M.; Sheykhi, M. Energy, environmental and economic evaluations of a CCHP system driven by Stirling engine with helium and hydrogen as working gases. Energy 2019, 174, 1251–1266. [Google Scholar] [CrossRef]
- Afzali, S.F.; Mahalec, V. Novel performance curves to determine optimal operation of CCHP systems. Appl. Energy 2018, 226, 1009–1036. [Google Scholar] [CrossRef]
- Das, B.K.; Al-Abdeli, Y.M.; Kothapalli, G. Effect of load following strategies, hardware, and thermal load distribution on stand-alone hybrid CCHP systems. Appl. Energy 2018, 220, 735–753. [Google Scholar] [CrossRef]
- Gu, W.; Lu, S.; Wu, Z.; Zhang, X.; Zhou, J.; Zhao, B.; Wang, J. Residential CCHP microgrid with load aggregator: Operation mode, pricing strategy, and optimal dispatch. Appl. Energy 2017, 205, 173–186. [Google Scholar] [CrossRef]
- Luo, Z.; Wu, Z.; Li, Z.; Cai, H.; Li, B.; Gu, W. A two-stage optimization and control for CCHP microgrid energy management. Appl. Therm. Eng. 2017, 125, 513–522. [Google Scholar] [CrossRef]
- Morales, J.M.; Conejo, A.J.; Madsen, H.; Pinson, P.; Zugno, M. Integrating Renewables in Electricity Markets: Operational Problems; Springer Science & Business Media: Berlin, Germany, 2013; Volume 205. [Google Scholar]
- Mago, P.J.; Chamra, L.M.; Ramsay, J. Micro-combined cooling, heating and power systems hybrid electric-thermal load following operation. Appl. Therm. Eng. 2010, 30, 800–806. [Google Scholar] [CrossRef]
- Feng, L.; Dai, X.; Mo, J.; Ma, Y.; Shi, L. Analysis of energy matching performance between CCHP systems and users based on different operation strategies. Energy Convers. Manage. 2019, 182, 60–71. [Google Scholar] [CrossRef]
- Dong, X.; Quan, C.; Jiang, T. Optimal planning of integrated energy systems based on coupled CCHP. Energies 2018, 11, 2621. [Google Scholar] [CrossRef]
- Lu, S.; Li, Y.; Xia, H. Study on the configuration and operation optimization of CCHP coupling multiple energy system. Energy Convers. Manage. 2018, 177, 773–791. [Google Scholar] [CrossRef]
- Kou, Y.; Bie, Z.; Wang, X.; Liu, F. ADMM-Based Multiperiod Optimal Energy Flow of a Regional Integrated Multi-Energy Microgrid. Energy Procedia 2019, 159, 180–185. [Google Scholar] [CrossRef]
- Soheyli, S.; Mayam, M.H.S.; Mehrjoo, M. Modeling a novel CCHP system including solar and wind renewable energy resources and sizing by a CC-MOPSO algorithm. Appl. Energy 2016, 184, 375–395. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, F.; Wang, R.; Kazemtabrizi, B.; Shi, J. Uncertainty-resistant Stochastic MPC Approach for Optimal Operation of CHP Microgrid. Energy 2019, 179, 1265–1278. [Google Scholar] [CrossRef]
- Wang, J.; Zhong, H.; Xia, Q.; Kang, C.; Du, E. Optimal joint-dispatch of energy and reserve for CCHP-based microgrids. IET Gener. Transm. Distrib. 2017, 11, 785–794. [Google Scholar] [CrossRef]
- Shams, M.H.; Shahabi, M.; Khodayar, M.E. Stochastic day-ahead scheduling of multiple energy Carrier microgrids with demand response. Energy 2018, 155, 326–338. [Google Scholar] [CrossRef]
- Grover-Silva, E.; Heleno, M.; Mashayekh, S.; Cardoso, G.; Girard, R.; Kariniotakis, G. A stochastic optimal power flow for scheduling flexible resources in microgrids operation. Appl. Energy 2018, 229, 201–208. [Google Scholar] [CrossRef]
- Marino, C.; Marufuzzaman, M.; Hu, M.; Sarder, M.D. Developing a CCHP-microgrid operation decision model under uncertainty. Comput. Ind. Eng. 2018, 115, 354–367. [Google Scholar] [CrossRef]
- Li, C.; Xu, Y.; Yu, X.; Ryan, C.; Huang, T. Risk-averse energy trading in multienergy microgrids: a two-stage stochastic game approach. IEEE Trans. Ind. Inf. 2017, 13, 2620–2630. [Google Scholar] [CrossRef]
- Narayan, A.; Ponnambalam, K. Risk-averse stochastic programming approach for microgrid planning under uncertainty. Renew. Energy 2017, 101, 399–408. [Google Scholar] [CrossRef]
- Marino, C.; Quddus, M.A.; Marufuzzaman, M.; Cowan, M.; Bednar, A.E. A chance-constrained two-stage stochastic programming model for reliable microgrid operations under power demand uncertainty. Sustainable Energy Grids Networks 2018, 13, 66–77. [Google Scholar] [CrossRef]
- Wang, L.; Li, Q.; Ding, R.; Sun, M.; Wang, G. Integrated scheduling of energy supply and demand in microgrids under uncertainty: A robust multi-objective optimization approach. Energy 2017, 130, 1–14. [Google Scholar] [CrossRef]
- Ji, L.; Niu, D.X.; Huang, G.H. An inexact two-stage stochastic robust programming for residential micro-grid management-based on random demand. Energy 2014, 67, 186–199. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, B.; Li, Q.; Song, W.; Li, G. Robust distributed optimization for energy dispatch of multi-stakeholder multiple microgrids under uncertainty. Appl. Energy 2019, 255, 113845. [Google Scholar] [CrossRef]
- Ji, L.; Huang, G.; Xie, Y.; Zhou, Y.; Zhou, J. Robust cost-risk tradeoff for day-ahead schedule optimization in residential microgrid system under worst-case conditional value-at-risk consideration. Energy 2018, 153, 324–337. [Google Scholar] [CrossRef]
- Saberi, K.; Pashaei-Didani, H.; Nourollahi, R.; Zare, K.; Nojavan, S. Optimal performance of CCHP based microgrid considering environmental issue in the presence of real time demand response. Sustainable Cities Soc. 2019, 45, 596–606. [Google Scholar] [CrossRef]
- Varasteh, F.; Nazar, M.S.; Heidari, A.; Shafie-khah, M.; Catalão, J.P. Distributed energy resource and network expansion planning of a CCHP based active microgrid considering demand response programs. Energy 2019, 172, 79–105. [Google Scholar] [CrossRef]
- Mohammadkhani, N.; Sedighizadeh, M.; Esmaili, M. Energy and emission management of CCHPs with electric and thermal energy storage and electric vehicle. Therm. Sci. Eng. Prog. 2018, 8, 494–508. [Google Scholar] [CrossRef]
- Vahid-Pakdel, M.J.; Nojavan, S.; Mohammadi-Ivatloo, B.; Zare, K. Stochastic optimization of energy hub operation with consideration of thermal energy market and demand response. Energy Convers. Manage. 2017, 145, 117–128. [Google Scholar] [CrossRef]
- Najafi, A.; Falaghi, H.; Contreras, J.; Ramezani, M. Medium-term energy hub management subject to electricity price and wind uncertainty. Appl. Energy 2016, 168, 418–433. [Google Scholar] [CrossRef]
- Davatgaran, V.; Saniei, M.; Mortazavi, S. Optimal bidding strategy for an energy hub in energy market. Energy 2018, 148, 482–493. [Google Scholar] [CrossRef]
- Zhou, Y.; Wei, Z.; Sun, G.; Cheung, K.W.; Zang, H.; Chen, S. A robust optimization approach for integrated community energy system in energy and ancillary service markets. Energy 2018, 148, 1–15. [Google Scholar] [CrossRef]
- Hu, H.; Wang, Y.R.; Zeng, B.; Zhang, J.H.; Shi, J.Q. CVaR-based economic optimal dispatch of integrated energy system. Electr. Power Autom. Equip. 2017, 37, 209–219. (in Chinese). [Google Scholar]
- Liu, G.; Xu, Y.; Tomsovic, K. Bidding strategy for microgrid in day-ahead market based on hybrid stochastic/robust optimization. IEEE Trans. Smart Grid 2016, 7, 227–237. [Google Scholar] [CrossRef]
- Najafi-Ghalelou, A.; Nojavan, S.; Zare, K.; Mohammadi-Ivatloo, B. Robust scheduling of thermal, cooling and electrical hub energy system under market price uncertainty. Appl. Therm. Eng. 2019, 149, 862–880. [Google Scholar] [CrossRef]
- Tian, M.W.; Ebadi, A.G.; Jermsittiparsert, K.; Kadyrov, M.; Ponomarev, A.; Javanshir, N.; Nojavan, S. Risk-based stochastic scheduling of energy hub system in the presence of heating network and thermal energy management. Appl. Therm. Eng. 2019, 159, 113825. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Mohammadi-Ivatloo, B. Stochastic risk-constrained scheduling of smart energy hub in the presence of wind power and demand response. Appl. Therm. Eng. 2017, 123, 40–49. [Google Scholar] [CrossRef]
- Ding, H.; Pinson, P.; Hu, Z.; Song, Y. Optimal offering and operating strategies for wind-storage systems with linear decision rules. IEEE Trans. Power Syst. 2016, 31, 4755–4764. [Google Scholar] [CrossRef]
- Tavakoli, M.; Shokridehaki, F.; Akorede, M.F.; Marzband, M.; Vechiu, I.; Pouresmaeil, E. CVaR-based energy management scheme for optimal resilience and operational cost in commercial building microgrids. Int. J. Electr. Power Energy Syst. 2018, 100, 1–9. [Google Scholar] [CrossRef]
- Jadidbonab, M.; Babaei, E.; Mohammadi-ivatloo, B. CVaR-constrained scheduling strategy for smart multi carrier energy hub considering demand response and compressed air energy storage. Energy 2019, 174, 1238–1250. [Google Scholar] [CrossRef]
- Huang, M.; Wang, X.; Zhang, S. Analysis of an electricity market equilibrium model with penalties for wind power’s bidding deviation. In Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015; pp. 35–40. [Google Scholar]


| Ref. | Research Object | EM Participation | Considered Uncertainties | Optimization Model | Risk Management | DRP |
|---|---|---|---|---|---|---|
| [14] | CCHP micro-grid | No | renewable power output | multi-stage optimization method | No | No |
| [15] | CCHP micro-grid | No | renewable power output | MPC method | No | EDRP |
| [16] | CCHP micro-grid | No | renewable power output | joint-dispatch scheme | No | No |
| [17] | micro-grid | No | renewable power output | SO method | No | EDRP, TDRP |
| [18] | micro-grid | No | renewable power output; electrical load | SO method | No | EDRP |
| [19,20,21,22] | CCHP micro-grid | No | renewable power output | SO method | No | No |
| [23] | micro-grid | No | renewable power output; electrical load | RO method | No | No |
| [24,25] | micro-grid | No | renewable power output; electrical load | RO method | No | No |
| [26] | micro-grid | No | renewable power output; electrical load | RO method | Yes | No |
| [27] | CCHP micro-grid | No | renewable power output; | RO method | No | EDRP |
| [28] | CCHP micro-grid | No | renewable power output; | SO method | No | EDRP |
| [29] | CCHP system | No | renewable power output; | Multi-objective optimization | No | EDRP |
| [30] | EH | Yes | renewable power output; EM prices | SO method | No | EDRP, TDRP |
| [31] | EH | Yes | renewable power output; EM prices | SO method | Yes | No |
| [32] | EH | Yes | renewable power output; EM prices | SO method | No | No |
| [33] | MRIES | Yes | renewable power output; EM prices | RO method | No | No |
| [34] | MRIES | Yes | renewable power output; EM prices | bi-level optimization | Yes | No |
| [35] | micro-grid | Yes | renewable power output; EM prices | SO method | No | No |
| [36] | multi-energy hub systems | Yes | renewable power output; EM prices | RO method | No | EDRP |
| Gaps |
| |||||
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 3.14 DKK/m3 | HAC,max | 320 kW | |
| 100 kWh | |||
| 0.35 | 180 kWh | ||
| 0.10 | 40 kWh | ||
| 0.75 | 250 kWh | ||
| 0.95 | 450 kWh | ||
| 0.95 | 100 kWh | ||
| 0.90 | 80 kW | ||
| 0.90 | 3 m/s | ||
| 0.80 | 13.1 m/s | ||
| 1 | 27 m/s | ||
| 4 | 7.92 | ||
| 0.70 | −23.76 | ||
| 60 kW | 0 | ||
| 200 kW | 0 | ||
| 30 kW | 0 | ||
| 2 h | 0.20 | ||
| 2 h | 0.20 | ||
| 500 kW | 0.20 | ||
| 40 kW | 0.20 | ||
| 40 kW | 0.20 | ||
| 100 kW | 0.20 | ||
| 100 kW | 0.40 | ||
| 240 kW | 0.90 | ||
| 140 kW |
| Models from Case | Arithmetic Average Scenario for Uncertainties | EM Participation | Stochastic Scenarios for Uncertainties | CVaR and Its Related Constraints | DRPs and Its Related Constraints | Termed as |
|---|---|---|---|---|---|---|
| 1 |  |  | deterministic model | |||
| 2 |  |  | SO model | |||
| 3 |  |  |  | model without DRPs | ||
| 4 |  |  |  |  | our proposed model | |
| 5 |  |  | islanded model |
| Case | Average Electrical Energy Selling to EMs (kW) | Average Electrical Energy Purchasing from EMs (kW) | ||
|---|---|---|---|---|
| Day-Ahead Stage | Real-Time Stage | Day-Ahead Stage | Real-Time Stage | |
| 1 | 100.0000 | 71.1993 | 66.2234 | 57.1591 |
| 2 | 91.8457 | 68.9668 | 62.4450 | 47.5966 |
| 3 | 82.4444 | 55.6556 | 38.9432 | 37.5924 |
| 4 | 83.8937 | 60.5208 | 48.2081 | 41.0695 |
| Case | AOC (DKK) | COC (DKK) |
|---|---|---|
| 1 | 639.5264 | 1297.5089 |
| 2 | 678.1488 | 1254.3559 |
| 3 | 690.2398 | 1178.6985 |
| 4 | 644.3196 | 1149.1882 |
| Case | Average Electrical Energy Selling to EMs (kW) | Average Electrical Energy Purchasing from EMs (kW) | ||
|---|---|---|---|---|
| Day-Ahead Stage | Real-Time Stage | Day-Ahead Stage | Real-Time Stage | |
| 1 | 82.3510 | 82.3510 | 62.4054 | 46.9530 |
| 2 | 72.3767 | 72.3767 | 59.8434 | 38.5721 |
| 3 | 61.3761 | 61.3761 | 38.8951 | 21.9265 |
| 4 | 67.4751 | 67.4751 | 43.7239 | 26.0192 |
| Case | AOC (DKK) | COC (DKK) |
|---|---|---|
| 1 | 358.2047 | 490.0226 |
| 2 | 386.9608 | 478.8715 |
| 3 | 397.9516 | 435.8498 |
| 4 | 364.0544 | 404.5357 |
| Case | Computational Time (s) | |
|---|---|---|
| The Typical Winter Day | The Typical Summer Day | |
| 1 | 5.15 | 6.11 |
| 2 | 10.13 | 10.24 |
| 3 | 11.36 | 12.04 |
| 4 | 11.92 | 12.82 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yang, Y.; Tang, L.; Sun, W.; Zhao, H. A Stochastic-CVaR Optimization Model for CCHP Micro-Grid Operation with Consideration of Electricity Market, Wind Power Accommodation and Multiple Demand Response Programs. Energies 2019, 12, 3983. https://doi.org/10.3390/en12203983
Wang Y, Yang Y, Tang L, Sun W, Zhao H. A Stochastic-CVaR Optimization Model for CCHP Micro-Grid Operation with Consideration of Electricity Market, Wind Power Accommodation and Multiple Demand Response Programs. Energies. 2019; 12(20):3983. https://doi.org/10.3390/en12203983
Chicago/Turabian StyleWang, Yuwei, Yuanjuan Yang, Liu Tang, Wei Sun, and Huiru Zhao. 2019. "A Stochastic-CVaR Optimization Model for CCHP Micro-Grid Operation with Consideration of Electricity Market, Wind Power Accommodation and Multiple Demand Response Programs" Energies 12, no. 20: 3983. https://doi.org/10.3390/en12203983
APA StyleWang, Y., Yang, Y., Tang, L., Sun, W., & Zhao, H. (2019). A Stochastic-CVaR Optimization Model for CCHP Micro-Grid Operation with Consideration of Electricity Market, Wind Power Accommodation and Multiple Demand Response Programs. Energies, 12(20), 3983. https://doi.org/10.3390/en12203983





