Control Strategy for Electric Vehicle Charging Station Power Converters with Active Functions

Abstract

Based on the assumption that vehicles served by petrol stations will be replaced by Electric Vehicles (EV) in the future, EV public charging station facilities, with off-board fast chargers, will be progressively built. The power demand of these installations is expected to cause great impact on the grid, not only in terms of peak power demanded but also in terms of power quality, because most battery chargers behave as non-linear loads. This paper presents the proposal of a novel comprehensive global control strategy for the power electronic converters associated with bidirectional three-phase EV off-board fast chargers. The Charging Station facility Energy Management System (CS-EMS) sends to each individual fast charger the active and reactive power setpoints. Besides, in case the charger has available capacity, it is assigned to compensate a fraction of the harmonic current demanded by other loads at the charging facility. The proposed approach works well under distorted and unbalanced grid voltages. Its implementation results in improvement in the power quality of each fast charger, which contributes to improvement in the power quality at the charging station facility level, which can even provide ancillary services to the distribution network. Simulation tests are conducted, using a 100 kW power electronic converter model, under different load and grid conditions, to validate the effectiveness and the applicability of the proposed control strategy.

1. Introduction

Electric vehicles (EV) represent the most likely successor to conventional internal combustion engine vehicles. Over the past few years, sales have steadily increased, and this trend is expected to continue over the next few years [1]. To perform the battery charging process, EVs rely on a charging station, which can be found at home, at work, or at a public charging station. Typically, on-board chargers are slow chargers, while off-board chargers are fast chargers. Both solutions come with advantages and disadvantages [2]. On-board chargers have limited power ratings due to space, weight, and cost restrictions, while off-board chargers can be designed for high charging rates with fewer restrictions. The different charging modes and their characteristics are summarized in

Table 1. EV charging modes according to IEC 61851-1 [3].

Charging Mode	Maximum Current	Maximum Charging Power	Charging Time for Recharging 20 kWh (1)
Mode 1	16 A, AC, 1-phase	3.7 kW	5 h
Mode 2	32 A, AC, 3-phase	22 kW	1 h
Mode 3	63 A, AC, 3-phase	44 kW	0.5 h
Mode 4	400 A, DC	approx. 200 kW	6 min (2)

¹ Sufficient for ca. 100–150 km electric driving. ² Charging up to approx. 80% SOC.

(from IEC 61851-1 [3]). Current forecasts, driven by European Distribution System Operators (DSO), suggest that, by 2030, AC power levels are expected to increase only slightly, since they will be constrained by existing connection points. However, fast DC chargers will grow to more than 150 kW (even up to 300 kW) [4].

Although most EV charging processes today take place at homes, it is clear that access to public fast DC charging stations could help mitigate the so-called ‘range anxiety’, which is one of the reasons considered for doubting buying an electric car. Therefore, the development of a charging infrastructure is a work in progress and likely the greatest long-term challenge for electric vehicles [5]. On the assumption that vehicles served by the gas stations will be replaced by EVs in the future, EV Charging Station facilities (CS) will be progressively built to meet this energy demand.

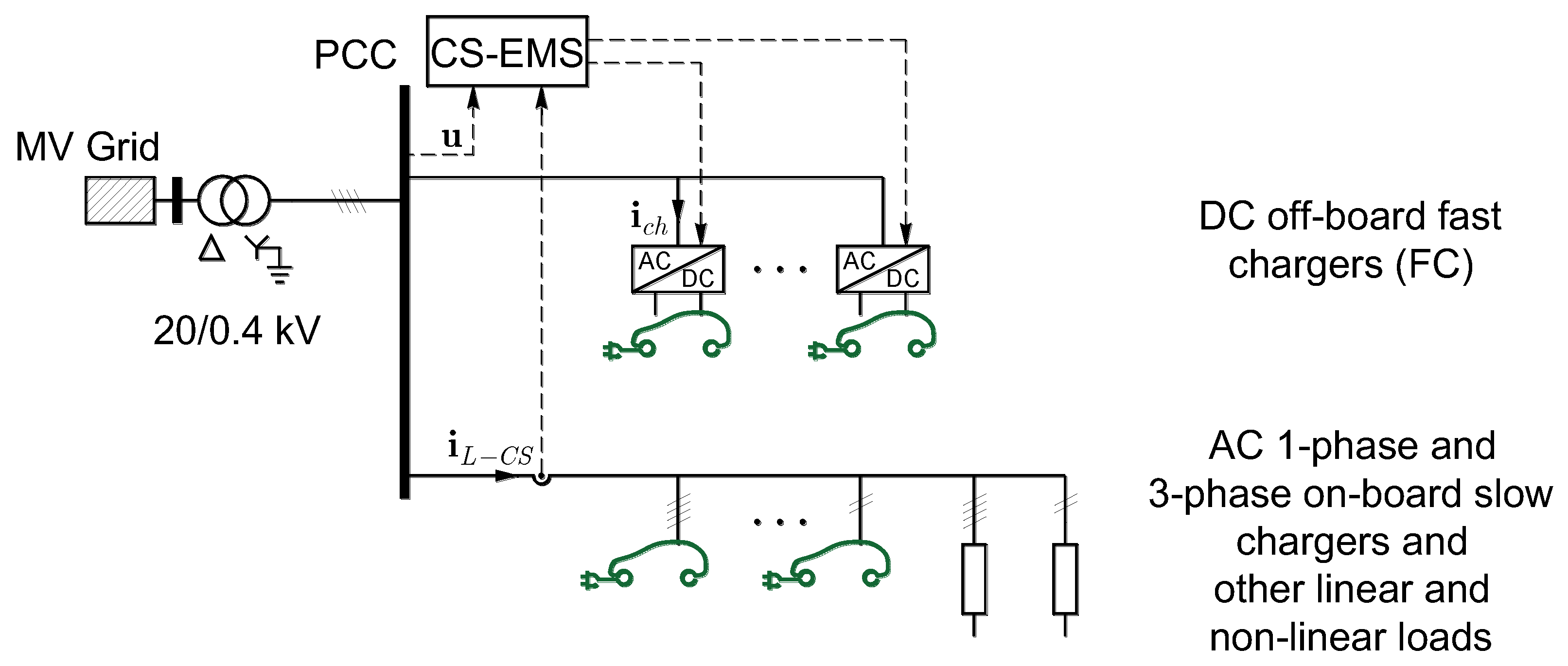
Considering that the network inside a CS is a three-phase four-wire Low Voltage (LV) network 230/400 V, which is typical in EU and permits the connection of both AC single-phase (230 V) loads and also AC three-phase (400 V) loads. As an illustrative case, suppose that there are 10 fast DC off-board charging piles, which are three-phase AC/DC voltage source converters (VSC), of about 100 kW per pile. There is also a parking zone equipped with 20 AC charging piles, both 1-phase and 3-phase, of about 30 kW on average, and a commercial facility (about 100 square meters) for shopping and another services of about 10 kW of installed power (based on an estimation of about 100 W per square meter). The global power will be about 1500 to 2000 kW, which is about the same as a residential building or office building [6].

A load of this magnitude is expected to require a connection to the Medium Voltage (MV) distribution network. Therefore, distribution system operators need to be informed in order to coordinate and facilitate the connection of these stations. However, the impact is not only in terms of the power demanded. Since the chargers are based on power electronic converters, the quality of supply will also be greatly affected. From the AC side, most battery chargers on the market behave as non-linear loads, which causes harmonic distortion, reactive consumption, and imbalances. These impacts on LV networks have been extensively documented and measured [7,8,9].

Figure 1 shows the architecture of an example of typical CS. The currents drawn by the entire CS, viewed from the LV side of the MV/LV transformer will be disturbed and unbalanced, not only by the chargers itself, but also by the other non-linear and unbalanced loads. Due to these currents and even the ones from other clients connected to the same MV network, the grid voltages will be disturbed as well. In this situation, the majority of the proposed control strategies aim to avoid the introduction of additional disturbances into the network (following recommendations from IEEE Standard 519-1992 [10]). However, they do not work properly in the presence of the mentioned distorted and unbalanced grid voltage waveforms. Consequently, the integration of EV needs research on new and more adequate control strategies.

It is important to note that the origin of the problems caused by the chargers is also part of the solution. The power electronic converters, which act as the interface between the grid and the batteries, have the potential to behave in an active way, by providing various active functions or ancillary services to support the power system operation, such as frequency control, voltage control [11], operating reserve, controllable load, and Power Quality (PQ) improvement [12]. This is in the context of what is often referred to as the vehicle-to-grid (V2G) concept. In the case of the off-board chargers, the AC/DC converter, which includes the DC link capacitors, is suitable to use as an active filter, even without a car connected for charging. Precisely, the strategies for these power electronic converters, following different compensation objectives from the setpoints provided by the CS-EMS, is one goal of this work.

Some works addressing bidirectional EV chargers, found in the technical literature, are focused on trying to alleviate the impact on the network by using strategies based on active power flow control coordination between chargers [13,14]. Control strategies considering the reactive power control are applied to single-phase chargers [15,16,17,18] and to three-phase chargers [19,20]. Charging/discharging with constant current or a constant voltage strategy are considered in Reference [21]. The work presented in Reference [22] achieves the control of the current demanded by a synchronous rectifier under normal and abnormal grid voltage conditions, but it does not perform active functions. In Reference [23], it is demonstrated that a single-phase EV on-board charger can operate both as a static synchronous compensator (STATCOM) and as an active power filter. However, it cannot work well under unbalanced and distorted grid voltages and cannot perform the phase balancing function. In contrast, three-phase chargers can compensate the unbalanced currents demanded by the loads connected at the same Point of Common Coupling (PCC). This is done by the charger studied in Reference [24], but it does not include a harmonic compensation capability. In References [25,26], a global control strategy was proposed and validated, which allows a single-phase charger to operate simultaneously with an active (P mode) and reactive (Q mode) power setpoints. It compensates the load current harmonics (H mode), in all the cases, under normal and abnormal grid conditions. The authors in Reference [27] apply a synchronverter strategy to a charging station, which can provide ancillary services such as frequency control or power reserves, as well as supply or absorb reactive power. However, it cannot provide H control and does not work properly under a disturbed grid. Reference [28] uses a strategy that is able to obtain sinusoidal grid currents and a unitary power factor even with distorted grid voltages, but it does not perform the H function nor imbalance load currents’ compensation. In the case of Reference [29], the Conservative Power Theory is applied, which implies that it does not work in the case of distorted or unbalanced source voltage, as demonstrated by Czarnecki in Reference [30].

From the previously mentioned studies, it can be asserted that the benefits of including a local harmonic and imbalance control strategy, operating simultaneously with the active and reactive controllers, in the case of a three-phase charger and under abnormal grid conditions have not been thoroughly investigated. This provides a global perspective on the convenience to address a different approach. With this objective, this paper starts from authors’ previous studies [25,26] and extends them to a three-phase system, adding the capability of imbalance load currents’ compensation (I mode).

Therefore, the main contribution of this paper is the proposal and validation of a novel comprehensive global control strategy for the power electronic converters associated with bidirectional three-phase EV fast chargers, which allows them to operate simultaneously with P, Q, H, and I control in a coordinated manner and, in all the cases, under distorted and unbalanced grid voltages.

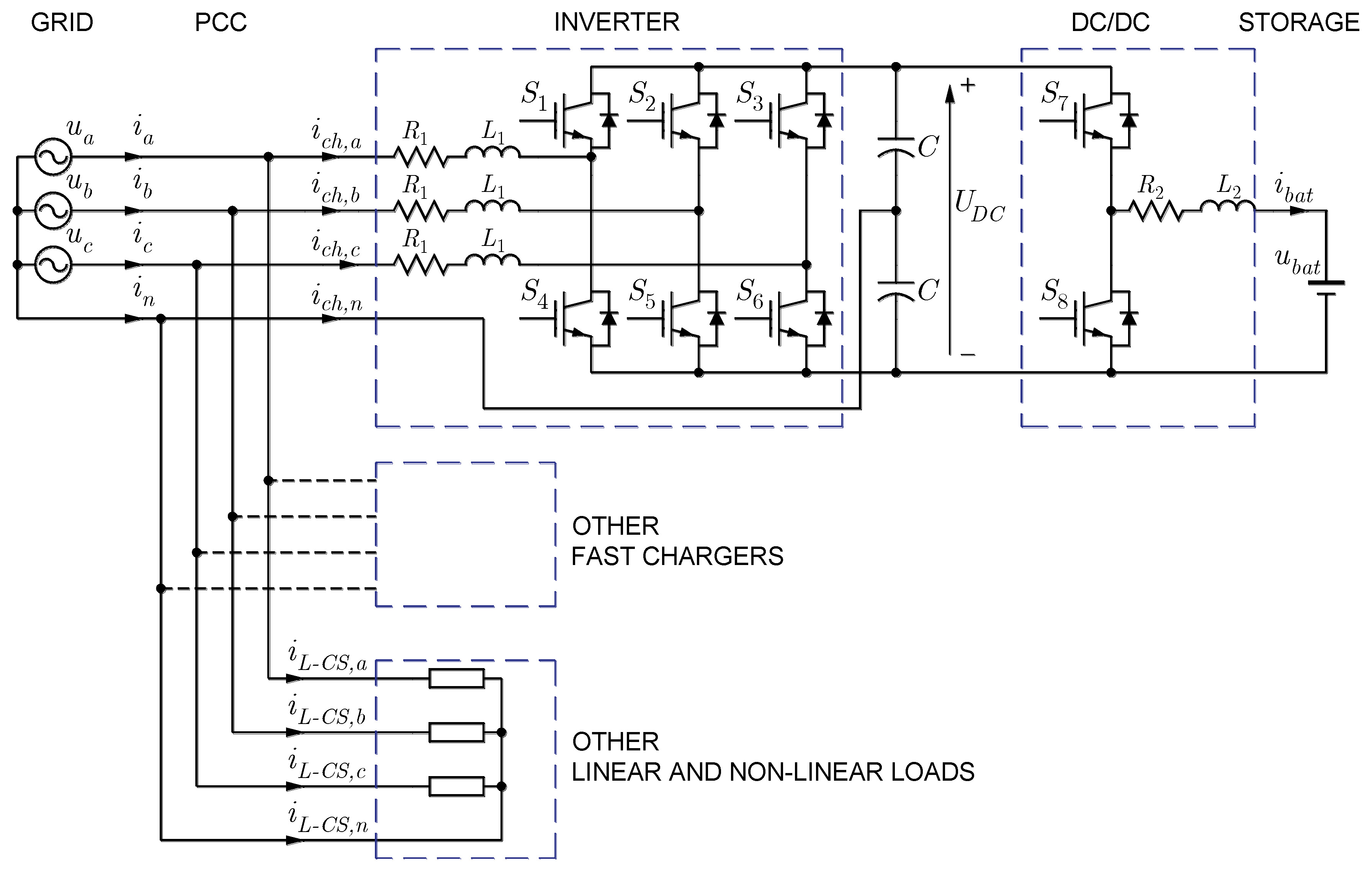
The paper is organized in the following manner. In Section 2, first, the control strategies to control active power and reactive power are presented. Then, the harmonic and imbalance control are added, with the aim of compensating the imbalance and harmonic consumption. In Section 3, the simulation model is explained, including the charger topology and control stage, where the strategies are implemented. The implemented model is based on electrical models with realistic parameters, using advanced versions of the elements, based on previous author’s works. A set of simulation tests are carried out in Section 4 showing the effectiveness of the strategies in different situations, which cover several representative cases. Lastly, conclusions are summarized in Section 5.

2. Proposed Control Strategy

Consider an EV Fast Charging point (FC), which is part of a CS. The control strategy generates the reference currents, $i_{ch}^{\ast }$ (see Figure 1), which must be provided by FC, in such a way that (i) active and reactive power setpoints sent by the CS-EMS are satisfied, and (ii) harmonic and unbalanced currents demanded by the other loads connected at the PCC are compensated. The former objective is a prioritized one, while the latter is at the expense of the remaining capacity, i.e., attempting to ensure that the FC rated power is not exceeded. This set of signals for the desired phase currents will be tracked by generating the corresponding switching signals for the electronic converter by means of the appropriate closed-loop switching control technique, such as hysteresis or dead-beat control. The implementation of this strategy in each individual FC will contribute to improving the operational performance of the four-wire LV network, because line currents will tend to be balanced, with the power factor close to one and free of harmonic content.

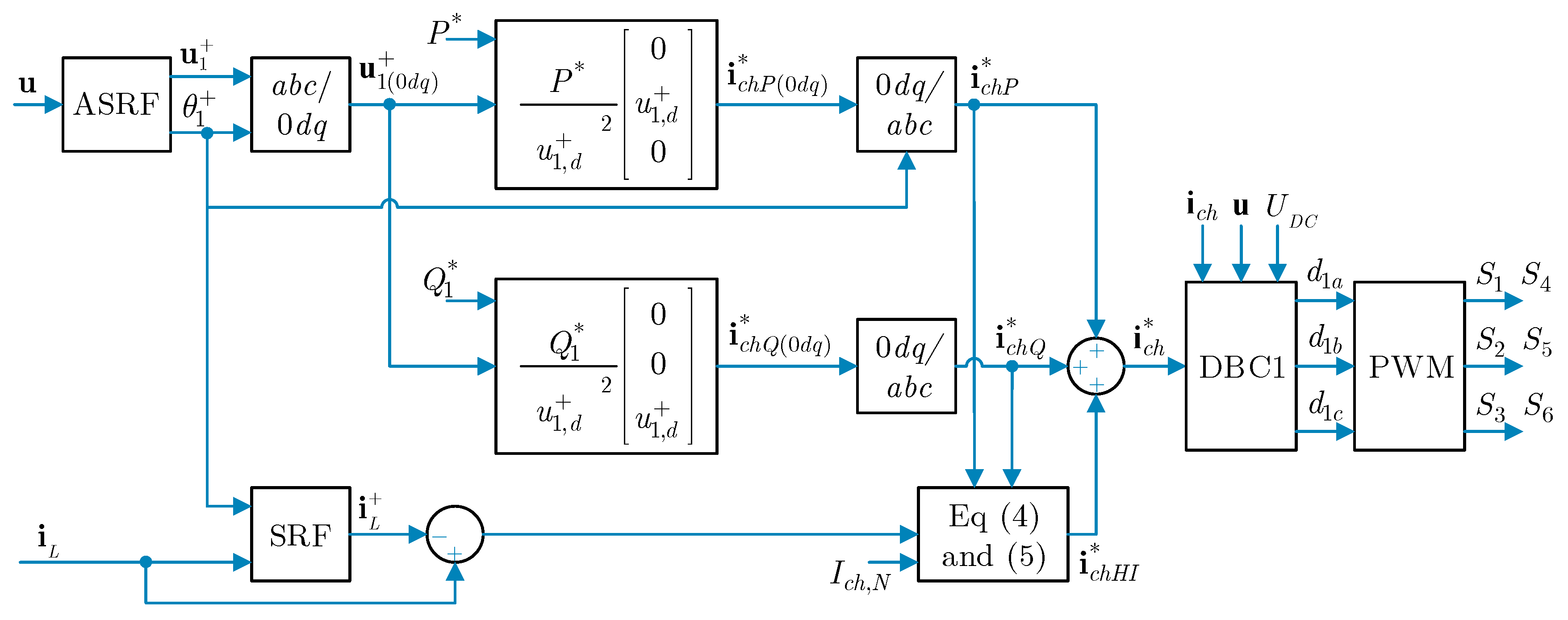
The charger reference current vector is generated by adding three separate control functions: active power control, reactive power control, and load current harmonics and imbalance reduction, i.e., $i_{ch}^{\ast }=i_{chP}^{\ast }+i_{chQ}^{\ast }+i_{chHI}^{\ast }$. In the following, these functions are explained and the corresponding reference current vectors are obtained.

2.1. Active Power Control

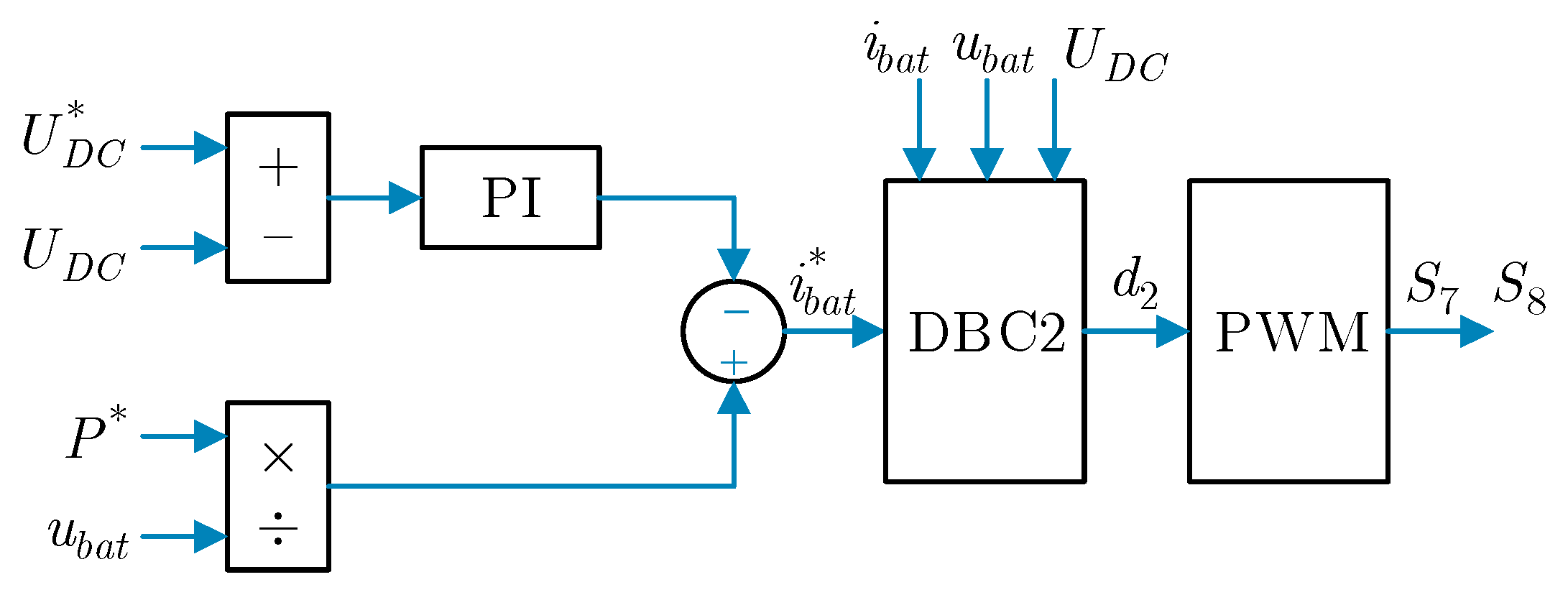
The CS-EMS sends a three-phase active power setpoint $P^{\ast }$ to each individual FC. Two modes of operation are considered: Grid to Charger mode (G2C-P mode), when the FC is extracting the active power from the grid to charge the storage system (sign criterion $P^{\ast }>0$), and the Charger to Grid mode (C2G-P mode), when the FC is injecting active power from the storage device into the grid (sign criterion $P^{\ast }<0$). The setpoints might be determined according to different criteria, which depends on commercial or economic consideration. These are out of the scope of this paper. Nevertheless, it is useful to provide some comments on this matter.

• In the G2C-P mode, the setpoint will be determined according to the power demanded by the EV battery, assuming that the customer will likely want to charge at different speeds (and, hence, at different power levels) associated with a choice on tariffs, which, in turn, might be associated with previous electric energy market negotiations done by the aggregator or the CS manager [31].
• On the other hand, with regard to the C2G-P mode, it seems logical that a customer who uses an FC would want to charge, not to discharge his/her EV. However, there might be reasons to do that, such as incentive tariffs. Besides, the possible use of the so-called Second Life Batteries (SLB) installed at the FC as back-up storage, implies both modes (G2C-P mode and C2G-P mode). According to Reference [32], by 2030, there will be one million battery packs retiring from electric vehicles per year. However, those used batteries could still retain up to 70%–80% of the original capacity that can be further utilized in less-demanding applications. The use of SLB would provide the CS with higher active power flow flexibility, which allows the bi-directional active power interchange with the grid and, hence, helps in the previously mentioned commercial tasks.

To carry out these modes of operation, a sinusoidal current (SC) control strategy is derived from the Perfect Harmonic Cancelation (PHC) strategy proposed in Reference [33]. The strategy causes that the current injected into the grid be sinusoidal and in phase with the positive-sequence fundamental component of the grid voltage. It guarantees the FC to operate with the unity displacement power factor (dPF) and the charger current to have neither harmonic content nor imbalance. The reference charger current in the 0dq reference frame is given by the following current vector (see Figure 1 and Figure 2 for current and voltage reference directions).

$$i_{chP\left(0dq\right)}^{\ast }=\frac{P^{\ast }}{{\left(u_{1,d}^{+}\right)}^2}\left[\begin{array}{c}0\\ u_{1,d}^{+}\\ 0\end{array}\right],$$

(1)

where $u_{1,d}^{+}$ is the d-axis coordinate of the positive-sequence fundamental component of the grid voltage space vector $u={\left(u_a{u}_b{u}_c\right)}^T$. This component can be calculated by using a phase-locked-loop system, such as the Auto-Adjustable Synchronous Reference Frame (ASRF) proposed in Reference [34].

2.2. Reactive Power Control

It is possible to provide voltage support at the PCC to which the FC is connected, or a proper reactive power management of the EV charging station, which can improve Volt-Var Optimization (VVO) solutions for the distribution network. This might be convenient [35]. Both cases would be motivated by economical reason based on the tariffs applicable by the DSO [12].

Again, the CS-EMS is responsible for calculating and sending a fundamental three-phase reactive power setpoint $Q_1^{\ast }$ to each individual FC. Two modes of operation are considered: the G2C-Q mode, which is when the fundamental three-phase reactive power is absorbed by the FC ($Q_1^{\ast }>0$), and the C2G-Q mode, which is when the FC injects fundamental three-phase reactive power to the grid ($Q_1^{\ast }<0$).

To accomplish with the reactive power setpoint, a quadrature SC (QSC) control strategy is used in this case, which is also derived from the PHC strategy [33]. This approach causes the current demanded or injected into the grid to be sinusoidal, balanced, and in quadrature with the positive-sequence fundamental component of the grid voltage. The reference charger current in the 0dq reference frame is given by the equation below.

$$i_{chQ\left(0dq\right)}^{\ast }=\frac{Q_1^{\ast }}{{\left(u_{1,d}^{+}\right)}^2}\left[\begin{array}{c}0\\ 0\\ u_{1,d}^{+}\end{array}\right].$$

(2)

2.3. Load Current Harmonics and Imbalance Reduction

This function makes use of the converter capacity not used by the active power and reactive power controls to compensate the harmonics and imbalances present in the CS load currents. In other words, the idea is that the charger behaves like an Active Power Filter (APF), as a secondary function, ensuring that the charger does not exceed its nominal parameters. This will improve the power quality and imbalance ratios locally and, therefore, will contribute to the global improvement of those parameters at the CS level. In this case, there is only one direction mode of operation. It will be named the Charger to Grid Harmonic and Imbalance mode (C2G-H-I mode).

The proposed Total Harmonic and Imbalance Compensation (THIC) control strategy aims to set the charger reference currents so that the total grid currents (chargers plus load currents) are sinusoidal, balanced, and in phase with the respective phase-to-neutral grid voltages. The CS-EMS measures the total load current at the PCC $i_{L-CS}$ and allocates a fraction of it to each FC. The charger reference currents have to be equal and opposed to the harmonic and fundamental unbalanced components (negative-sequence and zero-sequence terms) of the assigned load currents fraction. Let the load current fraction assigned to an FC be represented by the vector $i_L={(i_{L,a} i_{L,b} i_{L,c})}^T$, composed, in turn, by the fundamental component vectors (positive-sequence $i_{L1}^{+}$, negative-sequence $i_{L1}^{-}$, and zero-sequence $i_{L1}^0$) and the harmonic component vector $i_{Lh}$, which means $i_L=i_{L1}^{+}+i_{L1}^{-}+i_{L1}^0+i_{Lh}$. Thus, the reference charger currents, which contribute to compensate harmonics and imbalances in the load currents, will be given by the current vector.

$$i_{chHI}^{\ast }=-\left(i_L-i_{L1}^{+}\right).$$

(3)

To extract $i_{L1}^{+}$ from the load current vector $i_L,$ a synchronous reference frame (SRF) can be employed, which operates with the fundamental phase angle delivered by the previously mentioned ASRF.

This reference current has to be limited to prevent the inverter overload. Therefore, when all functions are operating simultaneously, the rated Root Medium Square (RMS) current of the charger, $I_{ch,N}$, must not be surpassed. Let $I_{chP}$ and $I_{chQ}$ be the RMS values of the reference currents for the P and Q control, respectively. Thus, the maximum RMS value of reference currents for the harmonic and imbalance control is obtained from the equation below.

$$I_{chHI,\max }=\sqrt{I_{ch,N}^2-I_{chP}^2-I_{chQ}^2}.$$

(4)

Taking into account this limit, the reference charger current will be obtained from the equations below.

$$\begin{array}{ll}{i}_{chHI}^{\ast }=-(i_L-i_{L1}^{+})\hfill & \mathrm{if}{I}_{chHI}\le I_{chHI,\max }\hfill \\ i_{chHI}^{\ast }=-(i_L-i_{L1}^{+})\frac{I_{chHI,\max }}{I_{chHI}}\hfill & \mathrm{if}{I}_{chHI}>I_{chHI,\max }\hfill \end{array},$$

(5)

where $I_{chHI}$ is the highest RMS value of the current $i_{chHI}^{\ast }$. Since this current could be unbalanced, this value corresponds to the phase with the highest load.

3. Fast Charger Power Structure and Control System

A three-phase power converter model for an FC has been developed. It receives P and Q setpoints from the CS-EMS, controls the current demanded/injected from/into the grid, and manages the charge/discharge of the battery.

3.1. Topology

The topology of each FC is displayed in Figure 2. It uses two power converters: an AC/DC converter to interface with the AC grid and a DC/DC converter to manage the charge/discharge of the battery and to adapt the battery voltage $u_{bat}$ to the DC link. The AC/DC converter is a three-phase three-leg Voltage Source Inverter (VSI) with a split DC link, formed by switches S1 to S6 and an inductor $L_1$ (with resistance $R_1$). The DC/DC converter has a half bridge bidirectional buck-boost DC/DC topology, consisting of two switches (S7 and S8) and one inductor $L_2$ (with resistance $R_2$). The currents drawn from the grid are $i_{ch,a}$, $i_{ch,b}$, $i_{ch,c},$ and the current absorbed by the battery is $i_{bat}$. A representation of the other charging station facility’s unbalanced and non-linear loads is also included in Figure 2.

3.2. Global Control System

The block diagram of the global control system for the VSI is displayed in Figure 3. The inputs are the measured phase-to-neutral grid voltage, $u={\left(u_a{u}_b{u}_c\right)}^T$, and the assigned fraction of the measured load current, $i_L={\left(i_{L,a}{i}_{L,b}{i}_{L,c}\right)}^T$. The other inputs are the setpoints $P^{\ast }$ and $Q_1^{\ast }$ provided by the CS-EMS and the RMS nominal charger current, $I_{ch,N}$, which has a known value. From $u$, the block ASRF extracts the positive-sequence fundamental component voltage vector, $u_1^{+}={\left(u_{1,a}^{+}{u}_{1,b}^{+}{u}_{1,c}^{+}\right)}^T$ and its fundamental phase angle ${\theta }_1^{+}$. This angle is used as an input for the SRF block, which is employed to obtain $i_{L1}^{+}$. The block abc/0dq translates $u_1^{+}$ into the 0dq reference frame, i.e., $u_{1\left(0dq\right)}^{+}={\left(0u_{1,d}^{+}{u}_{1,q}^{+}\right)}^T$. From here, there are two different parts to implement the SC strategy using Equation (1) and the QSC strategy from Equation (2). By means of the inverse transformation 0dq/abc, the reference currents $i_{chP}^{\ast }$ and $i_{chQ}^{\ast }$ are obtained. On the other hand, at the bottom, the part that performs the THIC strategy from Equations (4) and (5) appears, which yields $i_{chHI}^{\ast }$. Its inputs are $i_L$, $I_{ch,N}$, and also $i_{chP}^{\ast }$ and $i_{chQ}^{\ast }$ to calculate its respective RMS values. Lastly, the output is the total reference charger current $i_{ch}^{\ast }={\left(\begin{array}{ccc}{i}_{ch,a}^{\ast }& i_{ch,b}^{\ast }& i_{ch,c}^{\ast }\end{array}\right)}^T$, calculated by adding the reference current obtained with each independent control algorithm. It is interesting to note that the CS-EMS calculates only $P^{\ast }$, $Q_1^{\ast },$ and $i_L$ by measuring at the PCC. The remaining calculations are done locally by the converter control system.

The control strategy of the bidirectional DC/DC converter is displayed in Figure 4. The electrical magnitude that is followed as a reference for this converter is the battery current. Its reference value is obtained by taking into account the active power balance on the side of the battery, neglecting the losses. Since the active power imposed by the P control has to be extracted from the battery, the battery current must be the following.

$$i_{bat}^{\ast }=\frac{P^{\ast }}{u_{bat}}.$$

(6)

The DC/DC converter is in charge of regulating the DC bus voltage to its reference value $U_{DC}^{\ast }$, by means of a Proportional-Integral (PI) controller. This control action also leads to compensate the power losses in the transfer of energy between the grid and the battery. The DC/DC control needs to measure the battery voltage $u_{bat}$ and the DC bus voltage $U_{DC}$ and also uses the $P^{\ast }$ value as inputs provided by the CS-EMS and the reference DC bus voltage. The output is the reference battery current $i_{bat}^{\ast }$.

Dead-beat controllers are used to generate the switching signals of the converters, by trying to reduce to zero the difference between the reference and measured currents at the end of each switching period $T_S$. For each converter leg, $T_{ON}$ is defined as the time interval while the upper switch of that leg is in the on-state (the operation of the two switches of one leg is complementary, so the bottom switch is in the off state) and its duty cycle d as the relation $d=T_{ON}/T_S$. According to Reference [25], the duty cycle $d_{1i}$ (i = a, b, c) necessary to achieve the measured variable $i_{ch,i}$ to be equal to the reference value $i_{ch,i}^{\ast }$ at the end of the switching period $T_S$ for the i-leg of the VSI is obtained from the equation below.

$$d_{1i}=\frac{\left(u_i+U_{DC}/2\right)T_S-\left(i_{ch,i}^{\ast }-i_{ch,i}\right)L_1-i_{ch,i}{R}_1{T}_S}{T_S{U}_{DC}} i=a,b,c.$$

(7)

This operation is executed by the block DBC1 (Dead-Beat Controller 1) in Figure 3.

Analogously, the duty cycle $d_2$ for the DC/DC converter is obtained from the equation below.

$$d_2=\frac{u_{bat}{T}_S+\left(i_{bat}^{\ast }-i_{bat}\right)L_2+i_{bat}{R}_2{T}_S}{T_S{U}_{DC}}$$

(8)

This operation is executed by the block DBC2 (Dead-Beat Controller 2) in Figure 4.

Lastly, these duty cycle values are converted into the corresponding switching signals for the gates of the converter switches by means of a modulation technique such as Pulse Width Modulation (PWM blocks): S1-S6 for the VSI and S7-S8 for the DC/DC converter.

The transfer functions and controllers have been implemented in their discrete form by means of the Tustin method. This fact provides a step toward the real system performance analysis such as the control strategy being implemented in any microcontroller or DSP control system. At the same time, all measurements are sampled before processing at 10 kHz, which is achievable in modern controllers. However, a modelling challenge to be addressed in the future would be the inclusion of the digital delays produced by a real system (sensors, analogue to digital conversions, duty cycle updating, etc.) in the measurement feedback.

The practical implementation includes some blocks, such as ASRF and Park transformations, considered to have a high computational burden. These features would require the use of a microcontroller with a floating-point unit. The practical feasibility is justified by taking into consideration authors’ previous works [26,36], where strategies with similar computational requirements were experimentally implemented and tested.

4. Simulation Results and Analysis

4.1. Case Study Description

According to the topology and control system described before, a simulation model for FC has been developed in Matlab-Simulink to test the proposed active functions’ control strategies. The switching frequency was considered at 10 kHz (switching period $T_S={10}^{-4}$ s). Then, the time step for the simulation was taken at $T_m={10}^{-6} \mathrm{s}$. The LV voltage network (rated at 230/400 V) was supposed to be distorted and unbalanced, with values according to the limits proposed in EN 50160 [37] and EN 61000-2-2:2002 [38], shown in

Table 2. LV network distortion and imbalance limits according to EN 50160 and EN 61000-2-2:2002.

Individual Harmonic Distortion (%)				Total Harmonic Distortion THD (%)	${\mathit{U}}^{-}/{\mathit{U}}^{+}$	${\mathit{U}}^0/{\mathit{U}}^{+}$
HD3	HD5	HD7	HD9		(%)	(%)
5	5.5	4	7.6	7.83	2	2

$U^{-}/U^{+}$ is the RMS negative to positive sequence voltage ratio and $U^0/U^{+}$ is the RMS zero to positive sequence voltage ratio.

.

A CHAdeMO 1.2 FC [39] has been proposed, with rated parameters 200 kW, 500 V, and 400 A. From the three-phase 230/400 V grid, the corresponding current demand is 288.67 A. Therefore, the RMS nominal charger current $I_{ch, N}$ is 290 A and the main parameter values are shown in

Table 3. Main parameter values for the simulation of the three-phase charger.

Parameter	Value	Unit
$R_1$	$1\times {10}^{-3}$	Ω
$L_1$	$0.5\times {10}^{-3}$	H
C	$2.2\times {10}^{-3}$	F
$R_2$	$1\times {10}^{-3}$	Ω
$L_2$	$5.2\times {10}^{-3}$	H
$U_{DC}^{\ast }$	1200	V
$U_{n, bat}$ (Battery nominal voltage)	500	V
$SO{C}_i$ (initial battery SOC)	40	%

. These parameter values have been selected according to the design criteria proposed in Reference [40].

To demonstrate the behavior of the system, the simulation has been conducted in the following cases:

• Case A. Charging the EV battery at maximum power: $P^{\ast }$ = 200 kW. CS demand without harmonics nor imbalance. RMS value of load current $I_L$ = 200 A.
• Case B. Discharging the battery and injecting fundamental reactive power: $P^{\ast }$ = −160 kW, $Q_1^{\ast }$ = 120 kVAr. CS demand without harmonics and imbalance. RMS value of load current $I_L$ = 200 A.
• Case C. Charging the EV battery and demanding fundamental reactive power: $P^{\ast }$ = 120 kW and $Q_1^{\ast }$ = −120 kVAr. CS demand with maximum emission limits of odd harmonic currents up to the 9th order established by the EN-IEC-61000-3-4 standard [41], in low-voltage power supply systems for equipment with rated current greater than 16 A and power less than 33$S_{cc}$ (where $S_{cc}$ is the short-circuit power corresponding to the main connections). Harmonic content specified in

  Table 4. Harmonic content of the CS current (maximum limits established by EN-IEC-61000-3-4 for industrial consumers with power < 33$S_{cc}$ ) for cases C-E.

  Individual Harmonic Distortion (%)				Total Harmonic Distortion THD (%)
  HD3	HD5	HD7	HD9
  21.6	10.7	14.4	7.6	25.44

  and RMS value of load current $I_L$ = 206.37 A.
• Case D. Charging the EV battery and injecting fundamental reactive power: $P^{\ast }$ = 120 kW and $Q_1^{\ast }$ = 120 kVAr. CS demand with harmonic and unbalanced components. Maximum emission limits of odd harmonic currents as in case C and unbalanced load currents with ratios $I^{-}/I^{+}$ = 10%, $I^0/I^{+}$ = 10%. RMS value of the equivalent load current, according to Std. IEEE-1459:2010 [42], $I_{Le}$ = 208.3 A.
• Case E. Charging the EV battery and injecting fundamental reactive power: $P^{\ast }$ = 158 kW and $Q_1^{\ast }$ = 120 kVAr. CS demand with the same harmonic and unbalanced components as in Case D. $I_{Le}$ = 208.3 A.

4.2. Results

Simulation results for every case are displayed in Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. From top to bottom and from left to right, the figures present source voltages and currents, charger currents, load currents, battery voltage, reference, and measured battery current, reference charger currents for the H-I control mode, the reference, and the measured dc bus voltage.

The battery has an initial state of charge $SO{C}_i$. The AC/DC converter operates initially as a rectifier. Then the DC/DC converter starts to operate, which leads the DC-link voltage to its nominal value (1200 V) and, afterwards, the three control modes (P, Q, and H-I) are activated.

In cases A (Figure 5) and B (Figure 6), the CS demand has no harmonics nor unbalanced components, so the H-I control is not needed and, therefore, the FC draws from the grid sinusoidal and balanced currents. In case A, it is considered the operation of an EV charging at maximum power, 200 kW. Soon there is no reactive power setpoint provided from the CS-EMS and only the P control is activated. The charger current is in phase with the positive-sequence fundamental source voltage, which achieves a unity dPF. On the other hand, case B takes into account a situation where the CS-EMS send active and reactive power setpoints to the FC. Since the active power setpoint is negative, the battery is discharging, and $i_{bat}$ has a negative value.

In case C (Figure 7), the CS demands balanced but distorted currents with the maximum odd harmonic currents up to the 9th order allowed by the EN-IEC-61000-3-4 standard for industrial consumers. The active and reactive power setpoints permit the charger to still have sufficient capacity to take over the total compensation of the harmonics demanded by the CS, so the source current is balanced and sinusoidal. Harmonic content of the load, grid, and charger currents are collected in

Table 5. Load, grid, and charger current of the harmonic content for case C.

Variable	Total RMS Value (A)	Individual RMS Value (A)					THD (%)
	I	I1	I3	I5	I7	I9
Load current iL	206.37	200	43.2	21.4	14.4	7.6	25.44
Grid current i	410.58	410.26	2.13	3.37	3.13	1.8	3.93
Charger current ich	251.98	246.40	43.12	21.10	14.05	7.44	21.43

. The Total Harmonic Distortion (THD) of the CS current is 25.44% while this value is below 4% in the source current, due to the operation of the charger H control.

Figure 8 shows the results of case D, where the CS demands harmonic and unbalanced currents. The harmonic content of this current is the same as in case C (see Table 4) and the unbalanced load currents ratios due to a negative-sequence and zero-sequence fundamental components are $I^{-}/I^{+}$ = 10%, $I^0/I^{+}$ = 10%. In this case, the requirements from the CS-EMS setpoints and the harmonic and imbalance content of the CS are compatible with the charger nominal current, so the FC performs a full compensation and the source current is balanced and sinusoidal. The harmonic and imbalance contents of the load, grid, and charger currents are summarized in

Table 6. Load, grid, and charge of the current harmonic and imbalanced content for case D.

Variable	Phase	Total RMS (A)	Individual RMS Value (A)					THD (%)	${\mathit{I}}^{-}$	${\mathit{I}}^0$
		I	I1	I3	I5	I7	I9		(A)	(A)
Load current iL	Phase a	245.33	240	43.2	21.4	14.4	7.6	21.20	20	20
	Phase b	187.05	180	43.2	21.4	14.4	7.6	28.27
	Phase c	187.05	180	43.2	21.4	14.4	7.6	28.27
Grid current i	Phase a	415.53	415.3	2.2	3.3	3.1	1.8	3.55	0.7	1.5
	Phase b	422.94	422.7	2.1	3.4	3.2	1.8	3.53
	Phase c	408.83	408.5	2.1	3.3	3.1	2.0	3.97
Charger current ich	Phase a	221.82	215.5	43.1	21.2	14.0	7.4	24.34	20	18.6
	Phase b	274.02	268.9	43.2	21.1	14.1	7.4	19.55
	Phase c	261.17	255.8	43.2	21.1	14.1	7.3	20.68

. One can notice that the THD has been reduced from 21%-28% in the CS current, depending on the considered phase, to a value below 4% in the source currents. Regarding the imbalance, if one compares the negative-sequence fundamental component in the CS and the source currents, it has been reduced from 20 A to 0.7 A, while the zero-sequence fundamental component has decreased from 20 A to 1.5 A.

Case E has been proposed to validate the operation of the saturated H-I control. In this case (Figure 9), the harmonic and imbalance CS current components are the same as the ones considered in case D. However, the active power setpoint has been increased to 158 kW, so the RMS value of the available FC current is 16.24 A, while the RMS value of the harmonic and unbalanced CS current to compensate is 58.21 A. It means that it is not possible to fully attend the compensation requirements, so the charger performs a partial compensation, since it can be seen by comparing the reference charger currents for the H-I control mode in cases D and E (see Figure 8 and Figure 9). Consequently, the current demanded from the grid in this case is not sinusoidal nor balanced. The harmonic and imbalance content of the load, grid, and charger currents are shown in

Table 7. Load, grid, and charge of the current harmonic and imbalance content for case E.

Variable	Phase	Total RMS (A)	Individual RMS Value (A)					THD (%)	${\mathit{I}}^{-}$	${\mathit{I}}^0$
		I	I1	I3	I5	I7	I9		(A)	(A)
Load current iL	Phase a	245.33	240	43.2	21.4	14.4	7.6	21.20	20	20
	Phase b	187.05	180	43.2	21.4	14.4	7.6	28.27
	Phase c	187.05	180	43.2	21.4	14.4	7.6	28.27
Grid current i	Phase a	495.58	493.8	32.3	16.1	11.1	5.7	8.25	15.0	15.8
	Phase b	455.14	453.3	32.5	16.1	11.1	5.7	9.05
	Phase c	451.78	449.9	32.4	16.2	11.2	5.6	9.14
Charger current ich	Phase a	280	279.3	10.9	5.4	3.5	1.9	6.85	4.8	4.6
	Phase b	289.9	289.2	10.7	5.4	3.4	2.0	6.55
	Phase c	288.4	287.8	10.8	5.3	3.4	2.0	6.71

. The THD of the source current has been reduced to approximately 9% and the negative-sequence and zero-sequence fundamental components of the source current are around 15 A. These results confirm that the FC saturates the harmonic and imbalance load current compensation to ensure that the charger does not exceed its RMS nominal current.

Power terms according to power definitions proposed in Standard IEEE-1459:2010 are collected in

Table 8. Power terms according to Standard IEEE-1459:2010.

Case	S (kVA)	P (kW)	N (kVA)	Q1 (kVAr)	PF	dPF
A	202.4	200	31.08	0	0.99	1
B	201.8	−158.4	125.03	−120.8	0.77	0.78
C	186.11	118.96	143.12	−121.6	0.64	0.69
D	185.03	120.70	140.24	118.8	0.65	0.73
E	200.9	158.8	123.06	118.6	0.80	0.82

for the five cases. S is the apparent power, P is the active power, N is the non-active power, $Q_1$ is the fundamental reactive power, PF is the power factor, and dPF is the displacement power factor.

5. Conclusions

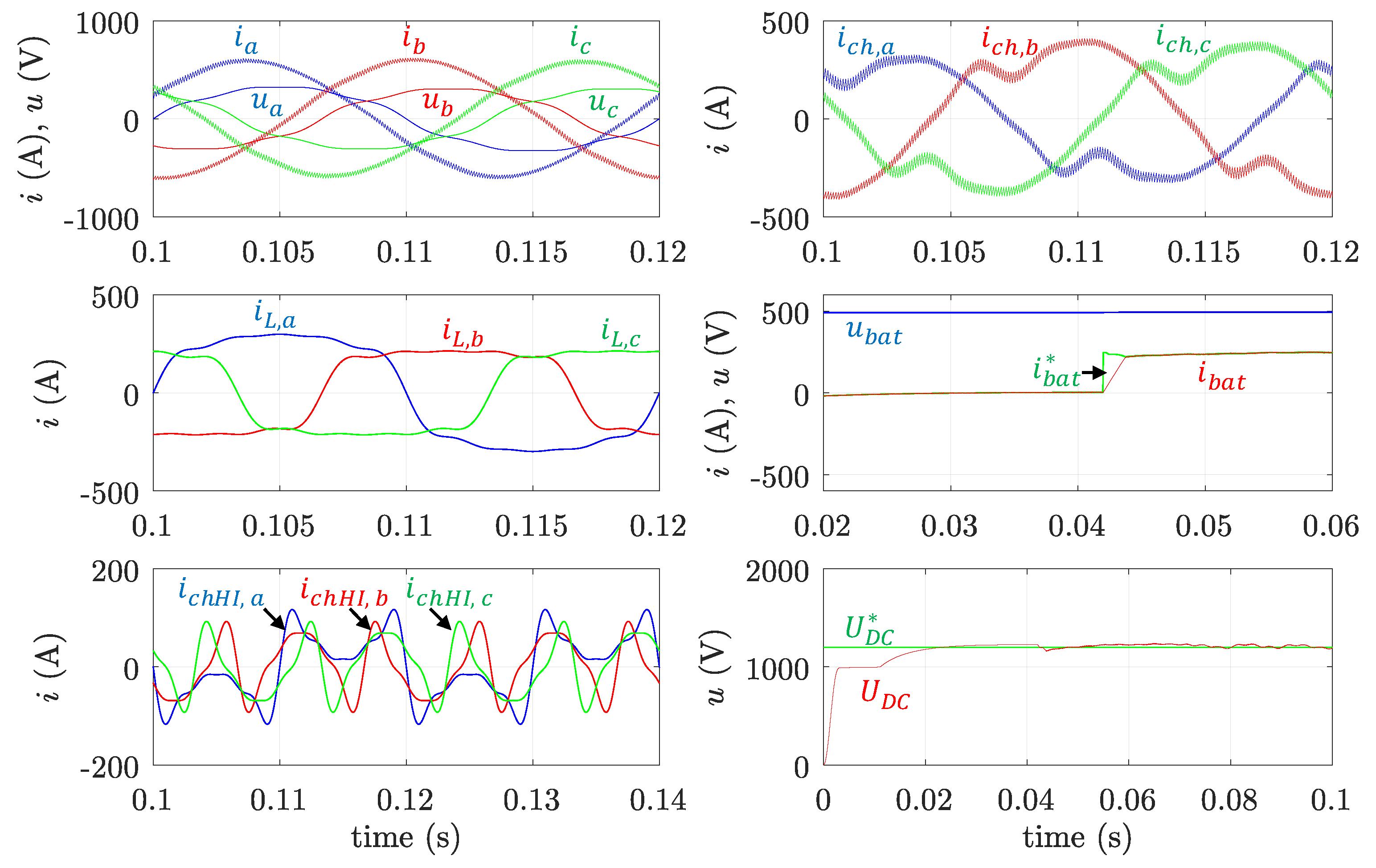
Control strategies for local FC regarding active power and reactive power control in EV-CS have been proposed. Additionally, a control strategy to reduce harmonic content and imbalances in the current demanded by the whole EV-CS is presented. This control only comes into operation once the CS-EMS verifies that the FC has available capacity and, if necessary, saturates the harmonic load current compensation to ensure that the charger does not exceed its nominal parameters. The main contributions of the paper propose the QSC strategy to control fundamental reactive power and the saturated THIC strategy.

A three-phase FC, located at an EV-CS, has been implemented by simulation to test the proposed strategy. Simulation results showing the currents injected/demanded by the FC charger following the setpoints provided by the CS-EMS with active, reactive, harmonic, and imbalance control are presented under distorted and unbalanced LV grid conditions.

There are no potential conflicts among the active, reactive, and harmonic compensation, since each control is devoted to a different component of the charger current. The lack of interaction is one of the advantages of the proposed global control strategy, which allows the charger to operate simultaneously with P, Q, and H I control.

These results validate the correct operation of the proposed control strategy and demonstrate that local FC in EV-CS can contribute to the smart grid goals, by providing ancillary services and improving the global power quality of the LV network.

Although the effectiveness has been demonstrated, a modelling challenge to be addressed in the future could be the inclusion of digital delays produced by a real system (sensors, analogue to digital conversions, duty cycle updating, etc.) in the measurement feedbacks. Furthermore, the authors’ ongoing research is carrying out experimental tests of the control strategy.

Practical implementation will be interesting for both the EV-CS owner and DSO. On one hand, the optimization of energy management, the PQ improvement (which contributes to increase energy efficiency and helps to comply with grid connection standards) and the possibility to offer ancillary services, might generate economical revenues for the EV-CS owner. On the other hand, an overall PQ improvement at the network level and the availability of the EV-CS as new ancillary service providers for DSOs, will contribute to the EV integration and achieving the smart grid goals.