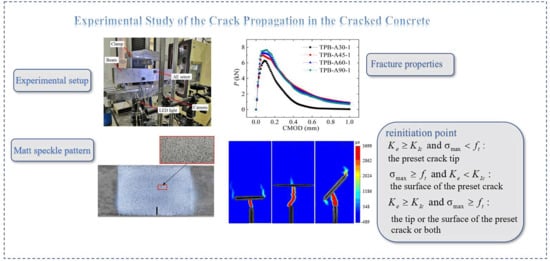
Experimental Study of Crack Propagation in Cracked Concrete
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Beams
2.2. Materials
2.3. Experimental Setup
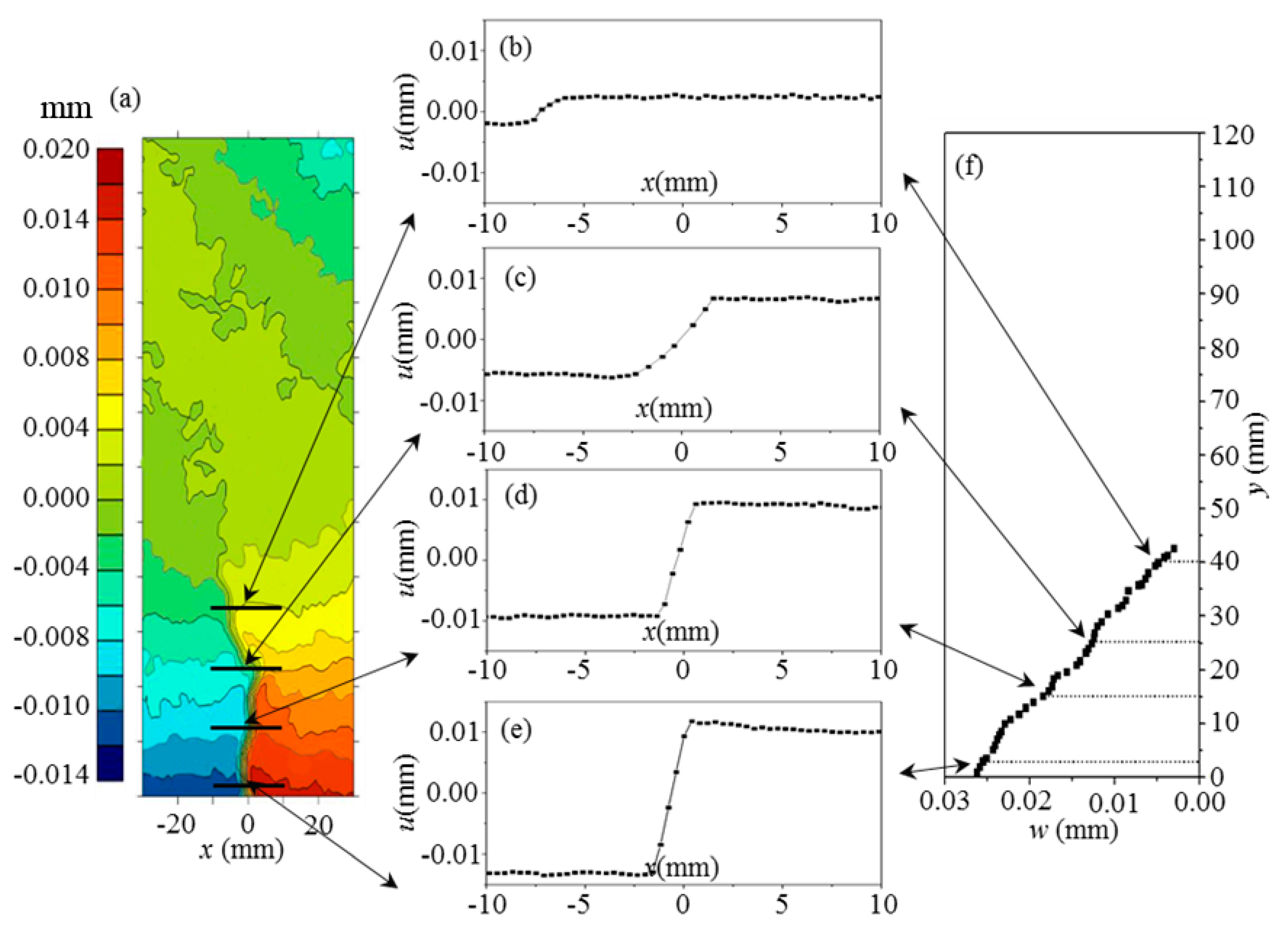
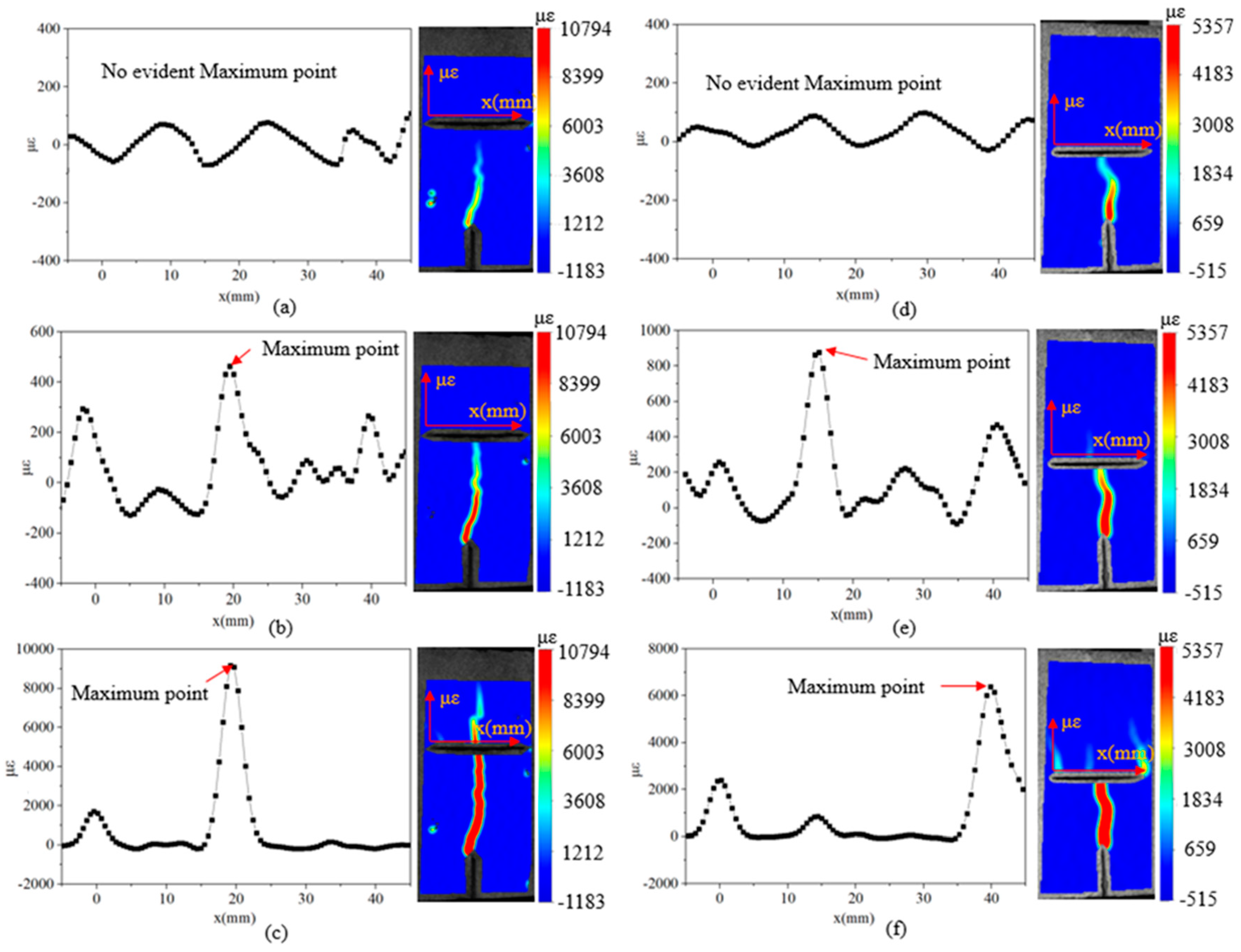
2.4. DIC Technology
3. Results and Discussion
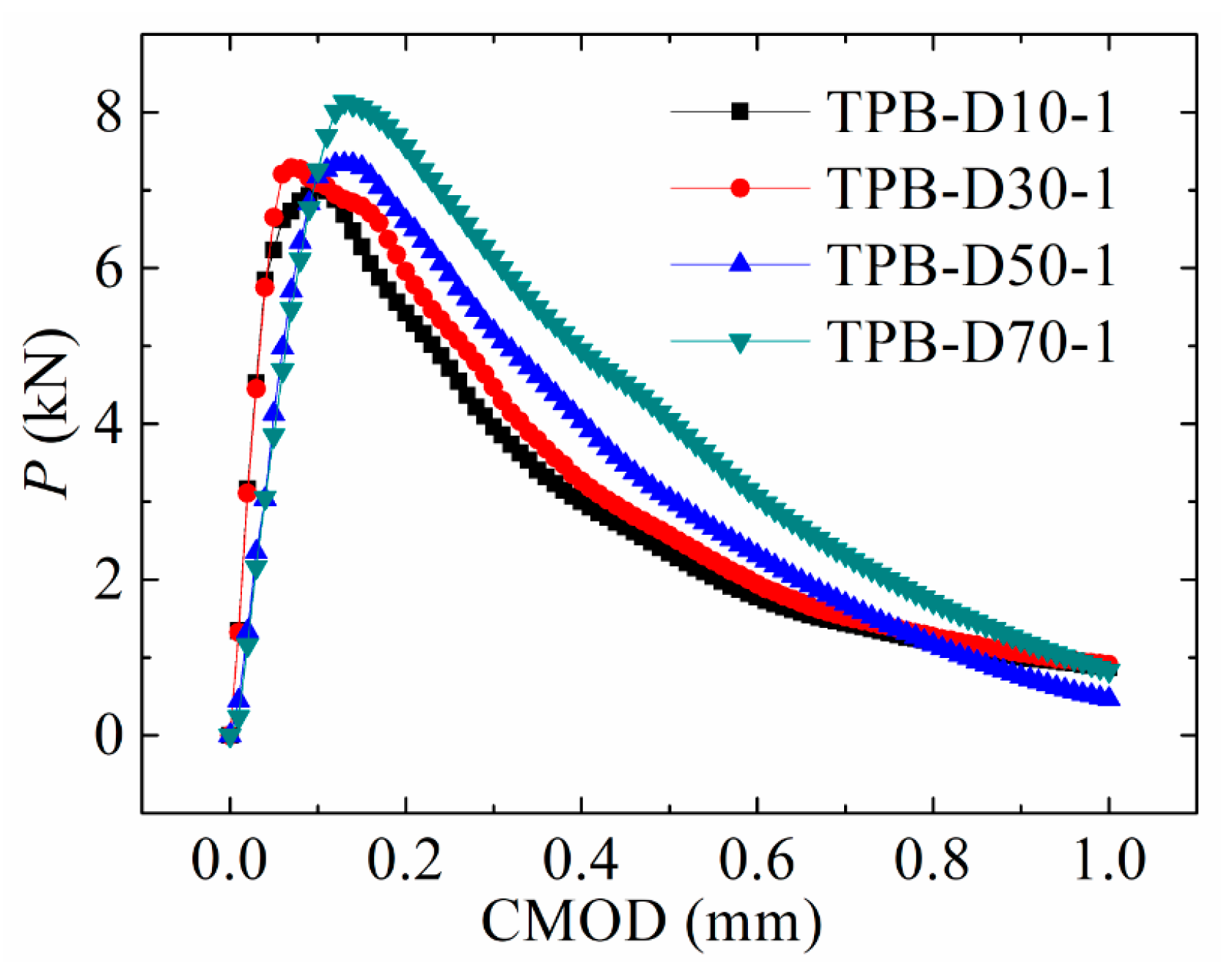
3.1. Preset Crack Position
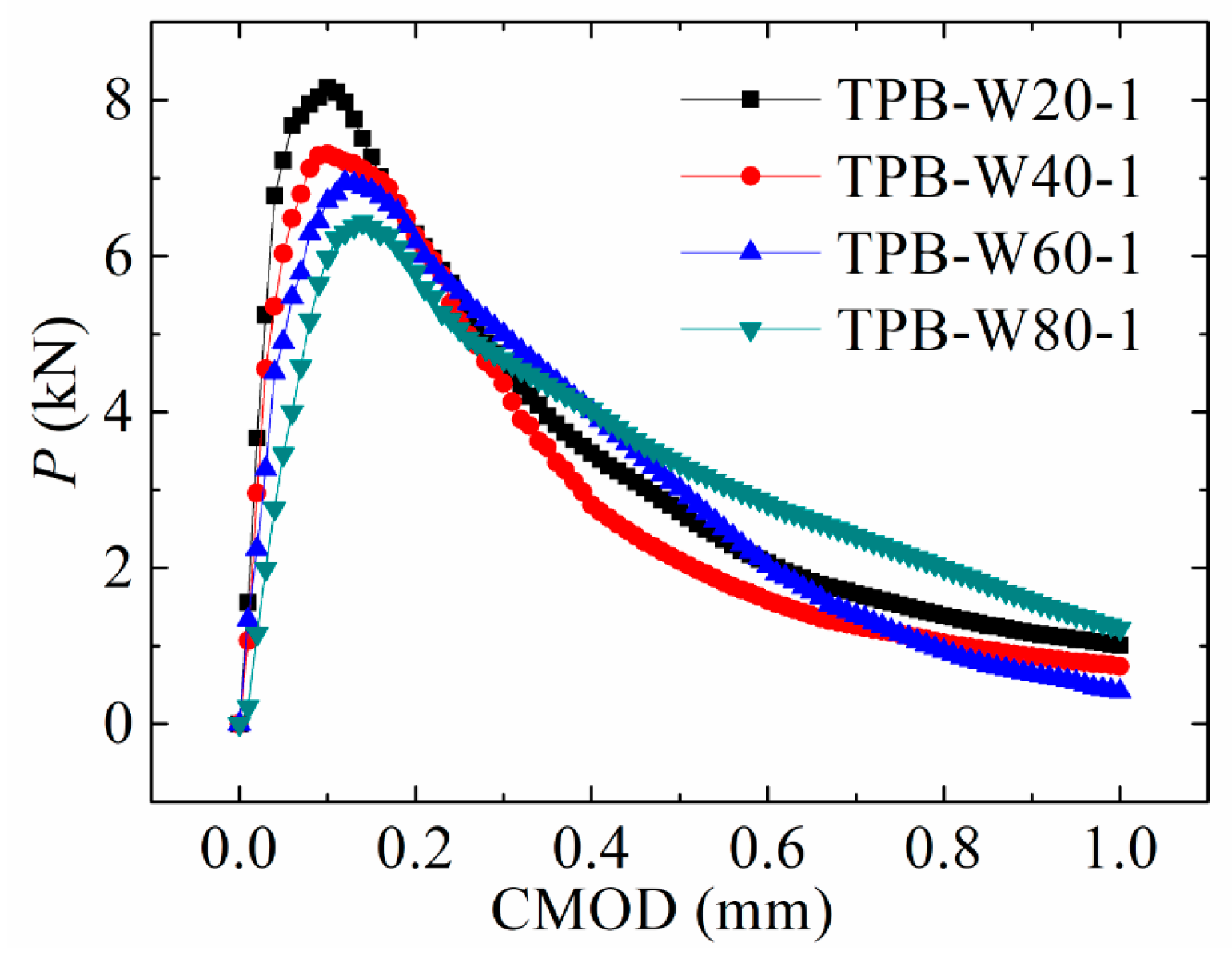
3.2. Preset Crack Length
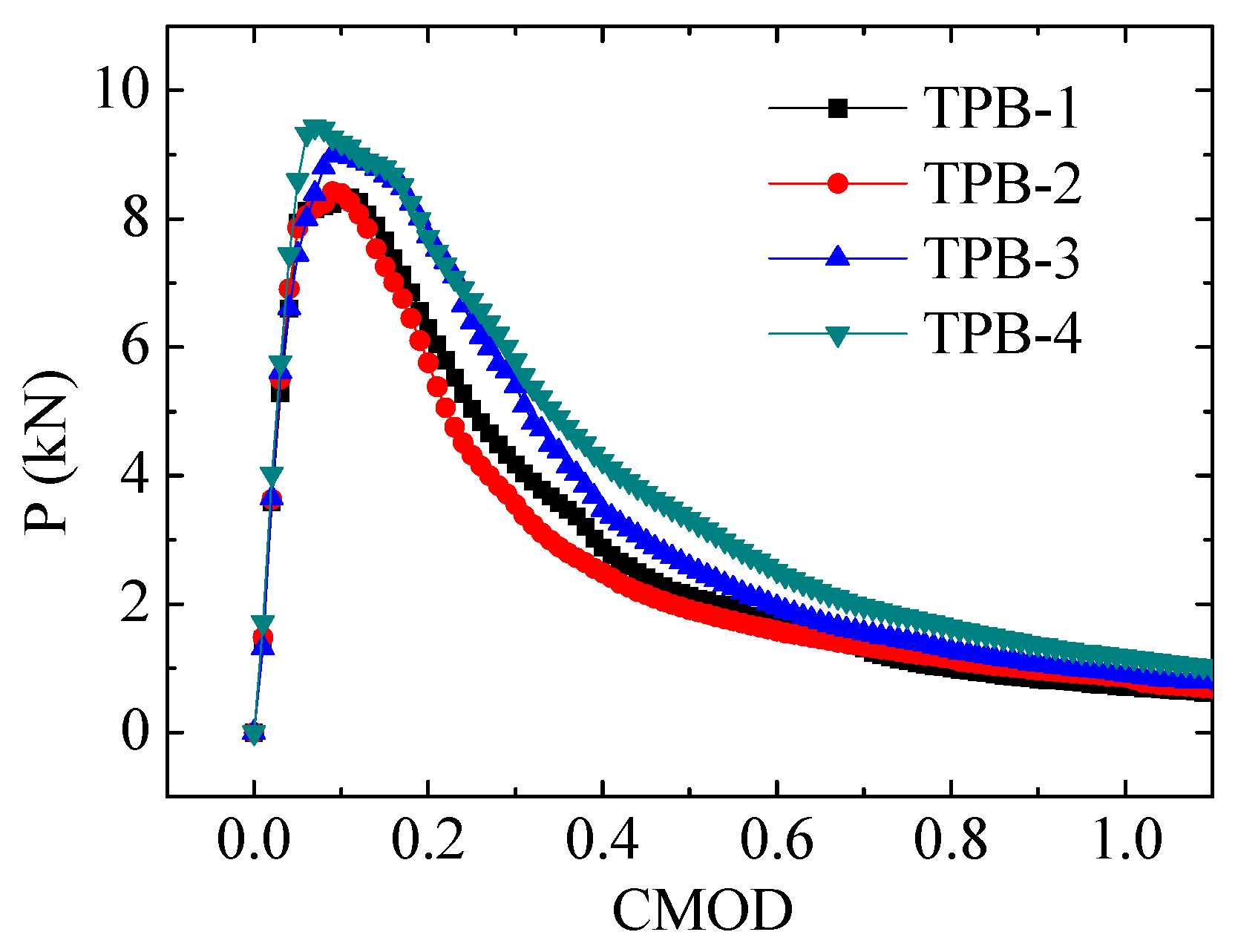
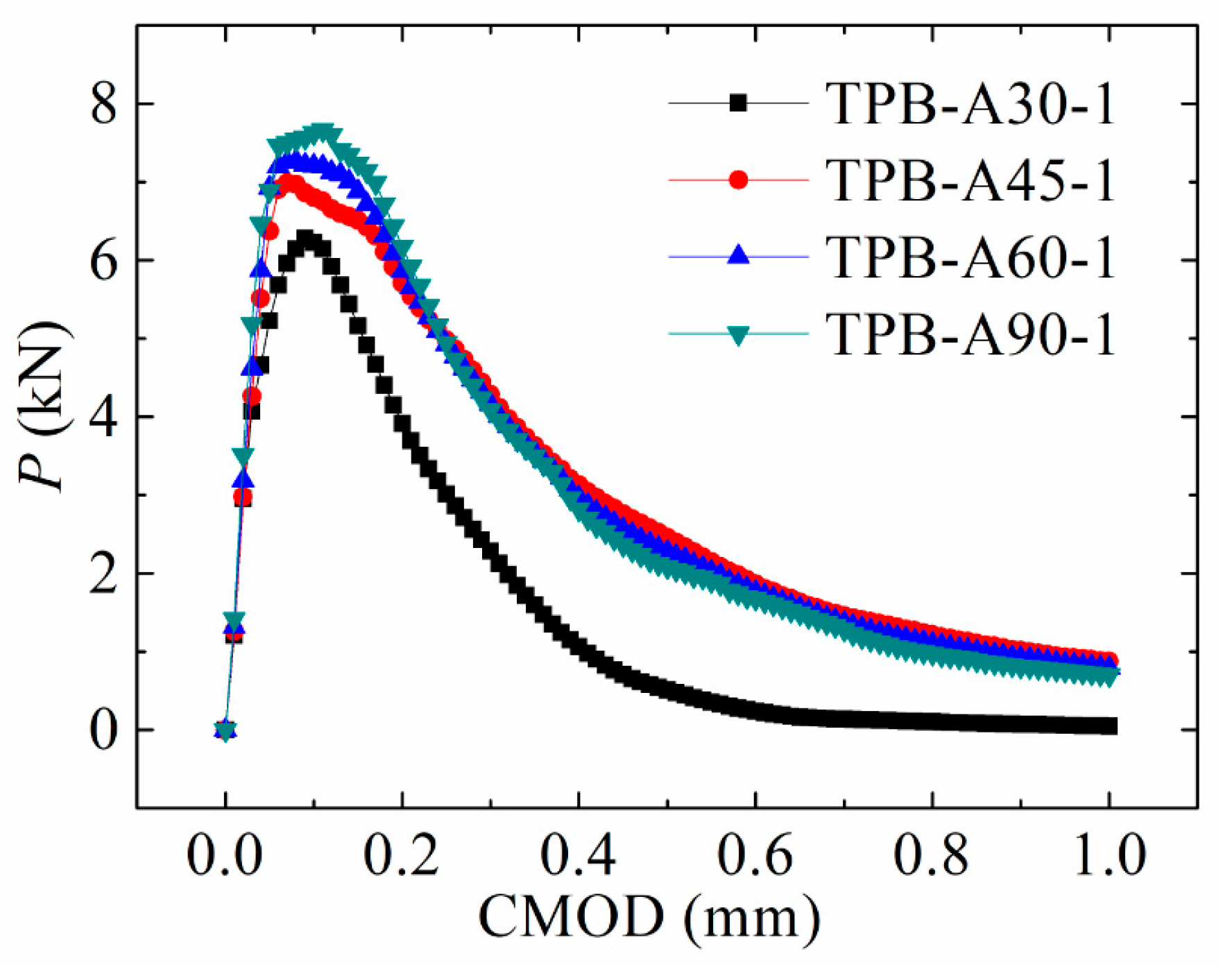
3.3. Approach Angle
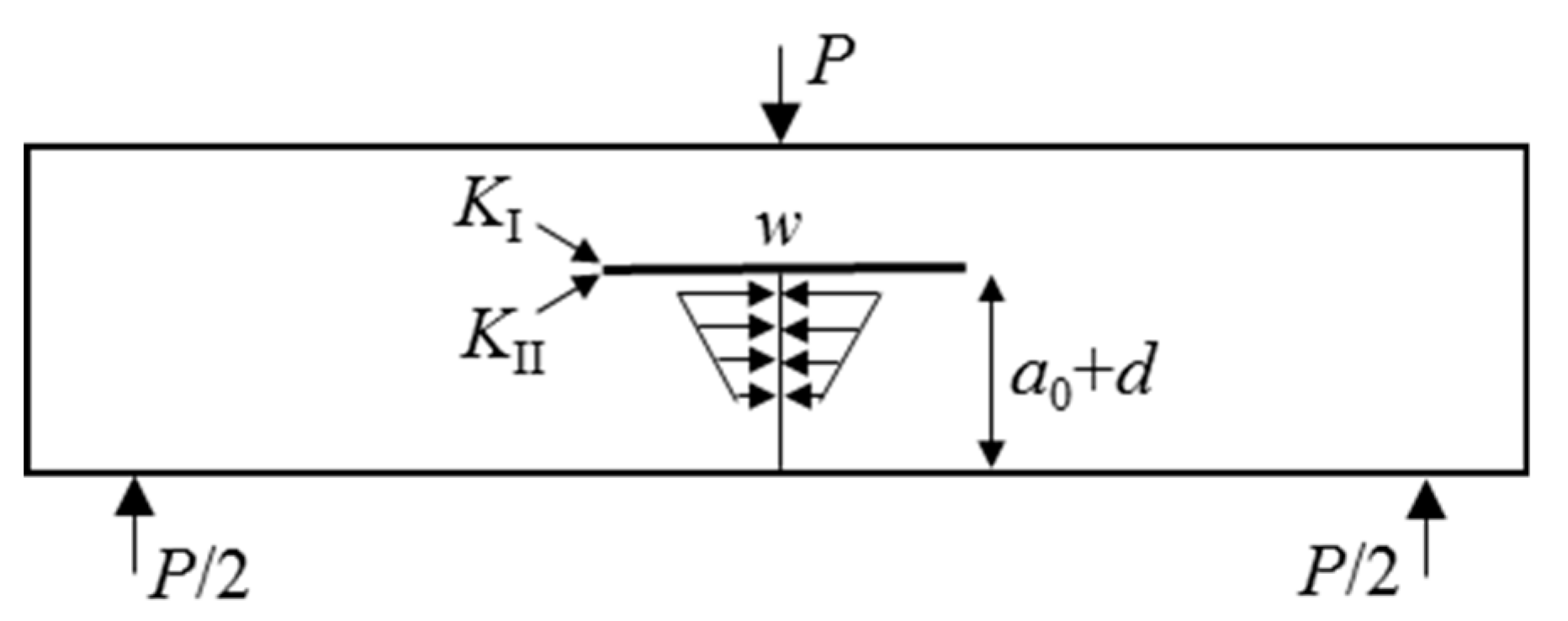
4. Criterion of Crack Restart Point after Intersection
4.1. Traditional Criterion of Restarting Crack after Crack Intersection
4.2. Improved Criterion of Restarting Crack after Crack Intersection
- When Ke ≥ KIc and σmax < ft, the crack will restart at the preset crack tip;
- When Ke < KIc and σmax ≥ ft, the crack will restart at the point on the surface of the preset crack;
- When Ke ≥ KIc and σmax ≥ ft, the crack will restart at the crack tip or at the point on the surface of the preset crack or both occur.
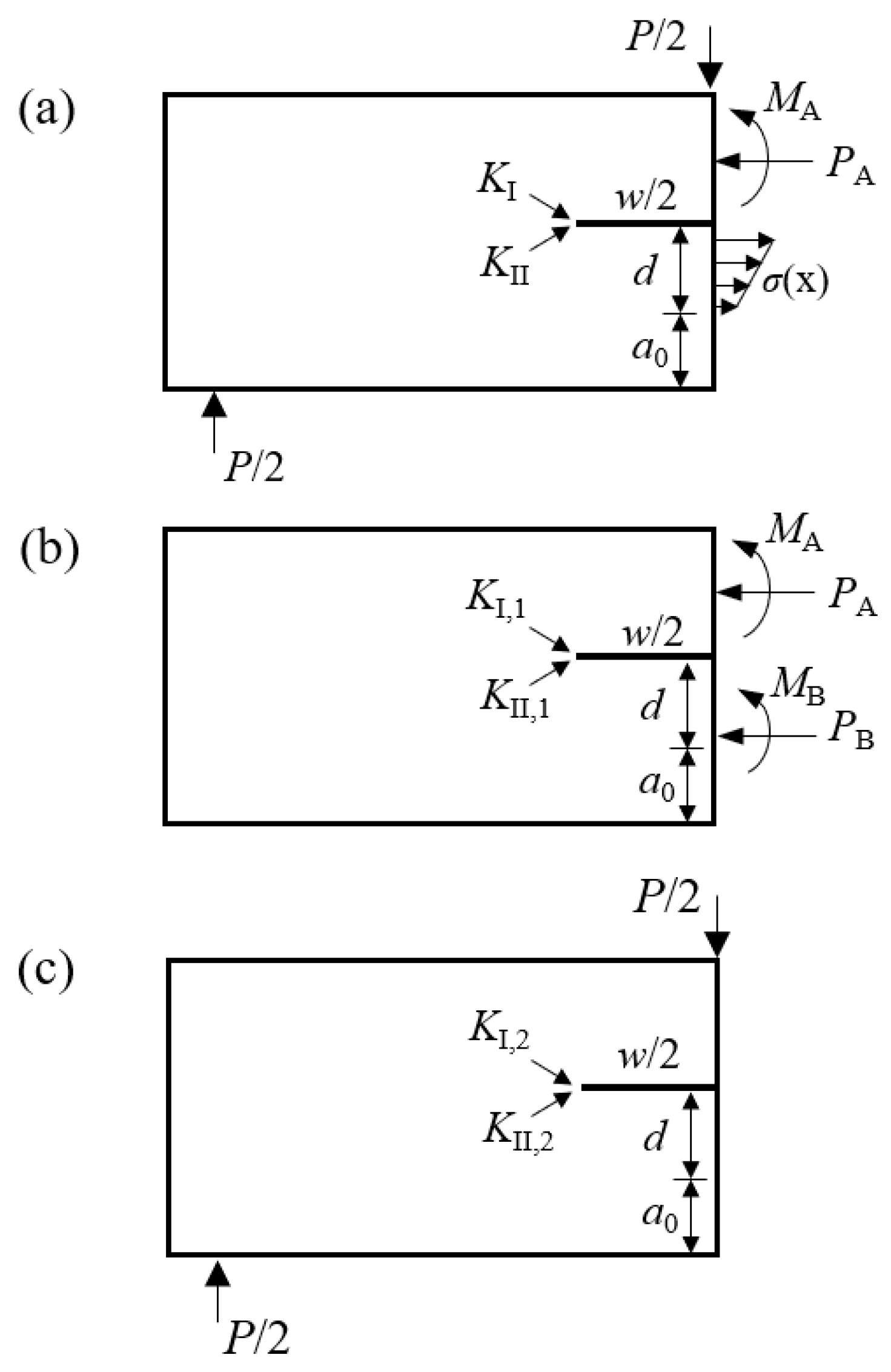
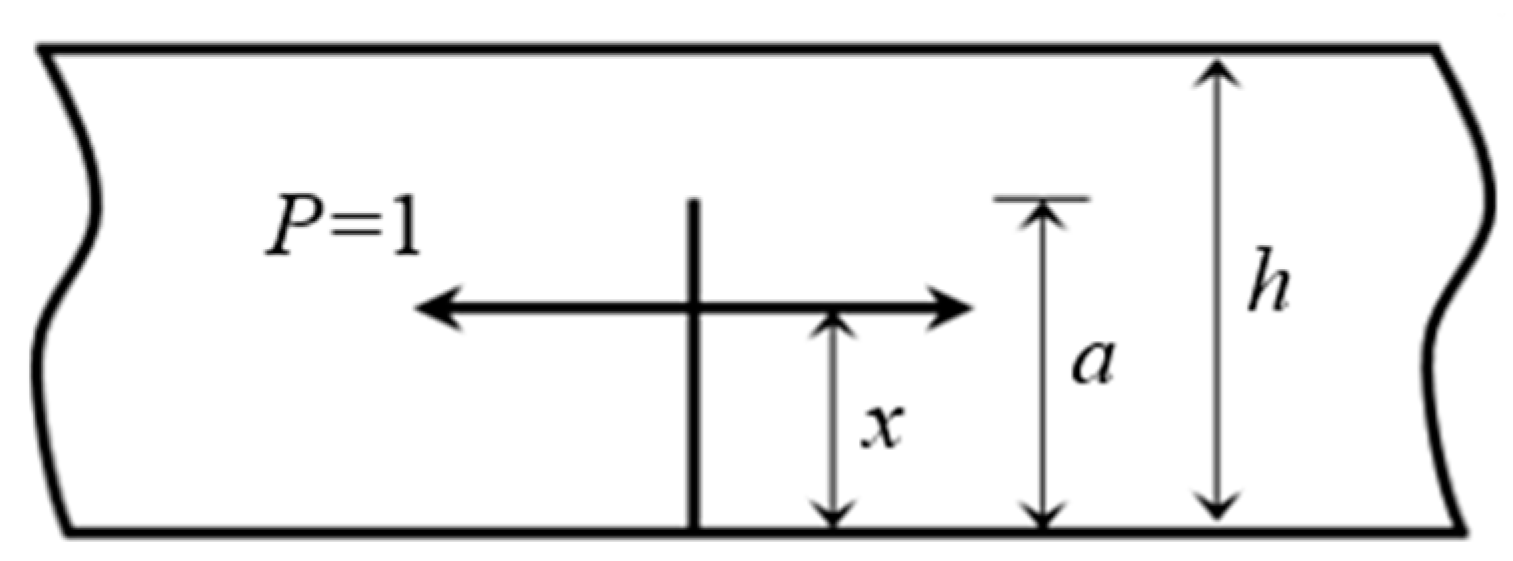
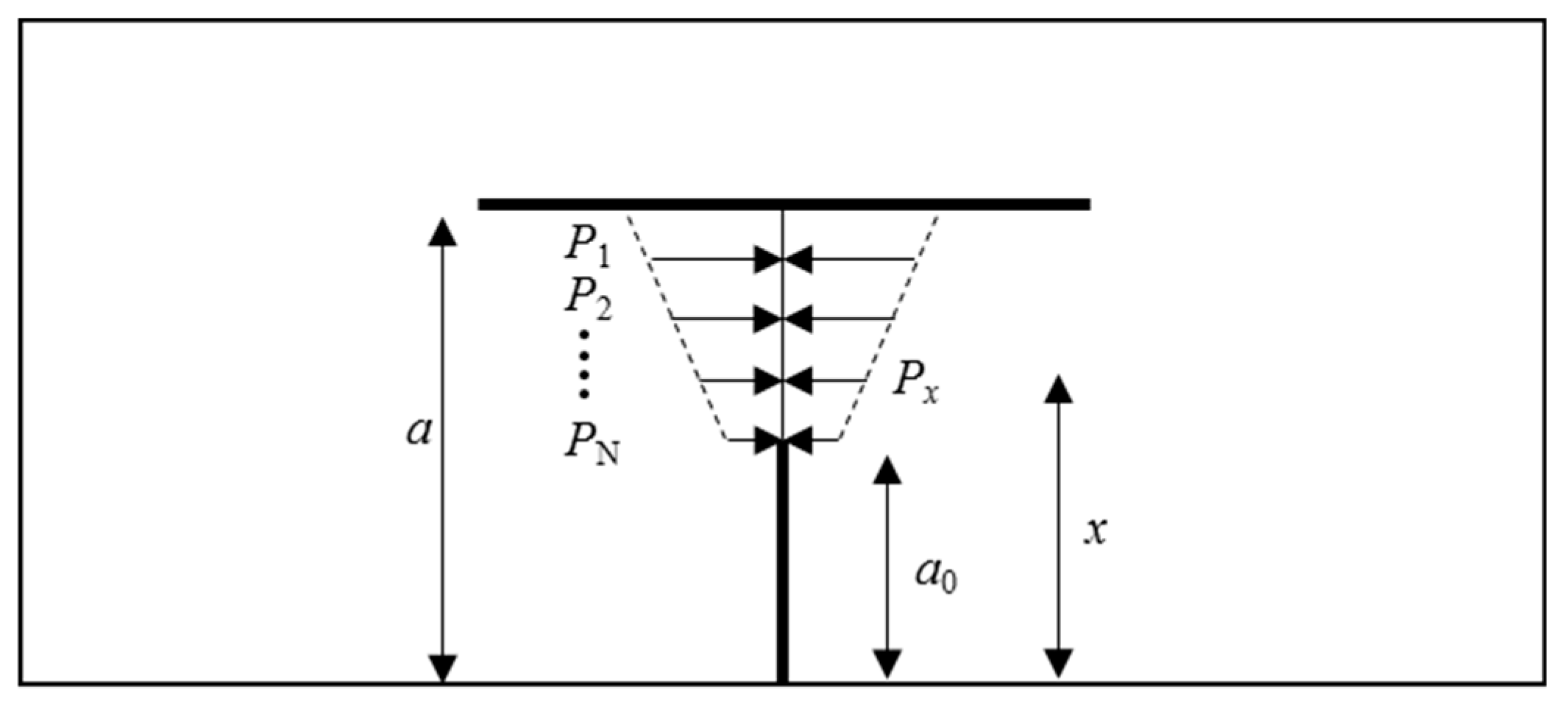
4.3. Determination of the SIF of the Preset Crack Tip
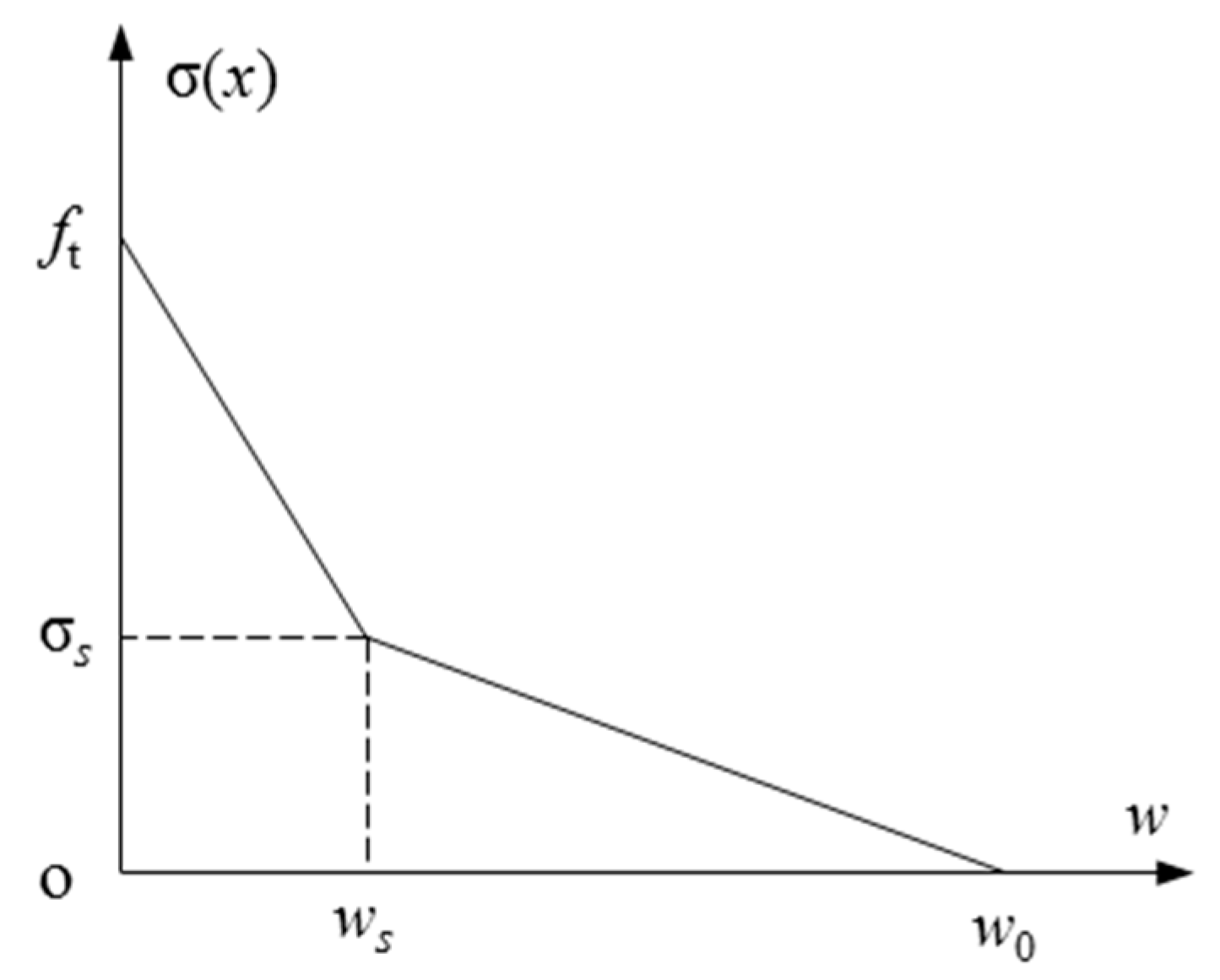
4.4. Determination of the Stress on the Preset Crack Upper Surface
4.5. Comparison of the Predicted and Experimental Results
5. Conclusions
- The edge crack of the test beams with different distances between the preset and the edge cracks vertically crosses through the preset crack when the relative distance was sufficiently long. The relative distance of the two cracks greatly influenced the peak load of the P-CMOD curve. The peak load was high when the relative distance was long;
- The edge crack of the test beams with different preset crack lengths vertically crosses through the preset crack when such length was sufficiently long. The preset crack length greatly influenced the critical CMOD of the P-CMOD curve. The critical CMOD was high when the preset crack length was long;
- The edge crack of the test beams with different approach angles vertically crosses through the preset crack when the approach angle was close to 90°. The approach angle greatly influenced crack propagation path and the carrying capacity. Such a path was close to upright and the peak load was high when the approach angle was large;
- The improved crack initiation criterion for predicting the crack propagation path after interaction was proposed by combining the maximum circumferential stress theory and fracture toughness criterion. The predicted results were compared with the experimental outcomes of the reinitiation after crack interaction. Results indicated that the improved criterion accurately predicted the aforementioned path after crack interaction;
- The DIC technology can effectively observe the crack intersection in concrete by this work. The accuracy crack opening displacement obtained by DIC technology indicated that it had good application prospects in investigating the complex problem of multiple crack propagation processes.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Beugelsdijk, L.J.L.; de Pater, C.J.; Sato, K. Experimental hydraulic fracture propagation in a multi-fractured medium. In Proceedings of the SPE Asia Pacific Conference on Integrated Modelling for Asset Management, Yokohama, Japan, 25–26 April 2000. [Google Scholar]
- Blanton, T.L. An experimental study of interaction between hydraulically induced and pre-existing fractures. In Proceedings of the SPE Unconventional Gas Recovery Symposium, Pittsburgh, PA, USA, 16–18 May 1982. [Google Scholar]
- Chen, Z.; Jeffrey, R.; Zhang, X.; Kear, J. Finite Element Simulation of a Hydraulic Fracture Interacting with a Natural Fracture. In Proceedings of the SPE Asia Pacific Unconventional Resources Conference and Exhibition, Brisbane, Australia, 9−11 November 2015. Paper SPE-176970-MS. [Google Scholar]
- Hubbert, M.K.; Willis, D.G. Mechanics of hydraulic fracturing. Trans. Soc. Pet. Eng. AIME 1957, 210, 153–163. [Google Scholar]
- Xu, S.; Reinhardt, H.W. Determination of double- K criterion for crack propagation in quasi-brittle fracture, Part III: Compact tension specimens and wedge splitting specimens. Int. J. Fract. 1999, 98, 179–193. [Google Scholar] [CrossRef]
- Xu, S.; Reinhardt, H.W. A simplified method for determining double-K fracture parameters for three-point bending tests. Int. J. Fract. 2000, 104, 181–209. [Google Scholar] [CrossRef]
- Mishin, V.M.; Sarrak, V.I. Critical local tensile stress as criterion of delayed brittle failure. Strength Mater. 1985, 17, 348–352. [Google Scholar] [CrossRef]
- Brizmerm, V.; Kligerman, Y.; Etsion, I. The effect of contact conditions and material properties on the elasticity terminus of a spherical contact. Int. J. Solids Struct. 2006, 43, 5736–5749. [Google Scholar] [CrossRef]
- Guo, H.; Aziz, N.I.; Schmidt, L.C. Rock cutting study using linear elastic fracture mechanics. Eng. Fract. Mech. 1992, 41, 771–778. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Lin, P. Numerical study of stress distribution and crack coalescence mechanisms of solid containing multiple holes. Int. J. Rock Mech. Min. Sci. 2015, 79, 41–54. [Google Scholar] [CrossRef]
- Darby, M.I. A fracture mechanics approach to the failure of graphite in laboratory tests. Int. J. Fract. 1976, 12, 745–757. [Google Scholar]
- Lei, W.S. Fracture probability of a randomly oriented microcrack under multi-axial loading for the normal tensile stress criterion. Theor. Appl. Fract. Mech. 2016, 85, S016784421530166X. [Google Scholar] [CrossRef]
- Jenq, Y.S.; Shah, S.P. A Fracture toughness criterion for concrete. Eng. Fract. Mech. 1985, 21, 1055–1069. [Google Scholar] [CrossRef]
- Margolin, B.Z.; Shvetsova, V.A.; Gulenko, A.G.; Kostylev, V.I. Application of a new cleavage fracture criterion for fracture toughness prediction for RPV steels. Fatigue Fract. Eng. Mater. Struct. 2010, 29, 697–713. [Google Scholar] [CrossRef]
- Xu, Y.; Dai, F.; Zhao, T.; Xu, N.-W.; Liu, Y. Fracture toughness determination of cracked chevron notched Brazilian disc rock specimen via griffith energy criterion incorporating realistic fracture profiles. Rock Mech. Rock Eng. 2016, 49, 3083–3093. [Google Scholar] [CrossRef]
- Gu, H.; Weng, X.; Lund, J.; Mack, M.; Ganguly, U.; Suarez-Rivera, R. Hydraulic fracture crossing natural fracture at nonorthogonal angles: A criterion and its validation. SPE Prod. Oper. 2012, 27, 20–26. [Google Scholar] [CrossRef]
- Fu, W.; Ames, B.C.; Bunger, A.P.; Savitski, A.A. Impact of partially cemented and non-persistent natural fractures on hydraulic fracture propagation. Rock Mech. Rock Eng. 2016, 49, 4519–4526. [Google Scholar] [CrossRef]
- Hassan, F.; Hossain, M.M.; Sarmadivaleh, M. Numerical and experimental investigation of the interaction of natural and propagated hydraulic fracture. J. Nat. Gas Sci. Eng. 2017, 37, 409–424. [Google Scholar]
- Wang, W.; Olson, J.E.; Prodanovi, M.; Schultz, R.A. Interaction between cemented natural fractures and hydraulic fractures assessed by experiments and numerical simulations. J. Pet. Sci. Eng. 2018, 167, 506–516. [Google Scholar] [CrossRef]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of digital image correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Almeida, O.D.; Lagattu, F.; Brillaud, J. Analysis by a 3D DIC technique of volumetric deformation gradients: Application to polypropylene/EPR/talc composites. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1210–1217. [Google Scholar] [CrossRef]
- Vogel, D.; Dudek, R.; Keller, J.; Michel, B. Combining DIC techniques and finite element analysis for reliability assessment on micro and nanoscale. In Proceedings of the 5th Electronics Packaging Technology Conference (EPTC 2003), Singapore, 12 December 2003. [Google Scholar]
- Tan, Y.Q.; Lei, Z.; Meng, G.; Li-yan, S. Investigation of the deformation properties of asphalt mixtures with DIC technique. Construct. Build. Mater. 2012, 37, 581–590. [Google Scholar]
- Helm, J.D. Digital image correlation for specimens with multiple growing cracks. Exp. Mech. 2008, 48, 753–762. [Google Scholar] [CrossRef]
- Li, D.; Huang, P.; Guo, X.; Zheng, X.; Lin, J.; Chen, Z. Fatigue crack propagation behavior of RC beams strengthened with CFRP under cyclic bending loads. Fatigue Fract. Eng. Mater. Struct. 2017, 41, 1–11. [Google Scholar] [CrossRef]
- Wu, Z.M.; Rong, H.; Zheng, J.J.; Xu, W.; Dong, W. An experimental investigation on the FPZ properties in concrete using digital image correlation technique. Eng. Fract. Mech. 2011, 78, 2978–2990. [Google Scholar] [CrossRef]
- Chen, H.; Su, R. Tension softening curves of plain concrete. Constr. Build Mater. 2013, 44, 440–451. [Google Scholar] [CrossRef]
- Erdoga, F.; Sih, G.C. On the crack extension in plates under plane loading and transverse shear. J. Basic Eng. Trans. ASME 1963, 85, 519–525. [Google Scholar] [CrossRef]
- Wang, X.L.; Shi, F.; Liu, C.; Lu, D.T.; Liu, H.; Wu, H.A. Extended finite element simulation of fracture network propagation in formation containing frictional and cemented natural fractures. J. Nat. Gas Sci. Eng. 2017, 50, 309–324. [Google Scholar] [CrossRef]
- Su, H.; Li, J.; Wen, Z.; Zhou, F. A bi-criteria combined evaluation approach for reinforcement effect of gravity dam with cracks. Int. J. Solids Struct. 2018, 147, 238–253. [Google Scholar] [CrossRef]
- Gu, H.; Weng, X.; Lund, J.B.; Mack, M.G.; Ganguly, U.; Suarez-Rivera, R. Hydraulic fracture crossing natural fracture at non-orthogonal angles, a criterion, its validation and applications. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 24–26 January 2011. [Google Scholar]
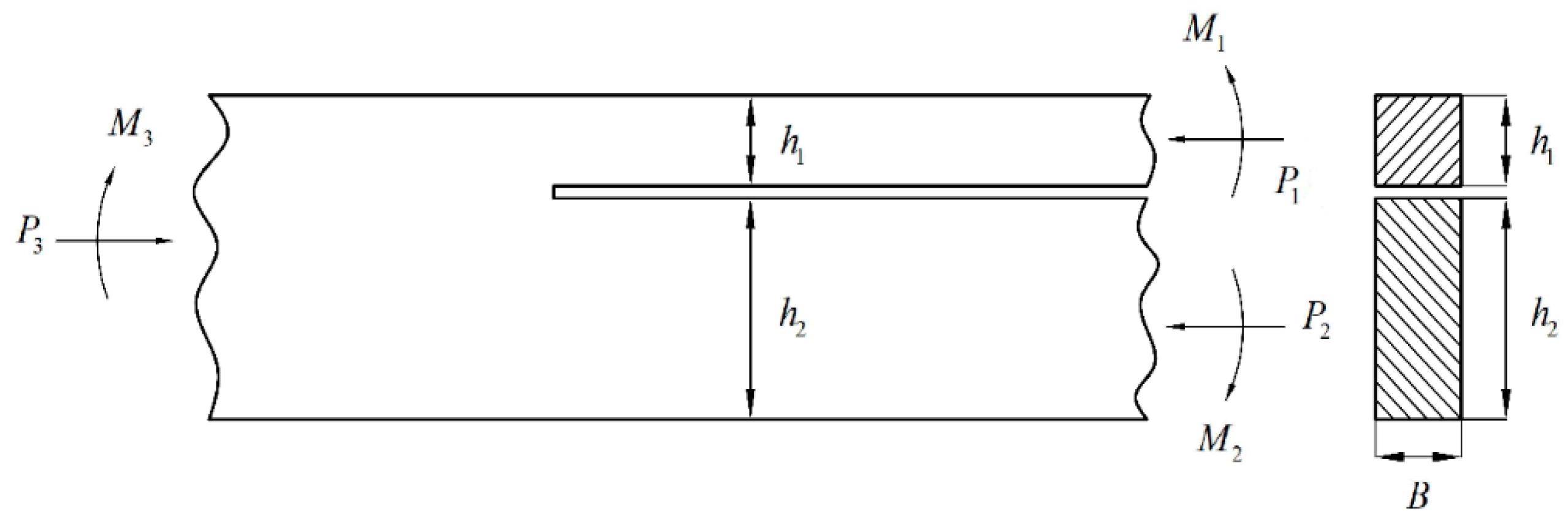
- Aamodt, B.; Bergan, P.G. On the principle of superposition for stress intensity factors. Eng. Fract. Mech. 1976, 8, 437–440. [Google Scholar] [CrossRef]
- Murakami, Y.; Keer, L.M. Stress Intensity Factors Handbook; Pergamon Press: London, UK, 1989; Volume 3. [Google Scholar]
- Petersson, P.E. Crack Growth and Development of Fracture Zones in PLAIN Concrete and Similar Materials; Report TVBM-1006; Division of Building Materials, Lund Institute of Technology: Lund, Sweden, 1981. [Google Scholar]
- Cheung, Y.K.; Woo, C.W.; Wang, Y.H. The stress intensity factor for a double edge cracked plate by boundary collocation method. Int. J. Fract. 1988, 37, 217–231. [Google Scholar] [CrossRef]
- Gao, Y.C. Plane stress dynamic plastic field near a propagating crack tip. Int. J. Fract. 1987, 34, 111–129. [Google Scholar] [CrossRef]
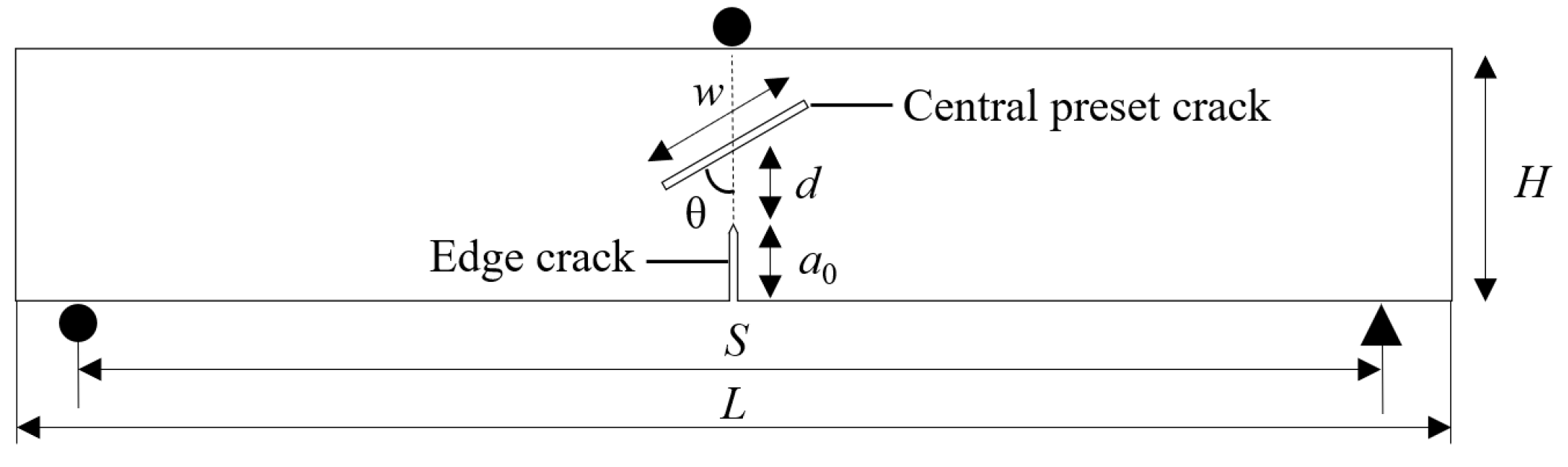


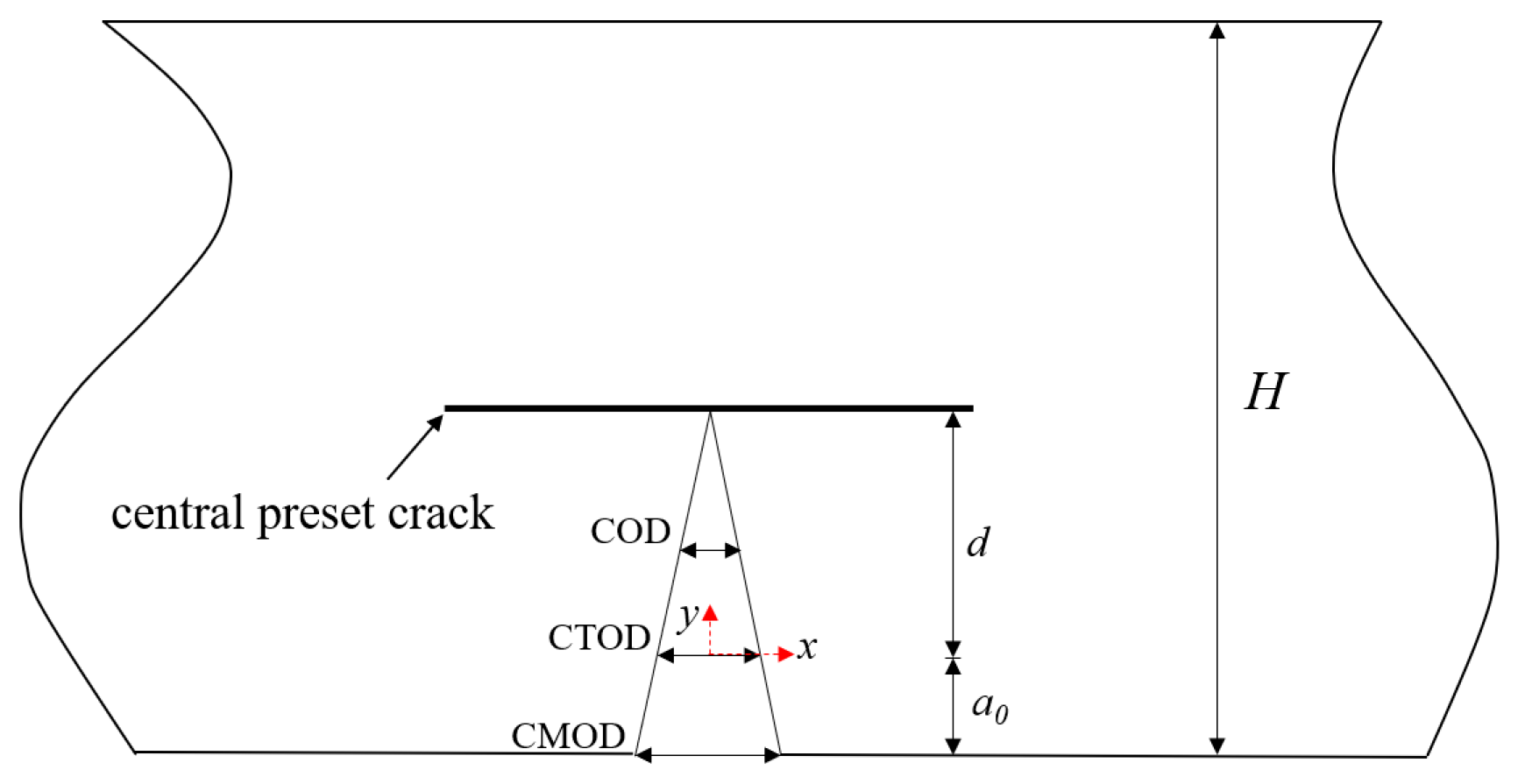



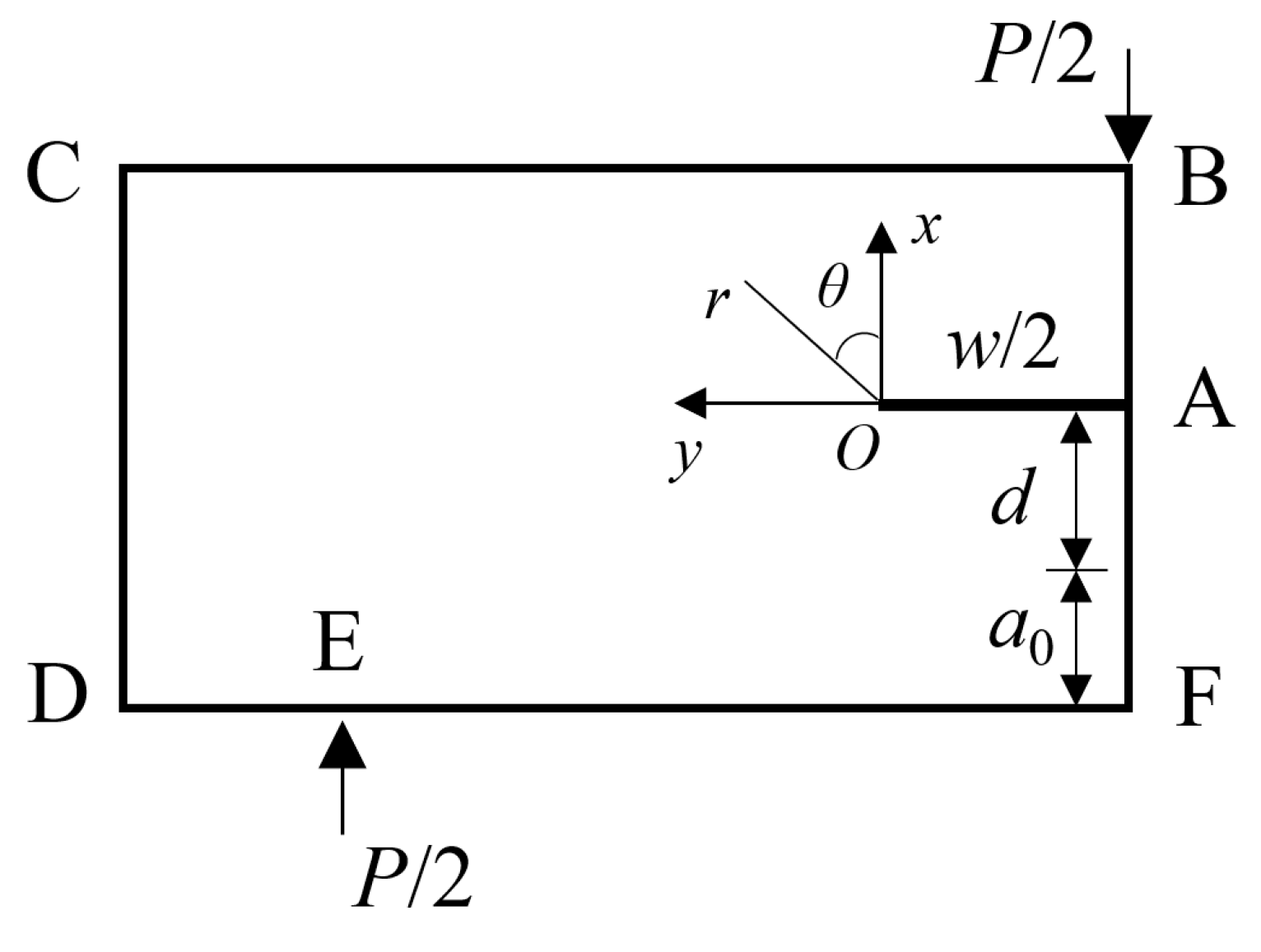
| Test Beam | a0 (mm) | d (mm) | w (mm) | θ (°) |
|---|---|---|---|---|
| TPB-D10 | 30 | 10 | 40 | 90 |
| TPB-D30 | 30 | 30 | 40 | 90 |
| TPB-D50 | 30 | 50 | 40 | 90 |
| TPB-D70 | 30 | 70 | 40 | 90 |
| TPB-W20 | 30 | 30 | 20 | 90 |
| TPB-W40 | 30 | 30 | 40 | 90 |
| TPB-W60 | 30 | 30 | 60 | 90 |
| TPB-W80 | 30 | 30 | 80 | 90 |
| TPB-A30 | 30 | 30 | 60 | 30 |
| TPB-A45 | 30 | 30 | 60 | 45 |
| TPB-A60 | 30 | 30 | 60 | 60 |
| TPB-A90 | 30 | 30 | 60 | 90 |
| Water/Cement Ratio | Cement (kg/m3) | Water (kg/m3) | Sand (kg/m3) | Aggregate (kg/m3) |
|---|---|---|---|---|
| 0.47 | 468 | 219 | 641 | 1301 |
| Test Beam | E (GPa) | Pini (kN) | CMODini (mm) | Pmax (kN) | CMODc (mm) |
|---|---|---|---|---|---|
| TPB-D10-1 | 32.05 | 6.24 | 0.08 | 6.98 | 0.11 |
| TPB-D10-2 | 34.23 | 6.07 | 0.11 | 7.13 | 0.13 |
| TPB-D10-3 | 33.17 | 5.92 | 0.09 | 6.72 | 0.12 |
| Average | 33.15 | 6.08 | 0.09 | 6.94 | 0.12 |
| TPB-D30-1 | 31.35 | 6.20 | 0.05 | 7.21 | 0.08 |
| TPB-D30-2 | 33.27 | 5.88 | 0.05 | 7.89 | 0.10 |
| TPB-D30-3 | 30.19 | 5.93 | 0.06 | 6.83 | 0.08 |
| Average | 31.60 | 6.00 | 0.05 | 7.31 | 0.09 |
| TPB-D50-1 | 34.03 | 5.81 | 0.07 | 7.32 | 0.11 |
| TPB-D50-2 | 32.37 | 5.95 | 0.07 | 7.01 | 0.12 |
| TPB-D50-3 | 31.13 | 6.16 | 0.08 | 8.03 | 0.12 |
| Average | 32.51 | 5.97 | 0.07 | 7.45 | 0.12 |
| TPB-D70-1 | 35.21 | 5.82 | 0.05 | 8.12 | 0.08 |
| TPB-D70-2 | 32.43 | 6.09 | 0.06 | 7.96 | 0.09 |
| TPB-D70-3 | 33.15 | 5.92 | 0.05 | 8.35 | 0.07 |
| Average | 33.60 | 5.94 | 0.05 | 8.14 | 0.08 |
| TPB-W20-1 | 32.65 | 6.11 | 0.06 | 8.09 | 0.07 |
| TPB-W20-2 | 33.38 | 5.84 | 0.06 | 8.21 | 0.08 |
| TPB-W20-3 | 34.26 | 6.05 | 0.07 | 7.82 | 0.10 |
| Average | 33.43 | 6.00 | 0.06 | 8.04 | 0.08 |
| TPB-W40-1 | 35.21 | 6.08 | 0.07 | 7.31 | 0.11 |
| TPB-W40-2 | 33.61 | 5.95 | 0.07 | 7.99 | 0.12 |
| TPB-W40-3 | 33.25 | 5.98 | 0.07 | 6.93 | 0.10 |
| Average | 34.02 | 6.00 | 0.07 | 7.41 | 0.11 |
| TPB-W60-1 | 30.23 | 5.93 | 0.07 | 6.95 | 0.13 |
| TPB-W60-2 | 34.21 | 6.24 | 0.09 | 7.14 | 0.14 |
| TPB-W60-3 | 33.15 | 6.21 | 0.07 | 6.96 | 0.12 |
| Average | 32.53 | 6.12 | 0.08 | 7.02 | 0.13 |
| TPB-W80-1 | 30.25 | 5.96 | 0.07 | 6.32 | 0.15 |
| TPB-W80-2 | 33.59 | 5.84 | 0.07 | 6.81 | 0.15 |
| TPB-W80-3 | 31.62 | 6.11 | 0.07 | 6.37 | 0.14 |
| Average | 31.82 | 5.99 | 0.07 | 6.50 | 0.15 |
| TPB-A30-1 | 33.35 | 5.02 | 0.08 | 6.27 | 0.13 |
| TPB-A30-2 | 31.31 | 4.97 | 0.06 | 5.62 | 0.11 |
| TPB-A30-3 | 34.15 | 5.17 | 0.08 | 6.18 | 0.11 |
| Average | 32.94 | 5.05 | 0.07 | 6.36 | 0.12 |
| TPB-A45-1 | 34.31 | 5.96 | 0.07 | 6.98 | 0.10 |
| TPB-A45-2 | 35.08 | 6.13 | 0.09 | 7.25 | 0.11 |
| TPB-A45-3 | 30.12 | 5.99 | 0.09 | 6.51 | 0.13 |
| Average | 33.17 | 6.03 | 0.08 | 6.91 | 0.11 |
| TPB-A60-1 | 28.54 | 6.13 | 0.07 | 7.21 | 0.11 |
| TPB-A60-2 | 29.79 | 5.98 | 0.06 | 7.04 | 0.09 |
| TPB-A60-3 | 31.52 | 6.02 | 0.06 | 7.08 | 0.09 |
| Average | 29.95 | 6.04 | 0.06 | 7.11 | 0.10 |
| TPB-A90-1 | 30.01 | 5.97 | 0.08 | 7.63 | 0.09 |
| TPB-A90-2 | 36.13 | 6.14 | 0.09 | 7.26 | 0.11 |
| TPB-A90-3 | 29.55 | 5.99 | 0.08 | 6.65 | 0.12 |
| Average | 31.90 | 6.03 | 0.08 | 7.18 | 0.11 |
| Boundary | φ0 | ∂φ0/∂n |
|---|---|---|
| AB | 0 | 0 |
| BC | 0 | |
| CD | ||
| DE | 0 | |
| EF | 0 | |
| FA | 0 |
| Test Beam | Restart Point | |||||
|---|---|---|---|---|---|---|
| Experiment | Predicted | |||||
| TPB-D10-1 | 6.58 | 0.43 | 0.67 | 3.03 | Tip | Tip |
| TPB-D30-1 | 6.87 | 0.48 | 0.73 | 3.82 | Tip & Middle | Tip & Middle |
| TPB-D50-1 | 6.98 | 0.59 | 0.48 | 4.15 | Near middle | Middle |
| TPB-D70-1 | 7.09 | 0.62 | 0.45 | 4.23 | Middle | Middle |
| TPB-W20-1 | 6.63 | 0.56 | 0.71 | 3.17 | Tip | Tip |
| TPB-W40-1 | 6.82 | 0.50 | 0.68 | 3.83 | Tip & Middle | Tip & Middle |
| TPB-W60-1 | 6.95 | 0.43 | 0.43 | 4.05 | Middle | Middle |
| TPB-W80-1 | 6.11 | 0.40 | 0.41 | 3.96 | Middle | Middle |
| TPB-A30-1 | 6.12 | - | 0.65 | 3.23 | Tip | Tip |
| TPB-A45-1 | 6.79 | - | 0.71 | 3.45 | Tip | Tip |
| TPB-A60-1 | 7.05 | - | 0.67 | 3.84 | Near tip | Tip & Middle |
| TPB-A90-1 | 7.11 | - | 0.42 | 4.02 | Middle | Middle |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Hu, S. Experimental Study of Crack Propagation in Cracked Concrete. Energies 2019, 12, 3854. https://doi.org/10.3390/en12203854
Wang S, Hu S. Experimental Study of Crack Propagation in Cracked Concrete. Energies. 2019; 12(20):3854. https://doi.org/10.3390/en12203854
Chicago/Turabian StyleWang, Siyao, and Shaowei Hu. 2019. "Experimental Study of Crack Propagation in Cracked Concrete" Energies 12, no. 20: 3854. https://doi.org/10.3390/en12203854
APA StyleWang, S., & Hu, S. (2019). Experimental Study of Crack Propagation in Cracked Concrete. Energies, 12(20), 3854. https://doi.org/10.3390/en12203854