Effect of Channel Diameter on the Combustion and Thermal Behavior of a Hydrogen/Air Premixed Flame in a Swirl Micro-Combustor
Abstract
1. Introduction
2. Methodology
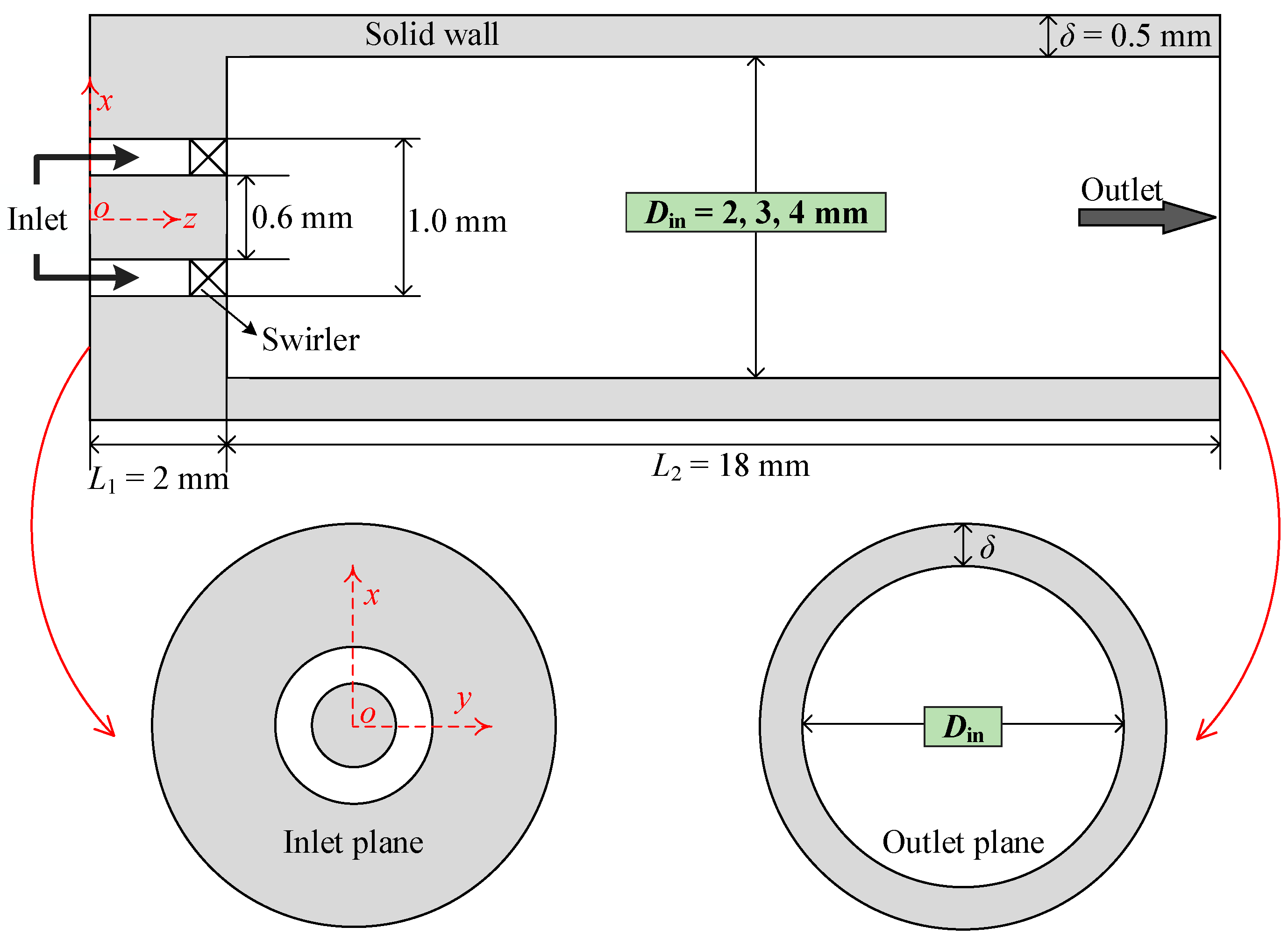
2.1. Physical Model
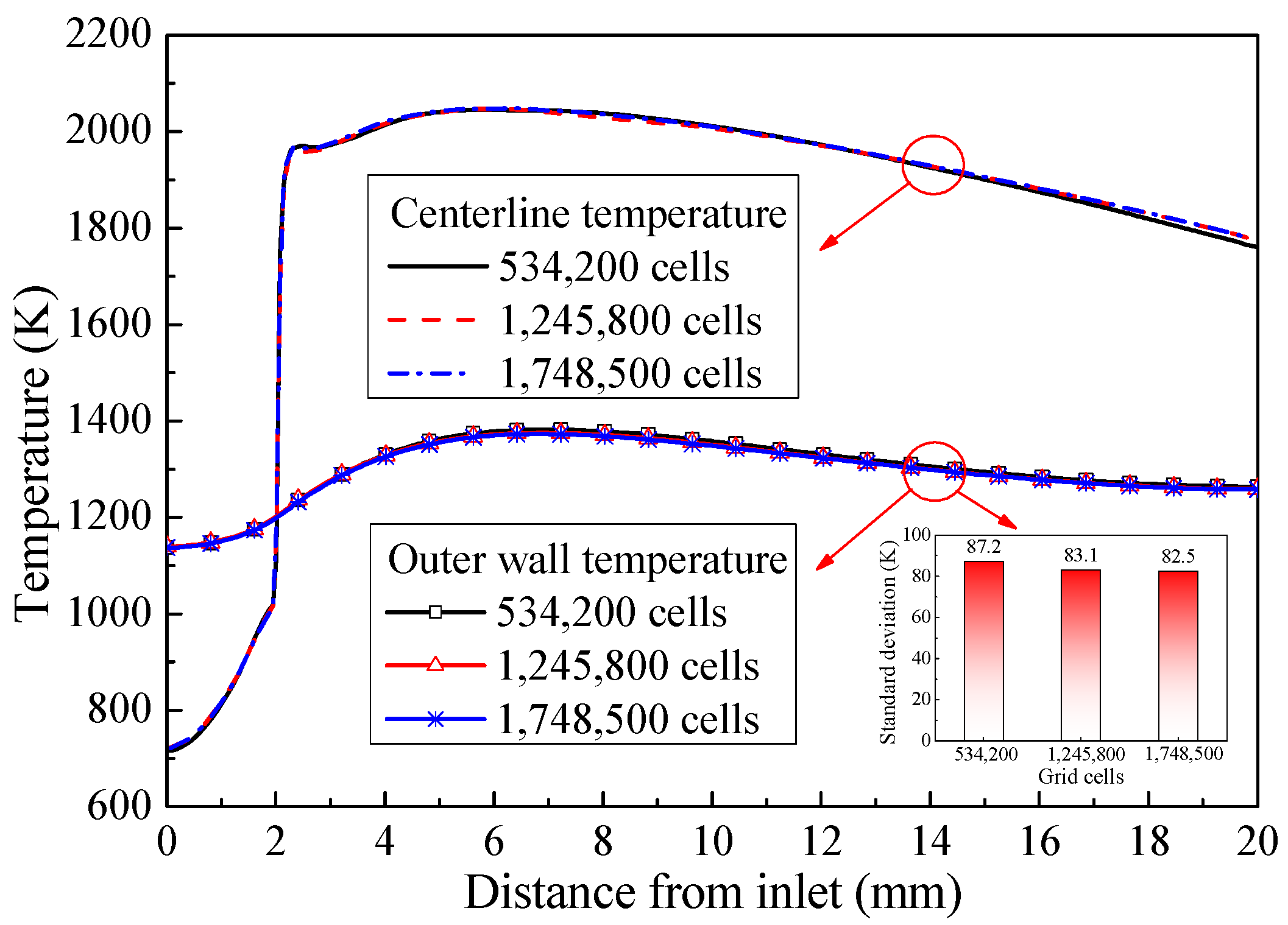
2.2. Computational Models
3. Results and Discussion
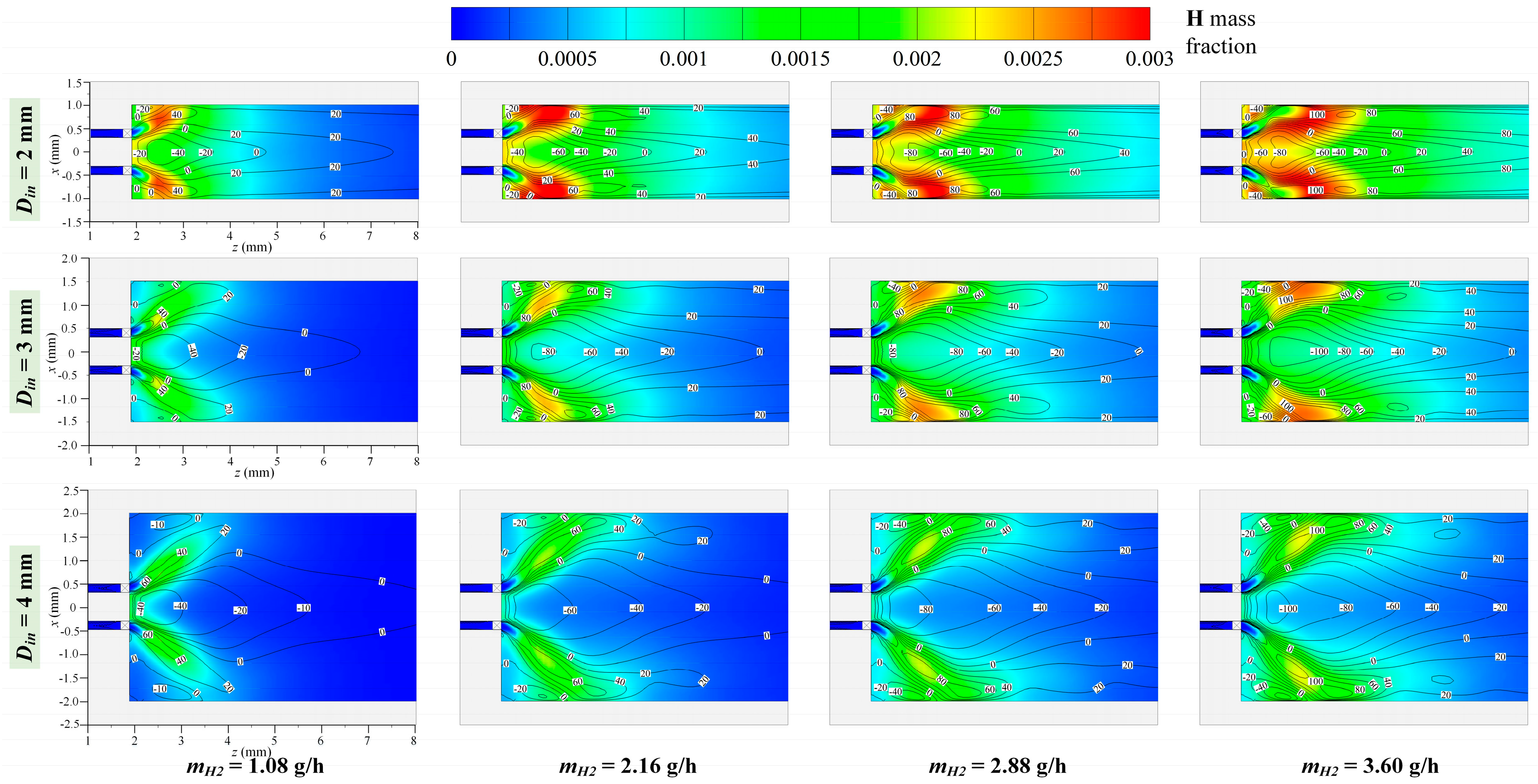
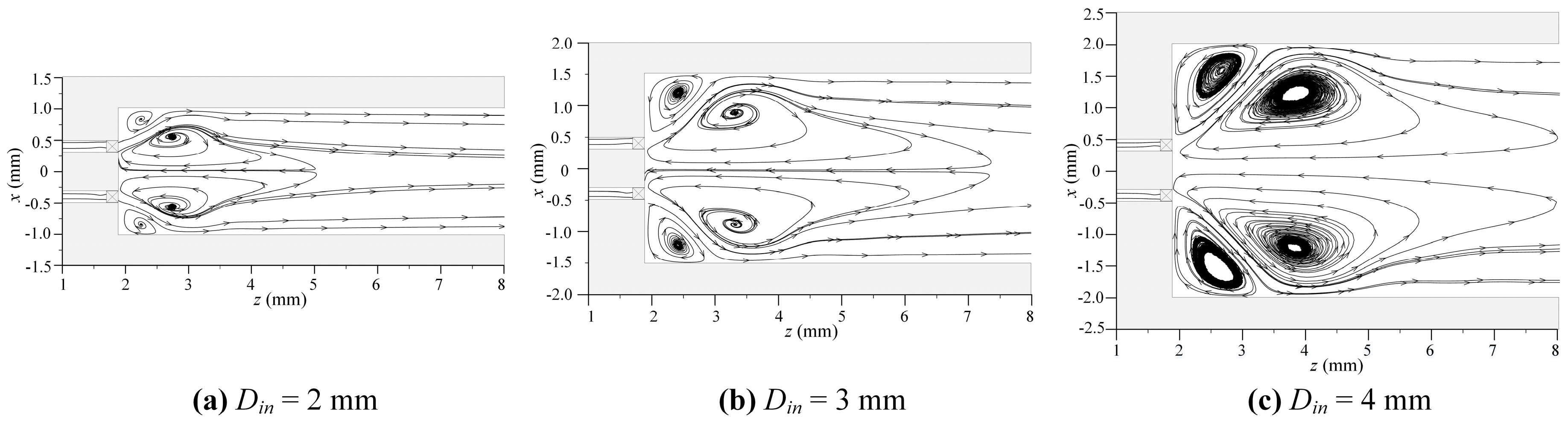
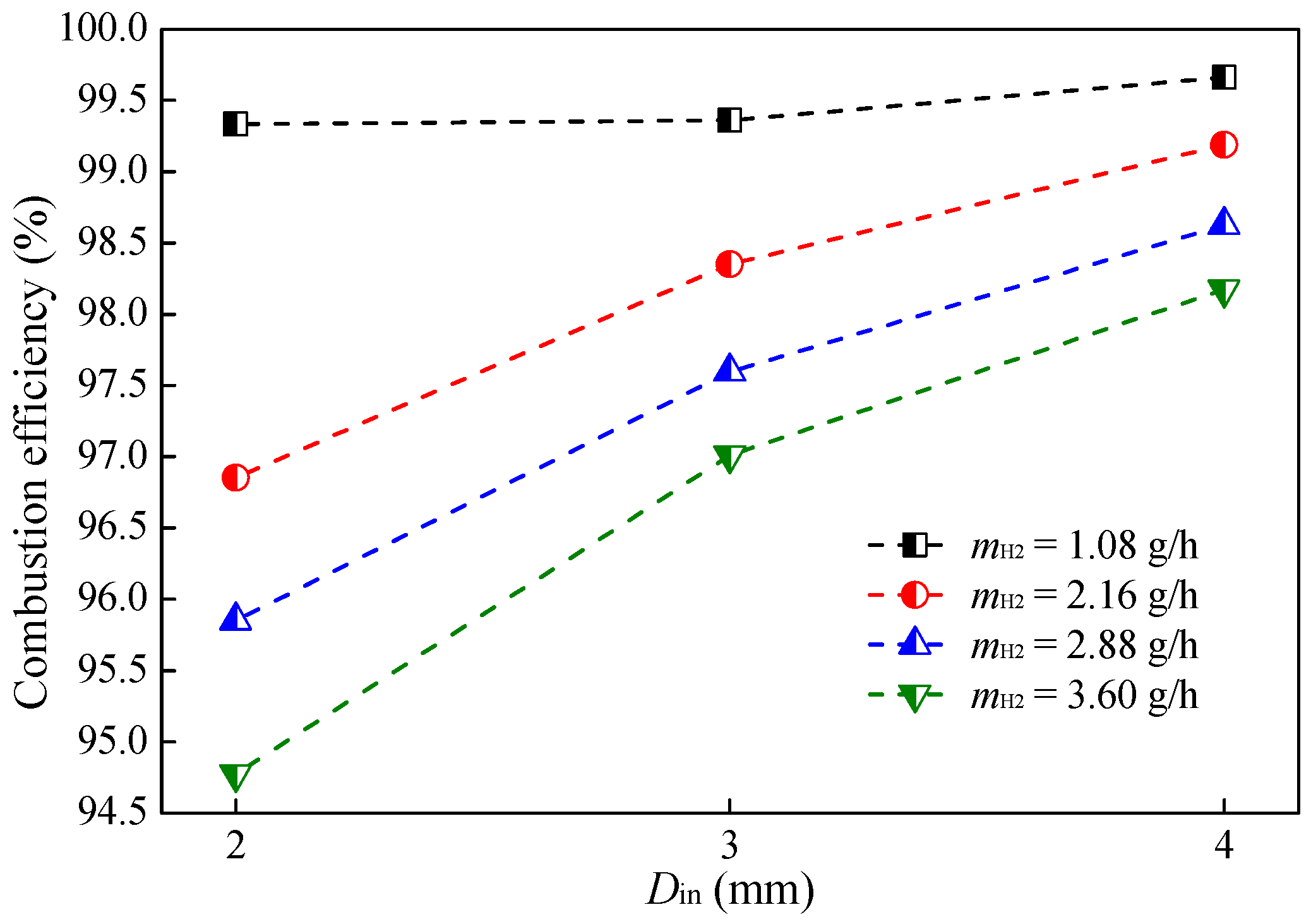
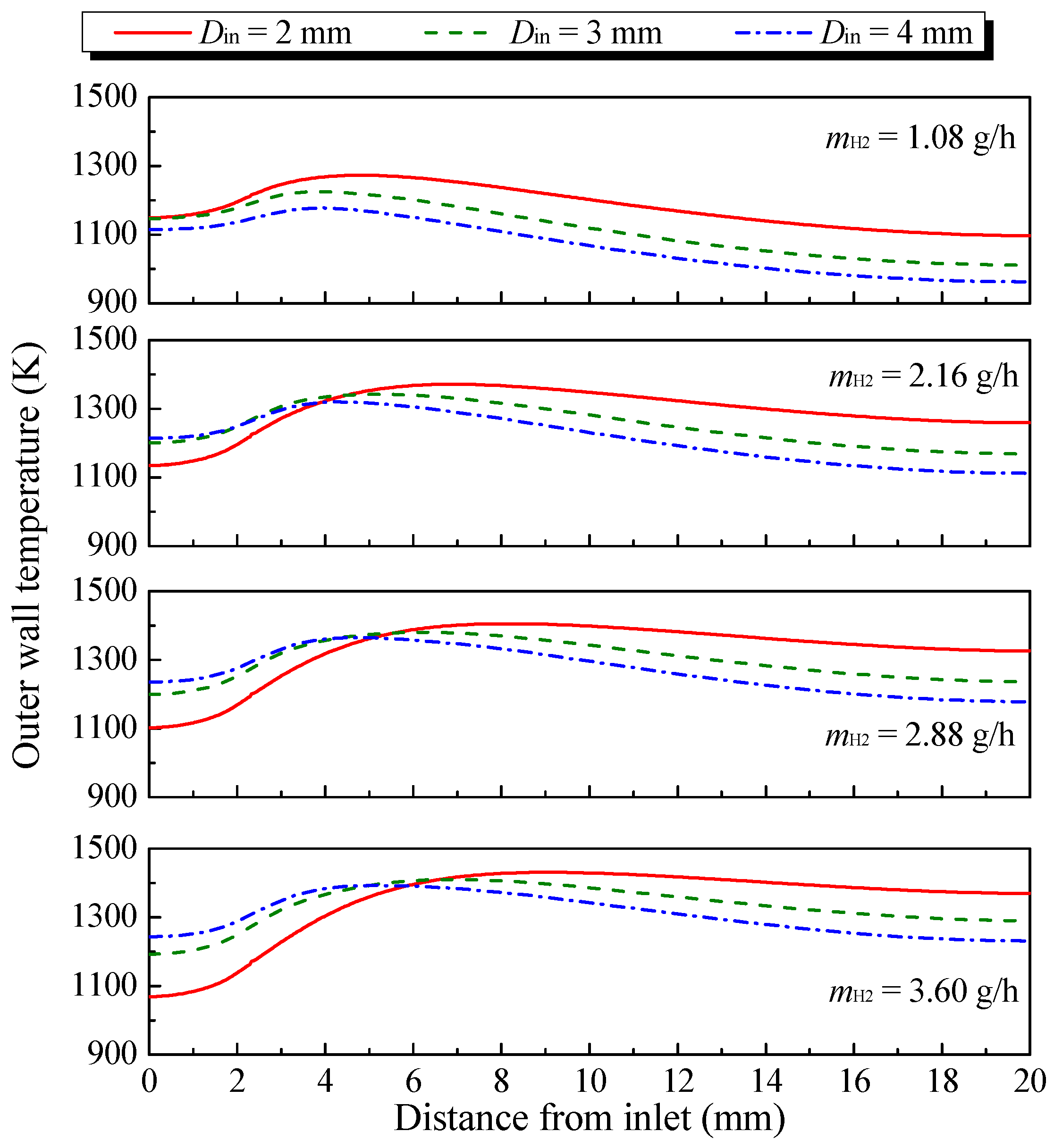
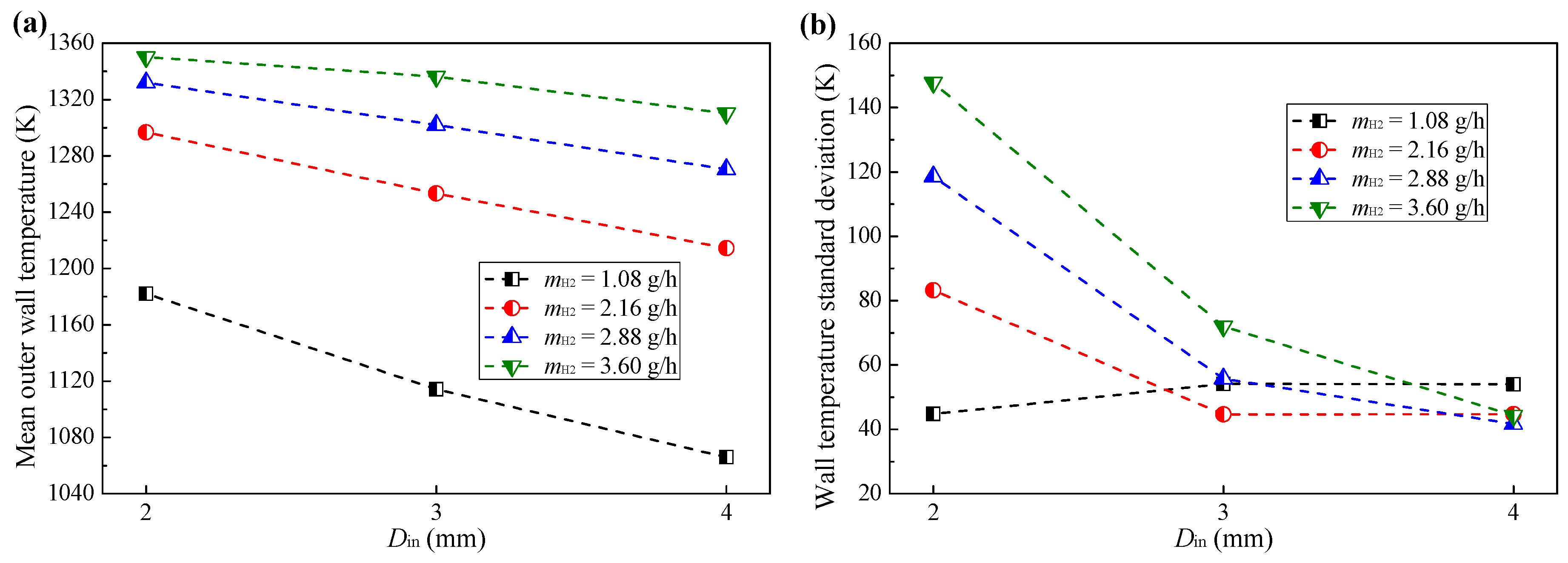
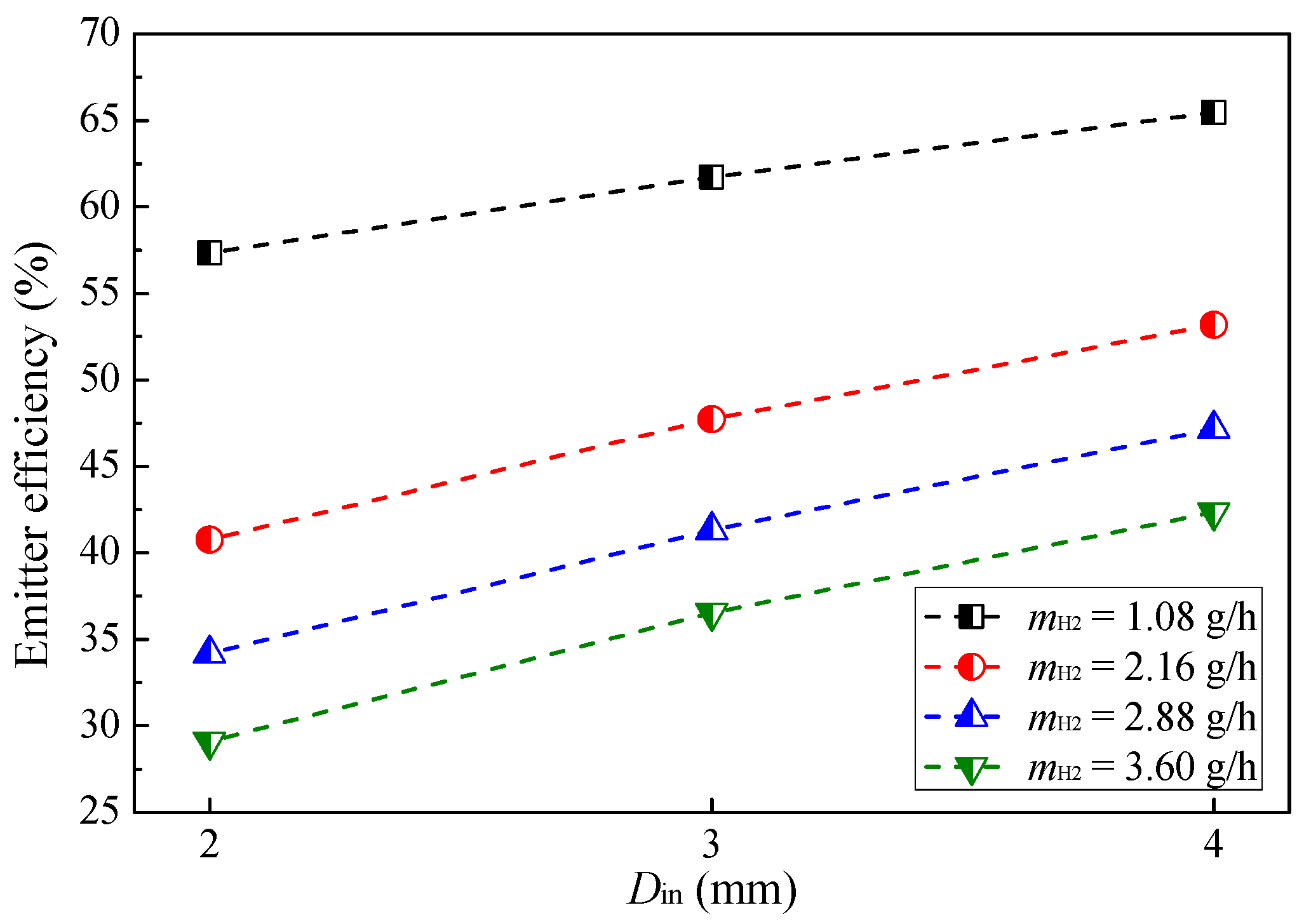
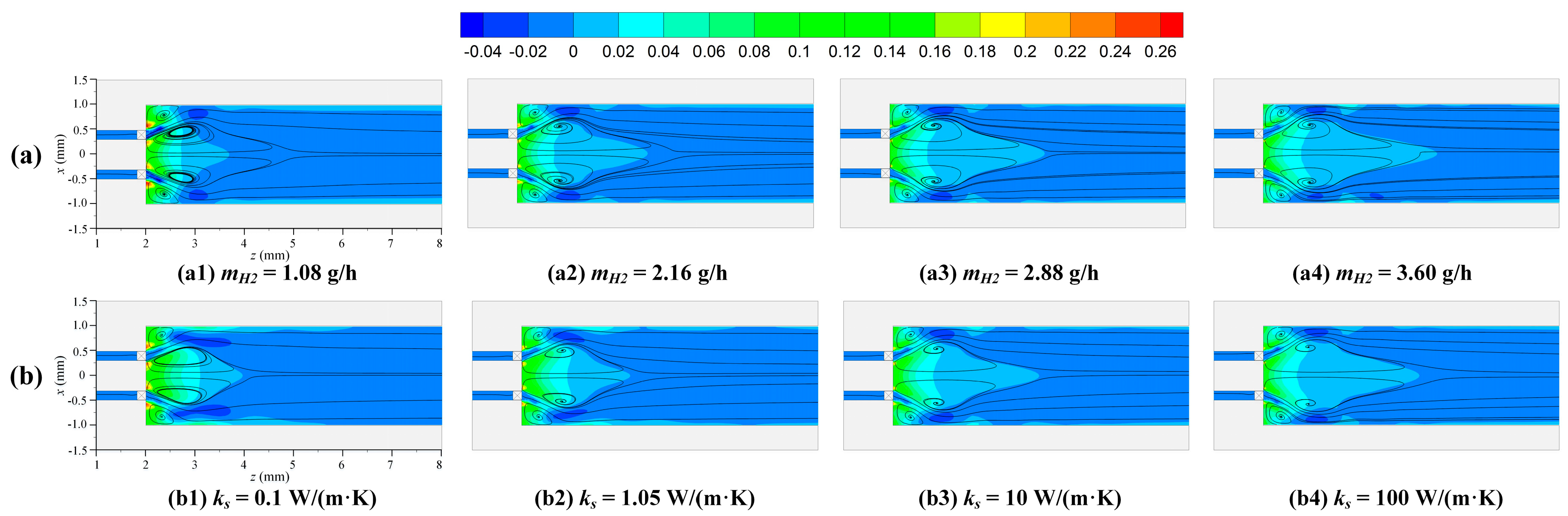
3.1. Effect of Hydrogen Mass Flow Rate
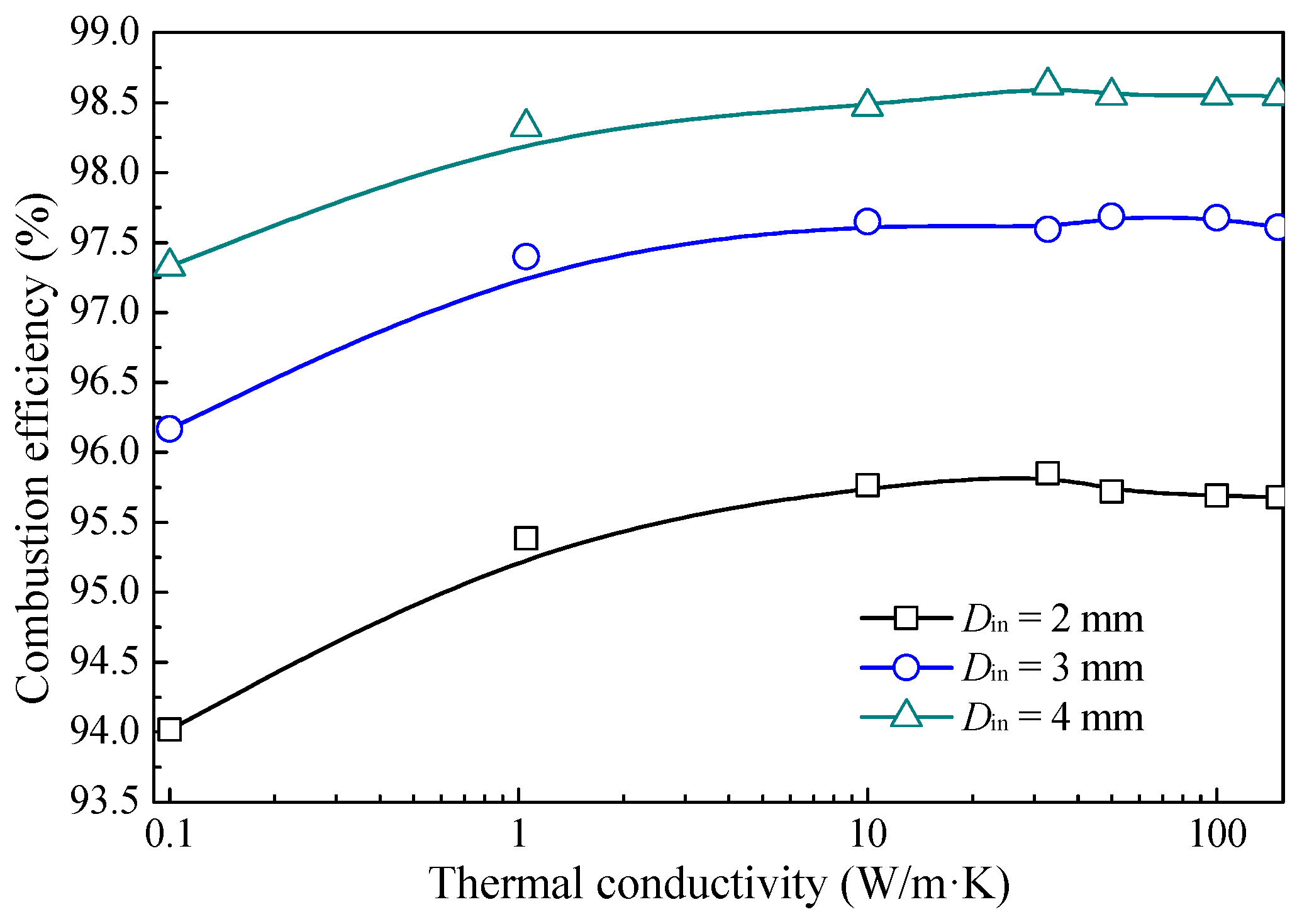
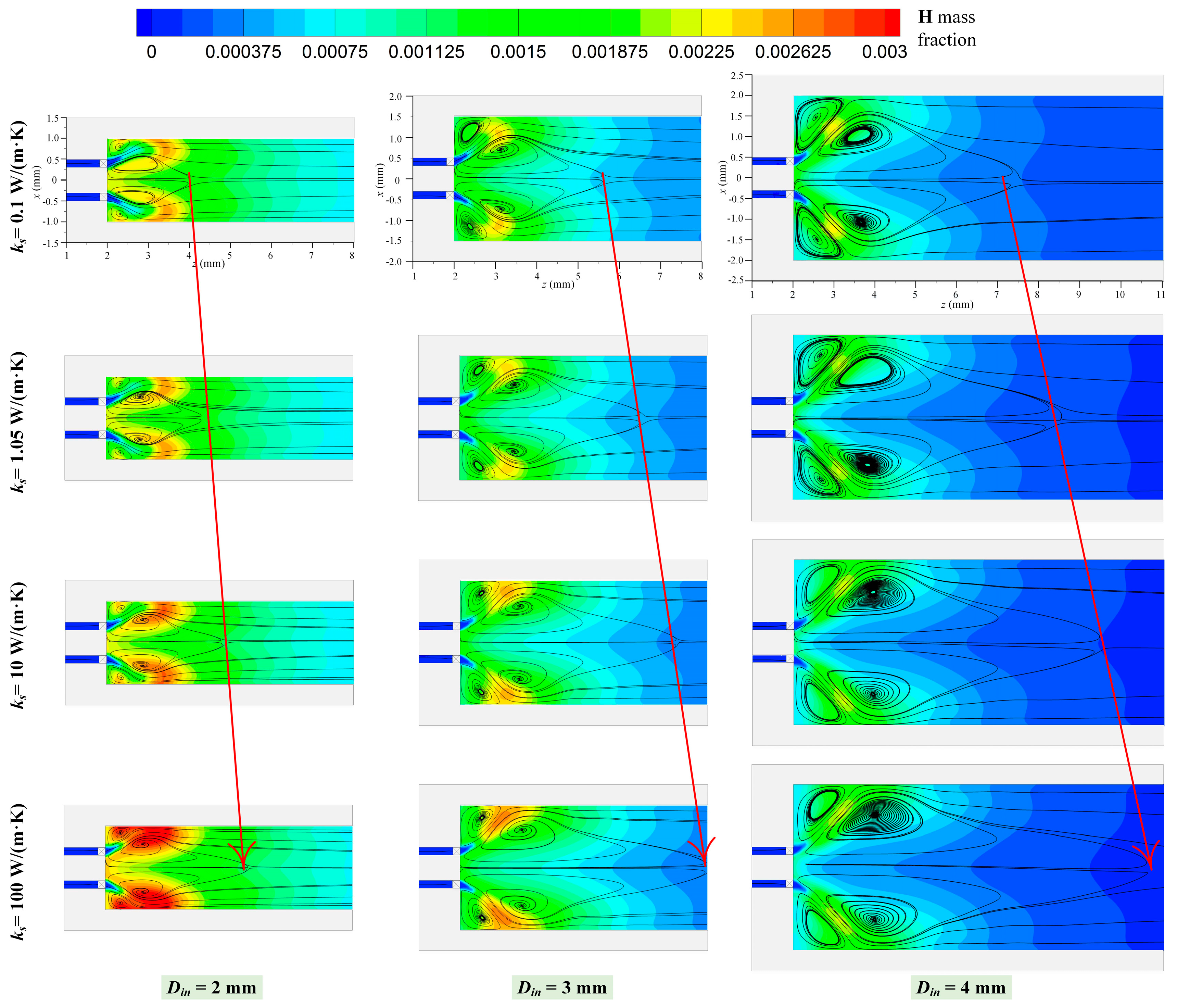
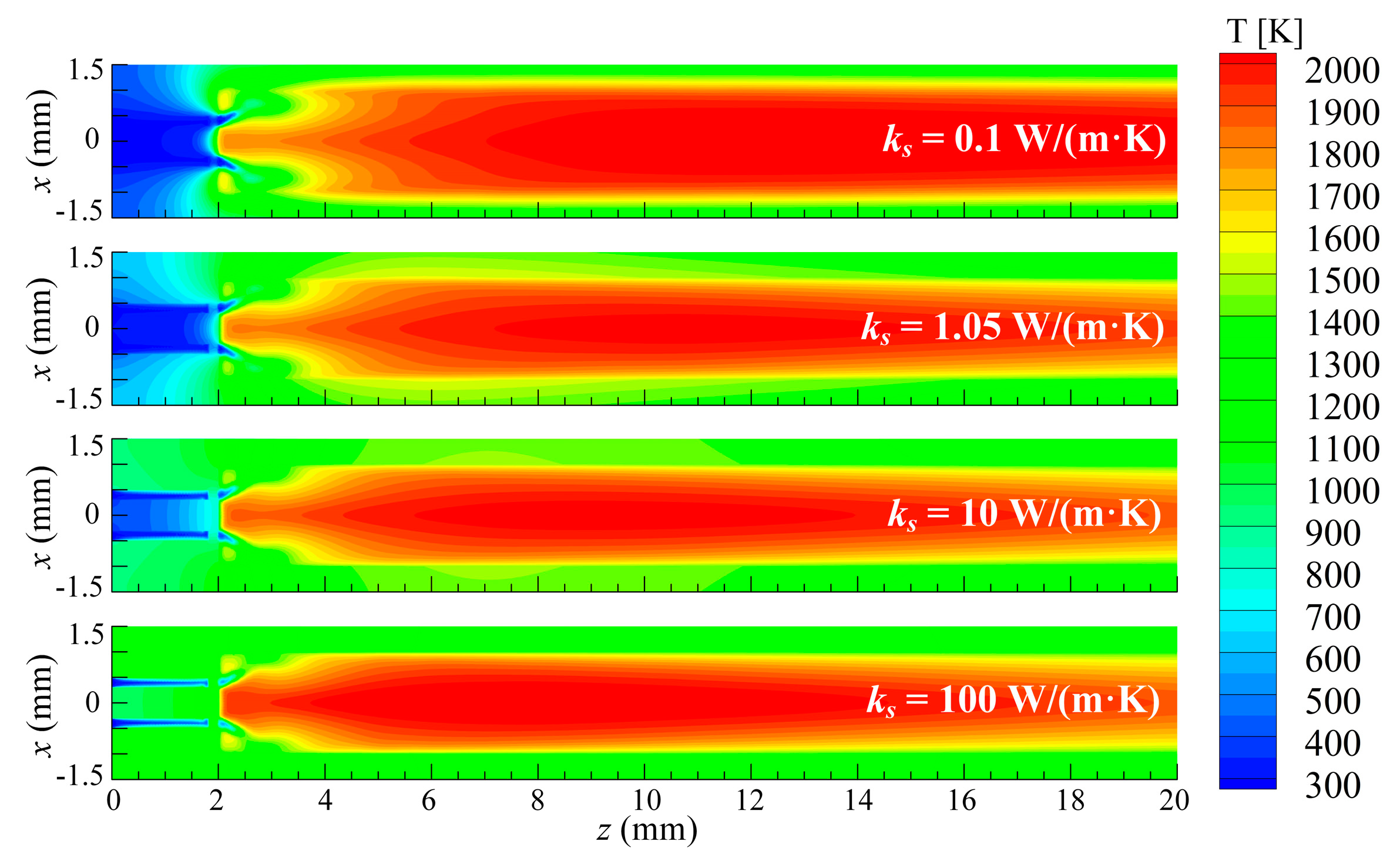
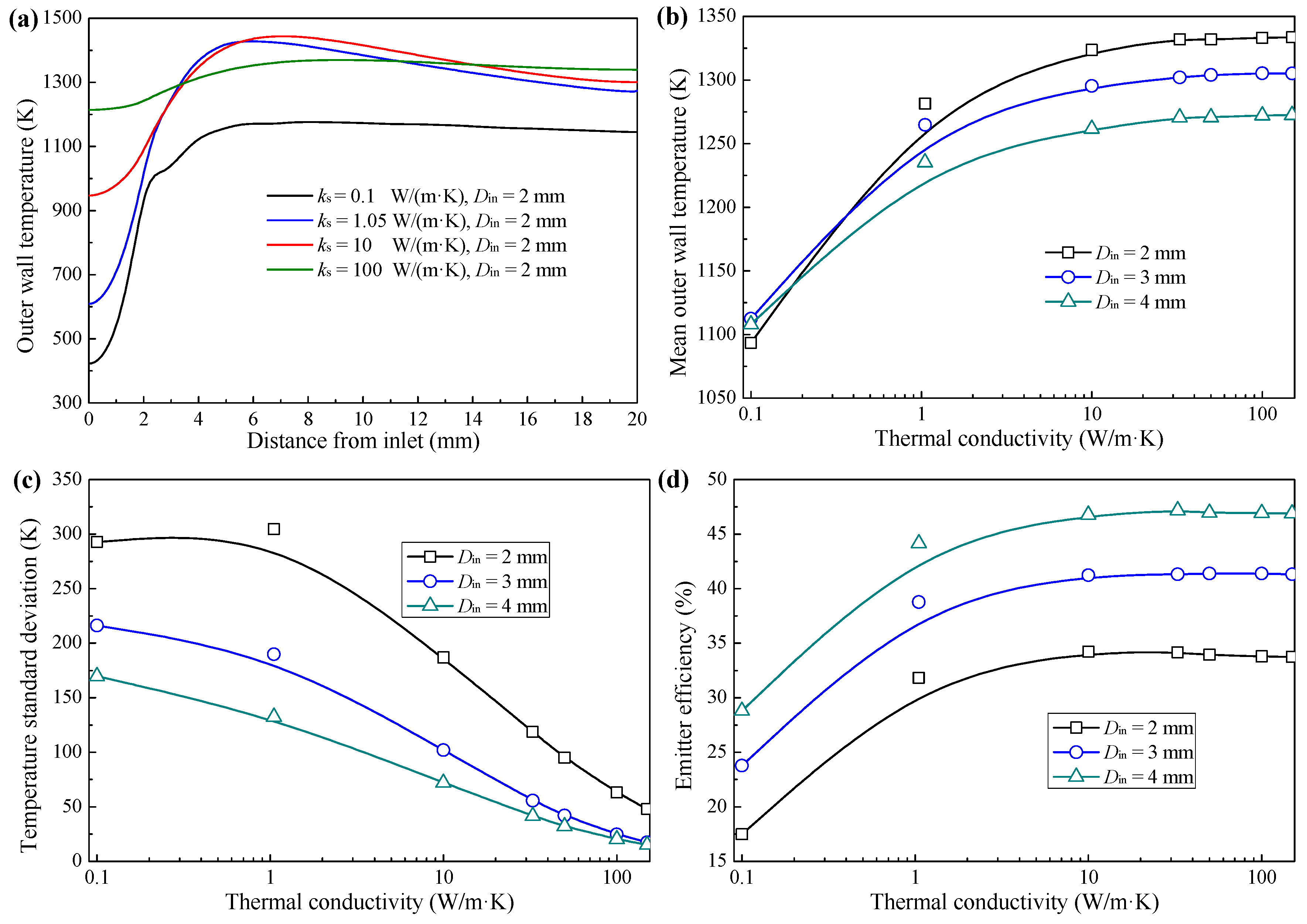
3.2. Effect of Thermal Conductivity
3.3. Effect of Preferential Transport
4. Conclusions
- (1)
- The formation of inner and corner recirculation zones with low local velocities in the swirl MC was due to the swirling flow facilitating flame anchoring;
- (2)
- The local equivalence ratio was larger in the recirculation zones, which confirms that the recirculation zones helped to create a radical pool, thereby anchoring the flame to there;
- (3)
- Although parameters such as channel diameter, inlet mass flow rate, and thermal conductivity of the solid wall changed, the flame root was firmly anchored to the starting position of the recirculation zones;
- (4)
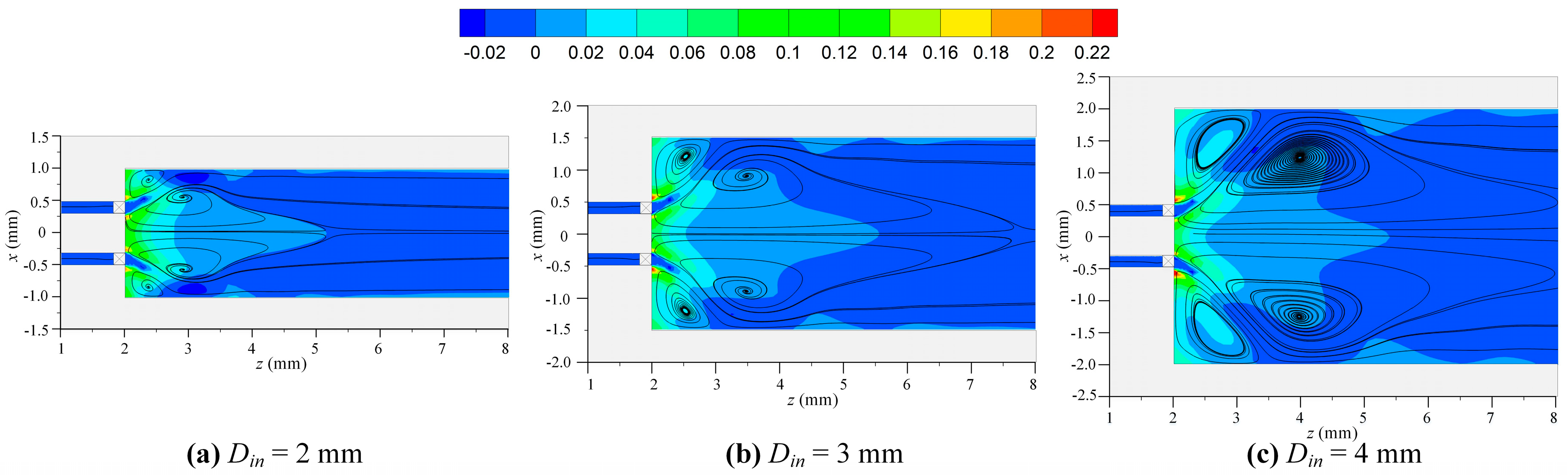
- The combustion intensity was stronger in the MC with a small Din of 2 mm, which had a higher wall temperature. But, a more uniform wall temperature and a larger emitter efficiency was obtained in the MC with Din = 4 mm;
- (5)
- Increasing the thermal conductivity enhanced the thermal performance of the combustion efficiency and emitter efficiency when the thermal conductivity was no greater than approximately 10 W/m·K because of the better preheating and heat transfer performances;
- (6)
- There was a critical point of thermal conductivity (approximately between 10 and 30 W/m·K) that can increase the thermal performance of an MC. When thermal conductivity exceeds the critical thermal conductivity, continuing to increase thermal conductivity has a negligible impact on thermal performance. Nevertheless, the wall temperature standard deviation decreases with increasing thermal conductivity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hosseini, S.E. Micro-power generation using micro-turbine (moving) and thermophotovoltaic (non-moving) systems. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233. [Google Scholar] [CrossRef]
- Ju, Y.; Maruta, K. Microscale combustion: Technology development and fundamental research. Prog. Energy Combust. Sci. 2011, 37, 669–715. [Google Scholar] [CrossRef]
- Chou, S.K.; Yang, W.M.; Chua, K.J.; Li, J.; Zhang, K.L. Development of micro power generators—A review. Appl. Energy 2011, 88, 1–16. [Google Scholar] [CrossRef]
- Burugupally, S.; Weiss, L. Power Generation via Small Length Scale Thermo-Mechanical Systems: Current Status and Challenges, a Review. Energies 2018, 11, 2253. [Google Scholar] [CrossRef]
- Waitz, I.A.; Gauba, G.; Tzeng, Y.S. Combustors for micro-gas turbine engines. J. Fluids Eng. 1998, 12, 109–117. [Google Scholar] [CrossRef]
- Mehra, A.; Zhang, X.; Ayon, A.A.; Waitz, I.A.; Spadaccini, C.M. A six-wafer combustion system for a silicon micro gas turbine engine. J. Microelectromech. Syst. 2000, 9, 517–527. [Google Scholar] [CrossRef]
- Yang, W.M.; Jiang, D.Y.; Chou, S.K.; Chua, K.J.; Karthikeyan, K.; An, H. Experimental study on micro modular combustor for micro-thermophotovoltaic system application. Int. J. Hydrogen Energy 2012, 37, 9576–9583. [Google Scholar] [CrossRef]
- Yang, W.M.; Chou, S.K.; Shu, C.; Xue, H.; Li, Z.W.; Li, D.T.; Pan, J.F. Microscale combustion research for application to micro thermophotovoltaic systems. Energy Convers. Manag. 2003, 44, 2625–2634. [Google Scholar] [CrossRef]
- Li, Y.-H.; Hong, J.R. Power generation performance of hydrogen-fueled micro thermophotovoltaic reactor. Int. J. Hydrogen Energy 2018, 43, 1459–1469. [Google Scholar] [CrossRef]
- Yang, W.M.; Chou, S.K.; Shu, C.; Li, Z.W.; Xue, H. A prototype microthermophotovoltaic power generator. Appl. Phys. Lett. 2004, 84, 3864–3866. [Google Scholar] [CrossRef]
- Yang, W.; Chou, S.; Shu, C.; Xue, H.; Li, Z. Effect of wall thickness of micro-combustor on the performance of micro-thermophotovoltaic power generators. Sens. Actuators A Phys. 2005, 119, 441–445. [Google Scholar]
- Yan, J.; Liao, X.; Yan, D.; Chen, Y. Review of Micro Thermoelectric Generator. J. Microelectromech. Syst. 2018, 27, 1–18. [Google Scholar] [CrossRef]
- Yadav, S.; Sharma, P.; Yamasani, P.; Minaev, S.; Kumar, S. A prototype micro-thermoelectric power generator for micro-electromechanical systems. Appl. Phys. Lett. 2014, 104, 123903. [Google Scholar] [CrossRef]
- Aravind, B.; Raghuram, G.K.S.; Kishore, V.R.; Kumar, S. Compact design of planar stepped micro combustor for portable thermoelectric power generation. Energy Convers. Manag. 2018, 156, 224–234. [Google Scholar] [CrossRef]
- Hosseini, S.; Owens, E.; Krohn, J.; Leylek, J. Experimental investigation into the effects of thermal recuperation on the combustion characteristics of a non-premixed meso-scale vortex combustor. Energies 2018, 11, 3390. [Google Scholar] [CrossRef]
- Wan, J.; Fan, A.; Maruta, K.; Yao, H.; Liu, W. Experimental and numerical investigation on combustion characteristics of premixed hydrogen/air flame in a micro-combustor with a bluff body. Int. J. Hydrogen Energy 2012, 37, 19190–19197. [Google Scholar] [CrossRef]
- Wan, J.; Fan, A.; Yao, H.; Liu, W. Experimental investigation and numerical analysis on the blow-off limits of premixed CH4/air flames in a mesoscale bluff-body combustor. Energy 2016, 113, 193–203. [Google Scholar] [CrossRef]
- Bagheri, G.; Hosseini, S.E.; Wahid, M.A. Effects of bluff body shape on the flame stability in premixed micro-combustion of hydrogen–air mixture. Appl. Therm. Eng. 2014, 67, 266–272. [Google Scholar] [CrossRef]
- Hosseini, S.E.; Wahid, M.A. Investigation of bluff-body micro-flameless combustion. Energy Convers. Manag. 2014, 88, 120–128. [Google Scholar] [CrossRef]
- Lloyd, S.A.; Weinberg, F.J. A burner for mixtures of very low heat content. Nature 1974, 251, 47–49. [Google Scholar] [CrossRef]
- Kim, N.; Kato, S.; Kataoka, T.; Yokomori, T.; Maruyama, S.; Fujimori, T.; Maruta, K. Flame stabilization and emission of small Swiss-roll combustors as heaters. Combust. Flame 2005, 141, 229–240. [Google Scholar] [CrossRef]
- Wang, W.; Zuo, Z.; Liu, J. Numerical study of the premixed propane/air flame characteristics in a partially filled micro porous combustor. Energy 2019, 167, 902–911. [Google Scholar] [CrossRef]
- Li, J.; Li, Q.; Wang, Y.; Guo, Z.; Liu, X. Fundamental flame characteristics of premixed H2–air combustion in a planar porous micro-combustor. Chem. Eng. J. 2016, 283, 1187–1196. [Google Scholar] [CrossRef]
- Marbach, T.L.; Sadasivuni, V.; Agrawal, A.K. Investigation of a Miniature Combustor Using Porous Media Surface Stabilized Flame. Combust. Sci. Technol. 2007, 179, 1901–1922. [Google Scholar] [CrossRef]
- Mikami, M.; Maeda, Y.; Matsui, K.; Seo, T.; Yuliati, L. Combustion of gaseous and liquid fuels in meso-scale tubes with wire mesh. Proc. Combust. Inst. 2013, 34, 3387–3394. [Google Scholar] [CrossRef]
- Yang, W.M.; Chua, K.J.; Pan, J.F.; Jiang, D.Y.; An, H. Development of micro-thermophotovoltaic power generator with heat recuperation. Energy Convers. Manag. 2014, 78, 81–87. [Google Scholar] [CrossRef]
- Tang, A.; Cai, T.; Deng, J.; Xu, Y.; Pan, J. Experimental investigation on combustion characteristics of premixed propane/air in a micro-planar heat recirculation combustor. Energy Convers. Manag. 2017, 152, 65–71. [Google Scholar] [CrossRef]
- Alipoor, A.; Saidi, M.H. Numerical study of hydrogen-air combustion characteristics in a novel micro-thermophotovoltaic power generator. Appl. Energy 2017, 199, 382–399. [Google Scholar] [CrossRef]
- Chou, S.K.; Yang, W.M.; Li, J.; Li, Z.W. Porous media combustion for micro thermophotovoltaic system applications. Appl. Energy 2010, 87, 2862–2867. [Google Scholar] [CrossRef]
- Akhtar, S.; Khan, M.N.; Kurnia, J.C.; Shamim, T. Investigation of energy conversion and flame stability in a curved micro-combustor for thermo-photovoltaic (TPV) applications. Appl. Energy 2017, 192, 134–145. [Google Scholar] [CrossRef]
- Yang, X.; He, Z.; Dong, S.; Tan, H. Enhancement of thermal performance by converging-diverging channel in a micro tube combustor fueled by premixed hydrogen/air. Int. J. Hydrogen Energy 2019, 44, 1213–1226. [Google Scholar] [CrossRef]
- Tang, A.; Pan, J.; Yang, W.; Xu, Y.; Hou, Z. Numerical study of premixed hydrogen/air combustion in a micro planar combustor with parallel separating plates. Int. J. Hydrogen Energy 2015, 40, 2396–2403. [Google Scholar] [CrossRef]
- Amani, E.; Alizadeh, P.; Moghadam, R.S. Micro-combustor performance enhancement by hydrogen addition in a combined baffle-bluff configuration. Int. J. Hydrogen Energy 2018, 43, 8127–8138. [Google Scholar] [CrossRef]
- Tang, A.; Xu, Y.; Pan, J.; Yang, W.; Jiang, D.; Lu, Q. Combustion characteristics and performance evaluation of premixed methane/air with hydrogen addition in a micro-planar combustor. Chem. Eng. Sci. 2015, 131, 235–242. [Google Scholar] [CrossRef]
- Yang, W.M.; Chou, S.K.; Shu, C.; Li, Z.W.; Xue, H. Research on micro-thermophotovoltaic power generators. Sol. Energy Mater. Sol. Cells 2003, 80, 95–104. [Google Scholar] [CrossRef]
- Lee, S.I.; Um, D.H.; Kwon, O.C. Performance of a micro-thermophotovoltaic power system using an ammonia-hydrogen blend-fueled micro-emitter. Int. J. Hydrogen Energy 2013, 38, 9330–9342. [Google Scholar] [CrossRef]
- Nadimi, E.; Jafarmadar, S. The numerical study of the energy and exergy efficiencies of the micro-combustor by the internal micro-fin for thermophotovoltaic systems. J. Clean. Prod. 2019, 235, 394–403. [Google Scholar] [CrossRef]
- Gentillon, P.; Singh, S.; Lakshman, S.; Zhang, Z.; Paduthol, A.; Ekins-Daukes, N.J.; Chan, Q.N.; Taylor, R.A. A comprehensive experimental characterisation of a novel porous media combustion-based thermophotovoltaic system with controlled emission. Appl. Energy 2019, 254, 113721. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, L.; He, Z.; Dong, S.; Tan, H. Comparative study of combustion and thermal performance in a swirling micro combustor under premixed and non-premixed modes. Appl. Therm. Eng. 2019, 160, 114110. [Google Scholar] [CrossRef]
- Yang, X.; He, Z.; Niu, Q.; Dong, S.; Tan, H. Numerical analysis of turbulence radiation interaction effect on radiative heat transfer in a swirling oxyfuel furnace. Int. J. Heat Mass Transf. 2019, 141, 1227–1237. [Google Scholar] [CrossRef]
- Ali Beskok, G.E.K. A model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophys. Eng. 1999, 3, 43–77. [Google Scholar] [CrossRef]
- Norton, D.G.; Vlachos, D.G. A CFD study of propane/air microflame stability. Combust. Flame 2004, 138, 97–107. [Google Scholar] [CrossRef]
- Norton, D.G.; Vlachos, D.G. Combustion characteristics and flame stability at the microscale: A CFD study of premixed methane/air mixtures. Chem. Eng. Sci. 2003, 58, 4871–4882. [Google Scholar] [CrossRef]
- Yan, Y.; Xu, F.; Xu, Q.; Zhang, L.; Yang, Z.; Ran, J. Influence of controllable slit width and angle of controllable flow on hydrogen/air premixed combustion characteristics in micro combustor with both sides–slitted bluff body. Int. J. Hydrogen Energy 2019, 44, 20482–20492. [Google Scholar] [CrossRef]
- Li, J.; Chou, S.K.; Li, Z.W.; Yang, W.M. A comparative study of H2-air premixed flame in micro combustors with different physical and boundary conditions. Combust. Theory Model. 2008, 12, 325–347. [Google Scholar] [CrossRef]
- Wan, J.; Fan, A.; Yao, H.; Liu, W. Flame-anchoring mechanisms of a micro cavity-combustor for premixed H2/air flame. Chem. Eng. J. 2015, 275, 17–26. [Google Scholar] [CrossRef]
- Wan, J.; Fan, A.; Yao, H.; Liu, W. Effect of thermal conductivity of solid wall on combustion efficiency of a micro-combustor with cavities. Energy Convers. Manag. 2015, 96, 605–612. [Google Scholar] [CrossRef]
- Barlow, R.S.; Dunn, M.J.; Magnotti, G. Preferential transport effects in premixed bluff-body stabilized CH4/H2 flames. Combust. Flame 2015, 162, 727–735. [Google Scholar] [CrossRef]
- Barlow, R.S.; Dunn, M.J.; Sweeney, M.S.; Hochgreb, S. Effects of preferential transport in turbulent bluff-body-stabilized lean premixed CH4/air flames. Combust. Flame 2012, 159, 2563–2575. [Google Scholar] [CrossRef]
- Katta, V.; Roquemore, W.M. C/H atom ratio in recirculation-zone-supported premixed and nonpremixed flames. Proc. Combust. Inst. 2013, 34, 1101–1108. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; He, Z.; Zhao, L.; Dong, S.; Tan, H. Effect of Channel Diameter on the Combustion and Thermal Behavior of a Hydrogen/Air Premixed Flame in a Swirl Micro-Combustor. Energies 2019, 12, 3821. https://doi.org/10.3390/en12203821
Yang X, He Z, Zhao L, Dong S, Tan H. Effect of Channel Diameter on the Combustion and Thermal Behavior of a Hydrogen/Air Premixed Flame in a Swirl Micro-Combustor. Energies. 2019; 12(20):3821. https://doi.org/10.3390/en12203821
Chicago/Turabian StyleYang, Xiao, Zhihong He, Lei Zhao, Shikui Dong, and Heping Tan. 2019. "Effect of Channel Diameter on the Combustion and Thermal Behavior of a Hydrogen/Air Premixed Flame in a Swirl Micro-Combustor" Energies 12, no. 20: 3821. https://doi.org/10.3390/en12203821
APA StyleYang, X., He, Z., Zhao, L., Dong, S., & Tan, H. (2019). Effect of Channel Diameter on the Combustion and Thermal Behavior of a Hydrogen/Air Premixed Flame in a Swirl Micro-Combustor. Energies, 12(20), 3821. https://doi.org/10.3390/en12203821







