A Weekend Load Forecasting Model Based on Semi-Parametric Regression Analysis Considering Weather and Load Interaction
Abstract
:1. Introduction
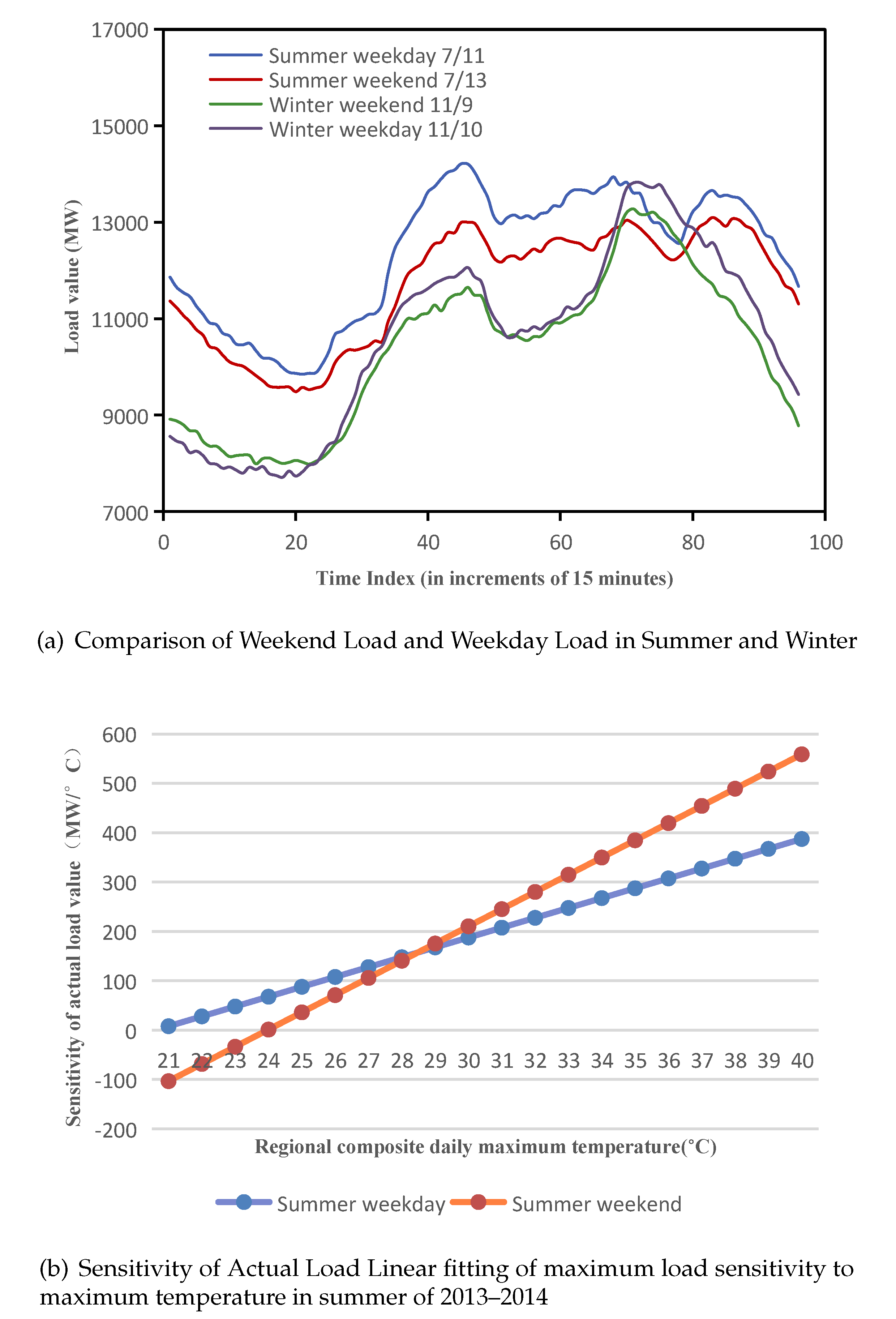
2. The Interaction of Meteorology and Load
3. The Semi-Parametric Regression Theory
3.1. Semi-Parametric Regression Model
- xβ reflects the parameters part of the known part of the laws, that is, the meteorological factors that are clearly related to the load to be predicted;
- g(z) + reflects a non-parametric part and has no definite function relationship with the load to be solved, i.e., the meteorological factors that is not clearly related to the load to be predicted.
3.2. Parameters Estimation Calculation
- Model standardization: Set = E(g(z)), E(g(z)) < ∞, and so:
- Get the fitting weight value: According to the non-parametric part (z, y) of the historical sample set, the regression model is established:After the b is obtained by the least-squares method, the point-by-point residuals and residual squares can be obtained:The larger residuals and its corresponding square value h, the worse the regression fitting. The fitting weight is found as follows:where n is the number of samples.
- Two-stage estimation of regression coefficients: and , which are the initial estimates of and , can be obtained by least-squares regression analysis of the normalized regression model (9) based on the parameter section of the historical sample set (x, y). Then the equation can be converted to:By the Equation (15), and , which are the final estimates of and , can be obtained by the least square method again. Then the Semi-parametric regression model is shown below:
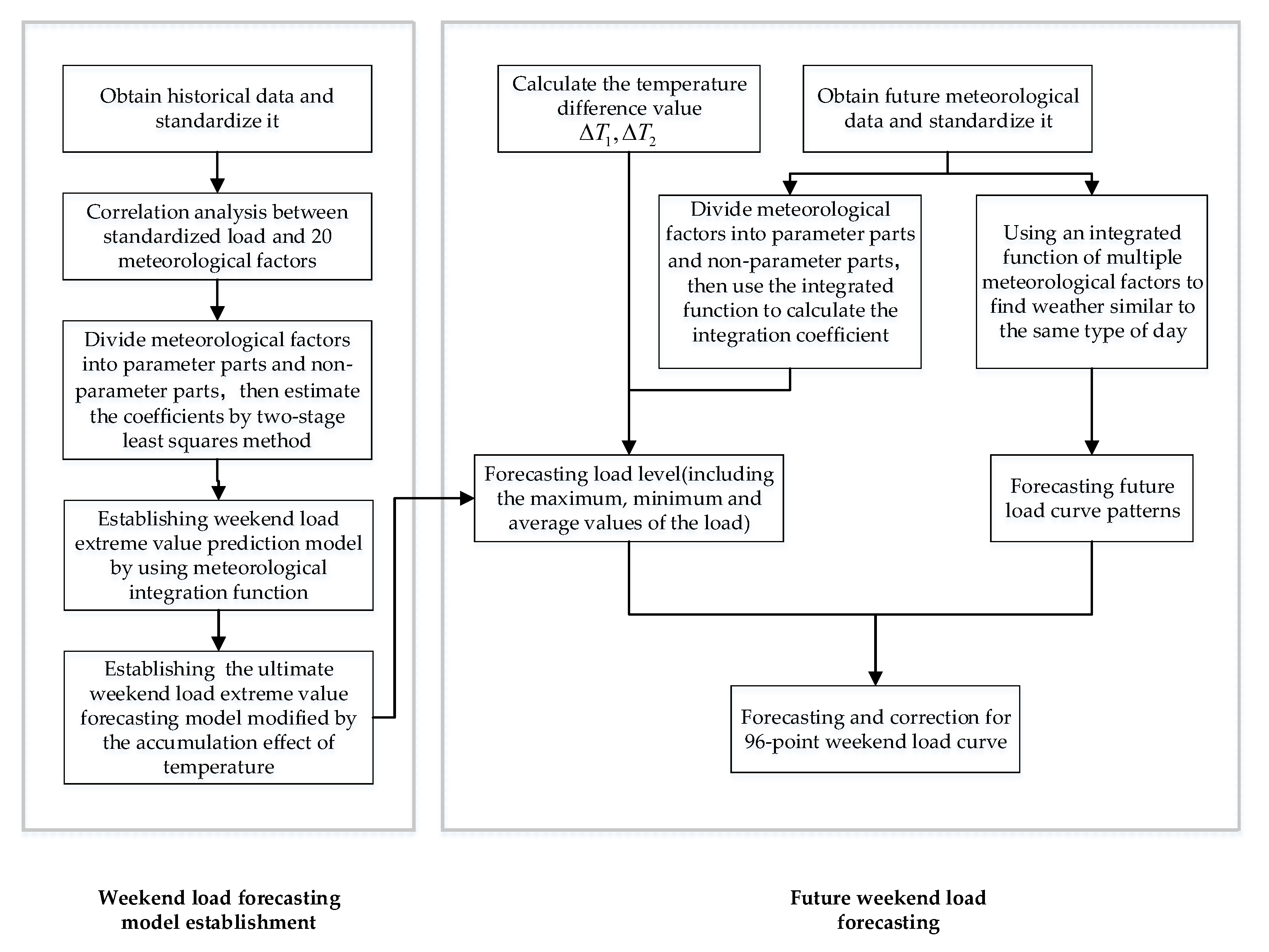
4. Load Forecasting of the Weekend Based on Semi-Parametric Regression
- According to the correlation analysis result of each meteorological factor and the load standard value, the standard load of the Semi-parameter can be selected among the independent parameters of the parametric and nonparametric part in the model.The independent variables of the parameter part can be expressed as follows:And the independent variables of the nonparametric part can be expressed as follows:where n and q are the number of the parametric parts and the non-parametric parts of the meteorological factors, respectively.
- Standardizing the sample sets of meteorological and load. And integrating the identified meteorological factors that characteristics with parametric and nonparametric by Equation (17).
- Based on the independent variable of the parametric part, calculating regression coefficient of standardized regression model by least squares, then and which are the initial estimates of parameters in the Semi-parametric regression model can be obtained.
- Calculate the g of the non-parametric part at this time by Equation (14).
5. Temperature Accumulation Effect Correction
6. Weekend Load Forecasting Model Construction
6.1. Forecasting of Weekend Load Level
6.2. Forecasting of Weekend Load Curve Model
6.3. Forecasting and Correction for 96-Point Weekend Load Curve
6.4. The Judgment Basis for Load Forecasting Results
7. Specific Example and Results Analysis
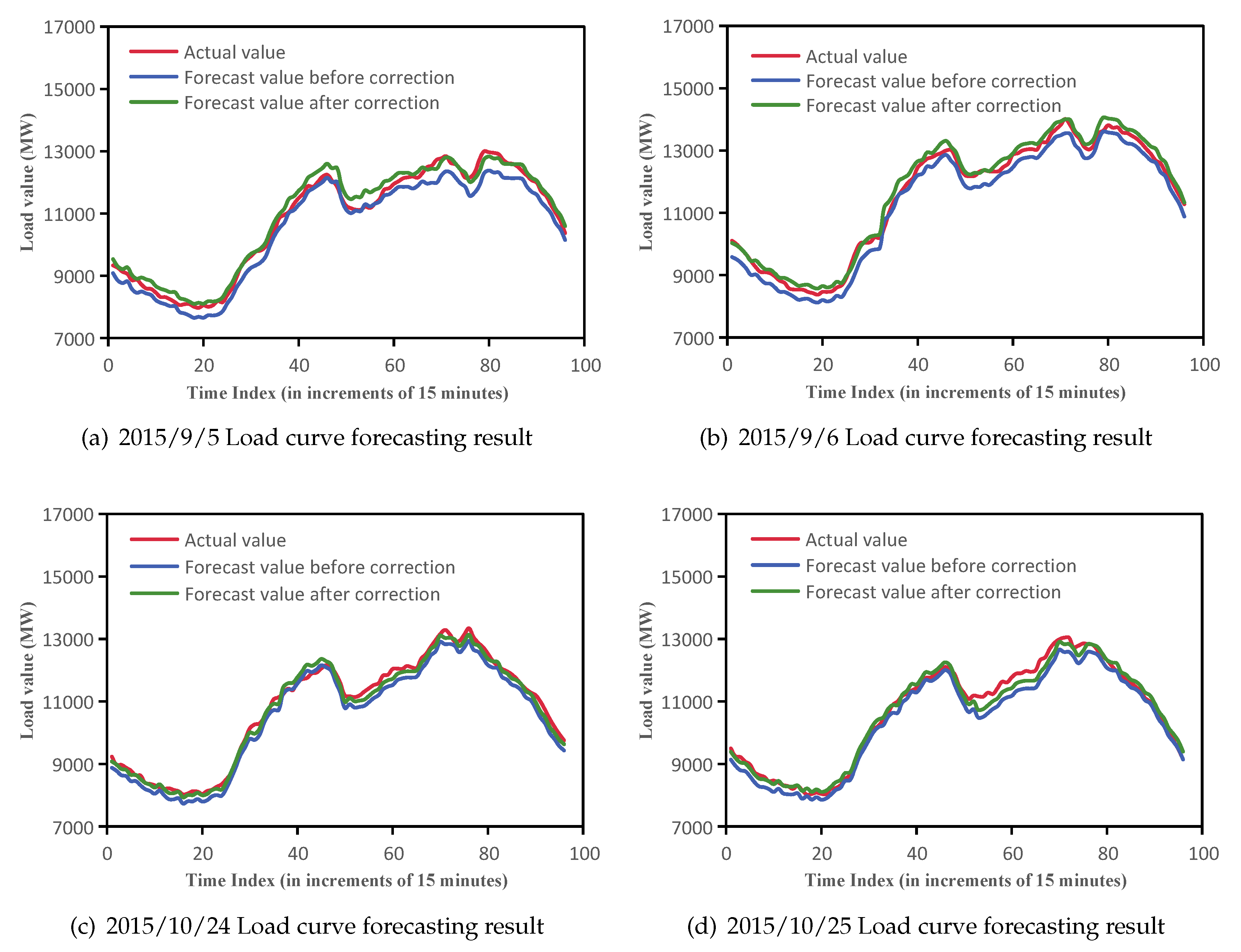
7.1. Sample Load Forecasting Based on Semi-Parametric Method
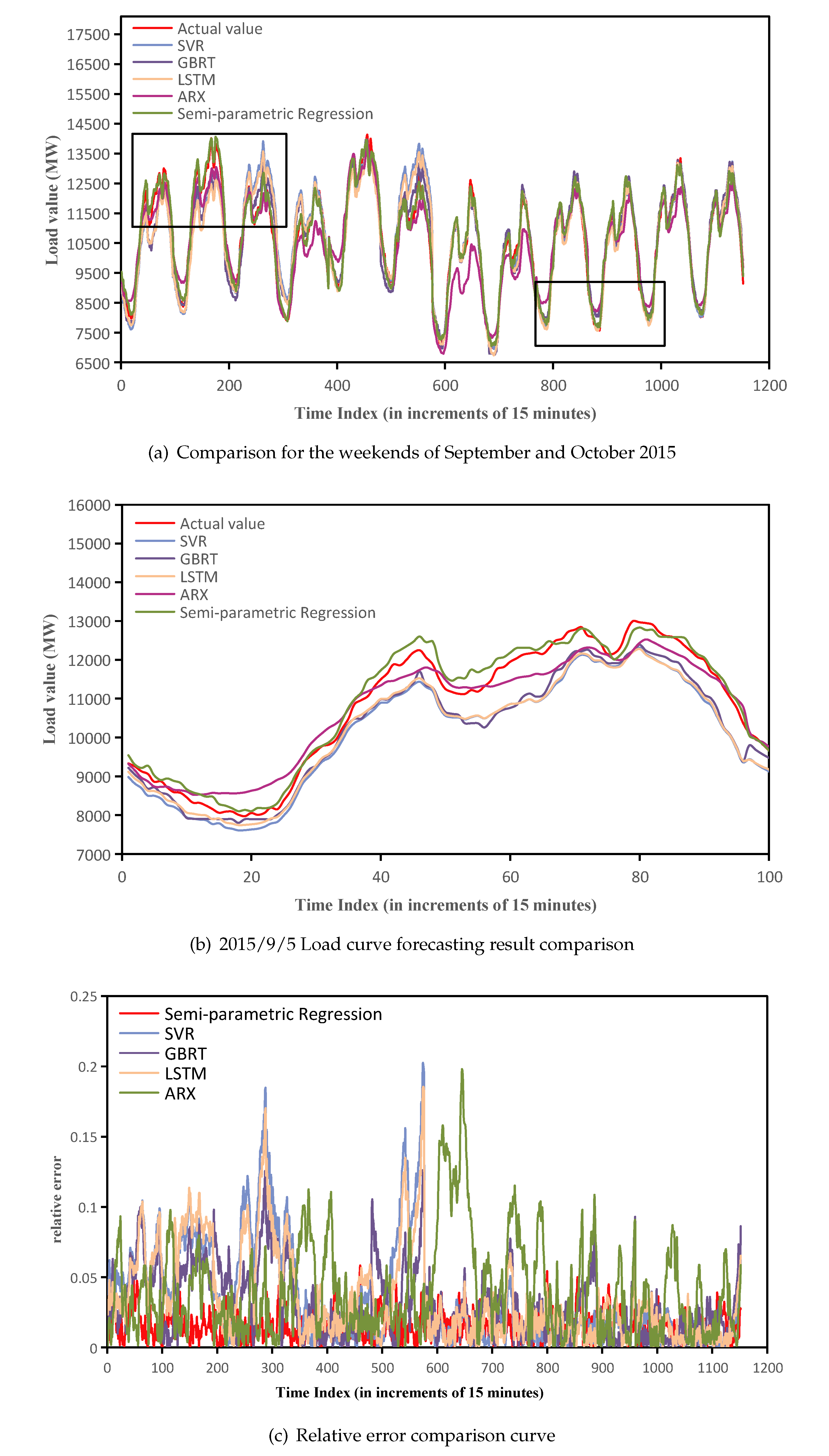
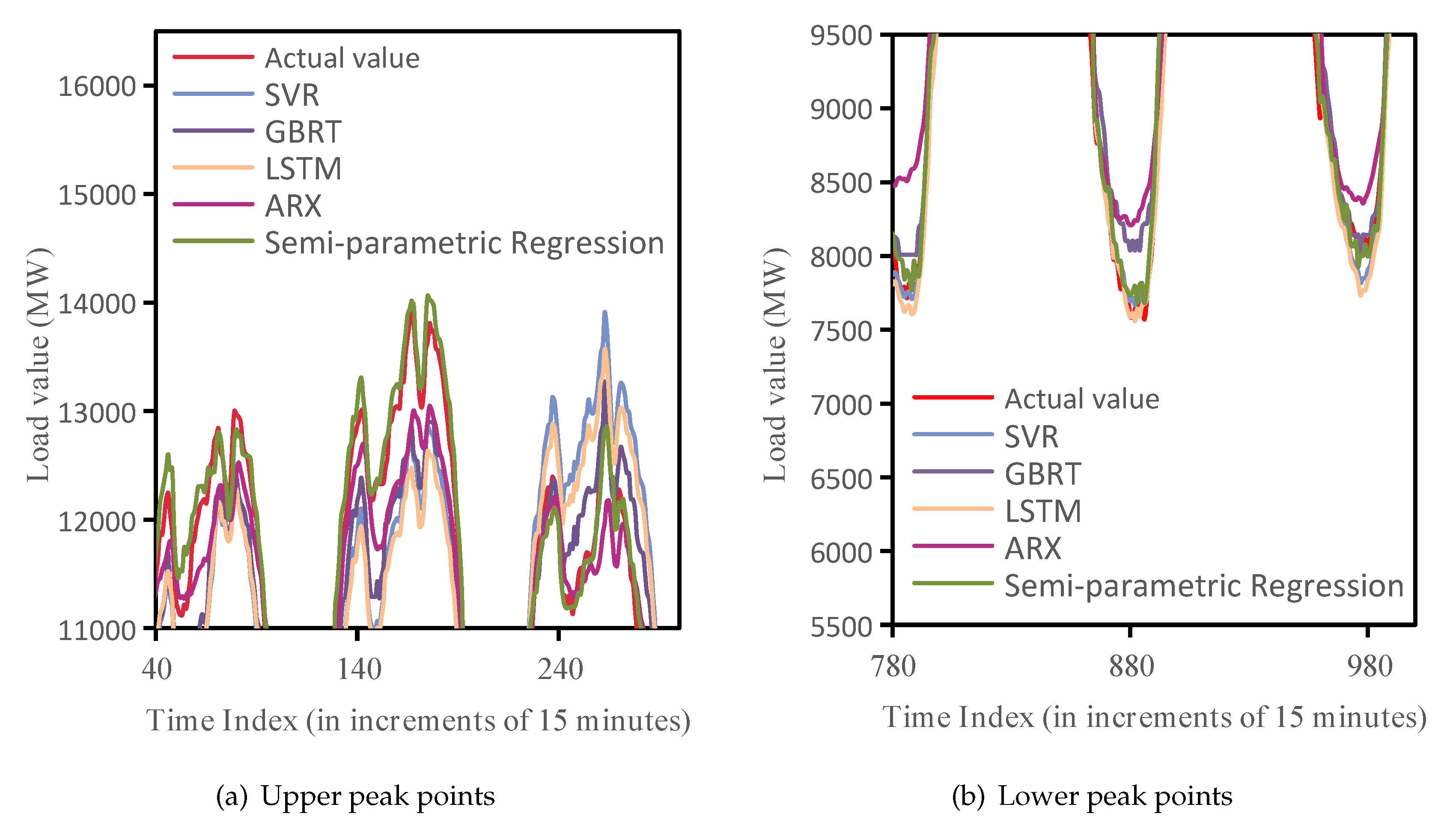
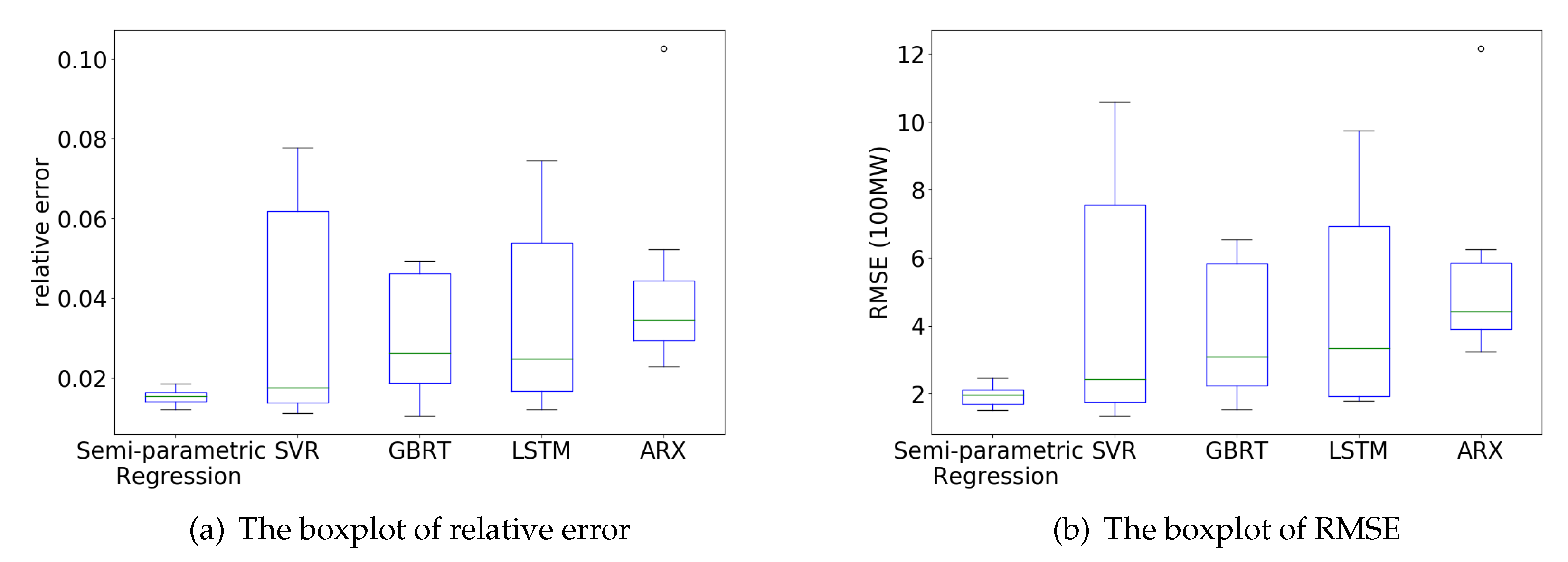
7.2. Comparison and Analysis of Model Prediction Results
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gao, C.; Li, Q.; Su, W.; Li, Y. Temperature correction model research considering temperature cumula-tive effect in short-term load forecasting. Trans. China Electromech. Soc. 2015, 30, 242–248. [Google Scholar]
- Li, C.; Yang, P.; Liu, W.; Li, D.; Wang, Y. An analysis of ac-accumulation effect of temperature in short-term load fore-casting. Autom. Electr. Power Syst. 2009, 33, 96–99. [Google Scholar]
- Buitrago, J.; Asfour, S. Short-Term Forecasting of Electric Loads Using Nonlinear Autoregressive Artificial Neural Networks with Exogenous Vector Inputs. Energies 2017, 10, 40. [Google Scholar] [CrossRef]
- Bennett, C.; Stewart, R.A.; Lu, J.W. Autoregressive with Exogenous Variables and Neural Network Short-Term Load Forecast Models for Residential Low Voltage Distribution Networks. Energies 2014, 7, 2938–2960. [Google Scholar] [CrossRef]
- Tian, C.S.; Hao, Y. A Novel Nonlinear Combined Forecasting System for Short-Term Load Forecasting. Energies 2018, 11, 712. [Google Scholar] [CrossRef]
- Cai, G.W.; Wang, W.J.; Lu, J.H. A Novel Hybrid Short Term Load Forecasting Model Considering the Error of Numerical Weather Prediction. Energies 2016, 9, 994. [Google Scholar] [CrossRef]
- Niu, D.X.; Dai, S.Y. A Short-Term Load Forecasting Model with a Modified Particle Swarm Optimization Algorithm and Least Squares Support Vector Machine Based on the Denoising Method of Empirical Mode Decomposition and Grey Relational Analysis. Energies 2017, 10, 408. [Google Scholar] [CrossRef]
- Hong, W.C.; Fan, G.F. Hybrid Empirical Mode Decomposition with Support Vector Regression Model for Short Term Load Forecasting. Energies 2019, 12, 1093. [Google Scholar] [CrossRef]
- Al-Musaylh, M.S.; Deo, R.C.; Li, Y.; Adamowski, J.F. Two-phase particle swarm optimized-support vector regression hybrid model integrated with improved empirical mode decomposition with adaptive noise for multiple-horizon electricity demand forecasting. Appl. Energy 2018, 217, 422–439. [Google Scholar] [CrossRef]
- Liu, T.X.; Jin, Y.; Gao, Y.Y. A New Hybrid Approach for Short-Term Electric Load Forecasting Applying Support Vector Machine with Ensemble Empirical Mode Decomposition and Whale Optimization. Energies 2019, 12, 1520. [Google Scholar] [CrossRef]
- Wu, X.; He, J.; Zhang, P.; Hu, J. Power system short-term load forecasting based on improved random forest with grey relation projection. Autom. Electr. Power Syst. 2015, 39, 50–55. [Google Scholar]
- Wu, X.; He, J.; Yip, T.; Jian, L.; Ning, L. A two-stage random forest method for short-term load forecasting. In Proceedings of the Power & Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016. [Google Scholar]
- Moon, J.; Kim, Y.; Son, M.; Hwang, E. Hybrid Short-Term Load Forecasting Scheme Using Random Forest and Multilayer Perceptron. Energies 2018, 11, 3283. [Google Scholar] [CrossRef]
- Chen, M.; Yuan, J.; Liu, D.; Tao, L. An adaption scheduling based on dynamic weighted random forests for load demand forecasting. J. Supercomput. 2017, 1–19. [Google Scholar] [CrossRef]
- Kong, W.; Zhao, Y.D.; Hill, D.J.; Luo, F.; Yan, X. Short-Term Residential Load Forecasting based on Resident Behaviour Learning. IEEE Trans. Power Syst. 2017, 33, 1087–1088. [Google Scholar] [CrossRef]
- Wang, S.X.; Wang, X.; Wang, S.M.; Wang, D. Bi-directional long short-term memory method based on attention mechanism and rolling update for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2019, 109, 470–479. [Google Scholar] [CrossRef]
- Kuo, P.H.; Huang, C.J. A High Precision Artificial Neural Networks Model for Short-Term Energy Load Forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef]
- Feng, Y.; Xu, X.F.; Meng, Y. Short-Term Load Forecasting with Tensor Partial Least Squares-Neural Network. Energies 2019, 12, 990. [Google Scholar] [CrossRef]
- Fallah, S.N.; Ganjkhani, M.; Shamshirband, S.; Chau, K.W. Computational Intelligence on Short-Term Load Forecasting: A Methodological Overview. Energies 2019, 12, 393. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Single and Multi-Sequence Deep Learning Models for Short and Medium Term Electric Load Forecasting. Energies 2019, 12, 149. [Google Scholar] [CrossRef]
- Jiao, R.H.; Su, C.J.; Lin, B.Y.; Mo, R.F. Short Term-Load Forecasting Based on Meteorological Correcting Grey Model. In Unifying Electrical Engineering and Electronics Engineering; Springer: New York, NY, USA, 2014. [Google Scholar]
- Li, G.D.; Wang, C.H.; Masuda, S.; Nagai, M. A research on short term load forecasting problem applying improved grey dynamic model. Int. J. Electr. Power Energy Syst. 2011, 33, 809–816. [Google Scholar] [CrossRef]
- Wang, H.; Yang, K.; Xue, L.Y.; Shuang, L. The Study of Long-term Electricity Load Forecasting Based on Improved Grey Prediction. In Proceedings of the International Conference on Machine Learning & Cybernetics, Tianjin, China, 14–17 July 2013. [Google Scholar]
- Zhang, Y. The Application of Semi-parametric Re-gression Model in Long-middle Term Load Forecast-ing. In Power System and Its Automation School of Electrical Engineering; Zhengzhou University: Zhengzhou, China, 2010. [Google Scholar]
- Goude, Y.; Nedellec, R.; Kong, N. Local Short and Middle Term Electricity Load Forecasting With Semi-Parametric Additive Models. IEEE Trans. Smart Grid 2014, 5, 440–446. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Liu, S. Short-term Load Forecasting Considering the Acaccumulation effects of Tem-peratures. IEEE Trans. Smart Grid 2013, 40, 49–54. [Google Scholar]
- Gregorczuk, M.; Cena, K. Distribution of Effective Temperature over the surface of the Earth. Int. J. Biometeorol. 1967, 11, 145–149. [Google Scholar] [CrossRef]
- Du, Y.; Lin, L.; Mou, D.; He, X. Analysis of the Impact of Comprehensive Meteorological Index on Electric Power Load. J. Chongqing Univ. 2006, 29, 56–60. [Google Scholar]
- Tromp, S.W. Medical Biometeorology; Elsevier: Amsterdam, The Netherlands, 1963. [Google Scholar]
- Zar, J.H. Significance Testing of the Spearman Rank Correlation Coefficient. Publ. Am. Stat. Assoc. 1972, 67, 578–580. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1987, 100, 441–471. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, X.; Zheng, H.; Yao, H.; Liu, J.; Zhang, C.; Peng, H.; Jiao, J. A Fault Diagnosis Model of Power Transformers Based on Dissolved Gas Analysis Features Selection and Improved Krill Herd Algorithm Optimized Support Vector Machine. IEEE Access 2019, 7, 102803–102811. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, Z.; Hong, W.C. A Hybrid Seasonal Mechanism with a Chaotic Cuckoo Search Algorithm with a Support Vector Regression Model for Electric Load Forecasting. Energies 2018, 11, 1009. [Google Scholar] [CrossRef]
- Ma, S.; Chen, X.; Liao, Y.; Gang, W.; Ding, X.; Kai, C. The variable weight combination load forecasting based on grey model and semi-parametric Regression Model. In Proceedings of the Tencon IEEE Region 10 Conference, Xi’an, China, 22–25 October 2013. [Google Scholar]
- Wang, X.; Chen, Z.; Yang, S. Forecasting modeling and simulation analysis of a power system in China, based on a class of Semi-parametric regression ap-proach. S. Afr. J. Ind. Eng. 2012, 23, 154–168. [Google Scholar]
- Ferraty, F.; Goia, A.; Salinelli, E.; Vieu, P. Peak-Load Forecasting Using a Functional Semi-Parametric Approach. In Topics in Nonparametric Statistics; Springer: New York, NY, USA, 2014. [Google Scholar]
- Robinson, P.M. Root-N-Consistent Semiparametric Regression. Econometrica 1988, 56, 931–954. [Google Scholar] [CrossRef]
- Li, Q. Nonparametric Econometrics: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Li, J.; Qi, X. Principles of Statistics, 3rd ed.; Shanghai Fudan University Press: Shanghai, China, 2005; pp. 340–341. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Zhang, Y. Short-Term Residential Load Forecasting based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Fattaheian-Dehkordi, S.; Fereidunian, A.; Gholami-Dehkordi, H.; Lesani, H. Hour-ahead demand forecasting in smart grid using support vector regression (SVR). Int. Trans. Electr. Energy Syst. 2015, 24, 1650–1663. [Google Scholar] [CrossRef]
- Papadopoulos, S.; Karakatsanis, I. Short-term electricity load forecasting using time series and ensemble learning methods. In Proceedings of the 2015 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 20–21 February 2015. [Google Scholar]
- Guo, Y.; Nazarian, E.; Ko, J.; Rajurkar, K. Hourly cooling load forecasting using time-indexed ARX models with two-stage weighted least squares regression. Energy Convers. Manag. 2014, 80, 46–53. [Google Scholar] [CrossRef]
| Meteorological Factors | Summer Correlation | Winter Correlation |
|---|---|---|
| Maximum temperature | 0.7554 ** | −0.6415 ** |
| Mean temperature | 0.7637 ** | −0.6372 ** |
| Minimum temperature | 0.6651 ** | −0.5678 ** |
| Maximum humidity | −0.3972 ** | −0.1061 |
| Mean humidity | −0.5036 ** | 0.0078 |
| Minimum humidity | −0.5382 ** | 0.0878 |
| Average wind speed | −0.0450 | 0.1614 ** |
| Rainfall | −0.3607 ** | 0.1039 ** |
| Maximum temperature humidity index | 0.7159 ** | −0.6375 ** |
| Mean temperature humidity index | 0.6754 ** | −0.6342 ** |
| Minimum temperature humidity index | 0.3520 ** | −0.5797 ** |
| Maximum effective temperature | 0.7373 ** | −0.6236 ** |
| Mean effective temperature | 0.7260 ** | −0.6226 ** |
| Minimum effective temperature | 0.5501 ** | −0.5683 ** |
| Maximum comfort index | 0.6744 ** | −0.6173 ** |
| Mean comfort index | 0.6253 ** | −0.6114 ** |
| Minimum comfort index | 0.3438 ** | −0.5618 ** |
| Maximum chillness humidity index | −0.7569 ** | 0.6321 ** |
| Mean chillness humidity index | −0.7642 ** | 0.6257 ** |
| Minimum chillness humidity index | −0.6744 ** | 0.5662 ** |
| Month | January | February | March | April |
| E | 0.0274 | 0.0293 | 0.0268 | 0.0214 |
| Month | May | June | July | August |
| E | 0.0259 | 0.0287 | 0.0293 | 0.0264 |
| Month | September | October | November | December |
| E | 0.0153 | 0.0229 | 0.0296 | 0.0197 |
| Date | Actual Value | Forecasting Value | A | A | A | A | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Max | Mean | Min | Max | Mean | Min | |||||
| 9/5 | 13,002 | 10,797 | 7973 | 12,832 | 10,727 | 8202 | 96.26% | 96.99% | 96.81% | 97.85% |
| 9/6 | 14,014 | 11,556 | 8371 | 14,463 | 11,605 | 8569 | 95.95% | 96.98% | 97.11% | 98.20% |
| 9/12 | 12,875 | 10,986 | 8959 | 12,557 | 10,713 | 8692 | 95.23% | 96.71% | 96.50% | 97.81% |
| 9/13 | 12,373 | 10,227 | 7918 | 12,351 | 10,592 | 8179 | 95.38% | 95.99% | 97.10% | 98.32% |
| 9/19 | 14,133 | 11,885 | 9018 | 14,190 | 12,108 | 9281 | 95.61% | 96.92% | 97.01% | 98.04% |
| 9/20 | 12,774 | 10,997 | 9204 | 12,558 | 10,704 | 8978 | 96.81% | 96.58% | 96.64% | 98.23% |
| 10/10 | 12,614 | 9755 | 7152 | 12,401 | 9706 | 7324 | 94.32% | 95.91% | 97.11% | 98.11% |
| 10/11 | 12,019 | 9535 | 6977 | 12,240 | 9826 | 7247 | 96.30% | 96.88% | 97.39% | 98.37% |
| 10/17 | 12,789 | 10,354 | 7716 | 12,875 | 10,722 | 7969 | 95.51% | 96.84% | 97.64% | 97.87% |
| 10/18 | 12,480 | 10,175 | 7571 | 12,740 | 10,478 | 7782 | 96.33% | 97.04% | 97.26% | 98.03% |
| 10/24 | 13,344 | 10,768 | 8025 | 12,877 | 10,207 | 7798 | 97.06% | 97.31% | 97.12% | 98.57% |
| 10/25 | 13,046 | 10,661 | 8016 | 12,840 | 10,665 | 8105 | 96.53% | 96.98% | 97.05% | 98.36% |
| Date | SVR | GBRT | LSTM | ARX | Semi-Parametric Regression |
|---|---|---|---|---|---|
| 5 September 2015 | 6.01% | 4.92% | 5.31% | 3.22% | 1.84% |
| 6 September 2015 | 6.88% | 4.58% | 7.44% | 4.44% | 1.54% |
| 12 September 2015 | 6.70% | 4.74% | 5.59% | 2.39% | 1.21% |
| 13 September 2015 | 5.93% | 4.13% | 4.88% | 4.43% | 1.40% |
| 19 September 2015 | 1.91% | 1.39% | 2.92% | 3.52% | 1.53% |
| 20 September 2015 | 7.78% | 4.87% | 6.37% | 2.79% | 1.62% |
| 10 October 2015 | 1.57% | 1.88% | 1.60% | 10.26% | 1.59% |
| 11 October 2015 | 1.57% | 2.71% | 2.01% | 5.23% | 1.41% |
| 17 October 2015 | 1.11% | 1.82% | 1.68% | 3.71% | 1.76% |
| 18 October 2015 | 1.37% | 2.54% | 1.73% | 3.35% | 1.68% |
| 24 October 2015 | 1.36% | 1.04% | 1.58% | 2.98% | 1.22% |
| 25 October 2015 | 1.18% | 2.02% | 1.20% | 2.28% | 1.40% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Lu, M.; Zhang, Y.; Huang, J. A Weekend Load Forecasting Model Based on Semi-Parametric Regression Analysis Considering Weather and Load Interaction. Energies 2019, 12, 3820. https://doi.org/10.3390/en12203820
Li B, Lu M, Zhang Y, Huang J. A Weekend Load Forecasting Model Based on Semi-Parametric Regression Analysis Considering Weather and Load Interaction. Energies. 2019; 12(20):3820. https://doi.org/10.3390/en12203820
Chicago/Turabian StyleLi, Bin, Mingzhen Lu, Yiyi Zhang, and Jia Huang. 2019. "A Weekend Load Forecasting Model Based on Semi-Parametric Regression Analysis Considering Weather and Load Interaction" Energies 12, no. 20: 3820. https://doi.org/10.3390/en12203820
APA StyleLi, B., Lu, M., Zhang, Y., & Huang, J. (2019). A Weekend Load Forecasting Model Based on Semi-Parametric Regression Analysis Considering Weather and Load Interaction. Energies, 12(20), 3820. https://doi.org/10.3390/en12203820






