A Power Control Mean Field Game Framework for Battery Lifetime Enhancement of Coexisting Machine-Type Communications

Abstract

Machine-type communications (MTC) enable the connectivity and control of a vast category of devices without human intervention. This study considers a hybrid coexisting wireless cellular network for traditional and MTC devices along with the need for an energy efficient power allocation mechanism for MTC devices. A model is presented for the interference and battery lifetime of MTC devices and a battery lifetime maximization problem is formulated. Conventional game designs are unable to address the demands of a densified user environment because of the dimensional difficulty presented when attempting to achieve a converged solution that would lead to a stable equilibrium. The MTC power control problem is modeled as a differential game and a mean field game (MFG) for massive number of MTC nodes estimates the power allocation policy with system utility defined in terms of the experienced interference and reliability. The formulated power control MFG is solved using a finite difference method and analyzed using extensive simulations. The solution provides an optimal power control strategy for MTC devices, enabling them to prolong their battery lives with the implemented energy efficient power allocation scheme.

1. Introduction

The evolution of next-generation wireless cellular networks has seen a rapid increase in development of novel algorithms and network architectures for evolving applications. This can be attributed to a rapid increase in the difference between service requirements and new service categories as defined by International Telecommunication Union (ITU-R) [1], whereas previous generations focused on spectrally efficient and bandwidth-hungry applications. Fifth-generation (5G) networks are foreseen to experience challenges including increased user capacity and spectrum shortage, energy starvation, and dense deployments as a result of diverse service demands.

The provision of enhanced mobile broadband (eMBB) along with ultra-reliable low latency communication (uRLLC) and massive machine-type communications (mMTC) demands complex network architecture with dynamic service structure for diverse user applications. MTC is defined as a communication design in which user devices produce, exchange, and analyze data without any human devices or intervention. MTC is broadly categorized as either mMTC or uRLLC [2] given the specific quality of service (QoS) constraints. mMTC usually supports a denser user environment characterized by low complexity and power requirements with varying QoS. Examples of the use of such devices include surveillance systems, smart agriculture, smart metering, sensor networks, remote control and diagnostics [3,4]. In contrast, uRLLC devices are highly sensitive to end-to-end latency and require high reliability with comparatively moderate service rates. Autonomous vehicles/drones, remote healthcare, automated cyber-physical systems and traffic management, are some examples of uRLLC applications [4].

The 3GPP and IEEE have defined specific features for MTC such as time-dependent, infrequent transmission and low mobility [3,4,5] to facilitate network design. The resource and traffic requirements of MTC devices are usually distinct from those of human type communication (HTC) devices. The traffic requirements of MTC and HTC devices are distinct and an advanced remodeling of the infrastructure of deployed networks is required to accommodate extensive demands of MTC devices (MTCDs) in terms of low latency and reliability as well as massive connectivity. By 2024, the number of MTCDs is expected to reach 4.1 billion [6], presenting a motivation for research and development of MTC traffic trends in future networks. A distributed resource management approach would suit a dense MTC network to avoid network overload in terms of processing and traffic demands. Key targets for a distributed design include the ability to accommodate the scalability, random deployment of devices, minimal signaling overhead and limited energy supply, inhomogeneity amongst devices and the availability of incomplete information. The need for a coexisting cellular network is becoming a reality with evolved services being offered to cellular subscribers. The primary aim of HTC devices is to improve data throughput with services such as HD video, telepresence and virtual reality. A spectrally efficient service architecture with high energy consumption is required to improve the data rates of user devices [7]. Remote sensing MTC devices need efficient design and power consumption control to enhance their battery life expectancy. The absence of a recharging option for MTCDs necessitates the design of an energy efficient power control scheme for these devices.

Contributions

The notion of the mean field for coexisting MTC and HTC users is explored by considering consumed power and reliability to design multi-dimensional user state dynamics. Mean field existence for an MTC ecosystem is only possible if the user devices satisfy certain conditions. Each device would have to maximize its utility by considering the channel state and available spectrum resources as well as the interference it experiences. Implemented via an MFG approach, a converged solution is established by meeting a mean field equilibrium condition. Hamilton-Jacobi-Bellman (HJB) and Fokker-Planck-Kolmogorov (FPK) equations are formulated for the proposed game theoretic design and solved using a finite difference scheme. The contributions of this paper are described as follows:

• Battery lifetime modeling is performed for battery-limited MTC nodes and the notions of an individual as well as network lifetimes are introduced and proven to equate to energy efficiency and power control in the discussed coexisting network.
• The uplink power control design in a coexisting HTC/MTC network is formulated as a stochastic differential game (SDG) by selecting appropriate state dynamics.
• A mean field game (MFG) for the MTC network is formulated which can accommodate a massive number of devices. State space of remaining battery energy and interference is considered to find an optimal power control policy for MTC transmit power allocations.
• A modified utility function is proposed for the formulated MFG depending on the signal-to-interference-plus-noise-ratio (SINR) thresholding and experienced interference power. A mean field approximation (MFA) technique is utilized to modify the formulated utility function to more appropriately adapt to the converted MFG design.
• The proposed MFG is solved using finite difference scheme with Lax-Freidrichs technique being utilized to solve the coupled FPK and HJB system of equations.
• Equilibrium analysis for the SDG as well as MFG design is performed by considering the formulated cost function.

The remainder of the paper is organized as follows: In Section 2, a detailed literature review has been presented, along with the identification of problem and related solutions with their shortcomings. In Section 3, network and system architecture is described and a problem model is formulated to be solved using game theory in later sections. In Section 4, an SDG is proposed for the presented problem along with possible limitations in the extension of this game for a massive number of user devices. In Section 5, a mean field game formulation is provided to find an optimal power control policy design for transmit power allocation of MTCDs. Section 6 presents the simulation design and results to visualize the proposed solution to the problem being discussed along with an evaluation of different performance parameters.

2. Literature Review

Providing massive access to MTCDs is a challenging task within itself and network congestion is the most likely occurrence when a large number of MTCDs access the base station simultaneously. Existing scheduling designs for MTCDs can be categorized as [8]: (i) channel-based, that schedules devices with the highest SINR to maximize throughput [9,10,11]; (ii) delay-based, that schedules according to delay budget of user devices for resources [10,12]; (iii) fairness-based, that guarantees a fair distribution of resources to devices [13]; and (iv) hybrid design, that considers a combination of the aforementioned and other metrics such as buffer status along with power consumption [9,14].

The need for a scalable connectivity and energy-efficient scheduling design is a key requirement for the efficient cellular operation of MTCDs. MTC metric design has been based on throughput, propagation delay, transmit power, and impact on QoS of HTC devices [8]. Uplink scheduling with hybrid access for MTC along with HTC nodes over cellular networks was proposed [14]. A rather simplistic energy consumption model can be designed for MTC, considering only the transmit power for reliable data transmission and neglecting any other source of energy consumption. The energy efficient operation of MTC over LTE networks is studied [15], and it was shown that an energy efficient design is not possible with the LTE physical layer. A power-efficient uplink scheduler design utilizing LTE system specification for delay-sensitive traffic over was investigated [16]; however, the considered traffic characteristics and delay models are not applicable in the case of MTC. Narrowband-IoT (NB-IoT) has seen considerable efforts in the domain of massive connectivity as well as coverage and battery lifetime maximization [17,18]. However, the battery consumption model proposed in these works for mMTC devices needs to be modified to depict the diversity in service requirements of NB-IoT devices. There is also a need to address the problem of battery lifetime improvement in coexisting environments which has been addressed in this work.

Game theory helps by determining strategic interactions as well as by providing a depiction of the rational behavior of users and the design of a distributed approach for a reliable solution. Resource management can be implemented efficiently by modeling a given network scenario as a game, with the players being the users in contention for different resources. A hierarchal game model for optimal resource allocation in a heterogeneous network was proposed [19]. Two non-cooperative sub-games were played sequentially in an attempt to overcome the problems of interference management and user rate maximization, respectively. Users optimized their connectivity with either a femtocell or macrocell based on a tradeoff between experienced interference and minimum rate requirement. Optimal power allocation schemes using game theory design to maximized user utilities for two-tier femtocell, ultra-dense and NOMA networks were proposed [20,21,22]. Interference coordination was achieved for device-to-device (D2D) links underlying cellular network using a distributed power control scheme [23]. A power control design with Nash equilibrium (NE) was designed for each link to guarantee interference minimization. Utility function modeling and reaching a stable equilibrium for a large number of users becomes increasingly difficult. Conventional game theory models cannot be used for massive user networks and advanced game models are required to efficiently design and model user behavior to reach a converged solution strategy. MFG is an advanced game theory framework a mean field characterizing the space-time dynamics, i.e., a player can make an optimal decision by only conforming with the mean field, instead of consulting the strategies of every other player in the game. MFG decision making is distributed with reduced information and control overheads [24,25,26,27]. MFG becomes more relevant for a large number of players as mean field approaches to a real value for increasing number of players [28,29,30,31,32]. Many works have been reported in which MFG theory is utilized to optimize energy utilization [33] and medium access control of devices [34]. However, no prior work has focused on utilizing the concept of a mean field for energy efficient resource management and a scheduling solution for MTC devices over a cellular network.

3. Architecture and Problem Formulation

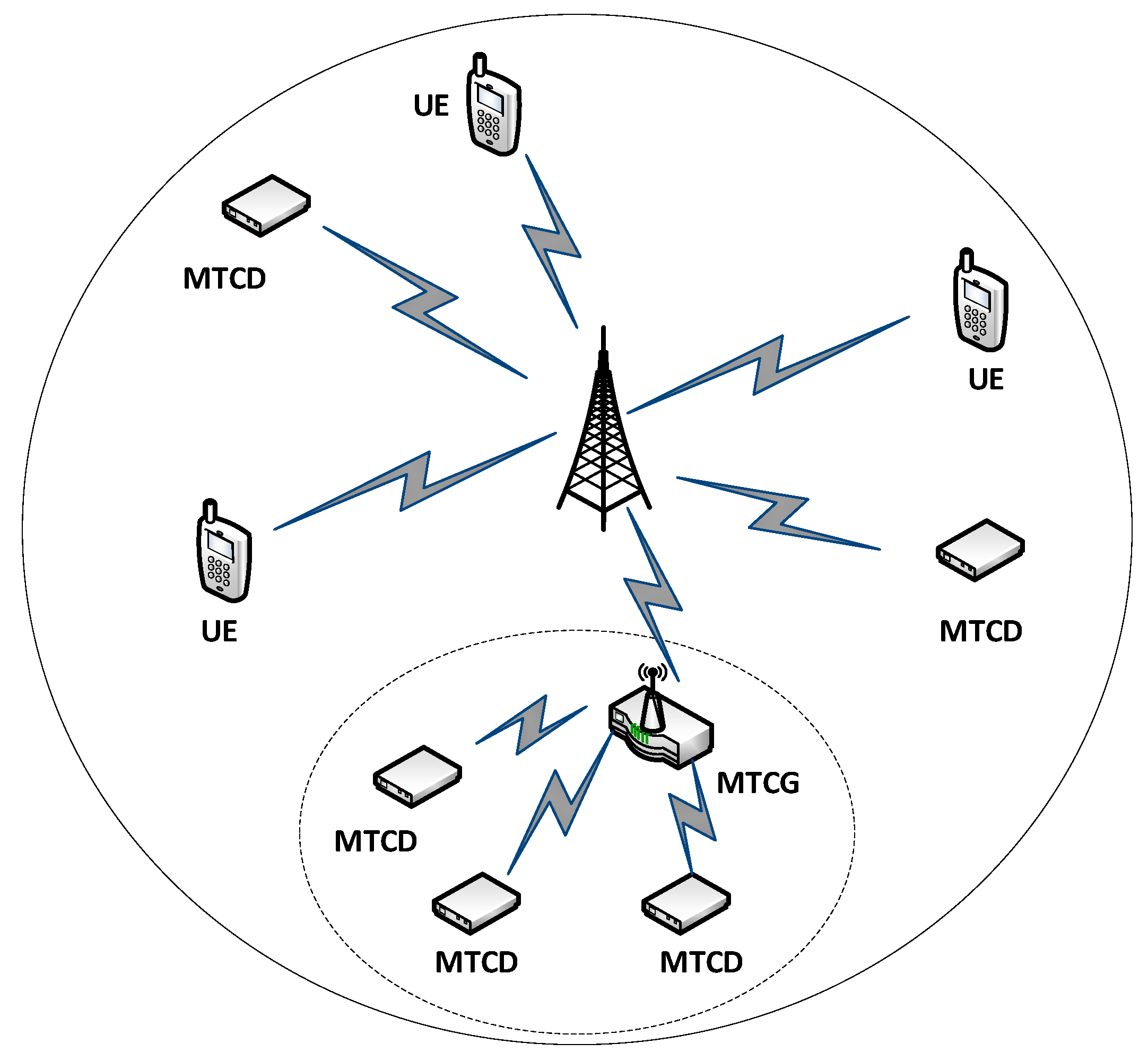
3.1. Network Model

The network model for the hybrid cellular MTC and HTC access framework is shown in Figure 1. Each MTC node considers the following steps for the realization of an energy efficient access solution for MTC nodes, which are to be accommodated in the existing cellular network. First, all MTCDs estimate their respective channel response (channel state information – CSI) to enable accurate modeling and information retrieval of the current experienced network environment. Service and node constraints are also considered for MTC nodes to be effectively integrated along with traditional HTC devices to avoid any service disruptions. Second, after determination of the device and context information, access provision to MTC nodes is performed. This includes user scheduling considerations for mMTC and uRLLC nodes according to their specific service QoS constraints. mMTC devices are arranged in clusters to simplify resource access as well as to address any congestion conditions, which have a high probability of occurring because of the massive connectivity requirement of these devices. Similarly, uRLLC devices are scheduled according to their requirements because of the event-driven nature of their traffic. Third, an SDG is formulated for the proposed energy-aware MTC design with a focus on the transmit power control of MTCDs. A mean field (MF) approximation is proposed as a possible solution to the formulated SDG which depends entirely on the accuracy of mean field modeling of the state dynamics of MTC nodes within a combined MTC/HTC cellular infrastructure. Lastly, a strategy based on the MF approximated solution is achieved by using a finite difference method for solving the MF equations to obtain converged energy-aware power and scheduling control. The equilibrium condition for the proposed game theory design is discussed and analyzed and includes the uniqueness, feasibility, and suitability with respect to the described network architecture.

3.2. System Model

A single cell is considered with diverse distribution of MTC and HTC devices with differing service requirements coexisting. A base station (BS) is at the center of this cell environment with a massive number of MTC users randomly distributed over the entire cell area as depicted in Figure 1. Consider a total of N users being present in the BS coverage with J conventional HTC and K MTC devices. uRLLC service nodes are provided a direct connectivity to the BS in order to ensure low latency and reliable communication link. Direct access to BS by mMTC devices may cause a serious congestion problem due to massive concurrent access event by all devices. A clustered approach is considered for mMTC devices which are grouped and relayed to counteract any congestion at the BS. An MTC gateway (MTCG) is responsible for relaying data of connected MTCDs to the BS for a seamless access experience. An MTCG can either be an MTC device itself or an HTC device relaying for the connected mMTC devices. Because of privacy and data integrity concerns, an mMTC device is selected as the gateway node such that battery lifetime and energy consumption are improved. A decode-and-forward (DF) protocol [35] is used to relay MTCDs traffic for the proposed cellular environment. The selection of a combined access protocol based on a typical LTE-A time-frequency resource division is considered to provide access to HTC and MTC users. Consider an m_th mMTC device with b_m data bits to be transmitted using a time period -T_i. An MTCG has a minimum rate requirement of b_h bits and the transmission times allocated to MTCD and MTCG are denoted, respectively, as t_m and t_h. This involves a two-stage operation in the uplink frame through which each MTCD communicates with the BS via MTCG. The uplink resource is allocated directly to the MTC and HTC devices to comply with the reliability condition and ensure minimum delay.

3.2.1. Hybrid Interference Model

Interference experienced by either the HTC and or the MTC users is modeled considering the interactions in the proposed hybrid coexisting environment. Inter-domain is the interference between HTC and MTC nodes whereas intra-domain is the interference between either amongst MTC or HTC devices, respectively. The intra-domain interference received by a k_th transmitting mMTC node from other i_th mMTC nodes in a cluster at any time t is expressed as:

$$i_k\left(t\right)= {\displaystyle \sum }_{i=1, i\ne k}^K{p}_i\left(t\right)G_{i,k}\left(t\right),$$

(1)

where $p_i\left(t\right)$ is the transmit power required for i_th MTCD, i ∈ K and $G_{i,k}\left(t\right)$ is the experienced channel gain between k_th and i_th MTCDs, i ∈ K, respectively. Here, (1) describes the interference caused by a single k_th MTCD transmitting device to all the other MTCDs at time t. The inter-domain interference is defined as an interaction between MTC and HTC users along with any possible MTCGs. The inter-domain interference received by a k_th MTCD from j_th HTC node can be defined as:

$$I{’}_k\left(t\right)= {\displaystyle \sum }_{j=1}^J{P}_j\left(t\right)G_{j,k}\left(t\right),$$

(2)

where $P_j\left(t\right)$ is the transmit power of the any j_th HTC device and $G_{j,k}\left(t\right)$ is the experienced channel gain between any j_th HTC and the k_th MTCD device. Now, the achievable SINR for any k_th MTCD with a transmit power of $p_k\left(t\right)$ and channel gain of $g_k\left(t\right)$ with a noise variance δ⁻² at time instant t is:

$${\gamma }_k\left(t\right)= \frac{p_k\left(t\right)g_k\left(t\right)}{i_k\left(t\right)+I{’}_k\left(t\right)+ {\sigma }^2 }, { }_{}$$

(3)

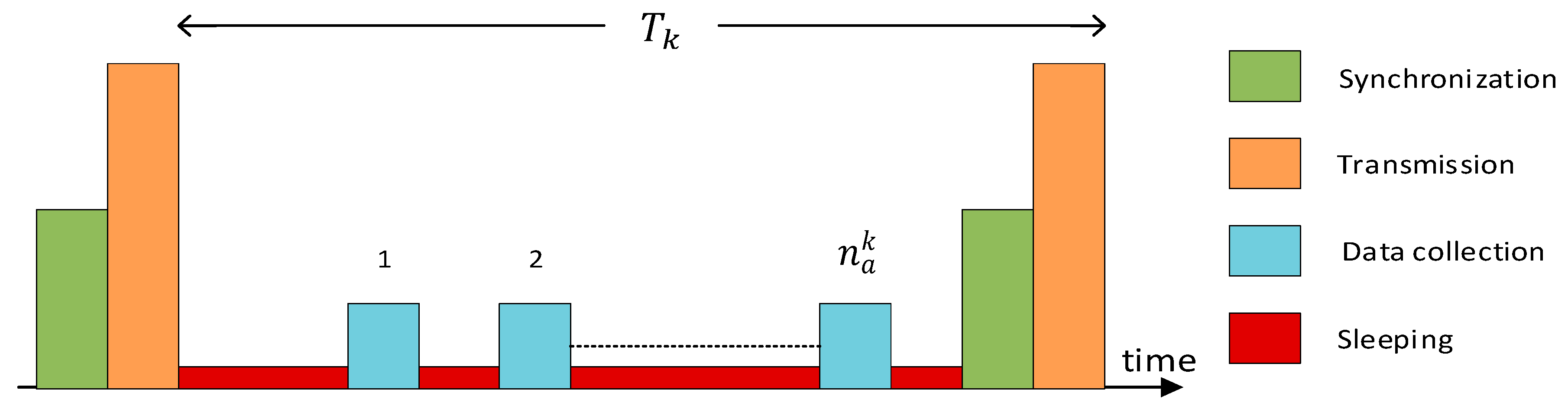
3.2.2. Individual Battery Lifetime

The optimization of expected battery lifetimes of MTC devices is an important consideration to enhance device performance and ensure a longer period of operation in the absence of recharging opportunity. Accurate modeling of the battery consumption pattern of MTCDs becomes critical considering the variance of energy consumption levels during the duty cycle of a typical MTC node as shown in Figure 2. The energy consumption per device is considered as a semi-regenerative process with regeneration occurring at the end of each interval of successful data transmission. The remaining battery energy of any k_th MTCD at time instant t^o is denoted as E_k(t^o), and the transmission interval period and the average packet size being denoted as T_k and D_k respectively. Power consumption for sleeping and transmission modes is denoted as $p_s$ and ($p_k$ + $p_e$) respectively, where $p_e$ is the consumed power by the electronic components during data transmission and $p_k$ is the required transmit power necessary for reliable data transmission. The expected battery lifetime of MTC devices for each transmission interval T_k for any node k is defined as the direct product of ratio between remaining energy to average energy consumption and the data transmission interval period described as:

$$L_k\left(t^o\right)=\frac{E_k\left(t^o\right)T_k}{E_s+p_s\left[T_k-\frac{D_k}{R_k}-n_a^k{T}_a^k\right]+n_a^k{T}_a^k{p}_a+\frac{D_k}{R_k}\left[p_e+\eta p_k \right]},$$

(4)

where R_k is the averaged data rate for any k_th MTCD, η is the inverse of the efficiency of power amplifier, and E_s is the averaged static energy consumption for synchronization, admission control, etc, in each data transmission interval. $p_a$ is the consumed power during data collection in the active mode with a duration of T_a^k and n_a^k being the total number of active modes during each data transmission interval T-_k. The consumed energy in transmitting and non-transmitting modes is denoted as É_s^k and É_d^k, respectively. The simplified form of individual battery lifetime in (4) is as follows:

$$L_k\left(t^o\right)= \frac{E_k\left(t^o\right)T_k}{ {\mathsf{É}}_s^k+ {\mathsf{É}}_d^k},$$

(5)

where:

$$\begin{gathered} {\mathsf{É}}_s^k= E_s+ p_s\left[T_k- \frac{D_k}{R_k}- n_a^k{T}_a^k\right] + n_a^k{T}_a^k{p}_a \\ {\mathsf{É}}_d^k= \frac{D_k}{R_k}\left[p_e+ \eta p_k\right]. \end{gathered}$$

(6)

3.2.3. Battery Lifetime and Energy Efficiency

There exists a direct relation between the battery lifetime and the achievable energy efficiency of wireless devices shown in detail by Miao [36]. The energy efficiency of any k_th- MTCD during the transmission is defined as:

$$U_k\left(R_k\right)= \frac{R_k}{p_e+ \eta p_k\left(R_k\right)}.$$

(7)

It is shown that when $p_k$(R_k) is strictly convex in R_k, with U_k(R_k) being strictly quasi-concave. This shows that an optimal R_k can be found that maximizes the energy efficiency. The battery lifetime in (5) can now be rewritten as:

$$L_k\left(t^o\right) = \frac{E_k\left(t^o\right)T_k}{D_k} \frac{R_k}{p_e+ \eta \left[p_k+{\mathsf{É}}_s^k \frac{R_k}{D_k\eta }\right]}.$$

(8)

Now, define $p_k$(R_k) as $p_k$(R_k) + É_s^k R_k/ ηD_k, which will be strictly convex in R_k given $p_k$(R_k) remains strictly convex. Hence, (8) can be written in terms of energy efficiency as follows:

$$L_k\left(t^o\right)= \frac{E_k\left(t^o\right)T_k}{D_k} \frac{R_k}{p_e+ {\dot{p}}_k }= \frac{E_k\left(t^o\right)T_k}{D_k} {\mathsf{Ú}}_k\left(R_k\right).$$

(9)

The direct dependence of lifetime over energy efficiency Ú_k(R_k) is evident from the mentioned expression. Hence, maximization of the battery life is equivalent to energy efficiency maximization and the proposed game takes advantage of this relation.

3.2.4. Network Battery Lifetime

Network battery lifetime is defined as the total time from network deployment to the time when the network is considered to be no longer functional. In the case of MTC-centric design, uRLLC devices have higher priority and therefore they contribute to the determination of the boundary condition of network functionality. A shortest individual lifetime (SIL) is deemed suitable to define and propose the notion of network lifetime defined as:

$$L_n\left(t^o\right)=\min L_k\left(t^o\right).$$

(10)

Massive connectivity can be partially supported by existing LTE-A cellular networks by adopting a clustering design for mMTC nodes. For simplicity, mMTC devices are assumed to have similar communication requirements including packet size and generation patterns. To maximize the lifetime of nodes clustered together in mMTC groups, all the members of the respective group perform gateway functionality. This helps in reducing the possibility of a single node experiencing battery drainage and causing a network failure condition as per SIL criterion. This approach also ensures the maximum possible SIL for each cluster. Let us denote the average cluster size of these mMTC nodes as s. The cluster forming problem in the context of mMTC nodes is considered at a reference point in time where E_i(t^o) = E_o and E_o represent the full battery capacity. The member and gateway transmit power levels are denoted by $p_t^m$ and $p_t^g$, respectively. In each data transmission period of clustered communication design, a node may either be in the gateway mode or the member mode with probabilities 1/s or (1 – 1/s), respectively. Hence, the expected life of battery for each mMTC node in a cluster centered at a distance $d_g$ from the BS is expressed as the product of the ratio between the remaining battery energy to the averaged energy consumption in each transmission interval and cluster reporting period is defined as:

$$L_g\left(d_g, s\right)= \frac{E_o T_g}{\frac{1}{s} {\mathsf{É}}_g+\left(1- \frac{1}{s}\right){\mathsf{É}}_m},$$

(11)

where:

$$\begin{gathered} {\mathsf{É}}_g= E_s^g+ \frac{\left(s-1\right) \mathsf{Ď}}{R_m}{p}_l+\left[ 1+ {\mathsf{\mu }}_c\left(s-1\right)\right]\mathsf{Ď}\frac{p_e+ \eta p_t^g }{R_g}, \\ {\mathsf{É}}_m= E_s+ \mathsf{Ď}\frac{p_e+ \eta p_t^m }{R_m}, \end{gathered}$$

(12)

where T_g is the cluster transmission interval, Ď is the average packet size, $p_l$ is the power consumption in listening mode, and $\left(s-1\right) \mathsf{Ď}{P}_l/R_m$ models the energy consumption of the gateway during the reception of data from other nodes in the cluster. In addition, µ_c is the coefficient for the compression of the packet length on gateway nodes, and E_s^g is the averaged static energy consumed in gateway mode for a node. R_m and R_g are the data rates of the respective nodes communicating within and outside the cluster as provided in an example [37].

To meet the mission-critical service requirements a direct link needs to be established to the BS. The air interface for the proposed joint HTC/MTC design is modeled considered as 3GPP LTE Release 13 [38] with time-frequency distribution of resources. For an LTE uplink power control mechanism, the transmit power for the uplink for each MTCD can be acquired using the downlink path loss estimation as:

$$P_{UL}\left(c_k,{\delta }_k\right)= c_k{P}_o{\beta }_k{ϴ}_k\left[2^{\frac{1.25TBS\left(c_k,{\delta }_k\right)}{c_k,N_s{N}_{sc}}}-1\right],$$

(13)

where c_k denotes the number of physical resource block pairs (PRBPs) allocated to a node k, β_k is the compensation factor and the estimated downlink path loss is defined as θ_k. The number of symbols and subcarriers in a PRBP are denoted as N_s and N_sc respectively. The transport block size (TBS) is the function of c_k and the TBS index, defined as shown in Table 7.1.7.2.1-1 [38]. The TBS index denoted by δ_k ∈ {0… 33} is dependent on the selected modulation and coding scheme (MCS) from Table 8.6.1-1 provided in [38]. P_o is a user-specific value, defined as $P_o= {\beta }_k\left[{\gamma }_{th}+P_n\right]+ \left[1- {\beta }_k\right]P_{max}$ which depends on the required SINR level ${\gamma }_{th}$. P_max is defined as the maximum allowed transmitting power with P_n being the noise power in each resource block. The expected battery lifetime for a direct communication MTCD node i within its time-to-transmit interval (TTI) can be defined as:

$$L_k\left(t^o\right) = \frac{E_i\left(t^o\right)T_k}{E_s^k+ TTI\left[P_e+ \eta P_{UL}\left(c_k,{\delta }_k\right)\right]}.$$

(14)

3.3. Problem Formulation

An energy efficient uplink scheduling and transmit power control mechanism can be obtained using the described system model for both the direct and relayed communication design for mMTC and uRLLC nodes. For a hybrid HTC/MTC co-existing design this has been formulated as:

$$ma{x}_{c_k,{\delta }_k}{L}_n^{sil}$$

(15)

subject to:

$$\begin{gathered} \mathrm{C}1:{{\displaystyle \sum }}_{k\in K}{c}_k\le \left|C\right|, \\ \mathrm{C}2: D_k \le TBS\left(c_k,{\delta }_k\right), \forall k \in A \\ \mathrm{C}3: P_{UL}\left(c_k,{\delta }_k\right) \le P_{max}, \forall k \in A \\ \mathrm{C}4: \delta k\in \left\{0,\dots ,33\right\};c_k\in \left\{1,\dots ,\left|C\right|\right\}, \forall k \in A \end{gathered}$$

where K is the set of schedulable devices, L_n^sil depends on the individual battery lifetimes for mMTC and uRLLC devices. |C| is the set of available PRBPs, e.g., 110 when considering an LTE system with a bandwidth of 20 MHz. This battery lifetime maximization problem for coexisting mMTC and HTC devices is modeled into an energy efficient power control problem for MTC devices. This leads to an improved utilization of available energy in battery reserves of MTC devices by consideration of interference and QoS requirements of both MTC and HTC devices. This paper proposes an approach based on differential and mean field game theory to solve this optimization problem, resulting in mean field-based power control for MTCDs.

4. Stochastic Differential Power Control Game

A promising direction in game theory is to design the method of transmit power control to improve the energy consumption of MTC users. This problem is modeled by utilizing the concept of a stochastic differential game with a proven Nash equilibrium existence. According to (9) the energy efficiency of MTCDs is directly proportional to the battery lifetime. Hence, the formulated problem is solved by manipulating the transmit power of MTCDs to optimize the energy consumption and eventually the operating time to prolong the network lifetime. The proposed SDG framework utilizes the concept of utility maximization for its players to come up with optimal control by considering system state and actions taken by players. The accuracy of the system state and utility model is of prime importance to the ability of an SDG to obtain an optimal control policy for its players.

The transmit power control problem is a continuous time problem and an SDG design must be defined for all points in time from starting timing instant T_i to final time instant T_f. Typically, a stochastic differential game consists of an independent set of players $\mathcal{K}$ = {1,…,K} (the MTC nodes) with associated action set $\mathcal{P}$_k and the corresponding state space $\mathcal{S}$_k. A utility function ϴ_k is a measure that analyses the performance of chosen actions and strategies by each player from set $\mathcal{K}$. A control policy $\mathcal{C}$_k is the set of power values to achieve an optimal power control objective.

4.1. State Space Model

The variables in terms of system dynamics include the remaining battery energy of the MTC node along with the experienced interference and channel gain. These variables will help in the formulation of the state space model for the proposed SDG power control. An MTC user transmits only for a finite amount of time due to limited battery energy. The consumed power is related to the available battery energy for node k at time t as E_k(t) by a generic relation:

$$d{E}_k\left(t\right)= -p_k\left(t\right)dt,$$

(16)

The total interference experienced by an MTC node considering the intra-domain and inter-domain interference behavior as already defined in equations (1) and (2) is represented as:

$$I_k\left(t\right)=i_k\left(t\right)+ I{’}_k\left(t\right)={\displaystyle \sum }_{i=1, i\ne k}^K{p}_i\left(t\right)G_{i,k}\left(t\right)+{\displaystyle \sum }_{j=1}^J{P}_j\left(t\right)G_{j,k}\left(t\right).$$

(17)

The interference state can now be shown as:

$$d{I}_k\left(t\right)= \frac{\partial }{{\partial }_t}{I}_k\left(t\right)$$

(18)

Hence, the state space for the considered SDG scenario is defined as:

$$S_k\left(t\right)=\left[ E_k\left(t\right), I_k\left(t\right)\right].$$

(19)

Here, the remaining energy, as well as the interference caused by the k_th MTC node, is considered as variables of the state space, which are acquired as the proposed differential game is solved using mean field approximation. During transmission, a device has a certain cost associated with the operation as described in the proposed state dynamics. The available energy at all devices continues to decrease during operation, so selection of the transmitting power for each device affects the battery life.

4.2. Utility Function

In differential game theory, the objective of each player is to maximize its own individual utility to determine the optimal control strategy for the defined problem. Each MTCD seeks to minimize its power consumption and eventually maximize its battery lifetime, which can be achieved only by defining an appropriate utility. Depending on the state space already defined (19), the utility function can be defined as:

$${ϴ}_k\left(t\right)={\left({\gamma }_k\left(t\right)- {\gamma }_{th}\left(t\right)\right)}^2+ \mathsf{\Omega }{p}_k\left(t\right),$$

(20)

where ${\gamma }_{th}$ is the SINR threshold value that is required to establish a reliable communication link assumed to be the same for all k MTC nodes. The inclusion of $\mathsf{\Omega }$ guarantees the conformity between units of both transmit power and SINR difference. Moreover, it is fairly obvious and can be easily proven that (20) is convex in terms of $p_k\left(t\right)$. In the proposed work, reliability for uRLLC devices is ensured by specifying an SINR threshold ${\gamma }_{th}$, which ensures the establishment of a serviceable link with the BS.

4.3. Optimal Control Policy

The utility function defined above depends on SINR performance as well as the value of the transmitting power selected by each MTC node. In the proposed design, each MTC device devises an optimal power control policy $C_k{}^{*}\left(t\right)$ where t ∈ [T_i, T_f]. A generic optimal control strategy and value function is usually defined as:

$$C_k{}^{*}\left(t\right)=\arg \underset{p_k\left(t\right)}{min}\mathbb{E}\left[{{\displaystyle \int }}_{T_i}^{T_f}{ϴ}_k(t) dt+ {ϴ}_k\left(T_f\right)\right],$$

(21)

$$V_k\left(t, S_k\left(t\right)\right)=\underset{p_k\left(t\right)}{min}\mathbb{E}\left[{{\displaystyle \int }}_{T_i}^{T_f}{ϴ}_k(t)dt+ {ϴ}_k\left(T_f,S_k\left(t\right)\right) \right],$$

(22)

where ${ϴ}_k\left(T_f\right)$ and ${ϴ}_k\left(T_f,S_k\left(t\right)\right)$ are the values for the utility and value functions at the final state $T_f$. Given the information about the optimal control problem, NE can exist for the above problem as shown later in this section. A power control profile ${\mathcal{C}}_k{}^{*}\left(t\right)= p_k{}^{*}\left(t\right)$, ∀ ∈ K is the Nash equilibrium of if and only if [25]:

$${\mathcal{C}}_k{}^{*}\left(t\right)=\arg \underset{p_k\left(t\right)}{min}\mathbb{E}\left[{{\displaystyle \int }}_{T_i}^{T_f}{ϴ}_k(p_k(t),p_{-k}{}^{*}\left(t\right)) dt+ {ϴ}_k\left(T_f\right)\right].$$

(23)

subject to:

$$\begin{gathered} S_k\left(t\right)=\left[ E_k\left(t\right), I_k\left(t\right)\right], \\ d{E}_k\left(t\right)= -p_k\left(t\right)dt, \\ d{I}_k\left(t\right)= \frac{\partial }{{\partial }_t}{I}_k\left(t\right). \end{gathered}$$

where $p_{-k}{}^{*}\left(t\right)$ is the transmit power vector of all MTC devices except the k_th device. The optimal control policy ensures that no player can lower the utility further by adopting a power control policy other than the optimal policy.

4.4. Stability and Equilibrium Analysis

The optimal control theory and the Bellman’s optimality principle [39] dictates that a partial differential equation (PDE) known as the HJB equation must be satisfied by the value function (22). It also convenes that value function (22) is the solution to the HJB equation and it gives the minimum utility solution to any dynamic differential game system with the associated utility function (20). The HJB equation is formulated from [40] as:

$$-{\partial }_t{V}_k\left(t, S_k\left(t\right)\right) =\underset{p_k\left(t\right)}{min}\left[{ϴ}_k(t, S_k\left(t\right), p_k\left(t\right))+{\partial }_t{S}_k\left(t\right) .▽{ϴ}_k\left(t,S_k\left(t\right)\right) \right],$$

(24)

where the Hamiltonian is defined as:

$$H\left(p_k\left(t\right), S_k\left(t\right),▽{ϴ}_k\left(t,S_k\left(t\right)\right)\right) =\underset{p_k\left(t\right)}{min}\left[{ϴ}_k(t, S_k\left(t\right), p_k\left(t\right))+ {\partial }_t{S}_k\left(t\right) .▽{ϴ}_k\left(t,S_k\left(t\right)\right) \right].$$

The NE is guaranteed for the proposed differential game if a unique solution can be found to the HJB Equation (24). The solution to the formulated HJB equation can exists only if the Hamiltonian is smooth [40] which in turn is guaranteed due to the continuity of the utility function. There exists at least one NE for the differential game Ꞡ whose existence is dependent on the unique solution of the HJB equation in differential game. A total of K players are included in the proposed game design, which means a solution of K PDEs is to be found in unison to each other leading to an exponential increase in complexity. Thus, a converged solution leading to NE is not practical for a large number of devices using the defined differential game model. A possible approach to solving this practical implementation problem is to seek the help of mean field concept.

5. Mean Field Power Control Game

In this section, the concept of mean field is introduced along with its significance and suitability in solving the formulated SDG using MFG theory. The suitability of MFG for a larger set of players is rooted in the independent design and formulation of HJB and the FPK coupled system of equations. The formulated power control problem for MTCDs has been represented as a coupled system of equations with the mean field approximation being utilized to determine a feasible equilibrium condition.

5.1. Mean Field Game

5.1.1. Mean Field and Player Interactions

The definition of mean field is core to the design and solution of MFG and the mean field is defined as the statistical distribution of state behavior of the game as:

$$m\left(t,S\right)=\underset{K\to \infty }{\lim }\frac{1}{K} {\displaystyle \sum }_{k=1}^K{𝟙}_{\left\{S_k\left(t\right)=S\right\}},$$

(25)

where 𝟙 represents an indicator function which is one if the given condition is true and zero elsewise. $S_k\left(t\right)=\left[ E_k\left(t\right), I_k\left(t\right)\right]$ is the state space dynamics of the power control game. Here, the mean field depicts the probability distribution of states over the player set at any given time instant.

Conventional game theory designs are unable to withstand the demands of a densified user environment because of the dimensional difficulty associated with achieving a converged solution. An MFG design utilizes large user numbers to balance out their effect on the game and only provides brief information about individual players. This also simplifies the design as the player numbers continue to grow in a real-time environment. HJB equation is used to model an individual player’s relation with the mean field and the collective behavior of all the players as per chosen actions is modeled by an FPK equation [40]. These coupled FPK and HJB equations are known as backward and forward equations, respectively according to the nature of their interactions with the mean field. The conversion of a differential power control game for MTCDs to an MFG power control design requires the fulfillment of the following necessary properties:

• Individual player makes a small contribution towards mass of all the other players and the MFG. This property ensures that the players act in a more rational and independent manner while choosing the optimal control policy.
• The action selection by each player depends on its own interests and only interacts with the mean field of players instead of participating in individual interactions.
• The continuity property of the mean field model is ensured by the provision of the massive number of MTC devices for power control.
• When analyzing a K-player game, the MFA technique is used to model the actions of the players and prove the exchangeability property.

Moreover, solutions to the MFGs can be obtained in a distributive manner and the behavior of all the players can be described by a single control strategy. These properties ensure that MFG can indeed provide an optimal transmit power control policy for a massive number of MTC users in the proposed network environment. The modelling of the mass effect of all players (the mean field) must be based on realistic parameters and it poses a major design challenge in application of mean field concept for solving problems in wireless communications.

5.1.2. Mean Field Utility Function

The formulated utility function (20) needs to be adapted to accommodate a large number of players in the mean field domain. Interference dynamics defined by (1) and (2) can be easily modified to conform with large number of MTC users as:

$$i_k{}^m\left(t\right)= {\displaystyle \sum }_{i=1, i\ne k}^K{p}_k\left(t\right)G_{i,k}\left(t\right)≋\left(K-1\right) p_k{}^m\left(t\right){\overline{G}}_{i,k}{}^m\left(t\right).$$

(26)

Here, $p_k{}^m\left(t\right)$ is the transmit power for by k_th MTC user required while estimating parameters for the MFG. ${\overline{G}}_{i,k}{}^m\left(t\right)$ is defined as the mean field channel gain for MTC devices. The power received at the BS is defined as:

$$P_k{}^{RX}\left(t\right)= P_k{}^m\left(t\right)G_k\left(t\right)+ i_k{}^m\left(t\right),$$

(27)

where $G_k\left(t\right)$ is the channel gain and $P_k{}^m\left(t\right)G_k\left(t\right)$ is the total received signal power. Further, $i_k{}^m\left(t\right)$ is the induced interference to the intended signal. The mean field SINR can be defined using (26) and (27) as:

$${\gamma }_k{}^m\left(t\right)= \frac{p_k\left(t\right)g_k\left(t\right)}{\left(K-1\right)P_k{}^m\left(t\right)G_{k,i}{}^m\left(t\right)+ {\sigma }^2}.$$

(28)

Hence, the modified mean field utility function can now be formulated as:

$${ϴ}_k{}^m\left(t\right)={\left({\gamma }_k{}^m\left(t\right)- {\gamma }_{th}\left(t\right)\right)}^2+ \mathsf{\Omega }{p}_k\left(t\right).$$

(29)

Formulation of the power control MFG can now be completed after including the mean field approximations in the interference dynamics and utility function for players.

5.1.3. Mean Field Game Formulation and Equilibrium Analysis

The mean field game can be formulated given the definition of utility function by completing the coupled system of equations. Hence, the FPK equation is formulated as defined by Lasry et al. in [40] in the following way:

$${\partial }_{t}m\left(t,S\right)+ ▽\left(m\left(t,S\right)· {\partial }_{t}S\left(t\right)\right)=0.$$

(30)

This completes the required set of coupled equations i.e. (24) and (30), necessary to complete the formulations of the proposed power control MFG. Figure 3a shows the interactions along with the forward and backward nature of the respective equations while completing the MFG design. This interactive design helps to solve the MFG and to devise an optimal control policy that considers the player dynamics and interactions within the domain of the MTCD architecture. An eventual mean MFG equilibrium condition is achieved when a converged optimal power control strategy is devised by solving both the HJB and FPK equations. The convergence of the proposed mean field-based power control framework is independent of the number of players in the game. Rather, it is more directly dependent on the method utilized to solve the formulated forward and backward PDEs. The mean field equilibrium (MFE) can be defined as a stable and converged set of the optimal control policy depicted through the optimal value function v^*(t, S) and the mean field function m^*(t, S). As shown in Figure 3a, v(t, S) is obtained by solving the HJB equation backward in time whereas m(t, S) is obtained by solving FPK forward in time.

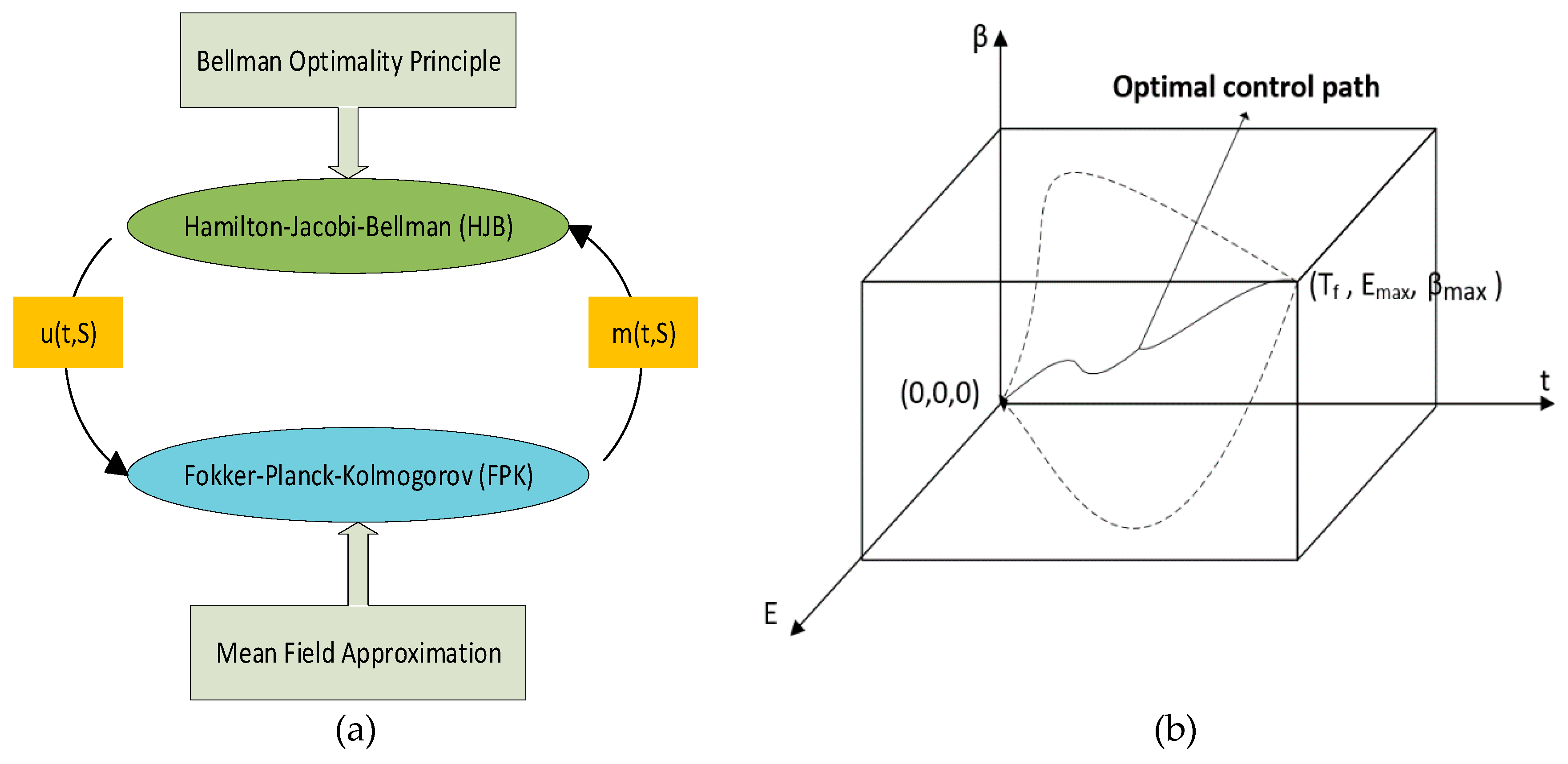
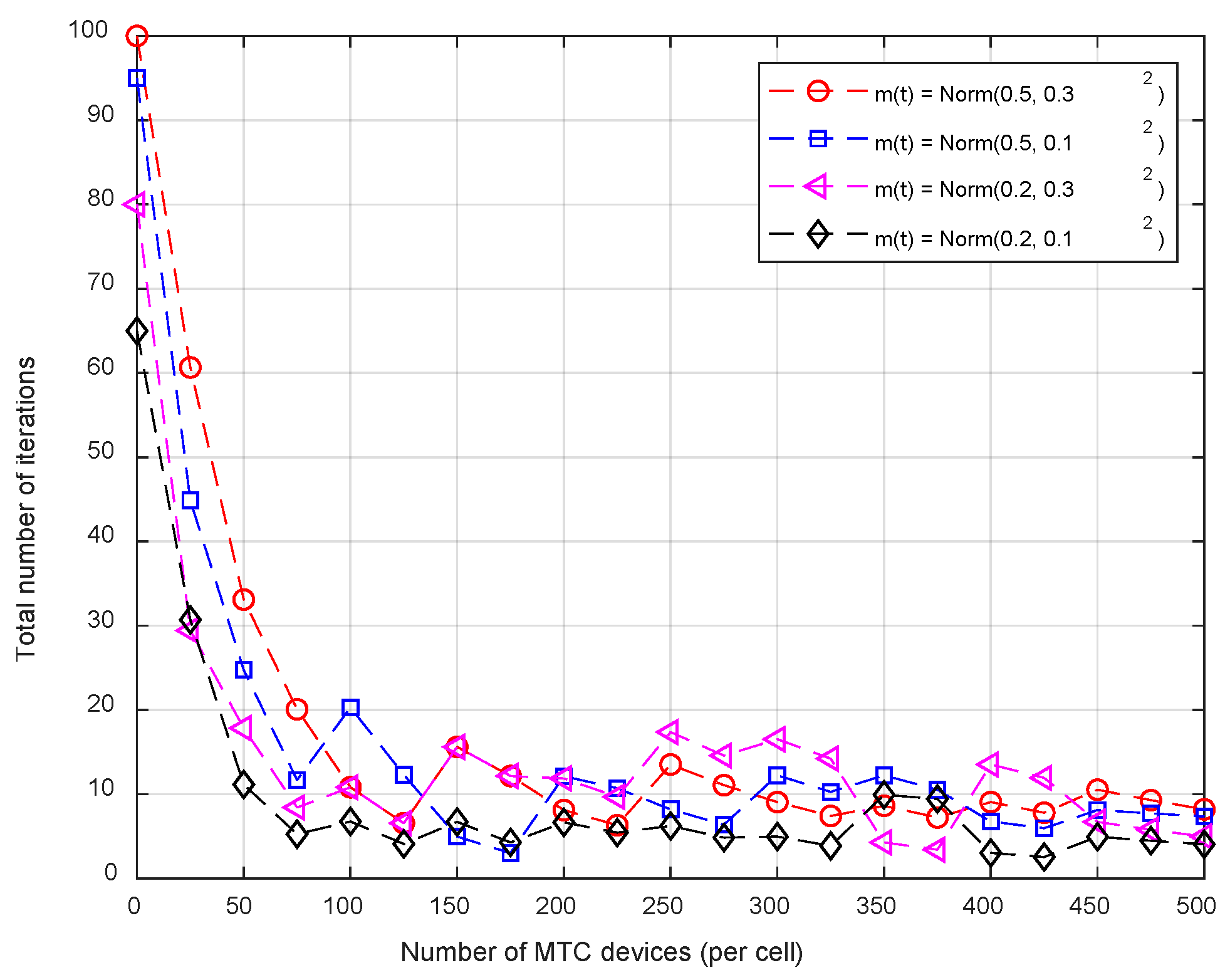
5.2. Finite Difference-Based MFG Solution

The MFE for the proposed power control MFG is achieved by formulating a solution strategy using the finite difference based scheme [40] to solve the coupled system of equations. Specifically, the Lax-Freidrichs technique is utilized as compared to other finite difference methods in order to obtain a guarantee regarding improved accuracy in time and space and the positivity of the mean field [41]. In the proposed design using the finite difference method, energy state [0, E_max], interference state [0, β_max] and the time [0, T_f] are discretized and mapped onto the X-, Y- and Z-axis, respectively as depicted in the Figure 3b. Multiple solutions may exist in the discrete state and action space depending on the chosen values for the mean field, interference and battery energy of the MTC devices. For convenience, the starting time instant of the MFG, T_i, is assumed to be zero. An optimal control policy is found by iterating for different values of the interference and energy states with corresponding time instances within the defined mean field game design.

5.2.1. Solving HJB and FPK Equations

The discretized form of the FPK equation is solved after application of the Lax-Friedrichs scheme and converts to (31). Here, $M\left(i,j,k\right), P\left(i,j,k\right), \omega \left(i,j,k\right)$ represent the values of the mean field, transmit power, and interference energy at any time instant i with the energy level j and interference state k within the discretized state space:

$$\begin{array}{c}M\left(i+1,j,k\right)\hfill \\ =\frac{\left[M\right(i,j-1,k)+M(i,j+1,k)+M(i,j,k-1)+M(i,j,k+1\left)\right]}{2}\hfill \\ +\frac{{\delta }_t\left[M\right(i,j+1,k\left)P\right(i,j+1,k)-M(i,j-1,k\left)P\right(i,j-1,k\left)\right]}{2{\delta }_E}\hfill \\ +\frac{{\delta }_t\left[M\right(i,j,k+1\left)P\right(i,j,k+1\left)\omega \right(i,j,k+1)-M(i,j,k-1\left)P\right(i,j,k-1\left)\omega \right(i,j,k-1)-M(i,j,k-1\left)P\right(i,j,k-1\left)\omega \right(i,j,k-1\left)\right]}{2{\delta }_{\mathsf{\beta }}}.\hfill \end{array}$$

(31)

The Hamiltonian in the HJB equation limits the applicability of the finite difference method in its conventional form to solve the HJB equation. Hence, the HJB equation is converted to an optimal control problem itself with the FPK equation now acting as a constraint. The newly formulated control problem is defined as:

$$\underset{P_k\left(t\right)}{\underbrace{min}}\mathbb{E}\left[{{\displaystyle \int }}_o^{T_f}{ϴ}_k{}^m\left(t\right)dt+ {ϴ}_k{}^m\left(T_f\right)\right]$$

(32)

subject to:

$${\partial }_{t}m\left(t,S\right)+ {▽}_{E}m\left(t,S\right)E\left(t\right)+ {▽}_{\beta }m\left(t,S\right)\beta \left(t\right) =0.$$

By employing a Lagrange multiplier, a solution to the modified form of the above-stated HJB equation can be found just as the FPK equation. The Lagrangian $L(m\left(t,S\right),p\left(t,S\right),\lambda \left(t,S\right)$ is obtained by setting ${ϴ}_k{}^m\left(T_f\right)=0$ as shown in (33).

The finite difference scheme can now be applied directly to solve the FPK and the newly proposed control problem (32) along with the HJB equation. The discretization as discussed above is now applied to formulate the 3D-state space of the power control MFG and the Lagrangian is defined as (34). According to the defined Lagrangian in (34), $\Gamma , \zeta , \varphi$ are defined as (35)–(37), respectively. $M\left(i,j,k\right), P\left(i,j,k\right), U\left(i,j,k\right), \lambda \left(i,j,k\right)$ represent the values of the discretized mean field, transmit power, utility as well as the Lagrange multipliers at any time instant t with battery energy level j, and experiencing interference state k in the multidimensional MFG state space:

$$L\left(m\left(t,S\right),p\left(t,S\right),\lambda \left(t,S\right)\right)=\underset{t=0}{\overset{T_f}{{\displaystyle \int }}}\underset{E=0}{\overset{E_{max}}{{\displaystyle \int }}}\underset{\beta =0}{\overset{{\beta }_{max}}{{\displaystyle \int }}}\left[{ϴ}_k{}^m\left(t,S\right)m\left(t,S\right)+\lambda \left(t,S\right)\left({\partial }_{t}m\left(t,S\right) {▽}_{E}m\left(t,S\right)E\left(t\right)+{▽}_{\beta }m\left(t,S\right)\beta \left(t\right)\right)\right]dtdEd\beta ,$$

(33)

$$L_d = {\delta }_t{\delta }_E{\delta }_{\beta }{\displaystyle \sum }_{i=1}^{X+1}{\displaystyle \sum }_{j=1}^{Y+1}{\displaystyle \sum }_{k=1}^{Z+1}\left[M\left(i,j,k\right)U\left(i,j,k\right)+\lambda \left(i,j,k\right)\left(\Gamma +\varphi + \zeta \right)\right],$$

(34)

$$\Gamma =\frac{1}{{\delta }_t}\left[M\left(i+1,j,k\right)-\frac{1}{2}M\left(i,j+1,k\right)+M\left(i,j-1,k\right)+M\left(i,j,k+1\right)+M\left(i,j,k-1\right)\right],$$

(35)

$$\zeta = \frac{1}{2{\delta }_E} \left[M\left(i,j+1,k\right)P\left(i,j+1,k\right)-M\left(i,j-1,k\right)P\left(i,j-1,k\right)\right] ,$$

(36)

$$\varphi = \frac{1}{2{\delta }_{\beta }}\left[M\left(i,j,k+1\right)P\left(i,j,k+1\right)\omega \left(i,j,k+1\right)-M\left(i,j,k-1\right)P\left(i,j,k-1\right)\omega \left(i,j,k-1\right)\right] .$$

(37)

For a converged optimal control policy, decision variables denoted as (P^*, M^*, $\lambda$^*) must satisfy the Karush-Kuhn-Tucker (KKT) conditions for the discretized state space. An optimal control policy for any point (i, j, k) can be found by minimizing (38) against the given constraints. The iterative updates for the Langrangian are performed in step-sizes defined by (38) and through evaluation of the expression $\delta L_d/\delta P\left(i,j,k\right)=0$. Now, the formulation of $\lambda \left(i-1,j ,k\right)$ is defined as (39):

$$\frac{\delta L_d}{\delta P\left(i,j,k\right)}={\displaystyle \sum }_{j=1}^{Y+1}{\displaystyle \sum }_{k=1}^{Z+1}M\left(i,j,k\right)\frac{\delta U\left(i,j,k\right)}{\delta P\left(i,j,k\right)}+\left[\frac{M\left(i,j,k\right)}{2{\delta }_E}+\frac{M\left(i,j,k\right)\omega \left(i,j,k\right)}{2{\delta }_{\beta }}\right]\left[\lambda \left(i,j+1,k\right)-\lambda \left(i,j-1,k\right)\right],$$

(38)

$$\begin{array}{cc}\lambda \left(i-1,j ,k\right)\hfill & =\frac{\left[\lambda \left(i,j+1,k\right)+\lambda \left(i,j-1,k\right)\right]+\left[\lambda \left(i,j,k+1\right)+\lambda \left(i,j,k+1\right)\right]}{2}\hfill \\ & -\frac{1}{2}{\delta }_{t}P\left(i,j,k\right)\left[\frac{\omega \left(i,j,k\right)}{{\delta }_{\beta }}+\frac{1}{{\delta }_E}\right]\left[\lambda \left(i,j+1,k\right)-\lambda \left(i,j-1,k\right)\right]\hfill \\ & +{\delta }_{t}U\left(i,j,k\right).\hfill \end{array}$$

(39)

One can solve the formulated Equation (39) for finding the value of required transmit power level for MTC devices P(i,j,k) at any arbitrary point (i,j,k) of the discretized 3D grid.

5.2.2. Power Control Scheme

The derived expressions for the FPK and HJB equations using the finite difference scheme can now be used to derive an optimal power control policy using the mean field concept. Each MTC user tweaks it’s transmit power level individually to reduce battery energy consumption during each transmit interval. An iterative solution method is proposed for solving Equations (31), (38) and (39) to obtain a converged solution using finite difference method. Algorithm 1 describes the proposed algorithm to obtain an optimal power control policy by evaluating against different available policies and finding the power level for each policy.

Algorithm 1: Finite difference method for optimal mean field, Lagrangian and transmission power evaluation

Initialization:M(0, 0, 0), P(X + 1, 0, 0), λ(X + 1, 0, 0), Iter = 1 repeat Step 1: Mean field evaluation for alli = 1: 1: Xdo   for allj = 1: 1: Ydo    for allk = 1: 1: Kdo     Calculate mean field M(i + 1, j, k) using Equation (31)      if P(i, j + 1, k) = 0       M(i + 1, j + 1, k + 1) = M(i, j, k)      else: M(i + 1, j + 1, k + 1) = 0    end   end end Step 2: Lagrangian evaluation for all i = X + 1: −1: 1 do

for allj = 1: 1: Y+1do    for all k = 1: 1: K do     Calculate λ(i−1,j,k) using Equation (39)    end   end end for Step 3: Transmission power evaluation for all i = 1: 1: X + 1 do   for all j = 1: 1: Y + 1 do    for all k = 1: 1: K do     Calculate P(i−1,j,k) using Equation (38)    end   end end until Iter ≥ Itermax

Each MTC user evaluates the mean field, Langrangian multipliers and eventually an optimal value for the transmit power until convergence is achieved. The concept of MFE is distinct from the notion of Nash equilibrium (NE) for conventional games (or HJB based control i.e. the SDG design) as the later considers the actual state value before taking any action leading to an exponential increase with the increasing number of players. MFG based control relies on the approximated distribution of states with MFE being achieved only asymptotically when K → ∞. The conventional SDG design sought the solution through evaluation of K PDEs which has now been reduced to exactly two (HJB and FPK) following the approximation of state space through mean field interactions instead of individual player interactions. By solving the set of MFG PDEs, a stable solution scheme can be devised even for very dense environments with larger K values. MFE is guaranteed for the proposed solution approach by considering the properties of Hessian as proven in [24]. For any discrete point (i,j,k), the Hessian is positive for the values of $\left(i,j,k\right), P\left(i,j,k\right), and I\left(i,j,k\right)$ and the objective function as defined in the newly formulated control problem of the HJB Equation (32). The positivity of the Hessian ensures that the formulated HJB optimization problem is convex and an optimal solution for this convex problem can be found only if the KKT conditions are met. Another important observation from this result is that the convergence of the optimization problem in (32) is the MFE of the proposed mean field power control game. In the proposed algorithm, the convergence is obtained by observing the condition that the difference between mean field values in consecutive iterations is greater than or equal to 10⁻⁵ or the maximum iteration value Iter_max.

6. Performance Evaluation and Discussion

A brief description of the simulation setup utilized to test the proposed model and solution schemes is provided along with the results of the simulation performed in MATLAB environment. The mean field structure is depicted along with the distribution of energy as well as the transmit power for the MTC nodes in the context of the formulated MFG. Then a more in-depth evaluation of the optimal power control policy along with a study of the energy efficiency as well as the battery lifetime maximization achieved by the MTC nodes is presented.

6.1. Simulation Setup

A simulation setup is devised to analyze the model and solution of proposed MFG-based power control scheme with a total system bandwidth of 20 MHz. A hybrid network environment is simulated, consisting of random numbers of HTC and MTC devices generated as a PPP independent of each other. The total number of MTC nodes included in the simulation design varies between 100 to 500, with 10-100 HTC nodes in each cell of the cellular network. For simplicity, the throughput and maximum transmit power level for all MTCD devices are assumed to be similar. The path loss (PL) model used for simulations is $128.1+37.6{\log }_{10}d$ with d being the distance in km and the std. dev. of shadow fading being 3 dB. The background noise power is 2 × 10⁻⁹ W with power spectral density (PSD) of −170 dBm/Hz. An LTE-A framework [38] is adopted with a frame duration of 10 ms and the receiver sensitivity threshold of 0.1 mW. The total simulation time is set as T = 5 s consisting of a total of 500 frames of data. A battery energy rating of 200 μJ is defined with the maximum transmit power for the MTC devices being 50 mW. As mentioned above, an MTC device will be required to match an SINR threshold, which is required for establishing a communication link, and no additional power is allocated to nodes after this SINR criterion is met.

A clustering model is utilized for MTC devices in close proximity to lower the burden of a massive number of devices simultaneously accessing the network. The discretization of the state space grid is performed with a 50 × 50 × 50 grid with the respective player states analyzed at different time instances for the duration of the MFG. Here, the value for the maximum energy level E_max as well as the maximum tolerable interference level β_max- for each MTCD is defined as 0.5 J and 6 × 10⁻⁶ W, respectively.

6.2. Simulation Results

The optimization of the transmit power allocation process to the MTCDs is the primary objective of the proposed power control scheme to prolong network and battery life. The power control problem is complex to solve and susceptible to complex interference patterns due to massive number of devices and the lack of an external power source. The proposed scheme is analyzed in different device densities and available battery energy levels to test its robustness and the obtained results are presented along with brief discussions.

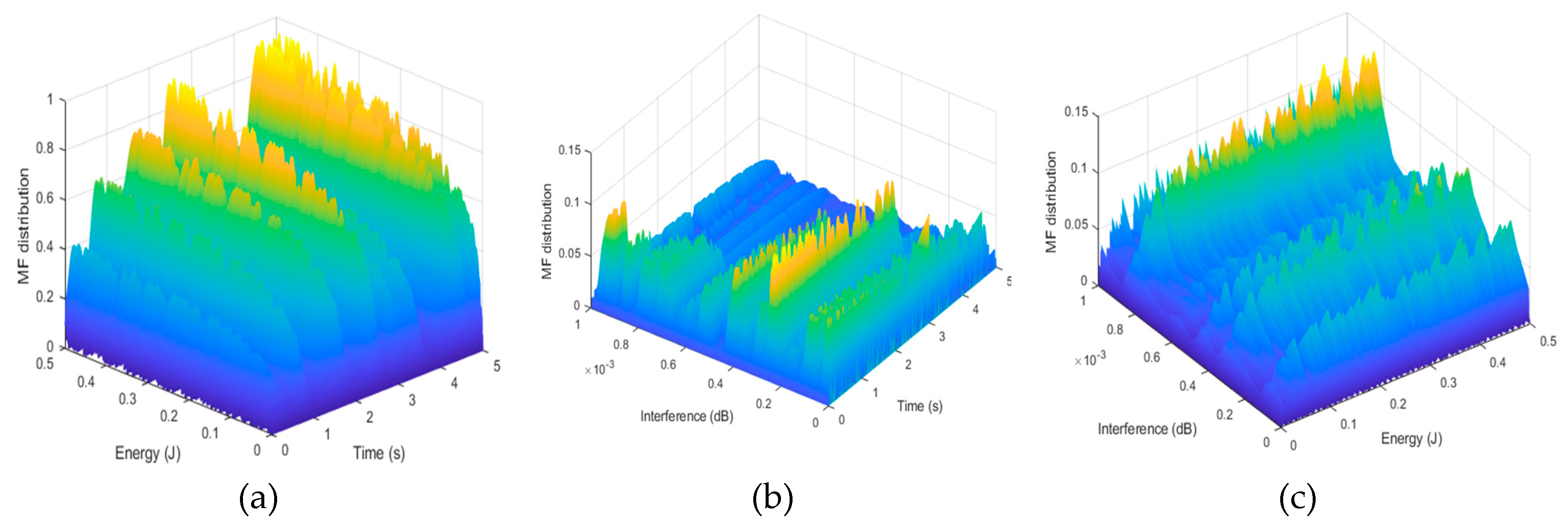
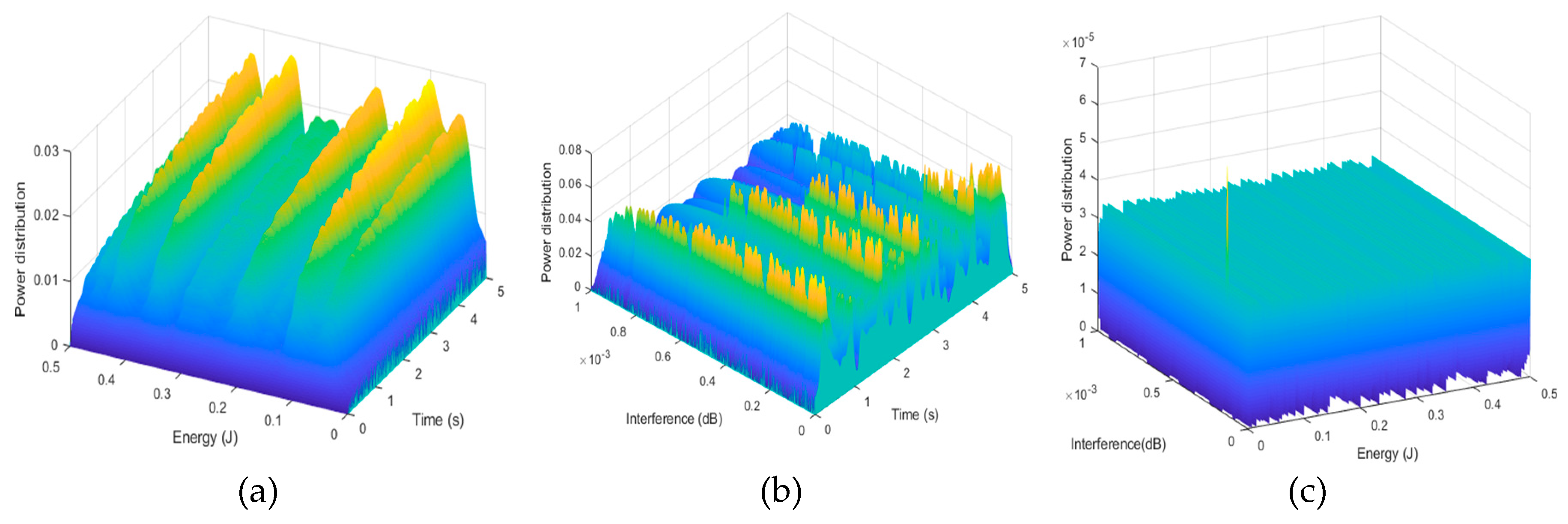
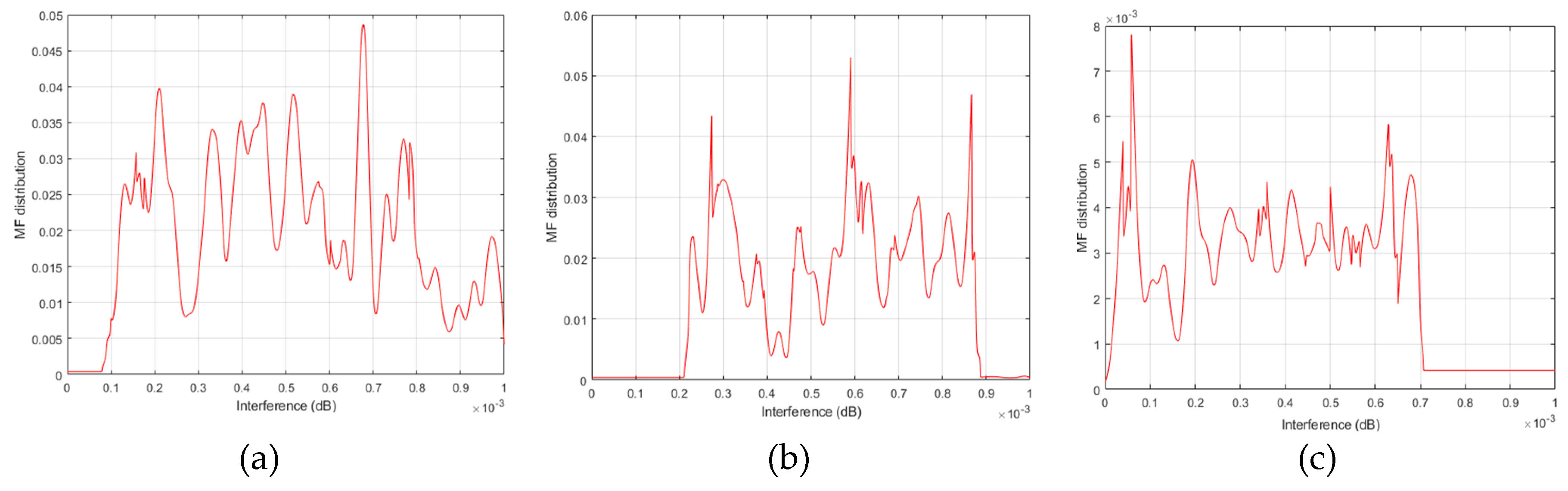
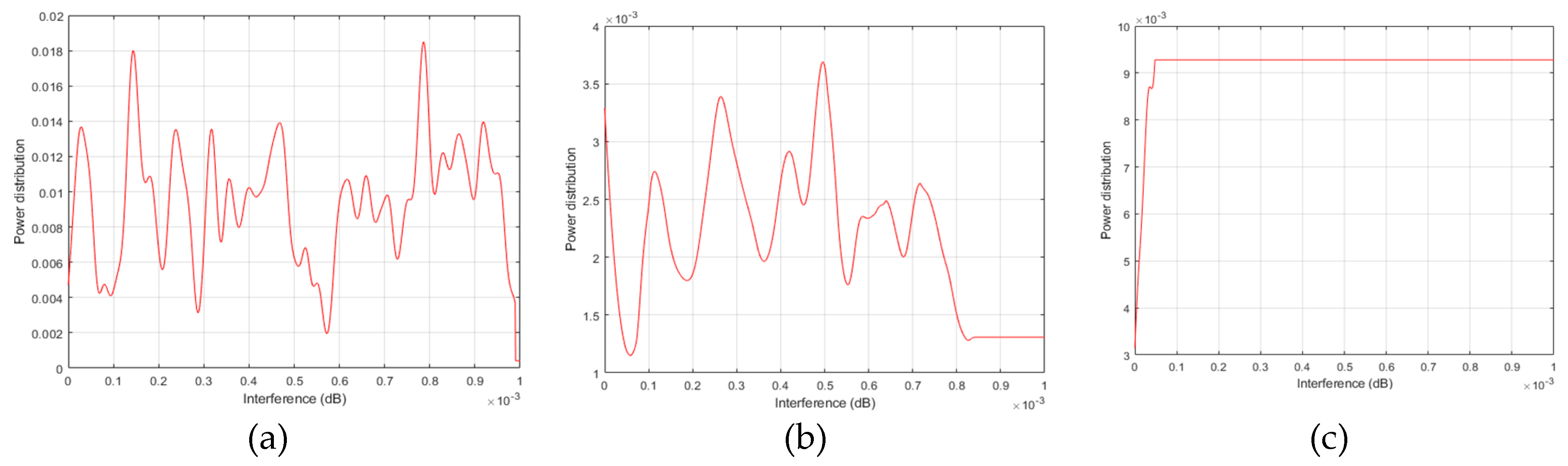
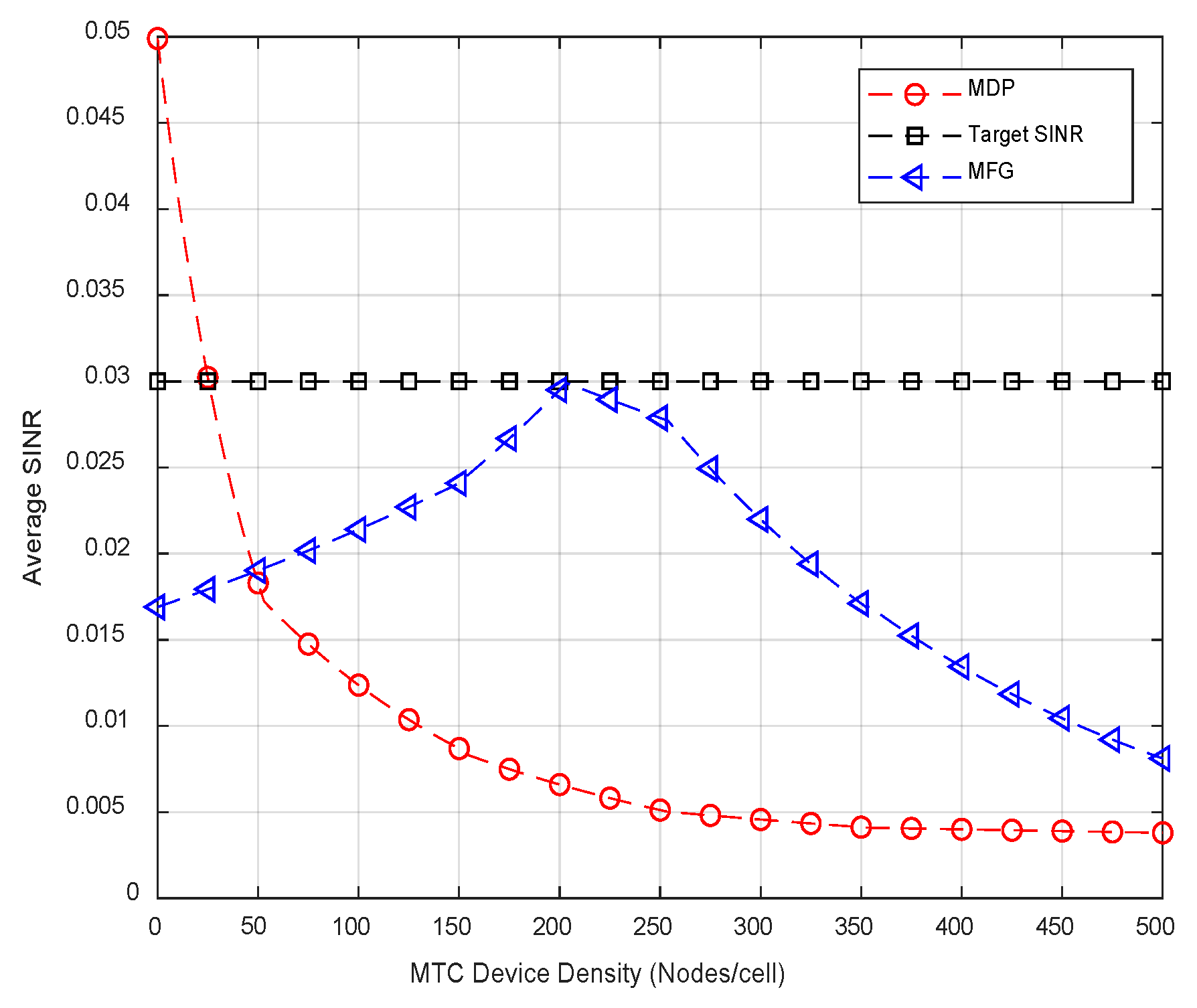
6.2.1. Mean Field Power Control Policy

The mean field or the collective device distribution for the massive MTC nodes is depicted in terms of the multi-dimensional state dynamics. An individual analysis is performed due to the complex multi-dimensional structure of the mean field as well as the power control policy. The mean field behavior of the MTC nodes is analyzed separately and depicted as different plots according to the observed dimensional dependence on energy, interference, and time. The plots are organized into three distinct scenarios accordingly as an MF distribution with (a) fixed interference but variable energy and time, (b) fixed energy with variable interference and time, (c) fixed time but variable energy and interference, respectively, as shown in Figure 4. Similarly, the impact of state behavior of the optimal power policy is depicted in Figure 5.

Figure 4 and Figure 5 represent the collective behavior or the mean field of MTCDs as well as the respective power policies in the defined grid for the Lax-Freidrichs scheme. The random pattern in the structure of both the mean field and power distribution over entire state space is due to the randomness in interference and player interactions. Hence, deducing anything meaningful about the power control strategy from the mean field and power distributions seems difficult. This information can be obtained by sampling the distributions at distinct time intervals to gain insight into the behavior of MTC players in the discussed MFG design.

To determine the impact of interference and player interactions on the mean field and the transmit power levels of MTC users the behavior of mean field and power distributions at different time instances is plotted in Figure 6 and Figure 7. After some time, a convergent behavior in the mean field and power distribution can be observed, in spite of differing levels of interference induced at different time instances. This equilibrium behavior for the mean field and power distribution near final stages of the time domain indicate the sufficiency of the proposed MFG based power control design for MTC devices. A comparison with respect to the number of required iterations for the convergence of the proposed power control scheme provides further insight into the equilibrium of the proposed MFG.

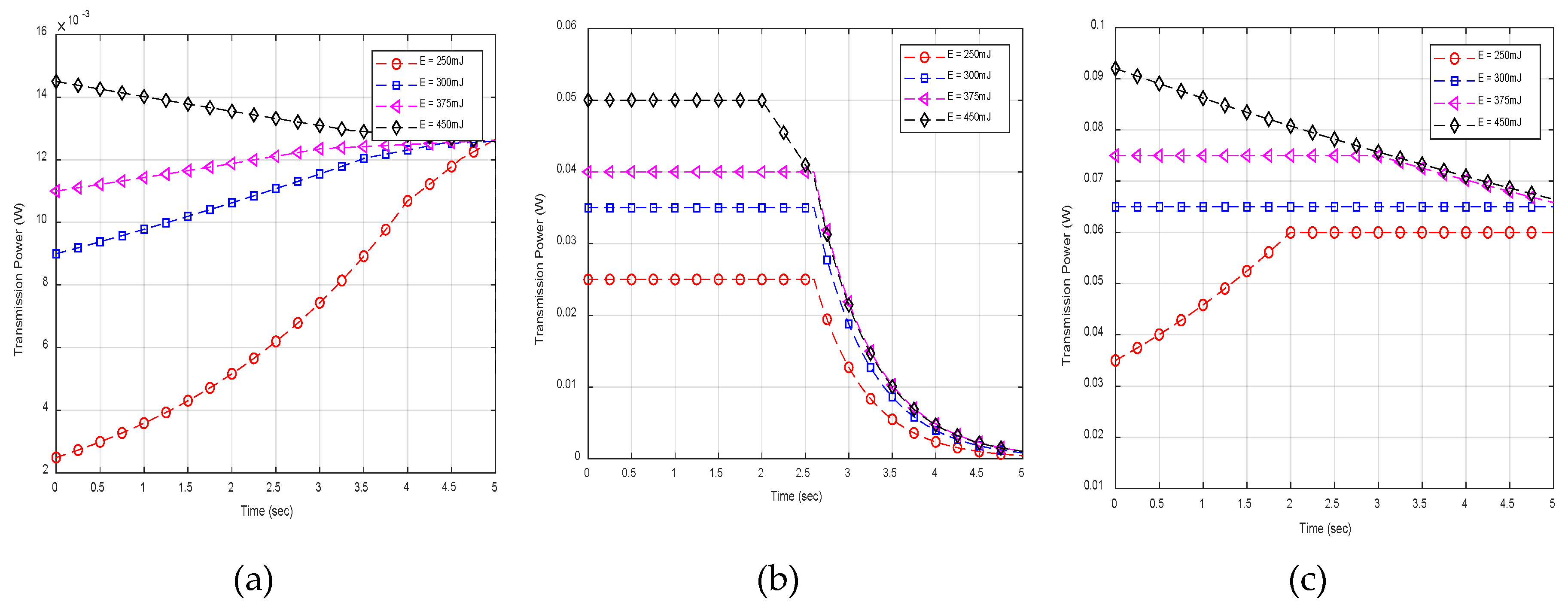
6.2.2. MTC Power Allocation and Battery Energy State

Extensive simulations are performed by considering different user densities and with changing levels of interference and battery energy levels to evaluate the impact of proposed power control scheme. The results of the simulation were analyzed by varying the MTC user densities present in service area of the cell for three particular cases. Case-I: low density scenario (150 nodes), Case-II: medium density scenario (300 nodes) and Case-III: high density scenario (500 nodes). Figure 8 shows the results obtained as a result of different simulations performed on described MTC user scenarios. The allocated power is compared for different energy levels of the batteries of these devices.

Figure 8a depicts power allocation pattern for Case-I with 150 MTC users in the cell along with a random number of HTC users. The convergence condition for this simulation setup is taken as the point of satisfaction of the reliability condition for MTC users. Higher initial battery energy allocate higher initial transmit power to the MTC users and devices with lower initial battery energy tend to conserve energy by allocating lower transmit powers. The allocated transmit power is adapted to a lower level after sometime for high battery energy devices owing to battery discharge cycle and the reliability condition. Lower energy level devices are allocated lower transmit power at the start of the MFG which is gradually increased with the progression of the game. This is partially due to lower MTC node density which incurs less interference on MTC users as compared to more dense scenarios and partially due to the decreasing powers allocated to MTC users having higher initial battery energy. It is observed that the effect of the interference state is simpler due to the relatively lower MTC user density. The results are shown in Figure 8b, which were obtained when the MTC user density (300 nodes) is increased to observe the effect on the power allocation. More power is allocated to each MTC node because of increased interference due to the increased MTC device numbers. Similar to the low MTC density case, higher initial battery level devices are allocated more transmission power. After some time, the allocated amount of power declines because the available energy in the batteries of MTC devices decreases and the interference increases as a result of relatively higher MTC device density. Figure 8c depicts the case with the highest MTC user density causing increased interference experienced by MTC devices and the consequent need for a higher amount of allocated power to reach the SINR threshold. MTC users with high initial battery energy levels perform the same way as the low and medium device density cases with higher power allocations initially with an eventual decline with the progression of the MFG. The MTC devices with lower levels of battery energy initially allocate power levels required to be within the SINR threshold. So, the transmit power increases until they satisfy the defined criterion with the power levels being held constant until the end of the game simulation maintained for the duration of the game or upon a significant drop in the battery level of the MTC devices.

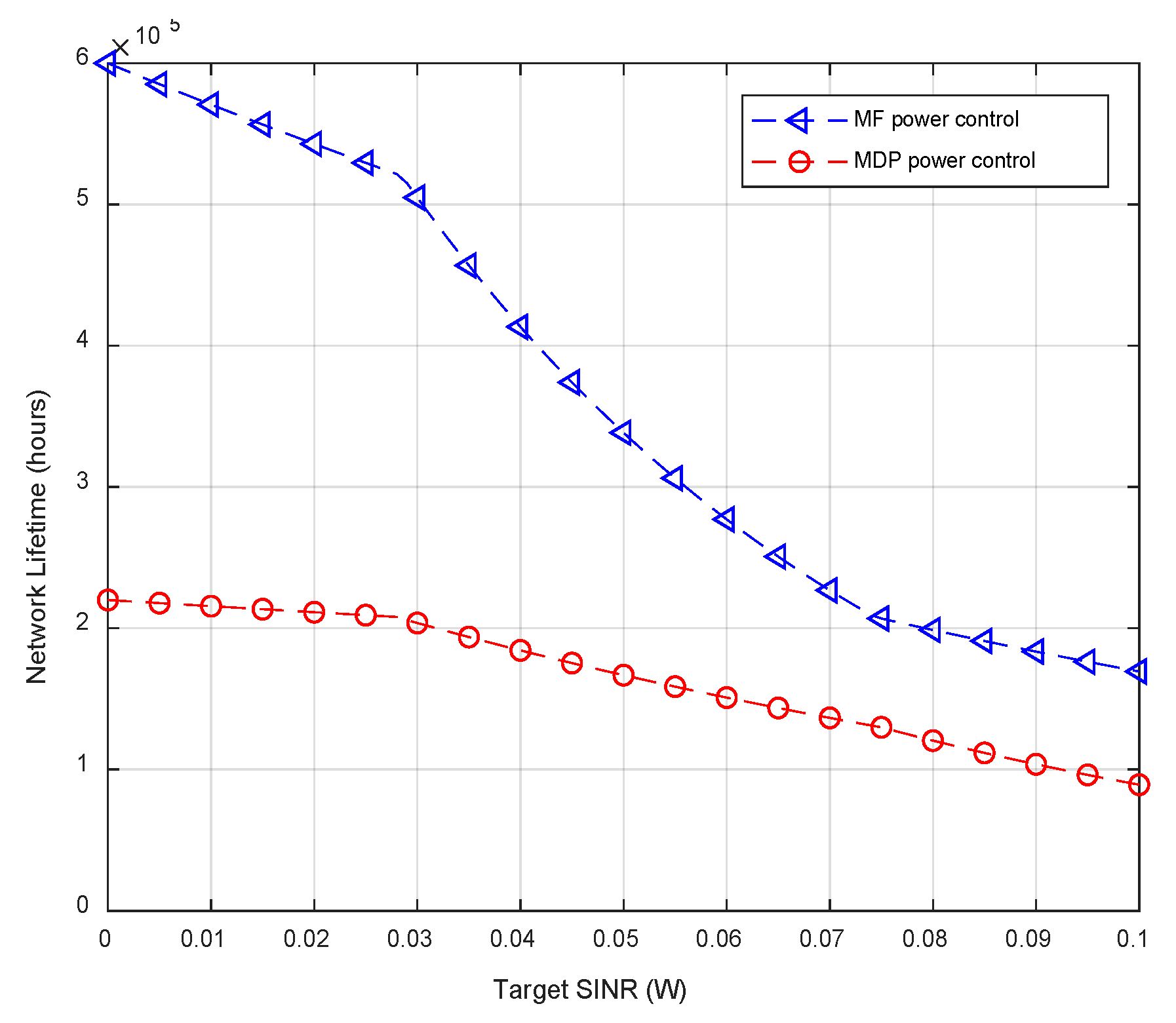
6.2.3. Energy Efficiency and Network Lifetime

The relationship between energy efficiency, allocated transmit power and the expected battery lifetime is an important one and it is described in Figure 9 and Figure 10 in detail. In the designed simulation environment, the SINR behavior of MTC devices is observed at different densities in the simulated cellular network considering the MFG based optimal power control policy. An increase in average SINR of the MTC users is observed with the increase of user density which can be attributed to increasingly dense network environment causing complex interference to all MTC and HTC users. As already observed, MTC devices tend to increase the allocated transmit power levels to counter this experienced interference. Due to increased MTC user density, the intra-MTC device interference takes the dominant role instead of the HTC device impairments after a certain point in the increasingly dense environment. Hence, an eventual drop in allocated power degrades the averaged SINR specifically for the MTC devices beyond this point in the density SINR graph. This behavior of the coexisting hybrid network environment of HTC and MTC devices ensures that the proposed MFG centered power control scheme can indeed achieve the highest possible SINR for the MTC devices. In comparison to the approaches involving a Markov decision process (MDP) based power control, the proposed MFG-based power control gets a more closely matched average SINR value to the target SINR. One can describe the MDP-based approach as a basic stochastic game design with individual optimal decision policies for each player instead of a global optimal policy for all players. Figure 9 provides a comparison of this MDP-based [42] and MFG-based power control scheme in terms of the averaged SINR according to different MTC device densities and their proximity to the target SINR value. It is clear that the MDP based power control scheme fails to support an increasingly dense MT environment with the expected decrease observed in the average SINR mainly due to increased interference levels. This experiment further highlights the importance of the achievable SINR in different MTC user densities as a key design target to ensure an energy efficient MFG-based power control.

The network lifetime of MTC devices using the SIL design was analyzed with respect to the target SINR value ${\gamma }_{th}$. It is clear from Equation (13) that the required value of P_o is directly related to the value of ${\gamma }_{th}$. Hence, the required transmit power needed by MTC devices to achieve their respective target SINR values directly affects their battery lifetimes. A comparative study of the proposed MFG based optimal power control scheme is done with an MDP-based power control mechanism and the results are shown in Figure 10. A decrease in network lifetime is observed for both of these schemes because of the direct dependence of the transmit power level and the value of the target SINR as expressed by Equation (13). The proposed MFG-based approach outperforms the MDP-based design by prolonging the lifetime of MTCDs by a factor of 3 before the optimal threshold value and by almost twice after the optimal value is attained. This proves the effectiveness of the proposed MFG-based design for battery lifetime enhancement for increasingly dense MTC network environment in coexistence with traditional HTC users. The convergence of the coupled system of PDEs using finite difference scheme can converge to an asymptotic NE known as the MFE as discussed in detail in Section 5.

Figure 11 depicts the exact behavior when multiple simulations are run using different initial state distributions (or mean field distributions) with the proposed algorithm converging rapidly to MFE within a limited number of iterations. This expected behavior is the premise of MFG and its explained benefits as compared to conventional game designs. Moreover, this also makes mean field based solutions a potential candidate for solving complex problems in ultra-dense networks.

7. Conclusions

In this work, a battery energy improvement mechanism is proposed for the scenario of coexisting HTC and MTC users in a bid to improve network and individual lifetimes of MTC devices. A differential game model for power control deemed suitable for modeling MTC user interactions with the environment and HTC users is proposed. The conversion of this differential game to a mean field game is presented that motivated by the dimensional difficulty in solving the differential game and due to an ultra-dense network requirement of the mMTC devices. This mean field game optimizes the power allocation procedure for the MTC devices by finding an optimal control policy to conserve and maximize the battery lifetimes. The solution to this proposed power control problem is found using the mean field approximation theory by solving a set of well-known PDEs known as the forward and backward set of equations or HJB and FPK set of equations. The simulation results justify the application of mean field game theory to reduce complexity and improve energy consumption efficiency of the MTC users in a coexisting network environment.

The authors intend to work on applications of mean field game theory in order to propose low complexity solutions to ease the curse of dimensionality in radio resource management and to improve latency for uRLLC applications.