Solar Panels as Tip Masses in Low Frequency Vibration Harvesters
Abstract
1. Introduction
2. Experimental Set-up
2.1. Harvesters Design and Realisation
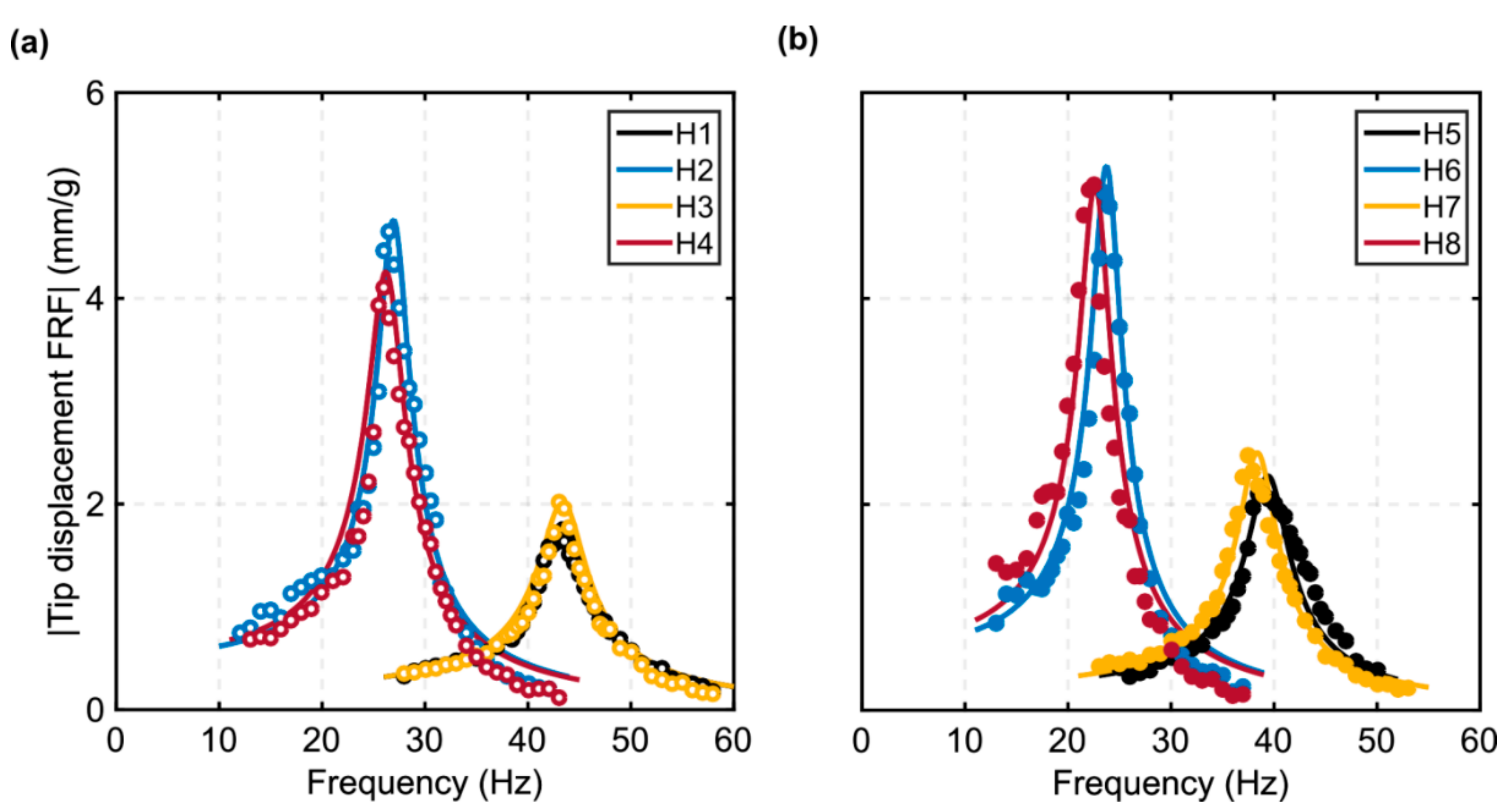
2.2. Harvesters Identification
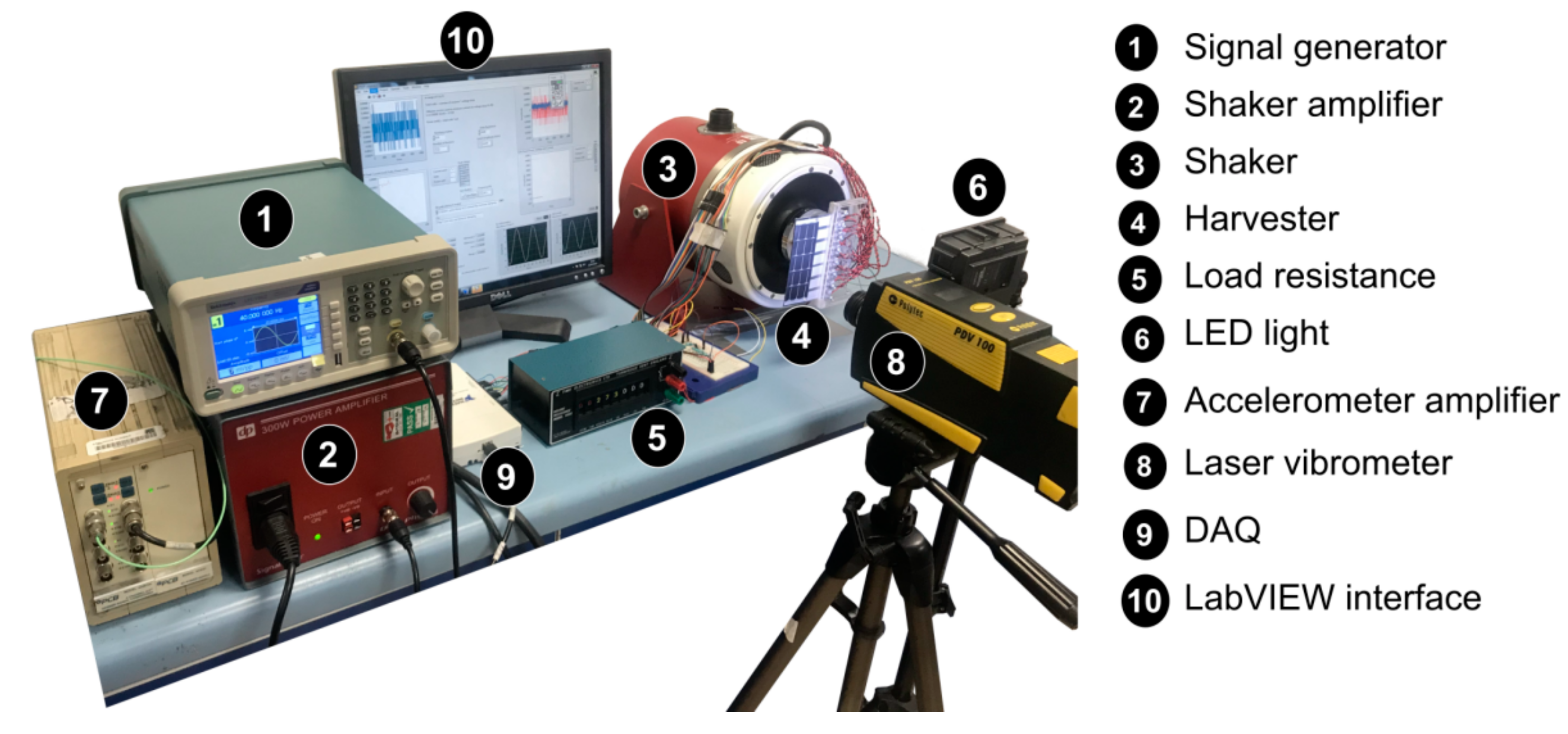
2.3. Experimental Apparatus
3. Considerations for Harvesters with Flexible Solar Panels
3.1. Model for an Equivalent Concentrated Tip Mass
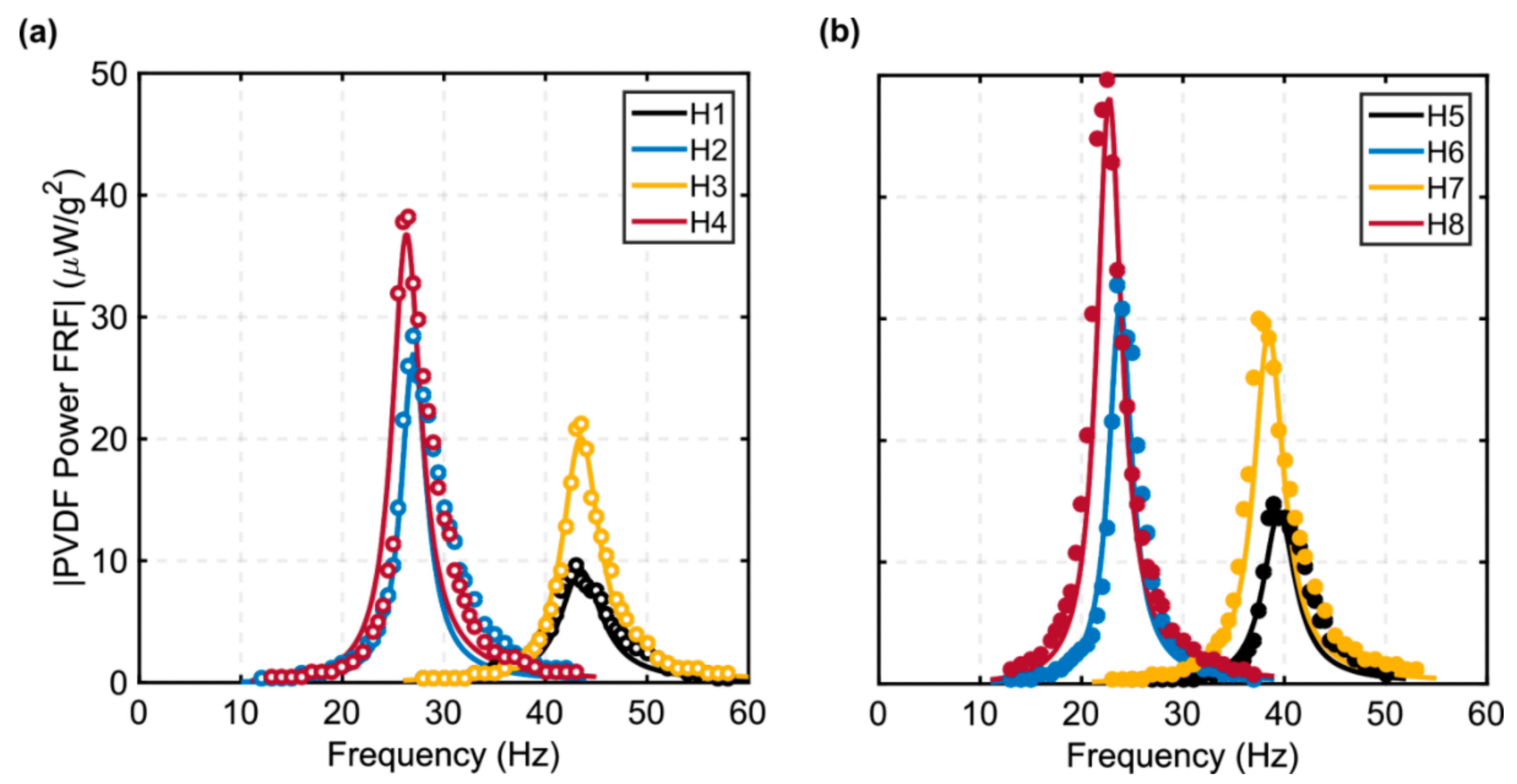
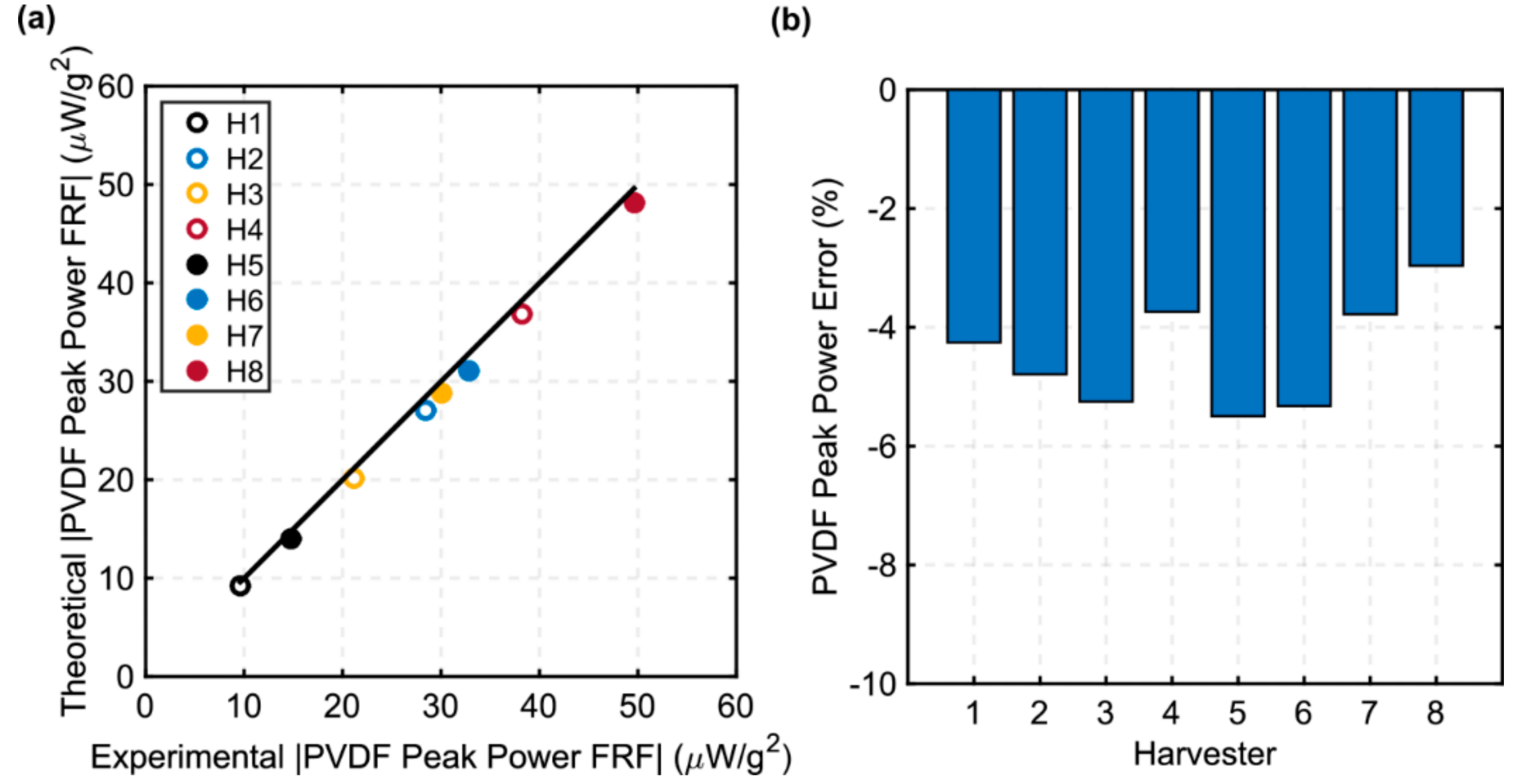
3.2. Equivalent Concentrated Tip Mass Model vs. Experimental Measurements
4. Considerations for Harvesters with Rigid Solar Panels
4.1. Model for a Distributed Tip Mass
4.2. Flexible vs. Rigid Solar Panels
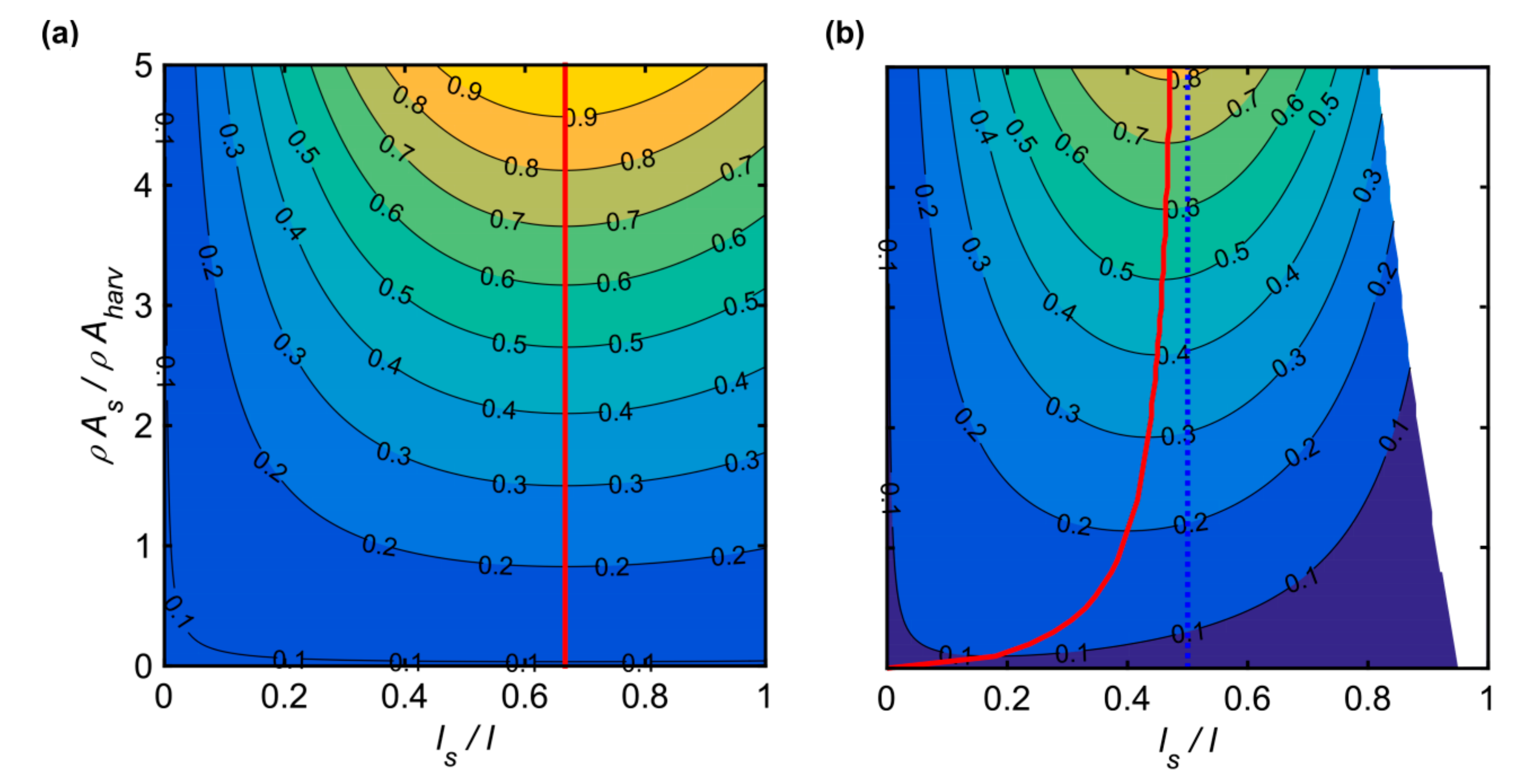
5. Optimum Tip Mass Configuration
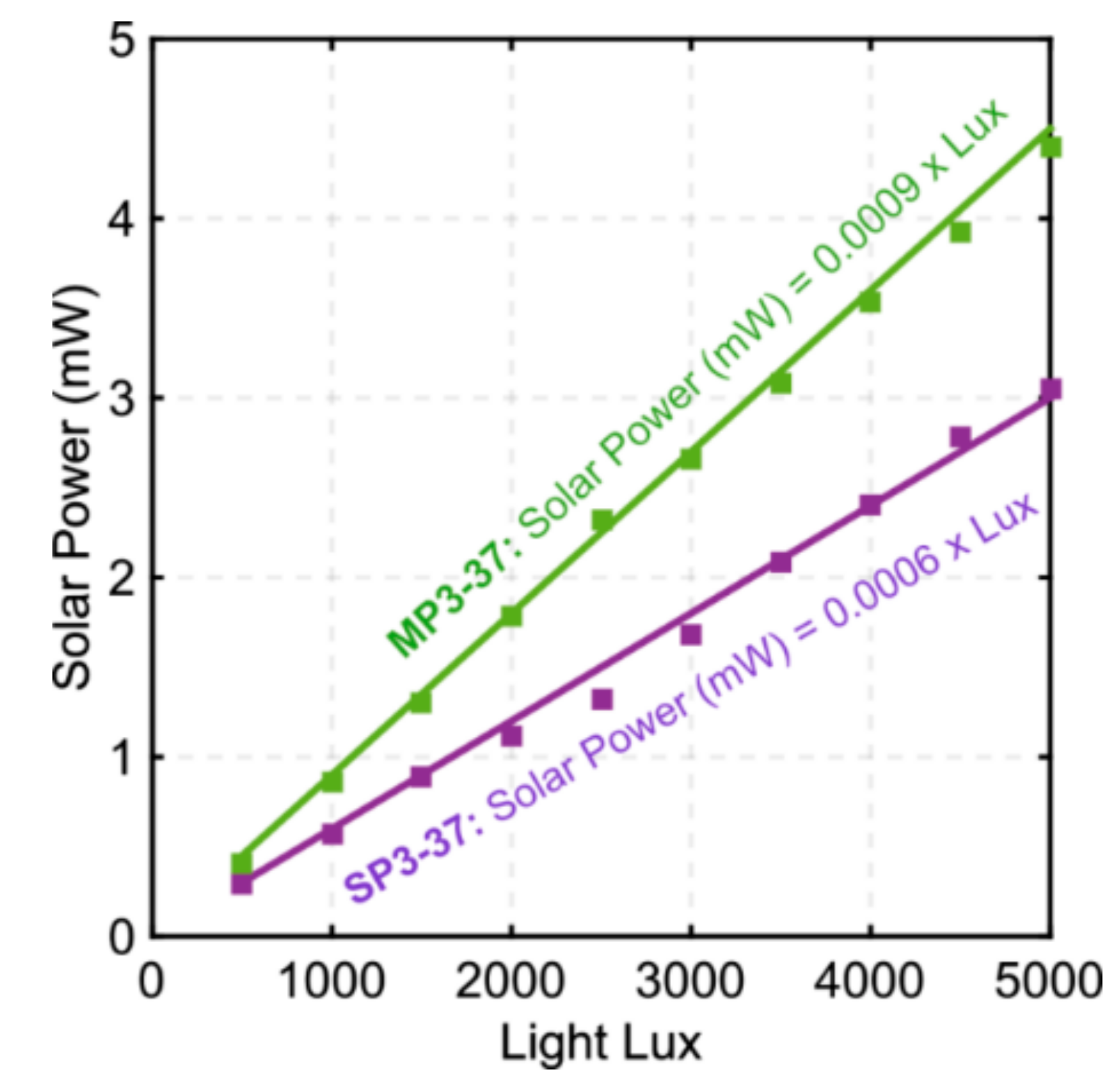
6. Solar Power
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Erturk, A.; Inman, D.J. A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters. J. Vib. Acoust. 2008, 130, 041002. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Renno, J.M.; Daqaq, M.F.; Inman, D.J. On the optimal energy harvesting from a vibration source. J. Sound Vib. 2009, 320, 386–405. [Google Scholar] [CrossRef]
- Stanton, S.C.; Erturk, A.; Mann, B.P.; Inman, D.J. Nonlinear piezoelectricity in electroelastic energy harvesters: Modeling and experimental identification. J. Appl. Phys. 2010, 108, 074903. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Najar, F.; Nayfeh, A.H.; Ayed, S.B. An energy harvester using piezoelectric cantilever beams undergoing coupled bending–torsion vibrations. Smart Mater. Struct. 2011, 20, 115007. [Google Scholar] [CrossRef]
- Orrego, S.; Shoele, K.; Ruas, A.; Doran, K.; Caggiano, B.; Mittal, R.; Kang, S.H. Harvesting ambient wind energy with an inverted piezoelectric flag. Appl. Energy 2017, 194, 212–222. [Google Scholar] [CrossRef]
- Li, S.; Lipson, H. Vertical-stalk flapping-leaf generator for wind energy harvesting. In Proceedings of the ASME 2009 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Oxnard, CA, USA, 21–23 September 2009. [Google Scholar]
- Li, S.; Yuan, J.; Lipson, H. Ambient wind energy harvesting using cross-flow fluttering. J. Appl. Phys. 2011, 109, 026104. [Google Scholar] [CrossRef]
- Nabawy, M.R.A.; Silva-Leon, J.; O’Connor, J.; Kennaugh, A.; Cioncolini, A.; Revell, A. Simultaneous energy harvesting using dual piezo-solar devices. In Proceedings of the IUTAM Symposium on Critical Flow Dynamics Involving Moving/Deformable Structures with Design Applications, Santorini, Greece, 18–22 June 2018. [Google Scholar]
- Silva-Leon, J.; Cioncolini, A.; Nabawy, M.R.A.; Revell, A.; Kennaugh, A. Simultaneous wind and solar energy harvesting with inverted flags. Appl. Energy 2019, 239, 846–858. [Google Scholar] [CrossRef]
- Cioncolini, A.; Nabawy, M.R.A.; Silva-Leon, J.; O’Connor, J.; Revell, A. An experimental and computational study on inverted flag dynamics for simultaneous wind–solar energy harvesting. Fluids 2019, 4, 87. [Google Scholar] [CrossRef]
- Vatansever, D.; Hadimani, R.L.; Shah, T.; Siores, E. An investigation of energy harvesting from renewable sources with PVDF and PZT. Smart Mater. Struct. 2011, 20, 055019. [Google Scholar] [CrossRef]
- Hobeck, J.D.; Inman, D.J. Artificial piezoelectric grass for energy harvesting from turbulence-induced vibration. Smart Mater. Struct. 2012, 21, 105024. [Google Scholar] [CrossRef]
- Song, J.; Zhao, G.; Li, B.; Wang, J. Design optimization of PVDF-based piezoelectric energy harvesters. Heliyon 2017, 3, e00377. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Shiono, S.; Hamada, H.; Fujita, T.; Higuchi, K.; Maenaka, K. Low-frequency energy harvesting using a laminated PVDF cantilever with a magnetic mass. In Proceedings of the Power MEMS 2010: The 10th International Workshop on Micro and Nanotechnology for Power Generation and Energy Conversion Applications, Leuven, Belgium, 30 November–3 December 2010; pp. 375–378. [Google Scholar]
- Cao, Z.; Zhang, J.; Kuwano, H. Vibration energy harvesting characterization of 1 cm2 Poly (vinylidene fluoride) generators in vacuum. Jpn. J. Appl. Phys. 2011, 50, 09ND15. [Google Scholar] [CrossRef]
- Rammohan, S.; Ramya, C.M.; Kumar, S.J.; Jain, A.; Pratap, R. Low frequency vibration energy harvesting using arrays of PVDF piezoelectric bimorphs. J. Inst. Smart Struct. Syst. 2014, 3, 18–27. [Google Scholar]
- Tsukamoto, T.; Umino, Y.; Shiomi, S.; Yamada, K.; Suzuki, T. Bimorph piezoelectric vibration energy harvester with flexible 3D meshed-core structure for low frequency vibration. Sci. Technol. Adv. Mater. 2018, 19, 660–668. [Google Scholar] [CrossRef] [PubMed]
- Chandwani, J.; Somkuwar, R.; Deshmukh, R. Multi-band piezoelectric vibration energy harvester for low-frequency applications. Microsyst. Technol. 2019, 25, 3867–3877. [Google Scholar] [CrossRef]
- Jacobson, M.Z.; Delucchi, M.A. A path to sustainable energy by 2030. Sci. Am. 2009, 301, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Haji, M.N.; Kluger, J.M.; Sapsis, T.P.; Slocum, A.H. A symbiotic approach to the design of offshore wind turbines with other energy harvesting systems. Ocean Eng. 2018, 169, 673–681. [Google Scholar] [CrossRef]
- Iqbal, M.; Khan, F.U. Hybrid vibration and wind energy harvesting using combined piezoelectric and electromagnetic conversion for bridge health monitoring applications. Energy Convers. Manag. 2018, 172, 611–618. [Google Scholar] [CrossRef]
- Gambier, P.; Anton, S.R.; Kong, N.; Erturk, A.; Inman, D.J. Piezoelectric, solar and thermal energy harvesting for hybrid low-power generator systems with thin-film batteries. Meas. Sci. Technol. 2011, 23, 015101. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations, 2nd ed.; Adison-Wesley Publishing Company: New York, NY, USA, 1990; pp. 22–23. [Google Scholar]
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131. [Google Scholar] [CrossRef]
- Kim, M.; Hoegen, M.; Dugundji, J.; Wardle, B.L. Modeling and experimental verification of proof mass effects on vibration energy harvester performance. Smart Mater. Struct. 2010, 19, 045023. [Google Scholar] [CrossRef]
- Kim, J.E.; Kim, Y.Y. Analysis of piezoelectric energy harvesters of a moderate aspect ratio with a distributed tip mass. J. Vib. Acoust. 2011, 133, 041010. [Google Scholar] [CrossRef]
- Strutt, J.W. (Lord Rayleigh). The Theory of Sound; Macmillan: London, UK, 1877. [Google Scholar]
- Roundy, S.; Wright, P.K.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.; Kwak, B.M. Design optimization of piezoelectric energy harvester subject to tip excitation. J. Mech. Sci. Technol. 2012, 26, 137–143. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: West Sussex, UK, 2011; pp. 19–130. [Google Scholar]
- Nabawy, M.R.A.; Crowther, W.J. Dynamic electromechanical coupling of piezoelectric bending actuators. Micromachines 2016, 7, 12. [Google Scholar] [CrossRef] [PubMed]
- Nabawy, M.R.A.; Parslew, B.; Crowther, W.J. Dynamic performance of unimorph piezoelectric bending actuators. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2015, 229, 118–129. [Google Scholar] [CrossRef]
- Aldraihem, O.J.; Wetherhold, R.C.; Singh, T. Distributed control of laminated beams: Timoshenko theory vs. Euler-Bernoulli theory. J. Intell. Mater. Syst. Struct. 1997, 8, 149–157. [Google Scholar] [CrossRef]
- Minnaert, B.; Veelaert, P. Which type of solar cell is best for low power indoor devices. In Innovation for Sustainable Production: i-SUP 2010; Ghent University, Department of Electronics and Information Systems: Ghent, Belgium, 2010. [Google Scholar]
- Minnaert, B.; Veelaert, P. A proposal for typical artificial light sources for the characterization of indoor photovoltaic applications. Energies 2014, 7, 1500–1516. [Google Scholar] [CrossRef]
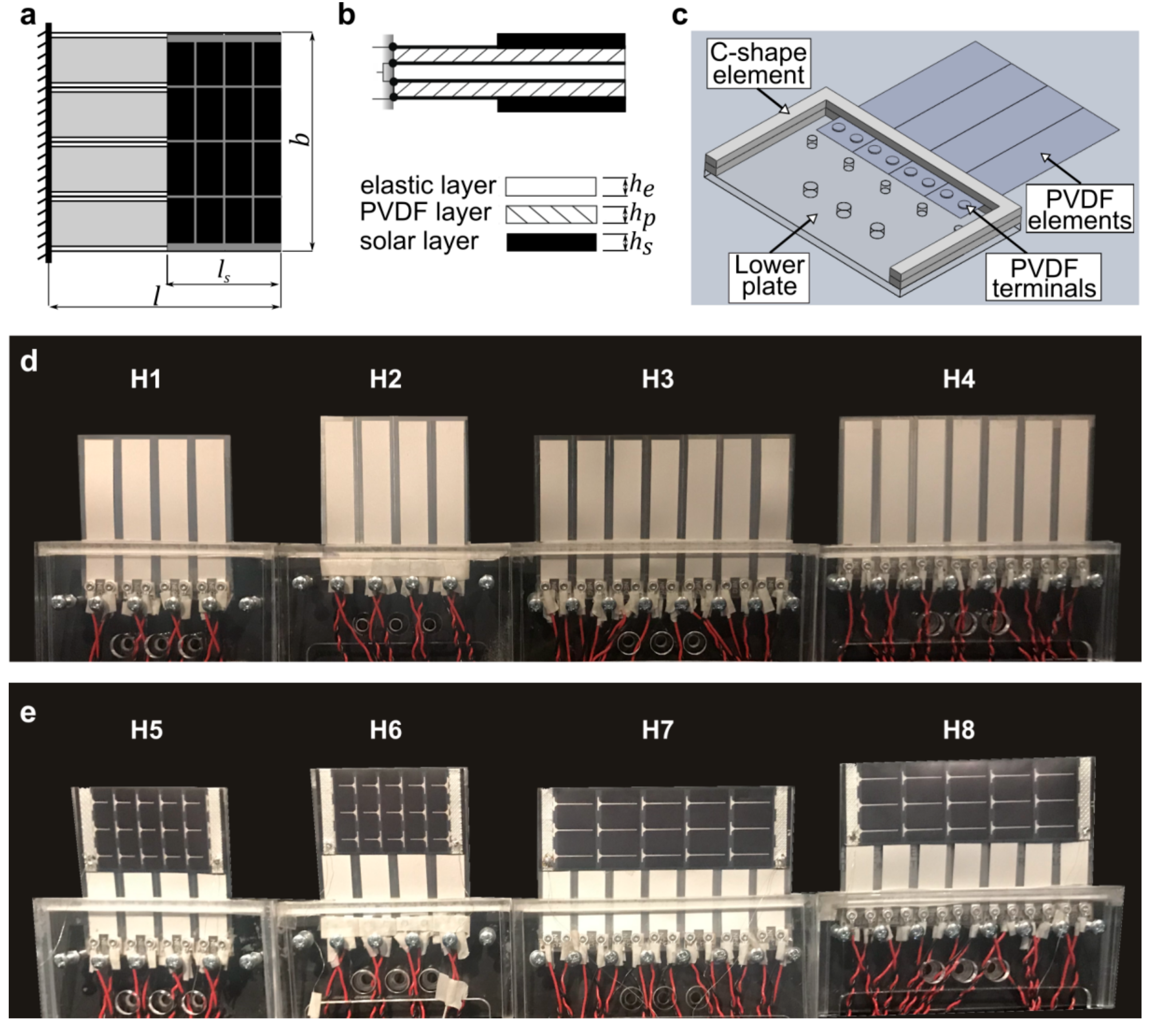



| Harvester | No of PVDFs | Solar Panel | Length (mm) | Width (mm) | Beam aspect ratio | |
|---|---|---|---|---|---|---|
| H1 | 8 (4 /side) | NA | 48 | 64 | 96 | NA |
| H2 | 8 (4 /side) | NA | 58 | 64 | 116 | NA |
| H3 | 14 (7 /side) | NA | 48 | 112 | 96 | NA |
| H4 | 14 (7 /side) | NA | 58 | 112 | 116 | NA |
| H5 | 8 (4 /side) | SP3-37 | 48 | 64 | 96 | 22.4 |
| H6 | 8 (4 /side) | SP3-37 | 58 | 64 | 116 | 42.4 |
| H7 | 14 (7 /side) | MP3-37 | 48 | 112 | 96 | 22.4 |
| H8 | 14 (7 /side) | MP3-37 | 58 | 112 | 116 | 42.4 |
| Harvester | H1 | H2 | H3 | H4 | H5 | H6 | H7 | H8 |
|---|---|---|---|---|---|---|---|---|
| Natural frequency, (Hz) | 43.5 | 27.0 | 43.5 | 26.3 | 39.5 | 23.8 | 38.5 | 22.7 |
| Damping ratio, | 0.057 | 0.056 | 0.051 | 0.066 | 0.049 | 0.058 | 0.047 | 0.066 |
| Stiffness, (N/m) | 81.17 | 37.88 | 142.1 | 62.87 | 97.68 | 42.93 | 161.5 | 68.46 |
| Optimum load resistance for PVDFs, (kOhm) | 161 | 258 | 92 | 152 | 179 | 293 | 104 | 176 |
| Lux | Resistance (kOhm) | |
|---|---|---|
| PowerFilm SP3-37 | PowerFilm MP3-37 | |
| 500 | 15.4 | 2.82 |
| 1000 | 8.80 | 1.54 |
| 1500 | 7.00 | 1.10 |
| 2000 | 5.00 | 0.88 |
| 2500 | 4.70 | 0.65 |
| 3000 | 3.76 | 0.57 |
| 3500 | 2.82 | 0.49 |
| 4000 | 2.82 | 0.49 |
| 4500 | 2.35 | 0.41 |
| 5000 | 2.35 | 0.41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Nabawy, M.R.A.; Cioncolini, A.; Revell, A. Solar Panels as Tip Masses in Low Frequency Vibration Harvesters. Energies 2019, 12, 3815. https://doi.org/10.3390/en12203815
Wang J, Nabawy MRA, Cioncolini A, Revell A. Solar Panels as Tip Masses in Low Frequency Vibration Harvesters. Energies. 2019; 12(20):3815. https://doi.org/10.3390/en12203815
Chicago/Turabian StyleWang, Jie, Mostafa R. A. Nabawy, Andrea Cioncolini, and Alistair Revell. 2019. "Solar Panels as Tip Masses in Low Frequency Vibration Harvesters" Energies 12, no. 20: 3815. https://doi.org/10.3390/en12203815
APA StyleWang, J., Nabawy, M. R. A., Cioncolini, A., & Revell, A. (2019). Solar Panels as Tip Masses in Low Frequency Vibration Harvesters. Energies, 12(20), 3815. https://doi.org/10.3390/en12203815









